EJERCICIO EXTRAS FCA 6 E TURNO NOCTURNO SENSEY
|
|
|
- Ana del Río Álvarez
- hace 8 años
- Vistas:
Transcripción
1 PROGRAMACIÓN LINEAL? LA PROGRAMACIÓN LINEAL SE APLICA A MODELOS DE OPTIMIZACIÓN EN LOS QUE LAS FUNCIONES OBJETIVO Y RESTRICCIONES SON ESTRICTAMENTE LINEALES. -VARIABLES Y PARÁMETROS. SON INCÓGNITAS QUE DEBEN DETERMINARSE RESOLVIENDO EL MODELO O PROBLEMAS EN CUESTIÓN MIENTRAS QUE LOS PARÁMETROS YA CONOCIDOS QUE RELACIONAN A LAS VARIABLES DE DECISIÓN CON LAS RESTRICCIONES, CON LA FUNCIÓN OBJETIVO Y LOS PARÁMETROS DEL MODELO, PUEDEN SER DETERMINISTICOS O PROBABILISTICOS. -FUNCIÓN OBJETIVO LA FUNCIÓN OBJETIVO DEFINE LA MEDIDA DEL SISTEMA COMO UNA FUNCIÓN MATEMÁTICA DE LAS VARIABLES DE DECISIÓN POR LO QUE LA SOLUCIÓN ÓPTIMA SERÁ AQUELLA QUE PRODUZCA EL MAYOR VALOR DE LA FUNCIÓN OBJETIVO SUJETA A LAS RESTRICCIONES. -RESTRICCIONES SON LAS LIMITACIONES TECNOLÓGICAS DEL SISTEMA Y LAS CUALES PUEDEN APARECER DE FORMA IMPLÍCITA O EXPLICITA Y ESTAS A SU VEZ RESTRINGEN LAS VARIABLES DE DECISIÓN A UN RANGO DE VALORES FACTIBLES. ALGUNOS EJEMPLOS UN GRANJERO PROBLEMA # 1 UN GRANJERO TIENE 100 ACRES EN LOS CUALES PUEDE SEMBRAR DOS CULTIVOS. DISPONE DE $3000 A FIN DE CUBRIR EL COSTO DEL SEMBRADO. EL GRANJERO PUEDE CONFIAR EN UN TOTAL DE 1350 HRS.- HOMBRE DESTINADAS A LA RECOLECCIÓN DE LOS DOS CULTIVOS Y EN EL CUADRO SE MUESTRA LOS SIGUIENTES DATOS POR ACRE: CULTIVOS COSTO DE PLANTAR DEMANDA HRS.-HOMBRE UTILIDAD PRIMERO $20 5HRS. $100 SEGUNDO $40 20HRS $300 DE DECISION X1 = LA CANTIDAD DE PRODUCCIÓN DEL PRIMER CULTIVO EN ACRES X2 = LA CANTIDAD DE PRODUCCIÓN DEL SEGUNDO CULTIVO EN ACRE MAX Z = 100X X2 (EL PROGRAMA DE PRODUCCIÓN SIEMPRE DEBE ELEGIRSE DE MODO QUE MAXIMICE LA UTILIDAD TOTAL). 3.-RESTRICIONES X1 +X2 < (2) ESTA ECUACIÓN SE DEBE A QUE SOLO TIENE 100 ACRES PARA LOS CULTIVOS. 5X1 + 20X2 < (3) 20X1 + 40X2 < (4) LO QUE QUEDA PLANTEADO X1 + X2 > 0
2 UNA COMPAÑÍA PROBLEMA # 2 UNA COMPAÑÍA PRODUCE DOS PRODUCTOS, AY B. CADA UNIDAD DE A REQUIERE 2 HRS. EN CADA MAQUINA Y 5 HRS. EN UNA SEGUNDA MAQUINA. CADA UNIDAD DE B DEMANDA 4HRS. EN LA PRIMERA MAQUINA Y 3 HRS. EN LA SEGUNDA MAQUINA. SE DISPONE DE 100 HRS. A LA SEMANA EN LA PRIMERA MAQUINA Y DE 110 HRS. EN LA SEGUNDA MAQUINA. SI LA COMPAÑÍA OBTIENE UNA UTILIDAD DE $70 POR CADA UNIDAD DE A Y $50 POR CADA UNIDAD DE B CUÁNTO DEBERÁ DE PRODUCIRSE DE CADA UNIDAD CON OBJETO DE MAXIMIZAR LA UTILIDAD TOTAL? PRODUCTO HRS. HRS. UTILIDAD MAQUINA1 MAQUINA 2 A 2 5 $70 KILO B 4 3 $50 KILO DE DECISION X1 = LA CANTIDAD DE PRODUCCIÓN DE A EN UNIDADES X2 = CANTIDAD DE PRODUCCIÓN DE B EN UNIDADES MAX Z = 70X1 + 50X2.. (1) 3.-RESTRICIONES 2X1 + 4X2 < (2) 5X1 + 3X2 < 110. (3) LO QUE QUEDA PLANTEADO X1 + X2 > 0 PROBLEMA # 3 UN NUTRICIONISTA UN NUTRICIONISTA ASESORA A UN INDIVIDUO QUE SUFRE UNA DEFICIENCIA DE HIERRO Y VITAMINA B, Y LE INDICA QUE DEBE DE INGERIR AL MENOS 2400 MG DE VITAMINA B-1 (TIAMINA) Y 1500 MG DE VITAMINA B- 2 (RIBOFLAVINA) DURANTE CIERTO PERIODO DE TIEMPO. EXISTEN 2 PÍLDORAS DE VITAMINAS DISPONIBLES, LA MARCA A Y LA MARCA B, CADA PÍLDORA DE LA MARCA A CONTIENE 40 MG DE HIERRO. 10 MG DE VITAMINA B-1, 5 MG DE VITAMINA B-2 Y CUESTA 6 CENTAVOS. CADA PÍLDORA DE LA MARCA B CONTIENE 10 MG DE HIERRO, 15 MG DE VITAMINA B-1 Y DE VITAMINA B-2 Y CUESTA 8 CENTAVOS. CUALES COMBINACIONES DE PÍLDORAS DEBE COMPRAR EL PACIENTE PARA CUBRIR SUS REQUERIMIENTOS DE HIERRO Y VITAMINA AL MENOR COSTO? MARCA A MARCA B REQUERIMIENTOS MÍNIMOS HIERRO 40 MG 10 MG 2400 MG VITAMINA B-1 10 MG 15 MG 2100 MG VITAMINA B-2 5 MG 15 MG 1500 MG DE DECISION X1- A 40MG HIERRO 10MG B1 5MG B2
3 X2 B - 10 MG HIERRO 15 MG B1 15 MG B2 2.-FUNCIÓN OBJETIVO MIN Z = 6X1 + 8X2 A 6CENTAVOS B 8CENTAVOS 3.-RESTRICIONES 40 X1 + 10X X1 + 15X X1 + 15X CNN X1, X2, 0 LA FTM PROBLEMA # 4 VAMOS A CONSIDERAR EL PROBLEMA DE LA FTM PARA DETERMINAR CUANTAS UNIDADES DE CADA COMEDOR FABRICAR PARA VENDER. LA FTM PRODUCE LOS TIPOS DE COMEDOR AMERICANOS VIRGINIA (V), MASSACHUSSETS (M). LA FTM LOGRA UNA UTILIDAD (= PRECIO NETOS DE VETA-COSTO VARIABLES DE FABRICACIÓN) DE $200 Y $240 DE LAS VENTA DE UN COMEDOR VIRGINIA Y UNO MASSACHUSSETS, RESPECTIVAMENTE. LA FTM HA EXPERIMENTADO UNA ALTA DEMANDA DE AMBOS COMEDORES. EN CONSECUENCIA, EL GERENTE GENERAL CREE QUE PUEDE VENDER TODOS LOS COMEDORES QUE PRODUZCA. LOS COMEDORES REQUIEREN TIEMPO0 DE PROCESO EN CONSTRUCCIÓN Y DE PINTURA (P). LOS REQUERIMIENTOS Y CAPACIDADES DE PRODUCCIÓN DIARIOS ESTA EN LA TABLA RECURSOS REQUERIDOS PARA PRODUCIR 1 UNIDAD TIEMPO DE CONSTRUCCIÓN C (HORAS) TIEMPO DE PINTURA P (HORAS) VIRGINIA V PRODUCTO MASSACHUSSETS M RECURSOS DISPONIBLES (CAPACIDAD) UNIDAD UNITARIA $200 $ ENTONCES, PARA DETERMINAR LA MEJOR UTILIDAD OPTIMA COMBINACIÓN DE COMEDORES V Y M QUE SE DEBE PRODUCIR DIARIAMENTE, LA FTM TIENE QUE ASIGNAR SUS CAPACIDADES LIMITADAS (RECURSOS ESCASOS) DE DEPARTAMENTOS C Y P DEL MISMO QUE PUEDA LOGRAR SU OBJETIVO. X1-6 HORAS 8 HORAS (P) X2 12 HORAS 4 HORAS (P) 2.- FUNCIÓN OBJETIVO. MÁX. Z = 200 X X2
4 120 HRS. EN CONSTRUCCIÓN 64 HRS. EN PINTURA 6X X X1 + 4X2 64 CNN X1, X2 > 0 UN FRUTERO PROBLEMA # 5 UN FRUTERO NECESITA 16 CAJAS DE NARANJAS, 5 DE PLÁTANOS Y 20 DE MANZANAS. DOS MAYORISTAS PUEDEN SUMINISTRARLE PARA SATISFACER SUS NECESIDADES, PERO SOLO VENDEN LA FRUTA EN CONTENEDORES COMPLETOS. EL MAYORISTA A ENVÍA EN CADA CONTENEDOR 8 CAJAS DE NARANJAS, 1 DE PLÁTANOS Y 2 DE MANZANAS. EL MAYORISTA B ENVÍA EN CADA CONTENEDOR 2 CAJAS DE NARANJAS, 1 DE PLÁTANOS Y 7 DE MANZANAS. SABIENDO QUE EL MAYORISTA A SE ENCUENTRA A 150 KM. DE DISTANCIA EL; MAYORISTA B A 300 KM., CALCULAR CUANTOS CONTENEDORES HABRÁ DE COMPRAR CADA MAYORISTA, CON EL OBJETO DE AHORRAR TIEMPO Y DINERO, REDUCIENDO AL MÍNIMO LA DISTANCIA DE LO SOLICITADO. MAYORISTA MAYORISTA NECESIDADES MÍNIMAS A B NARANJAS CAJAS PLÁTANOS CAJAS MANZANAS CAJAS DISTANCIAS 150 KM. 300 KM. X1 8 CAJAS DE NARANJAS 1 CAJA DE PLÁTANOS 2 CAJAS DE MANZANAS X2 2 CAJAS DE NARANJAS 1 CAJA DE PLÁTANOS 7 CAJAS DE MANZANAS 2.-FUNCIÓN OBJETIVO MIN Z = 150X X2 16 CAJAS DE NARANJAS 5CAJAS DE PLÁTANO 20 CAJAS DE MANZANAS 8X1 + 2X2 16 X1 + X2 5 2X1 + 7X2 20
5 COMPAÑÍA MINERA PROBLEMA # 6 UNA COMPAÑÍA TIENE DOS MINAS A PRODUCE DIARIAMENTE 1 TONELADA DE CARBÓN DE ANTRACITA DE ALTA CALIDAD 2 TONELADAS DE CARBÓN DE CALIDAD MEDIA Y 4 TONELADAS DE CARBÓN DE BAJA CALIDAD; LA MINA B PRODUCE 2 TONELADAS DE CADA DE LAS TRES CLASES. LA COMPAÑÍA NECESITA 70 TONELADAS DE CARBÓN DE ALTA CALIDAD, 130 DE CALIDAD MEDIA Y 150 DE BAJA CALIDAD LOS GASTOS DIARIOS DE LA MINA A ASCIENDEN A 150 DÓLARES Y LOS DE LA MINA B A 200 DÓLARES CUANTOS DÍAS DEBERÁ TRABAJAR EN CADA MINA PARA QUE LA FUNCIÓN DE SEA MÍNIMA? FUNCIÓN OBJETIVO (MINIMIZAR) F(X) = 150X + 200Y MINA A MINA B NECESIDADES MÍNIMAS ALTA MEDIA BAJA COSTE DIARIO 150$ 200$ 1.- VARIABLES X1 1TON. ALTA CALIDAD 2TON. MEDIA CALIDAD 4TON. BAJA CALIDAD X2 2TON. ALTA CALIDAD 2TON. MEDIA CALIDAD 2TON. BAJA CALIDAD 2.-FUNCIÓN OBJETIVO MIN Z = 150X X2 X 1+ X2 70 2X1 + 2X X 1+ 2X2 150 PROBLEMA # 7 UNA EMPRESA CONSTRUCTORA UNA EMPRESA CONSTRUCTORA DISPONE DE DOS TIPOS DE CAMIONES C1 Y C2 Y QUIERE TRANSPORTAR 100T DE ARENA A UNA OBRA. SABIENDO QUE DISPONE DE 6 CAMIONES TIPO C1 CON CAPACIDAD PARA 15T Y CON UN COSTE DE 4000PTS POR VIAJE Y DE 10 CAMIONES TIPO C2 CON UNA CAPACIDAD DE 5T Y CON UN COSTE DE 3000PTS POR VIAJE. X1 6 CAMIONES TIPO C1 X2 10 CAMIONES TIPO C2
6 2.-FUNCIÓN OBJETIVO F.O MIN. Z = 4000X1+3000X2 6X1 < 15 10X2 < 5 SEGUROS PRIMO PROBLEMA # 8 LA COMPAÑÍA DE SEGUROS PRIMOS ESTA EN PROCESO DE INTRODUCIR DOS NUEVAS LÍNEAS DE PRODUCCIÓN. SEGURO DE RIESGO ESPECIAL E HIPOTECAS. LAS GANANCIAS ESPERADAS ES DE $5.00 POR EL SEGURO DE RIESGO ESPECIAL Y $20 POR UNIDAD DE HIPOTECA. LA ADMINISTRACIÓN DESEA ESTABLECER LAS CUOTAS DE VENTA DE LAS NUEVAS LÍNEAS PARA MAXIMIZAR LA GANANCIA TOTAL ESPERADA. LOS REQUERIMIENTOS DE TRABAJO SON LOS SIGUIENTES. HORAS HOMBRE POR UNIDAD DEPTO. RIESGO ESPECIAL HIPOTECAS HORAS HOMBRE DISPONIBLE SUSCRIPCIONES ADMINISTRACIÓN RECLAMACIONES X1 3HRS SUSCRIPCIÓN 0HRS ADMINISTRACIÓN 2HRS RECLAMACIONES X2 2HRS SUSCRIPCIÓN 1HR ADMINISTRACIÓN 0HRS RECLAMACIONES 2.-FUNCIÓN OBJETIVO MÁX. Z = 5X1 + 20X2 3X1 + 2X2 < X1 + X2 < 800 2X1 + 0X2 < 1200 PROBLEMA # 9 UN FABRICANTE UN FABRICANTE ESTA TRATANDO DE DECIDIR SOBRE LAS CANTIDADES DE PRODUCCIÓN PARA DOS ARTÍCULOS; MESAS SILLAS. SE CUENTA CON 96 UNIDADES DE MATERIAL Y CON 72 HORAS DE MANO DE OBRA. CADA MESA REQUIERE 12 UNIDADES DE MATERIAL Y 6 HORAS DE MANO DE OBRA. POR OTRA PARTE, LAS SILLAS USAN 6 UNIDADES DE MATERIAL CADA UNA Y REQUIEREN 12 HORAS DE MANO DE OBRA POR SILLA. EL MARGEN DE CONTRIBUCIÓN ES EL MISMO PARA LAS SILLAS $5.00 POR UNIDAD. EL FABRICANTE PROMETIÓ CONSTRUIR POR LO MENOS 2 MESAS.
7 X1 12U/MATERIAL 6HRS X2 6U/MATERIAL 12HRS MAXIMIZAR Z= 5X1 + 5X2 96U/MATERIAL 72HRS. EXISTE UNA LIMITACIÓN MÁS. EL FABRICANTE PROMETIÓ PRODUCIR POR LO MENOS DOS MESAS. ESTO PUEDE EXPRESARSE COMO: X1 2 12X1 + 8X2 96 6X1 + 12X2 72 X1 2 COMPAÑÍA X PROBLEMA # 10 UNA COMPAÑÍA PRODUCE 2 PRODUCTOS A Y B. CADA UNO DE LOS CUALES REQUIERE TIEMPO EN TRES MAQUINAS, COMO SE INDICA A CONTINUACIÓN. PRODUCTO HRS. MAQUINA 1 HRS. MAQUINA 2 HRS. MAQUINA 3 UTILIDAD A $250 KG. B $300 KG. SI EL NUMERO DE HORAS DISPONIBLES EN CADA MAQUINA AL MES DE 200 EN LA MAQUINA UNO, 240 EN LA MAQUINA DOS, 190 EN LA MAQUINA TRES. DETERMINE CUANTAS UNIDADES DE CADA PRODUCTO DEBEN PRODUCIRSE A FIN DE MAXIMIZAR LA UTILIDAD. X1 2HRS/MAQ.1 4HRS/MAQ.2 3HRS/MAQ.3 X2 5HRS/MAQ.1 1HR/MAQ.2 2HRS/MAQ FUNCION OBJETIVO MAX. Z= 250 X X2
8 2X1 + 5X X1 + 1X X1 + 2X2 190 COMPAÑÍA DESTILADORA PROBLEMA # 11 UNA COMPAÑÍA DESTILADORA TIENE DOS GRADOS DE GÜISQUI EN BRUTO (SIN MEZCLAR) I Y II, DE LOS CUALES PRODUCE DOS MARCAS DIFERENTES. LA MARCA REGULAR CONTIENE UN 50% DE CADA UNO DE LOS GRADOS I Y II. MIENTAS QUE LA MARCA SÚPER CONSTA DE DOS TERCERAS PARTES DEL GRADO I Y UNA TERCERA PARTE DE GRADO II. LA COMPAÑÍA DISPONE DE 3000 GALONES DE GRADO I Y 2000 GALONES DEL GRADO II PARA MEZCLAR. CADA GALÓN DE LA MARCA REGULAR PRODUCE UNA UTILIDAD DE $5 MIENTRAS QUE CADA GALÓN DEL SÚPER PRODUCE UNA UTILIDAD DE $6. CUANTOS GALONES DE CADA MARCA DEBERÍA PRODUCIR LA COMPAÑÍA A FIN DE MAXIMIZAR SUS UTILIDADES? X X MAX. Z = 5X1 + 6X2 RESTRICCIONES 1500 X X X X PROBLEMA # 12 DOS PRODUCTOS X EN UNA EMPRESA SE FABRICAN DOS PRODUCTOS, CADA PRODUCTO DEBE PASAR POR UNA MAQUINA DE ENSAMBLE A Y OTRA DE TERMINADO B, ANTES DE SALIR A LA VENTA, EL PRODUCTO 1 SE VENDE A $ 60 Y EL PRODUCTO 2 A $ 50 POR UNIDAD. LA SIGUIENTE TABLA MUESTRA EL TIEMPO REQUERIDO POR CADA PRODUCTO. PRODUCTO MAQUINA A MAQUINA B 1 2H 3H 2 4H 2H TOTAL DISPONIBLE 48H 36 H X1 2HRS. 3HRS. X2 4HRS 2HRS
9 MAX Z = 60 X X2 2 X1 + 4 X X1 + 2 X2 36 COMPAÑIA DE CELULARES PROBLEMA # 13 UNA COMPAÑÍA FABRICA 2 TIPOS DE CELULARES DIFERENTES, PARA FABRICARLOS SE UTILIZAN 30 GR. DE UN PRODUCTO A Y 15 GR. DE UN PRODUCTO B PARA EL PRIMER TIPO. PARA EL SEGUNDO TIPO SE UTILIZAN 13 GR. DEL PRODUCTO A Y 23 GR. DEL PRODUCTO B. LA GANANCIA DEL PRIMER CELULAR ES DE $100 PESOS Y DEL SEGUNDO TIPO DE CELULAR ES DE $75 PESOS SI CUANTA CON: 300 GR. DEL PRODUCTO A 250 GR. DEL PRODUCTO B CUÁNTAS CANTIDADES DE CADA TIPO DE CELULAR DEBE PRODUCIR LA COMPAÑÍA PARA MAXIMIZAR SUS GANANCIAS? X1 30GR. 13GR. X2 15GR. 23GR. MAX Z = 100 X X2 30 X X X X2 250 PROBLEMA #14 UN FABRICANTE DE PALILLOS UN FABRICANTE DE PALILLOS DE DIENTES PRODUCE DOS CLASES DE PALILLOS, REDONDOS, RECTANGULARES, LOS DEPARTAMENTOS DE PRODUCCIÓN TAMBIÉN SON DOS EL DE CORTE Y EL DE EMPAQUE, EL PRIMERO PUEDE PROCESAR 350 CAJAS DE PALILLOS REDONDOS O 626 DE PALILLOS RECTANGULARES POR HORA LOS DOS, EL DEPARTAMENTO DE EMPAQUE PUEDE PROCESAR 600 CAJAS DE PALILLOS REDONDOS Y 300 CAJAS DE PALILLOS RECTANGULARES. LA CONTRIBUCIÓN DE COSTO PARA LA CAJA DE PALILLOS REDONDOS ES DE $0.030 Y PARA LA DE RECTANGULARES ES DE $0.040 Y $0.045 RESPECTIVAMENTE. DE DECISION REDONDO = X1 RECTANGULARES = X2 2.- FUNCION OBJETIVO MIN Z= X1 X2
10 MAX Z = X1 X2 MIN Z = 0.30 X X2 (COSTO) MAX Z = 0.40 X X2 (UTILIDAD) 3.- RESTRICCIONES RESTRICCIONES CORTE 350 C/HR (REDONDO) 625 C/HR (RECTANGULARES) EMPAQUE 600 C/HR (REDONDO) 300 C/HR (RECTANGULARES) COSTOS $0.30 / UNIDAD $0.35/UNIDAD UTILIDAD $0.40 / PIEZA $0.45/PIEZA CORTE X X2 = 975 EMPAQUE X X2 = 900 UN AVIÓN DE CARGA PROBLEMA # 15 UN AVIÓN DE CARGA TIENE 3 COMPARTIMIENTOS PARA ALMACENAR: DELANTERO, CENTRAL Y TRASERO ESTOS COMPARTIMENTOS TIENEN UN LIMITE TANTO DE PESO COMO DE ESPACIO. COMPARTIMIENTO CAP. DE PESO (TONELADAS) CAP. DE ESPACIO (PIES CÚBICOS) DELANTERO CENTRAL TRASERO PARA MANTENER EL AVIÓN BALANCEADO, ES EL PESO DE LA CARGA DE LOS RESPECTIVOS COMPARTIMIENTOS DEBE SER PROPORCIONAL A SU CAPACIDAD SE ENCUENTRA CON OFERTA PARA LOS SIGUIENTES ENVÍOS PARA UN VUELO PRÓXIMO YA QUE SE CUENTA CON ESPACIO DISPONIBLE. CARGA PESO (TONELADAS) VOLUMEN (PIES CÚBICOS) GANANCIAS (TONELADAS) FUNCION OBJETIVO MAX 350X X X X4
11 3.- RESTRICIONES 20X1 + 16X2 + 25X3 + 13X4 12(D) 20X1 + 16X2 + 25X3 + 13X4 18 (C) 20X1 + 16X2 + 25X3 + 13X4 10 (T) 500X1 + 70X X X4 7, X1 + 70X X X4 9, X1 + 70X X X4 5,000 COMPAÑÍA GILLETTE PROBLEMA # 16 LA COMPAÑÍA GILLETTE PRODUCE HOJAS PARA RASURAR ACTUALMENTE PRODUCE 2 TIPOS DE HOJAS DE RASURAR DE ACERO INOXIDABLE Y LA DE ALUMINIO. LA 1RA REQUIERE PARA SER PRODUCIDA 8 UNIDADES DE ACERO AL CARBÓN T 2 UNIDADES DE ALEACIONES DE ÁCIDO POR CADA 100 HOJAS MIENTRAS QUE LA DE ALUMINIO REQUIERE DE 4 UNIDADES DE ACERO AL CARBÓN Y 6 UNIDADES DE ALEACIÓN DE ÁCIDO PARA CADA 100 HOJAS. COMO RESULTADO DE UN RECIENTE ESTUDIO LA COMPAÑÍA TIENE UN INVENTARIO DE 24 MIL UNIDADES DE ACERO AL CARBÓN Y 10MI UNIDADES DE ALEACIÓN DE ÁCIDO, LOS CUALES ESTÁN DISPONIBLES PARA LA PRODUCCIÓN DE LOS 2 TIPOS DE HOJAS QUE REPORTAN EN ORDEN RESPECTIVO Y POR CADA 100 HOJAS DICHA COMPAÑÍA TIENE UNA GANANCIA DE 1 PESO Y 1.5 DE UTILIDAD RESPECTIVAMENTE LOS CUALES DESEA INCREMENTAR. X1 8U/ACERO 2U/AL. ÁCIDO X2 4U/ACERO 6U/AL. ÁCIDO MAX Z = 1X X2 RESTRICCIONES 8X1 + 4X X1 + 6X PROBLEMA # 17 ESPECIES INDIAN C.A LA COMPAÑÍA ESPECIES INDIAN C.A TIENE UN STOCK LIMITADO DE DOS HIERBAS QUE SE UTILIZAN EN LA PRODUCCIÓN DE ADEREZOS ESPECIES INDIAN C.A USA LOS DOS INGREDIENTES HB1 Y HB2, PARA PRODUCIR YA SEA CURRY O PIMENTÓN. EL DEPARTAMENTO DE MERCADOTECNIA INFORMA QUE AUNQUE LA EMPRESA PUEDE VENDER TODO EL PIMENTÓN QUE PUEDE PRODUCIR, SOLO PUEDE VENDER HASTA UN MÁXIMO DE 1500 BOTELLAS DE CURRY. LAS HIERBAS NO UTILIZADAS SE PUEDEN VENDER A $375 LA ONZA DE HB1 Y A $167 LA ONZA DE HB2. UTILIZANDO EL MÉTODO GRÁFICO, DETERMINE EL CONSUMO DE ESPECIAS QUE MAXIMICE EL INGRESO DE LA EMPRESA. ADEREZO INGREDIENTES (ONZAS / BOT.) HB1 HB2 DEMANDA (BOTELLAS) PRECIO DE VENTA POR BOTELLA ($) CURRY PIMENTÓN 2 3 ILIMITADA 1300
12 DISPONIBILIDAD (ONZAS) X1 5ONZ. /CURRY 2ONZ. / PIMENTÓN X2 3ONZ. /CURRY 3ONZ. /PIMENTÓN MAXIMIZAR Z= 2750 X X2 MAXIMIZAR Z= 2750 X X2 5X1 + 3X X1 + 3X2 1 X X FABRICA DE CARROS PROBLEMA # 18 EN UNA FÁBRICA DE CARROS SE CONSTRUYEN 2 TIPOS DE AUTOS, EL Z Y EL GT-R, EL PRIMERO UTILIZA 6 CILINDROS MIENTRAS QUE EL SEGUNDO 10, TAMBIÉN EL PRIMERO UTILIZA 2 FRENOS Y EL SEGUNDO 4. PERO EN CUANTO A VÁLVULAS EL; PRIMERO OCUPA 24 MIENTRAS QUE EL SEGUNDO 16. SI EL PRIMER AUTO SE VENDE EN $25,000 Y EL SEGUNDO EN $38,000 COMO PODEMOS SACAR UNA UTILIDAD MÁXIMA SI CONSIDERAMOS QUE EL ALMACÉN TIENE SOLO 75 CILINDROS, 45 FRENOS Y 160 VÁLVULAS. X1 6CIL. 2 FRENOS 24 VÁLVULAS X2 10CIL. 4 FRENOS 16 VÁLVULAS MAX Z = 25,000 X1 + 38,000 X2 6X1 + 10X2 75 2X1 + 4X X1 + 16X2 160 PROBLEMA # 19 COMPAÑIA XYZ LA COMPAÑÍA X Y Z PRODUCE JUGUETES, LOS OSOS BOBBY Y TEDDY. CADA UNO DE ESTOS PRODUCTOS DEBE SER PROCESADO EN 2 MAQUINAS DIFERENTES. UNA MAQUINA TIENE 12 HRS. DE CAPACIDAD DISPONIBLES Y LA OTRA 8. CADA BOBBY PRODUCIDO NECESITA 2 HRS. DE TIEMPO EN CADA MAQUINA.
13 CADA TEDDY PRODUCIDO REQUIERE 3HRS, DE TIEMPO EN LA PRIMERA MAQUINA Y 1HRS. EN LA SEGUNDA MAQUINA. LA GANANCIA INCREMENTA ES DE $ 6.00 POR CADA BOBBY Y DE $7.00 POR CADA TEDDY VENDIDOS Y LA FIRMA PUEDE VENDER TANTAS UNIDADES DE CADA PRODUCTO COMO FABRICANTE. EL PROBLEMA ES DETERMINAR CUANTAS UNIDADES DE BOBBY Y TEDDY DEBEN PRODUCIRSE. X1 2HRS. 2HRS. X2 3HRS. 1HR. MAX Z = 6X1 + 7X2 3,-RESTRICCIONES 2X1 + 3X2 12 HRS. 2X1 + 1X2 8 HRS. PROBLEMA # 20 COMPAÑÍA TEXTIL UNA COMPAÑÍA TEXTIL TIENE UNA PLANTA DE PRODUCCIÓN DE FIBRAS SINTÉTICAS Y EN LA LÍNEA DE PRODUCCIÓN PROCESA 2 CLASES DE FIBRAS: LA F1 Y LA F2 LA PRODUCCIÓN EN EL DEPARTAMENTO DE HILANDERÍA REQUIERE DE 20 Y 40 HRS. P/CADA MIL LB., ESTE DEPARTAMENTO CUENTA CON UNA DISPONIBILIDAD DE 2000 HRS. AL MES. EN EL DEPARTAMENTO DE ESTIRAMIENTO REQUIERE DE 60 Y 80 HRS. PARA CADA 1000 LB. DE F1 Y F2 RESPECTIVAMENTE, ESTE DEPARTAMENTO TIENE DISPONIBILIDAD DE 4800 HRS. AL MES Y EL DEPARTAMENTO DE CORTE REQUIERE DE 100 Y 60 HRS. PARA SACAR MIL LIBRAS DE DICHAS FIBRAS CONTANDO CON UNA DISPONIBILIDAD DE 6000 HRS. MENSUALMENTE LAS VENTAS LIMITAN LAS VENTAS DE PRODUCCIÓN DE F1 A UN MÁXIMO DE LB. AL MES. CUÁNTO DEBERÁ DE PRODUCIRSE DE CADA FIBRA EN EL FIN DE MAXIMIZAR UTILIDADES SABIENDO QUE LAS CONTRIBUCIONES DE LAS FIBRAS F1 Y F2 SON 100 Y 150 PARA CADA MIL FIBRAS RESPECTIVAMENTE? X1 20HRS 60HRS. 100HRS. X2 40HRS. 80HRS. 60HRS. 2.-FUNCION OBJETIV0 MAXIMIZAR 100X X2 20X1 + 40X X1 + 80X X1 + 60X X1 + X LA FABRICA ACE
14 PROBLEMA # 21 LA FABRICA ACE TIENE LA OPCIÓN DE PRODUCIR DOS PRODUCTOS EN PERIODOS DE ACTIVIDAD HOLGADA. PARA LA PRÓXIMA SEMANA LA PRODUCCIÓN SE HA PROGRAMADO PARA QUE LA MAQUINA QUE MUELE ESTE LIBRE 20HRS. Y LA MANO DE OBRA CALIFICADA TENGA 16HRS. DE TIEMPO DISPONIBLE. EL PRODUCTO 1 REQUIERE 8HRS. DE TIEMPO MAQUINA Y 4HRS. DE MANO DE OBRA CALIFICADA. EL PRODUCTO 1 CONTRIBUYE $7DLLS. POR UNIDAD A LAS UTILIDADES Y EL PRODUCTO 2 CONTRIBUYE CON $5DLLS. MAQUINA P1 8HRS 4HRS MANO DE OBRA P2 4HRS 4HRS MÁX. Z = 7X1+5X2 8X1+4X2<20 4X1+4X1<16 LA MAIN SNOWMOBIL PROBLEMA # 22 LA MAIN SNOWMOBIL COMPANY FABRICA DOS CLASES DE MAQUINAS, CADA UNA REQUIERE DE UNA TÉCNICA DIFERENTE DE FABRICACIÓN. LA MAQUINA DE LUJO REQUIERE DE 18HRS. DE MANO DE OBRA, 9 HORAS DE PRUEBA Y PRODUCE UNA UTILIDAD DE $400 DLLS. LA MAQUINA ESTÁNDAR REQUIERE DE 3 HRS. DE MANO DE OBRA, 4 HRS. DE PRUEBA Y PRODUCE UNA UTILIDAD DE $200 DLLS. SE DISPONE DE 800 HRS. PARA MANO DE OBRA Y 600 HRS. PARA PRUEBA CADA MES. SE HA PRONOSTICADO QUE LA DEMANDA MENSUAL PARA EL MODELO DE LUJO NO ES MAS DE 50 Y DE LA MAQUINA ESTÁNDAR NO ES MAS DE 150. LA GERENCIA DESEA SABER EL NUMERO DE MAQUINAS DE CADA MODELO, QUE DEBERÁ PRODUCIRSE PARA MAXIMIZAR LA UTILIDAD TOTAL. X1 18HRS. 9HRS X2 3HRS 4HRS MAX Z= 400X1+200X2 18X1+3X2 < 800 9X1+4X2 < 600
15 UN JOYERO PROBLEMA # 23 UN JOYERO FABRICA DOS TIPOS DE ANILLOS: LOS ANILLOS A1 PRECISAN 1GRAMO DE ORO Y 5 DE PLATA VENDIÉNDOLOS A $40 DLLS. CADA UNO. PARA LOS ANILLOS A2 EMPLEA 1.5 GRAMOS DE ORO Y 1 GRAMO DE PLATA Y LOS VENDE A $50 DLLS. EL JOYERO DISPONE EN SU TALLER DE 750 GRAMOS DE CADA METAL. CALCULAR CUANTOS ANILLOS DEBE FABRICAR DE CADA CLASE PARA OBTENER EL MÁXIMO BENEFICIO? A1 A2 1 GRAMO DE ORO 5 GRAMO DE PLATA 1.5 GRAMOS DE ORO 1 GRAMO DE PLATA MAX Z = 40X1+50X2 X1+1.5X2 < 750 5X1+X2 < 750 FABRICACIÓN DE MOBILIARIO PROBLEMA # 24 UNA EMPRESA, ESPECIALIZADA EN LA FABRICACIÓN DE MOBILIARIO PARA CASAS DE MUÑECAS, PRODUCE CIERTO TIPO DE MESAS Y SILLAS QUE VENDE A 2000 PST. Y 3000 PST. POR UNIDAD RESPECTIVAMENTE. DESEA SABER CUANTAS UNIDADES DE CADA ARTÍCULO DEBE FABRICAR DIARIAMENTE UN OPERARIO PARA MAXIMIZAR LOS INGRESOS TENIÉNDOSE LAS SIGUIENTES RESTRICCIONES: -EL NÚMERO TOTAL DE UNIDADES DE LOS DOS TIPOS NO PODRÁ EXCEDER DE 4 POR DÍA Y OPERARIO. -CADA MESA REQUIERE 2 HRS. PARA SU FABRICACIÓN; CADA SILLA 3 HRS. LA JORNADA LABORAL MÁXIMA ES DE 10 HRS. -EL MATERIAL UTILIZADO EN CADA MESA CUESTA 400 PST. EL UTILIZADO EN CADA SILLA CUESTA 200 PST. CADA OPERARIO DISPONE DE 1200 PST. DIARIAS PARA MATERIAL. X1 2 HRS. MESAS 400 PST X2 3 HRS. SILLAS 200 PST. MAX Z = 2000X1+3000X2 2X1+3X2 < X1+200X2 < 1200 X1+X2 < 0 X1, X2 > 0
16 LA COMPAÑÍA IBM PROBLEMA # 25 LA COMPAÑÍA IBM PRODUCE 2 TIPOS DE IMPRESORAS DE LUJO Y LA COMÚN LA PRIMERA TIENE UN PRECIO DE $100 DLLS. Y LA COMÚN A UN PRECIO DE $120 DLL PARA ELLO SE CUENTA CON UNA CAPACIDAD DE PRODUCCIÓN LIMITADA YA QUE LA PRIMERA IMPRESORA NECESITA DE 3HRS. DE MANO DE OBRA DIRECTA Y 4HRS. PARA EL ACABADO, Y LA SEGUNDA MAQUINA REQUIERE DE 6HRS. DE MANO DE OBRA DIRECTA Y 2HRS. DE ACABADO. CUANTAS IMPRESORAS Y DE QUE TIPO HAY QUE PRODUCIR PARA MAXIMIZAR LAS UTILIDADES, IBM CUENTA CON 60HRS. DE MANO DE OBRA Y 32HRS. DE ACABADO. X1 3HRS. MANO DE OBRA 4HRS. ACABADO FINO X2 6HRS. MANO DE OBRA 2HRS. ACABADO FINO MAX Z = 100X1+120X2 RESTRICCIONES 3X1+6X2 < 60 4X1+2X2 < 32 LA COMPAÑÍA WORLD LIGHT PROBLEMA # 26 LA COMPAÑÍA WORD LIGHT PRODUCE 2 DISPOSITIVOS PARA LÁMPARAS (PRODUCTO 1 Y 2), QUE REQUIEREN PARTES DE METAL Y COMPONENTES ELÉCTRICOS. LA ADMINISTRACIÓN DESEA DETERMINAR CUANTAS UNIDADES DE CADA PRODUCTO FABRICAR PARA MAXIMIZAR LAS GANANCIAS. -POR CADA UNIDAD DEL PRODUCTO 1 SE REQUIEREN 1 UNIDAD DE PARTE DE METAL Y 2 UNIDADES DE COMPONENTES ELÉCTRICOS. -POR CADA UNIDAD DEL PRODUCTO 2 NECESITAN 3 UNIDADES DE PARTES DE METAL Y 2 UNIDADES DE COMPONENTES ELÉCTRICOS. LA COMPAÑÍA TIENE 200 UNIDADES DE PARTES DE METAL Y 300 DE COMPONENTES ELÉCTRICOS. CADA UNIDAD DEL PRODUCTO 1 DA UNA GANANCIA DE $1 PESO, Y CADA UNIDAD DEL PRODUCTO, HASTA 60 UNIDADES DA UNA GANANCIA DE $2 PESOS. CUALQUIER EXCESO DE 60 UNIDADES DEL PRODUCTO 2 NO TIENE GANANCIA, POR LO QUE FABRICAR MAS DE 60 ESTA FUERA DE CONSIDERACIÓN. 1.- VARIABLES P1 1 UNIDAD DE METAL 2 UNIDADES DE ELÉCTRICOS P2 3 UNIDADES DE METAL 2 UNIDADES ELÉCTRICAS 2.-FUNCIÓN OBJETIVO MAX Z = X1+X2 X1+3X2 < 200 2X1+ 2X2 < X2 > 0
17 UN EMPRESARIO PROBLEMA #27 UN EMPRESARIO TIENE LA OPCIÓN DE INVERTIR EN DOS PLANES: EL PLAN A GARANTIZA QUE CADA DÓLAR INVERTIDO GANARA $0.70 UN AÑO DESPUÉS, Y EL PLAN B GARANTIZA QUE CADA DÓLAR INVERTIDO GANARA $2 A LOS 2 AÑOS. EN EL PLAN A SE PUEDEN HACER PERIODOS MÚLTIPLOS DE 2 AÑOS, CÓMO DEBA DE INVERTIR $ EL EMPRESARIO PARA MAXIMIZAR LAS GANANCIAS AL FINAL DE 3 AÑOS? GANANCIA $.70 DLLS $ 2 DLLS PLAN A 1 AÑO PLAN B 2 AÑOS MAX Z =.70X1+2X2 X1 > 1 X2 < 2 X1+X2 < PROBLEMA # 28 COMPAÑÍA DE NUECES UNA COMPAÑÍA VENDE DOS MEZCLAS DIFERENTES DE NUECES. LA MEZCLA MÁS BARATA CONTIENE UN 80% DE CACAHUATES Y UN 20 % DE NUECES, MIENTRAS QUE LA MÁS CARA CONTIENE 50% DE CADA TIPO. CADA SEMANA LA COMPAÑÍA OBTIENE 1800 KILOS DE CACAHUATE Y 1200 KILOS DE NUECES DE SUS FUENTES DE SUMINISTROS. CUANTOS KILOS DE CADA MEZCLA DEBERÍA PRODUCIR A FIN DE MAXIMIZAR LAS UTILIDADES SI LAS GANANCIAS SON DE $10 POR CADA KILO DE LA MEZCLA MÁS BARATA Y DE $ 15 POR CADA KILO DE LA MEZCLA MÁS CARA? MEZCLA CACAHUATE NUEZ GANANCIA POR SEMANA BARATA 80% 20% $10 POR KILO CARA 50% 50% $ 15 POR KILO X1 = LA CANTIDAD DE MEZCLA DE LA MARCA BARATA EN KILOGRAMOS X2 = LA CANTIDAD DE MEZCLA DE LA MARCA CARA EN KILOGRAMOS
18 2.-FUNCIÓN OBJETIVO MAX Z = 10X1+15X2 80X1+50X2 < X1+50X2 < 1200 LA CARNICERIA VILLAGE BUTCHER PROBLEMA # 29 LA CARNICERÍA VILLAGE BUTCHER, TRADICIONALMENTE HACE UN EMBUTIDO DE CARNE MOLIDA UTILIZANDO CARNE DE RES Y DE PUERCO, LA MOLIDA DE RES CONTIENE 80% DE CARNE Y 20% DE GRASA Y CUESTA.80DLLS POR LIBRA. LA MOLIDA DE PUERCO CONTIENE 68% DE CARNE Y 32% DE GRASA Y CUESTA.60DLL. LA LIBRA. CUÁNTO DEBE USAR DE CADA CLASE DE CARNE (RES Y PUERCO) PARA PRODUCIR UNA LÍNEA DE SU EMBUTIDO, SI QUIERE MINIMIZAR EL COSTO Y MANTENER EL CONTENIDO DE GRASA EN NO MAS DEL 25%. 80% % CARNE 20% % GRASA MIN Z =.80X1 +.60X2 RESTRICCIONES 20X1 + 32X2 < 25 X1 + X2 = 0 PROBLEMA # 30 UNA EMPRESA DE TARJETAS GRAFICAS UNA EMPRESA FABRICA DOS TIPOS DE TARJETAS GRÁFICAS, DE 16MB Y 32MB DE MEMORIA, RESPECTIVAMENTE. SE UTILIZAN DOS MÁQUINAS QUE EMPLEAN 2 MIN. EN FABRICAR LAS DE 16MB Y 3 MIN. EN FABRICAR LAS DE 32MB. LA CADENA DE MONTAJE SÓLO PUEDE FUNCIONAR, COMO MÁXIMO, 300 MINUTOS DIARIOS. ADEMÁS CADA MÁQUINA TIENE UNA CAPACIDAD MÁXIMA DE FABRICACIÓN DIARIA DE 125 UNIDADES, ENTRE LAS CUALES NO PUEDE HABER MÁS DE 90 TARJETAS DE 16MB NI MÁS DE 80 TARJETAS DE 32MB, SIENDO EL BENEFICIO NETO DE LAS PRIMERAS DE 45$ Y EL DE LAS SEGUNDAS DE 60$. CUÁNTAS TARJETAS DE 16MB Y 32MB DEBEN FABRICAR DIARIAMENTE CADA MÁQUINA PARA QUE EL BENEFICIO SEA MÁXIMO? 2 MIN. EN FABRICAR 16 MB 3 MIN., 32 MB MÁX. Z = 45X1+60X2
19 X1+3X2 < 300 X1 + X2 < 125 X1 < 90 X2 < 80 UNA TIENDA DE ANIMALES 31. UNA TIENDA DE ANIMALES HA DETERMINADO QUE CADA HÁMSTER DEBERÍA RECIBIRLA MENOS 70 UNIDADES DE PROTEÍNA. 100 UNIDADES DE CARBOHIDRATOS Y 20 UNIDADES DE GRASA. SI LA TIENDA VENDE LOS SEIS TIPOS DE ALIMENTOS MOSTRADOS EN LA TABLA. QUÉ MEZCLA DE ALIMENTO SATISFACE LAS NECESIDADES A UN COSTO MÍNIMO PARA LA TIENDA? ALIMENTO A B C D E F PROTEÍNAS (UNIDADES / ONZA) CARBOHIDRATOS (UNIDADES / ONZA) GRASA (UNIDADES / ONZA) COSTO (ONZA) ,.VARIABLES QUÉ ES LO QUE VAMOS A MINIMIZAR? X1 = LA CANTIDAD A MEZCLAR DE A X2 = LA CANTIDAD A MEZCLAR DE B X3 = LA CANTIDAD A MEZCLAR DE C X4 = LA CANTIDAD A MEZCLAR DE D X5 = LA CANTIDAD A MEZCLAR DE E X6 = LA CANTIDAD A MEZCLAR DE F MIN W = 2X1 + 3X2 + 5X3 + 6X4 + 8X5 + 8X6 20X1 + 30X2 + 40X3 + 40X4 + 45X5 + 30X6 < PROTEÍNA 50X1 + 30X2 + 20X3 + 25X4 + 50X5 + 20X6 < CARBOHIDRATOS 4X1 + 9X2 + 11X3 + 10X4 + 9X5 + 10X6 < GRASA X1, X2, X3, X4 > 0
-.PROGRAMACION LINEAL.- Problemas resueltos
 -.PROGRAMACION LINEAL.- Problemas resueltos EJEMPLO 1. Un expendio de carnes de la ciudad acostumbra preparar la carne para albondigón con una combinación de carne molida de res y carne molida de cerdo.
-.PROGRAMACION LINEAL.- Problemas resueltos EJEMPLO 1. Un expendio de carnes de la ciudad acostumbra preparar la carne para albondigón con una combinación de carne molida de res y carne molida de cerdo.
TP1 Programación Lineal - 2009
 Problema Trabajo Práctico Nº 1 de cerdo. Una carnicería 1 La carne prepara vaca hamburguesas contiene 80% con de carne una combinación y 20% de grasa de carne y le molida cuesta de $5 vaca el kilo, y carne
Problema Trabajo Práctico Nº 1 de cerdo. Una carnicería 1 La carne prepara vaca hamburguesas contiene 80% con de carne una combinación y 20% de grasa de carne y le molida cuesta de $5 vaca el kilo, y carne
EJERCICIOS RESUELTOS DE PROGRAMACIÓN LINEAL
 EJERCICIOS RESUELTOS DE PROGRAMACIÓN LINEAL 1.- Un estudiante reparte propaganda publicitaria en su tiempo libre. La empresa A le paga 0,05 por impreso repartido y la empresa B, con folletos más grandes,
EJERCICIOS RESUELTOS DE PROGRAMACIÓN LINEAL 1.- Un estudiante reparte propaganda publicitaria en su tiempo libre. La empresa A le paga 0,05 por impreso repartido y la empresa B, con folletos más grandes,
PROGRAMACIÓN LINEAL. a) Dibuja dicha región y determina sus vértices. b) Calcula el mínimo de la función objetivo z = 4x + 5y, en el recinto anterior.
 PROGRAMACIÓN LINEAL 1. La región factible de un problema de programación lineal es la intersección de primer cuadrante con los tres semiplanos definidos por las siguientes inecuaciones: x y x y x y + 1
PROGRAMACIÓN LINEAL 1. La región factible de un problema de programación lineal es la intersección de primer cuadrante con los tres semiplanos definidos por las siguientes inecuaciones: x y x y x y + 1
EJERCICIOS. Calcula la producción diaria de los artículos A y B que maximiza el beneficio
 EJERCICIOS EJERCICIO 1 En una granja de pollos se da una dieta "para engordar" con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado solo se encuentran
EJERCICIOS EJERCICIO 1 En una granja de pollos se da una dieta "para engordar" con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado solo se encuentran
x + y 4 2x + 3y 10 4x + 2y 12 x 0, y 0
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PROBLEMAS DE PROGRAMACIÓN LINEAL JUNIO 2000. OPCIÓN B. Una empresa especializada en la fabricación de mobiliario para casas de muñecas, produce cierto tipo de mesas y
PRUEBAS DE ACCESO A LA UNIVERSIDAD PROBLEMAS DE PROGRAMACIÓN LINEAL JUNIO 2000. OPCIÓN B. Una empresa especializada en la fabricación de mobiliario para casas de muñecas, produce cierto tipo de mesas y
Programación Lineal: Modelos PLE
 Programación Lineal: Modelos PLE CCIR / Matemáticas euresti@itesm.mx CCIR / Matemáticas Programación Lineal: Modelos PLE euresti@itesm.mx 1 / 35 Introduccion Introduccion En esta lectura se verán cómo
Programación Lineal: Modelos PLE CCIR / Matemáticas euresti@itesm.mx CCIR / Matemáticas Programación Lineal: Modelos PLE euresti@itesm.mx 1 / 35 Introduccion Introduccion En esta lectura se verán cómo
11.1. Diferentes situaciones sobre regiones factibles y óptimos. 1. Maximizar la función F(x,y) = 40x + 50y sujeta a las restricciones:
 11.1. Diferentes situaciones sobre regiones factibles y óptimos. 1. Maximizar la función F(x,y) = 40x + 50y sujeta a las restricciones: 0 0 (1) 2x + 5y 50 (3) 3x + 5y 55 (5) x (2) 5x + 2y 60 (4) x + y
11.1. Diferentes situaciones sobre regiones factibles y óptimos. 1. Maximizar la función F(x,y) = 40x + 50y sujeta a las restricciones: 0 0 (1) 2x + 5y 50 (3) 3x + 5y 55 (5) x (2) 5x + 2y 60 (4) x + y
CANTABRIA / JUNIO 04. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / BLOQUE 1 / OPCIÓN A
 CANTABRIA / JUNIO 04. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / BLOQUE 1 / OPCIÓN A BLOQUE 1 OPCIÓN A Un fabricante de coches lanza una oferta especial en dos de sus modelos, ofreciendo
CANTABRIA / JUNIO 04. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES / ÁLGEBRA / BLOQUE 1 / OPCIÓN A BLOQUE 1 OPCIÓN A Un fabricante de coches lanza una oferta especial en dos de sus modelos, ofreciendo
I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS PROGRAMACIÓN LINEAL
 I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS PROGRAMACIÓN LINEAL x + y 1 Dada la región del plano definida por las inecuaciones 0 x 3 0 y 2 a) Para qué valores (x, y) de dicha región es máxima
I E S CARDENAL CISNEROS -- DEPARTAMENTO DE MATEMÁTICAS PROGRAMACIÓN LINEAL x + y 1 Dada la región del plano definida por las inecuaciones 0 x 3 0 y 2 a) Para qué valores (x, y) de dicha región es máxima
MATEMÁTICAS PARA LA ECONOMIA II G.E.C.O. Curso 2012/2013
 MATEMÁTICAS PARA LA ECONOMIA II G.E.C.O. Curso 2012/2013 Relación de Ejercicios N o 3 1. Resolver los siguientes programas lineales primero gráficamente y después por el método del simplex. (a) Z = x +
MATEMÁTICAS PARA LA ECONOMIA II G.E.C.O. Curso 2012/2013 Relación de Ejercicios N o 3 1. Resolver los siguientes programas lineales primero gráficamente y después por el método del simplex. (a) Z = x +
TALLER 2: Programación Lineal-Planteamiento de problemas con dos variables
 TALLER 2: Programación Lineal-Planteamiento de problemas con dos variables En cada caso plantear el problema y encontrar la solución por el método grafico. Utilice el software QSB para verificar la solución.
TALLER 2: Programación Lineal-Planteamiento de problemas con dos variables En cada caso plantear el problema y encontrar la solución por el método grafico. Utilice el software QSB para verificar la solución.
Programación lineal -1-
 Programación lineal 1. (j99) Los alumnos de un instituto pretenden vender dos tipos de lotes, A y B, para sufragarse los gastos del viaje de estudios. Cada lote de tipo A consta de una caja de mantecados
Programación lineal 1. (j99) Los alumnos de un instituto pretenden vender dos tipos de lotes, A y B, para sufragarse los gastos del viaje de estudios. Cada lote de tipo A consta de una caja de mantecados
Ejemplos de planteamientos de Programación Lineal
 Ejemplos de planteamientos de Programación Lineal 1. Una familia campesina es propietaria de 125 acres y tiene fondos para $40 000 para invertir. Sus miembros pueden producir un total de 3 500 horashombre
Ejemplos de planteamientos de Programación Lineal 1. Una familia campesina es propietaria de 125 acres y tiene fondos para $40 000 para invertir. Sus miembros pueden producir un total de 3 500 horashombre
02 Ejercicios de Selectividad Programación Lineal
 Ejercicios propuestos en 009 1.- [009-1-B-1] En un examen se propone el siguiente problema: F x, y = 6x+ 3y en la región Indique dónde se alcanza el mínimo de la función determinada por las restricciones
Ejercicios propuestos en 009 1.- [009-1-B-1] En un examen se propone el siguiente problema: F x, y = 6x+ 3y en la región Indique dónde se alcanza el mínimo de la función determinada por las restricciones
Programación Lineal. Programación Lineal
 Programación Lineal Modelo General Max Z = c 1 + C 2 +... c n, s.a. a 11 + a 12 +... + a 1n b 1 a 21 + a 22 +... + a 2n b 2.. a m1 + a m2 +... + a mn b m 0, 0, x 3 0,..., 0 Programación Lineal Interpretación
Programación Lineal Modelo General Max Z = c 1 + C 2 +... c n, s.a. a 11 + a 12 +... + a 1n b 1 a 21 + a 22 +... + a 2n b 2.. a m1 + a m2 +... + a mn b m 0, 0, x 3 0,..., 0 Programación Lineal Interpretación
Programación Lineal. f(x,y) = 2 x + y. Cuántas soluciones hay? Solución:
 Programación Lineal 2 x + y 2 1.- alcula los puntos del recinto 2x y 2 que hacen mínima o máxima la función y 2 f(x,y) = 2 x + y. uántas soluciones hay? Solución: Representemos el sistema de inecuaciones
Programación Lineal 2 x + y 2 1.- alcula los puntos del recinto 2x y 2 que hacen mínima o máxima la función y 2 f(x,y) = 2 x + y. uántas soluciones hay? Solución: Representemos el sistema de inecuaciones
Programación Lineal Continua/ Investigación Operativa. EJERCICIOS DE INVESTIGACIÓN OPERATIVA. Hoja 1
 EJERCICIOS DE INVESTIGACIÓN OPERATIVA. Hoja 1 1. Una empresa que fabrica vehículos quiere determinar un plan de producción semanal. Esta empresa dispone de 5 fábricas que producen distintos elementos del
EJERCICIOS DE INVESTIGACIÓN OPERATIVA. Hoja 1 1. Una empresa que fabrica vehículos quiere determinar un plan de producción semanal. Esta empresa dispone de 5 fábricas que producen distintos elementos del
PROGRAMACIÓN LINEAL-SELECTIVIDAD (MADRID)
 PROGRAMACIÓN LINEAL-SELECTIVIDAD (MADRID) 1.- (Junio 99). Los alumnos de un instituto pretenden vender dos tipos de lotes, A y B, para sufragar los gastos del viaje de estudios. Cada lote de tipo A consta
PROGRAMACIÓN LINEAL-SELECTIVIDAD (MADRID) 1.- (Junio 99). Los alumnos de un instituto pretenden vender dos tipos de lotes, A y B, para sufragar los gastos del viaje de estudios. Cada lote de tipo A consta
PROGRAMACIÓN LINEAL. Ejemplo a) Dibuja el recinto formado por los puntos que cumplen las siguientes condiciones:
 PROGRAMACIÓN LINEAL CONTENIDOS: Desigualdades e inecuaciones. Sistemas lineales de inecuaciones. Recintos convexos. Problemas de programación lineal. Terminología básica. Resolución analítica. Resolución
PROGRAMACIÓN LINEAL CONTENIDOS: Desigualdades e inecuaciones. Sistemas lineales de inecuaciones. Recintos convexos. Problemas de programación lineal. Terminología básica. Resolución analítica. Resolución
PROGRAMACIÓN LINEAL. Solución: Sea: x = cantidad invertida en acciones A y = cantidad invertida en acciones B. La función objetivo es: x y + 100 100
 PROGRAMACIÓN LINEAL 1. A una persona le tocan 10 millones de pesos en una lotería y le aconsejan que las invierta en dos tipos de acciones, A y B. Las de tipo A tienen más riesgo pero producen un beneficio
PROGRAMACIÓN LINEAL 1. A una persona le tocan 10 millones de pesos en una lotería y le aconsejan que las invierta en dos tipos de acciones, A y B. Las de tipo A tienen más riesgo pero producen un beneficio
Programación lineal. 1º) En la región del plano determinada por, hallar las
 Programación lineal 1º) En la región del plano determinada por, hallar las coordenadas de los puntos en los que la función alcanza su valor mínimo y máximo. Máximo en el punto y mínimo en el punto. 2º)
Programación lineal 1º) En la región del plano determinada por, hallar las coordenadas de los puntos en los que la función alcanza su valor mínimo y máximo. Máximo en el punto y mínimo en el punto. 2º)
1º Dibuja las regiones factibles definidas por los siguientes sistemas:
 Departamento de Matemáticas 2º de bachillerato Matemáticas II aplicadas a las Ciencias Sociales Tema 3: Programación lineal. 1º Dibuja las regiones factibles definidas por los siguientes sistemas: 0,3
Departamento de Matemáticas 2º de bachillerato Matemáticas II aplicadas a las Ciencias Sociales Tema 3: Programación lineal. 1º Dibuja las regiones factibles definidas por los siguientes sistemas: 0,3
1.- Dibuja la región del plano determinada por estas desigualdades: Existe alguna restricción que se pueda suprimir sin que varíe la solución?
 HOJA DE EJERCICIOS 1.- Dibuja la región del plano determinada por estas desigualdades: x + y 4x + y 0 y 0 x + y 5, y calcula el máximo de la función F( x, y) = x + y en esta región. (Sol. (-1,4)). Existe
HOJA DE EJERCICIOS 1.- Dibuja la región del plano determinada por estas desigualdades: x + y 4x + y 0 y 0 x + y 5, y calcula el máximo de la función F( x, y) = x + y en esta región. (Sol. (-1,4)). Existe
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD OPCIÓN A
 a) (1 punto) Dada la matriz a 1 A, calcule el valor de a para que A a 0 sea la matriz nula. 1 1 t b) ( puntos) Dada la matriz M, calcule la matriz M M. 1 1 x 1 Sea la función f definida mediante f ( x).
a) (1 punto) Dada la matriz a 1 A, calcule el valor de a para que A a 0 sea la matriz nula. 1 1 t b) ( puntos) Dada la matriz M, calcule la matriz M M. 1 1 x 1 Sea la función f definida mediante f ( x).
SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE TRANSPORTE Y ASIGNACION.
 UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA DE LA PRODUCCIÓN INGENIERÍA INDUSTRIAL SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE
UNIVERSIDAD NACIONAL DE LA PLATA FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA DE LA PRODUCCIÓN INGENIERÍA INDUSTRIAL SOLUCION DE MODELOS DE PROGRAMACION LINEAL EN UNA HOJA DE CALCULO. PROBLEMAS DE
Tipo de máquina Tiempo disponible. (h/maq. Por semana) Fresadora 500 Torno 350 Rectificadora 150
 Ejercicios Tema 1. 1.- Utilizar el procedimiento gráfico para resolver los siguientes P.L. a) Max z = 10x 1 + 20x 2 s.a x 1 + 2x 2 15 x 1 + x 2 12 5x 1 + 3x 2 45 x 1,x 2 0 b) Max z = 2x 1 + x 2 s.a. x
Ejercicios Tema 1. 1.- Utilizar el procedimiento gráfico para resolver los siguientes P.L. a) Max z = 10x 1 + 20x 2 s.a x 1 + 2x 2 15 x 1 + x 2 12 5x 1 + 3x 2 45 x 1,x 2 0 b) Max z = 2x 1 + x 2 s.a. x
Análisis de los datos
 Universidad Complutense de Madrid CURSOS DE FORMACIÓN EN INFORMÁTICA Análisis de los datos Hojas de cálculo Tema 6 Análisis de los datos Una de las capacidades más interesantes de Excel es la actualización
Universidad Complutense de Madrid CURSOS DE FORMACIÓN EN INFORMÁTICA Análisis de los datos Hojas de cálculo Tema 6 Análisis de los datos Una de las capacidades más interesantes de Excel es la actualización
Unidad 4 Programación lineal
 Unidad 4 Programación lineal PÁGINA 79 SOLUCIONES 1. Las regiones quedan: a) b) 2. El sistema pedido es: x y > 1 2x + y < 7 y > 1 1 PÁGINA 91 SOLUCIONES 1. Sumando los kilos de todos los sacos, obtenemos
Unidad 4 Programación lineal PÁGINA 79 SOLUCIONES 1. Las regiones quedan: a) b) 2. El sistema pedido es: x y > 1 2x + y < 7 y > 1 1 PÁGINA 91 SOLUCIONES 1. Sumando los kilos de todos los sacos, obtenemos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2002 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2002 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
UNIVERSIDAD DE OCCIDENTE
 UNIVERSIDAD DE OCCIDENTE UDO - ESTELI Por la Excelencia Académica Carrera: Ingeniería en Computación y Sistemas Nombre de la asignatura: Métodos de Optimización I Año académico: Quinto año Cuatrimestre:
UNIVERSIDAD DE OCCIDENTE UDO - ESTELI Por la Excelencia Académica Carrera: Ingeniería en Computación y Sistemas Nombre de la asignatura: Métodos de Optimización I Año académico: Quinto año Cuatrimestre:
ÁLGEBRA 2º Ciencias Sociales PAU- LOGSE
 . (Jun. 205 Opción A) Dadas las matrices A = ( a 2 + 2 2 ), B = ( ) y C = (c 0 0 b 0 c ) Calcula las matrices A B y B C. Calcula los valores de a, b y c que cumplen A B B C. Sol.- 2. (Jun. 205 Opción B)
. (Jun. 205 Opción A) Dadas las matrices A = ( a 2 + 2 2 ), B = ( ) y C = (c 0 0 b 0 c ) Calcula las matrices A B y B C. Calcula los valores de a, b y c que cumplen A B B C. Sol.- 2. (Jun. 205 Opción B)
UTILIDAD BRUTA, GASTOS Y UTILIDAD NETA MARGEN BRUTO
 UTILIDAD BRUTA, GASTOS Y UTILIDAD NETA MARGEN BRUTO Margen y alza se aplican a lo que un operador de tienda produce en una sola venta de un solo artículo. Margen Bruto y Utilidad Bruta se refieren a lo
UTILIDAD BRUTA, GASTOS Y UTILIDAD NETA MARGEN BRUTO Margen y alza se aplican a lo que un operador de tienda produce en una sola venta de un solo artículo. Margen Bruto y Utilidad Bruta se refieren a lo
Modelo 2014. Problema 2A.- Septiembre 2012. Ejercicio 1A. Septiembre 2010. F.M. Ejercicio 1A. Septiembre 2010. F.G. Ejercicio 1B.
 Modelo 2014. Problema 2A.- (Calificación máxima: 2 puntos) Un astillero recibe un encargo para reparar barcos de la flota de un armador, compuesta por pesqueros de 500 toneladas y yates de 100 toneladas.
Modelo 2014. Problema 2A.- (Calificación máxima: 2 puntos) Un astillero recibe un encargo para reparar barcos de la flota de un armador, compuesta por pesqueros de 500 toneladas y yates de 100 toneladas.
Ejercicios y problemas
 Ejercicios problemas Problemas 28. Un granjero desea crear una granja de pollos de dos razas,a B. Dispone de 9 000 para invertir de un espacio con una capacidad limitada para 7 000 pollos. Cada pollo de
Ejercicios problemas Problemas 28. Un granjero desea crear una granja de pollos de dos razas,a B. Dispone de 9 000 para invertir de un espacio con una capacidad limitada para 7 000 pollos. Cada pollo de
Colección de Problemas IV
 1.- Una compañía se dedica a la elaboración de 2 productos, la demanda de estos productos es de 200 unidades para cada uno de ellos. La compañía podrá elaborar los productos o comprarlos a un proveedor.
1.- Una compañía se dedica a la elaboración de 2 productos, la demanda de estos productos es de 200 unidades para cada uno de ellos. La compañía podrá elaborar los productos o comprarlos a un proveedor.
PPL PARA RESOLVER CON SOLVE
 PPL PARA RESOLVER CON SOLVE 1. Una compañía posee dos minas: la mina A produce cada día 1 tonelada de hierro de alta calidad, 3 toneladas de calidad media y 5 de baja calidad. La mina B produce cada día
PPL PARA RESOLVER CON SOLVE 1. Una compañía posee dos minas: la mina A produce cada día 1 tonelada de hierro de alta calidad, 3 toneladas de calidad media y 5 de baja calidad. La mina B produce cada día
Matemáticas aplicadas a las ciencias sociales II PL
 Matemáticas aplicadas a las ciencias sociales II PL 1) Una imprenta local edita periódicos y revistas. Para cada periódico necesita un cartucho de tinta negra y otro de color, y para cada revista uno de
Matemáticas aplicadas a las ciencias sociales II PL 1) Una imprenta local edita periódicos y revistas. Para cada periódico necesita un cartucho de tinta negra y otro de color, y para cada revista uno de
4.3 INTERPRETACIÓN ECONÓMICA DE LA DUALIDAD
 4.3 INTERPRETACIÓN ECONÓMICA DE LA DUALIDAD El problema de programación lineal se puede considerar como modelo de asignación de recursos, en el que el objetivo es maximizar los ingresos o las utilidades,
4.3 INTERPRETACIÓN ECONÓMICA DE LA DUALIDAD El problema de programación lineal se puede considerar como modelo de asignación de recursos, en el que el objetivo es maximizar los ingresos o las utilidades,
Problemas de Investigación Operativa y Programación Matemática
 Problemas de Investigación Operativa y Programación Matemática Omar J. Casas López Septiembre 2002 Tema I : Introducción 1. Una factoría fabrica dos tipos de productos, A y B. Para su elaboración se requieren
Problemas de Investigación Operativa y Programación Matemática Omar J. Casas López Septiembre 2002 Tema I : Introducción 1. Una factoría fabrica dos tipos de productos, A y B. Para su elaboración se requieren
5. [2012] [EXT-A] Se estima que el beneficio anual B(t), en %, que produce cierta inversión viene determinado por el tiempo t en
![5. [2012] [EXT-A] Se estima que el beneficio anual B(t), en %, que produce cierta inversión viene determinado por el tiempo t en 5. [2012] [EXT-A] Se estima que el beneficio anual B(t), en %, que produce cierta inversión viene determinado por el tiempo t en](/thumbs/27/11076258.jpg) . [204] [ET-A] Dada la función f(x) = x2-8x+6 x 2-8x+5 a) Su dominio y puntos de corte con los ejes. -x+5, 0 x 2. [204] [JUN-A] En una sesión, el valor de cierta acción, en euros, vino dado por la función:
. [204] [ET-A] Dada la función f(x) = x2-8x+6 x 2-8x+5 a) Su dominio y puntos de corte con los ejes. -x+5, 0 x 2. [204] [JUN-A] En una sesión, el valor de cierta acción, en euros, vino dado por la función:
EJERCICIOS METODO SIMPLEX
 EJERCICIOS METODO SIMPLEX 1. Un empresario pretende fabricar dos tipos de congeladores denominados A y B. Cada uno de ellos debe pasar por tres operaciones antes de su comercialización: Ensamblaje, pintado
EJERCICIOS METODO SIMPLEX 1. Un empresario pretende fabricar dos tipos de congeladores denominados A y B. Cada uno de ellos debe pasar por tres operaciones antes de su comercialización: Ensamblaje, pintado
Tema 1. - SISTEMAS DE ECUACIONES.
 Matemáticas aplicadas CCSS. Ejercicios modelo Selectividad - Tema. - SISTEMAS DE ECUACIONES. Ejercicio. ( ) a) ( puntos) Determine dos números sabiendo que al dividir el mayor por el menor obtenemos 7
Matemáticas aplicadas CCSS. Ejercicios modelo Selectividad - Tema. - SISTEMAS DE ECUACIONES. Ejercicio. ( ) a) ( puntos) Determine dos números sabiendo que al dividir el mayor por el menor obtenemos 7
1. Cortar y teñir el material 2. Coser 3. Terminar (insertar el porta sombrilla, los separadores de palos, etc.) 4. Inspeccionar y embalar
 UN PROBLEMA SENCILLO DE MAXIMIZACION La compañía Par, Inc. Es un pequeño fabricante de equipo y accesorios para golf cuyos administradores han decidido incursionar en el mercado de las bolsas para bastones
UN PROBLEMA SENCILLO DE MAXIMIZACION La compañía Par, Inc. Es un pequeño fabricante de equipo y accesorios para golf cuyos administradores han decidido incursionar en el mercado de las bolsas para bastones
PROGRAMACIÓN LINEAL Teoría General de Programación Lineal y Fase de Formulación y Construcción de Modelos.
 PROGRAMACIÓN LINEAL Objetivo: Proponer en forma cuantitativa acciones o decisiones a tomar para optimizar sistemas donde existan recursos escasos y se presenten relaciones lineales, mediante la teoría
PROGRAMACIÓN LINEAL Objetivo: Proponer en forma cuantitativa acciones o decisiones a tomar para optimizar sistemas donde existan recursos escasos y se presenten relaciones lineales, mediante la teoría
SISTEMAS DE ECUACIONES LINEALES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS
 1 SISTEMAS DE ECUACIONES LINEALES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS 102. PAU Universidad de Oviedo Fase General OPCIÓN A junio 2010 Dos amigos, Ana y Nicolás, tienen en total 60 euros. Además se
1 SISTEMAS DE ECUACIONES LINEALES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS 102. PAU Universidad de Oviedo Fase General OPCIÓN A junio 2010 Dos amigos, Ana y Nicolás, tienen en total 60 euros. Además se
1.2 SISTEMAS DE PRODUCCIÓN
 19 1.2 SISTEMAS DE PRODUCCIÓN Para operar en forma efectiva, una empresa manufacturera debe tener sistemas que le permitan lograr eficientemente el tipo de producción que realiza. Los sistemas de producción
19 1.2 SISTEMAS DE PRODUCCIÓN Para operar en forma efectiva, una empresa manufacturera debe tener sistemas que le permitan lograr eficientemente el tipo de producción que realiza. Los sistemas de producción
Unidad 1 Modelos de programación lineal
 Unidad 1 Modelos de programación lineal La programación lineal comenzó a utilizarse prácticamente en 1950 para resolver problemas en los que había que optimizar el uso de recursos escasos. Fueron de los
Unidad 1 Modelos de programación lineal La programación lineal comenzó a utilizarse prácticamente en 1950 para resolver problemas en los que había que optimizar el uso de recursos escasos. Fueron de los
Programación Lineal. Ejercicio nº 1.- a) Representa gráficamente las soluciones de la inecuación: 2x y 3
 Programación Lineal Ejercicio nº.- a) Representa gráficamente las soluciones de la inecuación: b) Averigua cuál es la inecuación cuas soluciones corresponden al siguiente semiplano: Ejercicio nº.- a) Representa
Programación Lineal Ejercicio nº.- a) Representa gráficamente las soluciones de la inecuación: b) Averigua cuál es la inecuación cuas soluciones corresponden al siguiente semiplano: Ejercicio nº.- a) Representa
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 PROGRAMACIÓNLINEAL 1.0septiembre1995 UnaempresadeautomóvilestienedosplantasPyQdemontajedevehículosenlasqueproducetresmodelosA,ByC.Dela plantapsalensemanalmente10unidadesdelmodeloa,30delby15delc,ydelaq,20unidadesdelmodeloa,20delby70del
PROGRAMACIÓNLINEAL 1.0septiembre1995 UnaempresadeautomóvilestienedosplantasPyQdemontajedevehículosenlasqueproducetresmodelosA,ByC.Dela plantapsalensemanalmente10unidadesdelmodeloa,30delby15delc,ydelaq,20unidadesdelmodeloa,20delby70del
TRABAJO PRÁCTICO. Destinos 1 2 3 Oferta (u.) A 10 8 4 45 B 9 5 7 50 C 3 6 9 45 D 5 7 6 30 Demanda (u.) 90 30 50
 1 TRABAJO PRÁCTICO TEMA:TEORÍA DE TRANSPORTE Y ASIGNACIÓN PERSONAL 1) Una empresa tiene tres fábricas en distintos lugares del país que abastecen a 5 puestos minoristas. Los costos de envío de 1 Tn. de
1 TRABAJO PRÁCTICO TEMA:TEORÍA DE TRANSPORTE Y ASIGNACIÓN PERSONAL 1) Una empresa tiene tres fábricas en distintos lugares del país que abastecen a 5 puestos minoristas. Los costos de envío de 1 Tn. de
CAPÍTULO 3. HERRAMIENTA DE SOFTWARE DE PLANEACIÓN DE
 CAPÍTULO 3. HERRAMIENTA DE SOFTWARE DE PLANEACIÓN DE INVENTARIO Y PROCESO Objetivos del capítulo Desarrollar una herramienta de software de planeación de inventario con los datos obtenidos del capítulo
CAPÍTULO 3. HERRAMIENTA DE SOFTWARE DE PLANEACIÓN DE INVENTARIO Y PROCESO Objetivos del capítulo Desarrollar una herramienta de software de planeación de inventario con los datos obtenidos del capítulo
Unidad 7 Aplicación de máximos y mínimos
 Unidad 7 Aplicación de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Interpretará el concepto de ingreso y costos marginal. Aplicará la función de ingresos en problemas de maimización. Aplicará
Unidad 7 Aplicación de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Interpretará el concepto de ingreso y costos marginal. Aplicará la función de ingresos en problemas de maimización. Aplicará
DIRECCIÓN FINANCIERA Y CONTROL DE GESTIÓN
 APARTADO 5: Gestión de la cadena DIAPOSITIVA Nº: 11 EJERCICIO RESUELTO Nº 1: CASO PRÁCTICO Empresa ALMA CASO PRÁCTICO Empresa ALMA La empresa ALMA, S.A. se dedica a la fabricación y comercialización de
APARTADO 5: Gestión de la cadena DIAPOSITIVA Nº: 11 EJERCICIO RESUELTO Nº 1: CASO PRÁCTICO Empresa ALMA CASO PRÁCTICO Empresa ALMA La empresa ALMA, S.A. se dedica a la fabricación y comercialización de
Ejercicios resueltos de Programación Lineal
 Investigación Operativa I 009 Ejercicios resueltos de Programación Lineal Mauricio estrella Erika Beatriz Palacin Palacios Pajuelo Daniel PREGUNTA Ingeniería de Sistemas y Computación UNDAC 3..6 la empresa
Investigación Operativa I 009 Ejercicios resueltos de Programación Lineal Mauricio estrella Erika Beatriz Palacin Palacios Pajuelo Daniel PREGUNTA Ingeniería de Sistemas y Computación UNDAC 3..6 la empresa
GESTIÓN DE DEMANDA: SISTEMAS DE TARIFICACIÓN DE SERVICIOS
 GESTIÓN DE DEMANDA: SISTEMAS DE TARIFICACIÓN DE SERVICIOS La tarificación es un instrumento muy común que genera eficiencia en la gestión de demanda de servicios públicos como la electricidad, el abastecimiento
GESTIÓN DE DEMANDA: SISTEMAS DE TARIFICACIÓN DE SERVICIOS La tarificación es un instrumento muy común que genera eficiencia en la gestión de demanda de servicios públicos como la electricidad, el abastecimiento
MA4011: Modelación y Optimización EjemplosProfr. Eduardo Uresti, Agosto-Diciembre 2010
 MA4011: Modelación y Optimización EjemplosProfr. Eduardo Uresti, Agosto-Diciembre 2010 1. Un fabricante produce semanalmente un solo artículo para dos clientes. Este artículo es un insumo para ambos clientes
MA4011: Modelación y Optimización EjemplosProfr. Eduardo Uresti, Agosto-Diciembre 2010 1. Un fabricante produce semanalmente un solo artículo para dos clientes. Este artículo es un insumo para ambos clientes
www.aulamatematica.com
 www.aulamatematica.com APLIICACIIÓN DE DERIIVADAS:: PROBLEMAS DE OPTIIMIIZACIIÓN CON 1 VARIIABLE.. 004 Los costes de fabricación C(x) en euros de cierta variedad de galletas dependen de la cantidad elaborada
www.aulamatematica.com APLIICACIIÓN DE DERIIVADAS:: PROBLEMAS DE OPTIIMIIZACIIÓN CON 1 VARIIABLE.. 004 Los costes de fabricación C(x) en euros de cierta variedad de galletas dependen de la cantidad elaborada
Unidad 2 Método gráfico de solución
 Unidad 2 Método gráfico de solución Los problemas de programación lineal (pl) que sólo tengan dos variables de decisión pueden resolverse gráficamente, ya que, como se ha visto en los Antecedentes, una
Unidad 2 Método gráfico de solución Los problemas de programación lineal (pl) que sólo tengan dos variables de decisión pueden resolverse gráficamente, ya que, como se ha visto en los Antecedentes, una
LOGISTICA D E COMPRAS
 LOGISTICA D E COMPRAS 1. - Concepto de compras OBTENER EL (LOS) PRODUCTO(S) O SERVICIO(S) DE LA CALIDAD ADECUADA, CON EL PRECIO JUSTO, EN EL TIEMPO INDICADO Y EN EL LUGAR PRECISO. Muchas empresas manejan
LOGISTICA D E COMPRAS 1. - Concepto de compras OBTENER EL (LOS) PRODUCTO(S) O SERVICIO(S) DE LA CALIDAD ADECUADA, CON EL PRECIO JUSTO, EN EL TIEMPO INDICADO Y EN EL LUGAR PRECISO. Muchas empresas manejan
TEMA 4: PROPORCIONALIDAD Y PORCENTAJES
 TEMA : PROPORCIONALIDAD Y PORCENTAJES.1Razones y proporciones Página 90 ejercicio 1 Elige la respuesta correcta en cada caso: a) La razón de 5 y15 es: 1 2, 1 3, 2 3 5 15 15 5 5 5 1 3 Tareas 05-12-12: todos
TEMA : PROPORCIONALIDAD Y PORCENTAJES.1Razones y proporciones Página 90 ejercicio 1 Elige la respuesta correcta en cada caso: a) La razón de 5 y15 es: 1 2, 1 3, 2 3 5 15 15 5 5 5 1 3 Tareas 05-12-12: todos
CAPITULO IV DESARROLLO DEL MRP
 CAPITULO IV DESARROLLO DEL MRP 59 NATURALEZA DE LA PLANEACIÓN Y CONTROL Qué es la Planeación y el Control? Toda actividad productiva se desarrolla en base a operaciones que se diseñan y supervisan en diferentes
CAPITULO IV DESARROLLO DEL MRP 59 NATURALEZA DE LA PLANEACIÓN Y CONTROL Qué es la Planeación y el Control? Toda actividad productiva se desarrolla en base a operaciones que se diseñan y supervisan en diferentes
El fabricante desea planificar el proceso de producción y para ello establece las siguientes metas ordenadas por orden de importancia:
 Titulación: Ingeniero en Organización Industrial Asignatura: Investigación Operativa Curso: 2010/2011 RECOPILACIÓN EXÁMENES PRÁCTICAS Programación Multiobjetivo 1. [JUNIO 2010] (4.5 puntos) En el proceso
Titulación: Ingeniero en Organización Industrial Asignatura: Investigación Operativa Curso: 2010/2011 RECOPILACIÓN EXÁMENES PRÁCTICAS Programación Multiobjetivo 1. [JUNIO 2010] (4.5 puntos) En el proceso
Trabajo Práctico con ejercicios de repaso
 1 Trabajo Práctico con ejercicios de repaso Asignatura: Investigación Operativa Tema: Programación Lineal Luego de haber resuelto los ejercicios propuestos por la Cátedra, te ofrecemos una serie de problemas
1 Trabajo Práctico con ejercicios de repaso Asignatura: Investigación Operativa Tema: Programación Lineal Luego de haber resuelto los ejercicios propuestos por la Cátedra, te ofrecemos una serie de problemas
Tema 4: Problemas Aritméticos
 Tema 4: Problemas Aritméticos 4.1 Proporcionalidad simple. Vamos a en primer lugar a responder a dos preguntas: Cuándo se dice que dos magnitudes son directamente proporcionales? Se dice que son directamente
Tema 4: Problemas Aritméticos 4.1 Proporcionalidad simple. Vamos a en primer lugar a responder a dos preguntas: Cuándo se dice que dos magnitudes son directamente proporcionales? Se dice que son directamente
EL PROGRAMA DE AUTOENVÍO DE JEUNESSE : AYUDÁNDOLE A HACER CRECER SU NEGOCIO
 EL PROGRAMA DE AUTOENVÍO DE JEUNESSE : AYUDÁNDOLE A HACER CRECER SU NEGOCIO El programa de Autoenvío de Jeunesse juega un papel crucial en ayudarle a hacer crecer su negocio. Para poder ganar Comisiones
EL PROGRAMA DE AUTOENVÍO DE JEUNESSE : AYUDÁNDOLE A HACER CRECER SU NEGOCIO El programa de Autoenvío de Jeunesse juega un papel crucial en ayudarle a hacer crecer su negocio. Para poder ganar Comisiones
Matemáticas y Problemas de Lógica
 Capitulo Cinco Segunda Lección Matemáticas y Problemas de Lógica Conceptos y Habilidades Tratados: Aritmética Materiales Necesarios: Papel Lápiz o pluma Materiales Provistos: Problemas en formato de redacción
Capitulo Cinco Segunda Lección Matemáticas y Problemas de Lógica Conceptos y Habilidades Tratados: Aritmética Materiales Necesarios: Papel Lápiz o pluma Materiales Provistos: Problemas en formato de redacción
Ecuaciones Problemas Ejercicios resueltos
 Ecuaciones Problemas Ejercicios resueltos 1. En el siguiente dibujo todos los autos son iguales: Determinar el largo de cada auto. Sea x el largo de cada auto. De acuerdo a la figura, la ecuación que modela
Ecuaciones Problemas Ejercicios resueltos 1. En el siguiente dibujo todos los autos son iguales: Determinar el largo de cada auto. Sea x el largo de cada auto. De acuerdo a la figura, la ecuación que modela
2) Se ha considerado únicamente la mano de obra, teniéndose en cuenta las horas utilizadas en cada actividad por unidad de página.
 APLICACIÓN AL PROCESO PRODUCTIVO DE LA EMPRESA "F. G. / DISEÑO GRÁFICO". AÑO 2004 Rescala, Carmen Según lo explicado en el Informe del presente trabajo, la variación en la producción de páginas web de
APLICACIÓN AL PROCESO PRODUCTIVO DE LA EMPRESA "F. G. / DISEÑO GRÁFICO". AÑO 2004 Rescala, Carmen Según lo explicado en el Informe del presente trabajo, la variación en la producción de páginas web de
GUIA DE EJERCICIOS. d) 12x - 9y + 2 = 0 e) 2x+ y - 6 = 0
 ECUACIÓN DE LA RECTA Y PENDIENTE GUIA DE EJERCICIOS ) Encontrar la pendiente de la recta determinada por cada uno de los guientes pares de números: a) (, ) y (5, ) b) (, -3) y (-, ) c) (, 6) y (8, 56)
ECUACIÓN DE LA RECTA Y PENDIENTE GUIA DE EJERCICIOS ) Encontrar la pendiente de la recta determinada por cada uno de los guientes pares de números: a) (, ) y (5, ) b) (, -3) y (-, ) c) (, 6) y (8, 56)
Por qué Invertir en Tecnología: Criterios Objetivos para Analizar el Ahorro de Costes de la Inversión
 Por qué Invertir en Tecnología: Criterios Objetivos para Analizar el Ahorro de Costes de la Inversión En estos tiempos de incertidumbre por la situación económica actual, ante la disyuntiva de realizar
Por qué Invertir en Tecnología: Criterios Objetivos para Analizar el Ahorro de Costes de la Inversión En estos tiempos de incertidumbre por la situación económica actual, ante la disyuntiva de realizar
de la empresa Al finalizar la unidad, el alumno:
 de la empresa Al finalizar la unidad, el alumno: Identificará el concepto de rentabilidad. Identificará cómo afecta a una empresa la rentabilidad. Evaluará la rentabilidad de una empresa, mediante la aplicación
de la empresa Al finalizar la unidad, el alumno: Identificará el concepto de rentabilidad. Identificará cómo afecta a una empresa la rentabilidad. Evaluará la rentabilidad de una empresa, mediante la aplicación
5: LA FUNCIÓN PRODUCTIVA DE LA EMPRESA
 5: LA FUNCIÓN PRODUCTIVA DE LA EMPRESA 1. EL ÁREA DE PRODUCCIÓN DE LA EMPRESA: PRODUCIR: consiste en incrementar la utilidad de los bienes para satisfacer necesidades humanas. Ello implica realizar todas
5: LA FUNCIÓN PRODUCTIVA DE LA EMPRESA 1. EL ÁREA DE PRODUCCIÓN DE LA EMPRESA: PRODUCIR: consiste en incrementar la utilidad de los bienes para satisfacer necesidades humanas. Ello implica realizar todas
Selectividad Junio 2008 JUNIO 2008 PRUEBA A
 Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES
 PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
XI OLIMPIADA PRIMARIATHALES FASE COMARCAL RECICLAMOS, REUTILIZAMOS,..
 RECICLAMOS, REUTILIZAMOS, REDUCIMOS CONTAMINACIÓN Con este problema te proponemos trabajar con unos acompañantes que siempre tenemos cerca, los vemos todos los días en las papeleras de la clase, de nuestra
RECICLAMOS, REUTILIZAMOS, REDUCIMOS CONTAMINACIÓN Con este problema te proponemos trabajar con unos acompañantes que siempre tenemos cerca, los vemos todos los días en las papeleras de la clase, de nuestra
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 4 Pág. Página 60 FRIGORÍFICO 480 FACILIDADES DE PAGO EN TODOS LOS ARTÍCULOS: 25% A LA ENTREGA RESTO: EN 2 MENSUALIDADES SIN RECARGO En esta unidad vas a revisar algunas técnicas y razonamientos que se
4 Pág. Página 60 FRIGORÍFICO 480 FACILIDADES DE PAGO EN TODOS LOS ARTÍCULOS: 25% A LA ENTREGA RESTO: EN 2 MENSUALIDADES SIN RECARGO En esta unidad vas a revisar algunas técnicas y razonamientos que se
GUÍA PARA LAS FAMILIAS To Para Obtener Asistencia Financiera
 GUÍA PARA LAS FAMILIAS To Para Obtener Asistencia Financiera sss.nais.org/parents GUÍA PARA LAS FAMILIAS Para obtener asistencia financiera Haciendo que la educación independiente sea una realidad. Usted
GUÍA PARA LAS FAMILIAS To Para Obtener Asistencia Financiera sss.nais.org/parents GUÍA PARA LAS FAMILIAS Para obtener asistencia financiera Haciendo que la educación independiente sea una realidad. Usted
5.4 Una flecha será ensamblada en un cojinete como se muestra a continuación.
 PROBLEMAS 5.1. El famoso juego 7-11, requiere que el jugador lance dos dados una v. más veces hasta tomar la decisión de que se gana o se pierde el juego. El juego se gana si en el primer lanzamiento los
PROBLEMAS 5.1. El famoso juego 7-11, requiere que el jugador lance dos dados una v. más veces hasta tomar la decisión de que se gana o se pierde el juego. El juego se gana si en el primer lanzamiento los
GUÍA PARA LAS FAMILIAS
 GUÍA PARA LAS FAMILIAS Para Obtener Asistencia Financiera Hacer de la educación independiente una realidad. Usted ha tomado la decisión de invertir en una educación independiente para su hijo. La educación
GUÍA PARA LAS FAMILIAS Para Obtener Asistencia Financiera Hacer de la educación independiente una realidad. Usted ha tomado la decisión de invertir en una educación independiente para su hijo. La educación
Listado de Trabajo TRANSPORTE
 Listado de Trabajo TRANSPORTE Problema 1 Una compañía de servicios Informáticos, recibe pedidos de sus productos desde tres diferentes ciudades, en las siguientes cantidades: La ciudad A pide 18 Pc portatiles.
Listado de Trabajo TRANSPORTE Problema 1 Una compañía de servicios Informáticos, recibe pedidos de sus productos desde tres diferentes ciudades, en las siguientes cantidades: La ciudad A pide 18 Pc portatiles.
Programación lineal. Observación: La mayoría de estos problemas se han propuesto en exámenes de selectividad
 1 Observación: La mayoría de estos problemas se han propuesto en exámenes de selectividad 1. Dibuja la región del plano definida por las siguientes inecuaciones: x 0, 0 y 2, y + 2x 4 Representando las
1 Observación: La mayoría de estos problemas se han propuesto en exámenes de selectividad 1. Dibuja la región del plano definida por las siguientes inecuaciones: x 0, 0 y 2, y + 2x 4 Representando las
Guía de Ejercicios. Matemática 11
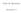 Guía de Ejercicios Matemática 11 Matemática 11 Resolver: 1) 5 + 3x 31 3x 5) 3(2x 1) > 4+5(x 1) 6) x + 4 3 > 2x 3 +1 4 1 7) 4 (2x 1) x
Guía de Ejercicios Matemática 11 Matemática 11 Resolver: 1) 5 + 3x 31 3x 5) 3(2x 1) > 4+5(x 1) 6) x + 4 3 > 2x 3 +1 4 1 7) 4 (2x 1) x
Resortes y fuerzas. Analiza la siguiente situación. Ley de Hooke. 2do Medio > Física Ley de Hooke. Qué aprenderé?
 2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
EB-5 Visa $1,000,000 USD
 EB-5 Visa $1,000,000 USD Resumen Ejecutivo El solicitante de la Visa EB-5 debe invertir un mínimo de $ 1,000,000 USD. El nombre de la empresa, que es una obra en proceso, ABC, LLC fue creada específicamente
EB-5 Visa $1,000,000 USD Resumen Ejecutivo El solicitante de la Visa EB-5 debe invertir un mínimo de $ 1,000,000 USD. El nombre de la empresa, que es una obra en proceso, ABC, LLC fue creada específicamente
SISTEMA CON UN SERVIDOR
 TALLER 6 : Problemas de Líneas de Espera. 1.SISTEMA CON UN SERVIDOR. Una compañía estatal tiene un numero de estaciones para el pesado de camiones a lo largo de una gran autopista, para verificar que el
TALLER 6 : Problemas de Líneas de Espera. 1.SISTEMA CON UN SERVIDOR. Una compañía estatal tiene un numero de estaciones para el pesado de camiones a lo largo de una gran autopista, para verificar que el
CAPITULO VI ESTRATEGIAS DE OUTSOURCING
 CAPITULO VI ESTRATEGIAS DE OUTSOURCING Cuando una compañía decide llevar a cabo un proceso de outsourcing debe definir una estrategia que guíe todo el proceso. Hay dos tipos genéricos de estrategia de
CAPITULO VI ESTRATEGIAS DE OUTSOURCING Cuando una compañía decide llevar a cabo un proceso de outsourcing debe definir una estrategia que guíe todo el proceso. Hay dos tipos genéricos de estrategia de
Administración Logística de Materiales
 Administración Logística de Materiales Para un mejor conocimiento de la industria acerca de distribución física, manufactura y compras, se estableció el programa de administración logística de materiales.
Administración Logística de Materiales Para un mejor conocimiento de la industria acerca de distribución física, manufactura y compras, se estableció el programa de administración logística de materiales.
PCGeek. Descripción del problema
 PCGeek Descripción del problema Ejercicio de Ingeniería del Software I Ejercicio de Ingeniería del Software I Página 1 de 9 1 Introducción... 3 1.1 Organización de la empresa... 3 2 Gestión del almacén...
PCGeek Descripción del problema Ejercicio de Ingeniería del Software I Ejercicio de Ingeniería del Software I Página 1 de 9 1 Introducción... 3 1.1 Organización de la empresa... 3 2 Gestión del almacén...
Colegio Portocarrero. Curso 2014-2015. Departamento de matemáticas. Repaso de todo. Con solución
 Repaso de todo Con solución Gauss, matrices, programación lineal, límites, continuidad, asíntotas, cálculo de derivadas. Problema 1: En una confiteria se dispone de 24 kg de polvorones y 15 kg de mantecados,
Repaso de todo Con solución Gauss, matrices, programación lineal, límites, continuidad, asíntotas, cálculo de derivadas. Problema 1: En una confiteria se dispone de 24 kg de polvorones y 15 kg de mantecados,
Obesidad y las dietas
 Obesidad y las dietas Qué es una dieta? Qué dieta es la recomendable para mí? Quién debe indicarla? Cuánto tiempo debo seguirla? INTRODUCCIÓN La obesidad es un problema de salud a nivel mundial. Durante
Obesidad y las dietas Qué es una dieta? Qué dieta es la recomendable para mí? Quién debe indicarla? Cuánto tiempo debo seguirla? INTRODUCCIÓN La obesidad es un problema de salud a nivel mundial. Durante
Introducción a las redes de computadores
 Introducción a las redes de computadores Contenido Descripción general 1 Beneficios de las redes 2 Papel de los equipos en una red 3 Tipos de redes 5 Sistemas operativos de red 7 Introducción a las redes
Introducción a las redes de computadores Contenido Descripción general 1 Beneficios de las redes 2 Papel de los equipos en una red 3 Tipos de redes 5 Sistemas operativos de red 7 Introducción a las redes
PROBLEMAS DE PROGRAMACIÓN LINEAL
 PROBLEMAS DE PROGRAMACIÓN LINEAL A.- Problemas generales B.- Problemas con porcentajes C.- Problemas de dietas D.- Problemas para profundizar A.- PROBLEMAS GENERALES Ejercicio 1.- En una fábrica se construyen
PROBLEMAS DE PROGRAMACIÓN LINEAL A.- Problemas generales B.- Problemas con porcentajes C.- Problemas de dietas D.- Problemas para profundizar A.- PROBLEMAS GENERALES Ejercicio 1.- En una fábrica se construyen
BREVE MANUAL DE SOLVER
 BREVE MANUAL DE SOLVER PROFESOR: DAVID LAHOZ ARNEDO PROGRAMACIÓN LINEAL Definición: Un problema se define de programación lineal si se busca calcular el máximo o el mínimo de una función lineal, la relación
BREVE MANUAL DE SOLVER PROFESOR: DAVID LAHOZ ARNEDO PROGRAMACIÓN LINEAL Definición: Un problema se define de programación lineal si se busca calcular el máximo o el mínimo de una función lineal, la relación
Buscando las soluciones óptimas (Una experienciacon alumnos de Estalmat-Canarias)
 Buscando las soluciones óptimas (Una experienciacon alumnos de Estalmat-Canarias) El objetivo de esta experiencia es iniciar de un modo práctico a estos alumnos en la interpretación gráfica y el manejo
Buscando las soluciones óptimas (Una experienciacon alumnos de Estalmat-Canarias) El objetivo de esta experiencia es iniciar de un modo práctico a estos alumnos en la interpretación gráfica y el manejo
Licencia. Todos los derechos reservados. Este reporte puede ser distribuido libremente pero queda
 Licencia copyright www.segurodevidaparapadres.com Todos los derechos reservados. Este reporte puede ser distribuido libremente pero queda estrictamente prohibida cualquier modificación del mismo. El contenido
Licencia copyright www.segurodevidaparapadres.com Todos los derechos reservados. Este reporte puede ser distribuido libremente pero queda estrictamente prohibida cualquier modificación del mismo. El contenido
SECADORA COMERCIAL DOBLE T-50X2 EXPRESS DE 50 LIBRAS DE CAPACIDAD EN CADA CANASTILLA
 SECADORA COMERCIAL DOBLE T-50X2 EXPRESS DE 50 LIBRAS DE CAPACIDAD EN CADA CANASTILLA Capacidad en peso ropa seca 2 x 50 libras(2 x 22.7 kg) Altura de gabinete 79 1/4 pulgadas(201.3 cm) Anchura de gabinete
SECADORA COMERCIAL DOBLE T-50X2 EXPRESS DE 50 LIBRAS DE CAPACIDAD EN CADA CANASTILLA Capacidad en peso ropa seca 2 x 50 libras(2 x 22.7 kg) Altura de gabinete 79 1/4 pulgadas(201.3 cm) Anchura de gabinete
Análisis e interpretación de estados financieros INTERPRETACIÓN DEL ANÁLISIS FINANCIERO
 INTERPRETACIÓN DEL ANÁLISIS FINANCIERO Método de razones simples, cálculo e interpretación de los indicadores 1 Liquidez 1. Capital neto de trabajo (CNT)=Activo circulante - Pasivo circulante. Se define
INTERPRETACIÓN DEL ANÁLISIS FINANCIERO Método de razones simples, cálculo e interpretación de los indicadores 1 Liquidez 1. Capital neto de trabajo (CNT)=Activo circulante - Pasivo circulante. Se define
PCLabs. Práctica de Ingeniería del Software I Curso 2008/09. Descripción del problema
 PCLabs Práctica de Ingeniería del Software I Curso 2008/09 Descripción del problema Introducción... 1 Organización de la empresa... 1 Gestión del almacén... 2 Gestión de pedidos de clientes... 3 Gestión
PCLabs Práctica de Ingeniería del Software I Curso 2008/09 Descripción del problema Introducción... 1 Organización de la empresa... 1 Gestión del almacén... 2 Gestión de pedidos de clientes... 3 Gestión
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. Página 4 En la última semana, los 0 monos de un parque natural han comido 0 kg de fruta. Acaban de traer monos más y disponemos de 080 kg de fruta. Para cuántos días tenemos? (Averigua previamente
Pág. Página 4 En la última semana, los 0 monos de un parque natural han comido 0 kg de fruta. Acaban de traer monos más y disponemos de 080 kg de fruta. Para cuántos días tenemos? (Averigua previamente
