SEMINARIO DE SISTEMAS DINÁMICOS. En torno a la fórmula de Pesin
|
|
|
- Javier Torres Cruz
- hace 5 años
- Vistas:
Transcripción
1 FACULTAD DE ATEÁTICAS PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE SEINARIO DE SISTEAS DINÁICOS En torno a la fórmula de Pesin Expositor: Felipe Riquelme Resumen El objetivo de este charla es estudiar relaciones entre la geometría de una variedad Riemanniana suave compacta, las propiedades ergódicas entregadas por un difeomorfismo de la variedad en sí misma. Nuestro punto de partida será el teorema de Oseledets, el cual nos proporciona una descomposición del espacio tangente en direcciones asintoticamente contractantes expansivas. A continuación, utilizando esta descomposición, buscaremos mesurar la entropía métrica respecto a medidas borelianas de probabilidad, invariantes por el difeomorfismo. Demostraremos usaremos la desigualdad de Ruelle para maorar la entropía métrica por un término que depende de los exponentes de Lapunov. Será de particular interés responder a la siguiente pregunta: Bajo qué condiciones existe igualdad en la desigualdad de Ruelle? Concluiremos la charla con una respuesta precisa, dando lugar entonces a la fórmula de Pesin.
2 . Preliminares.. Teorema de Oseledets Durante todo este documento, denotará una variedad Riemanniana compacta de clase C f : un difeomorfismo de clase C. Decimos que x es un punto regular de f si existen números λ x) >... > λ m x) subespacios vectoriales de T x, E x),..., E m x), tales que T x = E x)... E m x) lím n log D xf n )u = λ j x) para todo u E j x), no nulo, para todo j m. En tal caso, los números la descomposición son únicos, por lo que llamamos a los λ j x) exponentes de Lapunov a los espacios E j x) espacios característicos. Definición... Sea X un espacio métrico compacto T : X X una aplicación continua. Decimos que un conjunto medible Λ X es de medida total, si para toda medida µ T X) se tiene µλ) =. Una primera aproximación para entender la dinámica del difeomorfismo, desde la perspectiva de la teoría ergódica, está dada por el siguiente teorema Teorema..2. Teorema de Oseledets) El conjunto Λ de puntos regulares de f es un boreliano de medida total. ás aún, las funciones x λ j x), x dime j x)), definidas sobre Λ, son medibles. Recordemos que una medida µ f ) se dice ergódica si se satisface una de las siguientes propiedades equivalentes ) Si A es un conjunto medible, invariante por f, entonces µa) {0, }. 2) Si g : R es una función que satisface g = g f, entonces g es constante µ-c.t.p. Por lo que, luego de la definición de punto regular de f, las aplicaciones x λ j x) x dime j x)) son f-invariantes, luego constantes casi en todas partes) para medidas ergódicas en f ). Para concluir esta subsección, introduciremos una función que será fundamental a lo largo de toda este documento. Definimos χ : R como λ j x)dime j x)), si ha exponentes de Lapunov positivos χx) = λ jx)>0 0,en otro caso la cual es uniformemente acotada superiormente debido a la continuidad de norma de la diferencial de f sobre, la cual es una variedad compacta. Proposición..3. Sea x Λ E u x) = λ jx)>0 E jx). Entonces lím n log det D xf n ) E u x)) = λ jx)>0 λ j x)dime j x))
3 .2. Entropía Sean P Q dos particiones de, denotaremos por Px) al elemento átomo) de la partición P que contiene a x P Q la partición generada por P Q, es decir, que contiene a todas las intersecciones entre elementos de P Q. Definimos la entropía métrica de P respecto a la medida µ f ) como H µ P) = P P µp ) log µp ) la entropía de P relativa a Q como H µ P Q) = [ µq) ) ] µp Q) µp Q) log µq) µq) Q Q P P = ) µp Q) µp Q) log µq) P P,Q Q Bajo estas condiciones es posible probar que H µ P Q) = H µ Q) + H µ P Q). Decimos que P es más fina que Q si para todo elemento P de P existe un elemento Q de Q tal que P Q. Si P es más fina que otra partición R, entonces H µ P Q) H µ R Q) H µ Q P) H µ Q R). Definimos también la entropía de f relativa a P como h µ f, P) = lím n H µ n f j P. j=0 De lo anterior es posible mostrar que h µ f, P) = lím H µ n P f j P j= donde la secuencia {H µ P n j= f j P)} n es decreciente. Esto implica h µ f, P) H µ P f P). Finalmente definimos la entropía métrica de f como h µ f) = sup h µ f, P). P Un resultado que nos será útil es el siguiente. Consideremos una sucesión creciente de particiones P n ) n, tales que la σ-algebra generada por la unión de los elementos de las particiones P n es la σ-algebra boreliana, salvo por conjuntos de medida cero también conocida como sucesión generatriz). Entonces h µ f) = lím h µf, P n ). Otra forma de entender a la entropía métrica de una partición es la siguiente. Para una partición P se tiene H µ P) = log µpx))dµx). Si escribimos Pn a la particion n j=0 f j P, entonces tenemos la fórmula h µ f, P) = lím n log µpn x))dµx). El teorema de Shannon-cillan-Breiman asegura la convergencia en L de la sucesión de funciones /n log µp n x))) n N si la entropia métrica de P es finita. Esto implica que ) h µ f, P) = lím n log µpn x)) dµx). 2
4 2. Desigualdad de Ruelle Teorema Ruelle) Para toda medida µ f ) se tiene h µ f) χdµ ) La idea de la demostración consiste en trabajar sobre una sucesión generatriz de particiones adecuada, que permita medir el comportamiento de los exponentes de Lapunov. Ha tres pasos fundamentales, los cuales buscan maorar la entropía por términos que miden la dinámica aproximando linealmente. Demostración: La compacidad de permite reducirse al caso donde es una subvariedad inmersa isométricamente en R l. Afirmación : Existe una vecindad abierta U de un difeomorfismo f 0 : U f 0 U) U que extiende f que satisface D x f 0 )T x ) = T fx) ), D x f 0 ) Tx) /2 para todo x. En efecto, es cerrada en R l por lo que para cada R l existe x = π) en que verifica d, x) = d, ). Esto implica que pertenece al espacio afín T x ) ortogonal a T x que pasa por x. Escribimos entonces B ε T x ) ) como la bola de radio ε centrada en x contenida en ese espacio. Esto implica que para cada ε > 0, el conjunto ε = { R l d, ) < ε} es igual a ε = B ε T x ) ). x La continuidad del radio de inectividad de la exponencial normal sobre, la compacidad, permiten encontrar ε 0 > 0 tal que para todos x, x 2 distintos, se tiene B ε0 T x ) ) B ε0 T x2 ) ) =. La contrucción de f 0 resulta natural sobre el abierto ε0. Consideremos ahora la partición P n de R l, n, definida por los átomos de la forma donde q,..., q l ) Z l. q /n, q + )/n] q 2 /n, q 2 + )/n]... q l /n, q l + )/n] Afirmación 2: Podemos suponer que para todo n, P P n, se tiene µ P ) = 0. Consideremos un índice j fijo, x R notemos por T j x) la intersección de con el hiperplano definido por la ecuación x j = x. Escribimos Σ j = {x R µt j x)) 0}. Como µ es una medida de probabilidad, Σ j es a lo más numerable. Como R/Q es no numerable, podemos encontrar x = x,..., x l ) tal que para todo q Q todo j [, l], uno tenga µt j x j + q)) = 0. Si trasladamos de modo que x,..., x l ) sea el origen, entonces se tiene la afirmación buscada. La sucesión de particiones P n ) n genera entonces la tribu boreliana de, salvo por un conjunto de medida nula. Así, h µ f) = lím h µf, P n ). 3
5 Por otro lado, h µ f, P n ) H µ P n f P n )), entonces la concavidad de la función x logx) muestra H µ P n f µb f A)) µb f ) A)) P n )) = µa) log µa) µa) A P n B P n µa) log {B P n B f A) }. A P n Si escribimos ν f,n x) := {B P n B f A) } para x A, entonces h µ f, P n ) log ν f,n x)dµx). El teorema de convergencia dominada de Lebesgue muestra que para ν f x) = lím sup ν f,n x) se tiene h µ f) log ν f x)dµx). Si ahora consideramos f n prolongada por f0 n, la desigualdad anterior permanece siendo cierta, entonces h µ f) = n h µf n ) n log ν f nx)dµx). Como f0 n es un difeomorfismo sobre su imagen, entonces podemos usar la linearización de la aplicación para mostrar que, si Q 0 = [, ] l ν f nx) sup {P P + D x f0 n )Q 0 ) P }. Si considero un paralelepípedo Q que contiene a Q 0, el último término de la desigualdad anterior es maorado por ν f nx) sup {P P + D x f0 n )Q) P }. Afirmación 3: Si llamamos φa,..., a l ) el número maximal de átomos de P que pueden intersectar a un paralelepípedo de lados con largo a,..., a l, entonces φa,..., a l ) C a i> a i donde C es una constante que depende solo de l. La demostración de la afirmación anterior no es mu complicada de mostrar por lo que la asumiremos cierta. Consideremos entonces un paralelepípedo Q como antes donde los vectores {u,..., u l } que lo definen estén o bien en un espacio característico E i x) o bien en T x ). Esto implica que sup {P P + D x f n 0 )Q) P } C D xf n 0 )ui > D x f n 0 )u i por lo tanto lím sup n log ν f nx) λ ix)>0 λ i x)dime i x)) = χx). Nuevamente gracias al teorema de convergencia dominada de Lebesgue, es posible mostrar que h µ f) = lím n h µf n ) lím sup n log ν f nx)dµx) entonces h µ f) χx)dµx). 4
6 3. Teorema de Pesin Teorema Pesin) Sea una variedada Riemanniana compacta, de clase C f : un difeomorfismo de clase C +α, α > 0. Si µ f ) es absolutamente continua respecto a la medida de Lebesgue λ definida sobre, entonces h µ f) = χdµ 2) La demostración de este teorema consta esencialmente de dos etapas. Solo daremos un resumen de la prueba, dejando los detalles al lector. Primera Etapa: Consideremos µ f-invariante absolutamente continua respecto a otra medida ν. Sea además ρ : 0, ) función tal que log ρ es integrable respecto a µ. Se define Entonces S n f, ρ, x) = { 0 j n, df j x), f j )) ρf j x))} h ν f, ρ, x) = lím sup n log νs nf, ρ, x)). h µ f) h ν f, ρ, x)dµx). Para demostrar esto, consideramos r n = e n U n = {x r n+ ρx) < r n }. Ya que nµu n ) = U n ndµx) U n [ log ρx)]dµx), la integrabilidad de log ρ implica la convergencia de la serie de término general nµu n ). Uno construe entonces una partición P, utilizando la existencia de C > 0 tal que para todo 0 < r diam) existe una partición P r ) de con átomos de diámetro menor o igual a r tal que P r C ) dim. r Los átomos de P son entonces aquellos de la forma U n P ) para P P rn+. En este caso, para x U n, diampx) r n+ ρx), la convergencia de nµu n ) implica, junto a la concavidad de x log x, que P tiene entropía finita. Escribimos P n = n j=0 f j P, entonces h µ f) h µ f, P) = La continuidad absoluta de µ respecto a ν implica que µp n x)) lím νp n x)) = lím ) n log µpn x)) dµx). ) dµ x) dν en ν - casi todas partes. Así obtenemos lím n log µpn x)) ) = lím ) n log νpn x)) + lím ) n log µpn x)) νp n x)) luego lím ) n log µpn x)) = lím ) n log νpn x)) 5
7 para ν- casi todas partes. Finalmente, como diampx) ρx) se tiene P n x) S n f, ρ, x), por lo tanto lím /n log νpn x))) h ν f, ρ, x) lo que implica que h µ f) h ν f, ρ, x)dµx). Segunda Etapa: Supongamos ahora que f C +α que λ es la medida de Lebesgue. La demostración del teorema de Pesin se reduce a encontrar para cada ε > 0, un entero N, ρ : 0, ) un conjunto compacto K tales que log ρ sea µ-integrable, µk c ) ε h λ f N, ρ, x) N[χx) ε] 4NC ε ε para x K C 0. En efecto, en tal caso se tendría h µ f) = N h µf N ) h λ f N, ρ, x)dµx) N N[χx) ε] 4NC ε εdµx) N K K h λ f N, ρ, x)dµx) N χx)dµx) 4C ε ε N ε donde C es una cota superior para χx) en µ-casi todos x. K χx)dµx) ε Claramente, si lo anterior es cierto para todo ε > 0, la igualdad en 2) debe ser cierta. 4C ε + N + C + ) Las ideas principales de esta parte de la demostración son las siguientes: Primero debemos considerar E u x) = λ E ix)>0 ix) E 0 x) = λ E ix) 0 ix). Si escribimos Σ j = {x dime u x) = j} µ j A) = µa Σ j )/µσ j ) cuando µσ j ) 0, la linealidad de la entropía permite escribir h µ f) = µσ h j) 0 µ j f Σj ), por lo tanto, es suficiente reducirse al caso cuando = Σ j. Luego, usando el hecho que estos subespacios tienen dimensión constante en µ- casi todas partes sobre, podemos estudiar a asimilándolo a un espacio vectorial, bajo la elección de un atlas adecuado. Esto permite hablar de gráficos dispersión de aquellos gráficos. El hecho que λ sea la medida de Lebesgue, permite escribir λa) = Bx) λ +Eu x)a + E u x)))dλ E0 x)) E 0 x) donde λ E 0 x) λ +E u x) son las medidas de Lebesgue sobre los dos espacios afines Bx) es el ángulo entre aquellos dos espacios. Denotando por Λ n ) = S n f N, ρ, x) + E u x)) minorizando h λ f N, ρ, x) como sigue n ) log h λ f N, ρ, x) = lím sup lím sup lím sup n log ínf E 0 x) λ +E u x)λ n ))dλ E 0 x) E 0 x) ) sup E 0 x) λ +E u x)λ n )) ) n log λ +E u x)λ n )). 6
8 Considerando ε > 0 fijo, los teoremas de Egorov Birkhoff muestran la existencia de K, N, λ > β > tales que µk c ) ε, escribiendo g = f N se tiene, v E u x), D x g n )v λ n v, x K, n N, v E 0 x), D x g n )v β n v, /nn) log detd x g n ) E u x) χx) ε. Escogemos ahora c > 0 suficientemente pequeño tal que existe a > 0 con la propiedad siguiente: Si x K son tales que dx, ) < a, entonces para todo subespacio E T que es un E 0 x), E u x))-gráfico de dispersión c, satisface log detd g) E log detd x g) Eu x) ε. Si definimos entonces ρx) = mína, ξ Nx) ) donde Nx) = mín{n g n x) K} ξ es suficientemente pequeño, se tiene la propiedad de que si x K, g n x) K, E 0 x) Λ n ), entonces g n Λ n )) es un gráfico donde uno puede maorar la dispersión, entonces, es posible maorar su volumen. Esto implica C 0 detd z g n ) TzΛ n) dλz). Λ n) De esta forma, escribiendo S n = {0 j < n g j x) K}, n suficientemente grande, se deduce log detd z g n ) TzΛ n) = n log detd gj z)g) Tg j z) g j Λ n)) j=0 j S n ) log detd gj z)g) Tg j z) g j Λ n)) NC n S n ) log detdgj x)g) Eu g j x)) ) nε NC n S n ) j S n n log detdg j x)g) E u g j x)) ) nε 2NC n S n ) j=0 nnχx) ε) nε 2NC n S n ) nnχx) ε) nε 4NnC ε. donde C es una constante positiva adecuada. Así, C 0 > λλ n )) expnnχx) ε 4C ε) ε)) la conclusión es evidente pues en tal caso se tiene n log λλ n)) N[χx) ε] 4NC ε ε por lo tanto h λ f N, ρ, x) N[χx) ε] 4NC ε ε. Referencias [] Gilles, R., Formules) de Pesin, Séminaire de Théorie spectrale et géométrie, tome ), p [2] Ledrappier, F., Quelques propriétés des exposants caractéristiques, Ecole d Ete de Probabilites de Saint-Flour XII 985), [3] añé, R., A proof of Pesin s formula, Ergodic Theor Dnamical Sstems, vol., iss., pp , 98. [4] añé, R., Ergodic Theor and Differentiable Dnamics, Springer-Verlag, 987. [5] Walters, P., An Introduction to Ergodic Theor, Springer-Verlag,
Ejercicios de teoría de la medida
 Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Teoremas de Tonelli y Fubini
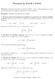 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Cursillo intensivo de Elementos de la Teoría Ergódica.
 Cursillo intensivo de Elementos de la Teoría Ergódica. Eleonora Catsigeras Instituto de Matemática. Facultad de Ingeniería. Universidad de la República. Montevideo. URUGUAY. eleonora@fing.edu.uy Curso
Cursillo intensivo de Elementos de la Teoría Ergódica. Eleonora Catsigeras Instituto de Matemática. Facultad de Ingeniería. Universidad de la República. Montevideo. URUGUAY. eleonora@fing.edu.uy Curso
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Medida y Probabilidad
 Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
2. CONSTRUCCIÓN DE MEDIDAS.
 2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
2. CONSTRUCCIÓN DE MEDIDAS. 1. MEDIDAS EXTERIORES. (2,1,1) Definición. Una medida exterior es una aplicación µ : P(X) [0, + ] que cumple: (a) µ ( ) = 0. (b) Monotonía: Si A B, entonces µ (A) µ (B). (c)
El Teorema de Recurrencia de Poincaré
 El Teorema de Recurrencia de Poincaré Pablo Lessa 9 de octubre de 204. Recurrencia de Poincaré.. Fracciones Continuas Supongamos que queremos expresar la relación que existe entre los números 27 y 0. Una
El Teorema de Recurrencia de Poincaré Pablo Lessa 9 de octubre de 204. Recurrencia de Poincaré.. Fracciones Continuas Supongamos que queremos expresar la relación que existe entre los números 27 y 0. Una
Ejercicios Análisis II
 Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
Ejercicios Análisis II Ejercicios resueltos del libro Real and Complex Analysis de Walter Rudin Mauricio Bravo Vera mauro.bravo@gmail.com Segundo semestre 2010 Índice general 1. Integración Abstracta
1. Propiedades básicas de las medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
2.3. Aplicaciones del teorema de Baire a espacios de Banach
 40 CAPÍTULO. COMPLETITUD Y CATEGORÍAS.3. Aplicaciones del teorema de Baire a espacios de Banach En esta sección, veremos algunas aplicaciones del teorema de Baire a espacios vectoriales normados. En particular,
40 CAPÍTULO. COMPLETITUD Y CATEGORÍAS.3. Aplicaciones del teorema de Baire a espacios de Banach En esta sección, veremos algunas aplicaciones del teorema de Baire a espacios vectoriales normados. En particular,
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Parte 6. Descomposición de medidas.
 Parte 6. Descomposición de medidas. Se generaliza el concepto de medida. Al principio admitiremos medidas a valores reales (positivos y negativos). Luego definiremos medidas complejas. Definición 1 Sea
Parte 6. Descomposición de medidas. Se generaliza el concepto de medida. Al principio admitiremos medidas a valores reales (positivos y negativos). Luego definiremos medidas complejas. Definición 1 Sea
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
1. Unicidad de Medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
Parte 4: Teoremas de convergencia.
 Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
x i yi (2M 1) i (3) i
 CURSO DE TEORÍA ERGÓDICA 2008 - V 1. El shift de Bernoulli: punto de vista topológico Sea Σ 2 = {0, 1} Z el espacio del shift de dos símbolos. Llamaremos Σ M = {0, 1..., M 1} Z el espacio del shift de
CURSO DE TEORÍA ERGÓDICA 2008 - V 1. El shift de Bernoulli: punto de vista topológico Sea Σ 2 = {0, 1} Z el espacio del shift de dos símbolos. Llamaremos Σ M = {0, 1..., M 1} Z el espacio del shift de
CÁLCULO INTEGRAL. HOJA 1. v(q) = Π n i=1(b i a i ). Definimos también el volumen de un rectángulo cerrado como el volumen de su interior.
 CÁLCULO INTEGRAL. HOJA 1. MEDIDA EXTERIOR DE LEBESGUE. CONJUNTOS MEDIBLES EN R N. MEDIDA DE LEBESGUE. Si Q = (a 1, b 1 )... (a n, b n ) es un rectángulo abierto de R n, definimos el volumen de Q como el
CÁLCULO INTEGRAL. HOJA 1. MEDIDA EXTERIOR DE LEBESGUE. CONJUNTOS MEDIBLES EN R N. MEDIDA DE LEBESGUE. Si Q = (a 1, b 1 )... (a n, b n ) es un rectángulo abierto de R n, definimos el volumen de Q como el
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
1. El espacio del shift y su topología.
 TEORIA ERGODICA Eleonora Catsigeras Apuntes para el curso de Maestría en Matemática. Abril de 2005. CAPITULO 4 TRANSFORMACIONES DE BERNOULLI 1. El espacio del shift y su topología. Sea K = {0, 1,..., k
TEORIA ERGODICA Eleonora Catsigeras Apuntes para el curso de Maestría en Matemática. Abril de 2005. CAPITULO 4 TRANSFORMACIONES DE BERNOULLI 1. El espacio del shift y su topología. Sea K = {0, 1,..., k
diám A = x,y A d(x,y) si A es acotado si A no es acotado. {d(x,y) : x,y A}
 Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Problemas con soluciones
 Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
1. Funciones medibles
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 4: Construcción de la integral de Lebesgue EPN, verano 2009 1. Funciones medibles Un concepto de medibilidad
Parte 5: Integración en espacios producto.
 Parte 5: Integración en espacios producto. Definición 1 Sean (X; M, µ) y (Y, N, ν) espacios de medida. Se define la σ álgebra producto M N como la σ álgebra generada por los llamados rectángulos medibles,
Parte 5: Integración en espacios producto. Definición 1 Sean (X; M, µ) y (Y, N, ν) espacios de medida. Se define la σ álgebra producto M N como la σ álgebra generada por los llamados rectángulos medibles,
Cambio de Variables en la Integral Múltiple
 Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Mariano Suárez-Alvarez. 7 de mayo, Límites superiores y límites inferiores
 ĺımsup y ĺıminf Mariano Suárez-Alvarez 7 de mayo, 2013 1.1. Definiciones 1. Límites superiores y límites inferiores 1.1. Sea (a n ) n 1 una sucesión de números reales que es acotada superiormente. Si para
ĺımsup y ĺıminf Mariano Suárez-Alvarez 7 de mayo, 2013 1.1. Definiciones 1. Límites superiores y límites inferiores 1.1. Sea (a n ) n 1 una sucesión de números reales que es acotada superiormente. Si para
Conjuntos Medibles. Preliminares
 Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Intersección y suma de subespacios
 Intersección y suma de subespacios Objetivos Demostrar que la intersección y la suma de dos subespacios de un espacio vectorial también son sus subespaicios Requisitos Espacio vectorial, subespacio vectorial
Intersección y suma de subespacios Objetivos Demostrar que la intersección y la suma de dos subespacios de un espacio vectorial también son sus subespaicios Requisitos Espacio vectorial, subespacio vectorial
Práctica 5 Martingalas a tiempo discreto
 Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Extensión de medidas
 Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2).
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 3: Lema de Baire y Teorema clásicos del Análisis Funcional EPN, verano 2012 Definición 1 (Espacio de
Métodos matemáticos: Análisis funcional
 Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
Métodos matemáticos: Análisis funcional Conceptos y resultados fundamentales Curso 2011/2012 Aquí encontrarás los Teoremas hay que saber para el primer parcial ( 1) así como las definiciones, problemas
Apuntes sobre la integral de Lebesgue
 Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Guía Semana 1 1. RESUMEN. Universidad de Chile. Ingeniería Matemática
 1. RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Guía Semana 1 Geometría. Dados x, y Ê N, su producto interno canónico (o producto punto) es x
1. RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Guía Semana 1 Geometría. Dados x, y Ê N, su producto interno canónico (o producto punto) es x
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
Índice general. 4. Subgrupos de Lie Subgrupos de Lie Subvariedades Teorema de Cartan... 7
 Índice general 4. Subgrupos de Lie 3 4.1. Subgrupos de Lie.......................... 3 4.2. Subvariedades............................ 6 4.3. Teorema de Cartan......................... 7 1 2 ÍNDICE GENERAL
Índice general 4. Subgrupos de Lie 3 4.1. Subgrupos de Lie.......................... 3 4.2. Subvariedades............................ 6 4.3. Teorema de Cartan......................... 7 1 2 ÍNDICE GENERAL
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Análisis real y complejo. Análisis Funcional
 UNIVERSIDAD DE SEVILLA Análisis real y complejo. Análisis Funcional Máster Universitario en Matemática Avanzada Luis Bernal González Departamento de Análisis Matemático Sevilla, febrero de 212 Disponible
UNIVERSIDAD DE SEVILLA Análisis real y complejo. Análisis Funcional Máster Universitario en Matemática Avanzada Luis Bernal González Departamento de Análisis Matemático Sevilla, febrero de 212 Disponible
Teoría de la Integración
 Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
Licenciatura en Matemáticas y Física Universidad de Antioquia 1 Introducción 2 3 Introducción Para toda persona con formación matemática superior, es conocida la teoría de la integración de Riemann. Sin
Tema 10: Teorema de Hahn-Banach. 14 y 17 de junio de 2010
 Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Tema 10: Teorema de Hahn-Banach 14 y 17 de junio de 2010 1 Versión anaĺıtica Enunciado del teorema Dual topológico Teoremas de extensión Duales de subespacios y cocientes Límites de Banach 2 Separación
Índice. Funciones de varias variables reales I Espacios normados. Revisando con perspectiva. Se puede hacer de forma más general?
 Índice Funciones de varias variables reales I Espacios normados José Manuel Mira Departamento de Matemáticas Universidad de Murcia Grado en Matemáticas 2013-2014 (18-09-2013) 1 Espacios normados. El espacio
Índice Funciones de varias variables reales I Espacios normados José Manuel Mira Departamento de Matemáticas Universidad de Murcia Grado en Matemáticas 2013-2014 (18-09-2013) 1 Espacios normados. El espacio
Ejercicios de Análisis Funcional
 Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Ejercicios de Análisis Funcional Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada ANÁLISIS FUNCIONAL Relación de Ejercicios N o 1 1. Dar un ejemplo de una distancia en un espacio
Cambio de Variables en la Integral Múltiple
 Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz
 Capítulo 3 La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz n este capítulo definiremos la Propiedad de Radon-Nikodým en un espacio de Banach X y estableceremos su equivalencia con
Capítulo 3 La Propiedad de Radon-Nikodým y el Teorema de Representación de Riesz n este capítulo definiremos la Propiedad de Radon-Nikodým en un espacio de Banach X y estableceremos su equivalencia con
1 Espacios de Banach:
 Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
1. Convergencia en medida
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
Acotación y compacidad
 Lección 8 Acotación y compacidad Para subconjuntos de un espacio métrico, estudiamos ahora la noción de acotación, que como ocurría con la complitud, no es una noción topológica, pero se conserva en un
Lección 8 Acotación y compacidad Para subconjuntos de un espacio métrico, estudiamos ahora la noción de acotación, que como ocurría con la complitud, no es una noción topológica, pero se conserva en un
1. La topología inducida.
 PRACTICO 4. ESPACIOS METRICOS. 1. La topología inducida. Sea (M, d) un espacio métrico. La bola abierta de centro x y radio r es el conjunto B(x; r) = {y M : d(x, y) < r}. La bola cerrada de centro x y
PRACTICO 4. ESPACIOS METRICOS. 1. La topología inducida. Sea (M, d) un espacio métrico. La bola abierta de centro x y radio r es el conjunto B(x; r) = {y M : d(x, y) < r}. La bola cerrada de centro x y
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
INTRODUCCIÓN A LOS ESPACIOS DE FUNCIONES. Problemas
 Problemas Curso 2013-2014 Problemas 1. Sea E un espacio normado. Si a, b son elementos de E, probar: (a) 1 2 (a + b) 2 1 2 a 2 + 1 2 b 2. (b) a max{ a + b, a b }. 2. Demostrar que en un espacio normado,
Problemas Curso 2013-2014 Problemas 1. Sea E un espacio normado. Si a, b son elementos de E, probar: (a) 1 2 (a + b) 2 1 2 a 2 + 1 2 b 2. (b) a max{ a + b, a b }. 2. Demostrar que en un espacio normado,
1. Funciones Medibles
 1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
1 Longitud y Medida Longitud Medida Exterior Conjuntos Medibles Ejercicios... 20
 Contenido Introducción 1 1 Longitud y Medida 3 1.1 Longitud............................. 3 1.2 Medida Exterior........................ 12 1.3 Conjuntos Medibles...................... 13 Ejercicios...............................
Contenido Introducción 1 1 Longitud y Medida 3 1.1 Longitud............................. 3 1.2 Medida Exterior........................ 12 1.3 Conjuntos Medibles...................... 13 Ejercicios...............................
Teorema de Hahn-Banach
 Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
1. Continuidad. Universidad de Chile Subsucesiones. Ingeniería Matemática
 1. Continuidad 1.1. Subsucesiones Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Importante: Visita regularmente http://www.dim.uchile.cl/~calculo.
1. Continuidad 1.1. Subsucesiones Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Importante: Visita regularmente http://www.dim.uchile.cl/~calculo.
Capítulo La integral de Riemann
 Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
Capítulo 5 Integración 1. La integral de iemann Empecemos por recordar la integral de iemann de una función acotada f : [a, b]. Una partición P de [a, b] es un subconjunto finito P [a, b] tal que a, b
11.1. Funciones uniformemente continuas
 Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Teoría de Calderón-Zygmund con medidas generales
 Teoría de Calderón-Zygmund con medidas generales José Manuel Conde Alonso Seminario de Doctorandos UCM Consejo Superior de Investigaciones Científicas - Universidad Autónoma de Madrid 15 de octubre de
Teoría de Calderón-Zygmund con medidas generales José Manuel Conde Alonso Seminario de Doctorandos UCM Consejo Superior de Investigaciones Científicas - Universidad Autónoma de Madrid 15 de octubre de
Integrales paramétricas
 5 Integrales paramétricas Página 1 de 29 1. uchas de las funciones que se manejan en Análisis atemático no se conocen mediante expresiones elementales, sino que vienen dadas a través de series o integrales.
5 Integrales paramétricas Página 1 de 29 1. uchas de las funciones que se manejan en Análisis atemático no se conocen mediante expresiones elementales, sino que vienen dadas a través de series o integrales.
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
Ejercicios resueltos
 Ejercicios resueltos 25 de septiembre de 29 2 1 Ejercicios Tema I Ejercicio 1 Demostrar que una clase no vacía A es un álgebra en Ω si y sólo si se verifican las siguientes propiedades: i) Si A A entonces
Ejercicios resueltos 25 de septiembre de 29 2 1 Ejercicios Tema I Ejercicio 1 Demostrar que una clase no vacía A es un álgebra en Ω si y sólo si se verifican las siguientes propiedades: i) Si A A entonces
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
Observación: Aceptaremos que la función f no este definida para un número finito de términos como por ejemplo f(n) = n 5.
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07- Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07- Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
1. Campos vectoriales y formas diferenciales
 Capítulo Orientación. Campos vectoriales formas diferenciales En este capítulo introduciremos el concepto de orientación, mu importante en el análisis de variedades, en particular la teoriá de integración.
Capítulo Orientación. Campos vectoriales formas diferenciales En este capítulo introduciremos el concepto de orientación, mu importante en el análisis de variedades, en particular la teoriá de integración.
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
CÁLCULO INTEGRAL. HOJA 9.
 CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
El espacio euclideano
 Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
Una norma en un espacio lineal (o vectorial) X es una función. : X R con las siguientes propiedades: (a) x 0, para todo x X (no negatividad);
 MATEMÁTICA APLICADA II Segundo cuatrimestre 20 Licenciatura en Física, Universidad Nacional de Rosario Espacios de Banach. Introducción Frecuentemente estamos interesados en qué tan grande. es una función.
MATEMÁTICA APLICADA II Segundo cuatrimestre 20 Licenciatura en Física, Universidad Nacional de Rosario Espacios de Banach. Introducción Frecuentemente estamos interesados en qué tan grande. es una función.
Análisis de Fourier. Resumen de los apuntes de D. Antonio Cañada Villar. Sergio Cruz Blázquez. Curso 2015/2016
 Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Introducción. Capítulo Introducción. Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos
 Capítulo 1 Introducción 1.1. Introducción Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos La distribución de esta variable aleatoria es Definimos M n = máx i n X i. P (M n x) = P
Capítulo 1 Introducción 1.1. Introducción Sea {X n, n 1} una sucesión de v.a.i.i.d. con f.d. común F y definamos La distribución de esta variable aleatoria es Definimos M n = máx i n X i. P (M n x) = P
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 2012
 AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
AMARUN www.amarun.org Comisión de Pedagogía - Diego Chamorro Análisis Funcional (Nivel 2). Lección n 1: Aplicaciones Lineales EPN, verano 212 Introducción Algunas fechas: 197: Noción de Operador lineal
Teoremas de la función inversa, función implícita y del rango constante
 Teoremas de la función inversa, función implícita y del rango constante Pablo Zadunaisky 13 de marzo de 2015 A lo largo de este documento usamos varias normas sobre espacios vectoriales de dimensión finita,
Teoremas de la función inversa, función implícita y del rango constante Pablo Zadunaisky 13 de marzo de 2015 A lo largo de este documento usamos varias normas sobre espacios vectoriales de dimensión finita,
Práctica 3 Esperanza Condicional
 1. Generalidades Práctica 3 Esperanza Condicional 1. Sea (X i ) i I una familia de variables aleatorias definidas sobre un mismo espacio medible (Ω, F) y sea Y otra variable aleatoria en este espacio.
1. Generalidades Práctica 3 Esperanza Condicional 1. Sea (X i ) i I una familia de variables aleatorias definidas sobre un mismo espacio medible (Ω, F) y sea Y otra variable aleatoria en este espacio.
6. Ortogonalidad. Universidad de Chile Conjuntos ortogonales y ortonormales. Ingeniería Matemática SEMANA 12: ORTOGONALIDAD
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 7- SEMANA : ORTOGONALIDAD 6 Ortogonalidad 6 Conjuntos ortogonales y ortonormales Recordemos que la proyección de u sobre v
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 7- SEMANA : ORTOGONALIDAD 6 Ortogonalidad 6 Conjuntos ortogonales y ortonormales Recordemos que la proyección de u sobre v
Cálculo diferencial e integral I. Eleonora Catsigeras
 Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
Sobre un Teorema de Kakutani vía Martingalas
 Sobre un Teorema de Kakutani vía Martingalas Jesús Daniel Arroyo Relión * 1. Preliminares El teorema de Kakutani es un importante resultado de la teoría de la medida. Fue demostrado en 1946 por Shizuo
Sobre un Teorema de Kakutani vía Martingalas Jesús Daniel Arroyo Relión * 1. Preliminares El teorema de Kakutani es un importante resultado de la teoría de la medida. Fue demostrado en 1946 por Shizuo
ANÁLISIS FUNCIONAL Notas de curso. M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid
 ANÁLISIS FUNCIONAL Notas de curso M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid 2 de septiembre de 22 Índice general. La integral de Lebesgue 3.. Introducción............................................
ANÁLISIS FUNCIONAL Notas de curso M.A. Rodríguez Departamento de Física Teórica II Universidad Complutense de Madrid 2 de septiembre de 22 Índice general. La integral de Lebesgue 3.. Introducción............................................
Cambio de variables en la integral múltiple.
 Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
Cambio de variables en la integral múltiple. En este apartado vamos a generalizar la fórmula g(b) g(a) f(x) dx = b a f(g(t)) g (t) dt al caso de funciones de n variables. Como la región de integración
Sucesiones y convergencia
 Capítulo 2 Sucesiones y convergencia 1. Definiciones Una de las ideas fundamentales del análisis es la de límite; en particular, el límite de una sucesión. En este capítulo estudiaremos la convergencia
Capítulo 2 Sucesiones y convergencia 1. Definiciones Una de las ideas fundamentales del análisis es la de límite; en particular, el límite de una sucesión. En este capítulo estudiaremos la convergencia
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Resumen de Análisis Matemático IV
 Resumen de Análisis Matemático IV 1. Funciones inversas e implícitas y extremos condicionados 1.1. Teorema de la función inversa Teorema de la función inversa: Sea A abierto de R n, f : A R n tal que f
Resumen de Análisis Matemático IV 1. Funciones inversas e implícitas y extremos condicionados 1.1. Teorema de la función inversa Teorema de la función inversa: Sea A abierto de R n, f : A R n tal que f
Extensión de medidas
 Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
Extensión de medidas Problemas para examen Semianillos de conjuntos 1. Escriba la definición de semianillo de conjuntos. 2. Convenio: el conjunto vacío pertenece a cualquier semianillo. En los siguientes
Nociones topológicas elementales de R n
 Nociones topológicas elementales de R n 1 Espacio vectorial R n Consideremos el conunto R n de las n-uplas de números reales, donde n es un número natural arbitrario fio. Los elementos de R n, que llamamos
Nociones topológicas elementales de R n 1 Espacio vectorial R n Consideremos el conunto R n de las n-uplas de números reales, donde n es un número natural arbitrario fio. Los elementos de R n, que llamamos
Departamento de Ingeniería Matemática - Universidad de Chile
 5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
5. Principio de inducción Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Introducción al Álgebra 08-1 5.1. Principio de inducción: Primera forma Importante: Visita
COMPLECIÓN DE CUERPOS CONVEXOS. Helmuth Villavicencio Fernández 1. (Recibido: 26/01/ Aceptado: 18/11/2014) COMPLETION OF CONVEX BODIES
 PESQUIMAT, Revista de la F.C.M. de la Universidad Nacional Mayor de San Marcos Vol. XVIII N o 1, pp. 16-20, Lima -Perú, Abril 2015 COMPLECIÓN DE CUERPOS CONVEXOS Helmuth Villavicencio Fernández 1 (Recibido:
PESQUIMAT, Revista de la F.C.M. de la Universidad Nacional Mayor de San Marcos Vol. XVIII N o 1, pp. 16-20, Lima -Perú, Abril 2015 COMPLECIÓN DE CUERPOS CONVEXOS Helmuth Villavicencio Fernández 1 (Recibido:
Ejercicios Variable Real
 UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
UNIVERSIDAD AUTÓNOMA DE MADRID FACULTAD DE MATEMÁTICAS Ejercicios Variable Real Antonio Córdoba (Manuel Mellado Cuerno) 1º Cuatrimestre del curso 2016-2017 manuel.mellado@estudiante.uam.es 2 Capítulo 1
Notas del Primer Capítulo del Libro Análisis Funcional de W. Rudin
 1 Notas del Primer Capítulo del Libro Análisis Funcional de W. Rudin Alejandra García García Estas notas son el trabajo desarrollado dentro del seminario de Análisis que se ha impartido durante los primeros
1 Notas del Primer Capítulo del Libro Análisis Funcional de W. Rudin Alejandra García García Estas notas son el trabajo desarrollado dentro del seminario de Análisis que se ha impartido durante los primeros
1 Continuidad uniforme
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 NOTAS 6: ESPACIOS MÉTRICOS II: COMPLETITUD 1 Continuidad uniforme Denición. Sean (M, d 1 ) y
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 NOTAS 6: ESPACIOS MÉTRICOS II: COMPLETITUD 1 Continuidad uniforme Denición. Sean (M, d 1 ) y
: k }, es decir. 2 k. k=0
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Integrales paramétricas propias
 Integrales paramétricas propias ISABEL ARRERO Departamento de Análisis atemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Tipos de integrales paramétricas 1 2.1. Simples..............................................
Integrales paramétricas propias ISABEL ARRERO Departamento de Análisis atemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Tipos de integrales paramétricas 1 2.1. Simples..............................................
Variedades diferenciables
 Capítulo 10 Variedades diferenciables 1. Variedades diferenciables en R n A grandes rasgos, una variedad diferenciable es un conjunto que, localmente, es difeomorfo al espacio euclideano. En este capítulo
Capítulo 10 Variedades diferenciables 1. Variedades diferenciables en R n A grandes rasgos, una variedad diferenciable es un conjunto que, localmente, es difeomorfo al espacio euclideano. En este capítulo

 Espacios L p con 0
Espacios L p con 0