Árboles: Árbol Abarcador Minimal CSI / ITESM
|
|
|
- Pablo Casado Castilla
- hace 5 años
- Vistas:
Transcripción
1 Árboles: Árbol Abarcador Minimal CSI / ITESM Árboles:Árbol Abarcador Minimal p.1/5
2 Árboles Abarcador (Spanning Tree): Definición Un árbol abarcador para un grafo G es un subgrafo de G que contien todos los értices (abarca) y es árbol. Árboles:Árbol Abarcador Minimal p./5
3 Árboles Abarcador (Spanning Tree): Definición Un árbol abarcador para un grafo G es un subgrafo de G que contien todos los értices (abarca) y es árbol. Resultado: Todo grafo conexo tien un árbol abarcador. Árboles:Árbol Abarcador Minimal p./5
4 Ejemplos árboles abarcadores para un grafo Considere el grafo: e 1 1 e 1 1 e e 4 e e e Árboles abarcadores son: e e e e 4 e e Árboles:Árbol Abarcador Minimal p./5
5 Grafos Con Peso (Weighted Graphs) Un árbol con peso es un grafo donde cada lado tiene un número asociado o peso. Árboles:Árbol Abarcador Minimal p.4/5
6 Grafos Con Peso (Weighted Graphs) Un árbol con peso es un grafo donde cada lado tiene un número asociado o peso. Normalmente, al peso de un lado e se le designa por w(e). Árboles:Árbol Abarcador Minimal p.4/5
7 Grafos Con Peso (Weighted Graphs) Un árbol con peso es un grafo donde cada lado tiene un número asociado o peso. Normalmente, al peso de un lado e se le designa por w(e). La suma de todos los pesos de todos los lados de un grafo con peso se llama el peso del grafo. Árboles:Árbol Abarcador Minimal p.4/5
8 Grafos Con Peso (Weighted Graphs) Un árbol con peso es un grafo donde cada lado tiene un número asociado o peso. Normalmente, al peso de un lado e se le designa por w(e). La suma de todos los pesos de todos los lados de un grafo con peso se llama el peso del grafo Árboles:Árbol Abarcador Minimal p.4/5
9 Grafos Con Peso (Weighted Graphs) Un árbol con peso es un grafo donde cada lado tiene un número asociado o peso. Normalmente, al peso de un lado e se le designa por w(e). La suma de todos los pesos de todos los lados de un grafo con peso se llama el peso del grafo Peso total del grafo = 19 Árboles:Árbol Abarcador Minimal p.4/5
10 Árbol Abarcador Minimal (Minimum Spanning Tree) Un árbol abarcador minimal para un grafo G es un árbol abarcador tal que cualquier otro árbol abarcador para G no tiene un peso total menor. Árboles:Árbol Abarcador Minimal p.5/5
11 Árbol Abarcador Minimal (Minimum Spanning Tree) Un árbol abarcador minimal para un grafo G es un árbol abarcador tal que cualquier otro árbol abarcador para G no tiene un peso total menor. Considere el grafo: Peso árbol abarcador= Árboles:Árbol Abarcador Minimal p.5/5
12 MST: Algoritmo de Kruskal Entrada: Un grafo conexo con peso. 1 Inicialice T a tener todos los értices de G y no tener lados. Sea E el conjunto de todos los lados de G y m := 0. Mientras (m < n 1) hacer a Encuentre en E el lado e más pequeño. b Borre e de E. c Si al añadir e a T no se forma un ciclo, entonces añadir e a T. d Incrementar m en 1. Salida: T. Árboles:Árbol Abarcador Minimal p.6/5
13 Algoritmo de Kruskal: Ejemplo Fase de Inicialización: m := 0 Árboles:Árbol Abarcador Minimal p.7/5
14 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a peso: m := Árboles:Árbol Abarcador Minimal p.8/5
15 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a peso: m := No forma un ciclo en T: Árboles:Árbol Abarcador Minimal p.8/5
16 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a peso: m := No forma un ciclo en T: se añade a T y m := m + 1 Árboles:Árbol Abarcador Minimal p.8/5
17 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: a 4 peso: m := Árboles:Árbol Abarcador Minimal p.9/5
18 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: a 4 peso: m := No forma un ciclo en T: Árboles:Árbol Abarcador Minimal p.9/5
19 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: a 4 peso: m := No forma un ciclo en T: se añade a T y m := m + 1 Árboles:Árbol Abarcador Minimal p.9/5
20 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a 4 peso: m := 4 Árboles:Árbol Abarcador Minimal p.10/5
21 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a 4 peso: m := 4 No forma un ciclo en T: Árboles:Árbol Abarcador Minimal p.10/5
22 Algoritmo de Kruskal: Ejemplo 1 1 Encuentre el lado más pequeño: 1 a 4 peso: m := 4 No forma un ciclo en T: se añade a T y m := m + 1 Árboles:Árbol Abarcador Minimal p.10/5
23 Algoritmo de Kruskal: Ejemplo 1 1 El algoritmo termina pues m () es igual a n 1 (4 1 = ). 1 4 m := Árboles:Árbol Abarcador Minimal p.11/5
24 MST: Algoritmo de Prim Entrada: Un grafo conexo con peso. 1 Tome un értice de G y sea T el grafo con un értice y sin ningún lado. Sea V el conjunto de todos los értices de G excepto. Desde i igual 1 hasta n 1 hacer: a Encuentre un lado e que conecte un értice de V con alguno de T y que sea lo más pequeño posible. Sea w el extremo de e que está en V. b Añada el értice w y el lado e al grafo T. c Borre el értice w de V. Salida: T. Árboles:Árbol Abarcador Minimal p.1/5
25 Algoritmo de Prim: Ejemplo Fase de Inicialización: i := 0 Árboles:Árbol Abarcador Minimal p.1/5
26 Algoritmo de Prim: Ejemplo i := 0; Determinar el menor lado que une un értice de T (rojos) con otro de V (negros): el menor lado es Se añade el értice y el lado y se aumenta i. Árboles:Árbol Abarcador Minimal p.14/5
27 Algoritmo de Prim: Ejemplo i := 1; Determinar el menor lado que une un értice de T (rojos) con otro de V (negros): el menor lado es Se añade el értice y el lado y se aumenta i. Árboles:Árbol Abarcador Minimal p.15/5
28 Algoritmo de Prim: Ejemplo i := ; Determinar el menor lado que une un értice de T (rojos)con otro de V (negros): el menor lado es Se añade el értice y el lado y se aumenta i. Árboles:Árbol Abarcador Minimal p.16/5
29 Algoritmo de Prim: Ejemplo 1 1 El algoritmo termina pues i () es igual a n 1 (4 1 = ). 1 4 i := ; Árboles:Árbol Abarcador Minimal p.17/5
30 Algoritmo de Paseos Cortos Entrada: Un grafo conexo con peso y un értice de él o. 1 Defina V el conjunto de todos los értices de G. Etiquete los értices de V con l() = y PathTo() = ɛ. Etiquete a l( 0 ) = 0. Mientras V no sea acío hacer: a b Elija el értice de V con menor índice posible. Llámero i. Para cada uno de los értices j de V adyacentes a i hacer: Si l( i ) + w( o,i j ) < l( j ) entonces hacer l( j ) = l( i ) + w( i, j ) y PathTo( j ) = PathTo( i ) i. c Borre el értice i de V. Salida: Las funciones índice de cada értice y la función PathTo. Árboles:Árbol Abarcador Minimal p.18/5
31 Ejemplo de Paseos Cortos Inicialización l() P atht o() oferta 0 0 ɛ 1 ɛ ɛ ɛ 4 ɛ 5 ɛ Árboles:Árbol Abarcador Minimal p.19/5
32 Ejemplo de Paseos Cortos: Vértice con mínimo índice 0 : afectación posible a los adyacentes l() PathTo() oferta de ɛ 1 ɛ 1 ɛ ɛ 4 ɛ 4 5 ɛ Árboles:Árbol Abarcador Minimal p.0/5
33 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ ɛ ɛ Árboles:Árbol Abarcador Minimal p.0/5
34 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ ɛ ɛ 0 sale Árboles:Árbol Abarcador Minimal p.0/5
35 Ejemplo de Paseos Cortos: Vértice con mínimo índice 1 : afectación posible a los adyacentes l() PathTo() oferta de ɛ ɛ 8 ɛ ɛ 6 Árboles:Árbol Abarcador Minimal p.1/5
36 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ Árboles:Árbol Abarcador Minimal p.1/5
37 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ sale. Árboles:Árbol Abarcador Minimal p.1/5
38 Ejemplo de Paseos Cortos: Vértice con mínimo índice 4 : afectación posible a los adyacentes l() PathTo() oferta de ɛ ɛ Árboles:Árbol Abarcador Minimal p./5
39 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ Árboles:Árbol Abarcador Minimal p./5
40 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ ɛ sale. Árboles:Árbol Abarcador Minimal p./5
41 Ejemplo de Paseos Cortos: Vértice con mínimo índice 5 : afectación posible a los adyacentes l() PathTo() oferta de ɛ ɛ Árboles:Árbol Abarcador Minimal p./5
42 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ Árboles:Árbol Abarcador Minimal p./5
43 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ sale. Árboles:Árbol Abarcador Minimal p./5
44 Ejemplo de Paseos Cortos: Vértice con mínimo índice : afectación posible a los adyacentes l() PathTo() oferta de 0 0 ɛ Árboles:Árbol Abarcador Minimal p.4/5
45 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ Árboles:Árbol Abarcador Minimal p.4/5
46 Ejemplo de Paseos Cortos: Vértices afectados: l() P atht o() oferta 0 0 ɛ sale. Árboles:Árbol Abarcador Minimal p.4/5
47 Ejemplo de Paseos Cortos: Conclusión Caminos más cortos desde 0 : l() P atht o() 0 0 ɛ Árboles:Árbol Abarcador Minimal p.5/5
Algoritmos voraces (greedy)
Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 21 de marzo de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Algoritmos voraces 21 de marzo de 2018 1 / 45 1 Algoritmos voraces (greedy) Aplicaciones de
ARBOLES GENERADORES. Orlando Arboleda Molina. 16 de septiembre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
5.6 Árbol generador de un grafo
88 5.6 Árbol generador de un grafo Definición 5.59. Sea G un grafo simple. Un árbol generador de G es un subgrafo de G que es un árbol y contiene todos los vértices de G. Ejemplo 5.60. Un grafo y algunos
Árboles. no es un árbol porque no es conexo. Sin embargo, cada componente conexa es un árbol y, este tipo de grafo se llama bosque.
Ejemplos Árboles Un grafo sin lazos, es un árbol si es conexo y no contiene ciclos. Tenemos que: es un árbol. no es un árbol porque contiene un ciclo. no es un árbol porque no es conexo. Sin embargo, cada
5.4 Caminos mínimos: Algoritmo de Dijkstra
81 5.4 Caminos mínimos: Algoritmo de Dijkstra Al observar nuestro mapa de carreteras se pueden considerar las distancias en km que hay entre las ciudades, a cada arista se le asigna el valor correspondiente
Análisis y Diseño de Algoritmos Árboles de Mínima Expansión (Minimum Spanning Trees) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
Análisis y Diseño de Algoritmos Árboles de Mínima Expansión (Minimum Spanning Trees) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Cableado de Circuitos Electrónicos 2 Diseño
Algoritmos Codiciosos y problemas de Optimización en Grafos
Algoritmos odiciosos y problemas de Optimización en Grafos B10 onceptos Un árbol es un grafo conexo y sin circuitos. Un árbol trivial es un grafo que consiste de un solo vértice. Un grafo sin circuitos
3.0.-ARBOLES ABARCADORES Y COMPONENTES CONEXOS CONCEPTO DE ARBOL ABARCADOR Y SU RELACION CON LOS RECORRIDOS.
3.0.-ARBOLES ABARCADORES Y COMPONENTES CONEXOS 3.1.- CONCEPTO DE ARBOL ABARCADOR Y SU RELACION CON LOS RECORRIDOS. 3.2.- BOSQUES Y COMPONENTES CONEXOS. NEXON LENIN CEFERINO POMPOSO Los árboles son particularmente
Análisis de algoritmos
Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Algebra Matricial y Teoría de Grafos
Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Representación y manipulación de grafos: caminos, expansión, cortes y flujos
Un grafo G es un par de conjuntos G =(V,E) Representación y manipulación de grafos: caminos, expansión, cortes y flujos V = un conjunto de n vértices u, v, w V E = un conjunto de m aristas V = n, E = m
Algoritmos en Teoría de Grafos
Algoritmos en Teoría de Grafos Jesús García López de Lacalle Algoritmos en Teoría de Grafos 1. Introducción 2. Conectividad 3. Caminos mínimos y distancias 4. Planificación y optimización de tareas 5.
Teoría de Grafos Introducción Grafos isomorfos
Capítulo 1 Teoría de Grafos 1.1. Introducción Definición. Denominaremos pseudomultigrafo a una terna (V,E, γ), donde V y E son conjuntos y γ : E {{u,v}: u,v V }. El conjunto V se denomina conjunto de vértices
Minimum Spanning Tree (Árbol de Expansión Mínima) Agustín J. González ELO320: Estructura de datos y Algoritmos
Minimum Spanning Tree (Árbol de Expansión Mínima) Agustín J. González ELO320: Estructura de datos y Algoritmos 1 Introducción Lo que realmente se minimiza es el peso del árbol obtenido. No se minimiza
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Algoritmo de Kruskal
Algoritmo de Kruskal Curso de Teoría Algebraica de Grafos Facultad de Ingeniería Universidad de la República 4 de mayo de 202 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un
Algoritmos sobre Grafos
Sexta Sesión 27 de febrero de 2010 Contenido Deniciones 1 Deniciones 2 3 4 Deniciones sobre Grafos Par de una lista de nodos y una lista de enlaces, denidos a su vez como pares del conjunto de nodos.
Algoritmos Voraces. Diseño y Análisis de Algoritmos
Algoritmos Voraces Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 Ejemplos básicos 3 Cambio de monedas 4 Problema de la mochila 5 Problemas de planificación de tareas 6 Patrones
Francisco J. Hernández López
Francisco J. Hernández López fcoj23@cimat.mx Estructura de datos no lineales donde cada componente o nodo puede tener uno o más predecesores (a diferencia de los árboles) y sucesores Un grafo esta formado
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Teoría de Grafos. Herramientas de programación para procesamiento de señales
Teoría de Grafos Herramientas de programación para procesamiento de señales Indice Nociones básicas: Definiciones Ejemplos Propiedades Nociones avanzadas: Grafos planares Árboles Representación en computadora
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
Análisis de Algoritmos Teoría de grafos
Análisis de Algoritmos Teoría de grafos Dra. Elisa Schaeffer elisa.schaeffer@gmail.com PISIS / FIME / UANL Teoría de grafos p. 1 Grafos Un grafo G es un par de conjuntos G = (V,E) Teoría de grafos p. 2
Trayectorias y circuitos Eulerianos y Hamiltonianos,
Trayectorias y circuitos Eulerianos y Hamiltonianos, Eulerianos Trayectoria de Euler: recorrer una gráfica G utilizando cada arista de la gráfica sólo una vez, puede ser necesario o no comenzar y terminar
Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos.
Matemática Discreta y Lógica 2 1. Árboles Árboles Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos. Como un lazo es un ciclo de longitud 1, un árbol
Capítulo 4: Grafos Clase 4: Árboles
Capítulo 4: Grafos Clase 4: Árboles Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 12 Árboles Los árboles son una clase particular de grafos que
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
Ciclos Hamiltonianos Algoritmo de la Ruta Más Corta. Matemática Discreta. Agustín G. Bonifacio UNSL. Teoría de Grafos II
UNSL Teoría de Grafos II y Ejemplos Un ciclo en un grafo que contiene cada vértice justo una vez, excepto por el vértice inicial y el final que aparece dos veces, recibe el nombre de ciclo de Hamilton.
TEMA IV TEORÍA DE GRAFOS
TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Conceptos Simples, Problemas Difíciles Héctor Ramírez C. 1 1 Departamento de Ingeniería Matemática Universidad de Chile Curso MA3701: Optimización Héctor Ramírez C. (U.
Los grafos estrella extendida: reconocimiento y propiedades estructurales
Los grafos estrella extendida: reconocimiento y propiedades estructurales CONICET/ Departamento de Matemática, Universidad Nacional de La Plata LXV Reunión Anual de Comunicaciones Científicas de la UMA,
MATROIDES Y EL ALGORITMO VORAZ
MATROIDES Y EL ALGORITMO VORAZ Natalia Castro - 19 de octubre de 2016 Algoritmos de Aproximación IMERL - Facultad de Ingeniería - UdelaR Edmonds loco-problem Edmonds se enfoca en algoritmos better than
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal.
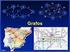Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal. Jose Aguilar 1 Grafo de carreteras entre ciudades Mcbo Coro Pto. Cabello Valera Bqto Valencia Maracay Caracas Acarigua Barinas San
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg "Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.")
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
1. Caminos Mínimos en un Grafo sin Pesos 2. Caminos Mínmos en un Grafo ponderado. 1. Algoritmo de Dijkstra
Tema - Soluciones Greedy para Problemas de Optimización sobre un Grafo Tema - Soluciones Greedy para Problemas de Optimización sobre un Grafo Germán Moltó Escuela Técnica Superior de Ingeniería Informática
Modelos de Redes: Árbol. M. En C. Eduardo Bustos Farías
Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación
Computación Geométrica Descomposición en polígonos monótonos
Computación Geométrica Descomposición en polígonos monótonos Introducción a la Geometría Computacional Copyright 2010-2011 Universidad de Alicante 1 Ejemplos Introducción a la Geometría Computacional Copyright
Grafos. 19 de diciembre de 2013
Grafos 19 de diciembre de 2013 Grafo Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de pares de vértices, llamados aristas (edges en inglés) que pueden ser orientados
Análisis de algoritmos
Demostración laboratorio: Martes 14 de Julio de 2015 Entrega vía Web: Domingo 19 de Julio de 2015 Demostración laboratorio y Entrega vía Web (Extraordinario): Martes 21 de Julio de 2015 M. en C. Edgardo
Teoría de grafos y optimización en redes
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]
![Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]](/thumbs/66/55246007.jpg "Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]")
Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Grafos
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Grafos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas a partir
Computación Geométrica Tema 5: Triangulación de polígonos. Triangulación por descomposición. Descomposición en polígonos monótonos.
Computación Geométrica Tema 5: Triangulación de polígonos Triangulación por descomposición Descomposición en polígonos monótonos! Un polígono cualquiera no monótono puede ser descompuesto en polígonos
Tema 5 Árboles y Grafos.
Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Razonamiento Geométrico Tema 5: Triangulación de polígonos. Sesión 10: Descomposición en polígonos monótonos
Razonamiento Geométrico Tema 5: Triangulación de polígonos Sesión 10: Descomposición en polígonos monótonos Triangulación de polígonos Copyright 2002-2003 Universidad de Alicante 1 Triangulación por descomposición
Teoría de redes y optimización en redes
Teoría de redes y optimización en redes Pedro Sánchez Martín Contenidos Definiciones básicas Árbol generador mínimo de expansión Camino mínimo Algoritmo Dkstra Algoritmo Bellman-Ford Fluo máximo Fluo de
Apuntes de Teórico de Programación 3. Apuntes de Teórico PROGRAMACIÓN 3. Greedy. Versión 1.1
Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas).
TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv
DEFINICIÓN 1: Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv φ donde: V = {v 1, v 2,, v n }: conjunto finito de vértices o nodos. A = {a 1, a 2,, a n }: conjunto finito de aristas o lados
Gráficas : teoría, aplicaciones e interacciones : II
J. Ramírez Alfonsín Université Montpellier 2, Francia Facultad de Ciencias, UNAM, México 22 de Enero de 2013 1 Ciclos 2 Gráficas hamiltonianas 3 Arboles 4 Gráficas Eulerianas 5 Gráficas dirigidas 6 Problema
Definiciones: conjuntos, grafos, y árboles. Agustín J. González ELO 320: Estructura de Datos y Algoritmos. 2002
Definiciones: conjuntos, grafos, y árboles Agustín J. González ELO 320: Estructura de Datos y Algoritmos. 2002 1 Conjuntos (sets) y Grafos (graphs) Un Conjunto es una colección de objetos distintos. No
Árboles generadores mínimos (MST) comp-420
Árboles generadores mínimos (MST) comp-420 Árboles generadores mínimos (MST) Sea G=(V,E) una gráfica conectada y no-dirigida con V vértices y E aristas. Cada arista (u,v) E tiene un peso w(u,v), que es
Matemáticas Discretas
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2016 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Sesión 4: Teoría de Grafos
Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Grafos. CCIR / Depto Matemáticas CB102
CB102 Conceptos Los grafos son una técnica de modelación de problemas atractiva y útil. Problemas de diferentes áreas pueden ser modelados mediante su uso: redes de transporte de bienes de consumo, redes
En la fig. 1 se representa el grafo, G=(V,A) donde: V = {1, 2, 3, 4, 5, 6} A = { {1,2}, {1,3}, {1,5}, {3}, {3,4}, {4,5}, {5,6} }
Unidad 1 Parte 1 - Teoría de Grafos Introducción En este capítulo veremos la noción matemática de grafo y propiedades de los mismos. En capítulos subsiguientes veremos las estructuras de datos utilizadas
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
1. GRAFOS : CONCEPTOS BASICOS
1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
Grafos. Amalia Duch Brown Octubre de 2007
Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Caminos y Flujos optimales. 2da y 3er clase 2007
Caminos y Flujos optimales 2da y 3er clase 2007 ESQUELETOS OPTIMALES (mínimo) Esqueleto de G =(X,U) es un subgrafo que es un árbol y que contiene todos los vértices de G. Esqueleto Mínimo de G = (X, U,
Algoritmos de Aproximación
Algoritmos de Aproximación Clase 3 Problema de Steiner y TSP Pablo Romero Lunes 8 de agosto de 2016, Montevideo, Uruguay. Contenidos 1 Cubrimiento de Vértices 2 Agenda 1 Cubrimiento de Vértices 2 Definición
Árboles. Un grafo no dirigido es un árbol si y sólo si existe una ruta unica simple entre cualquiera dos de sus vértices.
ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
Árboles de Expansión Mínima. Matemática Discreta. Agustín G. Bonifacio UNSL
UNSL Árboles Definiciones y Ejemplos Caracterización Un árbol T es un grafo simple que satisface lo siguiente: si v y w son vértices en T, entonces existe una trayectoria simple única de v a w. Un árbol
Algoritmos y Estructuras de Datos III
Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Estructura de ciclos en MSDs (Minimally Strong Digraphs)
(Minimally Strong Digraphs) 28 de marzo de 2017 Jesús García MSD versus trees 21 de marzo de 2017 Luis M. Pozo 1 MSD Definición Árbol (grafo conexo minimal) Caracterización MSD versus trees Árbol Árbol
ANÁLISIS Y DISEÑO DE ALGORITMOS
ANÁLISIS Y DISEÑO DE ALGORITMOS CURSO 26/27 BOLETÍN DE PROBLEMAS: ALGORITMOS VORACES Ejercicio 1 Sean n personas, representadas por los Enteros : 1..n, puestas en círculo, y m, un Entero no negativo cualquiera,
Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios
CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
TEORÍA DE GRAFOS PROPUESTA PARA ESCUELAS SECUNDARIAS
TEORÍA DE GRAFOS PROPUESTA PARA ESCUELAS SECUNDARIAS Fabián Nouche Instituto Superior del Profesorado Dr. Joaquín V. González Ciudad de Buenos Aires (Argentina) fnouche@yahoo.com.ar RESUMEN En este trabajo,
Grafos. Algoritmos y Estructuras de Datos III
Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Algorítmica y Complejidad
Departamento Informática Aplicada Algorítmica y omplejidad Tema Algoritmos sobre Grafos urso 0- Grafos. onceptos, Definiciones y Representación. onectividad y recorrido. Árboles de expansión 4. aminos
OBJETIVOS ÍNDICE BIBLIOGRAFÍA
OBJETIVOS Tema 9: GRAFOS Primera Parte Estructuras de Datos y Algoritmos Curso 2002/03 Definiciones formales de grafo y conceptos relacionados Estructuras de datos para representar grafos Algoritmos para
CLAVE V
CLAVE-962-2-V-2-00 -2017 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CURSO: Matemática para computación 2 SEMESTRE: Segundo CÓDIGO DEL CURSO: 962 TIPO DE EXAMEN:
Capítulo 7. Grafos. Continuar
Capítulo 7. Grafos Continuar Introducción Uno de los primeros resultados de la teoría de grafos fue el que obtuvo Leonhard Euler en el siglo XVIII al resolver el problema de los puentes de Königsberg.
Estructuras de Datos y Algoritmos. Grafos
Estructuras de Datos y Algoritmos Grafos Definiciones Grafo modelo para representar relaciones entre elementos de un conjunto. Grafo: (V,E), V es un conjunto de vértices o nodos, con una relación entre
Estructura de Datos Página 1 de 13 ESTRUCTURA DE DATOS
Estructura de Datos Página 1 de 13 ESTRUCTURA DE DATOS Contenido TEMA 4. Grafos 4.1. Grafos 4.1.1. Definición 4.1.2.Conceptos 4.2. Modelado de problemas típicos 4.3. Representación de un grafo a través
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
TIPOS ABSTRACTOS DE DATOS EN HASKELL
TIPOS ABSTRACTOS DE DATOS EN HASKELL ÍNDICE GENERAL 1. Introducción a Haskell 2. Tipos abstractos de datos en Haskell 3. TAD Grafo 4. TAD Montículos 5. Bibliografía INTRODUCCIÓN A HASKELL 1. Introducción
MÉTODOS RISI 2(3), COMPUTACIONALES (2005) ORIENTADOS A LA OBTENCIÓN DEL ÁRBOL EMST: UN APORTE AL PROBLEMA DE STEINER
MÉTODOS RISI 2(3), COMPUTACIONALES 38-42 (2005) ORIENTADOS A LA OBTENCIÓN DEL ÁRBOL EMST: UN APORTE AL PROBLEMA DE STEINER Rev. investig. sist. inform. Facultad de Ingeniería de Sistemas e Informática
Teoría de grafos. Coloración de vértices
Teoría de grafos Coloración de vértices Problema: cuántas jaulas son necesarias para transportar a estos cinco animales de forma que lleguen sanos y salvos a un mismo destino? León Hámster Si dos animales
GRAFOS. Prof. Ing. M.Sc. Fulbia Torres
ESTRUCTURAS DE DATOS 2006 Prof. DEFINICIÓN Un grafo consta de un conjunto de nodos(o vértices) y un conjunto de arcos (o aristas). Cada arco de un grafo se especifica mediante un par de nodos. Denotemos
Entregable 4.- RESUELTO. Semana del 5 de octubre al 11 de octubre
Entregable 4.- RESUELTO Semana del 5 de octubre al 11 de octubre 1. Resuelve los siguientes sistemas de ecuaciones 1. 2x = 5 en Z 7 3x = 1 en Z 5 x = 3 en Z 8 2. 2x = 1 en Z 6 x = 4 en Z 11 3x = 2 en Z
Aplicación de Ordenamiento en Línea: Construcción Eficiente del Árbol Cobertor
Aplicación de Ordenamiento en Línea: Construcción Eficiente del Árbol Cobertor Mínimo * Rodrigo Paredes Centro de Investigación de la Web, Universidad de Chile, Depto. de Ciencias de la Computación, Santiago,
Escuela de algoritmos de aproximación
Escuela de algoritmos de aproximación Módulo 3: Algoritmos de aproximación para problemas de ruteo Francisco Javier Zaragoza Martínez Universidad Autónoma Metropolitana Unidad Azcapotzalco ITAM, de septiembre
Grafos eulerianos. Introducción a los grafos eulerianos GRAFOS EULERIANOS. Contenido. Contenido Introducción a los grafos eulerianos
Grafos eulerianos Introducción a los grafos eulerianos Como saber si un grafo es euleriano Cristina Jordán Lluch Instituto de Matemáticas Multidisciplinar Grupo de Modelización Físico-Matemática Los puentes
Digrafos fuertemente conexos minimales (MSD) vs árboles
Digrafos fuertemente conexos minimales (MSD) vs árboles 21 de marzo de 2017 Digrafos fuertemente conexos minimales (MSD) 21vsde árboles marzo de 2017 1 / 26 Preliminares Deniciones(I): Grafo, digrafo,
Tema 1: Introducción a la Teoría de Grafos
Tema 1: Introducción a la Teoría de Grafos MATEMÁTICA A DISCRETA Nociones básicas Subgrafos. Operaciones con grafos Formas de definir un grafo Isomorfismo de grafos Tema 1: 1 Nociones básicas: Grafo: G
Capítulo 5 Introducción a la teoría de grafos
Capítulo 5 Introducción a la teoría de grafos 5.1. Terminología básica y tipos de grafos Una primera aproximación a la teoría de grafos la tenemos cuando observamos un mapa de carreteras: ciudades (vértices)
TEMA 5 El tipo grafo. Tipo grafo
TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
Cualquier vértice que esté en un ciclo tiene al menos grado 2 (el recíproco no es cierto).
.4 Grafos no dirigidos acíclicos: Árboles.4 Grafos no dirigidos acíclicos: Árboles Hasta ahora hemos buscado caminos y estudiado la conexión de un grafo, sin entrar en el estudio de los ciclos y la aciclicidad.
Tema 6.2: Camino de Menor Valor. CMV: Objetivo. CMV: ejemplo. Ejemplo. Camino de menor valor
Tema.: Camino de Menor Valor Modelización Matemática Máster en Ingeniería de Caminos, Canales y Puertos Camino de menor valor Algoritmos Algoritmo de Dijkstra Algoritmo de Bellman-Ford Ignacio Montes Departamento
M06/5/MATHL/HP3/SPA/TZ0/XX MATEMÁTICAS NIVEL SUPERIOR PRUEBA 3. Lunes 15 de mayo de 2006 (tarde) 1 hora INSTRUCCIONES PARA LOS ALUMNOS
IB MATEMÁTICAS NIVEL SUPERIOR PRUEBA 3 DIPLOMA PROGRAMME PROGRAMME DU DIPLÔME DU BI PROGRAMA DEL DIPLOMA DEL BI 06715 Lunes 15 de mayo de 006 (tarde) 1 hora INSTRUCCIONES PARA LOS ALUMNOS No abra esta
Matemáticas Discretas Tc1003 Teoría de Grafos
Definición. Sea A un grafo. A recibe el nombre de árbol sí y sólo si: A es conexo. A no contiene circuitos. Ejemplos: Definición. Sea A un árbol. Un vértice de grado 1 se llama una hoja. Un vértice de
Algorítmica y Complejidad. Tema 4 Algoritmos sobre grafos.
Algorítmica y Complejidad Tema. Algorítmos sobre grafos. Conceptos, Definiciones y Representación.. Conectividad y recorrido.. Árboles de expansión.. Caminos mínimos. Algorítmos sobre grafos. Conceptos,
Deseamos interconectar entre si todos los ordenadores de un edificio
Teoría de grafos Deseamos interconectar entre si todos los ordenadores de un edificio Tres problemas de conexión: Conectar una serie de ordenadores por pares Procurar que la distancia por cable entre dos
Estructuras de Datos ARBOLES Y GRAFOS
Estructuras de Datos ARBOLES Y GRAFOS Rosa Barrera Capot rosa.barrera@usach.cl Grafo? Características Permiten Modelar un problema Aplicaciones: Ingeniería de Sistemas Modelado de Redes Ingeniería Industrial
LAS TORRES DE HANOI-6 Si quieres saber más
LAS TORRES DE HANOI-6 Si quieres saber más Viaje al país del conocimiento Para este viaje utilizaremos un código: Disco 1: disco mayor Disco 2: disco siguiente al 1 Disco 3: disco siguiente al 2 I: torre