Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURAS III
|
|
|
- Francisco Javier Bustamante Rey
- hace 7 años
- Vistas:
Transcripción
1 Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURAS III Introducción a la Teoría de Elementos Finitos (Elementos Resorte, Barra y Viga) Autores: Ing. Santiago Pezzotti Ing. Federico Antico
2 1-Introducción El método de los elementos finitos (MEF en castellano o FEM en inglés) es un método de cálculo utilizado en diversos problemas de ingeniería, que se basa en considerar al cuerpo o estructura dividido en elementos discretos, con determinadas condiciones de vínculo entre sí, generándose un sistema de ecuaciones que se resuelve numéricamente y proporciona el estado de tensiones y deformaciones. También se utiliza en matemáticas como método nodal aproximado para resolver ecuaciones diferenciales en forma numérica. Es un procedimiento numérico aplicable a un gran número de problemas con condiciones de borde impuestas (en las estructuras las condiciones de borde serian: restricciones y cargas externas). Varios de estos problemas no tienen solución analítica o es muy difícil obtenerla, por lo que se convierte en la única alternativa de resolución. Con este método se pueden resolver sistemas los cuales no son fáciles de resolver mediante modelos matemáticos simples. Existen dos tipos de caminos para su formulación, basándose en el principio de los trabajos virtuales, es decir, formulaciones variacionales, o mediante el método de Garlekin, Método directo o bien con Raleigh Ritz.. Si bien fue originalmente desarrollado para el análisis de estructuras, con este método se pueden representar entre otros, los siguientes fenómenos físicos: Fenómenos termodinámicos: distribución de temperaturas en un sólido. Simulación de efectos dinámicos: Choque de dos cuerpos. Geomecánica: Comportamiento de la corteza terrestre. 2- Concepto La base del método de los elementos finitos es la representación de un cuerpo por un ensamble de subdivisiones llamadas elementos. Estos elementos se interconectan a través de puntos llamados nodos. Una manera de discretizar un cuerpo o estructura es dividirla en un sistema equivalente de cuerpos pequeños, tal que su ensamble representa el cuerpo original. La solución que se obtiene para cada unidad se combina para obtener la solución total. Por ende, La solución del problema consiste en encontrar los desplazamientos de estos puntos y a partir de ellos, las deformaciones y las tensiones del sistema analizado. Las propiedades de los elementos que unen a los nodos, están dadas por el material asignado al elemento, que definen la rigidez del mismo, y la geometría de la estructura a modelizar (a partir de las Leyes de la Elástica). Las deformaciones y las fuerzas externas se relacionan entre si mediante la rigidez y las relaciones constitutivas del elemento. Trabajando en régimen elástico, las ecuaciones que definen el sistema pueden expresarse de forma matricial como se muestra a continuación: Donde : [K]: es la matriz rigidez del sistema {δ}: es el vector desplazamientos {F}: es el vector de esfuerzos [K].{δ}={F} Página 1/26
3 Los tipos de elementos utilizados generalmente en la resolución a través de Fem son: Elementos Lineales (1-D) Estos pueden ser: o o o o Resorte Barras Vigas Caños Elementos Planos (2-D) Estos pueden ser: o o membranas placas Elementos Sólidos (3-D) Es importante destacar que se puede utilizar combinaciones de estos elementos actuando en conjunto. Página 2/26
4 3-Proceso de Análisis por Elementos Finitos El proceso de análisis por elementos finitos se puede describir como: Modelado Geométrico Modelado de Elementos Finitos Definición del Ambiente Análisis Corroboración de Resultados Modelado Geométrico: Creación del modelo matemático del objeto o del conjunto. Reproducción del sólido en forma precisa y de la geometría de la superficie. Modelado de Elementos Finitos: Subdividir la geometría del modelo en elementos discretos. Asignar las propiedades del material y del elemento. Definición del Ambiente: Aplicar las cargas y las condiciones de borde para simular el ambiente de la operación. Análisis: Computar los resultados (tensiones, deformaciones, etc.) a partir de análisis estáticos, dinámicos o de transferencia de calor. Corroboración de Resultados: Comparar los resultados con los criterios de diseño. Rediseñar la estructura y repetir el proceso si fuese necesario. En la actualidad la utilización de este método ha crecido notablemente debido a la utilización de software avanzado (además de un hardware potente que debe poseer gran velocidad y mucha memoria). Los software mas utilizados en la actualidad son: Msc Nastran Msc Patran Ansys Dyna 3D Abaqus Página 3/26
5 Cabe destacar que la utilización de software no implica la obtención del resultado exacto y real, es solo una aproximación y esta en el criterio del usuario el saber discernir entre un resultado coherente y uno que no lo es; además de conocer los márgenes de error y las limitaciones del modelo y el método. 4- Método Directo Página 4/26
6 4-1-Elemento Resorte Dado un resorte con fuerzas aplicadas en la dirección longitudinal del mismo: El sistema se compone de: Dos Nodos: i, j Constante Elástica del Resorte: k El mismo esta sometido: Fuerzas en los Nodos: f i, f j El elemento tiene dos grados de libertad, en el sentido longitudinal del elemento, cualquier desplazamiento de los nodos en el sentido normal al elemento no generara esfuerzos internos: Dos desplazamientos: u i, u j La relación entre la fuerza F y el desplazamiento Δ en régimen lineal será: F= K.Δ donde Δ=u j -u i Donde K es la rigidez del elemento o la constante elástica del resorte. Haciendo equilibrio de fuerzas internas en los Nodos: Nodo i: Nodo j: Expresado matricialmente: O bien, k.u =f Donde: k: es la matriz rigidez u: es la vector desplazamiento f: es la vector de fuerzas internas Página 5/26
7 4-2-Sistema de Resortes Considerando un par de resortes en serie: Para el Elemento 1: Para el Elemento 2: Donde es la fuerza interna local del Nodo i actuando en el Elemento m (i=1,2). Considerando la condición de equilibrio estático de fuerzas: F externas = F internas Nodo 1: Nodo 2: Nodo 3: Desarrollando con los valores de las fuerzas internas en función de la rigidez de cada elemento: Página 6/26
8 De forma Matricial: O bien, Donde: K.U=F K: es la matriz rigidez del sistema completo de resortes Se puede plantear por separado y luego plantear superposición: Planteando superposición se obtiene: A modo de ejemplo si consideramos un sistema que posee las siguientes condiciones: Reemplazando: Se reduce a: Página 7/26
9 Y, Como incógnita tenemos: Resolviendo, Reemplazando se obtiene la fuerza de reacción: Como conclusión, para un sistema de n nodos, el método de elementos finitos permite generar n ecuaciones, las cuales deberán tener n incógnitas para ser un sistema definido. Las incógnitas podrán ser parte del vector desplazamiento o ser parte del vector fuerza. Cada nodo deberá tener su desplazamiento o su fuerza actuante como condición de borde impuesta. Este sistema permite, cómo veremos más adelante resolver sistemas isoestáticos e hiperestáticos sin necesidad de cambiar el método. Página 8/26
10 4-3-Elemento Barra en Una Dimensión Consideremos una barra de sección constante: El sistema se compone de: Dos Nodos: i, j Modulo de Elasticidad E Área de la Sección Transversal A Longitud del Elemento L El mismo esta sometido: Fuerzas en los Nodos: f i, f j El elemento tiene dos grados de libertad, en el sentido longitudinal del elemento, cualquier desplazamiento de los nodos en el sentido normal al elemento no generara esfuerzos internos: Dos desplazamientos: u i, u j Sabiendo que la rigidez a tracción / compresión de una barra es: Y haciendo una analogía con el elemento resorte, tenemos que: Por lo tanto, O bien, Página 9/26
11 Por lo tanto, la ecuación de equilibrio del Elemento será: Para la resolución de este sistema se procede de la misma manera que en el elemento resorte. 4-4-Elemento Barra en Dos Dimensiones Local Global x,y X,Y u i,v i u i,v i 1 grado de Libertad 2 grados de Libertad Nota: El desplazamiento lateral v i no contribuye a la deformación de la barra. La idea es trabajar con las coordenadas globales, por lo tanto se deben hacer las siguientes transformaciones: Donde: Página 10/26
12 Escrito en forma matricial: O bien, Donde la matriz transformación: Donde la relación con la matriz ortogonal: A modo de ejemplo, se puede decir que para un sistema de elemento barra con dos nodos tenemos que: O bien, Con, Las fuerzas nodales son transformadas de la misma manera: Para obtener la matriz rigidez en dos dimensiones: En el sistema local de coordenadas tenemos que: Página 11/26
13 Esto se puede escribir en su totalidad como: O bien, Utilizando las transformaciones Obtenemos: Multiplicando ambos lados por T T y como T T *T=I, obtenemos: La matriz rigidez en el sistema global quedara de la siguiente manera: La cual es una matriz simétrica de 4X4. Escrita de manera explicita tenemos que: Donde los cosenos directores l y m son: 4-5-Elemento Viga Página 12/26
14 Se considera una viga en el plano. Esta toma esfuerzos de Corte, Axiles y Momentos, todas consideradas en el plano. Cada Nodo posee tres Grados de Libertad (u, v, q). Un elemento que toma estas cargas, tiene asociado para el calculo a E, J, l y A. El sistema se compone de: Dos Nodos: i, j Modulo de Elasticidad E Área de la Sección Transversal A Longitud del Elemento L Momento de Inercia I El mismo esta sometido: Fuerzas en los Nodos: F i, F j, V i, V j Momento en los Nodos: M i, M j Habrá tres grados de libertad por cada nodo Cuatro desplazamientos: u i, u j, v i, v j Dos Giros: θ i, θ j Para crear la Matriz Rigidez se suponen casos con desplazamientos unitarios, que luego mediante Superposición se ensamblan y dan forma a dicha matriz. Se adoptan giros en sentido horario y desplazamientos positivos. Se supone u i =1 u j, v i, v j, θ i, θ j =0 Página 13/26
15 Aplicando la Ley de Hooke, tal como se hace con elemento barra, tenemos que: Por lo tanto, Realizando un equilibrio de fuerzas, H EA = l i u i H i = EA l H j EA = l Se supone v i =1 u i, u j, v j, θ i, θ j = 0 Se puede demostrar calculando por Método de las Fuerzas que para un Desplazamiento Transversal en el extremo i, los esfuerzos en el sistema son: 12EJ 6EJ V i = M 3 i = 2 l l V j 12EJ l 6EJ l = M 3 j = 2 Se supone θ i =1 H = 0 H = 0 i j Página 14/26
16 u i, u j, v i, v j, θ j = 0 De la misma manera que en el caso anterior, tenemos que: V i = 6EJ 2 l 4EJ M i = l V j = 6EJ 2 l 2EJ M j = l H = 0 H = 0 i j Procediendo de forma análoga para los desplazamientos del Nodo j, obtendremos los restantes coeficientes de la Matriz Rigidez del Elemento. 5- Ejemplos Prácticos Página 15/26
17 5-1-Elemento Resorte Sea un sistema de resortes en serie, con una carga P aplicada: Datos: Se pide: Solución a) Encontrar la matriz rigidez del sistema. b) Desplazamientos en los Nodos 2 y 3. c) Las fuerzas en los empotramientos (Nodos 1 y 4). d) La fuerza en el resorte 2. a) La matriz rigidez de cada elemento es: Aplicando el principio de superposición se obtiene la matriz rigidez del sistema completo: Página 16/26
18 o bien, La Ecuación Matricial de Equilibrio quedara de la siguiente manera: b) Aplicando las Condiciones de Borde: en la Ecuación Matricial de Equilibrio y tachando la primera y cuarta fila y columna, tenemos que: Cuya solución es: Página 17/26
19 c) Con la primera y cuarta fila de la Ecuación de Equilibrio, y con los datos de los desplazamientos ya calculados, tenemos que: d) La ecuación de equilibrio del elemento 2 es: donde, Por lo tanto se puede calcular, la fuerza como: 5-2- Sistema de Resortes Sea un sistema de resortes en serie-paralelo con cargas aplicadas: Página 18/26
20 Se pide: Para el Sistema de Resortes de la figura, cuyos nodos fueron numerados de forma arbitraria, encontrar la Matriz Rigidez Global. Solución: Se construye una Tabla de Conectividad de Elementos: La matriz rigidez de cada elemento: Por lo tanto, aplicando el Principio de Superposición, obtendremos la Matriz Rigidez Global del Sistema: Página 19/26
21 5-3-Elemento Barra Sean dos barras de igual Longitud, igual Modulo de Elasticidad y el Área de una es dos veces la de la otra: Se pide: Hallar el desplazamiento en el Nodo 2. Solución: La Matriz Rigidez de cada elemento: Elemento 1 Elemento 2 Aplicando el Principio de Superposición, obtenemos la Matriz Rigidez Global, y así, obtenemos la Ecuación de Equilibrio. Aplicando las Condiciones de Borde: Página 20/26
22 y reemplazando, se obtiene: Para hallar el desplazamiento en el Nodo 2, utilizamos solo la segunda fila: Por lo tanto, 5-4-Elemento Barra en Dos Dimensiones Sean dos barras idénticas que poseen el mismo Modulo de Elasticidad, la misma Área Transversal y la misma Longitud: Página 21/26
23 Se pide: Hallar el desplazamiento del Nodo 2. Solución: En el sistema Local de Coordenadas, la matriz rigidez de los elementos es: Estas matrices no pueden ser ensambladas juntas, ya que cada una esta en diferentes Sistemas Coordinados. Por esta razón se debe trabajar con un Sistema Coordenado Global. Trabajaremos con cada elemento por separado: Elemento 1: La matriz rigidez del elemento 1 respecto a la Terna Global es: Elemento 2: La matriz rigidez del elemento 1 respecto a la Terna Global es: Página 22/26
24 Aplicando el Principio de Superposición, podemos armar la Ecuación de Equilibrio: Utilizando las Condiciones de Borde: Consideramos solo la tercer y cuarta fila, junto a la tercer y cuarta columna, y obtenemos: Resolviendo: 5-5-Elemento Viga Sea una viga empotrada-empotrada, con una carga P aplicada en L/2 y un Momento actuando en el mismo punto: Página 23/26
25 Se pide: a) Hallar la Rotación y Deflexión del Nodo 2. b) Hallar las Reacciones de Vinculo en los Empotramientos. Nota: Para este ejemplo, se tomo como convención que el momento antihorario es positivo. No solo como condición de borde, sino en el análisis matricial, y es por eso que la matriz rigidez difiere en signos con la de la explicación de la pagina 15. Solución: a) La Matriz Rigidez de cada Elemento es: La Ecuación de Equilibrio Global es: Página 24/26
26 Aplicando las Condiciones de Borde: Reemplazamos y obtenemos: Por lo tanto, resolviendo: b) Reemplazando en la Matriz Global, tenemos: Resolviendo tenemos, Página 25/26
27 6- Referencias Análisis de Estructuras mediante el Método de los Elementos Finitos. Ing. Ruben Lopez Triaca. Universidad Nacional del Centro de la Provincia de Buenos Aires. Introduction to Finite Element Method. Yijun Liu. University of Cincinnati. Finite Elements in Solids and Structures. Astley. Resistencia de Materiales. Stiopin Página 26/26
ESTRUCTURAS III Para alumnos de la carrera de Ingeniería Aeronáutica y Mecánica de la UNLP
 Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURAS III Para alumnos de la carrera de Ingeniería Aeronáutica y Mecánica de la UNLP Introducción a la Teoría de Elementos Finitos (Tratamiento
Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURAS III Para alumnos de la carrera de Ingeniería Aeronáutica y Mecánica de la UNLP Introducción a la Teoría de Elementos Finitos (Tratamiento
INDICE Prefacio 1. Esfuerzo Parte A. Conceptos generales. Esfuerzo Parte B. Análisis de esfuerzo de barras cargadas axialmente
 INDICE Prefacio XV 1. Esfuerzo 1-1. Introducción 1 Parte A. Conceptos generales. Esfuerzo 1-2. Método de las secciones 3 1-3. Definición de esfuerzo 4 1-4. Tensor esfuerzo 7 1-5. Ecuaciones diferenciales
INDICE Prefacio XV 1. Esfuerzo 1-1. Introducción 1 Parte A. Conceptos generales. Esfuerzo 1-2. Método de las secciones 3 1-3. Definición de esfuerzo 4 1-4. Tensor esfuerzo 7 1-5. Ecuaciones diferenciales
20 Dinámica + elementos finitos (caso lineal) Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales
 20 Dinámica + elementos finitos (caso lineal) Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Ecuaciones de la elástodinámica Las ecuaciones diferenciales
20 Dinámica + elementos finitos (caso lineal) Diego Andrés Alvarez Marín Profesor Asociado Universidad Nacional de Colombia Sede Manizales 1 Ecuaciones de la elástodinámica Las ecuaciones diferenciales
ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250)
 Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS
 Instituto Tecnológico de Sonora Ciudad Obregón, Sonora. Análisis Estructural, Plan de Estudios 2009 Ing. Jesús Horacio Zazueta Villaseñor MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS 1 Supuestos para el
Instituto Tecnológico de Sonora Ciudad Obregón, Sonora. Análisis Estructural, Plan de Estudios 2009 Ing. Jesús Horacio Zazueta Villaseñor MÉTODO DE LA RIGIDEZ PARA ARMADURAS PLANAS 1 Supuestos para el
Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación
 Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación DIFERENCIAS FINITAS Ayudante: Rodrigo Torres Aguirre El método
Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación DIFERENCIAS FINITAS Ayudante: Rodrigo Torres Aguirre El método
ν= 0.3; E=1.8e10; t= 0.05; q=-0.5;
 Analisis de placas y lamina 56 7.- COMPARACIÓN DE MÉTODOS MEDIANTE EJEMPLOS NUMÉRICOS DE CÁLCULO DE PLACAS A continuación se va ha hacer un análisis comparativo de los resultados obtenidos, para el cálculo
Analisis de placas y lamina 56 7.- COMPARACIÓN DE MÉTODOS MEDIANTE EJEMPLOS NUMÉRICOS DE CÁLCULO DE PLACAS A continuación se va ha hacer un análisis comparativo de los resultados obtenidos, para el cálculo
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
Conceptos básicos de sistemas de ecuaciones diferenciales en la simulación de procesos ambientales y químicos
 Conceptos básicos de sistemas de ecuaciones diferenciales en la simulación de procesos ambientales y químicos Apellidos, nombre Departamento Centro Torregrosa López, Juan Ignacio (jitorreg@iqn.upv.es)
Conceptos básicos de sistemas de ecuaciones diferenciales en la simulación de procesos ambientales y químicos Apellidos, nombre Departamento Centro Torregrosa López, Juan Ignacio (jitorreg@iqn.upv.es)
Carrera: MCT - 0525. Participantes Representantes de las academias de Ingeniería Mecánica de Institutos Tecnológicos. Academia de Ingeniería
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Mecánica de Materiales I Ingeniería Mecánica MCT - 0525 2 3 7 2.- HISTORIA DEL
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Mecánica de Materiales I Ingeniería Mecánica MCT - 0525 2 3 7 2.- HISTORIA DEL
Celosía plana. Definición
 Celosías planas Celosía plana. Definición Modelo idealizado de una estructura reticular, formada por barras rectas de canto despreciable frente a su longitud. Barras unidas en sus extremos mediante articulaciones
Celosías planas Celosía plana. Definición Modelo idealizado de una estructura reticular, formada por barras rectas de canto despreciable frente a su longitud. Barras unidas en sus extremos mediante articulaciones
ASIGNATURA: TEORÍA DE ESTRUCTURAS Y CONSTRUCCIONES INDUSTRIALES
 ASIGNATURA: TEORÍA DE ESTRUCTURAS Y CONSTRUCCIONES INDUSTRIALES EXPERIENCIA PILOTO DE CRÉDITOS EUROPEOS UNIVERSIDADES ANDALUZAS DATOS BÁSICOS DE LA ASIGNATURA NOMBRE: Teoría de estructuras y construcciones
ASIGNATURA: TEORÍA DE ESTRUCTURAS Y CONSTRUCCIONES INDUSTRIALES EXPERIENCIA PILOTO DE CRÉDITOS EUROPEOS UNIVERSIDADES ANDALUZAS DATOS BÁSICOS DE LA ASIGNATURA NOMBRE: Teoría de estructuras y construcciones
Programa de la asignatura. ASIGNATURA: Elasticidad y Resistencia de Materiales. Código: 141212004 Titulación: INGENIERO INDUSTRIAL Curso: 2º
 ASIGNATURA: Elasticidad y Resistencia de Materiales Código: 141212004 Titulación: INGENIERO INDUSTRIAL Curso: 2º (2012 / 2013) Profesor(es) responsable(s): - MARIANO VICTORIA NICOLÁS Departamento: ESTRUCTURAS
ASIGNATURA: Elasticidad y Resistencia de Materiales Código: 141212004 Titulación: INGENIERO INDUSTRIAL Curso: 2º (2012 / 2013) Profesor(es) responsable(s): - MARIANO VICTORIA NICOLÁS Departamento: ESTRUCTURAS
Tema 9. Espacio de Estados : Representación y propiedades importantes
 Ingeniería de Control Tema 9. Espacio de Estados : Representación y propiedades importantes Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Esquema del tema 9.1. Representación de sistemas discretos en
Ingeniería de Control Tema 9. Espacio de Estados : Representación y propiedades importantes Daniel Rodríguez Ramírez Teodoro Alamo Cantarero Esquema del tema 9.1. Representación de sistemas discretos en
1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte
 Trabajo Práctico Cálculo de Vigas. 1 Introducción 1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte Como se explicó
Trabajo Práctico Cálculo de Vigas. 1 Introducción 1.1 Estructuras isostáticas e hiperestáticas; cálculo de los diagramas de características en vigas, momento flector y esfuerzo de corte Como se explicó
CAPÍTULO V 10 EJERCICIOS RESUELTOS
 CAPÍTULO V 10 EJERCICIOS RESUELTOS Este último capítulo contiene 10 ejercicios complementarios (propuestos por los alumnos de la asignatura) que permiten poner en práctica los conocimientos adquiridos
CAPÍTULO V 10 EJERCICIOS RESUELTOS Este último capítulo contiene 10 ejercicios complementarios (propuestos por los alumnos de la asignatura) que permiten poner en práctica los conocimientos adquiridos
Asignatura: CÁLCULO DE ESTRUCTURAS (Código 452) AEROPUERTOS
 Asignatura: CÁLCULO DE ESTRUCTURAS (Código 452) Especialidad: AEROPUERTOS Curso/Cuatrimestre: TERCER CURSO / PRIMER CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 6,0 Conocimientos previos: Departamento:
Asignatura: CÁLCULO DE ESTRUCTURAS (Código 452) Especialidad: AEROPUERTOS Curso/Cuatrimestre: TERCER CURSO / PRIMER CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 6,0 Conocimientos previos: Departamento:
Asignatura: TEORÍA DE ESTRUCTURAS (Código 531) EQUIPOS Y MATERIALES
 Asignatura: TEORÍA DE ESTRUCTURAS (Código 531) Especialidad: EQUIPOS Y MATERIALES Curso/Cuatrimestre: SEGUNDO CURSO / PRIMER CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 7,5 Conocimientos previos: Departamento:
Asignatura: TEORÍA DE ESTRUCTURAS (Código 531) Especialidad: EQUIPOS Y MATERIALES Curso/Cuatrimestre: SEGUNDO CURSO / PRIMER CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 7,5 Conocimientos previos: Departamento:
La ecuación de segundo grado para resolver problemas.
 La ecuación de segundo grado para resolver problemas. Como bien sabemos, una técnica potente para modelizar y resolver algebraicamente los problemas verbales es el uso de letras para expresar cantidades
La ecuación de segundo grado para resolver problemas. Como bien sabemos, una técnica potente para modelizar y resolver algebraicamente los problemas verbales es el uso de letras para expresar cantidades
Herramientas digitales de auto-aprendizaje para Matemáticas
 real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
3. Funciones y gráficas
 Componente: Procesos físicos. Funciones gráficas.1 Sistemas coordenados En la maoría de estudios es necesario efectuar medidas relacionadas con los factores que intervienen en un fenómeno. Los datos que
Componente: Procesos físicos. Funciones gráficas.1 Sistemas coordenados En la maoría de estudios es necesario efectuar medidas relacionadas con los factores que intervienen en un fenómeno. Los datos que
Lección 1. Algoritmos y conceptos básicos.
 Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Figura 1.3.1. Sobre la definición de flujo ΔΦ.
 1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
Aplicaciones de las integrales dobles
 Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS. Este capítulo comprende diversas propiedades geométricas de secciones (para casos
 CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
EJERCICIOS RESUELTOS DE SISTEMAS LINEALES
 EJERCICIOS RESUELTOS DE SISTEMAS LINEALES 1. Dado el sistema de ecuaciones lineales: 2x + 3y 3 4x +5y 6 a) Escribir la expresión matricial del sistema. b) Discutir el sistema. c) Resolver el sistema por
EJERCICIOS RESUELTOS DE SISTEMAS LINEALES 1. Dado el sistema de ecuaciones lineales: 2x + 3y 3 4x +5y 6 a) Escribir la expresión matricial del sistema. b) Discutir el sistema. c) Resolver el sistema por
Representantes de las academias de Ingeniería Civil de los Institutos Tecnológicos.
 l.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Resistencia de Materiales Carrera : Ingeniería Civil Clave de la asignatura: Horas teorías - Horas prácticas - créditos: 2-4-8 2.- HISTORIA DEL PROGRAMA
l.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Resistencia de Materiales Carrera : Ingeniería Civil Clave de la asignatura: Horas teorías - Horas prácticas - créditos: 2-4-8 2.- HISTORIA DEL PROGRAMA
Análisis Estructural - 2009 Trabajo práctico de dinámica estructural: Superposición modal
 Análisis Estructural - 9 Enunciado Dada la estructura de la Figura, idealizada mediante un marco con vigas rígidas y columnas inextensibles, sometida a una carga armónica lateral de 8 t, se pide: ) Determinar
Análisis Estructural - 9 Enunciado Dada la estructura de la Figura, idealizada mediante un marco con vigas rígidas y columnas inextensibles, sometida a una carga armónica lateral de 8 t, se pide: ) Determinar
ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO. Mercedes López Salinas
 ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO Mercedes López Salinas PhD. Ing. Civil elopez@uazuay.edu.ec ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil y
ETAPAS BÁSICAS DEL ANÁLISIS MATRICIAL DE UN SISTEMA DISCRETO Mercedes López Salinas PhD. Ing. Civil elopez@uazuay.edu.ec ELEMENTOS FINITOS Facultad de Ciencia y Tecnología Escuela de Ingeniería Civil y
Fig. 18. Flexión asimétrica o inclinada de una viga con sección transversal doblemente simétrica
 8. Flexión Asimétrica (Biaxial) de Vigas 8.1 Introducción En esta sección, el análisis de la flexión en elementos-vigas, estudiado en las secciones precedentes, es ampliado a casos más generales. Primero,
8. Flexión Asimétrica (Biaxial) de Vigas 8.1 Introducción En esta sección, el análisis de la flexión en elementos-vigas, estudiado en las secciones precedentes, es ampliado a casos más generales. Primero,
3. Resolver triángulos rectángulos utilizando las definiciones de las razones trigonométricas.
 Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
INSTITUTO TECNOLÓGICO DE TIJUANA ECUACIONES DIFERENCIALES. Portafolio Parte 2
 INSTITUTO TECNOLÓGICO DE TIJUANA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE ENERO JUNIO 2014 INGENIERÍA EN SISTEMAS COMPUTACIONALES ECUACIONES DIFERENCIALES Portafolio Parte 2 Indicadores 19-23, 25,
INSTITUTO TECNOLÓGICO DE TIJUANA DEPARTAMENTO DE SISTEMAS Y COMPUTACIÓN SEMESTRE ENERO JUNIO 2014 INGENIERÍA EN SISTEMAS COMPUTACIONALES ECUACIONES DIFERENCIALES Portafolio Parte 2 Indicadores 19-23, 25,
PNF en Mecánica Vibraciones Mecánicas Prof. Charles Delgado
 Vibraciones en máquinas LOS MOVIMIENTOS VIBRATORIOS en máquinas se presentan cuando sobre las partes elásticas actúan fuerzas variables. Generalmente, estos movimientos son indeseables, aun cuando en algunos
Vibraciones en máquinas LOS MOVIMIENTOS VIBRATORIOS en máquinas se presentan cuando sobre las partes elásticas actúan fuerzas variables. Generalmente, estos movimientos son indeseables, aun cuando en algunos
CAPITULO 7.SERIES DE FOURIER. 7.1. Sistemas de funciones ortogonales
 CAPITULO 7.SERIES DE FOURIER La publicación por Fourier (1768-1830) de la " Teoría analítica del calor ", fue de una influencia decisiva en las matemáticas posteriores. Se supone en ella que cualquier
CAPITULO 7.SERIES DE FOURIER La publicación por Fourier (1768-1830) de la " Teoría analítica del calor ", fue de una influencia decisiva en las matemáticas posteriores. Se supone en ella que cualquier
FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación
 FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación Unidad 1: El movimiento de los cuerpos i. Objetivos Observar las distintas magnitudes físicas que se ponen de manifiesto
FÍSICA Y QUÍMICA 4º ESO. OBJETIVOS, CONTENIDOS Y CRITERIOS DE EVALUACIÓN. 1ª Evaluación Unidad 1: El movimiento de los cuerpos i. Objetivos Observar las distintas magnitudes físicas que se ponen de manifiesto
TEMA I. Teoría de Circuitos
 TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos. 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos. 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
Advanced Engineering for Real Solutions CURSO BÁSICO DE ELEMENTOS FINITOS 1.3 PARTE 1: ELEMENTO BARRA EN 1D
 CURSO BÁSICO DE ELEMENTOS FINITOS.3 PARTE : ELEMENTO BARRA EN D Sistema MEF Modelos Matemáticos Derivación de la matriz de rigidez Álgebra matricial y solución de ecuaciones Métodos Numéricos Ingeniería
CURSO BÁSICO DE ELEMENTOS FINITOS.3 PARTE : ELEMENTO BARRA EN D Sistema MEF Modelos Matemáticos Derivación de la matriz de rigidez Álgebra matricial y solución de ecuaciones Métodos Numéricos Ingeniería
FLEXIÓN DE UNA VIGA DELGADA EN VOLADIZO BAJO LA HIPÓTESIS DE NO LINEALIDAD GEOMÉTRICA
 VIII Congreso Nacional de Propiedades Mecánicas de Sólidos, Gandia 00 933-94 FLEXIÓN DE UNA VIGA DELGADA EN VOLADIZO BAJO LA HIPÓTESIS DE NO LINEALIDAD GEOMÉTRICA T. Beléndez a, M. Pérez-Polo b, y A. Beléndez
VIII Congreso Nacional de Propiedades Mecánicas de Sólidos, Gandia 00 933-94 FLEXIÓN DE UNA VIGA DELGADA EN VOLADIZO BAJO LA HIPÓTESIS DE NO LINEALIDAD GEOMÉTRICA T. Beléndez a, M. Pérez-Polo b, y A. Beléndez
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL
 U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL RESISTENCIA DE MATERIALES SILABO I. DATOS GENERALES CODIGO CARRERA
U N I V E R S I D A D A L A S P E R U A N A S FACULTAD DE INGENIERÍAS Y ARQUITECTURA ESCUELA ACADÉMICO PROFESIONAL DE INGENIERÍA INDUSTRIAL RESISTENCIA DE MATERIALES SILABO I. DATOS GENERALES CODIGO CARRERA
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
Sistema de ecuaciones algebraicas
 Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Espacio de estado.- el espacio n dimensional cuyos ejes de coordenadas consisten en el eje X1, X2... Xn y se denomina espacio de estado
 ANÁLII DE ITEMA DE CONTROL CON EL EPACIO DE ETADO La teoria de control clásica se basa en técnicas gráficas de tanteo y error mientras el control moderno es mas preciso Además se puede usar en sistemas
ANÁLII DE ITEMA DE CONTROL CON EL EPACIO DE ETADO La teoria de control clásica se basa en técnicas gráficas de tanteo y error mientras el control moderno es mas preciso Además se puede usar en sistemas
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO 82 Sea T una transformación afín definida por sus ecuaciones: = 2+ 2x y ' = 2+ 2y z' = 2+ 2z a) Clasificar T y hallar sus elementos característicos b)
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL ESPACIO 82 Sea T una transformación afín definida por sus ecuaciones: = 2+ 2x y ' = 2+ 2y z' = 2+ 2z a) Clasificar T y hallar sus elementos característicos b)
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES
 CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES P ÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 215-216 MATERIA: MATEMÁTICAS II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Después
UNIVERSIDADES P ÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO 215-216 MATERIA: MATEMÁTICAS II MODELO INSTRUCCIONES GENERALES Y VALORACIÓN Después
Solución de sistemas de ecuaciones lineales: Introducción y conceptos generales
 Solución de sistemas de ecuaciones lineales: Introducción y conceptos generales Ing. Jesús Javier Cortés Rosas M. en A. Miguel Eduardo González Cárdenas M. en A. Víctor D. Pinilla Morán * 2011 Resumen
Solución de sistemas de ecuaciones lineales: Introducción y conceptos generales Ing. Jesús Javier Cortés Rosas M. en A. Miguel Eduardo González Cárdenas M. en A. Víctor D. Pinilla Morán * 2011 Resumen
Mecánica Vectorial Cap. 3. Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D.
 Mecánica Vectorial Cap. 3 Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D. Cómo tener éxito en Matemáticas? Paso 1: El trabajo duro triunfa sobre el talento natural. Paso 2: Mantenga una mente abierta.
Mecánica Vectorial Cap. 3 Juan Manuel Rodríguez Prieto I.M., M.Sc., Ph.D. Cómo tener éxito en Matemáticas? Paso 1: El trabajo duro triunfa sobre el talento natural. Paso 2: Mantenga una mente abierta.
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales El sistema de ecuaciones lineales como modelo matemático de problemas Los sistemas de ecuaciones lineales permiten el planteamiento de problemas y soluciones que toman en
Sistemas de Ecuaciones Lineales El sistema de ecuaciones lineales como modelo matemático de problemas Los sistemas de ecuaciones lineales permiten el planteamiento de problemas y soluciones que toman en
Curso de Elemento Finito con el software ALGOR
 Curso de Elemento Finito con el software ALGOR Facultad de Ingeniería, UNAM www.algor.com M. en I. Alejandro Farah Instituto de Astronomía, UNAM www.astroscu.unam.mx/~farah Contenido general: - La teoría
Curso de Elemento Finito con el software ALGOR Facultad de Ingeniería, UNAM www.algor.com M. en I. Alejandro Farah Instituto de Astronomía, UNAM www.astroscu.unam.mx/~farah Contenido general: - La teoría
TRA NSFORMACIO N ES LIN EA LES
 TRA NSFORMACIO N ES LIN EA LES C o m p uta c i ó n G r á fica Tipos de Datos Geométricos T Un punto se puede representar con tres números reales [x,y,z] que llamaremos vector coordenado. Los números especifican
TRA NSFORMACIO N ES LIN EA LES C o m p uta c i ó n G r á fica Tipos de Datos Geométricos T Un punto se puede representar con tres números reales [x,y,z] que llamaremos vector coordenado. Los números especifican
Tema 1. Álgebra lineal. Matrices
 1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
10. 1 Definición de espacio euclídeo.
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS 10. ESPACIOS EUCLÍDEOS 10. 1 Definición de espacio euclídeo. Producto escalar
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS 10. ESPACIOS EUCLÍDEOS 10. 1 Definición de espacio euclídeo. Producto escalar
[GEOGEBRA] Innovación Educativa. Ricardo Villafaña Figueroa
![[GEOGEBRA] Innovación Educativa. Ricardo Villafaña Figueroa [GEOGEBRA] Innovación Educativa. Ricardo Villafaña Figueroa](/thumbs/40/21834013.jpg) 2009 Innovación Educativa [GEOGEBRA] Una introducción a la geometría interactiva y cálculo visual a través de, una herramienta computacional sin costo que facilita y apoya la enseñanza y el análisis de
2009 Innovación Educativa [GEOGEBRA] Una introducción a la geometría interactiva y cálculo visual a través de, una herramienta computacional sin costo que facilita y apoya la enseñanza y el análisis de
Estática. Equilibrio de una Partícula
 Estática 3 Equilibrio de una Partícula Objetivos Concepto de diagrama de cuerpo libre para una partícula. Solución de problemas de equilibrio de una partícula usando las ecuaciones de equilibrio. Índice
Estática 3 Equilibrio de una Partícula Objetivos Concepto de diagrama de cuerpo libre para una partícula. Solución de problemas de equilibrio de una partícula usando las ecuaciones de equilibrio. Índice
CURSO: MECÁNICA DE SÓLIDOS II UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO: MECÁNICA DE SÓLIDOS II PROFESOR: ING. JORGE A. MONTAÑO PISFIL CURSO DE
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO: MECÁNICA DE SÓLIDOS II PROFESOR: ING. JORGE A. MONTAÑO PISFIL CURSO DE
TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL
 INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación Numérica y Control
INTRODUCCIÓN AL MÉTODO DE LOS ELEMENTOS FINITOS TRABAJO PRÁCTICO 4 PROBLEMA DE ELASTICIDAD LINEAL Estudiante FREDY ANDRÉS MERCADO NAVARRO Pasaporte: 98 773.532 Maestría en Simulación Numérica y Control
TRATAMIENTO METODOLÓGICO DE LA UNIDAD 3 DE 9NO GRADO SISTEMA DE ECUACIONES LINEALES
 TRATAMIENTO METODOLÓGICO DE LA UNIDAD 3 DE 9NO GRADO SISTEMA DE ECUACIONES LINEALES I). Lugar que ocupa la unidad. La unidad Sistema de ecuaciones lineales es la tercera unidad dentro del programa de Matemática
TRATAMIENTO METODOLÓGICO DE LA UNIDAD 3 DE 9NO GRADO SISTEMA DE ECUACIONES LINEALES I). Lugar que ocupa la unidad. La unidad Sistema de ecuaciones lineales es la tercera unidad dentro del programa de Matemática
PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO
 PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO Parte I: MOMENTOS DE INERCIA Objetivo: Determinar experimentalmente el momento de inercia de un disco respecto a su centro de gravedad y respecto a distintos
PRÁCTICA: MOMENTOS DE INERCIA Y PÉNDULO FÍSICO Parte I: MOMENTOS DE INERCIA Objetivo: Determinar experimentalmente el momento de inercia de un disco respecto a su centro de gravedad y respecto a distintos
GEOMETRÍA ANALÍTICA EN EL PLANO
 GEOMETRÍA ANALÍTICA EN EL PLANO Coordenadas cartesianas Sistema de ejes Cartesianos: Dicho nombre se debe a Descartes, el cual tuvo la idea de expresar un objeto geométrico como un punto o una recta, mediante
GEOMETRÍA ANALÍTICA EN EL PLANO Coordenadas cartesianas Sistema de ejes Cartesianos: Dicho nombre se debe a Descartes, el cual tuvo la idea de expresar un objeto geométrico como un punto o una recta, mediante
Calcular el momento en el apoyo central, y dibujar los diagramas de esfuerzos. 6 m
 Elasticidad y Resistencia de Materiales Escuela Politécnica Superior de Jaén UNIVERSIDAD DE JAÉN Departamento de Ingeniería Mecánica y Minera Mecánica de Medios Continuos y Teoría de Estructuras Relación
Elasticidad y Resistencia de Materiales Escuela Politécnica Superior de Jaén UNIVERSIDAD DE JAÉN Departamento de Ingeniería Mecánica y Minera Mecánica de Medios Continuos y Teoría de Estructuras Relación
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Matemáticas 4 Enero 2016
 Laboratorio #1 Vectores I.- Calcule el producto escalar de los dos vectores y el coseno del ángulo entre ellos. 1) u = 3i + 2j 4k; v = i + 5j 3k 2) u = i + 2j 3k; v = 1i 2j + 3k 3) u = 1 2 i + 1 3 j +
Laboratorio #1 Vectores I.- Calcule el producto escalar de los dos vectores y el coseno del ángulo entre ellos. 1) u = 3i + 2j 4k; v = i + 5j 3k 2) u = i + 2j 3k; v = 1i 2j + 3k 3) u = 1 2 i + 1 3 j +
Tema 5: Sistemas de Ecuaciones Lineales
 Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
2.- Sistemas de ecuaciones Lineales
 .- Sistemas de ecuaciones Lineales..- Definición, Clasificación de los sistemas lineales y tipos de solución. Definición Una ecuación lineal con las variables escribirse en la forma,..., n es una ecuación
.- Sistemas de ecuaciones Lineales..- Definición, Clasificación de los sistemas lineales y tipos de solución. Definición Una ecuación lineal con las variables escribirse en la forma,..., n es una ecuación
Asignatura: CÁLCULO DE ESTRUCTURAS (Código 142) AERONAVES
 Asignatura: CÁLCULO DE ESTRUCTURAS (Código 142) Especialidad: AERONAVES Curso/Cuatrimestre: SEGUNDO CURSO / SEGUNDO CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 4,5 Conocimientos previos: Departamento:
Asignatura: CÁLCULO DE ESTRUCTURAS (Código 142) Especialidad: AERONAVES Curso/Cuatrimestre: SEGUNDO CURSO / SEGUNDO CUATRIMESTRE Tipo de Materia: TRONCAL Créditos: 4,5 Conocimientos previos: Departamento:
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Elasticidad. Bogotá D.C., 10 de marzo de 2014. *d.villota@javeriana.edu.co, *mara.salgado90@gmail.com, *aguirrek@javeriana.edu.co.
 Elasticidad Mara Salgado 1*, Diego Villota Erazo 1*, Katherine Aguirre Guataqui 1*. Bogotá D.C., 10 de marzo de 2014 Departamento de Matemáticas, Laboratorio de Física Biomecánica, pontificia Universidad
Elasticidad Mara Salgado 1*, Diego Villota Erazo 1*, Katherine Aguirre Guataqui 1*. Bogotá D.C., 10 de marzo de 2014 Departamento de Matemáticas, Laboratorio de Física Biomecánica, pontificia Universidad
2. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM
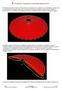 . ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
. ANÁLISIS DEL TECHO DE UN AUDITORIO MEDIANTE FEM El Objetivo es analizar el techo en forma de cono con abertura de un auditorio circular de diámetro igual a m, la altura total del cono sería.m, pero a
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de innovación didáctica Departamento de Matemáticas Universidad de Extremadura Índice Puntos y vectores en En R 3, conviene distinguir
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de innovación didáctica Departamento de Matemáticas Universidad de Extremadura Índice Puntos y vectores en En R 3, conviene distinguir
Estática. Carrera: MTM-0520 3-2-8. Participantes Representante de las academias de ingeniería Mecatrónica de los Institutos Tecnológicos.
 .- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Estática Ingeniería Mecatrónica MTM-00 --.- HISTORIA DEL PROGRAMA Lugar y fecha
.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos: Estática Ingeniería Mecatrónica MTM-00 --.- HISTORIA DEL PROGRAMA Lugar y fecha
Lección 13: Resolución algebraica de sistemas de ecuaciones
 GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
Métodos numéricos para Ecuaciones Diferenciales Ordinarias
 Métodos numéricos para Ecuaciones Diferenciales Ordinarias Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya (Barcelona) http://www-lacan.upc.es
Métodos numéricos para Ecuaciones Diferenciales Ordinarias Laboratori de Càlcul Numèric (LaCàN) Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya (Barcelona) http://www-lacan.upc.es
Coordenadas polares. Representación de puntos con coordenadas polares. Por ejemplo
 Instituto de Matemática Cálculo Integral Profesora Elisabeth Ramos Coordenadas polares El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del
Instituto de Matemática Cálculo Integral Profesora Elisabeth Ramos Coordenadas polares El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del
Suponemos un Mecanismo simple de colapso: (Dejo para los alumnos probar otros mecanismos simples como los de vigas)
 Determinar la carga de Colapso Unidades de longitud, m para todas las barras m = número de articulaciones pásticas posibles gh = número de grados de hiperestaticidad ms = número de mecanismos simples m:=
Determinar la carga de Colapso Unidades de longitud, m para todas las barras m = número de articulaciones pásticas posibles gh = número de grados de hiperestaticidad ms = número de mecanismos simples m:=
Figura 3.-(a) Movimiento curvilíneo. (b) Concepto de radio de curvatura
 Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
4. Método Simplex de Programación Lineal
 Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
Temario Modelos y Optimización I 4. Método Simplex de Programación Lineal A- Resolución de problemas, no particulares, con representación gráfica. - Planteo ordenado de las inecuaciones. - Introducción
GEOMETRÍA EN EL ESPACIO.
 GEOMETRÍA EN EL ESPACIO. Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y. Cada punto viene determinado por tres coordenadas
GEOMETRÍA EN EL ESPACIO. Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y. Cada punto viene determinado por tres coordenadas
Ejemplo 1.5 (Página 138).
 Ejemplo.5 (Página 8). THE FINITE ELEMENT METHOD IN ENGINEERING FOURTH EDITION Elsevier Science & Technology Books December. La viga dispone de una sección rectangular con cm de ancho y cm de altura y la
Ejemplo.5 (Página 8). THE FINITE ELEMENT METHOD IN ENGINEERING FOURTH EDITION Elsevier Science & Technology Books December. La viga dispone de una sección rectangular con cm de ancho y cm de altura y la
I IDENTIFICACION DE LA ASIGNATURA
 UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE CIENCIA DEPARTAMENTO DE FISICA I IDENTIFICACION DE LA ASIGNATURA NOMBRE : ALGEBRA CODIGO : 25003 NIVEL : 1º año T-E-L : 4-4-0 CARRERA : INGENIERÍA FÍSICA CARACTER
UNIVERSIDAD DE SANTIAGO DE CHILE FACULTAD DE CIENCIA DEPARTAMENTO DE FISICA I IDENTIFICACION DE LA ASIGNATURA NOMBRE : ALGEBRA CODIGO : 25003 NIVEL : 1º año T-E-L : 4-4-0 CARRERA : INGENIERÍA FÍSICA CARACTER
1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO
 1 1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos
1 1. PRODUCTO ESCALAR. ESPACIO EUCLÍDEO Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos
1. SISTEMAS DE ECUACIONES DIFERENCIALES
 1 1 SISTEMAS DE ECUACIONES DIFERENCIALES 11 SISTEMAS LINEALES DE PRIMER ORDEN Un sistema de ecuaciones diferenciales del tipo dx 1 dt a 11 tx 1 + a 1n tx n + f 1 t dx n dt a n1 tx 1 + a nn tx n + f n t
1 1 SISTEMAS DE ECUACIONES DIFERENCIALES 11 SISTEMAS LINEALES DE PRIMER ORDEN Un sistema de ecuaciones diferenciales del tipo dx 1 dt a 11 tx 1 + a 1n tx n + f 1 t dx n dt a n1 tx 1 + a nn tx n + f n t
MÉTODO DE LOS ELEMENTOS FINITOS.
 de MÉTODO DE LOS ELEMENTOS FINITOS. Castillo Madrid, 23 de Noviembre de 26 Índice de 2 3 4 de de El de los Elementos Finitos (M.E.F.) es un procedimiento numérico para resolver ecuaciones diferenciales
de MÉTODO DE LOS ELEMENTOS FINITOS. Castillo Madrid, 23 de Noviembre de 26 Índice de 2 3 4 de de El de los Elementos Finitos (M.E.F.) es un procedimiento numérico para resolver ecuaciones diferenciales
Método de fórmula general
 Método de fórmula general Ahora vamos a utilizar el método infalible. La siguiente fórmula, que llamaremos «fórmula general» nos ayudará a resolver cualquier ecuación cuadrática. Fórmula General La fórmula
Método de fórmula general Ahora vamos a utilizar el método infalible. La siguiente fórmula, que llamaremos «fórmula general» nos ayudará a resolver cualquier ecuación cuadrática. Fórmula General La fórmula
Ejemplo 1.8 (Página 248).
 Ejemplo.8 (Página 8). INTRODUCCIÓN A ESTUDIO DEL ELEMENTO FINITO EN INGENIERÍA SEGUNDA EDICIÓN Tirupathi R. Chandrupatla Ashok D. Belegundu Prentice Hall, México, 999 Para la viga y carga mostrada en la
Ejemplo.8 (Página 8). INTRODUCCIÓN A ESTUDIO DEL ELEMENTO FINITO EN INGENIERÍA SEGUNDA EDICIÓN Tirupathi R. Chandrupatla Ashok D. Belegundu Prentice Hall, México, 999 Para la viga y carga mostrada en la
UNIVERSIDAD TECNOLOGICA DE PEREIRA PROGRAMA DE TECNOLOGIA ELECTRICA
 UNIVERIDAD TECNOLOGICA DE PEREIRA PROGRAMA DE TECNOLOGIA ELECTRICA Curso Básico de Análisis de istemas Eléctricos de Potencia Antonio Escobar Zuluaga Pereira - Risaralda - Colombia Febrero - 2011 2 ELEMENTO
UNIVERIDAD TECNOLOGICA DE PEREIRA PROGRAMA DE TECNOLOGIA ELECTRICA Curso Básico de Análisis de istemas Eléctricos de Potencia Antonio Escobar Zuluaga Pereira - Risaralda - Colombia Febrero - 2011 2 ELEMENTO
Tema 2. Sistemas de ecuaciones lineales
 Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
1. Hallar por el método de Cross los diagramas de momento flector y de esfuerzo
 1. allar por el método de ross los diagramas de momento flector y de esfuerzo cortante, así como las reacciones de la estructura de la figura, empleando el método de superposición en las barras cargadas.
1. allar por el método de ross los diagramas de momento flector y de esfuerzo cortante, así como las reacciones de la estructura de la figura, empleando el método de superposición en las barras cargadas.
11. ANÁLISIS CINEMÁTICO POR MÉTODOS
 11. NÁLISIS CINEMÁTICO POR MÉTOOS NUMÉRICOS 11.1. Introducción En los capítulos anteriores se han estudiado los métodos tradicionales para el estudio cinemático y dinámico de mecanismos, basados en la
11. NÁLISIS CINEMÁTICO POR MÉTOOS NUMÉRICOS 11.1. Introducción En los capítulos anteriores se han estudiado los métodos tradicionales para el estudio cinemático y dinámico de mecanismos, basados en la
02 Elementos finitos para tensión/ compresión axial. Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales
 02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
02 Elementos finitos para tensión/ compresión axial Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 El método de los elementos finitos El método de los elementos
PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN.
 PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN. INTRODUCCIÓN. A continuación se presenta un método simplificado para encontrar la matriz de rigidez de un pórtico constitutivo
PROPUESTA SIMPLIFICADA PARA ENCONTRAR LA MATRIZ DE RIGIDEZ DE UN PÓRTICO DE HORMIGÓN. INTRODUCCIÓN. A continuación se presenta un método simplificado para encontrar la matriz de rigidez de un pórtico constitutivo
ax 2 +bx+c=0 ax 2 +bx=0 ax 2 +c=0 ax 2 =0 SESIÓN 2. Ecuaciones cuadráticas o de segundo grado.
 SESIÓN. Ecuaciones cuadráticas o de segundo grado. Comenzamos con la definición de ecuación de segundo grado. Ejemplos: 3y-y = 3x -48= Son ejemplos de ecuaciones de segundo grado, pues el mayor exponente
SESIÓN. Ecuaciones cuadráticas o de segundo grado. Comenzamos con la definición de ecuación de segundo grado. Ejemplos: 3y-y = 3x -48= Son ejemplos de ecuaciones de segundo grado, pues el mayor exponente
TEORÍA TEMA 8. 1. Concepto de BARRA Y ESFUERZO INTERNO EN LAS BARRAS. 2. Materialización de esfuerzo de tracción y compresión
 TEORÍA TEMA 8 1. Concepto de BARRA Y ESFUERZO INTERNO EN LAS BARRAS. 2. Materialización de esfuerzo de tracción y compresión 3. Sistema reticulado. Su generación CONDICIÓN DE RIGIDEZ (Relación entre el
TEORÍA TEMA 8 1. Concepto de BARRA Y ESFUERZO INTERNO EN LAS BARRAS. 2. Materialización de esfuerzo de tracción y compresión 3. Sistema reticulado. Su generación CONDICIÓN DE RIGIDEZ (Relación entre el
ÁREA DE INGENIERÍA QUÍMICA Prof. Isidoro García García. Operaciones Básicas de Transferencia de Materia. Tema 1
 ÁREA DE INGENIERÍA QUÍMICA Operaciones Básicas de Transferencia de Materia Los procesos químicos modifican las condiciones de una determinada cantidad de materia: modificando su masa o composición modificando
ÁREA DE INGENIERÍA QUÍMICA Operaciones Básicas de Transferencia de Materia Los procesos químicos modifican las condiciones de una determinada cantidad de materia: modificando su masa o composición modificando
220093 - Ecuaciones Diferenciales
 Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 205 - ESEIAAT - Escuela Superior de Ingenierías Industriales, Aeroespacial y Audiovisual de Terrassa 749 - MAT - Departamento
Unidad responsable: Unidad que imparte: Curso: Titulación: Créditos ECTS: 2016 205 - ESEIAAT - Escuela Superior de Ingenierías Industriales, Aeroespacial y Audiovisual de Terrassa 749 - MAT - Departamento
1. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado:
 CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
Expresiones algebraicas
 Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
UNIDAD Nº 6: TEOREMA DE LOS TRABAJOS VIRTUALES
 UNIDAD Nº 6: TEOREMA DE LOS TRABAJOS VIRTUALES 1 Trabajo de fuerzas generalizadas. Teorema de los trabajos virtuales. Aplicaciones. TRABAJO DE FUERZAS GENERALIZADAS. Considérese un cuerpo sometido a un
UNIDAD Nº 6: TEOREMA DE LOS TRABAJOS VIRTUALES 1 Trabajo de fuerzas generalizadas. Teorema de los trabajos virtuales. Aplicaciones. TRABAJO DE FUERZAS GENERALIZADAS. Considérese un cuerpo sometido a un
1. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM
 . ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
. ANALISIS DE UN RESERVORIO CIRCULAR MEDIANTE FEM Analizar la pared de un reservorio circular de radio interior m, espesor de la pared.m, altura de la pared desde la losa de fondo m. Considerar solamente
