Hoja de Prácticas tema 2: Derivación de Funciones de Varias Variables. (d) z = arctan(xy) (e) z = arcsin(x+y) (f) z = x y. x 2 +y 2 +z 2, ω xx =
|
|
|
- María José Valenzuela Sosa
- hace 7 años
- Vistas:
Transcripción
1 Cálculo II EPS (Grado TICS) Curso Hoja de Prácticas tema 2: Derivación de Funciones de Varias Variables 1. Hallar las derivadas parciales primera y segunda de las siguientes funciones: (a) z = x 2 sin(y 2 ) (b) z = e x2 +y 2 (c) ω = x 2 +y 2 +z 2 (d) z = arctan(xy) (e) z = arcsin(x+y) (f) z = x y (g) z = log(1+x 2 +y 2 ) Solución: (a) z x = 2xsin(y 2 ), z xx = 2sin(y 2 ), z y = 2yx 2 cos(y 2 ), z yy = 2x 2 sin(y 2 ) 4y 2 sin(y 2 ), z xy = z yx = 4xycos(y 2 ). (b) z x = 2xe x2 +y 2, z xx = (2+4x 2 )e x2 +y 2, z y = 2ye x2 +y 2, z yy = (2+4y 2 )e x2 +y 2, z xy = z yx = 4xye x2 +y 2. (c) ω x = x x 2 +y 2 +z 2, ω y = ω yy = x 2 +z 2 (x 2 +y 2 +z 2 ) 3/2, ω zz = ω xz = ω zx = y x 2 +y 2 +z 2, ω z = z x 2 +y 2 +z 2, ω xx = x 2 +y 2 (x 2 +y 2 +z 2 ) 3/2, ω xy = ω yx = xz (x 2 +y 2 +z 2 ) 3/2, ω yz = ω zy = yz (x 2 +y 2 +z 2 ) 3/2. y 2 +z 2 (x 2 +y 2 +z 2 ) 3/2, xy (x 2 +y 2 +z 2 ) 3/2, y (d) z x = 1+x 2 y 2, z x y= 1+x 2 y 2, z xx= 2xy3 (1+x 2 y 2 ) 2, z yy= 2x3 y (1+x 2 y 2 ) 2, z xy=z yx = 1 x2 y 2 (1+x 2 y 2 ) 2. (e) z x = z y = 1 1 (x+y) 2, z xx = z yy = z xy = z yx = x+y (1 (x+y) 2 ) 3/2. (f)z x = yx y 1, z y = (logy)x y, z xx = y(y 1)x y 2, z yy = (logy) 2 x y, z xy = z yx = (1+ylogx)x y 1. (g) z x = 2x 1+x 2 +y 2, z y = 2y 1+x 2 +y 2, z xx = 2(1+x2 y 2 ) (1+x 2 +y 2 ) 2, z yy = 2(1+y2 x 2 ) (1+x 2 +y 2 ) 2, z xy = z yx = 4xy (1+x 2 +y 2 ) 2.
2 2. Comprobar que la función f(x,y) = log(x 2 +y 2 ) satisface la ecuación de Laplace en dos dimensiones. NOTA: La ecuación de Laplace en dos dimensiones es: 2 f 2 x + 2 f 2 y = 0. Solución: Dado que hay simetría entre las variables x e y, se tiene el resultado ya que f x = 2x x 2 +y 2 2 f 2 x = 2y2 2x 2 (x 2 +y 2 ) 2 2 f 2 y = 2x2 2y 2 (x 2 +y 2 ) 2.
3 3. Hallar el vector gradiente de las siguientes funciones en los puntos que se indican: a) f(x,y) = x 3 y 2 e x 2 en P = (2,1) b) f(x 1,x 2,x 3 ) = x x2 2 x4 3 en P = (1,1,3) c) f(x,y) = log(x 2 +y 2 +1) en P = (2,2) Solución: (a) f(x,y) ( P) = (3x 2 y 2 e x 2, 2ye x 2 ) P = (11, 2). (b) f(x 1,x 2,x 3 ) ( P) = (3x 2 1,4x 2, 4x 3 3 ) P = (3,4, 108). (c) f(x,y) ( P) = (2x/(x 2 +y 2 +1),2y/(x 2 +y 2 +1)) P = (4/9,4/9).
4 4. Considérense las siguientes funciones de dos variablesy los puntos del dominio que se indican: i) z = x 2 +y 2 puntos: (1,0), ( 3/2,1/2) y (0,1) ii) z = xy puntos: (2,1/2), (-1/2,-2) iii) z = y x 2 puntos: (0,1), (1,1) Se pide en cada caso por separado: a. Determinar y representar gráficamente las curvas de nivel que pasan por los puntos indicados. b. Calcular el gradiente de las funciones en dichos puntos y determinar las direcciones en las que las correspondientes derivadas direccionales se anulan. c. Representar sobre las curvas de nivel y en los puntos dados, a través de vectores, las direcciones de máximo crecimiento, de máximo decrecimiento y de variación nula. Solución: i.a) Representemos primero la curva de nivel z = 1 y los puntos sobre ella: ii.a) Representemos primero la curva de nivel z = 1 y los puntos sobre ella: x y x y 5 ii.c) Representemos primero la curva de nivel y = 1 y los puntos sobre ella: x y 2
5 5. En los siguientes ejercicios hallar la derivada direccional de la función dada, en el punto y la dirección del vector v: (a) f(x,y) = x 2 +y 2 +e x 2 en P = (2,1) con v = (1, 1) (b) f(x,y,z) = xy +y 2 z +5z 1 en P = (1,1,1) con v = (1,2,1) (c) f(x,y) = e x2 +y 2 en P = (2,1) con v = ( 3,4) (d) f(x,y,z) = x y z2 en P = (1,1,2) con v = (3,4,0) Solución: Debemos recordar que si tenemos un vector v no unitario, debemos hacerlo unitario, esto es, ω = v/ v y entonces D v f(p) = D ω f(p) = w f(p). (a) En este caso como v = (1, 1) su módulo v = 1 2 +( 1) 2 = 2, por tanto es ω = (1/ 2, 1/ 2) y f(p) = (5,2), y por tanto D v f(p) = 3/ 2 (b) En este caso ω = (1/ 6,2/ 6,1/ 6) y f(p) = (1,3,6), por tanto D v f(p) = 13/ 6 (c) En este caso ω = ( 3/5,4/5) y f(p) = (4e 5,2e 5 ), por tanto D v f(p) = 4/5e 5 (d) Al igual que en los otros casos se sigue que D v f(p) = 1/5
6 6. En los siguientes ejercicios hallar los valores de las constantes a y b para que: (a) La derivada direccional del campo escalar f(x,y) = 2x 2 y a x en la dirección del vector y n = (2,0) en el punto P = (1, 1) sea nula. (b) La derivada direccional del campo escalar f(x,y) = xy 3 ax 2 + 3y 4 en la dirección del vector n = (3, 4) en el punto P = ( 1,1) sea igual a 3. (c) La derivada direccional del campo escalar f(x,y,z) = axyz 2 +3x+y 4z en la dirección del vector n = ( 1,1,2) en el punto P = (2,0, 1) sea nula. (d) La derivada direccional del campo escalar f(x,y,z) = ax 2 y + by 2 z +3z 2 x en la dirección del vector n = ( 1,1, 2) en el punto P = (0,1, 1) sea igual a 3. Solución: (a) En este caso D (2,0) (1,1) = (1,0) ( 4+a,2+a) = 4+a. Si nos dicen que dicho valor es cero, entonces a = 4 (b) En este caso D (3, 4) ( 1,1) = (3/5, 4/5) (1+2a,9) = (6a 33)/5. Si nos dicen que dicho valor es igual a 3, entonces a = 8 (c) En este caso D ( 1,1,2) (2,0, 1) = ( 1/ 6,1/ 6,2 6) (3,2a + 1, 4) = (2a 10)/ 6. Si nos dicen que dicho valor es cero, entonces a = 5 (d) En este caso D ( 2,1, 2) (0,1, 1) = ( 2/3,1/3, 2/3) (3, 2b,b) = ( 6 4b)/3. Si nos dicen que dicho valor es igual a 3, entonces b = 15/4, y a puede tomar cualquier valor.
7 7. Calcular aproximadamente el valor de la expresión (2 01) 3 +(1 01) 3 mediante el diferencial de la función adecuada. Solución: Consideremos la función z = x 3 +y 3 en el punto P = (2,1), entonces entorno a dicho punto dado que la función es diferenciable se tiene que entorno al punto P, z z(p)+ z x P (x 2)+ z y P (y 1) = 3+2(x 2)+ 1 (y 1), 2 luego (2 01) 3 +(1 01) Es diferenciable en el (1,2) ya que lim (x,y) (2,1) x 3 +y 3 3 2(x 2) (y 1)/2 x 3 +y (x 2) 3(y 1) = lim (x 2) 2 +(y 1) 2 (x,y) (2,1) 6 (x 2) 2 +(y 1) 2 (x 2) 2 (x+4)+(y 1) 2 (y +2) = lim (x,y) (2,1) 6 = lim (x 2) 2 +(y 1) 2 (x,y) (2,1) 2(x 2) 2 +(y 1) 2 2 (x 2) 2 +(y 1) 2 Y este límite es 0 pues el númerador tiene grado mayor que el denominador y es homogéneo.
8 8. El volumen de uncono circular recto, deradio r y altura h, es V = 1/3πr 2 h. Calcular, utilizando una aproximación lineal, una cota superior al error cometido en el cálculo del volumen si las mediciones del radio y la altura son 2 y 5, respectivamente, con un error máximo de 1/8. Solución: En este caso en un entorno del punto (r,h) = (2,5) se tiene V 20 3 π π(r 2)+ 4 3 π(h 5), y dado que el error máximo es de 1/8, entonces debemos asumir que r real 2 = 1/8, y h real 5 = 1/8, así se tiene que V real 20 3 π = π. Por tanto una cota superopr del error cometido es π.
9 9. Determinar la ecuación del plano tangente y la recta normal a las siguientes superficies en el punto indicado: (a) z = x 2 +y 2 en P = (3,4,25) (b) z = sin(xy) en (1,π,0) (c) x 2 +y 2 +z 2 = 49 en P = (6,3,2) (d) xy +yz +xz 1 = 0 en P = (1,1,0) (e) x 2 y 2 +xz 2y 3 = 10 en P = (2,1,4) Solución: (a) El gradiente es f(p) = (6,8, 1) así el planotangente es π : 6(x 3)+8(y 4) (z 25) = 0, y la normal n : (x 3,y 4,z 25) = t(6,8, 1). (b) El gradiente es f(p) = ( π, 1, 1) así el planotangente es π : π(x 1)+(y π)+(z 0) = 0, y la normal n : (x 1,y π,z 0) = t(π,1,1). (c) El gradiente es f(p) = (12,6,4) así el planotangente es π : 6(x 6)+3(y 3)+2(z 2) = 0, y la normal n : (x 6,y 3,z 2) = t(6,3,2). El resto de apartados se hacen de la misma forma.
10 10. (a) Hallar el punto de las siguientes superficies z = f(x,y) en que el plano tangente es horizontal: i) z = 3 x 2 y 2 +6y, ii) z = 3x 2 +2y 2 3x+4y 5 (b) Hallar los planos tangentes a la superficie x 2 +2y 2 +3z 2 = 21 que a la vez son paralelos al plano π : x+4y +6z = 0. (c) Hallar el plano tangente y la recta normal a la superficie x 2 yz +3y 2 2xz 2 +8z = 0 en el punto P = (1,2, 1). Solución: (a) Para la primera superície se otiene que f(x,y) = ( 2x, 2y +6), que se anula, o sea, es horizontal, para (x,y) = (0,3), luego el punto asociado a la superficie será para z = 12, es decir P = (0,3,12); para la segunda superficie es análoga obteniendose el punto P = (1/2, 1, 31/4). (b) Son los planos paralelos cuando los gradientes sean proporcionales, y esto sucede en los puntos (1,2,2), y ( 1, 2, 2). (c) 6(x 1)+11(y 2)+14(z +1) = 0, r (1 6t,2+11t, 1+14t), t R.
11 11. a) Se describe la superficie de una montaña mediante la ecuación: z = h(x,y) = x y 2 Un alpinista está en el punto P = (500,300,3390) En qué dirección debe moverse para ascender lo más rápido posible? b) La temperatura T en un punto (x,y) de una placa metálica viene dada por T(x,y) = 400 2x 2 y 2 Hallar las direcciones de aumento y disminución más rápido de la temperatura, en el punto (10,10). Solución: Debe ir en la dirección del gradiente, en este caso h(500,300) = ( 1, 2 4). Luego debemos ir sobre el plano XY en la dirección ( 1, 2 4). En el segundo caso la dirección del aumento más rápido de la temperatura viene dada por el gradiente y el mínimo por la dirección puesta. Es decir, T(10,10) = ( 40, 20). Luego la disminución más rápida es en la dirección (2,1) y el aumento más rapido es en la dirección menos (-2,-1).
12 12. La temperatura de una cierta región del espacio está determinada por la función T(x,y,z) = (x 2 +y 2 )exp( x 2 2y 2 3z 2 ) En qué dirección se establece el flujode calor en el punto (1,1,1)? Solución: En la dirección de máxima disminución de temperatura, es decir en la dirección v = T(1,1,1) = (2e 6,6e 6,12e 6 ), o cualquier proporcional positiva, por ejemplo (1,3,4).
13 13. La altitud z del terreno en una región, en unidades adecuadas,está determinada por la función z(x,y) = 1 (x 2 +3y 2 )exp(1 x 2 y 2 ), donde (x,y) son las coordenadas de un punto en un plano de referencia horizontal. Supóngase que una pelota de baloncesto se suelta en el punto de coordenadas (1/ 2,1 2, 1) En qué dirección comenzará a moverse la pelota? Resuélvase la misma cuestión para el punto ( 1/ 3, 2/3, 4/3). Solución: En este caso el gradiente será z(1/ 2,1 2) = [( 2x+2x(x 2 +3y 2 ), 6y +2y(x 2 +3y 2 ) ) exp(1 x 2 y 2 ) ] (1/ 2,1 2) Así En el segundo caso, z(1/ 2,1 2) = ( 2, 2). z( 1/ 3, 2/3) = ( 8 3/9,4 6/9).
14 14. Aplicar la regla de la cadena para hallar las derivadas que a continuación se indican: (a) z = e xy2 con x = tcost, y = tsint. Hallar z t en t = π 2. (b) ω = xy +yz +xz con x = scost, y = ssint, z = t. Hallar ω s y ω t en s = 2 y t = π 3. (c) ω = x 2 + 2xy +y 2 + z 2 con x = s 2 + r 2, y = r/s, z = 4s 3. Hallar ω r y ω s en s = 2 y r = 4. Solución: Teniendo en cuenta la teoría vista (a) Para t = π/2 se tiene que x = 0, y = π/2, así z z x z y (π/2) = (π/2)+ t x t y t (π/2) = (y2 e xy2 (cost tsint)+(2xye xy2 (sint+tcost) por tanto z π2 (π/2) = t 4 ( π 2 ) = π3 8 (b) En este caso, si s = 2 y t = π/3, entonces x = 1, y = 3, y z = π/3, así ( ω ω s (2,π/3) = x x s + ω y y s + ω ) z (2, π/3) z s ( ) = (y +z)(cost)+(x+z)(sint)+(x+y) 0 (2,π/3) = 3+ ( 3+1)π. 6 ( ω ω t (2,π/3) = x x t + ω y y t + ω ) t (2, π/3) z s ( ) = (y +z)( ssint)+(x+z)(scost)+(x+y) 1 (2,π/3) = 3 1+ (1 3)π. 3 (c) Si s = 2 y r = 4, entonces x = 20, y = 2, y z = 32, así ( ω ω s (2,4) = x x s + ω y y s + ω ) z (2,4) z s ( ) = (2x+2y)(2s) (2x+2y)(r/s 2 )+(2z)(12s 2 ) (2,4) = = ω r (2,4) = ( ω x x r + ω y y r + ω z ( (2x+2y)(2r) (2x+2y)(1/s)+(2z) 0 ) z (2,4) r ) (2,4) = 374.
15 15. La ecuación y 4 +x 3 y 2 xy 2 +xy = 2 representa unacurvaen el planoxy, determinar la ecuación de la recta tangente a esa curva en el punto (1,1). Solución: Si asumimos que y = y(x), en primer lugar derivamos respecto a x, obteniendo 4y 3 y +3x 2 y 2 +2x 3 yy y 2 2xyy +y +xy = 0, por tanto si lo evaluamos en x = 1 (se asume que se ha comprobado que el punto (1,1) satisface la ecuación inicial). Se tiene 4y (1)+3+2y (1) 1 2y (1)+1+y (1) = 0 y (1) = 3/5 por tanto la tangente es y 1 = 3 5 (x 1)
16 16. Demostrar que la superficie en R 3 de ecuación z 3 +xz +y = 0 define una función diferenciable z = g(x,y) en un entorno del punto (1,2). Calcular el gradiente de g en dicho punto (1,2). Solución: Está claro que z 3 + xz + y = 0 es una función continua pues es un polinomio y también es claro que no podemos despejar de una forma clara la variable z en términos de x e y fácilmente, de hecho la función es C 1. Y para (x,y) = (1,2) se tiene z 3 +z +2 = 0 que resulta como solución z(1,2) = 1. Además si tomamos F(x,y,z) = z 3 +xz +y, F z (1,2, 1) = (3z2 +x)(1,2, 1) = 4 0, Luego sabemos por teoría que se sigue el resultado. Ya que estamos, además para calcular las derivadas parciales (o direccionales) se hace 3z 2 z x +z +xz x = 0, 3z 2 z y +1 = 0, z x (1,2) = 1 4, z y(1,2) = 1 3. Y en un entorno de (x,y) = (1,2) se sigue Así el gradiente será z(1,2) = (1/4, 1/3). z(x,y) (x 1) 1 (y 2). 3
17 17. Suponiendo que las relaciones que a continuación se indican definen la variable z como función implícita de x y y, hallar z x y z y. a) x 2 y +z +e z +5 = 0, b) x 2 +y 2 +z 2 x ye z = 5, c) x z = y x. Solución: Al igual que en ejercicios anteriores: a)2xy +z x +z x e z = 0, x 2 +z y +z y e z = 0, por tanto z x = 2xy 1+e z, z x = x2 1+e z b) 2x+z 2 +2zxz x yz x e z = 0, 2y +2zxz y e z yz y e z = 0, z x = 2x+z2 ye z 2zx, z y = 2y ez ye z 2zx c) zx z 1 +z x x z logx = y x logy, z y x z logx = xy x 1 logy, z x = yx logy zx z 1 x z logx = xlogy z xlogx, z y = xyx 1 x z logx = x ylogx.
18 18. Estudiar si el sistema de ecuaciones: { y 2 +z 2 x 2 +2 = 0 yz +xz xy 1 = 0 define dos funciones implícitas y = y(x), z = z(x) en un entorno del punto (x,y,z) = (2,1,1) y hallar las derivadas de las mismas en el punto x = 2. Solución: Si tomamos la función F(x,y,z) = (y 2 +z 2 x 2 +2,yz +xz xy 1), está claro que F(2,1,1) = (0,0), así lo que hace falta es comprobar que la derivada de F respecto a x en el punto x = 2 no se anula, pero de hecho si se cumplen ambas condiciones se tiene que 2yy +2zz 2x = 0, y z +yz +z +xz y xy = 0, esdecirqueobtenemosunsistemaquetienesoluciónparaelpuntodadoy (2) = 3/2yz (2) = 1/2 y por tanto F y (2,1,1) = (2y,z x) (2,1,1) = (2,1) 0, F z (2,1,1) = (2z,y +z) (2,1,1) = (2,2) 0. Por tanto el resultado es cierto, si definen dos funciones implícitas y = y(x), z = z(x) en un entorno del punto (x,y,z) = (2,1,1), y las derivadas las hemos calculado previamente: y (2) = 3 2, y z (2) = 1 2.
19 19. Suponiendo que el sistema de ecuaciones: { u 2 v = 2x+y u 2v 2 = x 2y define las variables u y v como funciones de x e y. Hallar u x, u y, v x, y u y. Solución: Lo dejamos para que el estudiante lo resuelva.
Problema 1. Calcula las derivadas parciales de las siguientes funciones: (d) f(x, y) = arctan x + y. (e) f(x, y) = cos(3x) sin(3y),
 Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Práctica 3: Diferenciación I
 Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
2. Sea f(x, y) = x 2 2xy+y 2. Aquí el discriminante es igual a cero. Qué son los puntos críticos: mínimos locales, máximos locales o puntos silla?
 1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 . DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
. DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
Hoja 2: Derivadas direccionales y diferenciabilidad.
 Sonia L. Rueda ETS Arquitectura. UPM Curso 2011-2012. 1 CÁLCULO Hoja 2: Derivadas direccionales y diferenciabilidad. 1. Sea f : R 2 R la función definida por x 4 (x 2 +y 2 ) 2, (x, y) (0, 0) 0, (x, y)
Sonia L. Rueda ETS Arquitectura. UPM Curso 2011-2012. 1 CÁLCULO Hoja 2: Derivadas direccionales y diferenciabilidad. 1. Sea f : R 2 R la función definida por x 4 (x 2 +y 2 ) 2, (x, y) (0, 0) 0, (x, y)
Prueba de Funciones de varias variables. 5 de noviembre de 2012 GRUPO A
 5 de noviembre de 1 GRUPO A xy5 si y x x y 1.- Consideremos f(xy)=. Se pide: 1 si y=x a) Existe el límite: lím f(xy)? xy 1 b) Es continua la función en (1)? c) Es diferenciable la función en (1)? ( puntos).-
5 de noviembre de 1 GRUPO A xy5 si y x x y 1.- Consideremos f(xy)=. Se pide: 1 si y=x a) Existe el límite: lím f(xy)? xy 1 b) Es continua la función en (1)? c) Es diferenciable la función en (1)? ( puntos).-
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
1. Hallar la ecuación paramétrica y las ecuaciones simétricas de la recta en los siguientes casos:
 A. Vectores ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos, Superficies en el espacio Para terminar el 3 de septiembre.. Sean v = (0,, ) y w = (,, 4)
A. Vectores ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos, Superficies en el espacio Para terminar el 3 de septiembre.. Sean v = (0,, ) y w = (,, 4)
x 2 y si x 3y 2 si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.
 FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 010 Práctica 3: Diferenciación Derivadas parciales y direccionales 1. Sea f una función continua en x = a. Probar que f es derivable en x =
Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 010 Práctica 3: Diferenciación Derivadas parciales y direccionales 1. Sea f una función continua en x = a. Probar que f es derivable en x =
ANALISIS II Computación. Práctica 4. x 3. x 2 + y 2. x 2 + y 2 si (x, y) (0, 0) 0 si (x, y) = (0, 0)
 facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
Tema 3: Diferenciabilidad de funciones de varias variables
 Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 2009-2010. Tema 3: Diferenciabilidad de funciones de varias variables 1. Calcular las dos derivadas parciales de primer orden:
Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 2009-2010. Tema 3: Diferenciabilidad de funciones de varias variables 1. Calcular las dos derivadas parciales de primer orden:
Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos
 Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
(1.5 p.) 2) Hallar el polinomio de Taylor de grado 3 de la función g(x) = e 1 x2 centrado en x 0 = 1 y usarlo para dar una aproximación de e 5/4.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Examen final 0 de enero de 0.75 p. Se considera la función escalar de una variable real fx = lnlnx. lnx a Calcular el
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Examen final 0 de enero de 0.75 p. Se considera la función escalar de una variable real fx = lnlnx. lnx a Calcular el
x 2 + ln(x + z) y = 0 yz + e xz 1 = 0 define una curva C regular en un entorno de (1, 1, 0) y halle el plano normal a C en dicho punto.
 1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
(3 p.) 3) Se considera la superficie z = z(x, y) definida implícitamente por la ecuación. 3x 2 z x 2 y 2 + 2z 3 3yz = 15.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
TRABAJO EN GRUPO 04/2009 Permutación 1 Ingeniería Técnica de Obras Públicas (E.T.S.E.C.C.P.B.)
 TRABAJO EN GRUPO 04/2009 Permutación 1 Ingeniería Técnica de Obras Públicas (E.T.S.E.C.C.P.B.) Problema 1 (i) Probar que el sistema { ln(x 2 + y 2 + 1) + z 2 = π sen(z 2 ) (x 2 + y 2 ) 3 2 + xz = 0, dene
TRABAJO EN GRUPO 04/2009 Permutación 1 Ingeniería Técnica de Obras Públicas (E.T.S.E.C.C.P.B.) Problema 1 (i) Probar que el sistema { ln(x 2 + y 2 + 1) + z 2 = π sen(z 2 ) (x 2 + y 2 ) 3 2 + xz = 0, dene
MATE1207 Primer parcial - Tema B MATE-1207
 MATE7 Primer parcial - Tema B MATE-7. Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
MATE7 Primer parcial - Tema B MATE-7. Si su respuesta y justificación son correctas obtendrá el máximo puntaje. Si su respuesta es incorrecta podrá obtener créditos parciales de acuerdo a su justificación.
c) Calcular las asíntotas horizontales y verticales de f y representar de forma aproximada
 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Soluciones Matemáticas II Examen Final 2º Parcial 3-Julio-07. 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =.
 Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
1.6 Ejercicios resueltos
 Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Clase 4: Diferenciación
 Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Funciones de varias variables
 Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Curso 2010/ de julio de (2.75 p.) 1) Se considera la función f : (0, ) (0, ) definida por
 Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Capítulo 3. Funciones con valores vectoriales
 Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
2 t, y t = 2 sin 2t, z t = 3e 3t. ( 2 sin 2t) + z. t = 0. = f u (2, 3)u s (1, 0) + f v (2, 3)v s (1, 0) = ( 1)( 2) + (10)(5) = 52
 TALLER : Regla de la cadena, derivadas direccionales y vector gradiente Cálculo en varias variables Universidad Nacional de Colombia - Sede Medellín Escuela de matemáticas 1. Use la regla de la cadena
TALLER : Regla de la cadena, derivadas direccionales y vector gradiente Cálculo en varias variables Universidad Nacional de Colombia - Sede Medellín Escuela de matemáticas 1. Use la regla de la cadena
Matemáticas III Andalucía-Tech
 Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Primer Examen Parcial Tema A Cálculo Vectorial Marzo 5 de 2016
 rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
Problema 1 (i) Probar que el sistema. y 2 + z 2 x 2 + 2 = 0 yz + xz xy 1 = 0,
 Capítulo 1 Función implícita Problema 1 (i Probar que el sistema y + z x + 0 yz + xz xy 1 0 dene dos funciones implícitas y y(x z z(x en un entorno del punto (x y z ( 1 1. (ii Sea α la curva parametrizada
Capítulo 1 Función implícita Problema 1 (i Probar que el sistema y + z x + 0 yz + xz xy 1 0 dene dos funciones implícitas y y(x z z(x en un entorno del punto (x y z ( 1 1. (ii Sea α la curva parametrizada
Soluciones de los ejercicios del primer examen parcial
 Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
E.T.S.I. Industriales y Telecomunicación Curso PRUEBAS DE EVALUACIÓN
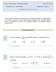 E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
Funciones de varias variables
 Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
CONJUNTO. (2,1,3) y v 3. (0,1, 1) y u 3. (2,0,3, 1), u 3
 CONJUNTO n.- Considerar los vectores u = (, -, 2) y v = (2, -, ) de a) Escribir, si es posible, los vectores (, 7, -4) y (2, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el vector
CONJUNTO n.- Considerar los vectores u = (, -, 2) y v = (2, -, ) de a) Escribir, si es posible, los vectores (, 7, -4) y (2, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el vector
Lección 11: Derivadas parciales y direccionales. Gradiente. Introducción al Cálculo Infinitesimal I.T.I. Gestión
 Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
gradiente de una función? Para esos valores, calcule la función potencial.
 CAMPOS CONSERVATIVOS. FUNCIÓN POTENCIAL 1. Sea F = 4xy 3x ( z (, 2x (, 2x, z. Demuestre que Fdl trayectoria C. es independiente de la 2. Dado el campo vectorial F = 3x ( + 2y y ( e 3, 2x 2ye 3. Es posible
CAMPOS CONSERVATIVOS. FUNCIÓN POTENCIAL 1. Sea F = 4xy 3x ( z (, 2x (, 2x, z. Demuestre que Fdl trayectoria C. es independiente de la 2. Dado el campo vectorial F = 3x ( + 2y y ( e 3, 2x 2ye 3. Es posible
Funciones reales de varias variables
 PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
Ejercicios típicos del primer parcial
 Ejercicios típicos del primer parcial El primer examen parcial tiene tres ejercicios teóricos y dos prácticos. Los límites entre los dos tipos de ejercicios son difusos. A continuación se proponen ejercicios
Ejercicios típicos del primer parcial El primer examen parcial tiene tres ejercicios teóricos y dos prácticos. Los límites entre los dos tipos de ejercicios son difusos. A continuación se proponen ejercicios
Funciones Implícitas.
 CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Temas 4 y 5. Teoremas de inversión local. Extremos.
 Problemas de Diferenciación de Funciones de Varias Variables Curso 2013-2014 Temas 4 y 5. Teoremas de inversión local. Extremos. 1. Sea U R n abierto convexo y f : U R. Decimos que f es convexa si: f(tx+(1
Problemas de Diferenciación de Funciones de Varias Variables Curso 2013-2014 Temas 4 y 5. Teoremas de inversión local. Extremos. 1. Sea U R n abierto convexo y f : U R. Decimos que f es convexa si: f(tx+(1
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Definición valor extremo: Si f(x,y) està definida en una regiòn R y P 0 =(a, es un punto de R, entonces: a) f(a, es un valor máximo local de f si f(a, f(x,y) para todos los
APLICACIONES DE LA DERIVADA Definición valor extremo: Si f(x,y) està definida en una regiòn R y P 0 =(a, es un punto de R, entonces: a) f(a, es un valor máximo local de f si f(a, f(x,y) para todos los
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0100. (1) Obtener la ecuación de la recta tangente a la curva x 3 + y 3 6xy =0
 CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0100 (1) Obtener la ecuación de la recta tangente a la curva x + y 6xy =0 en el punto, 8 ). (2) A un depósito cilíndrico de base circular de
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0100 (1) Obtener la ecuación de la recta tangente a la curva x + y 6xy =0 en el punto, 8 ). (2) A un depósito cilíndrico de base circular de
Índice general. Referencias 50
 Índice general 1. UNIDAD I: Derivadas parciales 2 1.1. Funciones de varias variables.............................. 2 1.1.1. Funciones de dos o más variables....................... 6 1.1.2. Derivadas parciales
Índice general 1. UNIDAD I: Derivadas parciales 2 1.1. Funciones de varias variables.............................. 2 1.1.1. Funciones de dos o más variables....................... 6 1.1.2. Derivadas parciales
1. Introducción a las funciones de varias variables 1. Diferenciación
 Problemas de DFVV, Curso 2017/18 1 1. Introducción a las funciones de varias variables 1. Diferenciación en R n 1.1. Espacios métricos, normados y euclídeos Problema 1.1 Prueba la desigualdad de Young:
Problemas de DFVV, Curso 2017/18 1 1. Introducción a las funciones de varias variables 1. Diferenciación en R n 1.1. Espacios métricos, normados y euclídeos Problema 1.1 Prueba la desigualdad de Young:
Ejercicios recomendados: Cálculo III
 Ejercicios recomendados: Cálculo III Cátedra de MA 1003 II ciclo 2017 Los ejemplos que siguen están tomados del libro: Claudio Pita Ruiz Cálculo Vectorial Prentice-Hall Hispanoamericana México 1995 Ejemplos
Ejercicios recomendados: Cálculo III Cátedra de MA 1003 II ciclo 2017 Los ejemplos que siguen están tomados del libro: Claudio Pita Ruiz Cálculo Vectorial Prentice-Hall Hispanoamericana México 1995 Ejemplos
Hoja 5. Diferenciabilidad de funciones de varias variables.
 CÁLCULO Hoja 5. Diferenciabilidad de funciones de varias variables. 1. Dada la función < 4x 3 x 2 + y 2 si x; y) 6= 0; 0) a) Estudiar la continuidad de f. b) Hallar las derivadas arciales y direccionales
CÁLCULO Hoja 5. Diferenciabilidad de funciones de varias variables. 1. Dada la función < 4x 3 x 2 + y 2 si x; y) 6= 0; 0) a) Estudiar la continuidad de f. b) Hallar las derivadas arciales y direccionales
CAPÍTULO 4: DERIVADAS DE ORDEN SUPERIOR. En este capítulo D denota un subconjunto abierto de R n.
 April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
April 15, 2009 En este capítulo D denota un subconjunto abierto de R n. 1. Introducción Definición 1.1. Dada una aplicación f : D R, definimos la derivada parcial segunda de f como D ij f = 2 f = ( ) x
Integración sobre curvas
 Problemas propuestos con solución Integración sobre curvas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Integral de línea de campos escalares 1
Problemas propuestos con solución Integración sobre curvas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Integral de línea de campos escalares 1
Problemas resueltos del Boletín 4
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Problemas de Cálculo Matemático E.U.A.T. CURSO Segundo cuatrimestre. Problemas del Tema 9. Funciones de dos variables.
 1 Problemas de Cálculo Matemático E.U.A.T. CURSO 2003-2004 Segundo cuatrimestre Problemas del Tema 9. Funciones de dos variables. 1. Determinar el dominio de cada una de las siguientes funciones: f(x,
1 Problemas de Cálculo Matemático E.U.A.T. CURSO 2003-2004 Segundo cuatrimestre Problemas del Tema 9. Funciones de dos variables. 1. Determinar el dominio de cada una de las siguientes funciones: f(x,
Tema 6 Funciones reales de varias variables
 Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
(x x 0 ) y 0. O bien z z 0 = x 0. y notamos a este límite ᾱ (t 0 ) = dᾱ dt (t 0).
 O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
OPCIÓN A. Determinar la ecuación de la recta tangente a la curva yy = llll (xx 11) que sea paralela a la. Solución:
 Nota sobre la puntuación de las preguntas: Los puntos asignados a las distintas preguntas son orientativos. En muchos casos, las preguntas pueden contestarse de varias formas distintas y el corrector debe
Nota sobre la puntuación de las preguntas: Los puntos asignados a las distintas preguntas son orientativos. En muchos casos, las preguntas pueden contestarse de varias formas distintas y el corrector debe
FUNCIONES DE. 1.- Determinar y representar gráficamente el dominio de las siguientes funciones: a) f (x) = x 2 16 b) f (x) = x 2 1.
 FUNCIONES DE n EN m Nota: se entenderá log log0 = y ln = log e - Determinar y representar gráficamente el dominio de las siguientes funciones: a) f () = 6 b) f () = c) f () = d) f () = e) f () = + + +
FUNCIONES DE n EN m Nota: se entenderá log log0 = y ln = log e - Determinar y representar gráficamente el dominio de las siguientes funciones: a) f () = 6 b) f () = c) f () = d) f () = e) f () = + + +
Escuela Politécnica Superior de Málaga. CÁLCULO
 Escuela Politécnica Superior de Málaga. CÁLCULO 4. Funciones de varias variables. 1. Describe y dibuja en el plano el dominio de las siguientes funciones en el espacio: f(x, y) = f(x, y) = 36 4x 2 9y 2
Escuela Politécnica Superior de Málaga. CÁLCULO 4. Funciones de varias variables. 1. Describe y dibuja en el plano el dominio de las siguientes funciones en el espacio: f(x, y) = f(x, y) = 36 4x 2 9y 2
1.- FUNCIONES REALES DE DOS Y TRES VARIABLES REALES. Funciones reales de dos variables reales independientes
 1.- FUNCIONES REALES DE DOS Y TRES VARIABLES REALES Funciones reales de dos variables reales independientes A) DOMINIO E IMAGEN TRABAJO PRÁCTICO Nº 1A.M. II - 014 1. Determine el conjunto de puntos donde
1.- FUNCIONES REALES DE DOS Y TRES VARIABLES REALES Funciones reales de dos variables reales independientes A) DOMINIO E IMAGEN TRABAJO PRÁCTICO Nº 1A.M. II - 014 1. Determine el conjunto de puntos donde
Sistemas no lineales
 Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
2 Estudio local de funciones de varias variables.
 a t e a PROBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CURSO 2009 2010 2 Estudio local de funciones de varias variables. 2.1 Derivadas de orden superior. Problema 2.1 Sea
a t e a PROBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CURSO 2009 2010 2 Estudio local de funciones de varias variables. 2.1 Derivadas de orden superior. Problema 2.1 Sea
MATEMÁTICAS II Notas de clase
 MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
EXAMEN TEMA 2:Funciones de varias variables
 GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) f(x, y) = x 2 y 2 ln(x 2 + y 2 ) y determine si satisface o no la ecuación en derivadas parciales:
 GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) CÁLCULO III (OTOÑO 207) - Calcule las derivadas parciales f x y f y i) ln(y + x 2 + y 2 ) xy ii) +x 2 +y 2 iii) arcsin(x/y) iv) (x 2 + y 2 )e xy v) x2 y 2 x 2 +y
GUÍA DE EJERCICIOS (DIFERENCIABILIDAD) CÁLCULO III (OTOÑO 207) - Calcule las derivadas parciales f x y f y i) ln(y + x 2 + y 2 ) xy ii) +x 2 +y 2 iii) arcsin(x/y) iv) (x 2 + y 2 )e xy v) x2 y 2 x 2 +y
Extremos de funciones de varias variables
 Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
DERIVADAS DE FUNCIONES DE VARIAS VARIABLES. Curvas Paramétricas. Dada una curva paramétrica
 ANÁLISIS MATEMÁTICO BÁSICO DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Curvas Paramétricas Dada una curva paramétrica γ : [a, b] R R n t γ(t) = (f 1 (t), f 2 (t),, f n (t)), donde las funciones f k : [a,
ANÁLISIS MATEMÁTICO BÁSICO DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Curvas Paramétricas Dada una curva paramétrica γ : [a, b] R R n t γ(t) = (f 1 (t), f 2 (t),, f n (t)), donde las funciones f k : [a,
Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 11 - Problemas 1, 3
 página 1/7 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 11 - Problemas 1, 3 Hoja 11. Problema 1 Resuelto por José Antonio Álvarez Ocete (septiembre 2014) 1. Sea la circunferencia
página 1/7 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 11 - Problemas 1, 3 Hoja 11. Problema 1 Resuelto por José Antonio Álvarez Ocete (septiembre 2014) 1. Sea la circunferencia
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1. El sistema: F(x,y,z) = =
 > 1. El sistema: F(x,y,z) = = Define implícitamente a la función (y, z) =f(x) en un entorno del punto x0=1. Encuentre la ecuación EXPLICITA de la recta tangente a la curva definida por f en el punto x0.
> 1. El sistema: F(x,y,z) = = Define implícitamente a la función (y, z) =f(x) en un entorno del punto x0=1. Encuentre la ecuación EXPLICITA de la recta tangente a la curva definida por f en el punto x0.
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900 (1) La posición vertical de una pelota está dada por h(t) = 128 + 16t 16t 2 en donde t se mide en segundos y h(t) se mide en pies. Durante
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900 (1) La posición vertical de una pelota está dada por h(t) = 128 + 16t 16t 2 en donde t se mide en segundos y h(t) se mide en pies. Durante
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Clase 1: Funciones de Varias Variables
 Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Derivación de funciones de varias variables.
 Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
El cuestionario virtual estara disponible los días 11, 12, 13, 14, 15 y 16 de enero.
 Fundamentos de Matematicas. Prueba de Evaluación a Distancia. Curso 016-17 Se debe marcar una sola respuesta correcta. Cada pregunta acertada suma 1 punto, las incorrectas restan 0.. Las preguntas en blanco
Fundamentos de Matematicas. Prueba de Evaluación a Distancia. Curso 016-17 Se debe marcar una sola respuesta correcta. Cada pregunta acertada suma 1 punto, las incorrectas restan 0.. Las preguntas en blanco
UNIVERSIDAD DE SEVILLA. DEPARTAMENTO DE ECONOMÍA APLICADA I. BOLETÍN DE PROBLEMAS DE MATEMÁTICAS I. GRADO EN ECONOMÍA.
 UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables.
 AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
DERIVADAS DE FUNCIONES DE VARIAS VARIABLES
 DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Definicion 1. Sea Ω R n un abierto f : Ω R n R m y a Ω. Se define la derivada direccional de f en el punto a y en la dirección u como D u f(a) h 0 f(a + hu) f(a)
DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Definicion 1. Sea Ω R n un abierto f : Ω R n R m y a Ω. Se define la derivada direccional de f en el punto a y en la dirección u como D u f(a) h 0 f(a + hu) f(a)
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) y = ex cos y. e x cos y e x sin y. y 2.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
