Modelos Autoconsistentes de Galaxias Espirales: Modelos de Halo-Disco-Núcleo
|
|
|
- Tomás Miranda Fidalgo
- hace 7 años
- Vistas:
Transcripción
1 Universidad Juáre Autónoma de Tabasco División Académica de Ciencias Básicas Licenciatura en Computación Modelos Autoconsistentes de Galaias Espirales: Modelos de Halo-Disco-Núcleo Tesis que presenta William de la Cru de los Santos Para obtener el grado de Licenciado en Computación Director de tesis Alejandro Gonále Sánche Cunduacán Tabasco, Méico Noviembre 25
2
3 Resumen Por más de una decada un gran número de autores han mencionado la importancia de las órbitas ergódicas en modelos de potenciales de galaias espirales elípticas. Esto tiene importantes consecuencias para la construcción de modelos densidad-potencial: Merrit [3] comenta que las órbitas ergódicas son mucho menos útiles que las órbitas regulares para reforar la figura de la galaia. Por otro lado, también han mostrado que las órbitas ergódicas son un componente significante de la densidad [8, 9, 2, 3]; por ejemplo en modelos triaiales con una concentración de masa central. La construcción de estos modelos utiliando la entropía Kolmogorov Sinai es el objetivo principal de esta tesis.
4
5 Índice general Índice de tablas iv. Introducción.. El problema de la autoconsistencia Solución propuesta Organiación de la tesis Dinámica de las galaias elípticas espirales Galaias Elípticas Correlación de parámetros en galaias elípticas Galaias espirales Distribución de la luminosidad del disco Correlación de parámetros en galaias espirales Materia oscura Conclusiones Modelos auto-consistentes de galaias 3.. Introducción La ecuación de Boltmann sin colisiones El método de Schwarschild Órbitas potencial gravitacional Pares densidad-potencial Modelo triaial de Disco + Halo + Núcleo Órbitas estelares en modelos de galaias triaiales Conclusiones Nueva aproimación; entropía Kolmogorov-Sinai Introducción Divergencia eponencial El máimo eponente de Lapunov La entropía Kolmogorov-Sinai Entropía para la dinámica del espacio de estados La identidad Pesin Integración Monte Carlo v
6 4.5. Conclusiones Modelos de sistemas de Halo-Disco-Núcleo; resultados Estabilidad del método Conservación de la energía Residuo fraccional de la energía Comportamiento asintótico de los eponentes de Lapunov Distribución de los eponentes de Lapunov Modelo con halo esférico sin disco sin núcleo Modelo con halo esférico + disco + bulge Modelo con halo esférico + núcleo Modelo con halo esférico + disco + núcleo Modelos con halo triaial Presencia de un núcleo central de masa Conclusiones Conclusiones trabajo futuro 65 Código fuente 69 Referencias 95
7 Índice de figuras 2.. La secuencia de Hubble es un esquema de clasificación para galaias inventado por Edwin Hubble en 926. Imagen tomada de Wikipedia Curvas de rotación de galaias espirales publicadas por Sander (996) de Blok & McGaugh (998). El radio (eje horiontal) esta dado en kpc en todos los casos la velocidad (eje vertical) esta en km s. Los puntos muestran las curvas de rotación de líneas de 2 cm observadas, las líneas punteadas son las curvas de rotación Newtonianas, las líneas solidas las medidas de MOND [6] Método de Schwarschild para calcular numéricamente la función de distribución f En la iquierda se muestra un sistema contenido en un cilindro con una división del espacio en celdas de igual volumen en la derecha se muestran órbitas pasando por una celda. El número total de órbitas que pasan por una celda se le llama número de ocupación este representa la densidad del sistema en la celda Gráfica del potencial Isochrone (arriba) la densidad generada (abajo) con b =,5 G = M = en unidades unitarias La gráfica de arriba muestra la densidad superficial del potencial de Kumin normaliado con a = la gráfica de abajo muestra la velocidad circular para a=,2,3,4,5; conforme a es más grande la densidad inicial es maor, por lo tanto la máima velocidad circular es menor lo que se observa en las curvas Gráficas de contorno de la densidad de Miamoto-Nagia para las raones b/a =.2 (arriba), b/a = (en medio) b/a = (abajo), también se muestra un ejemplo de órbita para cada gráfica de densidad con valores iniciales (R,, v R, v ) = (-.2,.,.,-.) GM = Contornos de igual densidad en el plano (R, ) para ρ L, cuando q Φ =. (arriba), q Φ =.95 (en medio) q Φ =.7 (abajo). Cuando q Φ =,7 la densidad es negativa cerca del eje para 7R c ; también se muestra un ejemplo de órbita para cada gráfica de densidad, con valores iniciales (R,, v R, v ) = (.5,-.5,.5,.2) con v = R c = vii
8 3.7. Familia de órbitas regulares que se encuentran en el modelo dado por (3.28), de halo esférico (p=q=) sin disco sin núcleo. Cada órbita tiene su proección en el plano XY, YZ XZ Familia de órbitas regulares que se encuentran en el modelo dado por (3.28), de halo triaial (p=.9, q=.8) sin disco sin núcleo. Cada órbita tiene su proección en el plano XY, YZ XZ Familia de órbitas regulares que se encuentran en el modelo dado por (3.28), de halo triaial (p=.9, q=.8) sin disco con núcleo (GM C =.2, 2 % de la masa total; b c =. kpc). Cada órbita tiene su proección en el plano XY, YZ XZ Familia de órbitas regulares que se encuentran en el modelo dado por (3.28), de halo triaial (p=.9, q=.8) con disco (GM D =.3 M, a D =3 kpc) sin núcleo. Cada órbita tiene su proección en el plano XY, YZ XZ Familia de órbitas regulares que se encuentran en el modelo dado por (3.28), de halo triaial (p=.9, q=.8) con disco (GM D =.3 M, a D =3 kpc) con núcleo (GM C =.2, 2 % de la masa total; b c =. kpc). Cada órbita tiene su proección en el plano XY, YZ XZ Eponentes de Lapunov (arriba) su mapa de bifurcación para la ecuación logística (abajo). Cuando los LEs son negativos o cero la órbita es periódica, cuando son maores que cero se observa una bifurcación en el mapa Una región de un espacio de estados dividido en pequeñas celdas, cada una de igual longitud L Gráficas de la energía para cuatro órbitas integradas con la rutina NAG D2CJF con una tolerancia de 7 con un tiempo de integración de Mr para un modelo de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) sin disco sin núcleo Residuo fraccional de la energía para las órbitas integradas de la figura 5. su valor de correlación lineal del residuo fraccional el tiempo de integración LEs en función del tiempo de tres óbitas integradas, para un modelo de galaia de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) sin disco sin núcleo. El tiempo de integración fue de 2 Mr. Se observan que los tres pares opuestos de LEs se mantienen durante el tiempo de integración sólo durante los tiempos iniciales no son bien definidos LEs en función del tiempo de tres óbitas integradas, para un modelo de galaia de halo triaial (p=.9, q=.8, r =. kpc, v =.2 3 km/s) sin disco sin núcleo; el tiempo de integración fue de 3 Mr. Como se espera para una órbita ergódica ha al menos un LE positivo uno igual a cero
9 5.5. La CDF de los LEs para un modelo de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) sin disco sin núcleo, empleando el método MC (arriba) con condiciones iniciales uniformes (abajo) Histogramas de frecuencias de los LEs de la figura 5.5, para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) La CDF de los LEs para un modelo de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) con disco + bulge (a D =3 kpc, b D = kpc, GM D =.3 M ), para el método MC (arriba), el método tradicional (abajo) Histogramas de frecuencias de los LEs de la figura 5.7, para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) La CDF de los LEs para un modelo de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) con núcleo (GM C =.2 (.2 % de la masa total), b c =. kpc), para el método MC (arriba), el método tradicional (abajo) Histogramas de frecuencias de los LEs de la figura 5.9, para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) La CDF de los LEs para un modelo de galaia de halo + disco + núcleo, con parámetros de la tabla 5., para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) Histograma de frecuencias de los LEs de la figura 5., para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) CDF de los LEs para un modelo de halo triaial (p=.8, q=.9, r =. kpc, v =.2 3 km/s) sin disco sin núcleo (arriba) para un modelo de halo triaial (p=.8, q=.9, r =. kpc, v =.2 3 km/s) con disco + bulge (a D =3 kpc, b D = kpc, GM D =.3 M ) (abajo), para el método MC (curva roja), el método tradicional (curva aul) Histograma de frecuencias de los LEs de la figura 5.3 (abajo), para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) CDF de los LEs para un modelo de halo triaial (p=.8, q=.9, r =. kpc, v =.2 3 km/s) con núcleo (GM C =.2 (2 % de la masa total), b c =. kpc), para el método MC (curva roja), el método tradicional (curva aul) CDF de los LEs para un modelo de halo triaial con disco + núcleo, con parámetros de la tabla 5. (con p=.8 q=.9), para el método MC (curva roja), el método tradicional (curva aul) Histograma de frecuencias de los LEs de la figura 5.5, para el método MC (arriba) empleando condiciones iniciales uniformes (abajo) CDFs para un modelo de halo esférico (p=q=, r =. kpc, v =.2 3 km/s) con núcleo (GM C =.2 (2 % de la masa total), b c =. kpc), para los radios de -2 kpc (verde), 2-4 kpc (aul), 4-6 kpc (magenta), 6-8 kpc (negro) 2-4 kpc (rojo)
10
11 Índice de tablas 4.. Tipos de movimientos que caracteria el eponente de Lapunov Parámetros del modelo de halo esférico + disco + núcleo i
12
13 Capítulo Introducción Recientemente se ha mencionado la importancia de las órbitas ergódicas en modelos de potenciales de galaias. Estas son un componente significante de la densidad [8, 9, 2, 3], a que llenan todo su espacio fase disponible; por ejemplo en modelos triaiales con una concentración de masa central. Esto tiene importantes consecuencias para la construcción de modelos densidad-potencial de galaias en especial en la construcción de modelos de halo + disco + núcleo... El problema de la autoconsistencia El problema de la selección de órbitas para la construcción de modelos autoconsistentes de densidad-potencial, en el conteto del método de Schwarschild [7], ha sido el método estándar para comprobar que la densidad obtenida a través de la superposición de las órbitas, es la misma que la densidad analítica obtenida mediante la ecuación de Poisson que conecta la densidad con el potencial. La construcción de la biblioteca de órbitas se lleva a cabo empleando condiciones iniciales, posiciones velocidades, etraídas de una distribución uniforme sobre el espacio fase del sistema. Sí las órbitas ergódicas son importantes en la construcción de modelos de galaias, como halos triaiales con un disco una concentración de masa central, como se menciona en [7, 8, 9, 2, 3], entonces el muestreo uniforme es incapa de encontrar aquellas órbitas ergódicas con más peso estadístico para reforar la figura de la galaia..2. Solución propuesta La selección de las órbitas se realió calculando el Eponente de Lapunov, el cual es una medida de la divergencia eponencial de una órbita con respecto a otra órbita mu cercana. De la teoría de sistemas dinámicos se sabe que la integral de los eponentes de Lapunov sobre todo el espacio fase del sistema es una cantidad conocida como la Entropía Kolmogorov-Sinai que describe su grado de estocásticidad. Entonces se plantea el problema de la selección de órbitas como un problema de Integración de
14 2 CAPÍTULO. INTRODUCCIÓN Monte Carlo; encontrando sólo aquellas órbitas con eponentes de Lapunov (órbitas ergódicas) que más contribuen a la integral..3. Organiación de la tesis La organiación de la tesis es como sigue: en el capítulo 2 se revisan las propiedades generales de las galaias elípticas espirales; en el capítulo 3 se describe la construcción de modelos densidad-potencial de galaias de disco, el modelo empleado en el presente trabajo el método de Schwarschild, en el capítulo 4 se desarrolla el método propuesto, en el capítulo 5 se ehiben los resultados finalmente en el capítulo 6 se presentan las conclusiones trabajo a futuro por desarrollar.
15 Capítulo 2 Dinámica de las galaias elípticas espirales 2.. Galaias Elípticas Las galaias elípticas son elipsoides sin estructura, compuestas principalmente por sistemas de población II o sistemas de Halo que son estrellas viejas entre a 2 M que ehiben poca o ninguna rotación, con poco gas, pero grandes velocidades σ de dispersión. Las galaias elípticas parecen tener curvas de luminosidad características la cual se allana a como el radio de la galaia R, tal luminosidad característica se puede ajustar por la le de Hubble como sigue: I(R) = I + (R/R c ) 2 (2.) donde I es la brillantes de la superficie central R c es el radio del núcleo. Las galaias elípticas pueden ehibir rotación en su eje menor o sobre sus ejes maores en muchos casos sobre ambos, algunas galaias parecen rotar primariamente cerca de sus ejes menores. Muchas galaias elípticas tienen rutas de polvo producidas por material frío interestelar distribuido en discos o anillos. Medidas cinemáticas de la velocidad muestran que en muchos casos este gas frío rota es distinto a la componente estelar subacente. Muchas galaias elípticas contienen de 9 a masas solares de gas a temperaturas de 7 K, esto es comparable al gas presente en galaias espirales. El gas caliente frecuentemente forma una atmósfera de presión alrededor de la galaia. La Masa solar es una unidad de medida utiliada en astronomía astrofísica para medir comparativamente la masa de las estrellas otros objetos astronómicos mu masivos. Su símbolo convencional su valor son: M =, kg 3
16 4 CAPÍTULO 2. DINÁMICA DE LAS GALAXIAS ELÍPTICAS Y ESPIRALES 2.2. Correlación de parámetros en galaias elípticas La luminosidad de las galaias elípticas esta altamente correlacionada con su velocidad de dispersión; esto es generalmente epresado como una le eponencial: L σ n donde L es la luminosidad de la galaia, σ es la velocidad de dispersión el eponente n es cerca de 4. La velocidad de dispersión está correlacionada con la luminosidad de acuerdo a la le de Faber-Jackson: σ p 22(L/L ),25 km s (2.2) donde L =, h 2 L 2. Otra correlación significante es también vista entre el radio efectivo R e el brillo superficial I e a ese radio, esto es: R e I e,33. La maoría de las relaciones de tipo Faber-Jackson son intrínsecas, es decir, estas reflejan las propiedades reales de las galaias. Datos modernos muestran que las galaias elípticas obedecen una relación de la forma: R e σ,4 I e,9 que define el llamado plano fundamental. El brillo superficial de una galaia elíptica decae suavemente con el radio, la brillantes superficial característica de la maoría de las galaias se pueden ajustar por la le de Vaucouleurs: I(R) = I() ep( kr,25 ) I e ep{ 7,67[(R/R e ),25 ]} (2.3) donde R e es el radio efectivo del isofoto (o superficie de igual intensidad luminosa) conteniendo la mitad de la luminosidad total I e es la brillantes superficial a R e. La función de luminosidad φ(l) describe el número relativo de galaias de diferentes luminosidades, es definida tal que φ(l)dl es el número de galaias en el intervalo de luminosidad L L + dl en una unidad de volumen representativa del universo. Una aproimación analítica a φ(l) es la le de Schechter, esta es φ(l)dl = n ( L L ) α ep( L/L ) dl L, (2.4) donde n =,2 2 h 3 Mpc 3, α =,25, L =, h 2 L en la banda visible Galaias espirales Estas son galaias como la nuestra o como M3 (la galaia Andrómeda) la cual contiene un disco prominente compuesto de estrellas de población I o sistemas de disco, son estrellas jóvenes que ehiben rotación; en estas galaias se encuentra la presencia de gas polvo. Las galaias espirales contienen un esferoide de estrellas de población II, las cuales su composición química, cinemática evolución histórica es diferente de las estrellas del disco se cree se han formado al mismo tiempo de 2 La luminosidad del sol L = 3,83 33 erg s
17 2.4. DISTRIBUCIÓN DE LA LUMINOSIDAD DEL DISCO 5 Figura 2.: La secuencia de Hubble es un esquema de clasificación para galaias inventado por Edwin Hubble en 926. Imagen tomada de Wikipedia. formación de la galaia, en contraste a las estrellas en el disco, las cuales se han formado a una raón constante a lo largo de la historia de la galaia. En todos estos sistemas el disco contiene braos espirales, los cuales varían grandemente en su longitud, grado de enrrollamiento prominencia de una galaia espiral a otra, pero casi siempre están presentes. La distribución del brillo superficial en galaias espirales de disco obedecen la le eponencial I(R) = I ep( R/R d ) (2.5) donde R d = 3,5 ±,5kpc 3 I 4L pc 2. Las curvas de velocidad circular v c de la maoría de las galaias espirales son casi planas, es decir v c (r) independiente de r, ecepto cerca del centro donde la velocidad circular cae a cero, la velocidad circular típica se encuentra entre 2 3 km s Distribución de la luminosidad del disco Fuera de sus centros, las galaias de disco típicamente tienen una luminosidad característica de tipo eponencial, i.e. la brillantes superficial decae eponencialmente con el radio. La componente más importante de la luminosidad proviene de una región pequeña que se ajusta por una función sech() característica de una capa auto-gravitatoria con velocidad de dispersión independiente de. Una función que ajusta la distribución de luminosidad en galaias de disco es: { L ep( r/h)sech 2 (/ ), si r/h < 4,2 ±,6 L(r, ) = (2.6), de otro modo, 3 El pársec o parsec (símbolo pc) es una unidad de longitud utiliada en astronomía. pársec = 3, m
18 6 CAPÍTULO 2. DINÁMICA DE LAS GALAXIAS ELÍPTICAS Y ESPIRALES donde L es la densidad de luminosidad en el medio plano al centro del disco, h es la longitud de escala radial es la altura vertical. Para las galaias espirales con un bulge (disco espiral hinchado en el centro) en los cuales domina la luminosidad total; se le puede ajustar la le de Vaocouleurs (2.3) como en galaias elípticas. El gas interestelar el polvo destacan en galaias espirales de tipo Sa posteriores según la clasificación de Hubble (vea la figura 2.). La maoría de esta materia interestelar se encontra en un disco con un ancho o grosor significantemente más pequeña que del disco estelar. La distribución radial de gas en galaias de disco no siempre sigue una distribución eponencial, algunas galaias tienen agujeros negros en sus centros, mientras que en otras el gas se etiende más allá del disco estelar a unos 5-25 kpc Correlación de parámetros en galaias espirales Alrededor de un 8 % de las galaias espirales conocidas presentan una barra en su centro, una gran fracción de galaias de disco tienen barras. El brillo superficial entre la barra con frecuencia es casi constante. Muchas galaias barradas también contienen anillos luminosos, los más notables son aquellos en los cuales el anillo encierra sólo a la barra, estos son conocidos como anillos internos, los más comunes son los anillos eteriores, los cuales tienen típicamente el diámetro de varias veces el de la barra. Esta estructura oval de luminosidad son llamados Lenses. La cercana coneión entre las barras, anillos internos lenses sugiere una coneión en la evolución formación de las galaias. Algunas observaciones establecen la presencia de halos negros, de ahí de que las curvas de rotación de las galaias de disco sean planas, lo cual sugiere la eistencia de materia oscura Materia oscura Virtualmente toda la información que poseemos del universo ha venido a nosotros a través de fotones provenientes de estrellas, gas de hidrógeno, raos-x desde gas ioniado, etc; aún no ha raón para suponer que cada tipo de materia en el universo debe de emitir un tren leíble de fotones; incluso entre un tipo dado de objetos astronómicos, no ha raón a priori porque la masa la luminosidad deban de estar bien correlacionadas. Este punto es bien ilustrado por la función de luminosidad en la Secuencia Principal, del vecindario solar. Estrellas más brillantes que el sol contribuen 95 % de la luminosidad, mientras estrellas más opacas que el sol contienen al menos 75 % de la masa. Por lo tanto, incluso modestas variaciones en el número relativo de baja-masa alta-masa de estrellas puede producir cambios sustanciales en la raón total masa-lu Υ. Sin embargo, las raones de masa-lu en partes centrales bien estudiadas de muchas galaias elípticas espirales de algún modo consiguen ser las mismas. El material de naturalea desconocida que es responsable de esta discrepancia es llamada Materia oscura. Así, se usa el término materia oscura para
19 2.6. MATERIA OSCURA 7 denotar cualquier forma de materia de quien su eistencia es inferida solamente por sus efectos gravitacionales. La primera evidencia de materia oscura fue encontrada por el astrónomo Frit Zwick en 993; Zwick basó su trabajo sobre medidas de la velocidad radial de sistemas de galaias pertenecientes al cluster Coma. El afirmaba que las galaias individuales tenían velocidades radiales que diferían de la velocidad promedio del cluster, con una dispersión RMS cerca de 7 kms. El concluo que virtualmente toda la masa del cluster esta en una forma de materia oscura invisible, que es indetectable ecepto a través de su fuera gravitacional. Ostriker (974) Einasto (974) han propuesto que ha grandes cantidades de materia oscura alrededor incluso en galaias aisladas: ellos argumentan que la materia oscura en galaias espirales esta localiada en Halos gigantes, etendiéndose varias veces el radio de la materia luminosa conteniendo la maoría de la masa total de la galaia. La evidencia más robusta de la eistencia de materia oscura proviene de las curvas de rotación de galaias espirales [9]. Empleando las emisión de hidrógeno de 2 cm, las velocidades de nubes de hidrógeno neutro se pueden medir como una función del radio r a partir del centro de la galaia. En casi todos los casos, después de alejarse del centro (r = ), las velocidades aumentan proporcionalmente a r hasta un r máimo para a partir de ahi mantenerse. Para un sistema esférico, la atracción gravitacional ejercida sobre un punto de masa a un radio r, por el segundo teorema de Newton es: donde F = dφ dr M = r ˆr = GM ˆr, (2.7) r2 ρ(r )r 2 dr (2.8) es la masa encerrada a un radio r. Se define la velocidad circular v c (r) la velocidad de escape v esc como v c 2 = r dφ dr = r F = GM r, (2.9) v esc 2 = 2 Φ(r), (2.) donde v esc es la velocidad mínima para escapar del campo de fuera gravitacional representado por Φ. De (2.9) (2.) se obtiene que la velociad circular es v c = GMr /2. Sí la velocidad circular se mantiene constante a grandes radios según los datos que se tienen actualmente, se tiene que M /2 r /2 const, M /2 const r = /2 r/2 const (2.) por lo tanto se obtiene que la masa M(r) r a grandes radios, lo que implica que la materia debe de eistir a radios maores que el disco visible de las galaias espirales. La figura 2.2 muestra algunas curvas de rotación obtenidas recientemente por Sander (996) de Blok & McGaugh (998) [6]. Las medidas ópticas fueron usualmente
20 8 CAPÍTULO 2. DINÁMICA DE LAS GALAXIAS ELÍPTICAS Y ESPIRALES restringidas a partes internas de las galaias, principalmente el comportamiento característico de las curvas de rotación del disco fueron divididas en 3 regiones [5]:. Una región en la cual la velocidad crece linealmente con la distancia desde el centro. 2. Una región donde la velocidad alcana un máimo entonces comiena a declinar (este es llamado radio de Turnover). 3. Una región Kepleriana en la cual el potencial del disco parece un punto de masa, así que la velocidad de rotación decae como r /2. Una ve que r se vuelve más grande que la etensión de la masa, uno espera que la velocidad sea r /2, pero esto no se observa, lo que muestra que no se conoce la etensión real de los halos de materia oscura alrededor de las galaias espirales. Si se aproima el halo a una configuración esférica de radio suficientemente grande tal que la fuera gravitacional del disco pueda ser ignorada, entonces una curva de rotación con velocidad constante v c implica que la masa del halo incrementa linealmente con el radio más allá del último punto medido. La densidad del halo correspondiente es ρ(r) = dm(r) 4πr 2 dr = v c 2 4πGr 2. (2.2) La densidad del halo debe caer bajo el valor dado por la densidad ρ a radios pequeños, a que curvas de rotación observadas se mantienen planas incluso cuando la masa del disco contribue una fracción sustancial a la curva de rotación. Las curvas de rotación proporcionan la más directa evidencia de materia oscura en otras galaias espirales. Sin embargo, las curvas de rotación no dan indicación de la etensión máima del halo de materia oscura a que son aun planas al punto donde la brillantes superficial cae por debajo de los límites detectables. Así, es posible que el halo de materia oscura termine cerca de los bordes del disco visible, por otro lado puede igualmente etenderse muchas veces más, quiás incluso a varios cientos de kpc, o traslaparse con el halo de otra galaia Conclusiones Es importante diferenciar los tipos de sistemas estelares, como las galaias elípticas espirales. Es necesaria una comprensión de la influencia que tiene la materia oscura sobre las galaias espirales; para entender la dinámica de las mismas poder interpretar los resultados obtenidos de acuerdo a las suposiciones hechas. La estructura de las galaias espirales está conformada por: un halo triaial de materia obscura, un disco en su centro un bulbo o concentración central, este será el sistema que analiaremos en esta tesis.
21 2.7. CONCLUSIONES 9 Figura 2.2: Curvas de rotación de galaias espirales publicadas por Sander (996) de Blok & McGaugh (998). El radio (eje horiontal) esta dado en kpc en todos los casos la velocidad (eje vertical) esta en km s. Los puntos muestran las curvas de rotación de líneas de 2 cm observadas, las líneas punteadas son las curvas de rotación Newtonianas, las líneas solidas las medidas de MOND [6].
22 CAPÍTULO 2. DINÁMICA DE LAS GALAXIAS ELÍPTICAS Y ESPIRALES
23 Capítulo 3 Modelos auto-consistentes de galaias 3.. Introducción La importancia de comprender la estructura las lees físicas subacentes que gobiernan la dinámica evolución de los sistemas galácticos es la principal meta en el estudio de sistemas estelares; a fin de comprender algunos de los problemas claves en astrofísica que relacionan el origen, evolución estructura del universo. El análisis de la morfología estabilidad de las órbitas de estrellas individuales en estos sistemas galácticos es esencial para desarrollar una teoría viable acerca del comportamiento de las galaias como un todo. Basandose en observaciones se pueden dividir a las galaias de acuerdo a su forma en espirales (barradas o no barradas), elípticas e irregulares. En la literatura las galaias elípticas se denotan como En donde n = a c a los parametros a c son los ejes maor menor, respectivamente. El rango de las elípticas va desde esféricas E hasta altamente atachadas E7. Las observaciones de galaias elípticas sólo proporcionan una proección de la línea de visión de su forma, dejando la duda de una posible simetría aial. Aunque recientemente las galaias elípticas fueron consideradas como aisimétricas (oblata) debido a su rotación. Se ha observado que la maoría de las galaias elípticas rotan significantemente más lento (de 7-8 km/h) de lo que se espera de un cuerpo fluido con la misma raón aial que seria de unos 2-3 km/h. Estas observaciones dan cabida a la siguiente pregunta: son las galaias elípticas aisimétricas o completamente triaiales?. Binne [4] ha propuesto que el atachamiento de las galaias elípticas se debe principalmente a que la distribución de velocidad es anisotrópica que por lo menos los modelos triaiales son probablemente aisimétricos. Brevemente se comenta que Schwarschild en [7] propuso un método para construir modelos triaiales auto-consistentes que se vera más adelante. Las galaias elípticas son sistemas de entre 7 a 2 estrellas tienen un radio aproimado de 5 kpc [5]. Una colisión es un encuentro entre estrellas cuando el efecto gravitacional debido a sus masas domina el campo gravitatorio del resto de la galaia. Resultados recientes muestran que el tiempo necesario para que se produca una colisión es de 9 r un factor de 9 más grande que la edad de la galaia, el
24 2 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS cual es de,5 r; esto justifica el tratamiento de las estrellas en una galaia como puntos con masa a las galaias como sistemas sin colisiones [5]. Esto también permite usar una distribución de masa continua para así obtener una aproimación al campo gravitacional de las galaias La ecuación de Boltmann sin colisiones La distribución de masa en un galaia sin colisiones se describe a través de una función de distribución (DF) del espacio fase f(, v, t) que satisface la ecuación de Boltmann sin colisiones (EBC) dada por: f f + v f Φ t v = (3.) donde Φ es el potencial gravitacional del sistema. Para que la DF tenga significado físico debe de ser no-negativa. En los modelos en equilibrio se tiene que f =. La integración de la DF sobre el espacio de velocidades t produce la densidad de masa ρ() del sistema: ρ(, t) = f(, v, t)d 3 v. (3.2) Dada la densidad de masa ρ, el potencial gravitacional Φ() se puede calcular por medio de la ecuación de Poisson: 2 Φ = 4πGρ (3.3) donde G es la constante gravitacional. No toda la densidad de masa es debido a la materia luninosa, sino también ha contribuciones importantes de materia oscura, tal como la eistencia de halos de materia oscura o agujeros negros en los centros de las galaias. Para obtener un modelo dinámico de un sistema galáctico se deben resolver las ecuaciones (3.)-(3.3) simultáneamente. Si se pueden resolver, entonces se habla de un modelo auto-consistente, para ello se pueden adoptar una de las siguientes aproimaciones:. Dada la densidad ρ resolvemos (3.)-(3.3) para f. 2. Dada la DF f resolvemos (3.)-(3.3) para ρ. En cualquiera de estas aproimaciones, es útil emplear el teorema de Jeans que relaciona la DF las coordenadas del espacio fase. Todas las integrales aisladas de movimiento I(, v) que se conservan en un potencial dado satisfacen (3.). Las integrales aisladas de movimiento la DF se relacionan por medio del teorema de Jeans, el cual dice que la DF depende de las coordenadas del espacio fase (, v) sólo a través de tres integrales aisladas de movimiento f(i, I 2, I 3 ). Si el sistema admite menos integrales de movimiento que grados de libertad las órbitas son caóticas (estocásticas o irregulares); esto significa que cada
25 3.2. EL MÉTODO DE SCHWARZSCHILD 3 órbita llenara densamente la porción del espacio fase delimitado por la(s) curva(s) de la integral(es) constante de movimiento que obedece. Sí por otro lado, el número de integrales aisladas de movimiento es igual al número de grados de libertad la órbita es regular El método de Schwarschild Las galaias triaiales tienen tres planos de reflección simétricos, pero los ejes no son simétricos. En un potencial triaial, la fuera no es radial por lo que ningún componente del momento angular se conserva. Esta ausencia de simetría hace de las galaias triaiales un problema de tres grados de libertad. La maoría de las galaias triaiales tienen eactamente una sola integral de movimiento, la energía de la órbita E (definido como el valor del Hamiltoniano). Sin embargo, los modelos numéricos muestran que porciones mu pequeñas de las órbitas en sistemas triaiales son regulares [7, 8, 9, 2, 3]. Estas órbitas admiten dos integrales de movimiento I 2 I 3 además de la energía orbital entonces la DF es f(e, I 2, I 3 ). Sin embargo, a que estas integrales aisladas de movimiento no se conocen analíticamente no se puede construir una DF que represente a una galaia. En [7] se propuso un método numérico para calcular una configuración 3-dimensional auto-consistente para sistemas estelares sin colisiones en equilibrio dinámico. Densidad Potencial Programación lineal Órbitas No-negativo mínimos cuadrados Distribución de la densidad de órbitas individuales Figura 3.: Método de Schwarschild para calcular numéricamente la función de distribución f. El método de Schwarschild es una aproimación estándar para verificar sí un
26 4 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS modelo es auto-consistente o no, que a grandes rasgos consiste en 4 pasos: ) escoger una distribución de densidad, 2) calcular el potencial a partir de la ecuación de Poisson, 3) integrar n órbitas finalmente 4) reproducir la densidad por medio de la superposición orbital. Para llevarlo a cabo se divide el espacio en celdas, a sea de igual masa o volumen, así se puede saber el tiempo que una órbita estuvo en cada celda. Comúnmente se emplea programación lineal para resolver el problema en muchas otras ocasiones mínimos cuadrados. La figura 3. muestra un esquema del método de Schwarschild. En la última etapa del método de Schwarschild se calculan los números de ocupación que es el número de veces que cada órbita pasa por una celda determinada por el índice i, esto proporciona una aproimación a la función de distribución del espacio fase f(, v). La principal contribución del método de Schwarschild es que f se obtiene numéricamente sin conocimiento eplícito de las integrales de movimiento. El procedimiento general del método de Schwarschild se detalla abajo. Procedimiento general a) Escoger una distribución de densidad. La distribución de densidad se puede dar numérica o analíticamente, pero por costo computacional se recomienda en lo posible representarla analíticamente para facilitar los cálculos en el paso b. El espacio ocupado por el modelo se divide en N celdas la distribución de densidad se representara por la masa D(J) con J = hasta N lugares en cada celda. El espacio se divide a sea en celdas de igual volumen o igual masa (figura 3.2) dependiendo de la geometría de la distribución se contiene en una esfera o un cilindro. b) Derivación del potencial gravitacional. Dada la distribución de densidad, el potencial se puede calcular por medio de la ecuación de Poisson (3.3). Por costo computacional es conveniente que el potencial sus primeras tres derivadas parciales se pueden epresar al menos parcialmente algebraicas, en lugar de totalmente numéricas. Para nuestros propositos este paso no es necesario, a que se tiene la epresión del potencial, por el cual también la densidad vía (3.3). c) Cálculo de las órbitas. Dado el potencial gravitacional, cualquier órbita descrita por sus parámetros iniciales se puede calcular empleando cualquier método de integración. Es necesario que el tiempo de integración sea lo suficientemente grande, digamos oscilaciones dentro del sistema para asegurarnos que la órbita represente las características del sistema. Durante el cálculo o integración de una órbita, ciertos datos tienen que ser guardados para futuras investigaciones como las velocidades posiciones. Aquí, sólo se necesita guardar la fracción de tiempo que una órbita pasa en una celda (números de ocupación) dependiendo de la división hecha en el paso a (figura 3.2). Así, cuando el cálculo de una órbita designada por el índice I, se guarda la fracción de tiempo B(I, J) en la celda con índice J = hasta N. Los valores B se pueden considerar como una
27 3.2. EL MÉTODO DE SCHWARZSCHILD 5 representación de la distribución de densidad producida por la superposición orbital. Figura 3.2: En la iquierda se muestra un sistema contenido en un cilindro con una división del espacio en celdas de igual volumen en la derecha se muestran órbitas pasando por una celda. El número total de órbitas que pasan por una celda se le llama número de ocupación este representa la densidad del sistema en la celda. d) Reproducción de la distribución de densidad del modelo. Después del cálculo de digamos M órbitas la pregunta restante es: puede la distribución de densidad D(J) ser reproducida por una superposición de M órbitas por medio de los números de ocupacion B(I, J), si cada órbita ocupa aleatoriamente un número apropiado de celdas con números de ocupación C(I)? o más precisamente, puede el siguiente conjunto de ecuaciones: M C(I) B(I, J) = D(J) (J =,..., N) (3.4) I= tener una solución física aceptable, por ejemplo, una en la cual todos los números de ocupación sean no negativos, es decir C(I) (I =,..., M). (3.5) Las ecuaciones (3.4) (3.5) representan un problema típico de programación lineal para el cual eisten métodos para calcular una solución o probar la no eistencia de una solución. Si para un caso en particular, la programación lineal da la respuesta Sin solución para las condiciones (3.4) (3.5), dos alternativas se pueden considerar: podría ser que las M órbitas incluidas no cubren suficientemente los tipos rangos de los parámetros de todas las órbitas posibles. En este caso, se necesita calcular órbitas adicionales con el objetivo de incrementar la variedad en las tablas B(I, J), entoces el método de programación lineal se repite agregando las nuevas órbitas. Por otro lado, si la respuesta sigue siendo Sin solución entonces la interpretación posible podría ser que la distribución elegida puede no corresponder a una configuración en equilibrio en vista de la eistencia de tres integrales de movimiento para la maoría de las órbitas. En
28 6 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS contraste, en la situación en que la programación lineal proporciona una solución para las condiciones (3.4) (3.5) se puede concluir que la distribución de densidad escogida corresponde a una configuración dinámica en equilibrio que esta configuración se puede representar por medio de una superposición de órbitas donde cada celda es ocupada por un número de estrellas dada por la solución de la programación lineal. La librería de órbitas empleando la aproimación de Schwarschild se puede contruir como sigue: muestrear uniformemente el espacio fase para obtener las condiciones iniciales (posiciones velocidades), integrar las ecuaciones de movimiento sobre grandes escalas de tiempo calcular los números de ocupación. Esto no asegura de que siempre se tendrán las órbitas que más peso estadístico tengan para reforar la forma de la galaia; por otro lado, varios autores mencionan la importancia de las órbitas ergódicas en modelos de potenciales de galaias. La ergodicidad de cada órbita se puede determinar vía su Eponente de Lapunov (LE), el cual mide la raón a la cual una órbita eperimenta una perturbación lineal desde su traectoria imperturbada. Una órbita regular tiene un LE igual a cero, mientras una órbita ergódica tiene al menos un LE positivo Órbitas potencial gravitacional Mucha de la masa de una galaia reside en estrellas. Para calcular el potencial de un gran número de estrellas se debe en principio sumar el potencial de cada punto de masa de todas las estrellas. Por supuesto, esto no es práctico para estrellas en una galaia típica, para la maoría de los propositos es suficiente modelar el potencial como una distribución de densidad uniforme que sea proporcional a la densidad local en la galaia. Para calcular la fuera F() sobre una unidad de masa a la posición que es generado por la atracción gravitacional de una distribución de masa ρ() se emplea la le del inverso al cuadrado de la gravitación de Isaac Newton. La fuera F() se puede obtener sumando las pequeñas contribuciones de la fuera total de cada pequeño elemento de volumen δ 3 localiada a, es decir: Entonces, δf() = G 3 δm( ) = G 3 ρ( )δ 3. (3.6) F = G d3 ρ( )d 3. (3.7) Se define el potencial gravitacional Φ(X) como ρ( ) Φ() = G d3 (3.8) del cual se deriva que
29 3.3. ÓRBITAS Y POTENCIAL GRAVITACIONAL 7 F() = Gρ( ) d3 = Φ. (3.9) El potencial es útil porque siendo un campo escalar, es más fácil de visualiar que el campo de fuera. Además, en muchas situaciones la mejor forma de obtener F es primero calcular el potencial entonces tomar su gradiente Pares densidad-potencial La densidad generada por un potencial gravitacional se puede conocer a través de (3.3) considerando que cada estrella es un punto de masa donde no eisten colisiones. A esta relación del potencial con la densidad se le conocen como modelos de galaias densidad-potencial. Los siguientes son ejemplos de modelos densidad-potencial. Potenciales esféricos Punto de masa: el potencial la fuera Kepleriana están dados por: Φ(r) = GM r, f r = Φ(r) = GM ˆr. (3.) r2 El movimiento de las órbitas se describe por la ecuación m r = m Φ(r), su mometum angular por unidad de masa es J = r (mṙ), del mismo modo J = r (m r) + ṙ (mṙ) = r F a que ṙ (mṙ) =. Sí Φ(r) depende únicamente de r no de r, entonces por lo tanto f = Φ = dφ ˆr (3.) dr dj = r (mf) = mdφr ṙ =. (3.2) dt dr El momentum angular alrededor del origen se conserva, lo que quiere decir que el movimiento se sustenta sobre un plano (r ˆr en el plano). Potencial Isocrono: Un potencial más realista es el potencial isocrono, el cual fue diseñado para dar una densidad constante alta cerca del centro decae como ρ r 4 para r grande (figura 3.3), consistente con muchos resultados empíricos de astronomía galáctica. El potencial isochrone tiene una escala longitud b masa total M GM Φ(r) = b + (3.3) b 2 + r 2
30 8 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS la densidad es [ ] 3(b + a)a 2 r 2 (b + 3a) ρ(r) = M 4π(b + a) 3 a 3 (3.4) donde a = b 2 + r Phi Rho r Figura 3.3: Gráfica del potencial Isochrone (arriba) la densidad generada (abajo) con b =,5 G = M = en unidades unitarias. Potenciales aisimétricos
31 3.3. ÓRBITAS Y POTENCIAL GRAVITACIONAL 9 Potencial de Plummer: Considere el potencial esférico Φ P = GM r2 + b, (3.5) 2 de la ecuación de Poisson (3.3) se tiene que la densidad correspondiente al potencial, es ( ) ) 5 3M ρ P (r) = ( + r2 2. (3.6) 4πb 3 b 2 En 9 H.C. Plummer usó este par densidad-potencial (3.5)-(3.6) para ajustar observaciones de cúmulos globulares, es conocido como el modelo de Plummer. Potencial de Plummer-Kumin: también conocido como el modelo de Toomre está dado por GM Φ K (R, ) =, (3.7) R 2 + (a + ) 2 con densidad superficial Σ K (R) = am. (3.8) 2π(R 2 + a 2 3/2 ) La densidad superficial se define como Σ K = ρ(r, )d. La figura 3.4 muestra la densidad superficial velocidad circular del potencial de Kumin; la densidad en R = es M/2πa 2 ; la velocidad circular en R = es infinita donde la densidad superficial sería cero, v c crece desde R = para a hasta alcanar la velocidad máima que le permite la densidad inicial en R = 2a. Potencial Miamoto-Nagai [4]: es una combinación del modelo de Plummer- Kumin (3.7) el modelo esférico de Plummer (3.5) para cúmulos globulares está dado por: Φ M (R, ) = GM R 2 + (a + b ) 2. (3.9) Cuando a =, Φ M se reduce al modelo esférico de Plummer (3.5), cuando b =, Φ M se reduce al modelo de Kumin (3.7). Dependiendo de la elección de los parámetros a b, Φ M puede representar el potencial de cualquier disco infinítamente delgado hasta un disco con una concentración de masa central. De (3.3) la densidad generada por el potencial es
32 2 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS Sigma Vc R Figura 3.4: La gráfica de arriba muestra la densidad superficial del potencial de Kumin normaliado con a = la gráfica de abajo muestra la velocidad circular para a=,2,3,4,5; conforme a es más grande la densidad inicial es maor, por lo tanto la máima velocidad circular es menor lo que se observa en las curvas.
33 3.3. ÓRBITAS Y POTENCIAL GRAVITACIONAL 2 ρ M (R, ) = ( ) b 2 M ar 2 + (a b 2 )(a b 2 ) 2 4π [ R2 + (a b 2 ) 2], (3.2) 5/2 (2 + b 2 ) 3/2 la cual es no-negativa en cualquier lugar en el espacio. El potencial de Miamoto-Nagai involucra pocos parámetros: la dimensión de la galaia a, el grosor galáctico b, la masa de la galaia M. Con estos tres parámetros, el modelo de Miamoto-Nagai cubre un amplio rango de configuraciones aisimétricas de galaias. La figura 3.5 muestra contornos de la densidad generado por el potencial como función de la raón b/a; conforme b/a decrementa la distribución de masa se vuelve cada ve más llana; también se muestra un ejemplo de órbita para cada densidad generada. La ecuación (3.2) muestra que la disposición de materia es oblato en lugar de prolato, a que ρ(, ) > ρ(, ) para a. Pero que la distribución de masa es generalmente esferoidal, ecepto cerca del centro galáctico donde el campo de densidad (3.2) tiende a una forma esferoidal oblata. Potencial logarítmico: a que los modelos de Plummer-Kumin (3.5)-(3.7) tienen una masa finita, la velocidad circular asociada con este potencial decae en una manera Kepleriana, es decir v c R /2 para R grande. Si para R grande, v c v es una constante entonces dφ/dr R por lo tanto Φ v 2 ln R + constant en esta región. Por lo tanto considere el siguiente potencial Φ L = ) 2 v 2 ln (R 2 c + R constant, (3.2) donde R c es el radio del núcleo, v es constante, q Φ. De la ecuación (3.3) la densidad generada por el potencial Φ L es q 2 Φ ( ) v 2 ρ L (R, ) = (2q 2 Φ + )Rc 2 + R 2 + 2( 2 q 2 Φ )2 4πGqΦ 2 (Rc 2 + R q 2. (3.22) Φ )2 Para R pequeños, ρ L tiende al valor ρ L (, ) = (4πG) (2 + q 2 Φ )(v /R c ) 2, cuando R o es grande ρ L decae como R 2 o 2. Las superficies equipotenciales de Φ L son elipses de raón aial q Φ, pero de la figura 3.6 muestra que las superficies equidensidad son algo más planas, también se muestra un ejemplo de órbita para cada densidad generada. La velocidad circular v c al radio R en el plano ecuatorial (R, ) de Φ L es v c = v R R 2 c + R 2. (3.23)
34 22 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS R R Figura 3.5: Gráficas de contorno de la densidad de Miamoto-Nagia para las raones b/a =.2 (arriba), b/a = (en medio) b/a = (abajo), también se muestra un ejemplo de órbita para cada gráfica de densidad con valores iniciales (R,, v R, v ) = (-.2,.,.,-.) GM =.
35 3.3. ÓRBITAS Y POTENCIAL GRAVITACIONAL 23 Este potencial se puede generaliar para simular una figura triaial el cual ha sido estudiado con detalle en [5]. En general, sepuede escribir en términos de coordenadas cartesianas como Φ H = 2 v2 ln(r p 2 + q 2 ). (3.24) Las equipotenciales son elipsoides con raones /p 2 /q 2 entre el medio eje largo corto largo respectivamente Modelo triaial de Disco + Halo + Núcleo Se generaliaron los modelos anteriores en tres dimensiones espaciales, para el modelo de una galaia con componentes de halo, disco núcleo, el potencial total es igual a la suma de cada componente individual a que los potenciales son conservativos. Se empleó un potencial logarítmico (3.24) para modelar el halo de la galaia (con parámetros de triaialidad p q): Halo: Φ H = 2 v2 ln(r p 2 + q 2 ). (3.25) Se modeló el disco bulge usando el potencial de Miamoto-Nagai (3.9) donde los parámetros a b determinan la concentración de masa central llanura del sistema: GM D Disco: Φ D = (a D + ( 2 + b 2 D )/2 ). (3.26) 2 Se incluó una esfera de Plummer (3.5) para modelar el núcleo central de masa para el sistema Así, el potencial total es GM C Núcleo: Φ C =. (3.27) b 2 c la densidad en cualquier región del sistema es Φ = Φ Halo + Φ Disco + Φ Núcleo (3.28) ρ(,, ) = 2 Φ 4πG. (3.29) Los parámetros del halo v la máima velocidad de rotación r el radio del núcleo donde el potencial es casi armónico están en unidades de km/s kpc respectivamente. Los valores que se emplearon fueron v =.2 igual a 2 km/s r = igual a kpc, respectivamente. Los parámetros del disco GM D que representa la masa del disco esta en unidades para la cual la constante gravitacional es la unidad, a D la concentración de masa central está dada en kpc b D que determina la llanura del disco también esta
36 24 CAPÍTULO 3. MODELOS AUTO-CONSISTENTES DE GALAXIAS R R R R Figura 3.6: Contornos de igual densidad en el plano (R, ) para ρ L, cuando q Φ =. (arriba), q Φ =.95 (en medio) q Φ =.7 (abajo). Cuando q Φ =,7 la densidad es negativa cerca del eje para 7R c ; también se muestra un ejemplo de órbita para cada gráfica de densidad, con valores iniciales (R,, v R, v ) = (.5,-.5,.5,.2) con v = R c =.5.
El primer paso para investigar la evolución de galaxias es comprender las propiedades actuales de esas galaxias. Galaxias Elípticas
 El primer paso para investigar la evolución de galaxias es comprender las propiedades actuales de esas galaxias. Galaxias Elípticas Familia que agrupa varias clases de galaxias cd: masivas y luminosas,
El primer paso para investigar la evolución de galaxias es comprender las propiedades actuales de esas galaxias. Galaxias Elípticas Familia que agrupa varias clases de galaxias cd: masivas y luminosas,
Ayudantía 11. Astronomía FIA Ayudante: Felipe Garrido Goicovic
 Ayudantía 11 Astronomía FIA 0111 Ayudante: Felipe Garrido Goicovic fagarri1@uc.cl 1.- Remanentes estelares provenientes del colapso nuclear de una supernova, con diámetro ~ 20 km y una inmensa densidad.
Ayudantía 11 Astronomía FIA 0111 Ayudante: Felipe Garrido Goicovic fagarri1@uc.cl 1.- Remanentes estelares provenientes del colapso nuclear de una supernova, con diámetro ~ 20 km y una inmensa densidad.
Galaxia espiral Messier 31 (2.5 millones de años luz=775 kpc)
 Galaxia espiral Messier 31 (2.5 millones de años luz=775 kpc) galaxias espirales barradas y la nuestra? Como sabemos cómo es, si estamos dentro? imagen de la Vía Láctea vista desde el hemisferio sur Herschel
Galaxia espiral Messier 31 (2.5 millones de años luz=775 kpc) galaxias espirales barradas y la nuestra? Como sabemos cómo es, si estamos dentro? imagen de la Vía Láctea vista desde el hemisferio sur Herschel
Astrofísica " Extragaláctica! INTRODUCCIÓN!
 Astrofísica " Extragaláctica! INTRODUCCIÓN! INTRODUCCIÓN Un sistema estelar es un grupo de estrellas ligadas gravitacionalmente. Varian en ~14 ordenes de magnitud en tamaños y masas: desde estrellas binarias
Astrofísica " Extragaláctica! INTRODUCCIÓN! INTRODUCCIÓN Un sistema estelar es un grupo de estrellas ligadas gravitacionalmente. Varian en ~14 ordenes de magnitud en tamaños y masas: desde estrellas binarias
Estructura estelar estática
 Estructura estelar estática Introducción A lo largo de su existencia, una estrella se encuentra en un estado de equilibrio delicado. Pequeños cambios pueden provocar inestabilidades locales o globales.
Estructura estelar estática Introducción A lo largo de su existencia, una estrella se encuentra en un estado de equilibrio delicado. Pequeños cambios pueden provocar inestabilidades locales o globales.
CÚMULOS Y GALAXIAS. Las Mega estructuras del Universo
 CÚMULOS Y GALAXIAS Las Mega estructuras del Universo Introducción Hasta el momento hemos visto los componentes básicos del Universo... Pero, Cómo interactúan estos objetos? Nos afecta a nosotros lo que
CÚMULOS Y GALAXIAS Las Mega estructuras del Universo Introducción Hasta el momento hemos visto los componentes básicos del Universo... Pero, Cómo interactúan estos objetos? Nos afecta a nosotros lo que
Nuestra galaxia: la Vía Láctea
 Nuestra galaxia: la Vía Láctea Las estrellas y los cúmulos de estrellas, el gas y el polvo, rayos cósmicos, radiación, campos magnéticos se agrupan en estructuras denominadas Galaxias. Nosotros formamos
Nuestra galaxia: la Vía Láctea Las estrellas y los cúmulos de estrellas, el gas y el polvo, rayos cósmicos, radiación, campos magnéticos se agrupan en estructuras denominadas Galaxias. Nosotros formamos
AST Temario. Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo
 AST 0111 Temario Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo Distribución de Cúmulos Abiertos en la Vía Láctea Distribución de Cúmulos Globulares en
AST 0111 Temario Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo Distribución de Cúmulos Abiertos en la Vía Láctea Distribución de Cúmulos Globulares en
Introducción a las Ciencias de la Tierra y el Espacio II 2011 (www.astronomia.edu.uy/cte2) Práctica Nro. 3. Materia oscura del halo galáctico NOMBRE:
 Práctica Nro. 3 Materia oscura del halo galáctico NOMBRE: FECHA DE ENTREGA: Objetivos Estimaremos la masa de la galaxia NGC 2742 por dos métodos diferentes: uno basado en la curva de rotación de la galaxia
Práctica Nro. 3 Materia oscura del halo galáctico NOMBRE: FECHA DE ENTREGA: Objetivos Estimaremos la masa de la galaxia NGC 2742 por dos métodos diferentes: uno basado en la curva de rotación de la galaxia
La Distribución de las Estrellas
 ESTRUCTURA GALÁCTICA Y DINÁMICA ESTELAR Recuentos de Estrellas y Cinemática Estelar 1 Dr. César A. Caretta Departamento de Astronomía Universidad de Guanajuato La Distribución de las Estrellas 1 Distancias
ESTRUCTURA GALÁCTICA Y DINÁMICA ESTELAR Recuentos de Estrellas y Cinemática Estelar 1 Dr. César A. Caretta Departamento de Astronomía Universidad de Guanajuato La Distribución de las Estrellas 1 Distancias
LAS GALAXIAS Y EL UNIVERSO
 LAS GALAXIAS Y EL UNIVERSO Introducción Tour por las Galaxias Distribución de Galaxias en el espacio. Masas de Galaxias y Materia Oscura Formación y Evolución de Galaxias Estructuras de Gran Escala Qué
LAS GALAXIAS Y EL UNIVERSO Introducción Tour por las Galaxias Distribución de Galaxias en el espacio. Masas de Galaxias y Materia Oscura Formación y Evolución de Galaxias Estructuras de Gran Escala Qué
Johan H. Knapen, Instituto de Astrofísica de Canarias, La Laguna, Tenerife
 Las galaxias barradas Johan H. Knapen, Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife Introducción Las estrellas forman parte de galaxias, y nuestra estrella, el Sol, forma parte de nuestra
Las galaxias barradas Johan H. Knapen, Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife Introducción Las estrellas forman parte de galaxias, y nuestra estrella, el Sol, forma parte de nuestra
Dinámica de la rotación Momento de un vector con respecto a un punto: vectores r y F y el sentido viene dado por la regla
 00-0 Dinámica de la rotación Momento de un vector con respecto a un punto: M El momento del vector con respecto al punto O se define como el producto vectorial M r O Es un vector perpendicular al plano
00-0 Dinámica de la rotación Momento de un vector con respecto a un punto: M El momento del vector con respecto al punto O se define como el producto vectorial M r O Es un vector perpendicular al plano
Repaso de electrostática y magnetostática. 1. En cada una de las siguientes distribuciones de carga:
 Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
LA ESCALA DEL UNIVERSO
 LA ESCALA DEL UNIVERSO LA ESCALA DEL UNIVERSO Tierra Sistema solar Estrellas vecinas Vía Láctea Grupo Local galáctico Supercúmulo de Virgo Supercúmulo Local Universo observable DISPOSICIÓN DE LAS GALAXIAS
LA ESCALA DEL UNIVERSO LA ESCALA DEL UNIVERSO Tierra Sistema solar Estrellas vecinas Vía Láctea Grupo Local galáctico Supercúmulo de Virgo Supercúmulo Local Universo observable DISPOSICIÓN DE LAS GALAXIAS
1. Suponiendo que los planetas Venus y la Tierra describen órbitas circulares alrededor del Sol, calcula: =365 (1,08. 1, m
 Física º Bachillerato Ejercicios resueltos 1. ASRONOMÍA 1.1. Introducción 1.. Astronomía pre-newtoniana 1. Suponiendo que los planetas Venus y la ierra describen órbitas circulares alrededor del Sol, calcula:
Física º Bachillerato Ejercicios resueltos 1. ASRONOMÍA 1.1. Introducción 1.. Astronomía pre-newtoniana 1. Suponiendo que los planetas Venus y la ierra describen órbitas circulares alrededor del Sol, calcula:
Electromagnetismo I. Semestre: TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Galaxias. Yago Ascasibar. Introducción a la Astronomía Programa Universidad para Mayores (PUMA) UAM, 26/04/2012
 Yago Ascasibar Programa Universidad para Mayores (PUMA) UAM, 26/04/2012 1 2 Eĺıpticas Espirales Otros tipos 3 La Vía Láctea La Vía Láctea La Vía Láctea Galileo Galilei (1564 1642) La Vía Láctea William
Yago Ascasibar Programa Universidad para Mayores (PUMA) UAM, 26/04/2012 1 2 Eĺıpticas Espirales Otros tipos 3 La Vía Láctea La Vía Láctea La Vía Láctea Galileo Galilei (1564 1642) La Vía Láctea William
Astronomía. Ayudantía 13 Prof. Jorge Cuadra Ayudante: Paulina González
 Astronomía Ayudantía 13 Prof. Jorge Cuadra Ayudante: Paulina González 1.- Los brazos espirales en una galaxia son delineados por: a) Enanas blancas. b) Estrellas tipo O y B. c) Estrellas de tipo solar.
Astronomía Ayudantía 13 Prof. Jorge Cuadra Ayudante: Paulina González 1.- Los brazos espirales en una galaxia son delineados por: a) Enanas blancas. b) Estrellas tipo O y B. c) Estrellas de tipo solar.
a) Analice la continuidad en (1,0). E1) Dada F : IR 2 π g : D IR 2 I R 2 2 2
 Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Física 3: Septiembre-Diciembre 2011 Clase 8, Miércoles 5 de octubre de 2011
 Clase 8 Flujo Eléctrico y ley de Gauss Flujo eléctrico El signo del flujo eléctrico Por su definición el flujo eléctrico a través de una cierta superficie puede ser positivo, negativo o nulo. De hecho
Clase 8 Flujo Eléctrico y ley de Gauss Flujo eléctrico El signo del flujo eléctrico Por su definición el flujo eléctrico a través de una cierta superficie puede ser positivo, negativo o nulo. De hecho
PARES POTENCIAL DENSIDAD PARA MODELOS DE GALAXIAS COMPUESTOS DE DISCOS DELGADOS Y HALOS ESFEROIDALES
 Planteamiento del problema PARES POTENCIAL DENSIDAD PARA MODELOS DE GALAXIAS COMPUESTOS DE DISCOS DELGADOS Y HALOS ESFEROIDALES Fernando Cortés Serrano Universidad Industrial de Santander Facultad de Ciencias
Planteamiento del problema PARES POTENCIAL DENSIDAD PARA MODELOS DE GALAXIAS COMPUESTOS DE DISCOS DELGADOS Y HALOS ESFEROIDALES Fernando Cortés Serrano Universidad Industrial de Santander Facultad de Ciencias
Familias de Soluciones Exactas No Locales de las Ecuaciones de Einstein
 Familias de Soluciones Exactas No Locales de las Ecuaciones de Einstein Héctor Hernández Universidad de Los Andes, Mérida, Venezuela H. Hernández. Bucaramanga 2012 1 INTRODUCCIÓN La relación curvatura
Familias de Soluciones Exactas No Locales de las Ecuaciones de Einstein Héctor Hernández Universidad de Los Andes, Mérida, Venezuela H. Hernández. Bucaramanga 2012 1 INTRODUCCIÓN La relación curvatura
1) Principio de Inercia. Todo cuerpo que se mueve libremente(no está sometido a una fuerza) se mueve en una línea recta(o está en reposo).
 Leyes de Newton Sea = pr mvr el momentum lineal de una partícula.m es la masa (inercial) y la velocidad. vr 1) Principio de Inercia. Todo cuerpo que se mueve libremente(no está sometido a una fuerza) se
Leyes de Newton Sea = pr mvr el momentum lineal de una partícula.m es la masa (inercial) y la velocidad. vr 1) Principio de Inercia. Todo cuerpo que se mueve libremente(no está sometido a una fuerza) se
Medios materiales y desarrollo multipolar.
 Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
Masas estelares. Estrellas binarias
 Capítulo 7 Masas estelares. Estrellas binarias 7.1. Masas estelares # Masa magnitud fundamental de las estrellas Determina la producción de energía ( ) evolución Constante durante la mayor parte de la
Capítulo 7 Masas estelares. Estrellas binarias 7.1. Masas estelares # Masa magnitud fundamental de las estrellas Determina la producción de energía ( ) evolución Constante durante la mayor parte de la
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
MECÁNICA CLÁSICA CINEMATICA. FAyA Licenciatura en Química Física III año 2006
 Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático.
 Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
CAPITULO 1 LAS GALAXIAS
 CAPITULO 1 LAS GALAXIAS 1998, José María Atencia Comentarios y sugerencias a: jmat@leame.com INDICE DE CONTENIDOS 1. Información del Copyright. 2. Introducción. 3. Las galaxias. 3.1. Observación. 3.2.
CAPITULO 1 LAS GALAXIAS 1998, José María Atencia Comentarios y sugerencias a: jmat@leame.com INDICE DE CONTENIDOS 1. Información del Copyright. 2. Introducción. 3. Las galaxias. 3.1. Observación. 3.2.
EJERCICIOS DE SELECTIVIDAD CAMPO GRAVITACIONAL
 EJERCICIOS DE SELECTIVIDAD CAMPO GRAVITACIONAL P1- JUNIO 2010 A) Deduzca la expresión de la energía cinética de un satélite en órbita circular alrededor de un planeta en función del radio de la órbita
EJERCICIOS DE SELECTIVIDAD CAMPO GRAVITACIONAL P1- JUNIO 2010 A) Deduzca la expresión de la energía cinética de un satélite en órbita circular alrededor de un planeta en función del radio de la órbita
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
VIII. MOMENTOS DE INERCIA
 VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
VIII. MOMENTOS DE INERCIA Recordemos que el momento estático es la suma de los productos de cada elemento de un cuerpo por su distancia a un eje. El momento de inercia, es cambio es la suma de los productos
2.- Cuánto valen el potencial y la intensidad del campo gravitatorio creado por la Tierra en un punto de su superficie?
 PROBLEMAS 1.- Con una órbita de 8000 Km de radio gira alrededor de la Tierra un satélite de 500 Kg de masa. Determina: a) su momento angular b) su energía cinética c) su energía potencial d) su energía
PROBLEMAS 1.- Con una órbita de 8000 Km de radio gira alrededor de la Tierra un satélite de 500 Kg de masa. Determina: a) su momento angular b) su energía cinética c) su energía potencial d) su energía
Instituto de Física Universidad de Guanajuato Agosto 2007
 Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
ANALISIS MATEMATICO I (2012)
 ANALISIS MATEMATICO I (0) TRABAJO PRÁCTICO Funciones cuadráticas Ejercicio. Hacer una representación gráfica aproimada de las siguientes funciones cuadráticas:. f() =. f() = + 4 3. f() = +, Ejercicio.
ANALISIS MATEMATICO I (0) TRABAJO PRÁCTICO Funciones cuadráticas Ejercicio. Hacer una representación gráfica aproimada de las siguientes funciones cuadráticas:. f() =. f() = + 4 3. f() = +, Ejercicio.
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
CLASIFICACIÓN MORFOLÓGICA
 CLASIFICACIÓN MORFOLÓGICA Las galaxias presentan una gran variedad de formas. Espiral Espiral+barra elíptica irregular El objetivo de la clasificación morfológica es: 1) Reconocer el arquetipo al que pertenece
CLASIFICACIÓN MORFOLÓGICA Las galaxias presentan una gran variedad de formas. Espiral Espiral+barra elíptica irregular El objetivo de la clasificación morfológica es: 1) Reconocer el arquetipo al que pertenece
(ε c ) max. y b. (ε t ) max. Fig.11. Distribución de deformaciones unitarias por flexión en sección compuesta por dos materiales.
 6. Vigas (Elementos) Compuestos por dos o más Materiales Las ecuaciones obtenidas en la Sección 3 se basan en la hipótesis que el material que forma la sección del elemento, además de ser lineal-elástico,
6. Vigas (Elementos) Compuestos por dos o más Materiales Las ecuaciones obtenidas en la Sección 3 se basan en la hipótesis que el material que forma la sección del elemento, además de ser lineal-elástico,
VII Olimpiada Nacional de Astronomía y Astronáutica. Evaluación Nivel Enseñanza Básica
 VII Olimpiada Nacional de Astronomía y Astronáutica Evaluación Nivel Enseñanza Básica 2015 NOMBRE COMPLETO: RUT: SEXO: FECHA DE NACIMIENTO: TELÉFONO: CORREO ELECTRÓNICO: DIRECCIÓN: CURSO: CUÁNTAS VECES
VII Olimpiada Nacional de Astronomía y Astronáutica Evaluación Nivel Enseñanza Básica 2015 NOMBRE COMPLETO: RUT: SEXO: FECHA DE NACIMIENTO: TELÉFONO: CORREO ELECTRÓNICO: DIRECCIÓN: CURSO: CUÁNTAS VECES
DM y DE. Probablemente, los bariones son una componente minoritaria del Universo. DM y DE Pero... DE no es la energía de la DM.
 DM y DE Probablemente, los bariones son una componente minoritaria del Universo. DM y DE Pero... DE no es la energía de la DM. Es otra cosa Materia oscura Hay razones científicas y sentimentales para pensar
DM y DE Probablemente, los bariones son una componente minoritaria del Universo. DM y DE Pero... DE no es la energía de la DM. Es otra cosa Materia oscura Hay razones científicas y sentimentales para pensar
Física 3: Septiembre-Diciembre 2011 Clase 13,Lunes 24 de octubre de 2011
 Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Movimientos planetarios complejos Movimientos retrogrados. Un poco de historia
 Gravedad Movimientos planetarios complejos Movimientos retrogrados Un poco de historia Un poco de historia Ya en el 400 a.c. Eudoxo desarrolla un modelo para explicar el movimiento planetario, con esferas
Gravedad Movimientos planetarios complejos Movimientos retrogrados Un poco de historia Un poco de historia Ya en el 400 a.c. Eudoxo desarrolla un modelo para explicar el movimiento planetario, con esferas
Cuáles son las características aleatorias de la nueva variable?
 Apuntes de Estadística II. Ingeniería Industrial. UCAB. Marzo 203 CLASES DE ESTADÍSTICA II CLASE 5) UNA TRANSFORMACIÓN DE DOS VARIABLES. Sea Z = g(, ) una función de las variables aleatorias e, tales que
Apuntes de Estadística II. Ingeniería Industrial. UCAB. Marzo 203 CLASES DE ESTADÍSTICA II CLASE 5) UNA TRANSFORMACIÓN DE DOS VARIABLES. Sea Z = g(, ) una función de las variables aleatorias e, tales que
Electromagnetismo I. Semestre: TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 214-2 TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz 1.- Problema: (2pts) a) Una carga puntual q está localizada en el centro de un cubo
Electromagnetismo I Semestre: 214-2 TAREA 2 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz 1.- Problema: (2pts) a) Una carga puntual q está localizada en el centro de un cubo
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN
 Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS SATÉLITES 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10 11 m. Si Júpiter tiene un período de aproximadamente
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS SATÉLITES 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10 11 m. Si Júpiter tiene un período de aproximadamente
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Astronomía. Ayudantía 11 Prof. Jorge Cuadra Ayudante: Paulina González
 Astronomía Ayudantía 11 Prof. Jorge Cuadra Ayudante: Paulina González 1.- Cuales de las siguientes propiedades son necesarias para determinar la distancia a una estrella? : (Mas de una puede ser correcta)
Astronomía Ayudantía 11 Prof. Jorge Cuadra Ayudante: Paulina González 1.- Cuales de las siguientes propiedades son necesarias para determinar la distancia a una estrella? : (Mas de una puede ser correcta)
CAMPO GRAVITATORIO º bachillerato FÍSICA
 Ejercicio 1. Modelo 2.014 La masa del Sol es 333183 veces mayor que la de la Tierra y la distancia que separa sus centros es de 1,5 10 8 km. Determine si existe algún punto a lo largo de la línea que los
Ejercicio 1. Modelo 2.014 La masa del Sol es 333183 veces mayor que la de la Tierra y la distancia que separa sus centros es de 1,5 10 8 km. Determine si existe algún punto a lo largo de la línea que los
T10. RELATIVIDAD GENERAL (II): GRAVEDAD Y ESPACIOTIEMPO
 T10. RELATIVIDAD GENERAL (II): GRAVEDAD Y ESPACIOTIEMPO 1. Relatividad de las medidas del tiempo 2. Relatividad de las medidas espaciales 3. Métrica, curvatura y geodésicas 3.1 Concepto de métrica 3.2
T10. RELATIVIDAD GENERAL (II): GRAVEDAD Y ESPACIOTIEMPO 1. Relatividad de las medidas del tiempo 2. Relatividad de las medidas espaciales 3. Métrica, curvatura y geodésicas 3.1 Concepto de métrica 3.2
AUXILIAR 1 PROBLEMA 1
 AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
Astronomía Extragaláctica
 Astronomía Extragaláctica Cap. 4: Galaxias espirales y lenticulares Profesor: Sergio A. Cellone Facultad de Ciencias Astronómicas y Geofísicas Universidad Nacional de La Plata, Argentina curso 2015 Cap.
Astronomía Extragaláctica Cap. 4: Galaxias espirales y lenticulares Profesor: Sergio A. Cellone Facultad de Ciencias Astronómicas y Geofísicas Universidad Nacional de La Plata, Argentina curso 2015 Cap.
PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA
 Departamento de Física Aplicada Universidad de Castilla-La Mancha Escuela Técnica Superior Ing. Agrónomos PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA Materiales * Varilla delgada con orificios practicados
Departamento de Física Aplicada Universidad de Castilla-La Mancha Escuela Técnica Superior Ing. Agrónomos PRÁCTICA 6: PÉNDULO FÍSICO Y MOMENTOS DE INERCIA Materiales * Varilla delgada con orificios practicados
Una nueva vision de los Cúmulos Globulares
 Una nueva vision de los Cúmulos Globulares Dr. Oscar Mario Martinez Bravo FCFM-BUAP Seminario del Cuerpo de Gravitacion, Particulas y Campos FCFM-BUAP " Cuando el grupo esta formado por mas de una docena
Una nueva vision de los Cúmulos Globulares Dr. Oscar Mario Martinez Bravo FCFM-BUAP Seminario del Cuerpo de Gravitacion, Particulas y Campos FCFM-BUAP " Cuando el grupo esta formado por mas de una docena
s(t) = 5t 2 +15t + 135
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E000, 1-1-000 (A) Primer parcial (1) Se lanza una pelota hacia arriba a una velocidad de 15 m/seg desde el borde de un acantilado a 15 m arriba del suelo.
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E000, 1-1-000 (A) Primer parcial (1) Se lanza una pelota hacia arriba a una velocidad de 15 m/seg desde el borde de un acantilado a 15 m arriba del suelo.
Componentes de la Vía-Láctea
 ESTRUCTURA GALÁCTICA Y DINÁMICA ESTELAR Componentes de la Vía-Láctea Dr. César A. Caretta Departamento de Astronomía Universidad de Guanajuato Componentes de la Vía-Láctea 1 La Vía-Láctea en óptico/visible
ESTRUCTURA GALÁCTICA Y DINÁMICA ESTELAR Componentes de la Vía-Láctea Dr. César A. Caretta Departamento de Astronomía Universidad de Guanajuato Componentes de la Vía-Láctea 1 La Vía-Láctea en óptico/visible
Campo Eléctrico. Es el portador de la fuerza eléctrica. q 2. q 1
 Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
Campo Eléctrico Es el portador de la fuerza eléctrica. q 1 q 2 E1 E2 Por qué se usa el campo eléctrico? Porque es útil simplificar el problema separándolo en partes. Porque nos permite pensar en una situación
CURSOS DE ASTROFÍSICA, DE NOVIEMBRE DE Instituto de Geofísica y Astronomía Calle 212, N 2906 entre 29 y 31, La Coronela,
 CURSOS DE ASTROFÍSICA, 14-25 DE NOVIEMBRE DE 2016 Instituto de Geofísica y Astronomía Calle 212, N 2906 entre 29 y 31, La Coronela, La Lisa, La Habana, Cuba Por : Dominique BALLEREAU Observatorio de París,
CURSOS DE ASTROFÍSICA, 14-25 DE NOVIEMBRE DE 2016 Instituto de Geofísica y Astronomía Calle 212, N 2906 entre 29 y 31, La Coronela, La Lisa, La Habana, Cuba Por : Dominique BALLEREAU Observatorio de París,
Introducción: Las galaxias y sus componentes
 Introducción: Las galaxias y sus componentes Cúmulos de estrellas Nebulosas: Nubes de polvo, residuos de explosiones de estrellas, etc -A principios del siglo XX se creía que nuestra galaxia era todo el
Introducción: Las galaxias y sus componentes Cúmulos de estrellas Nebulosas: Nubes de polvo, residuos de explosiones de estrellas, etc -A principios del siglo XX se creía que nuestra galaxia era todo el
Interacción Electrostática
 Interacción Electrostática Área Física Resultados de aprendizaje Reconocer las características de las cargas eléctricas en diversos problemas. Resolver problemas de electrostática mediante las leyes de
Interacción Electrostática Área Física Resultados de aprendizaje Reconocer las características de las cargas eléctricas en diversos problemas. Resolver problemas de electrostática mediante las leyes de
Mecánica Clásica - 2do. cuatrimestre de 2011 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.
 Mecánica Clásica - 2do. cuatrimestre de 20 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.. Escriba el hamiltoniano, las ecuaciones de Hamilton y construya los diagramas de
Mecánica Clásica - 2do. cuatrimestre de 20 Guía 7: Ecuaciones de Hamilton, transformaciones canónicas. Hamilton Jacobi.. Escriba el hamiltoniano, las ecuaciones de Hamilton y construya los diagramas de
Temario. Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo
 Temario Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo Gas en la Vía Láctea El gas (nubes de HI, HII, CO) y polvo se mueven de manera más ordenada que
Temario Distancias Movimientos y tiempos La Radiación Los Planetas Las Estrellas Las Galaxias El Universo Gas en la Vía Láctea El gas (nubes de HI, HII, CO) y polvo se mueven de manera más ordenada que
El l modelo «iceberg»
 El l modelo «iceberg» El Universo y las galaxias que contiene no son exactamente como parecen. Investigaciones recientes nos hacen replantearnos la forma de ver las galaxias espirales, las estructuras
El l modelo «iceberg» El Universo y las galaxias que contiene no son exactamente como parecen. Investigaciones recientes nos hacen replantearnos la forma de ver las galaxias espirales, las estructuras
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL El universo y el sistema solar
 SOLUCIONARIO GUÍA ESTÁNDAR ANUAL El universo y el sistema solar SGUICES028CB32-A16V1 Solucionario guía El universo y el sistema solar Ítem Alternativa Habilidad 1 B Reconocimiento 2 A Reconocimiento 3
SOLUCIONARIO GUÍA ESTÁNDAR ANUAL El universo y el sistema solar SGUICES028CB32-A16V1 Solucionario guía El universo y el sistema solar Ítem Alternativa Habilidad 1 B Reconocimiento 2 A Reconocimiento 3
Nacimiento, vida y muerte de las estrellas
 1 Nacimiento, vida y muerte de las estrellas Por Juanjo Gabiña La galaxia Andrómeda también conocida como Galaxia espiral M31 como todas las demás galaxias, es un colosal sistema cósmico integrado por
1 Nacimiento, vida y muerte de las estrellas Por Juanjo Gabiña La galaxia Andrómeda también conocida como Galaxia espiral M31 como todas las demás galaxias, es un colosal sistema cósmico integrado por
Departamento de Física Aplicada III
 Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
Astrofísica del Sistema Solar. Atmósferas planetarias (2da. Parte)
 Astrofísica del Sistema Solar Atmósferas planetarias (2da. Parte) UNLP 2do. Semestre 2016 Perfil de temperatura: Tierra Nubes: Se dice que una atmósfera esta saturada cuando el contenido de vapor de un
Astrofísica del Sistema Solar Atmósferas planetarias (2da. Parte) UNLP 2do. Semestre 2016 Perfil de temperatura: Tierra Nubes: Se dice que una atmósfera esta saturada cuando el contenido de vapor de un
VII Olimpiada Nacional de Astronomía y Astronáutica. Evaluación Nivel Enseñanza Media. Prueba de Alternativas
 VII Olimpiada Nacional de Astronomía y Astronáutica NOMBRE COMPLETO: RUT: SEXO: FECHA DE NACIMIENTO: TELÉFONO: CORREO ELECTRÓNICO: DIRECCIÓN: CURSO: Evaluación Nivel Enseñanza Media Prueba de Alternativas
VII Olimpiada Nacional de Astronomía y Astronáutica NOMBRE COMPLETO: RUT: SEXO: FECHA DE NACIMIENTO: TELÉFONO: CORREO ELECTRÓNICO: DIRECCIÓN: CURSO: Evaluación Nivel Enseñanza Media Prueba de Alternativas
Función de Green, método de imágenes y separación de variables.
 Física Teórica 1 Guia 2 - Green, imágenes y separación 1 cuat. 2014 Función de Green, método de imágenes y separación de variables. Método de imágenes y función de Green. 1. Una esfera conductora de radio
Física Teórica 1 Guia 2 - Green, imágenes y separación 1 cuat. 2014 Función de Green, método de imágenes y separación de variables. Método de imágenes y función de Green. 1. Una esfera conductora de radio
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN
 Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS LEYES DE KEPLER 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10¹¹ m. Si Júpiter tiene un período de
Física P.A.U. GRAVITACIÓN 1 GRAVITACIÓN PROBLEMAS LEYES DE KEPLER 1. El período de rotación de la Tierra alrededor del Sol es un año y el radio de la órbita es 1,5 10¹¹ m. Si Júpiter tiene un período de
01 - LEY DE COULOMB Y CAMPO ELÉCTRICO. 3. Dos cargas puntuales cada una de ellas de Dos cargas iguales positivas de valor q 1 = q 2 =
 01 - LEY DE COULOMB Y CAMPO ELÉCTRICO DISTRIBUCIONES DISCRETAS DE CARGAS 1. Tres cargas están a lo largo del eje x, como se ve en la figura. La carga positiva q 1 = 15 [µc] está en x = 2 [m] y la carga
01 - LEY DE COULOMB Y CAMPO ELÉCTRICO DISTRIBUCIONES DISCRETAS DE CARGAS 1. Tres cargas están a lo largo del eje x, como se ve en la figura. La carga positiva q 1 = 15 [µc] está en x = 2 [m] y la carga
Posición de un Cuerpo. Elementos para la descripción del movimiento. Vector de Posición y Vector Desplazamiento
 1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω
 ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
Alonso Fernández Galián
 Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Examen de Análisis de
 Pagína 1 de 6 (D1) Sistema Binario de Pulsar A través de búsquedas sistemáticas durante las últimas décadas, los astrónomos han encontrado un gran número de pulsares de milisegundos (período de giro
Pagína 1 de 6 (D1) Sistema Binario de Pulsar A través de búsquedas sistemáticas durante las últimas décadas, los astrónomos han encontrado un gran número de pulsares de milisegundos (período de giro
El campo magnético de las corrientes estacionarias
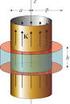 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Mm R 2 v= mv 2 R 24 5,98 10
 POBLEMAS CAMPO GAVIAOIO. FÍSICA ºBO 1. Un satélite artificial describe una órbita circular alrededor de la ierra. En esta órbita la energía mecánica del satélite es 4,5 x 10 9 J y su velocidad es 7610
POBLEMAS CAMPO GAVIAOIO. FÍSICA ºBO 1. Un satélite artificial describe una órbita circular alrededor de la ierra. En esta órbita la energía mecánica del satélite es 4,5 x 10 9 J y su velocidad es 7610
PROBLEMAS DE FUNDAMENTOS DE FÍSICA II
 PROBLEMAS DE FUNDAMENTOS DE FÍSICA II Grupo 511. CURSO 2016/2017. Interacción Magnética. 1.-Encontrar la densidad de corriente supuesta uniforme que se requiere en un alambre horizontal de Al para hacerlo
PROBLEMAS DE FUNDAMENTOS DE FÍSICA II Grupo 511. CURSO 2016/2017. Interacción Magnética. 1.-Encontrar la densidad de corriente supuesta uniforme que se requiere en un alambre horizontal de Al para hacerlo
AGUJEROS NEGROS 1.0. J.L.F. Barbón. IFT UAM/CSIC Madrid
 AGUJEROS NEGROS 1.0 J.L.F. Barbón IFT UAM/CSIC Madrid UN AGUJERO NEGRO es una región en la que la luz está atrapada por efecto de la gravedad m γ = E γ c 2 El concepto básico de agujero negro se
AGUJEROS NEGROS 1.0 J.L.F. Barbón IFT UAM/CSIC Madrid UN AGUJERO NEGRO es una región en la que la luz está atrapada por efecto de la gravedad m γ = E γ c 2 El concepto básico de agujero negro se
FUNCIONES PRÁCTICA N 2
 Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
Por una cuerda tensa se propagan dos ondas armónicas: y 1 (x, t) = +0, 02 sen(2 t + 20 x) e
 Opción A. Ejercicio 1 [a] Eplique el fenómeno de interferencia entre dos ondas. (1 punto) Por una cuerda tensa se propagan dos ondas armónicas: y 1 (, t) = +0, 0 sen( t + 0 ) e y (, t) = 0, 0 sen( t 0
Opción A. Ejercicio 1 [a] Eplique el fenómeno de interferencia entre dos ondas. (1 punto) Por una cuerda tensa se propagan dos ondas armónicas: y 1 (, t) = +0, 0 sen( t + 0 ) e y (, t) = 0, 0 sen( t 0
Balance Global de Energía
 Balance Global de Energía Balance de energía 1a Ley de la Termodinámica El balance básico global se establece entre la energía proveniente del sol y la energía regresada al espacio por emisión de la radiación
Balance Global de Energía Balance de energía 1a Ley de la Termodinámica El balance básico global se establece entre la energía proveniente del sol y la energía regresada al espacio por emisión de la radiación
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Estándar Anual. Física. Ejercicios PSU. Ciencias Básicas. Guía práctica El universo y el sistema solar GUICES028CB32-A16V1.
 Estándar Anual Nº Guía práctica El universo y el sistema solar Física Programa 1. El sistema solar está ubicado en A) B) C) D) E) 2. GUICES028CB32-A16V1 3. Ciencias Básicas Ejercicios PSU el centro de
Estándar Anual Nº Guía práctica El universo y el sistema solar Física Programa 1. El sistema solar está ubicado en A) B) C) D) E) 2. GUICES028CB32-A16V1 3. Ciencias Básicas Ejercicios PSU el centro de
Práctico 2: Mecánica lagrangeana
 Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
INDICE Capítulo 1. Mediciones Capítulo 2. Movimiento Unidimensional Capítulo 3. Vectores Capítulo 4. Movimiento Bidimensional y Tridimensional
 INDICE Capítulo 1. Mediciones 1 1.1. Las cantidades físicas, patrones y unidades 1 1.2. El sistema internacional de unidades 2 1.3. Patrón de tiempo 3 1.4. Patrón de masa 7 1.6. Precisión y cifras significativas
INDICE Capítulo 1. Mediciones 1 1.1. Las cantidades físicas, patrones y unidades 1 1.2. El sistema internacional de unidades 2 1.3. Patrón de tiempo 3 1.4. Patrón de masa 7 1.6. Precisión y cifras significativas
Mediante este programa se persigue desarrollar las siguientes habilidades:
 PROPÓSITO: El programa de esta asignatura está dirigido a los estudiantes del primer semestre de la Facultad de Ingeniería, con la finalidad de ofrecerles una capacitación teórica práctica en los principios
PROPÓSITO: El programa de esta asignatura está dirigido a los estudiantes del primer semestre de la Facultad de Ingeniería, con la finalidad de ofrecerles una capacitación teórica práctica en los principios
El momento angular y las Leyes de Kepler
 El momento angular y las Leyes de Kepler 1. Define el momento angular de una partícula de masa m y velocidad v respecto a un punto O. Pon un ejemplo razonado y de ley o fenómeno físico que sea una explicación
El momento angular y las Leyes de Kepler 1. Define el momento angular de una partícula de masa m y velocidad v respecto a un punto O. Pon un ejemplo razonado y de ley o fenómeno físico que sea una explicación
El momento angular y las Leyes de Kepler
 El momento angular y las Leyes de Kepler 1. Define el momento angular de una partícula de masa m y velocidad v respecto a un punto O. Pon un ejemplo razonado y de ley o fenómeno físico que sea una explicación
El momento angular y las Leyes de Kepler 1. Define el momento angular de una partícula de masa m y velocidad v respecto a un punto O. Pon un ejemplo razonado y de ley o fenómeno físico que sea una explicación
CAPÍTULO III Electrostática
 CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Mecánica y fluidos. Temario. Webpage:
 Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Las Nubes de Magallanes (MC)
 Las Nubes de Magallanes (MC) Más fáciles de estudiar que la Galaxia Compleja evolución galáctica En la secuencia: SMC - LMC - La Galaxia: Luminosidad, masa, [Fe/H], contenido gas (estudio de la variación
Las Nubes de Magallanes (MC) Más fáciles de estudiar que la Galaxia Compleja evolución galáctica En la secuencia: SMC - LMC - La Galaxia: Luminosidad, masa, [Fe/H], contenido gas (estudio de la variación
Luis P. Chimento, Mónica I. Forte y Martín G. Richarte Departamento de Física, Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires
 Luis P. Chimento, Mónica I. Forte y Martín G. Richarte Departamento de Física, Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires (arxiv:1106.0781) En la métrica FRW plana, proponemos
Luis P. Chimento, Mónica I. Forte y Martín G. Richarte Departamento de Física, Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires (arxiv:1106.0781) En la métrica FRW plana, proponemos
Planetas. El sistema solar también se compone de cinco planetas enanos: Plutón, Ceres, Eris, Makemake y Haumea.
 Planetas Según la Unión Astronómica Internacional (UAI), los planetas son cuerpos celestes que orbitan alrededor de una estrella dada. Deben tener suficiente masa para producir la fuerza gravitatoria que
Planetas Según la Unión Astronómica Internacional (UAI), los planetas son cuerpos celestes que orbitan alrededor de una estrella dada. Deben tener suficiente masa para producir la fuerza gravitatoria que
Principios de Mecánica
 Principios de Mecánica Salamanca, 2006-2007 Índice 1. Unidades y dimensiones 1 1. Unidades................................. 1 1..1 Sistema Internacional...................... 1 2. Ecuación de dimensiones........................
Principios de Mecánica Salamanca, 2006-2007 Índice 1. Unidades y dimensiones 1 1. Unidades................................. 1 1..1 Sistema Internacional...................... 1 2. Ecuación de dimensiones........................
Física 2º Bach. Campo eléctrico 19/02/ Calcula: a) La intensidad del campo eléctrico en el centro M de la base de un triángulo
 Física 2º Bach. Campo eléctrico 19/02/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTOS /UNO] 1. Dos conductores esféricos concéntricos huecos, de radios 6,00 y 10,0 cm, están cargados con
Física 2º Bach. Campo eléctrico 19/02/10 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [3 PUNTOS /UNO] 1. Dos conductores esféricos concéntricos huecos, de radios 6,00 y 10,0 cm, están cargados con
Índice. Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento. Ejemplos. Leyes de la Dinámica en SRNI.
 Índice Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento Ejemplos Leyes de la Dinámica en SRNI Ejemplos Teorema de la Cantidad de Movimiento. Conservación. Teorema del Momento
Índice Leyes de Newton Interacción Gravitatoria Reacción en Apoyos Leyes del Rozamiento Ejemplos Leyes de la Dinámica en SRNI Ejemplos Teorema de la Cantidad de Movimiento. Conservación. Teorema del Momento
Cúmulos estelares. Asociados generalmente a regiones HII
 Cúmulos estelares Los procesos de formación estelar tienen lugar en las nubes moleculares. Como consecuencia se originan los cúmulos abiertos o galácticos. Asociados generalmente a regiones HII Los cúmulos
Cúmulos estelares Los procesos de formación estelar tienen lugar en las nubes moleculares. Como consecuencia se originan los cúmulos abiertos o galácticos. Asociados generalmente a regiones HII Los cúmulos
