XII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN ANALOGÍAS Y ANÁLISIS DIMENSIONAL
|
|
|
- Ricardo Villalobos González
- hace 7 años
- Vistas:
Transcripción
1 XII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN ANALOGÍAS Y ANÁLISIS DIMENSIONAL XII..- ANALOGÍA ENTRE LA TRANSMISIÓN DE CALOR Y LA CANTIDAD DE MOVI- MIENTO EN LUJO TURBULENTO CAPA LIMITE TÉRMICA SOBRE PLACA PLANA.- En una corriente fluida que circula sobre una placa plana en régimen turbulento, se pueden distinguir dentro de la capa límite según una misma sección transversal, tres subcapas de fluido contenidas en la capa límite térmica, con unos límites de separación no muy bien diferenciados, ig XII.. a) La primera, subcapa viscosa, se encuentra en las proximidades de la pared; en ella prácticamente no existen remolinos y, por lo tanto, la variación de la cantidad de movimiento se debe exclusivamente a la viscosidad. b) La segunda zona, subcapa de transición, se corresponde con un régimen intermedio, y en ella se proce una variación de la cantidad de movimiento debido a la viscosidad y a la turbulencia. c) La tercera zona, subcapa turbulenta, se corresponde con la parte principal de la corriente que ocupa casi toda la sección transversal del tubo; es la zona en la que existen turbulencias de intensidad relativamente pequeña, aunque los remolinos sean grandes; los gradientes de la velocidad respecto a la distancia a la pared son relativamente pequeños, por lo que las variaciones de la cantidad de movimiento predominantes, son debidas a los esfuerzos de Reynolds τ turb en régimen turbulento. En lo que sigue se supondrá que tanto los gradientes de temperatura dentro de la capa límite térmica, como los gradientes de velocidades dentro de la capa límite hidrodinámica están perfectamente desarrollados y superpuestos, cumpliéndose que δ 3 = Pr, por lo que para Pr =, las dos δ T capas límite coinciden. Analogías y análisis dimensional.xii.-
2 Si Pr <, la capa límite térmica es más gruesa que la hidrodinámica y cuando Pr >, sucede todo lo contrario. ig XII..- Subcapas de la capa límite térmica en régimen turbulento Conctividad térmica.- Dentro de la subcapa viscosa el calor fluye principalmente por concción, aunque también interviene algo la convección, debido a que en esa zona existe algún remolino; a medida que se avanza transversalmente dentro de la capa límite, los efectos de la turbulencia se hacen más notorios, predominando la transmisión de calor por convección. En los fluidos ordinarios con números de Prandtl superiores a,6 la concción térmica es totalmente despreciable en la subcapa turbulenta, y puede llegar a ser considerable en la zona de transición cuando el número de Prandtl se aproxime a la unidad; para números de Prandtl elevados, la concción térmica es despreciable en esa zona. Cantidad de movimiento.- El esfuerzo cortante en régimen turbulento sigue una regla similar a lo anterior respecto a la viscosidad. Bajo ciertas condiciones ideales, existe una correspondencia exacta entre el flujo de calor y la variación de la cantidad de movimiento; sin embargo, en un caso general, esta correspondencia será sólo aproximada y el considerarla como exacta podría concir a grandes errores. Expresión general de la relación básica de la analogía entre el calor y la cantidad de movimiento.- Cuando se conoce el coeficiente de rozamiento λ entre el fluido y la pared del concto por el que circula, se puede determinar el coeficiente de transferencia de calor h C, mediante la analogía entre la transferencia de calor y la cantidad de movimiento. El esfuerzo cortante τ en la capa límite turbulenta se compone de dos sumandos: τ = τ visc + τ turb = η - ρ u * v * en la que τ turb se conoce como esfuerzo de Reynolds, siendo u * la velocidad de agitación o fluctuación de la velocidad instantánea u i alrededor del valor medio u : u i = u ± u * = u ± u agit Analogías y análisis dimensional.xii.-
3 mientras que v * es la fluctuación transversal de la velocidad instantánea v i de la forma: v i = v ± v * = v ± v agit Para el flujo turbulento de calor, se puede considerar que el flujo total de calor q* está compuesto! por una componente - conctiva q cond " #- turbulenta q turb q * = q cond + q turb = - k dt + ρ c v * T *, en la que: T i = T ± T *, es la temperatura instantánea T = T, es la temperatura media del fluido T *, es la temperatura debida a la fluctuación El término u * v * se obtiene a partir del significado físico del nº de Prandtl que sugiere que la fluctuación u * de la velocidad se relaciona con u * l m a través de la ecuación: en la que l m es la longitud de mezcla del espesor δ de la cantidad de movimiento de la capa límite hidrodinámica. Asimismo, la fluctuación transversal v * se admite es del mismo orden de magnitud que u * pero de signo opuesto: v * - l m ; u* v* = - (l m ) = - ε m en la que la difusividad turbulenta de la cantidad de movimiento es, ε m = l m Para hallar la relación del término v * T * con el gradiente de temperaturas local medio, se aplica un método similar, en la forma: T * - l c dt y v * = l c en la que l c es la longitud de mezcla del espesor de energía δ 3 de la capa límite, por lo que se puede poner: v * T * = - l c dt = - ε dt c siendo la difusividad turbulenta del calor, ε c = l c Sustituyendo estos valores en las ecuaciones de τ y de q*, se obtiene: τ = η + ρ ε m ; τ ρ = (ν + ε m ) q* = - k dt + ρ c v* T* = - k dt - ρ c dt ε c = - (k + ρ c ε c ) dt Analogías y análisis dimensional.xii.-3
4 q* ρ c = - ( k ρ c + ε c ) dt = - (α + ε c ) dt ecuaciones que divididas entre sí, proporcionan las relaciones básicas para la circulación de fluidos por tuberías: τ q* = - ν + ε m c (α + ε c ) dt ν y α, son propiedades del fluido en las que ; a partir de ellas se decen las analogías entre la ε m y ε c, lo son del flujo transferencia de calor y la cantidad de movimiento. XII..- ANALOGÍA DE REYNOLDS Esta analogía es de aplicación al flujo de fluidos por tubos rectos de sección circular; se puede estudiar en su forma más general, teniendo en cuenta que la relación entre las difusividades moleculares α y ν es igual a la relación entre las difusividades ε m y ε c. Como el número de Prandtl es una relación entre difusividades, se puede poner: ν α = ε m ε c = Pr ; ν = α Pr ; ε m = ε c Pr τ q * = τ q * = - ν + ε m c (α + ε c ) dt = - (α Pr + ε m Pr ) c (α + ε c ) dt = - Pr c dt u = - c t Pr q* T dt u T = c t p Pr q (T * p - T ) en la que τ y q * se toman en la superficie. Al ser: π d L τ = P π d 4 q* = h C (T p - T ) P = 4 L τ d = λ L ρ u d ; τ = λ ρ u = C w = λ 4 = C w ρ u C w λ ρ u u = Pr h resulta: C (T p - T ) (T p - T ) = C w λ ρ u h C = C w λ ρ u Pr h C Pr Nu St = Re Pr = h C λ = c p ρ u Pr = C w Pr que concuerda bastante bien con: C w = St x Pr /3, para números de Pr próximos a la unidad. -, 4 < Re < 5 Si los valores de λ se toman de la ecuación: λ =,4 Re d, en el campo: L d =,63 4 Re, siendo d L la distancia necesaria para que en el flujo turbulento el factor de fricción λ llegue a ser constante, se tiene: Analogías y análisis dimensional.xii.-4
5 Nu = St Re d Pr = λ 3 Pr Re d Pr =,4 4 < Re < 5 ;,5 < Pr < ; L d > 6 Re d, 3 Pr =,3 Re d, 3 Pr Reynolds propuso que todo el flujo está formado por una región altamente turbulenta, es decir, no considera la presencia de la subcapa viscosa, ni la subcapa de transición, por lo que las difusividades moleculares del momento ν y del calor α son despreciables en comparación con las difusividades turbulentas m ν << τ, por lo que no intervienen en el proceso. α << τ c Si se considera Pr =, resulta, ε m = ε c, por lo que: τ q = τ * q* = - ε m ε c c dt = - c dt! ecuación que se puede integrar entre las condiciones de la pared, T = T p " # u = u! del flujo principal, T = T ", obteniéndose: # u = u y las condiciones medias T q* dt = - T p τ c u T p - T = q* u = q * u q* τ c τ c = h C (T p - T ) = h q * u C τ c deciéndose: h C = τ c u = τ = λ u ρ = λ ρ u c El número de Stanton es: St = XII.3.- ANALOGÍA DE PRANDTL Nu Re Pr = h C ρ u c = λ = C w Prandtl considera al flujo dividido en dos zonas, viscosa y turbulenta: - En la zona viscosa supone predominan las difusividades moleculares - En la zona turbulenta supone predominan las difusividades turbulentas τ q = τ * q* Para la subcapa viscosa se tiene que ε m << ν ε c << α = - ν α c dt = - Pr c dt dt = - Pr q * τ c p T = T que integrada entre las condiciones de la pared p u = T = T i proporciona: u = u i T p - T = - Pr q * τ c p u y las del borde de la subcapa viscosa Analogías y análisis dimensional.xii.-5
6 Para la subcapa turbulenta se supone que ν << ε m, y si ε α << ε m y ε c son del mismo orden: ε m = ε c = ε, c se obtiene: τ q = τ * q* = - ε m ε c c dt = - c dt dt = - q * τ c que integrada entre los límites u = u ; T = T proporciona la diferencia de temperaturas entre el u = u ; T = T borde de la capa límite y el borde de la subcapa turbulenta: T - T = q * τ c p (u - u ) y sumada a la obtenida anteriormente T p - T resulta: T p - T = q * τ c p Pr u + q * * u (u - u ) = q { + u (Pr - )} τ c p τ c p u Como el coeficiente de transmisión de calor h C y el factor de fricción λ para el flujo por el interior del tubo, son de la forma: q* = h C (T p - T ) ; τ = λ ρ u sustituidos en la ecuación anterior, se obtiene: h C = λ ρ c u + u u (Pr - ) ; St = h C ρ c u = λ { + u u (Pr - )} La velocidad u del borde de la subcapa viscosa, se determina con ayuda de la ley de distribución de velocidades para flujos turbulentos, por ejemplo, mediante la siguiente ecuación empírica: τ ρ = ( u 5 ) = λ u ; u u = 5 λ y el número de St = λ + 5 λ (Pr - ) se rece a la analogía de Reynolds haciendo Pr =. XII.4.- ANALOGÍA DE VON KÀRMÀN Von Kàrmàn amplió la analogía de Prandtl, dividiendo el campo de flujo en tres subcapas diferentes, viscosa, de transición y turbulenta. Hizo suposiciones similares a las de Prandtl sobre las magnitudes relativas de las difusividades moleculares y turbulentas del calor, y de las variaciones de la cantidad de movimiento en la subcapa viscosa y en la zona turbulenta, incorporando además los efectos de la subcapa de transición, considerando que las difusividades molecular ν y turbulenta Analogías y análisis dimensional.xii.-6
7 ε m de esta subcapa, eran del mismo orden de magnitud. La analogía de Kàrmàn entre la transferencia de calor y la cantidad de movimiento en un flujo turbulento, dentro de un tubo circular, se expresa por la siguiente ecuación: St = h C Nu Re Pr = = λ ρ c u + 5 λ {(Pr - ) + ln 5 Pr + 6 } = λ = 4 C w = + 5 C w C w / {(Pr - ) + ln 5 Pr + 6 } Si: C w =,576 5 Re x, resulta: Nu x =, Re x, Pr +,49 Re x -, {(Pr - ) + ln 5 Pr + 6 } Para un flujo totalmente desarrollado hidrodinámicamente el valor del coeficiente de rozamiento λ se obtiene del diagrama de Moody, ig X., o de las ecuaciones que lo definen, de la forma: Para tuberas lisas: ε d = λ =,364 Re -,5 ; < Re < 5 Blasius = log ( Re λ λ,5 ) ; Re > 5 ª Ec. de Kàrmàn-Prandtl Para tuberías rugosas = log ( ε/d λ 3,7 +,5 ) ; λ = f (Re, ε Re λ d ) Colebrook-White = log d λ ε +,74 ; λ = f ( ε ) ª Ec. de Kàrmàn-Prandtl d = log d λ ε +,4 ; λ = f ( ε d ) Nikuradse XII.5.- ANALOGÍA DE COLBURN Colburn modifica la ecuación de la analogía de Reynolds, por otra de la forma: St = l Pr, para tubos ;,7 < Pr < 6 ; Re >. /3 para placas ;,7 < Pr < 6 ; Re > 3,5. 5 Como la mayor resistencia a la transmisión de calor procede de la capa de fluido que se mueve en régimen turbulento, las propiedades del fluido se toman a la temperatura media de película, que representa fielmente las propiedades físicas de esta capa. Para tubos lisos, los números de Stanton y Nuselt son de la forma: λ St = = λ =,46 Pr /3 Re-, = Nu =,3 Re, Pr /3 -,,3 Re = Pr /3 h C ρ c u = Nu Re Pr ecuación que es casi idéntica a la de Dittus-Boelter, diferenciándose en que no especifica si se trata de un calentamiento o un enfriamiento. Analogías y análisis dimensional.xii.-7
8 ig XII..- Diagrama de Moody Analogías y análisis dimensional.xii.-
9 Para Re >, la relación L no influye en los fluidos que se calientan d Para tener en cuenta el efecto de las variaciones radiales de la viscosidad debidas al gradiente de temperatura (pared calefactora-fluido), se introce el factor adimensional ( η ),4 que se utiliza únicamente cuando la viscosidad varía marcadamente con la temperatura, tomando la η p ecuación que determina el valor de h C la forma: h C =,3 k d Re, Pr /3 ( η η p ),4 forma: La analogía de Colburn define un factor adimensional Ψ, función del nº de Reynolds, de la Ψ = h C c G ( c η k )/3 =,3 ( d i G µ )-, que se utiliza en gran número de ecuaciones empíricas; con carácter aproximado: Ψ = λ XII.6.- ANÁLISIS DIMENSIONAL TEOREMA DE BUCKINGHAN.- El Teorema establece que en un problema físico en el que intervienen n variables linealmente independientes, que incluyen m dimensiones, las variables se pueden agrupar en (n-m) parámetros π adimensionales, linealmente independientes. Algunas de las variables que pueden intervenir en un determinado fenómeno son:, fuerza ; L, longitud ; u, velocidad ; ρ, densidad ; η, viscosidad dinámica ; g, gravedad ; cs, velocidad del sonido; σ, tensión superficial; k, conctividad térmica del fluido; c, calor específico a presión constante; h C, coeficiente de convección. Las dimensiones son: Longitud L, masa M, tiempo t y temperatura T Las fuerzas que pueden intervenir en un fenómeno son: inercia (debida a un gradiente de presiones) elástica gravedad viscosidad (rozamiento) capilaridad (tensión superficial) Si A, A,..., A n son las variables consideradas, como presión, velocidad, viscosidad, etc., que se supone son esenciales a la hora de resolver un problema, podemos suponer vienen relacionadas me Analogías y análisis dimensional.xii.-9
10 diante una expresión funcional de la forma: ( A, A,..., A n ) = y si, π, π,..., π n-m, representan los parámetros adimensionales que agrupan a las variables, A, A,..., A n, que incluyen, entre todas ellas, las m dimensiones, el Teorema de Buckinghan establece la existencia de una ecuación, función de estos parámetros, de la forma: f (π, π,..., π n m ) = El método que permite obtener los parámetros π consiste en seleccionar m de las n variables A i, las cuales pueden tener diferentes dimensiones, pero deben ser linealmente independientes, de forma que contengan entre todas ellas las m dimensiones, pudiéndose emplear como variables repetitivas al combinarlas con las variables A restantes, formándose así cada parámetro adimensional π. Por ejemplo se puede suponer que A, A y A 3 contienen las dimensiones (M, L, t), masa, longitud y tiempo, no necesariamente en cada una de ellas, pero sí en forma colectiva. El primer parámetro π adimensional es: π = A x A x A 3 x 3 A 4 El segundo parámetro π adimensional es: π = A y A y A 3 y 3 A 5 z y así sucesivamente hasta el parámetro: π n m = A z A z A 3 3 A n Los exponentes de estas ecuaciones se tienen que examinar de tal manera que cada parámetro π resulte adimensional; se sustituyen las dimensiones de las variables A i y los exponentes de M, L, t,... se igualan a cero por separado, formándose un sistema de ecuaciones (tres para el ejemplo propuesto), con tres incógnitas para cada parámetro π, pudiéndose determinar los exponentes x, y, z, y por lo tanto, los parámetros π correspondientes. Ecuación general de resistencia.- Las variables que intervienen en el movimiento de un so- lido inmerso en una corriente fluida se relacionan mediante la ecuación A L = f (V, L, ρ, η ), siendo la matriz correspondiente de la forma /AL V L ρ η M L t Si por ejemplo se eligen como variables linealmente independientes V, L, ρ, resulta -3 = - y como el número de variables n que intervienen en el fenómeno es 5 y el número de dimensiones m es 3, el número de parámetros π adimensionales que se pueden formar son, π y π, de la forma: π = (V ) x (L) x (ρ ) x 3 η = (L t - ) x (L) x (M L -3 ) x 3 (M L - t - ) = Analogías y análisis dimensional.xii.-
11 π = (V ) y (L) y (ρ ) y 3 Los parámetros π y π son: A L = (L t - ) y (L) y (M L -3 ) y 3 (M L - t - ) = = (L ) x +x -3 x 3 - (M ) x 3 + (t ) - x - = (L ) (M ) (t ) = (L ) y +y -3 y 3 - (M ) y 3 + (t ) - y - = (L ) (M ) (t ) x 3 + = x + = x + x - 3 x 3 - = y 3 + = y + y - 3 y 3 - = y + = x = - ; x = - ; x 3 = - ; π = V - L - ρ η = Re - y = - ; y = ; y 3 = - ; π = V - ρ - A L A L = π ρ V = ( π ) ρ V = C w ρ V que es la forma que toma la ecuación de resistencia, ya demostrada anteriormente. Ecuación general de la pérdida de carga en una concción cilíndrica.- En un concto de sección circular la pérdida de presión debida a la fricción se conoce como pérdida de carga P, que multiplicada por la sección transversal A T tiene que ser igual a la pérdida por fricción, o fuerza de arrastre, en la forma: = P π d 4 P = = ( π ) ρ V A L = C w ρ V π d L d ( π ) ρ V L = λ ρ V d L = ρ C w V L d en la que el valor de λ se determina mediante formulación empírica o ábacos y diagramas, de entre los que destaca el diagrama de Moody. MÉTODO BÁSICO DE ANÁLISIS DIMENSIONAL.- Consiste en recir al mínimo el número de variables que pueden intervenir en un problema, formando con las mismas una serie de grupos adimensionales independientes. En este método todas las ecuaciones racionales se pueden hacer adimensionales con un cierto número de términos independientes; las variables se acomodan en una ecuación dimensional única, de forma que la combinación de variables para formar grupos o términos adimensionales, proporciona un número de grupos independientes siempre menor que el de variables originales. El proceso se puede iniciar identificando sólo aquellas variables que son significativas del problema; después se agrupan en una ecuación funcional y se determinan sus dimensiones. Como aplicación directa del método, vamos a hacer un estudio inicial de la transmisión de ca Analogías y análisis dimensional.xii.-
12 lor desde un tubo cilíndrico a un fluido que circula por su interior en régimen turbulento. Si se considera un flujo en convección forzada, y que el tubo está limpio y sin incrustaciones, los coeficientes de película h C se determinan experimentalmente como función de un cierto número de factores que representan las características dinámicas del flujo y las propiedades físicas del fluido. El rozamiento del fluido supone un intercambio de energía entre él y la superficie interna del tubo, mientras que la transmisión de calor por convección forzada supone un intercambio de energía térmica entre la superficie del tubo y el fluido; ambos fenómenos dependen del grado de turbulencia del fluido. En general, el rozamiento de un fluido en circulación forzada depende de los siguientes factores: - Diámetro interior del tubo d i - Longitud del tubo L - Velocidad media del fluido u en el intervalo correspondiente a la longitud L - Densidad del fluido ρ - Viscosidad dinámica del fluido η - Rugosidad relativa del tubo ε /d i La transmisión de calor depende de la conctividad k del fluido y de su calor específico a presión constante c ; la determinación del coeficiente h C de la transmisión de calor por convección forzada, se puede iniciar a partir de la ecuación: Q A L ΔT = h C = φ (d i, u, ρ, η, L, k, c, ε d i ) ó (d i, u, ρ, η, L, k, c, ε d i ) = y que adimensionalmente se puede expresar mediante la siguiente matriz: di u L ρ η k c hc M L -3 - t T de 7 variables y cuyo discriminante es de razón 4, por lo que habrá que especificar de antemano el valor de 3 variables cualesquiera. El valor de h C se puede expresar en la forma adimensional siguiente: h c = d i a u b ρ c η d L e k f c i (M t -3 T - ) = (L) a (L t - ) b (M L -3 ) c (M L - t - ) d (L) e (M L t -3 T - ) f (L t - T - ) i = = M c+d+f L a+b-3c-d+e+f+i t -b-d-3f-i T -f-i Analogías y análisis dimensional.xii.-
13 c + d + f = a + b - 3 c - d + e + f + = Identificando coeficientes se obtiene el sistema de 4 ecuaciones: b + d + 3 f + i = 3 f + i = linealmente independientes, con 7 incógnitas, pudiéndose fijar 3 incógnitas, por ejemplo (i, b, e) y poner las 4 restantes en función de ellas, quedando: f = - i d = - c - f = i - c = 3 - b - 3 f - i = 3 - b i - i = - b + i c = b a = - b + 3 c + d - e - f - i = - + b - e por lo que: h c = d ī +b-e u b ρ b η -b+i L e k -i c i = ( d i ) - ( d i u ρ ) b ( d i k η L )-e ( h c k ) i que a su vez se puede poner en la forma: h C d i k = ϕ ( d i u ρ, d i η L, h c ) k y que para la transmisión de calor por convección forzada, indica que si se efectúan una serie de pruebas que difieran solamente en el valor de la velocidad u, con los valores que así se obtengan, junto con los de h C medidos experimentalmente, se pueden determinar la función o funciones que ligan a los grupos adimensionales Re = d i u ρ η = d i u ν ; Nu = h C d i k ; Pr = c η k que sólo serán válidas para valores particulares de los demás grupos adimensionales; por lo tanto: Nu = ϕ ( Re, Pr, d i L ) modelo que no admite cambios de estado en el fluido que circula; la formulación desarrollada es muy adecuada para estudiar la influencia de la velocidad u sobre el coeficiente de transmisión de calor por convección forzada h C de un sistema cualquiera, pues estas dos variables aparecen una sola vez. El procedimiento normal para determinar los exponentes (b, e, i) a partir de datos experimentales consiste en igualar el calor transmitido al fluido por convección, con la variación de entalpía que experimenta por esta causa. Calor transmitido al fluido por convección: Q = h C A L (T p - T ) Variación de la entalpía del fluido: Analogías y análisis dimensional.xii.-3
14 Q = m c (T sal - T ent ) = A T u ρ c (T sal - T ent ) = G A T c (T sal - T ent ) = G A T (i sal - i ent ) G es la velocidad másica= 36 u ρ, kg/m hora, viniendo u en m/seg en la que: A T es el área de la sección transversal del tubo correspondiente al diámetro int erior A L es el área de la superficie de la pared en contacto con el fluido Igualándolas se obtiene: h C c G = A T (T sal - T ent ) A L (T p - T ) = St = Nu Re Pr El número de Stanton St se calcula a partir de datos de Laboratorio. Para fluidos que se calientan en el interior de tubos, se aplica satisfactoriamente la ecuación de Dittus-Boelter, función de los números de Nusselt, Reynolds y Prandtl, de la forma: Nu =,3 Re, Pr,4, siendo: Pr= ν α = c η k Nu= h C ΔT k ΔT L = h C L k!- El coeficiente de convección h c ( Kcal/hora m C) # en la que: "- La conctividad térmica k del fluido ( Kcal/m C) # $ - La velocidad másica G ( kg/m hora) El número de Nusselt es la relación entre el calor transmitido por convección y el calor transmitido por concción, siendo L la longitud característica. Analogías y análisis dimensional.xii.-4
XIII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN, ANALOGÍAS Y ANÁLISIS DIMENSIONAL
 XIII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN, ANALOGÍAS Y ANÁLISIS DIMENSIONAL XIII.1.- ANALOGÍA ENTRE LA TRANSMISIÓN DE CALOR Y LA CANTIDAD DE MOVI- MIENTO EN LUJO TURBULENTO CAPA LIMITE TÉRMICA SOBRE PLACA
XIII.- TRANSMISIÓN DE CALOR POR CONVECCIÓN, ANALOGÍAS Y ANÁLISIS DIMENSIONAL XIII.1.- ANALOGÍA ENTRE LA TRANSMISIÓN DE CALOR Y LA CANTIDAD DE MOVI- MIENTO EN LUJO TURBULENTO CAPA LIMITE TÉRMICA SOBRE PLACA
Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
 Tema 7. Expresiones del actor de ricción 1. Introducción. Factor de ricción en régimen laminar 3. Subcapa laminar. Comportamiento hidrodinámico de tuberías 4. Experiencias de Nikuradse 5. Valor del coeiciente
Tema 7. Expresiones del actor de ricción 1. Introducción. Factor de ricción en régimen laminar 3. Subcapa laminar. Comportamiento hidrodinámico de tuberías 4. Experiencias de Nikuradse 5. Valor del coeiciente
Dinámica de Fluidos. Mecánica y Fluidos VERANO
 Dinámica de Fluidos Mecánica y Fluidos VERANO 1 Temas Tipos de Movimiento Ecuación de Continuidad Ecuación de Bernouilli Circulación de Fluidos Viscosos 2 TIPOS DE MOVIMIENTO Régimen Laminar: El flujo
Dinámica de Fluidos Mecánica y Fluidos VERANO 1 Temas Tipos de Movimiento Ecuación de Continuidad Ecuación de Bernouilli Circulación de Fluidos Viscosos 2 TIPOS DE MOVIMIENTO Régimen Laminar: El flujo
INDICE 1.- CÁLCULO DE CHIMENEA DE EVACUACIÓN DE HUMOS SEGÚN LA NORMA EN DATOS DE PARTIDA... 2
 INDICE 1.- CÁLCULO DE CHIMENEA DE EVACUACIÓN DE HUMOS SEGÚN LA NORMA EN 13384-1.... 2 1.1.- DATOS DE PARTIDA.... 2 1.2.- CAUDAL DE LOS PRODUCTOS DE COMBUSTIÓN.... 2 1.3.- DENSIDAD MEDIA DE LOS HUMOS...
INDICE 1.- CÁLCULO DE CHIMENEA DE EVACUACIÓN DE HUMOS SEGÚN LA NORMA EN 13384-1.... 2 1.1.- DATOS DE PARTIDA.... 2 1.2.- CAUDAL DE LOS PRODUCTOS DE COMBUSTIÓN.... 2 1.3.- DENSIDAD MEDIA DE LOS HUMOS...
INTRODUCCIÓN A LA CONVECCIÓN
 Diapositiva 1 INTRODUCCIÓN A LA CONVECCIÓN JM Corberán, R Royo 1 Diapositiva 1. CLASIFICACIÓN SEGÚN: ÍNDICE 1.1. CAUSA MOVIMIENTO FLUIDO - Forzada - Libre 1.. CONFIGURACIÓN DE FLUJO: - Flujo externo -
Diapositiva 1 INTRODUCCIÓN A LA CONVECCIÓN JM Corberán, R Royo 1 Diapositiva 1. CLASIFICACIÓN SEGÚN: ÍNDICE 1.1. CAUSA MOVIMIENTO FLUIDO - Forzada - Libre 1.. CONFIGURACIÓN DE FLUJO: - Flujo externo -
REGIMENES DE CORRIENTES O FLUJOS
 LINEAS DE CORRIENTE Ø Las líneas de corriente son líneas imaginarias dibujadas a través de un fluido en movimiento y que indican la dirección de éste en los diversos puntos del flujo de fluidos. Ø Una
LINEAS DE CORRIENTE Ø Las líneas de corriente son líneas imaginarias dibujadas a través de un fluido en movimiento y que indican la dirección de éste en los diversos puntos del flujo de fluidos. Ø Una
TEMA 1. MECANISMOS BÁSICOS DE TRANSMISIÓN DE CALOR
 TEMA 1. MECANISMOS BÁSICOS DE TRANSMISIÓN DE CALOR El calor: Es una forma de energía en tránsito. La Termodinámica y La Transferencia de calor. Diferencias. TERMODINAMICA 1er. Principio.Permite determinar
TEMA 1. MECANISMOS BÁSICOS DE TRANSMISIÓN DE CALOR El calor: Es una forma de energía en tránsito. La Termodinámica y La Transferencia de calor. Diferencias. TERMODINAMICA 1er. Principio.Permite determinar
Universidad Nacional de Córdoba. Facultad de Ciencias Exactas Físicas y Naturales. Cátedra de Mecánica de los Fluidos. Carrea de Ingeniería Civil
 Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
CAPITULO 6. Análisis Dimensional y Semejanza Dinámica
 CAPITULO 6. Análisis Dimensional y Semejanza Dinámica Debido a que son pocos los flujos reales que pueden ser resueltos con exactitud sólo mediante métodos analíticos, el desarrollo de la mecánica de fluidos
CAPITULO 6. Análisis Dimensional y Semejanza Dinámica Debido a que son pocos los flujos reales que pueden ser resueltos con exactitud sólo mediante métodos analíticos, el desarrollo de la mecánica de fluidos
Mecánica de Fluidos. Análisis Diferencial
 Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
MECANICA DE LOS FLUIDOS
 MECANICA DE LOS FLUIDOS 6 ANALISIS DIMENSIONAL Y SEMEJANZA HIDRAULICA Ing. Alejandro Mayori 6 ANALISIS DIMENSIONAL Y SEMEJANZA HIDRAULICA 6.1 Introducción - Teoría matemática y resultados experimentales
MECANICA DE LOS FLUIDOS 6 ANALISIS DIMENSIONAL Y SEMEJANZA HIDRAULICA Ing. Alejandro Mayori 6 ANALISIS DIMENSIONAL Y SEMEJANZA HIDRAULICA 6.1 Introducción - Teoría matemática y resultados experimentales
ECUACIONES DIMENSIONALES
 ECUACIONES DIMENSIONALES 1. En la expresión x = k v n / a, x = distancia, v = velocidad, a = aceleración y k es una constante adimensional. Cuánto vale n para que la expresión sea dimensionalmente homogénea?
ECUACIONES DIMENSIONALES 1. En la expresión x = k v n / a, x = distancia, v = velocidad, a = aceleración y k es una constante adimensional. Cuánto vale n para que la expresión sea dimensionalmente homogénea?
DEPARTAMENTO DE INGENIERÍA QUÍMICA. Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESTADO NO ESTACIONARIO
 DEPARAMENO DE INGENIERÍA QUÍMICA Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESADO NO ESACIONARIO 1. INRODUCCIÓN El sistema al que se va a plantear el balance de energía calorífica consiste
DEPARAMENO DE INGENIERÍA QUÍMICA Laboratorio de Ingeniería Química BALANCE DE ENERGÍA EN ESADO NO ESACIONARIO 1. INRODUCCIÓN El sistema al que se va a plantear el balance de energía calorífica consiste
PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA
 PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA OBJETIVO GENERAL: Familiarizar al alumno con los sistemas de torres de refrigeración para evacuar el calor excedente del agua. OBJETIVOS ESPECÍFICOS: Investigar
PRÁCTICA 10. TORRE DE REFRIGERACIÓN POR AGUA OBJETIVO GENERAL: Familiarizar al alumno con los sistemas de torres de refrigeración para evacuar el calor excedente del agua. OBJETIVOS ESPECÍFICOS: Investigar
LABORATORIO DE FENÓMENOS COLECTIVOS
 LABORATORIO DE FENÓMENOS COLECTIVOS LA VISCOSIDAD DE LOS LÍQUIDOS CRUZ DE SAN PEDRO JULIO CÉSAR RESUMEN La finalidad de esta práctica es la determinación de la viscosidad de diferentes sustancias (agua,
LABORATORIO DE FENÓMENOS COLECTIVOS LA VISCOSIDAD DE LOS LÍQUIDOS CRUZ DE SAN PEDRO JULIO CÉSAR RESUMEN La finalidad de esta práctica es la determinación de la viscosidad de diferentes sustancias (agua,
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA AREA DE TECNOLOGÍA DEPARTAMENTO DE ENERGÉTICA UNIDAD CURRICULAR: TRANSFERENCIA DE CALOR
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA AREA DE TECNOLOGÍA DEPARTAMENTO DE ENERGÉTICA UNIDAD CURRICULAR: TRANSFERENCIA DE CALOR Convección Profesor: Ing. Isaac Hernández Isaachernandez89@gmail.com
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA AREA DE TECNOLOGÍA DEPARTAMENTO DE ENERGÉTICA UNIDAD CURRICULAR: TRANSFERENCIA DE CALOR Convección Profesor: Ing. Isaac Hernández Isaachernandez89@gmail.com
SENSORES DE FLUJO. Transducers for Biomedical Measurements: Principles and Applications, R.S.C. Cobbold, Ed. John Wiley & Sons
 SENSORES DE FLUJO Referencias bibliográficas Transducers for Biomedical Measurements: Principles and Applications, R.S.C. Cobbold, Ed. John Wiley & Sons Sensores y acondicionamiento de señal, R. Pallás
SENSORES DE FLUJO Referencias bibliográficas Transducers for Biomedical Measurements: Principles and Applications, R.S.C. Cobbold, Ed. John Wiley & Sons Sensores y acondicionamiento de señal, R. Pallás
Análisis Dimensional y Semejanza
 87 Capítulo 8 Análisis Dimensional y Semejanza Dado que el número de problemas que se puede resolver en forma puramente analítica es pequeño, la gran mayoría requiere algún grado de resultados empíricos
87 Capítulo 8 Análisis Dimensional y Semejanza Dado que el número de problemas que se puede resolver en forma puramente analítica es pequeño, la gran mayoría requiere algún grado de resultados empíricos
Cuarta Lección. Principios de la física aplicados al vuelo.
 Capítulo II. Termodinámica y Física de los Fluidos aplicadas a procesos naturales. Tema. El proceso de vuelo de las aves y de los ingenios alados. Cuarta Lección. Principios de la física aplicados al vuelo.
Capítulo II. Termodinámica y Física de los Fluidos aplicadas a procesos naturales. Tema. El proceso de vuelo de las aves y de los ingenios alados. Cuarta Lección. Principios de la física aplicados al vuelo.
UNIVERSIDAD NACIONAL DEL SANTA ESCUELA DE INGENIERIA EN ENERGIA MODULO SEMANA 9 IMPEDANCIA EN SERIE DE LINEAS DE TRANSMISION : RESISTENCIA
 UNIVERSIDAD NACIONAL DEL SANTA ESCUELA DE INGENIERIA EN ENERGIA MODULO SEMANA 9 CURSO: SISTEMAS ELECTRICOS DE POTENCIA PROFESOR : MSC. CESAR LOPEZ AGUILAR INGENIERO EN ENERGIA INGENIERO MECANICO ELECTRICISTA
UNIVERSIDAD NACIONAL DEL SANTA ESCUELA DE INGENIERIA EN ENERGIA MODULO SEMANA 9 CURSO: SISTEMAS ELECTRICOS DE POTENCIA PROFESOR : MSC. CESAR LOPEZ AGUILAR INGENIERO EN ENERGIA INGENIERO MECANICO ELECTRICISTA
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas.
 Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli.
 Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli. Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Presión de un fluido Presión depende de la profundidad P = ρ
Física para Ciencias: Principio de Arquímedes, Ecuaciones de Continuidad y Bernoulli. Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Presión de un fluido Presión depende de la profundidad P = ρ
PROBLEMAS DE NAVIDAD 2001
 PROBLEMAS DE NAVIDAD 2001 PROBLEMAS DE NAVIDAD 2001 Navidad 2001-1 Para la conducción cuya sección transversal se representa en la figura se pide: Calcular el caudal de agua que puede trasegar suponiendo
PROBLEMAS DE NAVIDAD 2001 PROBLEMAS DE NAVIDAD 2001 Navidad 2001-1 Para la conducción cuya sección transversal se representa en la figura se pide: Calcular el caudal de agua que puede trasegar suponiendo
UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA
 UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA UNIDAD III. HIDROCINEMÁTICA Introducción. La hidrocinemática o cinemática de los líquidos se ocupa del estudio de las partículas que integran
UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA UNIDAD III. HIDROCINEMÁTICA Introducción. La hidrocinemática o cinemática de los líquidos se ocupa del estudio de las partículas que integran
PÉRDIDAS DE CARGA. E.T.S. Ingenieros Industriales. Curso PRÁCTICAS DE MECÁNICA DE FLUIDOS ÍNDICE. Área de Mecánica de Fluidos
 Prácticas de Mecánica de Fluidos Pérdidas de Carga 1/10 UNIVERSIDAD DE OVIEDO E.T.S. Ingenieros Industriales 3 er curso Curso 004-005 PRÁCTICAS DE MECÁNICA DE FLUIDOS PÉRDIDAS DE CARGA ÍNDICE 1. Introducción
Prácticas de Mecánica de Fluidos Pérdidas de Carga 1/10 UNIVERSIDAD DE OVIEDO E.T.S. Ingenieros Industriales 3 er curso Curso 004-005 PRÁCTICAS DE MECÁNICA DE FLUIDOS PÉRDIDAS DE CARGA ÍNDICE 1. Introducción
ECUACIONES ADIMENSIONALES Y ORDENES DE MAGNITUD
 CUACIONS ADIMNSIONAS Y ORDNS D MAGNITUD Prof. C. Dopazo Área de Mecánica de Fluidos Centro Politécnico Superior Universidad de Zaragoza Septiembre 2005 Índice PROBMA TRMICO 4 2 PROBMA MASICO 5 3 ORDNS
CUACIONS ADIMNSIONAS Y ORDNS D MAGNITUD Prof. C. Dopazo Área de Mecánica de Fluidos Centro Politécnico Superior Universidad de Zaragoza Septiembre 2005 Índice PROBMA TRMICO 4 2 PROBMA MASICO 5 3 ORDNS
Campo de velocidades se puede representar mediante una función potencial φ, escalar
 Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
T 1 T 2. x L. Con frecuencia es importante el valor de la resistencia térmica multiplicado por el área de flujo de calor, en este caso sera
 1. ey de Fourier ué flujo de calor es necesario hacer pasar a través de una barra circular de madera de 5 cm de diámetro y 10 cm de longitud, cuya temperatura en los extremos es de 50 C y 10 C en sus extremos?
1. ey de Fourier ué flujo de calor es necesario hacer pasar a través de una barra circular de madera de 5 cm de diámetro y 10 cm de longitud, cuya temperatura en los extremos es de 50 C y 10 C en sus extremos?
Mecánica de Fluidos. Docente: Ing. Alba V. Díaz Corrales
 Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
Mecánica de Fluidos Docente: Ing. Alba V. Díaz Corrales Mecánica de Fluidos Contenido Fluidos incompresibles Ecuación de continuidad Ecuación de Bernoulli y aplicaciones Líneas de cargas piezométricas
Problemas métricos. 1. Problemas afines y problemas métricos
 . Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
. Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
7. Difracción n de la luz
 7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
7. Difracción n de la luz 7.1. La difracción 1 7. Difracción de la luz. 2 Experiencia de Grimaldi (1665) Al iluminar una pantalla opaca con una abertura pequeña, se esperaba que en la pantalla de observación
CENTRIFUGACIÓN. Fundamentos. Teoría de la centrifugación
 CENTRIFUGACIÓN Fundamentos. Teoría de la centrifugación Fuerzas intervinientes Tipos de centrífugas Tubular De discos Filtración centrífuga 1 SEDIMENTACIÓN Se basa en la diferencia de densidades entre
CENTRIFUGACIÓN Fundamentos. Teoría de la centrifugación Fuerzas intervinientes Tipos de centrífugas Tubular De discos Filtración centrífuga 1 SEDIMENTACIÓN Se basa en la diferencia de densidades entre
INTERCAMBIADORES DE CALOR (CONCEPTOS)
 INTERCAMBIADORES DE CALOR (CONCEPTOS Intercambiador de calor Los intercambiadores de calor son equipos de transferencia de calor. Pueden clasificarse según su construcción o el servicio que prestan. 1
INTERCAMBIADORES DE CALOR (CONCEPTOS Intercambiador de calor Los intercambiadores de calor son equipos de transferencia de calor. Pueden clasificarse según su construcción o el servicio que prestan. 1
5. PÉRDIDAS DE CARGA EN CONDUCTOS CERRADOS O TUBERIAS
 5. PÉRIAS E CARGA EN CONUCTOS CERRAOS O TUBERIAS 5. Perfiles de Velocidad: Laminar y Turbulento 5. Radio Hidráulico para Secciones no Circulares 5.3 Pérdidas Primarias y Secundarias 5.4 Ecuación de arcy
5. PÉRIAS E CARGA EN CONUCTOS CERRAOS O TUBERIAS 5. Perfiles de Velocidad: Laminar y Turbulento 5. Radio Hidráulico para Secciones no Circulares 5.3 Pérdidas Primarias y Secundarias 5.4 Ecuación de arcy
Transferencia de Calor por convección Natural CAPÍTULO 3 DE CALOR POR CONVECCIÓN NATURAL. En convección natural el flujo resulta solamente de la
 CAPÍTULO 3 TRANSFERENCIA DE CALOR POR CONVECCIÓN NATURAL 3.1 Definición de Convección Natural. En convección natural el flujo resulta solamente de la diferencia de temperaturas del fluido en la presencia
CAPÍTULO 3 TRANSFERENCIA DE CALOR POR CONVECCIÓN NATURAL 3.1 Definición de Convección Natural. En convección natural el flujo resulta solamente de la diferencia de temperaturas del fluido en la presencia
CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO)
 GENERALIDADES. CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO) El bombeo hidráulico tipo jet es un sistema artificial de producción especial, a diferencia del tipo pistón, no ocupa partes móviles y
GENERALIDADES. CAPITULO VII BOMBEO HIDRÁULICO TIPO JET (A CHORRO) El bombeo hidráulico tipo jet es un sistema artificial de producción especial, a diferencia del tipo pistón, no ocupa partes móviles y
CONSIDERACIONES GENERALES SOBRE ESTÁTICA
 CONSIDERACIONES GENERALES SOBRE ESTÁTICA Índice 1. CONCEPTOS ÚTILES 2 1.1. Configuración geométrica de un sistema....................... 2 1.2. Ligaduras....................................... 2 1.3. Coordenadas
CONSIDERACIONES GENERALES SOBRE ESTÁTICA Índice 1. CONCEPTOS ÚTILES 2 1.1. Configuración geométrica de un sistema....................... 2 1.2. Ligaduras....................................... 2 1.3. Coordenadas
ELECTRODINAMICA. Nombre: Curso:
 1 ELECTRODINAMICA Nombre: Curso: Introducción: En esta sesión se estudiara los efectos de las cargas eléctricas en movimiento en diferentes tipos de conductores, dando origen al concepto de resistencia
1 ELECTRODINAMICA Nombre: Curso: Introducción: En esta sesión se estudiara los efectos de las cargas eléctricas en movimiento en diferentes tipos de conductores, dando origen al concepto de resistencia
Vertedores y compuertas
 Vertedores y compuertas Material para el curso de Hidráulica I Se recomienda consultar la fuente de estas notas: Sotelo Ávila Gilberto. 2002. Hidráulica General. Vol. 1. Fundamentos. LIMUSA Editores. México.
Vertedores y compuertas Material para el curso de Hidráulica I Se recomienda consultar la fuente de estas notas: Sotelo Ávila Gilberto. 2002. Hidráulica General. Vol. 1. Fundamentos. LIMUSA Editores. México.
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS
 TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
TUTORIAL BÁSICO DE MECÁNICA FLUIDOS El tutorial es básico pues como habréis visto en muchos de ellos es haceros entender no sólo la aplicación práctica de cada teoría sino su propia existencia y justificación.
Capa Límite Superficial
 Capa ímite Superficial Física Ambiental. ema 6. ema6. FA (prof. RAMOS 1 ema 6.- Capa ímite Superficial. Capa límite: justificación. Flujos laminar y turbulento, características físicas: números de Reynolds.
Capa ímite Superficial Física Ambiental. ema 6. ema6. FA (prof. RAMOS 1 ema 6.- Capa ímite Superficial. Capa límite: justificación. Flujos laminar y turbulento, características físicas: números de Reynolds.
LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA:
 LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA: LABORATORIO DE MECÁNICA DE FLUIDOS PRESENTADO A: ING. VLADIMIR QUIROZ
LABORATORIO #6 DEMOSTRACIÓN DEL TOREMA DE BERNOULLI LUIS CARLOS DE LA CRUZ TORRES GILDARDO DIAZ CARLOS ROJAS PRESENTADO EN LA CÁTEDRA: LABORATORIO DE MECÁNICA DE FLUIDOS PRESENTADO A: ING. VLADIMIR QUIROZ
HIDRODINÁMICA. Profesor: Robinson Pino H.
 HIDRODINÁMICA Profesor: Robinson Pino H. 1 CARACTERÍSTICAS DEL MOVIMIENTO DE LOS FLUIDOS Flujo laminar: Ocurre cuando las moléculas de un fluido en movimiento siguen trayectorias paralelas. Flujo turbulento:
HIDRODINÁMICA Profesor: Robinson Pino H. 1 CARACTERÍSTICAS DEL MOVIMIENTO DE LOS FLUIDOS Flujo laminar: Ocurre cuando las moléculas de un fluido en movimiento siguen trayectorias paralelas. Flujo turbulento:
Módulo 3: Fluidos reales
 Módulo 3: Fluidos reales 1 Fluidos reales Según la ecuación de Bernouilli, si un fluido fluye estacionariamente (velocidad constante) por una tubería horizontal estrecha y de sección transversal constante,
Módulo 3: Fluidos reales 1 Fluidos reales Según la ecuación de Bernouilli, si un fluido fluye estacionariamente (velocidad constante) por una tubería horizontal estrecha y de sección transversal constante,
Resistencia de Materiales 1A. Profesor Herbert Yépez Castillo
 Resistencia de Materiales 1A Profesor Herbert Yépez Castillo 2014-2 2 Capítulo 5. Torsión 5.4 Ángulo 3 Un par es un momento que tiende a hacer girar respecto a su eje longitudinal. Su efecto es de interés
Resistencia de Materiales 1A Profesor Herbert Yépez Castillo 2014-2 2 Capítulo 5. Torsión 5.4 Ángulo 3 Un par es un momento que tiende a hacer girar respecto a su eje longitudinal. Su efecto es de interés
QUÍMICA FÍSICA II Grupo A. Tercer control, 10 de mayo de Escoged 2 de las 3 preguntas que os propongo, cada una de las preguntas vale 5 puntos.
 QUÍMICA FÍSICA II Grupo A. Tercer control, 10 de mayo de 2011 Escoged 2 de las 3 preguntas que os propongo, cada una de las preguntas vale 5 puntos. 1. Qué significado tienen los parámetros termodinámicos
QUÍMICA FÍSICA II Grupo A. Tercer control, 10 de mayo de 2011 Escoged 2 de las 3 preguntas que os propongo, cada una de las preguntas vale 5 puntos. 1. Qué significado tienen los parámetros termodinámicos
MECÁNICA DE FLUIDOS. Docente: Ing. Alba Díaz Corrales
 MECÁNICA DE FLUIDOS Docente: Ing. Alba Díaz Corrales Fecha: 1 de septiembre 2010 Mecánica de Fluidos Tipo de asignatura: Básica Específica Total de horas semanales: 6 Total de horas semestrales: 84 Asignatura
MECÁNICA DE FLUIDOS Docente: Ing. Alba Díaz Corrales Fecha: 1 de septiembre 2010 Mecánica de Fluidos Tipo de asignatura: Básica Específica Total de horas semanales: 6 Total de horas semestrales: 84 Asignatura
EJERCICIOS RESUELTOS DE INECUACIONES
 EJERCICIOS RESUELTOS DE INECUACIONES 1. Resolver las inecuaciones: a) 3-8 - 7 b) 6-5 > 1-10 a) Para resolver la inecuación, se pasan los términos con al primer miembro y los independientes al segundo quedando
EJERCICIOS RESUELTOS DE INECUACIONES 1. Resolver las inecuaciones: a) 3-8 - 7 b) 6-5 > 1-10 a) Para resolver la inecuación, se pasan los términos con al primer miembro y los independientes al segundo quedando
MECANICA DE LOS FLUIDOS
 MECANICA DE LOS FLUIDOS 7 FUNDAMENTOS DEL FLUJO DE FLUIDOS Ing. Alejandro Mayori Flujo de Fluidos o Hidrodinámica es el estudio de los Fluidos en Movimiento Principios Fundamentales: 1. Conservación de
MECANICA DE LOS FLUIDOS 7 FUNDAMENTOS DEL FLUJO DE FLUIDOS Ing. Alejandro Mayori Flujo de Fluidos o Hidrodinámica es el estudio de los Fluidos en Movimiento Principios Fundamentales: 1. Conservación de
QUÉ ES LA TEMPERATURA?
 1 QUÉ ES LA TEMPERATURA? Nosotros experimentamos la temperatura todos los días. Cuando estamos en verano, generalmente decimos Hace calor! y en invierno Hace mucho frío!. Los términos que frecuentemente
1 QUÉ ES LA TEMPERATURA? Nosotros experimentamos la temperatura todos los días. Cuando estamos en verano, generalmente decimos Hace calor! y en invierno Hace mucho frío!. Los términos que frecuentemente
Laboratorio de Propiedades Termofísicas. Centro Nacional de Metrología
 Medición de la conductividad térmica de materiales sólidos conductores Leonel Lira Cortés Laboratorio de Propiedades Termofísicas División Termometría, Área Eléctrica Centro Nacional de Metrología INTRODUCCION
Medición de la conductividad térmica de materiales sólidos conductores Leonel Lira Cortés Laboratorio de Propiedades Termofísicas División Termometría, Área Eléctrica Centro Nacional de Metrología INTRODUCCION
CORRIENTE CONTINUA I : RESISTENCIA INTERNA DE UNA FUENTE
 eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
eman ta zabal zazu Departamento de Física de la Materia Condensada universidad del país vasco euskal herriko unibertsitatea FACULTAD DE CIENCIA Y TECNOLOGÍA UNIVERSIDAD DEL PAÍS VASCO DEPARTAMENTO de FÍSICA
MEDICIÓN DE CONDUCTIVIDAD TÉRMICA
 MEDICIÓN DE CONDUCTIVIDAD TÉRMICA Introducción: Las soluciones de la Ley de Fourier en su formulación diferencial, empleando las condiciones de borde adecuadas, permite resolver el problema de conducción
MEDICIÓN DE CONDUCTIVIDAD TÉRMICA Introducción: Las soluciones de la Ley de Fourier en su formulación diferencial, empleando las condiciones de borde adecuadas, permite resolver el problema de conducción
HIDRAULICA DE POTENCIA. Unidad 1. Bases físicas de la hidráulica
 HIDRAULICA DE POTENCIA Unidad 1. Bases físicas de la hidráulica Presión Este término se refiere a los efectos de una fuerza que actúa distribuida sobre una superficie. La fuerza causante de la presión
HIDRAULICA DE POTENCIA Unidad 1. Bases físicas de la hidráulica Presión Este término se refiere a los efectos de una fuerza que actúa distribuida sobre una superficie. La fuerza causante de la presión
1 Introducción. 2 Modelo. Hipótesis del modelo MODELO DE REGRESIÓN LOGÍSTICA
 MODELO DE REGRESIÓN LOGÍSTICA Introducción A grandes rasgos, el objetivo de la regresión logística se puede describir de la siguiente forma: Supongamos que los individuos de una población pueden clasificarse
MODELO DE REGRESIÓN LOGÍSTICA Introducción A grandes rasgos, el objetivo de la regresión logística se puede describir de la siguiente forma: Supongamos que los individuos de una población pueden clasificarse
Representación en el espacio de estado. Sistemas Control Embebidos e Instrumentación Electrónica UNIVERSIDAD EAFIT
 Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Representación en el espacio de estado Representación en espacio de estado Control clásico El modelado y control de sistemas basado en la transformada de Laplace, es un enfoque muy sencillo y de fácil
Mecánica de Sistemas y Fenómenos Ondulatorios Práctico 4
 Práctico 4 Ejercicio 1 Considere el sistema de la figura, formado por masas puntuales m unidas entre sí por resortes de constante K y longitud natural a. lamemos y n al desplazamiento de la n-ésima masa
Práctico 4 Ejercicio 1 Considere el sistema de la figura, formado por masas puntuales m unidas entre sí por resortes de constante K y longitud natural a. lamemos y n al desplazamiento de la n-ésima masa
http://saeti.itson.mx/otrosusuarios/plandosmilnueveconsprogamplioimpma.asp?materia...
 Page 1 of 5 Departamento: Dpto Cs. Agua y Medio Ambiente Nombre del curso: TRANSFERENCIA DE CALOR CON LABORATORIO Clave: 004269 Academia a la que pertenece: Academia de Ingeniería Química Aplicada en Operaciones
Page 1 of 5 Departamento: Dpto Cs. Agua y Medio Ambiente Nombre del curso: TRANSFERENCIA DE CALOR CON LABORATORIO Clave: 004269 Academia a la que pertenece: Academia de Ingeniería Química Aplicada en Operaciones
Ejercicios Propuestos Transporte eléctrico.
 Ejercicios Propuestos Transporte eléctrico. 1. La cantidad de carga que pasa a través de una superficie de área 1[ 2 ] varía con el tiempo de acuerdo con la expresión () =4 3 6 2 +6. (a) Cuál es la intensidad
Ejercicios Propuestos Transporte eléctrico. 1. La cantidad de carga que pasa a través de una superficie de área 1[ 2 ] varía con el tiempo de acuerdo con la expresión () =4 3 6 2 +6. (a) Cuál es la intensidad
INTERCAMBIADORES DE CALOR
 1 OBJETO: INTERCAMBIADORES DE CALOR Estudio del comportamiento de un cambiador de calor de carcasa y tubos. Determinación de su coeficiente global de transmisión de calor, DMLT, F, eficiencia, NUT, y pérdidas
1 OBJETO: INTERCAMBIADORES DE CALOR Estudio del comportamiento de un cambiador de calor de carcasa y tubos. Determinación de su coeficiente global de transmisión de calor, DMLT, F, eficiencia, NUT, y pérdidas
RESUMEN DEL PROGRAMA (parte de Hidráulica)
 Código de la asignatura: 68202, 60203 Nombre de la asignatura: Hidráulica y máquinas agrícolas Créditos: 6 (3 Hidráulica) Año académico: 2007-2008 Titulación: Ingeniero Técnico Agrícola (Hortofruticultura
Código de la asignatura: 68202, 60203 Nombre de la asignatura: Hidráulica y máquinas agrícolas Créditos: 6 (3 Hidráulica) Año académico: 2007-2008 Titulación: Ingeniero Técnico Agrícola (Hortofruticultura
Unidad 1: SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS
 Unidad 1: SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS 1.1.- SISTEMAS DE ECUACIONES LINEALES Ecuación lineal Las ecuaciones siguientes son lineales: 2x 3 = 0; 5x + 4y = 20; 3x + 2y + 6z = 6; 5x 3y + z 5t =
Unidad 1: SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS 1.1.- SISTEMAS DE ECUACIONES LINEALES Ecuación lineal Las ecuaciones siguientes son lineales: 2x 3 = 0; 5x + 4y = 20; 3x + 2y + 6z = 6; 5x 3y + z 5t =
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES.
 TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
TEMA 1: SISTEMAS MODELADOS POR ECUACIONES DIFERENCIALES EN INGENIERÍA QUÍMICA. CLASIFICACIÓN. GENERALIDADES. 1. INTRODUCCIÓN. PLANTEAMIENTO DE PROBLEMAS EN INGENIERÍA QUÍMICA 2. PROBLEMAS EXPRESADOS MEDIANTE
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO 1. Un condensador se carga aplicando una diferencia de potencial entre sus placas de 5 V. Las placas son circulares de diámetro cm y están separadas
SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO 1. Un condensador se carga aplicando una diferencia de potencial entre sus placas de 5 V. Las placas son circulares de diámetro cm y están separadas
TEMA PE9. PE.9.2. Tenemos dos espiras planas de la forma y dimensiones que se indican en la Figura, siendo R
 TEMA PE9 PE.9.1. Los campos magnéticos de los que estamos rodeados continuamente representan un riesgo potencial para la salud, en Europa se han establecido recomendaciones para limitar la exposición,
TEMA PE9 PE.9.1. Los campos magnéticos de los que estamos rodeados continuamente representan un riesgo potencial para la salud, en Europa se han establecido recomendaciones para limitar la exposición,
Termodinámica y Máquinas Térmicas
 Termodinámica y Máquinas Térmicas Tema 04. Funciones de Estado Inmaculada Fernández Diego Severiano F. Pérez Remesal Carlos J. Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica
Termodinámica y Máquinas Térmicas Tema 04. Funciones de Estado Inmaculada Fernández Diego Severiano F. Pérez Remesal Carlos J. Renedo Estébanez DPTO. DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA Este tema se publica
Sistemas de ecuaciones lineales
 Ecuación lineal con n incógnitas Sistemas de ecuaciones lineales Es cualquier expresión del tipo: a 1 x 1 + a 2 x 2 + a 3 x 3 +... + a n x n = b, donde a i, b. Los valores a i se denominan coeficientes,
Ecuación lineal con n incógnitas Sistemas de ecuaciones lineales Es cualquier expresión del tipo: a 1 x 1 + a 2 x 2 + a 3 x 3 +... + a n x n = b, donde a i, b. Los valores a i se denominan coeficientes,
Figura 10.1: Resultante de fuerzas horizontal y vertical sobre un perfil alar.
 116 Capítulo 1 Capa Límite n cuerpo que este inmerso en un flujo eperimenta una fuerza resultante debido a la acción entre el flujo y el cuerpo. Esta es la fuerza resultante de los esfuerzos de corte en
116 Capítulo 1 Capa Límite n cuerpo que este inmerso en un flujo eperimenta una fuerza resultante debido a la acción entre el flujo y el cuerpo. Esta es la fuerza resultante de los esfuerzos de corte en
TUBERIAS. Ricardo García San José Ingeniero Industrial (Noviembre 2.000) TUBERIAS
 TUBERIAS Ricardo García San José Ingeniero Industrial (Noviembre 2.000) TUBERIAS INDICE 1.- MATERIALES... 3 2.- PERDIDAS DE CARGA... 4 2.1.- FACTORES QUE INFLUYEN EN LAS PERDIDAS DE CARGA... 4 2.2.- REGIMENES
TUBERIAS Ricardo García San José Ingeniero Industrial (Noviembre 2.000) TUBERIAS INDICE 1.- MATERIALES... 3 2.- PERDIDAS DE CARGA... 4 2.1.- FACTORES QUE INFLUYEN EN LAS PERDIDAS DE CARGA... 4 2.2.- REGIMENES
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
Espacio afín. 1. Rectas en el espacio. Piensa y calcula. Aplica la teoría
 6 Espacio afín 1. Rectas en el espacio Piensa y calcula Calcula las coordenadas de un vector que tenga la dirección de la recta que pasa por los puntos A2, 1, 5 y B3, 1, 4 AB 1, 2, 1 Aplica la teoría 1.
6 Espacio afín 1. Rectas en el espacio Piensa y calcula Calcula las coordenadas de un vector que tenga la dirección de la recta que pasa por los puntos A2, 1, 5 y B3, 1, 4 AB 1, 2, 1 Aplica la teoría 1.
Álgebra Lineal Ma1010
 Álgebra Ma1010 Departamento de Matemáticas ITESM Álgebra - p. 1/31 En este apartado se introduce uno de los conceptos más importantes del curso: el de combinación lineal entre vectores. Se establece la
Álgebra Ma1010 Departamento de Matemáticas ITESM Álgebra - p. 1/31 En este apartado se introduce uno de los conceptos más importantes del curso: el de combinación lineal entre vectores. Se establece la
Trabajo Práctico n 2. Robotización de un Puente Grúa. Presentación. Restricciones. Curso 2011
 Trabajo Práctico n 2 Robotización de un Puente Grúa Presentación Este problema consiste en desarrollar un sistema de control automático que permita robotizar la operación de un puente grúa para la carga
Trabajo Práctico n 2 Robotización de un Puente Grúa Presentación Este problema consiste en desarrollar un sistema de control automático que permita robotizar la operación de un puente grúa para la carga
El modelo semiclásico de las propiedades de transporte: Objetivo
 El modelo semiclásico de las propiedades de transporte: Objetivo En el estudio de las propiedades de transporte se usa una aproximación que se basa en los principios usado para el estudio de los electrones
El modelo semiclásico de las propiedades de transporte: Objetivo En el estudio de las propiedades de transporte se usa una aproximación que se basa en los principios usado para el estudio de los electrones
PLANIFICACIÓN Y MANEJO DEL AGUA EN LA AGRICULTURA IRRIGADA. Roberto P. Marano
 PLANIFICACIÓN Y MANEJO DEL AGUA EN LA AGRICULTURA IRRIGADA Relación suelo-agua Roberto P. Marano Retención de agua La matriz del suelo retiene agua por dos mecanismos: * el agua puede ser adsorbida a las
PLANIFICACIÓN Y MANEJO DEL AGUA EN LA AGRICULTURA IRRIGADA Relación suelo-agua Roberto P. Marano Retención de agua La matriz del suelo retiene agua por dos mecanismos: * el agua puede ser adsorbida a las
Mecánica y fluidos. Webpage: Departamento de FísicaF Universidad de Sonora. Dinámica de Fluidos
 Mecánica y fluidos Webpage: http://paginas.fisica.uson.mx/qb 007 Departamento de FísicaF Universidad de Sonora Dinámica de Fluidos 1 Temario 7. Dinámica de fluidos Dinámica de fluidos (.5 semanas) 1. Características
Mecánica y fluidos Webpage: http://paginas.fisica.uson.mx/qb 007 Departamento de FísicaF Universidad de Sonora Dinámica de Fluidos 1 Temario 7. Dinámica de fluidos Dinámica de fluidos (.5 semanas) 1. Características
CAPÍTULO PRINCIPIOS DE FLUIDIZACIÓN. La fluidización es la levitación de una masa (lecho) de partículas por la acción de un fluido
 CAPÍTULO 3 PRINCIPIOS DE FLUIDIZACIÓN La fluidización es la levitación de una masa (lecho) de partículas por la acción de un fluido que se observa cuando el lecho entra en contacto con un flujo vertical
CAPÍTULO 3 PRINCIPIOS DE FLUIDIZACIÓN La fluidización es la levitación de una masa (lecho) de partículas por la acción de un fluido que se observa cuando el lecho entra en contacto con un flujo vertical
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
DEPARTAMENTO DE FÍSICA DE LA UNIVERSIDAD DE SONORA ORGANIZACIÓN DE LA MATERIA DE FÍSICA III
 DEPARTAMENTO DE FÍSICA DE LA UNIVERSIDAD DE SONORA ORGANIZACIÓN DE LA MATERIA DE FÍSICA III HERMOSILLO, SONORA, OCTUBRE DEL 2005 NOMBRE: FISICA III CON LABORATORIO UNIDAD REGIONAL: CENTRO EJE BÁSICO DE
DEPARTAMENTO DE FÍSICA DE LA UNIVERSIDAD DE SONORA ORGANIZACIÓN DE LA MATERIA DE FÍSICA III HERMOSILLO, SONORA, OCTUBRE DEL 2005 NOMBRE: FISICA III CON LABORATORIO UNIDAD REGIONAL: CENTRO EJE BÁSICO DE
Capítulo 10. Efectos de superficie. Sistema respiratorio
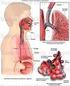 Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
Prólogo RANALD V. GILES
 Prólogo Este libro ha sido concebido con el principal propósito de complementar los textos ordinarios (de mecánica de los fluidos e hidráulica. Se basa en la convicción del autor de que el esclarecimiento
Prólogo Este libro ha sido concebido con el principal propósito de complementar los textos ordinarios (de mecánica de los fluidos e hidráulica. Se basa en la convicción del autor de que el esclarecimiento
2.- Ecuaciones de primer grado
 3º ESO E UNIDAD 8.- ECUACIONES. SISTEMAS DE ECUACIONES PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------
3º ESO E UNIDAD 8.- ECUACIONES. SISTEMAS DE ECUACIONES PROFESOR: RAFAEL NÚÑEZ -------------------------------------------------------------------------------------------------------------------------------------
JUNIO Opción A
 Junio 010 (Prueba Específica) JUNIO 010 Opción A 1.- Discute y resuelve según los distintos valores del parámetro a el siguiente sistema de ecuaciones: a x + a y + az 1 x + a y + z 0.- Una panadería se
Junio 010 (Prueba Específica) JUNIO 010 Opción A 1.- Discute y resuelve según los distintos valores del parámetro a el siguiente sistema de ecuaciones: a x + a y + az 1 x + a y + z 0.- Una panadería se
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA
 CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
Introdución a la capa límite laminar bidimensional y estacionaria
 Introdución a la capa límite laminar bidimensional y estacionaria M. Rodríguez 1 Introducción En los movimientos a altos números de Reynolds (basado en la longitud característica del movimiento), los efectos
Introdución a la capa límite laminar bidimensional y estacionaria M. Rodríguez 1 Introducción En los movimientos a altos números de Reynolds (basado en la longitud característica del movimiento), los efectos
DILATACIÓN PREGUNTAS PROBLEMAS
 DILATACIÓN 1. Qué es la temperatura? PREGUNTAS PROBLEMAS 1. Dos barras idénticas de fierro (α = 12 x 10-6 /Cº) de 1m de longitud, fijas en uno de sus extremos se encuentran a una temperatura de 20ºC si
DILATACIÓN 1. Qué es la temperatura? PREGUNTAS PROBLEMAS 1. Dos barras idénticas de fierro (α = 12 x 10-6 /Cº) de 1m de longitud, fijas en uno de sus extremos se encuentran a una temperatura de 20ºC si
PRÁCTICO DE MÁQUINAS PARA FLUIDOS II
 44) En la instalación de la figura la bomba gira a 1700rpm, entregando un caudal de agua a 20 o C de 0.5m 3 /s al tanque elevado. La cañería es de acero galvanizado, rígida y de 500mm de diámetro y cuenta
44) En la instalación de la figura la bomba gira a 1700rpm, entregando un caudal de agua a 20 o C de 0.5m 3 /s al tanque elevado. La cañería es de acero galvanizado, rígida y de 500mm de diámetro y cuenta
PRÁCTICA Nº 5. MEDIDORES DE FLUJO PARA FLUIDOS COMPRESIBLES
 República bolivariana de Venezuela La Universidad del Zulia Facultad de Ingeniería Escuela de Ingeniería Química Laboratorio de Operaciones Unitarias I PRÁCTICA Nº 5. MEDIDORES DE FLUJO PARA FLUIDOS COMPRESIBLES
República bolivariana de Venezuela La Universidad del Zulia Facultad de Ingeniería Escuela de Ingeniería Química Laboratorio de Operaciones Unitarias I PRÁCTICA Nº 5. MEDIDORES DE FLUJO PARA FLUIDOS COMPRESIBLES
V B. g (1) V B ) g, (2) +ρ B. =( m H. m H (3) ρ 1. ρ B. Aplicando al aire la ecuación de estado de los gases perfectos, en la forma.
 Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
BALANCE DE MASA Y ENERGÍA EN TUBERIAS Y ACCESORIOS HIDRAULICOS (C206)
 UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE INGENIERIA MECÁNICA AREA DE TERMOFLUIDOS GUIA DE LABORATORIO DE MECANICA DE FLUIDOS BALANCE DE MASA Y ENERGÍA EN TUBERIAS Y ACCESORIOS HIDRAULICOS (C06)
UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE INGENIERIA MECÁNICA AREA DE TERMOFLUIDOS GUIA DE LABORATORIO DE MECANICA DE FLUIDOS BALANCE DE MASA Y ENERGÍA EN TUBERIAS Y ACCESORIOS HIDRAULICOS (C06)
Glosario. Agregación geométrica: modificación de la longitud típica de los planos de escurrimiento con el aumento de escala.
 G.1 Glosario Agregación ( up-scaling ): proceso de pasaje de descripciones de procesos (modelos) o variables de una escala menor a otra mayor (Blöshl et al., 1997). Agregación geométrica: modificación
G.1 Glosario Agregación ( up-scaling ): proceso de pasaje de descripciones de procesos (modelos) o variables de una escala menor a otra mayor (Blöshl et al., 1997). Agregación geométrica: modificación
LISTA DE SÍMBOLOS. Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro
 LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
LISTA DE SÍMBOLOS Capítulo 2 EJEMPLOS Y TEORIA DE LAS VIBRACIONES PARAMÉTRICAS 2.1 Introducción T - Periodo Ω - Frecuencia a- parámetro b- parámetro 2.1.1 Rigidez Flexiva que Difiere en dos Ejes x- Desplazamiento
Anexo1: Ejemplo práctico: Cálculo disipador con ventilación forzada.
 Anexo1. Ejemplo práctico, pg 1 Anexo1: Ejemplo práctico: Cálculo disipador con ventilación forzada. Para clarificar conceptos y ver la verdadera utilidad del asunto, haremos el siguiente ejemplo práctico
Anexo1. Ejemplo práctico, pg 1 Anexo1: Ejemplo práctico: Cálculo disipador con ventilación forzada. Para clarificar conceptos y ver la verdadera utilidad del asunto, haremos el siguiente ejemplo práctico
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
Elementos Uniaxiales Sometidos a Carga Axial Pura
 Elementos Uniaiales Sometidos a Carga ial ura Definición: La Tensión representa la intensidad de las fuerzas internas por unidad de área en diferentes puntos de una sección del sólido aislada (Fig. 1a).
Elementos Uniaiales Sometidos a Carga ial ura Definición: La Tensión representa la intensidad de las fuerzas internas por unidad de área en diferentes puntos de una sección del sólido aislada (Fig. 1a).
4. DISCUSIÓN DE RESULTADOS
 4. DISCUSIÓN DE RESULTADOS 4.1 Revisión bibliográfica La revisión bibliográfica aportó la información, datos y ecuaciones matemáticas para poder tener un punto de partida y sustentar este trabajo con datos
4. DISCUSIÓN DE RESULTADOS 4.1 Revisión bibliográfica La revisión bibliográfica aportó la información, datos y ecuaciones matemáticas para poder tener un punto de partida y sustentar este trabajo con datos
