Forma y simetría. Enseñanza adaptada a personas ciegas a través de los modelos cristalográficos
|
|
|
- José Ángel Cuenca Campos
- hace 7 años
- Vistas:
Transcripción
1 Forma y simetría. Enseñanza adaptada a personas ciegas a través de los modelos cristalográficos Mª Victoria López-Acevedo Cornejo. Juan Carlos Chicote González. Javier Goñi López Departamento de Cristalografía y Mineralogía. Facultad de CC Geológicas. Universidad Complutense. C/ José Antonio Nováis nº Madrid vcornejo@geo.ucm.es jcchicote@yahoo.es correo_javi@hotmail.com Resumen: El presente trabajo constituye un curso completo de Cristalografía Morfológica, adaptado a la enseñanza de personas ciegas. En él se pone de manifiesto el carácter transversal de esta disciplina y sus posibilidades para el desarrollo intelectual y sensitivo de personas con discapacidad visual. La metodología se basa en el reconocimiento háptico de los modelos cristalográficos y es aplicable en Educación Especial. Palabras clave: Forma. Simetría. Personas ciegas. Háptico. Cristalografía Morfológica. INTRODUCCIÓN Y PROGRAMA La palabra cristal se deriva de la palabra griega crystallos que significa hielo y también cristal de roca. En la actualidad, se aplica a la materia sólida que posee una estructura atómica interna ordenada. Sin embargo, considerado exclusivamente desde un punto de vista macroscópico, el cristal se define como un sólido homogéneo que a veces presenta formas poliédricas de gran belleza. El estudio morfológico de estos poliedros tuvo gran importancia en el desarrollo de la Cristalografía, que se inició con la búsqueda de las relaciones geométricas y simétricas que se podían apreciar entre las caras de un cristal. En aquella búsqueda, hubo unos elementos clave que fueron los modelos cristalográficos o réplicas idealizadas de dichos poliedros, realizadas en cerámica, madera o vidrio, que facilitaron las medidas y observaciones necesarias para solucionar las incógnitas planteadas (Fig. 1). En otro orden de cosas, la geometría es posiblemente uno de los temas de estudio que más se utilizan para la educación de personas ciegas o con discapacidad visual, ya que resulta casi imprescindible para la adecuada construcción mental de sus representaciones espaciales. En este sentido, se ha diseñado el presente curso, que se 1
2 centra en la adquisición del conocimiento de la forma y la simetría, a través de la percepción táctil de los modelos cristalográficos descritos. Estos modelos, conocidos familiarmente como tarugos, se emplean tradicionalmente para el estudio y la enseñanza de la forma y la simetría de los cristales. La gran variedad de modelos disponibles y además, la posibilidad de clasificarlos en unos pocos grupos, según criterios perfectamente definidos y reconocibles, contribuyen a enriquecer y ampliar, casi exponencialmente, las oportunidades de aprendizaje en este terreno. De esta manera, se pone de manifiesto el carácter interdisciplinar de la Cristalografía, que cruza sus tradicionales límites de conocimiento, para adentrarse en otros campos de estudio, como es la Educación y más concretamente la Educación Especial, transfiriendo sus métodos y proporcionando, en este caso, nuevos recursos para el aprendizaje de personas ciegas o con discapacidad visual y que puede tener incidencia en diversas materias relacionadas con el arte o las ciencias en general. Figura 1. Ejemplares de la colección de modelos cristalográficos (Foto: Natalie Paco). El programa del curso consta de los siguientes capítulos: 1. Historia. Elementos de la cristalografía morfológica 2. Las formas cristalinas: sus nombres. 3. Sistemas de referencia: cruces axiales. Los siete sistemas cristalinos. Particularidades del sistema hexagonal. 4. Concepto de simetría: elementos de simetría. 5. Simetría de rotación y de reflexión: planos y ejes. 6. La inversión: el centro de inversión. 7. Lo más difícil: los ejes de inversión. 8. Sistemas y simetría: características simétricas de los sistemas cristalinos. 9. Las 32 clases de simetría. 10. Descripción de los modelos cristalográficos: pasos a seguir. 2
3 En todos los capítulos se incluye un apartado de prácticas, relacionadas con el tema tratado, en el que se describen los materiales y las actividades necesarias para su ejecución. Los modelos cristalográficos de las fotografías que ilustran este curso pertenecen a la colección del Departamento de Cristalografía y Mineralogía de la Facultad de CC Geológicas de la Universidad Complutense de Madrid. Las fotografías han sido tomadas por Pablo Marro (portada), Natalie Paco y Mª Victoria López - Acevedo. La narración ha sido hecha por Mª Victoria López - Acevedo. Historia HISTORIA. ELEMENTOS DE LA CRISTALOGRAFÍA MORFOLÓGICA La Cristalografía Morfológica o Cristalografía Clásica, como también se denomina, se inserta en un área de conocimiento muy amplia, que se ocupa de estudiar la compleja organización de las partículas atómicas que constituyen la materia cristalina, así como de todas las propiedades y utilidades que se derivan de ella. Este orden, casi invisible, tiene sin embargo una manifestación macroscópica muy directa: efectivamente, las bellas formas poliédricas que a menudo presentan los minerales (que son cristales naturales) son el reflejo de dicha organización interna y, muy posiblemente, fueron estas formas y la fascinación que ejercieron en los primeros científicos, las responsables del nacimiento de esta ciencia. Uno de los principales objetivos de aquellos primeros científicos, estudiosos de los cristales, era encontrar explicaciones para esas morfologías tan regulares y simétricas. Esto exigía describir y representar el mayor número posible de ellas, sin embargo, los ejemplares naturales completos, bien cristalizados y de buen tamaño, son relativamente escasos. Por esta razón, se les ocurrió realizar modelos artificiales, grandes e idealizados, que facilitaran las medidas y comprobaciones, necesarias para establecer las primeras leyes cristalográficas y encontrar las explicaciones que buscaban. Las primeras colecciones de modelos que se hicieron, fueron diseñadas por Jean Baptiste Romé de L Isle, Moldeados a mano, con arcilla que después cocía en un horno, estos modelos destacan por su valor estético y sobre todo por su gran interés para la Historia de la Cristalografía (Fig. 2). Sin embargo, desde el punto de vista docente, fueron más interesantes unas réplicas de madera, ideadas por el abate Haüy, , y comercializadas posteriormente por la firma alemana Krantz que, a finales del siglo 19, diseñó alrededor de 900 prototipos que han servido de base para la enseñanza de la cristalografía en todo el mundo, hasta el día de hoy. Estos modelos de madera se conocen familiarmente como los tarugos y constituyen un material didáctico excepcional para el estudio de las formas y la simetría (Fig. 3). 3
4 Figura 2. Modelos de arcilla (Romé de L Isle, XVIII) que simulan cristales cúbicos. Figura 3. Retrato de Haüy y algunos de sus modelos de madera (Musée de Minéralogie. Ecole des Mines de Paris). Elementos de la cristalografía morfológica Apoyándose en estos modelos, cristalógrafos y mineralogistas, fueron desarrollando una teoría de la simetría, respaldada por un imponente soporte matemático, descubrieron que no todos los cristales se ajustan bien a un sistema de ejes cartesiano ortogonal, sino que existen hasta siete sistemas de ejes de referencia 4
5 diferentes, idearon unos índices para relacionar las caras cristalinas con sus correspondientes ejes y finalmente, asignaron un nombre específico a cada forma o grupo de formas que identificaban en los poliedros. Estos elementos que se vienen utilizando desde entonces para describir las morfologías de los poliedros cristalinos, se pueden concretar en: Unos elementos de simetría que se agrupan en 32 clases de simetría. Unos ejes de referencia o cruz axial. Existen siete cruces axiales o siete sistemas cristalinos. Un nombre específico para cada forma o grupo de formas que constituyen los poliedros cristalinos. Unos índices para denominar caras y direcciones, que fueron bautizados con el nombre de los científicos que los idearon: Weiss y Miller. De esta manera, la Cristalografía Morfológica quedó consagrada definitivamente como la ciencia del orden y la simetría y los modelos cristalográficos como las herramientas que lo habían hecho posible. Forma y simetría: introducción e historia. Prácticas Con el fin de complementar la visión histórica que se ha dado acerca del origen de los modelos cristalográficos que van a servir de base para este curso, así como introducir y fomentar el interés por la forma, su abstracción y su comprensión espacial, se sugieren dos tipos de actividades: 1. Visita al Museo Geominero del Instituto Geológico y Minero de España (IGME. Calle Ríos Rosas, 23. Madrid) donde tienen una guía en Braille, para que las personas ciegas puedan hacer un recorrido táctil por el museo. Este recorrido consta de numerosos ejemplares de minerales y fósiles, todos ellos con su etiqueta en Braille, que se pueden tocar, comprobando propiedades como dureza, temperatura o densidad, y disfrutando de su belleza geométrica. 2. Visita al Museo Tiflológico de la Organización Nacional de Ciegos Españoles (ONCE. Calle La Coruña, 18. Madrid) donde se pueden tocar obras artísticas y material tiflológico perceptible a través del tacto, entre el que destacan las maquetas de algunos símbolos de la arquitectura e ingeniería mundial, como la torre Eiffel o la Alambra, entre otros. 5
6 FORMAS CRISTALINAS: SUS NOMBRES Uno de los elementos más importantes que sirvieron de base para las primeras descripciones morfológicas de los cristales fueron los nombres de los poliedros y demás formas geométricas que se reconocían en ellos. Estos nombres, la mayoría de origen griego o latino, con algunas modificaciones, se utilizan actualmente para designar a las formas cristalinas, que se definen como conjuntos de caras que están relacionadas por su simetría. La mayoría de estas formas corresponden a figuras geométricas, conocidas por todos y de muy fácil comprensión, por lo que vamos a describirlas, aunque aún no se haya iniciado el estudio de la simetría, ya que su conocimiento resulta casi imprescindible, a la hora de trabajar rigurosamente con los modelos cristalográficos. Estas formas cristalinas pueden ser abiertas, cuando no encierran un espacio, y cerradas cuando si lo encierran. Entre las formas abiertas se tienen: La pirámide que está constituida por un conjunto de caras triangulares, idénticas, unidas en un vértice común. Para cerrar la pirámide es necesaria otra forma. Lo más simple es hacerlo con una base. Esta base se considera otra forma cristalina abierta. Se trata de una cara aislada sin equivalente por simetría y se denomina pedión (que podría derivar del griego pedion que significa plano, o también del latín pedis que significa pie). El prisma está constituido por un conjunto de caras paralelas e idénticas, con forma rectangular. Para cerrar el prisma es necesaria otra forma. Lo más simple es hacerlo con dos polígonos iguales y paralelos o bases. Estas bases o pareja de caras paralelas, se consideran otra forma cristalina abierta que se denomina pinacoide (que podría derivar del griego pinakes que significa tablillas). El domo y el esfenoide son dos formas abiertas consistentes en dos caras no paralelas. La diferencia entre una y otra está en el elemento de simetría que las relaciona (un plano o un eje, respectivamente). Cuando aparecen en los poliedros cristalinos (obviamente combinadas con otras) se pueden distinguir por su apariencia: Si recuerdan al tejado de una casa, se tratará del domo (que etimológicamente significa casa, derivado del latín domus ) y si recuerdan a una cuña, se tratará del esfenoide (que etimológicamente significa cuña, del griego esfen ). 6
7 Entre las formas cerradas se tienen: Escalenoedro. poliedro formado por caras idénticas, que tienen forma de triángulo escaleno. Los hay de 8 y 12 caras. Trapezoedro. poliedro formado por caras idénticas, que tienen forma de trapezoide. Los hay de 6, 8 y 12 caras. (Recordar que un trapezoide es un cuadrángulo tal que ninguno de sus cuatro lados es paralelo a otro). Romboedro. poliedro formado por caras idénticas, que tienen forma de rombo. Tiene 6 caras. Las formas del sistema cúbico son todas cerradas y tienen nombres especiales. Algunas de éstas son las siguientes: Cubo o hexaedro. 6 caras cuadradas idénticas. Octaedro. 8 caras idénticas, con forma de triángulo equilátero. Rombododecaedro. 12 caras idénticas, con forma de rombo. Tetraedro. 4 caras idénticas, con forma de triángulo equilátero. Dodecaedro trapezoidal. 12 caras idénticas, con forma de trapezoide. Dodecaedro pentagonal o piritoedro. 12 caras idénticas, con forma pentagonal. El mineral pirita adopta esta forma con mucha frecuencia. Icosaedro. 20 caras idénticas, con forma de triángulo equilátero. Todas las formas descritas hasta el momento, ya sean abiertas o cerradas, se consideran formas simples. En los poliedros cristalinos, éstas pueden aparecer aisladas (solo en el caso de las cerradas) o combinadas con otras, en cuyo caso se habla de formas compuestas. Algunas de las más comunes son: Pirámide y pedión. Dos o más pirámides y pedión. Bipirámide que son dos pirámides unidas por la base. Prisma y pinacoide. Dos o más prismas y pinacoide. Prisma y bipirámide. Prisma y romboedro. Biesfenoide que son dos esfenoides interpenetrados, una auténtica cuña!. Etc. Las formas cúbicas también pueden combinarse entre ellas. Por ejemplo: Cubo y octaedro dan un cubo de vértices truncados. Dos tetraedros dan un tetraedro de vértices truncados. 7
8 Finalmente, aunque el estudio de los Sistemas Cristalinos no se ha iniciado aún, es importante adelantar que la única restricción que limita estas combinaciones, es que siempre se realizan entre formas pertenecientes al mismo Sistema Cristalino. Prácticas con las formas cristalinas. Materiales y actividades Modelos cristalográficos de cartulina: Envases de medicamentos, cajas de cerillas o cucuruchos doblados longitudinalmente en tres, cuatro o seis partes iguales, pueden servir para estudiar y entender las formas abiertas y las compuestas: Un envase prismático de sección cuadrada, al que se le hayan recortado las solapas, será un buen ejemplo de prisma. Las solapas recortadas serán el pinacoide. Una caja de cerillas será una combinación de tres pinacoides. Si extraemos el cajoncito de las cerillas nos quedan dos pinacoides, el correspondiente al rascador y el grande. Ambos modelos (envase y caja de cerillas) son muy útiles para diferenciar entre un verdadero prisma, en el que todas sus caras son idénticas (el envase) y la combinación de pinacoides, donde las caras son iguales dos a dos (la caja de cerillas). El cucurucho plegado es una pirámide. Si queremos cerrarla con una base plana, esta sería el pedión, mientras que si la cerramos con otra pirámide igual, tendremos una bipirámide, etc. En el mercado se pueden conseguir colecciones de modelos cristalográficos recortables, similares a los ejemplares que se muestran en las figuras 4 a 6, que pueden servir para construir las formas descritas. Tarugos: Colección de tarugos en los que se identifiquen las diferentes formas cristalinas estudiadas, (Figs. 6 a 14). 8
9 Figura 4. Prisma trigonal y pinacoide. 9
10 Figura 5. Pirámide trigonal. 10
11 Figura 6.- Pirámide tetragonal y pedión. 11
12 Figura 7. Colecciones de formas hexagonales: bipirámides, prismas con bipirámide y prismas con bipirámide y pinacoide que trunca los vértices de las bipirámides (Foto: Natalie Paco). Figura 8. Colecciones de formas tetragonales: Prismas y pinacoide, bipirámides truncadas por un pedión, prismas con biesfenoide, biesfenoides, pinacoides, bipirámides, etc. (Foto: Natalie Paco). 12
13 Figura 9. Colección de pinacoides y prismas (Foto: Natalie Paco). Figura 10. Domo y otras formas (Foto: Natalie Paco). 13
14 Figura 11. Colección de formas cúbicas: cubos, cubos con octaedro, octaedros, etc. (Foto: Natalie Paco). Figura 12. Colección de formas cúbicas: pentagonododecaedros o piritoedros. Dos tetraedros. Tetraedros (Foto: Natalie Paco). 14
15 Figura 13. Colección de formas romboédricas, realizadas en madera de roble: romboedros con prisma, romboedro con prisma y pinacoide, romboedros alargados, simple y con aristas biseladas. Escalenoedro con prisma y pinacoide. Trapezoedro (Foto: Natalie Paco). Figura 14. Dodecaedros trapezoidales cúbicos (Foto: Natalie Paco). 15
16 SISTEMAS DE REFERENCIA: CRUCES AXIALES La cruz axial es un sistema de ejes a, b y c que sirven de referencia para situar las caras, aristas, vértices y elementos de simetría del cristal. Se supone que se cortan en su centro geométrico y que están limitados por caras, aristas o vértices importantes del mismo. Estos ejes no tienen siempre que ser perpendiculares entre sí (cartesianos), sino que hay otras relaciones angulares más acordes con las diferentes formas cristalinas existentes. Se denomina alfa al ángulo que forman los ejes b y c, beta al que forman a y c, y gamma al que forman a y b. De hecho, se consideran siete sistemas de ejes de referencia o siete cruces axiales, caracterizados por unas relaciones angulares y de longitud específicas. Estas diferentes cruces constituyen los siete sistemas cristalinos que se describen a continuación (Fig. 15): Triclínico a distinto de b distinto de c y alfa distinto de beta distinto de gamma y distintos de 90 grados. Monoclínico a distinto de b distinto de c y alfa igual gamma igual a 90 grados y beta distinto de 90 grados. Ortorrómbico o rómbico a distinto de b distinto de c y alfa igual beta igual gamma igual a 90 grados. Tetragonal a igual b distinto de c y alfa igual beta igual gamma igual a 90 grados. Cúbico, isométrico o regular a igual b igual c y alfa igual beta igual gamma igual a 90 grados. Hexagonal a igual b distinto de c y alfa igual beta igual a 90 grados y gamma igual a 120 grados. 16
17 Trigonal o romboédrico a igual b igual c y alfa igual beta igual gamma distintos de 90 grados. Cruz triclínica a c b a c Cruz monoclínica Cruz rómbica b c a b Figura 15. Modelos de cruces axiales realizados en metal. La posición de los ejes a, b y c está marcada en triclínica, monoclínica y rómbica. Los cristales siempre van a pertenecer a alguno de estos sistemas. Para elegir la cruz más adecuada a un determinado poliedro cristalino, se pueden seguir tres vías (dependiendo del caso): 1ª Tomarla paralela a aristas reales o posibles, que se corten en un vértice también real o posible (una arista posible sería una arista biselada y un vértice posible sería un vértice truncado). 2ª Tomarla paralela a las perpendiculares a las caras mejor desarrolladas. 3ª Hacerla coincidir con sus elementos de simetría más importantes: cada uno de estos sistemas, además de estas relaciones angulares y de longitud, se caracterizan por una simetría específica, que se verá en el capítulo de simetría. Finalmente, para orientar correctamente el poliedro que vamos a estudiar, se toma el eje c vertical frente a nosotros, la parte positiva hacia arriba y la negativa hacia abajo, el eje b horizontal frente a nosotros, la parte positiva a nuestra derecha y la negativa a nuestra izquierda y el eje a apuntando directamente a nosotros, la parte positiva hacia nosotros y la negativa en la dirección opuesta. Y con respecto a los ángulos, el ángulo alfa (definido por b y c) es el que se opone al eje a, el ángulo beta 17
18 (definido por a y c) es el que se opone al eje b y el ángulo gamma (definido por a y b) es el que se opone al eje c. Particularidades del sistema hexagonal Para facilitar el trabajo y los cálculos que se realizan con el sistema hexagonal, se suele utilizar un cuarto eje, denominado i (latina y minúscula). Este eje i es coplanario con a y b y forma un ángulo de 120 grados con cada uno de ellos. Es decir, la cruz axial hexagonal quedaría ligeramente modificada: a igual b igual i distinto de c y alfa igual beta igual a 90 grados y gamma igual a 120 grados (Fig. 16). c i a b a a Figura 16. Cruz axial hexagonal. Está marcada la posición de los ejes a, b, i y c. Al orientar una cruz hexagonal frente a nosotros debemos tener en cuenta que el eje i tendrá su parte negativa apuntando hacia nosotros (situada entre a y b positivos) y su parte positiva en la dirección opuesta. Por último, debes saber que esta cruz hexagonal, se suele utilizar también para trabajar con el sistema Trigonal o Romboédrico, porque resulta mucho más operativa que la suya propia. Recomendaciones: Para recordar el nombre y las características de cada sistema, es muy útil conocer su etimología y significado: 18
19 Clino: inclinado. Triclínico: triplemente inclinado. Monoclínico: un ángulo NO es recto. Orto: cualidad de recto, perpendicular. Ortorrómbico: se refiere a un prisma recto de sección rómbica. Un prisma recto se podrá mantener perpendicular sobre una superficie plana. Los paralelepípedos ortorrómbicos se mantienen así sobre una superficie plana. Por el contrario, los monoclínicos parecen inclinarse hacia atrás (o hacia delante) y los triclínicos además, se inclinan hacia un lado. Gono: ángulo. Tetragonal: cuatro ángulos. Hexagonal : seis ángulos. Trigonal: tres ángulos. Edron: cara. Romboédrico: es otra denominación del sistema trigonal. Se refiere a la forma más característica del sistema, el romboedro, que es un poliedro que tiene todas sus caras en forma de rombo. Cubicus: cúbico. Se refiere a la forma más característica del sistema, el cubo, que es uno de los cinco sólidos platónicos. Iso-métricus: igual medida El sistema isométrico (cúbico y regular) se caracteriza por tres ejes de la misma longitud. 1. Regularis: regular. Se refiere a un poliedro cuyas caras y ángulos sólidos son iguales. El cubo (cúbico e isométrico) es un gran ejemplo de poliedro regular. Materiales. PRÁCTICAS CON LAS CRUCES AXIALES Modelos tridimensionales de las siete cruces axiales (Fig. 17): se pueden realizar fácilmente con palillos largos (como los que se utilizan en la cocina para preparar pinchos morunos), insertados en una bola de plastelina. 19
20 Figura 17. Modelos de cruces axiales triclínica (izqda.), rómbica (centro) y hexagonal (dcha.). Realizados en metal. También se puede utilizar, en lugar de la plastelina, alguna arcilla polimérica que aunque requiere algo más de elaboración, pues hay que endurecerla en un horno, resulta más resistente y duradera. Pequeños alicates de corte. Tarugos o paralelepípedos característicos de los siete Sistemas Cristalinos: combinaciones de tres pinacoides para triclínico, monoclínico y rómbico (son paralelepípedos, que recuerdan a cajas de cerillas, triplemente inclinados, inclinados y rectos, respectivamente). Prismas para tetragonal y hexagonal (son prismas rectos de sección cuadrada y hexagonal, respectivamente). Cubo para el cúbico. Romboedros alargado y aplastado para el romboédrico (Fig. 18). Figura 18. Tarugos de madera. Primera fila, de dcha. a izada.: prismas tetragonal y hexagonal. Segunda fila: pinacoides (rómbico, monoclínico y triclínico). Tercera fila: tres romboedros (aplastado, intermedio y alargado) y cubo. 20
21 Prismas ortorrómbico y clinorrómbico (son prismas de sección rómbica, recto e inclinado, respectivamente) (Fig. 19). Figura 19. Prismas ortorrómbico (dcha.) y clinorrómbico (izada.). Los ejes de la cruz axial están marcados con chinchetas corcheteras. Prisma hexagonal con romboedro inscrito en su interior y romboedro (el prisma está dividido en dos mitades. Al separarlas deja ver en su interior un molde hueco con forma de romboedro, en el que se puede encajar este) (figura 20 A, B). Figura 20. A. Prisma hexagonal y romboedro. B. El romboedro queda inscrito en el prisma hexagonal. Se comprueba la compatibilidad entre las dos cruces axiales. Con cinta adhesiva en las aristas correspondientes se indica la posición de los ejes a, b y c. Con chinchetas corcheteras se marcan las entradas de los ejes que se van a cortar en el interior del prisma hexagonal (y de los prismas ortorrómbico y clinorrómbico). Con pegatinas escritas en Braille se indica la posición de los ángulos alfa (con una a), beta (con una b) y gamma (con una g). 21
22 Actividades. Se sugieren dos tipos de actividades: 1. Reconocimiento directo de las siete cruces axiales Reconocer las diferentes cruces axiales en modelos preparados previamente por el profesor (o el alumno prepara sus propias cruces): Para preparar las cruces se toman grupos de tres palillos que serán los ejes a, b y c, respectivamente. Estos se cortan con los alicates, para que tengan las longitudes requeridas por la cruz axial que se esté fabricando. Por ejemplo, todos de longitudes diferentes en el caso del triclínico, donde a, b y c son diferentes. Una vez cortados se irán insertando en una bola de plastelina o de la pasta de moldear que se vaya a utilizar. La bola debe quedar situada en el punto medio de cada uno de los ejes. Al insertarlos, iremos teniendo en cuenta las relaciones angulares requeridas por la cruz axial que se esté fabricando. Por ejemplo, para el triclínico, primero insertaremos vertical el palillo correspondiente al eje c. Después insertaremos el b, horizontal pero sin formar un ángulo de 90 grados con el palillo c. Y finalmente insertaremos el palillo a, apuntando hacia nosotros y de manera que tampoco forme un ángulo de 90 grados con b ni con c. Estas cruces se pueden mantener de pie si se insertan, por ejemplo, en una pequeña pirámide de plastelina, que actúe como base. 2. Relacionar las cruces axiales con los diferentes tarugos Localizar las siete cruces axiales en diferentes paralelepípedos. En unos casos se reconocen coincidiendo con las aristas más importantes y en otros (prisma hexagonal) se adivinan en el interior de la figura, cortándose en su centro geométrico. Orientar las cruces correctamente. Comparar las distintas posiciones que adoptan estos poliedros al situarlos sobre una superficie plana (los que tienen su eje c formando 90 grados con los otros ejes (a y b) quedan perpendiculares a ella y los que forman un ángulo distinto 22
23 de 90 grados quedan inclinados, estos últimos llevan en su denominación el prefijo clino ). Por ejemplo, las combinaciones de pinacoides en los sistemas ortorrómbico, monoclínico y triclínico, recuerdan a cajas de cerillas que se mantienen rectas en el caso del rómbico, se inclinan hacia atrás en el monoclínico y hacia atrás y hacia un lado en el triclínico. Relacionar el nombre de cada sistema con su etimología y tratar de asociarlo a la forma de los paralelepípedos y demás poliedros representativos. Reconocer un verdadero prisma ortorrómbico, de sección rómbica, y adivinar su cruz axial en el interior, cortándose en su centro geométrico. Compararlo con el prisma clinorrómbico (según lo que hemos estudiado hasta ahora, este prisma clinorrómbico pertenecería al sistema monoclínico). Reconocer y comparar el cubo y el romboedro. Finalmente, relacionar las cruces hexagonal y romboédrica, jugando con el prisma hexagonal y su romboedro inscrito. CONCEPTO DE SIMETRÍA: ELEMENTOS DE SIMETRÍA Antes de iniciar este capítulo, conviene recordar lo que se entiende intuitivamente por simetría: nuestro cuerpo, nuestras manos y en general, la mayor parte de los objetos que nos rodean son simétricos, constan de dos o más porciones idénticas, relacionadas entre si por una determinada operación. Por ejemplo, nuestro cuerpo está formado, idealmente, por dos mitades idénticas, cada mitad es el reflejo de la otra mitad. Si suponemos un plano que separe estas dos mitades, resulta que cada porción situada en un lado de dicho plano tiene su imagen simétrica situada al otro lado, exactamente a la misma distancia de él: las dos orejas, los dos ojos, los dos pies, etc. La operación en este caso es la reflexión y el operador que la realiza es ese plano que ha dividido nuestro cuerpo en dos mitades. El concepto de reflexión está interiorizado en las personas que utilizan pauta y punzón para escribir las letras en Braille: las letras se escriben al clavar el punzón en el reverso del papel, usando una pauta o regleta dividida en cajetines, cada uno de los cuales consta de una matriz de seis puntos (que es el signo generador y permite desarrollar 64 caracteres diferentes). Es decir, las letras se escriben en bajo relieve y además, de derecha a izquierda, resultando unos puntos (letras) en alto relieve, sobre el anverso del papel, que se leen de izquierda a derecha. Ambas cosas, letras inscritas (de derecha a izquierda) y letras leídas (de izquierda a derecha) tienen simetría especular. 23
24 Finalmente, la huella que nuestro dedo percibe al leer el documento Braille, es la imagen especular de lo que está escrito, huella y escrito son simétricos por un plano de reflexión que actúa como un espejo, que estaría situado entre el dedo y el documento. Está propiedad, la simetría, es también la propiedad más importante del medio cristalino, por lo que no es de extrañar que los cristales constituyan, en conjunto, uno de los ejemplos de simetría más variados, completos y mejor estudiados que existen. Recordemos aquí que dicha cualidad, era uno de los cuatro pilares en los que se apoyaba la Cristalografía Morfológica. Los poliedros cristalinos, presentan externamente una simetría que se describe en función de unos elementos u operadores) de simetría. Estos elementos hacen coincidir puntos homólogos del cristal, caras, aristas, etc. mediante una operación de simetría. Estos elementos y las operaciones que realizan son los siguientes: Planos. Realizan la reflexión. Ejes. Realizan la operación del giro. Centro. Realizan la inversión. A veces, los elementos se asocian y realizan operaciones mixtas, por ejemplo los: Ejes de inversión que combinan giro e inversión. CONCEPTO DE SIMETRÍA. PRÁCTICAS Como actividad complementaria en este capítulo de introducción a la simetría, se sugiere una reflexión acerca de las características simétricas de los objetos que nos rodean: al hacerlo, nos daremos cuenta inmediatamente de que hay muy pocos objetos que sean asimétricos. La mayoría son simétricos y entre ellos, lo dominante es la simetría por reflexión. Casi todas las cosas, objetos e incluso animales de nuestro entorno, presentan simetría especular. Materiales y actividades Una práctica interesante consistiría en buscar ejemplos de "cosas" asimétricas, frente a otras simétricas y entre estas últimas, intentar dilucidar si solo tienen un único plano de reflexión o si por el contrario, se adivina en ellas un grado mayor de simetría, como dos o más planos, o una simetría diferente de la especular. Por ejemplo, se podrían utilizar las fichas de un dominó como material de trabajo en este caso. Si nos fijamos en la disposición de los puntos que indican su valor, que suelen estar en bajorrelieve, comprobaremos que se trata de una colección 24
25 excepcional, en la que se reúnen todas las distribuciones que hemos citado. Así, entre sus 28 fichas, hay: 11 completamente asimétricas. 10 con un único plano de reflexión que las divide longitudinalmente. 5 que tienen dos planos de reflexión perpendiculares entre si, que las dividen transversal y longitudinalmente. Estas últimas son algunas de las denominadas dobles. Finalmente, quedan el dos y el tres doble, en las que se adivina simetría, pero de otro tipo. En este caso, no se trata de simetría especular, sino de rotación. En ellas, el grupo de dos o tres puntos que está situado en una mitad de la ficha, se repite en la otra mitad, gracias a un giro de 180 grados, alrededor de un imaginario eje, que se supone perpendicular a la ficha, clavado en su punto medio exactamente. Esta operación del giro se estudiará con más detalle en el capítulo siguiente. Planos SIMETRÍA DE ROTACIÓN Y DE REFLEXIÓN: PLANOS Y EJES Su funcionamiento se ha descrito al iniciar el apartado de simetría, en los ejemplos. La operación que realizan se denomina reflexión. Los podemos tomar como planos imaginarios que dividen a los poliedros en dos mitades idénticas. Estas dos mitades, simétricas por reflexión, se dice que son enantiomorfas o formas opuestas (de enantios que significa opuesto), es decir que, aunque son idénticas no se pueden superponer (pensemos en nuestras manos que son simétricas por reflexión. Si se superponen no coinciden y para que coincidan, se tienen que situar palma contra palma o dorso contra dorso). Los planos se indican con la letra m (minúscula) y gráficamente se representan mediante una línea continua. Ejes de Rotación (también se denominan Ejes Propios) Para entender su funcionamiento, podemos pensar en los mismos molinos de viento que Don Quijote veía como peligrosos gigantes. Las aspas de estos molinos, consistentes en cuatro paletas idénticas dispuestas en torno a un eje, son un claro ejemplo de simetría de rotación. Efectivamente, dicho eje actúa como un eje cuaternario, que repite la paleta cada 90 grados, un total de cuatro veces en un giro completo de 360 grados. 25
26 En el caso de los poliedros cristalinos los podemos tomar como ejes imaginarios que atraviesan dichos poliedros y que los hacen girar 360 grados, repitiendo a intervalos iguales, sus caras, aristas y vértices. El número de intervalos indica el orden del eje: Por ejemplo, si la repetición se produce cuatro veces (como en las aspas del molino de viento), el orden del eje será 4, además como los intervalos deben ser iguales, tendremos que dicha repetición tendrá lugar cada 90 grados (360 grados partido 4). Nótese que el cuarto giro lleva a coincidir el elemento que está girando, cara, arista o vértice, con el elemento de partida. A este eje de orden 4, también se le llama cuaternario y se representa gráficamente mediante un cuadrado. Resumen: eje cuaternario o de orden 4, se representa gráficamente mediante un cuadrado y repite las caras, aristas y vértices del cristal cuatro veces, cada 90 grados, hasta completar un giro de 360 grados. La materia cristalina presenta estos ejes de orden 4 o cuaternarios que acabamos de estudiar y además, puede presentar ejes de orden seis, tres, dos y uno, que reciben el nombre de senario, ternario, binario y monario, respectivamente. Está claro que dividiendo 360 grados por el orden del eje, calculamos el número de grados que corresponde a cada intervalo de repetición, así que estos ejes van a repetir los elementos del cristal, caras, aristas y vértices, cada 60 grados, 120 grados, 180 grados y 360 grados, respectivamente. Resumen: Eje senario o de orden 6, se representa gráficamente mediante un hexágono y repite las caras, aristas y vértices del cristal seis veces, cada 60 grados, hasta completar un giro de 360 grados. Eje ternario o de orden 3, se representa gráficamente mediante un triángulo y repite las caras, aristas y vértices del cristal tres veces, cada 120 grados, hasta completar un giro de 360 grados. Eje binario o de orden 2, se representa gráficamente mediante una elipse y repite las caras, aristas y vértices del cristal dos veces, cada 180 grados, hasta completar un giro de 360 grados. Eje monario o de orden 1. Lleva a la identidad después de un único giro de 360 grados (nuestro cuerpo está atravesado por un eje monario que después de hacernos dar una vuelta completa, nos deja igual que estábamos antes de darla). El orden de los ejes, en general, se expresa mediante la letra n (minúscula). Nota aclaratoria. Es posible que en este punto, alguien se haya preguntado por 26
27 qué no se habla de ejes de orden 5 o de orden mayor que 6. La razón es que la simetría que presenta externamente un poliedro cristalino, es un reflejo de la simetría con que se distribuyen las partículas materiales (átomos, iones o moléculas) que constituyen su estructura interna. Dicha distribución tiene un carácter periódico, es decir, que esas partículas materiales, con su simetría específica, se repiten paralelamente a sí mismas, rellenando completamente el espacio cristalino. Para comprender que esta repetición es incompatible con la presencia de dichos ejes, podemos intentar cubrir una superficie plana, a base de acoplar pentágonos, heptágonos u octógonos, paralelamente a sí mismos. Comprobaremos que es imposible hacerlo pues siempre quedarán huecos sin cubrir. Sin embargo, esto no significa que no exista esta simetría en otro tipo de medios. Por ejemplo, la simetría pentagonal, es relativamente frecuente en los seres vivos, como los erizos o las estrellas de mar. Materiales PRÁCTICAS CON PLANOS Y EJES Objetos para estudiar el funcionamiento de planos y ejes. Colecciones de: 1. Formas idénticas (de 2 a 6 piezas), preferiblemente asimétricas y con cierto volumen para que sean fácilmente identificables al tacto. Ej. Flechas, notas musicales, pequeños juguetes (soldaditos, etc), figuras de ajedrez, etc. 2. Figuras geométricas que incluyan un hexágono, un cuadrado, un triángulo equilátero, una elipse y una esferita. Todas ellas con cierto volumen, para que sean fácilmente identificables al tacto. En el mercado hay una amplia gama de juegos magnéticos, que ofrecen desde piezas variadísimas, pensadas para construir todo tipo de formas y figuras geométricas, hasta otras más específicas como las del ajedrez y similares. Además de su versatilidad, tienen la ventaja de que permiten construcciones relativamente estables, que se pueden retocar y revisar tantas veces como sea necesario, así como disfrutar del resultado final, sin temor a descolocarlas. Además son necesarios una regla, varita o lapicero y un molinillo de viento. 27
28 Modelos cristalográficos Colección de tarugos sencillos: combinaciones de tres pinacoides para triclínico, monoclínico y rómbico. Prismas para tetragonal y hexagonal. Cubo para el cúbico. Romboedros alargado y aplastado para el romboédrico (Fig. 18). Prismas ortorrómbico y clinorrómbico (Fig. 19). Otros tarugos más complejos (Fig. 21). Airón-fix de terciopelo, para indicar la posición de ejes y planos en los tarugos más representativos. Actividades Figura 21. Modelos cristalográficos (Foto: Natalie Paco). Se sugieren dos tipos de actividades: 1. Simulación del funcionamiento de planos y ejes Se sitúa la regla sobre una mesa, apuntando hacia nosotros. Se supone que debe actuar como un plano de reflexión. A continuación, se colocan nuestras manos sobre la mesa, con las palmas hacia abajo, a ambos lados de la regla y a la misma distancia de ella. Esta disposición constituye un claro ejemplo de simetría especular. 28
29 Después de entender el ejemplo, se toman parejas de figuras idénticas y se sitúan a ambos lados de dicha regla, de manera que entre ellas también exista la misma simetría especular. Por ejemplo, los caballos del ajedrez quedarán enfrentados, mirándose, o bien de perfil, mirando los dos en la misma dirección, o enfadados, dándose la espalda (Fig. 22). Figura 22. Simetría especular entre dos caballos de ajedrez. Se sopla el molinillo de viento para que gire. Este molinillo actúa como lo haría un eje de rotación. Los molinillos más comunes tienen cuatro o seis aspas, que serían un eje cuaternario y senario, respectivamente. Se elige alguna figura geométrica y se sitúa sobre la superficie. Se puede construir con las piezas del juego magnético. Esta figura representa un eje de rotación que se supone perpendicular a dicha superficie. Por ejemplo, la elipse representa al eje binario, que gira dos veces, 180 grados cada vez. A continuación se elige una pareja de figuras idénticas, como los dos caballos del ajedrez. Uno se sitúa en contacto con el binario y se deja allí, mientras que el otro, partiendo de la misma posición que el primero, se hace girar 180 grados sobre la superficie de la mesa, en torno al binario. Los dos caballos quedarán diametralmente opuestos y su hocico indicará el sentido del giro (habitualmente se gira en sentido antihorario). 29
30 Finalmente, se compara la diferencia entre las posiciones de los dos caballos relacionados por el plano de reflexión y los dos relacionados por el eje binario. Este mismo ejercicio se realiza con los otros ejes, construyendo las figuras correspondientes en cada caso, y haciendo girar en torno a ellos las formas que se tienen, incluyendo las propias piezas del juego, etc. La esferita representa al eje monario (Fig. 23). Figura 23.- Diferentes etapas en la operación de los ejes ternario, cuaternario y senario. Abajo a la derecha, se tiene la operación completa. Realizado con un juego magnético. 30
31 2. Reconocer ejes y planos en los tarugos Reconocer los ejes y planos marcados con terciopelo en los tarugos sencillos (fig. 24). Figura 24. Tarugos sencillos. Delante, de izqda. a dcha. Pinacoides (triclinico, rómbico y monoclínico) y prisma tetragonal. Detrás prisma trigonal, trapezoedro trigonal y prisma hexagonal. Con sus principales elementos de simetría marcados con terciopelo. Relacionar las morfologías del cubo y el romboedro (utilizar los dos tipos de romboedros, alargado y aplastado). Reconocer el eje ternario en los tres casos: en los romboedros alargados, dicho eje está definido por los vértices en los que se juntan tres ángulos agudos, en los aplastados está definido por los vértices en los que se juntan tres obtusos y en el cubo, los tres ángulos son de 90 grados. Comprobar que en el cubo se reconocen cuatro ejes ternarios en total (mientras que en los romboedros solo hay uno). Reconocer ejes y planos en los tarugos más complejos. LA INVERSIÓN: EL CENTRO DE INVERSIÓN La operación que realiza se denomina inversión y consiste en que cambia el signo de las coordenadas de un punto. Por ejemplo, un punto p de coordenadas x, y, z, se invierte a pinv de coordenadas menos x, menos y, menos z. El punto p y su inverso 31
32 pinv, quedan situados en los extremos de una línea recta que pasa por el centro de inversión y a la misma distancia de él. Un buen ejemplo de inversión son las antípodas que geográficamente, constituyen el lugar de la superficie terrestre que está diametralmente opuesto a otro lado (el diámetro que une a las dos antípodas pasa por el centro de la tierra). Por ejemplo, Las antípodas de Madrid están en Weber, Nueva Zelanda: Las coordenadas geográficas (aproximadas) de Madrid son: 40 grados Norte y 3 grados Oeste (latitud y longitud, respectivamente). Diametralmente opuesto está Weber, de coordenadas 40 grados Sur y 177 grados Este (latitud y longitud, respectivamente). De esta manera se pone de manifiesto que si colocamos en Madrid a una figura humana que mira hacia el Polo Norte y que tiene su brazo izquierdo extendido hacia la costa este de los Estados Unidos, en América del Norte, su antípoda situada en Weber, estará mirando hacia la Antártida, en el Polo Sur, y tendrá su brazo izquierdo extendido hacia Chile, en la costa oeste de América del Sur. Estas coordenadas también se podrían expresar como: Madrid: 40 grados y menos 3 grados (latitud y longitud) Weber: menos 40 grados y 3 grados (latitud y longitud) De esta segunda forma, lo que se evidencia claramente es el cambio de signo en las coordenadas, provocado por el centro de inversión. El centro de inversión se expresa mediante la letra i (latina minúscula). Nota aclaratoria: Quizás sea interesante recordar los conceptos de latitud y longitud: Latitud: es la distancia angular entre el ecuador y un punto determinado del planeta, medida a lo largo del meridiano que pasa por ese punto. La latitud se mide en grados, entre 0 y 90; y puede representarse de dos formas: 1. Indicando a qué hemisferio pertenece la coordenada. 2. Añadiendo valores positivos para referirse al norte y negativos para referirse al sur. (Así, 40 grados de latitud norte, podría indicarse como 40 grados norte o como 40 grados. Y 40 grados de latitud sur podría indicarse como 40 grados sur o como menos 40 grados). 32
33 La longitud, expresa la distancia angular entre un punto dado de la superficie terrestre y el meridiano que se considere como 0 grados, tomando como centro angular el centro de la Tierra. En la actualidad, ese meridiano 0 es el meridiano de Greenwich (que pasa por Londres y casi, casi por Madrid, etc.). Se mide en grados y existen varias maneras de medirla y expresarla: 1. Entre 0 y 180 grados, indicando a qué hemisferio pertenece (este u oriental y oeste u occidental). 2. Entre 0 y 180 grados positivos, en dirección este, o negativos, en dirección oeste. Así, 3 grados de longitud oeste, puede indicarse como 3 grados oeste y como menos 3 grados. Y 177 grados de longitud este como 177 grados este o como 177 grados. Materiales PRÁCTICAS CON EL CENTRO DE INVERSIÓN Objetos para estudiar el funcionamiento del centro Miniglobo terraqueo. Cordón fino y adaptable para marcar algunos meridianos estratégicos sobre la superficie del globo. Parejas de figuras idénticas de un tamaño que permita adherirlas a la superficie del globo, preferiblemente asimétricas y con cierto volumen (de madera, cartón pluma, plástico, etc.). Ej. notas musicales, figuras de juguete, polígonos irregulares, etc. Cinta adhesiva normal y de doble cara. Modelos cristalográficos Colección de tarugos en los que se identifique claramente la presencia del centro. Otros tarugos más complejos. Ejemplares triclínicos en los que solo hay centro de inversión (Fig. 25). 33
34 Figura 25. Ejemplares triclínicos en los que solo hay centro de inversión. Airón-fix de terciopelo, para indicar la posición de las caras que están invertidas en los tarugos más representativos. Actividades Se sugieren dos tipos de actividades: 1. Simulación del funcionamiento del centro de inversión Con la cinta adhesiva se sitúan algunos meridanos sobre la superficie del globo. Ej. Se sitúa el meridiano de Greenwich. Con el adhesivo de doble cara se pegan las parejas de figuras, en una posición y en su antípoda. Por ejemplo en Madrid y en Weber, Nueva Zelanda. Se comprueba que todos los puntos de la figura quedan realmente invertidos en las dos posiciones (Fig. 26). 34
35 P N MADRID WEBER (NZ) Meridiano de GREENWICH P S Figura 26. Se ha situado el meridiano de Greenwich en el miniglobo. Con el adhesivo de doble cara se adhieren dos cangrejos, uno en Madrid y otro en su antípoda, en Weber (Nueva Zelanda). El de Madrid mira hacia el Polo Norte y señala con su pinza izquierda hacia la costa este de los EEUU en América del Norte y el otro mira al Polo Sur y señala con su pinza izquierda la costa de chile en el oeste de América del Sur. 2. Reconocer el centro de inversión en los tarugos Reconocer las caras invertidas, marcadas con terciopelo en los tarugos sencillos (Fig. 27). Reconocer la presencia del centro en los tarugos más complejos. Observar el tipo morfológico de los modelos triclínicos (Fig. 25). Todos parecen triplemente inclinados, como aplastados y torcidos. Figura 27. Las caras invertidas están indicadas con trazo discontinuo en los dos tarugos centrales. 35
36 LO MÁS DIFÍCIL: LOS EJES DE INVERSIÓN Estos ejes, que también se denominan EJES IMPROPIOS, realizan la operación mixta del giro seguido de la inversión, y al igual que en los otros ejes (propios), esta operación doble se repite tantas veces como sea el orden del eje. Desde un punto de vista conceptual, se trata posiblemente de la operación más difícil de entender de todas las que hemos estudiado hasta el momento, ya que requiere hacer abstracción mental de algunos de sus pasos. Para estudiar su funcionamiento hemos seleccionado el cuaternario de inversión que como veremos más adelante, es el más importante, por ser el único que realiza una operación nueva que no tiene ninguna equivalencia. En primer lugar vamos a imaginar que dicho eje cuaternario coincide con el eje c de alguna de nuestras cruces axiales ortogonales y que el centro de inversión, que participa en esta operación mixta, coincide a su vez, con el origen de dicha cruz. Ahora, vamos a suponer que dicho eje actúa sobre un punto de coordenadas x, y, z (todas positivas). Esta sería la posición 1. El eje gira este punto 90 grados, en sentido antihorario, como haría un cuaternario normal (propio), hasta la posición menos x, y, z que no es definitiva, ya que seguidamente debe invertirlo para alcanzar la posición 2, de coordenadas x, menos y, menos z (recordar que el centro de inversión cambia el signo de todas las coordenadas de un punto). El eje continúa con su recorrido, girando 90 grados el punto 2, siempre en sentido antihorario, hasta alcanzar la posición x, y, menos z que no es definitiva ya que debe invertirse hasta alcanzar la posición 3 de coordenadas menos x, menos y, z. El recorrido continúa, girando este punto 3 hasta x, menos y, z e invirtiéndolo para alcanzar la posición 4 de coordenadas menos x, y, menos z. A partir de aquí y siguiendo el mismo procedimiento, se regresaría a la posición 1 y se daría por terminada la operación (recordar que las operaciones de los ejes, ya sean propios o impropios, se realizan siempre hasta completar los 360 grados que llevan al punto de partida). Esta operación del cuaternario de inversión, ha dado como resultado final cuatro posiciones homólogas, que rodean al eje y se sitúan a 90 grados una de otra, igual que haría un cuaternario propio, pero con la diferencia de que el signo de la coordenada z varía alternativamente, de positivo a negativo, entre una y otra. Es decir, en total se han obtenido las 4 posiciones siguientes: 36
37 Posición 1: x, y, z. Posición 2: x, menos y, menos z. Posición 3: menos x, menos y, z. Posición 4: menos x, y, menos z. Si ahora nos apoyamos en el modelo desarrollado para explicar el funcionamiento del centro de inversión, basado en el concepto geográfico de antípodas, podemos planificar un fantástico viaje en avión, alrededor del globo terráqueo, que nos va a ayudar a comprender un poco mejor el funcionamiento de este eje. En este viaje se visitarán cuatro países, dos en el Trópico de Cáncer y dos en el Trópico de Capricornio, pero llegaremos a ellos haciendo el mismo recorrido loco que haría un cuaternario de inversión, situado en la misma posición que el eje Norte- Sur del globo. 1. El viaje se inicia en Puerto Rico, en el Trópico de Cáncer, país al que asignaremos unas coordenadas x, y, z (que se corresponden con la anterior posición 1). 2. El avión vuela por el Trópico de Cáncer, en sentido antihorario, recorriendo un cuarto de Trópico (que traducido en grados serían 90) hasta llegar al sur de Libia, de coordenadas menos x, y, z. Sin embargo, al llegar a este país, el comandante del avión no permite bajar a nadie, reposta gasolina, y parte para un viaje larguíííísimo, invirtiéndose hasta las antípodas de Libia en las Islas Sociedad de la Polinesia Francesa, en el Trópico de Capricornio, de coordenadas x, menos y, menos z (que se corresponden con la anterior posición 2). Estas islas le gustan mucho al comandante. Así que deja que los pasajeros se bajen y disfruten, comprobando que efectivamente, la gente que vive en el hemisferio sur no camina cabeza abajo. 3. El viaje continúa, ahora por el Trópico de Capricornio, otro cuarto de Trópico en sentido antihorario, hasta llegar a Bolivia, de coordenadas x, y, menos z, donde el comandante, nuevamente, no permite a nadie descender del avión, reposta gasolina y reanuda el vuelo hacia las antípodas de Bolivia, en Hong Kong, en el Trópico de Cáncer. En este país, de coordenadas menos x, menos y, z (que se corresponden con la anterior posición 3), el comandante vuelve a permitir que los viajeros se bajen de la nave y hagan un poquito de turismo. 4. El viaje sigue, esta vez por el Trópico de Cáncer, hasta las Islas Hawai, de coordenadas x, menos y, z, donde nuevamente no deja bajar a nadie y después de repostar, reanuda rápidamente el vuelo hasta las antípodas de Hawai en 37
38 Botswana, en el Trópico de Capricornio, de coordenadas menos x, y, menos z (que se corresponden con la anterior posición 4) donde les permite hacer su último recorrido turístico. Efectivamente, a partir de este punto el avión tiene como meta regresar al punto de partida, para lo cual, primero vuela por el trópico de Capricornio hasta Australia, de coordenadas menos x, menos y, menos z, y desde allí se invierte hasta Puerto Rico, donde termina el viaje. El resultado final es que se han visitado los países siguientes: Puerto Rico en el Trópico de Cáncer, de coordenadas: x, y, z. Se corresponde con la Posición 1. Islas Sociedad en el Trópico de Capricornio, de coordenadas: x, menos y, menos z. Se corresponde con la Posición 2. Hong Kong en el Trópico de Cáncer, de coordenadas: menos x, menos y, z. Se corresponde con la Posición 3. Botswana en el Trópico de Capricornio, de coordenadas: menos x, y, menos z. Se corresponde con la Posición 4. Y entre uno y otro país, el avión ha repostado gasolina en las antípodas de todos ellos: Australia de Puerto Rico, Libia de las Islas Sociedad, Bolivia de Hong Kong y las Islas Hawai de Botswana. En el caso de los ejes de inversión de orden 1, 2, 3, y 6, esta operación mixta equivale a la que realizarían conjuntamente dos elementos (de los que ya conocemos): Un eje propio (de orden mitad que el de inversión) y un plano en el caso de los ejes de inversión de orden par (menos 2 y menos 6). Un eje propio (del mismo orden que el de inversión) y un centro en el caso de los ejes de inversión de orden impar (menos 1 y menos 3). Solo el eje cuaternario de inversión que hemos estudiado en el ejemplo, realiza una operación nueva que no tiene ninguna equivalencia. Los ejes de inversión se expresan mediante un número que indica el orden del eje con un signo menos encima (como un súper-rayado) y se habla de ellos añadiendo un menos delante, por ejemplo, el menos tres, es el ternario de inversión, etc. Para representarlos gráficamente se utiliza el mismo icono que en los ejes propios, pero con una lentejita inscrita dentro de él. 38
39 PRÁCTICAS CON LOS EJES DE INVERSIÓN Materiales Objetos para estudiar el funcionamiento de los ejes de inversión El miniglobo terráqueo de la práctica 5.1. Alambres finitos y cinta adhesiva normal y de doble cara. Etiquetas adhesivas con las iniciales PR (de Puerto Rico), B (de Bolivia), L (de Libia), BW (de Botswana), HK (de Hong Kong), A (de Australia), HW (de Hawai) e IS (de Islas Sociedad), escritas en Braille. Etiquetas adhesivas con forma de flecha o triangulares. Estas figuras también se pueden hacer de plástico duro recortado, fieltro, etc., con cinta adhesiva de doble cara en su base. Simularán pequeños aviones Modelos tridimensionales de cruces axiales, como las preparadas en la práctica Colección de pinzas de pequeño tamaño, similares a las de tender la ropa Modelos cristalográficos Tarugos en los que se identifique claramente la presencia del cuaternario de inversión. Es decir, el tetraedro y el biesfenoide tetragonal, este último aislado o combinado con un prisma (Fig. 28). Figura 28. Colección de modelos tetragonales: biesfenoides (hilera central). Dos biesfenoides con prisma (detrás) (Foto Natalie Paco). 39
40 Actividades Se sugieren dos tipos de actividades: 1. Simulación del funcionamiento de los ejes de inversión Con el globo terráqueo Se resaltan los Trópicos de Cáncer y de Capricornio, con el mismo tipo de alambres finitos que se emplearon en la práctica 5.1, para marcar los meridianos estratégicos. Se sitúan las pegatinas escritas en Braille sobre los países correspondientes: Puerto Rico (PR), Bolivia (B), Libia (L), Botswana (BW), Hong Kong (HK), Australia (A), Hawai (HW) e Islas Sociedad (IS). Después: Se pega el primer avión en Puerto Rico. Desde Puerto Rico, se gira el globo 90 grados en sentido antihorario, hasta Libia y desde ahí se invierte a sus antípodas en las Islas Sociedad, donde se pega un segundo avión. Desde las Islas Sociedad, se gira el globo hasta Bolivia, otros 90 grados, siempre en sentido antihorario, y se invierte a Hong Kong donde se coloca un tercer avión. Desde Hong Kong, se gira el globo otros 90 grados, hasta las Islas Hawai y se invierte a Botswana donde se sitúa un cuarto avión. Desde Botswana, se termina el viaje girando 90 grados hasta Australia e invirtiendo a Puerto Rico, donde termina el viaje. Este recorrido es el mismo que haría un eje cuaternario de inversión situado en la posición del eje Norte-Sur terrestre. Con las cruces axiales Con las cruces axiales y las minipinzas se puede seguir el recorrido de los ejes de inversión. Por ejemplo, vamos a simular la operación del cuaternario. Este eje reproduce puntos homólogos cuatro veces, en posiciones que distan 90 grados entre sí, y que están alternativamente derechas e invertidas. Es decir, si suponemos que dicho cuaternario coincide con el eje c de las cruces axiales, las posiciones homólogas generadas por él, tendrán la coordenada z con signo positivo y negativo alternativamente. 40
41 Se toma la cruz tetragonal o la cúbica y también cuatro pinzas, que representarán a los cuatro puntos homólogos que genera el eje. Se coloca una pinza en el extremo positivo del eje a, mirando hacia arriba, para indicar que su coordenada z es positiva. Esta es la posición 1. Desde esa posición 1 se supone un giro de 90 grados en sentido antihorario, hasta b positivo, seguido de una inversión al extremo negativo del eje b, donde colocaremos una segunda pinza, mirando hacia abajo, para indicar que su coordenada z es negativa. Esta será la posición 2. Desde esa posición 2 se supone un giro de 90 grados en sentido antihorario, hasta a positivo, seguido de una inversión al extremo negativo del eje a, donde colocaremos una tercera pinza, mirando hacia arriba, para indicar que su coordenada z es positiva. Esta será la posición 3. Desde esa posición 3 se supone un giro de 90 grados en sentido antihorario, hasta b negativo, seguido de una inversión al extremo positivo del eje b, donde colocaremos una cuarta pinza, mirando hacia abajo, para indicar que su coordenada z es negativa. Esta será la posición 4. De esta manera se tienen cuatro pinzas, situadas en los extremos positivos y negativos de los ejes a y b, a 90 grados unas de otras, mirando alternativamente hacia arriba y hacia abajo, para indicar el signo positivo o negativo de la coordenada z. Concretamente, las dos pinzas del eje a miran hacia arriba porque tienen z positivo y las dos del eje b miran hacia abajo porque tienen z negativo. Utilizando las otras cruces axiales se puede simular la operación de los otros ejes de inversión y comprobar las equivalencias descritas. Por ejemplo, vamos a simular la operación del binario: Para ello, se toma una cruz ortogonal y se coloca una pinza en el extremo positivo del eje a, mirando hacia arriba, para indicar que la coordenada z es positiva. Esta será la posición 1. Para buscar la posición 2 tomamos otra pinza, la hacemos girar 180 grados desde la posición 1, en sentido antihorario, hasta llegar al extremo negativo del eje a, desde donde se invierte hasta alcanzar nuevamente el extremo positivo del eje a, donde la colocaremos mirando hacia abajo, para indicar que su coordenada z es negativa. Se comprende claramente que la posición 1 y la posición 2, están relacionadas por un plano de reflexión que es la equivalencia descrita para el binario de inversión. 41
42 2. Reconocer el eje de inversión en los tarugos seleccionados Antes de intentar visualizar la actuación del cuaternario de inversión en tetraedro y biesfenoide tetragonal, es interesante reflexionar acerca de cómo divide el espacio un sistema de tres ejes, similar a nuestras cruces axiales. Lo hace en ocho octantes, cuatro con valores positivos de z y otros cuatro con valores negativos: Vamos a numerar del 1 al 4, los z-positivos, empezando por el que también tiene positivas x e y, y continuando en sentido antihorario. Y del 5 al 8 los z-negativos, empezando por el que está debajo del uno y continuando en sentido antihorario. Tetraedro y biesfenoide tetragonal, son poliedros constituidos por cuatro caras iguales con forma de triángulo, equilátero el tetraedro e isósceles el biesfenoide tetragonal. Son formas que recuerdan a cuñas, equidimensional el tetraedro y alargada el biesfenoide tetragonal. Situando imaginariamente en estos poliedros, sus correspondientes cruces axiales, se comprueba como dos de sus caras quedarán situadas en dos octantes opuestos, z-positivos, por ejemplo 1 y 3, mientras que las otras dos caras, se situarán en los octantes z-negativos 6 y 8, también opuestos y que no coinciden bajo los positivos, sino que están intercalados entre ellos. SISTEMAS Y SIMETRÍA: RECONOCIMIENTO DE LOS SISTEMAS A PARTIR DE LOS ELEMENTOS DE SIMETRÍA Como ya adelantamos en alguno de los capítulos anteriores, cada sistema cristalino está caracterizado por una simetría específica, además de por su cruz axial. Esto se traduce en la presencia de un elemento o elementos característicos, e indica inequívocamente el sistema cristalino al que pertenece el poliedro que los posee. Estos elementos son los siguientes, para cada sistema: Triclínico. Como mínimo un eje monario y como máximo un centro. Monoclínico. Como mínimo un elemento de simetría binaria, que puede ser un eje binario o un plano, y como máximo dos elementos de simetría binaria, que serán un eje binario y un plano perpendicular a él. Ortorrómbico. Como mínimo tres elementos de simetría binaria, que pueden ser tres ejes binarios o un binario y dos planos, y como máximo seis elementos de simetría binaria, es decir, tres ejes binarios perpendiculares y tres planos perpendiculares a todos ellos. 42
43 Tetragonal. Un eje cuaternario, aislado o con otros elementos de simetría, siempre que éstos no sean otros ejes cuaternarios. Cúbico. Cuatro ejes ternarios, que se sitúan en la misma posición que las diagonales mayores del cubo. Hexagonal. Un eje senario, aislado o con otros elementos de simetría. Trigonal (romboédrico). Un eje ternario, aislado o con otros elementos de simetría, siempre que estos no sean otros ejes ternarios. que: Además, estos elementos ocupan posiciones fijas en cada Sistema, de manera Los ejes de giro coinciden con los ejes a, b o c de la cruz axial, excepto en el cúbico: En el cúbico, sus cuatro ejes ternarios característicos, coinciden con las cuatro diagonales equidistantes de los ejes a, b y c de su cruz axial. Los ejes de giro de mayor orden se hacen coincidir con el eje c, excepto en el monoclínico: En el monoclínico, el único eje binario que puede tener, se hace coincidir con el eje b. Los planos ocupan dos posiciones bien definidas: o son perpendiculares a los ejes de giro, o los contienen ya que, la línea de intersección de dos o más planos siempre es un eje de giro. En el monoclínico, el único plano que puede llegar a tener, siempre se hace coincidir con el plano perpendicular al eje b (es decir, con el plano definido por a y c). Finalmente, el centro de inversión en el triclínico, se hace coincidir con el origen de la cruz axial, en el centro geométrico del poliedro. RECONOCIMIENTO DE LOS SISTEMAS A PARTIR DE LOS ELEMENTOS DE SIMETRÍA. PRÁCTICAS Materiales y actividades A partir de una colección de modelos cristalográficos variados, se sugieren dos tipos de actividades: 43
44 1. Reconocimiento del sistema al que pertenece cada modelo, por la presencia del elemento o elementos característicos Se puede empezar por los casos más fáciles, por ejemplo, la presencia de ejes senarios o cuaternarios se detecta rápidamente, los tarugos de estos sistemas muestran secciones hexagonales o cuadradas que rápidamente inducen a pensar en la presencia de estos ejes, que a su vez indican inequívocamente que se trata del sistema hexagonal y tetragonal, respectivamente (Fig. 29). Figura 29. Prismas tetragonal (izquierda) y hexagonal (derecha). En las formas trigonales se reconocen secciones pseudo-hexagonales o pseudotriangulares. Es importante reconocer el romboedro y buscar en el su eje ternario (Fig. 30). Figura 30. Tarugos trigonales. 44
45 El tipo morfológico ayuda también a buscar la simetría característica: Las formas cúbicas son siempre muy equidimensionales (sus ejes a, b y c son iguales). Cuando encontremos poliedros con estas características, podemos buscar los cuatro ejes ternarios del cúbico. Para hacernos una idea de cómo se sitúan estos ejes en estos poliedros, pensemos que en un cubo irían de vértice a vértice opuesto (Fig. 31). Figura 31. Tarugos cúbicos. Las formas ortorrómbicas suelen ser muy simétricas, algo aplanadas y con secciones rectangulares o rómbicas. Si son prismáticas se mantienen rectas sobre cualquier superficie (sus ejes a, b y c son perpendiculares entre si). Recordar la caja de cerillas (Fig. 32). Figura 32. Tarugos rómbicos. 45
46 Los poliedros monoclínicos recuerdan mucho a los rómbicos pero siempre se van a inclinar hacia un lado cuando se colocan sobre una superficie (su ángulo beta es diferente de 90 grados) (Fig. 33). Figura 33. Tarugos monoclínicos. Finalmente, los triclínicos son poliedros muy aplastados, triplemente inclinados y muy poco simétricos. Efectivamente, lo máximo que pueden tener es un centro que invierte todas sus caras (Fig. 25). 2. Relacionar los elementos de simetría característicos del Sistema con la cruz axial correspondiente Empezando por los más fáciles como antes, los ejes senario y cuaternario del hexagonal y el tetragonal, se harán coincidir con el eje c. En el trigonal también se hace coincidir el ternario con el eje c, pero tomando la cruz axial hexagonal. En el cúbico, los cuatro ejes ternarios se situarán equidistantes de a, b y c. En el rómbico los binarios se harán coincidir con los ejes a, b y c. En el caso de que solo haya un binario, éste se hará coincidir con el eje c. En el monoclínico, su único eje binario se hace coincidir con el eje b. En el triclínico, el centro se supone coincidente con el centro geométrico del poliedro. Como práctica final se sugiere desordenar la colección de tarugos y reordenarla, agrupándola por sistemas. Y además, repetir esta operación hasta que se realice sin cometer ningún fallo. 46
47 LAS 32 CLASES DE SIMETRÍA A lo largo de los capítulos precedentes, hemos tenido la oportunidad de comprobar como los elementos de simetría estudiados pueden encontrarse aislados o combinados con otros en un mismo poliedro, lo cual depende, lógicamente, de la forma del poliedro. Por ejemplo, el paralelepípedo más representativo del sistema ortorrómbico, es la combinación de pinacoides, que recuerda a la caja de cerillas. En este poliedro hay tres ejes binarios, perpendiculares entre sí. Cada uno de ellos, relaciona parejas de caras homólogas del poliedro: en la caja de cerillas se diferencian tres tipos de caras, las más pequeñas que forman el cajoncito, las intermedias que llevan pegado el rascador y las dos más grandes. Los binarios se sitúan perpendiculares a cada tipo de cara y coinciden además, con los ejes de la cruz axial. Además de estos binarios, hay tres planos de reflexión mutuamente perpendiculares. En cada intersección de dos planos se aloja un binario y cada binario tiene un plano perpendicular. Para estudiar estas combinaciones de elementos de simetría, habrá que tener en cuenta que cumplen una serie de normas: Primera. Todos los elementos que se combinan se cortan en un punto (como si fueran un ramo de flores). Por ello a esta simetría se la denomina puntual. Por ejemplo en la caja de cerillas, los tres ejes y los tres planos confluyen en un punto que coincide con el origen de la cruz axial y con el centro geométrico de la caja. Segunda. Todos los elementos que se combinan deben guardar unas relaciones angulares específicas. Por ejemplo en la caja de cerillas, tanto los ejes como los planos, guardan relaciones de ortogonalidad entre sí. Tercera. La presencia de algunos elementos implica obligatoriamente la presencia de otros. Dentro de esta categoría se contemplan cuatro casos: 1. Las combinaciones de ejes deben ser ternarias como mínimo. Es decir que, o bien se tienen poliedros con un único eje de rotación, o si hay más ejes presentes, serán tres como mínimo. Además, estas combinaciones de ejes no pueden formar ángulos cualesquiera (solo se van a encontrar valores de 90 47
48 grados, 45 grados, 120 grados, 60 grados, 30 grados y otros muy específicos en las agrupaciones correspondientes al sistema cúbico). Por ejemplo, en el sistema ortorrómbico, la simetría mínima característica son tres binarios, perpendiculares entre sí, o bien un binario situado en la intersección de dos planos perpendiculares. En ningún caso hay combinaciones de solo dos ejes. 2. Un eje de orden n que tiene un binario perpendicular a él, genera otros ejes binarios, tantos como sea el orden del eje, que también son perpendiculares a él. Por ejemplo, en el sistema ortorrómbico, hay un eje binario, de orden dos, que coincide con el eje c de la cruz axial y dos binarios perpendiculares a el. 3. Un eje de orden n contenido en un plano, genera otros planos, tantos como sea el orden del eje. El eje queda situado en la intersección de todos esos planos. Por ejemplo, en el sistema ortorrómbico, una de sus agrupaciones características, consiste en un binario situado en la intersección de dos planos perpendiculares. 4. Un eje de orden n y un plano m perpendiculares, generan automáticamente un centro de inversión, situado en la intersección de ambos. Por ejemplo, en el sistema ortorrómbico, la agrupación de los tres ejes binarios, con tres planos perpendiculares, existe además un centro de inversión, que coincide con el origen de todo. En la caja de cerillas se puede comprobar como cada pareja de caras homólogas esta relacionada por un centro, además de por los binarios y los planos que se han detectado. El origen de estas normas es puramente matemático. Cada elemento de simetría constituye un grupo matemático y todas las combinaciones que se hagan con ellos están gobernadas por la Teoría de Grupos. Estas normas restringen el número de combinaciones de elementos posibles, de hecho solo hay 32 combinaciones que reciben el nombre de clases de simetría (o 32 grupos puntuales de simetría). A continuación se indican los símbolos y las combinaciones de elementos que constituyen cada una de estas clases: Clases que solo tienen un eje propio. Hay cinco. Se representan como n, siendo n el orden del eje: 48
49 Clase 1 (un eje monario). Clase 2 (un eje binario). Clase 3 (un eje ternario). Clase 4 (un eje cuaternario). Clase 6 (un eje senario). Clases que solo tienen un eje de inversión. Hay cinco. Se representan como menos n, siendo n el orden del eje: Clase menos 1 (equivale al centro de inversión) Clase menos 2 (equivale al plano. El binario de inversión, por convenio, siempre se representa como un plano. Por ejemplo, los poliedros monoclínicos, que pertenecen a esta clase, se dice que pertenecen a la clase m). Clase menos 3 (equivale a un ternario propio más un centro de inversión) Clase menos 4 (no tiene equivalencia). Clase menos 6 (equivale al ternario propio más un plano perpendicular a él. En los poliedros que pertenecen a esta clase, se adivina mucho mejor el ternario con su plano perpendicular que el senario de inversión, sin embargo, por convenio se dice que pertenecen a la clase menos 6). Clases con un eje propio y un plano perpendicular. Hay tres. Se representan como n/m, siendo n el orden del eje y m el plano: Clase 2/m (un eje binario perpendicular a un plano). Clase 4/m (un eje cuaternario perpendicular a un plano). Clase 6/m (un eje senario perpendicular a un plano). Clases con un eje propio situado en la intersección de dos o más planos. Hay cuatro. Se representan como nmm o nm, siendo n el orden del eje y m el plano: Clase 2mm (un eje binario en la intersección de dos planos m, que forman entre ellos un ángulo de 90 grados). Clase 3m (un eje ternario en la intersección de tres planos m, que forman entre ellos un ángulo de 60 grados). 49
50 Clase 4mm (un eje cuaternario en la intersección de cuatro planos m, que forman entre ellos un ángulo de 45 grados). Clase 6mm (un eje senario en la intersección de seis planos m, que forman entre ellos un ángulo de 30 grados). Clases consistentes en agrupaciones de tres ejes propios. Hay seis. Se representan como nnn o nn, siendo n el orden de los ejes que se agrupan: Clase 222 (tres ejes binarios perpendiculares entre si) Clase 32 (un eje ternario y tres ejes binarios perpendiculares a él, que forman entre ellos un ángulo de 60 grados). Clase 422 (un eje cuaternario y cuatro ejes binarios perpendiculares a él, que forman entre ellos un ángulo de 45 grados). Clase 622 (un eje senario y seis ejes binarios perpendiculares a él, que forman entre ellos un ángulo de 30 grados). Clase 23 (cuatro ejes ternarios, que se disponen coincidiendo con las diagonales mayores de un cubo y tres ejes binarios ortogonales entre sí, que se disponen coincidiendo con las perpendiculares a las caras del cubo, o con los ejes a, b y c de la cruz axial. Todos ellos se cortan en el centro geométrico del cubo). Clase 432 (cuatro ejes ternarios, que se disponen coincidiendo con las diagonales mayores de un cubo, tres cuaternarios ortogonales entre sí, que se disponen coincidiendo con las perpendiculares a las caras del cubo y seis binarios que coinciden con las diagonales menores del cubo. Todos ellos se cortan en el centro geométrico del cubo). Clases consistentes en agrupaciones de un eje propio y dos de inversión. Hay tres. Esta es la única posibilidad de que se agrupen ejes propios e impropios. Se representan como menos nnm Puesto que el binario de inversión siempre se representa como un plano, la m que figura en estas clases, hace referencia al binario de inversión que se ha combinado con los otros ejes: Clase menos 42m (un cuaternario de inversión que es la intersección de dos planos m y dos binarios perpendiculares a él, que se intercalan con los planos, formando unos con otros, ángulos de 45 grados). Clase menos 62m (un senario de inversión que es la intersección de tres planos m y tres binarios perpendiculares a él, que se intercalan con los planos, formando unos con otros, ángulos de 60 grados). 50
51 Clase menos 43m (cuatro ejes ternarios, que se disponen coincidiendo con las diagonales mayores de un cubo, tres cuaternarios de inversión ortogonales entre sí, y cuatro planos). Clases que se obtienen añadiendo un centro a las clases consistentes en agrupaciones de ejes propios. Hay seis. Surgen unas clases con muchos elementos de simetría: Clase 2/m 2/m 2/m, formada por tres ejes binarios perpendiculares entre si y tres planos perpendiculares a cada uno de los binarios. Clase menos 3 2/m, formada por un eje ternario de inversión, situado en la intersección de tres planos, y tres ejes binarios perpendiculares al ternario e intercalados entre los planos m. Clase 4/m 2/m 2/m, formada por un cuaternario con un plano perpendicular y cuatro binarios perpendiculares al cuaternario. Cada uno de estos binarios tiene además un plano perpendicular a él. Clase 6/m 2/m 2/m, formada por un senario con un plano perpendicular y seis binarios perpendiculares al senario. Cada uno de estos binarios tiene además un plano perpendicular a él. Clase 2/m menos 3, formada por tres ejes binarios, cada uno con un plano perpendicular, combinados con cuatro ejes ternarios de inversión. Clase 4/m menos 3 2/m, formada por tres ejes cuaternarios, cada uno con un plano perpendicular, cuatro ejes ternarios de inversión y seis ejes binarios, cada uno con un plano perpendicular. PRÁCTICAS DE LAS 32 CLASES DE SIMETRÍA Materiales Caja de cerillas de tamaño grande, chinchetas corcheteras y cinta adhesiva. Tablita con las clases de simetría escritas en Braille. Colección de modelos cristalográficos (Figs. 34 y 35). 51
52 Figura 34. Modelos cristalográficos. Varios sistemas y clases. Figura 35. Modelos cristalográficos. Varios sistemas y clases. 52
53 Actividades Se sugieren dos tipos de actividades: 1. Reconocimiento de los elementos de simetría de la clase 2/m 2/m 2/m del rómbico Sobre la caja de cerillas, marcar con chinchetas la posición de los tres binarios y con cinta adhesiva la posición de los tres planos que tiene la figura. Comprobar que en este poliedro, además de los elementos indicados, existe un centro de inversión. 2. Buscar elementos de simetría en los modelos cristalográficos y determinar la clase a que pertenecen ayudándose con la tablita. Empezar por los más fáciles. Las formas tetragonales y hexagonales se reconocen enseguida. Buscar en ellas los ejes binarios y los planos y decidir la clase que se trate. Por ejemplo, si un tarugo tetragonal tiene un plano m perpendicular al cuaternario, podrá ser de la clase 4/m, pero si además tiene ejes binarios, lo más seguro es que sea de la clase 4/m 2/m 2/m. Si el tarugo no tiene plano perpendicular al cuaternario, es fácil que sea de las clases 4mm o 422. Habrá que buscar binarios o planos para decidir. Etc. A continuación se muestra la lista de símbolos que deben ir en la tablita Braille. Las clases se han agrupado por sistemas: Triclínico 1, menos 1 Monoclínico 2, m, 2/m Ortorrómbico 222, 2mm, 2/m 2/m 2/m Tetragonal 4, menos 4, 4/m, 4mm, 422, menos 42m, 4/m 2/m 2/m Cúbico 23, 432, menos 43m, 2/m menos 3, 4/m menos 3 2/m 53
54 Trigonal 3, menos 3, 3m, 32, menos 3 2/m Hexagonal 6, menos 6, 6/m, 6mm, 622, menos 62m, 6/m 2/m 2/m DESCRIPCIÓN DE LOS MODELOS CRISTALOGRÁFICOS: PASOS A SEGUIR A continuación se resume el procedimiento para describir sistemáticamente los modelos cristalográficos, de acuerdo con los criterios y normas que se han estudiado en los capítulos precedentes: Primero. Se busca la característica simétrica. Por ejemplo, se va a describir un prisma recto de sección cuadrada. En él se reconoce inmediatamente la presencia de un eje cuaternario, que indica inequívocamente que pertenece al sistema tetragonal. Segundo. Se especifican las formas cristalinas que lo componen. Al saber que se trata de un poliedro tetragonal se puede definir como una combinación de prisma tetragonal y pinacoide. Tercero. Se sitúa la cruz axial y se orienta el poliedro correctamente. Como norma, se hacen coincidir, lo más estrechamente posible, los elementos de simetría detectados con los ejes de la cruz axial. En el prisma tetragonal, se hace coincidir el cuaternario con el eje c. Situamos este eje vertical frente a nosotros. El poliedro queda vertical frente a nosotros. Los ejes a y b están contenidos en un plano perpendicular a dicho eje, de manera que el eje a apunte hacia nosotros y el b quede horizontal frente a nosotros. Ambos ejes pueden suponerse perpendiculares a las caras del prisma, o bien apuntando a la mitad de las aristas entre dichas caras. Cuarto. Se buscan otros elementos de simetría que puedan estar presentes en las clases del sistema al que pertenece el modelo. Para ello es muy útil disponer de una tablita con las 32 Clases de Simetría. En general los planos son muy fáciles de reconocer, por ello se recomienda buscarlos en primer lugar. En las clases tetragonales puede haber planos y ejes binarios. El prisma del ejemplo tiene un plano de simetría perpendicular al cuaternario, por tanto solo podrá ser de dos clases: la 4/m o la 4/m 2/m 2/m. 54
55 Para decidir entre una u otra habrá que buscar ejes binarios o más planos. Colocando el prisma horizontalmente, se reconocen cuatro ejes binarios, que van de centro de cara a centro de cara del prisma, y de centro de arista a centro de arista; y que forman 45 grados unos con otros. Además, dos de estos binarios coinciden con los ejes a y b de la cruz axial. En resumen, el poliedro debe pertenecer a la clase 4/m 2/m 2/m. Quinto. Finalmente se buscan los demás elementos de simetría que deben estar presentes. En el prisma del ejemplo se tendrán cuatro planos m que dividen al prisma longitudinalmente. Estos planos además, son perpendiculares a los ejes binarios. En las figuras 36 y 37 se muestran tarugos tetragonales de diferentes clases de simetría. Figura 36. Tarugos tetragonales. De izquierda a derecha: prismas (4/m2/m2/m), bipirámides con prisma y pedión (4), Biesfenoides con prisma y biesfenoides (menos 42m) (foto Natalie Paco). 55
56 Figura 37. Tarugos tetragonales. De arriba abajo: bipirámides con prisma y pinacoide (4/m) y bipirámides con prisma (4/m2/m2/m) (foto Natalie Paco). RECURSOS ELECTRÓNICOS Mª Victoria López-Acevedo Cornejo. Juan Carlos Chicote González. Javier Goñi López Forma y simetría. Enseñanza adaptada a personas ciegas a través de los modelos cristalográficos. Vídeo. Consultado 29 de septiembre de Disponible en: Recibido: 8 enero Aceptado: 24 septiembre
Módulo 3. Introducción a la cristalografía
 Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
UNIDAD 1: LA MATERIA CRISTALINA
 UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Mª Victoria López-Acevedo Cornejo 1 ; Juan Carlos Chicote González 1 ; Javier Goñi López 1 y Ana López-Herce Cid 2
 Experiencias e Ideas para el aula Forma y simetría en la naturaleza. Enseñanza adaptada a personas ciegas a través de métodos cristalográficos Shape and symmetry in nature for blind people: a special educational
Experiencias e Ideas para el aula Forma y simetría en la naturaleza. Enseñanza adaptada a personas ciegas a través de métodos cristalográficos Shape and symmetry in nature for blind people: a special educational
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
TEMA 5: Cuerpos geométricos CONTENIDOS:
 CONTENIDOS: - Prismas y pirámides: descripción, elementos y clasificación. - Cilindro, cono y esfera: descripción y elementos. - Realización de clasificaciones de cuerpos geométricos atendiendo a diferentes
CONTENIDOS: - Prismas y pirámides: descripción, elementos y clasificación. - Cilindro, cono y esfera: descripción y elementos. - Realización de clasificaciones de cuerpos geométricos atendiendo a diferentes
SIMETRÍA INFINITA. nt = kt
 SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
1. Dualidad de poliedros. 2. Prismas y antiprismas. 3. Estructuras espaciales. 4. Secciones y simetrías de poliedros. 5. Macizamiento del espacio
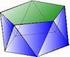 5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
5. Poliedros Matemáticas 2º ESO 1. Dualidad de poliedros 2. Prismas y antiprismas 3. Estructuras espaciales 4. Secciones y simetrías de poliedros 5. Macizamiento del espacio 6. Coordenadas en el espacio
GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS. NOMBRE. FECHA: 03/10/2018. Tercero básico
 GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS NOMBRE. FECHA: 03/10/2018. Tercero básico 1- Qué son los cuerpos geométricos? Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho
GUÍA CUERPOS GEOMÉTRICOS Nº1 POLIEDROS NOMBRE. FECHA: 03/10/2018. Tercero básico 1- Qué son los cuerpos geométricos? Un sólido o cuerpo geométrico es una figura geométrica de tres dimensiones (largo, ancho
Un punto divide a una recta en dos semirrectas. Ese punto es el origen de ambas semirrectas.
 Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas. Ese punto es el origen
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos
 Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos
 Gráficos por Computadora MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos Objetos básicos Punto, Línea, Plano y Espacio Punto: Ubicación, sin longitud, anchura ni altura. (El punto representa
Gráficos por Computadora MSC J. Fco. Jafet Pérez L. Conceptos Geométricos Objetos Básicos Objetos básicos Punto, Línea, Plano y Espacio Punto: Ubicación, sin longitud, anchura ni altura. (El punto representa
a 2 = = 1600 ; a = 40 A = = 80. Iguales A = 361 1:150
 uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
La palabra poliedro está compuesta por dos palabras griegas: poli (muchos) y edro (planos, caras).
 Sólidos Platónicos Título: Sólidos Platónicos. Target: Profesores de Matemáticas. Asignatura: Matemáticas. Autor: Emiliana Oliván Calzada, Licenciada en Matemáticas, Profesora de Matemáticas en Educación
Sólidos Platónicos Título: Sólidos Platónicos. Target: Profesores de Matemáticas. Asignatura: Matemáticas. Autor: Emiliana Oliván Calzada, Licenciada en Matemáticas, Profesora de Matemáticas en Educación
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA CUNOR - CARRERA DE GEOLOGÍA CURSO DE MINERALOGÍA GENERAL PRÁCTICA No. 1 Realización de modelos Cristalográficos en 3D. ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA CUNOR - CARRERA DE GEOLOGÍA CURSO DE MINERALOGÍA GENERAL PRÁCTICA No. 1 Realización de modelos Cristalográficos en 3D. ÍNDICE DE SISTEMAS Y MODELOS CRISTALOGRÁFICOS
2.2 Simetría en los sólidos cristalinos
 2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
2.2 Simetría en los sólidos cristalinos Observación: Distribución de las caras en los cristales Sentido de proporción y equilibrio geométrico Simetría externa de los cristales permite: - Placer estético
TEMA 4. Geometría. Teoría. Matemáticas
 1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
POLIEDROS. ÁREAS Y VOLÚMENES.
 7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
7. POLIEDROS. ÁREAS Y VOLÚMENES. EN ESTA UNIDAD VAS A APRENDER CUERPOS GEOMÉTRICOS POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES CARACTERÍSTICAS DEFINICIÓN ELEMENTOS DEFINICIÓN ELEMENTOS - Tetaedro.
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS.
 TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS. LOS POLÍGONOS El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los vértices.
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS. LOS POLÍGONOS El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los vértices.
TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO
 Matemáticas Aplicadas Tema: Movimiento de los cuerpos geométricos. TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO Transformación isométrica Isometría proviene del griego iso, prefijo que significa
Matemáticas Aplicadas Tema: Movimiento de los cuerpos geométricos. TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO Transformación isométrica Isometría proviene del griego iso, prefijo que significa
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección...
 TEMA 8 RECTAS Y ÁNGULOS TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección....... Línea recta Cada una de las partes en
TEMA 8 RECTAS Y ÁNGULOS TIPOS DE LÍNEAS Las rectas no tienen principio ni fin. La recta es una línea formada por una serie de puntos en una misma dirección....... Línea recta Cada una de las partes en
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
Dibujo y geometría descriptiva II 2014
 ` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
` CONTENIDO 1. Conceptos básicos Cuerpos geométricos Intersección 2. Intersección entre planos y sólidos. 3. Intersección de plano con prisma 4. Intersección de plano con cilindro. 5. Intersección de sólido
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
GEOGRAFÍA. Qué es un mapa mental?
 GEOGRAFÍA Qué es un mapa mental? Se llama mapa mental a la imagen que cada uno tiene del lugar donde vive es decir una representación íntima, personal, que sirve para actuar en el territorio. Si se compara
GEOGRAFÍA Qué es un mapa mental? Se llama mapa mental a la imagen que cada uno tiene del lugar donde vive es decir una representación íntima, personal, que sirve para actuar en el territorio. Si se compara
Contenido. Tema 11. Geometría en el espacio. 1. Poliedros Regulares o sólidos Platónicos Teorema de Euler Prismas...
 Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
Tema 11. Geometría en el espacio Contenido 1. Poliedros Regulares o sólidos Platónicos... 2 2. Teorema de Euler... 3 3. Prismas... 3 4. Pirámides... 5 5. Cilindro... 7 6. Cono... 8 7. Esfera... 9 8. Coordenadas
SISTEMASS DE REPRESENTACIÓNN Geometría Básica
 SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
SISTEMASS DE REPRESENTACIÓNN Geometría Básica Coordinadora de Cátedra: Ing. Canziani, Mónica Profesores: Arq. Aubin, Mónica Arq. Magenta, Gabriela Ing. Medina, Noemí Ing. Nassipián, Rosana V. Ing. Borgnia,
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
CLASIICAR POLIEDROS OBJETIVO 1 Nombre: Curso: eca: POLIEDROS Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los polígonos que limitan al poliedro se llaman caras. Los
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA
 MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA Área matemática: Geometría Primer periodo 20XX Habilidad(es)
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA Área matemática: Geometría Primer periodo 20XX Habilidad(es)
Módulo diseñado por: Docente María Cristina Marín Valdés
 Módulo diseñado por: Docente María Cristina Marín Valdés I.E. Eduardo Fernández Botero Amalfi (Ant) 2018 CONTENIDOS CONTENIDO PÁGINA Concepto de poliedros. 3 Clases de poliedros 3 Teorema de Euler. 4 Áreas
Módulo diseñado por: Docente María Cristina Marín Valdés I.E. Eduardo Fernández Botero Amalfi (Ant) 2018 CONTENIDOS CONTENIDO PÁGINA Concepto de poliedros. 3 Clases de poliedros 3 Teorema de Euler. 4 Áreas
APLICACIÓN DE DESARROLLOS
 TEMA: DESARROLLOS DESARROLLOS Es el proceso de trazar una superficie geométrica sobre un plano de tal manera que se pueda extender para mostrar la superficie desarrollada. De tal manera que al cortarla
TEMA: DESARROLLOS DESARROLLOS Es el proceso de trazar una superficie geométrica sobre un plano de tal manera que se pueda extender para mostrar la superficie desarrollada. De tal manera que al cortarla
INSTITUCIÓN EDUCATIVA TÉCNICA SAGRADO CORAZÓN Aprobada según Resolución No NIT DANE SOLEDAD ATLÁNTICO.
 Página 1 de 22 GUÍA N 1 ÁREA: MATEMATICAS GRADO: 601 602 603 Docente: NANCY DE ALBA PERIODO: PRIMERO IH (en horas): 4 EJE TEMÁTICO POLÍGONOS CUERPOS GEOMÉTRICOS Y MOVIMIENTOS EN EL PLANO. DESEMPEÑO Identifica
Página 1 de 22 GUÍA N 1 ÁREA: MATEMATICAS GRADO: 601 602 603 Docente: NANCY DE ALBA PERIODO: PRIMERO IH (en horas): 4 EJE TEMÁTICO POLÍGONOS CUERPOS GEOMÉTRICOS Y MOVIMIENTOS EN EL PLANO. DESEMPEÑO Identifica
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
UNIDAD 1 EXPRESIÓN GRÁFICA.
 UNIDAD 1 EXPRESIÓN GRÁFICA. 1.1 Expresión gráfica. 1.2 El boceto y el croquis. 1.3 La escala de dibujo. 1.4 El sistema diédrico: vistas. 1.5 Perspectivas: isométrica y caballera. 1.6 Acotación y normalización.
UNIDAD 1 EXPRESIÓN GRÁFICA. 1.1 Expresión gráfica. 1.2 El boceto y el croquis. 1.3 La escala de dibujo. 1.4 El sistema diédrico: vistas. 1.5 Perspectivas: isométrica y caballera. 1.6 Acotación y normalización.
UNIDAD 11 Figuras en el espacio
 Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
TEMA 5. Geometría. Teoría. Matemáticas
 1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
POLIEDROS. POLIEDROS Prof. Annabella Zapattini. Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos.
 POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí,
 CONOCE LAS MATEMÁTICAS. CEIP Manuel Siurot (La Palma del Cdo.) Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí, llamadas BASES (que pueden ser
CONOCE LAS MATEMÁTICAS. CEIP Manuel Siurot (La Palma del Cdo.) Definición: Un prisma es un cuerpo geométrico (un poliedro) que tiene dos bases iguales y paralelas entre sí, llamadas BASES (que pueden ser
Preparado por el Arqto. Jing Chang Lou
 POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
POLIIEDROS A P U N T E D O C E N T E Preparado por el Arqto. Jing Chang Lou U N I V ER S I D A D D E C H I L E F AC U L T A D D E A R Q U I T EC T U R A Y U R B A N I S MO D EPARTAMENTO C I ENCIAS DE L
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
ACTIVIDADES PARA LA SESIÓN SEXTA
 ACTIVIDADES PARA LA SESIÓN SEXTA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 6 POLIEDROS ARQUIMEDIANOS 1. Qué se ve en la imagen?
ACTIVIDADES PARA LA SESIÓN SEXTA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 6 POLIEDROS ARQUIMEDIANOS 1. Qué se ve en la imagen?
INSTITUCIÓN EDUCATIVA HÉCTOR ABAD GÓMEZ
 Nombre del Documento: Evaluación de tercer período de geometría grado 8 Versión 01 Página 1 Evaluación de tercer periodo de geometría Grado: 8 Docente: Janny Lucia Bueno Valencia que son polígonos congruentes
Nombre del Documento: Evaluación de tercer período de geometría grado 8 Versión 01 Página 1 Evaluación de tercer periodo de geometría Grado: 8 Docente: Janny Lucia Bueno Valencia que son polígonos congruentes
unidad 10 Cuerpos geométricos
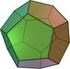 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
TEMA 9: CUERPOS GEOMÉTRICOS
 1 TEMA 9: CUERPOS GEOMÉTRICOS CUERPOS GEOMETRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos.
1 TEMA 9: CUERPOS GEOMÉTRICOS CUERPOS GEOMETRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos geométricos.
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
CIENCIAS SOCIALES: SEXTO DE PRIMARIA CBM NUESTRA SEÑORA DE LOS ÁNGELES (EL ESPARRAGAL-MURCIA)
 CIENCIAS SOCIALES: SEXTO DE PRIMARIA CBM NUESTRA SEÑORA DE LOS ÁNGELES (EL ESPARRAGAL-MURCIA) Los planos son representaciones geográficas que indican o marcan ubicaciones de una localidad, un lugar de
CIENCIAS SOCIALES: SEXTO DE PRIMARIA CBM NUESTRA SEÑORA DE LOS ÁNGELES (EL ESPARRAGAL-MURCIA) Los planos son representaciones geográficas que indican o marcan ubicaciones de una localidad, un lugar de
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia
 geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
LOS SOLIDOS CLÁSICOS. Daniela Valdés Torres
 LOS SOLIDOS CLÁSICOS Daniela Valdés Torres La geometría de los solidos clásicos es la base para el diseño de los balones de futbol, de los mapamundis, refugios portátiles, pendientes esféricos masivos,
LOS SOLIDOS CLÁSICOS Daniela Valdés Torres La geometría de los solidos clásicos es la base para el diseño de los balones de futbol, de los mapamundis, refugios portátiles, pendientes esféricos masivos,
Se dice que un poliedro es regular cuando sus caras son polígonos regulares iguales y sus ángulos poliedros tienen el mismo número de caras.
 LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
5to Parcial de Geometría Euclidiana. 2) Sea p un polígono tal que se puede descomponer en n polígonos simples
 5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
ACTIVIDADES PARA LA SESIÓN PRIMERA
 ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
ACTIVIDADES PARA LA SESIÓN PRIMERA AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Sesión 1 1. Los poliedros regulares convexos: Cuántos
GEOMETRÍA DEL ESPACIO
 GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
GEOMETRÍA DEL ESPACIO Lic. Saúl Villamizar Valencia 33 1 GEOMETRÍA DEL ESPACIO Definición: Es la parte de la geometría que estudia las propiedades de las figuras y sólidos geométricos cuyos elementos
Lámina 1a. Cálculo mental diario
 Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
!!!!!!!!! TEMA 1: DIBUJO 1.INSTRUMENTOS 2.SOPORTES 3.BOCETOS, CROQUIS Y PLANOS 4.VISTAS 5.PERSPECTIVAS
 TEMA 1: DIBUJO 1.INSTRUMENTOS 2.SOPORTES 3.BOCETOS, CROQUIS Y PLANOS 4.VISTAS 5.PERSPECTIVAS 1.INSTRUMENTOS Lápices Son los principales instrumentos de trazado. Se fabrican en madera y llevan en su interior
TEMA 1: DIBUJO 1.INSTRUMENTOS 2.SOPORTES 3.BOCETOS, CROQUIS Y PLANOS 4.VISTAS 5.PERSPECTIVAS 1.INSTRUMENTOS Lápices Son los principales instrumentos de trazado. Se fabrican en madera y llevan en su interior
Poliedros Regulares- Patricia Muñoz. Poliedros Regulares. D.I. Patricia Muñoz. Laboratorio de Morfología SICyT - FADU - UBA
 Poliedros Regulares- Patricia Muñoz 1 Poliedros Regulares D.I. Patricia Muñoz Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU - UBA Poliedros
Poliedros Regulares- Patricia Muñoz 1 Poliedros Regulares D.I. Patricia Muñoz Laboratorio de Morfología SICyT - FADU - UBA Cátedra de Morfología Especial 1 Carrera de Diseño Industrial FADU - UBA Poliedros
6. Mosaicos y movimientos. en el plano
 6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
Matemáticas UNIDAD 11 CUBOS Y PRISMAS RECTOS SECTOR. Material de apoyo complementario para el docente. Preparado por: Irene Villarroel SEMESTRE: 2
 SECTOR Material de apoyo complementario para el docente UNIDAD 11 CUBOS Y PRISMAS RECTOS SEMESTRE: 2 DURACIÓN: 3 semanas Preparado por: Irene Villarroel Diseño Gráfico por: www.genesisgrafica.cl UNIDAD
SECTOR Material de apoyo complementario para el docente UNIDAD 11 CUBOS Y PRISMAS RECTOS SEMESTRE: 2 DURACIÓN: 3 semanas Preparado por: Irene Villarroel Diseño Gráfico por: www.genesisgrafica.cl UNIDAD
Grupos espaciales de simetría
 Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
Lámina 1a. Cálculo mental diario
 Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
ES U. Número de publicación: REGISTRO DE LA PROPIEDAD INDUSTRIAL. Número de solicitud: U Int. Cl.
 k 19 REGISTRO DE LA PROPIEDAD INDUSTRIAL ESPAÑA 11 k Número de publicación: 1 011 706 1 k Número de solicitud: U 8803681 51 k Int. Cl. 4 : A63F 9/00 k 1 SOLICITUD DE MODELO DE UTILIDAD U k Fecha de presentación:
k 19 REGISTRO DE LA PROPIEDAD INDUSTRIAL ESPAÑA 11 k Número de publicación: 1 011 706 1 k Número de solicitud: U 8803681 51 k Int. Cl. 4 : A63F 9/00 k 1 SOLICITUD DE MODELO DE UTILIDAD U k Fecha de presentación:
unidad 11 Transformaciones geométricas
 unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60 con regla y compás Página 1 La cuerda de un arco de 60 (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso:
unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60 con regla y compás Página 1 La cuerda de un arco de 60 (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso:
Remedial Unidad N 3 Matemática Sexto Año Básico 2017
 v Remedial Unidad N 3 Matemática Sexto Año Básico 2017 GUÍA DE TRABAJO REMEDIAL N 1 UNIDAD N 3 Nombre Curso 6 año básico Fecha Objetivo Habilidad cognitiva Tiempo Reconocer elementos propios de las de
v Remedial Unidad N 3 Matemática Sexto Año Básico 2017 GUÍA DE TRABAJO REMEDIAL N 1 UNIDAD N 3 Nombre Curso 6 año básico Fecha Objetivo Habilidad cognitiva Tiempo Reconocer elementos propios de las de
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA VI: Geometría 3D (III)
 UNIDAD DIDÁCTICA VI: Geometría 3D (III) 1 ÍNDICE Página: 2 SUPERFICIES PRISMÁTICAS.. 2 2.1 PRISMAS 2 3 SUPERFICIES PIRAMIDALES.. 3 3.1 PIRÁMIDES 4 4 SECCIONES PLANAS. 5 5 DESARROLLOS Y TRANSFORMADAS...
UNIDAD DIDÁCTICA VI: Geometría 3D (III) 1 ÍNDICE Página: 2 SUPERFICIES PRISMÁTICAS.. 2 2.1 PRISMAS 2 3 SUPERFICIES PIRAMIDALES.. 3 3.1 PIRÁMIDES 4 4 SECCIONES PLANAS. 5 5 DESARROLLOS Y TRANSFORMADAS...
DIBUJO GEOMÉTRICO. - Segmento: es una parte limitada de la recta comprendida entre dos puntos que por lo tanto se nombraran con mayúscula.
 DIBUJO GEOMÉTRICO 1. SIGNOS Y LÍNEAS. A. El punto: es la intersección de dos rectas. Se designa mediante una letra mayúscula y se puede representar también con un círculo pequeño o un punto. A B C D X
DIBUJO GEOMÉTRICO 1. SIGNOS Y LÍNEAS. A. El punto: es la intersección de dos rectas. Se designa mediante una letra mayúscula y se puede representar también con un círculo pequeño o un punto. A B C D X
Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja?
 Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
MATEMÁTICAS Y SU DIDÁCTICA
 MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2009 2010 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2009 2010 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
PAUTAS PARA RELIZAR EL EXAMEN DE LOS TEMAS 1 Y 2.
 PAUTAS PARA RELIZAR EL EXAMEN DE LOS TEMAS 1 Y 2. 1. Vocabulario: el alumno debe definir correctamente los siguientes términos: Geografía. Geografía física. Geografía humana. Meridiano. Paralelo. Latitud.
PAUTAS PARA RELIZAR EL EXAMEN DE LOS TEMAS 1 Y 2. 1. Vocabulario: el alumno debe definir correctamente los siguientes términos: Geografía. Geografía física. Geografía humana. Meridiano. Paralelo. Latitud.
ESTRU R C U T C UR U A R S A D E D LOS O MAT A ERI R AL A ES
 ESTRUCTURAS DE LOS MATERIALES Cristalina CRISTALINOS METALES COMPUESTOS IÓNICOS COMPUESTOS COMPLEJOS COV.-ION. SÓLIDOS COVALENTES COVALENTE PURO SÓLIDOS MOLECULARES NO CRISTALINOS (AMORFOS) VIDRIOS INORGÁNICOS
ESTRUCTURAS DE LOS MATERIALES Cristalina CRISTALINOS METALES COMPUESTOS IÓNICOS COMPUESTOS COMPLEJOS COV.-ION. SÓLIDOS COVALENTES COVALENTE PURO SÓLIDOS MOLECULARES NO CRISTALINOS (AMORFOS) VIDRIOS INORGÁNICOS
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
 Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
11 CONOCER LOS POLIEDROS Y DIFERENCIAR
 REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
PÁGINA 98. a) Tetraedro = 2 Cubo = 2 Octaedro = 2 Dodecaedro = 2 Icosaedro = 2
 PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DEL BAJO CAUCA
 Las matemáticas, históricamente, comenzaron con la geometría. La geometría es la ciencia que estudia la forma y posición de la figuras y nos enseña a medir su extensión. Geometría (del griego geo, tierra,
Las matemáticas, históricamente, comenzaron con la geometría. La geometría es la ciencia que estudia la forma y posición de la figuras y nos enseña a medir su extensión. Geometría (del griego geo, tierra,
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría. Ángulos. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Los elementos básicos de la Geometría Plana son el punto, la línea, y el plano.
 GEOMETRÍA PLANA Dibujo Geométrico La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras planas y tridimensionales en el espacio. La palabra procede de dos
GEOMETRÍA PLANA Dibujo Geométrico La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras planas y tridimensionales en el espacio. La palabra procede de dos
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
2. ELEMENTOS GEOGRÁFICOS
 1. CONCEPTO DE TOPOGRAFÍA (topo = lugar, grafos = descripción). La topografía es la ciencia que estudia el conjunto de principios y procedimientos que tienen por objeto la representación gráfica de la
1. CONCEPTO DE TOPOGRAFÍA (topo = lugar, grafos = descripción). La topografía es la ciencia que estudia el conjunto de principios y procedimientos que tienen por objeto la representación gráfica de la
Figura 1 Figura 2 Figura 3
 Sesión 1. Áreas en tangram y tramas 1. Este ejercicio se realiza con las piezas del Tangram. Figura 1 Figura 2 Figura 3 a) Tomando como unidad de superficie la figura 1, calcular la superficie de la figura
Sesión 1. Áreas en tangram y tramas 1. Este ejercicio se realiza con las piezas del Tangram. Figura 1 Figura 2 Figura 3 a) Tomando como unidad de superficie la figura 1, calcular la superficie de la figura
Enlace con el hogar no. 28 H Actividad
 For use after Unit Four, Session 2. NOMBRE FECHA Enlace con el hogar no. 28 H Actividad NOTA PARA LA FAMILIA DEL ALUMNO El Origami es el arte tradicional japonés de doblar papel o papiroflexia y es una
For use after Unit Four, Session 2. NOMBRE FECHA Enlace con el hogar no. 28 H Actividad NOTA PARA LA FAMILIA DEL ALUMNO El Origami es el arte tradicional japonés de doblar papel o papiroflexia y es una
 http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
http://www.matesymas.es/ MATERIAL PLOT El material PLOT está formado por láminas de cartulina troquelada y gomas elásticas de colores para realizar las uniones. De las láminas de cartulina se obtienen
