TRIANGULACIONES Y HOMOLOGÍA SIMPLICIAL
|
|
|
- Lidia Figueroa Rubio
- hace 6 años
- Vistas:
Transcripción
1 Pro Mathematica Vol. XVIII, Nos , 2004 TRIANGULACIONES Y HOMOLOGÍA SIMPLICIAL Christian Valqui Resumen La fórmula de Poincaré-Euler para poliedros convexos se generaliza a través de triangulaciones y la homología simplicial. Esto permite captar de manera intuitiva la idea de homología. O Sección Matemática, Departamento de Ciencias, PUCP
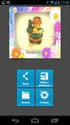
2 1 La Fórmula de Poincaré-Euler Euler se dio cuenta en 1752 que en un poliedro convexo siempre se cumple la relación V -A+e = 2, donde V, A y e son los números de Vértices, Aristas y Caras respectivamente. Esto se verifica rápidamente en un tetraedro (V=4, A=6, C=4), en un cubo (V=8, A=12, C=6) y en un dodecaedro (V=12, A=30, C=20). Figura 1.1 Dodecaedro, Tetraedro y Cubo Figura 1.2 Pelota de fútbol También vale para una pelota de futbol estándar con doce paños pentagonales y 20 hexagonales (V=60, A=90, C=32). Una demostración bastante simple es debido a Thurston [2]: Coloquemos el poliedro en el espacio, de modo que ninguna arista esté horizontal- en particular, hay un único vértice máximo U y un único mínimo L. Calculemos la cantidad V- A+ e poniendo un signo "+" en cada vértice y en el centro de cada cara, y un signo "-" en el centro de cada arista. Mostraremos que todos los signos se cancelan entre sí, excepto los dos signos "+" en U y L. 68
3 + + Figura 1.3 Se gira contra el reloj Para esto desplazamos los signos de los vértices y las aristas hacia una cara adyacente. La dirección es determinada por la regla de que cada signo se mueve horizontalmente, en contra del sentido del reloj, visto desde arriba. De esta manera, cada cara recibe los signos correspondientes a un intervalo abierto de su frontera, Arista-cara-arista-... -arista -cara-arista, es decir, una suma total de = Figura 1.4 Una cara recibe = -1 69
4 Sumando al + 1 que teníamos al centro de la cara, obtenemos una suma total de cero en cada cara. Lo que queda como suma final de todo el poliedro es +2, correspondiente a U y L. O Sí el poliedro P no es convexo la suma alternada nos va a dar la característica de Euler (ver definición 3.1), x(p) =V- A+ e (1.1) siempre y cuando las caras sean polígonos homeomorfos a polígonos convexos. Como ejemplos veamos poliedros que son homeomorfos a superficies de característica cero (el toro T) y -2 (el bítoro BT). En el primer caso cortamos las caras inferior y superior en trapecios (polígonos convexos) y tenemos que e= 16, A= 32 y V = 16, (ver figura) Figura 1.5 Poliedro homeomorfo al toro y la suma alternada nos da x(t) = O. Sí juntamos dos toros según la figura Figura 1.6 Bitoro se pierden dos caras, pero ninguna esquina ni arista, de modo que e = 30, A= 64 y V= 32. Así V- A+ e= -2 = x(bt). Notemos que se puede asumir que los poliedros sólo tienen caras triangulares, pues al partir un polígono en un triángulo y en un polígono 70
5 con un lado menos, V - A + e se mantiene constante, pues la cantidad V de vértices no cambia, e aumenta en + 1, pero también A aumenta en +l. Si hacemos esto con el toro obtenemos una triangulación del toro con e = 32, A= 48 y V = 16 (ver figura) Figura l. 7 Toro triangulado En lo que sigue vamos a formalizar el concepto de triangulación para poder definir la homología simplicial y analizar su relación con las fórmulas mostradas anteriormente. 2 Triangulaciones En esta parte vamos a generalizar el concepto de triangulación de una superficie, que no es otra cosa que el cubrimiento de la superficie con triángulos de tal manera, que si dos triángulos se intersecan, tienen una lado completo o una esquina en común. Los triángulos son 2-símplices, y en el caso general consideramos n-símplices. Definición 2.1 El n-símplice estándar ~n está dado por ~n:={(xo,...,xn)ejrn+l, tq n LXi=1yxi;::O, \fi} i=o Las k-caras del n-símplice estándar son los subconjuntos El 0-símplice estándar es el punto {1} e JR, el 1-símplice es un trozo de recta, el 2-símplice es un triángulo (ver figura) y el 3-símplice es un 71
6 tetraedro (contenido en IR 4 ). Figura 2.1 Los 0,1,2-símplices estándar Las O-caras de.6. 3 son las esquinas, las 1-caras son las aristas, las 2-caras son las caras propiamente dichas y la única 3-cara es el.6. 3 mismo. Definición 2.2 Sea X un espacio de Hausdorff. Un atlas simplicial de X es un conjunto S de funciones continuas de algún.ó.n a X {las funciones de un.ó.n para n fijo forman un subconjunto de S denotado por Sn) que cumplen las siguientes condiciones: 1. X= UsES Im(s) 2. Todo s es inyectivo. Como X es de Hausdorff y.ó.n compacto esto implica que s(.ó.n) = Im(s) es cerrado y homeomorfo a.ó.n- 3. Cualesquiera dos funciones s, t E S están relacionadas linealmente entre sí. Esto significa que si s :.Ó.m ~ X y t :.Ó.n ~ X tienen imágenes no disjuntas, entonces s- 1 t(.ó.n) es una cara de.ó.m (y recíprocamente}, además s- 1 t es una función lineal. Si s- 1 t preserva el orden de los vértices para todo s, t, se dice que el atlas S es ordenado. 4. La topología de X está dada por S. Esto significa que A C X es cerrado si y solamente si A n Im(s) es cerrado para todo s. Ejemplos de atlas simpliciales: a) Como primer ejemplo tenemos los poliedros con caras triangulares como el tetraedro o el poliedro de la figura 1.5. Aquí se considera a los triángulos como imágenes de Componiendo estas triangulaciones con homeomorfismos de poliedros con superficies obtenemos triangulaciones de superficies. Verifiquemos en este ejemplo 72
7 las condiciones de la definición: La condición 1, X es igual a la unión, significa que los triángulos cubren a todo el poliedro (o superficie), mientras que la condición 2 significa que los triángulos son no degenerados, es decir imágenes inyectivas de ~2 La condición 3 significa que la intersección de dos triángulos debe ser un lado común a ambos, o sino una esquina. En particular, un lado de un triángulo no puede ser la unión de dos lados de otros dos triángulos (ver figura). Figura 2.2 Esto NO es triangulación del cuadrado La última condición 4 se cumple en nuestro caso poniendo la topología inducida en la superficie como subespacio de IR 3. El objetivo de esta condición es poder seguir usando las herramientas de la topología en espacios simpliciales de dimensión infinita. b) X= ~n, S= {Id} e) X = ~n y S se forma de todas las inclusiones ordenadas de símplices menores como caras, es decir con s~,...,ik :~k ~ ~n, (to,..., tk) r-t L tjei;. k j=o Por ejemplo sg' 2 = d incluye ~ 1 como cara en ~ 2, según la fórmula de arriba, tenemos s~' 2 (t 1,t 2 ) = (h,o,t 2 ) (ver figura). 73
8 Figura 2.3 s~' 2 = é~: ~1 como cara de ~2 d) Si cjj: ~n ~En = {x E ~n, llxll :S 1}, se puede formar el atlas cjjs = { cjj os, s E S} para cada uno de los dos ejemplos anteriores. Se puede demostrar las siguientes afirmaciones [1, Prop.V.7.2, V.7.4 y V.7.5]: l. Todo atlas (ordenado) está contenido en un único atlas maximal (ordenado). 2. Todo atlas maximal contiene a un atlas maximal ordenado que se llama triangulación. 3. Para un atlas simplicial ordenado S son equivalentes: a) S es maximal, b) s E Sn :::::} s o é~ E Sn-1 para todo e~, donde é~ son las inclusiones de las (n- 1)-caras en ~n e) Dado un punto PE X, existe un únicos E S (en un único Sn) o de modo que P E s(~n) Notemos que en el ejemplo b) el atlas (X= ~n' S= {Id}) no es maximal; un punto de una arista no está en el interior (relativo) de la imagen del único mapa s = Id E S. 74
9 3 Homología Simplicial Partiendo de un espacio triangulado (X, S) construimos un complejo de cadenas de grupos abelianos. La homología de este complejo es por definición la homología simplicial de X. Definimos SPn := Grupo abeliano libre generado por Sn y el diferencial an : SPn -+ SPn-1 dado por n an(s) = z) -l)is o e~ i=o en la base y extendido linealmente. Definimos la homología simplicial HSP(X) como la homología del complejo (SPn, an)nen Sea por ejemplo la triangulación del 2-símplice estándar: Entonces SP 0 e 0 ZEBe 1 ZEBe 2 Ze::'ZEBZEBZ=Z 3 S~ ~ZEB~ZEB~Ze::'ZEBZEBZ=~ SP2 IdZe::'Z Obviamente SPn = {O} paran ~ {0, 1, 2}, y los diferenciales relevantes (no nulos) al' a2 están dados de la siguiente manera en los generadores: El diferencial a 2 está definido por y al definido a través de ~ r-r eo - el ~ r-r eo - e2 ~ r-r el - e2. Es un cálculo directo verificar que el núcleo de a 1 es justamente la imagen de a 2 (Ejercicio para el lector). Sabemos además que 3 = dim(spl) = 75
10 dim(im(81)) + dim(ker(81)), que Ker(8 0 ) = SPo y que Ker(82) =O. Entonces podemos calcular la homología HSPn(X) = Ker(on)/ Im(on+d Y obtenemos H 0 ~ Z, H1 = {O} y H2 = {0}. Si tomamos como X solamente el triángulo que es el borde de ó 2, horneom orfo a 8 1, obtenemos usando los cálculos anteriores que H (S1 ) = { Z k = O, 1 k o k, :. o, 1 Notemos que hemos usado el hecho que un homeomorfismo da lugar a un isomorfismo en los complejos simpliciales y por tanto induce un isomorfismo en la homología. Extendiendo nuestro resultado se puede verificar (aunque los cálculos involucrados se hacen cada vez más largos) que para las esferas unitarias sn ~ Ón se tiene H (Sn) = { Z k= O, n k O k ;j:. O, n (3.1) Notemos que aquí usamos el símbolo H(X), que es la homología usual construida a partir del complejo singular de un espacio. Es un teorema (ver [1, Prop. V.8. 7]) que la homología simplicial coincide con esta homología, en particular no depende de la triangulación escogida. Este resultado del cálculo de la homología para sn es uno de los primeros resultados importantes de las teorías homológicas, pues demuestra que las esferas no pueden ser homeomorfas entre sí (este es un resultado del cual no conozco prueba alguna que no use homología). Veremos ahora la fórmula de Poincaré-Euler bajo la luz de los resultados nuevos. Definición 3.1 Dado un espacio triangulado X de dimensión finita n, la característica de Euler está dada por Además tenemos que n x(x) := 2) -1);dim(H;(X)). i=o dim(h;(x)) = dim(ker8;jim(8i+1)) dim(k er(o;)) - dim(im(8hl)) 76
11 y dim(k er(oi)) + dim(im(oi)) = dim(spi) Esto nos permite calcular x(x) L) -1)idim(Hi(SP(X))) :~::) -1)i [dim(ker(oi))- dim(im(oi+l))] "L)-1)idim(Ker(oi)) + "L:(-1)i+ 1 dim(im(8h )) L:(-1)idim(Ker(oi)) + "L:(-1)idim(Im(8i)) L( -1)i (dim(ker(oi)) + dim(im(oi))) L( -1)idim(SPi)) Notemos que dim(spi) es el número de i-símplices de la triangulación. En el caso de una superficie triangulada como en la primera parte es entonces el número de los vértices (0-símplices), de las aristas (1- símplices) y de las caras triangulares (2-símplices) respectivamente, de modo que la última suma alternada no es otra cosa que V - A + C, con lo cual queda probada la fórmula (1.1). Notemos que la homología de un poliedro convexo es la misma que la de S 2, y la característica de Euler de S 2 es 2 (Ya conocemos la homología de las esferas por (3.1)) con lo cual vemos que la fórmula de Euler es un caso particular del cálculo de invariantes homológicas. Espero que este breve paseo por los orígenes de las teorías homológicas motive a estudiar más a fondo esta herramienta que se ha vuelto indispensable en la matemática moderna. Referencias [1] ALBRECHT DOLD: Lectures on Algebraic Topology. Grundlehren der mathematischen Wissenschaften Springer Verlag (1972). 77
12 [2] W.P. THURSTON: The Geometry and Topology of Three-Dimensional Manifolds. Notas no publicadas. Referencia encontrada en / /junkyard/ euler / charges.html. Christian Valqui Sección Matemática, Departamento de Ciencias Pontificia Universidad Católica del Perú cvalqui@pucp. edu. pe 78
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton
 Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
POLIEDROS. POLIEDROS Prof. Annabella Zapattini. Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos.
 POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
POLIEDROS Definición: Llamamos poliedro a la región del espacio limitada por polígonos planos. Definiciones: Llamamos caras de un poliedro a los polígonos que lo definen. Llamamos aristas a los segmentos
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
3-variedades. Una 3-variedad es un espacio topologico (hausdorff y segundo numerable) que es localmente homeomorfo a R3.
 3-Variedades 3-variedades Las 3- variedades son espacios que localmente se parecen al espacio euclidiano. Dos variedades son iguales si es posible deformar continuamente a una para obtener la otra Una
3-Variedades 3-variedades Las 3- variedades son espacios que localmente se parecen al espacio euclidiano. Dos variedades son iguales si es posible deformar continuamente a una para obtener la otra Una
TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS
 TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS Ejercicio 4.1.- Relación 4. Compacidad. Conexión Supongamos que A es compacto y sea A α Λ B α un recubrimiento de A por bolas abiertas. Entonces, como
TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS Ejercicio 4.1.- Relación 4. Compacidad. Conexión Supongamos que A es compacto y sea A α Λ B α un recubrimiento de A por bolas abiertas. Entonces, como
Clasificación de superficies compactas
 Clasificación de superficies compactas Fuente: http://topologia.wordpress.com/2009/01/03/clasificacion-de-superficies-i/ Apuntes basados en las referencias: C. Koswniowski, Topología algebraica, 1986,
Clasificación de superficies compactas Fuente: http://topologia.wordpress.com/2009/01/03/clasificacion-de-superficies-i/ Apuntes basados en las referencias: C. Koswniowski, Topología algebraica, 1986,
Clasificación de superficies compactas
 Clasificación de superficies compactas Hemos visto al principio de curso superficies sencillas como la esfera, el toro, el cilindro, la banda de Möbius, el plano proyectivo, la botella de Klein. Todas
Clasificación de superficies compactas Hemos visto al principio de curso superficies sencillas como la esfera, el toro, el cilindro, la banda de Möbius, el plano proyectivo, la botella de Klein. Todas
Superficies. Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Esfera Toro Abierto del plano
 Superficies Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Ejemplos: Esfera Toro Abierto del plano Superficies abiertas y cerradas Hay muchas maneras de
Superficies Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Ejemplos: Esfera Toro Abierto del plano Superficies abiertas y cerradas Hay muchas maneras de
Poliedros regulares. CAPÍTULO 1 - Teorema de Euler. Poliedros regulares convexos (solidos platónicos)
 Poliedros regulares CAPÍTULO 1 - Teorema de Euler (1-a) Poliedros regulares convexos (solidos platónicos) (1-b) Leonhard Paul Euler Demostró un teorema referido a los poliedros. Fue matemático y físico.
Poliedros regulares CAPÍTULO 1 - Teorema de Euler (1-a) Poliedros regulares convexos (solidos platónicos) (1-b) Leonhard Paul Euler Demostró un teorema referido a los poliedros. Fue matemático y físico.
58 7. ESPACIOS COCIENTE
 CAPíULO 7 Espacios cociente En esta sección estudiamos el cociente de un espacio vectorial por un subespacio W. Este cociente se define como el conjunto cociente de por una relación de equivalencia conveniente.
CAPíULO 7 Espacios cociente En esta sección estudiamos el cociente de un espacio vectorial por un subespacio W. Este cociente se define como el conjunto cociente de por una relación de equivalencia conveniente.
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Ampliación de Topología
 Ampliación de Topología Problemas. Curso 2003 04 Homotopía de aplicaciones y tipos de homotopía 1. Sea X un espacio, y sea f: S 1 X una aplicación continua. Demostrar que f es homótopa a una aplicación
Ampliación de Topología Problemas. Curso 2003 04 Homotopía de aplicaciones y tipos de homotopía 1. Sea X un espacio, y sea f: S 1 X una aplicación continua. Demostrar que f es homótopa a una aplicación
Complejos Simpliciales y Poliedros (Introducción) Notas - Ejercicios Guiados
 Complejos Simpliciales y Poliedros (Introducción) Notas - Ejercicios Guiados Un poliedro es un espacio topológico que admite una triangulación por un complejo simplicial. Las triangulaciones permiten analizar
Complejos Simpliciales y Poliedros (Introducción) Notas - Ejercicios Guiados Un poliedro es un espacio topológico que admite una triangulación por un complejo simplicial. Las triangulaciones permiten analizar
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Se dice que un poliedro es regular cuando sus caras son polígonos regulares iguales y sus ángulos poliedros tienen el mismo número de caras.
 LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
LOS POLIEDROS: El cubo, la pirámide, la esfera, el cilindro... son figuras sólidas. Observando tales figuras, vemos que algunos sólidos, como el cubo y la pirámide, tienen su superficie exterior formada
1. Espacios topológicos compactos.
 PRACTICO 6. COMPACIDAD. 1. Espacios topológicos compactos. Definición 1 Un cubrimiento de un conjunto X es una familia de subconjuntos de X cuya unión da X. Un cubrimiento de un espacio es abierto si cada
PRACTICO 6. COMPACIDAD. 1. Espacios topológicos compactos. Definición 1 Un cubrimiento de un conjunto X es una familia de subconjuntos de X cuya unión da X. Un cubrimiento de un espacio es abierto si cada
Teorema de punto fijo de Lefschetz: Versión topológica y versiones combinatorias.
 Teorema de punto fijo de Lefschetz: Versión topológica y versiones combinatorias. E.G. Minian La versión clásica (topológica) del teorema de punto fijo de Lefschetz da condiciones suficientes para que
Teorema de punto fijo de Lefschetz: Versión topológica y versiones combinatorias. E.G. Minian La versión clásica (topológica) del teorema de punto fijo de Lefschetz da condiciones suficientes para que
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS Desarrollo de los Poliedros Regulares.
 1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
1 38. CUERPOS SÓLIDOS: DESARROLLOS Y TRANSFORMADAS. 38.1. Desarrollo de los Poliedros Regulares. 38.1.1. Tetraedro. Dado que los poliedros regulares tienen sus caras iguales, el desarrollo de los mismos
Hablemos de la esfera.
 Hablemos de la esfera. Cristián U. Sánchez Les propongo mirar una prueba de la conocida? profunda fórmula sobre los poliedros debida a Euler: V L + C = 2 y de paso revisar algunas ideas sobre la esfera
Hablemos de la esfera. Cristián U. Sánchez Les propongo mirar una prueba de la conocida? profunda fórmula sobre los poliedros debida a Euler: V L + C = 2 y de paso revisar algunas ideas sobre la esfera
Figura 1.7 Además, para poliedros específicos puede ser muy fácil establecer una correspondencia adecuada entre sus puntos y los de la esfera. Por eje
 1.2 Equivalencia topológica Existen diversas demostraciones del teorema de Euler. Hemos elegido la anterior por dos razones. La primera, su elegancia; muchas de las restantes demostraciones usan inducción
1.2 Equivalencia topológica Existen diversas demostraciones del teorema de Euler. Hemos elegido la anterior por dos razones. La primera, su elegancia; muchas de las restantes demostraciones usan inducción
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos
![Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos Semana02[1/23] Conjuntos. 9 de marzo de Conjuntos](/thumbs/53/31721818.jpg) Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
Semana02[1/23] 9 de marzo de 2007 Introducción Semana02[2/23] La teoría de conjuntos gira en torno a la función proposicional x A. Los valores que hacen verdadera la función proposicional x A son aquellos
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS
 APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Estructura de la frontera de un conjunto convexo. Los politopos
 Capítulo 2 Estructura de la frontera de un conjunto convexo. Los politopos Cuando hablamos de polígonos y poliedros (cubos, prismas, etc.) es bien conocido por todos el significado de los términos vértice
Capítulo 2 Estructura de la frontera de un conjunto convexo. Los politopos Cuando hablamos de polígonos y poliedros (cubos, prismas, etc.) es bien conocido por todos el significado de los términos vértice
Parte 2: Definición y ejemplos de topologías.
 Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Parte 2: Definición y ejemplos de topologías. 22 de marzo de 2014 1. Definiciones y propiedades básicas. Definición 1 Sea X un conjunto. Una familia T de subconjuntos de X es una topología de X si se cumplen:
Geometría convexa y politopos, día 2
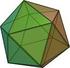 Geometría convexa y politopos, día 2 Alexey Beshenov (cadadr@gmail.com) 9 de agosto de 2016 2. La envolvente convexa 2.1. Definición. Si X R n es cualquier conjunto, entonces la envolvente convexa de X
Geometría convexa y politopos, día 2 Alexey Beshenov (cadadr@gmail.com) 9 de agosto de 2016 2. La envolvente convexa 2.1. Definición. Si X R n es cualquier conjunto, entonces la envolvente convexa de X
Descomposición en valores singulares de una matriz
 Descomposición en valores singulares de una matriz Estas notas están dedicadas a demostrar una extensión del teorema espectral conocida como descomposición en valores singulares (SVD en inglés) de gran
Descomposición en valores singulares de una matriz Estas notas están dedicadas a demostrar una extensión del teorema espectral conocida como descomposición en valores singulares (SVD en inglés) de gran
TEMA 5. Geometría. Teoría. Matemáticas
 1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
1 La Geometría trata sobre las formas y sus propiedades. A su vez, se puede dividir en: Geometría plana: trata de las figuras en el plano, (dos dimensiones) Geometría tridimensional: trata de figuras en
Subespacios de espacios vectoriales
 Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
IES FONTEXERÍA MUROS. 14-II-2014 Nombre y apellidos:.
 IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
11 CONOCER LOS POLIEDROS Y DIFERENCIAR
 REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
REPASO Y APOYO OBJETIVO 1 11 CONOCER LOS POLIEDROS Y DIERENCIAR LOS POLIEDROS REGULARES Nombre: Curso: echa: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos.
unidad 10 Cuerpos geométricos
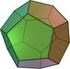 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
Teoría de la Dimensión
 Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Descomposición de dos Anillos de Funciones Continuas
 Miscelánea Matemática 38 (2003) 65 75 SMM Descomposición de dos Anillos de Funciones Continuas Rogelio Fernández-Alonso Departamento de Matemáticas Universidad Autónoma Metropolitana-I 09340 México, D.F.
Miscelánea Matemática 38 (2003) 65 75 SMM Descomposición de dos Anillos de Funciones Continuas Rogelio Fernández-Alonso Departamento de Matemáticas Universidad Autónoma Metropolitana-I 09340 México, D.F.
Cuestiones de Álgebra Lineal
 Cuestiones de Álgebra Lineal Algunas de las cuestiones que aparecen en esta relación están pensadas para ser introducidas en un plataforma interactiva de aprendizaje de modo que los parámetros a, b que
Cuestiones de Álgebra Lineal Algunas de las cuestiones que aparecen en esta relación están pensadas para ser introducidas en un plataforma interactiva de aprendizaje de modo que los parámetros a, b que
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
 Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
Reconocer y utilizar las propiedades sencillas de la topología métrica.
 3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
3 Funciones continuas De entre todas las aplicaciones que pueden definirse entre dos espacios métrico, las aplicaciones continuas ocupan un papel preponderante. Su estudio es fundamental no sólo en topología,
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Cuerpos geométricos. Cuerpos redondos Cuerpos de revolución. Poliedros (más importantes)
 Cuerpos geométricos Cuerpos redondos Cuerpos de revolución Poliedros (más importantes) Cuerpo geométrico limitado por caras que son polígonos Cuerpo geométrico que se obtiene a partir de una figura plana
Cuerpos geométricos Cuerpos redondos Cuerpos de revolución Poliedros (más importantes) Cuerpo geométrico limitado por caras que son polígonos Cuerpo geométrico que se obtiene a partir de una figura plana
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
El espacio euclideano
 Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos
 Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Cálculo Avanzado Segundo Cuatrimestre de 2012 Práctica 2 -Cardinalidad- A. Propiedades básicas de los Conjuntos Ejercicio 1. Demostrar las siguientes igualdades de conjuntos: i) B i I A i = i I(B A i ).
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
Representaciones Matriciales de Grafos Isomorfismos de Grafos Grafos Planos. Matemática Discreta. Agustín G. Bonifacio UNSL. Teoría de Grafos III
 UNSL Teoría de Grafos III Matriz de Adyacencia Matriz de Incidencia a b c d e a 0 1 0 0 1 b 1 0 1 0 1 c 0 1 2 0 1 d 0 0 0 0 2 e 1 1 1 2 0 Dado un grafo G = (V,E), la matriz de adyacencia de G, denotada
UNSL Teoría de Grafos III Matriz de Adyacencia Matriz de Incidencia a b c d e a 0 1 0 0 1 b 1 0 1 0 1 c 0 1 2 0 1 d 0 0 0 0 2 e 1 1 1 2 0 Dado un grafo G = (V,E), la matriz de adyacencia de G, denotada
Caras, aristas y vértices
 1 Introducción Caras, aristas y vértices Juan Sabia La idea motivadora de este trabajo fue escribir un texto de matemática que, por un lado, pudiera ser leído directamente por estudiantes de la escuela
1 Introducción Caras, aristas y vértices Juan Sabia La idea motivadora de este trabajo fue escribir un texto de matemática que, por un lado, pudiera ser leído directamente por estudiantes de la escuela
Poliedros Regulares en el 3-Toro.
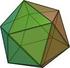 Poliedros Regulares en el 3-Toro. Antonio Montero Daniel Pellicer PCCM, UMSNH-UNAM CCM,UNAM XXVIII Coloquio Víctor Neumann-Lara de Teoría de las Gráficas Combinatoria y sus Aplicaciones Morelia, Marzo
Poliedros Regulares en el 3-Toro. Antonio Montero Daniel Pellicer PCCM, UMSNH-UNAM CCM,UNAM XXVIII Coloquio Víctor Neumann-Lara de Teoría de las Gráficas Combinatoria y sus Aplicaciones Morelia, Marzo
REGULARES.
 Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Diédrico Poliedros REGULARES http://www.edu.xunta.es/contidos/premios/p2004/b/poliedros/poliedros.html POLIEDROS Los poliedros son los cuerpos geométricos limitados por polígonos. Poliedros regulares son
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
3-variedades. Los ejemplos mas simples de variedades abiertas son los abiertos de R 3.
 3-variedades Una 3-variedad es un espacio topológico hausdorff y con base numerable localmente homeomorfo a R 3. Una 3-variedad con borde es un espacio topológico (hausdorf y con base numerable) localmente
3-variedades Una 3-variedad es un espacio topológico hausdorff y con base numerable localmente homeomorfo a R 3. Una 3-variedad con borde es un espacio topológico (hausdorf y con base numerable) localmente
Maquetería 02: Poliedros, cuerpos redondos y su construcción
 Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Maquetería 02: Poliedros, cuerpos redondos y su construcción Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
Tema 2: Determinantes
 Tema 2: Determinantes 1. Introducción En este tema vamos a asignar a cada matriz cuadrada de orden, un número real que llamaremos su determinante y escribiremos. Vamos a ver cómo se calcula. Consideremos
Tema 2: Determinantes 1. Introducción En este tema vamos a asignar a cada matriz cuadrada de orden, un número real que llamaremos su determinante y escribiremos. Vamos a ver cómo se calcula. Consideremos
Ejercicios de Análisis Funcional. Curso
 Ejercicios de Análisis Funcional Curso 2010-2011 1 1 Preliminares de espacios normados Problema 1.1. Demostrar que para 1 < p < la norma. p en R 2 verifica la siguiente propiedad: Si x, y R 2 con x y y
Ejercicios de Análisis Funcional Curso 2010-2011 1 1 Preliminares de espacios normados Problema 1.1. Demostrar que para 1 < p < la norma. p en R 2 verifica la siguiente propiedad: Si x, y R 2 con x y y
1. Poliedros regulares. 2. Fórmula de Euler. 3. Poliedros semiregulares. 4. Poliedros de Catalán. 5. Prismas y antiprismas. 6. Dualidad de poliedros
 7. Poliedros Ámbito científico 1. Poliedros regulares 2. Fórmula de Euler 3. Poliedros semiregulares 4. Poliedros de Catalán 5. Prismas y antiprismas 6. Dualidad de poliedros 7. Dipirámides y deltaedros
7. Poliedros Ámbito científico 1. Poliedros regulares 2. Fórmula de Euler 3. Poliedros semiregulares 4. Poliedros de Catalán 5. Prismas y antiprismas 6. Dualidad de poliedros 7. Dipirámides y deltaedros
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Material educativo. Uso no comercial 12.1 NOCIONES BÁSICAS. Definición 72. Ángulo diedro. Definimos el ángulo diedro que notamos P AB.
 12.1 NOCIONES BÁSICAS Definición 72. Ángulo diedro. Sean 1, 2 distintos, AB, P 1, P AB, Q 2, Q AB. Definimos el ángulo diedro que notamos P AB Q a la figura : P : Q AB. Esto es P AB Q : P : Q AB. Ver figura
12.1 NOCIONES BÁSICAS Definición 72. Ángulo diedro. Sean 1, 2 distintos, AB, P 1, P AB, Q 2, Q AB. Definimos el ángulo diedro que notamos P AB Q a la figura : P : Q AB. Esto es P AB Q : P : Q AB. Ver figura
Cálculo diferencial e integral I. Eleonora Catsigeras
 Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
F-ESPACIOS. 1.- Introducción
 F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Teorema de Lagrange. En esta sección demostramos algunos hechos básicos sobre grupos, que se pueden deducir de la definición
 Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones. 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides.
 Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
18 de enero de 2015 CIMAT. Homología persistente. Malors Espinosa Lara. Introducción. Filtraciones. persistente. Números de Betti persistentes
 s CIMAT 18 de enero de 2015 Plan de la exposición s 1. 2. 3. 4 Persistentes. 5 persistencia. 6. La idea de la homología s La homología permite entender las distintas clases de agujeros de un objeto. Clases
s CIMAT 18 de enero de 2015 Plan de la exposición s 1. 2. 3. 4 Persistentes. 5 persistencia. 6. La idea de la homología s La homología permite entender las distintas clases de agujeros de un objeto. Clases
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
A mi muy querida profesora que con ansias debe estar esperando mi trabajo. I. Introducción pag. 4
 MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
MONOGRAFÍA NOMBRE : COLEGIO : GRADO : IVº B TEMA : Geometría del Espacio PROFESORA : FECHA : 30 de Noviembre DEDICATORIA A mi muy querida profesora que con ansias debe estar esperando mi trabajo índice
Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es
 2. LA FUNCIÓN VOLUMEN Definición 9. Volumen de un poliedro convexo Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es un poliedro convexo, X E. Definimos una función que
2. LA FUNCIÓN VOLUMEN Definición 9. Volumen de un poliedro convexo Sea P el conjunto de todos los poliedros convexos del espacio, esto es P X / X es un poliedro convexo, X E. Definimos una función que
GEOMETRÍA POLIEDROS. Los ángulos diedros y los ángulos poliedros determinados por las caras son los ángulos diedros y ángulos poliedros del poliedro.
 GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
GEOMETRÍA POLIEDROS Poliedro. Un poliedro es la unión de cuatro o más regiones poligonales tales que cada uno de sus lados pertenecen precisamente a dos regiones adyacentes no coplanares. Las regiones
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Introducción a la Teoría de Grafos
 Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
INTRODUCCIÓN A LOS POLIEDROS
 INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
INTRODUCCIÓN A LOS POLIEDROS AUTORIA MIGUEL ÁNGEL GUERRERO MOLINA TEMÁTICA POLIEDROS ETAPA BACHILLERATO Resumen Este artículo pretende dar una visión general de los poliedros. Trataremos su clasificación,
Tipo de triángulo según sus ángulos Característica Dibujo
 TEMA 7 - LUGARES GEOMÉTRICOS Y FIGURAS PLANAS 1º. Completa la tabla siguiente donde se indica la clasificación de los triángulos según sus ángulos y donde, además, aparezca un dibujo de cada tipo. Tipo
TEMA 7 - LUGARES GEOMÉTRICOS Y FIGURAS PLANAS 1º. Completa la tabla siguiente donde se indica la clasificación de los triángulos según sus ángulos y donde, además, aparezca un dibujo de cada tipo. Tipo
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
Introducción. Este trabajo será realizado con los siguientes fines :
 Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
Introducción Este trabajo será realizado con los siguientes fines : Aprender mas sobre la geometría analítica. Tener mejores conceptos sobre ella ; los cuales me pueden ayudar con las pruebas ICFES. Otro
Formulaciones equivalentes del Axioma de Elección
 Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Formulaciones equivalentes del Axioma de Elección MARU SARAZOLA Resumen En este documento presentamos algunas formulaciones equivalentes del axioma de elección. En la primera sección, se presenta el enunciado
Semana04[1/17] Funciones. 21 de marzo de Funciones
![Semana04[1/17] Funciones. 21 de marzo de Funciones Semana04[1/17] Funciones. 21 de marzo de Funciones](/thumbs/73/69418199.jpg) Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Espacios Vectoriales. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21
 Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
TEORÍAS HOMOLÓGICAS Y ESCISIÓN
 Pro Mathematica Vol. XV, Nos. 29-30 TEORÍAS HOMOLÓGICAS Y ESCISIÓN Christian Valqui Resumen Veremos algunos aspectos de topología algebraica) en particular ilustraremos la clasificación de superficies
Pro Mathematica Vol. XV, Nos. 29-30 TEORÍAS HOMOLÓGICAS Y ESCISIÓN Christian Valqui Resumen Veremos algunos aspectos de topología algebraica) en particular ilustraremos la clasificación de superficies
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Aplicaciones lineales.
 Tema 4 Aplicaciones lineales. Definición 4. Sea f: V W una aplicación entre los espacios vectoriales reales V y W. Se dice que f es una aplicación lineal si: a f(u + v = f(u + f(v; u, v V, b f(ku = kf(u;
Tema 4 Aplicaciones lineales. Definición 4. Sea f: V W una aplicación entre los espacios vectoriales reales V y W. Se dice que f es una aplicación lineal si: a f(u + v = f(u + f(v; u, v V, b f(ku = kf(u;
