Departamento de Matemáticas
|
|
|
- Celia Mendoza Chávez
- hace 5 años
- Vistas:
Transcripción
1 MA5 Clase 8: Ecuaciones Diferenciales Ordinarias Elaborado por los profesores Edgar Cabello y Marcos González Es muy común encontrar que los modelos matemáticos que se necesitan para el estudio de problemas de nuestra actividad diaria tienen implícitas ecuaciones que dependen de una función y sus derivadas. Estas ecuaciones, llamadas ecuaciones diferenciales, son el objetivo a estudiar en el resto del curso. Veamos la definición formal. Definiciones y ejemplos Definición Una ecuación diferencial ordinaria, o más brevemente EDO, es una ecuación de la forma F(x,y,y,y,...,y (n) ) = 0, donde F es una función de n + variables e y es una función de x, y (n) indica la n-ésima derivada de y respecto de x. Ejemplo Algunos ejemplos de ecuaciones diferenciales ordinarias son los siguientes:. + xy = 0,. y + y + x = cosx, 3. (x + y ) (x + y) = 0, 4. y + xy = 0, 5. y + y = 0, 6. (y ) 4 + 3y + y = 0, d 3 x x 4xy = 0, ( ) 3 8. = cosx. Definición Se dice que una EDO tiene orden n si la derivada de mayor orden que aparece en la ecuación es la derivada n-ésima.
2 Por ejemplo, damos a continuación una tabla con algunas ecuaciones diferenciales y sus respectivos órdenes: Ecuación Orden y + xy = e x y + p(x)y = 0 y (4) + xy = senx 4 x 3 y (3) y + 6y = e x 3 y x + y = e x cosx y e x + y x + y x + = y x d ( ) y (3) + 5 4y = e x Definición 3 Una solución de una EDO de orden n, es una función y = φ(x) definida en un intervalo abierto (a,b), la cual tiene derivada de al menos orden n, tal que al hacer la sustitución y = φ(x) en la ecuación diferencial ordinaria, ésta se convierte en una identidad en (a, b). La gráfica de la solución y = φ(x) de la EDO es llamada curva integral de la EDO. Observemos que la integral indefinida (o anti-derivada) de una función f, es la solución de una ecuación diferencial del tipo y = f (x). Por ejemplo, y = ln(x ) +C es solución de y = x. En vista de esto, podemos decir que cada procedimiento que estudiemos para resolver una ecuación diferencial (es decir, hallar todas sus soluciones) es una generalización de la integración de funciones. Ejemplo Verifique que, para todas las constantes reales a y b y = acosx + bsenx es solución de y + 4y = 0. Solución: En efecto, y = (acosx + bsenx) = ( asenx + bcosx) = 4acosx 4bsenx = 4(acosx + bsenx) = 4y. Ejemplo 3 La curva y = senx + cosx es solución de la ecuación diferencial y + y = 0.
3 f (x) Gráfica de f (x) = sen(x) + cos(x) Ejemplo 4 La curva y = e x es solución de la ecuación diferencial y + y 6y = 0. f (x) Gráfica de f (x) = e x Definición 4 Una EDO F(x,y,y,y,...,y (n) ) = 0 se llama lineal si F es lineal en las variables y,y,y,...,y (n), es decir, la ecuación es de la forma Ejemplo 5 a n (x)y (n) + a n (x)y (n ) + + a (x)y + a 0 (x)y = g(x).. La ecuación y = y es lineal y tiene por solución y = e x. x x 3
4 . La ecuación yy = x no es lineal y tiene por solución x y = c, c R. 3. La ecuación (y ) x 3 x + y = (y ) 4 e x no es lineal. 4. La ecuación y xy = x es lineal. Definición 5 Una EDO de primer orden y = f (x,y) sujeta a la condición y(x 0 ) = y 0 es llamado un problema de valor inicial. La condición y(x 0 ) = y 0 se denomina condición inicial. Ejemplo 6 La ecuación diferencial y = y tiene solución general y = Ke x. Si además se tiene el valor y() =, entonces, sustituyendo x = e y = en y = Ke x obtenemos = Ke, de donde K = e. Por lo tanto, y = e e x es la solución del problema de valor inicial { y = y y() =. Origen de algunas ecuaciones diferenciales. Caida Libre Es conocido que el recorrido vertical de un cuerpo que cae libremente viene dado por d s = g, donde s dt es la distancia recorrida, t es el tiempo y g la aceleración. Supongamos que queremos una función s que describa la distancia vertical de una partícula en caida libre, desde el punto en el cual cae, y supongamos que dicho punto está suficientemente cerca de la superficie de la Tierra de modo que podamos suponer la aceleración de gravedad, denotada por g, constante. Entonces, sabemos que s satisface la ecuación diferencial d s dt = g.. Elongación de resorte Para encontrar el desplazamiento vertical x(t) de una masa sujeta a un resorte se usan las leyes empíricas siguientes: la segunda ley de Newton y la ley de Hooke. La segunda ley de Newton nos dice que la fuerza total que actúa sobre una particula en movimiento está dada por F = m a, donde m es la masa de la partícula y a es la aceleración (la cual está dada por x (t)). La ley de Hooke nos dice que la fuerza de restitución de un resorte estirado es proporcional a su elongación s + x. Es decir, existe una constante κ > 0 tal que κ(s + x) es dicha fuerza de restitución. Comparando estas fórmulas para la fuerza total, obtenemos una ecuación diferencial para la elongación del resorte x, a saber, m d x = κ(s+x) donde x es el dt desplazamiento vertical de una masa sujeto a un resorte, m es la masa y κ la constante de proporcionalidad. 4
5 f (x) Gráfica de f (x) = cos( x ), la solución de y = y, y(0) =, y (0) = 0..3 El Péndulo Simple Una masa m de peso W se suspende del extremo de una varilla de longitud constante R. Suponiendo que el movimiento se realiza en un plano vertical, queremos determinar el ángulo de desplazamiento θ, medido con respecto a la vertical, en función del tiempo t. Recordemos que el arco s, que barre un ángulo θ en un círculo de radio R, está dado por s = Rθ. Por lo tanto, la aceleración angular es a = d s dt = θ Rd dt. Ahora, en virtud de la segunda ley de Newton, tenemos que F = ma = mr d θ dt, mientras que si calculamos la fuerza directamente (como la componente vertical del vector aceleración la masa de la particula), tenemos que F = mgsenθ y, en suma, mr d θ dt = mgsenθ. 3 Ecuación diferencial asociada a una ecuación. Definición 6 Una ecuación de la forma F(x,y,c,c ) = 0 es llamada una familia de curvas -paramétrica. Ejemplo 7 Las siguientes ecuaciones son familias de curvas -paramétricas:. (x c ) + (y c ) = 9,. c e x+c + cosx = e x. x 5
6 . Dada la ecuación y = C e x +C, podemos buscar la EDO asociada. Esta ecuación es -paramétrica por lo tanto la EDO es de segundo orden. Derivamos y = C e x +C y se tiene = C e x y la segunda derivada d y = C e x. De aquí se tiene que d y =.. Consideremos la ecuación y = cx 3, encontremos su ecuación diferencial. Derivando obtenemos y = 3cx. Despejamos c de la ecuación y = cx 3 se tiene que c = y, siempre que x 0. Sustituyendo x3 ( y ) el valor de c en la ecuación y = 3cx se tiene y = 3 x 3 x = 3 y. De donde x x = 3y. 3. Consideremos la ecuación x 3 3x y = c, encontremos su ecuación diferencial. Derivando obtenemos 3x 6xy + 3x y = 0. Ahora despejamos y de esta última ecuación para obtener y = 6xy 3x 3x. Es decir, y = y x. Ejemplo 8 Encontrar la ecuación diferencial asociada con:. x = c(y b) + a Solución: Por una parte, derivando con respecto a y la ecuación x = c(y b) + a resulta = c(y b) y, por otra parte, despejando c en x = c(y b) + a se tiene que c = x a. En suma, (y b) = x a (y b). Es decir, (y b) = x a (y b).. y = cx Solución: y = cx y = cx. Como c = y x se tiene que y = y x x y = y x. 3. (x ) + (y + ) = c. Solución: Diferenciando (x ) +(y+) = c se obtiene (x )+(y+) = 0. Por lo tanto, = x, siempre que y. y + La familia de círculos dada corresponde a dos familias de semi-círculos y = + c (x ), () y = c (x ). () En la ecuación () tenemos una familia de soluciones de la ecuación diferencial para y >. En la ecuación () tenemos una familia de soluciones de la ecuación diferencial para y <. Si le damos valores iniciales a = x para y = cuando x =, se debe elegir c de (), ya y + que >, = + c 9 ó c = 8. Así, y = 8 (x ) es la solución que se busca. 6
7 4 Trayectorias Ortogonales Definición 7 Sea C una curva dada y F una familia de curvas. Se dice que C es una trayectoria ortogonal de la familia F si C corta ortogonalmente a todas las curvas de F. Procedimiento para determinar las trayectorias ortogonales de una familia de curvas dadas. i) Se halla la ecuación diferencial F(x,y,y ) = 0. ii) Se halla la ecuación diferencial ortogonal F(x,y, ). Ejemplo 9 Encuentre una ecuación diferencial satisfecha por la familia ortogonal a la familia y = c x. Solución: y = c x luego y = c x = c ( ), entonces y = y x x x. La ecuación diferencial ordinaria que satisface la familia ortogonal es y = x y, es decir, yy = x... Encuentre la familia ortogonal a la familia dada de curvas (x ) + (y ) = r. Solución: Derivando (x ) + (y ) = r se tiene que (x ) + (y )y = 0, de donde y = x y. Ahora y = f (x) = y x =, con lo cual la ecuación diferencial buscada es = y x, es decir, (x )y = y. 3. Encuentre una ecuación diferencial satisfecha por la familia ortogonal a la familia y = cx + x. Solución: Derivando y = cx + x, se tiene que ( + x)c cx c y = ( + x) =. Por lo tanto, ( + x) de donde y = y x + x. y = c + x + x = cx + x x( + x) = y x( + x), La ecuación diferencial ordinaria satisfecha por la familia ortogonal a la familia F es y = x + x y o yy + x + x = 0. Correcciones y gráficos: Boris Iskra May 3, 008 7
1. Introducción a las ecuaciones diferenciales. ( Chema Madoz, VEGAP, Madrid 2009)
 1. Introducción a las ecuaciones diferenciales ( Chema Madoz, VEGAP, Madrid 009) 1 Profesores: Manuel Abejón (grupos A y B) Bartolo Luque (grupos C y D) Página del departamento de Matemática Aplicada y
1. Introducción a las ecuaciones diferenciales ( Chema Madoz, VEGAP, Madrid 009) 1 Profesores: Manuel Abejón (grupos A y B) Bartolo Luque (grupos C y D) Página del departamento de Matemática Aplicada y
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Tema 7: Ecuaciones diferenciales. Conceptos fundamentales. Integración de algunas ecuaciones diferenciales. Aplicaciones.
 Tema 7: Ecuaciones diferenciales. Conceptos fundamentales. Integración de algunas ecuaciones diferenciales. Aplicaciones. 1. Introducción y ejemplos. Las ecuaciones diferenciales ordinarias, e. d. o.,
Tema 7: Ecuaciones diferenciales. Conceptos fundamentales. Integración de algunas ecuaciones diferenciales. Aplicaciones. 1. Introducción y ejemplos. Las ecuaciones diferenciales ordinarias, e. d. o.,
Ecuaciones diferenciales en la Química. Modelos.
 Capítulo 1 Ecuaciones diferenciales en la Química. Modelos. 1.1 Introducción. Muchos fenómenos naturales (físicos, químicos, biológicos, etc. ) responden, en sus resultados, a formulaciones matemáticas
Capítulo 1 Ecuaciones diferenciales en la Química. Modelos. 1.1 Introducción. Muchos fenómenos naturales (físicos, químicos, biológicos, etc. ) responden, en sus resultados, a formulaciones matemáticas
Problemas resueltos del Boletín 4
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Sistemas no lineales
 Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
Tema 4 Sistemas no lineales Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 2005 2006 Tema 4. Sistemas no lineales 1. Sistemas no lineales de ecuaciones diferenciales. Integrales
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE
 TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
TEMA 9. MOVIMIENTO ARMÓNICO SIMPLE Un movimiento periódico es aquel que describe una partícula cuando las variables posición, velocidad y aceleración de su movimiento toman los mismos valores después de
UNIDAD II Ecuaciones diferenciales con variables separables
 UNIDAD II Ecuaciones diferenciales con variables separables UNIDAD ECUACIONES DIFERENCIALES CON VARIABLES SEPARABLES Ecuaciones diferenciales de primer orden y de primer grado. Una ecuación diferencial
UNIDAD II Ecuaciones diferenciales con variables separables UNIDAD ECUACIONES DIFERENCIALES CON VARIABLES SEPARABLES Ecuaciones diferenciales de primer orden y de primer grado. Una ecuación diferencial
INDICE. Introducción 1. Movimiento vibratorio armónico simple (MVAS) 1. Velocidad en el MVAS 2. Aceleración en el MVAS 2. Dinámica del MVAS 3
 INDICE Introducción 1 Movimiento vibratorio armónico simple (MVAS) 1 Velocidad en el MVAS Aceleración en el MVAS Dinámica del MVAS 3 Aplicación al péndulo simple 4 Energía cinética en el MVAS 6 Energía
INDICE Introducción 1 Movimiento vibratorio armónico simple (MVAS) 1 Velocidad en el MVAS Aceleración en el MVAS Dinámica del MVAS 3 Aplicación al péndulo simple 4 Energía cinética en el MVAS 6 Energía
Tema 6: Ecuaciones diferenciales lineales.
 Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
ECUACIONES DIFERENCIALES
 ECUACIONES DIFERENCIALES INGENIERÍA (NIVEL LICENCIATURA) Curso Básico - Primavera 2017 Omar De la Peña-Seaman Instituto de Física (IFUAP) Benemérita Universidad Autónoma de Puebla (BUAP) 1 / Omar De la
ECUACIONES DIFERENCIALES INGENIERÍA (NIVEL LICENCIATURA) Curso Básico - Primavera 2017 Omar De la Peña-Seaman Instituto de Física (IFUAP) Benemérita Universidad Autónoma de Puebla (BUAP) 1 / Omar De la
Indice. Cinemática de la Partícula Introducción
 Indice Cinemática de la Partícula Introducción Un fenómeno que siempre está presente y que observamos a nuestro alrededor es el movimiento. La cinemática es la parte de la Física que describe los posibles
Indice Cinemática de la Partícula Introducción Un fenómeno que siempre está presente y que observamos a nuestro alrededor es el movimiento. La cinemática es la parte de la Física que describe los posibles
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
Ecuaciones diferenciales Profesores: Eusebio Valero (grupos A y B) Bartolo Luque (grupos C y D)
 Ecuaciones diferenciales Profesores: Eusebio Valero (grupos A B) Encargado de responder a todas las preguntas de la asignatura de todas las tutorías. Bartolo Luque (grupos C D) Este no tiene ni idea. No
Ecuaciones diferenciales Profesores: Eusebio Valero (grupos A B) Encargado de responder a todas las preguntas de la asignatura de todas las tutorías. Bartolo Luque (grupos C D) Este no tiene ni idea. No
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Contenido. 3. Ecuaciones diferenciales de orden superior. 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/53 53
 Contenido 3. Ecuaciones diferenciales de orden superior 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/53 53 Contenido: Tema 03 3. Ecuaciones diferenciales de orden
Contenido 3. Ecuaciones diferenciales de orden superior 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/53 53 Contenido: Tema 03 3. Ecuaciones diferenciales de orden
Ecuaciones Diferenciales Ordinarias
 Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Física y Química 1º Bachillerato LOMCE. Bloque 3: Trabajo y Energía. Trabajo y Energía
 Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
2xy 3x 2 y 2 y(0) = 1
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
ECUACIONES DE RECTAS Y PLANOS
 ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
ECUACIONES DE RECTAS Y PLANOS Una recta en el plano está determinada cuando se dan dos puntos cualesquiera de la recta, o un punto de la recta y su dirección (su pendiente o ángulo de inclinación). La
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 3 de febrero de 2005 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Considera la función f!x"! ln! x ""!. Se
Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 3 de febrero de 2005 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :. Considera la función f!x"! ln! x ""!. Se
2.4 Ecuaciones diferenciales de Bernoulli
 .4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
.4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
CAPÍTULO 1 INTRODUCCION
 CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
Análisis Dinámico: Ecuaciones diferenciales
 Análisis Dinámico: Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: 1 / 51 Introducción Solución genérica Solución de
Análisis Dinámico: Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: 1 / 51 Introducción Solución genérica Solución de
Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Semestre de Otoño, 2012
 Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Ecuaciones lineales de segundo orden
 Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL
 Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
1. La capacidad límite del hábitat de un rebaño en vida salvaje es L. El ritmo de crecimiento dn dt
 AMPLIACIÓN DE MATEMÁTICAS Relación 3 005/006 1. La capacidad límite del hábitat de un rebaño en vida salvaje es L. El ritmo de crecimiento dn dt del rebaño, es proporcional a las oportunidades de crecimiento
AMPLIACIÓN DE MATEMÁTICAS Relación 3 005/006 1. La capacidad límite del hábitat de un rebaño en vida salvaje es L. El ritmo de crecimiento dn dt del rebaño, es proporcional a las oportunidades de crecimiento
ECUACIONES DIFERENCIALES CARLOS RUZ LEIVA
 ECUACIONES DIFERENCIALES CARLOS RUZ LEIVA Definición de ecuación diferencial Una ecuación que relaciona una función desconocida y una o más de sus derivadas se llama ecuación diferencial. Instituto de
ECUACIONES DIFERENCIALES CARLOS RUZ LEIVA Definición de ecuación diferencial Una ecuación que relaciona una función desconocida y una o más de sus derivadas se llama ecuación diferencial. Instituto de
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
2DA PRÁCTICA CALIFICADA
 2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
2DA PRÁCTICA CALIFICADA DINÁMICA (IC 244) ALUMNOS : CARITAS BARRIENTOS, Ronald ROBLES ROCHA, Hamilton TORRES PÉREZ, Walter A. TORO VELARDE, William DOCENTE : Ing. CASTRO PÉREZ, Cristian CINÉTICA DE UNA
Ecuaciones Diferenciales
 VOLUMEN 1 Ecuaciones Diferenciales 11 de Mayo de 2009 cuaciones Diferenciales Introducción Qué es una E. D.? Solución de E. D. Introducción Muchas de las leyes de la naturaleza, en física, química o astronomía,
VOLUMEN 1 Ecuaciones Diferenciales 11 de Mayo de 2009 cuaciones Diferenciales Introducción Qué es una E. D.? Solución de E. D. Introducción Muchas de las leyes de la naturaleza, en física, química o astronomía,
Esta relación se obtiene mediante el denominado modelo dinámico, que relaciona matemáticamente:
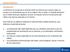 Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Introducción La dinámica se ocupa de la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento que en el se origina. Por lo tanto, el modelo dinámico de un robot tiene por objetivo conocer
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
2. Actividad inicial: Crecimiento del dinero.
 Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
Selectividad Matemáticas II junio 2015, Andalucía (versión 3)
 Selectividad Matemáticas II junio 05, Andalucía (versión 3) Pedro González Ruiz 7 de junio de 05. Opción A Problema. Se quiere construir un depośito abierto de base cuadrada y paredes verticales con capacidad
Selectividad Matemáticas II junio 05, Andalucía (versión 3) Pedro González Ruiz 7 de junio de 05. Opción A Problema. Se quiere construir un depośito abierto de base cuadrada y paredes verticales con capacidad
Sistemas de ecuaciones diferenciales y el uso de operadores
 Sistemas de ecuaciones diferenciales y el uso de operadores En la clase anterior resolvimos algunos sistemas de ecuaciones diferenciales sacándole provecho a la notación matricial. Sin embrago, algunos
Sistemas de ecuaciones diferenciales y el uso de operadores En la clase anterior resolvimos algunos sistemas de ecuaciones diferenciales sacándole provecho a la notación matricial. Sin embrago, algunos
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Introducción y algunos métodos de solución) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López
Ecuaciones Diferenciales Ordinarias (Introducción y algunos métodos de solución) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López
Diferenciación SEGUNDA PARTE
 ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
Clase 4: Diferenciación
 Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Clase 4: Diferenciación C.J Vanegas 27 de abril de 2008 1. Derivadas Parciales Recordemos que la definición de derivada parcial: sea fa R R, definida sobre un f(x) f(x 0 ) intervalo abierto A. f es derivable
Tema 3: Diferenciabilidad de funciones de varias variables
 Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 2009-2010. Tema 3: Diferenciabilidad de funciones de varias variables 1. Calcular las dos derivadas parciales de primer orden:
Departamento de Matemáticas. Universidad de Jaén. Análisis Matemático II. Curso 2009-2010. Tema 3: Diferenciabilidad de funciones de varias variables 1. Calcular las dos derivadas parciales de primer orden:
Movimiento armónico simple.
 1 Movimiento armónico simple. 1.1. Concepto de movimiento armónico simple: Su ecuación. Supongamos un muelle que cuelga verticalmente, y de cuyo extremo libre pende una masa m. Si tiramos de la masa y
1 Movimiento armónico simple. 1.1. Concepto de movimiento armónico simple: Su ecuación. Supongamos un muelle que cuelga verticalmente, y de cuyo extremo libre pende una masa m. Si tiramos de la masa y
* e e Propiedades de la potenciación.
 ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
2 Deniciones y soluciones
 Deniciones y soluciones Sabemos que la derivada de una función y(x) es otra función y (x) que se determina aplicando una regla adecuada. Por ejemplo, la derivada de y = e 3x es dx = 6xe3x. Si en la última
Deniciones y soluciones Sabemos que la derivada de una función y(x) es otra función y (x) que se determina aplicando una regla adecuada. Por ejemplo, la derivada de y = e 3x es dx = 6xe3x. Si en la última
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN
 APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN Movimiento de rotación Qué tienen en común los movimientos de un disco compacto, las sillas voladoras, un esmeril,
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 10 CINEMÁTICA DE ROTACIÓN Movimiento de rotación Qué tienen en común los movimientos de un disco compacto, las sillas voladoras, un esmeril,
Física Ciclo Dos Ed Media Capacitación 2000 MOVIMIENTO ARMÓNICO SIMPLE (M.A.S)
 MOVIMIENTO ARMÓNICO SIMPLE (M.A.S) Movimiento Armónico Simple es aquel que en la aceleración está siempre apuntando hacia la posición del equilibrio y es directamente proporcional al desplazamiento. También
MOVIMIENTO ARMÓNICO SIMPLE (M.A.S) Movimiento Armónico Simple es aquel que en la aceleración está siempre apuntando hacia la posición del equilibrio y es directamente proporcional al desplazamiento. También
Ecuaciones Diferenciales (MA-841)
 Ecuaciones Diferenciales (MA-841) Ecuaciones de Departmento de Matemáticas / CSI ITESM Ecuaciones de Ecuaciones Diferenciales - p. 1/16 Ecuaciones de Iniciaremos nuestras técnicas de solución a ED con
Ecuaciones Diferenciales (MA-841) Ecuaciones de Departmento de Matemáticas / CSI ITESM Ecuaciones de Ecuaciones Diferenciales - p. 1/16 Ecuaciones de Iniciaremos nuestras técnicas de solución a ED con
3 Cálculo diferencial en varias variables
 Introducción Derivadas parciales. Derivadas parciales de orden superior Función diferenciable. Diferencial total. Regla de la cadena. Derivadas de una función definida de manera implícita. (*) Derivación
Introducción Derivadas parciales. Derivadas parciales de orden superior Función diferenciable. Diferencial total. Regla de la cadena. Derivadas de una función definida de manera implícita. (*) Derivación
Soluciones a los ejercicios propuestos: Matemáticas III. Curso Tema 4. (a) Determinar si f es localmente invertible en (0, 0, 0).
 Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
Hoja de Problemas Ecuaciones Diferenciales Ordinarias
 Unidad docente de Matemáticas Matemáticas (CC. Químicas) Hoja de Problemas Ecuaciones Diferenciales Ordinarias 1. Comprobar si la función indicada en cada caso es una solución de la ecuación diferencial
Unidad docente de Matemáticas Matemáticas (CC. Químicas) Hoja de Problemas Ecuaciones Diferenciales Ordinarias 1. Comprobar si la función indicada en cada caso es una solución de la ecuación diferencial
Lista sobre Solución por Series.
 UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS MA-1005 Ecuaciones Diferenciales para Ingenieía ESCUELA DE MATEMÁTICA Segundo Ciclo del 2015 Lista sobre Solución por Series. Solución de ecuaciones diferenciales
UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS MA-1005 Ecuaciones Diferenciales para Ingenieía ESCUELA DE MATEMÁTICA Segundo Ciclo del 2015 Lista sobre Solución por Series. Solución de ecuaciones diferenciales
Preliminares Problemas de Valor Inicial Problemas de Contorno ECUACIONES DIFERENCIALES ORDINARIAS
 ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
LAS ECUACIONES VARIACIONALES DE EULER
 LAS ECUACIONES VARIACIONALES DE EULER Los conceptos de máximo y de mínimo -de extremo o extremal, en definitivade una expresión funcional, es algo corriente en el análisis matemático, y las condiciones
LAS ECUACIONES VARIACIONALES DE EULER Los conceptos de máximo y de mínimo -de extremo o extremal, en definitivade una expresión funcional, es algo corriente en el análisis matemático, y las condiciones
Selectividad Matemáticas II septiembre 2014, Andalucía
 Selectividad Matemáticas II septiembre 14, Andalucía Pedro González Ruiz 17 de septiembre de 14 1. Opción A Problema 1.1 Sabiendo que lím x cos(3x) e x +ax xsen(x) Sea l el límite pedido. Tenemos: es finito,
Selectividad Matemáticas II septiembre 14, Andalucía Pedro González Ruiz 17 de septiembre de 14 1. Opción A Problema 1.1 Sabiendo que lím x cos(3x) e x +ax xsen(x) Sea l el límite pedido. Tenemos: es finito,
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5
 Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
CÁLCULO III (0253) PRIMER PARCIAL (33.33%) SECCIONES 02 Y 04 27/03/09. . π
 UCV FIUCV CÁLCULO III (05) PRIMER PARCIAL (%) SECCIONES 0 Y 04 7/0/09 Una curva C está definida por y = sen(x) x 0 y = x x 0 x + (y + ) = x 0 a Parametrice la curva C en sentido horario ( puntos) b Encuentre
UCV FIUCV CÁLCULO III (05) PRIMER PARCIAL (%) SECCIONES 0 Y 04 7/0/09 Una curva C está definida por y = sen(x) x 0 y = x x 0 x + (y + ) = x 0 a Parametrice la curva C en sentido horario ( puntos) b Encuentre
Examen de Física-1, 1 Ingeniería Química Examen final. Enero de 2015 Problemas (Dos puntos por problema).
 Examen de Física-, Ingeniería Química Examen final. Enero de 205 Problemas (Dos puntos por problema). Problema : La posición de una partícula móvil en el plano Oxy viene dada por : x(t) = 2 t 2 y(t) =
Examen de Física-, Ingeniería Química Examen final. Enero de 205 Problemas (Dos puntos por problema). Problema : La posición de una partícula móvil en el plano Oxy viene dada por : x(t) = 2 t 2 y(t) =
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
Tema 3: Cinemática del punto
 Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
Ecuaciones Diferenciales Tema 1. Parte 1: Ecuaciones Diferenciales
 Ecuaciones Diferenciales Tema 1. Parte 1: Ecuaciones Diferenciales Ester Simó Mezquita Matemática Aplicada IV 1 1. Qué es una Ecuación Diferencial Ordinaria? 2. Solución de una EDO 3. Tipos de EDO 4. Solución
Ecuaciones Diferenciales Tema 1. Parte 1: Ecuaciones Diferenciales Ester Simó Mezquita Matemática Aplicada IV 1 1. Qué es una Ecuación Diferencial Ordinaria? 2. Solución de una EDO 3. Tipos de EDO 4. Solución
APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 4 MOVIMIENTO ARMÓNICO SIMPLE
 MOVIMIENTO ARMÓNICO SIMPLE APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 4 MOVIMIENTO ARMÓNICO SIMPLE El movimiento armónico simple, o también llamado M.A.S., se trata de una clase de
MOVIMIENTO ARMÓNICO SIMPLE APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 4 MOVIMIENTO ARMÓNICO SIMPLE El movimiento armónico simple, o también llamado M.A.S., se trata de una clase de
Física Ondas 10/11/06
 Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
sea a lo largo de la curva solución de la ecuación diferencial xy, = 5x
 1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
Dinámica del Sólido Rígido
 Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
Dinámica del Sólido Rígido El presente documento de clase sobre dinámica del solido rígido está basado en los contenidos volcados en la excelente página web del curso de Física I del Prof. Javier Junquera
CINEMÁTICA: ESTUDIO DEL MOVIMIENTO. Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos.
 CINEMÁTICA: ESTUDIO DEL MOVIMIENTO Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos. 1. Cuándo un cuerpo está en movimiento? Para hablar de reposo o movimiento
CINEMÁTICA: ESTUDIO DEL MOVIMIENTO Cinemática es la parte de la Física que estudia la descripción del movimiento de los cuerpos. 1. Cuándo un cuerpo está en movimiento? Para hablar de reposo o movimiento
Guillermo Carrión Santiago 4 de enero de 2013
 física I Guillermo Carrión Santiago 4 de enero de 2013 Espero que a todos os sirva y que podáis estudiar física como un matemático lo haría y sin patadas en el estomago. Si encontráis alguna errata avisad
física I Guillermo Carrión Santiago 4 de enero de 2013 Espero que a todos os sirva y que podáis estudiar física como un matemático lo haría y sin patadas en el estomago. Si encontráis alguna errata avisad
Sistemas de Ecuaciones Diferenciales
 Semana 8 - Clase 5// Tema 4: Sistemas y Series Sistemas de Ecuaciones Diferenciales Cuando consideramos la evolución de sistemas con varios grados de libertad o con varias partículas, naturalmente arribamos
Semana 8 - Clase 5// Tema 4: Sistemas y Series Sistemas de Ecuaciones Diferenciales Cuando consideramos la evolución de sistemas con varios grados de libertad o con varias partículas, naturalmente arribamos
Universidad Carlos III de Madrid
 Ejercicio 2 3 4 5 6 7 8 total Puntos Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 9 de septiembre de 2005 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :.
Ejercicio 2 3 4 5 6 7 8 total Puntos Universidad Carlos III de Madrid Departamento de Economía Examen final de Matemáticas I 9 de septiembre de 2005 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO :.
CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO
 MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO Unidad Académica Profesional Tianguistenco Licenciatura en Ingeniería de Plásticos Unidad de Aprendizaje:
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO Unidad Académica Profesional Tianguistenco Licenciatura en Ingeniería de Plásticos Unidad de Aprendizaje: Análisis Numérico y Ecuaciones Diferenciales Unidad 1.
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO Unidad Académica Profesional Tianguistenco Licenciatura en Ingeniería de Plásticos Unidad de Aprendizaje: Análisis Numérico y Ecuaciones Diferenciales Unidad 1.
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
1.1. Clasificación de las ecuaciones diferenciales
 Capítulo 1 1.1. Clasificación de las ecuaciones diferenciales Una ecuación diferencial tiene como incógnita una función y que puede depender de una, y(x), o de más variables independientes, y(x 1,...,
Capítulo 1 1.1. Clasificación de las ecuaciones diferenciales Una ecuación diferencial tiene como incógnita una función y que puede depender de una, y(x), o de más variables independientes, y(x 1,...,
Ecuaciones Diferenciales
 Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
BORRADOR. Ecuaciones diferenciales ordinarias de primer orden Definición y ejemplos
 Capítulo 3 Ecuaciones diferenciales ordinarias de primer orden 3.1. Definición y ejemplos La definición formal de una ecuación diferencial ordinaria (EDO) es la de una expresión F(x,y,y,y,...,y (n) ) =
Capítulo 3 Ecuaciones diferenciales ordinarias de primer orden 3.1. Definición y ejemplos La definición formal de una ecuación diferencial ordinaria (EDO) es la de una expresión F(x,y,y,y,...,y (n) ) =
MECÁNICA CLÁSICA CINEMATICA. FAyA Licenciatura en Química Física III año 2006
 Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un
 TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un elemento de masa dm que gira a una distancia r del eje de
TRABAJO Y ENERGIA EN ROTACIÓN. Consideremos un cuerpo que gira alrededor de un eje tal como se muestra en la figura. La energía cinética de un elemento de masa dm que gira a una distancia r del eje de
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
850 CAPÍTULO 12 Funciones vectoriales
 850 CAPÍTULO Funciones vectoriales Eploración de velocidad Considérese el círculo dado por Usar una herramienta de graficación en modo paramétrico para repretar este círculo para varios valores de. Cómo
850 CAPÍTULO Funciones vectoriales Eploración de velocidad Considérese el círculo dado por Usar una herramienta de graficación en modo paramétrico para repretar este círculo para varios valores de. Cómo
Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial
 Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial Sergio Blanes http://personales.upv.es/ serblaza Instituto de Matemtica Multidisciplinar Universidad Politécnica de Valencia Edificio 8-G, entrada
Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial Sergio Blanes http://personales.upv.es/ serblaza Instituto de Matemtica Multidisciplinar Universidad Politécnica de Valencia Edificio 8-G, entrada
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
Práctica 3: Diferenciación I
 Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Ecuaciones diferenciales ordinarias de primer orden
 Capítulo 3 Ecuaciones diferenciales ordinarias de primer orden 3.1. Definición y ejemplos La definición formal de una ecuación diferencial ordinaria (EDO) es la de una expresión F(x,y,y,y,...,y (n) ) =
Capítulo 3 Ecuaciones diferenciales ordinarias de primer orden 3.1. Definición y ejemplos La definición formal de una ecuación diferencial ordinaria (EDO) es la de una expresión F(x,y,y,y,...,y (n) ) =
Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y
 CINEMÁTICA CINEMÁTICA (MRU) CONCEPTO DE CINEMÁTICA Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y de
CINEMÁTICA CINEMÁTICA (MRU) CONCEPTO DE CINEMÁTICA Estudia las propiedades geométricas de las trayectorias que describen los cuerpos en movimiento mecánico, independientemente de la masa del cuerpo y de
ECUACIONES DIFERENCIALES
 ECUACIONES DIFERENCIALES DEFINICIÓN Ecuación Diferencial es una ecuación que contiene las derivadas o diferenciales de una función de una o más variables. 1. Si hay una sola variable independiente, las
ECUACIONES DIFERENCIALES DEFINICIÓN Ecuación Diferencial es una ecuación que contiene las derivadas o diferenciales de una función de una o más variables. 1. Si hay una sola variable independiente, las
CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen
 CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
Tema 3: Espacios eucĺıdeos
 Marisa Serrano, Zulima Fernández Universidad de Oviedo 25 de noviembre de 2009 email: mlserrano@uniovi.es Índice 1 2 3.1 V, R espacio vectorial, la aplicación : V V R ( v, u) v u a) v 1, v 2, u V α, β
Marisa Serrano, Zulima Fernández Universidad de Oviedo 25 de noviembre de 2009 email: mlserrano@uniovi.es Índice 1 2 3.1 V, R espacio vectorial, la aplicación : V V R ( v, u) v u a) v 1, v 2, u V α, β
Ecuaciones Diferenciales Ordinarias.
 Wilson Herrera 1 Ecuaciones Diferenciales Ordinarias. 1. Comprobar si las relaciones dadas son integrales de las ecuaciones diferenciales indicadas o no lo son (C=const): 1.2) y 3 = 1 x + C x 3, xy2 dy
Wilson Herrera 1 Ecuaciones Diferenciales Ordinarias. 1. Comprobar si las relaciones dadas son integrales de las ecuaciones diferenciales indicadas o no lo son (C=const): 1.2) y 3 = 1 x + C x 3, xy2 dy
DERIVADAS DE FUNCIONES DE VARIAS VARIABLES. Curvas Paramétricas. Dada una curva paramétrica
 ANÁLISIS MATEMÁTICO BÁSICO DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Curvas Paramétricas Dada una curva paramétrica γ : [a, b] R R n t γ(t) = (f 1 (t), f 2 (t),, f n (t)), donde las funciones f k : [a,
ANÁLISIS MATEMÁTICO BÁSICO DERIVADAS DE FUNCIONES DE VARIAS VARIABLES Curvas Paramétricas Dada una curva paramétrica γ : [a, b] R R n t γ(t) = (f 1 (t), f 2 (t),, f n (t)), donde las funciones f k : [a,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Cálculo Integral Agosto 2015
 Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Selectividad Matemáticas II junio 2017, Andalucía
 Selectividad Matemáticas II junio 07, Andalucía Pedro González Ruiz 3 de junio de 06. Opción A Problema. Se quiere hacer una puerta rectangular coronada por un semicírculo como el de la figura. El hueco
Selectividad Matemáticas II junio 07, Andalucía Pedro González Ruiz 3 de junio de 06. Opción A Problema. Se quiere hacer una puerta rectangular coronada por un semicírculo como el de la figura. El hueco
