3.1 EXPRESIONES TEÓRICAS DE MODOS DE VIBRACIÓN Y SUS CURVATURAS

Transcripción

1 MODEOS FEM. EXPRESIONES TEÓRICAS DE MODOS DE VIBRACIÓN Y SUS CURVATURAS a forma del modo de vibración del modelo teórico es la de una viga en voladizo, la cual viene dada por la siguiente ecuación, según lo recogido en el capítulo Analysis of undamped free vibrations (Clough, Penzien 975): sen( a ) senh( a ) ( x) A sen( a x) senh( a x) x cos( a ) cosh( a ) ( cosh( a x) cos( a )) donde A es la amplitud del modo (no conocida a priori) y a una constante cuyo valor varía dependiendo de si es primer, segundo o tercer modo de vibración. m a constante a tiene la siguiente expresión a ω, de lo que se deriva que E I la frecuencia es ω a E I. Del ejemplo E8- (Clough, Penzien 975), se m extrae que las expresiones que definen las frecuencias de los tres primeros modos de vibración son las siguientes: ω (.875) E I m ω (.69) E I m ω (7.855) E I m Para transformar la fórmula primera de la frecuencia en esta última se procede como sigue: ω a E I m a E I m E I ( a ) m Por lo tanto, se deduce que el valor de la constante a para los tres primeros modos de vibración se obtiene de igualar la expresión anterior con cada una de las expresiones de la frecuencia para cada modo. Primer modo vibración:.875 a a.875 7

2 Segundo modo vibración: Tercer modo vibración:.69 a a a a es la longitud total del vástago, cuyo valor puede ser 5.9m ó.5m en función de la altura a la que se considere el empotramiento, estudio que se desarrollará en próximos apartados. A partir del estudio realizado por Romero en su Proyecto Fin de Carrera (pág.6) (Romero Ordóñez 7), la expresión anterior que describe la forma del modo se puede simplificar agrupando constantes, para el posterior ajuste de las amplitudes y de las pendientes. ( sen( a x) senh( a x) ) C ( cosh( a x) cos( a )) ( x) C donde [I] x C A C sen( a ) senh( a ) A cos( a ) cosh( a ) Para la obtención de los valores de C y C Romero propone (Romero Ordóñez 7) la resolución de un sistema sobredeterminado donde x i es la coordenada de la sección i, Clin i y de dicha sección. Acel i son las amplitudes de los clinómetros y de los acelerómetros os datos manejados para la obtención de las constantes son las amplitudes de los tres acelerómetros, instalados en el vástago a diferentes alturas ( Acel a x. 657m, Acel a x. m y Acel a x. 687m ). Por ello el sistema de ecuaciones no tendrá en cuenta las amplitudes de los clinómetros y el sistema quedará de la siguiente forma: sen( a x sen( a x sen( a x ) senh( a x ) ) senh( a x ) ) senh( a x ) cosh( a x cosh( a x cosh( a x ) cos( a x ) cos( a x ) cos( a x ) C ) ) C Acel Acel Acel 8

3 Resolviendo este sistema directamente los valores de C y C no cumplen las relaciones [I] y por tanto la expresión (x) no refleja en ese caso la forma del primer modo de una viga en voladizo. Para que se cumplan, se propone en este trabajo introducir ambas en el sistema a resolver, de forma que sólo exista una incógnita C A. sen( a ) senh( a ) D cos( a ) cosh( a ) C C D sen( a x sen( a x sen( a x ) senh( a x ) ) senh( a x ) ) senh( a x ) cosh( a x cosh( a x cosh( a x ) cos( a x ) cos( a x ) cos( a x ) C ) ) C Acel Acel Acel S S Acel S C S C Acel S C S C D Acel Quedando el siguiente sistema de ecuaciones: [ S S D] [ C ] [ Acel] Este mismo proceso es el que se seguirá para determinar el primer modo analítico a partir de los valores numéricos de cualquier modelo de elementos finitos, que más adelante serán descritos. Para estos casos x i es la coordenada de la sección i y Acel i el valor del desplazamiento de la misma sección obtenido del análisis modal de cada modelo. a expresión de la curvatura analítica no es más que la derivada segunda de la función del modo analítico. ( cosh( a x) a cos( a x ) sen( a ) senh( a ) " ( x) A sen( a x) a senh( a x) a ) a cos( a ) cosh( a ) Sabiendo que: C A sen( a ) senh( a ) D cos( a ) cosh( a ) [II] 9

4 C A D a expresión de la curvatura queda: ( sen( a x) senh( a x) ) C a ( cosh( a x) cos( a )) "( x) C a [III] x El valor de la curvatura en el extremo del vástago (x) tiene que ser nulo. Esto se deduce al sustituir en la función [II] el valor en la variable x. Para que esto siga cumpliéndose al sustituir los valores de C y C en la expresión [III] habrá que tener en cuenta al resolver el sistema sobredeterminado la relación entre estas constantes, expuesta con anterioridad. De otra forma la expresión de la curvatura obtenida no sería correcta.. ESCAADO DE OS MODOS Se parte de la necesidad de escalar los datos numéricos y experimentales para poder trabajar con única escala y así poder comparar coherentemente los resultados. Existen varias alternativas a la hora de realizar el escalado de los modos. Por un lado está la normalización del vector de datos a norma unidad. Por otro lado se tiene el escalado del vector desplazamiento de tal forma que el valor de éste en la sección del acelerómetro sea la unidad. Por último el escalado de los datos tal que la suma de los desplazamientos en las secciones de los acelerómetros al cuadrado sea la unidad. En el estudio realizado se ha optado por la última opción de escalado. Esto es debido a que con esta forma de normalización no se obliga a que ningún punto de la curva pase por un valor determinado. Si esto ocurriese podría provocar la pérdida de información a la hora de trabajar con los modos numéricos, y por tanto en la posterior obtención de los parámetros modales, llegando a falsear las comparaciones con los distintos resultados. [ A... A acel... A acel... A acel... A n ] num ( A A A ) [...] [ ] α escalado... num α acel acel acel α

5 . MODEO D.. SEECCIÓN DE TIPO DE EEMENTOS El modelo monodimensional de la estructura portante del Giraldillo se diseña como una viga en voladizo compuesta por tres tramos de diferente sección y dos masas puntuales (una en el extremo libre del vástago y otra a cm por encima de la unión superior) que representan el reparto de masa de la escultura entre esos dos puntos. Para la selección de los tipos de elementos a usar en la caracterización del modelo D se ha partido de un pequeño ejercicio, el cual consiste en una viga en voladizo de sección constante con una carga puntual en su extremo libre. A partir de este diseño sencillo lo que se pretende es comprobar que el elemento viga y el elemento masa elegidos tengan un correcto comportamiento ante el análisis modal. Para ello se determinarán, a partir del cálculo matricial, las frecuencias de este sistema para compararlas con las frecuencias resultantes del modelo de elementos finitos, haciendo uso de los elementos a examinar. Al ser un ejercicio bidimensional se ha escogido como elemento viga BEAM y como elemento masa MASS. El elemento elástico BEAM es un elemento uniaxial con tres grados de libertad en cada nodo: desplazamientos en las direcciones x e y y rotación alrededor del eje z. El elemento MASS hace referencia a una masa estructural puntual con seis grados de libertad: M x, M y, M z, I xx, I yy e I zz. Para iniciar el ejercicio se caracteriza la estructura con las siguientes propiedades: A m m Mkg I m kg ρ 785 m E 9 N m as frecuencias obtenidas del análisis modal en ANSYS son: 9, y 96.5Hz.

6 Para la resolución matricial de este caso se parte de las matrices de masa y rigidez siguientes: 56 M M M ρa EI EI EI EI EA K 6 6 M K ω De esta forma los valores de la frecuencia son:.5, 56.5, 6.7Hz. Como se observa al comparar los resultados de los dos métodos de cálculo las frecuencias no coinciden, eso es debido a que la matriz de masa del elemento BEAM que emplea ANSYS tiene la siguiente expresión: ( ) ( ) ), ( ), ( ), ( ), ( M M r E r C r C r A m A M in ε ρ donde m : masa añadida por unidad de longitud ( m ) in ε : pretensión ( in ε ) ( ) ), ( r r A ( ) ), ( r r C ( ) ), ( r r E

7 donde r I A EI GA s s : radio de giro G : módulo a cortante s A A : área a cortante; s F s F : constante de deflexión por cortante s s Como SHEARZ entonces F A. Por lo tanto los términos de la matriz de masa quedan de la siguiente forma (para m): 6 A( r) r 5 5 C( r) r E( r) r 5 5 M ρ A A( r, ) C( r, ) M C( r, ) E( r, ) M Resolviendo matricialmente el cálculo de las frecuencias y haciendo uso de la matriz de masa en función de r, se obtienen las frecuencias: 9.7,.8 y 96.5Hz, coincidentes con las resultantes del análisis modal del modelo de elementos finitos. En el caso más habitual de barras esbeltas, el valor de r se puede despreciar. Así, en el caso de un perfil de características A.m e I 5 m las frecuencias obtenidas del modelo en ANSYS son:.57, 7.68 y 5.87Hz. as resultantes a partir del cálculo matricial, en función de r, son:.566, y 5.866Hz. Y por último las obtenidas del cálculo matricial suponiendo r, son:.57, y 56.6Hz. De este ejercicio se concluye que los elementos seleccionados tendrán un comportamiento adecuado al tipo de análisis y a la estructura a examinar. Puesto que la estructura es tridimensional se ha optado por usar un elemento viga BEAM, el cual tiene un comportamiento similar al del BEAM, con la diferencia de ser tridimensional y por tanto presentar seis grados de libertad en cada nodo.

8 .. MODEO VÁSTAGO GIRADIO Análisis de sensibilidad de parámetros de detección de daño. El diseño monodimensional del modelo del vástago está basado en las características descritas en el apartado. Puesto que a priori se desconoce la cota del empotramiento del modelo del que se disponen los datos experimentales de referencia, se ha optado por diseñar dos modelos con las dos posibles alternativas de empotramiento. El primero consta de tres tramos de longitudes (de abajo hacia arriba) 8, 75 y 7mm, y el segundo modelo de 9, 75 y 7mm. Dichos tramos están definidos con elementos BEAM. as propiedades de los dos primeros tramos serán las correspondientes a un kg material ST5 ( E GPa, ρ 785, υ. ) y las del tercer tramo las de un m kg material AISI 6 ( E 9GPa, ρ 8, υ. ). m Para poder comparar con los resultados experimentales es necesario que la frecuencia del primer modo de vibración del modelo sea.5hz, ya que éste es el valor de la frecuencia natural del experimental. Para ello se distribuyen los 5kg del Giraldillo entre los dos puntos de apoyo en el vástago, situación que fue indicada anteriormente, en cuyos nodos se define un elemento masa MASS. Tras varias iteraciones el reparto de masa queda de la siguiente forma: Masa superior (kg) Masa inferior (kg) Frecuencia (Hz) Modelo tramo 8mm Modelo tramo 9mm.5

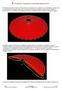
9 .. VAIDACIÓN MODEOS D POR COMPARACIÓN CON EXPERIMENTA. DETERMINACIÓN ONGITUD DE EMPOTRAMIENTO DE VÁSTAGO A partir del análisis modal de los dos modelos de elementos finitos anteriormente definidos, se han obtenido dos vectores de desplazamiento nodal (uno por cada modelo) correspondientes al primer modo de vibración. Para poder comparar estos resultados con los datos experimentales se procede a normalizar según la última alternativa de escalado descrita en el apartado.. os datos experimentales de los que se dispone son los correspondientes a los de los tres acelerómetros distribuidos por el vástago. A partir de estos se ha obtenido una curva del primer modo haciendo uso de la expresión analítica del modo, es decir, se obtiene lo que se denominará como modo experimental aproximado. Representando gráficamente las curvas del modo numérico de los dos modelos, el modo experimental y el modo experimental interpolado se tiene lo siguiente (Fig. ):.9 er MODO MODEO D.8 modo D 8 escalado modo D 9 escalado modo acel modo exp aprox.7 Desplazamiento USUM ongitud Fig.. Comparación del primer modo de vibración de los modelos D y los resultados del modelo experimental 5

10 Para determinar la longitud de empotramiento del vástago se pueden comparar las dos curvas de los modelos monodimensionales con la experimental aproximada, observándose que el modelo que sigue un comportamiento similar al del experimental es el de 9mm de longitud en el tramo. En el análisis experimental se consideró que la longitud del primer tramo era de 8mm, por eso se observa que en el origen exista esa diferencia entre ambas curvas. Pero una vez salvado el origen ambas curvas tienden prácticamente a una, a medida que se recorre el vástago. Por lo tanto se concluye que la estructura portante del Giraldillo consta de tres tramos de longitudes 9, 75 y 7mm. A partir de esto se procederá al diseño del modelo en tres dimensiones de acuerdo con estas longitudes.. MODEO D.. SEECCIÓN DE TIPO DE EEMENTOS Para la selección de los tipos de elementos a usar en la caracterización del modelo tridimensional se parte de unos sencillos ejercicios de una viga en voladizo de.5m de longitud. Esta barra en un primer caso será un tubo hueco de propiedades: ext. mm e. 7mm med 8. 6mm I y I x π I z ext m ( ).688 m int Y en un segundo caso será un cilindro de características: mm I y I z m I x m 6

11 Para cada perfil descrito se diseñan unos modelos de elementos finitos en D, D y DD, y se someten a un análisis modal con el fin de comparar las frecuencias resultantes entre ellas, tomando como referencia la primera frecuencia de vibración del modelo monodimensional, cuyo elemento viga es BEAM. os elementos a evaluar son para los modelos con perfil tubular los elementos lámina SHE6 y SHE9, y para los modelos con perfil circular macizo los elementos sólido SOID5 y SOID95 (Fig. ). El elemento SHE6, usado para modelar superficies planas, está definido por cuatro nodos con seis grados de libertad en cada nodo: desplazamientos en las direcciones x, y y z y rotaciones alrededor de los ejes x, y y z. El SHE9, especialmente adecuado para modelar superficies curvas, está definido por ocho nodos con tres grados de libertad en cada nodo: desplazamientos en las direcciones x, y y z. os elementos SOID5 Y SOID95 están definidos por ocho y veinte nodos, respectivamente, con tres grados de libertad por nodo: desplazamientos en las direcciones x, y y z. El SOID5 es usado en el modelado de estructuras sólidas tridimensionales con contornos lineales, y para los casos con contornos cuadráticos se emplea el SOID95. PERFI TUBUAR BEAM SHE 6 ó SHE 9 SHE 6 ó SHE 9 BEAM PERFI CIRCUAR MACIZO BEAM SOID 5 ó SOID 95 SOID 5 ó SOID 95 BEAM Fig.. Ejercicios para la selección de los tipos de elementos del modelo tridimensional 7

12 a primera frecuencia del modelo D, para el caso del perfil tubular, es de.8hz. as diferentes alternativas de caracterización del modelo D, el cual será diseñado con el diámetro medio del perfil, son usar el elemento SHE6 o el SHE9. Con el SHE6, partiendo de un tamaño de elemento de.8, la frecuencia es de 7.Hz, la cual dista mucho del valor de referencia. Para llegar a dicha frecuencia hay que disponer de un mallado muy fino con tamaños de elementos inferiores a.7, por lo que complica la resolución de un modelo tan sencillo, por el hecho de manejar un elevado número de elementos. Al emplear el SHE9, partiendo de un tamaño de elemento de.8, la frecuencia es de.55hz. a diferencia con la frecuencia de referencia es muy pequeña. De esta forma se puede usar una malla más tosca, facilitando la resolución del modelo. a primera frecuencia del modelo D, para el perfil circular macizo, es de.98hz. Con el SOID5, partiendo de un tamaño de elemento de., la frecuencia es de.9hz, cuyo valor dista con el de referencia. Para alcanzar esta frecuencia hay que reducir el tamaño de los elementos por debajo de., lo que complica el cálculo del modelo al definir un número tan elevado de elementos. Haciendo lo mismo con el SOID95, para un tamaño de elemento de., la frecuencia es de.65hz. Este valor es más próximo al de referencia por lo que la malla a usar puede presentar un menor número de elementos que si se usase el SOID5. Después de haberse ejecutado estos cuatro ejercicios se concluye que el elemento lámina SHE9 y el elemento sólido SOID95 son los que presentan un comportamiento más adecuado y práctico para el análisis del modelo en tres dimensiones. Por último se crean unos modelos combinando D y D con el objeto de comprobar que la unión rígida entre los tramos D y D, la cual se describe en el siguiente subapartado, responde correctamente a cualquier tipo de análisis. En el caso del perfil hueco se definen los tramos D con elementos BEAM y los tramos D con elementos SHE9, y en el caso del perfil macizo los tramos D se caracterizan igual que el anterior y los tramos D con elementos SOID95. 8

13 Para el primer caso y un tamaño de elemento de.5 se obtiene una frecuencia de.96hz y para el segundo caso, y el mismo tamaño de elemento, la frecuencia es de.76hz. Ambas frecuencias son próximas a sus valores de referencia, por lo que la selección de estos elementos para el diseño del vástago en tres dimensiones es la más adecuada... MODEO VÁSTAGO GIRADIO Una vez decidida la cota de empotramiento del modelo, analizado en el subapartado.., y el tipo de elementos a utilizar, se procede al diseño en tres dimensiones del modelo de elementos finitos del vástago del Giraldillo junto con los elementos de unión descritos, en dimensiones y propiedades, en el capítulo. Con la idea de simplificar el modelo, de tal manera que el número de elementos no sea muy elevado, se ha optado por diseñar tramos del vástago monodimensionales. Para que esta simplificación no afecte al comportamiento de la estructura en el análisis a realizar, se establece una unión rígida consistente en acoplar todos los desplazamientos y giros del nodo extremo del tramo monodimensional con los nodos de la superficie en contacto del tramo tridimensional. A continuación (Fig. ) se muestra un ejemplo gráfico: SHE9 BEAM Node master Node slave Fig.. Esquema acoplamiento tramos D y D Puesto que las dos uniones que presenta la estructura portante son diseñadas en tres dimensiones, los tramos del vástago próximos a ellas también serán tridimensionales, quedando el resto monodimensional. En el esquema de la figura (Fig. ) se muestran las longitudes de los diferentes tramos: 9

14 Fig.. Esquema estructura portante del Giraldillo usada en el diseño D os tramos de vástago con perfil tubular, es decir, los tramos y, son diseñados a partir del diámetro medio. Esto hace que entre la superficie del vástago y el hueco de la brida y las cartelas no exista contacto. Para solucionar esto se rellena ese espacio mediante una unión rígida haciendo uso de un material con un elevado módulo elástico y una baja densidad ( E E y ρ siguiente aspecto (Fig. 5): acero ). Dicha unión presenta el ámina unión rígida Diámetro medio Anillo sólido unión rígida Fig. 5. Unión rígida entre vástago tubular y el hueco de la brida y las cartelas En la caracterización del modelo de elementos finitos se han usado los siguientes tipos de elementos para las distintas partes del mismo: elementos BEAM para los

15 tramos del vástago monodimensionales; SHE9 para los tramos del vástago de perfil tubular y las cartelas; SOID95 para los tramos de vástago de perfil macizo y las bridas, y MASS para las cargas puntuales de la masa del Giraldillo. En la siguiente figura (Fig. 6) se muestra un esquema con los tipos de elementos y materiales asociados a cada parte del modelo: SOID95 / AISI 6 SHE9 / ST5 SOID95 / AISI 6 SOID95 / ST5 MASS SHE9 / ST5 SHE9 / ST5 BEAM / AISI 6 DETAE A MASS SHE9 / ST5 BEAM / ST5 A SHE9 / ST5 B SOID95 / ST5 SHE9 / ST5 SHE9 / ST5 DETAE B Fig. 6. Esquema con tipos de elementos y materiales asociados a cada parte del modelo D Para hacer un mallado coherente entre las distintas partes tridimensionales de la estructura se procede a dividir las áreas de los perfiles tubulares y los volúmenes de las bridas y del perfil macizo. De esta manera los nodos generados tras el mallado, en las líneas y superficies comunes entre elementos estructurales resultantes de la

16 división, coincidirán. Esto permitirá además realizar una unión nodo a nodo entre cada pareja de bridas, dando lugar a lo que se denominará modelo sin tornillos. A continuación se exponen una serie de imágenes ilustrativas de las divisiones practicadas en el modelo y el mallado resultante según esta división (de Fig. 7a Fig. ): Fig. 7. Imagen D de la unión inferior

17 Fig. 8. Imagen D de la unión superior Fig. 9. Imagen D mallado de la unión inferior

18 Fig.. Detalle mallado de la unión inferior Fig.. Imagen D mallado unión superior

19 Fig.. Detalle mallado de la unión superior Una vez terminado el diseño del modelo, y considerando el mismo reparto de masa que en el caso monodimensional, tras el análisis modal la primera frecuencia de vibración resultante es.6hz. Para comparar con los datos experimentales se reparte la masa de tal manera que la frecuencia sea.5hz. Tras varias iteraciones el reparto queda de la siguiente forma: Masa superior (kg) Masa inferior (kg) Frecuencia (Hz) Modelo D.6 tramo 9mm

20 .. SIMUACIÓN DE TORNIOS Análisis de sensibilidad de parámetros de detección de daño. Continuando con el diseño del modelo de elementos finitos, y con el fin de que éste se aproxime a la estructura real, se procede a la simulación de los tornillos. En el caso anterior, había una unión nodo a nodo de los nodos coincidentes entre cada par de bridas, y ahora se procede a desconectar dichos nodos y simular la unión entre las bridas mediante tornillos. En cada unión entre tramos de vástago hay ocho tornillos, que serán diseñados como unas barras que atraviesan las bridas por los huecos destinados a ello. Por lo tanto los tornillos de la unión inferior tendrán una longitud de 6mm y los de la unión superior mm. Para que dichos tornillos queden fijos en sus extremos a las superficies de las bridas se establece una unión rígida, consistente en acoplar todos los desplazamientos y giros de cada nodo extremo del tornillo con los nodos del borde del orificio de la superficie de la brida. A continuación (Fig. ) se muestra un esquema: Node master Node slave Fig.. Esquema acoplamiento entre el extremo del tornillo y el borde del orificio os tornillos serán caracterizados con elementos tipo BEAM. Para las dos uniones que presenta la estructura los tornillos poseen propiedades y medidas diferentes. En la tabla siguiente se listan las características de los tornillos en función de la unión: 6

21 Unión Inferior Métrica Diámetro (mm) I y I z (m ) I x (m ) Material M A-8 (Inox): 9 N E m ρ 8 m kg Unión Superior M A-7 (Inox): 9 N E 5 m ρ 796 m kg Para comprobar el efecto que provoca en la estructura la presencia de tornillos pretensados se ha hecho inicialmente un modelo con tornillos sin pretensar y otro considerando una pretensión en ellos. os tornillos de la unión inferior poseen un apriete de 5Nm y los de la unión superior de 5Nm. Este apriete se introduce en el modelaje como una deformación inicial: Apriete 5Nm N KN A 5mm E N mm ε inicial N.665 E A Apriete 5Nm N 57KN A 5mm E 5 N mm ε inicial N.9 E A Una vez terminado el diseño de los modelos, y considerando el mismo reparto de masa que en el caso tridimensional descrito en el subapartado anterior (Masa superiorkg y Masa inferior69kg), se obtiene una primera frecuencia de vibración de.8hz para ambos modelos, con tornillos sin pretensar y con tornillos pretensados. a frecuencia disminuye en un.6% respecto a la del modelo sin tornillos (.5Hz), lo que significa que en el modelo con tornillos las uniones entre bridas es más flexible, siéndolo incluso más que en la estructura real. El efecto de la pretensión en los tornillos o de cualquier tipo de carga externa no se refleja en los resultados del análisis en el dominio de la frecuencia, de ahí que la 7

22 frecuencia sea la misma en ambos casos. Para analizar dicho efecto habría que someter los modelos a un análisis transitorio en el dominio del tiempo... VAIDACIÓN DE MODEOS D: COMPARACIÓN CON MODEO D Y EXPERIMENTA A partir del análisis modal de los modelos de elementos finitos diseñados en el subapartado anterior, se obtiene un vector de desplazamiento nodal para cada uno de ellos, correspondiente al primer modo de vibración. El tamaño de estos vectores es de nodos para el modelo tridimensional sin tornillos (acoplamiento entre bridas nodo a nodo) y de nodos para el modelo con tornillos. Con el fin de comparar estos resultados con los del modelo monodimensional y con los datos experimentales, se programa una función en Matlab la cual selecciona de entre todos los nodos aquellos que representan la forma del modo de los modelos tridimensionales como si el diseño fuese monodimensional. os nodos seleccionados son aquellos que en su posición indeformada se encuentran sobre el eje Z o, en su defecto, los más próximos a dicho eje, es decir, los nodos situados en la generatriz más cercana al eje Z. Según esto el tamaño del vector de desplazamiento de los modelos sin tornillos y con tornillos es de 6 nodos, en ambos casos, un número de datos considerablemente más manejable que el inicial. as coordenadas de posición de dichos nodos son iguales para todos los diseños tridimensionales. En las siguientes imágenes se muestra el modelo tridimensional (Fig. ) y el conjunto de nodos que representarán la forma del modo a comparar con los demás modelos (Fig. 5). 8

23 Fig.. Imagen modelo de elementos finitos D del vástago Fig. 5. Conjunto de nodos usados para representar la forma del modo del modelo D 9

24 Para comparar los resultados numéricos de los modelos tridimensionales con los demás casos se procede a normalizar los vectores de desplazamiento de igual manera que se hizo en el modelo monodimensional. Puesto que los datos experimentales de los que se dispone son hasta la posición del acelerómetro, en las gráficas se analizará la forma del modo de los modelos hasta dicha posición. En un primer análisis comparativo, se representan gráficamente la curva del modo numérico del modelo tridimensional sin tornillos y la del monodimensional, el modo experimental y el modo experimental aproximado por la expresión teórica del modo (Fig. 6)..9 er MODO (vastago 9 y modonum escalado).8.7 modo D 9 escalado modo D 9 escalado modo acel modo exp aprox.6 Desplazamiento ongitud Fig. 6. Comparación del primer modo de vibración de los modelos D y D con los resultados del modelo experimental A la vista de esta gráfica se observa que el modo del modelo tridimensional sin tornillos tiene un comportamiento similar al del modelo monodimensional. a diferencia entre ambas curvas está en la definición y caracterización de las uniones en el diseño tridimensional, pero a efectos prácticos dicha desviación puede considerarse despreciable. Esto permite que ante estudios de la estructura portante en los que la definición de las uniones no se vea alterada se puede hacer uso del modelo monodimensional, facilitando la obtención de resultados y el posterior manejo de los mismos.

25 Por último, en la siguiente gráfica (Fig. 7) son representadas las curvas de los modos numéricos de los modelos tridimensionales sin tornillos, con tornillos sin pretensado y con tornillos pretensados, el modo experimental y el modo experimental aproximado por la expresión teórica del modo er MODO vastago 9 (modonum escalado con tornillos pretensados y sin pretensado) modo D 9 escalado sin tornillos modo D 9 escalado con tornillos sin pretensado modo D 9 escalado con tornillos pretensado modo acel modo exp aprox.6 Desplazamiento ongitud Fig. 7. Comparación del primer modo de vibración de los modelos D sin tornillos y con tornillos con los resultados del modelo experimental Como se muestra en la gráfica las curvas de los modos de los modelos con tornillos (sin pretensado y con pretensado) son iguales, esto se debe a que la pretensión en los tornillos no afecta a los resultados del análisis en el dominio de la frecuencia. Comparando estas dos curvas con la del modelo sin tornillos ésta última presenta un comportamiento prácticamente idéntico a las anteriores. as diferencias existentes versan en torno a lo descrito en la gráfica anterior, pero en este caso son menores ya que en los tres modelos están definidas las uniones y lo que diferencia a un caso de otro es la presencia o no de tornillos. as formas de los modos de estos modelos tridimensionales y del monodimensional, junto con la del modo experimental serán tomadas como referencia en posteriores cálculos comparativos y análisis de sensibilidad.