Tema 8: Torsión. Tema 8: TORSIÓN 1 2 G. T x. Prof.: Jaime Santo Domingo Santillana E.P.S.-Zamora (U.SAL.)

Transcripción

1 ea 8: orsión ea 8: ORSIÓN Prof: Jaie Sano Doingo Sanillana EPS-Zaora (USL) - 008

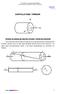
2 ea 8: orsión 8-INRODUCCIÓN Una sección de un eleeno esrucural esá soliciada a orsión cuando el Moeno resulane de las fuerzas ineriores iene la coponene M z y Fig8a Crierios de signos para los Moenos orsores >0 si su senido es el de la noral saliene de la sección n n <0 si su senido es conrario al de la noral saliene en la sección n n Fig8 En ese ea se esudiarán eleenos esrucurales en los que odas sus secciones esén soliciadas a orsión Diagraas de Moenos orsores l igual que ocurre con los diagraas correspondienes de la racción-copresión y de la Fleión, los diagraas de Moenos orsores indicarán el Moeno orsor correspondiene a cada sección del eleeno esrucural Se desarrollará uno de esos diagraas a ravés de un ejeplo:

3 Sección 8: Inroducción rao L M M M M M e M n M in M L L M M rao L + - M e M M in M n M M Fig8 - M ipos de orsión que se podrán dar: -orsión unifore: Se dice que una arra raaja a ORSIÓN UNIFORME cuando se cuplan las dos condiciones siguienes: el único esfuerzo presene es un Moeno orsor, que es consane a lo largo de ella y adeás los ereos de la arra pueden alaear lireene M M L M + Fig8 En la orsión unifore, dado que el alaeo que se pueda producir es el iso en odas las secciones, se podrá afirar que las ensiones norales serán cero (σ 0), y sólo dará lugar a ensiones coranes:

4 ea 8: orsión B-orsión no unifore: Se dirá que la orsión no es unifore cuando no se cuplan algunas de las dos condiciones aneriores, coo sería el caso de los dos ejeplos siguienes: Ejeplo Ejeplo M M M M Fig84 M ce M Fig La sección de la izquierda esá eporada y no podrá alaear lireene M El Moeno orsor no es consane a lo largo de la arra - En la orsión no unifore, el alaeo posile de las diferenes secciones no será el iso, por lo que se producirán ensiones norales: σ y ensiones coranes: En la siguiene figura se uesra el efeco del alaeo de una arra IPE lainada soeida a orsión no unifore (caso del ejeplo ) Se oserva cóo deido al alaeo, las alas de la viga se fleionan y por ano aparecerán en ellas ensiones norales σ Fig86 4

5 Sección 8: Inroducción Oservaciones: Para edir la suscepiilidad al alaeo por orsión de una deerinada sección se uiliza el denoinado ódulo de alaeo : I a y para edir la suscepiilidad la orsión se uiliza el ódulo de orsión : I os valores se pueden calcular u oener de alas Las piezas soeidas a orsión no unifore en las que el ódulo de alaeo (I a ) sea nulo o de pequeño valor con respeco al ódulo de orsión (I ), se adie aplicar el cálculo coo si fuera orsión unifore Ésos casos se darán en los siguienes ipos de secciones: secciones acizas de gran espesor secciones cerradas de pequeño espesor secciones aieras de pequeño espesor foradas por recángulos que se coran en un puno 5

6 ea 8: orsión Secciones ás adecuadas para raajar a orsión En las piezas soeidas a orsión cae disinguir dos ipos: el de las piezas cuya principal función es la ransisión de un par orsor, sólo o coinado con esfuerzos de fleión o ailes, (es el caso de piezas usadas principalene en las áquinas: ejes, ec) y el de piezas en las cuales la orsión es un efeco secundario indeseale (es el caso, no uy frecuene, de algunas piezas de esrucuras de edificación, coo las vigas carril o las correas en fachadas laerales) Las piezas correspondienes al prier ipo indicado, se proyecan con secciones acizas de gran espesor o cerradas de pequeño espesor: SECCIONES DE RN ESPESOR (MCIZS) Circulares Circulares huecas Recangulares SECCIONES CERRDS DE PEQUEÑO ESPESOR Circulares Recangulares Las SECCIONES BIERS DE PEQUEÑO ESPESOR no son apropiadas para ese ipo de soliciación y deen raar de eviarse su uilización o ien eplear disposiciones consrucivas adecuadas para eviar que la orsión se presene en ellas Por ello su cálculo no es frecuene y es esudiado con ás profundidad en asignauras de Esrucuras Meálicas 6

7 Sección 8: ensiones y deforaciones en piezas de sección aciza: circular y circular hueca 8-ENSIONES Y DEFORMCIONES EN PIEZS DE SECCIÓN MCIZ: CIRCULR Y CIRCULR HUEC - CÁLCULO DE ENSIONES Considérese una pieza de sección circular y sea el oeno orsor en una de sus secciones z y Fig87 Las relaciones ensiones Soliciaciones visas en 7 serían para ese caso: 0 σ y 0 y z 0 z ( ) N d V d V d y z d M 0 σ z d M 0 σ y d z y y z (8) Pero al igual que ocurría en la racción-copresión y en la Fleión, ésas ecuaciones, por si solas, no perien calcular el valor de las ensiones originadas por el Moeno orsor y hará que recurrir nuevaene a hipóesis siplificaivas que han sido coproadas eperienalene Para ese caso será: Hipóesis de Coulo: Las secciones ransversales circulares de la pieza peranecen planas durane la orsión, girando coo un odo rígido alrededor del eje noral a la sección 7

8 ea 8: orsión Coo consecuencia de dicha hipóesis se deduce que los radios de las secciones ransversales giran, peraneciendo recos, ienras que las generarices de la superficie laeral (línea -), se ransfora en hélices (curva - ) Fig88 Se deosrará a coninuación que en la orsión de piezas de sección circular no se producen ensiones norales, es decir que: σ 0 Se supone en prier lugar que eisen ensiones norales σ Si fuese así, ésas deerían presenar una disriución no consane, pues si fuese consane, es decir: σ ce, en virud de la priera de las relaciones de la ecuación (8), se endría: σ d ( si σ ce) σ d σ 0 No se cupliría dicha relación Osea que endría que ser: σ ce Si σ ce, por la ley de Hooke: ε σ ce E con lo cual se endría que las deforaciones lineales ε serían diferenes para los disinos punos de una sección y ésa por ano se alaearía, conradiciendo la Hipóesis de Coulo Conclusión: σ 0 (8) O lo que es lo iso: La orsión en secciones circulares sólo produce ensiones coranes 8

9 Sección 8: ensiones y deforaciones en piezas de sección aciza: circular y circular hueca Cálculo de las ensiones coranes Se considera una reanada de la pieza de longiud d ϕ ϕ +dϕ d Fig89 Mienras que la sección izquierda gira, alrededor del eje, un ángulo ϕ (ángulo de giro a orsión), la sección de la derecha hará girado, en el iso senido, un ángulo ϕ + dϕ lo que supone un giro relaivo a orsión de ésa sección con respeco a la anerior de valor dϕ Se oa sore dicha reanada un prisa coo el indicado en la siguiene figura d a c d Fig80 Coo consecuencia del giro de orsión relaivo, dϕ, enre las dos secciones laerales de dicha reanada, el prisa se deforará, de al fora que la cara laeral derecha girará un ángulo dϕ con respeco a la cara laeral izquierda, dando lugar a la siguiene figura, (que se apliará para poder oservarse ejor dicha deforación) La cara acd del prisa se ransforará en la a c d, sufriendo una deforación angular γ d a γ dϕ r c c a d γ c c d Fig8 9

10 ea 8: orsión La deforación angular γ se podrá oener por: r dϕ ag γ γ r ϑ (8) a d dϕ denoinando θ "ángulo de orsión uniario" (84) d La deforación angular γ es el resulado de la acción de las ensiones coranes que acúan sore las caras laerales del prisa El valor de ésas se podrá oener a parir de la Ley de Hooke: γ γ ( según 8) r ϑ (85) Ecuación que indica que: en una sección circular, las ensiones coranes producidas por el Moeno orsor, son proporcionales a la disancia r al cenro de la isa y perpendiculares al vecor de posición r sí pues, la disriución de ensiones coranes en una sección circular será la que se indica en las siguienes figuras a a d r c a r R a z siendo: Fig8 y a r ϑ y a ( cuando r R) R ϑ la ensión corane áia: a, se dará en los punos del orde de la sección circular La cuara ecuación de la relación ensiones-soliciaciones, ecuaciones (8) era: ( y z) d ( ver figura) r d y susiuyendo el valor de dado en (85) : y ϑ ángulo de orsión uniario (86) I o Fig8 siendo: I o Módulo de rigidez a la orsión (equivalene al ódulo de rigidez a la fleión: EI z, viso en el ea 5º) 0 z y r ϑ r d ϑ r d ϑ I o de donde : dr r O y d z z

11 Sección 8: ensiones y deforaciones en piezas de sección aciza: circular y circular hueca Susiuyendo finalene el valor oenido en (86), para el cálculo del ángulo de orsión uniario, en la ecuación (85): r r ϑ r (87) I I o o epresión final para el cálculo de la ensión corane deida a la orsión, en el caso de arras de sección circular Por lo viso anes: a R ( r R) (88) I I o o Wo R siendo : W o I o / R Módulo resisene a la orsión (equivalene al ódulo de resisene a la fleión: W z I z / y a, viso en el ea 5º) Oservación: Ésas fórulas serán aién aplicales a las arras acizas de sección circular hueca SECCIÓN CIRCULR SECCIÓN CIRCULR HUEC a a a R a z a R i R e a z y a y a 4 π R I o ( r R) a 4 π Re π Ri Io ( r R ) a e 4 Fig84a Fig84

12 ea 8: orsión B- CÁLCULO DE DEFORMCIONES Las deforaciones que se provocan en una arra soeida a orsión son los IROS a ORSION: ϕ, que se producen, al girar sus secciones ransversales alrededor del eje geoérico OX de la isa El valor de ésos giros será: El ángulo de orsión uniario según la ecuación (86) era: dϕ ϑ dϕ d I I o o d e inegrando esa ecuación enre dos secciones y B de la arra: B d ϕb ϕ B ϕ (89) I o iro relaivo enre dos secciones y B de la arra Caso paricular: Si I o ce, la ecuación (89) se podrá epresar: d S ϕ B ϕ B ϕ I I B o B o (80) Epresión que nos dice: el giro relaivo deido a la orsión enre dos secciones y B, es igual al área del diagraa de oenos orsores enre las dos secciones, dividido por el ódulo de rigidez a la orsión: I o Signos: ϕ B > 0 B gira en senido anihorario respeco a (siepre que las secciones consideradas y B, la sección esé a la izquierda de la B) Oservación final: Según lo indicado en 8, las fórulas oenidas para las ensiones y las deforaciones serán válidas ano para el caso de orsión Unifore coo para el de orsión no Unifore

13 Sección 8: ensiones y deforaciones en piezas de sección aciza no circulares 8-ENSIONES Y DEFORMCIONES EN PIEZS DE SECCIÓN MCIZ NO CIRCULRES La hipóesis de Coulo: las secciones ransversales peranecen planas durane la orsión, válida para las secciones circulares, no es válida sin eargo para oro ipo de secciones y por ano en ésas oras, las secciones se alaearán Fig85 No osane, en ese ipo de secciones, el ódulo de alaeo I a es pequeño coparado con el ódulo de orsión I y enonces, según lo indicado en 8, se podrá esudiarlas coo si esuvieran soeidas a orsión Unifore, aunque se esuviera en el caso de orsión no Unifore sí pues, en ese ipo de secciones soeidas a orsión, sólo aparecerán ensiones coranes La deerinación eaca de ensiones y deforaciones en una pieza de sección cualquiera soeida a orsión, se dee a Sain-Venan y fora pare de la eoría de la Elasicidad quí se epondrán a coninuación los resulados que se oienen al aplicar dicha eoría al caso se piezas de sección recangular CSO DE SECCIÓN RECNULR: µ h a (8) se da en el puno edio del lado ayor h a ϑ β h (8) Fig86 Los valores de µ y de β dependen de la relación h/: h/,5,75, µ 0,08 0, 0,9 0,46 0,58 0,67 0,8 0,99 0,07 0, 0, β 0,4 0,96 0,4 0,9 0,49 0,6 0,8 0,99 0,07 0, 0,

14 ea 8: orsión 84-ENSIONES Y DEFORMCIONES EN PIEZS DE SECCIONES BIERS DE PEQUEÑO ESPESOR Ya se indicó en 8 que ese ipo de secciones no son apropiadas para el raajo a orsión y para los casos en que la orsión aparezca coo efeco secundario, para eviar la ecesiva deforación o roura a la que pueda dar lugar, deerán eplearse disposiciones consrucivas adecuadas para eviar el efeco de dichas consecuencias En ese ipo de secciones sólo se va a esudiar el caso de la orsión Unifore Oservación: Según se dijo aneriorene los casos de secciones aieras de pequeño espesor foradas por recángulos que se coran en un puno, coo sería el cado de las secciones en L o en siple, aunque esén soeidas a orsión no unifore, su cálculo se hará coo si fuera orsión unifore CSO DE ORSIÓN UNIFORME: Para conocer la disriución de ensiones coranes a lo largo de la sección se uiliza el denoinado Méodo de analogía de la erana, propueso por Prandl y que dice: las ensiones coranes no dependen de la curvaura del conorno de la sección, siendo prácicaene las isas que si dicho conorno fuese reco De acuerdo con ello: equivalene s s Fig87 En virud de ello, y en el caso de espesor consane ce, se podrán aplicar las isas fórulas (8) y (8) visas aneriorene para el caso de sección recangular: a µ h M M ϑ µ s β h β s Y en ese caso, coo h >>, es decir, s >>, los coeficienes µ y β valdrán (ver ala en 8): µ 0, / β 0, / sí pues las forulas quedarán: 4 a s ϑ (8) (84) s

15 Sección 84: ensiones y deforaciones en piezas de sección aiera de pequeño espesor La eoría de Prandl aién dice: las ensiones coranes áias se dan en los ordes del conorno, llevando en aos lados senidos opuesos y se adie que su variación es lineal a lo largo del espesor a a equivalene a a s a a a a s Fig88 Casos pariculares: En el caso de que el espesor de la sección no sea consane: ce, las ecuaciones aneriores se generalizarán de la siguiene fora: a () a s 0 ds (85) s Fig89 a ( a) a ϑ s 0 ds (86) s En el caso de que el espesor de la sección no sea consane: ce, pero que ésa esuviese forada por varios eleenos de espesor consane, las ecuaciones aneriores serían ahora: a ( ) s s a ( a) a La ensión corane áia para cualquier espesor se oendrá: Fig80 a ϑ i si i si (87) (88) a ( ) (89) I 5

16 ea 8: orsión 85-ENSIONES Y DEFORMCIONES EN PIEZS DE SECCIONES CERRDS DE PEQUEÑO ESPESOR En ese ipo de secciones, según lo que se indicó en la sección 8, el cálculo que hareos será válido ano para la orsión unifore coo para la orsión no unifore, por lo ano las ensiones norales serán cero (σ 0) y sólo hará ensiones coranes () - CÁLCULO DE ENSIONES Se considera una reanada de una pieza de longiud d soeida a un Moeno orsor a a c d e d Fig8 Se sae que las ensiones coranes en los punos del conorno: a a, han de ser angenes al iso y dado el pequeño espesor () de la sección, se adie que esán disriuidas uniforeene a lo largo del iso Esaleciendo el equilirio de fuerzas del eleeno cde, que se represena a coninuación apliado: c c c c d d e F 0 d d c c c c (flujo corane)ce el flujo corane: es consane a lo largo de la sección ransversal Fig8 Coo consecuencia de ello, las ensiones coranes (), serán ayores donde el espesor () sea enor, (al revés de lo que ocurre en las secciones aieras de pequeño espesor) c c c c c 6 d e si Fig8 > c < c

17 Sección 84: ensiones y deforaciones en piezas de secciónes cerradas de pequeño espesor oando ahora oenos respeco del cenro de gravedad de la sección, de odas las fuerzas que acúan en la isa: ds df r d S df ds z s longiud línea edia y despejando y Fig84 df r ds r ( coo ce) r ds d s s s (80) siendo: área encerrada por la línea edia de la sección ransversal Fig85 La ensión corane áia, por lo viso anes, se dará donde el espesor sea ínio, resulando siendo su valor: a (8) B- CÁLCULO DE DEFORMCIONES Para el cálculo de deforaciones se parirá de la ecuación oenida en, aplicándola a la reanada de la pieza aneriorene descria de longiud d: d e du in siendo: d e dϕ raajo que realiza el oeno orsor du u dv + dv dv ds d d ( y z ) ( ce) V V V s d s ds energía alacenada en la reanada durane la deforación provocada por M 7

18 ea 8: orsión igualando aas epresiones: d dϕ dϕ ds ds ds d s s s (y coo ce) s ds ds ϑ (coo ) y despejando : ϑ 4 s ds s ϑ ds 4 (8) s Casos pariculares: Si ce s θ a (8) (84) 4 Si el espesor de la sección no es consane: ce, pero ésa esuviese forada por varios eleenos de espesor consane: a (85) θ 4 si (86) i in OBSERVCIÓN FINL: CUDRO RESUMEN Con el ojeo de unificar las fórulas que se han oenido para los diferenes ipos de secciones, se podrá adopar un forao general, único para odas ellas, que sería el siguiene: a W (87) siendo: I oeno de inercia orsor equivalene ϑ I (88) siendo: W ódulo resisene a la orsión equivalene Los valores de I y de W para cada una de las secciones se oendrán coparando las fórulas oenidas para cada una de las secciones esudiadas con las dadas coo forao general sí endreos: 8

19 Sección 85: ensiones y deforaciones en piezas de sección cerrada de pequeño espesor a) sección circular : coparando las fórulas específicas oenidas para la sección circular: ϑ I o (86) a (87) W o con las generales de forao único: ϑ I (88) a W (87) resulará: I I o π R 4 W W o I o R π R (89) ) sección recangular : coparando las fórulas específicas oenidas para la sección recangular: ϑ (8) a (8) β h µ h con las generales de forao único: ϑ I (88) a (87) W resulará: I β h W µ h (80) c) secciónes aieras de pequeño espesor: copararando las fórulas específicas oenidas para las secciones aieras de pequeño espesor ce: ϑ (84) a (8) s s con las generales de forao único: ϑ I resulará: I (88) a (87) W s W s (8) Oservación: La Noraiva española NBE-E-95 corrige esos valores afecándolos de un coeficiene α de la siguiene fora: I α s W α s (8) 9

20 ea 8: orsión siendo el valor de α: α SECCIÓN,, Y para el caso esudiado de que el espesor de la sección no sea consane: ce, pero que ésa esuviese forada por varios eleenos de espesor consane, coparando de nuevo las ecuaciones oenidas para ese caso específico con las fórulas generales únicas, y ya incluyendo el valor α correcor que incluye la noraiva española NBE- E-95, sería: I α si i W α si i (8) d) secciónes cerradas de pequeño espesor: copararando las fórulas específicas oenidas para las secciones cerradas de pequeño espesor ce θ 4 s (84) a (8) con las generales de forao único: ϑ I (88) a (87) W resulará 4 I W in s (84) Si el espesor de la sección no es consane: ce, pero ésa esuviese forada por varios eleenos de espesor consane: 4 I W in si i (85) 0

21 Sección 85: ensiones y deforaciones en piezas de sección cerrada de pequeño espesor Ejeplos -SECCIÓN CIRCULR DE PEQUEÑO ESPESOR -SECCIÓN RECNULR DE PEQUEÑO ESPESOR r ce Fig86 r r r s I r W r s r ) 4( 4 in π π π π π π h in 4 4 h h s I h W h s h i i + + Fig87

22 ea 8: orsión 86-INRODUCCIÓN L DIMENSIONMIENO RESISENCI DE VIS MEÁLICS SOLICIDS ORSIÓN (Noraiva DB-SE-) RESISENCI DE LS SECCIONES ORSIÓN El esfuerzo orsor de cualquier sección puede dividirse en dos coponenes: + w (86) siendo: : coponene correspondiene a la orsión unifore w : coponene correspondiene a la orsión de alaeo En las piezas de secciones acizas de gran espesor o en las cerradas de pequeño espesor puede despreciarse la coponene w, con lo cual: En las piezas de secciones aieras de pequeño espesor puede despreciarse la coponene de orsión unifore, con lo cual: w La coproación a resisencia puede realizarse de acuerdo a la epresión de Von Misses Oservación: En esa asignaura al y coo dijios aneriorene, an sólo diensionareos, en el caso de la orsión, con secciones acizas de gran espesor o cerradas de pequeño espesor Crierio de diensionaieno de Von Misses: σ σ * * co + f yd Se calcularán las ensiones coranes deidas a y las ensiones norales y coranes deidas a w Con los valores oenidos de odas esas ensiones se inroducirán en la fórula de Von Misses