UNIDAD IV Poliedros SESIÓN 19 Poliedros Radiales: Prismas
|
|
|
- María Mercedes González Gil
- hace 7 años
- Vistas:
Transcripción
1 SISTMS RPRSNTIÓN 0 POLIROS UNI IV Poliedos SSIÓN 9 Poliedos Radiales: Pismas Joge Luis aldeón Salcedo
2 SISTMS RPRSNTIÓN 0 POLIROS 4. oncepto y clasificación de sólidos geométicos Un sólido geomético es una egión del espacio limitada po cietas supeficies que pueden se planas o cuas. ependiendo de las caacteísticas que pesentan esas supeficies, es posible ealiza una clasificación como la que se muesta en la Tabla #. TL # : lasificación de los Sólidos Geométicos de acuedo a la supeficie que los define. POLIROS IRRGULRS RGULRS O PLTÓNIOS S RGULR RTOS S IRRGULR PRISMS S RGULR OLIUOS S IRRGULR S RGULR RTS S IRRGULR PIRÁMIS S RGULR OLIUS S IRRGULR OMINIONS Y PRTS OTROS POOLIROS Tetaedo, Hexaedo, Octaedo, odecaedo, Icosaedo. SRROLLLS ONOS URPOS RONOS SÓLIOS OMPUSTOS RGLOS O SIMPL URVTUR LOS ILINROS onoide, ilindoide, Hipeboloide de una oja, etc. OL RVOLUIÓN sfea, Too, lipsoide de Reolución, etc. URVTUR NO RVOLUIÓN RSULTO L OMINIÓN SÓLIOS ISTINT NTURLZ. La deteminación de los distintos elementos que componen un sólido geomético y el tazado de su poyección constituyen la síntesis de todos los temas estudiados peiamente en este libo. s entonces obligatoio el buen dominio de los conocimientos teóicos y de los pocedimientos instumentales peliminaes, paa loga el coecto empleo de las eamientas con las que se cuenta paa obtene buenos esultados en la esolución de los poblemas que an de se abodados. Los Poliedos son cuepos cuya supeficie limitante está compuesta exclusiamente po planos (supeficie po iédica), l los cuales confoman un númeo deteminado de ca as. su ez, los segmentos de ecta geneados po la intesección de caas adyacentes constituyen las aistas del poliedo. stas aistas conegen en un númeo no infeio a 3 en puntos denominados étices del poliedo. Joge Luis aldeón Salcedo
3 SISTMS RPRSNTIÓN 0 POLIROS 4.2 Poyección cilíndica otogonal de un Poliedo La poyección de cualquie poliedo sobe un plano siempe es un polígono, cuyos étices son el esultado de la intesección ente los ayos poyectantes tangentes al sólido que pasan po sus étices y el plano de poyección consideado. ico polígono constituye, a su ez, la poyección de la Línea de ontono paente del poliedo en el plano de poyección; esta línea poligonal ceada puede no se plana sino alabeada, es isible en la poyección y es la fontea ente las caas isibles y las no isibles del sólido. H G ualquie étice de un poliedo se poyecta dento de la poyección de la línea de contono apaente coespondiente. Po ota pate, esta línea no es la misma en la poyección oizontal y en la etical, po lo que la isibilidad debe se analizada sepaadamente. ig. 4.: Poyección ilíndica Otogonal n la ig. 4. se muesta la poyección de de un Poliedo. un cubo GH sobe el plano oizontal. La poyección del poliedo es el polígono G H, poyección oizontal de la poligonal alabeada GH, que es la línea de contono apaente en la poyección oizontal consideada. omo puede obsease en la figua, las caas GH, y G se encuentan po encima de la línea de contono apaente, po lo que las aistas comunes a esas caas se epesentan con línea continua en la poyección. Po el contaio, las caas estantes se allan po debajo de la mencionada línea, lo que justifica el tazado de las poyecciones de las aistas, y H con línea de tazos, pues son aistas inisibles en la poyección. 4.3 Pismas Los poliedos iegulaes pesentan caas y aistas de difeentes tamaños. Pueden se clasificados en pismas y piámides, en función de la supeficie poliédica que los limita. l P sma, i es un poliedo limitado po una supeficie pismática, la cual se compone de planos cuyas intesecciones ente sí son paalelas. ada una de esas intesecciones es la ecta común a dos planos como máximo. fin de limita el espacio dento de la supeficie pismática, ésta es cotada po dos planos paalelos y, dando luga a dos polígonos iguales llamados bases y en la ig los cuales pueden se egulaes o no. Las demás caas del pisma son denominadas caas lateales, que son las caas de la supeficie pismática, cuyo númeo es igual al númeo de étices que tienen los polígonos que confoman las bases y constituyen, en cualquie caso, paalelogamos. H G PH Joge Luis aldeón Salcedo
4 SISTMS RPRSNTIÓN 0 POLIROS J O SS O PLNOS S SUP. PRISMÁTI R LTRL ig. 4.2: Pisma simismo, las aistas esultantes de la intesección ente las caas lateales del sólido eciben el nombe de aistas lateales, siendo aistas básicas las esultantes de la intesección ente la supeficie pismática y los planos que contienen a las bases, es deci, los lados de los polígonos base. La ecta que pasa po los centos O y O de cada una de las dos bases del pisma se denomina eje del sólido, y es paalela a sus aistas lateales. Si este eje - y po consiguiente las aistas lateales es pependicula a los planos de base, el pisma seá ecto; si es oblicuo a dicos planos, el sólido se denomina oblicuo. La meno distancia ente los planos de base se conoce como ltua del pisma (H), y esulta se igual al segmento O O si se tata de pismas ectos. Los siguientes tópicos efeentes a pismas se enfocan exclusiamente en aquellos cuya base es un polígono egula y en los que el eje es pependicula a los planos base, es deci, pismas ectos de base egula Secciones Notables de Pismas Rectos de ase Regula Las secciones más impotantes desde el punto de ista geomético en cualquie pisma ecto de base egula son las Secciones Sencillas (ig. 4.3) y las Secciones Pincipales (ig. 4.4). Las Secciones Sencillas de un pisma son el esultado de la intesección ente planos paalelos al eje del sólido y el popio sólido. Su foma es de paalelogamos con dos lados Joge Luis aldeón Salcedo
5 SISTMS RPRSNTIÓN 0 POLIROS opuestos de longitud igual a la del segmento del eje OO. Las secciones sencillas seán ectangulaes si el sólido es ecto. K K M M O O ig. 4.3: Secciones sencillas de Pisma Recto con ase Regula. L L Las Secciones Pincipales de un pisma contienen las dimensiones más eleantes del poliedo: la altua y la diagonal de base o altua de base, dependiendo del númeo de étices que ésta tenga. Resultan al secciona este poliedo mediante planos que poseen las siguientes caacteísticas:. ontienen al eje del sólido. 2. ontienen a uno de los étices básicos. e lo anteio se infiee que las secciones pincipales son paalelogamos ectángulos si el pisma es ecto con dos lados opuestos de longitud igual a la del segmento OO, en tanto que los otos dos lados tienen una longitud igual a la diagonal de base, paa el caso de pismas con un númeo de étices básicos pa (ig. 4.4-a), o a la altua de base, si se tata de pismas con un númeo de étices básicos impa (ig. 4.4-b). l númeo de secciones sencillas en un pisma es indeteminado; po el contaio, el númeo de secciones pincipales es igual al númeo de étices básicos que posee el poliedo. s eidente que, si el pisma consideado es un pisma ecto, cada uno de los planos de sección sencilla y de sección pincipal es pependicula a los planos de base. O M O O ig. 4.4-a O ig. 4.4-b M ig. 4.4: Sección Pincipal de un Pisma Recto con ase Regula. Joge Luis aldeón Salcedo
6 SISTMS RPRSNTIÓN 0 POLIROS Poyección cilíndica otogonal de un Pisma Recto de ase Regula. Las caacteísticas de la poyección de la línea de contono apaente de un pisma ecto de base egula sobe un deteminado plano de poyección, dependen de la posición elatia ente este plano y el eje del poliedo. sí, si el eje es paalelo al plano de poyección, el pisma se poyecta como un ectángulo de altua igual a la altua del pisma (ig. 4.5-a); si el eje es pependicula al plano de poyección, el pisma se poyecta como un polígono igual a la base (ig. 4.5-b); finalmente, si el eje es oblicuo al plano de poyección, el esultado es un polígono genealmente iegula con un númeo de lados mayo a cuato (ig. 4.5-c). Si en el pime caso el ectángulo coesponde a una sección pincipal, la posición del pisma en elación con el plano de poyección se considea una posición notable, ya que la sección pincipal es un polígono que contiene dos dimensiones fundamentales del pisma: la altua y una diagonal de caa o una altua de caa, dependiendo del númeo de étices básicos que posee. PH ig. 4.5-a PH = = = PH ig. 4.5-b ig. 4.5-c ig. 4.5: Poyección cilíndica otogonal de un Pisma Recto de ase Regula. Joge Luis aldeón Salcedo
7 SISTMS RPRSNTIÓN 0 POLIROS simismo, el segundo caso constituye ota posición notable del pisma con especto al plano de poyección, dado que la poyección coespondiente epesenta el edadeo tamaño de las bases del poliedo. omo egla geneal puede establecese que si se conoce la sección pincipal de un pisma, o una de las bases y la magnitud de la altua del poliedo, éste queda completamente deteminado. π LT 0 P P π R R d R a R ig. 4.6-a onsidéese el siguiente ejemplo (ig. 4.6): se quiee constui las poyecciones diédicas de un pisma ecto de base egula exagonal, conocidos los étices y y el punto P, éste último sobe el plano que contiene a la sección pincipal, y sabiendo que las aistas básicas tienen una longitud a. Se tomaá la solución de meno cota paa el étice. Los puntos conocidos en un pincipio pemiten defini el plano de una de las secciones pincipales. Su constucción seá la clae paa la esolución de este poblema. Joge Luis aldeón Salcedo
8 SISTMS RPRSNTIÓN 0 POLIROS π 0 LT P P π ig. 4.6-b l pime paso consiste en alla una poyección en la que el plano π, definido po los puntos, y P y que contiene a la sección pincipal. apaezca en edadeo tamaño. sto se a ealizado aplicando un abatimiento en tono a la taza oizontal π. continuación, se a constuido un exágono auxilia de lado igual a la longitud a de las aistas básicas del pisma, obteniéndose así la longitud d de la diagonal de base (ig. 4.6-a). Luego se constuye una semicicunfeencia de diámeto igual a la longitud R R, sobe la cual se encuenta R po se el aco capaz de noenta gados. xisten dos soluciones paa ese aco; se a tomado la de meno cota. Haciendo cento en R y con adio igual a la diagonal de base d, se taza un aco que cota al anteio en R, luego, aplicando paalelismo ente ectas, se detemina el punto R (ig. 4.6-a). Seguidamente, se allan las poyecciones diédicas de los étices y, paa luego constui el plano de base infeio, el cual es pependicula a las aistas lateales y y contiene a los puntos y. Mediante un abatimiento de los puntos y del plano en tono a su taza oizontal, se a logado constui el edadeo tamaño de la base infeio, a pati del cual se obtienen las poyecciones diédicas de dica base. n ista de que se tata de un pisma ecto de base exagonal egula, existe paalelismo ente las aistas lateales y ente las aistas básicas opuestas, po lo que se a apoecado esa elación en la constucción de la caa supeio (ig. 4.6-b). inalmente, es necesaio analiza las pates isibles y las no isibles en cada una de las dos poyecciones diédicas. Siendo el étice de meno cota, es un punto inisible en la Joge Luis aldeón Salcedo
9 SISTMS RPRSNTIÓN 0 POLIROS poyección oizontal, po tanto, la aistas conegentes en ese étice son inisibles en dica poyección, a menos que sean pate de la línea de contono apaente. e igual manea, se deteminan las aistas no isibles en poyección etical; siendo el étice de meno uelo, las aistas conegentes en este étice seán inisibles, a menos que fomen pate de la línea de contono apaente (ig. 4.6-c). π LT P P π ig. 4.6-c JRIIOS PROPUSTOS. etemine la doble poyección otogonal de un pisma ecto de base exagonal egula sabiendo que sobe la ecta e se encuenta el eje del sólido y que es un étice básico. La altua del poliedo es de 60mm. Visibilidad. e [ ( 40,4,53),2( 70,9,28) ] ( 50,08,9) 2. etemine la doble poyección otogonal de un pisma ecto de base tiangula equilátea sabiendo que sobe la ecta m se encuenta la aista lateal del sólido y que el punto M es el punto medio del eje OO. Visibilidad. M [ ( 30,97,63),2( 70,74,30 ] ( 77,40,58) m ) Joge Luis aldeón Salcedo
10 SISTMS RPRSNTIÓN 0 POLIROS 3. etemine las poyecciones diédicas de un pisma e4cto de base cuadada, sabiendo que X es un punto peteneciente a la aista. efina la isibilidad del sólido. X ( 64,32,00) ( 40,36,5) ( 94,42,65) Joge Luis aldeón Salcedo
6.1. SUPERFICIE PRISMÁTICA Y PRISMA
 6 6.1. SUPERFICIE PRISMÁTICA Y PRISMA 6.. SUPERFICIE PIRAMIDAL Y PIRÁMIDE 6.. CUERPOS REDONDOS. 6.4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemina áeas de supeficies. Detemina volúmenes de sólidos. 14 Inicialmente
6 6.1. SUPERFICIE PRISMÁTICA Y PRISMA 6.. SUPERFICIE PIRAMIDAL Y PIRÁMIDE 6.. CUERPOS REDONDOS. 6.4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemina áeas de supeficies. Detemina volúmenes de sólidos. 14 Inicialmente
12 Cuerpos. en el espacio. 1. Elementos básicos en el espacio. Dibuja a mano alzada un punto, una recta, un romboide y un cubo.
 12 uepos en el espacio 1. Elementos básicos en el espacio ibuja a mano alzada un punto, una ecta, un omboide y un cubo. P I E N S A Y A L U L A Recta Punto Romboide ubo ané calculista 489,6 : 7,5 = 65,28;
12 uepos en el espacio 1. Elementos básicos en el espacio ibuja a mano alzada un punto, una ecta, un omboide y un cubo. P I E N S A Y A L U L A Recta Punto Romboide ubo ané calculista 489,6 : 7,5 = 65,28;
UNIDAD 4: CIRCUNFERENCIA CIRCULO:
 UNIDD 4: CIRCUNFERENCI CIRCULO: CONTENIDO: I. CONCEPTO DE CIRCUNFERENCI: Es una cuva ceada y plana cuyos puntos equidistan de un punto llamado cento. Una cicunfeencia se denota con la expesión: O C, y
UNIDD 4: CIRCUNFERENCI CIRCULO: CONTENIDO: I. CONCEPTO DE CIRCUNFERENCI: Es una cuva ceada y plana cuyos puntos equidistan de un punto llamado cento. Una cicunfeencia se denota con la expesión: O C, y
9 Cuerpos geométricos
 865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
SISTEMA DIÉDRICO II Paralelismo, perpendicularidad y distancias Verdaderas magnitudes lineales TEMA 9 PARALELISMO
 SSTEMA ÉRCO Paalelismo, pependiculaidad y distancias Vedadeas magnitudes lineales Objetivos y oientaciones metodológicas TEMA 9 Esta unidad temática es fundamental y, a la vez, su explicación se puede
SSTEMA ÉRCO Paalelismo, pependiculaidad y distancias Vedadeas magnitudes lineales Objetivos y oientaciones metodológicas TEMA 9 Esta unidad temática es fundamental y, a la vez, su explicación se puede
Arista Los polígonos que limitan al poliedro se llaman caras. Tetraedro Cubo Octaedro Dodecaedro Icosaedro
 OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
GEOMETRÍA. 1. Sin resolver el sistema, determina si la recta 2x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia
 Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombe: Cuso: eca: POLIEDROS poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Los polígonos que limitan al poliedo se llaman caas. Los lados de las
CLASIICAR POLIEDROS OBJETIVO 1 Nombe: Cuso: eca: POLIEDROS poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Los polígonos que limitan al poliedo se llaman caas. Los lados de las
CUERPOS REDONDOS. LA ESFERA TERRESTRE
 IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
TEMA 9: FORMAS GEOMÉTRICAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
Matemáticas 4º ESO Fernando Barroso Lorenzo GEOMETRÍA ANALÍTICA. r r
 Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS
 INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. Página 68 Reconoce, nomba y descibe figuas geométicas que apaecen en esta ilustación. Respuesta libe. Po ejemplo: cilindo, otoedo, cono, pisma tiangula Recueda otas figuas geométicas que foman pate
Pág. Página 68 Reconoce, nomba y descibe figuas geométicas que apaecen en esta ilustación. Respuesta libe. Po ejemplo: cilindo, otoedo, cono, pisma tiangula Recueda otas figuas geométicas que foman pate
1 Halla la mediatriz del segmento AB. 2 Traza la recta perpendicular a la recta r por el punto A.
 1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
TANGENCIAS (Julio Catalán)
 NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
A continuación obligamos, aplicando el producto escalar, a que los vectores:
 G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
Capítulo 8 Geometría del Espacio
 Capítulo 8 Geometía del Espacio Intoducción Esta ama de la geometía, también denominada Esteeometía, se ocupa de las popiedades y medidas de figuas geométicas en el espacio tidimensional. Estas figuas
Capítulo 8 Geometía del Espacio Intoducción Esta ama de la geometía, también denominada Esteeometía, se ocupa de las popiedades y medidas de figuas geométicas en el espacio tidimensional. Estas figuas
plano de la siguiente pirámide está compuesto por un cuadrado (base) y cuatro (4) triángulos isósceles. Longitud del lado del cuadrado 3 cm
 Matemáticas 9 Bimeste: III Númeo de clase: 26 Clase 26 Esta clase tiene video Tema: Áea y volumen de las piámides Actividad 60 1 El áea total de una piámide se puede calcula a pati de su desaollo plano.
Matemáticas 9 Bimeste: III Númeo de clase: 26 Clase 26 Esta clase tiene video Tema: Áea y volumen de las piámides Actividad 60 1 El áea total de una piámide se puede calcula a pati de su desaollo plano.
Puntos, rectas y planos en el espacio. Problemas métricos en el espacio
 1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
ACTIVIDADES INCLUIDAS EN LA PROPUESTA DIDÁCTICA: DE AMPLIACIÓN
 ág. 1 ENUNCIADOS 1 Giando una de las piezas de este mecano, la goma se defoma, peo siempe detemina un paalelogamo. o qué? ( Cómo es un cuadiláteo cuyas diagonales se cotan en sus puntos medios?) 2 ocedimiento
ág. 1 ENUNCIADOS 1 Giando una de las piezas de este mecano, la goma se defoma, peo siempe detemina un paalelogamo. o qué? ( Cómo es un cuadiláteo cuyas diagonales se cotan en sus puntos medios?) 2 ocedimiento
Sistema diédrico: punto, recta y plano. sta Unidad inicia el desarrollo del sistema diédrico, que abarca tres unidades didácticas.
 UNIDD 7 Sistema diédico: punto, ecta y plano E sta Unidad inicia el desaollo del sistema diédico, que abaca tes unidades didácticas. El sistema diédico pesenta cieta dificultad paa imagina las figuas en
UNIDD 7 Sistema diédico: punto, ecta y plano E sta Unidad inicia el desaollo del sistema diédico, que abaca tes unidades didácticas. El sistema diédico pesenta cieta dificultad paa imagina las figuas en
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
. Desarrollando esta ecuación vectorial, obtenemos: a = 3. : a = 2, b =, c = 0, y para w : a = 0, b =, c = -2.
 1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
GEOMETRÍA ANALÍTICA COORDENADAS POLARES. 2.1 Relación entre coordenadas polares y rectangulares de un punto
 COORDENADAS OLARES CONTENIDO 1. Coodenadas polaes de un punto. Coodenadas polaes gealizadas.1 Relación ente coodenadas polaes y ectangulaes de un punto. Cambio de sistema de coodenadas catesianas a polaes
COORDENADAS OLARES CONTENIDO 1. Coodenadas polaes de un punto. Coodenadas polaes gealizadas.1 Relación ente coodenadas polaes y ectangulaes de un punto. Cambio de sistema de coodenadas catesianas a polaes
de perfil, y se halla la tercera proyección tanto del punto P como de la recta r. La proyección r corta a los planos de proyección en H r
 Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
2.7 Cilindros, conos, esferas y pirámides
 UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
UNIDAD Geometía.7 Cilindos, conos, esfeas y piámides 58.7 Cilindos, conos, esfeas y piámides OBJETIVOS Calcula el áea y el volumen de cilindos, conos, esfeas y piámides egulaes Resolve poblemas de solidos
1. (JUN 04) Se consideran la recta y los planos siguientes: 4
 Matemáticas II Cuso.. (JUN ) Se considean la ecta los planos siguientes ; ;. Se pide (a) Detemina la posición elativa de la ecta con especto a cada uno de los planos. (b) Detemina la posición elativa de
Matemáticas II Cuso.. (JUN ) Se considean la ecta los planos siguientes ; ;. Se pide (a) Detemina la posición elativa de la ecta con especto a cada uno de los planos. (b) Detemina la posición elativa de
A B. Teniendo en cuenta que el lado de un pentágono regular es la sección aurea de su diagonal, se tiene la siguiente construcción:
 1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO
 EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO Detemina la posición elativa de las siguientes paejas de planos a) 8 ' 4 6 6 b) 6 7 ' 4 c) ' 6 7 d) 4 7 Dado el plano que contenga al punto A(-,, 4), detemina
EJERCICIOS DE GEOMETRÍA ANALITICA DEL ESPACIO Detemina la posición elativa de las siguientes paejas de planos a) 8 ' 4 6 6 b) 6 7 ' 4 c) ' 6 7 d) 4 7 Dado el plano que contenga al punto A(-,, 4), detemina
DIBUJO TÉCNICO I GEOMÉTRICO DESCRIPTIVA NORMALIZACIÓN SOLUCIONARIO EDITORIAL DONOSTIARRA
 DIBUJO TÉCNICO I SOLUCIONRIO GEOMÉTRICO DESCRIPTIV Ø EDITORIL DONOSTIRR NORMLIZCIÓN Ø Ø Ø F. JVIER RODRÍGUEZ DE BJO VÍCTOR ÁLVREZ BENGO DIBUJO TÉCNICO DIBUJO GEOMÉTRICO º Bachilleato SOLUCIONRIO EDITORIL
DIBUJO TÉCNICO I SOLUCIONRIO GEOMÉTRICO DESCRIPTIV Ø EDITORIL DONOSTIRR NORMLIZCIÓN Ø Ø Ø F. JVIER RODRÍGUEZ DE BJO VÍCTOR ÁLVREZ BENGO DIBUJO TÉCNICO DIBUJO GEOMÉTRICO º Bachilleato SOLUCIONRIO EDITORIL
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
Apuntes de Trigonometría Elemental
 Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
GEOMETRÍA. punto, la recta y el plano.
 MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Matemáticas para Maestros Primer Curso Grado en Primaria 2014/2015. Tema 2. Magnitudes Geométricas
 Tema 2. Magnitudes Geométicas 1. Intoducción En pime luga tataemos de una cualidad de las figuas planas (su extensión, lo que ocupan en el plano) llamada, genealmente, supeficie o áea. Algunos autoes establecen
Tema 2. Magnitudes Geométicas 1. Intoducción En pime luga tataemos de una cualidad de las figuas planas (su extensión, lo que ocupan en el plano) llamada, genealmente, supeficie o áea. Algunos autoes establecen
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
RELACION DE ORDEN: PRINCIPALES TEOREMAS
 RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
3.3.- Cálculo del campo eléctrico mediante la Ley de Gauss
 Lección 1. Campo Electostático en el vacío: Conceptos y esultados fundamentales 17..- Cálculo del campo eléctico mediante la Ley de Gauss La Ley de Gauss pemite calcula de foma sencilla el campo eléctico
Lección 1. Campo Electostático en el vacío: Conceptos y esultados fundamentales 17..- Cálculo del campo eléctico mediante la Ley de Gauss La Ley de Gauss pemite calcula de foma sencilla el campo eléctico
CUADRILÁTEROS. Cuadrado y Rectángulo.
 ibuja un NTÁN cuando nos dan el RI. 1. ibuja una cicunfeencia de adio el que nos dan.. ibuja dos diámetos pependiculaes (ojo que pasen po el cento de la cicunfeencia). 3. ibuja la mediatiz de uno de los
ibuja un NTÁN cuando nos dan el RI. 1. ibuja una cicunfeencia de adio el que nos dan.. ibuja dos diámetos pependiculaes (ojo que pasen po el cento de la cicunfeencia). 3. ibuja la mediatiz de uno de los
MAGNITUDES VECTORIALES:
 Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
3 y un vector director Supongamos también que P x, y,
 . Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
. Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
Tema 7 Problemas métricos
 Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
AXO-1 Z Z X Y X Y Z Z X Y X Y Z Z Y X Y X
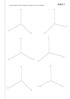 1- Halla los tiángulos de tazas coficientes de educción de estos ejes axonométicos O-1 2- Con los coeficientes de educción obtenidos en el ejecicio anteio, epesenta los siguientes puntos: =(3.5,2.0,4.0)
1- Halla los tiángulos de tazas coficientes de educción de estos ejes axonométicos O-1 2- Con los coeficientes de educción obtenidos en el ejecicio anteio, epesenta los siguientes puntos: =(3.5,2.0,4.0)
ECUACIONES DE LA RECTA
 Temas 6 y 7 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
Temas 6 y 7 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS
 IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
11 FORMAS GEOMÉTRICAS
 11 FRMS GEMÉTRIS EJERIIS PRPUESTS 11.1 Dos puntos deteminan una ecta. a) uántas ectas se pueden taza con un solo punto? b) ómo son las ectas que pasan po ese punto? a) Tantas como se quiea. b) Secantes,
11 FRMS GEMÉTRIS EJERIIS PRPUESTS 11.1 Dos puntos deteminan una ecta. a) uántas ectas se pueden taza con un solo punto? b) ómo son las ectas que pasan po ese punto? a) Tantas como se quiea. b) Secantes,
LEY DE GAUSS. Este enunciado constituye en realidad una de las principales leyes del Electromagnetismo.
 LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
4.- (1 punto) Como ya sabéis, el campo eléctrico creado por una carga en un punto P, es una magnitud vectorial que viene dada por la expresión E K u
 Nombe: Cuso: º Bachilleato B Examen I Fecha: 5 de febeo de 08 Segunda Evaluación Atención: La no explicación claa y concisa de cada ejecicio implica una penalización del 5% de la nota.- (,5 puntos) Halla
Nombe: Cuso: º Bachilleato B Examen I Fecha: 5 de febeo de 08 Segunda Evaluación Atención: La no explicación claa y concisa de cada ejecicio implica una penalización del 5% de la nota.- (,5 puntos) Halla
PREGUNTAS 1) El resultado de calcular. 100x es: A) ±10x B) 50 x C) 10x D) 10 x
 La siguiente colección de ejecicios es una muesta de lo que podía contene la Evaluación Diagnóstica de Matemática, que se toma paa ingesa a cusa cualquiea de las caeas que se ofecen en la FACULTAD DE CIENCIAS
La siguiente colección de ejecicios es una muesta de lo que podía contene la Evaluación Diagnóstica de Matemática, que se toma paa ingesa a cusa cualquiea de las caeas que se ofecen en la FACULTAD DE CIENCIAS
La ecuación implicita del plano que pasa por el punto P(1, 0, 1) con vectores AB (2,1,0) y AP (2,0,0) será:
 xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
Teorema para Calcular el área de un cuadrilátero
 Teoema paa alcula el áea de un cuadiláteo ilton Favio onaie eña El siguiente polema pulicado el 1 de Feeo del 2018, en la evista Tiangulos ai 1, nos pemitiá mosta algunos esultados inteesantes. olema 867
Teoema paa alcula el áea de un cuadiláteo ilton Favio onaie eña El siguiente polema pulicado el 1 de Feeo del 2018, en la evista Tiangulos ai 1, nos pemitiá mosta algunos esultados inteesantes. olema 867
POTENCIA TEMA2. Actividad 1
 x = 4,76 EI E GEERÍ Y IUJ ÉI ctividad La edia popocional x a los segentos a y b se obtiene sabiendo que la potencia de un punto especto de una cicunfeencia es igual al cuadado del segento toado sobe una
x = 4,76 EI E GEERÍ Y IUJ ÉI ctividad La edia popocional x a los segentos a y b se obtiene sabiendo que la potencia de un punto especto de una cicunfeencia es igual al cuadado del segento toado sobe una
El radio de una circunferencia mide 1,25 cm. Halla el ángulo que forman las tangentes a la circunferencia desde un punto situado a 4,8 cm del centro.
 T: TRIGNMETRÍ 1º T 7. RESLUIÓN E TRIÁNGULS RETÁNGULS L TNGENTE UN IRUNFERENI El adio de una cicunfeencia mide 1, cm. Halla el ángulo que foman las tangentes a la cicunfeencia desde un punto situado a cm
T: TRIGNMETRÍ 1º T 7. RESLUIÓN E TRIÁNGULS RETÁNGULS L TNGENTE UN IRUNFERENI El adio de una cicunfeencia mide 1, cm. Halla el ángulo que foman las tangentes a la cicunfeencia desde un punto situado a cm
FUNCIONES TRIGONOMÉTRICAS página 37
 página 37 página 38 2 2.1 UNA PROPIEDAD DE LOS TRIÁNGULOS Los tiángulos ectángulos tienen dos popiedades muy impotantes. De la pimea que a continuación se va a analiza nacen las llamadas Funciones Tigonométicas.
página 37 página 38 2 2.1 UNA PROPIEDAD DE LOS TRIÁNGULOS Los tiángulos ectángulos tienen dos popiedades muy impotantes. De la pimea que a continuación se va a analiza nacen las llamadas Funciones Tigonométicas.
TEMA PRELIMINAR. Los sistemas de representación son objeto de estudio en la geometría descriptiva, la cual se fundamenta en la geometría proyectiva.
 TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
Sistema de planos acotados
 Sistema de planos acotados ISBN 978-84-9048-146-2 4021P02 Sistema de planos acotados Conceptos básicos y ejecicios Vicente Rioja Castellano El objetivo fundamental de este libo es popociona una heamienta
Sistema de planos acotados ISBN 978-84-9048-146-2 4021P02 Sistema de planos acotados Conceptos básicos y ejecicios Vicente Rioja Castellano El objetivo fundamental de este libo es popociona una heamienta
MAGNITUDES ESCALARES Y VECTORIALES
 C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Los ángulos: Se pueden medi en: GRADOS RADIANES: El adián se define como el ángulo que limita un aco cuya longitud es igual al adio del aco. Po tanto, el ángulo, α,
FRANCISCO JAVIER GARCÍA CAPITÁN
 MÁXIMOS SIN DERIVDS FRNCISCO JVIER GRCÍ CPITÁN Resumen Este atículo eune vaios ejemplos de cómo calcula extemos sin necesidad de usa el cálculo difeencial Solo usaemos conocidas desigualdades ente las
MÁXIMOS SIN DERIVDS FRNCISCO JVIER GRCÍ CPITÁN Resumen Este atículo eune vaios ejemplos de cómo calcula extemos sin necesidad de usa el cálculo difeencial Solo usaemos conocidas desigualdades ente las
RECTAS EN EL ESPACIO.
 IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
π r. Cada círculo menor es de radio 2. Por
 Pueba CNU Venezuela, Septiembe de 004. Modelo. Soluciones. < Si, y z son enteos positivos, tales que z. Cuál de las siguientes epesiones es mayo que? z ( ) ( ) a) z b) z c) z d) z e) = ( ) < ( ) = < Solución:
Pueba CNU Venezuela, Septiembe de 004. Modelo. Soluciones. < Si, y z son enteos positivos, tales que z. Cuál de las siguientes epesiones es mayo que? z ( ) ( ) a) z b) z c) z d) z e) = ( ) < ( ) = < Solución:
z a3 Ecuaciones continuas de la recta: eliminando el parámetro de (2) = = u u u
 Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Ejercicios. 100 Capítulo 8 Construcciones geométricas
 jecicios 1. a. Taza la ecta (MN). b. Taza la semiecta [N). c. Taza el segmento [Q]. d. Taza el segmento []. e. Taza la ecta (). f. Taza la semiecta [).. 7. () [] [) (G) G () [) [) () [] [] [) (G) H 8.
jecicios 1. a. Taza la ecta (MN). b. Taza la semiecta [N). c. Taza el segmento [Q]. d. Taza el segmento []. e. Taza la ecta (). f. Taza la semiecta [).. 7. () [] [) (G) G () [) [) () [] [] [) (G) H 8.
La recta n forma un ángulo de 60 (trazar con reglas) con la recta r. Qué ángulos forma la recta n con la recta s? NOMBRE: Nº 1ºESO
 1. OCBULRIO BÁSICO 1. Dibuja las siguientes ectas siguiendo las instucciones: La ecta vetical es pependicula a las ectas s y q. La distancia ente estas dos ectas es de 20mm. o La ecta n foma un ángulo
1. OCBULRIO BÁSICO 1. Dibuja las siguientes ectas siguiendo las instucciones: La ecta vetical es pependicula a las ectas s y q. La distancia ente estas dos ectas es de 20mm. o La ecta n foma un ángulo
ALGEBRA Y GEOMETRÍA I
 FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
La ecuación implicita del plano que pasa por el punto P(1, 0, 1) con vectores AB (2,1,0) y AP (2,0,0) será:
 xyz0. Dados la ecta : y el punto P(, 0, ) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que pasa
xyz0. Dados la ecta : y el punto P(, 0, ) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que pasa
Fuerza magnética sobre conductores.
 Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Cinemática del Sólido Rígido (SR)
 Cinemática del Sólido Rígido (SR) OBJETIVOS Intoduci los conceptos de sólido ígido, taslación, otación y movimiento plano. Deduci la ecuación de distibución de velocidades ente puntos del SR y el concepto
Cinemática del Sólido Rígido (SR) OBJETIVOS Intoduci los conceptos de sólido ígido, taslación, otación y movimiento plano. Deduci la ecuación de distibución de velocidades ente puntos del SR y el concepto
EJERCICIOS DEL TEMA VECTORES
 EJERCICIOS DEL TEMA VECTORES 1) Considea el vecto w, siguiente: w Dibuja, en cada caso uno de los siguientes casos, un vecto v, que sumado con u dé como esultado w : a) b) c) d) u u u u 2) A la vista de
EJERCICIOS DEL TEMA VECTORES 1) Considea el vecto w, siguiente: w Dibuja, en cada caso uno de los siguientes casos, un vecto v, que sumado con u dé como esultado w : a) b) c) d) u u u u 2) A la vista de
Ángulos en la circunferencia
 MT-22 Clase Ángulos en la cicunfeencia pendizajes espeados Identifica los elementos de un cículo y una cicunfeencia. Calcula áeas y peímetos del secto y segmento cicula. Reconoce tipos de ángulos en la
MT-22 Clase Ángulos en la cicunfeencia pendizajes espeados Identifica los elementos de un cículo y una cicunfeencia. Calcula áeas y peímetos del secto y segmento cicula. Reconoce tipos de ángulos en la
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1
 TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
TALLER 3 GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA α CORBALÁN AÑO 2010
 Página 1 de 16 2010 www.amondelaguila.com PUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BCILLERTO. UTOR: RMON DEL GUIL α CORBLÁN ÑO 2010 G α 1 ch (α 2 ) Los apuntes que pesento solo petenden se un complemento
Página 1 de 16 2010 www.amondelaguila.com PUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BCILLERTO. UTOR: RMON DEL GUIL α CORBLÁN ÑO 2010 G α 1 ch (α 2 ) Los apuntes que pesento solo petenden se un complemento
ELIMINATORIA, 14 de abril de 2007 PROBLEMAS
 ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
1. Realiza las siguientes operaciones con segmentos. 1º a+2b-c. 2º a+c-b. 3º 3a+c-b NOMBRE: Nº 1ºESO 1.3. OPERACIONES CON SEGMENTOS
 1.3. OPERCIONES CON SEGMENTOS 1. Realiza las siguientes opeaciones con segmentos a b c 1º a+2b-c 1º 2º a+c-b 2º 3º 3a+c-b 3º TEM 1 - Opeaciones con segmentos página 3 1.3.2. TEOREM DE TLES 1. Divide el
1.3. OPERCIONES CON SEGMENTOS 1. Realiza las siguientes opeaciones con segmentos a b c 1º a+2b-c 1º 2º a+c-b 2º 3º 3a+c-b 3º TEM 1 - Opeaciones con segmentos página 3 1.3.2. TEOREM DE TLES 1. Divide el
Análisis de respuesta en frecuencia
 Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
5.2 PROBLEMAS PRACTICOS DE MÁXIMOS Y MINIMOS
 8. Un avión que vuela a velocidad constante de Km/h pasa sobe una estación teeste de ada a una altua de 1 Km. Y se eleva a un ángulo de º. qué velocidad aumenta la distancia ente el avión la estación de
8. Un avión que vuela a velocidad constante de Km/h pasa sobe una estación teeste de ada a una altua de 1 Km. Y se eleva a un ángulo de º. qué velocidad aumenta la distancia ente el avión la estación de
Situaciones 1: Dada una carga eléctrica puntual, determine el campo eléctrico en algún punto dado. r u r. r 2. Esmelkys Bonilla
 Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
Situaciones 1: Dada una caga eléctica puntual, detemine el campo eléctico en algún punto dado. E = k q 2 u 1.- Una caga puntual positiva, situada en el punto P, cea un campo eléctico E v en el punto, epesentado
Matemáticas II Hoja 6: Puntos, rectas y planos en el espacio
 Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
 FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
Al estar la fuerza dirigida hacia arriba y la intensidad del campo eléctrica hacia abajo, la carga de la esfera es negativa:
 PROLMS CMPO LÉCTRICO. FÍSIC CHILLRTO. Pofeso: Féli Muñoz Jiménez Poblema 1 Detemina la caga de una peueña esfea cagada de 1, mg ue se encuenta en euilibio en un campo eléctico unifome de 000 N /C diigido
PROLMS CMPO LÉCTRICO. FÍSIC CHILLRTO. Pofeso: Féli Muñoz Jiménez Poblema 1 Detemina la caga de una peueña esfea cagada de 1, mg ue se encuenta en euilibio en un campo eléctico unifome de 000 N /C diigido
DIBUJO TÉCNICO BACHILLERATO. Láminas resueltas del TEMA 4. TANGENCIAS. Departamento de Artes Plásticas y Dibujo
 DIBUJO ÉCNICO BACHILLERAO Láminas esueltas del EMA 4. ANGENCIAS. Depatamento de Ates lásticas y Dibujo 1.- Dibuja 2 cicunfeencias adio 10 mm. que sean ANGENES EXERIORES a la dada y ente ellas. 2.- Dibuja
DIBUJO ÉCNICO BACHILLERAO Láminas esueltas del EMA 4. ANGENCIAS. Depatamento de Ates lásticas y Dibujo 1.- Dibuja 2 cicunfeencias adio 10 mm. que sean ANGENES EXERIORES a la dada y ente ellas. 2.- Dibuja
0.2.4 Producto de un escalar por un vector. Vector unitario. 0.3 Vectores en el sistema de coordenadas cartesianas.
 VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
RECTAS EN EL ESPACIO
 IES Pade Poeda (Guadi UNIDAD 9 GEOMETRÍA AFÍN RETAS EN EL ESPAIO. EUAIONES DE LA RETA Una ecta queda deteminada po Un punto A ( a a a Un ecto de diección ( A ( A; se le llama deteminación lineal de la
IES Pade Poeda (Guadi UNIDAD 9 GEOMETRÍA AFÍN RETAS EN EL ESPAIO. EUAIONES DE LA RETA Una ecta queda deteminada po Un punto A ( a a a Un ecto de diección ( A ( A; se le llama deteminación lineal de la
RECTAS EN EL ESPACIO.
 IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
2. CURVAS EN EL SISTEMA POLAR
 2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO Geometría lineal Recta y Plano
 LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
( ) CIRCUNFERENCIA UNIDAD VIII VIII.1 DEFINICIÓN DE CIRCUNFERENCIA
 CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
TANGENCIAS ENTRE CIRCUNFERENCIAS
 1. Cicunfeencias tangentes EXERIORES a una cicunfeencia a la dada y ente ellas. Dada la cicunfeencia debemos dibuja una cicunfeencia que sea tangente a la pimea. Después vamos a dibuja ota cicunfeencia
1. Cicunfeencias tangentes EXERIORES a una cicunfeencia a la dada y ente ellas. Dada la cicunfeencia debemos dibuja una cicunfeencia que sea tangente a la pimea. Después vamos a dibuja ota cicunfeencia
SUPERPOSICIÓN DE M. A.S.
 SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
INTRODUCCION AL ANALISIS VECTORIAL
 JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
LINEA: Es una sucesión infinita de puntos. Pueden ser lineas curvas o líneas rectas.
 puntes geometía: Constucciones básicas º ESO LINE: Es una sucesión infinita de puntos. ueden se lineas cuvas o líneas ectas. LINE CUR. Es una sucesión infinita de puntos en difeentes diecciones. LINE RECT.
puntes geometía: Constucciones básicas º ESO LINE: Es una sucesión infinita de puntos. ueden se lineas cuvas o líneas ectas. LINE CUR. Es una sucesión infinita de puntos en difeentes diecciones. LINE RECT.
ÁNGULOS Y LONGITUDES DE ARCO
 I.E LEÓN XIII EL PEÑOL MATEMÁTICA GRADO: 0 TALLER Nº: EMETRE I ÁNGULO Y LONGITUDE DE ARCO REEÑA HITÓRICA Un Poblema de Ángulos en la Antigüedad. El matemático giego Eatostenes (apox 76 9 a.c.) midió la
I.E LEÓN XIII EL PEÑOL MATEMÁTICA GRADO: 0 TALLER Nº: EMETRE I ÁNGULO Y LONGITUDE DE ARCO REEÑA HITÓRICA Un Poblema de Ángulos en la Antigüedad. El matemático giego Eatostenes (apox 76 9 a.c.) midió la
