DIBUJO TÉCNICO I GEOMÉTRICO DESCRIPTIVA NORMALIZACIÓN SOLUCIONARIO EDITORIAL DONOSTIARRA
|
|
|
- Vanesa Vega Franco
- hace 7 años
- Vistas:
Transcripción
1 DIBUJO TÉCNICO I SOLUCIONRIO GEOMÉTRICO DESCRIPTIV Ø EDITORIL DONOSTIRR NORMLIZCIÓN Ø Ø Ø
2 F. JVIER RODRÍGUEZ DE BJO VÍCTOR ÁLVREZ BENGO DIBUJO TÉCNICO DIBUJO GEOMÉTRICO º Bachilleato SOLUCIONRIO EDITORIL DONOSTIRR Pokopandegi, nº - Pabellón Igaalde - Baio Igaa patado 67 - Teléfonos Fax SN SEBSTIÁN SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
3 INTRODUCCIÓN En esta oba se pesentan las espuestas, de un modo gáfico y azonado, de las actividades planteadas en el libo de Dibujo Técnico de º BCHILLERTO de los autoes F. Javie Rodíguez de bajo y Vícto Álvaez Bengoa. Este solucionaio va diigido, fundamentalmente, a los pofesoes/as que impaten la mateia de Dibujo Técnico de º Bachilleato, en las siguientes modalidades: Tecnología, Ciencias de la Natualeza y de la Salud y tes, con objeto de ayudales y guiales en la esolución de las actividades popuestas en el libo anteiomente citado. Paa facilita la compensión y ejecución del poceso de esolución de las actividades indicadas, nos ha paecido opotuno acompaña a la mayoía de las soluciones gáficas dadas, una seie de textos explicativos de las mismas, así como, señala cuáles son los fundamentos teóicos en los que se basa su esolución. Existen, po oto lado, una seie de temas en los que, po las azones que a continuación se exponen, no se ealiza ningún tipo de solución. Los temas y los motivos po los que no disponen de solucionaio, son: Tema : INSTRUMENTOS DE DIBUJO Las actividades popuestas consisten en la epoducción, a mano alzada y a limpio, de una seie de figuas sencillas que apaecen en el libo. Como su tazado y constucción no epesenta ningún tipo de dificultad y, además, la espuesta es la misma figua, no se ha ealizado solucionaio alguno. Tema : TRZDOS FUNDMENTLES EN EL PLNO. Las actividades popuestas consisten en la epoducción, a mano alzada y a limpio, de una seie de figuas sencillas que apaecen en el libo. Como su tazado y constucción no epesenta ningún tipo de dificultad y, además, la espuesta es la misma figua, no se ha ealizado solucionaio alguno. Tema 8: TNGENCIS Las actividades popuestas consisten en la epoducción, a escala, de una seie de figuas sencillas, que apaecen dibujadas en el libo, sobe tangencias. Como su tazado y constucción no epesenta ningún tipo de dificultad y, además, la espuesta es, pácticamente, la misma figua, no se ha ealizado solucionaio alguno. Tema 9: CURVS TÉCNICS Las actividades popuestas consisten en la epoducción, a escala, de dos figuas sencillas, que apaecen dibujadas en el libo, sobe aplicaciones del tema. Como su tazado y constucción no epesenta ningún tipo de dificultad y, además, la espuesta es, pácticamente, la figua popuesta, no se ha ealizado solucionaio alguno. Tema : GEOMETRÍ DESCRIPTIV. SISTEMS DE REPRESENTCIÓN La actividad popuesta consiste en la epoducción, a mano alzada y en los divesos sistemas indicados, de una seie de objetos sencillos que estén al alcance del alumno. Como su tazado y constucción no epesenta ningún tipo de dificultad y, además, los objetos son de libe elección po pate del alumno, no existe solucionaio de este tema. Tema : SISTEMS COTDOS l no existi popuesta de actividades, no pocede ealiza espuesta alguna. Tema 7: NORMLIZCIÓN: Rotulación nomalizada l no existi popuesta de actividades, no pocede ealiza espuesta alguna. Tema 9: RTE Y DIBUJO TÉCNICO Las actividades popuestas son abietas y de libe elección, en consecuencia, no se pesenta ninguna solución. DIBUJO GEOMÉTRICO SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
4 ctividad ESCLS TEM La difeencia estiba en que la escala de educción se aplica paa los objetos que, po su gan tamaño, no se pueden epesenta con las medidas eales sobe el papel o fomato nomalizado, y éstas se han de educi, y la de ampliación se utiliza cuando, po su pequeño tamaño, los objetos no se pueden epesenta con las medidas eales sobe el papel o plano industial y esta medidas deben se ampliadas. DIBUJO GEOMÉTRICO Tipo de escala Escala de educción Escala de ampliación Caacteísticas y aplicaciones Paa objetos de gan tamaño que no pueden epoducise, sobe el papel nomalizado, con las medidas eales, y po lo tanto, éstas se educen. Paa objetos de pequeño tamaño que no se pueden epesenta sobe fomatos nomalizados,... con las medidas eales, y éstas han de ampliase. ctividad La escala : no está nomalizada; sin embago, se pemite su uso aunque no se ecomienda. ctividad Las escalas nomalizadas de ampliación son: : 5: y 0: ctividad Escala = Medidas del objeto en el dibujo / Medidas del objeto en la ealidad = mm / mm mm del cuepo en el dibujo equivale a mm del cuepo en la ealidad. Escala = Dibujo / Realidad = mm / R = / ð Realidad = = mm =.600 m =,6 km ctividad 5 5 mm, puesto que, en los planos dibujados a escala, las cifas de cota que se ponen son siempe medidas eales de la pieza a constui. ctividad 6 Que la mayoía de las piezas u objetos, que apaecen epesentados en el plano, están dibujados a escala :, y que alguno se ha dibujado a escala :. ctividad 7 : (:) (5:) SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
5 ctividad 8. Paa la medida de 0 Escala = Medidas del objeto en el dibujo / Medidas del objeto en la ealidad = Dibujo / 0 = / 0 Medida del objeto en el dibujo = 0 / 0 = mm.. Paa la medida de 750 Escala = Medidas del objeto en el dibujo / Medidas del objeto en la ealidad = Dibujo / 750 = / 0 Medida del objeto en el dibujo = 750 / 0 = 75 mm. ctividad 9 Escala = Medidas del cuepo en el dibujo / Medidas del cuepo en la ealidad = / ð Medida del cuepo en la ealidad = / = mm. DIBUJO GEOMÉTRICO SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
6 o CONSTRUCCIÓN DE FORMS POLIGONLES (I) Tiángulos. Ángulos elacionados con la cicunfeencia TEM DIBUJO GEOMÉTRICO ctividad. Dibuja el lado b = 6 cm (C), y po el vétice constui el ángulo  utilizando el método gáfico de la figua adjunta.. Sobe el lado obtenido de este ángulo se lleva c = cm obteniéndose el vétice B.. Uni B con C paa completa el tiángulo. c = cm B a 7 0 C b = 6 cm SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
7 ctividad. Dibuja el lado b = 6 cm (C).. Constui el aco capaz del segmento C bajo el ángulo B = 5º. ^. Dibuja el ángulo C = 60º, y polonga el lado a hasta que cote al aco capaz, punto B.. Uni B con paa completa el tiángulo. B 5 o ^ DIBUJO GEOMÉTRICO c O a 60 o o 5 b = 6 cm C SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 6
8 ctividad. Dibuja el lado b = 6 cm (C).. Constui el aco capaz del segmento C bajo el ángulo Ê = 90º.. pati de se detemina el punto E al cota el aco capaz con un aco de adio h a = cm.. Uni E con C. pati de C, y sobe este último lado, lleva el valo de a = cm. paa obtene el vétice B. 5. Uni B con paa defini el tiángulo. a E B a = cm DIBUJO GEOMÉTRICO h = cm h a c a M C b = 6 cm SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 7
9 ctividad. Dibuja el lado a = cm (CB).. Dibuja la mediatiz del lado a, y a pati del punto M taza el aco de adio m a = cm.. Desde B, con adio el lado c = 5 cm, taza un aco que cota al anteio en.. Uniendo con C y B queda delimitado el tiángulo. c b c = 5 cm a m = cm DIBUJO GEOMÉTRICO C M B a = cm ctividad 5 ^. Se constuye el ángulo C = 60º.. Po un punto cualquiea del lado s de este ángulo, se taza una pependicula al mismo, y se lleva sobe ella la altua h b = 5 cm.. Po el extemo de h b, punto E, se dibuja una paalela t al lado s, que al cota al lado detemina el vétice B.. Halla la mediatiz del segmento CB, y desde M taza un aco de adio m a = 6 cm que cota al lado s en el vétice. 5. Uni con C y B paa foma el tiángulo. S h = 5 cm b m = 6 cm a b E c t h = 5 cm b 60 o C M a B SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 8
10 ctividad 6. Taza la altua h a = cm (E).. Po el extemo E, dibuja la ecta pependicula al segmento E.. pati de taza dos acos de adio c = 5 cm y b = 6 cm, que cotaán a la ecta en los puntos B y C espectivamente.. Uniendo con C y B queda definido el tiángulo. b = 6 cm b h = cm a c = 5 cm c DIBUJO GEOMÉTRICO C E a B ctividad 7 ^. Dibuja el ángulo C = 60º.. En un punto cualquiea, del lado del ángulo constuido, dibuja un ángulo de 5º.. Desde el vétice C, taza la pependicula al lado c del ángulo de 5º, y lleva sobe ella el valo de h = cm, c obteniendo N. ^. Po N, taza una paalela a c hasta que cote a los lados y s del ángulo C, obteniendo y B, con lo cual queda definido el tiángulo. s N c b h = cm c o 5 c o 5 60 o C a B SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 9
11 ctividad 8 Este ejecicio se esuelve po semejanza con oto tiángulo auxilia. ^ ^. Taza el tiángulo auxilia B C cuyos ángulos y B sean, espectivamente, de 5º y 60º. Paa ello, se toma un segmento cualquiea B C y se dibuja el aco capaz de este segmento bajo el ángulo de 5º; po B se taza el ángulo de 60º y se obtiene el vétice.. Taza la mediatiz del segmento B y se obtiene el punto N sobe el citado segmento.. En la polongación de CN, ecta t, y a la distancia m c = 6 cm, se encuenta el punto M, punto medio del lado c del tiángulo, que seá paalelo al lado B del tiángulo auxilia. m = 6 cm c 5 o b DIBUJO GEOMÉTRICO t M 5 o c N O 60 o 60 o B a B o 5 C SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 0
12 CONSTRUCCIÓN DE FORMS POLIGONLES (II) Cuadiláteos. Polígonos egulaes TEM5 DIBUJO GEOMÉTRICO ctividad. Dibuja la diagonal del cuadado d = C = 0 mm.. Taza la mediatiz del segmento C, y con cento en O dibuja la cicunfeencia de adio d/.. Uniendo los puntos, B, C y D queda definido el cuadado. d = 0 mm D O C B SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
13 ctividad Este ejecicio se esuelve po semejanza con oto cuadado auxilia.. Constui un cuadado cualquiea de lado L = B. Sobe la diagonal de este cuadado situa el punto N. Paa ello, se lleva a pati de el valo del segmento N = D + L. Uni el punto N con B y sobe la citada diagonal lleva el valo de D + L = 70 mm, definiendo el punto M.. Po el extemo M, se taza la paalela a NB, obteniendo el punto C en B. El segmento C es el lado L del cuadado cuyo lado y diagonal suman 70 mm, es deci, M = D + L = 70 mm.. Paa constui el oto cuadado, cuya difeencia ente la diagonal y el lado es igual a 0 mm, dibuja el aco NBP de cento en D. 5. Uni P con B, y po R (distancia de 0 mm llevada sobe la diagonal a pati de ) taza una paalela al segmento citado PB, obteniendo el punto C en la polongación de B. El segmento C es el lado L del cuadado cuya difeencia ente su diagonal y su lado es de 0 mm. ) DIBUJO GEOMÉTRICO D + L N M E D 70 0 P R D C B C L L SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
14 ctividad. Dibuja, a pati de, un ángulo ecto, y sobe sus lados lleva los valoes de L = 5 mm y de L + D = 80 mm, obteniendo los puntos E y N.. Uni E con N y dibuja la mediatiz del segmento EN. El punto B, luga donde esta mediatiz cota al segmento N, define el lado L del ectángulo.. Taza po B y po E paalelas a sus lados espectivos paa obtene el ectángulo BCE solicitado. E C DIBUJO GEOMÉTRICO D L = 5 D B N L L + D = 80 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
15 ctividad En el dibujo de esta actividad, se ha ealizado una figua de análisis y los cálculos pecisos paa compende mejo la constucción del ombo. O D + D = FIGUR DE NÁLISIS D = 90 DIBUJO GEOMÉTRICO D = 5 D - D = 8 D. Coloca, sobe una ecta, los datos: - = mm, y - = 8 mm.. Halla la mediatiz del segmento - y obtene el punto O º.. Teniendo en cuenta que el segmento - es el eje mayo del ombo, se halla la mediatiz de -, y sobe ella se lleva el valo del eje meno -, definiendo los puntos B y D.. Uni los vétices, B, C y D paa obtene el ombo solicitado. NÁLISIS DEL EJERCICIO (D + D ) - (D - D ) = D + D - D + D = D = - 8 = 0 mm D = 0 / = 5 mm D = - D = - 5 = 90 mm D - D = 90-5 = 8 mm D O O O C D = 5 B D = 90 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
16 RELCIONES GEOMÉTRICS Popocionalidad, semejanza, igualdad, equivalencia y simetía TEM6 DIBUJO GEOMÉTRICO ctividad -. Sobe una ecta lleva el segmento a = 0 mm y a continuación el b = 5 mm, obteniéndose los puntos, N y P.. pati de, y sobe una ecta cualquiea s, se toma el segmento b = 5 mm, obteniendo el punto M.. Uni los puntos M y N, y po P taza la paalela a MN, obteniendo el punto Q. El segmento x = MQ es el teceo popocional a los segmentos a y b. x Q s b = 5 M N P a = 0 b = 5 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
17 ctividad -. Sobe una ecta lleva el segmento a = 0 mm y, a continuación, el b = 0 mm, obteniéndose los puntos, N y P.. pati de, y sobe una ecta cualquiea s, se toma el segmento c = 70 mm, obteniendo el punto M.. Uni los puntos M y N, y po P taza la paalela a MN, obteniendo el punto Q. El segmento x = MQ es el cuato popocional solicitado. c = 70 M x Q s DIBUJO GEOMÉTRICO N P a = 0 b = 0 ctividad - Pime pocedimiento (Fig. ). Se toma el segmento a = 5 mm y, supepuesto con él, el segmento b = 0 mm.. Taza el aco capaz del segmento B sobe el ángulo de 90º, que es la semicicunfeencia de diámeto B = b = 0 mm, y po P la pependicula a B. El segmento x = M es el medio popocional ente los segmentos a y b. Segundo pocedimiento (Fig. ). Dibuja los segmentos a y b, uno a continuación del oto, y taza la semicicunfeencia de diámeto (a + b = 75 mm).. Po el punto P taza una pependicula al segmento B que cota a la semicicunfeencia en M. El segmento x = PM es la altua sobe la hipotenusa y medio popocional de los segmentos dados a y b. Fig. Fig. M x M x a = 5 P B P B b = 0 a = 5 b = 0 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 6
18 ctividad. Dibuja el segmento B de 0 mm de longitud.. Po el punto, y sobe una ecta cualquiea, se ealizan 5 divisiones iguales, y se toman, uno a continuación del oto, los valoes coespondientes a las divisiones, 5 y 7, obteniéndose, espectivamente, los puntos M, N y P.. Uni el punto P con el B, y po M y N taza sendas paalelas al segmento PB, deteminando los puntos N y M sobe el segmento B. Los segmentos M, M N y N B son popocionales, espectivamente, a, 5 y 7. 7 P DIBUJO GEOMÉTRICO 5 N M M N B 0 mm SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 7
19 ) ctividad Pime pocedimiento. Constui el pentágono egula BCDE de lado L = 5 mm. Paa ello: Se toma B y se taza la mediatiz de B. Se toma BM = B con ayuda del aco ; con cento en N y adio NM se taza el aco MF; el segmento F es la diagonal d del pentágono que se busca. Con adio d y centos en y B se tazan dos acos que se cotan en D. Con cento en y adio L = B se taza el aco, que cota en E el aco DE de cento en B; de la misma foma se obtiene el punto C.. Se toma un punto cualquiea P y se une con los vétices del pentágono. El segmento DP se divide en pates iguales y se fija el punto D, homólogo del D siendo D P = / DP.. Po D se taza la paalela a DC hasta que cote en C a CP; se sigue así po medio de paalelas constuyendo el pentágono D C C B B E E. (El punto P puede esta situado sobe el pentágono, exteio a él o dento del mismo). ) DIBUJO GEOMÉTRICO D D P E M C E B C N B F PRIMER PROCEDIMIENTO L = 5 d Segundo pocedimiento, po coodenadas. Se constuye el pentágono de L = 5 mm.. Como la azón de semejanza es R = /, se toma = /, B = / B y B = / B.. Los segmentos DN y C se dividen en tes pates iguales y se llevan las altuas coespondientes a los / obteniéndose los vétices C, D y E del pentágono semejante al dado con R = /. SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 8
20 E = = = Tece pocedimiento, sistema de la cuadícula D 0,5 SEGUNDO PROCEDIMIENTO C N B. Una vez dibujado el pentágono de L = 5 mm se constuye una cuadícula de lado l.. Se toma ota cuadícula de lado l = / l, y sobe ésta se macan los puntos, B, C, D y E que configuan el pentágono semejante al dado. E D C N B 7 = 0,5 / DIBUJO GEOMÉTRICO l D TERCER PROCEDIMIENTO 8,5 E C 5,6 = 8,5 / E l = / l D C 0,5 B B 7 = 0,5 / ctividad 5. Dibuja el cuadado BCD de lado l = 50 mm.. Po C taza una paalela a la diagonal DB hasta que cote a la polongación del segmento B en el punto E.. Uniendo los puntos, D y E se obtiene el tiángulo equivalente al cuadado de lado 50 mm. D C L = 50 mm B E SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 9
21 ctividad 6. Dibuja el polígono convexo iegula de 6 lados BCDEF.. Se toma una diagonal del polígono, po ejemplo, la DB, tal que deje aislado a un solo vétice, el C; se polonga el lado B hasta que cote a la paalela a la diagonal DB tazada po C; de este modo, se obtiene el vétice G del nuevo polígono GFED equivalente al dado peo con un lado menos.. Del mismo modo se pocede con las diagonales y obteniéndose el tiángulo final IGD semejante al polígono BCDEF. E D DIBUJO GEOMÉTRICO F C I H B G SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 0
22 ctividad 7 En la figua de análisis podemos apecia que el lado L del cuadado es igual a la media popocional x de los segmentos a y b, es deci, de los lados del ectángulo equivalente, dado que, según la definición de media popocional, a/x = x/b, y en consecuencia x = a b. Si tenemos en cuenta que, x = L = Áea del cuadado y a b = Áea del ectángulo, podemos establece que el cuadado de lado L = x es equivalente al ectángulo de lados a y b. Po oto lado, la mediatiz del lado CE del tiángulo ectángulo inscito en la semicicunfeencia debe pasa po el punto M, cento de la misma. b F H D a M G B C L = x b E Figua de análisis DIBUJO GEOMÉTRICO Método de constucción:. Dibuja el cuadado BCD de lado L = 60 mm.. Sobe la polongación del lado B, y a pati de B, situa el lado b = 0 mm del ectángulo que define el punto E. Uniendo E con C se foma el cateto meno del tiángulo ectángulo del aco capaz del segmento FE bajo el ángulo de 90º.. Taza la mediatiz, del lado CE, que cota al cuadado en el punto M cento del aco capaz; con cento en M, y adio igual al segmento ME, taza la semicicunfeencia que define el punto F. El segmento FB es el lado mayo del ectángulo equivalente.. Haciendo cento en B, y con adio BE, se obtiene el punto G y el ectángulo. L = 60 mm D C H G b = 0 F M B E a = 90 b = 0 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
23 ctividad DIBUJO GEOMÉTRICO SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
24 TRNSFORMCIONES GEOMÉTRICS Taslación, gio y homotecia TEM7 DIBUJO GEOMÉTRICO ctividad. Dibuja la figua poligonal F = BCDE y el vecto taslación VV = 5 cm.. pati de los puntos, B, C, D y E se tazan segmentos de igual magnitud y paalelos al vecto taslación, obteniéndose los puntos, B, C, D y E que al unilos se obtiene la figua tansfomada F de la F dada. V d = 5 cm C D F B V C T(C) E D T(D) F B T(B) E T(E) T() SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
25 o ctividad Obsevando la figua de análisis se deduce que el cento de gio, O, que tansfoma la ecta en equidista de ambas, po lo tanto, petenece a la bisectiz de uno de los ángulos que foman las ectas y. Teniendo en cuenta que este ángulo debe medi 60º, el ángulo de gio, siguiendo el sentido de las agujas del eloj, del punto, pie de la pependicula po O a la ecta, seá 0º, tal y como se apecia en dicha figua. Pocedimiento de constucción:. Po O se taza la pependicula a la ecta dada obteniendo el punto.. Se constuye el ángulo O de 0º, y se une O con paa obtene el segmento O.. l taza, po el punto, la pependicula al segmento O se obtiene la ecta tansfomada de y que foma con ella un ángulo de 60º. DIBUJO GEOMÉTRICO R() B R(B) 60 R() o 0 o o 0 60 o 0 60 o O O B d = cm FIGUR DE NÁLISIS ctividad lgunas de las múltiples aplicaciones pueden se: Estuctuas y edes modulaes. Paa el diseño de logotipos. En mosaicos decoativos. donos aquitectónicos. Señales, símbolos y anagamas. En quitectua. En Diseño Gáfico. En el diseño y talla de muebles. SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
26 ctividad El cento de gio que lleva al punto P a la posición P ha de petenece a la mediatiz del segmento PP, y lo mismo podía decise paa lleva el punto Q a la posición Q. Po lo tanto, el cento de gio de la tansfomación se encuenta en el punto de intesección de ambas mediatices, punto O. P P R(P) DIBUJO GEOMÉTRICO Q Q R(Q) O SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
27 ctividad 5 Dibujaemos, po ejemplo, un pentágono egula de L = 0 mm. Pime caso: la azón de homotecia es K = /. Paa valoes positivos de K, las paejas de puntos homotéticos u homólogos, po ejemplo, y, se hallan situados del mismo lado especto de O, y se dice que la homotecia es diecta. Teniendo en cuenta que dos figuas homotéticas son semejantes, paa su constucción seguiemos los mismos pasos y azonamiento de la actividad (pime pocedimiento) del tema 6. K = / D D DIBUJO GEOMÉTRICO E E C C O B B Segundo caso: la azón de homotecia es K = -/. Cuando la azón de homotecia es negativa, es deci, K = -/, los puntos homólogos, po ejemplo, y, están situados a distinto lado del cento O, y la homotecia se dice que es invesa. Teniendo en cuenta que una paeja de ectas homólogas son paalelas, caso de y, la constucción del pentágono B C D E es elativamente sencilla. Basta con halla, po ejemplo, E, y a pati de este punto taza paalelas al esto de lados del pentágono oigen. D B E C O C E B D K = -/ SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 6
28 Tece caso: la azón de homotecia es K = -. Cuando la azón de homotecia K = -, la homotecia es equivalente a una simetía cental, ya que y, B y B, etc, son siméticos de O, es deci, equidistan de O y están en línea ecta con él. Paa constui el pentágono homotético se une, po ejemplo, E con O, y sobe esta ecta, a pati de O, se lleva el valo del segmento EO hasta obtene E ; con el esto de puntos se pocede del mismo modo. Los lados homotéticos, po ejemplo, DE y D E, son paalelos. K = - E D DIBUJO GEOMÉTRICO B C O C B D E SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 7
29 CURVS TÉCNICS Elipse, hipébola y paábola Definición y tazado TEM0 DIBUJO GEOMÉTRICO ctividad º Detemina un punto de la cuva: Se dibujan los ejes B = a = 80 mm y CD = b = 50 mm. Con cento en C o D y adio a, se cota el eje mayo en F y F, focos de la cuva. Se toma un punto N cualquiea en el eje mayo; con adio N y cento en F se taza el aco y con adio NB y cento en F, se taza el aco ; estos dos acos se cotan en el punto M, que es el punto de la elipse que se ha solicitado. º Dibuja un cuadante de la cuva va po puntos aplicando su definición. Paa dibuja este cuadante se tazan una seie de puntos (,,, ) cualesquiea en el eje mayo. Con adios,, y y cento en F se taza una seie de acos y con adios B, B, B y B y cento en F se tazan otos acos; estos acos se cotaán espectivamente con los tazados desde F definiendo una seie de puntos, po ejemplo E, de la elipse, tal y como se ha visto en el punto anteio, que uniéndolos se dibuja el cuadante pedido. º Dibuja oto cuadante de la cuva po medio de haces poyectivos: Se constuye el ectángulo OCLB y se dividen los segmentos OB y LB en el mismo númeo de pates iguales, cinco en la figua. Los ayos D, D, D y D se cotan espectivamente con los ayos C, C, C y C en los puntos J, I, H y G de la elipse. º Dibuja oto cuadante de la cuva po medio de envolventes: Esta constucción se funda en que la cicunfeencia pincipal de diámeto a y cento O es el luga geomético de los pies de las pependiculaes tazadas po cada foco a las tangentes. Las envolventes son, pues, las tangentes. Se taza la cicunfeencia pincipal de cento O y adio O. Se toman una seie de puntos (,,, ) cualesquiea en esta cicunfeencia pincipal; se une, po ejemplo, con F y se taza la pependicula t po a F; la ecta t es tangente a la elipse en el punto K; epitiendo esta opeación con los puntos, y se obtienen una seie de tangentes que van envolviendo la cuva. SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 8
30 Método envolventes Método po puntos t M K C J F N O F E D G Método haces poyectivos H I L B 50 DIBUJO GEOMÉTRICO 80 ctividad º Constucción de la elipse po puntos. Se taza el eje mayo B = a = 00 mm y se dibuja su mediatiz. Con adio c = 0 mm y cento O, se sitúan sobe el eje mayo los focos F y F. Con cento en F o F y adio a = 50 mm, se cota a la mediatiz en C y D, extemos del eje meno de la elipse. pati de aquí se pocede como se ha descito en los apatados y de la actividad anteio. c = 0 C a = 50 G I b = 60 F O F B H J D a = 50 a = 50 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 9
31 º Tazado de la elipse po haces poyectivos. Se taza el eje mayo B = a = 00 mm y se dibuja su mediatiz. Con adio c = 0 mm y cento O, se sitúan sobe el eje mayo los focos F y F. Con cento en F o F y adio a = 50 mm, se cota a la mediatiz en C y D, extemos del eje meno de la elipse. Se constuye el ectángulo OCE y se dividen los segmentos O y E en el mismo númeo de pates iguales, cinco en la figua. Los ayos D, D, D y D se cotan espectivamente con los ayos C, C, C y C en puntos de la elipse. E c = 0 C a = 50 DIBUJO GEOMÉTRICO b = 60 F O F B D a = 50 a = 50 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 0
32 º Tazado de la elipse po puntos mediante la cicunfeencia pincipal y la de diámeto b. Se taza el eje mayo B = a = 00 mm y se dibuja su mediatiz. Con adio c = 0 mm y cento O, se sitúan sobe el eje mayo los focos F y F. Con cento en F o F y adio a = 50 mm, se cota a la mediatiz en C y D, extemos del eje meno de la elipse. Con cento en O, se taza la cicunfeencia pincipal de adio a = 50 mm y la de adio b = 0 mm. Se taza un adio cualquiea que cota en R y R a las dos cicunfeencias; po R se taza la paalela a B y po R la paalela a CD, que se cota con la anteio en el punto R de la elipse. Esta opeación se epite numeosas veces. c = 0 DIBUJO GEOMÉTRICO R a = 50 C R R b = 60 F O F B D a = 50 a = 50 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
33 º Tazado de la elipse po puntos mediante envolventes. Se taza el eje mayo B = a = 00 mm y se dibuja su mediatiz. Con adio c = 0 mm y cento O, se sitúan sobe el eje mayo los focos F y F. Con cento en F o F y adio a = 50 mm, se cota a la mediatiz en C y D, extemos del eje meno de la elipse. Se taza la cicunfeencia pincipal de cento O y adio O. Se toma un punto cualquiea L de esta cicunfeencia pincipal, se une con F y se taza la pependicula t po L a FL; la ecta t es tangente a la elipse en el punto K; epitiendo esta opeación se obtienen una seie de tangentes que van envolviendo la cuva. c = 0 DIBUJO GEOMÉTRICO a = 50 t C L K b = 60 F O F B D a = 50 a = 50 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
34 ctividad El cuadante de la cuva se ha dibujado po medio de haces poyectivos. Se taza el segmento FO = c = 60 mm y, pependicula a él, el semieje meno CO = b = 0 mm. Con adio CF y cento O, se taza un aco que cota a la polongación de OF en el punto, extemo del semieje mayo. Se constuye el ectángulo OCE y se dividen los segmentos O y E en el mismo númeo de pates iguales, cinco en la figua. Los ayos D, D, D y D se cotan espectivamente con los ayos C, C, C y C en puntos de la elipse. DIBUJO GEOMÉTRICO a = 7, E C b = 0 F O c = 60 a = 7, D SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
35 ctividad º Detemina un punto cualquiea de la cuva. Se dibujan los datos B = a = 0 mm y FF = c = 50 mm. Se toma un punto N cualquiea en el eje eal B y con adios N y BN y centos en F y F se tazan dos acos que se cotan en P, punto de la hipébola solicitado. F c = 50 O = 9, P B = 9, N F DIBUJO GEOMÉTRICO - = 0 P a = 0 º Constucción de la hipébola po puntos a pati de los ejes (Pime pocedimiento). Se dibujan los datos B = a = 0 mm y FF = c = 50 mm. Se toma un punto cualquiea en el eje eal B y con adios y B y centos en F y F se tazan dos acos que se cotan en M, punto de la hipébola. Paa obtene otos puntos de la cuva se toman los puntos y del eje eal. c = 50 M M F O B N F M M a = 0 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
36 º Constucción de la hipébola po medio de haces poyectivos (Segundo pocedimiento). Se dibujan los datos B = a = 0 mm y FF = c = 50 mm. Se halla, po el pocedimiento indicado en el apatado º de esta actividad, un punto cualquiea P de la cuva y se constuye el ectángulo BMPN. Se dividen los lados MP y PN en un númeo cualquiea de pates iguales que se unen con los puntos B y F, espectivamente. Los puntos de intesección de los ayos homónimos u homólogos de estos haces son puntos de la hipébola, en conceto, los puntos Q, R, S y T. De la misma foma se constuye la pate infeio de la cuva. F c = 50 O M T S R Q B P N F DIBUJO GEOMÉTRICO a = 0 º Constucción de la hipébola po envolventes (Tece pocedimiento). Se dibujan los datos B = a = 0 mm y FF = c = 50 mm. Se constuye la cicunfeencia pincipal de cento O y adio a = O = OB = 0 mm. l igual que en la elipse, basta toma puntos en la cicunfeencia pincipal, po ejemplo, los puntos,, y, uniles con F y taza las coespondientes pependiculaes, que son tangentes a la cuva, po ejemplo, en los puntos Q, R, S y T. c = 50 Q R S T F O B F a = 0 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
37 5º Constucción de las asíntotas. Se dibujan los datos B = a = 0 mm y FF = c = 50 mm. La cicunfeencia pincipal, de cento O y adio a = O = OB = 0 mm, cota a la de diámeto OF en los puntos T y T. Las ectas OT y OT son las asíntotas a y a. También se obtienen uniendo el punto O con los puntos R y S donde cota a la cicunfeencia de diámeto FF (adio = c) la pependicula po al eje eal. El tiángulo R--O es ectángulo y sus lados a, b y c. b R c = 50 c T a DIBUJO GEOMÉTRICO F O B F T S a a = 0 a SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 6
38 ctividad 5. Se dibujan los ejes de la hipébola de cento O; sobe el eje imaginaio, se lleva, a pati de O, el valo de b = 0 mm, fomándose el punto C.. Con adio C = c = 5 mm y cento C, se taza un aco que cota, en y B, al eje mayo.. Haciendo cento en O y adio c = 5 mm, se taza la cicunfeencia que cota al eje pincipal en los puntos F y F, focos de la cuva.. pati de aquí, se pocede como en el apatado de la actividad. M P DIBUJO GEOMÉTRICO T b = 0 c = 5 C Q P S 5 F O F N B U 5 Nota: Esta actividad se epesenta a escala : SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 7
39 ctividad 6 º Constucción de la diectiz y de la tangente en el vétice. Se dibuja el eje de simetía de la cuva y, sobe él, se sitúan los puntos, V y F a una distancia de 5 mm ente cada uno de ellos, dado que el vétice V es el punto medio del segmento F. Po y V, se tazan sendas pependiculaes al eje de simetía; estas ectas definen la diectiz d y la tangente en el vétice t v. º Obtene un punto y taza los adios vectoes del mismo. Definidos la diectiz d, el eje, el vétice V y la tangente en el vétice t v, se taza po un punto cualquiea del eje la pependicula a éste y con cento en F y adio - =, se cota a dicha pependicula, obteniendo el punto P y su simético, que son puntos de la cuva. Po el punto P, se taza una pependicula a la diectiz, obteniendo el punto N. Los segmentos PF y PN son los adios vectoes y se cumple que = PF = PN. DIBUJO GEOMÉTRICO 5,89 N P d t v 5,89 V F 5 5 SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 8
40 SISTEM DIÉDRICO I Repesentación del punto, ecta y plano ctividad TEM Paa epesenta estos puntos hemos de tene en cuenta las consideaciones siguientes: Un punto se puede da o defini po tes cotas o distancias a los tes planos, tal y como sucede en este ejecicio. Los valoes de la pimea distancia de cada uno de los puntos dados: (,-,-), B (-,-,-) y C (-,-,-) epesentan la distancia de los puntos al plano de pefil a (a -a ), situándose los valoes positivos a su izquieda y los negativos a la deecha. Los datos que apaecen en segundo luga: (-,,-), B (-,,-) y C (-,,-) indican la distancia al plano hoizontal o cota. Los valoes situados en tece luga: (-,-,), B (-,-,5) y C (-,-,-) epesentan la distancia de cada uno de los puntos al plano vetical o alejamiento. Los puntos del pime diedo tienen la poyección vetical po encima de la L.T. y la hoizontal po debajo. Los puntos del segundo diedo tienen las dos poyecciones po encima de la L.T. GEOMETRÍ DESCRIPTIV. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Se dibuja, en un punto cualquiea de la Línea de Tiea (L.T.), la ecta a -a que epesenta el plano de pefil.. El punto (,,) es un punto del pime cuadante, el B (-,,5) se encuenta situado también en el pime cuadante peo a la deecha del plano de pefil, dado que dista del mismo, y el punto C (-,,-), además de esta colocado al lado deecho del plano de pefil, petenece al º diedo o cuadante. C C B - O Unidades en centímetos B SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 9
41 ctividad. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Se dibuja, en un punto cualquiea de la Línea de Tiea (L.T.), la ecta a -a que epesenta el plano de pefil.. Se dibujan las poyecciones del punto dado P (-,,5).. Tazado de una ecta hoizontal de plano ( - ): La poyección vetical de la ecta (paalela a la L.T.) debe pasa po P. La poyección hoizontal de la ecta (puede se cualquiea) debe pasa po P. Donde cota a la LT se encuenta V, y en la intesección de la pependicula tazado po ese punto con se encuenta V, que son las poyecciones de la taza vetical V de la ecta. 5. Tazado de una ecta fontal de plano s (s -s ): La poyección hoizontal de la ecta s (paalela a la L.T.) debe pasa po P. La poyección vetical de la ecta s (puede se cualquiea) debe pasa po P. Donde s cota a la L.T. se encuenta H, s y en la intesección de la pependicula tazada po ese punto con s se encuenta H, que son las poyecciones de la taza hoizontal H de la ecta s. 6. Tazado de una vetical o de punta, especto al plano Hoizontal t (t -t ): La poyección vetical de la ecta t (pependicula a la L.T.) debe pasa po P. La poyección hoizontal de la ecta t (es un punto) debe coincidi con P. Donde t cota a la L.T. se encuenta H, t y en la intesección de la pependicula tazada po ese punto con t se encuenta H, que son las poyecciones de la taza hoizontal H de la ecta t. t s GEOMETRÍ DESCRIPTIV - t V P s O V H t H s 5 s P t H t H s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 0
42 ctividad. Se dibuja, en un punto cualquiea de la Línea de Tiea (LT), la ecta a -a que epesenta el plano de pefil.. Se sitúan todas las poyecciones de los puntos dados P (,,) y Q (,,), es deci: P (P,P,P) y Q (Q,Q,Q), tal y como se puede apecia en la figua.. Uniendo las poyecciones espectivas de los puntos obtenemos las poyecciones hoizontal (P -Q ) y vetical (P -Q ) de la ecta de pefil.. Sobe el plano de pefil a(a -a ), se halla la tecea poyección de la ecta, uniendo las poyecciones P y Q de los puntos. 5. La poyección de pefil de la ecta cota a los planos de poyección en H y V que son las tazas de la ecta ; estas tazas se efieen a la ecta en H -H y en V -V. V P V P GEOMETRÍ DESCRIPTIV Q Q H V O H P Q H SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
43 ctividad. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos un plano oblicuo cualquiea a po medio de sus tazas a -a. Estas tazas se cotan en un punto de la LT.. Paa situa cualquie ecta sobe un plano hay que tene en cuenta las siguientes consideaciones: Una ecta está situada en un plano cuando las tazas de la ecta están situadas sobe las tazas del mismo nombe del plano. Las ectas ( - ) y s (s -s ) están situadas en el plano a po esta V y V s en a y H y H sen a. Las tazas H -V y H s -V s pueden esta colocadas en cualquie punto de las tazas del mismo nombe del plano dado.. Paa situa cualquie punto sobe un plano hay que tene en cuenta las siguientes consideaciones: Un punto está en un plano cuando sus poyecciones están sobe las poyecciones del mismo nombe de una ecta contenida en dicho plano. Esta ecta puede se una oblicua cualquiea o mejo aún, po su sencillez, una hoizontal o una fontal. Los puntos ( - ), B(B -B ) y C(C -C ) están en el plano a po petenece a las ectas - y s -s de este plano. Estos puntos pueden esta colocados en cualquie luga de las ectas. V GEOMETRÍ DESCRIPTIV H V N H V s s C C s B s B V H s H s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
44 ctividad 5. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos un plano oblicuo cualquiea a po medio de sus tazas a -a. Estas tazas se cotan en un punto de la LT.. Paa situa cualquie ecta sobe un plano hay que tene en cuenta las siguientes consideaciones: Una ecta está situada en un plano cuando las tazas de la ecta están situadas sobe las tazas del mismo nombe del plano. Rectas hoizontales: Las ectas ( - ) y s(s -s ) están situadas en el plano a po esta V y V s en a y y s se paalelas a a. Las tazas V y V s pueden esta colocadas en cualquie punto de la taza vetical del plano dado. Rectas fontales: Las ectas t(t -t ) y u(u -u ) están situadas en el plano a po esta H t y H uen a y t y u se paalelas a a. Las tazas H t y H u pueden esta colocadas en cualquie punto de la taza hoizontal del plano dado. V s V s t u GEOMETRÍ DESCRIPTIV N H t V s V H u H t s t H u u ctividad 6 P. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta cualquiea, en este caso, la oblicua -.. Tazamos la paalela a la línea de tiea a una distancia de cm. cm. En el punto de intesección de esta paalela con, se encuenta la poyección vetical P del punto P. Paa halla la poyección hoizontal del punto, basta taza po P la pependicula a la L.T. hasta que cote en P a. P SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
45 ctividad 7. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos un punto P -P y una ecta oblicua - cualquiea.. Po la poyección P del punto, tazamos la poyección s de la hoizontal (paalela a la L.T.); en el punto de intesección de esta paalela con, se encuenta la poyección vetical del punto de intesección de ambas ectas.. Paa halla la poyección hoizontal del punto, se taza po la pependicula a la L.T., hasta que cote en a. 5. Se unen P y y tenemos la poyección hoizontal s, de la ecta hoizontal de plano solicitada. s s P P GEOMETRÍ DESCRIPTIV ctividad 8 Paa ealiza esta actividad, hemos de tene en cuenta que las tazas de un plano son los lugaes geométicos de las tazas de todas las ectas contenidas en dicho plano. ctividad 8-º: po una ecta hoizontal y un punto exteio.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta hoizontal - cualquiea, y un punto P -P exteio.. Deteminamos la taza V -V de la hoizontal.. Sobe la ecta -, se sitúa un punto cualquiea ( - ). 5. Se unen los puntos P y y tenemos la ecta oblicua s -s ; deteminamos las tazas H -H s s y V -V s s de esta ecta. 6. Uniendo las tazas veticales V y V s de las ectas, tenemos la taza vetical a del plano, y uniendo el punto N, intesección de esta taza con la L.T., y la taza hoizontal H, s obtenemos la taza hoizontal a. Esta taza hoizontal del plano es paalela a la poyección hoizontal de la fontal. El plano obtenido es un plano oblicuo. V s s V P N V V s s H s P H s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato
46 ctividad 8-º: po una ecta fontal y un punto exteio.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta fontal - cualquiea, y un punto P -P exteio.. Deteminamos la taza H -H de la fontal.. Sobe la ecta -, se sitúa un punto cualquiea ( - ). 5. Se unen los puntos P y y tenemos la ecta oblicua s -s ; deteminamos las tazas H -H s s y V -V s s de esta ecta. N 6. Uniendo las tazas hoizontales H y H sde las ectas, tenemos la taza hoizontal a del plano, y uniendo el punto N, intesección de esta taza con la L.T., y la taza vetical V, s obtenemos la taza vetical a. Esta taza vetical del plano es paalela a la poyección vetical s de la ecta fontal. El plano obtenido es un plano oblicuo. H V H s V s s s P P H H s s GEOMETRÍ DESCRIPTIV ctividad 8-º: po una ecta vetical y un punto exteio.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta vetical o de punta al P.H. - cualquiea, y un punto P -P exteio.. Deteminamos la taza H -H de la vetical.. Sobe la ecta -, se sitúa un punto cualquiea Se unen los puntos P y y tenemos la ecta oblicua (s -s ); deteminamos las tazas H -H s s y V -V s s de esta ecta. V s s P 6. Uniendo las tazas hoizontales H y H s de las ectas, tenemos la taza hoizontal a del plano, y uniendo el punto N, intesección de esta taza con la L.T., y la taza vetical V, s obtenemos la taza vetical a. Esta taza vetical del plano es paalela a la poyección vetical de la ecta de punta. El plano obtenido es un plano poyectante hoizontal y, en consecuencia, su taza hoizontal a contiene a las poyecciones hoizontales y s de sus ectas. V s N H s H P H H s s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
47 ctividad 8-º: po una ecta de pefil y un punto exteio.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta de pefil ( - ) cualquiea po medio de sus tazas H -H y V -V, y un punto P -P exteio.. Sobe la ecta ( - ), se sitúa un punto cualquiea ( - ).. Se unen los puntos P y y tenemos la ecta oblicua s(s -s ); deteminamos las tazas H -H s s y V -V s s de esta ecta. 5. Uniendo las tazas hoizontales H y H sde las ectas, tenemos la taza hoizontal a del plano, y uniendo N las tazas veticales V y V s de las ectas, obtenemos la taza vetical a. El plano obtenido es un plano oblicuo. V s V s s V s P H H V P H H s s GEOMETRÍ DESCRIPTIV ctividad 8-5º: po los puntos P(,,), Q(-,-,) y R(,,-5).. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Se dibuja, en un punto cualquiea de la Línea de Tiea (L.T.), la ecta a -a que epesenta el plano de pefil.. Dibujamos las poyecciones P -P, Q -Q y R -R de los puntos dados.. Se unen los puntos P y Q y tenemos la ecta - ; igualmente, se unen los puntos R y Q y tenemos la ecta s -s ; estas dos ectas se cotan en el punto Q y definen el plano. 5. Se hallan las tazas hoizontales H y H s de las ectas y s, y al unilas, tenemos la taza hoizontal b del plano. Se halla la taza vetical V s de la ecta s, y al unila con el punto de la L.T donde la cota la taza b obtenemos la taza vetical b del plano. Esta taza b es paalela a. El plano obtenido es un plano oblicuo. β P R s R s H s H s H V s V s - P H - β Q Q SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 6
48 ctividad 8-6º: po dos ectas que se cotan de las que no podemos halla las tazas.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Repesentamos dos ectas oblicuas - y s -s cualesquiea que se cotan en el punto P(P -P ) cuyas tazas no se puedan halla en el dibujo.. Tazamos una ecta hoizontal a -a cualquiea que cota a las ectas dadas en los puntos - y B -B, y deteminamos su taza vetical V -V. a a. Tazamos una ecta fontal b -b cualquiea que cota a las ectas dadas en los puntos C -C y D -D, y deteminamos su taza hoizontal H -H. b b 5. La taza a del plano se obtiene tazando, po la taza hoizontal H b de la ecta b, la ecta paalela a la poyección a ; la taza vetical a se obtiene tazando, po la taza vetical V a de la ecta a, la ecta paalela a la poyección b. El plano obtenido es un plano oblicuo. a s b s C C a P P B B D D b V a V a H H b b GEOMETRÍ DESCRIPTIV ctividad 9 ctividad 9-º: utilizando la tecea poyección. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Se dibuja, en un punto cualquiea de la Línea de Tiea (L.T.), la ecta a -a que epesenta el plano de pefil.. Repesentamos la ecta de pefil - definida po dos de sus puntos, po ejemplo, - y B -B.. Se halla la tecea poyección de la ecta, paa ello, se obtienen los puntos y B que, unidos, definen la poyección ; esta poyección cota a los planos de poyección en H y V que son las tazas pedidas y éstas se efieen a la ecta en H -H y en V -V. V V B B H V H B H SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 7
49 ctividad 9-º: sin ecui a la tecea poyección Paa esolve este ejecicio, basta con taza un plano a(a -a ) que pase po la ecta ( - ), fomada po los puntos ( - ) y B(B -B ), auxiliándose de dos ectas hoizontales (o fontales) abitaias a -a y b -b que pasen po los citados puntos y sean paalelas ente sí.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos la ecta de pefil - definida po dos de sus puntos, po ejemplo, - y B -B.. Se tazan dos ectas fontales abitaias a -a y b -b que pasen po - y B -B y sean paalelas ente sí.. Deteminamos las tazas H a y H b de las ectas a y b, y al unilas tenemos la taza hoizontal a del plano; esta taza, al cota a la L.T., define el punto N. 5. Dibujamos la taza vetical a del plano a que pasa po la ecta ( - ) y está definido po las fontales a - a y b -b. Esta taza vetical debe se paalela a las poyecciones a y b de las ectas a y b, y pasa po el punto N. N H H a a a a b B H H V H b B V b b H GEOMETRÍ DESCRIPTIV 6. Las tazas a y a del plano a cotan a la ecta - en sendos puntos, que son las tazas buscadas H y V. ctividad 0 Paa esolve esta actividad, hemos de ecoda la definición de línea de máxima pendiente de un plano: es la ecta de este plano que foma el mayo ángulo con el plano hoizontal, y se caacteiza poque su poyección hoizontal es pependicula a la taza hoizontal a del plano al que petenece.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos una ecta de máxima pendiente abitaia -, y deteminamos sus tazas H -H y V -V.. Po la taza H de esta ecta, dibujamos, pependiculamente a, la taza hoizontal a del plano, que al cota a la L.T. define el punto N.. Uniendo el punto N con la taza vetical V de la ecta definimos la taza a del plano. 5. Paa situa un punto cualquiea ( - ) en el plano a(a -a ) definido po la (l.m.p.), basta con coloca en y en, teniendo en cuenta que y deben petenece a una misma pependicula a L.T. N V H V H SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 8
50 ctividad En la esolución de esta actividad, hemos de tene en cuenta la condición que se debe cumpli paa que dos ectas ( - ) y s(s -s ) se coten: dos ectas se cotan en el espacio si las poyecciones del mismo nombe se cotan en puntos que están en una misma pependicula a L.T.; así, las ectas ( - ) y s(s -s ) se cotan en el punto P del espacio, si las poyecciones hoizontales y s se cotan en P y las veticales y s en P y ambos puntos están en la misma pependicula a L.T.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos un punto abitaio P -P.. Tazamos dos ectas oblicuas abitaias - y s -s que pasen po P -P, y deteminamos sus tazas H -H y V -V.. Uniendo las tazas hoizontales H y H s de las ectas y s, obtenemos la taza hoizontal a del plano, y uniendo las tazas veticales V y V s de las ectas y s, obtenemos la taza vetical a. El plano obtenido es un plano oblicuo. 5. Situa una ecta t(t -t ) en este plano a(a -a ) definido po las dos ectas y s que se cotan. Paa ello, tendemos en cuenta las consideaciones siguientes: Un plano oblicuo contiene cuato tipos de ectas: Rectas oblicuas. Rectas hoizontales de plano. Rectas fontales de plano. Rectas de pefil. Una ecta está situada en un plano cuando las tazas de la ecta, están situadas sobe las tazas del mismo nombe del plano. En la solución popuesta, se ha optado po situa una hoizontal t -t, de tal modo, que V t se debe enconta en a y t debe se paalela a a. GEOMETRÍ DESCRIPTIV V V s t P V t s V H s V s H V t N t P s H H s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 9
51 ctividad En la esolución de esta actividad, hemos de tene en cuenta las consideaciones siguientes: Dos ectas se cotan en el espacio si las poyecciones del mismo nombe se cotan en puntos que están en una misma pependicula a L.T.; así, las ectas ( - ) y s(s -s ) se cotan en el punto P del espacio, si las poyecciones hoizontales y s se cotan en P y las veticales y s en P y ambos puntos están en la misma pependicula a L.T. Un plano oblicuo contiene cuato tipos de ectas: Rectas oblicuas. Rectas hoizontales de plano. Rectas fontales de plano. Rectas de pefil. Una ecta está situada en un plano cuando las tazas de la ecta, están situadas sobe las tazas del mismo nombe del plano. Un punto está situado en un plano cuando sus poyecciones están sobe las poyecciones del mismo nombe de una ecta contenida en dicho plano.. Repesentamos la línea de tiea con línea llena fina y con dos tazos en sus extemos.. Dibujamos, po ejemplo, del punto cuya segunda poyección deseamos halla, y un punto abitaio P -P.. Tazamos dos ectas oblicuas abitaias - y s -s que pasen po P -P, y deteminamos sus tazas H -H y V -V.. Uniendo las tazas hoizontales H y H sde las ectas y s, obtenemos la taza hoizontal a del plano, y uniendo las tazas veticales V y V s de las ectas y s, obtenemos la taza vetical a. El plano obtenido es un plano oblicuo. 5. Tazamos, po ejemplo, la ecta fontal t -t que pase po y petenezca al plano a -a definido po las dos ectas y s que se cotan en P -P. 6. La poyección se encuenta en la intesección de t y una pependicula a L.T. tazada desde. GEOMETRÍ DESCRIPTIV t V V s P V s H s V s H H t N t P s H H t H s SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 50
52 SISTEM XONOMÉTRICO TEM GEOMETRÍ DESCRIPTIV Intoducción Todas las actividades se esuelven en el sistema axonomético isomético, y, po apidez y comodidad, no se aplica la escala de educción isomética. Los tes planos del sistema, al cotase, dividen al espacio en ocho tiedos; cuato situados po encima del plano XOY, y otos cuato po debajo del mismo. Paa designa cada tiedo consideamos los dos sentidos + y - de cada eje a pati del oigen O. Los ejes se designan po: X, Y y Z. Un punto del espacio se designa po una leta o po un númeo: ( - - ) ó (,5,6), siendo: : la poyección diecta. : la poyección sobe el plano XOY. : la poyección sobe el plano XOZ. : la poyección sobe el plano YOZ. Una ecta se designa po una leta minúscula: ( - - ), siendo: : la poyección diecta. : la poyección sobe el plano XOY. : la poyección sobe el plano XOZ. : la poyección sobe el plano YOZ. Un plano se designa po una leta giega: a (a -a -a ), siendo: a : la taza del plano a con el plano XOY. a : la taza del plano a con el plano XOZ. a : la taza del plano a con el plano YOZ. SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
53 ctividad. Repesentamos los tes ejes del sistema axonomético isomético que, al foma el mismo ángulo con el plano del cuado, se poyectan fomando ángulos de 0º ente sí.. Se dibujan las poyecciones de los cuato puntos, B, C y D, situados cada uno de ellos en uno de los tiedos situados po debajo del plano y distibuidos del modo siguiente: Punto : en el tiedo +X, +Y, -Z. Punto B: en el tiedo +X, -Y, -Z. Punto C: en el tiedo -X, -Y, -Z. Punto D: en el tiedo -X, +Y, -Z. Z C GEOMETRÍ DESCRIPTIV C D C D O C B B D Y D X B B SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
54 ctividad. Repesentamos los tes ejes del sistema axonomético isomético que, al foma el mismo ángulo con el plano del cuado, se poyectan fomando ángulos de 0º ente sí.. Se dibujan las poyecciones de los puntos, B, C, D, E, G, H y K, distibuidos del modo siguiente: Punto : sobe el plano XOY, y valoes (+X, +Y, Z=0). Punto B: sobe el plano XOZ, y valoes (+X, Y=0, +Z). Punto C: sobe el plano YOZ, y valoes (X=0, +Y, +Z). Punto D: sobe el plano XOY, y valoes (+X, -Y, Z=0). Punto E: sobe el plano XOY, y valoes (-X, -Y, Z=0). Punto G: sobe el plano XOZ, y valoes (-X, Y=0, +Z). Punto H: sobe el plano YOZ, y valoes (X=0, -Y, +Z). Punto K: sobe el plano XOY, y valoes (-X, +Y, Z=0). H H G G H Z B GEOMETRÍ DESCRIPTIV G K K K C C G E C E E O E D H B B D D D C K B X Y ctividad Z C C C. Repesentamos los tes ejes del sistema axonomético isomético que, al foma el mismo ángulo con el plano del cuado, se poyectan fomando ángulos de 0º ente sí.. Se dibujan las poyecciones de los puntos, B y C, distibuidos del modo siguiente: Punto : sobe el eje X, y valoes (+X, Y=0, Z=0). Punto B: sobe el eje Y, y valoes (X=0, +Y, Z=0). Punto C: sobe el eje Z, y valoes (X=0, Y=0, +Z). C O B Y B B B X SOLUCIONRIO - DIBUJO TÉCNICO I - Bachilleato 5
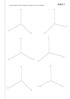
de perfil, y se halla la tercera proyección tanto del punto P como de la recta r. La proyección r corta a los planos de proyección en H r
 Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
UNIDAD 4: CIRCUNFERENCIA CIRCULO:
 UNIDD 4: CIRCUNFERENCI CIRCULO: CONTENIDO: I. CONCEPTO DE CIRCUNFERENCI: Es una cuva ceada y plana cuyos puntos equidistan de un punto llamado cento. Una cicunfeencia se denota con la expesión: O C, y
UNIDD 4: CIRCUNFERENCI CIRCULO: CONTENIDO: I. CONCEPTO DE CIRCUNFERENCI: Es una cuva ceada y plana cuyos puntos equidistan de un punto llamado cento. Una cicunfeencia se denota con la expesión: O C, y
SISTEMA DIÉDRICO II Paralelismo, perpendicularidad y distancias Verdaderas magnitudes lineales TEMA 9 PARALELISMO
 SSTEMA ÉRCO Paalelismo, pependiculaidad y distancias Vedadeas magnitudes lineales Objetivos y oientaciones metodológicas TEMA 9 Esta unidad temática es fundamental y, a la vez, su explicación se puede
SSTEMA ÉRCO Paalelismo, pependiculaidad y distancias Vedadeas magnitudes lineales Objetivos y oientaciones metodológicas TEMA 9 Esta unidad temática es fundamental y, a la vez, su explicación se puede
Sistema diédrico: punto, recta y plano. sta Unidad inicia el desarrollo del sistema diédrico, que abarca tres unidades didácticas.
 UNIDD 7 Sistema diédico: punto, ecta y plano E sta Unidad inicia el desaollo del sistema diédico, que abaca tes unidades didácticas. El sistema diédico pesenta cieta dificultad paa imagina las figuas en
UNIDD 7 Sistema diédico: punto, ecta y plano E sta Unidad inicia el desaollo del sistema diédico, que abaca tes unidades didácticas. El sistema diédico pesenta cieta dificultad paa imagina las figuas en
Matemáticas 4º ESO Fernando Barroso Lorenzo GEOMETRÍA ANALÍTICA. r r
 Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
Fenando Baoso Loenzo GEOMETRÍA ANALÍTICA 1. Dados los vectoes cuyas coodenadas son u = ( 10, 2) y v = (13, 2), calcula el módulo u 43 u 298621 del vecto esultante de la siguiente combinación lineal w =
. Desarrollando esta ecuación vectorial, obtenemos: a = 3. : a = 2, b =, c = 0, y para w : a = 0, b =, c = -2.
 1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
1 Sean los vectoes: v 1 ( 1, 1, 1) v (,, ) y v (, 1, ) Compueba que foman una base de V. Halla las coodenadas especto de dicha base de los vectoes u ( 1,, ) y w ( 1,, 1). Paa ve si son linealmente independientes
TEMA 9: FORMAS GEOMÉTRICAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
Puntos, rectas y planos en el espacio. Problemas métricos en el espacio
 1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
A continuación obligamos, aplicando el producto escalar, a que los vectores:
 G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
DIBUJO TÉCNICO BACHILLERATO. Láminas resueltas del TEMA 4. TANGENCIAS. Departamento de Artes Plásticas y Dibujo
 DIBUJO ÉCNICO BACHILLERAO Láminas esueltas del EMA 4. ANGENCIAS. Depatamento de Ates lásticas y Dibujo 1.- Dibuja 2 cicunfeencias adio 10 mm. que sean ANGENES EXERIORES a la dada y ente ellas. 2.- Dibuja
DIBUJO ÉCNICO BACHILLERAO Láminas esueltas del EMA 4. ANGENCIAS. Depatamento de Ates lásticas y Dibujo 1.- Dibuja 2 cicunfeencias adio 10 mm. que sean ANGENES EXERIORES a la dada y ente ellas. 2.- Dibuja
LINEA: Es una sucesión infinita de puntos. Pueden ser lineas curvas o líneas rectas.
 puntes geometía: Constucciones básicas º ESO LINE: Es una sucesión infinita de puntos. ueden se lineas cuvas o líneas ectas. LINE CUR. Es una sucesión infinita de puntos en difeentes diecciones. LINE RECT.
puntes geometía: Constucciones básicas º ESO LINE: Es una sucesión infinita de puntos. ueden se lineas cuvas o líneas ectas. LINE CUR. Es una sucesión infinita de puntos en difeentes diecciones. LINE RECT.
INTERSECCIONES. POSICIONES RELATIVAS. DISTANCIAS
 INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
INTERSECCIONES. POSICIONES RELATIAS. DISTANCIAS OBJETIOS 1 2 Reconoce el Sistema diédico o Sistema de Monge como el ecuso desciptivo gáfico más adecuado en el diseño industial y aquitectónico. 1 INTERSECCIÓN
A B. Teniendo en cuenta que el lado de un pentágono regular es la sección aurea de su diagonal, se tiene la siguiente construcción:
 1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
1. Dibuja el pentágono egula de diagonal 120 mm. D E O G AF/2 A B F Pate pimea: Dibujo del pentágono. Teniendo en cuenta que el lado de un pentágono egula es la sección auea de su diagonal, se tiene la
GEOMETRÍA. 1. Sin resolver el sistema, determina si la recta 2x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia
 Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
Puebas de Acceso a la Univesidad GEOMETRÍA Junio 94.. Sin esolve el sistema detemina si la ecta x y + = 0 es exteio secante ó tangente a la cicunfeencia (x ) + (y ) =. Razónalo. [5 puntos]. Dadas las ecuaciones
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Ángulos en la circunferencia
 MT-22 Clase Ángulos en la cicunfeencia pendizajes espeados Identifica los elementos de un cículo y una cicunfeencia. Calcula áeas y peímetos del secto y segmento cicula. Reconoce tipos de ángulos en la
MT-22 Clase Ángulos en la cicunfeencia pendizajes espeados Identifica los elementos de un cículo y una cicunfeencia. Calcula áeas y peímetos del secto y segmento cicula. Reconoce tipos de ángulos en la
POTENCIA TEMA2. Actividad 1
 x = 4,76 EI E GEERÍ Y IUJ ÉI ctividad La edia popocional x a los segentos a y b se obtiene sabiendo que la potencia de un punto especto de una cicunfeencia es igual al cuadado del segento toado sobe una
x = 4,76 EI E GEERÍ Y IUJ ÉI ctividad La edia popocional x a los segentos a y b se obtiene sabiendo que la potencia de un punto especto de una cicunfeencia es igual al cuadado del segento toado sobe una
APUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BACHILLERATO. AUTOR: RAMON DEL AGUILA α CORBALÁN AÑO 2010
 Página 1 de 16 2010 www.amondelaguila.com PUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BCILLERTO. UTOR: RMON DEL GUIL α CORBLÁN ÑO 2010 G α 1 ch (α 2 ) Los apuntes que pesento solo petenden se un complemento
Página 1 de 16 2010 www.amondelaguila.com PUNTES DE DIBUJO TÉCNICO: PRIMERO Y SEGUNDO DE BCILLERTO. UTOR: RMON DEL GUIL α CORBLÁN ÑO 2010 G α 1 ch (α 2 ) Los apuntes que pesento solo petenden se un complemento
RELACION DE ORDEN: PRINCIPALES TEOREMAS
 RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
1 Halla la mediatriz del segmento AB. 2 Traza la recta perpendicular a la recta r por el punto A.
 1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
1 Halla la mediatiz del segmento. 2 Taza la ecta pependicula a la ecta po el punto. 3 Taza la pependicula a la ecta desde el punto. uál es la distancia del punto a la ecta? 4 Dibuja dos ectas pependiculaes
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
TANGENCIAS (Julio Catalán)
 NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
NGENIS (Julio atalán) Los poblemas de tangencia que pueden pesentase son innumeables y van desde los muy sencillos a los más complejos, ecuiéndose paa su solución a pocedimientos muy distintos: desde los
Apuntes de Trigonometría Elemental
 Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
CUADRILÁTEROS. Cuadrado y Rectángulo.
 ibuja un NTÁN cuando nos dan el RI. 1. ibuja una cicunfeencia de adio el que nos dan.. ibuja dos diámetos pependiculaes (ojo que pasen po el cento de la cicunfeencia). 3. ibuja la mediatiz de uno de los
ibuja un NTÁN cuando nos dan el RI. 1. ibuja una cicunfeencia de adio el que nos dan.. ibuja dos diámetos pependiculaes (ojo que pasen po el cento de la cicunfeencia). 3. ibuja la mediatiz de uno de los
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
GEOMETRÍA ANALÍTICA COORDENADAS POLARES. 2.1 Relación entre coordenadas polares y rectangulares de un punto
 COORDENADAS OLARES CONTENIDO 1. Coodenadas polaes de un punto. Coodenadas polaes gealizadas.1 Relación ente coodenadas polaes y ectangulaes de un punto. Cambio de sistema de coodenadas catesianas a polaes
COORDENADAS OLARES CONTENIDO 1. Coodenadas polaes de un punto. Coodenadas polaes gealizadas.1 Relación ente coodenadas polaes y ectangulaes de un punto. Cambio de sistema de coodenadas catesianas a polaes
TANGENCIAS ENTRE CIRCUNFERENCIAS
 1. Cicunfeencias tangentes EXERIORES a una cicunfeencia a la dada y ente ellas. Dada la cicunfeencia debemos dibuja una cicunfeencia que sea tangente a la pimea. Después vamos a dibuja ota cicunfeencia
1. Cicunfeencias tangentes EXERIORES a una cicunfeencia a la dada y ente ellas. Dada la cicunfeencia debemos dibuja una cicunfeencia que sea tangente a la pimea. Después vamos a dibuja ota cicunfeencia
Tema 7 Geometría en el espacio Matemáticas II 2º Bachillerato 1
 Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
Tema Geometía en el espacio Matemáticas II º Bachilleato ÁNGULOS EJERCICIO 5 : λ Dados las ectas : λ, s : λ calcula el ángulo que foman: a) s b) s π el plano π : ; i j k a) Hallamos el vecto diecto de
ECUACIONES DE LA RECTA
 Temas 6 y 7 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
Temas 6 y 7 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
ECUACIONES DE LA RECTA
 Tema 6 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
Tema 6 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
9 Cuerpos geométricos
 865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
Tema 7 Problemas métricos
 Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
BLOQUE II. Geometría. 10. Elementos en el plano 11. Triángulos 12. Los polígonos y la circunferencia 13. Perímetros y áreas
 LOQUE II Geometía 0. Elementos en el plano. Tiángulos. Los polígonos y la cicunfeencia. Peímetos y áeas 0 Elementos en el plano. Elementos básicos en el plano Dibuja una ecta y contesta a las siguientes
LOQUE II Geometía 0. Elementos en el plano. Tiángulos. Los polígonos y la cicunfeencia. Peímetos y áeas 0 Elementos en el plano. Elementos básicos en el plano Dibuja una ecta y contesta a las siguientes
Cinemática del Sólido Rígido (SR)
 Cinemática del Sólido Rígido (SR) OBJETIVOS Intoduci los conceptos de sólido ígido, taslación, otación y movimiento plano. Deduci la ecuación de distibución de velocidades ente puntos del SR y el concepto
Cinemática del Sólido Rígido (SR) OBJETIVOS Intoduci los conceptos de sólido ígido, taslación, otación y movimiento plano. Deduci la ecuación de distibución de velocidades ente puntos del SR y el concepto
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
El radio de una circunferencia mide 1,25 cm. Halla el ángulo que forman las tangentes a la circunferencia desde un punto situado a 4,8 cm del centro.
 T: TRIGNMETRÍ 1º T 7. RESLUIÓN E TRIÁNGULS RETÁNGULS L TNGENTE UN IRUNFERENI El adio de una cicunfeencia mide 1, cm. Halla el ángulo que foman las tangentes a la cicunfeencia desde un punto situado a cm
T: TRIGNMETRÍ 1º T 7. RESLUIÓN E TRIÁNGULS RETÁNGULS L TNGENTE UN IRUNFERENI El adio de una cicunfeencia mide 1, cm. Halla el ángulo que foman las tangentes a la cicunfeencia desde un punto situado a cm
11 FORMAS GEOMÉTRICAS
 11 FRMS GEMÉTRIS EJERIIS PRPUESTS 11.1 Dos puntos deteminan una ecta. a) uántas ectas se pueden taza con un solo punto? b) ómo son las ectas que pasan po ese punto? a) Tantas como se quiea. b) Secantes,
11 FRMS GEMÉTRIS EJERIIS PRPUESTS 11.1 Dos puntos deteminan una ecta. a) uántas ectas se pueden taza con un solo punto? b) ómo son las ectas que pasan po ese punto? a) Tantas como se quiea. b) Secantes,
Tangencias y enlaces. Aplicaciones.
 DIBUJ Tangencias y Enlaces TEA 38: Tangencias y enlaces. Aplicaciones. Esquema:.- Intoducción. Email: pepaadoes@aakis.es Web: http://www.pepaadoesdeoposiciones.com.- Tazados de ectas tangentes...- Posiciones
DIBUJ Tangencias y Enlaces TEA 38: Tangencias y enlaces. Aplicaciones. Esquema:.- Intoducción. Email: pepaadoes@aakis.es Web: http://www.pepaadoesdeoposiciones.com.- Tazados de ectas tangentes...- Posiciones
3 y un vector director Supongamos también que P x, y,
 . Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
. Coodenadas o componentes de un vecto Sean dos puntos a, a2, a y, 2, vecto son: b a, b a, b a b b b del espacio. Entonces las coodenadas o componentes del. Dos vectoes, CD son equivalentes ( CD ) si tienen
BLOQUE II. Geometría. 10. Elementos en el plano 11. Triángulos 12. Los polígonos y la circunferencia 13. Perímetros y áreas
 LOQUE II Geometía 0. Elementos en el plano. Tiángulos. Los polígonos y la cicunfeencia. Peímetos y áeas 0 Elementos en el plano. Elementos básicos en el plano Dibuja una ecta y contesta a las siguientes
LOQUE II Geometía 0. Elementos en el plano. Tiángulos. Los polígonos y la cicunfeencia. Peímetos y áeas 0 Elementos en el plano. Elementos básicos en el plano Dibuja una ecta y contesta a las siguientes
Resolución de triángulos rectángulos
 Resolución de tiángulos ectángulos Ahoa vamos a aplica las funciones tigonométicas paa esolve tiángulos ectángulos. Resuelve el siguiente tiángulo ectángulo: Ejemplo y 60 Empezamos notando que podemos
Resolución de tiángulos ectángulos Ahoa vamos a aplica las funciones tigonométicas paa esolve tiángulos ectángulos. Resuelve el siguiente tiángulo ectángulo: Ejemplo y 60 Empezamos notando que podemos
CUERPOS REDONDOS. LA ESFERA TERRESTRE
 IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
IES PEÑAS NEGRAS. Geometía. º ESO. CUERPOS REDONDOS. LA ESFERA TERRESTRE 1. CUERPOS REDONDOS. Un cuepo edondo es un sólido que contiene supeficies cuvas. Dento de los cuepos edondos los más inteesantes
mediatrices de cada lado se cortan en un B, C..., etc, son iguales. el mismo centro y es tangente a los lados del polígono en 1, 2...
 POLÍONOS RULRS Polígono (vaios ángulos), es la figua plana limitada po vaios ánulos, los tiángulos y los cuadiláteos estudiados hasta ahoa son polígonos de y ángulos, espectivamente. Un polígono seá egula
POLÍONOS RULRS Polígono (vaios ángulos), es la figua plana limitada po vaios ánulos, los tiángulos y los cuadiláteos estudiados hasta ahoa son polígonos de y ángulos, espectivamente. Un polígono seá egula
La recta n forma un ángulo de 60 (trazar con reglas) con la recta r. Qué ángulos forma la recta n con la recta s? NOMBRE: Nº 1ºESO
 1. OCBULRIO BÁSICO 1. Dibuja las siguientes ectas siguiendo las instucciones: La ecta vetical es pependicula a las ectas s y q. La distancia ente estas dos ectas es de 20mm. o La ecta n foma un ángulo
1. OCBULRIO BÁSICO 1. Dibuja las siguientes ectas siguiendo las instucciones: La ecta vetical es pependicula a las ectas s y q. La distancia ente estas dos ectas es de 20mm. o La ecta n foma un ángulo
MAGNITUDES ESCALARES Y VECTORIALES
 C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
RECTAS Y ÁNGULOS. SEMIRRECTA.- Un punto de una recta la divide en dos semirrectas. La semirrecta tiene principio pero no tiene fin.
 RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
M a t e m á t i c a s I I 1
 Matemáticas II CSTILL-L MNCH CONVOCTORI SEPTIEMRE 00 SOLUCIÓN DE L PRUE DE CCESO UTOR: José Luis Péez Sanz Pime loque Llamamos al adio de la base y h a la altua del cilindo. Como la capacidad del depósito
Matemáticas II CSTILL-L MNCH CONVOCTORI SEPTIEMRE 00 SOLUCIÓN DE L PRUE DE CCESO UTOR: José Luis Péez Sanz Pime loque Llamamos al adio de la base y h a la altua del cilindo. Como la capacidad del depósito
1. (JUN 04) Se consideran la recta y los planos siguientes: 4
 Matemáticas II Cuso.. (JUN ) Se considean la ecta los planos siguientes ; ;. Se pide (a) Detemina la posición elativa de la ecta con especto a cada uno de los planos. (b) Detemina la posición elativa de
Matemáticas II Cuso.. (JUN ) Se considean la ecta los planos siguientes ; ;. Se pide (a) Detemina la posición elativa de la ecta con especto a cada uno de los planos. (b) Detemina la posición elativa de
Arista Los polígonos que limitan al poliedro se llaman caras. Tetraedro Cubo Octaedro Dodecaedro Icosaedro
 OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
OBJETIVO 1 CLASIICAR POLIEDROS NOMBRE: CURSO: ECHA: POLIEDROS Un poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Aista Los polígonos que limitan al poliedo se llaman caas. Caa
COLEGIO ESTRADA DE MARIA AUXILIADORA CIENCIA, TRABAJO Y VALORES: MI PROYECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (10 )
 COLEGIO ESTRADA DE MARIA AUILIADORA CIENCIA, TRABAJO VALORES: MI PROECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (0 ) Fecha: Nombe del estudiante: N O T A La nivelación es en foma de talle donde
COLEGIO ESTRADA DE MARIA AUILIADORA CIENCIA, TRABAJO VALORES: MI PROECTO DE VIDA NIVELACION DE MATEMATICAS GRADO DECIMO (0 ) Fecha: Nombe del estudiante: N O T A La nivelación es en foma de talle donde
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS
 IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
IV. SISTEMAS DE COORDENADAS Y ALGUNOS CONCEP TOS A. COORDENADAS POLARES Dado un punto en el plano catesiano, (coodenadas ectangulaes), dicho punto puede se epesentado con otas coodenadas (coodenadas polaes)
1. Realiza las siguientes operaciones con segmentos. 1º a+2b-c. 2º a+c-b. 3º 3a+c-b NOMBRE: Nº 1ºESO 1.3. OPERACIONES CON SEGMENTOS
 1.3. OPERCIONES CON SEGMENTOS 1. Realiza las siguientes opeaciones con segmentos a b c 1º a+2b-c 1º 2º a+c-b 2º 3º 3a+c-b 3º TEM 1 - Opeaciones con segmentos página 3 1.3.2. TEOREM DE TLES 1. Divide el
1.3. OPERCIONES CON SEGMENTOS 1. Realiza las siguientes opeaciones con segmentos a b c 1º a+2b-c 1º 2º a+c-b 2º 3º 3a+c-b 3º TEM 1 - Opeaciones con segmentos página 3 1.3.2. TEOREM DE TLES 1. Divide el
AXO-1 Z Z X Y X Y Z Z X Y X Y Z Z Y X Y X
 1- Halla los tiángulos de tazas coficientes de educción de estos ejes axonométicos O-1 2- Con los coeficientes de educción obtenidos en el ejecicio anteio, epesenta los siguientes puntos: =(3.5,2.0,4.0)
1- Halla los tiángulos de tazas coficientes de educción de estos ejes axonométicos O-1 2- Con los coeficientes de educción obtenidos en el ejecicio anteio, epesenta los siguientes puntos: =(3.5,2.0,4.0)
6.1. SUPERFICIE PRISMÁTICA Y PRISMA
 6 6.1. SUPERFICIE PRISMÁTICA Y PRISMA 6.. SUPERFICIE PIRAMIDAL Y PIRÁMIDE 6.. CUERPOS REDONDOS. 6.4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemina áeas de supeficies. Detemina volúmenes de sólidos. 14 Inicialmente
6 6.1. SUPERFICIE PRISMÁTICA Y PRISMA 6.. SUPERFICIE PIRAMIDAL Y PIRÁMIDE 6.. CUERPOS REDONDOS. 6.4. SÓLIDOS DE REVOLUCIÓN Objetivos: Detemina áeas de supeficies. Detemina volúmenes de sólidos. 14 Inicialmente
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
12 Cuerpos. en el espacio. 1. Elementos básicos en el espacio. Dibuja a mano alzada un punto, una recta, un romboide y un cubo.
 12 uepos en el espacio 1. Elementos básicos en el espacio ibuja a mano alzada un punto, una ecta, un omboide y un cubo. P I E N S A Y A L U L A Recta Punto Romboide ubo ané calculista 489,6 : 7,5 = 65,28;
12 uepos en el espacio 1. Elementos básicos en el espacio ibuja a mano alzada un punto, una ecta, un omboide y un cubo. P I E N S A Y A L U L A Recta Punto Romboide ubo ané calculista 489,6 : 7,5 = 65,28;
La ecuación implicita del plano que pasa por el punto P(1, 0, 1) con vectores AB (2,1,0) y AP (2,0,0) será:
 xyz0. Dados la ecta : y el punto P(, 0, ) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que pasa
xyz0. Dados la ecta : y el punto P(, 0, ) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que pasa
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Campo eléctrico. 3 m. respectivamente. Calcular el campo eléctrico en el punto A (4,3). Resp.:
 Campo eléctico 1. Calcula el valo de la fueza de epulsión ente dos cagas Q 1 = 200 µc y Q 2 = 300 µc cuando se hallan sepaadas po una distancia de a) 1 m. b) 2 m. c) 3 m. Resp.: a) 540 N, b) 135 N, c )
Campo eléctico 1. Calcula el valo de la fueza de epulsión ente dos cagas Q 1 = 200 µc y Q 2 = 300 µc cuando se hallan sepaadas po una distancia de a) 1 m. b) 2 m. c) 3 m. Resp.: a) 540 N, b) 135 N, c )
Ejercicios. 100 Capítulo 8 Construcciones geométricas
 jecicios 1. a. Taza la ecta (MN). b. Taza la semiecta [N). c. Taza el segmento [Q]. d. Taza el segmento []. e. Taza la ecta (). f. Taza la semiecta [).. 7. () [] [) (G) G () [) [) () [] [] [) (G) H 8.
jecicios 1. a. Taza la ecta (MN). b. Taza la semiecta [N). c. Taza el segmento [Q]. d. Taza el segmento []. e. Taza la ecta (). f. Taza la semiecta [).. 7. () [] [) (G) G () [) [) () [] [] [) (G) H 8.
ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
 FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
FACULTAD DE CIENCIAS Y TECNOLOGIA CARRERA DE INGENIERIA CIVIL 0.1 CURVAS EN R 3 ANALISIS VECTORIAL Y TENSORIAL SEMESTRE II/2015 PRACTICA # 3 UNIDAD 2 DIFERENCIACION VECTORIAL y OPERADORES DIFERENCIALES
UN CACHITO DE LA ALHAMBRA
 UN CACHITO DE LA ALHAMBRA Se llama mosaico a todo ecubimiento del plano mediante piezas llamadas teselas que no pueden supeponese, ni puede deja huecos sin ecubi y en el que los ángulos que concuen en
UN CACHITO DE LA ALHAMBRA Se llama mosaico a todo ecubimiento del plano mediante piezas llamadas teselas que no pueden supeponese, ni puede deja huecos sin ecubi y en el que los ángulos que concuen en
2. CURVAS EN EL SISTEMA POLAR
 2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
z a3 Ecuaciones continuas de la recta: eliminando el parámetro de (2) = = u u u
 Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Junio 2010 OPCIÓN A. A vemos que se diferencian en el cuadrado de la matriz unitaria. Dado que en este caso. por ser la matriz nula.
 Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Matemáticas II Hoja 6: Puntos, rectas y planos en el espacio
 Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
Pofeso: Miguel Ángel Baeza Alba (º Bachilleato) Matemáticas II Hoja 6: Puntos, ectas y planos en el espacio Ejecicio : a) Halla el punto de cote ente el plano 6x y + z y la ecta que pasa po el punto P
2λ λ. La ecuación del plano que buscamos es p: 5x 2y + 2z
 Poducto escala 060 Halla la ecuación de la ecta que cota a y s pependiculamente. x = 1 x = 6 µ : y = 11+ s: y = + µ z = 1+ z = + µ Hallamos un punto P y un punto Q s de modo que el vecto PQ sea pependicula
Poducto escala 060 Halla la ecuación de la ecta que cota a y s pependiculamente. x = 1 x = 6 µ : y = 11+ s: y = + µ z = 1+ z = + µ Hallamos un punto P y un punto Q s de modo que el vecto PQ sea pependicula
( ) CIRCUNFERENCIA UNIDAD VIII VIII.1 DEFINICIÓN DE CIRCUNFERENCIA
 CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
UNIDAD 11: PUNTOS, RECTAS Y PLANOS EN EL ESPACIO
 I.E.. Isabel Peillán y Quiós Matemáticas Depatamento de Matemáticas UNIDAD : Puntos, ectas y planos en el espacio UNIDAD : PUNTO, RECTA Y PLANO EN EL EPACIO Ecuaciones de la ecta Ecuaciones del plano Posiciones
I.E.. Isabel Peillán y Quiós Matemáticas Depatamento de Matemáticas UNIDAD : Puntos, ectas y planos en el espacio UNIDAD : PUNTO, RECTA Y PLANO EN EL EPACIO Ecuaciones de la ecta Ecuaciones del plano Posiciones
Fig. 1 Esquema para el cálculo de B
 P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
TEMA PRELIMINAR. Los sistemas de representación son objeto de estudio en la geometría descriptiva, la cual se fundamenta en la geometría proyectiva.
 TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
TEMA PRELIMINAR 1. Sistemas de Repesentación y Geometía. En esta pate de la intoducción, se tata de encuada el estudio de los sistemas de epesentación dento de lo que es la geometía. Paa ello se va a intenta
TALLER 3 GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA
 TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
TALLER GEOMETRÍA VECTORIAL Y ANALÍTICA FACULTAD DE INGENIERÍA UNIVERSIDAD DE ANTIOQUIA. 0- Pofeso: Jaime Andés Jaamillo González (jaimeaj@conceptocomputadoes.com) Pate del mateial ha sido tomado de documentos
4.- (1 punto) Como ya sabéis, el campo eléctrico creado por una carga en un punto P, es una magnitud vectorial que viene dada por la expresión E K u
 Nombe: Cuso: º Bachilleato B Examen I Fecha: 5 de febeo de 08 Segunda Evaluación Atención: La no explicación claa y concisa de cada ejecicio implica una penalización del 5% de la nota.- (,5 puntos) Halla
Nombe: Cuso: º Bachilleato B Examen I Fecha: 5 de febeo de 08 Segunda Evaluación Atención: La no explicación claa y concisa de cada ejecicio implica una penalización del 5% de la nota.- (,5 puntos) Halla
ELIMINATORIA, 14 de abril de 2007 PROBLEMAS
 ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
TEMA 3. TANGENCIAS 3º ESO
 EMA 3. ANGENCIAS 3º ESO 1 ANGENCIAS: Dos o más figuas geométicas son tangentes cuando únicamente tienen UN UNO EN COMÚN. Los casos que nosotos vamos a estudia son ente cicunfeencias o ente cicunfeencias
EMA 3. ANGENCIAS 3º ESO 1 ANGENCIAS: Dos o más figuas geométicas son tangentes cuando únicamente tienen UN UNO EN COMÚN. Los casos que nosotos vamos a estudia son ente cicunfeencias o ente cicunfeencias
ÁNGULOS Y LONGITUDES DE ARCO
 I.E LEÓN XIII EL PEÑOL MATEMÁTICA GRADO: 0 TALLER Nº: EMETRE I ÁNGULO Y LONGITUDE DE ARCO REEÑA HITÓRICA Un Poblema de Ángulos en la Antigüedad. El matemático giego Eatostenes (apox 76 9 a.c.) midió la
I.E LEÓN XIII EL PEÑOL MATEMÁTICA GRADO: 0 TALLER Nº: EMETRE I ÁNGULO Y LONGITUDE DE ARCO REEÑA HITÓRICA Un Poblema de Ángulos en la Antigüedad. El matemático giego Eatostenes (apox 76 9 a.c.) midió la
0.2.4 Producto de un escalar por un vector. Vector unitario. 0.3 Vectores en el sistema de coordenadas cartesianas.
 VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
VECTORES, OPERCIONES ÁSICS. VECTORES EN EL SISTEM DE C. CRTESINS 0.1 Vectoes escalaes. 0. Opeaciones básicas: 0..1 Suma de vectoes. 0.. Vecto opuesto. 0..3 Difeencia de vectoes. 0..4 Poducto de un escala
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
La ecuación implicita del plano que pasa por el punto P(1, 0, 1) con vectores AB (2,1,0) y AP (2,0,0) será:
 xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
xyz0 1. Dados la ecta : y el punto P(1, 0, 1) exteio a : x y z a) Halla la ecuación en foma geneal del plano que contiene a y a P b) Halla la ecuación (como intesección de dos planos) de la ecta s que
CAPÍTULO 15: TRIÁNGULOS RECTÁNGULOS
 PÍTULO 15: TRIÁNGULOS RETÁNGULOS Dante Gueeo-handuví Piua, 2015 FULTD DE INGENIERÍ Áea Depatamental de Ingenieía Industial y de Sistemas PÍTULO 15: TRIÁNGULOS RETÁNGULOS Esta oba está bajo una licencia
PÍTULO 15: TRIÁNGULOS RETÁNGULOS Dante Gueeo-handuví Piua, 2015 FULTD DE INGENIERÍ Áea Depatamental de Ingenieía Industial y de Sistemas PÍTULO 15: TRIÁNGULOS RETÁNGULOS Esta oba está bajo una licencia
Unidad 12: Posiciones y Métrica en el espacio.
 Unidad 12: Poicione y Mética en el epacio. 1) Poicione elativa en el epacio: a) De un punto con ecta y plano: a1) Un punto A petenece a una ecta i cumple u ecuacione geneale, en cao contaio e dice que
Unidad 12: Poicione y Mética en el epacio. 1) Poicione elativa en el epacio: a) De un punto con ecta y plano: a1) Un punto A petenece a una ecta i cumple u ecuacione geneale, en cao contaio e dice que
Leyes de Kepler. Antes de demostrar las tres leyes de Kepler, haré un análisis matemático de lo que es una elipse.
 Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1
 TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
Trigonometría. Positivo
 Seminaio Univesitaio de Ingeso 17 Tigonometía La tigonometía es una de las amas de la matemática, cuyo significado etimológico es la medición de los tiángulos. Se deiva del vocablo giego tigōno: "tiángulo"
Seminaio Univesitaio de Ingeso 17 Tigonometía La tigonometía es una de las amas de la matemática, cuyo significado etimológico es la medición de los tiángulos. Se deiva del vocablo giego tigōno: "tiángulo"
ALGEBRA Y GEOMETRÍA I
 FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
FACULTAD DE CIENCIAS EXACTAS, INGENIERÍA Y AGRIMENSURA ESCUELA DE FORMACIÓN BÁSICA DEPARTAMENTO DE MATEMÁTICA ALGEBRA Y GEOMETRÍA I El Plano Ricado Sagistá EL PLANO - Definición del plano como luga geomético
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO Geometría lineal Recta y Plano
 LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
CLASIFICAR POLIEDROS. Nombre: Curso: Fecha:
 CLASIICAR POLIEDROS OBJETIVO 1 Nombe: Cuso: eca: POLIEDROS poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Los polígonos que limitan al poliedo se llaman caas. Los lados de las
CLASIICAR POLIEDROS OBJETIVO 1 Nombe: Cuso: eca: POLIEDROS poliedo es un cuepo geomético que está limitado po cuato o más polígonos. Los polígonos que limitan al poliedo se llaman caas. Los lados de las
Con la medida del radio r dibujar una circunferencia y dibujar sus diámetros vertical y horizontal que pase por el centro. o
 * constucciones de cuadiáteos (pobemas de cuadiáteos 5.3- CUADRADO *conocido e ado. Se toma a medida de ado con e compás y a dibujamos sobe una ecta cuaquiea Con a medida de ado se dibuja un aco desde
* constucciones de cuadiáteos (pobemas de cuadiáteos 5.3- CUADRADO *conocido e ado. Se toma a medida de ado con e compás y a dibujamos sobe una ecta cuaquiea Con a medida de ado se dibuja un aco desde
IV. Geometría plana. v v2 2. u v = u v cos α
 Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
Talle de Matemáticas 16 IV. Geometía plana IR 2 = {(x, y)/x, y IR} puede identificase con el espacio de vectoes libes del plano utilizando la base canónica: v =(v 1,v 2 )=v 1 (1, 0) + v 2 (0, 1) = v 1
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. Página 68 Reconoce, nomba y descibe figuas geométicas que apaecen en esta ilustación. Respuesta libe. Po ejemplo: cilindo, otoedo, cono, pisma tiangula Recueda otas figuas geométicas que foman pate
Pág. Página 68 Reconoce, nomba y descibe figuas geométicas que apaecen en esta ilustación. Respuesta libe. Po ejemplo: cilindo, otoedo, cono, pisma tiangula Recueda otas figuas geométicas que foman pate
Cálculo diferencial e integral en una variable. Examen Febrero de 2018
 Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
XLIX Olimpiada Matemática Española
 XLIX Olimpiada Matemática Española Fase Local Melilla 1 de eneo de 01 Poblema 1 Escibimos en fila, peo no necesaiamente en oden, los númeos enteos desde el 1 al 01. Calculamos las medias de cada dos númeos
XLIX Olimpiada Matemática Española Fase Local Melilla 1 de eneo de 01 Poblema 1 Escibimos en fila, peo no necesaiamente en oden, los númeos enteos desde el 1 al 01. Calculamos las medias de cada dos númeos
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO
 SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
( ) TEMA V. 1. Ecuaciones del plano. Tema 5 : Rectas y planos en el espacio
 TEMA V. Ecuaciones del plano. Ecuaciones de la ecta. Haz de planos 4. Incidencia de planos y ectas 5. Ángulos en el espacio 6. Condiciones de pependiculaidad 7. Distancias en el espacio. Ecuaciones del
TEMA V. Ecuaciones del plano. Ecuaciones de la ecta. Haz de planos 4. Incidencia de planos y ectas 5. Ángulos en el espacio 6. Condiciones de pependiculaidad 7. Distancias en el espacio. Ecuaciones del
2x y 2z. Entonces Rang A = 4 > Rang A Sistema incompatible r y s no se cortan y el problema no tiene solución. = =
 Geometía analítica del epacio. Matemática II Mazo 04 Opción A Ejecicio. (untuación máxima: punto) z Calcula la ecuación de una efea que tiene u cento en la ecta x 3 y, y e tangente al plano x y z 4 0,,.
Geometía analítica del epacio. Matemática II Mazo 04 Opción A Ejecicio. (untuación máxima: punto) z Calcula la ecuación de una efea que tiene u cento en la ecta x 3 y, y e tangente al plano x y z 4 0,,.
