Funciones de varias variables
|
|
|
- Valentín García Serrano
- hace 9 años
- Vistas:
Transcripción
1 Funciones de varias variables BENITO J. GONZÁLEZ RODRÍGUEZ DOMINGO HERNÁNDEZ ABREU MATEO M. JIMÉNEZ PAIZ M. ISABEL MARRERO RODRÍGUEZ ALEJANDRO SANABRIA GARCÍA Departamento de Análisis Matemático Universidad de La Laguna Índice 1. Funciones de varias variables 1 2. Límites y continuidad 5 3. Derivadas parciales Interpretación geométrica La diferencial de una función Aplicaciones de la diferencial Derivadas parciales de orden superior Extremos de funciones de dos variables 17
2
3 FUNCIONES DE VARIAS VARIABLES 1/23 1. Funciones de varias variables Definición 1.1. Denotemos por R 2 = {(x,y) : x,y R} el plano euclídeo, y sea D R 2. Una aplicación f : D R (x,y) z = f (x,y) se denomina una función valuada real de dos variables reales. Es usual denotar por z = f (x,y) a estas funciones. Llamaremos variables independientes a x e y, y variable dependiente a z. El dominio de la función f es el conjunto Dom f = { (x,y) R 2 : f (x,y) R } R 2. Nótese que D Dom f. El conjunto Im f = {z = f (x,y) : (x,y) Dom f } R es la imagen o rango de f. Por último, la gráfica o grafo de f es el conjunto Grafo f = {(x,y, f (x,y)) : (x,y) Dom f } R 3. Geométricamente, el grafo de f se interpreta como una superficie en el espacio cuya proyección sobre el plano OXY es Dom f. Ejemplo 1.2. Hallar el dominio y el rango de la función f (x,y) = 16 4x 2 y 2. Esbozar su gráfica. RESOLUCIÓN. En primer lugar, nótese que el radicando ha de ser no negativo. Por tanto Dom f = { (x,y) R 2 : 16 4x 2 y 2 0 } = } {(x,y) R 2 : x2 4 + y2 16 1,
4 2/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Figura 1.1. Dominio, rango y gráfica de la función del Ejemplo 1.2. el cual constituye el recinto interior a la elipse de semiejes 2 y 4 en el plano OXY : x y2 16 = 1. Por otra parte, al ser 4x 2 +y 2 0, el valor máximo de f se toma en el punto (0,0), donde f (0,0) = 16 = 4; mientras que el valor mínimo se toma cuando 4x 2 +y 2 = 16, es decir, sobre la elipse anterior, donde la función es idénticamente nula. Así pues, Im f = {z = f (x,y) R : (x,y) Dom f } = {z R : 0 z 4}. El grafo de f viene dado por Grafo f = = {(x,y, ) } 16 4x 2 y 2 : (x,y) Dom f { ( x,y, ) } 16 4x 2 y 2 : x2 4 + y2 16 1, el cual puede ser representado como la mitad superior del elipsoide x y z2 16 = 1. En efecto: z = f (x,y), z 0 z = 16 4x 2 y 2, z 0 z 2 = 16 4x 2 y 2, z 0 x2 4 + y z2 = 1, z OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
5 FUNCIONES DE VARIAS VARIABLES 3/23 La Figura 1.1 muestra el dominio, rango y gráfica de la función considerada. Para visualizar una función de dos variables podemos auxiliarnos de sus curvas de nivel f (x,y) = c, c constante, que según las distintas aplicaciones en que se utilicen se denominan isobaras, isotermas, líneas equipotenciales, etc. Ejemplo 1.3. Dibujar las curvas de nivel de la función f (x,y) = 64 x 2 y 2 correspondientes a c = 0,1,2,3,...,8. RESOLUCIÓN. Las curvas de nivel para la función f vienen dadas por: f (x,y) = c 64 x 2 y 2 = c 64 x 2 y 2 = c 2 x 2 + y 2 = 64 c 2, las cuales son circunferencias en el plano OXY centradas en el origen y de radio 64 c 2. Por tanto, para los valores c = 0,1,2,3,...,8, los radios de las respectivas circunferencias son 8, 63, 60, 55,...,0. En la Figura 1.2 se da una representación gráfica de las curvas de nivel de f para estos valores de c. Figura 1.2. Curvas de nivel del Ejemplo 1.3. Al ser la función f constante sobre las curvas de nivel ( f (x,y) = c), podemos esbozar su gráfica como se muestra en la Figura 1.3.
6 4/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Figura 1.3. Gráfica de la función del Ejemplo 1.3. Figura 1.4. Gráfica de la función z = senθ/θ. Ejemplo 1.4. Realizar un esbozo de la gráfica de la función f (x,y) = sen(x2 + y 2 ) x 2 + y 2. RESOLUCIÓN. En primer lugar, nótese que las circunferencias C r de centro el origen y radio r 0 en el plano OXY, C r = {(x,y) R 2 : x 2 + y 2 = r 2 }, son curvas de nivel para dicha función. Esto quiere decir que la superficie correspondiente es una superficie de revolución, obtenida al girar alrededor del eje OZ la función de una variable real z = senθ θ (θ x 2 + y 2 ). La gráfica de esta última viene dada en la Figura 1.4. Su revolución alrededor del eje OZ produce el «sombrero mexicano» de la Figura 1.5. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
7 FUNCIONES DE VARIAS VARIABLES 5/23 Figura 1.5. «Sombrero mexicano». 2. Límites y continuidad Definición 2.1. Sea z = f (x,y) definida en un disco abierto (esto es, un círculo sin su circunferencia exterior) centrado en (x 0,y 0 ), excepto quizás en (x 0,y 0 ), y sea L R. Se dice que lím f (x,y) = L (x,y) (x 0,y 0 ) si ε > 0, δ > 0 : 0 < (x x 0 ) 2 + (y y 0 ) 2 < δ f (x,y) L < ε. Definición 2.2. La función z = f (x,y) es continua en el punto (x 0,y 0 ) de una región D si lím f (x,y) = f (x 0,y 0 ). (x,y) (x 0,y 0 ) Diremos que f es continua en D si lo es en todo punto de D. Si las funciones f, g son continuas en el punto (x 0,y 0 ), también son continuas en (x 0,y 0 ): 1. k f, con k R. 2. f ± g. 3. f g.
8 6/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA 4. f /g, siempre que g(x 0,y 0 ) 0. Ejemplo 2.3. Como consecuencia de las propiedades anteriores y del hecho que las funciones coordenadas x e y son continuas, se obtiene que los polinomios en x e y: p(x,y) = a 00 + a 10 x + a 01 y + a 20 x 2 + a 11 xy + a 02 y a nm x n y m, con a i j R (0 i n, 0 j m), son también continuos. Intuitivamente, el límite lím f (x,y) = L (x,y) (x 0,y 0 ) puede ser interpretado de la siguiente manera: cualquiera que sea la forma de acercarnos al punto (x 0,y 0 ) del plano OXY (esto es, a lo largo de semirrectas, parábolas, etc.), para (x,y) cerca de (x 0,y 0 ), los valores z = f (x,y) están cercanos a L. Formalizando esta idea de límite se pueden obtener las siguientes propiedades, particularmente útiles en situaciones prácticas. Límites iterados. Si los límites iterados son distintos, esto es: ( ) ( ) lím lím f (x,y) lím lím f (x,y), x x 0 y y 0 y y0 x x 0 podemos concluir que no existe lím f (x,y). (x,y) (x 0,y 0 ) Límites direccionales. Consideramos dos rectas que pasan por el punto (x 0,y 0 ): r 1 : y = y 0 + λ 1 (x x 0 ) r 2 : y = y 0 + λ 2 (x x 0 ) y son distintas, esto es, λ 1 λ 2. Si los límites direccionales lím f (x,y) = lím (x,y) (x 0,y 0 ) y r 1 (x,y) (x 0,y 0 ) y=y 0 +λ 1 (x x 0 ) f (x,y) = lím x x0 f (x,y 0 + λ 1 (x x 0 )) OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
9 FUNCIONES DE VARIAS VARIABLES 7/23 y lím f (x,y) = lím (x,y) (x 0,y 0 ) y r 2 (x,y) (x 0,y 0 ) y=y 0 +λ 2 (x x 0 ) son distintos, podemos concluir que no existe f (x,y) = lím x x0 f (x,y 0 + λ 2 (x x 0 )) lím f (x,y). (x,y) (x 0,y 0 ) Es importante hacer notar que, tanto en los límites iterados como en los direccionales, la igualdad de éstos no garantiza la existencia del límite doble. Luego, los criterios anteriores constituyen un método para probar la inexistencia del límite de una función en un determinado punto del plano. La idea anterior puede ser aplicada al caso más general en que consideramos curvas que pasan por el punto (x 0,y 0 ) en lugar de rectas, como por ejemplo parábolas, curvas polinomiales de grado n 3, etc. Ejemplo 2.4. Estudiar la continuidad de la función f (x,y) = x2 x 2 + y 2. RESOLUCIÓN. La función f (x,y) es una función racional, esto es, el cociente de dos polinomios. Al ser los polinomios funciones continuas, utilizando la propiedad 4 anterior podemos garantizar que f (x, y) es continua salvo quizás en aquellos puntos que anulen el denominador x 2 + y 2. Ahora bien, x 2 + y 2 = 0 x = 0 y = 0. La función f (x,y) no está definida en (0,0), luego podemos afirmar que es continua en todo su dominio Dom f = {(x,y) R 2 : (x,y) (0,0)}. Veamos si la función puede ser definida en el origen (0,0) de manera que sea continua en todo R 2. Esto es equivalente a probar que existe lím (x,y) (0,0) x 2 x 2 + y 2. Para ello comprobamos en primer lugar si coinciden los límites iterados. Ahora bien: ( lím lím x 0 y 0 x 2 x 2 + y 2 ) x 2 = lím x 0 x 2 = 1,
10 8/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA mientras que ( lím lím y 0 x 0 x 2 x 2 + y 2 ) 0 = lím y 0 y 2 = 0. Como los límites iterados no coinciden, podemos afirmar que no existe lím (x,y) (0,0) x 2 x 2 + y 2, con lo cual f no puede ser extendida continuamente a todo R 2. OBSERVACIÓN: Los límites direccionales en este caso vienen dados por: lím (x,y) (x,y) y=λx x 2 x 2 + y 2 = lím x 0 x 2 f (x,λx) = lím x 0 x 2 (1 + λ 2 ) = λ 2. Puesto que el límite depende de λ, existen rectas distintas a través de (0, 0) con límites direccionales distintos. Por tanto, al igual que con los límites iterados, podemos inferir que no existe lím (x,y) (0,0) x 2 x 2 + y Derivadas parciales Para determinar el efecto de un catalizador en un experimento, un químico puede realizarlo varias veces, con distintas cantidades de catalizador cada vez, mientras mantiene constantes todas las demás variables, como la temperatura o la presión. Análogamente, puede estudiar la influencia de la temperatura si hace variar ésta mientras mantiene constantes la proporción de catalizador y la presión; o de la presión, si la hace variar manteniendo constantes la cantidad de catalizador y la temperatura. Suponiendo que la función z = f (u, v, w) describe el resultado del experimento en términos de la proporción de catalizador u, la temperatura v y la presión w, cuál es el ritmo de cambio de f con respecto a cada una de sus variables independientes? Definición 3.1. El proceso que permite averiguar dicha razón de cambio se llama derivación parcial y el resultado se denomina derivada parcial de f respecto de la variable independiente elegida. Simbólicamente, si z = f (x, y): f (x + x,y) f (x,y) f x (x,y) = lím = f x 0 x x (x,y), OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
11 FUNCIONES DE VARIAS VARIABLES 9/23 f (x,y + y) f (x,y) f y (x,y) = lím = f y 0 y y (x,y). Nótese que en la definición de la derivada parcial f x (x,y) la variable y se mantiene constante, y análogamente ocurre con la variable x en la definición de f y (x,y). Esto viene a decir que la derivada parcial respecto a una de las variables es una derivada en el sentido usual de funciones de una variable real, mientras que el resto de variables que comparecen en la función permanecen constantes. Por lo tanto, en el cálculo de derivadas parciales es lícito el uso de las reglas de derivación para funciones de una variable real. Ejemplo 3.2. Hallar las derivadas parciales de la función f (x,y) = 3x x 2 y 2 + 2x 3 y. RESOLUCIÓN. Utilizando la definición de las derivadas parciales: f (x + x,y) f (x,y) f x (x,y) = lím x 0 x = lím x 0 = lím x 0 = lím x 0 = lím x 0 3(x + x) (x + x) 2 y 2 + 2(x + x) 3 y (3x x 2 y 2 + 2x 3 y) x 3(x + x) y 2 [x 2 + 2x x + ( x) 2 ] + 2y[x 3 + 3x 2 x + 3x( x) 2 + ( x) 3 ] (3x x 2 y 2 + 2x 3 y) x 3x x 2 y 2 + 2x 3 y + (3 2xy 2 + 6x 2 y) x + ( y 2 + 6xy)( x) 2 + 2y( x) 3 (3x x 2 y 2 + 2x 3 y) x [ (3 2xy 2 + 6x 2 y) + ( y 2 + 6xy) x + 2y( x) 2] = 3 2xy 2 + 6x 2 y. Análogamente: f (x,y + y) f (x,y) f y (x,y) = lím y 0 y 3x x 2 (y + y) 2 + 2x 3 (y + y) (3x x 2 y 2 + 2x 3 y) = lím y 0 y 3x x 2 [y 2 + 2y y + ( y) 2 ] + 2x 3 (y + y) (3x x 2 y 2 + 2x 3 y) = lím y 0 y 3x x 2 y 2 + 2x 3 y + ( 2x 2 y + 2x 3 ) y x 2 ( y) 2 (3x x 2 y 2 + 2x 3 y) = lím y 0 y [ = lím ( 2x 2 y + 2x 3 ) x 2 y ] y 0 = 2x 2 y + 2x 3. Las derivadas parciales anteriores pueden ser calculadas más fácilmente usando las reglas de derivación
12 10/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA para funciones de una variable real, tal como comentamos anteriormente. Así, al derivar respecto a x manteniendo y constante obtenemos: f x (x,y) = 3 2xy 2 + 6x 2 y. Derivando ahora respecto a y mientras mantenemos x constante: f y (x,y) = 2x 2 y + 2x 3. Ejemplo 3.3. Hallar las derivadas parciales de la función f (x,y) = xe x2y en el punto (1,ln2). RESOLUCIÓN. Las derivadas parciales en cualquier punto (x,y) vienen dadas por: f x (x,y) = e x2y + 2x 2 ye x2y, f y (x,y) = x 3 e x2y. Evaluándolas en el punto (1,ln2): f x (1,ln2) = e ln2 + 2ln2e ln2 = 2 + 4ln2, f y (1,ln2) = e ln2 = Interpretación geométrica Si y = y 0, entonces z = f (x,y 0 ) es la curva intersección de la superficie z = f (x,y) con el plano y = y 0. Por tanto, f (x 0 + x,y 0 ) f (x 0,y 0 ) f x (x 0,y 0 ) = lím x 0 x es la pendiente de la recta tangente a dicha curva en el punto (x 0,y 0, f (x 0,y 0 )). Nótese que tanto la curva como su tangente se hallan en el plano y = y 0. Análogamente ocurre con f y (x 0,y 0 ). Así pues, los valores de f x y f y en el punto (x 0,y 0 ) proporcionan las pendientes de la superficie en el punto (x 0,y 0, f (x 0,y 0 )), en las direcciones OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
13 FUNCIONES DE VARIAS VARIABLES 11/23 x e y, respectivamente (Figura 3.1). Figura 3.1. Interpretación geométrica de las derivadas parciales. Ejemplo 3.4. Hallar las pendientes de la superficie de ecuación f (x,y) = x2 2 y en el punto ( 1 2,1,2), en las direcciones x e y. RESOLUCIÓN. Las derivadas parciales en cualquier punto (x,y) vienen dadas por: f x (x,y) = x, f y (x,y) = 2y. En el punto ( 1 2,1,2): f x ( 1 2,1 ) = 1 2, f y ( ) 1 2,1 = 2. Tal y como se ha mencionado anteriormente, estas parciales proporcionan las pendientes de la superficie en dicho punto, en las direcciones x e y, respectivamente La diferencial de una función Definición 3.5. Supongamos que z = f (x,y) es una función definida en un conjunto abierto D, que (x 0,y 0 ) D, y que existen en este punto las derivadas parciales f x (x 0,y 0 ) y f y (x 0,y 0 ).
14 12/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Entonces se dirá que f es diferenciable en (x 0,y 0 ) si lím (h,k) (0,0) f (x 0 + h,y 0 + k) f (x 0,y 0 ) f x (x 0,y 0 )h f y (x 0,y 0 )k = 0. h 2 + k 2 El siguiente resultado garantiza que la mayoría de las funciones que manejamos habitualmente son diferenciables en determinados puntos. Teorema 3.6. Si la función f posee derivadas parciales continuas en un punto entonces es diferenciable en ese punto. Definición 3.7. Dada la función z = f (x,y) diferenciable en el punto (x 0,y 0 ), se denomina diferencial de f en dicho punto a la aplicación lineal dada por [dz(x 0,y 0 )] : R 2 R (x,y) f x (x 0,y 0 )x + f y (x 0,y 0 )y. Ejemplo 3.8. Hallar la diferencial de la función z = x 4 y 3 en el punto (1, 1). RESOLUCIÓN. Se tiene: [dz(1, 1)](x,y) = 4x 3y. En el punto ( 1,0), [dz( 1,0)](x,y) = 4x. Es importante fijar la idea de que la diferencial es una aplicación lineal Aplicaciones de la diferencial Considerando el límite que comparece en la Definición 3.5 y teniendo en cuenta que la diferencial de f en el punto (h,k) está dada por [d f (x 0,y 0 )](h,k) = f x (x 0,y 0 )h + f y (x 0,y 0 )k, OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
15 FUNCIONES DE VARIAS VARIABLES 13/23 observamos que dicho límite se puede escribir como f (x 0 + h,y 0 + k) f (x 0,y 0 ) [d f (x 0,y 0 )](h,k) lím = 0. (h,k) (0,0) h 2 + k 2 Tanto el numerador como el denominador de esta expresión tienden a cero cuando (h,k) (0,0), pero el valor del límite es cero. Por tanto, el numerador está más cerca de cero que h 2 + k 2 cuando (h,k) se aproxima a (0,0), y podemos escribir: f (x 0 + h,y 0 + k) f (x 0,y 0 ) [d f (x 0,y 0 )](h,k) 0, (h,k) (0,0); o, lo que es lo mismo: f (x 0 + h,y 0 + k) f (x 0,y 0 ) [d f (x 0,y 0 )](h,k) = f x (x 0,y 0 )h + f y (x 0,y 0 )k, (h,k) (0,0). (3.1) La relación anterior pone de manifiesto que la diferencial de f en el punto (x 0,y 0 ) es una buena aproximación de f (x 0 + h,y 0 + k) f (x 0,y 0 ) para (h,k) (0,0). Esto se verá más claro en el Ejemplo 3.9. Demostrar que la función f (x,y) = xe xy es diferenciable en el punto (1,0). Encontrar su diferencial en dicho punto y calcular aproximadamente f (1.1, 0.1). RESOLUCIÓN. Las parciales de f son: f x = e xy + xye xy, f y = x 2 e xy. Estas funciones son continuas en R 2, así que f es diferenciable en R 2. En el punto (1,0) se tiene f (1,0) = 1, f x (1,0) = 1, f y (1,0) = 1; en particular, la diferencial de f en (1,0) es [d f (1,0)](x,y) = x + y.
16 14/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA El punto (1,0) juega el papel de (x 0,y 0 ), mientras que (1.1, 0.1) representa a (x 0 + h,y 0 + k), esto es, un punto cercano a (1,0). En consecuencia h = 0.1 y k = 0.1, de modo que la diferencial en (1,0), evaluada en el punto (0.1, 0.1), vale 0. Ahora, en virtud de (3.1), f (1.1, 0.1) 1 0 f (1.1, 0.1) 1. El valor que proporciona la calculadora es, efectivamente, próximo a 1: f (1.1, 0.1) = 1.1 e 0.11 = Ejemplo Haciendo uso de la noción de diferencial de una función, hallar un valor aproximado de RESOLUCIÓN. Consideremos la función f (x,y) = x 3 /y 2. Queremos calcular, aproximadamente, f (2.01,0.999) mediante la diferencial de f. Para ello tomamos como (x 0,y 0 ) el punto (2,1), que es un punto próximo a (2.01,0.999) donde se conoce el valor de la función, y hallamos la diferencial de f en dicho punto. Se tiene: f (2,1) = 8, [d f (2,1)](x,y) = 12x 16y. El punto (2.01,0.999) jugará el papel de (x 0 + h,y 0 + k), que es el punto donde se pretende obtener el valor aproximado. Por tanto h = 0.01 y k = 0.001, y (3.1) permite escribir ( 0.001), o, lo que es equivalente, = Hemos obtenido un valor cercano al proporcionado por la calculadora, que es En conclusión, la diferencial de una función permite aproximar los valores de dicha función en el entorno de un punto. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
17 FUNCIONES DE VARIAS VARIABLES 15/ Derivadas parciales de orden superior Dada una función z = f (x,y) podemos calcular, en caso de existir, las derivadas parciales f x (x,y) y f y (x,y). Éstas a su vez vuelven a ser funciones de las variables x e y, por lo que cabe plantearse el cálculo de las derivadas parciales de las funciones derivadas parciales. Así, para f x (x,y) podemos calcular su derivada parcial tanto respecto de x como respecto de y; y análogamente para f y (x,y). Estas cuatro nuevas derivadas se denominan derivadas parciales de segundo orden. Definición La definición y notaciones comúnmente empleadas para las derivadas parciales de segundo orden son las siguientes: ( f x x ( f y x ( f x y ( f y y ) (x,y) = 2 f ) (x,y) = 2 f ) (x,y) = 2 f x 2 (x,y) = f xx(x,y). y x (x,y) = f xy(x,y). x y (x,y) = f yx(x,y). ) (x,y) = 2 f y 2 (x,y) = f yy(x,y). Definición Las derivadas parciales f xy (x,y) y f yx (x,y) se denominan también derivadas parciales cruzadas o mixtas. Teorema 3.13 (Schwarz). Si f xy (x,y) y f yx (x,y) existen y son continuas, entonces f xy (x,y) = f yx (x,y). Observación Repitiendo el proceso anterior se obtienen las derivadas parciales de orden superior (tercero, cuarto, etc.). Ejemplo Hallar las derivadas parciales de segundo orden de la función f (x,y) = 3xy 2 2y +5x 2 y 2, y evaluar f xy ( 1,2). RESOLUCIÓN. Las derivadas parciales de primer orden en cualquier punto (x,y) vienen dadas por: f x (x,y) = 3y xy 2, f y (x,y) = 6xy x 2 y.
18 16/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Figura 3.2. A = A(a,b,θ) = absenθ. Luego, las derivadas de segundo orden serán: f xx (x,y) = 10y 2, f yy (x,y) = 6x + 10x 2, f xy (x,y) = 6y + 20xy, f yx (x,y) = 6y + 20xy. Como cabría esperar f xy (x,y) = f yx (x,y), puesto que ambas parciales cruzadas son continuas (al ser polinomios en x e y), y vale el Teorema Además, f xy ( 1,2) = = 28. Ejemplo El área de un paralelogramo de lados adyacentes a y b, con ángulo θ entre ellos, viene dada por A = absenθ. a) Calcular la razón de cambio de A respecto de a para a = 10, b = 20, θ = π/6. b) Calcular la razón de cambio de A respecto de θ para a = 10, b = 20, θ = π/6. RESOLUCIÓN. La función área puede ser considerada como una función de tres variables (Figura 3.2). a) La razón de cambio de A respecto de a es: A a (a,b,θ) = bsenθ. Para a = 10, b = 20, θ = π/6: A a (10,20,π/6) = 20senπ/6 = 10. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
19 FUNCIONES DE VARIAS VARIABLES 17/23 b) La razón de cambio de A respecto de θ es: A θ (a,b,θ) = abcosθ. Para a = 10, b = 20, θ = π/6: A θ (10,20,π/6) = 200cosπ/6 = = Extremos de funciones de dos variables Definición 4.1. Sea z = f (x,y) ((x,y) D) una función de dos variables, definida en una región cerrada (esto es, que contiene a sus bordes) y acotada D del plano. Los valores f (a,b) y f (c,d) tales que f (a,b) f (x,y) f (c,d) ((a,b),(c,d) D) cualquiera que sea (x,y) D se denominan mínimo y máximo absolutos de f en D. Teorema 4.2. Si f es continua en una región cerrada y acotada D, entonces f alcanza sus extremos (máximo y mínimo) absolutos en, al menos, sendos puntos de D. Definición 4.3. Se dice que f tiene un mínimo relativo (respectivamente, máximo relativo) en (x 0,y 0 ) D, si f (x,y) f (x 0,y 0 ) (respectivamente, f (x,y) f (x 0,y 0 )) para todo (x,y) en un disco abierto centrado en (x 0,y 0 ). Para investigar los extremos relativos de f hay que determinar sus puntos críticos, que son aquellos (x 0,y 0 ) D tales que: al menos una de las parciales f x (x 0,y 0 ), f y (x 0,y 0 ) no existe, o bien ambas parciales existen, y f x (x 0,y 0 ) = f y (x 0,y 0 ) = 0.
20 18/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Figura 4.1. Mínimo relativo. Figura 4.2. Máximo relativo. La naturaleza de un punto crítico se discute recurriendo al determinante hessiano de f, constituido por las derivadas parciales de segundo orden: H(x,y) = f xx (x,y) f yx (x,y) f xy (x,y) f yy (x,y) = f xx f yy f xy f yx. Supongamos que f x (a,b) = f y (a,b) = 0. Entonces: 1. Si H(a,b) > 0 y f xx (a,b) > 0, entonces f tiene un mínimo relativo en (a,b, f (a,b)) (Figura 4.1). f xx (a,b) < 0, entonces f tiene un máximo relativo en (a,b, f (a,b)) (Figura 4.2). 2. Si H(a,b) < 0, entonces f tiene un punto de silla en (a,b, f (a,b)) (Figura 4.3). 3. Si H(a,b) = 0, el criterio no es concluyente. Figura 4.3. Punto de silla. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
21 FUNCIONES DE VARIAS VARIABLES 19/23 Figura 4.4. Gráfica de la función estudiada en el Ejemplo 4.4. Ejemplo 4.4. Identificar los extremos relativos de f (x,y) = x 3 + 4xy 2y RESOLUCIÓN. En primer lugar, para obtener los puntos críticos de f (x, y) resolvemos el sistema que resulta de igualar a cero las derivadas primeras: f x (x,y) = 3x 2 + 4y = 0 f y (x,y) = 4x 4y = 0 3x 2 4y = 0 x = y x(3x 4) = 0 x = y = 0 x = y = 4 3. Luego, (0, 0) y (4/3, 4/3) son puntos críticos de f. Se puede ver una representación gráfica de f en la Figura 4.4. Para estudiar la naturaleza de los puntos críticos formamos, en primer lugar, la matriz hessiana. Como f xx (x,y) = 6x, f yy (x,y) = 4, f xy (x,y) = f yx (x,y) = 4, tenemos: H(x,y) = 6x = 24x 16. Así pues: 1. H(0,0) = 16 < 0, por lo que (0,0, f (0,0)) = (0,0,1) es un punto de silla. La Figura 4.5 muestra una representación gráfica de la función cerca del punto de silla.
22 20/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA Figura 4.5. Ejemplo 4.4: punto de silla. 2. H(4/3,4/3) = 16 > 0 y f xx (4/3,4/3) = 24/3 < 0, por lo que (4/3, 4/3, f (4/3, 4/3)) = (4/3, 4/3, 59/27) es un máximo relativo. La Figura 4.6 muestra la gráfica de la superficie cerca del máximo local. Figura 4.6. Ejemplo 4.4: máximo relativo. Ejemplo 4.5. Identificar los extremos relativos de f (x,y) = x 2 y 2. RESOLUCIÓN. Los puntos críticos de f (x,y) son solución del sistema: f x (x,y) = 2xy 2 = 0 f y (x,y) = 2x 2 y = 0 x = 0 ó y = 0. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
23 FUNCIONES DE VARIAS VARIABLES 21/23 Figura 4.7. Superficie estudiada en el Ejemplo 4.5. Luego, los puntos críticos son de la forma (0,a) y (b,0), con a,b R. Construimos el hessiano: f xx (x,y) = 2y 2, f yy (x,y) = 2x 2, f xy (x,y) = f yx (x,y) = 4xy. Así pues, H(x,y) = 2y 2 4xy 4xy 2x 2 = 4x 2 y 2 16x 2 y 2 = 12x 2 y 2. Como H(0,a) = H(b,0) = 0 cualesquiera sean a,b R, estamos frente a un caso dudoso. Ahora bien: x 2 y 2 = f (x,y) f (0,a) = f (b,0) = 0 (x,y,a,b R); por tanto, todos los puntos críticos son mínimos absolutos de la función dada. Se puede ver la gráfica de la superficie en la Figura 4.7. Ejemplo 4.6. Hallar los extremos relativos y absolutos de la función f (x, y) = sen xy en la región cerrada determinada por 0 x π y 0 y 1.
24 22/23 B. GONZÁLEZ, D. HERNÁNDEZ, M. JIMÉNEZ, I. MARRERO, A. SANABRIA RESOLUCIÓN. Determinemos los puntos críticos de f (x,y): f x (x,y) = y cosxy = 0 f y (x,y) = x cosxy = 0 y = 0 cosxy = 0 xy = π 2 x = 0 cosxy = 0 xy = π 2. (ya que xy [0,π]) Por tanto, los puntos críticos son todos los de la hipérbola xy = π/2 y el punto (0,0). Como la función f (x,y) satisface que 1 f (x,y) 1, si (x,y) está en la hipérbola xy = π/2, necesariamente f (x, y) = sen π/2 = 1. Por tanto, estos puntos corresponden a máximos absolutos de f en la región considerada. Para analizar la naturaleza del punto (0,0) formamos el determinante hessiano. Las derivadas parciales de segundo orden son: f xx (x,y) = y 2 senxy, f yy (x,y) = x 2 senxy, f xy (x,y) = f yx (x,y) = cosxy xy senxy. Por tanto, H(x,y) = y 2 senxy cosxy xy senxy cosxy xy senxy x 2 senxy. Ahora H(0,0) = = 1 < 0, y en consecuencia (0,0, f (0,0)) = (0,0,0) es un punto de silla. No obstante, como 0 xy π se tiene 0 senxy 1, por lo que, en el recinto considerado, el punto (0,0) proporciona un mínimo absoluto. Para detectar otros posibles extremos absolutos hemos de analizar los puntos frontera: Si 0 x π, y = 0 entonces f (x,0) = 0 y, por tanto, en (x,0) la función toma un mínimo absoluto. Si 0 x π, y = 1 entonces f (x,1) = senx, que toma mínimos absolutos en x = 0, x = π y máximo absoluto en x = π/2. Por tanto, (0,1) y (π,1) son mínimos absolutos, mientras que (π/2,1) es un máximo absoluto de f (x,y) en el recinto considerado. Si x = 0, 0 y 1 entonces f (0,y) = 0 y, por tanto, en (0,y) la función toma un mínimo absoluto. OCW-ULL 2013 MATEMÁTICA APLICADA Y ESTADÍSTICA
25 FUNCIONES DE VARIAS VARIABLES 23/23 Figura 4.8. Puntos críticos de la superficie estudiada en el Ejemplo 4.6. Figura 4.9. Superficie estudiada en el Ejemplo 4.6. Si x = π, 0 y 1 entonces f (π,y) = senπy, que toma mínimos absolutos en y = 0, y = 1 y máximo absoluto en y = 1/2. Por tanto (π,0) y (π,1) son mí nimos absolutos, mientras que (π,1/2) es un máximo absoluto. La Figura 4.6 proporciona una representación gráfica de los puntos críticos en el plano OXY. En conclusión: xy = π/2 máximo absoluto. 0 x π, y = 0 f (x,0) = 0 (x,0) mínimo absoluto. x = 0, 0 y 1 f (0,y) = 0 (0,y) mínimo absoluto. x = π, y = 1 f (π,1) = 0 (π,1) mínimo absoluto. x = π/2, y = 1 f (π/2,1) = 1 (π/2,1) máximo absoluto. x = π, y = 1/2 f (π,1/2) = 1 (π,1/2) máximo absoluto. El grafo de f (x,y) en el recinto considerado se puede ver en la Figura 4.9.
Funciones de varias variables: problemas resueltos
 Funciones de varias variables: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ
Funciones de varias variables: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
9. Diferenciación de funciones reales de varias variables reales
 9.2. Extremos 9.2.1. POLINOMIOS DE TAYLOR Polinomios de Taylor y de McLaurin Se llama polinomio de Taylor de orden n 1 de la función f(x, y) en (a, b) al polinomio: f(a, b) f(a, b) n (x, y) = f(a, b) +
9.2. Extremos 9.2.1. POLINOMIOS DE TAYLOR Polinomios de Taylor y de McLaurin Se llama polinomio de Taylor de orden n 1 de la función f(x, y) en (a, b) al polinomio: f(a, b) f(a, b) n (x, y) = f(a, b) +
Funciones de varias variables. Continuidad
 Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad
 Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Función de dos variables
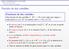 Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
8. FUNCIONES DE VARIAS VARIABLES.
 8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
8. FUNCIONES DE VARIAS VARIABLES. En este tema comenzamos el análisis de funciones de varias variables reales. Comenzaremos estudiando el espacio euclídeo n-dimensional para continuar el estudio (sencillo)
Tema 6 Funciones reales de varias variables
 Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Integración múltiple: integrales dobles
 Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna [email protected] Índice. Integrales iteradas 2. Teorema
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna [email protected] Índice. Integrales iteradas 2. Teorema
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 . DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
. DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
1. Funciones de varias variables
 Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Soluciones de los ejercicios del examen de Cálculo del 29 de junio de 2007 Primero de Ingeniería de Telecomunicación
 Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
CÁLCULO DIFERENCIAL Muestras de examen
 CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Límites y Continuidad de funciones de varias variables
 1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Lección 11: Derivadas parciales y direccionales. Gradiente. Introducción al Cálculo Infinitesimal I.T.I. Gestión
 Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Tema 4 Diferenciación de funciones de una y varias
 Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Tema 4 Diferenciación de funciones de una y varias variables. CÁLCULO DIFERENCIAL DE FUNCIONES DE UNA VARIABLE Definición.: Función derivable Sea f : R R definida en un entorno de a R, se dice que f es
Matemáticas III Andalucía-Tech
 Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Continuidad de funciones reales y vectoriales de variable vectorial
 Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
Capítulo 6 Continuidad de funciones reales y vectoriales de variable vectorial 6.1. Introducción Hasta el momento hemos estudiado funciones reales de variable real, es decir, funciones de la forma f :
FUNCIONES DE DOS VARIABLES
 FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
FUNCIONES DE DOS VARIABLES - Funciones de dos variables reales - Límites 3- Continuidad de funciones de dos variables 4- Derivabilidad de funciones de dos variables 5- Diferenciabilidad de funciones de
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
MATEMÁTICAS II Notas de clase
 MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular
Variables estadísticas bidimensionales: problemas resueltos
 Variables estadísticas bidimensionales: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO
Variables estadísticas bidimensionales: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO
Límites y Continuidad de funciones de varias variables
 1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
1- Se construe un depósito de propano adosando dos hemisferios a los etremos de un cilindro circular recto Epresar el volumen V de ese depósito en función del radio r del cilindro de su altura h - Determinar
TEORIA MATEMATICAS 5 PRIMER PARCIAL
 Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
Def: Grafica de una función TEORIA MATEMATICAS 5 PRIMER PARCIAL Sea:. Definimos la grafica de f como el subconjunto de formado por los puntos, de en los que es un punto de U. Simbólicamente grafica es:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Examen-Modelo para el curso 2014-2015 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Examen-Modelo para el curso 2014-2015 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Teoría de errores: problemas propuestos
 Teoría de errores: problemas propuestos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ ([email protected])
Teoría de errores: problemas propuestos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL MARRERO RODRÍGUEZ ([email protected])
Matemática II Tema 14: valores extremos
 Matemática II Tema 14: valores extremos 2012 2013 Índice Valores extremos y puntos silla 1 Criterio de las derivadas para extremos locales 1 Máximos y mínimos absolutos 5 Trabajo práctico 7 Valores extremos
Matemática II Tema 14: valores extremos 2012 2013 Índice Valores extremos y puntos silla 1 Criterio de las derivadas para extremos locales 1 Máximos y mínimos absolutos 5 Trabajo práctico 7 Valores extremos
Topología en R n. Continuidad de funciones de varias variables
 . Continuidad de funciones de varias variables María Muñoz Guillermo [email protected] U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
. Continuidad de funciones de varias variables María Muñoz Guillermo [email protected] U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Extremos de funciones de varias variables
 Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
2. Sea f(x, y) = x 2 2xy+y 2. Aquí el discriminante es igual a cero. Qué son los puntos críticos: mínimos locales, máximos locales o puntos silla?
 1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Licenciatura en Matemáticas Soluciones del examen final de Cálculo de septiembre de sena + 4sen(a/2) + 9sen(a/3) + + n 2 sen(a/n) n 2.
 Licenciatura en Matemáticas Soluciones del examen final de de septiembre de 00 Ejercicio 1. (a) Calcular: lím n sena + 4sen(a/) + 9sen(a/3) + + n sen(a/n) n (a + 1)(a + ) (a + n) (b) Estudiar la convergencia
Licenciatura en Matemáticas Soluciones del examen final de de septiembre de 00 Ejercicio 1. (a) Calcular: lím n sena + 4sen(a/) + 9sen(a/3) + + n sen(a/n) n (a + 1)(a + ) (a + n) (b) Estudiar la convergencia
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
EXAMEN TEMA 2:Funciones de varias variables
 GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Análisis Matemático 2
 Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
TERCER EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
(x x 0 ) y 0. O bien z z 0 = x 0. y notamos a este límite ᾱ (t 0 ) = dᾱ dt (t 0).
 O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
1.6 Ejercicios resueltos
 Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected] 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected] 2016 Licencia Creative Commons 4.0 Internacional J.
Derivación de funciones de varias variables.
 Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
UNIVERSIDAD COMPLUTENSE DE MADRID
 Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
Principales conceptos que se tendrán en cuenta en la elaboración de las pruebas de Acceso a la Universidad para los estudiantes provenientes del Bachillerato LOGSE de la materia "Matemáticas II" ÁLGEBRA
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Práctica 3: Diferenciación I
 Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos
 Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Práctica 1. Continuidad Ejercicios resueltos
 Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Cálculo integral de funciones de una variable: problemas propuestos
 Cálculo integral de funciones de una variable: problemas propuestos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL
Cálculo integral de funciones de una variable: problemas propuestos BENITO J. GONZÁLEZ RODRÍGUEZ ([email protected]) DOMINGO HERNÁNDEZ ABREU ([email protected]) MATEO M. JIMÉNEZ PAIZ ([email protected]) M. ISABEL
f, y el Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada ( xy, ) de D un
 Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Funciones de varias variables Función de dos variables Definición. Es una función f que asigna a cada pareja ordenada (, ) de D un único número real f (, ). El conjunto D es el dominio de f, el correspondiente
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Funciones de varias variables
 9 Versión: Funciones de varias variables 6 de noviembre de 7 En este tema introducimos algunos elementos básicos del cálculo diferencial en varias variables. Muchos procesos (físicos, biológicos,... )
9 Versión: Funciones de varias variables 6 de noviembre de 7 En este tema introducimos algunos elementos básicos del cálculo diferencial en varias variables. Muchos procesos (físicos, biológicos,... )
Límites y Continuidad de funciones de dos variables
 Límites y Continuidad de funciones de dos variables 1.- Si en un cierto punto ( a, b) R existe el lim f = L R a,b, entonces: f es continua en (a, b). b) Existen los límites reiterados de f en (a, b) y
Límites y Continuidad de funciones de dos variables 1.- Si en un cierto punto ( a, b) R existe el lim f = L R a,b, entonces: f es continua en (a, b). b) Existen los límites reiterados de f en (a, b) y
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
Guía Semana 7 1. RESUMEN 2. EJERCICIOS PROPUESTOS. Universidad de Chile. Ingeniería Matemática
 . RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
. RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
La integral doble sobre recintos no rectangulares
 La integral doble sobre recintos no rectangulares IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna [email protected] Índice 1. Introducción 1 2. Conjuntos de tipos I II 2 3. Aplicaciones
La integral doble sobre recintos no rectangulares IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna [email protected] Índice 1. Introducción 1 2. Conjuntos de tipos I II 2 3. Aplicaciones
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
