MATEMÁTICAS TAREAS DE VERANO
|
|
|
- Ana Sandoval Salinas
- hace 7 años
- Vistas:
Transcripción
1 MATEMÁTICAS TAREAS DE VERANO MATEMÁTICAS º ESO CRITERIOS DE CALIFICACIÓN CONVOCATORIA DE SEPTIEMBRE Para los alumnos de E.S.O. que obtengan una calificación final de Insuficiente, los profesores del Departamento propondrán unos ejercicios y problemas a realizar durante el verano, basados en una selección de estándares del curso. La prueba extraordinaria estará basada en los ejercicios y problemas propuestos para el verano y será calificado de 0 a 0. En el examen se establecerá claramente el valor de cada pregunta o el peso que tenga en la nota del mismo. En caso de obtener en el examen una nota inferior a, la calificación será INSUFICIENTE acompañada del número que mejor describa la calificación obtenida. En caso de obtener en el examen una nota igual o superior a, la calificación se obtendrá por redondeo. A CONTINUACIÓN FIGURAN LOS EJERCICIOS Y PROBLEMAS A REALIZAR DURANTE EL VERANO. Estos ejercicios son una guía para facilitar el estudio de la materia. Se recomienda el uso de un cuaderno específico para realizarlos y facilitar así el repaso final de la materia. TRABAJO VERANO º ESO (06 Página
2 TRABAJO DE VERANO MATEMÁTICAS ºESO NOMBRE:...CURSO: NÚMEROS NATURALES Y DIVISIBILIDAD Ejercicio nº.- Realiza las siguientes operaciones combinadas: : 6 7 (8 : ( 7 ( 6 : 8 (6: 0: Ejercicio nº.- Escribe cómo se leen los siguientes números a b c d Ejercicio nº.- Escribe con palabras la superficie de las siguientes islas y ordénalas de menor a mayor superficie: Groenlandia: km Nueva Guinea: 6 80 km Borneo: 7 km Madagascar: 70 km Ejercicio nº.- Escribe con cifras los siguientes números:: a Dieciocho millones trescientos ocho mil b Seiscientos veinticinco billones, tres mil catorce c Tres billones, ochenta y cinco millones cinco Ejercicio nº.- Un pastor tenía ovejas. Los lobos mataron a todas salvo a. Cuántas quedaron? Ejercicio nº 6.-Un ciclista realiza un viaje en varios días, el primero recorre 78 km, el segundo día sólo la mitad, porque llegó a un pueblo que quería visitar, el tercer día recorrió 8 por la mañana y 6 por la tarde. En total hay 0 km. Cuántos km tiene aún que recorrer? Escribe la frase matemática que indica todos los cálculos y responde la pregunta. Ejercicio nº 7.-En una mina trabajan 78 mineros que extraen diariamente carretillas de carbón. Todas las carretillas llenas pesan 06 kg, y cada una de ellas, vacía, 0 kg. TRABAJO VERANO º ESO (06 Página
3 Cuánto carbón extrae, por término medio, cada minero al día? Escribe la frase matemática que indica todos los cálculos y responde la pregunta. Ejercicio nº 8.-Se descargan de un barco 0 0 toneladas de carbón, llenando vagones de mercancías que pueden llevar 0 toneladas cada uno. Cuántos trenes se necesitan para transportar todo el carbón si cada tren está formado por 8 vagones? Escribe la frase matemática que indica todos Ejercicio nº.- Subraya la/s afirmación/nes correcta/s en cada caso: a En una granja hay.0 pollos,. puedo venderlos en grupos de y no me sobra ninguno;. puedo venderlos en grupos de, de 0 y de 0 y no me sobraría ninguno;. puedo venderlos en grupos de 0 y de 0 y no me sobraría ninguno;. puedo venderlos en grupos de, de 0 y de y no me sobraría ninguno. b Cualquier número que acabe en es divisible por y por ;. es divisible por, por y por ;. es divisible por 6 y por ;. es divisible por y por. Ejercicio nº 0.- De los siguientes números, hay uno que no es múltiplo de. Cuál? a b c 78 d 6 Ejercicio nº.-contesta: a Pueden dividirse los números,,, 7,,, 7 y por otro número que no sea el o ellos mismos, para obtener un cociente exacto? b Qué nombre reciben los números que sólo tienen como divisores el y ellos mismos? c Un número es primo cuando... a... sólo es divisible por sí mismo y por. b... es impar. c... sólo es divisible por sí mismo y por uno. Ejercicio nº.-halla los divisores de cada uno de estos números y señala cuáles son primos y cuáles compuestos:,,, 6, 7, Ejercicio nº.-si las descomposiciones factoriales de dos números son: y 7 Cuáles son su m.c.d. y su m.c.m.? TRABAJO VERANO º ESO (06 Página
4 a m.c.d = b m.c.d = m.c.m. = 7 m.c.m. = 7 c m.c.d = d m.c.d = m.c.m. = 7 m.c.m. = 7 Ejercicio nº.-los divisores de y son: Divisores de = {,,,, 6, } Divisores de = {,,,, 6, 8,, } Cuál es el m.c.d (,? a b c 8 d Ejercicio nº.-calcula el m.c.d. y el m.c.m. de los siguientes números a partir de sus descomposiciones factoriales a y 7 b 80, 6, 0 c 00 y 6. Ejercicio nº 6.-En una casa utilizan para la cocina una bombona de butano que dura 8 días; otra bombona para una estufa, que dura 6 días, y otra para el agua caliente, que dura 0 días. Cada cuántos días se acaban las tres bombonas al mismo tiempo? Ejercicio nº 7.-Los libros de una biblioteca se pueden empaquetar de en, de en y de 00 en 00, sin que sobre ninguno. Son más de 700 y menos de.000. Cuántos libros hay? Ejercicio nº 8.-En un restaurante ponen sopa de primer plato cada 6 días, ponen pollo de segundo plato cada días y ponen natillas de postre cada 8 días. Si hoy han coincidido los tres, cuándo volverán a coincidir? Ejercicio nº.-mi hermano pequeño hace grupos con sus canicas de 6 en 6, de 8 en 8 y de en y siempre sobran. Tiene menos de 0 canicas pero, cuántas tiene exactamente? a 6 canicas. b 0 canicas. c canicas. d canicas. Ejercicio nº 0.-Un bodeguero tiene vino de la clase A: litros; vino de la clase B: litros, y vino de la clase C: 7 litros. Desea envasar dichos vinos en toneles que sean lo más grandes posible, pero con la condición que han de salir igual número de toneles de cada clase de vino. Averigua cuántos toneles obtendrá y qué número de litros tendrán. Ejercicio nº.-maría le dice a su amiga que su hermano le deja la bicicleta cada 0 días. Su amiga le contesta que tiene mucha suerte porque a ella le toca la bicicleta cada 8 días. Por suerte para las dos, el próximo domingo día 8 ambas coinciden en tener bicicleta y deciden hacer una excursión. Averigua cuántos días pasarán para que vuelvan a coincidir las dos con bicicleta. TRABAJO VERANO º ESO (06 Página
5 Ejercicio nº.- Tres listones de madera miden respectivamente, cm, 6 cm y 0 cm. Quiero cortar a los tres en partes iguales de la mayor longitud posible. Cuál será la longitud del corte?. En cuántas partes quedaría dividido cada listón?. Ejercicio nº.- Al dividir dos números se obtiene de cociente y de resto: a Si el divisor es 8, cuánto vale el dividendo? b Si el dividendo es 8, cuánto vale el divisor? Ejercicio nº.- Completa la siguiente tabla poniendo V (verdadero o F (falso según corresponda, realizando las operaciones necesarias. Múltiplo de Múltiplo de Primo Compuesto Ejercicio nº.- Completa la tabla. Redondeo a las centenas Redondeo a los millares Redondeo a las decenas de millares Ejercicio nº 6.- Calcula: a 6 + b ( 6 + c 6 ( + d (6 + e ( f (7 7 : 6 Ejercicio nº 7.- Calcula: a b 78 8 c d : e 6 78 : 8 f : En las divisiones del ejercicio, expresa la relación entre el dividendo, el divisor, el cociente y el resto. Ejercicio nº 8.- Francisco tiene, Roberto tiene más que Francisco. Ramón tiene 7 menos que Roberto. Cuánto tienen entre los tres? TRABAJO VERANO º ESO (06 Página
6 POTENCIAS Y RAÍCES Ejercicio nº.- Tenemos cajas de aceite, cada una de las cuales contiene botellas de aceite y cada botella tiene una capacidad de litros. Si deseamos saber el total de litros que poseemos, podemos indicar = 7 y este producto puede expresarse en forma de potencia: = Indica los productos y potencias que correspondan en los casos siguientes: a El número de cajas es ; las botellas por caja son ; los litros de cada botella son, cuántos litros hay en total? b Son amigos y cada uno tiene euros. Cuántos euros reúnen entre todos? Ejercicio nº.- Expresa como una sola potencia: a b 0 6 : : c 0 8 : d Ejercicio nº.- Realiza las siguientes operaciones, realizando los pasos intermedios: a b c 00 : 8 = d = Ejercicio nº.- Escribe en forma de potencia con base números primos: a b 6 c 7 d 6 : 8 e : f 7 : g h 0 i ( j ( 6 k : l (7 : 7 8 Ejercicio nº.- Calcula, escribiendo los pasos intermedios: 0: 0 a 6 0 b c : 6 0 TRABAJO VERANO º ESO (06 Página 6
7 Ejercicio nº 6.-Luís tiene 8 años y dice que la edad de su abuelo es el cuadrado de la suya y que la edad de su abuela es el cubo de la edad de su hermana chica, que tiene años. Calcula la edad del abuelo y de la abuela de Luís. Ejercicio nº 7.- Las raíces cuadradas son necesarias para averiguar un número cuando conocemos su cuadrado. Es el caso del área de un cuadrado si deseamos conocer cuánto mide el lado de dicho cuadrado. Indica cuánto mide el lado en cada caso: a Área de un cuadrado m. b Área de un cuadrado cm. c Área de un cuadrado 8 dm. d Área de un cuadrado 00 mm. Ejercicio nº 8.- Calcula: a b c 0 d e 0 0 Ejercicio nº.- Calcula el valor de las siguientes potencies de 0: a 0 b 0 c 0 8 d 0 Ejercicio nº 0.- Expresa los números siguientes como el producto de un número natural por una potencia de 0: a b 00 c d 00 Ejercicio nº.- Calcula: a b 6 : 8 c : d : 6 Ejercicio nº.- Expresa como una sola potencia y calcula su valor: a b : c ( : d ( e ( : f (6 6 : (66 6 Ejercicio nº.- Expresa como una potencia de 0: a 000 b c d Ejercicio nº.- Una finca tiene forma cuadrada y mide m de lado. Si el metro cuadrado se paga a 00. Cuánto vale la finca?. Ejercicio nº.- Ana y Ester tienen monedas. Ana tiene elevado al cuadrado y Ester tiene elevado a la sexta. Quién tiene más?. Razona tu respuesta. Ejercicio nº 6.- Silvia tiene cinco faldas, cinco camisetas y cinco pares de zapatos. De cuántas maneras diferentes puede combinar dichas prendas?. TRABAJO VERANO º ESO (06 Página 7
8 NÚMEROS ENTEROS Ejercicio nº.- Escribe los números enteros comprendidos entre - y +. Ejercicio nº.- Ordena con el signo < los números siguientes y represéntalos en la recta real: -; +; -; +, ; -; + Ejercicio nº.- Utiliza los números enteros para expresar: a El año 0 antes de Cristo. b Me han ingresado euros en mi cuenta de ahorros. c Mi pueblo se encuentra a metros sobre el nivel del mar. d Mi coche se encuentra aparcado en la ª planta del sótano de unos grandes almacenes. e La temperatura media de mi pueblo en el verano es de º grados. f La temperatura media de mi pueblo en el invierno es de º grados bajo cero. g El año del descubrimiento de América. Ejercicio nº.- Forma el opuesto de los números: a - b +6 c - d +7 Ejercicio nº.- Cuál es el número entero comprendido entre - y -? a b - 6 c d - Ejercicio nº 6.- Calcula: 6 6 Ejercicio nº 7.- Calcula 6 6 Ejercicio nº 8.- El primero de mes al señor García le ingresaron en su cuenta bancaria, que tenía 6 euros, su sueldo de.7 euros.en la primera semana sacó 6 euros y en la siguiente volvió a sacar 7 euros; el día 0 ingresó euros que le tocaron en un juego de azar; el día le cargaron en su cuenta la letra del coche, que eran 8 euros. Qué dinero le queda a final de mes? (Expresa las operaciones en una sola expresión de números enteros. TRABAJO VERANO º ESO (06 Página 8
9 Ejercicio nº.- En un juego, Antonio ganó 8 canicas, después perdió, más tarde ganó, después ganó y finalmente perdió 8. Cuál fue el resultado al cabo del juego? Ejercicio nº 0.- Indica los números que están representados por letras en la recta: Ejercicio nº.- Realiza las siguientes operaciones con números enteros, escribiendo todos los pasos intermedios: a 6 7 b d 0 0: 0 c 6 0 Ejercicio nº.- Estudia los movimientos de la cuenta y calcula el saldo que tenía el 6 de noviembre (6 - XI, sabiendo que el de octubre ( X tenía un saldo positivo en su cuenta de 0. BANCO WW EXTRACTO DE MOVIMIENTOS FECHA D H CONCEPTO 6 - X 0 Extracción cajero - X Devolución comisión - X 8 Abono nómina - XI 8 Gasto tarjeta comercio - XI 00 Extracción cajero - XI 7 Préstamo hipotecario - XI 6 Recibo luz Ejercicio nº.- Completa las siguientes frases: a El valor de es.. b El valor absoluto de se escribe. y vale.. c De los siguientes números: -, +, +, +78, -, + 6 no son naturales los números: d El resultado de : es TRABAJO VERANO º ESO (06 Página
10 FRACCIONES y EXPRESIONES DECIMALES Ejercicio nº.- Calcula cuatro fracciones equivalentes en cada caso: = Ejercicio nº.- Simplifica estas fracciones hasta obtener su fracción irreducible: Cuál es? 6 Ejercicio nº.- De las siguientes fracciones hay una que es equivalente a Ejercicio nº.- Elige la respuesta correcta: Las fracciones pueden transformarse en otras equivalentes por simplificación: a Multiplicando el numerador y denominador por un número. b Dividiendo el numerador y denominador por un mismo número. c Dividiendo el numerador y denominador por diferentes números. d Multiplicando el numerador y denominador por diferentes números. Ejercicio nº.- Elige la respuesta correcta: Las fracciones pueden transformarse en otras equivalentes por amplificación: a Multiplicando los dos términos de dicha fracción por números primos diferentes. b Multiplicando los dos términos de dicha fracción por un mismo número. c Dividiendo los dos términos de dicha fracción por números cualesquiera. d Dividiendo el numerador por un divisor común. Ejercicio nº 6.- Si observas las fracciones, también son cocientes indicados: 7 = = 0,; 0, 0, , de una cantidad es la mitad. 0, de una cantidad es la cuarta parte. 0,7 de una cantidad es las tres cuartas partes. Ejercicio nº 7.- Calcula los cocientes que representan las fracciones siguientes: (Fíjate en el ejercicio anterior 8 = = = = 0 TRABAJO VERANO º ESO (06 Página 0
11 Ejercicio nº 8.- Reduce a común denominador estos grupos de fracciones:,,,,,, 6 0 Ejercicio nº.- Completa para que las relaciones sean ciertas. 7 Ejercicio nº 0.- Ordena de mayor a menor las siguientes fracciones.,,,,, 0 8 Ejercicio nº.- Ordena estas fracciones: 0 a De mayor a menor:,,,, 7 8 b De menor a mayor:,,, 0 Ejercicio nº.- Calcula: a de 60 b de 0 c de 80 Ejercicio nº.- Al tostarse el café, éste pierde de su peso. Un comerciante tiene 80 kg de café verde. Cuánto pesará este café después de tostarlo? Ejercicio nº.- Con 8 céntimos de euro, que son los 7 de mi dinero, compré un rotulador. Cuánto dinero tenía antes de la compra? Ejercicio nº.- El depósito de un coche tiene una capacidad de 8 litros de gasolina. Si se gasta en un viaje, cuántos le quedan al volver del viaje? 6 Ejercicio nº 6.- Voy por la página 8 y llevo leídos los tiene el libro? Ejercicio nº 7.- A una sesión de cine asisten 6 espectadores, siendo niños hay en el cine? de un libro. Cuántas páginas a b 8 c 8 d 7 niños. Cuántos TRABAJO VERANO º ESO (06 Página
12 TRABAJO VERANO º ESO (06 Página Ejercicio nº 8.-. Calcula y simplifica: f e d c b a Ejercicio nº.- Calcula y simplifica: d c b a Ejercicio nº 0.- Calcula y simplifica: : - : d c b a Ejercicio nº.- De un rollo de cuerda de 60 metros, Raúl ha cortado del total, Pedro cortó del total y Juan, 6 del total. Qué fracción del rollo de cuerda han cortado entre los tres?. Cuántos metros quedan?. Razona tus respuestas. Ejercicio nº.-.ordena de menor a mayor las siguientes fracciones reduciéndolas previamente a común denominador: 8, 8, 7,. Ejercicio nº.- Un comerciante vendió las tres cuartas partes de un cargamento de naranjas a un frutero. Después vendió dos terceras partes del resto a un supermercado y aún le quedaron 0 kg de naranjas. Cuál era el peso final del cargamento?. Razona tu respuesta. Ejercicio nº.- Resuelve las siguientes operaciones con fracciones, simplificando al máximo el resultado y escribiendo el proceso de resolución paso a paso. 8 7 : : 6 d c b a Ejercicio nº.- De qué tipo son los siguientes decimales ' 0 8; '78;?. Exprésalos en forma de fracción, simplificando el resultado.
13 Ejercicio nº 6.- Ana ha comprado tres sobres a 0,8 cada uno y tres tarjetas a 0, cada una. Si ha pagado con un billete de 0, cuánto dinero le han devuelto?. Ejercicio nº 7.- Rául compra en unos grandes almacenes por valor de 8, euros. Gasta la cuarta parte en libros, y del resto, la mitad en camisetas. Cuánto ha gastado en camisetas? Ejercicio nº 8.- Tres cuartos de kilo de bacalao han costado euros. Cuánto cuesta un kilo?. Ejercicio nº.- Una bolsa de arroz, de tres cuartos de kilo, cuesta,80. A cómo sale el kilo?. Ejercicio nº 0.- Se han sembrado de alfalfa los / de la superficie de una finca, y aún quedan 600 metros cuadrados sin sembrar. Cuál es la superficie total de la finca?. Ejercicio nº.- Rosario ha sacado / del dinero que tenía en la hucha y aún le quedan euros. Cuánto tenía antes de abrirla?. PROPORCIONALIDAD Y PORCENTAJES Ejercicio nº.- Indica qué proporciones son ciertas: , Ejercicio nº.- Indica cuáles de las siguientes expresiones se refieren a magnitudes directamente e inversamente proporcionales: a El número de días trabajados y el importe que se cobra. b La cantidad de trigo que cabe en un saco y el peso del mismo. c Las horas que funciona un tractor y la cantidad de gasoil que consume. d La velocidad con la que se hace un trabajo y el tiempo que se tarda en acabarlo. e El número de grifos de una fuente y el tiempo que tarda en llenarse. f El número de personas que hacen un trabajo y los días que tardan en acabarlo. g El número de trabajadores de una empresa y el importe de las nóminas que debe pagar el empresario. h El número de trabajadores que hacen un edificio y el tiempo que tardan en acabarlo. i El tiempo que está abierto un grifo y la cantidad de agua que arroja. TRABAJO VERANO º ESO (06 Página
14 Ejercicio nº.- Averigua el término que falta: x 0 x 8 Ejercicio nº.- La pista del recreo mide 60 m de larga. Tardamos minuto en recorrerla. Cuántos metros recorremos durante minutos? Supongamos que un paso tuyo mide 0 cm. Calcula las vueltas que das a la pista si das.000 pasos. Ejercicio nº.- Seis ovejas comen la hierba de un campo en días. Cuántas ovejas serían necesarias para agotarla hierba del campo en 8 días? Ejercicio nº 6.- Un niño decide repartir 00 cromos entre sus amigos directamente proporcional al tiempo que hace que conoce a cada uno. A José lo conoce hace años; a Luís lo conoce hace años y a María la conoce hace años. Cuántos cromos dará a cada uno? Ejercicio nº 7.- Por ' kg de cordero se pagan euros. Cuánto se pagará por 7 kg y 0 g? Ejercicio nº 8.- En una clase de º de ESO por cada alumnos hay alumnas. Si el número total de alumnos es. Cuántas alumnas hay? Ejercicio nº.- Un coche con velocidad media 7 Km/h tardar hora y cuarto en hacer el recorrido previsto. Otro coche hace el mismo recorrido en minutos. Son proporcionales? Por qué? De qué tipo? A qué velocidad media ha ido el segundo coche? Ejercicio nº 0.- Un barco tarda 6 minutos en ir de una isla a otra con una velocidad de 0 nudos/min. A veces, el barco se llena de pasajeros, sale antes y tiene que hacer el mismo recorrido en hora. A qué velocidad tendrá que ir? Ejercicio nº.- Para pintar una casa de plantas en 0 días se precisa de pintores. Si se quiere terminar en 6 días, de cuántos pintores habrá que disponer? Ejercicio nº.- Un recipiente se llena en h con un grifo que arroja l por minuto. Cuánto tiempo tardaría en llenarse con un grifo que arrojase 0' l por segundo? Ejercicio nº.- Un tractor siembra hectáreas en horas. Cuántas hectáreas sembrará en.000 minutos? Ejercicio nº.- En una granja de ovejas se realiza una tabla sobre nº de animales y kg de pienso que consumen. Completa los huecos: Ejercicio nº.-escribe estos porcentajes en forma de fracción y de número decimal: a 7% b % c 8% d 7% TRABAJO VERANO º ESO (06 Página
15 Ejercicio nº 6.- Si deseamos calcular el % de una cantidad se multiplica dicha cantidad por la fracción o por el número decimal. Ejemplo: Utilizando fracción % de Utilizando el número decimal o tanto por uno % de 00 0, 00 = 60 Resuelve utilizando las dos formas: a Averigua la cantidad que me descuentan de un libro que vale 0, si me rebajan el %. b Averigua los que sube un litro de aceite, si vale /litro y lo aumentan el 8%. Ejercicio nº 7.- Por un pantalón que marcaba 00, he pagado 80. Qué % me han descontado? Ejercicio nº 8.- Completa la tabla sobre disminuciones porcentuales: Disminuciones % Cantidades % disminuido Resultado 80 0% kg 7%.00 km 6% Ejercicio nº.- Compro un ordenador cuyo precio de venta al público es de.87 euros. Si por pagar al contado me descuentan un 6%, Cuánto tengo que pagar por el ordenador? Ejercicio nº 0.- El número de alumnos de un instituto es 6. El % de los alumnos del instituto son chicas. Cuál es el porcentaje de chicos? Cuántos chicos y chicas hay en el instituto? Ejercicio nº.- Juan Pedro compra un televisor que tiene marcado un precio de 6 euros. Si le hacen un descuento de un %, cuánto tiene que pagar Juan Pedro por el televisor? Ejercicio nº.- Una bicicleta de montaña cuesta 0, pero en la tienda hacen una rebaja del 0%, Cuánto pagará por la bicicleta finalmente? Ejercicio nº.- Un ordenador cuesta 00. Aparte hay que aplicarle un 7% de IVA. Cuánto costará el ordenador? TRABAJO VERANO º ESO (06 Página
16 ÁLGEBRA Los problemas deben contener: Datos, Identificación de las incógnitas, Planteamiento y Resolución, respondiendo a lo que se pregunte, no vale con indicar un número como solución del problema. Ejercicio nº.- Traduce a lenguaje algebraico los siguientes enunciados: a El cuádruplo de un número b El doble de un número menos cuatro unidades c El número anterior a un número n d El número posterior a un número n e El cuadrado de un número aumentado en unidades f El cociente de dos números g El producto de un número y la mitad de otro número h El triple del resultado de sumarle unidades a un número i La mitad del resultado de réstale unidades a un número Ejercicio nº.- Completa la siguiente tabla: Monomios x x x x 7x Coeficientes Parte literal Grado Ejercicio nº.- Calcula la suma de los siguientes monomios e indica los casos en los que no es posible. a x x b x y x y c ax ax x ax d e, x y, 8x Ejercicio nº.- Realiza las siguientes operaciones. Recuerda que sólo se pueden sumar o restar monomios semejantes. a - 7x + x - + x - x +x - = b x y - xy + - xy + - x y = Ejercicio nº.- La resta de los siguientes monomios: x - x es: a x b x c - x d No se pueden restar. TRABAJO VERANO º ESO (06 Página 6 y
17 Ejercicio nº 6.- Halla el resultado cuando sea posible x + x = 6x - x = x + x = -x + x = -8x x = x + x = x 8x = x + x = x x = 8x x = Ejercicio nº 7.- Reduce las siguientes expresiones x x + x x = x 7x + x x + x x = x x x = x x x + x = Ejercicio nº 8.- Calcula el resultado x. x = x. x = x. x = x 7. = 8x. x = x. 6 = Ejercicio nº.- Calcula el resultado de las siguientes operaciones con monomios x + x = x + x = x + 6x = 8x + x = x + x = x + x = 6x + x + x = x + x + x = x + 8x + x = 6x - x = 8x - x = x - x = x - 8x = x - 6x = x - x = x - x = 7x - 0x = x - x = x + 6x - x = x - x - x = x - x - x = x. x = x. x = x. x = a. a = a. 6a = b 6. b = TRABAJO VERANO º ESO (06 Página 7
18 x + 7x = x + x = x + 7x = x + 0x = x + x = x + x = x + x + 6x = x + x + x = x + x + 6x = 7x - x = x - x = 0x - x = x - x = x - x = x - 7x = 8x - x = 7x - x = x - 7x = x + x - 6x = x - 7x - x = x - x x = x. x = x. 6x = x. x = a. 6a = a. a 6 = b 6. b = Ejercicio nº0.- Resuelve estas ecuaciones: x a x b (x 0 = x c (x 6 0 = (x d (x 6 (x = (x Ejercicio nº.- Qué número hay que sumar a para obtener 7?. Ejercicio nº.- Averigua un número, sabiendo que si a su triple se le restan 0 unidades se obtiene el número aumentado en unidades. Ejercicio nº.- Se multiplica por al resultado de disminuir un número en unidades, de modo que da. De qué número se trata?. Ejercicio nº.- Halla dos números sabiendo que uno de ellos es el doble del otro, y que entre los dos suman. Ejercicio nº.- Un lápiz y un bolígrafo valen juntos 7. Cuánto vale cada uno si el bolígrafo vale 7 más que el lápiz?. Ejercicio nº 6.-Resuelve las siguientes ecuaciones: a x x 6 b 8x 7 x 8x c x x x 7 d 7 x x x 0 e x 0 6 x f x 6 x x g x x x h x 7x x 6x x i x x 7 x x j 8 x 6x x 7 x Ejercicio nº 7.- Halla el lado de un triángulo equilátero si su perímetro es 7 m. Ejercicio nº 8.- Calcula lo que miden los lados de un triángulo cuyo perímetro es de 8 cm, si sabemos que el segundo lado es el doble que el primero, y el tercer lado cm menos que el segundo. TRABAJO VERANO º ESO (06 Página 8
19 Ejercicio nº.- Halla las dimensiones (cuánto mide cada lado de un rectángulo, si su perímetro es de 0 m y la base mide 7 m más que la altura. Ejercicio nº 0.- Nerea se sube a una báscula junto con sus dos hijos (Ricardo y Juan y marca 87 kg. Averigua el peso de cada uno si sabemos que Ricardo pesa kg más que Juan y Nerea el doble que Juan y Ricardo juntos. Ejercicio nº.- Dos números enteros consecutivos suman. Cuáles son?. Ejercicio nº.- Di tres números consecutivos tales que el mayor es el doble del pequeño. Ejercicio nº.- La suma de tres números pares consecutivos es 7. Calcula dichos números. Ejercicio nº.- Al sumar tres números impares consecutivos obtenemos. Hállalos. Ejercicio nº.- En una reunión se sabe que hay el triple de mujeres que de hombres, y cuatro veces más niños que hombres. Cuántos hombres, mujeres y niños hay?. Ejercicio nº 6.- En un cesto hay 00 piezas de fruta. Se sabe que hay veces más naranjas que manzanas y el doble de peras que de manzanas y naranjas juntas. Cuántas frutas hay de cada clase? Ejercicio nº 7.- Un padre tiene 6 años y su hijo 7. Dentro de cuánto tiempo será la edad del padre el doble de la de su hijo? Ejercicio nº 8.- En una clase los aprobados son más que los suspensos. Si son un total de alumnos en la clase, cuántos aprobados y cuántos suspensos hay? Ejercicio nº.- Por tres kilos de naranjas y dos de peras, he pagado 6,0. A cómo está el kilo de cada una de esas frutas, si el de peras es veinte céntimos más caro que el de naranjas?. Ejercicio nº 0.- En una ferretería se venden clavos en cajas de tres tamaños diferentes. La caja grande contiene el doble de unidades que la mediana, y esta, el doble que la pequeña. Si compras una caja de cada tamaño, te llevas 0 unidades. Cuántos clavos tiene cada caja?. TRABAJO VERANO º ESO (06 Página
DIVIDENDO DIVISOR COCIENTE RESTO
 TEMA 1. NÚMEROS NATURALES 1. Realiza las siguientes operaciones combinadas: 20 460 25 418 256 27 5 16 60 54 :9 6 4 7 (8 4) 15: 5 ( 7 2) 4 (4 6) : 84 5 (6 : 2 5) 4 10 : 5 2. Completa la tabla calculando
TEMA 1. NÚMEROS NATURALES 1. Realiza las siguientes operaciones combinadas: 20 460 25 418 256 27 5 16 60 54 :9 6 4 7 (8 4) 15: 5 ( 7 2) 4 (4 6) : 84 5 (6 : 2 5) 4 10 : 5 2. Completa la tabla calculando
MATEMÁTICAS 2º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: Ejercicio nº 2.-
 MATEMÁTICAS º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: 5 6 1, 45 7 19 4 5, 5 1 4 9 Ejercicio nº.- Sitúa cada número (entero o natural) en el conjunto que
MATEMÁTICAS º ESO ENTEROS Y DIVISIBILIDAD. Ejercicio nº 1.- Rodea con un círculo los números enteros: 5 6 1, 45 7 19 4 5, 5 1 4 9 Ejercicio nº.- Sitúa cada número (entero o natural) en el conjunto que
EJERCICIOS RECUPERACIÓN MATEMÁTICAS 2º ESO
 NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
2º. Rellena los huecos que faltan y determina la constante de proporcionalidad:
 TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO ª EVALUACIÓN CURSO: 3º ESO PROPORCIONALIDAD NUMÉRICA 1º. Busca los valores para que las siguientes proporciones sean ciertas:... 0 45 5 45 5............,...
TRABAJO DE RECUPERACIÓN DE MATEMÁTICAS PENDIENTES DE º ESO ª EVALUACIÓN CURSO: 3º ESO PROPORCIONALIDAD NUMÉRICA 1º. Busca los valores para que las siguientes proporciones sean ciertas:... 0 45 5 45 5............,...
Cuadernillo 1. Actividades a realizar para la superación de la materia pendiente: Matemáticas 1º ESO
 Cuadernillo Actividades a realizar para la superación de la materia pendiente Matemáticas º ESO UNIDAD NÚMEROS NATURALES Actividad Calcula el cuadrado de los números de la siguiente tabla Números 0 8 Cuadrados
Cuadernillo Actividades a realizar para la superación de la materia pendiente Matemáticas º ESO UNIDAD NÚMEROS NATURALES Actividad Calcula el cuadrado de los números de la siguiente tabla Números 0 8 Cuadrados
Cuadernillo 1. Actividades a realizar para la superación de la materia pendiente:
 Cuadernillo 1 Actividades a realizar para la superación de la materia pendiente: Matemáticas 1º ESO Recuerda que: Habrá 2 cuadernillos cada uno con la mitad de las unidades que se trabajaron en el curso
Cuadernillo 1 Actividades a realizar para la superación de la materia pendiente: Matemáticas 1º ESO Recuerda que: Habrá 2 cuadernillos cada uno con la mitad de las unidades que se trabajaron en el curso
TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS...
 TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS... 1ª Realizar las siguientes divisiones: a) 345,83 : 6 = b) 23 : 0, 5 = c) 0,18 : 0,12 = d) 34,15 : 5 = e) 2,16 : 1,8 = f) 13,02 : 0,25=
TRABAJO DE SEPTIEMBRE DE MATEMÁTICAS 2º ESO... NOMBRE Y APELLIDOS... 1ª Realizar las siguientes divisiones: a) 345,83 : 6 = b) 23 : 0, 5 = c) 0,18 : 0,12 = d) 34,15 : 5 = e) 2,16 : 1,8 = f) 13,02 : 0,25=
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO)
 PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO) 1 NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación correspondiente
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO) 1 NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación correspondiente
4.- Realiza las siguientes operaciones: a) 3,25 (8,23 4,2)
 MATEMÁTICAS.- PRIMER CURSO ESO. Repasa durante el verano estos objetivos, realiza estos ejercicios y preséntalos el día del examen de recuperación en Septiembre. La prueba de Septiembre serán ejercicios
MATEMÁTICAS.- PRIMER CURSO ESO. Repasa durante el verano estos objetivos, realiza estos ejercicios y preséntalos el día del examen de recuperación en Septiembre. La prueba de Septiembre serán ejercicios
a) 45,9 12, 1 = b) 9,1 6,9 = c) 246,7 8,9 = 2.- Resuelve el ejercicio anterior como resta de fracciones de igual denominador.
 REFUERZO 2 1.- Resta los siguientes números decimales:, 12, 1 = b),1 6, = c) 26,7 8, = 2.- Resuelve el ejercicio anterior como resta de fracciones de igual denominador..- Resuelve el siguiente ejercicio
REFUERZO 2 1.- Resta los siguientes números decimales:, 12, 1 = b),1 6, = c) 26,7 8, = 2.- Resuelve el ejercicio anterior como resta de fracciones de igual denominador..- Resuelve el siguiente ejercicio
Departamento de Matemáticas Actividades de recuperación 2º ESO (Pendientes 1º)
 FICHA 1 NÚMEROS I Fecha límite de entrega: 17 de octubre 1. Rellena el cuadro: Nº en cifra Nº en letra 2.345.018 Ocho millardos 310.023 Dos billones, mil doscientos 2. Escribe en número o en letra: Tres
FICHA 1 NÚMEROS I Fecha límite de entrega: 17 de octubre 1. Rellena el cuadro: Nº en cifra Nº en letra 2.345.018 Ocho millardos 310.023 Dos billones, mil doscientos 2. Escribe en número o en letra: Tres
ECUACIONES E INECUACIONES
 ECUACIONES E INECUACIONES 1.- Escribe las expresiones algebraicas que representan los siguientes enunciados: a) Número de ruedas necesarias para fabricar x coches. b) Número de céntimos para cambiar x
ECUACIONES E INECUACIONES 1.- Escribe las expresiones algebraicas que representan los siguientes enunciados: a) Número de ruedas necesarias para fabricar x coches. b) Número de céntimos para cambiar x
TEMA 05 - EXPRESIONES ALGEBRAICAS
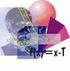 º ESO TEMA 05 - EXPRESIONES ALGEBRAICAS 1º. Indica las expresiones algebraicas correspondientes a los siguientes enunciados, utilizando una sola letra (x): a) El siguiente de un número, más tres unidades.
º ESO TEMA 05 - EXPRESIONES ALGEBRAICAS 1º. Indica las expresiones algebraicas correspondientes a los siguientes enunciados, utilizando una sola letra (x): a) El siguiente de un número, más tres unidades.
EJERCICIOS DE RECUPERACIÓN
 EJERCICIOS DE RECUPERACIÓN EJERCICIOS DE RECUPERACIÓN DE LA 1ª EVALUACIÓN Números Enteros 1º. Haz las siguientes sumas: a) (+10) + (+5) = b) (+7) + (+6) = c) ( 4) + ( 6) = d) ( 10) + ( 5) = e) ( 7) + (
EJERCICIOS DE RECUPERACIÓN EJERCICIOS DE RECUPERACIÓN DE LA 1ª EVALUACIÓN Números Enteros 1º. Haz las siguientes sumas: a) (+10) + (+5) = b) (+7) + (+6) = c) ( 4) + ( 6) = d) ( 10) + ( 5) = e) ( 7) + (
IDENTIFICAR LA RELACIÓN DE PROPORCIONALIDAD ENTRE MAGNITUDES
 OBJETIVO IDENTIICAR LA RELACIÓN DE PROPORCIONALIDAD ENTRE MAGNITUDES NOMBRE: CURSO: ECHA: Para multiplicar un número por 0, 00,.000... se desplaza la coma a la derecha tantos lugares como ceros tenga la
OBJETIVO IDENTIICAR LA RELACIÓN DE PROPORCIONALIDAD ENTRE MAGNITUDES NOMBRE: CURSO: ECHA: Para multiplicar un número por 0, 00,.000... se desplaza la coma a la derecha tantos lugares como ceros tenga la
Expresiones algebraicas
 Expresiones algebraicas Contenidos 1. Lenguaje algebraico Expresiones algebraicas Traducción de enunciados Valor numérico 2. Monomios Características Suma y resta Producto 3. Ecuaciones Solución de una
Expresiones algebraicas Contenidos 1. Lenguaje algebraico Expresiones algebraicas Traducción de enunciados Valor numérico 2. Monomios Características Suma y resta Producto 3. Ecuaciones Solución de una
2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6
 ACTIVIDADES TEMA 1 1.- Escribe con palabras los siguientes números: 1.034.456: 20.004.080: 100.060.201: 35.001.001: 2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6 3.- Ordena de
ACTIVIDADES TEMA 1 1.- Escribe con palabras los siguientes números: 1.034.456: 20.004.080: 100.060.201: 35.001.001: 2.- Representa los siguientes números en la recta númerica: 2,5,3,5,8,6 3.- Ordena de
c) Es 91 múltiplo de 7? y 7 divisor de 91?
 UNIDAD 1: NÚMEROS NATURALES (1 pto) Ejercicio nº 1.- a) Escribe los diez primeros múltiplos de 15: IES EL CORONIL b) Todos los divisores del 60 c) Es 91 múltiplo de 7? y 7 divisor de 91? (1 pto) Ejercicio
UNIDAD 1: NÚMEROS NATURALES (1 pto) Ejercicio nº 1.- a) Escribe los diez primeros múltiplos de 15: IES EL CORONIL b) Todos los divisores del 60 c) Es 91 múltiplo de 7? y 7 divisor de 91? (1 pto) Ejercicio
Expresiones algebraicas (1º ESO)
 Epresiones algebraicas (º ESO) Lenguaje numérico y lenguaje algebraico. El lenguaje en el que intervienen números y signos de operaciones se denomina lenguaje numérico. Lenguaje usual Lenguaje numérico
Epresiones algebraicas (º ESO) Lenguaje numérico y lenguaje algebraico. El lenguaje en el que intervienen números y signos de operaciones se denomina lenguaje numérico. Lenguaje usual Lenguaje numérico
PRUEBAS EXTRAORDINARIAS CURSO 2015/16 DEPARTAMENTO DIDÁCTICO: MATEMÁTICAS MATERIA: MATEMÁTICAS NIVEL: 1º ESO
 PRUEBAS EXTRAORDINARIAS CURSO 2015/16 DEPARTAMENTO DIDÁCTICO: MATEMÁTICAS MATERIA: MATEMÁTICAS NIVEL: 1º ESO CONTENIDOS MÍNIMOS Unidad 1: Números Naturales 1. Criterios de divisibilidad. 2. Descomposición
PRUEBAS EXTRAORDINARIAS CURSO 2015/16 DEPARTAMENTO DIDÁCTICO: MATEMÁTICAS MATERIA: MATEMÁTICAS NIVEL: 1º ESO CONTENIDOS MÍNIMOS Unidad 1: Números Naturales 1. Criterios de divisibilidad. 2. Descomposición
COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS. 1º ESO
 COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS. º ESO RELACIÓN 5: ALGEBRA Lenguaje algebraico, monomios polinomios EXPRESIÓN ALGEBRAICA Es un conjunto de números letras
COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS. º ESO RELACIÓN 5: ALGEBRA Lenguaje algebraico, monomios polinomios EXPRESIÓN ALGEBRAICA Es un conjunto de números letras
1) Calcula : a) b) 5+4 (7-1) c) 3-6:3 2 d) : ( 2) 8 ( 8) e) 2 3 [4 5 (3 2)] f) (6-2) g) 2-10:5 2 h)
![1) Calcula : a) b) 5+4 (7-1) c) 3-6:3 2 d) : ( 2) 8 ( 8) e) 2 3 [4 5 (3 2)] f) (6-2) g) 2-10:5 2 h) 1) Calcula : a) b) 5+4 (7-1) c) 3-6:3 2 d) : ( 2) 8 ( 8) e) 2 3 [4 5 (3 2)] f) (6-2) g) 2-10:5 2 h)](/thumbs/52/30004136.jpg) 1) Calcula : a) 2 6-2 2+3 5 b) 5+4 (7-1) c) 3-6:3 2 d) 4 + 32 : ( 2) 8 ( 8) e) 2 3 [4 5 (3 2)] f) 2 + 3 (6-2) g) 2-10:5 2 h) 22-15+3 i) 22-(15+3) j) 30-18-8 k) 30-(18-8) l) 45-30+15 m) 45-(30+15) n) 2
1) Calcula : a) 2 6-2 2+3 5 b) 5+4 (7-1) c) 3-6:3 2 d) 4 + 32 : ( 2) 8 ( 8) e) 2 3 [4 5 (3 2)] f) 2 + 3 (6-2) g) 2-10:5 2 h) 22-15+3 i) 22-(15+3) j) 30-18-8 k) 30-(18-8) l) 45-30+15 m) 45-(30+15) n) 2
1ª EVALUACIÓN. 1. Resuelve las siguientes operaciones combinadas. 2. Resuelve las siguientes operaciones combinadas
 1ª EVALUACIÓN TEMA: NÚMEROS NATURALES 1. Resuelve las siguientes operaciones combinadas 2. Resuelve las siguientes operaciones combinadas 3. Un camión de reparto transporta 15 cajas de refresco de naranja
1ª EVALUACIÓN TEMA: NÚMEROS NATURALES 1. Resuelve las siguientes operaciones combinadas 2. Resuelve las siguientes operaciones combinadas 3. Un camión de reparto transporta 15 cajas de refresco de naranja
5. El cociente de la división de dos números naturales vale 8 y el resto 66. Halla estos números, sabiendo que uno excede al otro en 570 unidades.
 PROBLEMAS ECUACIONES Y SISTEMAS 1. Una suma de 375 está formada por un mismo número de billetes de 10 que de 5 Hallar el número de billetes de cada clase. 2. En tres meses una fábrica de latas de sardinas
PROBLEMAS ECUACIONES Y SISTEMAS 1. Una suma de 375 está formada por un mismo número de billetes de 10 que de 5 Hallar el número de billetes de cada clase. 2. En tres meses una fábrica de latas de sardinas
MATEMÁTICAS-EJERCICIOS DE RECUPERACION PENDIENTES 1º E.S.O. 2º BLOQUE. Nombre y Apellidos:
 TEMA 7. SISTEMA METRICO DECIMAL 1. 2. Para pasar de una medida de superficie inferior a otra inmediatamente superior: a) Se multiplica el resultado de la medida por 100. b) Se multiplica el resultado de
TEMA 7. SISTEMA METRICO DECIMAL 1. 2. Para pasar de una medida de superficie inferior a otra inmediatamente superior: a) Se multiplica el resultado de la medida por 100. b) Se multiplica el resultado de
FICHAS REPASO 3º ESO. Para restar números enteros, se suma al minuendo el opuesto del sustraendo y después se aplican las reglas de la suma.
 FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
FICHAS REPASO º ESO OPERACIONES CON NÚMEROS ENTEROS El valor absoluto de un número entero es el número natural que resulta al prescindir del signo. Por ejemplo, el valor absoluto de es y el valor absoluto
Curso º ESO. UNIDADES 6 Y 7: EXPRESIONES ALGEBRAICAS Y ECUACIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas de Morón
 2º ESO UNIDADES 6 Y 7: EXPRESIONES ALGEBRAICAS Y ECUACIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas de Morón OBJETIVOS CONTENIDOS PROCEDIMIENTOS Lenguaje algebraico. Normas y Traducción
2º ESO UNIDADES 6 Y 7: EXPRESIONES ALGEBRAICAS Y ECUACIONES Departamento de Matemáticas IES Fray Bartolomé de las Casas de Morón OBJETIVOS CONTENIDOS PROCEDIMIENTOS Lenguaje algebraico. Normas y Traducción
TEMA 1. NÚMEROS NATURALES Y POTENCIAS
 TEMA 1. NÚMEROS NATURALES Y POTENCIAS 1. Escribe como se leen los siguientes números naturales: a) 15.684.985 = b) 59.800.197.400 = c).500.01.01 = d) 180.00.505 = e) 68.967 = f) 14.14.15.65 = g) 1.000.001.001.001=
TEMA 1. NÚMEROS NATURALES Y POTENCIAS 1. Escribe como se leen los siguientes números naturales: a) 15.684.985 = b) 59.800.197.400 = c).500.01.01 = d) 180.00.505 = e) 68.967 = f) 14.14.15.65 = g) 1.000.001.001.001=
RESOLUCIÓN ECUACIONES LINEALES
 Nombre: RESOLUCIÓN ECUACIONES LINEALES 1.- Resuelve las siguientes ecuaciones por tanteo: a) 6 x = 1 b) 8 + x = 3 c) 2x = 10 d) x + 2 = 6 e) 6 x = 6 f) x 1 = 3 2.- Calcula el valor de x por tanteo: a)
Nombre: RESOLUCIÓN ECUACIONES LINEALES 1.- Resuelve las siguientes ecuaciones por tanteo: a) 6 x = 1 b) 8 + x = 3 c) 2x = 10 d) x + 2 = 6 e) 6 x = 6 f) x 1 = 3 2.- Calcula el valor de x por tanteo: a)
COLEGIO INTERNACIONAL TORREQUEBRADA. Departamento de matemáticas. CUADERNO DE VERANO MATEMÁTICAS 1º ESO ALUMNO: Cuaderno de Verano Matemáticas 1ºESO
 CUADERNO DE VERANO MATEMÁTICAS 1º ESO ALUMNO: OPERACIONES COMBINADAS: En estas operaciones en caso que haya paréntesis o corchetes, deberás realizar primero las operaciones indicadas dentro de ellos. Seguirás
CUADERNO DE VERANO MATEMÁTICAS 1º ESO ALUMNO: OPERACIONES COMBINADAS: En estas operaciones en caso que haya paréntesis o corchetes, deberás realizar primero las operaciones indicadas dentro de ellos. Seguirás
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Trabajo de Matemáticas AMPLIACIÓN 3º ESO
 Trabajo de Matemáticas AMPLIACIÓN º ESO ACTIVIDADES DE AMPLIACIÓN TEMA : NÚMEROS FRACCIONARIOS O RACIONALES Problema nº Un grifo tarda en llenar un depósito horas y otro tarda en llenar el mismo depósito
Trabajo de Matemáticas AMPLIACIÓN º ESO ACTIVIDADES DE AMPLIACIÓN TEMA : NÚMEROS FRACCIONARIOS O RACIONALES Problema nº Un grifo tarda en llenar un depósito horas y otro tarda en llenar el mismo depósito
EJERCICIOS DE VERANO MATEMÁTICAS 1º ESO
 EJERCICIOS DE VERANO MATEMÁTICAS 1º ESO NOTA IMPORTANTE: Estos ejercicios deben ser entregados en septiembre, el mismo día del examen de recuperación de Matemáticas. No se utilizarán estas hojas para su
EJERCICIOS DE VERANO MATEMÁTICAS 1º ESO NOTA IMPORTANTE: Estos ejercicios deben ser entregados en septiembre, el mismo día del examen de recuperación de Matemáticas. No se utilizarán estas hojas para su
2 Quita paréntesis y calcula. a) (+5) ( 3) (+8) + ( 4) b) ( 7) (+5) + ( 6) + (+4) c) +( 9) (+13) ( 11) + (+5) d) (+8) + ( 3) ( 15) (+6) (+2)
 Matemáticas pendientes 2º E.S.O. Los números enteros suma y resta de números enteros 1 Calcula. a) 5 8 4 + 3 6 + 9 b) 10 11 + 7 13 + 15 6 c) 9 2 7 11 + 3 + 18 10 d) 7 15 + 8 + 10 9 6 + 11 2 Quita paréntesis
Matemáticas pendientes 2º E.S.O. Los números enteros suma y resta de números enteros 1 Calcula. a) 5 8 4 + 3 6 + 9 b) 10 11 + 7 13 + 15 6 c) 9 2 7 11 + 3 + 18 10 d) 7 15 + 8 + 10 9 6 + 11 2 Quita paréntesis
Números racionales e irracionales
 Números racionales e irracionales. Divisibilidad Calcula mentalmente: a) M.C.D. (, 8) b) M.C.D. (, 8) c) M.C.D. (, 9, ) d) m.c.m. (, ) e) m.c.m. (, 9) f ) m.c.m. (,, ) P I E N S A Y C A L C U L A a) b)
Números racionales e irracionales. Divisibilidad Calcula mentalmente: a) M.C.D. (, 8) b) M.C.D. (, 8) c) M.C.D. (, 9, ) d) m.c.m. (, ) e) m.c.m. (, 9) f ) m.c.m. (,, ) P I E N S A Y C A L C U L A a) b)
Alumnos pendientes 1º ESO pag.1. Dpto. de Matemáticas.- I.E.S. María Moliner
 Alumnos pendientes 1º ESO pag.1 Alumnos pendientes 1º ESO pag.2 Alumnos pendientes 1º ESO pag.3 DIVISIBILIDAD Escribe la palabra múltiplo o divisor según corresponda: El 4 es de 24 a. El 25 es de 5 b.
Alumnos pendientes 1º ESO pag.1 Alumnos pendientes 1º ESO pag.2 Alumnos pendientes 1º ESO pag.3 DIVISIBILIDAD Escribe la palabra múltiplo o divisor según corresponda: El 4 es de 24 a. El 25 es de 5 b.
FRACCIONES. a) c) e) 3. - Escribe las fracciones: - Catorce diecinueveavos:... - Ocho onceavos:...
 FRACCIONES. - Observa el gráfico y responde: a) Cuántos cuadrados ves? b) Cuántos cuadrados negros hay? c) Qué fracción del conjunto representan los cuadrados negros? d) Qué fracción del conjunto representan
FRACCIONES. - Observa el gráfico y responde: a) Cuántos cuadrados ves? b) Cuántos cuadrados negros hay? c) Qué fracción del conjunto representan los cuadrados negros? d) Qué fracción del conjunto representan
2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I. 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es?
 2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I PÁGINA 142 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es? 3x 8 = 25 Solución: 11 Si a cierta cantidad le restas su tercera parte y le sumas
2º ESO - PROBLEMAS UNIDAD 6: ECUACIONES I PÁGINA 142 1 ) Si al triple de un número le restas 8, obtienes 25. Qué número es? 3x 8 = 25 Solución: 11 Si a cierta cantidad le restas su tercera parte y le sumas
ALUMNOS DE 3ºESO QUE TIENEN SUSPENSAS LAS MATEMÁTICAS DE 2ºESO
 ALUMNOS DE ºESO QUE TIENEN SUSPENSAS LAS MATEMÁTICAS DE ºESO Departamento de Matemáticas Curso 015/016 ALUMNOS DE ºESO QUE TIENEN SUSPENSAS LAS MATEMÁTICAS DE ºESO Fecha límite de entrega: 0 de enero de
ALUMNOS DE ºESO QUE TIENEN SUSPENSAS LAS MATEMÁTICAS DE ºESO Departamento de Matemáticas Curso 015/016 ALUMNOS DE ºESO QUE TIENEN SUSPENSAS LAS MATEMÁTICAS DE ºESO Fecha límite de entrega: 0 de enero de
EJERCICIOS PARA NAVIDAD (RECUPERACIÓN PRIMERA EVALUACIÓN). CURSO: Fecha de entrega: Viernes. 14 de enero. Fecha de examen: Viernes, 21 de enero.
 º E.S.O. MATEMÁTICAS I.E.S. LOSADA EJERCICIOS PARA NAVIDAD (RECUPERACIÓN PRIMERA EVALUACIÓN). CURSO: 10-11 Fecha de entrega: Viernes. 1 de enero. Fecha de examen: Viernes 1 de enero. Alumno/a:. Grupo:
º E.S.O. MATEMÁTICAS I.E.S. LOSADA EJERCICIOS PARA NAVIDAD (RECUPERACIÓN PRIMERA EVALUACIÓN). CURSO: 10-11 Fecha de entrega: Viernes. 1 de enero. Fecha de examen: Viernes 1 de enero. Alumno/a:. Grupo:
1. ESQUEMA - RESUMEN Página EJERCICIOS DE INICIACIÓN Página EJERCICIOS DE DESARROLLO Página EJERCICIOS DE REFUERZO Página 25
 1. ESQUEMA - RESUMEN Página. EJERCICIOS DE INICIACIÓN Página 6. EJERCICIOS DE DESARROLLO Página 17 5. EJERCICIOS DE REFUERZO Página 5 1 1. ESQUEMA - RESUMEN Página 1.1. EXPRESIONES ALGEBRAICAS. 1.. VALOR
1. ESQUEMA - RESUMEN Página. EJERCICIOS DE INICIACIÓN Página 6. EJERCICIOS DE DESARROLLO Página 17 5. EJERCICIOS DE REFUERZO Página 5 1 1. ESQUEMA - RESUMEN Página 1.1. EXPRESIONES ALGEBRAICAS. 1.. VALOR
REFUERZO - MATEMÁTICAS OBJETIVOS MÍNIMOS
 OBJETIVOS MÍNIMOS Realizar operaciones con números enteros [ ] a) 18 ( 8 ) b) [ 1 ( 1 ) ] c) [ ( 8 9) ] 7 ( ) [ ] Realizar operaciones con fracciones 7 1 a) 1 1 b) c) : 1 7 7 1 1 d) : 1 1 e) 1 : 10 1 f)
OBJETIVOS MÍNIMOS Realizar operaciones con números enteros [ ] a) 18 ( 8 ) b) [ 1 ( 1 ) ] c) [ ( 8 9) ] 7 ( ) [ ] Realizar operaciones con fracciones 7 1 a) 1 1 b) c) : 1 7 7 1 1 d) : 1 1 e) 1 : 10 1 f)
TRABAJO DE MATEMÁTICAS. PENDIENTES DE 1º ESO. (2ª parte)
 TRABAJO DE MATEMÁTICAS PENDIENTES DE 1º ESO. (2ª parte) NÚMEROS RACIONALES REDUCCIÓN DE FRACCIONES AL MISMO DENOMINADOR Para reducir varias fracciones al mismo denominador se siguen los siguientes pasos:
TRABAJO DE MATEMÁTICAS PENDIENTES DE 1º ESO. (2ª parte) NÚMEROS RACIONALES REDUCCIÓN DE FRACCIONES AL MISMO DENOMINADOR Para reducir varias fracciones al mismo denominador se siguen los siguientes pasos:
2. Subraya los múltiplos de 4: Subraya los múltiplos de 2:
 TEMA 2. DIVISIBILIDAD Se dice que entre dos números hay una relación de divisibilidad cuando al dividir el mayor de ellos entre el menor la división es exacta. Se dice entonces que el número mayor es múltiplo
TEMA 2. DIVISIBILIDAD Se dice que entre dos números hay una relación de divisibilidad cuando al dividir el mayor de ellos entre el menor la división es exacta. Se dice entonces que el número mayor es múltiplo
1. a) Escribe los primeros cinco múltiplos de 16 que estén entre 75 y 150
 ACTIVIDADES DE PENDIENTES DE 2º eso. UNIDADES 1, 2, 3, 4 1. a) Escribe los primeros cinco múltiplos de 16 que estén entre 75 y 150 b) Escribe todos los divisores de 54 c) Escribe todos los divisores de
ACTIVIDADES DE PENDIENTES DE 2º eso. UNIDADES 1, 2, 3, 4 1. a) Escribe los primeros cinco múltiplos de 16 que estén entre 75 y 150 b) Escribe todos los divisores de 54 c) Escribe todos los divisores de
Pendientes 3 ESO Segunda Evaluación
 Pendientes 3 ESO Segunda Evaluación Polinomios 1 Efectúa las siguientes operaciones con monomios: 1 x 3 5x 3 = 3x x + 7x = 3 (x 3 ) (5x 3 ) = (x 3 y ) (5x 3 yz ) = 5 (1x 3 ) : (x) = 6 (18x 6 y z 5 ) :
Pendientes 3 ESO Segunda Evaluación Polinomios 1 Efectúa las siguientes operaciones con monomios: 1 x 3 5x 3 = 3x x + 7x = 3 (x 3 ) (5x 3 ) = (x 3 y ) (5x 3 yz ) = 5 (1x 3 ) : (x) = 6 (18x 6 y z 5 ) :
1. Responde a las preguntas:
 . Responde a las preguntas: a) Cuántas unidades de mil hay en 400 centenas? b) Cuántas centenas de millar hay en tres millones y medio? c) Cuántas decenas hay en 0 centenas? d) Cuántas unidades de mil
. Responde a las preguntas: a) Cuántas unidades de mil hay en 400 centenas? b) Cuántas centenas de millar hay en tres millones y medio? c) Cuántas decenas hay en 0 centenas? d) Cuántas unidades de mil
SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD
 SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD Ejercicio nº 1.- Subraya los pares de magnitudes que sean proporcionales: a) El peso de las naranjas compradas y el precio pagado por ellas. b) La estatura
SOLUCIONES MINIMOS 2º ESO TEMA 3 PROPORCIONALIDAD Ejercicio nº 1.- Subraya los pares de magnitudes que sean proporcionales: a) El peso de las naranjas compradas y el precio pagado por ellas. b) La estatura
Matemáticas 1º ESO TRABAJO VERANO Nombre y apellidos: CONTENIDOS PARA LA RECUPERACIÓN DE ÁREA EN SEPTIEMBRE
 Matemáticas 1º ESO TRABAJO VERANO 201 Nombre y apellidos: CONTENIDOS PARA LA RECUPERACIÓN DE ÁREA EN SEPTIEMBRE NÚMEROS REALES POTENCIAS Y RAÍCES POLINOMIOS Y FRACCIONES ALGEBRAICAS ECUACIONES. MAGNITUDES
Matemáticas 1º ESO TRABAJO VERANO 201 Nombre y apellidos: CONTENIDOS PARA LA RECUPERACIÓN DE ÁREA EN SEPTIEMBRE NÚMEROS REALES POTENCIAS Y RAÍCES POLINOMIOS Y FRACCIONES ALGEBRAICAS ECUACIONES. MAGNITUDES
MATEMÁTICAS 6º PRIMARIA
 CUADERNO DE ACTIVIDADES MATEMÁTICAS 6º PRIMARIA Nombre: Curso: 1 Descompón estos números. Fíjate en el ejemplo. 4.168 = 4 UM + 1 C + 6 D + 8 U 51.245 = 754.390 = 3.790.050 = 2 Rodea con rojo los múltiplos
CUADERNO DE ACTIVIDADES MATEMÁTICAS 6º PRIMARIA Nombre: Curso: 1 Descompón estos números. Fíjate en el ejemplo. 4.168 = 4 UM + 1 C + 6 D + 8 U 51.245 = 754.390 = 3.790.050 = 2 Rodea con rojo los múltiplos
EJERCICIOS DE REPASO DE MATEMÁTICAS 1º ESO
 EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO EJERCICIOS DE NÚMEROS NATURALES. ( + 7) + 0. ( 0 ). 6 + 7 + 8. 8 + 6 + ( 6 ) +. 6 ( 70 + 0) 600 6. : + 7 7. + 9 + 8 8. 7 ( ) 66 9. ( + 7) 8 7 0. + 6 0. + ( 9 7)
EJERCICIOS DE REPASO DE MATEMÁTICAS º ESO EJERCICIOS DE NÚMEROS NATURALES. ( + 7) + 0. ( 0 ). 6 + 7 + 8. 8 + 6 + ( 6 ) +. 6 ( 70 + 0) 600 6. : + 7 7. + 9 + 8 8. 7 ( ) 66 9. ( + 7) 8 7 0. + 6 0. + ( 9 7)
Tema 2. Divisibilidad 1º de Educación Secundaria Obligatoria
 Tema 2. Divisibilidad 1º de Educación Secundaria Obligatoria Contenidos 1. Múltiplos y divisores 1.1. Múltiplos y divisores 1.2. Propiedades de múltiplos y divisores 2. Números primos y compuestos 2.1.
Tema 2. Divisibilidad 1º de Educación Secundaria Obligatoria Contenidos 1. Múltiplos y divisores 1.1. Múltiplos y divisores 1.2. Propiedades de múltiplos y divisores 2. Números primos y compuestos 2.1.
5º lección TEMA 5.- LAS OPERACIONES CON FRACCIONES
 º lección TEMA.- LAS OPERACIONES CON FRACCIONES Para calcular la fracción de una cantidad, dividimos la cantidad entre el denominador y el resultado lo multiplicamos por el numerador. -. Calcula: Ejemplo
º lección TEMA.- LAS OPERACIONES CON FRACCIONES Para calcular la fracción de una cantidad, dividimos la cantidad entre el denominador y el resultado lo multiplicamos por el numerador. -. Calcula: Ejemplo
Actividades para preparar el examen de Proporcionalidad.
 Actividades para preparar el examen de Proporcionalidad. Departamento de Matemáticas del I.E.S. Salvador Serrano Segundo de ESO - Curso.0 -.0.- Contesta si son ciertas las siguientes afirmaciones:. a n
Actividades para preparar el examen de Proporcionalidad. Departamento de Matemáticas del I.E.S. Salvador Serrano Segundo de ESO - Curso.0 -.0.- Contesta si son ciertas las siguientes afirmaciones:. a n
CUADERNILLO RECUPERACIÓN PENDIENTES CURSO 2016/2017 MATEMÁTICAS 2º E.S.O.
 CUADERNILLO RECUPERACIÓN PENDIENTES CURSO 016/017 MATEMÁTICAS º E.S.O. 1ª EVALUACIÓN Tema 1: Números enteros. Divisibilidad. Tema : Fracciones. Tema : Números decimales. Tema 4: Sistema sexagesimal. Unidad
CUADERNILLO RECUPERACIÓN PENDIENTES CURSO 016/017 MATEMÁTICAS º E.S.O. 1ª EVALUACIÓN Tema 1: Números enteros. Divisibilidad. Tema : Fracciones. Tema : Números decimales. Tema 4: Sistema sexagesimal. Unidad
ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
 ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA Recordar: Una ecuación es una igualdad algebraica en la que aparecen letras (incógnitas) con valor desconocido. El grado de una ecuación viene dado por el eponente
ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA Recordar: Una ecuación es una igualdad algebraica en la que aparecen letras (incógnitas) con valor desconocido. El grado de una ecuación viene dado por el eponente
Lee y ordena estos números : : : :... Escribe el menor y mayor número de siete cifras significativas
 TEMA 1 - LOS NUMEROS Y LAS OPERACIONES Escribe los números siguientes: Medio millón:... Tres millones y medio:... Diez millones cien mil:... Cuatro millones cuatrocientos... Seis millones treinta mil:...
TEMA 1 - LOS NUMEROS Y LAS OPERACIONES Escribe los números siguientes: Medio millón:... Tres millones y medio:... Diez millones cien mil:... Cuatro millones cuatrocientos... Seis millones treinta mil:...
Actividades de refuerzo
 Actividades de refuerzo Matemáticas º E.S.O. ACTIVIDADES DE REFUERZO DE MATEMÁTICAS º E.S.O. Curso.0 Alumno/a: Curso: Grupo: I.E.S. ALVAREDA I.E,S. ALVAREDA Departamento de Matemáticas Junio.0 I.E.S. ALVAREDA
Actividades de refuerzo Matemáticas º E.S.O. ACTIVIDADES DE REFUERZO DE MATEMÁTICAS º E.S.O. Curso.0 Alumno/a: Curso: Grupo: I.E.S. ALVAREDA I.E,S. ALVAREDA Departamento de Matemáticas Junio.0 I.E.S. ALVAREDA
APRENDER MATEMÁTICAS TEMA 1 JUAN LUIS CHAMIZO BLÁZQUEZ - CARMEN GORDO CUEVAS PEDRO M. RIVERA LEBRATO 3
 TEMA 1 JUAN LUIS CHAMIZO BLÁZQUEZ - CARMEN GORDO CUEVAS PEDRO M. RIVERA LEBRATO 3 NÚMEROS NATURALES Los números naturales son los que sirven para contar. Los números naturales se representan de menor a
TEMA 1 JUAN LUIS CHAMIZO BLÁZQUEZ - CARMEN GORDO CUEVAS PEDRO M. RIVERA LEBRATO 3 NÚMEROS NATURALES Los números naturales son los que sirven para contar. Los números naturales se representan de menor a
COLEGIO INTERNACIONAL TORREQUEBRADA
 CUADERNO DE VERANO MATEMÁTICAS 2º ESO ALUMNO: LOS NÚMEROS ENTEROS CONTENIDOS. 1. Los números enteros 2. Valor absoluto de un número entero 3. Ordenación de números enteros 4. Representación de los números
CUADERNO DE VERANO MATEMÁTICAS 2º ESO ALUMNO: LOS NÚMEROS ENTEROS CONTENIDOS. 1. Los números enteros 2. Valor absoluto de un número entero 3. Ordenación de números enteros 4. Representación de los números
El producto de dos números es 4, y la suma de sus cuadrados 17. Cuáles son esos números?
 TEMA 4: INECUACIONES Y SISTEMAS SISTEMAS DE ECUACIONES NO LINEALES Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado. La resolución de estos sistemas se
TEMA 4: INECUACIONES Y SISTEMAS SISTEMAS DE ECUACIONES NO LINEALES Un sistema de ecuaciones es no lineal, cuando al menos una de sus ecuaciones no es de primer grado. La resolución de estos sistemas se
Profesor: Miguel Ángel Valverde. 1.- Teniendo en cuenta la jerarquía de las operaciones, calcula: (tema 1 libro texto)
 EJERCICIOS DE MATEMÁTICAS PARA 1º DE LA ESO. REPASO PARA EL VERANO 008 (Incluye ejercicios de ángulos, gráficas y funciones y geometría del plano y polígonos y cuerpos geométricos, que no se han dado en
EJERCICIOS DE MATEMÁTICAS PARA 1º DE LA ESO. REPASO PARA EL VERANO 008 (Incluye ejercicios de ángulos, gráficas y funciones y geometría del plano y polígonos y cuerpos geométricos, que no se han dado en
Ecuaciones de Primer Grado
 Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
UNITAT 1. ELS NOMBRES NATURALS.
 UNITAT 1. ELS NOMBRES NATURALS. 1. Escribe en tu cuaderno los siguientes números: a) Dos millones cuatrocientos mil b) Un millón, dos mil, cinco c) Tres mil, cuatro 2. Escribe en números romanos los siguientes
UNITAT 1. ELS NOMBRES NATURALS. 1. Escribe en tu cuaderno los siguientes números: a) Dos millones cuatrocientos mil b) Un millón, dos mil, cinco c) Tres mil, cuatro 2. Escribe en números romanos los siguientes
Ejercicios Pendientes Matemáticas 2º ESO Curso Números Enteros Los Números Enteros
 Los 1) 2) 1 3) 4) 5) 9) ) 2 11) 12) 16) 3 17) 18) 19) 4 20) 21) En qué orden se realizan las operaciones con números enteros Para resolver varias operaciones combinadas con números enteros, se debe seguir
Los 1) 2) 1 3) 4) 5) 9) ) 2 11) 12) 16) 3 17) 18) 19) 4 20) 21) En qué orden se realizan las operaciones con números enteros Para resolver varias operaciones combinadas con números enteros, se debe seguir
1. NÚMEROS NATURALES 2. POTENCIAS
 . NÚMEROS NATURALES. Aplica la propiedad distributiva y opera: a) 5 (9 5)= b) (8 5+4) 6= c) (9 6) = d) (9+4 0+) =. Opera: a) (6 4) 5+6 (7 5)= b) (0 5 4) 7 (8 4):= c) (6+5 ) 8 (4 ) (5 )= d) 5+(6 8) (0 )
. NÚMEROS NATURALES. Aplica la propiedad distributiva y opera: a) 5 (9 5)= b) (8 5+4) 6= c) (9 6) = d) (9+4 0+) =. Opera: a) (6 4) 5+6 (7 5)= b) (0 5 4) 7 (8 4):= c) (6+5 ) 8 (4 ) (5 )= d) 5+(6 8) (0 )
6 EL LENGUAJE ALGEBRAICO. ECUACIONES
 6 EL LENGUAJE ALGEBRAICO. ECUACIONES EJERCICIOS PROPUESTOS 6.1 El perímetro de un rectángulo viene dado por la epresión: y (: largo; y: ancho). Calcula el perímetro de cualquier rectángulo; el que tú elijas.
6 EL LENGUAJE ALGEBRAICO. ECUACIONES EJERCICIOS PROPUESTOS 6.1 El perímetro de un rectángulo viene dado por la epresión: y (: largo; y: ancho). Calcula el perímetro de cualquier rectángulo; el que tú elijas.
NÚMEROS Y OPERACIONES
 NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
Matemáticas. Tercero ESO. Curso 2012-2013. Exámenes
 Matemáticas. Tercero ESO. Curso 0-03. Exámenes . 9 de octubre de 0 Ejercicio. Calcular: 3 5 4 + 3 0 3 7 8 5 3 5 4 + 3 0 5 + 6 0 3 0 3 7 8 5 3 56 0 3 8 0 84 74 5 5 5 Ejercicio. Calcular: 5 6 [ ( 3 3 3 )]
Matemáticas. Tercero ESO. Curso 0-03. Exámenes . 9 de octubre de 0 Ejercicio. Calcular: 3 5 4 + 3 0 3 7 8 5 3 5 4 + 3 0 5 + 6 0 3 0 3 7 8 5 3 56 0 3 8 0 84 74 5 5 5 Ejercicio. Calcular: 5 6 [ ( 3 3 3 )]
2. Divisibilidad SOLUCIONARIO 2. NÚMEROS PRIMOS Y COMPUESTOS 1. MÚLTIPLOS Y DIVISORES PIENSA Y CALCULA
 16 SOLUCIONARIO 2. Divisibilidad 1. MÚLTIPLOS Y DIVISORES Calcula mentalmente e indica, de las siguientes divisiones, cuáles son exactas o enteras: a) 125 : 5 b) 28 : 6 c) 140 : 7 d) 23400 : 100 a) 25.
16 SOLUCIONARIO 2. Divisibilidad 1. MÚLTIPLOS Y DIVISORES Calcula mentalmente e indica, de las siguientes divisiones, cuáles son exactas o enteras: a) 125 : 5 b) 28 : 6 c) 140 : 7 d) 23400 : 100 a) 25.
SISTEMAS DE ECUACIONES
 URB. LA CANTERA, S/N. 988 HTTP:/WWW.MARIAAUXILIADORA.COM º ESO SISTEMAS DE ECUACIONES º. Empareja cada sistema con su solución. a) 8 0 b) c) d) ) =, = -/ ) = 8, = ) =, = ) =, = º. De entre los siguientes
URB. LA CANTERA, S/N. 988 HTTP:/WWW.MARIAAUXILIADORA.COM º ESO SISTEMAS DE ECUACIONES º. Empareja cada sistema con su solución. a) 8 0 b) c) d) ) =, = -/ ) = 8, = ) =, = ) =, = º. De entre los siguientes
001. Interpreta correctamente códigos (teléfonos, matrículas, NIF ).
 3.2.4 Criterios específicos de evaluación. 001. Interpreta correctamente códigos (teléfonos, matrículas, NIF ). 002. Calcula el total de elementos que se puedan codificar con una determinada clave. 003.
3.2.4 Criterios específicos de evaluación. 001. Interpreta correctamente códigos (teléfonos, matrículas, NIF ). 002. Calcula el total de elementos que se puedan codificar con una determinada clave. 003.
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 14 REFLEXIONA En esta unidad vas a estudiar las relaciones de proporcionalidad, que te ayudarán a superar muchos problemas aritméticos de los que se presentan todos los días. Completa la
Pág. 1 PÁGINA 14 REFLEXIONA En esta unidad vas a estudiar las relaciones de proporcionalidad, que te ayudarán a superar muchos problemas aritméticos de los que se presentan todos los días. Completa la
Números fraccionarios y decimales
 Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Fracciones + + EJERCICIOS resueltos. Operaciones combinadas + = Para resolver operaciones combinadas debemos tener en cuenta estas indicaciones:
 Operaciones combinadas Para resolver operaciones combinadas debemos tener en cuenta estas indicaciones: La misión de los paréntesis es la de unir o "empaquetar" aquello a lo que afectan. Los signos de
Operaciones combinadas Para resolver operaciones combinadas debemos tener en cuenta estas indicaciones: La misión de los paréntesis es la de unir o "empaquetar" aquello a lo que afectan. Los signos de
1:F 2:V 3:F 4:V 5:V 6:F 7:F 8:V 9:F 10:V 11:F 12:V 13:V 14:V 15:V 16:V 17:F 18:V. 49 no es múltiplo de 9: 49:9 no es exacta
 Tema 1: DIVISIBILIDAD Actividades para preparar el examen. Teoría: Contesta si son ciertas las afirmaciones: 1:F :V 3:F 4:V 5:V 6:F 7:F 8:V 9:F 10:V 11:F 1:V 13:V 14:V 15:V 16:V 17:F 18:V 19:V 0:V 1:F
Tema 1: DIVISIBILIDAD Actividades para preparar el examen. Teoría: Contesta si son ciertas las afirmaciones: 1:F :V 3:F 4:V 5:V 6:F 7:F 8:V 9:F 10:V 11:F 1:V 13:V 14:V 15:V 16:V 17:F 18:V 19:V 0:V 1:F
Ejercicios ( ) EJERCICIOS PRIMERA EVALUACIÓN PARA ALUMNOS CON MATEMATICAS DE 3º DE ESO PENDIENTE
 Pendientes º ESO Primera evaluación Pág. / 9 Temario TEMA.- NÚMEROS RACIONALES. Repaso breve de números racionales y operaciones en forma de fracción. Repaso de las formas decimales y de la fracción generatriz.
Pendientes º ESO Primera evaluación Pág. / 9 Temario TEMA.- NÚMEROS RACIONALES. Repaso breve de números racionales y operaciones en forma de fracción. Repaso de las formas decimales y de la fracción generatriz.
RESUMEN DE CONCEPTOS
 RESUMEN DE CONCEPTOS 1º ESO MATEMÁTICAS NÚMEROS NATURALES (1) Múltiplo de un número: Un número es múltiplo de otro si el segundo está contenido en el primero un número exacto de veces. Ejemplo: 16 es múltiplo
RESUMEN DE CONCEPTOS 1º ESO MATEMÁTICAS NÚMEROS NATURALES (1) Múltiplo de un número: Un número es múltiplo de otro si el segundo está contenido en el primero un número exacto de veces. Ejemplo: 16 es múltiplo
Alumno Fecha Actividad 13 Expresiones algebraicas 1º ESO
 Alumno Fecha Actividad 1 Expresiones algebraicas 1º ESO Las expresiones que resultan de combinar números y letras relacionándolos con las operaciones habituales se llaman expresiones algebraicas y se utilizan
Alumno Fecha Actividad 1 Expresiones algebraicas 1º ESO Las expresiones que resultan de combinar números y letras relacionándolos con las operaciones habituales se llaman expresiones algebraicas y se utilizan
APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA
 APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA 1º CURSO DEL CICLO DE GRADO SUPERIOR DE ADMINISTRACIÓN Y FINANZAS. CONTENIDO: Números enteros Fracciones Potencias Igualdades algebraicas notables
APÉNDICE MATEMÁTICO DEL MÓDULO DE: GESTIÓN FINANCIERA 1º CURSO DEL CICLO DE GRADO SUPERIOR DE ADMINISTRACIÓN Y FINANZAS. CONTENIDO: Números enteros Fracciones Potencias Igualdades algebraicas notables
UNIDAD DIDÁCTICA 4º. Temporalización. septiembre octubre noviembre diciembre enero febrero marzo abril mayo junio
 UNIDAD DIDÁCTICA 4º Etapa: Educación Primaria. Ciclo: 3º Curso 6º Área del conocimiento: Matemáticas Nº UD: 4º (8 sesiones de 60 minutos; a ocho sesiones por quincena) Título: Múltiplos y divisores. Temporalización
UNIDAD DIDÁCTICA 4º Etapa: Educación Primaria. Ciclo: 3º Curso 6º Área del conocimiento: Matemáticas Nº UD: 4º (8 sesiones de 60 minutos; a ocho sesiones por quincena) Título: Múltiplos y divisores. Temporalización
Materia: Matemáticas Curso 2015-2016. Alumno/a Curso: 4º ESO
 Materia: Matemáticas Curso 015-016 Alumno/a Curso: º ESO A continuación se describen los aprendizajes no adquiridos, así como las actividades programadas, las estrategias y los criterios de evaluación
Materia: Matemáticas Curso 015-016 Alumno/a Curso: º ESO A continuación se describen los aprendizajes no adquiridos, así como las actividades programadas, las estrategias y los criterios de evaluación
CUADERNO DE REPASO DE MATEMÁTICAS 1º ESO
 CUADERNO DE REPASO DE MATEMÁTICAS 1º ESO Indicaciones: 1. Presenta el trabajo en hojas cuadriculadas, tamaño A, y en una funda de plástico. 2. Realiza tus ejercicios de forma ordenada, escribiendo los
CUADERNO DE REPASO DE MATEMÁTICAS 1º ESO Indicaciones: 1. Presenta el trabajo en hojas cuadriculadas, tamaño A, y en una funda de plástico. 2. Realiza tus ejercicios de forma ordenada, escribiendo los
EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO
 EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO A continuación te presentamos una serie de ejercicios que deberás realizar y presentar obligatoriamente a tu profesor/a el día del examen. Puedes consultar
EJERCICIOS-RECUPERACIÓN ESTIVAL DE MATEMÁTICAS 1º ESO A continuación te presentamos una serie de ejercicios que deberás realizar y presentar obligatoriamente a tu profesor/a el día del examen. Puedes consultar
LOS NUMEROS Y LAS OPERACIONES
 LOS NUMEROS Y LAS OPERACIONES Sistema de numeración decimal. Lectura de números 1. Escribe los números siguientes: Medio millón:... Cuatro millones cuatrocientos... Tres millones y medio:... Seis millones
LOS NUMEROS Y LAS OPERACIONES Sistema de numeración decimal. Lectura de números 1. Escribe los números siguientes: Medio millón:... Cuatro millones cuatrocientos... Tres millones y medio:... Seis millones
ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO
 CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
Nombre: 90 X 40= = Calcula el termino que falta en cada operación. Escribe el número anterior y el posterior
 Calcula el termino que falta en cada operación 52.685 + = 87.652 6.753 = 6.397 + 34.476 = 56.987 39.455 = 11.247 624 X = 89.232 : 263 = 451 X 340 =294.100 144.795 : = 591 Escribe el número anterior y el
Calcula el termino que falta en cada operación 52.685 + = 87.652 6.753 = 6.397 + 34.476 = 56.987 39.455 = 11.247 624 X = 89.232 : 263 = 451 X 340 =294.100 144.795 : = 591 Escribe el número anterior y el
TEMA 2. POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA. POLINOMIOS Y FRACCIONES ALGEBRAICAS.. Repaso de polinomios - Epresión algebraica. Valor numérico - Polinomios. Operaciones con polinomios.. Identidades notables - Cuadrado de una suma de una diferencia
TEMA. POLINOMIOS Y FRACCIONES ALGEBRAICAS.. Repaso de polinomios - Epresión algebraica. Valor numérico - Polinomios. Operaciones con polinomios.. Identidades notables - Cuadrado de una suma de una diferencia
2 Divisibilidad. 1. Múltiplos y divisores
 2 Divisibilidad 1. Múltiplos y divisores Calcula mentalmente e indica, de las siguientes divisiones, cuáles son exactas o enteras: a) 125 : 5 b) 28 : 6 c) 140 : 7 d) 23 400 : 100 P I E N S A Y C A L C
2 Divisibilidad 1. Múltiplos y divisores Calcula mentalmente e indica, de las siguientes divisiones, cuáles son exactas o enteras: a) 125 : 5 b) 28 : 6 c) 140 : 7 d) 23 400 : 100 P I E N S A Y C A L C
La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación.
 La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación. Los contenidos mínimos de la materia son los que aparecen con un * UNIDAD 1: LOS NÚMEROS NATURALES
La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación. Los contenidos mínimos de la materia son los que aparecen con un * UNIDAD 1: LOS NÚMEROS NATURALES
CUADERNO Nº 6 NOMBRE:
 Ecuaciones Contenidos 1. Ecuaciones: ideas básicas Igualdades y ecuaciones Elementos de una ecuación Ecuaciones equivalentes 2. Reglas para resolver una ecuación Sin denominadores Con denominadores Resolución
Ecuaciones Contenidos 1. Ecuaciones: ideas básicas Igualdades y ecuaciones Elementos de una ecuación Ecuaciones equivalentes 2. Reglas para resolver una ecuación Sin denominadores Con denominadores Resolución
SOLUCIONES CONCEPTOS. centenas centésimas decenas. se escribe se lee parte entera parte decimal fracción. 0,023 Veintitrés milésimas 0 023
 SOLUCIONES CONCEPTOS 1.- Coloca cada número en el lugar adecuado: 103.578,9 décimas Unidades de millar centenas centésimas decenas Centenas de millar unidades Decenas de millar 3 5 9 7 1 8 0. Escribe con
SOLUCIONES CONCEPTOS 1.- Coloca cada número en el lugar adecuado: 103.578,9 décimas Unidades de millar centenas centésimas decenas Centenas de millar unidades Decenas de millar 3 5 9 7 1 8 0. Escribe con
Un número a es múltiplo de otro b cuando es el resultado de multiplicar este último por otro número c.
 DIVISIBILIDAD Múltiplos Un número a es múltiplo de otro b cuando es el resultado de multiplicar este último por otro número c. 18 = 2 9 18 es múltiplo de 2, ya que resulta de multiplicar 2 por 9. Tabla
DIVISIBILIDAD Múltiplos Un número a es múltiplo de otro b cuando es el resultado de multiplicar este último por otro número c. 18 = 2 9 18 es múltiplo de 2, ya que resulta de multiplicar 2 por 9. Tabla
PENDIENTES 1º ESO. Segundo examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del segundo examen de recuperación de MATEMÁTICAS DE 1º ESO Curso
 014 015 Preparación del segundo examen de recuperación de MATEMÁTICAS DE 1º ESO PENDIENTES 1º ESO Segundo examen DEPARTAMENTO DE MATEMÁTICAS 1.- Asocia un número entero a cada enunciado: NÚMEROS ENTEROS
014 015 Preparación del segundo examen de recuperación de MATEMÁTICAS DE 1º ESO PENDIENTES 1º ESO Segundo examen DEPARTAMENTO DE MATEMÁTICAS 1.- Asocia un número entero a cada enunciado: NÚMEROS ENTEROS
EJERCICIOS DE MATEMÁTICAS 1º ESO
 EJERCICIOS DE MATEMÁTICAS 1º ESO Realiza estos ejercicios y entrégaselos a tu profesor de Matemáticas en septiembre antes del examen. Te servirán para repasar toda la asignatura. 1.- Calcula: a) 3 4 +
EJERCICIOS DE MATEMÁTICAS 1º ESO Realiza estos ejercicios y entrégaselos a tu profesor de Matemáticas en septiembre antes del examen. Te servirán para repasar toda la asignatura. 1.- Calcula: a) 3 4 +
La unidad fraccionaria es cada una de las partes que se. Una fracción es el cociente de dos números enteros a y b,
 Unidad fraccionaria La unidad fraccionaria es cada una de las partes que se obtienen al dividir la unidad en n partes iguales. Definición de fracción Una fracción es el cociente de dos números enteros
Unidad fraccionaria La unidad fraccionaria es cada una de las partes que se obtienen al dividir la unidad en n partes iguales. Definición de fracción Una fracción es el cociente de dos números enteros
UNIDAD 1: DIVISIBILIDAD Y NÚMEROS ENTEROS
 UNIDAD 1: DIVISIBILIDAD Y NÚMEROS ENTEROS 1. *Representar números enteros sobre la recta numérica, compararlos y ordenarlos. 2. *Sumar y restar números enteros teniendo en cuenta el signo que presentan.
UNIDAD 1: DIVISIBILIDAD Y NÚMEROS ENTEROS 1. *Representar números enteros sobre la recta numérica, compararlos y ordenarlos. 2. *Sumar y restar números enteros teniendo en cuenta el signo que presentan.
3. Un número x dividido por 12 da como cociente 7 y resto 9. a) Halla x b) Qué número tienes que sumar a x para que la división por 12 sea exacta?
 . a) Expresa en forma polinómica: 8 b) Representa en el sistema binario el número. a) Calcula: (+).()+.(4) b) Escribe en forma de potencia: 6. Un número x dividido por da como cociente 7 y resto 9. a)
. a) Expresa en forma polinómica: 8 b) Representa en el sistema binario el número. a) Calcula: (+).()+.(4) b) Escribe en forma de potencia: 6. Un número x dividido por da como cociente 7 y resto 9. a)
