Investigación Operativa
|
|
|
- Ernesto Castro Soriano
- hace 7 años
- Vistas:
Transcripción
1 Investigación Operativa Unidad temática 3.3: Extensiones de la programación lineal. Programación con objetivos múltiples. Fundamentos y aplicaciones. Variables irrestrictas. Programación por objetivos. El modelo lineal, su formulación y solución. Objetivos unidireccionales. Preferencia y prioridad de objetivos. Introducción a la programación lineal paramétrica. Programación entera. Fundamentos y aplicaciones. El modelo lineal, su formulación y solución. Modelos mixtos. Usos de las variables auxiliares. Facultad de Ciencias Agrarias y Forestales Universidad Nacional de La Plata La Plata 13 de octubre del 2010 Pablo Yapura
2 Programación por Objetivos El modelo de decisión se ha desarrollado para resolver problemas en los que hay más de un objetivo relevante (objetivos contradictorios y soluciones de compromiso). El problema del uso múltiple de los bosques (y de las tierras en general) es probablemente el ejemplo más representativo de este tipo de situaciones y ha sido ampliamente estudiado. El modelo matemático busca minimizar las desviaciones en el cumplimiento de ciertas metas u objetivos, sujetas a ciertas restricciones que representan a las propias metas y a otras restricciones que representan límites físicos. Contrariamente a las restricciones físicas, las metas serán alcanzadas o satisfechas tanto como sea posible, pero no necesariamente de manera completa. Conseguir esta flexibilidad demanda el establecimiento de metas cuantitativamente explicitadas y una estructura de preferencias del responsable de la decisión para todas las metas identificadas, lo que finalmente constituye su mayor desventaja. Investigación Operativa Programación por objetivos y Programación entera Diapositiva 2
3 Programación por Objetivos El modelo matemático puede ser lineal (si se lo plantea como una extensión de la programación lineal), lo que implica que se puede usar el método símplex para resolverlo, con todas las ventajas asociadas (principalmente la eficiencia). El único concepto novedoso es el empleo de variables irrestrictas. Puesto que a las desviaciones se les debe permitir tomar valores negativos o positivos, es necesario superar la limitación del requerimiento de no negatividad de la programación lineal. Entonces, si se necesita representar una variable irrestricta en signo (sea x 1 ), se pueden definir: x + 1 = { x 1 si x de otro modo x 1 ={ x 1 si x de otro modo x 1 =x 1 + x 1 Investigación Operativa Programación por objetivos y Programación entera Diapositiva 3
4 Programación por Objetivos Puesto que las variables de desviación son linealmente dependientes, por el axioma de la independencia sólo una de ellas puede estar en la base (i.e. ser estrictamente positiva). El modelo matemático del predador y su presa formulado como un problema de programación por objetivos, en este caso con metas establecidas para el tiempo y la dieta nutritiva: Minimizar z=d 1 + d 1 d 2 + d 2 Sujeto a 4x 1 4x 2 d 1 + d 1 =150 tiempo 3x 1 2x 2 d 2 + d 2 =90 6x 1 8x x 1, x 2, d 1 +, d 1, d 2 +, d 2 0 función objetivo nutrientes calorías Investigación Operativa Programación por objetivos y Programación entera Diapositiva 4
5 Programación por Objetivos La representación geométrica del predador y su presa formulado como un problema de programación por objetivos, en este caso con metas establecidas para el tiempo y la dieta nutritiva: Investigación Operativa Programación por objetivos y Programación entera Diapositiva 5
6 Programación por Objetivos La solución del modelo con todas las combinaciones posibles para las dos metas (las unilaterales se indican como desigualdades mientras que las bilaterales se indican como igualdades): Parámetro Solución Holgura/Superávit Tiempo Nutrientes x 1 x 2 Punto Tiempo Nutrientes Calorías = 150 = 90 15,0 22,5 A = 90 = ,0 15,0 B ,0 22,5 A ,0 7,5 C ,0 22,5 A ,0 15,0 B ,0 7,5 C ,0 22,5 A Investigación Operativa Programación por objetivos y Programación entera Diapositiva 6
7 Investigación Operativa Unidad temática 3.3: Extensiones de la programación lineal. Programación con objetivos múltiples. Fundamentos y aplicaciones. Variables irrestrictas. Programación por objetivos. El modelo lineal, su formulación y solución. Objetivos unidireccionales. Preferencia y prioridad de objetivos. Introducción a la programación lineal paramétrica. Programación entera. Fundamentos y aplicaciones. El modelo lineal, su formulación y solución. Modelos mixtos. Usos de las variables auxiliares. Facultad de Ciencias Agrarias y Forestales Universidad Nacional de La Plata La Plata 3 de noviembre del 2010 Pablo Yapura
8 Es la extensión de la Programación Lineal (y de la Programación Matemática en particular) que se ha desarrollado para superar la limitación impuesta por el requerimiento de continuidad de las variables de la PL. En muchas situaciones reales lo más conveniente será ignorar este requerimiento de representación, resolver el problema de PL resultante y truncar (o redondear) la solución para convertirla en entera. Este procedimiento debe ser aplicado con precaución puesto que no garantiza que la solución entera así obtenida será óptima. Por lo demás, los problemas de programación entera sólo se distinguirán de su equivalente continuo por el agregado de las restricciones que establezcan que una o más, y tal vez todas, las variables deben ser enteras. Investigación Operativa Programación por objetivos y Programación entera Diapositiva 8
9 El agregado de estas restricciones (de integridad en las variables) redefine el espacio de soluciones factibles y, consecuentemente, resultará en valores óptimos que, como mucho, serán iguales a su equivalente continuo. De forma más general, en problemas de maximización se puede escribir: * * z MIP z LP Esta observación implica que normalmente las soluciones enteras serán interiores (y también inferiores o dominadas) y que, al no ser básicas, el simplex no podrá encontrarlas. Entonces, son necesarios otros algoritmos específicos para encontrar las soluciones enteras. Aunque no es el único, el algoritmo de ramificación y acotamiento ilustra bien los principios generales de los algoritmos de la programación entera (enumeración exhaustiva implícita; escasa eficiencia). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 9
10 Un transportista ha suscripto un contrato para transportar chips de madera desde la playa de una industria hasta el puerto, donde serán embarcados hacia el extranjero. Para el cumplimiento del contrato estudia la posibilidad de asignar dos camiones con capacidades de carga y costos operativo diferentes. La industria le ha adjudicado una cuota mínima de chips a transportar de 3000 t, los que serán remunerados a razón de 8 $.t 1 de chips transportada desde su playa al puerto, el que se encuentra a una distancia de 6,25 km. Los excedentes que el contratista pueda entregar serán recibidos y retribuidos al mismo precio que la industria ofrece para la cuota asignada. Por otra parte, el contrato no establece una cuota máxima de chips a transportar para mejorar las posibilidades de que sus contratistas obtengan algún retorno económico. El contrato establece que el transportista dispondrá de 60 días para entregar la cuota asignada con el único requisito de informar su plan de tareas antes de iniciarlas, pues la industria tiene otros contratos de transporte para la carga del barco suscriptos con anterioridad y además piensa usar camiones propios en caso de ser necesario. Investigación Operativa Programación por objetivos y Programación entera Diapositiva 10
11 El transportista acostumbra enviar sus camiones al taller para la realización de un service general cada 5000 km recorridos, para lo cual lleva un registro de la distancia que cada una de sus unidades ha recorrido. Esta información es crítica porque se estima que las unidades enviadas al service permanecerán inactivas un tiempo tal que dificultarían seriamente la posibilidad de cumplir el contrato una vez reincorporadas al trabajo. Habiendo considerado los tiempos de carga y descarga, junto con los turnos de sus choferes, ha estimado la cantidad de viajes diarios que cada uno de los camiones que asignará al cumplimiento del contrato pueden realizar y ha acordado que los camiones pueden pasar las horas fuera de servicio en la playa de estacionamiento de la industria. Toda la información relativa a los camiones se muestra en la siguiente tabla: Camión Capacidad de carga Costo operativo Viajes diarios Distancia recorrida* (t) ($.km 1 ) (cargas.día 1 ) (km) * Puestos en la playa de la industria Investigación Operativa Programación por objetivos y Programación entera Diapositiva 11
12 El contratista necesita determinar el número de cargas que le asignará a cada camión para maximizar el ingreso neto (sin considerar costos fijos) del contrato, evitando que las unidades cumplan los 5000 km previstos para su mantenimiento durante los 60 días asignados. Maximizar z=1,75 x 1 3,50 x 2 Sujeto a x 1 175,50 ; x 2 250,80 8 x 1 12 x /8 x 1 1/5 x 2 60 x i Z 0 Investigación Operativa Programación por objetivos y Programación entera Diapositiva 12
13 La solución óptima del problema relajado (Nodo 1). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 13
14 La solución óptima de la primera ramificación con la primera cota (Nodo 2). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 14
15 La solución óptima de la primera ramificación con la segunda cota (Nodo 3). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 15
16 La solución óptima de la segunda ramificación con la primera cota (Nodo 4). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 16
17 La solución no factible de la segunda ramificación con la segunda cota (Nodo 5). Investigación Operativa Programación por objetivos y Programación entera Diapositiva 17
18 El algoritmo de ramificación y acotamiento se puede representar mediante un diagrama de árbol que muestra el progreso en la búsqueda de la solución entera óptima: 1 x 1 * =78,72; x 2 * =250,8 z * =1015,56 x 1 78 x 1 79 x 1 * =78; x 2 * =250,80 z * =1014, x 1 * =79; x 2 * =250,625 z * =1015,44 x x x 1 * =80; x 2 * =250 z * =1015, Entera No factible Investigación Operativa Programación por objetivos y Programación entera Diapositiva 18
19 En el aprovechamiento de un rodal, el volumen total de madera a arrastrar es de 5000 m 3 y se debe decidir cuanto será asignado a dos medios diferentes: bueyes y motoarrastradores. Todos los rollizos deben ser arrastrados desde el rodal hasta una playa de trozas en la que serán cargados en camiones y trasladados hasta la industria. Para operar con los bueyes se necesita preparar una playa de trozas que cuesta 600 $, mientras que para los motoarrastradores la playa necesaria cuesta 1000 $. Por otra parte, si se decide operar con los dos medios, la playa costaría 1600 $. Los costos de arrastrar con bueyes se han estimado en 12 $.m 3 y los de hacerlo con motoarrastradores en 10 $.m 3. Si se desea minimizar el costo total de arrastrar la madera, incluyendo el costo de construir la playa de trozas, y se define a x 1 y x 2 como los volúmenes de madera a ser arrastrados por bueyes y motoarrastradores (en m 3 ), respectivamente, entonces la función objetivo se puede escribir como: Minimizar z=12 x 1 10 x 2 { 600 si x 1 0 x 2 = si x 1 =0 x si x 1 0 x 2 0 Investigación Operativa Programación por objetivos y Programación entera Diapositiva 19
20 Puesto que los costos fijos implican una violación del axioma de la proporcionalidad, para formular este problema como un programa lineal se pueden definir variables accesorias y restricciones accesorias: y 1= { 0 si x 1 =0 1 si x 1 0 y 2= { 0 si x 2 =0 1 si x 2 0 Minimizar z=12 x 1 10 x y y 2 Sujeto a x 1 x 2 =5000 x y 1 0 x y 2 0 x 1 0 ; x 2 0 ; y 1 ={0,1}; y 2 ={0,1} Investigación Operativa Programación por objetivos y Programación entera Diapositiva 20
Optimización combinatoria Flujo en redes. Investigación Operativa, Grado en Estadística y Empresa, 2011/12
 Optimización combinatoria Flujo en redes Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema Optimización combinatoria: definición y formulación de PE El problema
Optimización combinatoria Flujo en redes Prof. José Niño Mora Investigación Operativa, Grado en Estadística y Empresa, 2011/12 Esquema Optimización combinatoria: definición y formulación de PE El problema
MODELOS DE PROGRAMACION LINEAL VARIABLES Xij
 MODELOS DE PROGRAMACION LINEAL VARIABLES Xij 1. Construcción de modelos de programación lineal con variables Xij. 2. Aplicaciones en finanzas, marketing, producción. 3. Modelos de transporte y transbordo.
MODELOS DE PROGRAMACION LINEAL VARIABLES Xij 1. Construcción de modelos de programación lineal con variables Xij. 2. Aplicaciones en finanzas, marketing, producción. 3. Modelos de transporte y transbordo.
INVESTIGACION DE OPERACIONES PROGRAMACION LINEAL ENTERA
 INVESTIGACION DE OPERACIONES PROGRAMACION LINEAL ENTERA 1. Tipos de Modelo de Programación Lineal Entera. 2. Aplicaciones de las variables binarias (0-1) 1 1. Tipos de Modelo de Programación Lineal Entera
INVESTIGACION DE OPERACIONES PROGRAMACION LINEAL ENTERA 1. Tipos de Modelo de Programación Lineal Entera. 2. Aplicaciones de las variables binarias (0-1) 1 1. Tipos de Modelo de Programación Lineal Entera
Simulación y Optimización de Procesos Químicos. Titulación: Ingeniería Química. 5º Curso Optimización
 Simulación Optimización de Procesos Químicos Titulación: Ingeniería Química. 5º Curso Optimización MILP, MINLP (Mixed Integer (Non) Linear Programming). Octubre de 009. Optimización Discreta Programación
Simulación Optimización de Procesos Químicos Titulación: Ingeniería Química. 5º Curso Optimización MILP, MINLP (Mixed Integer (Non) Linear Programming). Octubre de 009. Optimización Discreta Programación
FORMULACIÓN DE MODELOS PROGRAMACIÓN LINEAL
 Clase # 4 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN LINEAL 4-1 CONTENIDO 1. Etapas en la Formulación del Modelo 2. Ejemplo 1: Asignación de Recursos 3. Ejemplo 2: Formulación de Dietas 4. Ejemplo 3: Programación
Clase # 4 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN LINEAL 4-1 CONTENIDO 1. Etapas en la Formulación del Modelo 2. Ejemplo 1: Asignación de Recursos 3. Ejemplo 2: Formulación de Dietas 4. Ejemplo 3: Programación
Es un procedimiento matemático que permite la planeación de actividades y la asignación de recursos productivos basados en criterios de optimización.
 PROGRAMACION LINEAL [Introducción] Es un procedimiento matemático que permite la planeación de actividades y la asignación de recursos productivos basados en criterios de optimización. Sirve para asignar
PROGRAMACION LINEAL [Introducción] Es un procedimiento matemático que permite la planeación de actividades y la asignación de recursos productivos basados en criterios de optimización. Sirve para asignar
FORMULACION DE PROBLEMAS LINEALES.
 FORMULACION DE PROBLEMAS LINEALES. La programación lineal son modelos destinados a la asignación eficiente de los recursos limitados en actividades conocidas con el objetivo de satisfacer las metas deseadas
FORMULACION DE PROBLEMAS LINEALES. La programación lineal son modelos destinados a la asignación eficiente de los recursos limitados en actividades conocidas con el objetivo de satisfacer las metas deseadas
Programación Entera. Nelson Devia C. IN Modelamiento y Optimización Departamento de Ingeniería Industrial Universidad de Chile
 IN3701 - Modelamiento y Optimización Departamento de Ingeniería Industrial Universidad de Chile 2011 Basado en Bertsimas, D., Tsitsiklis, J. (1997) Introduction to Linear Optimization Capítulos 10 y 11
IN3701 - Modelamiento y Optimización Departamento de Ingeniería Industrial Universidad de Chile 2011 Basado en Bertsimas, D., Tsitsiklis, J. (1997) Introduction to Linear Optimization Capítulos 10 y 11
MODELOS DE DECISIÓN. L.A. y M.C.E. Emma Linda Diez Knoth. 1 Colcio.j
 MODELOS DE DECISIÓN 1 Colcio.j MODELOS DE DECISIÓN a) Decisiones empresariales: Alcanzar las metas de la organización. Utilizar algún criterio o medida del rendimiento. La medida más común del rendimiento
MODELOS DE DECISIÓN 1 Colcio.j MODELOS DE DECISIÓN a) Decisiones empresariales: Alcanzar las metas de la organización. Utilizar algún criterio o medida del rendimiento. La medida más común del rendimiento
Programación entera 1
 Programación entera 1 1. El modelo de programación entera. 2. Aplicaciones de la programación entera. 3. Solución gráfica de problemas enteros. 4. El algoritmo de ramificación y acotación. 5. El algoritmo
Programación entera 1 1. El modelo de programación entera. 2. Aplicaciones de la programación entera. 3. Solución gráfica de problemas enteros. 4. El algoritmo de ramificación y acotación. 5. El algoritmo
Jesús Getán y Eva Boj. Marzo de 2014
 Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj 1 / 18 Jesús Getán y Eva Boj 2 / 18 Un Programa lineal consta de: Función objetivo. Modeliza
Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj 1 / 18 Jesús Getán y Eva Boj 2 / 18 Un Programa lineal consta de: Función objetivo. Modeliza
PROGRAMACION ENTERA: METODO DE BIFURCACIÓN Y ACOTAMIENTO
 PROGRAMACION ENTERA: METODO DE BIFURCACIÓN Y ACOTAMIENTO La mayor parte de los PE se resuelven en la práctica mediante la técnica de ramificación y acotamiento. En este método se encuentra la solución
PROGRAMACION ENTERA: METODO DE BIFURCACIÓN Y ACOTAMIENTO La mayor parte de los PE se resuelven en la práctica mediante la técnica de ramificación y acotamiento. En este método se encuentra la solución
Tema No. 3 Métodos de Resolución de Modelos de Programación Lineal. El Método Gráfico y Método Simplex Autoevaluación y Ejercicios Propuestos
 UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 3 Métodos de Resolución de Modelos
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA ÁREA DE TECNOLOGÍA DEPARTAMENTO DE GERENCIA INVESTIGACIÓN DE OPERACIONES PROFESOR: Dr. JUAN LUGO MARÍN Tema No. 3 Métodos de Resolución de Modelos
Programación Lineal Introducción
 Programación Lineal Introducción Curso: Investigación de Operaciones Ing. Javier Villatoro fjvillatoro.wordpress.com Curso: Catedrático: Investigación de Operaciones Ing. Javier Villatoro Comunicación
Programación Lineal Introducción Curso: Investigación de Operaciones Ing. Javier Villatoro fjvillatoro.wordpress.com Curso: Catedrático: Investigación de Operaciones Ing. Javier Villatoro Comunicación
PROGRAMACIÓN LINEAL PROGRAMACIÓN LINEAL.
 PROGRAMACIÓN LINEAL. La programación lineal es una técnica de modelado (construcción de modelos). La programación lineal (PL) es una técnica matemática de optimización, es decir, un método que trata de
PROGRAMACIÓN LINEAL. La programación lineal es una técnica de modelado (construcción de modelos). La programación lineal (PL) es una técnica matemática de optimización, es decir, un método que trata de
Programación Lineal Entera.
 Fundamentos de Investigación de Operaciones. S2/2003 Programación Lineal Entera. 1. El consejo directivo de la General Wheels Co. Está considerando siete grandes inversiones de capital. Estas inversiones
Fundamentos de Investigación de Operaciones. S2/2003 Programación Lineal Entera. 1. El consejo directivo de la General Wheels Co. Está considerando siete grandes inversiones de capital. Estas inversiones
Universidad de Managua Curso de Programación Lineal
 Universidad de Managua Curso de Programación Lineal Profesor: MSc. Julio Rito Vargas Avilés. Objetivos y Temáticas del Curso Estudiantes: Facultad de CE y A Año académico: III Cuatrimestre 2014 ORIENTACIONES
Universidad de Managua Curso de Programación Lineal Profesor: MSc. Julio Rito Vargas Avilés. Objetivos y Temáticas del Curso Estudiantes: Facultad de CE y A Año académico: III Cuatrimestre 2014 ORIENTACIONES
INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2016 UNIDAD DE APRENDIZAJE
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2016 UNIDAD DE APRENDIZAJE
UNIDAD 4 Programación Lineal
 MATEMÁTICAS APLICADAS A LAS C. SOCIALES 2 Unidad 4 UNIDAD 4 Programación Lineal TEORÍA (Editorial Editex) Repaso de 1º Inecuaciones lineales con dos incógnitas (Repaso de 1º)(Pág. 80) Actividad resuelta:
MATEMÁTICAS APLICADAS A LAS C. SOCIALES 2 Unidad 4 UNIDAD 4 Programación Lineal TEORÍA (Editorial Editex) Repaso de 1º Inecuaciones lineales con dos incógnitas (Repaso de 1º)(Pág. 80) Actividad resuelta:
Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut
 Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut 8.1 Para cada uno de los siguientes conjuntos, encontrar una desigualdad válida que agregada a la formulación
Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut 8.1 Para cada uno de los siguientes conjuntos, encontrar una desigualdad válida que agregada a la formulación
Universidad Nacional Autónoma de Nicaragua UNAN-Managua. Curso de Investigación de Operaciones
 Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Presentación del Programa de Investigación de Operaciones Estudiantes:
Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Presentación del Programa de Investigación de Operaciones Estudiantes:
UNIDAD II. PROGRAMACIÓN LINEAL
 UNIDAD II. PROGRAMACIÓN LINEAL OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Introducción
UNIDAD II. PROGRAMACIÓN LINEAL OBJETIVO DE APRENDIZAJE: El alumno identificará y analizará problemas de optimización de funciones y recursos para mejorar la operación de una organización. Introducción
U.N.Ju. Facultad de Ingeniería I. O. Trabajo Practico Nº 2: PL Grafico - Fecha: /abr/11
 U.N.Ju. Facultad de Ingeniería I. O. Trabajo Practico Nº 2: PL Grafico - Fecha: /abr/11 ALUMNO: CARRERA: L.U. Nº: FIRMA: Ejercicios: 1) Defina a La Programación Lineal. 2) Escriba la forma canónica de
U.N.Ju. Facultad de Ingeniería I. O. Trabajo Practico Nº 2: PL Grafico - Fecha: /abr/11 ALUMNO: CARRERA: L.U. Nº: FIRMA: Ejercicios: 1) Defina a La Programación Lineal. 2) Escriba la forma canónica de
CAPITULO 1: PERSPECTIVE GENERAL DE LA
 CONTENIDO CAPITULO 1: PERSPECTIVE GENERAL DE LA INVESTIGACION DE OPERACIONES 1 1.1 Modelos matemáticos de investigación de operaciones. 1 1.2 Técnicas de investigación de operaciones 3 1.3 Modelado de
CONTENIDO CAPITULO 1: PERSPECTIVE GENERAL DE LA INVESTIGACION DE OPERACIONES 1 1.1 Modelos matemáticos de investigación de operaciones. 1 1.2 Técnicas de investigación de operaciones 3 1.3 Modelado de
Técnicas de optimización. Introducción.
 Técnicas de optimización. Introducción. Diego A. Patino Pontificia Universidad Javeriana 18 de julio de 2016 1/ 20 Definición Composición Tipos de problemas Ejemplos 2/ 20 Qué es optimización? 3/ 20 Qué
Técnicas de optimización. Introducción. Diego A. Patino Pontificia Universidad Javeriana 18 de julio de 2016 1/ 20 Definición Composición Tipos de problemas Ejemplos 2/ 20 Qué es optimización? 3/ 20 Qué
Un sistema de ecuaciones diferenciales son aquellas que tienen varias posibilidades para su solución. Estas son:
 Unidad X: Programación lineal (continuación) Objetivo específico: Entender ampliamente el fenómeno del comportamiento de los modelos matemáticos para la resolución de problemas enfocados a las ecuaciones
Unidad X: Programación lineal (continuación) Objetivo específico: Entender ampliamente el fenómeno del comportamiento de los modelos matemáticos para la resolución de problemas enfocados a las ecuaciones
RESOLUCIÓN DE MODELOS DE PROGRAMACIÓN ENTERA
 11 de Junio de 2012 RESOLUCIÓN DE MODELOS DE PROGRAMACIÓN ENTERA MÉTODOS DE ENUMERACIÓN, RAMIFICACIÓN Y ACOTACIÓN Postgrado de Investigación de Operaciones Facultad de Ingeniería Universidad Central de
11 de Junio de 2012 RESOLUCIÓN DE MODELOS DE PROGRAMACIÓN ENTERA MÉTODOS DE ENUMERACIÓN, RAMIFICACIÓN Y ACOTACIÓN Postgrado de Investigación de Operaciones Facultad de Ingeniería Universidad Central de
Casos especiales de la P. L.
 Casos especiales de la P. L. Programación por Objetivos Proporciona una manera racional de intentar alcanzar varios objetivos de manera simultánea, jerarquizando los mismos o asociándoles una ponderación
Casos especiales de la P. L. Programación por Objetivos Proporciona una manera racional de intentar alcanzar varios objetivos de manera simultánea, jerarquizando los mismos o asociándoles una ponderación
Formule un modelo de programación lineal binaria que minimice la distancia máxima entre un distrito y su respectiva estación.
 Profesores: Daniel Espinosa, Roberto Cominetti. Auxiliares: Victor Bucarey, Pablo Lemus, Paz Obrecht. Coordinador: Matías Siebert. IN3701 - Modelamiento y Optimización Auxiliar 2 22 de Marzo de 2012 P1.
Profesores: Daniel Espinosa, Roberto Cominetti. Auxiliares: Victor Bucarey, Pablo Lemus, Paz Obrecht. Coordinador: Matías Siebert. IN3701 - Modelamiento y Optimización Auxiliar 2 22 de Marzo de 2012 P1.
Casos especiales de la P. L.
 Casos especiales de la P. L. Programación Lineal Entera Un modelo de programación lineal que no acepta soluciones fraccionales. En este caso, la formulación es similar a la de un problema general de programación
Casos especiales de la P. L. Programación Lineal Entera Un modelo de programación lineal que no acepta soluciones fraccionales. En este caso, la formulación es similar a la de un problema general de programación
MECU 3031 PROGRAMACION LINEAL
 MECU 3031 PROGRAMACION LINEAL La Programación Lineal La programación lineal es una técnica matemática. Se usa para determinar la solución de problemas que se plantean muy comúnmente en disciplinas como
MECU 3031 PROGRAMACION LINEAL La Programación Lineal La programación lineal es una técnica matemática. Se usa para determinar la solución de problemas que se plantean muy comúnmente en disciplinas como
Dirección de operaciones. SESIÓN # 2: Programación lineal
 Dirección de operaciones SESIÓN # 2: Programación lineal Contextualización Dentro de la sesión anterior conocimos el concepto y alcance de la administración de operaciones, dicho de otro modo el qué, ahora
Dirección de operaciones SESIÓN # 2: Programación lineal Contextualización Dentro de la sesión anterior conocimos el concepto y alcance de la administración de operaciones, dicho de otro modo el qué, ahora
Optimización de Problemas de Producción
 Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile Colaboran: Héctor Cancela - Antonio Mauttone - Carlos Testuri Depto. Investigación Operativa. Instituto de Computación. Facultad de
Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile Colaboran: Héctor Cancela - Antonio Mauttone - Carlos Testuri Depto. Investigación Operativa. Instituto de Computación. Facultad de
Algoritmo de ramificación y acotación
 Algoritmo de ramificación y acotación Investigación Operativa Ingeniería Técnica en Informática de Gestión UC3M Curso 08/09 Descripción de los objetivos En esta práctica desarrollaremos el algoritmo de
Algoritmo de ramificación y acotación Investigación Operativa Ingeniería Técnica en Informática de Gestión UC3M Curso 08/09 Descripción de los objetivos En esta práctica desarrollaremos el algoritmo de
Fundamentos de Programación Entera
 Fundamentos de Programación Entera Carlos Testuri Germán Ferrari Departamento de Investigación Operativa. Instituto de Computación. Facultad de Ingeniería. Universidad de la República 2012-2016 Facultad
Fundamentos de Programación Entera Carlos Testuri Germán Ferrari Departamento de Investigación Operativa. Instituto de Computación. Facultad de Ingeniería. Universidad de la República 2012-2016 Facultad
Introducción a la Programación Lineal. Juan Pablo Cobá Juárez Pegueros Investigación de Operaciones Ingeniería Mecánica Facultad de Ingeniería 2015
 Introducción a la Programación Lineal Juan Pablo Cobá Juárez Pegueros Investigación de Operaciones Ingeniería Mecánica Facultad de Ingeniería 2015 Historia La investigación de Operaciones se caracteriza
Introducción a la Programación Lineal Juan Pablo Cobá Juárez Pegueros Investigación de Operaciones Ingeniería Mecánica Facultad de Ingeniería 2015 Historia La investigación de Operaciones se caracteriza
Método Simplex. Ing. Ricardo Fernando Otero, MSc
 Método Simplex Ing. Ricardo Fernando Otero, MSc Forma estándar de un modelo de programación lineal Dirección de mejora: Maximizar Todas las restricciones deben ser El lado izquierdo debe contener solo
Método Simplex Ing. Ricardo Fernando Otero, MSc Forma estándar de un modelo de programación lineal Dirección de mejora: Maximizar Todas las restricciones deben ser El lado izquierdo debe contener solo
INTRODUCCIÓN A LOS MÉTODOS DE OPTIMIZACIÓN EN 2º BACHILLERATO
 INTRODUCCIÓN A LOS MÉTODOS DE OPTIMIZACIÓN EN 2º BACHILLERATO AUTORÍA ANTONIO GARCÍA JIMÉNEZ TEMÁTICA MATEMÁTICAS CIENCIAS SOCIALES ETAPA BACHILLERATO Resumen La optimización es una técnica muy importante
INTRODUCCIÓN A LOS MÉTODOS DE OPTIMIZACIÓN EN 2º BACHILLERATO AUTORÍA ANTONIO GARCÍA JIMÉNEZ TEMÁTICA MATEMÁTICAS CIENCIAS SOCIALES ETAPA BACHILLERATO Resumen La optimización es una técnica muy importante
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Introducción a la programación lineal
 Introducción a la programación lineal La programación lineal se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales. La técnica se aplica en una
Introducción a la programación lineal La programación lineal se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales. La técnica se aplica en una
Programación lineal por metas: una alternativa para la toma de decisiones
 Programación lineal por metas: una alternativa para la toma de decisiones Claudia Mayela Alcaraz Avendaño Instituto Tecnológico de Celaya [email protected] Introducción El presente artículo
Programación lineal por metas: una alternativa para la toma de decisiones Claudia Mayela Alcaraz Avendaño Instituto Tecnológico de Celaya [email protected] Introducción El presente artículo
Dualidad 1. 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. 5 Condiciones de holgura complementaria.
 Dualidad 1 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. Condiciones de holgura complementaria. 6 Solución dual óptima en la tabla. 7 Interpretación
Dualidad 1 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. Condiciones de holgura complementaria. 6 Solución dual óptima en la tabla. 7 Interpretación
INTRODUCCIÓN A LA MODELACIÓN MATEMÁTICA Y OPTIMIZACIÓN
 INTRODUCCIÓN A LA MODELACIÓN MATEMÁTICA Y OPTIMIZACIÓN Carlos Julio Vidal Holguín UNIVERSIDAD DEL VALLE FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA INDUSTRIAL Y ESTADÍSTICA 1. FORMULACIÓN DE MODELOS DE
INTRODUCCIÓN A LA MODELACIÓN MATEMÁTICA Y OPTIMIZACIÓN Carlos Julio Vidal Holguín UNIVERSIDAD DEL VALLE FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA INDUSTRIAL Y ESTADÍSTICA 1. FORMULACIÓN DE MODELOS DE
Componentes de la Programación Lineal
 Programación Lineal El desarrollo actual de la Programación Lineal para los negocios y la industria se debe al Dr. George Dantzig. Dantzig presentó su Método Simplex (1947) para resolver este tipo de problemas.
Programación Lineal El desarrollo actual de la Programación Lineal para los negocios y la industria se debe al Dr. George Dantzig. Dantzig presentó su Método Simplex (1947) para resolver este tipo de problemas.
TRANSPORTE Y TRANSBORDO
 TRANSPORTE Y TRANSBORDO En ésta semana estudiaremos un modelo particular de problema de programación lineal, uno en el cual su resolución a través del método simplex es dispendioso, pero que debido a sus
TRANSPORTE Y TRANSBORDO En ésta semana estudiaremos un modelo particular de problema de programación lineal, uno en el cual su resolución a través del método simplex es dispendioso, pero que debido a sus
CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA
 CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA Programación Lineal Entera Es una técnica que permite modelar y resolver problemas cuya característica principal es que el conjunto de soluciones factibles es discreto.
CAPÍTULO 4 PROGRAMACIÓN LINEAL ENTERA Programación Lineal Entera Es una técnica que permite modelar y resolver problemas cuya característica principal es que el conjunto de soluciones factibles es discreto.
Casos especiales de la P. L.
 Casos especiales de la P. L. Las redes: Las redes están presentes en diferentes lugares en la vida real: redes de transporte, flujo eléctrico y comunicaciones, por ejemplo. Las redes: También son ampliamente
Casos especiales de la P. L. Las redes: Las redes están presentes en diferentes lugares en la vida real: redes de transporte, flujo eléctrico y comunicaciones, por ejemplo. Las redes: También son ampliamente
Casos especiales de la P. L.
 Casos especiales de la P. L. Problemas de flujo mínimo Planteamiento del problema Son problemas de programación lineal con ciertas estructuras especiales Permiten ser trabajados con algoritmos especiales
Casos especiales de la P. L. Problemas de flujo mínimo Planteamiento del problema Son problemas de programación lineal con ciertas estructuras especiales Permiten ser trabajados con algoritmos especiales
Breve introducción a la Investigación de Operaciones
 Breve introducción a la Investigación de Operaciones Un poco de Historia Se inicia desde la revolución industrial, usualmente se dice que fue a partir de la segunda Guerra Mundial. La investigación de
Breve introducción a la Investigación de Operaciones Un poco de Historia Se inicia desde la revolución industrial, usualmente se dice que fue a partir de la segunda Guerra Mundial. La investigación de
1. Defina el problema de particionamiento. Escriba un ejemplo de este tipo de problema, junto con su formulación general en AMPL.
 DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA o. DIPLOMATURA DE ESTADÍSTICA Ampliación de la Investigación Operativa. Curso 00/0 a Prueba de Evaluación Continua. Fecha: 6-6-0. Defina el problema
DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA o. DIPLOMATURA DE ESTADÍSTICA Ampliación de la Investigación Operativa. Curso 00/0 a Prueba de Evaluación Continua. Fecha: 6-6-0. Defina el problema
Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones
 Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad
Curso: Teoría, Algoritmos y Aplicaciones de Gestión Logística. Modelos de Ubicación de Instalaciones Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad
La Programación Lineal. H. R. Alvarez A., Ph. D. 1
 La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES
 II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El estudiante, conocerá los fundamentos en que se basan las herramientas de la investigación de operaciones para la toma de decisiones.
II. INTRODUCCIÓN A LA INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El estudiante, conocerá los fundamentos en que se basan las herramientas de la investigación de operaciones para la toma de decisiones.
Teniendo en cuenta los valores de las variables se tienen 3 tipos de modelos lineales enteros:
 Tema 5 Programación entera En este tema introducimos problemas lineales en los que algunas o todas las variables están restringidas a tomar valores enteros. Para resolver este tipo de problemas se han
Tema 5 Programación entera En este tema introducimos problemas lineales en los que algunas o todas las variables están restringidas a tomar valores enteros. Para resolver este tipo de problemas se han
Casos especiales de la P. L.
 Casos especiales de la P. L. Las redes: Las redes están presentes en diferentes lugares en la vida real: redes de transporte, flujo eléctrico y comunicaciones, por ejemplo. Las redes: También son ampliamente
Casos especiales de la P. L. Las redes: Las redes están presentes en diferentes lugares en la vida real: redes de transporte, flujo eléctrico y comunicaciones, por ejemplo. Las redes: También son ampliamente
MÉTODO SIMPLEX MÉTODO DE SOLUCIÓN GRÁFICO
 MÉTODO SIMPLEX MÉTODO DE SOLUCIÓN GRÁFICO Investigación de Operaciones 1 Tipos de soluciones en problemas de PL Solución óptima finita única. Solución óptima finita múltiple. Solución ilimitada. Solución
MÉTODO SIMPLEX MÉTODO DE SOLUCIÓN GRÁFICO Investigación de Operaciones 1 Tipos de soluciones en problemas de PL Solución óptima finita única. Solución óptima finita múltiple. Solución ilimitada. Solución
7. PROGRAMACION LINEAL
 7. PROGRAMACION LINEAL 7.1. INTRODUCCION A LA PROGRMACION LINEAL 7.2. FORMULACION DE UN PROBLEMA LINEAL 7.3. SOLUCION GRAFICA DE UN PROBLEMA LINEAL 7.4. CASOS ESPECIALES DE PROBLEMAS LINEALES 7.4.1. Problemas
7. PROGRAMACION LINEAL 7.1. INTRODUCCION A LA PROGRMACION LINEAL 7.2. FORMULACION DE UN PROBLEMA LINEAL 7.3. SOLUCION GRAFICA DE UN PROBLEMA LINEAL 7.4. CASOS ESPECIALES DE PROBLEMAS LINEALES 7.4.1. Problemas
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA
 RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA SIMPLEX Y LINEAL ENTERA a Resuelve el siguiente problema con variables continuas positivas utilizando el método simple a partir del vértice
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA SIMPLEX Y LINEAL ENTERA a Resuelve el siguiente problema con variables continuas positivas utilizando el método simple a partir del vértice
Programación Lineal. - Si no: Sea j tal que c
 Programación Lineal El objetivo de este documento es hacer una breve introducción a la programación lineal que pueda contribuir al fácil manejo de la aplicación. La programación lineal es un procedimiento
Programación Lineal El objetivo de este documento es hacer una breve introducción a la programación lineal que pueda contribuir al fácil manejo de la aplicación. La programación lineal es un procedimiento
EJERCICIOS DE PROGRAMACIÓN LINEAL
 EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
PLE: Ramificación y Acotamiento
 PLE: Ramificación y Acotamiento CCIR / Depto Matemáticas TC3001 CCIR / Depto Matemáticas PLE: Ramificación y Acotamiento TC3001 1 / 45 La compañía TELFA fabrica mesa y sillas. Una mesa requiere 1 hora
PLE: Ramificación y Acotamiento CCIR / Depto Matemáticas TC3001 CCIR / Depto Matemáticas PLE: Ramificación y Acotamiento TC3001 1 / 45 La compañía TELFA fabrica mesa y sillas. Una mesa requiere 1 hora
Programación Lineal Entera. Programación Entera
 Programación Lineal Entera PE Programación Entera Modelo matemático, es el problema de programación lineal Restricción adicional de variables con valores enteros. Programación entera mita Algunas variables
Programación Lineal Entera PE Programación Entera Modelo matemático, es el problema de programación lineal Restricción adicional de variables con valores enteros. Programación entera mita Algunas variables
Departamento de Matemáticas. ITAM Programación lineal (+ extensiones). Objetivos y panorama del c
 Programación lineal (+ extensiones). Objetivos y panorama del curso. Departamento de Matemáticas. ITAM. 2008. Introducción Programación lineal http://allman.rhon.itam.mx/ jmorales La programación lineal
Programación lineal (+ extensiones). Objetivos y panorama del curso. Departamento de Matemáticas. ITAM. 2008. Introducción Programación lineal http://allman.rhon.itam.mx/ jmorales La programación lineal
El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés.
 Universidad Nacional de Ingeniería Sede: UNI-Norte II Semestre 2008 Investigación de Operaciones I El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés. martes, 21 de octubre de 2008 El Problema
Universidad Nacional de Ingeniería Sede: UNI-Norte II Semestre 2008 Investigación de Operaciones I El Problema del Transporte M.C. Ing. Julio Rito Vargas Avilés. martes, 21 de octubre de 2008 El Problema
INGENIERÍA EN MECATRÓNICA
 INGENIERÍA EN MECATRÓNICA HOJA DE ASIGNATURA CON DESGLOSE DE UNIDADES TEMÁTICAS 1. Nombre de la asignatura Optativa II Métodos cuantitativos para la toma de decisiones en administración 2. Competencias
INGENIERÍA EN MECATRÓNICA HOJA DE ASIGNATURA CON DESGLOSE DE UNIDADES TEMÁTICAS 1. Nombre de la asignatura Optativa II Métodos cuantitativos para la toma de decisiones en administración 2. Competencias
La Programación Lineal. H. R. Alvarez A., Ph. D. 1
 La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
Programación lineal: Algoritmo del simplex
 Programación lineal: Algoritmo del simplex Se considera la formulación estándar de un problema de programación lineal siguiendo la notación utilizada en las clases teóricas: Minimizar c t x sa: Ax = b
Programación lineal: Algoritmo del simplex Se considera la formulación estándar de un problema de programación lineal siguiendo la notación utilizada en las clases teóricas: Minimizar c t x sa: Ax = b
Tema 1. Modelos lineales y solución gráfica. 1.1 El modelo lineal
 Tema 1 Modelos lineales y solución gráfica La programación lineal es una importante rama de la Investigación Operativa. Esta técnica matemática consiste en una serie de métodos que permiten obtener la
Tema 1 Modelos lineales y solución gráfica La programación lineal es una importante rama de la Investigación Operativa. Esta técnica matemática consiste en una serie de métodos que permiten obtener la
INTRODUCCIÓN A LA PROGRAMACIÓN ENTERA
 INTRODUCCIÓN A LA PROGRAMACIÓN ENTERA Los problemas de programación lineal en que se requiere que algunas o todas las variables tomen valores enteros, son de programación entera. La programación entera
INTRODUCCIÓN A LA PROGRAMACIÓN ENTERA Los problemas de programación lineal en que se requiere que algunas o todas las variables tomen valores enteros, son de programación entera. La programación entera
CONTENIDO Prefacio CAPITULO 1: Qué es la investigación de operaciones? CAPITULO 2: Introducción a la programación lineal...
 CONTENIDO Prefacio XV CAPITULO 1: Qué es la investigación de operaciones? 1 1.1 Modelos de investigación de operaciones 1 1.2 Solución del modelo de investigación de operaciones.. 4 1.3 Modelos de colas
CONTENIDO Prefacio XV CAPITULO 1: Qué es la investigación de operaciones? 1 1.1 Modelos de investigación de operaciones 1 1.2 Solución del modelo de investigación de operaciones.. 4 1.3 Modelos de colas
Práctica 1. Introducción a la optimización mediante herramienta MS Excel Solver (I)
 Ingeniería de Telecomunicación Planificación Avanzada de Redes de Comunicaciones Curso 2006-2007 Pablo Pavón Mariño Práctica 1. Introducción a la optimización mediante herramienta MS Excel Solver (I) Objetivos
Ingeniería de Telecomunicación Planificación Avanzada de Redes de Comunicaciones Curso 2006-2007 Pablo Pavón Mariño Práctica 1. Introducción a la optimización mediante herramienta MS Excel Solver (I) Objetivos
Programación Matemática para Economistas 1
 Programación Matemática para Economistas 1 CAPÍTULO 4. TOMA DE DECISIONES MULTICRITERIO. 1.- Introducción. Los problemas de programación lineal vistos hasta ahora, no implicaban ninguna decisión. Una vez
Programación Matemática para Economistas 1 CAPÍTULO 4. TOMA DE DECISIONES MULTICRITERIO. 1.- Introducción. Los problemas de programación lineal vistos hasta ahora, no implicaban ninguna decisión. Una vez
FORMULACIÓN DE MODELOS DE PROGRAMACIÓN LINEAL (Parte 1)
 21 de Septiembre de 2017 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN LINEAL (Parte 1) Ingeniería Industrial Ingeniería Informática Facultad de Ingeniería Universidad Católica Andrés Bello 1 Puntos a tratar
21 de Septiembre de 2017 FORMULACIÓN DE MODELOS DE PROGRAMACIÓN LINEAL (Parte 1) Ingeniería Industrial Ingeniería Informática Facultad de Ingeniería Universidad Católica Andrés Bello 1 Puntos a tratar
Modelado en Programación Lineal y Entera en Modelado Cuantitativo para Problemas de Producción
 Modelado en Programación Lineal y Entera en Modelado Cuantitativo para Problemas de Producción Héctor Cancela - Antonio Mauttone Pedro Piñeyro - Luis Stábile - Carlos Testuri Depto. Investigación Operativa.
Modelado en Programación Lineal y Entera en Modelado Cuantitativo para Problemas de Producción Héctor Cancela - Antonio Mauttone Pedro Piñeyro - Luis Stábile - Carlos Testuri Depto. Investigación Operativa.
Programación Lineal. El método simplex
 Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
3.1. La Optimización Lineal El Planteamiento
 Gerardo Febres Última revisión: 2016.03.23 3.1. La Optimización Lineal 3.1.1.- El Planteamiento Planteemos un problema extremadamente sencillo. Hacer máximas las ganancias obtenidas al vender tornillos.
Gerardo Febres Última revisión: 2016.03.23 3.1. La Optimización Lineal 3.1.1.- El Planteamiento Planteemos un problema extremadamente sencillo. Hacer máximas las ganancias obtenidas al vender tornillos.
EXTENSIONES DE LA PROGRAMACIÓN LINEAL
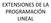 EXTENSIONES DE LA PROGRAMACIÓN LINEAL MODELOS OPTIMIZANTES MUNDO REAL ABSTRACCION OPERACION M MODELOS DE DECISIÓN NO RESTRINGIDOS RESTRINGIDOS MIN 6 / x 1 + 5 x 1 + 7 / x 2 + x 1.x 2 PROGRAMAS MATEMÁTICOS
EXTENSIONES DE LA PROGRAMACIÓN LINEAL MODELOS OPTIMIZANTES MUNDO REAL ABSTRACCION OPERACION M MODELOS DE DECISIÓN NO RESTRINGIDOS RESTRINGIDOS MIN 6 / x 1 + 5 x 1 + 7 / x 2 + x 1.x 2 PROGRAMAS MATEMÁTICOS
UNIDAD III. INVESTIGACIÓN DE OPERACIONES
 UNIDAD III. INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El alumno resolverá problemas utilizando la programación lineal y de proyectos para sugerir cursos de acción de mejora en las empresas turísticas
UNIDAD III. INVESTIGACIÓN DE OPERACIONES Objetivo de la unidad: El alumno resolverá problemas utilizando la programación lineal y de proyectos para sugerir cursos de acción de mejora en las empresas turísticas
Universidad Nacional Autónoma de Nicaragua UNAN-Managua. Curso de Investigación de Operaciones
 Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: FAREM-Carazo Unidad II Modelos de Programación Lineal
Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: FAREM-Carazo Unidad II Modelos de Programación Lineal
PROBLEMA 1. Considere el siguiente problema de programación lineal:
 PROBLEMA 1 Considere el siguiente problema de programación lineal: Sean h1 y h2 las variables de holgura correspondientes a la primera y segunda restricción, respectivamente, de manera que al aplicar el
PROBLEMA 1 Considere el siguiente problema de programación lineal: Sean h1 y h2 las variables de holgura correspondientes a la primera y segunda restricción, respectivamente, de manera que al aplicar el
Fundamentos de Investigación de Operaciones Modelos de Grafos
 Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Formulando con modelos lineales enteros
 Universidad de Chile 19 de marzo de 2012 Contenidos 1 Forma de un problema Lineal Entero 2 Modelando con variables binarias 3 Tipos de Problemas Forma General de un MILP Problema de optimización lineal
Universidad de Chile 19 de marzo de 2012 Contenidos 1 Forma de un problema Lineal Entero 2 Modelando con variables binarias 3 Tipos de Problemas Forma General de un MILP Problema de optimización lineal
Programación Lineal y Optimización Segundo Examen Parcial:Solución Profr. Eduardo Uresti, Enero-Mayo 2012
 Matrícula: Nombre: Programación Lineal y Optimización Segundo Examen Parcial: Profr. Eduardo Uresti, Enero-Mayo 2012 SÓLO HAGA 4 PROBLEMAS 1. Suponga que tiene una empresa que produce tres tipos de productos
Matrícula: Nombre: Programación Lineal y Optimización Segundo Examen Parcial: Profr. Eduardo Uresti, Enero-Mayo 2012 SÓLO HAGA 4 PROBLEMAS 1. Suponga que tiene una empresa que produce tres tipos de productos
Programación Entera TIPOS DE PROBLEMAS DE PROGRAMACIÓN EN ENTEROS. Comparación entre la programación lineal y la de enteros
 Comparación entre la programación lineal y la de enteros Programación Entera M. En C. Eduardo Bustos Farías En programación lineal, el algoritmo símplex siempre encuentra el óptimo global debido a que
Comparación entre la programación lineal y la de enteros Programación Entera M. En C. Eduardo Bustos Farías En programación lineal, el algoritmo símplex siempre encuentra el óptimo global debido a que
PROGRAMACIÓN LINEAL MÉTODO GRÁFICO
 1 PROGRAMACIÓN LINEAL MÉTODO GRÁFICO Dado un problema de programación lineal se debe: 1. Graficar cada una de las restricciones. 2. Encontrar el Polígono de factibilidad, que es la intersección de los
1 PROGRAMACIÓN LINEAL MÉTODO GRÁFICO Dado un problema de programación lineal se debe: 1. Graficar cada una de las restricciones. 2. Encontrar el Polígono de factibilidad, que es la intersección de los
