E.T.S.I. Agrónomos Grado en Biotecnología Matemáticas II 1 a prueba de la evaluación continua: soluciones

Transcripción

1 E.T.S.I. Agrónomos Grado en Biotecnología Matemáticas II a prueba de la evaluación continua: soluciones 4 de marzo de 04 Es importante que escribáis con claridad y expreséis con precisión los argumentos matemáticos que os permiten obtener los resultados a los que lleguéis. Es imprescindible que utilicéis las herramientas y las nociones matemáticas que se han introducido en este curso para obtener las soluciones de los problemas de este examen. Todos los ejercicios tienen el mismo valor. Tiempo: horas. La tabla refleja las observaciones de la densidad del agua de mar ρ como función de la salinidad S y de la temperatura T. a) Estimad el valor de la densidad cuando la salinidad es de 33,5 unidades y la temperatura de 7 unidades. b) Estimad el valor medio de la densidad del agua de mar para el rango de salinidades y temperaturas de las se tienen observaciones. Consideran el número de subintervalos en cada eje que permita utilizar el mayor número de datos. a) Para estimar el valor de la densidad cuando la salinidad es de 33,5 unidades y la temperatura de 7 unidades vamos a utilizar la aproximación lineal que proporcionan las derivadas parciales de las funciones diferenciables. Dado que no tenemos la expresión analítica de la función ρ(t, S) deberemos aproximar los valores de las derivadas parciales ρ S (33,5; 7) y ρ T (33,5; 7) para poder utilizar que ρ(33,5; 7) L(33,5; 7) = ρ(33; 6) + ρ S (33; 6)(0,5) + ρ T (33; 6)()

2 Aproximamos los valores de las derivadas parciales mediante el promedio de las derivada parcial con incremento de la variable independiente positivo y con incremento negativo: ρ S (33; 6) ( ) ρ(34; 6) ρ(33; 6) ρ(3; 6) ρ(33; 6) + = Por lo tanto = (6,77 6 5, + 6) = 0,775 ρ T (33; 6) ( ) ρ(33; 8) ρ(33; 6) ρ(33; 4) ρ(33; 6) + = = (5,73 6 6,3 + 6) = 0,5 4 ρ(33,5; 7) L(33,5; 7) = 6 + 0,3875 0,5 = 6,65 b) Para estimar el valor medio de la densidad del agua de mar para el rango de salinidades y temperaturas de las se tienen observaciones y considerar el número de subintervalos en cada eje que permita utilizar el mayor número de datos hemos de utilizar 6 subintervalos para la salinidad y otros 6 para la temperatura. En este caso los valores de la densidad estarán en los vértices de los rectángulos que genera la partición elegida. Si elegimos el valor de la densidad correspondiente al vértice más próximo al origen en cada rectángulo, la suma de Riemann de dicha partición se obtiene sumando todos los valores de la tabla excepto los de la primera fila y los de la última columna y multiplicado por dos, que es el área de cada rectángulo. El valor que se obtiene es 946,0 = 89,0 Entonces un valor aproximado de la densidad media del agua es 89,0/7 = 6,78. Este valor se ha obtenido dividiendo el valor de la suma de Riemann por el área de la región de los valores de salinidad y temperatura.. Para la función f(x, y) = e ax+by cos(x + y) + e ax+by sen(x + y) obtened los valores de a y b tales que en el punto (0, 0) la derivada direccional es máxima en la dirección de la bisectriz del primer cuadrante y tiene el valor 3. Como la dirección de máximo crecimiento debe ser la bisectriz del primer cuadrante el gradiente de f debe tener esa dirección; por lo tanto a y b deben ser tales que f f (0, 0) = (0, 0). x y Además como el valor de la derivada direccional en la dirección de máximo crecimiento es 3, debe verificarse ( ) ( ) f f (0, 0) + (0, 0) = 8. x y Se tiene que f x (x, y) = a exp(ax + by) cos(x + y) exp(ax + by) sin(x + y)+ +a exp(ax + by) sin(x + y) + exp(ax + by) cos(x + y) f y (x, y) = b exp(ax + by) cos(x + y) exp(ax + by) sin(x + y)+ +b exp(ax + by) sin(x + y) + exp(ax + by) cos(x + y)

3 Por lo tanto el valor de las derivadas parciales en (0, 0) es a + para la derivada parcial respecto de x y b + para la otra. La primera condición implica a = b, la segunda a =. 3. Un barco arroja al mar un vertido tóxico de metales pesados (se trata de mercurio fundamentalmente). Un estudio estima que al cabo de tres días la concentración de mercurio en la superficie alrededor del barco se puede aproximar por la función C(x, y) = 4x 4xy + 4y, considerando el barco en el origen de coordenadas. Un sistema de boyas de observación se sitúa a una distancia de 5 millas náuticas del barco formando una circunferencia. Las boyas tienen un dispositivo que dispara una alarma cuando la concentración de metales pesados es superior a 300 ppb (partes por billón). La alarma se disparó. Es buena la conclusión del estudio sobre la concentración de metales pesados que produjo el barco? Explicar por qué. Entre qué valores varía la concentración de mercurio a 5 millas náuticas del barco según la estimación del estudio? Debemos indagar sobre los valores de la concentración en una circunferencia centrada en el barco de radio 5 millas y debemos obtener los valores entre los que varía la concentración sobre dicha circunferencia. Si la función concentración estimada varía en un rango por debajo de 300 ppb, teóricamente no se dispararía la alarma y las conclusiones del estudio serían erróneas. Para evaluar el rango de variación de la concentración estimada debemos obtener los extremos absolutos de la función C en la circunferencia x + y = 5. Esta curva es la curva de nivel correspondiente al valor cero de la función g(x, y) = x + +y 5. Por lo tanto, hemos de obtener los puntos (x, y) que verifican las ecuaciones Este sistema es equivalente al sistema 8x 4y = xλ 4x + y = yλ x + y = 5. C(x, y) = λ g(x, y) g(x, y) = 0. x = y x + y = 5 Dado que x = y, de la segunda ecuación se obtiene x = ±5/. Volviendo a la primera ecuación, que es equivalente a x = ±y, se obtienen los puntos Dado que y (5/, 5/ ), ( 5/, 5/ ), (5/, 5/ ) y ( 5/, 5/ ). C(5/, 5/ ) = C( 5/, 5/ ) = 50 C(5/, 5/ ) = C( 5/, 5/ ) = 50 la concentración estimada varía entre 50 ppb y 50 ppb a una distancia de 5 millas del barco. Es decir, en una circunferencia de radio 5 millas y centrada en el barco, nunca se supera la concentración de 300 ppb. Una consecuencia del estudio es que la alarma de la boya no debe dispararse cuando su distancia al barco es de 5 millas. Teniendo en cuenta los datos de que se dispone podemos afirmar que la estimación de la concentración en el citado informe es errónea. }. 3

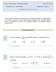
4 4. La temperatura de los puntos de una plancha es inversamente proporcional a la distancia a un cierto punto P de la misma. Obtened la temperatura media de la plancha en un disco de 5 unidades de radio. El punto P está en la circunferencia que delimita dicho disco y la temperatura en el punto de la circunferencia diametralmente opuesto a P es 00 C. Podemos colocar los ejes coordenados de forma que que el disco D está definido por D = {(x, y) x + y 0y} Dado que T (x, y) = k x + y se tiene que el punto opuesto a P sobe la circunferencia es (0, 0). Por lo tanto T (0, 0) = k/0 = 00, entonces k = 000. El área del disco es 5 y el promedio se calcula mediante la integral 5 D Utilizando coordenadas polares tenemos que Se obtiene 40 D 000 x + y = 40 D x + y dxdy D = {(θ, r) 0 θ, 0 r 0 sen θ} ( 0 sen θ dxdy =40 x + y 0 0 = 400 [ cos θ] 0 = 800 El promedio es 800/ 54, C. 5. Calcular la integral 3 y xe y dx dy ) dr dθ = sen θ dθ = en el orden que aparece y cambiando el orden de integración. Haced un esquema del recinto de integración. Figura : Recinto de integración 4

5 La figura muestra la región de integración, es decir, Como región tipo I se tiene que R = {(x, y) y 9, y x 3} R = {(x, y) x 3, y x } Calculando la integral como región tipo I se tiene = 3 x xe y dydx = Como región de tipo II se obtiene 3 3 [ e x ex ] 3 = e (e8 9). = [9ey ] 9 y xe y dxdy = [xe y ] x dx = 3 ( ) xe x ex dx = [ x e y] 3 y dy = (9e y ye y ) dy = ye y dy = (9e9 9e) [yey ] 9 + = (9e9 9e 9e 9 + e + e 9 e) = e (e8 9). e y dy = 5