ETSII Febrero Análisis Matemático.
|
|
|
- Paula Sáez Marín
- hace 5 años
- Vistas:
Transcripción
1 Departamento de Análisis Matemático ETSII Febrero Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese la función f : R R dada por f (x) = 2x2 + 6x + 10 x (x R). Se pide: a) Estudiar los intervalos de crecimiento y decrecimiento, los extremos absolutos y la imagen. b) Basándose en el apartado anterior, calcular el número de soluciones de la ecuación f (x) = m según el valor del número real m. Problema 3. (1.5 puntos) En un triángulo equilátero de lado 4 se inscribe un rectángulo apoyado en uno de sus lados. Calcular el área máxima que puede tener un rectángulo de esta forma (ver figura abajo). Problema 4. (1.5 puntos) Calcular el volumen del sólido de revolución obtenido al girar respecto al eje OX la función f (x) = 1 con x [0,1]. 1 + ex Problema 5. (2 puntos) (Ingeniería superior) Resolver la ecuación diferencial (3x + 2arctany)dx + x dy = y2 (Gestión y Sistemas) Calcular los extremos absolutos de la función f (x,y) = 2x 2 2xy + y 2 x en el cuadrado definido por {0 x 1, 0 y 1}. Granada 16 de febrero de 2000.
2 Departamento de Análisis Matemático ETSII Febrero Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese la función f : R R dada por f (x) = 2x2 + 6x + 10 x (x R). Se pide: a) Estudiar los intervalos de crecimiento y decrecimiento, los extremos absolutos y la imagen. b) Basándose en el apartado anterior, calcular el número de soluciones de la ecuación f (x) = m según el valor del número real m. Problema 3. (1.5 puntos) En un triángulo equilátero de lado 4 se inscribe un rectángulo apoyado en uno de sus lados. Calcular el área máxima que puede tener un rectángulo de esta forma (ver figura abajo). Problema 4. (1.5 puntos) Calcular el volumen del sólido de revolución obtenido al girar respecto al eje OX la función f (x) = 1 con x [0,1]. 1 + ex Problema 5. (2 puntos) (Ingeniería superior) Resolver la ecuación diferencial (3x + 2arctany)dx + x dy = y2 (Gestión y Sistemas) Calcular los extremos absolutos de la función f (x,y) = 2x 2 2xy + y 2 x en el cuadrado definido por {0 x 1, 0 y 1}. Granada 16 de febrero de 2000.
3 Departamento de Análisis Matemático Ingeniería Técnica en Informática de Sistemas. Análisis Matemático. Problema 1. Consideremos la función f :]0,+ [ R dada por f (x) = lnx x + 2 (x ]0,+ [). a) Calcular los intervalos de crecimiento y decrecimiento y los extremos relativos de f. Cuál es su imagen?. b) Calcular el número de soluciones de la ecuación f (x) = 0 en ]0,+ [. Problema 2. Se desea construir un cono usando una plancha circular de hojalata de radio R. Para ello, se toma un sector circular de dicha plancha y se une por los bordes rectos. Determinar el mayor volumen que puede tener un cono construido de esta forma. Problema 3. a) Calcular el área comprendida entre las curvas x = y 3 y x = y 2 en el primer cuadrante. b) Calcular el área comprendida entre las curvas y = 2x 2 e y = x 4 2x 2. c) Calcular el volumen del sólido de revolución obtenido al girar respecto del eje OY la región bajo 1 la curva y = x 2 (1 + x 2 con x [1,+ [. ) Problema 4. Calcular los siguientes ites: 1 cosx x 0 x + x 2 (e x + x) 1/x x 0 2 x 3 x x x Granada 13 de diciembre de 1999.
4 Departamento de Análisis Matemático ETSII Febrero Análisis Matemático. Problema 1. (2 puntos) Calcular, según el valor del parámetro real m, el número de soluciones de la ecuación e x = mx x R. Problema 2. (2 puntos) Consideremos un rectángulo cuya base se encuentra sobre el eje de abcisas y cuyos otros dos vértices se hallan sobre la gráfica de la función y = 4senx; 0 x π (ver figura de abajo). Encontrar el perímetro máximo que puede tener un rectángulo de esta forma. Problema 3. (2 puntos) Calcular el volumen del sólido de revolución obtenido al girar respecto al eje OX la función f (x) = x x 2 con x [0, ). + 4 Problema 4. (2 puntos) Consideremos la función f : R 2 R definida por f (x,y) = x 3 +y 2 +x 2 y+2y+1. a) Calcular los extremos relativos y puntos de silla de f en R 2. b) Calcular los extremos absolutos de f en el conjunto A = { (x,y) R 2 : x 0, y 0, x + y 2 } (triángulo de vértices (0,0), (2,0) y (0,2) ). Granada 1 de Febrero de 2001.
5 Departamento de Análisis Matemático ETSII Septiembre Análisis Matemático. Problema 1. (4 puntos) Calcular: (a) e 1 (b) x 1 (c) x + log(log x) dx x 2x x 4 3 x 1 4 x 3 e2001/x 1 log ( ) x+1 x (d) Volumen del sólido de revolución obtenido al hacer girar al rededor del eje OX la región limitada por x = y 3, x = 0, x = 8. Problema 2. (2 puntos) Se debe construir un canalón para lluvia a partir de una lámina metálica que tiene 30cm de ancho, doblando la tercera parte de la lámina de cada lado hasta que forme un ángulo θ (ver figura abajo). Cómo debe elegirse θ para que el canalón lleve la cantidad máxima de agua? Problema 3. (2 puntos) Consideremos la función f : R 2 R definida por f (x,y) = x 3 3xy + y 3. a) Calcular los extremos relativos y puntos de silla de f en R 2. b) Calcular los extremos absolutos de f en el conjunto A = { (x,y) R 2 : x 0, y 0, x + y 3 } (triángulo de vértices (0,0), (3,0) y (0,3) ). Granada 20 de septiembre de 2001.
6 Análisis Matemático 1 de Informática. Granada, 11 de Septiembre de ) Calcular el área del recinto: A = { (x,y) IR 2 : x 2 + y 2 1, x 2 + (y 1) 2 1 } 2.) De entre todas las cuerdas MN de la circunferencia unidad paralelas al eje OY, determinar la que forma con el origen O un triángulo de área máxima. 3.) Determinar el número de raíces reales de la función en el intervalo [ 2π,2π]. f (x) = xsenx + cosx 4.) Sea f : K IR la función definida por f (x,y) = f (x,y) = xy(1 x)(1 y), donde K es el cuadrado de vértices (0,0),(1,0),(1,1) y (0,1). Calcular los extremos absolutos de f en K.
7 Análisis Matemático 1 de Informática. Granada, 13 de Febrero de ) Responder razonadamente si son ciertas las siguientes afirmaciones: a) Sea f : [a, b] IR una función estrictamente creciente con f (a) f (b) < 0. Entonces c (a,b) tal que f (c) = 0. b) Toda función continua en un punto es derivable en dicho punto. Z 3 [ ] dx 1 3 c) 0 (x 1) 2 = = 1 x = 3 2. R x 2 0 sent t dt d) x 0 x 2 = 1. 2.) Consideremos un octógono en el que todos los ángulos interiores son iguales (y por tanto iguales a 135 ) y las longitudes de los lados alternados son iguales (ver figura). De entre todos los octógonos de este tipo de perímetro 8, calcular el que tenga mayor superficie. a b a b b a b a 3.) Sea f : K IR la función definida por f (x,y) = f (x,y) = (2x 2 + y 2 )e (x2 +y 2), donde A = { (x,y) IR 2 : x 2 + y 2 4 }. Calcular los extremos absolutos de f en A. 4.) Calcular Z (x 2 + y)dxdy, siendo A = { (x,y) IR 2 : x 0, y 0, 1 x 2 + y 2 4 }. A
8 1 Análisis Matemático 1 de Informática. Granada, 29 de Enero de Contestar razonadamente a los siguientes enunciados: a) Justifíquese cuáles de los siguientes conjuntos son compactos y cuáles no: 1) {x, y) R 2 ; x 2 + y 2 = 2}. 2) {x, y) [0, 1] [0, 1]; 0 x < y 1} 3) {x, y) R 2 ; x 2 + y 2 2}. b) Justifíquese si el punto (0, 0) es un éxtremo de la función f(x, y) = x + y y A = [ 1, 1] [ 1, 1] c) Justifíquese si el punto (0, 0) es un éxtremo de la función f(x, y) = x + y y A = [ 1, 1] [ 1, 1] d) Sea F la función definida mediante la expresión F (x) = 1+x 2 0 Calcular F (x) en los puntos donde sea posible. sen(t) dt. t 2. Calcular el área máxima de un trapecio, inscrito en una circunferencia de radio 1, cuya base coincide con el diámetro de dicha circunferencia. 3. Calcúlense los extremos de la función f(x, y) = 4x 3 + 3x 2 6x + 3y 2, en el conjunto A = {(x, y) R 2 : x 2 + y 2 1, x 0} 4. Calcúlese el volumen de madera desprendido al taladrar por el centro una bola de madera de 9cm de radio con una broca de 1 cm de radio.
9 1 Análisis Matemático 1 de Informática. Granada, 20 de Septiembre de Contestar razonadamente a los siguientes enunciados: a) Sea f : [a, b] R una función derivable en el intervalo abierto (a, b). Entonces existe un punto c (a, b) verificando que f (c) = f(b) f(a). b a b) El ite existe y vale 1 3. x 0 sin(x) 0 sin(t) dt t x 2. Hallar la longitud de la catenaria. Ecuación : f : [ a, a] R : f(x) = 1 2 a(ex/a + e x/a ) 3. Consideremos la parábola de ecuación y = f(x) = 4 x 2. Sea (a, f(a)) un punto en la gráfica de la mencionada parábola. Calcular a para que el triángulo que determina la recta tangente a la parábola en el punto (a, f(a)) con los semiejes positivos tenga área mínima. 4. Sea K = {(x, y) R 2 / y 0, 4x 2 + y 2 4}. Calcular los extremos absolutos de la función f : K R definida por f(x, y) = 4x 2 + y 2 16y 3, (x, y) K.
10 Análisis Matemático 1 de Informática. Granada, 21 de Diciembre de ) Intentaremos aproximar el log(1,5) con un error menor que A tal efecto se pide calcular el polinomio de Taylor de grado n, P n (x), de la función f (x) = log(1 + 20x) (x ( 20 1,+ ]). Calcular el menor n para el cual se verifica que el error cometido al aproximar log(1,5) mediante un determinado valor de P n (x) sea menor que ) Después de recibir un golpe, un espejo rectangular de base 1 y altura 2 se ha roto en una de sus esquinas y ha perdido un trozo en forma triangular de lados 0 < a < 2 y 0 < b < 1 (véase figura abajo). Pretendemos conseguir otro espejo rectangular cortando el trozo restante mediante dos paralelas a los lado (ver línea discontinua de la figura inferior). Calcular las dimensiones del espejo rectangular de mayor área que podemos conseguir de esta forma. 3.) Sea f (x) la función cuya gráfica es la línea recta que pasa por los puntos (0,r) y (h,r), donde r,r,h IR +. Cuando giramos la gráfica de f entre 0 y h alrededor del eje OX obtenemos un tronco de cono de radios r,r y altura h. Obtener, mediante la fórmula del volumen de un sólido de revolución, el volumen de dicho tronco de cono.
11 Ingeniero Técnico en Informática de Gestión y de Sistemas ANÁLISIS MATEMÁTICO. FEBRERO DE 2006 Problema 1. [2 puntos] (a) Demuéstrese que e log(x) x para todo x > 0. (b) Demuéstrese, usando el apartado anterior si se quiere, que e x/e x para todo x > 0. (c) Decidir razonadamente, usando de nuevo el apartado (a) si se quiere, cuál de los siguientes números es mayor: e 5 ó 5 e. Problema 2. [2 puntos] Calcula el volumen generado al girar alrededor del eje OX la gráfica de la función f (x) = cosh(x) con x [0, 7]. Nota: cosh(x) = ex +e x. 2 Problema 3. [2 puntos] Halla los puntos de la curva { x 2 xy + y 2 z 2 = 1 x 2 + y 2 = 1 que están más próximos al origen de coordenadas. Problema 4. [2 puntos] Calcula la integral x x 2 + y d(x,y) donde A = { (x,y) R 2 : x 2 + y 2 2x, x y }. 2 A Granada, 10 de febrero de 2006.
12 Ingeniero Técnico en Informática de Gestión y de Sistemas ANÁLISIS MATEMÁTICO. SEPTIEMBRE DE 2006 Problema 1. Demuéstrese que la desigualdad se verifica para todo x (0,1). 1 + x < e x < 1 1 x Problema 2. Usando un desarrollo de Taylor adecuado de la función f (x) = log(1 + x), aproximar log(1,25) con un error menor que Problema 3. Calcúlense los extremos absolutos y relativos de la función f : A R dada por f (x,y) = x 2 + 4xy + y 2, en el conjunto A = {(x,y) R R + 0 : x2 + y 2 1} {(x,y) R R : 2 2x + y, 2x y 2}. Problema 4. Calcular el volumen formado por la intersección de las esferas S 1 = {(x,y,z) R 3 : x 2 + y 2 + z 2 1} S 2 = {(x,y,z) R 3 : x 2 + y 2 + z 2 2z}. Granada, 11 de septiembre de 2006.
13 Ingeniero en Informática, Ingeniero Técnico en Informática de Gestión y de Sistemas ANÁLISIS MATEMÁTICO. CONVOCATORIA ORDINARIA DE FEBRERO DE 2007 Problema 1. Consideremos la función f : R R dada por f (x) = 3 2 x4 2x 3 6x 2 ( ) x R. Se pide: (a) Calcular la imagen de la función f. (b) Calcular el número de soluciones de la ecuación f (x) = m según los valores del parámetro m R. Problema 2. Consideremos la función Se pide: f (x) = log(x) x 1/4 ( x ]0,1] ). (a) Calcular el volumen obtenido al girar la gráfica bajo la función f respecto del eje OX. (b) Calcular el volumen obtenido al girar la gráfica bajo la función f respecto del eje OY. Problema 3. Calcúlense los extremos absolutos de la función f : Ω R dada por f (x,y) = e xy, en el conjunto Ω = { (x,y) R 2 : x 2 + 4y 2 8 }. Problema 4. Calcúlese el área del conjunto A = { (x,y) R 2 : (x 1) 2 + y 2 1, x 2 + (y 1) 2 1 }. Granada, 16 de febrero de 2007.
14 Ingeniero en Informática, Ingeniero Técnico en Informática de Gestión y de Sistemas ANÁLISIS MATEMÁTICO. SEPTIEMBRE DE 2007 Problema 1. Sea f : R + R la función definida por a) Calcular los puntos críticos de f. f (x) = x [sen(log(x)) cos(log(x))]. 2 b) Clasificar los puntos críticos obtenidos en el apartado anterior. c) Calcular la imagen de f. Problema 2. Usando un desarrollo de Taylor adecuado de la función f (x) = cosh(x) = ex + e x, 2 aproximar el valor de cosh(0,5) con un error menor que Problema 3. Consideremos la función a) Calcular y clasificar los puntos críticos de f. f : R 2 R f (x,y) = 3(x 2 1)y 2x 4. b) Calcular los extremos absolutos de f en el conjunto A = {(x,y) R 2 : y 2,y x 2 }. Problema 4. Calcular siendo A x 3 y sen( πy2 x )d(x,y), A = {(x,y) R 2 : x 3 y x}. Granada, 17 de Septiembre de 2007.
CÁLCULO ELEMENTAL PROBLEMAS. Valor absoluto. Funciones y sus gráficas
 CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
Problemas de Cálculo Matemático E.U.A.T. CURSO Primer cuatrimestre
 1 Problemas de Cálculo Matemático EUAT CURSO 00-003 Primer cuatrimestre Problemas del Tema 5 Teoremas relativos a funciones derivables y aplicaciones 1 La función f(x) = 1 3 x se anula para x 1 = 1 y para
1 Problemas de Cálculo Matemático EUAT CURSO 00-003 Primer cuatrimestre Problemas del Tema 5 Teoremas relativos a funciones derivables y aplicaciones 1 La función f(x) = 1 3 x se anula para x 1 = 1 y para
x 2 + 1, si x 0 1 x 2 si x < 0 e x, si x > 0 x si 0 x < 2 f(x) = x + 2 si 2 x < 3 2x 1 si 3 x < 4 tgx, 0 < x < π/4
 CÁLCULO. Curso 2003-2004. Tema 7. Derivabilidad.. Estudiar la continuidad y la derivabilidad de las funciones: {, si 0 (a) e, si > 0 2 +, si > 0 (b), si = 0 2. Dada la función (c) 2 si < 0 e, si > 0 2
CÁLCULO. Curso 2003-2004. Tema 7. Derivabilidad.. Estudiar la continuidad y la derivabilidad de las funciones: {, si 0 (a) e, si > 0 2 +, si > 0 (b), si = 0 2. Dada la función (c) 2 si < 0 e, si > 0 2
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones. 1. Estudiar la acotación de las siguientes funciones:
 Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS
 SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
Escuela Politécnica Superior de Málaga. CÁLCULO
 Escuela Politécnica Superior de Málaga. CÁLCULO. Cálculo en una variable.. Prueba que y 3 no son números racionales. En los números que se describen a continuación, Cuáles son racionales y cuales no? Encontrar
Escuela Politécnica Superior de Málaga. CÁLCULO. Cálculo en una variable.. Prueba que y 3 no son números racionales. En los números que se describen a continuación, Cuáles son racionales y cuales no? Encontrar
1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones:
 APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
Escuela Politécnica Superior de Málaga. CÁLCULO
 Escuela Politécnica Superior de Málaga. CÁLCULO. Cálculo en una variable.. En los números que se describen a continuación, Cuáles son racionales y cuales no? Encontrar la fracción generatriz para aquellos
Escuela Politécnica Superior de Málaga. CÁLCULO. Cálculo en una variable.. En los números que se describen a continuación, Cuáles son racionales y cuales no? Encontrar la fracción generatriz para aquellos
Área entre curvas. Ejercicios resueltos. 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x.
 Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
De x = 1 a x = 6, la recta queda por encima de la parábola.
 Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Aplicaciones físicas
 Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
Problemas propuestos con solución Aplicaciones físicas ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ulles Índice 1 Integral doble: valor medio 1 2 Integral doble:
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
x = 1 y que la recta tangente a la gráfica de la función en el punto de abcisa x=0 tiene la a)estudia y calcula las asístontas de la gráfica de f.
 Jueves 9 de noviembre de 17 Ejercicio 1. Problema de optimización. Se considera una ventana rectangular en la que el lado de arriba se ha sustituido por un triángulo equilátero. Calcula la longitud de
Jueves 9 de noviembre de 17 Ejercicio 1. Problema de optimización. Se considera una ventana rectangular en la que el lado de arriba se ha sustituido por un triángulo equilátero. Calcula la longitud de
a) Calcular las asíntotas, el máximo y el mínimo absolutos de f (x). 4. (SEP 04) Sabiendo que una función f (x) tiene como derivada
 Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Selectividad hasta el año incluido = 0. Página 1 de 13 ANÁLISIS
 ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
Más ejercicios y soluciones en fisicaymat.wordpress.com FUNCIONES
 FUNCIONES 1- a) Dibuje el recinto plano limitado por la parábola y=4x-x 2 y las tangentes a la curva en los puntos de intersección con el eje de las abscisas. b) Halle el área del recinto dibujado en a).
FUNCIONES 1- a) Dibuje el recinto plano limitado por la parábola y=4x-x 2 y las tangentes a la curva en los puntos de intersección con el eje de las abscisas. b) Halle el área del recinto dibujado en a).
EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable
 EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas
 UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
INTEGRACION EN VARIAS VARIABLES: Integrales dobles. 1. e x+y dy dx. 3. Evaluar las siguientes integrales en los recintos que se indican:
 INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
Ejercicios de Matemáticas I - Relación 5
 Ejercicios de Matemáticas - Relación 5. Calcula y simplifica todo lo que puedas las derivadas de las siguientes funciones: / f./d sen. C 3/ 2/f./D cos 2. 3 / 3/ f./d cos p 5/ f./d 2 C r C 4/ f./d 3p 6/
Ejercicios de Matemáticas - Relación 5. Calcula y simplifica todo lo que puedas las derivadas de las siguientes funciones: / f./d sen. C 3/ 2/f./D cos 2. 3 / 3/ f./d cos p 5/ f./d 2 C r C 4/ f./d 3p 6/
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
c) Demuestra que la función f(x) anterior y g(x) = 2x 1 se cortan al menos en un punto. (1 punto) 2
 Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Integración 416. a) Limitada por y = x 2 + 1,y = 0,x = 1,x = 1 alrededor del eje OX: b) Limitada por y = x,x = 4,y = 0 alrededor del eje OX:
 Integración 416 Problema 2 En los siguientes apartados usar el método de discos para hallar el volumen del sólido generado al girar la región dada entre los límites dados sobre el eje indicado: a) Limitada
Integración 416 Problema 2 En los siguientes apartados usar el método de discos para hallar el volumen del sólido generado al girar la región dada entre los límites dados sobre el eje indicado: a) Limitada
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2016-2017) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
PROBLEMAS DE CÁLCULO I
 INGENIERÍAS TÉCNICAS INDUSTRIALES PROBLEMAS DE CÁLCULO I UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas ING. TEC. IND. MECANICA, ELECTRICIDAD Y ELECTRÓNICA 24
INGENIERÍAS TÉCNICAS INDUSTRIALES PROBLEMAS DE CÁLCULO I UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas ING. TEC. IND. MECANICA, ELECTRICIDAD Y ELECTRÓNICA 24
INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx
![INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx](/thumbs/56/39119384.jpg) INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
Problemas Tema 3 Enunciados de problemas de Derivabilidad
 página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
+ ax 2 + bx) x. ( 2 sen(x) 0 (a + b sen(x) sen(2x))2 dx sea mínima.
 Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Ejercicio 2.- [2 5 puntos] Sea f : ( 2, + ) R la función
Opción A Ejercicio 1.- [2 5 puntos] Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Ejercicio 2.- [2 5 puntos] Sea f : ( 2, + ) R la función
Práctica 7. sen 2 x cos x dx. c) 3x 2 x 2 dx. f) 3. Hallar el área encerrada por las curvas:
 ANÁLISIS I MATEMÁTICA ANÁLISIS (Computación) Práctica 7 I. epaso: integración en una variable. Calcular: sen x. b) π sen x. c) El área entre las curvas y = sen x, y =, x =, x = π.. Calcular: x sen x. b)
ANÁLISIS I MATEMÁTICA ANÁLISIS (Computación) Práctica 7 I. epaso: integración en una variable. Calcular: sen x. b) π sen x. c) El área entre las curvas y = sen x, y =, x =, x = π.. Calcular: x sen x. b)
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Matemáticas II. * Análisis III: Integrales * o) x x. p) 3. q) 5. r) 1. s) e 2x 3 dx. t) 5 dx. u) x2 5 x 4. v) x3 3x 2 x 1. z) 3
 I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1
 Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1 Ejercicio 1: Estudiar el dominio, asíntotas, signo, crecimiento, decrecimiento, máximos y mínimos relativos de la función f(x) = e 2x
Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1 Ejercicio 1: Estudiar el dominio, asíntotas, signo, crecimiento, decrecimiento, máximos y mínimos relativos de la función f(x) = e 2x
EJERCICIOS PARA VERANO. MATEMÁTICAS I 1º BACH
 Desarrollar los siguiente valores absolutos f(x) = x² + 5x 4 - x - 2 f(x) = x² -4x + 3 + x - 3 f(x) = x x f(x) = x / x Resolver las ecuaciones exponenciales: Resolver los sistemas de ecuaciones exponenciales:
Desarrollar los siguiente valores absolutos f(x) = x² + 5x 4 - x - 2 f(x) = x² -4x + 3 + x - 3 f(x) = x x f(x) = x / x Resolver las ecuaciones exponenciales: Resolver los sistemas de ecuaciones exponenciales:
Integración en una variable (repaso)
 Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 2 Práctica 8: Integración Integración en una variable (repaso). Calcular: sen x. 2π sen x. El área entre las curvas y = sen x, y =, x =, x
Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 2 Práctica 8: Integración Integración en una variable (repaso). Calcular: sen x. 2π sen x. El área entre las curvas y = sen x, y =, x =, x
Boletín I. Cálculo diferencial de funciones de una variable
 CÁLCULO Boletín I. Cálculo diferencial de funciones de una variable 1. Demuestra que la ecuación x + sin x = Ejercicios básicos 1 x + 3 tiene al menos una raíz en [0, π]. 2. Justifica la existencia de
CÁLCULO Boletín I. Cálculo diferencial de funciones de una variable 1. Demuestra que la ecuación x + sin x = Ejercicios básicos 1 x + 3 tiene al menos una raíz en [0, π]. 2. Justifica la existencia de
Boletín II. Cálculo diferencial de funciones de una variable
 CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. Sea f la función dada por 5x 2. a) Utiliza la definición de derivada para demostrar que f (x) = 10x. b) Calcula
CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. Sea f la función dada por 5x 2. a) Utiliza la definición de derivada para demostrar que f (x) = 10x. b) Calcula
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
EJERCICIOS DE SELECTIVIDAD / COMUNIDAD DE MADRID MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II BLOQUE: ANÁLISIS
 EJERCICIOS DE SELECTIVIDAD / COMUNIDAD DE MADRID MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II BLOQUE: ANÁLISIS. Septiembre( 00 / OPCIÓN B / EJERCICIO ) (puntuación máima puntos) Se considera
EJERCICIOS DE SELECTIVIDAD / COMUNIDAD DE MADRID MATERIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II BLOQUE: ANÁLISIS. Septiembre( 00 / OPCIÓN B / EJERCICIO ) (puntuación máima puntos) Se considera
= λ + 1 y el punto A(0, 7, 5)
 94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
Integración múltiple: integrales dobles
 Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
APLICACIONES DE LAS DERIVADAS. 1. Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican:
 Matemáticas Aplicaciones de las derivadas APLICACIONES DE LAS DERIVADAS Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican: 5 a) f, c) f lntg, en en 8 b) f, en d)
Matemáticas Aplicaciones de las derivadas APLICACIONES DE LAS DERIVADAS Halla las rectas tangente y normal a las siguientes funciones en los puntos que se indican: 5 a) f, c) f lntg, en en 8 b) f, en d)
TEMA 2: CÁLCULO DIFERENCIAL DE UNA VARIABLE.
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Ingeniería Industrial (GITI/GITI+ADE) Ingeniería de Telecomunicación (GITT/GITT+ADE) CÁLCULO Curso 05-06 TEMA : CÁLCULO
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Ingeniería Industrial (GITI/GITI+ADE) Ingeniería de Telecomunicación (GITT/GITT+ADE) CÁLCULO Curso 05-06 TEMA : CÁLCULO
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1. [2 5 puntos] Calcula lim x 0 siendo Ln(1 + x) el logaritmo neperiano de 1 + x. Ln(1 + x) sen x, x sen x Ejercicio 2. Sea f : R R la función definida por f(x) = e x/3. (a) [1 punto]
Opción A Ejercicio 1. [2 5 puntos] Calcula lim x 0 siendo Ln(1 + x) el logaritmo neperiano de 1 + x. Ln(1 + x) sen x, x sen x Ejercicio 2. Sea f : R R la función definida por f(x) = e x/3. (a) [1 punto]
Funciones de una variable
 Ejercicios de Análisis Matemático Funciones de una variable Ejercicio 1. Supuesto que s t < x y, donde s,x R, t,y R+, prueba que s t < s + x t + y < x y Ejercicio 2. Discute la validez de las siguientes
Ejercicios de Análisis Matemático Funciones de una variable Ejercicio 1. Supuesto que s t < x y, donde s,x R, t,y R+, prueba que s t < s + x t + y < x y Ejercicio 2. Discute la validez de las siguientes
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
LA INTEGRAL DEFINIDA. APLICACIONES
 13 LA INTEGRAL DEFINIDA. APLICACIONES REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
13 LA INTEGRAL DEFINIDA. APLICACIONES REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
Se pide: estudiar su compatibilidad según los valores del parámetro a, y resolverlo cuando sea compatible.(3 puntos).
 PAU. CASTILLA Y LEON - 1998 a x + y z = z PR-1. Dado el sistema x + ay + z = x 3x + 3y + z = y Se pide: estudiar su compatibilidad según los valores del parámetro a, y resolverlo cuando sea compatible.(3
PAU. CASTILLA Y LEON - 1998 a x + y z = z PR-1. Dado el sistema x + ay + z = x 3x + 3y + z = y Se pide: estudiar su compatibilidad según los valores del parámetro a, y resolverlo cuando sea compatible.(3
Hallar el dominio de las siguientes funciones : 1. log F(x) = 234. F(x) = x F(x) = ln( F(x) = 9 3. x.calcular simplificando
 Hallar el dominio de las siguientes funciones : 4. F() = 3 8 0 6 5. F() = 3 7 6. F() = 6 7. F() = 9 4 8. F() = ln 9. F() = e e 30. F() = e 3 3. F() = log 7 3. F() = sen 33. F() = 3 8 34. F() = 3 3 4 35.
Hallar el dominio de las siguientes funciones : 4. F() = 3 8 0 6 5. F() = 3 7 6. F() = 6 7. F() = 9 4 8. F() = ln 9. F() = e e 30. F() = e 3 3. F() = log 7 3. F() = sen 33. F() = 3 8 34. F() = 3 3 4 35.
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 Opción A Ejercicio 1.- Sea la función f : (0, + ) R definida por f(x) = 1 +ln(x) donde ln denota la función x logaritmo neperiano. (a) [1 75 puntos] Halla los [ extremos ] absolutos de f (abscisas donde
Opción A Ejercicio 1.- Sea la función f : (0, + ) R definida por f(x) = 1 +ln(x) donde ln denota la función x logaritmo neperiano. (a) [1 75 puntos] Halla los [ extremos ] absolutos de f (abscisas donde
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
(1-mx)(2x+3) x 2 +4 = 6. x > -1
 . [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
. [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
Cálculo Diferencial Enero 2015
 Laboratorio # 1 Desigualdades I.- Determinar los valores de que satisfacen simultáneamente las dos ecuaciones dadas. y y y y II. - Determina los valores de que satisfagan al menos una de las condiciones.
Laboratorio # 1 Desigualdades I.- Determinar los valores de que satisfacen simultáneamente las dos ecuaciones dadas. y y y y II. - Determina los valores de que satisfagan al menos una de las condiciones.
Derivadas Parciales. Aplicaciones.
 RELACIÓN DE PROBLEMAS FUNDAMENTOS MATEMÁTICOS DE LA INGENIERÍA Curso 2004/2005 Escuela Universitaria de Ingeniería Técnica Agrícola Departamento de Matemática Aplicada I Tema 3. Derivadas Parciales. Aplicaciones.
RELACIÓN DE PROBLEMAS FUNDAMENTOS MATEMÁTICOS DE LA INGENIERÍA Curso 2004/2005 Escuela Universitaria de Ingeniería Técnica Agrícola Departamento de Matemática Aplicada I Tema 3. Derivadas Parciales. Aplicaciones.
EXAMEN DE MATEMÁTICAS I. Test
 Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
H K V T E X. Bachillerato por madurez. Victor Solano Mora. Examen I-2014
 M H K V T E X achillerato por madurez Examen I-014 HK V T E X xm: I-014 Pregunta 1 Uno de los factores de x 4 16y 4 es x + y x + 8y x + y (x y) Pregunta Uno de los factores de x 1 10x es 1 x x + x + 4
M H K V T E X achillerato por madurez Examen I-014 HK V T E X xm: I-014 Pregunta 1 Uno de los factores de x 4 16y 4 es x + y x + 8y x + y (x y) Pregunta Uno de los factores de x 1 10x es 1 x x + x + 4
Curso MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2011-2012 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
Tema 2. GEOMETRÍA ELEMENTAL Y ANALÍTICA.
 Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 2. Hoja 1 Tema 2. GEOMETRÍA ELEMENTAL Y ANALÍTICA. 1. Un solar de forma triangular tiene dos lados de longitudes 140,5 m y 170,6 m, y el
Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 2. Hoja 1 Tema 2. GEOMETRÍA ELEMENTAL Y ANALÍTICA. 1. Un solar de forma triangular tiene dos lados de longitudes 140,5 m y 170,6 m, y el
e x -1 2 e x [2013] [JUN] Dependiendo de los valores de a, estudia la continuidad de la función f(x) = . a si x = 0
![e x -1 2 e x [2013] [JUN] Dependiendo de los valores de a, estudia la continuidad de la función f(x) = . a si x = 0 e x -1 2 e x [2013] [JUN] Dependiendo de los valores de a, estudia la continuidad de la función f(x) = . a si x = 0](/thumbs/84/90930423.jpg) . [204] [ET-A] Sea = (x)2 x-. i) Determina el dominio de f. ii) Halla sus asíntotas. iii) Determina los extremos relativos y estudia la monotonía de f. iv) Dibuja la gráfica de f destacando los elementos
. [204] [ET-A] Sea = (x)2 x-. i) Determina el dominio de f. ii) Halla sus asíntotas. iii) Determina los extremos relativos y estudia la monotonía de f. iv) Dibuja la gráfica de f destacando los elementos
RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA.
 RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA. 1. Sea f : IR IR definida por f() = 2 + 1, IR. Probar, utilizando la definición, que f es derivable en cualquier punto de IR. Encontrar los
RELACIÓN 3a DE EJERCICIOS. MATEMÁTICAS 1. INGENIERÍA QUÍMICA. 1. Sea f : IR IR definida por f() = 2 + 1, IR. Probar, utilizando la definición, que f es derivable en cualquier punto de IR. Encontrar los
FUNCIONES. 7.(99).- Hallar la longitud de los lados del triángulo isósceles de área máxima cuyo perímetro sea 60 m.
 Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
Enunciados de problemas de selectividad. Matemáticas II. Funciones FUNCIONES.(97).- Hay alguna función f() que no tenga límite cuando y que, sin embargo, [f()] sí tenga límite cuando?. Si la respuesta
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V
 GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
en el intervalo - 1-cos(x) 2 si x > 0 sen(x)
 . [04] [ET-A] Sea la función f() = e -. Determinar sus intervalos de crecimiento y decrecimiento, etremos relativos, intervalos de concavidad y conveidad, puntos de infleión y asíntotas. Esbozar su gráfica..
. [04] [ET-A] Sea la función f() = e -. Determinar sus intervalos de crecimiento y decrecimiento, etremos relativos, intervalos de concavidad y conveidad, puntos de infleión y asíntotas. Esbozar su gráfica..
f (x) = 3(1 + x2 cos x)(x sin x 1) 2 x ( x + 7x) 2/3 cos 4 (tan x) ) 1/5 f (x) = 3x4 + 6x 3 9x 2 + 3x + 3 x(x 3 + 3x 1)
 1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
Cálculo diferencial en varias variables (Curso ) a) Estudiar la continuidad en el origen de las funciones dadas.
 CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
CÁLCULO Práctica 4.2 Cálculo diferencial en varias variables (Curso 2017-2018) 1. Sean f, h: IR 2 IR funciones definidas del siguiente modo: x 3 f(x, y) = x 2, (x, y) (0, 0) + y2 a) Estudiar la continuidad
LA CIRCUNFERENCIA. x y r. (x h) (y k) r. d(p; 0) x y r. d(p; C) (x h) (y k) r. Definición. Ecuación de la circunferencia. Geometría Analítica 3
 Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN
 APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN 1. Calcular, aplicando la definición de derivada: f (), siendo f (x) = 3x 1 1 f ( ), siendo f (x) = x 1 Solución: 1; 4. Determinar el dominio y la expresión de
APLICACIONES DE LA DERIVADA Y OPTIMIZACIÓN 1. Calcular, aplicando la definición de derivada: f (), siendo f (x) = 3x 1 1 f ( ), siendo f (x) = x 1 Solución: 1; 4. Determinar el dominio y la expresión de
Cálculo Integral Agosto 2015
 Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
ALGUNOS EJERCICIOS DE C. DIF.
 1 ALGUNOS EJERCICIOS DE C. DIF. 1.-Concepto de función Algunos ejercicios 1.1==En una circunferencia de radio 10 m, se inscribe un rectangulo. Expresar el area del rectangulo en funcion del lado x de la
1 ALGUNOS EJERCICIOS DE C. DIF. 1.-Concepto de función Algunos ejercicios 1.1==En una circunferencia de radio 10 m, se inscribe un rectangulo. Expresar el area del rectangulo en funcion del lado x de la
Análisis Matemático. Grupo D. Examen 1
 Análisis Matemático. Grupo D. Examen Apellidos, Nombre y Firma: Importante: En la puntuación de los problemas no sólo se tendrá en cuenta la solución obtenida sino la exposición correcta de los razonamientos
Análisis Matemático. Grupo D. Examen Apellidos, Nombre y Firma: Importante: En la puntuación de los problemas no sólo se tendrá en cuenta la solución obtenida sino la exposición correcta de los razonamientos
Examen de Matemáticas II (Modelo 2018) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 Problema (2,5 puntos) Dadas las matrices A = 0 0, y I = 0 0 0 0 0 se pide: 0 0 a) (,5 puntos) Obtener los valores de m para
Examen de Matemáticas II (Modelo 208) Selectividad-Opción A Tiempo: 90 minutos 0 Problema (2,5 puntos) Dadas las matrices A = 0 0, y I = 0 0 0 0 0 se pide: 0 0 a) (,5 puntos) Obtener los valores de m para
Pauta Auxiliar N 10 Aplicaciones de la Integral I Viernes 1 de Junio de 2012
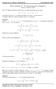 Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
tiene un máximo relativo en x = asíntota horizontal la recta y = 3. Razonar si para a = 2 y b = 3 la función f(x) tiene algún mínimo relativo.
 Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
Selectividad CCNN 006. [ANDA] [SEP-A] Sea f: la función definida por f() = -. a) Estudia la derivabilidad de f. b) Determina los intervalos de crecimiento y decrecimiento de f. c) Calcula los etremos relativos
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
Opción A Ejercicio 1.- Sea f : (0,+ ) R la función definida por f(x) = 3x + 1 x. (a) [1 5 puntos] Determina los intervalos de crecimiento y de decrecimiento y los extremos relativos de f (puntos donde
No. Nombre C.I. Firma. 1. Teoremas sobre funciones derivables. f (2) = c 1 ; f 0 (2) = c 2 ; f 00 (2) = 2c 3
 Fecha07//05 TRABAJO PR ACTICO SECCI ON 80 COORDINADOR PROF. RICHARD ROSALES R. No. Nombre C.I. Firma. Teoremas sobre funciones derivables. Sea f () una funcion al menos tres veces diferenciable en un entorno
Fecha07//05 TRABAJO PR ACTICO SECCI ON 80 COORDINADOR PROF. RICHARD ROSALES R. No. Nombre C.I. Firma. Teoremas sobre funciones derivables. Sea f () una funcion al menos tres veces diferenciable en un entorno
Aplicaciones de la derivada
 Aplicaciones de la derivada. Encontrar el punto sobre la grá ca de f (x) + x donde la recta tangente tiene la pendiente máxima y el punto donde la recta tangente tiene la pendiente mínima. Solución La
Aplicaciones de la derivada. Encontrar el punto sobre la grá ca de f (x) + x donde la recta tangente tiene la pendiente máxima y el punto donde la recta tangente tiene la pendiente mínima. Solución La
MATEMÁTICAS II - P.A.E.U. CÁLCULO DIFERENCIAL CUESTIONES
 MATEMÁTICAS II - P.A.E.U. CÁLCULO DIFERENCIAL CUESTIONES. Calcular a b 0 + siendo a, b >. (J9) Sol.: ab.. Hallar el máimo y el mínimo absoluto de f()=3-9+ en [0,]. (S9) Sol.: Má (0,); mín (3/,-/). 3. Puede
MATEMÁTICAS II - P.A.E.U. CÁLCULO DIFERENCIAL CUESTIONES. Calcular a b 0 + siendo a, b >. (J9) Sol.: ab.. Hallar el máimo y el mínimo absoluto de f()=3-9+ en [0,]. (S9) Sol.: Má (0,); mín (3/,-/). 3. Puede
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
APLICACIONES DE LAS DERIVADAS
 10 APLICACIONES DE LAS DERIVADAS REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: Relación de la curvatura con el signo de la segunda derivada
10 APLICACIONES DE LAS DERIVADAS REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: Relación de la curvatura con el signo de la segunda derivada
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Boletín III. Integración de funciones de una variable. Ejercicios básicos
 CÁLCULO Boletín III. Integración de funciones de una variable Ejercicios básicos. Demuestra que 8 4 4x es una primitiva de afirmativo justifica por qué; en caso negativo encuentra otra. x. Es su única
CÁLCULO Boletín III. Integración de funciones de una variable Ejercicios básicos. Demuestra que 8 4 4x es una primitiva de afirmativo justifica por qué; en caso negativo encuentra otra. x. Es su única
CALCULO VECTORIAL GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES
 GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
Cálculo Diferencial y Geometría Analítica Agosto 2016
 Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
Laboratorio # 1 Línea Recta I.- Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por los puntos
