TERCER EXAMEN EJERCICIOS RESUELTOS
|
|
|
- Soledad Franco Cabrera
- hace 5 años
- Vistas:
Transcripción
1 MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ). ) Calcula el área de dicha región. Solución. ) Puesto que tanto la circunferencia como la lemniscata se han visto en las clases con cierto detalle, calculamos sólo los elementos esenciales para dibujarlas. Para la circunferencia r = r θ) = senθ), multiplicamos por r obteniendo r = r senθ) y pasamos a coordenadas cartesianas: x + y = y. Completando el cuadrado nos queda x + y /) = /. Es decir, se trata de la circunferencia con centro en A =, /) y radio /. La lemniscata de ecuación r = r θ) = cosθ), de la que sabemos que es una curva con forma de, es simétrica con respecto a los dos ejes y al origen de coordenadas ya que r θ) = cos θ) = cosθ), r π θ) = cosπ θ)) = cos θ) = cosθ), r π + θ) = cosπ + θ)) = cosθ). Así que es suficiente con dibujarla en el primer cuadrante y extenderla por simetría. Su dominio de definición en el primer cuadrante viene dado por cosθ), es decir θ π/ y, por tanto, θ π/4. Para θ = el punto correspondiente es el, ) y luego se va acercando al origen, conforme θ crece, llegando a dicho punto en el otro extremo del dominio de definición θ = π/4. La circunferencia r = r θ) = senθ) y la lemniscata r = r θ) = cosθ).
2 Matemáticas II G. I. T. I.) La región limitada entre ambas curvas es la región sombreada en la figura. Para hallar el ángulo polar del punto P de corte, igualamos los radios de ambas curvas: senθ) = cosθ). Elevando al cuadrado y usando la fórmula del coseno del ángulo doble queda sen θ) = cosθ) = cos θ) sen θ) = sen θ). Luego sen θ) = /4 y, por tanto, senθ) = ±/ que, en el primer cuadrante, resulta θ = π/6. ) Por simetría, el área de la región completa será el doble del área en el primer cuadrante. A su vez, para aplicar la fórmula del área de una curva dada en coordenadas polares, tenemos que darnos cuenta de que el área en el primer cuadrante hay que separarla en dos casos: en el intervalo [, π/6], o sea, desde el origen hasta P por la parte inferior, la curva frontera es la circunferencia, mientras que en [π/6, π/4], o sea, desde P hasta el origen por la parte superior, la curva frontera es la lemniscata. En consecuencia, el área en el primer cuadrante es área en el primer cuadrante = π/6 Calculamos cada una de estas integrales por separado. Y, por otro lado, Luego el área total es π/6 r θ) dθ = π/6 sen θ) dθ = = θ ) senθ) π/6 π/4 r θ) dθ = π/4 cosθ) dθ = π/6 π/6 = ) / /4 = 4 área total = área en el primer cuadrante) = r θ) dθ + π/6 = π/4 π/6 r θ) dθ. cosθ) ) dθ+ ) π π/6 /4 = 8. senθ) 8 π π/4 π/ ) ) 8 = π
3 EJERCICIO. Ejercicios resueltos del tercer examen del curso 4 Considera la siguiente integral impropia en la que α R es un parámetro, e x xα dx. Para qué valores de α converge? Solución. La integral es impropia por dos motivos: porque está extendida hasta + y porque el denominador del integrando se anula para x =. Para determinar cuándo converge debemos separar la integral en dos y estudiar cada caso por separado, e x xα dx = e x xα dx + e x xα dx. Para estudiar la integral de segunda especie e x xα dx utilizaremos el criterio de comparación con una función de la forma x p. Para buscar el valor adecuado de p calculamos los términos principales de los desarrollos de Maclaurin de numerador y denominador. Puesto que el término principal x! puesto que e x = = x ) x x! + x5 5! = x! 5 5! +, = x 6 es un infinitésimo equivalente a ) en. Por otro lado, + x + x)! + x)! + ) = x + x)! el término principal x es un infinitésimo equivalente a e x ) en. De esa forma, lim x e x y comparamos el integrando con x +α porque = lim x x /6 x = lim x x / + x)! +, lim x e x x +α xα = lim x x /6 x x = /. Entonces, el criterio de comparación nos dice que la integral impropia si, y sólo si, la integral impropia e x xα dx converge x +α dx converge y, a su vez, también sabemos que esta integral converge si, y sólo si, + α >. En resumen, la integral impropia si, y sólo si, α >. e x xα dx converge
4 4 Matemáticas II G. I. T. I.) Para estudiar la integral de segunda especie e x xα dx utilizaremos el criterio de comparación con una función adecuada. En este caso, la función que más rápidamente crece es la exponencial e x del denominador, así que comparamos, por ejemplo, con e x y tenemos, cualquiera que sea el valor de α, lim e x xα e x = lim e x e x xα =, porque la exponencial e x en el denominador tiende a infinito más rápidamente que cualquiera de las demás funciones que aparecen. Como, por otro lado, sabemos que la integral el criterio de comparación nos dice que la integral de partida cualquier valor de α. En definitiva, uniendo los dos resultados obtenemos que la integral dada e x dx converge, e x xα dx converge para e x xα dx. converge si, y sólo si, α >.
5 EJERCICIO. Ejercicios resueltos del tercer examen del curso 4 5 Calcula el volumen de un depósito de agua que tiene forma del hemielipsoide de revolución que se obtiene al hacer girar alrededor del eje OY el tramo de la elipse de ecuación x 6 + y 9 = situado en el primer cuadrante. Solución. Los semiejes de la elipse x 6 + y 9 = valen 4, el horizontal, y, el vertical. El primer cuadrante de la elipse dada. El tramo de la elipse situado en el primer cuadrante podemos considerarlo como la gráfica de la función y = fx) = 4 6 x para x 4, así que el volumen que se pide viene dado por 4 volumen = π xfx) dx = π 4 x 6 x dx. Para calcular esta integral, hallamos una primitiva de x 6 x. Puesto que x es la derivada del radicando 6 x salvo por el factor ), la primitiva será 6 x ) /. Otra opción es hacer el cambio de variable t = 6 x, con lo que x dx = dt y tenemos x t 6 x dx = dt = t/ = 6 x ) /. Otra posibilidad es hacer el cambio de variable x = 4 senu), entonces dx = 4 cosu) du y tenemos x 6 x dx = 4 senu) cos u) du = 4 cos u) = 6 x ) /. Se haga como se haga, aplicando la Regla de Barrow resulta volumen = π 4 x 6 x dx = π 6 x ) / 4 = π 6 / ) = π. El cambio de variable x = 4 senu) también puede aplicarse directamente en la integral definida. Para ello observamos que para x = tenemos u = y para x = 4 tenemos u = π/, de forma que volumen = π 4 x 6 x dx = π π/ 4 senu) cos u) du = π ) 4 cos π/ u) = π.
6 6 Matemáticas II G. I. T. I.) Otro camino para hallar el volumen es utilizar la y como variable independiente, de manera que se trata de hallar el volumen de revolución alrededor del eje OY de la gráfica de la función dada por x = gy) = 4 9 y para y. Entonces volumen = π gy) ) dy = 6π 9 9 y ) dy. = 6π 9 9y y ) = 6π 7 9) = π. 9
7 EJERCICIO 4. ) Resuelve el problema de valor inicial ) Determina si la integral Ejercicios resueltos del tercer examen del curso 4 7 y + y = e x con y) =. yx) dx es convergente y, en ese caso, calcula su valor. ) Prueba que la ecuación yx) + = tiene una solución en el intervalo [, ] y determina su valor aproximado usando el método de Newton de la siguiente manera: debes dar tres pasos tomando x = como punto inicial no hace falta que compruebes las demás condiciones del Teorema de Convergencia). Solución. ) La ecuación diferencial y + y = e x es una ecuación lineal de primer orden, así que la resolveremos hallando la solución general de la ecuación homogónea asociada y una solución particular de la ecuación completa. La ecuación homogénea asociada y + y = es una ecuación en variables separadas, así que la escribimos como y /y = e integramos, obteniendo logy) = x + k, donde k es una constante de integración. Entonces su solución general es y h) x) = ce x, donde c es una constante arbitraria. Para hallar una solución particular de la ecuación completa usamos el método de variación de parámetros, ensayando una solución de la forma y p) x) = gx)e x. Entonces debe ocurrir [ gx)e x ] x) + gx)e x = e x. Haciendo la derivada resulta g x)e x gx)e x + gx)e x = e x luego g x) = y, por tanto, podemos tomar gx) = x y la solución particular es y p) x) = xe x. Como consecuencia es estos resultados, la solución general de y + y = e x es donde c es una constante arbitraria. yx) = y h) x) + y p) x) = c + x)e x, También podemos aplicar directamente la fórmula que proporciona la solución de una ecuación lineal de primer orden y + px)y = qx) yx) = [ ] c + qx)µx) dx µx) donde c es una constante arbitraria y la función µ, el factor integrante de la ecuación, es la función definida por µx) := e px) dx. En nuestro caso, px) = y qx) = e x, asó que µx) = e px) dt = e x y, en consecuencia, ] yx) = e [c x + e x e x dx = e x c + x). Una vez que tenemos la solución general yx) = c+x)e x, imponiendo la condición inicial y) = nos queda c =, así que la solución del problema de valor inicial es yx) = xe x.
8 8 Matemáticas II G. I. T. I.) ) Para ver si la integral pedida yx) dx = xe x dx es convergente y calcular su valor, lo más cómodo es hallar una primitiva del integrando. Usamos integración por partes con ux) = x y v x) = e x, con lo que u x) = y vx) = e x, y resulta xe x dx = xe x e x ) dx = xe x e x = + x)e x. Entonces, usando la definición de integral impropia r xe x dx = lim xe x dx = lim + x)e x r) = lim + r)e r ) ) =, r r r luego la integral converge y vale. La función yx) = xe x y el área que corresponde a la integral pedida. ) Puesto que yx) = xe x, la ecuación yx) + = nos queda xe x + =. Para ver que la ecuación xe x + = tiene una solución en el intervalo [, ] usamos el Teorema del Valor Intermedio de Bolzano: Puesto que gx) = xe x + es continua, g ) = e < y g) =, este teorema nos dice que, efectivamente, la ecuación xe x + = tiene una solución x en [, ]. La función gx) = xe x +.
9 Ejercicios resueltos del tercer examen del curso 4 9 Tal y como se pide, vamos determinar el valor aproximado de x usando tres pasos del Método de Newton x = como punto inicial. Para llevar a cabo las iteraciones del Método de Newton, calculamos g x) = x)e x. Entonces x = x gx ) g x ) = = x = x gx ) g x ) = e e x = x gx ) g x ) Luego la aproximación es x.577. = e e e.684 =.684 = )e.684
Soluciones de los ejercicios del del examen final de febrero
 Matemáticas II (GIC, curso 5 6) Soluciones de los ejercicios del del examen final de febrero EJERCICIO. Determina el ángulo polar de los puntos con tangente horizontal y los puntos con tangente vertical
Matemáticas II (GIC, curso 5 6) Soluciones de los ejercicios del del examen final de febrero EJERCICIO. Determina el ángulo polar de los puntos con tangente horizontal y los puntos con tangente vertical
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas II (GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Halla el área que encierra la curva C dada en polares por r = + sen(θ. Solución: Primero debemos hallar
Matemáticas II (GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Halla el área que encierra la curva C dada en polares por r = + sen(θ. Solución: Primero debemos hallar
Grado en Ingeniería en Tecnologías Industriales. Matemáticas II. Examen de Prueba. 1deDiciembrede2011. Curso
 Matemáticas II Grado en Ingeniería en Tecnologías Industriales 7 Grado en Ingeniería en Tecnologías Industriales Matemáticas II Examen de Prueba dediciembrede0 Curso 0-0 Ejercicio Sea C la curva situada
Matemáticas II Grado en Ingeniería en Tecnologías Industriales 7 Grado en Ingeniería en Tecnologías Industriales Matemáticas II Examen de Prueba dediciembrede0 Curso 0-0 Ejercicio Sea C la curva situada
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 17/01/2013
 MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Para saber si tiene asíntotas horizontales hacemos los límites en los infinitos.
 1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
Cálculo. Primer curso de Ingenieros de Telecomunicación. Curso Examen de Septiembre. 6 de Septiembre de 2002.
 Cálculo. Primer curso de Ingenieros de Telecomunicación. Curso -. Examen de Septiembre. 6 de Septiembre de. Primera parte Ejercicio. Un canal abierto cuya sección es un trapecio isósceles de bases horizontales,
Cálculo. Primer curso de Ingenieros de Telecomunicación. Curso -. Examen de Septiembre. 6 de Septiembre de. Primera parte Ejercicio. Un canal abierto cuya sección es un trapecio isósceles de bases horizontales,
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Soluciones de los ejercicios del examen de Cálculo del 29 de junio de 2007 Primero de Ingeniería de Telecomunicación
 Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen del 14 de Septiembre de 2000 Primera parte
 ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen de 1 de Septiembre de 2009 Primera parte
 ÁLULO Primer curso de ngeniero de Telecomunicación Examen de de Septiembre de 9 Primera parte Ejercicio. En un círculo de radio a se toma un diámetro POQ. Sobre la perpendicular al círculo en el punto
ÁLULO Primer curso de ngeniero de Telecomunicación Examen de de Septiembre de 9 Primera parte Ejercicio. En un círculo de radio a se toma un diámetro POQ. Sobre la perpendicular al círculo en el punto
Integrales Múltiples.
 CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 9 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Examen de Matemáticas 2 o de Bachillerato Mayo 2003
 Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
Examen de Matemáticas o de Bachillerato Mayo 1. (a) Dibuja el recinto limitado por las curvas y = e x+, y = e x y x =. (b) Halla el área del recinto considerado en el apartado anterior. (a) El dominio
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 19 de Junio de 2004 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 9 de Junio de 4 Primera parte Ejercicio. Un depósito subterráneo de gasolina tiene forma de cilindro elíptico con semieje orizontal a
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 9 de Junio de 4 Primera parte Ejercicio. Un depósito subterráneo de gasolina tiene forma de cilindro elíptico con semieje orizontal a
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Nombre y Apellidos: x e 1 x 1 x f(x) = ln(x) x
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.
 SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
SEMESTRE 018-1 SERIE CURVAS EN EL PLANO POLAR 1. Obtener las coordenadas cartesianas del punto B simétrico del punto A(5,30 ), respecto al polo.. Determinar las coordenadas polares del punto C simétrico
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate de mayo de 2016
 Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate 332 5 de mayo de 26 Nombre. Sección Número de Estudiante Profesor Número de puntos disponibles:
Universidad de Puerto Rico. Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas Examen Final Mate 332 5 de mayo de 26 Nombre. Sección Número de Estudiante Profesor Número de puntos disponibles:
Teorema 1 (Cambio de Variable en R n ).
 Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
Vamos a estudiar en este segundo capítulo sobre los cambios de variable para funciones de varias variables, algunos de los más habituales: los cambios de coordenadas a coordenadas polares en el plano,
Universidad Icesi Departamento de Matemáticas y Estadística
 Universidad Icesi Departamento de Matemáticas y Estadística Solución del segundo examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO.
Universidad Icesi Departamento de Matemáticas y Estadística Solución del segundo examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO.
Licenciatura en Matemáticas Soluciones del examen final de Cálculo de septiembre de sena + 4sen(a/2) + 9sen(a/3) + + n 2 sen(a/n) n 2.
 Licenciatura en Matemáticas Soluciones del examen final de de septiembre de 00 Ejercicio 1. (a) Calcular: lím n sena + 4sen(a/) + 9sen(a/3) + + n sen(a/n) n (a + 1)(a + ) (a + n) (b) Estudiar la convergencia
Licenciatura en Matemáticas Soluciones del examen final de de septiembre de 00 Ejercicio 1. (a) Calcular: lím n sena + 4sen(a/) + 9sen(a/3) + + n sen(a/n) n (a + 1)(a + ) (a + n) (b) Estudiar la convergencia
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
a n en las que n=1 s n = n + 1 Solución: a) Utilizando el criterios de D Alembert se obtiene que a n+1 n a n 3 > 1 n=1
 EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
Matemáticas II Matemáticas II CASTILLA Y LEÓN CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Prueba A Problemas a) f(x) x El denominador de f(x) nunca se anula; por
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Cálculo Integral Agosto 2015
 Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 10 de febrero de 2010
 CUESTIONES TIPO TEST Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- En un triángulo esférico rectángulo,
CUESTIONES TIPO TEST Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- En un triángulo esférico rectángulo,
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
Soluciones de los ejercicios del examen de Análisis Matemático Primer curso de Ingeniería Informática - Febrero de 2005
 Soluciones de los ejercicios del examen de Primer curso de Ingeniería Informática - Febrero de 25 Ejercicio. A Dados los puntos A, y 2,2, calcula el camino más corto para ir de A a pasando por un punto
Soluciones de los ejercicios del examen de Primer curso de Ingeniería Informática - Febrero de 25 Ejercicio. A Dados los puntos A, y 2,2, calcula el camino más corto para ir de A a pasando por un punto
PRIMER CONTROL. 13 de Noviembre de 2012.
 GRAO EN QUÍMICA. MATEMÁTICAS. (Evaluación continua) PRIMER CONTROL. 13 de Noviembre de 2012. 1.- Sea f : R 3 R 3 la aplicación lineal f(x, y, z) = (x + z, 2x + ay az, 4x + z), (a R) a) Matriz de la aplicación
GRAO EN QUÍMICA. MATEMÁTICAS. (Evaluación continua) PRIMER CONTROL. 13 de Noviembre de 2012. 1.- Sea f : R 3 R 3 la aplicación lineal f(x, y, z) = (x + z, 2x + ay az, 4x + z), (a R) a) Matriz de la aplicación
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-0---M-00-0 CURSO: Matemática Intermedia SEMESTRE: Primero CÓDIGO DEL CURSO: 0 TIPO DE EXAMEN: Eamen Final
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-0---M-00-0 CURSO: Matemática Intermedia SEMESTRE: Primero CÓDIGO DEL CURSO: 0 TIPO DE EXAMEN: Eamen Final
Universidad Diego Portales
 Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo II LABORATORIO Nº 0 Longitud de arco y Volumen de sólido de revolución Contenido: Longitud de arco en
Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo II LABORATORIO Nº 0 Longitud de arco y Volumen de sólido de revolución Contenido: Longitud de arco en
1. INTEGRALES DEFINIDAS E IMPROPIAS
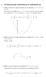 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3! + x5
 Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
EXAMEN DE MATEMÁTICAS I. Test
 Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
REPRESENTACIÓN GRÁFICA DE CURVAS - II
 REPRESENTACIÓN GRÁFICA DE CURVAS - II 1.- Representa gráficamente la función a) Dominio: f(x) es el cociente del valor absoluto de una función polinómica de 2º grado entre la variable x. Ambas son continuas
REPRESENTACIÓN GRÁFICA DE CURVAS - II 1.- Representa gráficamente la función a) Dominio: f(x) es el cociente del valor absoluto de una función polinómica de 2º grado entre la variable x. Ambas son continuas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Integración múltiple: integrales dobles
 Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Tema 13 La integral definida. Aplicaciones
 Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
Integración doble Integrales dobles sobre regiones no rectangulares
 Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
INTEGRALES. EL PROBLEMA DEL ÁREA III
 INTEGRALES. EL PROBLEMA DEL ÁREA III En esta relación de ejercicios vamos a aplicar el concepto de integral definida para calcular el área limitado por gráficas de funciones. Recuerda que para realizar
INTEGRALES. EL PROBLEMA DEL ÁREA III En esta relación de ejercicios vamos a aplicar el concepto de integral definida para calcular el área limitado por gráficas de funciones. Recuerda que para realizar
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
e x 1 + kx b) Halla los intervalos de crecimiento, decrecimiento, concavidad, así como los extremos y puntos de inflexión de la función:
 Matemáticas Convocatoria Extraordinaria 4 de junio de 14 1 3 puntos) a) Estudia el ite: en función del valor del parámetro real k e x 1 + kx x 1 cos x b) Halla los intervalos de crecimiento, decrecimiento,
Matemáticas Convocatoria Extraordinaria 4 de junio de 14 1 3 puntos) a) Estudia el ite: en función del valor del parámetro real k e x 1 + kx x 1 cos x b) Halla los intervalos de crecimiento, decrecimiento,
SEGUNDO EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Ejercicio 1 2 3 4 5 6 Total Puntos Departmento de Economía Matematicas I Examen Final 16 enero 2019 APELLIDOS: Duración: 2 horas. NOMBRE: ID: GRADO: GRUPO: (1) Sea la función
Universidad Carlos III de Madrid Ejercicio 1 2 3 4 5 6 Total Puntos Departmento de Economía Matematicas I Examen Final 16 enero 2019 APELLIDOS: Duración: 2 horas. NOMBRE: ID: GRADO: GRUPO: (1) Sea la función
Área entre curvas. Ejercicios resueltos. 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x.
 Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
De x = 1 a x = 6, la recta queda por encima de la parábola.
 Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN
 2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
COORDENADAS POLARES O CILÍNDRICAS
 COORDENADAS POLARES O CILÍNDRICAS Para definir la posición de un punto en un plano (o en el espacio) podemos utilizar distintos tipos de coordenadas, siendo las más normales las coordenadas rectangulares
COORDENADAS POLARES O CILÍNDRICAS Para definir la posición de un punto en un plano (o en el espacio) podemos utilizar distintos tipos de coordenadas, siendo las más normales las coordenadas rectangulares
Nombre y Apellidos: x (1 + ln(x)) si x > 0 f(x) = 0 si x = 0.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-M-2-00-202 CURSO: Matemática Intermedia I SEMESTRE: Segundo CÓDIGO DEL CURSO: 07 TIPO DE EXAMEN: Segundo
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2017 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 7 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Análisis Matemático 2
 MARTÍN MAULHARDT Análisis Matemático 2 UNA CUIDADOSA SELECCIÓN DE EJERCICIOS RESUELTOS CAPÍTULO 1 Geometría del Plano. El plano y el espacio constituyen el lugar geométrico sobre el cual vamos a trabajar
MARTÍN MAULHARDT Análisis Matemático 2 UNA CUIDADOSA SELECCIÓN DE EJERCICIOS RESUELTOS CAPÍTULO 1 Geometría del Plano. El plano y el espacio constituyen el lugar geométrico sobre el cual vamos a trabajar
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Y resolvemos esta indeterminación por L Hôpital, derivando arriba y abajo:
 1.- Considerad la función: f(x) = ln x x a) Dad el dominio de f y estudiad si tiene una asíntota horizontal. b) Calculad una primitiva de f usando el método de integración por partes. Indicación: Fijaos
1.- Considerad la función: f(x) = ln x x a) Dad el dominio de f y estudiad si tiene una asíntota horizontal. b) Calculad una primitiva de f usando el método de integración por partes. Indicación: Fijaos
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II ARAGÓN CONVOCATORIA JUNIO 009 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz. Algebra Opción A a) Las matrices correspondientes son: A m m m m m m A* El determinante
Matemáticas II Matemáticas II ARAGÓN CONVOCATORIA JUNIO 009 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz. Algebra Opción A a) Las matrices correspondientes son: A m m m m m m A* El determinante
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Ejercicios propuestos para el cálculo de áreas
 Aplicaciones geométricas y mecánicas de la integral definida 191 Ejercicios propuestos para el cálculo de áreas 1) Calcular el área de la figura limitada por la parábola verticales = 1, = y el eje OX y
Aplicaciones geométricas y mecánicas de la integral definida 191 Ejercicios propuestos para el cálculo de áreas 1) Calcular el área de la figura limitada por la parábola verticales = 1, = y el eje OX y
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Ejercicio 2 3 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 24 de Junio de 26 Duración del Examen: 2 horas. APELLIDOS: NOMBRE: DNI: Titulación:
Universidad Carlos III de Madrid Ejercicio 2 3 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 24 de Junio de 26 Duración del Examen: 2 horas. APELLIDOS: NOMBRE: DNI: Titulación:
CAPÍTULO 1. Geometría del Plano.
 CAPÍTULO 1 Geometría del Plano. El plano y el espacio constituyen los lugares geométricos sobre los cuales vamos a trabajar en casi todo este libro y donde se aplican los teoremas integrales en los cuales
CAPÍTULO 1 Geometría del Plano. El plano y el espacio constituyen los lugares geométricos sobre los cuales vamos a trabajar en casi todo este libro y donde se aplican los teoremas integrales en los cuales
Selectividad Matemáticas II septiembre 2017, Andalucía (versión 2)
 Selectividad Matemáticas II septiembre 07, Andalucía versión ) Pedro González Ruiz 6 de septiembre de 07. Opción A Problema. Una imprenta recibe un encargo para realizar una tarjeta rectangular con las
Selectividad Matemáticas II septiembre 07, Andalucía versión ) Pedro González Ruiz 6 de septiembre de 07. Opción A Problema. Una imprenta recibe un encargo para realizar una tarjeta rectangular con las
E.T.S.I. INFORMÁTICOS (UPM) SOLUCIONES EXAMEN FINAL (16/6/2014) 2 n 2 +n. n = (n 2 + 1) (n 2 3n) n n 2 3n = lím. n + 1 n. n 2 n = 3 2
 MATEMÁTICA APLICADA CÁLCULO E.T.S.I. INFORMÁTICOS UPM o G.I.I. SOLUCIONES EXAMEN FINAL 6/6/04 er EXAMEN PARCIAL. Calcule los siguientes ites, si existen: a n + n 3n. b n n + 3 n +n a El ite presenta una
MATEMÁTICA APLICADA CÁLCULO E.T.S.I. INFORMÁTICOS UPM o G.I.I. SOLUCIONES EXAMEN FINAL 6/6/04 er EXAMEN PARCIAL. Calcule los siguientes ites, si existen: a n + n 3n. b n n + 3 n +n a El ite presenta una
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 26 de Junio de 2007 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 6 de Junio de 7 Primera parte Ejercicio. Determinar los puntos de máxima y mínima pendiente de la gráfica de la función y = +x, x. Solución.
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 6 de Junio de 7 Primera parte Ejercicio. Determinar los puntos de máxima y mínima pendiente de la gráfica de la función y = +x, x. Solución.
r r a) Clasificar el sistema x = Ax en función del parámetro r R.
 Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
CLAVES DE CORRECCIÓN SEGUNDO PARCIAL MATEMÁTICA 2º Cuatrimestre 2017 SEGUNDO TURNO (22/11/2017) TEMA 1
 SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 17 SEGUNDO TURNO (/11/17) TEMA 1 Ejercicio 1 ( puntos) Dada la función exponencial f(x) = x 1, determinar el conjunto de negatividad y positividad. Ya que la función
SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 17 SEGUNDO TURNO (/11/17) TEMA 1 Ejercicio 1 ( puntos) Dada la función exponencial f(x) = x 1, determinar el conjunto de negatividad y positividad. Ya que la función
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 26 de Junio de 2008 Primera parte. =1, a,b > 0.
 ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
APLICACIONES DE LA INTEGRAL DEFINIDA
 APLICACIONES DE LA INTEGRAL DEFINIDA Objetivo: El alumno analizará y comprenderá el uso y la aplicación de la integral definida en la resolución de problemas REGIONES PLANAS LIMITADAS POR DOS CURVAS Sean
APLICACIONES DE LA INTEGRAL DEFINIDA Objetivo: El alumno analizará y comprenderá el uso y la aplicación de la integral definida en la resolución de problemas REGIONES PLANAS LIMITADAS POR DOS CURVAS Sean
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen, 7 de Septiembre de 2005 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen, 7 de Septiembre de 005 Primera parte Ejercicio 1. Un espejo plano de dimensiones 80 cm y 90 cm, se rompe por una esquina según una recta. De
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen, 7 de Septiembre de 005 Primera parte Ejercicio 1. Un espejo plano de dimensiones 80 cm y 90 cm, se rompe por una esquina según una recta. De
Apellidos: Nombre: Curso: 1º Grupo: C Día: 2- III- 16 CURSO
 EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 2008
 Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 8 MA- Practica: semana y/o Ejercicios sugeridos para la semana y/o. Cubre el siguiente material: Propiedades de la
Universidad Simón Bolívar Departamento de Matemáticas Puras y Aplicadas Enero - Marzo, 8 MA- Practica: semana y/o Ejercicios sugeridos para la semana y/o. Cubre el siguiente material: Propiedades de la
Segundo Parcial de Matemáticas II Grado Ingeniería Biomédica
 Segundo Parcial de Matemáticas II Grado Ingeniería Biomédica ETSII de alència. Junio de 08 Apellidos Nombre Instrucciones Comienza poniendo el nombre y apellidos. En la pregunta de erdadero o also marca
Segundo Parcial de Matemáticas II Grado Ingeniería Biomédica ETSII de alència. Junio de 08 Apellidos Nombre Instrucciones Comienza poniendo el nombre y apellidos. En la pregunta de erdadero o also marca
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M _SC
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-1-M-1-00-2018_SC CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN: Primer Parcial FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-1-M-1-00-2018_SC CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN: Primer Parcial FECHA DE
Fundamentos matemáticos. Tema 5 Derivación de funciones de una y varias variables
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
TEMA 4 SEGUNDO TURNO (22/11/2017) Ejercicio 1 (2 puntos) Respuesta. Ejercicio 2 (3 puntos) Respuesta. Material de uso exclusivamente didáctico 1
 SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 17 SEGUNDO TURNO (/11/17) TEMA 4 Ejercicio 1 ( puntos) Hallar las coordenadas del punto de la gráfica de la función h(x) = ln(x + x + 1) + 5x donde la pendiente
SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 17 SEGUNDO TURNO (/11/17) TEMA 4 Ejercicio 1 ( puntos) Hallar las coordenadas del punto de la gráfica de la función h(x) = ln(x + x + 1) + 5x donde la pendiente
Prueba º Bach C Análisis. Nombre:... 17/05/10. Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible 1 h. 30 min.
 Nota Prueba 3.04 º Bach C Análisis Nombre:... 7/05/0 Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible h. 30 min. OPCIÓN A. a) Calcula los siguientes límites: ln( + ) sen
Nota Prueba 3.04 º Bach C Análisis Nombre:... 7/05/0 Elige una de las dos opciones y contesta a todas sus preguntas. Tiempo disponible h. 30 min. OPCIÓN A. a) Calcula los siguientes límites: ln( + ) sen
Primer Parcial MA1002 Cálculo II ExMa
 Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
UNIDAD 5.C :INTEGRALES Y SUPERFICIES DE REVOLUCIÓN
 UNIDAD 5.C :INTEGRALES Y SUPERFICIES DE REVOLUCIÓN 5.C.1 Concepto de integral Primitiva de una función: Sea f una función definida en el intervalo (a,b). Llamamos primitiva, antiderivada o integral indefinida
UNIDAD 5.C :INTEGRALES Y SUPERFICIES DE REVOLUCIÓN 5.C.1 Concepto de integral Primitiva de una función: Sea f una función definida en el intervalo (a,b). Llamamos primitiva, antiderivada o integral indefinida
CUESTIONES RESUELTAS 3. INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA
 CUESTIONES RESUELTAS INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS º GRADO GESTIÓN AERONAÚTICA INTEGRAL DEFINIDA REGLA DE BARROW Sea f() una función discontinua en = y continua en el resto de puntos del intervalo
CUESTIONES RESUELTAS INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS º GRADO GESTIÓN AERONAÚTICA INTEGRAL DEFINIDA REGLA DE BARROW Sea f() una función discontinua en = y continua en el resto de puntos del intervalo
CLAVES DE CORRECCIÓN SEGUNDO PARCIAL MATEMÁTICA 2º
 SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 07 PRIMER TURNO (//07) TEMA Ejercicio ( puntos) Dada la función f(x) = a sen(x + π). Hallar el valor de la constante a R sabiendo que f ( π ) = a + Se sabe que
SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 07 PRIMER TURNO (//07) TEMA Ejercicio ( puntos) Dada la función f(x) = a sen(x + π). Hallar el valor de la constante a R sabiendo que f ( π ) = a + Se sabe que
CLAVES DE CORRECCIÓN SEGUNDO PARCIAL MATEMÁTICA 2º
 SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 07 PRIMER TURNO (//07) TEMA Ejercicio ( puntos) Hallar él o los puntos del gráfico de la función para los cuales la recta tangente sea horizontal f(x) = e x 3x
SEGUNDO PARCIAL MATEMÁTICA º Cuatrimestre 07 PRIMER TURNO (//07) TEMA Ejercicio ( puntos) Hallar él o los puntos del gráfico de la función para los cuales la recta tangente sea horizontal f(x) = e x 3x
1 a 0 a 1 1 F 32 (2) /2
 ESCUELA UNIVESITAIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial. Especialidad en Electricidad. Fundamentos Matemáticos de la Ingeniería Curso 00-006. Soluciones correspondientes al examen de la
ESCUELA UNIVESITAIA POLITÉCNICA DE SEVILLA Ingeniería Técnica Industrial. Especialidad en Electricidad. Fundamentos Matemáticos de la Ingeniería Curso 00-006. Soluciones correspondientes al examen de la
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
3. Cambio de variables en integrales dobles.
 GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
2 ln x dx. Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = 1 x dx dv = dx v = x y por tanto
 Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
METODOS MATEMATICOS DE LA FISICA II.
 METODOS MATEMATICOS DE LA FISICA II. EXAMEN DEL PRIMER PARCIAL 3 de enero de 24 GRUPO I (Pedro López Rodríguez).. (2.5 puntos) Calcular el flujo del campo F (x, y, z) = (x, y, 2z) a través de la superficie
METODOS MATEMATICOS DE LA FISICA II. EXAMEN DEL PRIMER PARCIAL 3 de enero de 24 GRUPO I (Pedro López Rodríguez).. (2.5 puntos) Calcular el flujo del campo F (x, y, z) = (x, y, 2z) a través de la superficie
Departamento de Matemática Aplicada a la I.T. de Telecomunicación
 Departamento de Matemática Aplicada a la I.T. de Telecomunicación ASIGNATURA: CÁLCULO I (Examen Final) CONVOCATORIA: FEBRERO FECHA: de Enero de 3 Duración del examen: 3 horas Fecha publicación notas: 8--3
Departamento de Matemática Aplicada a la I.T. de Telecomunicación ASIGNATURA: CÁLCULO I (Examen Final) CONVOCATORIA: FEBRERO FECHA: de Enero de 3 Duración del examen: 3 horas Fecha publicación notas: 8--3
( ) ( ) ( ) f h f h h h h. h 0 h h 0 h h 0 h h 0. f h f h h h h
 Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
