Teorema del punto fijo para funciones contractivas
|
|
|
- José Manuel José Miguel Valverde Lozano
- hace 5 años
- Vistas:
Transcripción
1 Teorema del punto fijo para funciones contractivas 1. Definición (función contractiva). Sea (X, d) un espacio métrico. Una función f : X X se llama contractiva (función contractante, contracción) si existe un L [0, 1) tal que a, b X d(f(a), f(b)) Ld(a, b). En otras palabras, una función X X se llama contractiva si es Lipschitz continua con un coeficiente de Lipschitz estrictamente menor que Definición (función corta, función estrictamente corta). Sea (X, d) un espacio métrico y sea f : X X. Se dice que f es corta o no-expansiva si a, b X d(f(a), f(b)) d(a, b). Se dice que f es estrictamente corta si a, b X d(f(a), f(b)) < d(a, b). 3. Hay funciones estrictamente cortas que no son contractivas. Obviamente cada función contractiva es estrictamente corta. No cada función estrictamente corta es contractiva. Por ejemplo, consideremos la función f : R R definida mediante la regla f(x) = arc tg(x). Como f (x) = 1 < 1 (x R), 1 + x2 el teorema del valor medio garantiza que f(a) f(b) < a b para cualesquier a, b R. Por otro lado, con la regla de L Hospital o con un uso apropiado de límites notables uno puede ver que f(x) f(0) lim = 1. x 0 x 0 Por consecuencia, y la función f no es contractiva. f(a) f(b) sup a,b R a b a b = 1, 4. Definición (punto fijo de una función). Sea X un conjunto, sea f : X X y sea p X. Se dice que p es un punto fijo de f si f(p) = p. Teorema del punto fijo para funciones contractivas, página 1 de 5
2 5. Lema (desigualdad fundamental para funciones contractivas). Sea (X, d) un espacio métrico y sea f : X X una función contractiva con un coeficiente L, L [0, 1). Entonces para cualesquiera a, b en X d(a, b) 1 ( ) d(a, f(a)) + d(b, f(b)). (1) Demostración. Aplicamos la desigualdad del triángulo y luego la suposición que f es contractiva con coeficiente L: d(a, b) d(a, f(a)) + d(f(a), f(b)) + d(f(b), b) d(a, f(a)) + Ld(a, b) + d(b, f(b)). Pasamos el sumando Ld(a, b) al lado izquierdo: ()d(a, b) d(a, f(a)) + (b, f(b)). (2) Por la hipótesis, L < 1, así que > 0. Dividimos ambos lados de (2) entre y obtenemos (1). 6. Lema (unicidad del punto fijo de funciones contractivas). Sea (X, d) un espacio métrico y sea f : X X una función contractiva. Supongamos que a, b X, f(a) = a y f(b) = b. Entonces a = b. Demostración. Aplicamos (1) a los puntos dados a y b. El lado derecho se anula, por eso concluimos que d(a, b) = 0 y a = b. 7. Definición (iteraciones de una función cuyo contradominio coincide con el dominio). Sea X un conjunto y sea f : X X. Para cada n en N 0 denotamos por f [n] la n-ésima iteración de f, definida de manera recursiva: f [0] := id X, f [n+1] := f [n] f. Aquí id X es la función identidad del conjunto X: id X : X X, id X (x) := x (x X). Notamos que f [n] : X X para cada n en N Propiedades de las iteraciones de una función. Sean X y f como en la definición anterior. Entonces de la propiedad asociativa de la composición de funciones se puede deducir que f [n+m] = f [m] f [n] = f [n] f [m] (m, n N 0 ). En particular, f [n+1] = f f [n]. Teorema del punto fijo para funciones contractivas, página 2 de 5
3 9. Lema (sobre las iteraciones de una función contractiva). Sea X un espacio métrico y sea f : X X una función contractiva con coeficiente L, L [0, 1). Entonces para cada n en N 1 la función f [n] es contractiva con coeficiente L n. Demostración. Se demuestra fácilmente por inducción. 10. Lema (sobre el límite de las iteraciones). Sea X un espacio métrico, sea f : X X una función continua y sea (x n ) n=0 una sucesión en X que converge a un punto p, p X. Entonces p es un punto fijo de f, esto es, f(p) = p. Demostración. Pasamos al límite en la igualdad f(x n ) = x n+1. Como f es continua, f(x n ) p. Por otro lado, x n+1 p. Entonces f(p) = p. 11. Lema (la órbita de un punto bajo una función contractiva es una sucesión de Cauchy). Sea X un espacio métrico, sea f : X X una función contractiva y sea x 0 un punto de X. Para cada n en N 1 definimos x n como f [n] (x 0 ). Entonces la sucesión (x n ) n=0 es de Cauchy. Primera demostración, usando la desigualdad fundamental. Para cualesquiera m, n en N 0 aplicamos la desigualdad fundamental (1) a los puntos x m y x n : d(x m, x n ) 1 ( d(xm, x m+1 ) + d(x n, x n+1 ) ). Notamos que d(x m, x m+1 ) = d(f [m] (x 0 ), f [m] (f(x 0 ))) L m d(x 0, f(x 0 )) y de manera similar d(x n, x n+1 ) L n d(x 0, f(x 0 )). Por eso d(x m, x n ) d(x 0, f(x 0 ))( L m + L n). Cuando m y n tienden a infinito, la expresión L m + L n tiende a cero. Segunda demostración, trabajando con sumas de progresiones geométricas. Notamos que d(x n, x n+1 ) L n d(x 0, f(x 0 )). Si n < m, entonces por la desigualdad del triángulo d(x n, x m ) m 1 j=n m 1 d(x j, x j+1 ) d(x 0, f(x 0 )) La última expresión tiende a cero, cuando n tiende a infinito. j=n L j d(x 0, f(x 0 )) L n. (3) Teorema del punto fijo para funciones contractivas, página 3 de 5
4 12. Teorema de Banach sobre el punto fijo de la función contractiva. Sea (X, d) un espacio métrico completo, X, y sea f : X X una función contractiva con coeficiente L [0, 1). Entonces: I. La función f tiene un único punto fijo; lo denotemos por p. II. Si x 0 X y la sucesión (x n ) n=1 está definida mediante la regla recursiva x n = f(x n 1 ), (4) entonces esta sucesión converge a p, y para cada n {1, 2,...} d(x n, p) d(x 0, f(x 0 )) L n. (5) Demostración. La demostración sale fácilmente de los lemas anteriores. Por el Lema 6, f no puede tener dos puntos fijos diferentes entre si. La existencia del punto fijo se demuestra de manera constructiva, simultáneamente con el inciso II. Sea x 0 X. Por el Lema 11, la sucesión (x n ) n=0 es de Cauchy. El espacio X es completo, por eso la sucesión tiene un límite. Lo denotamos por p. Por el Lema 10, p es un punto fijo de f. Aplicamos la desigualdad fundamental (1) a los puntos x n y p y obtenemos (5): d(x n, p) d(x n, x n+1 ) d(x 0, f(x 0 )) L n. 13. Observación. La desigualdad (5) también se puede deducir de (3), pasando al límite cuando m tiende al infinito. 14. Observación: el teorema del punto fijo de Banach es constructivo. La existencia del punto fijo en este teorema se demuestra de manera constructiva, a saber, se da una receta para aproximar el punto fijo. 15. Aplicaciones. El teorema del punto fijo se utiliza en numerosas aplicaciones, tanto teóricas como prácticas: para demostrar el teorema de la función implícita (es un camino de demostración), para demostrar la existencia y unicidad de soluciones de ciertas ecuaciones diferenciales, para justificar varios algoritmos de métodos numéricos y del álgebra lineal numérica. Teorema del punto fijo para funciones contractivas, página 4 de 5
5 16. Corolario del teorema de Banach para una función cuya potencia es contractiva. Sea (X, d) un espacio métrico completo, X, sea f : X X y sea N N 1 tales que la función f [N] es contractiva con un coeficiente L en [0, 1). Entonces la función f tiene un único punto fijo p, y para cada x 0 en X la sucesión (f [n] (x 0 )) n=0 converge a p. Demostración. Por el teorema sobre el punto fijo de una función contractiva, la función f [N] tiene un único punto fijo. Lo denotamos por p. Demostremos que p es un punto fijo de f. La igualdad f [N] (f(p)) = f(f [N] (p)) = f(p) muestra que f(p) es un punto fijo de f [N], y por la unicidad concluimos que f(p) = p. Demostremos que p es el único punto fijo de f. Si f tiene un punto fijo q, entonces es fácil mostrar por inducción que f [n] (q) = q para cada n en N 1 ; en particular, f [N] (q) = q, por lo cual q = p. Ahora elegimos x 0 en X y mostremos que la sucesión (f [n] (x 0 )) n=0 converge a p. Denotemos por M al número M := max 0 j<n d(f [j] (x 0 ), f [j+n] (x 0 )). Dado n en N 0, dividimos n con resto entre N, es decir, encontramos r en {0,..., N 1} y m en N 0 tales que n = mn + r. Aplicamos la desigualdad (5) a la iteración m de la función f [N] y al punto inicial f [r] (x 0 ). Entonces obtenemos que d(f [n] (x 0 ), p) Lm d(f [r] (x 0 ), f [N+r] (x 0 )) L n/n M. La última expresión tiende a 0 cuando n tiende a. Teorema del punto fijo para funciones contractivas, página 5 de 5
Teoremas de la función inversa, función implícita y del rango constante
 Teoremas de la función inversa, función implícita y del rango constante Pablo Zadunaisky 13 de marzo de 2015 A lo largo de este documento usamos varias normas sobre espacios vectoriales de dimensión finita,
Teoremas de la función inversa, función implícita y del rango constante Pablo Zadunaisky 13 de marzo de 2015 A lo largo de este documento usamos varias normas sobre espacios vectoriales de dimensión finita,
ECUACIONES DIFERENCIALES
 ECUACIONES DIFERENCIALES (Grupo A) Teoría Fundamental En esta parte del curso nos dedicaremos a establecer los resultados teóricos fundamentales del curso. Nos interesaremos por las condiciones de existencia
ECUACIONES DIFERENCIALES (Grupo A) Teoría Fundamental En esta parte del curso nos dedicaremos a establecer los resultados teóricos fundamentales del curso. Nos interesaremos por las condiciones de existencia
Departamento de Matemáticas
 MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
Teoremas de Tonelli y Fubini
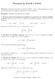 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
El Teorema de Contracción de Mapas
 El Teorema de Contracción de Mapas Carlos Gamez Escuela de Matemática Facultad de Ciencias Naturales y Matemática Universidad de El Salvador Presentación Beamer Esquema Introducción Contracción Punto Fijo,
El Teorema de Contracción de Mapas Carlos Gamez Escuela de Matemática Facultad de Ciencias Naturales y Matemática Universidad de El Salvador Presentación Beamer Esquema Introducción Contracción Punto Fijo,
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Polinomios (lista de problemas para examen)
 Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Soluciones de ecuaciones de una variable
 Análisis Numérico Soluciones de ecuaciones de una variable CNM-425 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft 2010. Reproducción permitida bajo
Análisis Numérico Soluciones de ecuaciones de una variable CNM-425 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft 2010. Reproducción permitida bajo
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple
 Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Transformación adjunta a una transformación lineal
 Transformación adjunta a una transformación lineal Objetivos. Estudiar la construcción y las propiedades básicas de la transformación lineal adjunta. Requisitos. Transformación lineal, producto interno,
Transformación adjunta a una transformación lineal Objetivos. Estudiar la construcción y las propiedades básicas de la transformación lineal adjunta. Requisitos. Transformación lineal, producto interno,
Series de Fourier absolutamente convergentes
 Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
Temas preliminares de Análisis Real
 Temas preliminares de Análisis Real Problemas para examen Usamos la notación A B en el siguiente sentido: A es un subconjunto de B, puede ser que A = B. Propiedades de las operaciones con conjuntos 1.
Temas preliminares de Análisis Real Problemas para examen Usamos la notación A B en el siguiente sentido: A es un subconjunto de B, puede ser que A = B. Propiedades de las operaciones con conjuntos 1.
Análisis Matemático I
 Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Teorema de Carathéodory
 Teorema de Carathéodory Objetivos. Dada una medida exterior ϕ, definir conjuntos Carathéodory-medibles respecto a ϕ, mostrar que esos conjuntos forman una σ-álgebra y la medida exterior ϕ restringida a
Teorema de Carathéodory Objetivos. Dada una medida exterior ϕ, definir conjuntos Carathéodory-medibles respecto a ϕ, mostrar que esos conjuntos forman una σ-álgebra y la medida exterior ϕ restringida a
11.1. Funciones uniformemente continuas
 Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
Lección 11 Continuidad uniforme Completando el análisis de los principales teoremas que conocemos sobre continuidad de funciones reales de variable real, estudiamos ahora la versión general para espacios
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija
 Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija Objetivos. Mostrar que la correspondencia entre vectores y columnas de sus coordenadas (respecto a una base fija) preserva
Correspondencia entre vectores y columnas de sus coordenadas respecto a una base fija Objetivos. Mostrar que la correspondencia entre vectores y columnas de sus coordenadas (respecto a una base fija) preserva
Valores y vectores propios
 Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Resolución numérica de ecuaciones no lineales
 Resolución numérica de ecuaciones no lineales Son muchas las situaciones en las que se presenta el problema de obtener las soluciones de ecuaciones de la forma f(x) = 0. En algunos casos existe una fórmula
Resolución numérica de ecuaciones no lineales Son muchas las situaciones en las que se presenta el problema de obtener las soluciones de ecuaciones de la forma f(x) = 0. En algunos casos existe una fórmula
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Series. Diremos que una serie de números complejos
 Series Una sucesión de números complejos a, a 2, a 3,..., a n,... en C converge al número complejo a (a n a) si para cada ɛ > 0, existe un N tal que a n a < ɛ siempre que n N. Diremos que una serie de
Series Una sucesión de números complejos a, a 2, a 3,..., a n,... en C converge al número complejo a (a n a) si para cada ɛ > 0, existe un N tal que a n a < ɛ siempre que n N. Diremos que una serie de
Taller de Cálculo Avanzado - Segundo Cuatrimestre de Práctica 3
 Taller de Cálculo Avanzado - Segundo Cuatrimestre de 2008 Práctica 3 Topología. Decir qué propiedades (abierto, cerrado, acotado) tienen los siguientes conjuntos. (a) Q. (b) N. (c) {x R : x > 0}. (d) (0,
Taller de Cálculo Avanzado - Segundo Cuatrimestre de 2008 Práctica 3 Topología. Decir qué propiedades (abierto, cerrado, acotado) tienen los siguientes conjuntos. (a) Q. (b) N. (c) {x R : x > 0}. (d) (0,
Guía Semana 7 1. RESUMEN 2. EJERCICIOS PROPUESTOS. Universidad de Chile. Ingeniería Matemática
 . RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
. RESUMEN FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08- Guía Semana 7 Teorema de la función inversa. Sea f : Ω Ê N Ê N, Ω abierto, una función de clase
diám A = x,y A d(x,y) si A es acotado si A no es acotado. {d(x,y) : x,y A}
 Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
El espacio euclideano
 Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
Capítulo 1 El espacio euclideano 1. Definiciones básicas El espacio Euclideano, denotado por R n, está definido por el conjunto (1.1) R n = {x = (x 1, x 2,..., x n ) : x i R}. Es decir, R n es efectivamente
Teorema de Kirk y estructura normal en espacios de Banach
 Teorema de Kirk y estructura normal en espacios de Banach Introducción En el anterior artículo se comentaron los llamados problemas del milenio de las matemáticas [8]. Sólo uno de ellos se ha podido resolver
Teorema de Kirk y estructura normal en espacios de Banach Introducción En el anterior artículo se comentaron los llamados problemas del milenio de las matemáticas [8]. Sólo uno de ellos se ha podido resolver
Subespacios de espacios vectoriales
 Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Boletín de Matemáticas Nueva Serie, Volumen XI No. 1 (2004), pp PUNTOS FIJOS COMUNES DE CONTRACCIONES GENERALIZADAS
 Boletín de Matemáticas Nueva Serie, Volumen XI No. 1 (2004), pp. 132 137 PUNTOS FIJOS COMUNES DE CONTRACCIONES GENERALIZADAS JAIME RODRÍGUEZ MONTES (*) To Jairo Charris in memoriam Resumen. Se demuestra
Boletín de Matemáticas Nueva Serie, Volumen XI No. 1 (2004), pp. 132 137 PUNTOS FIJOS COMUNES DE CONTRACCIONES GENERALIZADAS JAIME RODRÍGUEZ MONTES (*) To Jairo Charris in memoriam Resumen. Se demuestra
OCW-V.Muto El algoritmo de bisección Cap. VI CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO
 CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO En este capítulo comenzaremos a analizar uno de los problemas más básicos del análisis numérico: el problema de búsqueda de raíces. El problema
CAPITULO VI. EL ALGORITMO DE BISECCION 1. INTRODUCCION Y METODO En este capítulo comenzaremos a analizar uno de los problemas más básicos del análisis numérico: el problema de búsqueda de raíces. El problema
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Transformaciones lineales autoadjuntas (hermíticas)
 Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
Transformaciones lineales autoadjuntas (hermíticas) Objetivos. Estudiar propiedades elementales de transformaciones lineales autoadjuntas. Demostrar que para toda transformación lineal autoadjunta en un
TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES)
 TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES) Instrucciones: Resolver los 5 problemas justificando todas sus afirmaciones y presentando todos sus cálculos. 1. Sea F un campo.
TERCER EXAMEN PARCIAL ALGEBRA LINEAL I 23 DE MAYO DE 2014 (CON SOLUCIONES) Instrucciones: Resolver los 5 problemas justificando todas sus afirmaciones y presentando todos sus cálculos. 1. Sea F un campo.
10. Series de potencias
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 7-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
Propiedades de números enteros (lista de problemas para examen)
 Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Universidad Nacional Autónoma de México Licenciatura en Economía Cálculo Diferencial e Integral Continuidad
 1 Universidad Nacional Autónoma de México Licenciatura en Economía Cálculo Diferencial e Integral Continuidad Hasta hace muy poco se creía que una función continua siempre tenía una primera derivada cuyo
1 Universidad Nacional Autónoma de México Licenciatura en Economía Cálculo Diferencial e Integral Continuidad Hasta hace muy poco se creía que una función continua siempre tenía una primera derivada cuyo
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Series numéricas y de potencias. 24 de Noviembre de 2014
 Cálculo Series numéricas y de potencias 24 de Noviembre de 2014 Series numéricas y de potencias Series numéricas Sucesiones de números reales Concepto de serie de números reales. Propiedades Criterios
Cálculo Series numéricas y de potencias 24 de Noviembre de 2014 Series numéricas y de potencias Series numéricas Sucesiones de números reales Concepto de serie de números reales. Propiedades Criterios
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Fórmula integral de Cauchy
 Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
Prerrequisitos de la asignatura Álgebra Lineal Numérica
 Prerrequisitos de la asignatura Álgebra Lineal Numérica El propósito de Álgebra Lineal Numérica es analizar algoritmos típicos de álgebra lineal, optimizando la rapidez y la precisión. Para analizar la
Prerrequisitos de la asignatura Álgebra Lineal Numérica El propósito de Álgebra Lineal Numérica es analizar algoritmos típicos de álgebra lineal, optimizando la rapidez y la precisión. Para analizar la
Norma de Frobenius. Estos apuntes están escritos por Darío Coutiño Aquino y Egor Maximenko.
 Norma de Frobenius Estos apuntes están escritos por Darío Coutiño Aquino y Egor Maximenko. Objetivos. Dada una matriz A M m n (C), su norma de Frobenius (llamada también la norma de Hilbert Schmidt) se
Norma de Frobenius Estos apuntes están escritos por Darío Coutiño Aquino y Egor Maximenko. Objetivos. Dada una matriz A M m n (C), su norma de Frobenius (llamada también la norma de Hilbert Schmidt) se
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Olimpiada Iberoamericana de Matemática Universitaria 2012 Problemas, soluciones y criterios
 Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Espacios completos. 8.1 Sucesiones de Cauchy
 Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
Capítulo 8 Espacios completos 8.1 Sucesiones de Cauchy Definición 8.1.1 (Sucesión de Cauchy). Diremos que una sucesión (x n ) n=1 en un espacio métrico (X, d) es de Cauchy si para todo ε > 0 existe un
C alculo Noviembre 2010
 Cálculo Noviembre 2010 Series numéricas. Sucesiones Definición Una sucesión es una aplicación a : IN IR. Denotamos simplificadamente a n en vez de a(n). El límite de la sucesión (a n ) es l R si para
Cálculo Noviembre 2010 Series numéricas. Sucesiones Definición Una sucesión es una aplicación a : IN IR. Denotamos simplificadamente a n en vez de a(n). El límite de la sucesión (a n ) es l R si para
Métodos Matemáticos: Análisis Funcional
 Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Espacios eucĺıdeos Definición Se dice que un espacio vectorial E es un espacio eucĺıdeo si
Límites y continuidad
 Límites y continuidad Una sucesión en A C es una función que asocia a cada i N un punto a i A, y se le denota como {a i }. La sucesión {a i } es acotada si existe un real r tal que a i r para toda i. La
Límites y continuidad Una sucesión en A C es una función que asocia a cada i N un punto a i A, y se le denota como {a i }. La sucesión {a i } es acotada si existe un real r tal que a i r para toda i. La
: k }, es decir. 2 k. k=0
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Basado en el apunte del curso Cálculo (2do semestre), de Roberto Cominetti, Martín Matamala y Jorge San
5. Funciones analíticas y teoría del índice.
 Funciones de variable compleja. Eleonora Catsigeras. 25 Abril 2006. 47 5. Funciones analíticas y teoría del índice. 5.1. Definición y derivabilidad infinita de las funciones analíticas. Sea Ω un abierto
Funciones de variable compleja. Eleonora Catsigeras. 25 Abril 2006. 47 5. Funciones analíticas y teoría del índice. 5.1. Definición y derivabilidad infinita de las funciones analíticas. Sea Ω un abierto
TEMA 4. Series de potencias
 TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
TEMA 4 Series de potencias. Introducción En el tema anterior hemos estudiado la aproximación polinómica local de funciones mediante el polinomio de Taylor correspondiente. En particular, vimos para la
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Cuatro Problemas de Algebra en la IMO.
 Cuatro Problemas de Algebra en la IMO. Rafael Sánchez Lamoneda UCV. Escuela de Matemáticas Barquisimeto, 10 de Marzo de 2008 Introducción. El objetivo de esta conferencia es analizar cuatro problemas de
Cuatro Problemas de Algebra en la IMO. Rafael Sánchez Lamoneda UCV. Escuela de Matemáticas Barquisimeto, 10 de Marzo de 2008 Introducción. El objetivo de esta conferencia es analizar cuatro problemas de
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
COMPLEMENTO DEL TEÓRICO
 ÁLGEBRA I PRIMER CUATRIMESTRE - AÑO 2016 COMPLEMENTO DEL TEÓRICO El material de estas notas fue dictado en las clases teóricas pero no se encuentra en el texto que seguimos en las mismas ( Álgebra I -
ÁLGEBRA I PRIMER CUATRIMESTRE - AÑO 2016 COMPLEMENTO DEL TEÓRICO El material de estas notas fue dictado en las clases teóricas pero no se encuentra en el texto que seguimos en las mismas ( Álgebra I -
Métodos Matemáticos: Análisis Funcional
 Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Qué son esos espacios de Hilbert? Qué son esos espacios de Hilbert? David Hilbert Para relajarnos
Licenciatura en Ciencias y Técnicas Estadísticas Universidad de Sevilla http://euler.us.es/ renato/clases.html Qué son esos espacios de Hilbert? Qué son esos espacios de Hilbert? David Hilbert Para relajarnos
6. Teoría de Cauchy local.
 Funciones de variable compleja. Eleonora Catsigeras. 24 Abril 2006. 59 6. Teoría de Cauchy local. Dado un abierto Ω C, se denota con R Ω a un rectángulo contenido en Ω. R indica el conjunto de puntos que
Funciones de variable compleja. Eleonora Catsigeras. 24 Abril 2006. 59 6. Teoría de Cauchy local. Dado un abierto Ω C, se denota con R Ω a un rectángulo contenido en Ω. R indica el conjunto de puntos que
Análisis Numérico para Ingeniería. Clase Nro. 7
 Análisis Numérico para Ingeniería Clase Nro. 7 Sistemas de Ecuaciones No Lineales Temas a tratar: Método de Bisección. Método de Punto Fijo. Método de Punto Fijo Sistemático. Método de Newton-Raphson.
Análisis Numérico para Ingeniería Clase Nro. 7 Sistemas de Ecuaciones No Lineales Temas a tratar: Método de Bisección. Método de Punto Fijo. Método de Punto Fijo Sistemático. Método de Newton-Raphson.
3.4 El Teorema de Taylor. Extremos relativos
 3.4. EL TEOREMA DE TAYLOR. EXTREMOS RELATIVOS 103 3.4 El Teorema de Taylor. Extremos relativos La derivación está directamente relacionada con la posibilidad de aproximar localmente funciones suficientemente
3.4. EL TEOREMA DE TAYLOR. EXTREMOS RELATIVOS 103 3.4 El Teorema de Taylor. Extremos relativos La derivación está directamente relacionada con la posibilidad de aproximar localmente funciones suficientemente
Deducción de las fórmulas del método del gradiente conjugado
 Deducción de las fórmulas del método del gradiente conjugado Objetivos. Demostrar el teorema sobre los subespacios de Krylov en el método del gradiente conjugado. Requisitos. Subespacios generados por
Deducción de las fórmulas del método del gradiente conjugado Objetivos. Demostrar el teorema sobre los subespacios de Krylov en el método del gradiente conjugado. Requisitos. Subespacios generados por
Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación
![Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación](/thumbs/59/43345437.jpg) Tema 8 Ceros de funciones Versión: 23 de abril de 2009 8.1 Introducción Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación f(x) = 0. (8.1) La
Tema 8 Ceros de funciones Versión: 23 de abril de 2009 8.1 Introducción Dada f : [a, b] R R, continua, se plantea el problema de encontrar ceros de f, es decir raíces de la ecuación f(x) = 0. (8.1) La
F-ESPACIOS. 1.- Introducción
 F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
F-ESPACIOS 1.- Introducción Recordemos que un subconjunto A de un espacio topológico X se llama diseminado o raro (nowhere dense en ingés) si A=. Un subconjunto que se pueda escribir como unión numerable
Variable Compleja I ( ) Ejercicios resueltos. Las convergencias puntual y uniforme de sucesiones y series de funciones
 Variable Compleja I (205-6) Ejercicios resueltos Las convergencias puntual y uniforme de sucesiones y series de funciones Recordemos la definición de la convergencia uniforme: f n (z) f (z) en un conjunto
Variable Compleja I (205-6) Ejercicios resueltos Las convergencias puntual y uniforme de sucesiones y series de funciones Recordemos la definición de la convergencia uniforme: f n (z) f (z) en un conjunto
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Números naturales y recursividad
 Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Números naturales y recursividad Rafael F. Isaacs G. * Fecha: 12 de abril de 2004 Números naturales Cuál es el primer conjunto de números que estudiamos desde la escuela primaria? Se sabe que los números
Continuidad 2º Bachillerato. materiales Editorial SM
 Continuidad 2º Bachillerato materiales Editorial SM Continuidad en un punto: primera aproximación Estatura medida cada 5 años: hay grandes saltos entre cada punto y el siguiente. Estatura medida cada año:
Continuidad 2º Bachillerato materiales Editorial SM Continuidad en un punto: primera aproximación Estatura medida cada 5 años: hay grandes saltos entre cada punto y el siguiente. Estatura medida cada año:
ax + b (x 1)(x 4). c) (2.0 pto.) Sabiendo que f(0) = 2, escriba el desarrollo de Taylor de orden 3 para f en torno a x 0 = 0.
 Pauta Control 1 MA1002 Cálculo Diferencial e Integral Fecha: 21 de Abril de 2017 Problema 1. Considere la función f : R \ {1, 4} R, tal que su derivada es f (x) = ax + b (x 1)(x 4). a) (1.0 ptos.) Sabiendo
Pauta Control 1 MA1002 Cálculo Diferencial e Integral Fecha: 21 de Abril de 2017 Problema 1. Considere la función f : R \ {1, 4} R, tal que su derivada es f (x) = ax + b (x 1)(x 4). a) (1.0 ptos.) Sabiendo
Métodos Iterativos para Ecuaciones no Lineales
 This is page i Printer: Opaque this Métodos Iterativos para Ecuaciones no Lineales Dr. Oldemar Rodríguez Rojas Setiembre 001 ii This is page iii Printer: Opaque this Contents 1 Métodos iterativos para
This is page i Printer: Opaque this Métodos Iterativos para Ecuaciones no Lineales Dr. Oldemar Rodríguez Rojas Setiembre 001 ii This is page iii Printer: Opaque this Contents 1 Métodos iterativos para
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. Estabilidad
 ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. ESTABILIDAD DE LOS SISTEMAS NO LINEALES. PRINCIPIO DE LINEALIZACIÓN. TEOREMA DE GROBMAN-HARTMAN Estabilidad 1. Definición. Sea f : Ω R n R n un campo C 1, y
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 7. ESTABILIDAD DE LOS SISTEMAS NO LINEALES. PRINCIPIO DE LINEALIZACIÓN. TEOREMA DE GROBMAN-HARTMAN Estabilidad 1. Definición. Sea f : Ω R n R n un campo C 1, y
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
Tema 2: Series numéricas
 Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
Tema 2: Series numéricas Una serie infinita (o simplemente serie) es una suma formal de infinitos términos a + a 2 + a 3 + + + Al número se le denomin-ésimo término de la serie Se llama sucesión de sumas
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
Problemas con soluciones
 Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Departamento de Matemática, Universidad Técnica Federico Santa María, MAT-223. Problemas con soluciones 1) Muestre que si A es una base de una toplogía en X, entonces la topología generada por A es iqual
Método de Gradientes Conjugados.
 Método de Gradientes Conjugados. Lourdes Fabiola Uribe Richaud & Juan Esaú Trejo Espino. Instituto Politécnico Nacional Escuela Superior de Física y Matemáticas February 17, 2015 1 Método de Direcciones
Método de Gradientes Conjugados. Lourdes Fabiola Uribe Richaud & Juan Esaú Trejo Espino. Instituto Politécnico Nacional Escuela Superior de Física y Matemáticas February 17, 2015 1 Método de Direcciones
Matriz asociada a una transformación lineal respecto a un par de bases
 Matriz asociada a una transformación lineal respecto a un par de bases Ejercicios Objetivos Comprender cómo se describe una transformación lineal (que actúa en espacios vectoriales de dimensiones finitas)
Matriz asociada a una transformación lineal respecto a un par de bases Ejercicios Objetivos Comprender cómo se describe una transformación lineal (que actúa en espacios vectoriales de dimensiones finitas)
Definición de la matriz inversa
 Definición de la matriz inversa Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, habilidades básicas de resolver sistemas de ecuaciones Ejemplo El número real
Definición de la matriz inversa Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, habilidades básicas de resolver sistemas de ecuaciones Ejemplo El número real
Desarrollos en Serie.Series Funcionales Teorema de Rolle Enunciado
 Desarrollos en Serie.Series Funcionales Teorema de Rolle Enunciado Sea y=f(x) Contínua en [a,b] Derivable en (a,b) Cumpliendo f(a) = f(b) Se cumple que: Demostración Por el teorema de Weirstrasse, f(x)
Desarrollos en Serie.Series Funcionales Teorema de Rolle Enunciado Sea y=f(x) Contínua en [a,b] Derivable en (a,b) Cumpliendo f(a) = f(b) Se cumple que: Demostración Por el teorema de Weirstrasse, f(x)
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2
 ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
Nombre y Apellidos: e f(x) dx. Estudiar si converge la integral impropia
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Febrero 27 de Enero de 26 Nombre y Apellidos: DNI: 6.25 p.) ) Se considera la función f : [, ) R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Febrero 27 de Enero de 26 Nombre y Apellidos: DNI: 6.25 p.) ) Se considera la función f : [, ) R definida
Semana04[1/17] Funciones. 21 de marzo de Funciones
![Semana04[1/17] Funciones. 21 de marzo de Funciones Semana04[1/17] Funciones. 21 de marzo de Funciones](/thumbs/73/69418199.jpg) Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Semana04[1/17] 21 de marzo de 2007 Composición de funciones Semana04[2/17] Pensemos que tenemos tres conjuntos no vacíos A, B, C, y dos funciones, f : A B y g : B C, como en el siguiente diagrama: Figura:
Teorema de la Función Inversa (sistema f i : R n R) f 1 : U R. f n : U R
 Funciones de R n en R m 1 Teorema de la Función Inversa (sistema f i : R n R) Teorema 1. Sea U R n un abierto y sean f 1 : U R. f n : U R con derivadas parciales continuas. Considerar las ecuaciones f
Funciones de R n en R m 1 Teorema de la Función Inversa (sistema f i : R n R) Teorema 1. Sea U R n un abierto y sean f 1 : U R. f n : U R con derivadas parciales continuas. Considerar las ecuaciones f
Ecuaciones Diferenciales Ordinarias. Método Iterativo Teorema de Picard
 Apuntes de Ecuaciones Diferenciales Ordinarias II Método Iterativo Teorema de Picard Octavio Miloni 1 Soluciones por Iteración Vamos a resolver ecuaciones diferenciales a partir de un esquema iterativo,
Apuntes de Ecuaciones Diferenciales Ordinarias II Método Iterativo Teorema de Picard Octavio Miloni 1 Soluciones por Iteración Vamos a resolver ecuaciones diferenciales a partir de un esquema iterativo,
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
8. Consecuencias de la Teoría de Cauchy.
 Funciones de variable compleja. Eleonora Catsigeras. 8 Mayo 2006. 77 8. Consecuencias de la Teoría de Cauchy. 8.1. Principio del módulo máximo. Definición 8.1.1. Sea f una función continua en Ω. Se dice
Funciones de variable compleja. Eleonora Catsigeras. 8 Mayo 2006. 77 8. Consecuencias de la Teoría de Cauchy. 8.1. Principio del módulo máximo. Definición 8.1.1. Sea f una función continua en Ω. Se dice
Procesos de Control Semi-Markovianos con Costos Descontados
 Capítulo 1 Procesos de Control Semi-Markovianos con Costos Descontados 1.1. Introducción En este capítulo se introduce el problema de control óptimo semi-markoviano (PCO) con respecto al índice en costo
Capítulo 1 Procesos de Control Semi-Markovianos con Costos Descontados 1.1. Introducción En este capítulo se introduce el problema de control óptimo semi-markoviano (PCO) con respecto al índice en costo
Clase 2: Algoritmo de Euclídes
 Clase 2: Algoritmo de Euclídes Dr. Daniel A. Jaume, * 8 de agosto de 2011 1. Máximo común divisor Para entender que es el máximo común divisor de un par de enteros (no simultáneamente nulos). Lidearemos
Clase 2: Algoritmo de Euclídes Dr. Daniel A. Jaume, * 8 de agosto de 2011 1. Máximo común divisor Para entender que es el máximo común divisor de un par de enteros (no simultáneamente nulos). Lidearemos
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Continuidad. 5.1 Continuidad en un punto
 Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
Capítulo 5 Continuidad 5.1 Continuidad en un punto Definición 5.1.1 (Aplicación continua en un punto). Sean (X, τ) e (Y, τ ) dos espacios topológicos, y sea f : X Y una aplicación entre ellos. Diremos
a b = a 2 b 2 a 3 b 3 1 n = [ 1 ] n
![a b = a 2 b 2 a 3 b 3 1 n = [ 1 ] n a b = a 2 b 2 a 3 b 3 1 n = [ 1 ] n](/thumbs/81/82890600.jpg) Álgebra compleja C n Objetivos. En el espacio vectorial C n introducir la multiplicación por componentes y mostrar que C n con esta operación es una álgebra compleja asociativa y conmutativa con identidad.
Álgebra compleja C n Objetivos. En el espacio vectorial C n introducir la multiplicación por componentes y mostrar que C n con esta operación es una álgebra compleja asociativa y conmutativa con identidad.
Examen de Cálculo infinitesimal PROBLEMAS. 1 + a + a a n a n+1
 Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Método del Punto Fijo
 Método del Punto Fijo Carlos Uriel Herrera Felipe de Jesús Aguilar May 21, 2018 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias Físico Matemáticas 1 / 24 Contenido 1 Introducción Espacios
Método del Punto Fijo Carlos Uriel Herrera Felipe de Jesús Aguilar May 21, 2018 Benemérita Universidad Autónoma de Puebla Facultad de Ciencias Físico Matemáticas 1 / 24 Contenido 1 Introducción Espacios
Problemas de VC para EDVC elaborados por C. Mora, Tema 4
 Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Problemas de VC para EDVC elaborados por C. Mora, Tema 4 Ejercicio Determinar las funciones enteras f para las que Solución f( + w) = f()f(w), w C. En primer lugar, f(0) = f(0 + 0) = f(0)f(0) = f(0) 2,
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Teorema de Existencia y unicidad (caso n-dimensional).
 Teorema de Existencia y unicidad (caso n-dimensional). Sea U R n un conjunto abierto y V R un intervalo abierto en R. Considere la aplicación v : V U R n diferenciable con derivada continua en una vecindad
Teorema de Existencia y unicidad (caso n-dimensional). Sea U R n un conjunto abierto y V R un intervalo abierto en R. Considere la aplicación v : V U R n diferenciable con derivada continua en una vecindad
