Teoremas del Límite Central No-Conmutativos y Productos de Gráficas
|
|
|
- Esteban González Contreras
- hace 5 años
- Vistas:
Transcripción
1 Teoremas del Límite Central No-Conmutativos y Productos de Gráficas Marco Tulio Gaxiola Leyva CIMAT 16 de Octubre de 2014 Seminario Interinstitucional Centro Norte de México, de Combinatoria y Probabilidad Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
2 1 Probabilidad No-Conmutativa 2 Teoremas de Límite Central No-Conmutativos 3 Productos de gráficas Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
3 Probabilidad No-Conmutativa Definiciones básicas Definición (1) Un Espacio de Probabilidad No-Conmutativo es un par (A, ϕ) donde A es un álgebra compleja con unidad y ϕ : A C es un funcional lineal con ϕ(1 A ) = 1, donde 1 A es la unidad en A. (2) Si A es una *-álgebra y ϕ es un estado, es decir, cumple que ϕ(a a) 0 para toda a A, entonces el par (A, ϕ) es llamado *-EPNC. A los elementos de A se les llama variables aleatorias no-conmutativas, o solo variables aleatorias. A una variable aleatoria a A se le llama autoadjunta si se tiene que a = a. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
4 Probabilidad No-Conmutativa Definiciones básicas (Ejemplo) Las matrices cuadradas (de n n) con entradas reales es un *-álgebra. ϕ tr (M) = 1 n Tr(M). ϕ 1 (M) = M 11. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
5 Probabilidad No-Conmutativa Definiciones básicas Sea a (A, ϕ) una variable aleatoria autoadjunta, decimos que la distribución (con respecto al estado ϕ) de a es una medida µ en R, tal que ϕ(a m ) = x m µ(dx), m = 1, 2,.... Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
6 Probabilidad No-Conmutativa Nociones de independencia (Tensorial) Definición Sea (A, ϕ) un EPNC, decimos que a, b (A, ϕ) son independientes en el sentido tensorial si se cumple que ϕ(a m 1 b n1 a m k b n k ) = ϕ (a ) k i=1 m i ϕ (b ) k i=1 n i, para todo m j, n j N {0}, i = 1, 2,..., k. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
7 Probabilidad No-Conmutativa Nociones de independencia (Booleana) Definición Sea (A, ϕ) un EPNC, decimos que a, b (A, ϕ) son independientes en el sentido booleano si se cumple que ϕ(a m 1 b n1 a m k b n k ) = para todo m j, n j N {0}, i = 1, 2,..., k. k ϕ (a m i ) ϕ (b n i ), i=1 Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
8 Probabilidad No-Conmutativa Nociones de independencia (Monótona) Definición Sea (A, ϕ) un EPNC, decimos que a, b (A, ϕ) son independientes en el sentido monótono si se cumple que ϕ(a m 1 b n1 a m k b n k ) = ϕ (a ) k k i=1 m i ϕ (b n i ), para todo m j, n j N {0}, i = 1, 2,..., k. i=1 Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
9 Probabilidad No-Conmutativa Nociones de independencia (Ejemplos) Consideremos el EPNC (A, ϕ 1 ), donde A = M n n, la *-álgebra de las matrices cuadradas de n n, y ϕ 1 (M) = M 11, para M A. Sean A M m m y B M l l, tales que ml = n, sean I m e I l la matriz identidad de m m y l l, respectivamente, y P l y P m la proyección de rango 1 al espacio generado por (1, 0, 0,..., 0), donde el vector es de tamaño m y l, respectivamente, entonces (A I l ), (I m B) son independientes en el sentido tensorial (A P l ), (P m B) son independientes en el sentido booleano (A P l ), (I m B) son independientes en el sentido monótono, con respecto al funcional ϕ 1. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
10 ϕ tr ((A I l ) m 1 (I m B) n1 (A I l ) m k (I m B) n k ) = ϕ tr ((A m 1 I m 1 l )(I n 1 m B n 1 ) (A m k I m k l = ϕ tr ((A m 1 B n 1 ) (A m k B n k )) = ϕ tr ( A k i=1 m i B k i=1 n i = Tr m = Tr ml = Tr n (A k i=1 m i ) Tr l (B k i=1 n i (A ) k i=1 m i Tr I l lm ((A I l ) ) k i=1 m i Tr = ϕ tr ( (A I l ) k i=1 m i ) = Tr n ) )(I n k m B n k )) (A k i=1 m i B k i=1 n i (I m B ) k i=1 n i ((I m B) ) k i=1 m i ) n ϕ tr ((I m B) k i=1 m i ) ) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
11 Teoremas de Límite Central No-Conmutativos TLC Tensorial Teorema Sea {a n } n 1 (A, ϕ) una sucesión de variables aleatorias autoadjuntas en un *-EPNC, independientes en el sentido tensorial, tales que ϕ(a n ) = 0 y ϕ(a 2 n) = 1, para todo n 1, entonces se cumple que (( ) lim ϕ 1 m ) a i n n i=1 = 1 2π x m e x 2 /2 dx, m = 1, 2,.... Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
12 Teoremas de Límite Central No-Conmutativos TLC Booleano Teorema Sea {a n } n 1 (A, ϕ) una sucesión de variables aleatorias autoadjuntas en un *-EPNC, independientes en el sentido booleano, tales que ϕ(a n ) = 0 y ϕ(a 2 n) = 1, para todo n 1, entonces se cumple que (( ) lim ϕ 1 m ) a i = 1 n n 2 i=1 x m (δ 1 + δ 1 )dx, m = 1, 2,.... Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
13 Teoremas de Límite Central No-Conmutativos TLC Monótono Teorema Sea {a n } n 1 (A, ϕ) una sucesión de variables aleatorias autoadjuntas en un *-EPNC, independientes en el sentido monótono, tales que ϕ(a n ) = 0 y ϕ(a 2 n) = 1, para todo n 1, entonces se cumple que (( ) lim ϕ 1 m ) a i = 1 n n π i=1 2 2 x m dx, m = 1, 2, x 2 Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
14 Producto directo Definición Sean G 1 = (V 1, E 1 ) y G 2 = (V 2, E 2 ) dos gráficas. El producto directo de G 1 con G 2, denotado por G 1 G 2, es la gráfica con conjunto de vértices V = V 1 V 2 y conjunto de aristas E, de tal forma que para (v 1, w 1 ), (v 2, w 2 ) V 1 V 2 el arista e = (v 1, w 1 ) (v 2, w 2 ) E si, y solo si, alguna de las condiciones se satisface: 1. v 1 = v 2 y w 1 w 2 2. v 1 v 2 y w 1 = w 2. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
15 Producto directo (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
16 Producto directo (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
17 Producto directo (Ejemplo) Lo anterior se puede escribir en términos de las matrices de adyacencia A P2 y A K3, de la siguiente forma: A P2 K 3 = A P2 I 3 + I 3 A K3, donde I 3 es la matriz identidad de 3 3. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
18 Producto directo Teorema Sean G 1 = (V 1, E 1 ) y G 2 = (V 2, E 2 ) dos gráficas finitas, entonces la matriz de adyacencia de G 1 G 2, puede ser descompuesta como una suma en términos de las matrices de adyacencia A G1 y A G2 de la siguiente forma: A G1 G 2 = A G1 I V2 + I V1 A G2, donde I d es la matriz identidad de d d. Corolario A G1 G 2 (M V V, ϕ tr ) es la suma de dos variables aleatorias independientes en el sentido tensorial. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
19 Producto directo (TLC) Teorema Sea G = (V, E) una gráfica finita conexa. Sea G N el producto directo de la gráfica G consigo misma N veces, y sea A G N su matriz de adyacencia, entonces se cumple que lim N ϕ tr A G N ) 1/2 N ( V 2 E m = 1 2π x m e x 2 /2 dx, m = 1, 2,... Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
20 Producto booleano Definición Sean G 1 = (V 1, E 1, r 1 ) y G 2 = (V 2, E 2, r 2 ) dos gráficas con raíz. El producto booleano de G 1 con G 2, denotado por G 1 G 2, es la gráfica con conjunto de vértices V = V 1 V 2 y conjunto de aristas E, de tal forma que para (v 1, w 1 ), (v 2, w 2 ) V 1 V 2 el arista e = (v 1, w 1 ) (v 2, w 2 ) E si, y solo si, alguna de las condiciones se satisface: 1. v 1 = v 2 = r 1 y w 1 w 2 2. v 1 v 2 y w 1 = w 2 = r 2. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
21 Producto booleano (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
22 Producto booleano (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
23 Producto booleano (Ejemplo) Lo anterior se puede escribir en términos de las matrices de adyacencia A K3 y A C4, de la siguiente forma: A K3 C 4 = A K3 P 4 + P 3 A C4, donde P 4 y P 3 son la proyección de rango 1 al espacio generado por (1,0,0,0) y (1,0,0), respectivamente. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
24 Producto booleano Teorema Sean (G 1, e 1 ) y (G 2, e 2 ) dos gráficas con raíz, entonces la matriz de adyacencia de G 1 G 2, puede ser descompuesta como una suma en términos de las matrices de adyacencia A G1 y A G2 de la siguiente forma: A G1 G 2 = A G1 P V2 + P V1 A G2 Corolario A G1 G 2 (M V V, ϕ 1 ) es la suma de dos variables aleatorias independientes en el sentido booleano. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
25 Producto booleano (TLC) Teorema Sea G = (V, E, e 1 ) una gráfica finita conexa con raíz. Sea G N el producto booleano de la gráfica G consigo misma N veces, y sea A G N su matriz de adyacencia, entonces se cumple que lim N ϕ 1 (( ) m ) A G N = 1 Ndeg(e1 ) 2 x m (δ 1 + δ 1 )dx, m = 1, 2,... Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
26 Producto monótono Definición Sean G 1 = (V 1, E 1, r 1 ) y G 2 = (V 2, E 2, r 2 ) dos gráficas con raíz. El producto monótono de G 1 con G 2, denotado por G 1 r2 G 2, es la gráfica con conjunto de vértices V = V 1 V 2 y conjunto de aristas E, de tal forma que para (v 1, w 1 ), (v 2, w 2 ) V 1 V 2 el arista e = (v 1, w 1 ) (v 2, w 2 ) E si, y solo si, alguna de las condiciones se satisface: 1. v 1 = v 2 y w 1 w 2 2. v 1 v 2 y w 1 = w 2 = r 2. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
27 Producto monótono (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
28 Producto monótono (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
29 Producto monótono (Ejemplo) Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
30 Producto monótono (Ejemplo) En términos de las matrices de adyacencia se tiene que A K3 C 4 = A K3 P 4 + I 3 A C4, donde P 4 es la proyección de rango 1 al espacio generado por (1,0,0,0) e I 3 es la matriz identidad de 3 3. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
31 Producto monótono Teorema Sean (G 1, e 1 ) y (G 2, e 2 ) dos gráficas con raíz, entonces la matriz de adyacencia de G 1 G 2, puede ser descompuesta como una suma en términos de las matrices de adyacencia A G1 y A G2 de la siguiente forma: A G1 G 2 = A G1 P V2 + I V1 A G2 Corolario A G1 G 2 (M V V, ϕ 1 ) es la suma de dos variables aleatorias independientes en el sentido monótono. Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
32 Producto monótono (TLC) Teorema Sea G = (V, E, e 1 ) una gráfica finita conexa con raíz. Sea G N el producto monótono de la gráfica G consigo misma N veces, y sea A G N su matriz de adyacencia, entonces se cumple que lim N ϕ 1 (( ) m ) A G N = 1 Ndeg(e1 ) π 2 2 x m dx, m = 1, 2,... 2 x 2 Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
33 GRACIAS Marco Tulio Gaxiola Leyva (CIMAT) TLC s No-Conmutativos 16 de Octubre de / 33
Introducción a la Probabilidad No-Conmutativa
Introducción a la Probabilidad No-Conmutativa Tulio Gaxiola CIMAT 18 de abril de 2016 Sesión de Probabilidad No-Conmutativa, Matrices Aleatorias y Gráficas Tulio Gaxiola (CIMAT) EPNC y Gráficas 18 de abril
Espacios vectoriales con producto interno
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Preliminares. 1.1 Acciones de Grupo
Capítulo 1 Preliminares En este capítulo se presentan algunas definiciones y hechos fundamentales de la Teoría de Grupos y recordar nociones básicas de Álgebra Lineal. También se presentan algunos resultados
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
ELEMENTOS DE ANÁLISIS FUNCIONAL
ELEMENTOS DE ANÁLISIS FUNCIONAL Guillermo Ames Universidad Tecnológica Nacional - Facultad Regional Córdoba 2011 TEMA 3: ESPACIOS CON PRODUCTO INTERNO. ESPACIOS DE HILBERT. Espacios producto interno. Espacios
Lista de problemas de álgebra, 2016
Instituto Politécnico Nacional Escuela Superior de Física y Matemáticas Posgrado en Ciencias Físicomatemáticas Línea de Matemáticas Lista de problemas de álgebra 2016 Egor Maximenko: En mi opinión cualquier
4. Espacios vectoriales
Contents 4 Espacios vectoriales 2 4.1 Dependencia e independencia lineal.................................. 4 4.2 Subespacios vectoriales.............................................. 7 4.3 Bases y dimensión..................................................
Teoría de Anillos y Campos
Teoría de Anillos y Campos Presentación 2: anillos, homomorfismos e ideales Luis Felipe González Rivas UANL 21 de agosto de 2018 Contenido 1 Anillos 2 Homomorfismos 3 Ideales Luis Felipe González Rivas
Matrices de Toeplitz autoadjuntas y el teorema ĺımite de Szegő
Matrices de Toeplitz autoadjuntas y el teorema ĺımite de Szegő Egor Maximenko para un proyecto conjunto con Víctor Hugo Ibarra Mercado, Eliseo Sarmiento Rosales y José Eliud Silva Urrutia Instituto Politécnico
1. Algunas deniciones y resultados del álgebra lineal
. Algunas deniciones y resultados del álgebra lineal Denición. (Espacio vectorial o espacio lineal sobre R) Un espacio vectorial o espacio lineal sobre el campo de los números reales, R, es un conjunto
Repaso de álgebra de matrices y probabilidad. Javier Santibáñez (IIMAS, UNAM) Regresión Semestre / 58
Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
Análisis Funcional (Ejercicios-01)
Análisis Funcional (Ejercicios-1 1. Sea M un conjunto a lo más numerable y sea (M, 2 M, # el espacio de medida con # la medida de conteo. (i Demuestre que una función medible f es integrable si y sólo
Guía. Álgebra II. Examen parcial III. Transformaciones lineales. Teoremas los más importantes cuyas demostraciones se pueden incluir en el examen
Guía. Álgebra II. Examen parcial III. Transformaciones lineales. Teoremas los más importantes cuyas demostraciones se pueden incluir en el examen 1. Teorema de la representación matricial de una transformación
Examen de Admisión a la Maestría / Doctorado 24 de Junio de 2016
Examen de Admisión a la Maestría / Doctorado 4 de Junio de 6 Nombre: Instrucciones: En cada reactivo seleccione la respuesta correcta encerrando en un círculo la letra correspondiente. Puede hacer cálculos
Prerrequisitos de la asignatura Álgebra Lineal Numérica
Prerrequisitos de la asignatura Álgebra Lineal Numérica El propósito de Álgebra Lineal Numérica es analizar algoritmos típicos de álgebra lineal, optimizando la rapidez y la precisión. Para analizar la
Cuerpos Finitos. XXVII Escuela Venezolana de Matemáticas EMALCA. Edgar Martínez-Moro Sept. 2014
Cuerpos Finitos XXVII Escuela Venezolana de Matemáticas EMALCA Edgar Martínez-Moro Sept. 2014 Cuerpos y extensiones de cuerpos Un cuerpo (F, +, ) es un conjunto no vacío en el que se han definido dos operaciones
( 1 0 BLOQUE DE GEOMETRÍA TEMA 4: ESPACIOS VECTORIALES. ( 5+ 3i )+ ( 2 i )=7+ 2i. La suma de dos números complejos es un número complejo.
BLOQUE DE GEOMETRÍA TEMA 4: ESPACIOS VECTORIALES. Operaciones Binarias: Observamos las siguientes operaciones: ( 5+ 3i )+ ( 2 i )=7+ 2i. La suma de dos números complejos es un número complejo. ( 1 0 2
Estadística. Tema 2. Variables Aleatorias Funciones de distribución y probabilidad Ejemplos distribuciones discretas y continuas
Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Examen Extraordinario de Álgebra III, licenciatura
Examen Extraordinario de Álgebra III, licenciatura El Examen a Título de Suficiencia de Álgebra III abarca los siguientes temas: 1. Formas bilineales y cuadráticas. 2. Valores y vectores propios. 3. Forma
1. ESPACIOS DE HILBERT Y OPERADORES
1. ESPACIOS DE HILBERT Y OPERADORES 1. DEFINICIÓN, PROPIEDADES Y EJEMPLOS Definición. Sea H un espacio vectorial sobre el cuerpo C de los números complejos, un producto escalar sobre H es una aplicación
Métodos Estadísticos Multivariados
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Teoremas de Tonelli y Fubini
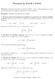Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Algebra Lineal. Gustavo Rodríguez Gómez. Verano 2011 INAOE. Gustavo Rodríguez Gómez (INAOE) Algebra Lineal Verano / 21
Algebra Lineal Gustavo Rodríguez Gómez INAOE Verano 2011 Gustavo Rodríguez Gómez (INAOE) Algebra Lineal Verano 2011 1 / 21 Espacios Vectoriales Espacios Vectoriales INAOE Gustavo Rodríguez Gómez (INAOE)
Momentos de Funciones de Vectores Aleatorios
Capítulo 1 Momentos de Funciones de Vectores Aleatorios 1.1 Esperanza de Funciones de Vectores Aleatorios Definición 1.1 Sea X = (X 1,..., X n ) un vector aleatorio (absolutamente continuo o discreto)
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
Departamento de Ingeniería Matemática - Universidad de Chile
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 08-2 SEMANA 7: ESPACIOS VECTORIALES 3.5. Generadores de un espacio vectorial Sea V un espacio vectorial
Tema 3 APLICACIONES LINEALES
Tema 3 APLICACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Definición y propiedades. Núcleo e imagen. Isomorfismos. Definición 1.1 Una aplicación f : V V entre dos espacios vectoriales
Bases ortogonales. Profesores Omar Darío Saldarriaga Ortíz. Hernán Giraldo
Bases ortogonales Profesores Omar Darío Saldarriaga Ortíz Iván Dario Gómez Hernán Giraldo 9 Definición Sea V un espacio vectorial y {v,..., v n} una base para V. decimos que {v,..., v n} es una base ortogonal
Clase de Álgebra Lineal
Clase de Álgebra Lineal M.Sc. Carlos Mario De Oro Facultad de Ciencias Básicas Departamento de matemáticas 04.2017 Page 1 Espacios vectoriales Definicion. Espacio Vectorial (E.V.) Un V espacio vectorial
Material para el examen parcial 1
Algebra Lineal 2, FAMAT-UG, aug-dic, 2009 Material para el examen parcial 1 (17 oct, 2009) Definiciones: Hay que saber las definiciones precisas de todos los siguientes términos, y conocer ejemplos concretos
1. MEDIDA E INTEGRACIÓN.
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
El Álgebra Lineal detrás de los buscadores de internet
El Álgebra Lineal detrás de los buscadores de internet 2 / 09 / 202 Bloques temáticos de Álgebra (EI) Sistemas lineales de ecuaciones Matrices & determinantes Espacios vectoriales Subespacios, transformaciones
Una Introducción Amable a la Teoría Infinita de Ramsey
Una Introducción Amable a la Teoría Infinita de Ramsey David J. Fernández Bretón djfernan@umich.edu http://www-personal.umich.edu/~djfernan Mathematics Department, University of Michigan Jueves 30 de julio
Clase 8 Matrices Álgebra Lineal
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
2. El Segundo Método de Estabilidad de Liapunov. 2. El Segundo Método de Estabilidad de Liapunov
2.1. Introducción. Funciones de Liapunov 2.1. Introducción. Funciones de Liapunov Consideremos el sistema no lineal autónomo (1.12) y = f (y) donde f : D R N R N, con f Lip loc (D) y f (0) = 0, D abierto
Geometría afín y proyectiva, 2016 SEMANA 3
Geometría afín y proyectiva, 2016 SEMANA 3 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
ALGEBRA LINEAL Segundo Semestre. Parte II
1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
ALGEBRA LINEAL Y GEOMETRÍA. REPASO DE ÁLGEBRA LINEAL-2: CAMBIOS DE BASE GRADO DE MATEMÁTICAS. CURSO
ALGEBRA LINEAL Y GEOMETRÍA. REPASO DE ÁLGEBRA LINEAL-2: CAMBIOS DE BASE GRADO DE MATEMÁTICAS. CURSO 2012-2013 José García-Cuerva Universidad Autónoma de Madrid 11 de febrero de 2013 JOSÉ GARCÍA-CUERVA
Análisis de Fourier. Resumen de los apuntes de D. Antonio Cañada Villar. Sergio Cruz Blázquez. Curso 2015/2016
Análisis de Fourier Resumen de los apuntes de D. Antonio Cañada Villar Curso 2015/2016 Sergio Cruz Blázquez Índice 1 El espacio L 2 (a, b) Definición y primeras notas El espacio L 1 (a, b) L 2 (a, b) como
Maestría en Matemáticas
Reactivos Propuestos para Examen de Admisión (ASN) Ingreso en Agosto de 203. Sea R el conjunto de los números reales y S el conjunto de todas las funciones valuadas en los reales con dominio en R. Muestre
Clase 1: Gráficas. Malors Espinosa Lara. 6 de Febrero de 2010
Clase : Gráficas. Malors Espinosa Lara 6 de Febrero de 00 Resumen Estudiaremos el capítulo del libro A course in Combinatorics. Daremos algunas definiciones de libro Combinatorics and Graph Theory, pues
Tema 1: Matrices. October 13, 2016
Tema 1: Matrices October 13, 2016 1 Matrices Las matrices se usan en muchos ámbitos de las ciencias: sociología, economía, hojas de cálculo, matemáticas, física,... Se inició su estudio en el siglo XIX
5. Aplicaciones Lineales
Contents 5 Aplicaciones Lineales 2 5.1 Aplicaciones lineales. Definición y propiedades........................ 2 5.2 Núcleo e Imagen.................................................... 3 5.3 Descomposición
Espacios Vectoriales
Espacios Vectoriales Pedro Díaz Navarro * Abril de 26. Vectores en R 2 y R 3 2. Espacios Vectoriales Definición (Espacio vectorial) Decimos que un conjunto no vacío V es un espacio vectorial sobre un cuerpo
Primera Escuela de Verano de Matemática y Física Universidad Central del Ecuador. Espacios Algebraicos de Probabilidad y Aplicaciones
Primera Escuela de Verano de Matemática y Física Universidad Central del Ecuador Espacios Algebraicos de Probabilidad y Aplicaciones 12 de junio 2013 Sean: El conjunto Ω = {ω 1, ω 2,, ω n}, La función
Cap. 3 : Variables aleatorias
Cap. 3 : Variables aleatorias Alexandre Blondin Massé Departamento de Informática y Matematica Université du Québec à Chicoutimi 16 de junio del 2015 Modelado de sistemas aleatorios Ingeniería de sistemas,
Anillos finitos locales
Anillos finitos locales XXVII Escuela Venezolana de Matemáticas EMALCA Edgar Martínez-Moro Sept. 2014 Estructura de los anillos finitos Un anillo conmutativo A es local si tiene un único ideal maximal
Álgebra Lineal 2015 Práctica 5: Diagonalización.
Álgebra Lineal 2015 Práctica 5: Diagonalización. 1. Sean T (a, b) = (4a b, b+2a), B = {(1, 0), (0, 1)} y C = {(1, 3), (2, 5)}. (a) Hallar la matriz camio de base de B a C, la matriz cambio de base de C
Valores propios de matrices de Toeplitz hermitianas: aproximación uniforme por medio de la función cuantil
Valores propios de matrices de Toeplitz hermitianas: aproximación uniforme por medio de la función cuantil Egor Maximenko http://esfm.egormaximenko.com usando trabajos conjuntos con Johan Manuel Bogoya,
Curso Propedéutico de Cálculo Sesión 7:
Curso Propedéutico de Cálculo Sesión 7: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 Esquema 1 2 3 4 Hasta ahora nos hemos enfocado en funciones
Notas núm dic, 2010
Mini-curso de introducción a los grupos de Lie, CIMAT, dic 2010 Notas núm. 1 6 dic, 2010 Temario del curso: Lunes, 6 dic: Definición y ejemplos de grupos de Lie y acciones de grupos de Lie. Martes, 7 dic:
TEMA VI: ESPACIOS DE HILBERT
TEMA VI: ESPACIOS DE HILBERT. Espacios con producto escalar Definición: Sea L un espacio vectorial sobre el cuerpo K (R ó C). Por un producto escalar (o interno) sobre L entedemos una aplicación :
Cumulantes en Probabilidad Libre de Tipo B
Universidad de Guanajuato Trabajo de tesis para obtener el título de Licenciado en Matemáticas Cumulantes en Probabilidad Libre de Tipo B Autor: Adrián de Jesús Celestino Rodríguez Director de Tesis: Dr.
Estadística III Repaso de Algebra Lineal
Repaso de Algebra Lineal Vectores Un vector columna de dimensión n 1 es una serie de números dispuestos como sigue: x 1 x 2 x =. x n Un vector fila de dimensión 1 p es una serie de números dispuestos como
MATEMÁTICAS DE 2º BACHILLER APLICADAS A LAS CIENCIAS SOCIALES
MATEMÁTICAS DE 2º BACHILLER APLICADAS A LAS CIENCIAS SOCIALES BLOQUE DE ÁLGEBRA Editorial SM TEMA 1: MATRICES Concepto de matriz Dimensión de una matriz Tipos de Matrices: o Matriz fila o Matriz columna
De la convergencia en distribución a la aproximación uniforme
De la convergencia en distribución a la aproximación uniforme Egor Maximenko utilizando trabajos juntos con Johan Manuel Bogoya, Albrecht Böttcher y Sergei Grudsky Instituto Politécnico Nacional, ESFM,
Departamento de Matemáticas
MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
2 Espacios vectoriales
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
520142: ALGEBRA y ALGEBRA LINEAL
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
Una Breve Introducción a los Números p-ádicos
Una Breve Introducción a los Números p-ádicos Seminario de Teoría de Números Luciano Sciaraffia R. Pontificia Universidad Católica de Chile 14 de agosto de 2018 Valores absolutos Definición Un valor absoluto
Introducción a la Teoría de la Información
Introducción a la Teoría de la Información Tasa de Entropía de un Proceso Estocástico. Facultad de Ingeniería, UdelaR (Facultad de Ingeniería, UdelaR) Teoría de la Información 1 / 13 Agenda 1 Procesos
EXAMEN DEPARTAMENTAL DE ÁLGEBRA LINEAL MUESTRA FIN TECATE UABC
EXAMEN DEPARTAMENTAL DE ÁLGEBRA LINEAL MUESTRA FIN TECATE UABC 1. REACTIVO MUESTRA De las opciones que se presentan elije la que corresponde a un ejemplo número complejo. A) 5-0i B) 5-3i C) 5-2k D) 5 2.
TEOREMA DE HAHN-BANACH.
TEOREMA DE HAHN-BANACH. Sea E un e.v y M un s.v. de E. Toda aplicación lineal T 0 : M F de M en otro e.v. F se extiende a una aplicación lineal T : E F. Por ejemplo, basta considerar un suplementario algebraico
Integral de Lebesgue
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Material para el examen final
Algebra Lineal 2, FAMAT-UG, ene-jun, 2004 Material para el examen final 31 de mayo, 2004 Definiciones: Hay que saber las definiciones precisas de todos los siguientes términos, y conocer ejemplos concretos
Algebra Lineal XIX: Rango de una Matriz y Matriz Inversa.
Algebra Lineal XIX: Rango de una Matriz y Matriz Inversa José María Rico Martínez Departamento de Ingeniería Mecánica Facultad de Ingeniería Mecánica Eléctrica y Electrónica Universidad de Guanajuato email:
PROLOGO... vi 0 CONCEPTOS PRELIMINARES CONJUNTOS RELACIONES DE EQUIVALENCIA FUNCIONES EJERCICIOS...
ÍNDICE PROLOGO... vi 0 CONCEPTOS PRELIMINARES... 1 0.1 CONJUNTOS... 3 0.2 RELACIONES DE EQUIVALENCIA... 6 0.3 FUNCIONES... 10 EJERCICIOS... 16 1 SISTEMAS DE ECUACIONES LINEALES Y MATRICES... 23 1. SISTEMAS
Divisibilidad Infinita Libre, Teoremas de Convergencia
Divisibilidad Infinita Libre, Teoremas de Convergencia Arturo Jaramillo Trabajo Conjunto con Octavio Arizmendi Arturo Jaramillo (The University of Kansas) Divisibilidad Infinita Libre 1 / 28 Fenómeno del
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
N o de examen: ESCRIBIR LAS RESPUESTAS AQUÍ Este examen consta de diez preguntas tipo verdadero/falso y diez ejercicios
N o de examen: NOMBRE: C.I.: Examen de Geometría y Álgebra Lineal 1 22 de julio de 2014 Instituto de Matemática y Estadística Rafael Laguardia Facultad de Ingeniería ESCRIBIR LAS RESPUESTAS AQUÍ 1 2 3
Valores y vectores propios
Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Introducción a la complejidad computacional
Introducción a la complejidad computacional definida sobre anillos arbitrarios 18 de junio de 2016 Fuente: http://www.utmmcss.com/ Por qué otro modelo? Continuo vs discreto. Intuición interiorizada del
Ma34a Probabilidades y Procesos Estocásticos 21 de Noviembre, Resumen No. 3
Ma34a Probabilidades y Procesos Estocásticos 21 de Noviembre, 2004 Resumen No. 3 Prof. Cátedra: M. Kiwi Prof. Auxiliares: M. Soto, R. Cortez 1 Variables Aleatorias 1.1 Variables Aleatorias Absolutamente
Sobre vectores y matrices. Independencia lineal. Rango de una matriz
Espacios vectoriales Llamaremos R 2 al conjunto de todos los pares ordenados de la forma (a 1, a 2 ) tal que a 1, a 2 R. Es decir: R 2 = {(a 1, a 2 ) : a 1, a 2 R} De la misma forma: R 3 = {(a 1, a 2,
ÁLGEBRA LINEAL I Práctica 5
ÁLGEBRA LINEAL I Práctica 5 Espacios vectoriales (Curso 2014 2015) 1. En el espacio vectorial real IR 2 consideramos los siguientes subconjuntos: (a) A = {(x y) IR 2 x 2 + y 2 = 1}. (b) B = {(x y) IR 2
Guía del Examen parcial II de Álgebra II, licenciatura
Guía del Examen parcial II de Álgebra II, licenciatura Teoremas los más importantes cuyas demostraciones se pueden incluir en el examen El estudiante tiene que escribir la demostración de manera breve
Álgebra Lineal Ivan D. Molina N. Universidad del Norte Enero del 2016 Ivan D. Molina N. (Universidad del Norte) Álgebra Lineal Enero del / 26
Álgebra Lineal Ivan D. Molina N. Universidad del Norte Enero del 2016 Ivan D. Molina N. (Universidad del Norte) Álgebra Lineal Enero del 2016 1 / 26 1 Subespacios y combinaciones lineales 2 Dependencia
REPASO DE ALGEBRA VECTORIAL
REPASO DE ALGEBRA VECTORIAL Vectores en R 2 : Un vector v en el plano R 2 = XY es un par ordenado de números reales (a,b). Los números reales a y b se llaman componentes del vector v. El vector cero es
Representaciones Matriciales de Grafos Isomorfismos de Grafos Grafos Planos. Matemática Discreta. Agustín G. Bonifacio UNSL. Teoría de Grafos III
UNSL Teoría de Grafos III Matriz de Adyacencia Matriz de Incidencia a b c d e a 0 1 0 0 1 b 1 0 1 0 1 c 0 1 2 0 1 d 0 0 0 0 2 e 1 1 1 2 0 Dado un grafo G = (V,E), la matriz de adyacencia de G, denotada
Álgebra II Primer Cuatrimestre 2007
Álgebra II Primer Cuatrimestre 2007 Práctica 5: Módulos, II 1. Localización de módulos 1.1. Localización de módulos. Sea A un anillo, S A un subconjunto central multiplicativamente cerrado y sea M un A-módulo
Notas de clase. Prof. Nora Arnesi
Notas de clase Este material está sujeto a correcciones, comentarios y demostraciones adicionales durante el dictado de las clases, no se recomienda su uso a aquellos alumnos que no concurran a las mismas
Guía. Álgebra III. Examen parcial III. Forma canónica de Jordan. Producto interno.
Guía. Álgebra III. Examen parcial III. Forma canónica de Jordan. Producto interno. Teoremas con demostraciones que se pueden incluir en el examen: 1. Fórmula para f(j m (λ)), donde J m (λ) es el bloque
Notas para un curso de Probabilidad y Estadística Borradores: Variables aleatorias (e)
Notas para un curso de Probabilidad y Estadística Borradores: Variables aleatorias (e) Apéndice 9 de marzo de 010 Las leyes físicas deben tener la simplicidad y belleza de las matemáticas. (Paul Adrien
EJEMPLO DE PREGU,TAS
EJEMPLO DE PREGU,TAS MATEMÁTICAS PRIMERO, SEGU,DO Y TERCERO DE BACHILLERATO 1. Lógica proposicional Esta competencia se refiere al conocimiento que usted posee sobre el lenguaje de las proposiciones y
Distribuciones multivariadas
Distribuciones multivariadas Si X 1,X 2,...,X p son variables aleatorias discretas, definiremos la función de probabilidad conjunta de X como p(x) =p(x 1,x 2,...,x k )=P (X 1 = x 1,X 2 = x 2,...,X p =
Comportamiento asintótico de estimadores
Comportamiento asintótico de estimadores Seguimos con variable X con función de densidad/masa f (x; θ). Queremos estimar θ. Dada una muestra aleatoria, definimos un estimador T = h(x 1,..., X n ) Esperamos/deseamos
0 a b X = b c 0. f X (A) = AX XA.
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Industriales Álgebra Lineal Convocatoria de Junio 8 de Junio de 2007 (3 ptos.). Sea V = {A M 3 3 (R) / A t = A}. (a) Demostrar que toda
Tema 5: ESPACIOS VECTORIALES
Tema 5: ESPACIOS VECTORIALES EUCLÍDEOS Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría I. Curso 2003/04 Licenciatura:
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
Opción A xcos(x)+b sen(x) Ejercicio 1.- [2 5 puntos] Sabiendo que lím x 0 x 3 es finito, calcula b y el valor del límite. Ejercicio 2.- Sean f : R R y g : R R las funciones definidas mediante f(x) = x(x
El Teorema de Fubini-Tonelli
Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
18 Experimentos aleatorios. Sucesos y espacio muestral. Frecuencia y probabilidad de un suceso.
PRIMER CURSO DE E.S.O Criterios de calificación: 80% exámenes, 10% actividades, 10% actitud y trabajo 1 Números naturales. 2 Potencias de exponente natural. Raíces cuadradas exactas. 3 Divisibilidad. Concepto
Tema 4: Estructura vectorial de R n.
TEORÍA DE ÁLGEBRA I: Tema 4. DIPLOMATURA DE ESTADÍSTICA 1 Tema 4: Estructura vectorial de R n. 1 Definiciones y propiedades Definición. 1.1 Denotaremos por R n al conjunto de todas las n-tuplas de números
Independencia lineal y rango Ejemplos. Rango. Rango y matriz inversa Teorema de Rouché-Frobenius revisitado
Independencia lineal y rango Ejemplos. Rango. Rango y matriz inversa Teorema de Rouché-Frobenius revisitado c Jana Rodriguez Hertz p. /2 Independencia lineal Si el sistema x A + x 2 A 2 + + x n A n = O
2.5 Ejercicios... 59
Índice General 1 Espacios vectoriales 1 1.1 Espacios vectoriales y subespacios......................... 1 1.1.1 Preliminares................................. 1 1.1.2 Espacios vectoriales.............................
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
Opción A Ejercicio 1.- [2 5 puntos] Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto. Ejercicio 2.- Sean
23 de noviembre de 2017
Representaciones de grupos finitos Cándido Martín González Universidad de Málaga http://agt2.cie.uma.es/tr.htm 23 de noviembre de 2017 Teorema Sea G un grupo finito. El número de clases de isomorfía de
Álgebra Lineal. Tema 11. El Teorema Espectral en R. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
Álgebra Lineal Tema. El Teorema Espectral en R Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Índice
Topología en R n. Continuidad de funciones de varias variables
. Continuidad de funciones de varias variables María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I (1 o Grado en Ingeniería Electrónica Industrial y Automática) M. Muñoz (U.P.C.T.) Continuidad
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Transformación adjunta a una transformación lineal
Transformación adjunta a una transformación lineal Objetivos. Estudiar la construcción y las propiedades básicas de la transformación lineal adjunta. Requisitos. Transformación lineal, producto interno,