1 TEORÍA BORROSA. 1.1 Conjuntos Borrosos CONTROL BORROSO
|
|
|
- Teresa Villalba Pérez
- hace 7 años
- Vistas:
Transcripción
1 TEORÍA BORROSA. Conjuntos Borrosos El concepto de conjunto borrosos fue introducido por primera vez por Lofti A. Zadeh, profesor de la Universidad de California Berkeley, en el año 964, en un intento de representar y manipular datos que no eran precisos. Dicho concepto dio paso a la denominada Teoría de los Subconjuntos Borrosos, ya que ciertas magnitudes pueden tomar valores que difícilmente se pueden clasificar en un conjunto determinado. La Teoría de Subconjuntos Borrosos permite la definición adecuada de conjuntos que modelan las situaciones de imprecisión antes expuestas. En la teoría clásica de conjuntos, un subconjunto A de un conjunto puede ser definido por una función característica A que puede tomar dos valores: y A : {,} La verdad o falsedad de la expresión x está en A viene dada por el par ordenado (x, A (x)), de forma que será cierta si el segundo elemento del par es y falsa cuando sea. De forma similar se puede definir un subconjunto borroso A de un conjunto, denominado universo de discurso, como el conjunto de pares ordenados (x, A (x)), siendo A la función de pertenencia al conjunto borroso A, definida como A : [,]
2 Dicha función puede tomar todos los valores del intervalo entre y. El valor representa la no-pertenencia al conjunto A y el valor representa la pertenencia total a dicho conjunto..2 Números Borrosos Un número borroso es un caso particular de conjunto borroso cuya función de pertenencia es continua, convexa y definida sobre un intervalo cerrado de los números reales. Dicha función de pertenencia puede adoptar diferentes formas siendo las más habituales las triangulares o trapezoidales que se caracterizan por un número reducido de parámetros, aunque también son habituales la gaussiana o la campana generalizada. En la Figura 3- se pueden observar ejemplos de las diferentes funciones de pertenencia comentadas..3 Variables lingüísticas Los conjuntos borrosos se pueden utilizar para representar variables lingüísticas cuyos valores son números borrosos que están definidos en términos lingüísticos. Al conjunto de estos números borrosos, que abarcan todo el universo de discurso de la variable, se le denomina partición borrosa. 2
3 Grados de Pertenencia Grados de Pertenencia Grados de Pertenencia Grados de Pertenencia Figura 3-.- Ejemplos de funciones de pertenencia triangular, trapeziodal, gaussiana y campana generalizada. El número de conjuntos borrosos que componen dicha partición se suele tomar según el grado de precisión requerido para esa variable. Tomar una gran cantidad de conjuntos borrosos (siete o más de siete, en general), tiene como ventaja el poder precisar las acciones que se van a llevar a cabo en el sistema en función de esta variable. La desventaja es que la base de conocimiento del sistema debe contemplar todos los términos lingüísticos (conjuntos), por lo que el tamaño de la misma crecerá enormemente. Por ejemplo, si la temperatura se interpreta como una variable lingüística, el conjunto de valores que puede tomar podría ser {muy fría, fría, media, templada, cálida, calurosa}. Cada uno de estos términos está caracterizado por un conjunto borroso definido en el universo de discurso ([-6ºC, 48ºC]) de la variable temperatura, tal y como muestra la figura
4 A Muy fría Fría Media Templada Cálida Calurosa temperatura (ºC) Figura Definición y partición borrosa de la variable lingüística temperatura..4 Operaciones con Conjuntos Borrosos Las operaciones que se definen en la lógica borrosa pueden reducirse a las definiciones clásicas si el grado de pertenencia a los conjuntos borrosos se limita al conjunto {,}. Por esta razón, se utiliza la misma notación que para los conjuntos concisos. Así se puede definir el complemento (Tabla 3-), la T-norma (o intersección) (Tabla 3-2) y la S-norma (o unión) (Tabla 3-3). Estándar c(x) = x x x Sugeno c ( x), con ager p p c( x) x, p Tabla 3-.- Definición de complementos básicos. Mínimo Lukasiewicz (producto acotado) T(x,y) = min{x,y} T(x,y) = max{x+y-,} 4
5 Producto algebraico T(x,y) = xy Producto drástico min T w ( x, y) T x y x, y si maxx, y xy ( )( x y xy) en otro caso Hamacher (, ), Frank Dubois and Prade x y s s, s T( x, y) logs s xy T ( x, y ), max x, y,, p p, p p ager T( x, y) min, x y Tabla Definición de T-normas básicas Máximo Lukasiewicz (suma acotada) Probabilística (suma algebraica) Suma drástica Hamacher Frank S(x,y) = max{x,y} S(x,y) = min{x+y,} S(x,y) = x+y-xy max S w ( x, y) x, y si minx, y en otro caso x y 2 xy S ( x, y ), ( ) xy S( x, y) logs x y s s, s s p p p ager S( x, y) min, x y, p Tabla Definición de S-normas básicas 5
6 Ejemplo: Dado los números borroso A (figura 3-3.a) y B (figura 3-3.b); se obtiene la intersección AB, esto es, la operación AND () utilizando la T-Norma mínimo en la figura 3-3.c. A B A B Figura Operación AND: (a) conjunto borroso A; (b) conjunto borroso B;(c) AB utilizando la T-Norma mínimo. 6
7 Ejemplo: Dado los números borroso A (figura 3.a) y B (figura 3.b); se obtiene la unión AB, esto es, la operación OR (O) utilizando la S-Norma máximo en la figura 3-4. AUB Figura Operación OR sobre los conjuntos borrosos A y B, AB..5 Reglas borrosas si-entonces Una regla borrosa del tipo si-entonces, tiene la siguiente forma: Si x es A entonces y es B siendo A y B valoraciones particulares de sendas variables lingüísticas. El término x es A se denomina antecedente, mientras que el término y es B se denomina consecuente. Ejemplos sencillos de tales reglas serían: Si la presión es alta, entonces el volumen es pequeño Si la temperatura es alta, entonces hace calor 7
8 Para poder utilizar una regla borrosa es necesario formalizar el significado de la expresión Si x es A entonces y es B, que abreviadamente se indica como AB. Para ello es útil definir esta relación borrosa binaria. Una relación borrosa binaria es un conjunto borroso R, sobre x ( e son dos universos de discurso), que asignan a cada elemento de x un número entre y. Esto es: R = {((x,y), R (x,y))(x,y) x } La relación borrosa asociada a la regla borrosa se puede obtener usando alguna de las T-normas citadas anteriormente, por ejemplo, si se usa el operador mínimo para la conjunción lógica (propuesto por Mamdani) tendremos: R m = (AB ) = min{( A (x), B (y)} / (x,y).6 El razonamiento borroso El razonamiento borroso (o aproximado) permite obtener conclusiones a partir de un conjunto de reglas borrosas y un conjunto de hechos borrosos conocidos. La regla de inferencia clásica es el Modus Ponens que nos permite inferir la verdad de la proposición B ( hace calor ), a partir de la verdad de la proposición A ( la temperatura es alta ) y de la implicación AB ( si la temperatura es alta, entonces hace calor ), de forma esquematizada tendríamos: Premisa (Regla): Si x es A ENTONCES y es B Premisa 2 (Hecho): x es A Consecuente (Conclusión): y es B Sin embargo, en muchos razonamientos humanos, el modus ponens es utilizado de una forma aproximada. Por ejemplo, si tenemos la misma regla de 8
9 implicación AB ( si la temperatura es alta, entonces hace calor ), y sabemos que la temperatura es más o menos alta (x es A ), entonces podemos inferir que hace más o menos calor (y es B ), que se podría esquematizar de la siguiente manera: Premisa (Regla): Si x es A ENTONCES y es B Premisa 2 (Hecho): x es A Consecuente (Conclusión): y es B donde A es más o menos A, y B es más o menos B. Este tipo de razomiento es el razonamiento borroso, siendo A, B, A y B conjuntos borrosos del universo del discurso correspondientes. A esta regla de inferencia también se le conoce como Modus Ponens Generalizado (GMP) ya que la regla de Modus Ponens es un caso especial de ésta. Por lo tanto, el razonamiento borroso nos permite obtener conclusiones a partir de reglas borrosas de tipo si-entonces y de hechos conocidos. La base de este procedimiento es la regla composicional de inferencia. Ésta es una generalización del concepto de curva. Una curva viene dada por una función que permite obtener el valor de y a partir del valor de x, mediante y=f(x), donde el papel de la variable independiente lo jugará el hecho (x es A ), el papel de la función lo tomará la relación borrosa asociada a la regla (AB) y finalmente, el papel de la variable dependiente será para una conclusión borrosa (y es B ), figura
10 A B y es B' y=b y=f(x) x=a x es A' Figura Regla compocisional de inferencia como generalización del concepto de curva. Entonces, sea R una relación borrosa sobre x, y sea A un conjunto borroso sobre. Para encontrar el conjunto borroso resultante B, construiremos una extensión cilíndrica de A, c(a), que tome como base A. La extensión cilíndrica se define como c(a) (x,y) = A (x), y por lo tanto es un conjunto borroso sobre x que nos permitirá calcular la intersección con el conjunto borroso de la relación borrosa R. Finalmente proyectamos esta intersección (c(a)r) sobre el domino, obteniendo así un conjunto borroso B que representa la conclusión. Veamos gráficamente cada uno de estos pasos. Partimos de la premisa que es la regla R= AB (en el concepto de curva sería la función y=f(x)), que nos da la relación borrosa R sobre x que vemos en la figura 3-6.
11 Grados de pertenencia Figura Relación borrosa R sobre y. La segunda premisa consiste en el hecho x es A (en el concepto de curva el valor x=a) para extender este hecho hasta que corte la relación borrosa tendremos que realizar la extensión cilíndrica de A, figura 3-7. Grados de pertenencia Figura Extensión cilíndrica de A, c(a ).
12 La intersección entre la extensión cilíndrica de A c(a ) y la relación borrosa R, figura 3-8, forma una región que es análoga al punto de corte x=a con la función y=f(x), en el concepto de curva. Grados de pertenencia Figura Intersección (mínimo) de la relación borrosa R y la Extensión cilíndrica de A. Proyectando la intersección de R c(a ) sobre el eje y, podremos inferir y como el conjunto borroso B sobre el eje, esto es la conclusión y es B, que se muestra en la figura 3-9. Membership Grades
13 Figura Proyección (máximo) sobre el eje de la intersección entre la relación borrosa R y la extensión cilíndrica de A para obtener la conclusión y es B. Podemos concluir que el conjunto borroso B inducido por las premisas x es A y la regla borrosa si x es A entonces y es B se define por: B = A R= A (AB) donde indica el operador composicional Si al aplicar la regla composicional de inferencia utilizamos el mínimo para la intersección de Rc(A ) obtenemos: B (y)= max x min[ A (x), R (x,y)] composición max-min Si la intersección de Rc(A ) se realiza con la operación producto tendríamos: B (y)=max x [ A (x) R (x,y)] composición max-producto 3
14 Regla composicional max-min min Max-Min Regla com posicional prod max-prod Antecedentes Consecuentes Conclusiones Hechos Figura 3-.- Razonamiento borroso utilizando regla composicional max-min en las tres gráficas superiores y utilizando max-prod en las tres gráficas inferiores. En la figura 3- se representa gráficamente el mecanismo de razonamiento aproximado para una regla con un antecedente. Las tres gráficas superiores se refieren a la regla composicional del tipo max-min. La primera gráfica (de izquierda a derecha) muestra como se componen el antecedente y el hecho. En este caso el hecho tiene asociada una función de pertenencia triangular, y el antecedente una función de pertenencia trapezoidal. La composición de ambas funciones de pertenencia mediante la operación max-min es lo que denominamos grado de compatibilidad. En este caso, como sólo hay un antecedente el grado de compatibilidad es igual a la fuerza de disparo de la regla. La siguiente gráfica se refiere al consecuente de la regla. La fuerza de disparo y la función de pertenencia asociada al consecuente son utilizadas para obtener la función de pertenencia del consecuente cualificado (resultado de la inferencia de la regla). En las tres gráficas superiores se utiliza el operador mínimo mientras que en las tres gráficas inferiores se utiliza el operador producto. Dependiendo del operador utilizado se obtiene un conjunto borroso resultado de la inferencia diferente. 4
15 .7 Una regla con un antecedente Este es el caso más sencillo, considerando una regla composicional de inferencia del tipo max-min, y una la implicación borrosa de Mamdani, tendremos: B (y)= max x min[ A (x), R (x,y)]= max x min[ A (x), min[ A (x), B (y)]] Simplificando tendríamos: B (y)= min{max x min[ A (x), A (x)], B (y)]}= min[w, B (y)] siendo w = max x min[ A (x), A (x)], que se denomina grado de compatibilidad entre el conjunto borroso del hecho (A ) y el antecedente (A). En otras palabras, primero encontramos el grado de compatibilidad w como el máximo de la región que resulta de la operación mínimo entre A (x) y A (x) (zona sombreada en el antecedente, figura 3-). La función de pertenencia del conjunto borroso B será igual a la función de pertenencia de B recortada por w (zona sombrada en el consecuente, figura 3-). min A' A B B' Figura 3-.-Interpretación gráfica del Modus Ponens Generalizado, utilizando la implicación borrosa de Mamdani (mínimo) y el operador composicional max-min. 5
16 .8 Una regla con múltiples antecedentes Una regla borrosa del tipo si-entonces con dos antecedentes es de la forma: Si x es A y es B ENTONCES z es C, la Generalización del Modus Ponens para este problema se esquematizaría de la siguiente manera: Premisa (Regla): SI x es A y es B ENTONCES z es C Premisa 2 (Hecho): x es A y es B Consecuente (Conclusión): z es C El método para obtener C se basa en utilizar una relación ternaria borrosa para describir esta regla con dos antecedentes, esto es, A x B C puede ser transformada, utilizando por ejemplo la implicación borrosa de Mamdani, como: R m = (A x B C ) = (A x B) x C= min{( A (x), B (y), C (z)} / (x,y,z) El resultado C es el siguiente: C = (A x B ) (A x B C) = [A (A C)] [B (B C)] Esto es, el resultado del consecuente C puede ser expresado como la intersección de C =[A (A C)] y C 2 =[B (B C)], cada uno de estos términos corresponde a la inferencia borrosa para el caso más simple con un solo antecedente. Utilizando el operador composiciona max-min tendremos: C (z)= min{max x min[ A (x), A (x)], max y min[ B (y), B (y)], C (z)} C (z)= min[w A,A, w B,B, C (z)] 6
17 Siendo w A,A y w B,B los grados de compatibilidad para los antecedentes A y B, respectivamente. El resultado de los grados de compatibilidad de los antecedentes se denomina fuerza de disparo de la regla: f u ((A,B );(A,B))= min[w A,A, w B,B ] Una representación gráfica de este procedimiento se muestra en la figura 3-2, que utiliza el implicador de Mamdani y la regla composicional max-min. El resultado C es igual a la función de pertenencia del conjunto borroso C recortada por la fuerza de disparo de la regla. min A' A B B' w C C' w 2 w Z Figura Interpretación gráfica del Modus Ponens Generalizado en una regla con múltiples antecedentes, utilizando el implicador borroso de Mamdani (mínimo) y el operador composicional max-min..9 Múltiples reglas con múltiples antecedentes El siguiente grado de complejidad lo obtenemos cuando en lugar de una sola regla se tienen varias. En ese caso se interpreta la relación borrosa sobre la que debemos componer los hechos como la unión de las relaciones borrosas de cada una de las reglas individuales. De este modo, dado el siguiente problema: Premisa (Regla): SI x es A y es B ENTONCES z es C Premisa 2 (Regla): SI x es A 2 y es B 2 ENTONCES z es C 2 Premisa 3 (Hecho): x es A y es B Consecuente (Conclusión): z es C 7
18 Tendremos que C se calcula mediante la siguiente expresión: C =(A x B ) (R R 2 ) =[(A x B ) R ] [(A x B ) R 2 ] = C C 2 donde C y C 2 son los conjuntos borrosos inferidos para la regla y 2 respectivamente. Utilizando el operador composicional max-min resulta, en términos de los grados de compatibilidad, lo siguiente: C (z)= max {min[w A,A, w B,B, C (z)], min[w A2,A, w B2,B, C2 (z)]} y en términos de las fuerzas de disparo, tenemos: C (z)=max{min[f((a,b );(A,B )), C (z)], min[f((a,b );(A 2,B 2 )), C2 (z)]} Denominamos consecuente cualificado al conjunto borroso que se obtiene cuando se opera la fuerza de disparo y el consecuente de una regla. Llamaremos salida conjunta a la agregación de todos los consecuentes cualificados. La figura 3-3 muestra gráficamente el razonamiento borroso para múltiples reglas con múltiples antecedentes, utilizando el implicador borroso de Mamdani y la regla de inferencia composicional max-min. Como se puede apreciar, en cada una de las reglas se realiza la inferencia empezando por la obtención de los grados de compatibilidad (operación max-min) representado por w A,A y w B,B en la primera y w A2,A y w B2,B en la segunda. A continuación se aplica el operador -lógico mediante una T-norma, en este caso la T-norma mínimo. El resultado es la fuerza de disparo de la regla (w y w 2 para la regla uno y dos respectivamente) que es utilizada junto a la función de pertenencia del consecuente y un método de inferencia para obtener el consecuente cualificado (C y C 2 para la regla uno y dos respectivamente). La regla composicional de inferencia utilizada es la T-norma mínimo. Los consecuentes cualificados obtedios se observan a la derecha de cada 8
19 una de las filas que representan las reglas. La agregación de los consecuentes cualificados se realiza en este caso mediante la aplicación de la S-norma máximo, cuyo resultado se observa en la parte inferior de la figura 32. El borde superior del área sombreada es la función de pertenencia asociada al conjunto borroso resultado de la inferencia con múltiples reglas y múltiples antecedentes. 9
20 min A' A B B' C w A,A' C' w B,B' w A 2 A' B 2 B' min w A2,A' C 2 Z C'2 w B2,B' w 2 Z max C' Figura Interpretación gráfica del Modus Ponens Generalizado para varias reglas con múltiples antecedentes, utilizando el implicador borroso de Mamdani (mínimo) y el operador composicional max-min. Z 2
21 . Sistemas de inferencia borrosa Los sistemas de inferencia borrosa constituyen una clase de algoritmos de cómputo basados en conjuntos borrosos y en el razonamiento aproximado. Se componen de tres elementos. En primer lugar un conjunto de reglas lógicas, con múltiples antecedentes y un consecuente, denominado base de reglas. En segundo lugar el llamado diccionario que contiene la definición de los conjuntos borrosos asociados a los antecedentes y consecuentes de las reglas. Por último, hay que definir un mecanismo de inferencia. Las entradas a este tipo de sistemas pueden ser tanto números concisos (crisp) como conjuntos borrosos. Cuando se trata de un número conciso hay que o bien considerarlo como un conjunto borroso particular, esto es, con pertenencia para un solo valor de su universo y en el resto (singleton), o bien convertirlo a un número borroso en un proceso llamado borrosificación (fuzzyfication). La salida del sistema es un conjunto borroso que se obtiene a partir de las entradas, las reglas y el mecanismo de inferencia elegido. Sin embargo, en muchas aplicaciones es necesario que la salida sea un valor numérico y no un número borroso. En esos casos se realiza un proceso de desborrosificación mediante el cual, el conjunto borroso se convierte a un valor del universo de salida representativo de la conclusión obtenida. En la figura 3-4 se presenta el diagrama de bloques de un sistema de inferencia borroso [Jang 997]. El proceso básico puede resumirse en las siguientes etapas: obtención de los grados de compatibilidad de las entradas con los antecedentes de las reglas, obtención de las fuerzas de disparo de las reglas, agregación de los consecuentes cualificados y finalmente, en los casos en los que se requiera la desborrosificación. 2
22 Regla w (Borroso) x es A y es B Regla 2 (Conciso o Borroso) x es A 2 w 2 y es B 2 (Borroso) Agregación (Borroso) Desborrosificación (Conciso) y Regla r w r x es A r y es B r (Borroso) Figura Diagrama de bloques de un sistema de inferencia borrosa. El cuadro rojo agrupa los componentes de un sistema de inferencia básico con salida borrosa. Una clasificación de los tipos más usuales de sistemas de inferencia borrosa se basa en el modelo utilizado para representar el consecuente de las reglas y en el método de agregación aplicado. Uno de los más utilizados y que es el que hemos utilizado en el planificador instruccional es el de Mamdani... MODELO BORROSO DE MAMDANI Este sistema fue propuesto [Mamdani 975] para el control de una máquina de vapor mediante un conjunto de reglas de control lingüísticas obtenidas de la experiencia de los operadores de la máquina. Este modelo toma como representación de los consecuentes, conjuntos borrosos que representan las valoraciones de una variable lingüística. Se admiten múltiples reglas con múltiples antecedentes. Cada regla debe tener el mismo conjunto de variables lingüísticas representadas en sus antecedentes. El método de inferencia borrosa, como se ha indicado anteriormente, admite un número de variantes. Concretamente en el modelo de Mamdani, estas variantes se refieren al operador -lógico donde normalmente se toma una T-norma, el operador Ológico se suele emplear una S-norma, el operador implicación normalmente implementado con una T-norma para calcular el consecuente cualificado y el operador de agregación corrientemente definido por una S-norma. En la figura 3-5 se puede observar un ejemplo. 22
23 min A B C C' w min Z A B 2 2 C 2 C' 2 w 2 Z x y max C' Z Centroide del área Figura Sistema de inferencia borroso de Mamdani utilizando el mínimo y máximo para la T-norma y S-norma, respectivamente. En este modelo se suele utilizar un desborrosificador para convertir el conjunto borroso de salida en un valor conciso. Existen diversos métodos para realizar este proceso, cuyos resultados se pueden ver en la figura 3-6: Desborrosificación basada en el centroide del área: se trata de calcular el centroide del conjunto borroso resultado de la agregación de todos los consecuentes cualificados. z ca Z Z z ( z) dz A A ( z) dz 23
24 Bisector del área: se trata de encontrar el valor numérico del elemento del universo del discurso que separa el área del conjunto borroso en dos mitades iguales. Media de los máximos: se buscan aquellos elementos del universo del discurso en donde la función de pertenencia del conjunto borroso tome su valor máximo, y se calcula la media de estos puntos. Mínimo de los máximos: el procedimiento es igual al anterior, únicamente varia en que se toma el menor de los puntos del universo del discurso en lugar de la media. Mayor de los máximos: Idem caso anterior pero esta vez se toma el mayor de los puntos. Área Mínimo de los máximos Mayor de los máximos Z Media de los máximos Centroide del área Bisector de área Figura Diferentes métodos de desborrosificación para obtener una valor conciso a la salida. 24
Sesión 9. Razonamiento con imprecisión. Año académico 2014/15. Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt
 Sesión 9 Razonamiento con imprecisión Año académico 2014/15 Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt 1 Índice Introducción Conjuntos borrosos Operaciones con conjuntos borrosos
Sesión 9 Razonamiento con imprecisión Año académico 2014/15 Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt 1 Índice Introducción Conjuntos borrosos Operaciones con conjuntos borrosos
SubTemas. Tema 1.4 Razonamiento Aproximado. Tópicos
 SubTemas 1.1 Introducción al control difuso 1.2 Teoría de conjuntos difusos 1.3 Representación del conocimiento 1.4 Razonamiento aproximado 1.5 Sistemas de inferencia difusos Tema 1.4 Razonamiento Aproximado
SubTemas 1.1 Introducción al control difuso 1.2 Teoría de conjuntos difusos 1.3 Representación del conocimiento 1.4 Razonamiento aproximado 1.5 Sistemas de inferencia difusos Tema 1.4 Razonamiento Aproximado
Sesión 9. Razonamiento con imprecisión. Semestre de otoño Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt
 Sesión 9 Razonamiento con imprecisión Semestre de otoño 2013 Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt 1 Índice Introducción Conjuntos borrosos Operaciones con conjuntos borrosos
Sesión 9 Razonamiento con imprecisión Semestre de otoño 2013 Profesores: Sascha Ossowski, Alberto Fernández y Holger Billhardt 1 Índice Introducción Conjuntos borrosos Operaciones con conjuntos borrosos
Control Borroso. Rosa Mª Aguilar Chinea Vanesa Muñoz Cruz
 Control Borroso Rosa Mª Aguilar Chinea Vanesa Muñoz Cruz Indice. Introducción 2. Conjuntos Borrosos 3. Variables Lingüísticas 4. Definición Lógica Borrosa 5. Operaciones con Conjuntos Borrosos 6. Reglas
Control Borroso Rosa Mª Aguilar Chinea Vanesa Muñoz Cruz Indice. Introducción 2. Conjuntos Borrosos 3. Variables Lingüísticas 4. Definición Lógica Borrosa 5. Operaciones con Conjuntos Borrosos 6. Reglas
Modelo posibilista: Objetivos. Conjuntos difusos. Conjuntos difusos/lógica difusa. Notas
 : Objetivos Introducción Intentamos representar la imprecisión del lenguaje Los expertos expresan su conocimiento como apreciaciones cualitativas Dos elementos: Variables definidas sobre un dominio (Universo
: Objetivos Introducción Intentamos representar la imprecisión del lenguaje Los expertos expresan su conocimiento como apreciaciones cualitativas Dos elementos: Variables definidas sobre un dominio (Universo
Modelo posibilista: Objetivos
 Introducción Modelo posibilista: Objetivos Intentamos representar la imprecisión del lenguaje Los expertos expresan su conocimiento como apreciaciones cualitativas Dos elementos: Variables definidas sobre
Introducción Modelo posibilista: Objetivos Intentamos representar la imprecisión del lenguaje Los expertos expresan su conocimiento como apreciaciones cualitativas Dos elementos: Variables definidas sobre
LOGICA DIFUSA. Dámaso López Aragón
 LOGICA DIFUSA Dámaso López Aragón Introducción La lógica difusa tiene su origen en la década de los 60, en la Universidad de Berkeley - California, la cual fue desarrollada por Lofti Zadeth a través de
LOGICA DIFUSA Dámaso López Aragón Introducción La lógica difusa tiene su origen en la década de los 60, en la Universidad de Berkeley - California, la cual fue desarrollada por Lofti Zadeth a través de
Lógica Borrosa o Difusa
 Lógica Borrosa o Difusa Introducción Ingenierías del Conocimiento EIE 1 Contenido Orígenes Conjuntos borrosos Operaciones con conjuntos borrosos Razonamiento borroso Representación del conocimiento Métodos
Lógica Borrosa o Difusa Introducción Ingenierías del Conocimiento EIE 1 Contenido Orígenes Conjuntos borrosos Operaciones con conjuntos borrosos Razonamiento borroso Representación del conocimiento Métodos
Tema 3. Razonamiento Aproximado Lección 3.2. Razonamiento con imprecisión
 Tema 3. Razonamiento Aproximado Lección 3.2. Razonamiento con imprecisión Referencias Bibliográficas (diapositivas): José Cuena. Sistemas Inteligentes. Conceptos, técnicas y métodos de construcción. Facultad
Tema 3. Razonamiento Aproximado Lección 3.2. Razonamiento con imprecisión Referencias Bibliográficas (diapositivas): José Cuena. Sistemas Inteligentes. Conceptos, técnicas y métodos de construcción. Facultad
Capítulo 2. disponibles las habilidades de los expertos a los no expertos. Estos programas tratan de
 Capítulo 2 Sistemas Expertos y Lógica Difusa 2.1 Sistemas Expertos Los sistemas expertos son programas computacionales diseñados para tener disponibles las habilidades de los expertos a los no expertos.
Capítulo 2 Sistemas Expertos y Lógica Difusa 2.1 Sistemas Expertos Los sistemas expertos son programas computacionales diseñados para tener disponibles las habilidades de los expertos a los no expertos.
LÓGICA Y CONJUNTOS DIFUSOS
 CPÍTULO 2 LÓGIC Y CONJUNTOS DIFUSOS 2.1 Introducción La lógica difusa es una metodología que proporciona una manera simple de obtener una conclusión a partir de información de entrada vaga, ambigua, imprecisa,
CPÍTULO 2 LÓGIC Y CONJUNTOS DIFUSOS 2.1 Introducción La lógica difusa es una metodología que proporciona una manera simple de obtener una conclusión a partir de información de entrada vaga, ambigua, imprecisa,
LÓGICA DIFUSA. Conjuntos difusos Blanca A. Vargas Govea Noviembre 2, 2012 Inteligencia Computacional
 LÓGICA DIFUSA Conjuntos difusos Blanca A. Vargas Govea vargasgovea@itesm.mx Noviembre 2, 2012 Inteligencia Computacional Sistemas de inferencia difusa 2 Observacio nes Inferencia difusa Fusificación Definir
LÓGICA DIFUSA Conjuntos difusos Blanca A. Vargas Govea vargasgovea@itesm.mx Noviembre 2, 2012 Inteligencia Computacional Sistemas de inferencia difusa 2 Observacio nes Inferencia difusa Fusificación Definir
Caso de estudio: Sistema de toma de decisiones
 5 Caso de estudio: Sistema de toma de decisiones En este capítulo se tomarán todas las celdas presentadas anteriormente, para la implementación de un sistema difuso de toma de decisiones. Esta estructura
5 Caso de estudio: Sistema de toma de decisiones En este capítulo se tomarán todas las celdas presentadas anteriormente, para la implementación de un sistema difuso de toma de decisiones. Esta estructura
Capítulo 2 Conjuntos. 2.1 Introducción. 2.2 Determinación de conjuntos. Definición:
 Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación.
 NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
Introducción al Control Borroso
 Introducción al Control Borroso Carlos Bordóns Alba Dpto. Ingeniería de Sistemas y Automática Escuela Superior de Ingenieros. Universidad de Sevilla Índice Introducción Reseña histórica Estado actual Fundamentos
Introducción al Control Borroso Carlos Bordóns Alba Dpto. Ingeniería de Sistemas y Automática Escuela Superior de Ingenieros. Universidad de Sevilla Índice Introducción Reseña histórica Estado actual Fundamentos
Conjuntos Difusos. Conjuntos Crisp x Difusos Definición Representación Propiedades Formatos Operaciones Hedges
 Conjuntos Difusos Conjuntos Crisp x Difusos Definición Representación Propiedades Formatos Operaciones Hedges Formatos de los Conjuntos La función Verdad de um conjunto fuzzy representa las propiedades
Conjuntos Difusos Conjuntos Crisp x Difusos Definición Representación Propiedades Formatos Operaciones Hedges Formatos de los Conjuntos La función Verdad de um conjunto fuzzy representa las propiedades
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo. Contenidos
 Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 1: Lunes 11 Viernes 16 de Marzo Complementos Contenidos Clase 1: Elementos de lógica: Conectivos, tablas de verdad, tautologías y contingencias.
Control borroso de la fuerza del efector de un Brazo Robot
 Control borroso de la fuerza del efector de un Brazo Robot Bautista Blasco, Susana: subautis@fdi.ucm.es Garmendia Salvador, Luis: lgarmend@fdi.ucm.es Departamento de Ingeniería del Software e Inteligencia
Control borroso de la fuerza del efector de un Brazo Robot Bautista Blasco, Susana: subautis@fdi.ucm.es Garmendia Salvador, Luis: lgarmend@fdi.ucm.es Departamento de Ingeniería del Software e Inteligencia
DESIGUALDADES. AXIOMA 1.- Tricotomía de los números reales. Si a y b son números reales entonces se cumple una y solo una de las relaciones
 DESIGUALDADES 4.1.- AXIOMAS DE ORDEN. Cualquier conjunto o Campo de números que satisface los siguientes 4 Axiomas se dice que es un conjunto de números ORDENADO. El conjunto o Campo de los números reales
DESIGUALDADES 4.1.- AXIOMAS DE ORDEN. Cualquier conjunto o Campo de números que satisface los siguientes 4 Axiomas se dice que es un conjunto de números ORDENADO. El conjunto o Campo de los números reales
Matrices 2º curso de Bachillerato Ciencias y tecnología
 MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
Apuntes de Inteligencia artificial (II)
 Apuntes de Inteligencia artificial (II) Tema 2 Razonamiento Aproximado Profesor: Daniel Manrique Índice 1. Introducción. 2. Razonamiento con imprecisión: lógica borrosa. 3. Razonamiento con incertidumbre.
Apuntes de Inteligencia artificial (II) Tema 2 Razonamiento Aproximado Profesor: Daniel Manrique Índice 1. Introducción. 2. Razonamiento con imprecisión: lógica borrosa. 3. Razonamiento con incertidumbre.
2.1 Descripción en espacio de estado de sistemas dinámicos
 2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
Licenciatura en Ingeniería en Sistemas Inteligentes
 Universidad Autónoma del Estado de México Unidad Académica Profesional Nezahualcóyotl Licenciatura en Ingeniería en Sistemas Inteligentes Unidad de aprendizaje: Lógica Difusa Relaciones Difusas Dra. Dora
Universidad Autónoma del Estado de México Unidad Académica Profesional Nezahualcóyotl Licenciatura en Ingeniería en Sistemas Inteligentes Unidad de aprendizaje: Lógica Difusa Relaciones Difusas Dra. Dora
Sistemas informáticos industriales. Algebra de Boole
 Sistemas informáticos industriales 2016 lgebra de oole lgebra oole Se denomina así en honor a George oole (1815-1864). El algebra de oole se emplea en sistema de control digitales, desde los sistemas de
Sistemas informáticos industriales 2016 lgebra de oole lgebra oole Se denomina así en honor a George oole (1815-1864). El algebra de oole se emplea en sistema de control digitales, desde los sistemas de
Control con Lógica Difusa
 Teoría de Control con Lógica Difusa Teoría Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolás de Hidalgo Facultad de Ingeniería Eléctrica Morelia, Michoacan Dr. Fernando Ornelas Tellez UMSNH-FIE
Teoría de Control con Lógica Difusa Teoría Dr. Fernando Ornelas Tellez Universidad Michoacana de San Nicolás de Hidalgo Facultad de Ingeniería Eléctrica Morelia, Michoacan Dr. Fernando Ornelas Tellez UMSNH-FIE
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: LA INTEGRAL DEFINIDA
 UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: LA INTEGRAL DEFINIDA La integral definida Anteriormente se mencionó que la Integral Indefinida da como resultado una familia de funciones
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: LA INTEGRAL DEFINIDA La integral definida Anteriormente se mencionó que la Integral Indefinida da como resultado una familia de funciones
TEMA 1: LÓGICA. p p Operador conjunción. Se lee y y se representa por. Su tabla de verdad es: p q p q
 TEMA 1: LÓGICA. Definición. La lógica es la ciencia que estudia el razonamiento formalmente válido. Para ello tiene un simbolismo que evita las imprecisiones del lenguaje humano y permite comprobar la
TEMA 1: LÓGICA. Definición. La lógica es la ciencia que estudia el razonamiento formalmente válido. Para ello tiene un simbolismo que evita las imprecisiones del lenguaje humano y permite comprobar la
a 21 x a 22,a 22,b 2,a 21,b 1,a 12
 UNA APROXIMACIÓN A LOS SISTEMAS DE ECUACIONES LINEALES CON CALC 1.- INTRODUCCIÓN El objeto del presente documento es ofrecer una aplicación de la hoja de cálculo al aprendizaje y a la comprensión de un
UNA APROXIMACIÓN A LOS SISTEMAS DE ECUACIONES LINEALES CON CALC 1.- INTRODUCCIÓN El objeto del presente documento es ofrecer una aplicación de la hoja de cálculo al aprendizaje y a la comprensión de un
Introducción a la Lógica
 Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
Tema 0 Introducción a la Lógica En cualquier disciplina científica se necesita distinguir entre argumentos válidos y no válidos. Para ello, se utilizan, a menudo sin saberlo, las reglas de la lógica. Aquí
ANALÓGICO vs. DIGITAL
 ANALÓGICO vs. DIGITAL Una señal analógica se caracteriza por presentar un numero infinito de valores posibles. Continuo Posibles valores: 1.00, 1.01, 200003,, infinitas posibilidades Una señal digital
ANALÓGICO vs. DIGITAL Una señal analógica se caracteriza por presentar un numero infinito de valores posibles. Continuo Posibles valores: 1.00, 1.01, 200003,, infinitas posibilidades Una señal digital
Matemáticas Básicas para Computación
 Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 6 Nombre: Álgebra Booleana Objetivo Durante la sesión el participante identificará las principales características
Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 6 Nombre: Álgebra Booleana Objetivo Durante la sesión el participante identificará las principales características
CORPORACION UNIFICADA NACIONA DE EDUCACION SUPERIOR DEPARTAMENTO DE CIENCIAS BASICAS FUNCIÓN Y RELACIÓN
 CORPORACION UNIFICADA NACIONA DE EDUCACION SUPERIOR DEPARTAMENTO DE CIENCIAS BASICAS AREA / COMPONENTE: FORMACIÓN BÁSICA CICLO DE FORMACIÓN: TECNICA FUNCIÓN Y RELACIÓN RELACION Dados los conjuntos A =
CORPORACION UNIFICADA NACIONA DE EDUCACION SUPERIOR DEPARTAMENTO DE CIENCIAS BASICAS AREA / COMPONENTE: FORMACIÓN BÁSICA CICLO DE FORMACIÓN: TECNICA FUNCIÓN Y RELACIÓN RELACION Dados los conjuntos A =
Estructuras Discretas. Teoremas. Técnicas de demostración. Reglas de Inferencia. Reglas de Inferencia Ley de Combinación.
 Estructuras Discretas Teoremas Técnicas de demostración Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 15 Definición: teorema
Estructuras Discretas Teoremas Técnicas de demostración Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 15 Definición: teorema
Sistemas Difusos. La mayoría de los fenómenos con los cuales nos deparamos son imprecisos Ejemplo: día Caliente (40, 35, 30, 29,5?
 Sistemas Difusos La mayoría de los fenómenos con los cuales nos deparamos son imprecisos Ejemplo: día Caliente (40, 35, 30, 29,5?) Imprecisión Intrínseca ayuda en la comprensión del problema. Fuzziness
Sistemas Difusos La mayoría de los fenómenos con los cuales nos deparamos son imprecisos Ejemplo: día Caliente (40, 35, 30, 29,5?) Imprecisión Intrínseca ayuda en la comprensión del problema. Fuzziness
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Arquitectura de Ordenadores Tutor: Antonio Rivero Cuesta Unidad Didáctica 1 Representación de la Información y Funciones Lógicas Tema 1 Representación de la Información
Centro Asociado Palma de Mallorca Arquitectura de Ordenadores Tutor: Antonio Rivero Cuesta Unidad Didáctica 1 Representación de la Información y Funciones Lógicas Tema 1 Representación de la Información
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
TEMA 3 ÁLGEBRA DE CONMUTACIÓN
 TEMA 3 ÁLGEBRA DE CONMUTACIÓN TEMA 3: Álgebra de Boole ÍNDICE. POSTULADOS DEL ÁLGEBRA DE CONMUTACIÓN 2. ÁLGEBRA DE BOOLE BIVALENTE O ÁLGEBRA DE CONMUTACIÓN 2. Teoremas del álgebra de conmutación 3. VARIABLES
TEMA 3 ÁLGEBRA DE CONMUTACIÓN TEMA 3: Álgebra de Boole ÍNDICE. POSTULADOS DEL ÁLGEBRA DE CONMUTACIÓN 2. ÁLGEBRA DE BOOLE BIVALENTE O ÁLGEBRA DE CONMUTACIÓN 2. Teoremas del álgebra de conmutación 3. VARIABLES
4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE
 Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 54 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable. En la
Prácticas de Matemáticas I y Matemáticas II con DERIVE-5 54 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable. En la
CONJUNTOS. Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas.
 CONJUNTOS CPR. JORGE JUAN Xuvia-Narón Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas. Un conjunto está formado por una serie de elementos susceptibles de poseer
CONJUNTOS CPR. JORGE JUAN Xuvia-Narón Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas. Un conjunto está formado por una serie de elementos susceptibles de poseer
LÓGICA DIFUSA. Inferencia: defusificación Blanca A. Vargas Govea Noviembre 13, 2012 Inteligencia Computacional
 LÓGICA DIFUSA Inferencia: defusificación Blanca A. Vargas Govea vargasgovea@itesm.mx Noviembre 13, 2012 Inteligencia Computacional Sistemas de inferencia difusa 2 Observacio nes Inferencia difusa Fusificación
LÓGICA DIFUSA Inferencia: defusificación Blanca A. Vargas Govea vargasgovea@itesm.mx Noviembre 13, 2012 Inteligencia Computacional Sistemas de inferencia difusa 2 Observacio nes Inferencia difusa Fusificación
Algebra de Boole: Teoremas
 Teorema 1: A + A = A Teorema 2: A A = A Teorema 3: A + 0 = A Teorema 4: A 1 = A Teorema 5: A 0 = 0 Teorema 6: A + 1 = 1 Teorema 7: (A + B) = A B Teorema 8: (A B) = A + B Teorema 9: A + A B = A Teorema
Teorema 1: A + A = A Teorema 2: A A = A Teorema 3: A + 0 = A Teorema 4: A 1 = A Teorema 5: A 0 = 0 Teorema 6: A + 1 = 1 Teorema 7: (A + B) = A B Teorema 8: (A B) = A + B Teorema 9: A + A B = A Teorema
Horas teoría-horas prácticas-horas trabajo adicional-horas totales-créditos
 ASIGNATURA: CONTROL INTELIGENTE I 1. DATOS DE LA ASIGNATURA Nombre de la asignatura: CONTROL INTELIGENTE I Línea de investigación o de trabajo: Horas teoría-horas prácticas-horas trabajo adicional-horas
ASIGNATURA: CONTROL INTELIGENTE I 1. DATOS DE LA ASIGNATURA Nombre de la asignatura: CONTROL INTELIGENTE I Línea de investigación o de trabajo: Horas teoría-horas prácticas-horas trabajo adicional-horas
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES
 SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Integración múltiple
 Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
Integración múltiple IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Integrales múltiples 1 3. Caso particular: la integral triple
MEDIDAS DE TENDENCIA CENTRAL
 MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
MEDIDAS DE TENDENCIA CENTRAL Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro
Una introducción a la Lógica Borrosa Matemática
 Una introducción a la Lógica Borrosa Matemática Marco Cerami Instituto de Investigación en Inteligencia Artificial (IIIA - CSIC) Bellaterra (Spain) cerami@iiia.csic.es SIMBa, 14 Febrero 2011 Marco Cerami
Una introducción a la Lógica Borrosa Matemática Marco Cerami Instituto de Investigación en Inteligencia Artificial (IIIA - CSIC) Bellaterra (Spain) cerami@iiia.csic.es SIMBa, 14 Febrero 2011 Marco Cerami
GUIA 4: ALGEBRA DE BOOLE
 GUIA 4: ALGEBRA DE BOOLE En 1854 George Boole introdujo una notación simbólica para el tratamiento de variables cuyo valor podría ser verdadero o falso (variables binarias) Así el álgebra de Boole nos
GUIA 4: ALGEBRA DE BOOLE En 1854 George Boole introdujo una notación simbólica para el tratamiento de variables cuyo valor podría ser verdadero o falso (variables binarias) Así el álgebra de Boole nos
Razonamiento bajo incertidumbre
 Inteligencia en Redes de Comunicaciones Razonamiento bajo incertidumbre Julio Villena Román jvillena@it.uc3m.es Razonamiento humano En el razonamiento humano hay que trabajar con la incertidumbre: la información
Inteligencia en Redes de Comunicaciones Razonamiento bajo incertidumbre Julio Villena Román jvillena@it.uc3m.es Razonamiento humano En el razonamiento humano hay que trabajar con la incertidumbre: la información
CURSO: 2º BACHILLERATO MATERIA: TECNOLOGÍA INDUSTRIAL II
 CURSO: ILLERATO MATERIA: TECNOLOGÍA INDUSTRIAL II BLOQUES DE CONTENIDO Bloque I Materiales partimos de los aprendizajes del curso anterior para continuar profundizando en la manera de determinar las propiedades
CURSO: ILLERATO MATERIA: TECNOLOGÍA INDUSTRIAL II BLOQUES DE CONTENIDO Bloque I Materiales partimos de los aprendizajes del curso anterior para continuar profundizando en la manera de determinar las propiedades
BLOQUE 1. LOS NÚMEROS
 BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
Algoritmos. Medios de expresión de un algoritmo. Diagrama de flujo
 Algoritmos En general, no hay una definición formal de algoritmo. Muchos autores los señalan como listas de instrucciones para resolver un problema abstracto, es decir, que un número finito de pasos convierten
Algoritmos En general, no hay una definición formal de algoritmo. Muchos autores los señalan como listas de instrucciones para resolver un problema abstracto, es decir, que un número finito de pasos convierten
Medidas de la pieza. Forma-posición elemento
 TOLERANCIAS DIMENSIONALES Introducción 1 - Podemos conseguir una dimensión exacta?. - Máquinas están sometidos a: desajustes, deformaciones de tipo elástico y térmico que dan lugar a imperfecciones dimensionales.
TOLERANCIAS DIMENSIONALES Introducción 1 - Podemos conseguir una dimensión exacta?. - Máquinas están sometidos a: desajustes, deformaciones de tipo elástico y térmico que dan lugar a imperfecciones dimensionales.
Un enunciado es toda frase u oración que se emite
 OBJETIO 2: Aplicar la lógica proposicional y la lógica de predicados en la determinación de la validez de una proposición dada. Lógica Proposicional La lógica proposicional es la más antigua y simple de
OBJETIO 2: Aplicar la lógica proposicional y la lógica de predicados en la determinación de la validez de una proposición dada. Lógica Proposicional La lógica proposicional es la más antigua y simple de
ELECTRÓNICA DIGITAL 1. INTRODUCCIÓN. SEÑALES ANALÓGICAS Y DIGITALES.
 1 ELECTRÓNICA DIGITAL 1. INTRODUCCIÓN. SEÑALES ANALÓGICAS Y DIGITALES. Podemos dividir la electrónica en dos grandes campos: la electrónica analógica y la electrónica digital, según el tipo de señales
1 ELECTRÓNICA DIGITAL 1. INTRODUCCIÓN. SEÑALES ANALÓGICAS Y DIGITALES. Podemos dividir la electrónica en dos grandes campos: la electrónica analógica y la electrónica digital, según el tipo de señales
ALUMNA: GRADO: MODALIDAD-10. PROFESOR: Hugo Nelson Ramírez Cárdenas
 ALUMNA: GRADO: MODALIDAD-10 FECHA: PROFESOR: Hugo Nelson Ramírez Cárdenas LOGROS 1. Representa en un diagrama la entrada y salida de datos del problema que desea resolver. 1. Analizo con mi equipo de trabajo
ALUMNA: GRADO: MODALIDAD-10 FECHA: PROFESOR: Hugo Nelson Ramírez Cárdenas LOGROS 1. Representa en un diagrama la entrada y salida de datos del problema que desea resolver. 1. Analizo con mi equipo de trabajo
SECCIÓN 7.3 INTRODUCCION A VECTORES. Capítulo 7
 SECCIÓN 7.3 INTRODUCCION A VECTORES Capítulo 7 Introducción Cantidades tales como área, volumen, longitud, temperatura y tiempo se componen únicamente de una magnitud y se pueden describir completamente
SECCIÓN 7.3 INTRODUCCION A VECTORES Capítulo 7 Introducción Cantidades tales como área, volumen, longitud, temperatura y tiempo se componen únicamente de una magnitud y se pueden describir completamente
Figura 1. Gráfica de la función.
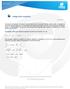 Integración numérica Por Iván Cruz Al momento de evaluar una integral definida dentro de un intervalo finito de valores o bien, al necesitar la obtención del área bajo una curva teniendo como datos de
Integración numérica Por Iván Cruz Al momento de evaluar una integral definida dentro de un intervalo finito de valores o bien, al necesitar la obtención del área bajo una curva teniendo como datos de
Erik Valdemar Cuevas Jiménez (Autor) Daniel Zaldívar Navarro (Autor) Sistemas de Control Neurodifuso Un enfoque utilizando NEFCON
 Erik Valdemar Cuevas Jiménez (Autor) Daniel Zaldívar Navarro (Autor) Sistemas de Control Neurodifuso Un enfoque utilizando NEFCON https://cuvillier.de/de/shop/publications/2114 Copyright: Cuvillier Verlag,
Erik Valdemar Cuevas Jiménez (Autor) Daniel Zaldívar Navarro (Autor) Sistemas de Control Neurodifuso Un enfoque utilizando NEFCON https://cuvillier.de/de/shop/publications/2114 Copyright: Cuvillier Verlag,
BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS
 Bloque V. Control y programación de sistemas automáticos pág. 1 Bloque V. Control y programación de sistemas automáticos pág. 2 BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS 1. LA INFORMACIÓN
Bloque V. Control y programación de sistemas automáticos pág. 1 Bloque V. Control y programación de sistemas automáticos pág. 2 BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS 1. LA INFORMACIÓN
BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS
 Bloque V. Control y programación de sistemas automáticos pág. 1 BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS 1. LA INFORMACIÓN BINARIA 1.1. Sistemas de numeración y códigos Def. Sistema de
Bloque V. Control y programación de sistemas automáticos pág. 1 BLOQUE V. CONTROL Y PROGRAMACIÓN DE SISTEMAS AUTOMÁTICOS 1. LA INFORMACIÓN BINARIA 1.1. Sistemas de numeración y códigos Def. Sistema de
Matemáticas Discretas Lógica
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Lógica Cursos Propedéuticos 2010 Ciencias Computacionales INAOE Lógica undamentos de Lógica Cálculo proposicional Cálculo de predicados
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Lógica Cursos Propedéuticos 2010 Ciencias Computacionales INAOE Lógica undamentos de Lógica Cálculo proposicional Cálculo de predicados
Introducción al Cálculo (16-O)
 Introducción al Cálculo (16-O) Planeación del Curso 26 de septiembre de 2016 1. Información General Grupo: CAT-02. Horario de clase: lunes, martes, jueves y viernes, de 10:00 a 11:30 horas. Salón de clase:
Introducción al Cálculo (16-O) Planeación del Curso 26 de septiembre de 2016 1. Información General Grupo: CAT-02. Horario de clase: lunes, martes, jueves y viernes, de 10:00 a 11:30 horas. Salón de clase:
Funciones. Cátedra de Matemática I
 Funciones Cátedra de Matemática I 2013 Definición Las funciones representan el principal objeto de análisis en el cálculo, ya que constituyen la clave para describir el mundo real en términos matemáticos
Funciones Cátedra de Matemática I 2013 Definición Las funciones representan el principal objeto de análisis en el cálculo, ya que constituyen la clave para describir el mundo real en términos matemáticos
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN
 INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
INTRODUCCION A LA INTELIGENCIA ARTIFICIAL MÓDULO 6- CÁLCULO DE PREDICADOS Y LÓGICA DE PRIMER ORDEN Referencias: Inteligencia Artificial Russell and Norvig Cap.6. Artificial Intellingence Nils Nilsson Ch.4
Determinar la incertidumbre al momento de desarrollar aplicativos en inteligencia artificial, haciendo uso de estructuras probabilísticas..
 Sistemas expertos e inteligencia artificial, Guia 5 1 Facultad : Ingeniería Escuela : Computación Asignatura: Sistemas expertos e Inteligencia Artificial Tema: RAZONAMIENTO CON INCERTIDUMBRE. Objetivo
Sistemas expertos e inteligencia artificial, Guia 5 1 Facultad : Ingeniería Escuela : Computación Asignatura: Sistemas expertos e Inteligencia Artificial Tema: RAZONAMIENTO CON INCERTIDUMBRE. Objetivo
Unidad Temática 3: Probabilidad y Variables Aleatorias
 Unidad Temática 3: Probabilidad y Variables Aleatorias 1) Qué entiende por probabilidad? Cómo lo relaciona con los Sistemas de Comunicaciones? Probabilidad - Definiciones Experimento aleatorio: Un experimento
Unidad Temática 3: Probabilidad y Variables Aleatorias 1) Qué entiende por probabilidad? Cómo lo relaciona con los Sistemas de Comunicaciones? Probabilidad - Definiciones Experimento aleatorio: Un experimento
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Conceptos previos. Revisión de Sistemas Lógicos Formatos Numéricos. Dpto. Ingeniería Electrónica y Comunicaciones
 Conceptos previos Revisión de Sistemas Lógicos Formatos Numéricos Revisión de Sistemas Lógicos Álgebra de Boole Base matemática de la Electrónica Digital Consta de dos elementos: 0 lógico y 1 lógico Tecnología
Conceptos previos Revisión de Sistemas Lógicos Formatos Numéricos Revisión de Sistemas Lógicos Álgebra de Boole Base matemática de la Electrónica Digital Consta de dos elementos: 0 lógico y 1 lógico Tecnología
ALGEBRA y ALGEBRA LINEAL. Primer Semestre CAPITULO I LOGICA Y CONJUNTOS.
 ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
ALGEBRA y ALGEBRA LINEAL 520142 Primer Semestre CAPITULO I LOGICA Y CONJUNTOS. DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas Universidad de Concepción 1 La lógica es
Medidas de Tendencia Central
 Medidas de Tendencia Central En cualquier análisis o interpretación, se pueden usar muchas medidas descriptivas que representan las propiedades de tendencia central, variación y forma para resumir las
Medidas de Tendencia Central En cualquier análisis o interpretación, se pueden usar muchas medidas descriptivas que representan las propiedades de tendencia central, variación y forma para resumir las
I UNIDAD ÁLGEBRA BOOLEANA Y COMPUERTAS LÓGICAS
 I UNIDAD ÁLGEBRA BOOLEANA Y COMPUERTAS LÓGICAS 1.1 Electrónica Digital Obviamente es una ciencia que estudia las señales eléctricas, pero en este caso son señales discretas, es decir, están bien identificadas,
I UNIDAD ÁLGEBRA BOOLEANA Y COMPUERTAS LÓGICAS 1.1 Electrónica Digital Obviamente es una ciencia que estudia las señales eléctricas, pero en este caso son señales discretas, es decir, están bien identificadas,
Contenido. BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática
 Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
El Control Difuso o FC, por sus siglas en ingles Fuzzy Control es considerado como la
 Capítulo 4 4.1 Introducción El o FC, por sus siglas en ingles Fuzzy Control es considerado como la aplicación más importante de la teoría de lógica difusa. La lógica difusa es una técnica diseñada para
Capítulo 4 4.1 Introducción El o FC, por sus siglas en ingles Fuzzy Control es considerado como la aplicación más importante de la teoría de lógica difusa. La lógica difusa es una técnica diseñada para
Estadística Inferencial. Estadística Descriptiva
 INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
INTRODUCCIÓN Estadística: Ciencia que trata sobre la teoría y aplicación de métodos para coleccionar, representar, resumir y analizar datos, así como realizar inferencias a partir de ellos. Recogida y
Matemáticas Discretas Relaciones y funciones
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
Fabio Prieto Ingreso 2003
 Fabio Prieto Ingreso 00. INECUACIONES CON UNA VARIABLE.. Inecuación lineal Llamaremos desigualdad lineal de una variable a cualquier epresión de la forma: a + b > 0 o bien a + b < 0 o bien a + b 0 o bien
Fabio Prieto Ingreso 00. INECUACIONES CON UNA VARIABLE.. Inecuación lineal Llamaremos desigualdad lineal de una variable a cualquier epresión de la forma: a + b > 0 o bien a + b < 0 o bien a + b 0 o bien
Probabilidad Condicional. Teorema de Bayes para probabilidades condicionales:
 Probabilidad Condicional Teorema de Bayes para probabilidades condicionales: Definición: Sea S el espacio muestral de un experimento. Una función real definida sobre el espacio S es una variable aleatoria.
Probabilidad Condicional Teorema de Bayes para probabilidades condicionales: Definición: Sea S el espacio muestral de un experimento. Una función real definida sobre el espacio S es una variable aleatoria.
El álgebra booleana fue estudiada por Pitágoras y George Boole.
 ALGEBRA DE BOOLE Centro CFP/ES ALGEBRA DE BOOLE El álgebra booleana fue estudiada por Pitágoras y George Boole. Con el álgebra booleana, partiendo de una serie de sentencias lógicas iniciales verdaderas
ALGEBRA DE BOOLE Centro CFP/ES ALGEBRA DE BOOLE El álgebra booleana fue estudiada por Pitágoras y George Boole. Con el álgebra booleana, partiendo de una serie de sentencias lógicas iniciales verdaderas
Tecnologías de Sistemas Inteligentes (IA95 022) Razonamiento Aproximado mediante Lógica Difusa
 Razonamiento Aproximado mediante Lógica Difusa c M. Valenzuela 1996, 1997, 2006 (23 de febrero de 2006) Este apunte está basado en (Driankov, Hellendoorn, y Reinfrank, 1996, capítulo 2) y (Klir y Yuan,
Razonamiento Aproximado mediante Lógica Difusa c M. Valenzuela 1996, 1997, 2006 (23 de febrero de 2006) Este apunte está basado en (Driankov, Hellendoorn, y Reinfrank, 1996, capítulo 2) y (Klir y Yuan,
Simulación de un controlador difuso mediante Matlab
 Control Inteligente Práctica 7 Simulación de un controlador difuso mediante Matlab José Gerardo Gomez,Diego Vallejo, Amarelis Quijano Mayo 22, 2015 Resumen En el presente documento se muestra el proceso
Control Inteligente Práctica 7 Simulación de un controlador difuso mediante Matlab José Gerardo Gomez,Diego Vallejo, Amarelis Quijano Mayo 22, 2015 Resumen En el presente documento se muestra el proceso
Tema 5: Álgebra de Boole Funciones LógicasL
 Tema 5: Álgebra de Boole Funciones LógicasL Ingeniería Informática Universidad Autónoma de Madrid 1 Álgebra de Boole.. Funciones LógicasL O B J E T I V O S Conocer el Álgebra de Boole, sus teoremas y las
Tema 5: Álgebra de Boole Funciones LógicasL Ingeniería Informática Universidad Autónoma de Madrid 1 Álgebra de Boole.. Funciones LógicasL O B J E T I V O S Conocer el Álgebra de Boole, sus teoremas y las
Desigualdades o inecuaciones lineales en una variable. Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 2017
 UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 017 Práctica 1- Números Reales Entre los conjuntos numéricos más conocidos con los que trabajaremos en esta práctica se encuentran los Naturales (N),
UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 017 Práctica 1- Números Reales Entre los conjuntos numéricos más conocidos con los que trabajaremos en esta práctica se encuentran los Naturales (N),
Que es la lógica difusa
 Que es la lógica difusa y por supuesto, para que sirve? Julio Waissman Vilanova Departamento de Matemáticas Universidad de Sonora Encuentro Universitario de Ciencia y Tecnología Plan de la presentación
Que es la lógica difusa y por supuesto, para que sirve? Julio Waissman Vilanova Departamento de Matemáticas Universidad de Sonora Encuentro Universitario de Ciencia y Tecnología Plan de la presentación
SISTEMA DE NUMEROS REALES
 SISTEMA DE NUMEROS REALES 1.1 Conjuntos Es una agrupación de objetos distintos (pero con algunas características en común), los que reciben el nombre de elementos. Generalmente se nombra a un conjunto
SISTEMA DE NUMEROS REALES 1.1 Conjuntos Es una agrupación de objetos distintos (pero con algunas características en común), los que reciben el nombre de elementos. Generalmente se nombra a un conjunto
Tema 8: Funciones I. Características.
 Tema 8: Funciones I. Características. Iniciamos la primera parte de los dos temas que vamos a dedicar al bloque de análisis, en el cual vamos a conocer y definir el concepto de función y los principales
Tema 8: Funciones I. Características. Iniciamos la primera parte de los dos temas que vamos a dedicar al bloque de análisis, en el cual vamos a conocer y definir el concepto de función y los principales
Una manera de describir un conjunto es por extensión y consiste en enumerar sus elementos entre llaves
 CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales.
 EL SISTEMA DE LOS NÚMEROS REALES Introducción El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales. Números tales como:1,3, 3 5, e,
EL SISTEMA DE LOS NÚMEROS REALES Introducción El ente básico de la parte de la matemática conocida como ANÁLISIS, lo constituye el llamado sistema de los número reales. Números tales como:1,3, 3 5, e,
La lógica borrosa: conjuntos borrosos, razonamiento aproximado y control borroso
 La lógica borrosa: conjuntos borrosos, razonamiento aproximado y control borroso Norma V. Ramírez Pérez, Instituto Tecnológico de Celaya normav@itc.mx, Martín Laguna Estrada Departamento de Mecatrónica
La lógica borrosa: conjuntos borrosos, razonamiento aproximado y control borroso Norma V. Ramírez Pérez, Instituto Tecnológico de Celaya normav@itc.mx, Martín Laguna Estrada Departamento de Mecatrónica
RAZONAMIENTO APROXIMADO
 RAZONAMIENTO APROXIMADO Sistemas Difusos (Fuzzy Systems) Introducción a la IA - LCC REALIDAD El conocimiento que necesitamos para desarrollar un Sistema basado en Conocimiento tiene muchas veces las siguientes
RAZONAMIENTO APROXIMADO Sistemas Difusos (Fuzzy Systems) Introducción a la IA - LCC REALIDAD El conocimiento que necesitamos para desarrollar un Sistema basado en Conocimiento tiene muchas veces las siguientes
MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano
 MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano Las representaciones pictóricas, suelen ser las opciones más adecuadas para mostrar el producto final plasmado
MÉTODOS DE PROYECCIÓN PARA LA REPRESENTACIÓN DE OBJETOS Unidad 1. El dibujo técnico en el plano Las representaciones pictóricas, suelen ser las opciones más adecuadas para mostrar el producto final plasmado
Sistemas de numeración
 platea.pntic.mec.es Autor: Luis González SISTEMAS DE NUMERACIÓN binario, octal y hexadecimal Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar
platea.pntic.mec.es Autor: Luis González SISTEMAS DE NUMERACIÓN binario, octal y hexadecimal Sistemas de numeración Un sistema de numeración es un conjunto de símbolos y reglas que permiten representar
GUIA 6: MAPAS DE KARNAUGH. A B C f A A
 RQUITETUR DEL OMPUTDOR Prof. Sandro ostantini GUI 6: MPS DE RNUGH Los mapas de arnaugh constituyen un método sencillo y apropiado para la minimización de funciones lógicas. El tamaño del mapa depende depende
RQUITETUR DEL OMPUTDOR Prof. Sandro ostantini GUI 6: MPS DE RNUGH Los mapas de arnaugh constituyen un método sencillo y apropiado para la minimización de funciones lógicas. El tamaño del mapa depende depende
Funciones: Aspectos básicos
 Funciones: Aspectos básicos Nombre: Curso:.. Producto cartesiano En teoría de conjuntos, el producto cartesiano de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son todos
Funciones: Aspectos básicos Nombre: Curso:.. Producto cartesiano En teoría de conjuntos, el producto cartesiano de dos conjuntos es una operación que resulta en otro conjunto cuyos elementos son todos
CONJUNTOS CIENTÍFICO, MAT. 2
 CONJUNTOS CIENTÍFICO, MAT. 2 PRIMERAS NOCIONES Conceptos primitivos: Conjunto y elemento de un conjunto. Formas de determinar un conjunto: 1) Decimos que un conjunto está determinado por extensión cuando
CONJUNTOS CIENTÍFICO, MAT. 2 PRIMERAS NOCIONES Conceptos primitivos: Conjunto y elemento de un conjunto. Formas de determinar un conjunto: 1) Decimos que un conjunto está determinado por extensión cuando
Diagramas de Veitch y Karnaugh
 Diagramas de Veitch y Karnaugh Estos diagramas permiten simplificar en forma sistemática las funciones Booleanas sin aplicar las propiedades propias del álgebra de Boole. Para entender como aplicar estos
Diagramas de Veitch y Karnaugh Estos diagramas permiten simplificar en forma sistemática las funciones Booleanas sin aplicar las propiedades propias del álgebra de Boole. Para entender como aplicar estos
Material educativo. Uso no comercial 1.4 MÉTODOS DE DEMOSTRACIÓN Método directo o Método de la hipótesis auxiliar
 1.4 MÉTODOS DE DEMOSTRACIÓN Designamos en esta forma las estrategias o esquemas más generales que identificamos en los procesos deductivos. Estos modelos están fundamentados lógicamente en teoremas o reglas
1.4 MÉTODOS DE DEMOSTRACIÓN Designamos en esta forma las estrategias o esquemas más generales que identificamos en los procesos deductivos. Estos modelos están fundamentados lógicamente en teoremas o reglas
