Teoría Electromagnética. Escalar: Número, cantidad: masa, carga, temperatura, volumen, edad, altura, etc.
|
|
|
- María Teresa Villalba Calderón
- hace 5 años
- Vistas:
Transcripción
1 Apéndice A: Cálculo Vectorial Escalar: Número, cantidad: masa, carga, temperatura, volumen, edad, altura, etc. Vector: Número + Dirección: velocidad, aceleración, desplazamiento, fuerza, campos, etc. F 1 F 2 W F 3 1
2 Suma: Operaciones algebraicas: B A B A C=A+B Resta: B C=A-B A A C=A-B B a) b) 2
3 Multiplicación por un escalar: A 2A -A -2A 3
4 Producto Escalar (Producto Punto): vector vector escalar A B = ABcosα B α A 4
5 El Producto Escalar es: Conmutativo: A B = B A Y distributivo: A (B + C) = A B + A C Magnitud de un vector: A A = AA cos(0) = A 2 A = A A Vector unitario (magnitud = 1): n ˆ = 5 n n n
6 Ejemplo A.1 Ley de los Cosenos: B C=A-B α A C C = (A B) (A B) = A A A B B A + B B C 2 = A 2 + B 2 2ABcosα 6
7 Producto Vectorial (Producto Cruz): vector vector vector A B = (ABsenα)ˆ n Saliendo n^ B α Entrando A Regla de la mano derecha: Los dedos de la mano derecha apuntan en dirección del primer vector (A); se enroscan hacia el segundo (B) a través del ángulo más pequeño (α); el pulgar apunta en dirección de n ˆ. 7
8 El producto cruz es: No conmutativo: Sí es distributivo: A B = B A A (B + C) = A B + A C Si los vectores A y B son paralelos: A B = 0 8
9 Geométricamente: A B = área de la superficie definida por A y B A B área vector 9
10 Productos múltiples: Producto de un vector por un producto punto: A(B C) = (B C)A Producto cruz de un vector por un producto cruz: A (B C) = B(A C) C(A B) Producto punto de un producto cruz: A (B C) = B (C A) = C (A B) 10
11 Volumen de paralelepípedo de lados A, B y C: C B A τ = C (A B) 11
12 Cartesiano Derecho: Sistemas Coordenados: z d (x,y,z) (x o,y o,z o ) d o ^i ^ k ^ j y x d o = x oˆ i + y oˆ j + z o ˆ k d = (x x o )ˆ i +(y y o )ˆ j + (z z o ) ˆ k 12
13 Distancia entre dos puntos: {[ ] d = (x x o )ˆ i + (y y o )ˆ j + (z z o )ˆ k [ ]} 1/ 2 (x x o )ˆ i + (y y o )ˆ j + (z z o )ˆ k ˆ i ˆ j = ˆ i k ˆ = ˆ j k ˆ = 0 ˆ i ˆ i = ˆ j ˆ j = k ˆ k ˆ =1 d = (x x o ) 2 +(y y o ) 2 +(z z o ) 2 13
14 Producto Escalar en Coordenadas Cartesianas: A B = (A xˆ i + A yˆ j + A z ˆ k ) (B xˆ i + B yˆ j + B z ˆ k ) = A x B x + A y B y + A z B z Producto Vectorial en Coordenadas Cartesianas: ˆ i i ˆ = ˆ j ˆ j = k ˆ k ˆ = 0 ˆ i ˆ j = ˆ j ˆ i = k ˆ ˆ j k ˆ = k ˆ ˆ j = ˆ i ˆ k ˆ i = ˆ i ˆ k = ˆ j 14
15 A B = ˆ i ˆ j ˆ k A x A y A z = B x B y B z (A y B z A z B y )ˆ i + (A z B x A x B z )ˆ j +(A x B y A y B x ) ˆ k Volumen: C ( A B) = C x C y C z A x A y A z B x B y B z 15
16 Esférico: z (r,θ,φ) r^ ^φ θ r ^ θ y φ x 0 r + 0 θ π 0 φ 2π 16
17 Equivalencia con sistema cartesiano: x = rsenθcosφ y = rsenθsenφ z = rcosθ Transformaciones inversas: r = x 2 + y 2 +z 2 θ = cos 1 z x 2 + y 2 + z 2 = tan 1 x 2 + y 2 z φ = tan 1 y x 17
18 Distancia del origen a cualquier punto: Vectores unitarios: d = rˆ r r ˆ = senθcosφˆ i +senθsenφˆ j + cosθk ˆ θ ˆ = cosθcosφˆ i + cosθsenφˆ j senθˆ k φ ˆ = senφˆ i + cosφˆ j ˆ i = senθcosφˆ r +cosθcosφˆ θ senφˆ φ ˆ j = senθsenφˆ r + cosθsenφˆ θ + cosφˆ φ k ˆ = cosθˆ r senθˆ θ 18
19 Derivadas de vectores unitarios: ˆ r θ = cosθcosφˆ i + cosθsenφˆ j senθˆ k = θ ˆ ˆ r φ = senθsenφˆ i + cosθcosφˆ j ˆ θ θ = senθcosφˆ i senθsenφˆ j cosθˆ k = ˆ r ˆ θ φ = cosθsenφˆ i + cosθcosφˆ j ˆ φ φ = cosφˆ i senφˆ j 19
20 Producto Escalar en coordenadas Esféricas: A B = (A rˆ r + A θˆ θ + A φˆ φ ) (B rˆ r + B θˆ θ + B φˆ φ ) = A r B r + A θ B θ + A φ B φ Producto Vectorial en Coordenadas Esféricas: A B = r ˆ ˆ θ ˆ φ A r A θ A φ = B r B θ B φ (A θ B φ A φ B θ )ˆ r + (A φ B r A r B φ )ˆ θ + (A r B θ A θ B r ) φ ˆ 20
21 Cilíndrico: z ^k ^φ r r^ (r,φ,z) d o y φ x 0 r + 0 φ 2π z + 21
22 Equivalencia con sistema cartesiano: x = rcosφ y = rsenφ z = z Transformaciones Inversas: r = x 2 + y 2 φ = tan 1 z = z y x 22
23 Distancia del origen a cualquier punto: d o = rˆ r + zˆ k d o = r 2 + z 2 Vectores unitarios: r ˆ = cosφˆ i + senφˆ j φ ˆ = senφˆ i + cosφˆ j k ˆ = k ˆ ˆ i = cosφˆ r senφˆ φ ˆ j = senφˆ r +cosφˆ φ k ˆ = k ˆ 23
24 Derivadas de vectores unitarios: ˆ r φ = senφˆ i + cosφˆ j ˆ φ φ = cosφˆ i senφˆ j = ˆ r Producto Escalar en Coordenadas Cilíndricas: A B = (A rˆ r + A φˆ φ + A z k ˆ ) (B rˆ r + B φ φ ˆ + B z k ˆ ) = A r B r + A φ B φ + A z B z 24
25 Producto Vectorial en Coordenadas Cilíndricas: A B = r ˆ ˆ φ ˆ k A r A φ A z = B r B φ B z (A φ B z A z B φ )ˆ r + (A z B r A r B z ) φ ˆ + (A r B φ A φ B r ) k ˆ 25
26 Operaciones diferenciales: Gradiente Divergencia Rotacional Operador diferencial Del ( Nabla ): Cartesianas: Esféricas: x ˆ i + y ˆ j + z ˆ k r r ˆ + 1 r θ ˆ θ + 1 rsenθ φ ˆ φ 26
27 Cilíndricas: r r ˆ + 1 r φ ˆ φ + z ˆ k Gradiente: Del actúa sobre una función escalar vector f = F F: dirección de máximo cambio de la función escalar F: pendiente en un punto dado 27
28 Ejemplo A.2.-Temperatura panel solar: T(x,y) = 25 [ 2 xy 5y2 2x +17y 4] 28
29 T(x,y) = T x ˆ i + T y ˆ j = 25 2 (y 2) i ˆ + 25 (x 10y +17) 2 ˆ j T(x = 4,y = 0) = 25ˆ i + (525/ 2)ˆ j T(x = 4,y = 0) = ( 25) 2 + (525/2) 2 = C/ m T(x = 2,y = 1.5) = ( 25/ 4)ˆ i + 50ˆ j T(x = 2,y =1.5) = ( 25/ 4) 2 + (50) 2 = C/ m 29
30 25 2 (y m 2) = 0 y m = (x m 10y m +17) = 0 x m = 3 T(x m,y m ) = 25 [ 2 (3)(2) 5(2)2 2(3)+17(2) 4] = 125 C Divergencia: Del actúa sobre una función vectorial escalar E = f 30
31 E = > 0 campo divergente : fuente 0 campo no divergente < 0 campo convergente : sumidero P P P 31
32 Rotacional: Del actúa sobre una función vectorial vector H = J 32
33 Derivadas de productos: ( fg) = f g + g f ( A B) = A ( B) +B ( A) + ( A )B + ( B )A ( fa) = f( A) + A ( f) ( A B) = B ( A) A ( B) ( A B) = ( B )A ( A )B + A( B) B( A) ( fa) = f( A) A ( f) 33
34 Derivadas de segundo orden: ( A) = 2 A + ( A) ( f ) = 2 f ( A) = 0 ( f ) = 0 ( A) = ( A) 2 A 2 A = ( A) ( A) 34
35 Operaciones integrales: integral de un vector línea superficie volumen Integral de un vector: Sigue siendo un vector El vector unitario debe ser constante x 1 x o ( xyzˆ i + y 3ˆ j + xz 2ˆ k )dx = 1 2 x2 yzˆ i + xy 3ˆ j x2 z 2 k ˆ x 1 x o 35
36 = 1 2 yz ( x x o )ˆ i + y 3 ( x 1 x o )ˆ j z2 ( 2 x 1 2 xo )ˆ k x 1 xyzdxˆ r 1 2 yz ( x x o )ˆ r x o r ˆ no es constante r ˆ = f ˆ i, ˆ j, k ˆ r ˆ = senθcosφˆ i + senθsenφˆ j + cosθk ˆ ( ) = x x 2 + y 2 + z 2 ˆ i + y x 2 + y 2 + z 2 ˆ j + z x 2 + y 2 + z 2 ˆ k 36
37 x 1 xyzdxˆ r x o = yz 2 x 2 1 x 1 + y 2 + z 2 y 2 + z 2 ( ) ln x 1 + x y 2 + z 2 x o x o 2 + y 2 + z 2 + y 2 + z 2 ( ) ln x o + x o 2 + y 2 + z 2 i ˆ +y 2 { z x y 2 + z 2 x 2 o + y 2 + z 2 }ˆ j + yz 2 x o 2 + y 2 + z 2 x o 2 + y 2 + z 2 { } ˆ k 37
38 Integral de línea: escalar b a F dl F dl Cartesiano: dl = dxˆ i + dyˆ j + dz ˆ k Esférico: dl = drˆ r + rdθ ˆ θ + rsenθdφ ˆ φ Cilíndrico: dl = drˆ r + rdφ ˆ φ + dz ˆ k 38
39 Ejemplo A.3.- F(x,y,z) = 3x2ˆ i + 2xzˆ j y 2 k ˆ (x o, y o, z o ). (0, 0, 0) Forma incorrecta: F dl = ( 3x 2ˆ i + 2xzˆ j y 2ˆ k ) dxˆ i + dyˆ j + dzk ˆ ( ) x o y o z o = 3x 2 dx + 2xzdy y 2 dz o o o = x o 3 + 2xy o z y 2 z o 39
40 Forma correcta: Se define una trayectoria z (x o,y o,z o ) III I y (x o,0,0) (x o,y o,0) II x Sub-trayectoria I: x: x=0 x=xo dx 0 y: y=0 y=0 dy=0 z: z=0 z=0 dz=0 40
41 x o x o I F dl = 3x 2ˆ i dxˆ i = 3x 2 3 dx = x o 0 0 Sub-trayectoria II: x: x=xo x=xo dx=0 y: y=0 y=yo dy 0 z: z=0 z=0 dz=0 y o y o F dl = 2xzˆ j dyˆ j = 2x o (0)dy = 0 II
42 Sub-trayectoria III: x: x=xo x=xo dx=0 y: y=yo y=yo dy=0 z: z=0 z=zo dz 0 z o z o F dl = y 2ˆ k dz k ˆ = 2 y odz III 0 0 = y o 2 zo F dl = I F dl + F dl + F dl II III = x o y o 2 z o = x o 3 y o 2 z o 42
43 Ejemplo físico: Trabajo W = F dl II b a I 43
44 Integral de superficie: escalar F da F da Cartesianas: da = ±dydzˆ i Esféricas: da = ±r 2 senθdθdφˆ r da = ±dxdzˆ j da = ±rdrdθˆ φ da = ±dxdy ˆ k da = ±rsenθdrdφ ˆ θ Cilíndricas: da = ±rdφdzˆ r da = ±drdzˆ φ da = ±rdrdφˆ k 44
45 Ejemplo A.4.- F(x,y,z) = 3x2 yˆ i + xyzˆ j y 3ˆ k z da V (0,0,c) da II da IV (a,0,0) da I (0,b,0) da III y x da VI 45
46 Cara anterior: da = +dydzˆ i x=a I F da = 3x 2 yˆ i dydzˆ i b c = 3a 2 ydydz = 3a 2 ydy dz = 3 2 a2 b 2 c 0 0 Cara posterior: da = dydzˆ i x=0 F da = 3x 2 yˆ i ( dydzˆ i ) = 3(0) 2 ydydz = II 0 46
47 Cara derecha: da = +dxdzˆ j y=b F da = xyzˆ j dxdzˆ j III a c = xyzdxdz = b xdx zdz = 1 4 a2 bc Cara izquierda: da = dxdzˆ j y=0 F da = xyzˆ j ( dxdzˆ j IV ) = x(0)zdxdz = 0 47
48 Cara superior: da = +dxdyˆ k z=c. V F da = ( y 3ˆ k ) dxdyˆ k a b Cara inferior: = y 3 dxdy = dx 0 0 da = dxdyˆ k z=0 y 3 dy = 1 4 ab4 F da = ( y 3ˆ k ) ( dxdyk ˆ ) VI a b = + y 3 dxdy = dx 0 0 y 3 dy = 1 4 ab4 48
49 Total: VI i=i F da = F da i = 3 2 a2 b 2 c a2 bc ab ab3 F da = 1 4 a2 bc(6b + c) Flujo de F F da = a través de superficie 49
50 Integral de volumen: escalar τ = volumen Cartesianas: dτ = dxdydz Esféricas: dτ = r2 senθdrdθdφ Cilíndricas: dτ = rdrdφdz Ejemplo A.5.-Volumen de esfera de radio R. τ = dτ = r2 senθdrdθdφ 50
51 z dτ y R x R 0 r 2 dr π 0 2π senθdθ dφ = 1 3 R3 (2)(2π) = 4 3 πr3 0 51
52 Teoremas fundamentales: Del De la Del Gradiente Divergencia Rotacional Teorema fundamental del gradiente: b ( f ) dl = f (b) f(a ) a ( f ) dl = 0 52
53 Teorema fundamental de la divergencia: ( F) dτ = F da da superficie cerrada que envuelve al volumen dτ. Ejemplo A.6.-Teorema de la Divergencia usando F(x,y, z) = 3x 2 yˆ i + xyzˆ j y 3ˆ k y el volumen definido por un paralelepídedo regular de lados x=a, y=b, y z=c. F = x ˆ i + y ˆ j + k z ˆ 3x 2 yˆ i + xyzˆ j y 3ˆ k ( ) = 6xy + xz = x(6y + z) 53
54 ( F)dτ = x(6y+ z)dxdydz a b c = xdx (6y + z)dydz b = 1 2 a2 6yc c2 dy = 1 4 a2 bc(6b + c) 0 ( F)dτ = 1 4 a2 bc(6b + c) 54
55 Teorema fundamental del rotacional: ( F) da = F dl dl perímetro que define la superficie abierta da. Si: F = f F = 0 ( f ) = 0 El rotacional de un gradiente es siempre cero 55
Sistemas de coordenadas
 Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Tema 1. Introducción
 Grado en Ingeniería Aeroespacial en Aeronavegación Tema 1. Introducción Felipe Alonso Atienza felipe.alonso@urjc.es @FelipeURJC Escuela Técnica Superior de Ingeniería de Telecomunicación Universidad Rey
Grado en Ingeniería Aeroespacial en Aeronavegación Tema 1. Introducción Felipe Alonso Atienza felipe.alonso@urjc.es @FelipeURJC Escuela Técnica Superior de Ingeniería de Telecomunicación Universidad Rey
APƒNDICE A: CçLCULO VECTORIAL
 430 Murphy APƒNDICE A: CçLCULO VECTORIAL A.1 INTRODUCCIîN La teor a electromagnžtica, como todas las ramas de la f sica, usa vectores para representar algunos conceptos y cantidades. Un nœmero ordinario
430 Murphy APƒNDICE A: CçLCULO VECTORIAL A.1 INTRODUCCIîN La teor a electromagnžtica, como todas las ramas de la f sica, usa vectores para representar algunos conceptos y cantidades. Un nœmero ordinario
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN
 SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
CAMPOS: CIRCULACIÓN Y FLUJO
 AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
Analisis Vectorial. 19 de octubre de 2011
 M.Sc. Alejandro Galo Roldan Physics Professor Head of the Physics Program at the National University of Honduras UNAH 19 de octubre de 2011.Sc. Alejandro Galo RoldanPhysics Professor Head of the Analisis
M.Sc. Alejandro Galo Roldan Physics Professor Head of the Physics Program at the National University of Honduras UNAH 19 de octubre de 2011.Sc. Alejandro Galo RoldanPhysics Professor Head of the Analisis
PEP 3. Responda 4 de los siguientes 9 problemas, escogiendo al menos uno de cada sección.
 Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Universidad de Santiago de Chile Cálculo odrigo Vargas do semestre 1 PEP Nombre: Nota: esponda de los siguientes 9 problemas, escogiendo al menos uno de cada sección. Sección 1. 1. Use coordenadas esféricas
Electromagnetismo II. Solución Tarea 1
 Electromagnetismo II Semestre: 216-1 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero por Carlos Maciel Escudero Tarea 1 1.- Problema: 1pts a Demuestra que la regla BAC-CAB se cumple,
Electromagnetismo II Semestre: 216-1 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero por Carlos Maciel Escudero Tarea 1 1.- Problema: 1pts a Demuestra que la regla BAC-CAB se cumple,
INTRODUCCIÓN AL CÁLCULO VECTORIAL
 1. INTRODUCCIÓN INTRODUCCIÓN AL CÁLCULO VECTORIAL Este capítulo es una revisión condensada de los principales conceptos del cálculo vectorial a modo de repaso de un tema que se supone más o menos conocido
1. INTRODUCCIÓN INTRODUCCIÓN AL CÁLCULO VECTORIAL Este capítulo es una revisión condensada de los principales conceptos del cálculo vectorial a modo de repaso de un tema que se supone más o menos conocido
EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS.
 c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
Matemáticas para ingeniería I. Ingeniería en Mecatrónica Lilia Meza Montes IFUAP Otoño 2016
 Matemáticas para ingeniería I Ingeniería en Mecatrónica Lilia Meza Montes IFUP Otoño 2016 Concepto de campo vectorial. Producto por escalar, producto interior y vectorial de campos vectoriales. Ejemplos
Matemáticas para ingeniería I Ingeniería en Mecatrónica Lilia Meza Montes IFUP Otoño 2016 Concepto de campo vectorial. Producto por escalar, producto interior y vectorial de campos vectoriales. Ejemplos
Dpto. Física y Mecánica. Operadores diferenciales
 Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Guía n 0: Herramientas de Física y Matemáticas
 Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
NOCIONES DE CALCULO VECTORIAL
 NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
ANALISIS MATEMATICO II (Ciencias- 2011) Trabajo Práctico 8
 ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
TEMA 0: Herramientas matemáticas
 1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
SERIE # 4 CÁLCULO VECTORIAL
 SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander. Monday, November 5, 2007 at 8:44 am (FA07.
 Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
Estática Profesor Herbert Yépez Castillo
 Estática 2015-2 Profesor Herbert Yépez Castillo Introducción 2.1 Escalares y vectores 2.2 Operaciones vectoriales 2.3 Suma vectorial de fuerzas 2.4 Suma de sistema de fuerzas coplanares 2.5 Vectores cartesianos
Estática 2015-2 Profesor Herbert Yépez Castillo Introducción 2.1 Escalares y vectores 2.2 Operaciones vectoriales 2.3 Suma vectorial de fuerzas 2.4 Suma de sistema de fuerzas coplanares 2.5 Vectores cartesianos
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Vectores Presentanción basada en el material contenido en: Serway, R. Physics for Scientists and Engineers. Saunders College Pub. 3rd edition.
 Vectores Presentanción basada en el material contenido en: Serway, R. Physics for Scientists and Engineers. Saunders College Pub. 3rd edition. Sistemas de Coordenadas Se usan ara describir la posición
Vectores Presentanción basada en el material contenido en: Serway, R. Physics for Scientists and Engineers. Saunders College Pub. 3rd edition. Sistemas de Coordenadas Se usan ara describir la posición
3.1 Integrales de línea. Integral en R Propiedades Longitud de arco Teorema de Green
 3.1 Integrales de línea Integral en R Propiedades Longitud de arco Teorema de Green Integración de una variable Operación inversa de la derivación. Integral definida de f de a a b, si el límite existe
3.1 Integrales de línea Integral en R Propiedades Longitud de arco Teorema de Green Integración de una variable Operación inversa de la derivación. Integral definida de f de a a b, si el límite existe
3. Expresar las siguientes figuras en (i) coordenadas cilíndricas (ii) coordenadas esféricas (a) x 2 + y 2 + z 2 = 25 (b) z 2 = 2(x 2 + y 2 ) B + 3
 ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
Definición. Tema 12: Teoremas de Integración del Cálculo Vectorial. Gradiente de un campo escalar. Rotacional de un campo vectorial.
 Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Definición valor extremo: Si f(x,y) està definida en una regiòn R y P 0 =(a, es un punto de R, entonces: a) f(a, es un valor máximo local de f si f(a, f(x,y) para todos los
APLICACIONES DE LA DERIVADA Definición valor extremo: Si f(x,y) està definida en una regiòn R y P 0 =(a, es un punto de R, entonces: a) f(a, es un valor máximo local de f si f(a, f(x,y) para todos los
Cálculo diferencial e integral 3
 Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
Cálculo diferencial e integral 3 Guía 1 1. Sean a 1,..., a n R n. Demuestra que el conjunto { W = x = (x 1,..., x n ) R n es un subespacio vectorial de R n. } n a i x i = 0 i=1 2. Sean W y V subespacios
I. Fundamentos matemáticos. ticos. Campos Electromagnéticos. ticos. 1. Coordenadas curvilíneas. Ingeniero de Telecomunicación
 I. Fundamentos matemá 1. Coordenadas curvilíneas Gabriel Cano Gómez, G 2009/10 Dpto. Física F Aplicada III (U. Sevilla) Campos Electromagné Ingeniero de Telecomunicación I. Fundamentos matemá Gabriel Cano
I. Fundamentos matemá 1. Coordenadas curvilíneas Gabriel Cano Gómez, G 2009/10 Dpto. Física F Aplicada III (U. Sevilla) Campos Electromagné Ingeniero de Telecomunicación I. Fundamentos matemá Gabriel Cano
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE. 2) Para cada una de las superficies dadas determine un vector normal y la ecuación del
 GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
(26, 10, 4) = (0.92, 0.36, 0.14) (26, 10, 4)
 CAPÍTULO 1 1.1. Dados los vectores M= 1a x + 4a y 8a z y N = 8a x + 7a y a z, encuentre: a) un vector unitario en la dirección de M + N. M + N = 1a x 4a y + 8a z + 16a x + 14a y 4a z = (6, 1, 4) De este
CAPÍTULO 1 1.1. Dados los vectores M= 1a x + 4a y 8a z y N = 8a x + 7a y a z, encuentre: a) un vector unitario en la dirección de M + N. M + N = 1a x 4a y + 8a z + 16a x + 14a y 4a z = (6, 1, 4) De este
UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS
 UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ESCUELA DE FÍSICA Laboratorios virtuales: Electricidad y Magnetismo I Uso de Mathematica: Campos Vectoriales y Sistemas de Coordenadas ELABORADO
UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ESCUELA DE FÍSICA Laboratorios virtuales: Electricidad y Magnetismo I Uso de Mathematica: Campos Vectoriales y Sistemas de Coordenadas ELABORADO
DINAMICA DEL PUNTO. Es el momento con respecto a un punto O de la cantidad de movimiento de una partícula móvil.
 DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
SERIE ÁLGEBRA VECTORIAL
 SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
Física para Ciencias: Vectores y Sistemas de Referencia
 Física para Ciencias: Vectores y Sistemas de Referencia Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Magnitudes Físicas Escalares: definidos por un número Ej.: masa, tiempo, presión, temperatura,
Física para Ciencias: Vectores y Sistemas de Referencia Dictado por: Profesor Aldo Valcarce 1 er semestre 2014 Magnitudes Físicas Escalares: definidos por un número Ej.: masa, tiempo, presión, temperatura,
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
1.5. Integral de línea de un campo Vectorial.
 .5. Integral de línea de un campo Vectorial. Sea F ( xyz,, un campo vectorial continuo sobre R donde F representa un campo de fuerzas aplicado sobre una partícula cuya trayectoria puede ser descrita por
.5. Integral de línea de un campo Vectorial. Sea F ( xyz,, un campo vectorial continuo sobre R donde F representa un campo de fuerzas aplicado sobre una partícula cuya trayectoria puede ser descrita por
Fuerte: Magnitud relativa = 1 Cohesión nuclear Rango de acción reducido Partícula mediadora: Mesón
 CAPÍTULO 1 INTRODUCCIÓN Las teorías de campo: Fuerte Electromagnética Débil Gravitacional Cada campo tiene una Fuerza Fundamental asociada: Fuerte: Magnitud relativa = 1 Cohesión nuclear Rango de acción
CAPÍTULO 1 INTRODUCCIÓN Las teorías de campo: Fuerte Electromagnética Débil Gravitacional Cada campo tiene una Fuerza Fundamental asociada: Fuerte: Magnitud relativa = 1 Cohesión nuclear Rango de acción
Sistemas de Coordenadas
 Vectores Sistemas de Coordenadas Se usan ara describir la posición de un punto en el espacio El sistema de coordenadas consiste de: Un punto de referencias fijo que se llama origen Ejes con una escala
Vectores Sistemas de Coordenadas Se usan ara describir la posición de un punto en el espacio El sistema de coordenadas consiste de: Un punto de referencias fijo que se llama origen Ejes con una escala
Examen Final de Cálculo Vectorial MATE PREGUNTAS ABIERTAS TEMA A Diciembre 6 de Nombre: Código:
 UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-112-4-V-1--217 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 112 TIPO DE EXAMEN: Examen Final Parcial FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-112-4-V-1--217 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 112 TIPO DE EXAMEN: Examen Final Parcial FECHA DE
INTEGRALES CURVILÍNEAS
 (Apuntes sin revisión para orientar el aprendizaje) INTEGRALES URVILÍNEAS (Material de apoyo y orientación para preparar el tema) Las integrales curvilíneas constituyen el estudio de funciones sobre curvas.
(Apuntes sin revisión para orientar el aprendizaje) INTEGRALES URVILÍNEAS (Material de apoyo y orientación para preparar el tema) Las integrales curvilíneas constituyen el estudio de funciones sobre curvas.
Breviario de cálculo vectorial
 Apéndice A Breviario de cálculo vectorial versión 16 de octubre de 2006 Este apéndice no pretende ser mas que un resumen de definiciones y fórmulas útiles acerca de la función delta de Dirac, cálculo vectorial
Apéndice A Breviario de cálculo vectorial versión 16 de octubre de 2006 Este apéndice no pretende ser mas que un resumen de definiciones y fórmulas útiles acerca de la función delta de Dirac, cálculo vectorial
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Vectores A A. Vector. A u AA. Segmento orientado en el espacio (módulo, dirección y sentido).
 Vectores Vector Segmento orientado en el espacio (módulo, dirección y sentido). A u AA A u A A A 1 ua 1 Ejemplo Vector velocidad módulo: 500 km/h sentido: el de avance Vector fuerza gravitatoria módulo:
Vectores Vector Segmento orientado en el espacio (módulo, dirección y sentido). A u AA A u A A A 1 ua 1 Ejemplo Vector velocidad módulo: 500 km/h sentido: el de avance Vector fuerza gravitatoria módulo:
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Sea S = F r(w ) una supercie cerrada que limita una región en el espacio W R 3
 4.3 Teorema de la ivergencia Gauss) ea = F r ) una supercie cerrada que limita una región en el espacio R 3 El teorema de la divergencia tambien conocido como teorema de Gauss) es una generalización del
4.3 Teorema de la ivergencia Gauss) ea = F r ) una supercie cerrada que limita una región en el espacio R 3 El teorema de la divergencia tambien conocido como teorema de Gauss) es una generalización del
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
GUÍA DE CÁLCULO VECTORIAL Academia de Matemáticas y Física I.C.
 1. Considere los siguientes vectores a = (2,3,1), b = (4, 1,3). Calcule: a) a + b b) 2a + 3b c) 3a b d) a + b e) 3a 2b f) 2 a + b 2. Halle las longitudes de los lados del triángulo ABC y determine si son
1. Considere los siguientes vectores a = (2,3,1), b = (4, 1,3). Calcule: a) a + b b) 2a + 3b c) 3a b d) a + b e) 3a 2b f) 2 a + b 2. Halle las longitudes de los lados del triángulo ABC y determine si son
W F l. ù û = Nxm º Joule. En SI: éë W. ù û. = Dinaxcm º Ergio. En CGS: é
 El trabajo W hecho sobre un objeto, por un agente externo ejerciendo una fuerza constante en el objeto, es el producto de la fuerza y de la magnitud del desplazamiento: W = F * l A F B W F l En SI: éë
El trabajo W hecho sobre un objeto, por un agente externo ejerciendo una fuerza constante en el objeto, es el producto de la fuerza y de la magnitud del desplazamiento: W = F * l A F B W F l En SI: éë
6. El teorema de la divergencia.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. Lección. Cálculo vectorial. 6. El teorema de la divergencia. Ya vimos una versión del teorema de Green en el plano que expresa la igualdad entre la integral doble
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. Lección. Cálculo vectorial. 6. El teorema de la divergencia. Ya vimos una versión del teorema de Green en el plano que expresa la igualdad entre la integral doble
Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal.
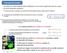 Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Electromagnetismo I P R E G U N T A S Y E J E R C I C I O S. Fecha: lunes, 8 de febrero del Simplificar la siguiente expresión: (2 2 (1+2+3)
 Electromagnetismo I Semestre: 206-2 Prof. Alejandro Reyes Coronado Ayud. Adrián Alejandro Bartolo González Ayud. José Ángel Castellanos Reyes de Examen Diagnóstico Fecha: lunes, 8 de febrero del 205. Simplificar
Electromagnetismo I Semestre: 206-2 Prof. Alejandro Reyes Coronado Ayud. Adrián Alejandro Bartolo González Ayud. José Ángel Castellanos Reyes de Examen Diagnóstico Fecha: lunes, 8 de febrero del 205. Simplificar
i j k xy yz xz = = Div Rot F = x y z
 Div Rot F, si F = ( xy, yz, xz) 1. Hallar: primero, debemos hallar rotor de la función vectorial. i j k Rot ( F ) = ( xy, yz, xz) =,, ( xy, yz, xz) = x y z xy yz xz ( xz) ( yz) ( xy) ( xz) ( yz) ( xy)
Div Rot F, si F = ( xy, yz, xz) 1. Hallar: primero, debemos hallar rotor de la función vectorial. i j k Rot ( F ) = ( xy, yz, xz) =,, ( xy, yz, xz) = x y z xy yz xz ( xz) ( yz) ( xy) ( xz) ( yz) ( xy)
a n en las que n=1 s n = n + 1 Solución: a) Utilizando el criterios de D Alembert se obtiene que a n+1 n a n 3 > 1 n=1
 EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
SERIE # 2 CÁLCULO VECTORIAL
 SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
VECTORES : Las Cantidades Vectoriales cantidades escalares
 VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
Fundamentos Matemáticos. Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla
 Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Índice Introducción I. Sistemas de coordenadas II. Campos escalares. Gradiente III.
Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Índice Introducción I. Sistemas de coordenadas II. Campos escalares. Gradiente III.
Electromagnetismo I. Solucion Examen Diagnóstico
 Electromagnetismo I Semestre: 05- Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza Escudero Examen Diagnóstico Resuelto por: Carlos Alberto Maciel Escudero Solucion
Electromagnetismo I Semestre: 05- Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza Escudero Examen Diagnóstico Resuelto por: Carlos Alberto Maciel Escudero Solucion
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
MAGNITUDES VECTORIALES
 MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
Elementos de análisis
 Elementos de análisis El estudio universitario del electromagnetismo en Física II requiere del uso de elementos de análisis en varias variables que el alumno adquirirá en la asignatura Análisis Matemático
Elementos de análisis El estudio universitario del electromagnetismo en Física II requiere del uso de elementos de análisis en varias variables que el alumno adquirirá en la asignatura Análisis Matemático
Tema 1: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 2/7 Campos escalares.
 Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte /7 Campos escalares. Gradiente Concepto de campo escalar: una magnitud que depende
Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte /7 Campos escalares. Gradiente Concepto de campo escalar: una magnitud que depende
Coordenadas Generalizadas en el Espacio
 Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Sistemas de coordenadas
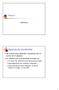 Tema 2 Vectores Sistemas de coordenadas Se utilizan para describir la posición de un punto en el espacio Un sistema de coordenadas consiste en un punto de referencia que llamaremos origen ejes específicos
Tema 2 Vectores Sistemas de coordenadas Se utilizan para describir la posición de un punto en el espacio Un sistema de coordenadas consiste en un punto de referencia que llamaremos origen ejes específicos
Matemáticas III Tema 6 Integrales de superficie
 Matemáticas III Tema 6 Integrales de superficie Rodríguez ánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba,. 214. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative Commons Attribution- NonComercial-hareAlike
Matemáticas III Tema 6 Integrales de superficie Rodríguez ánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba,. 214. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative Commons Attribution- NonComercial-hareAlike
Primer octante Segundo octante Tercer octante Cuarto octante P ( X, Y, Z ) P (-X, Y, Z ) P (-X,-Y, Z ) P ( X,-Y, Z )
 Capítulo VI. Álgebra vectorial Objetivo: El alumno aplicará el álgebra vectorial en la resolución de problemas geométricos. Contenido: 6.1. Cantidades escalares y cantidades vectoriales. Definición de
Capítulo VI. Álgebra vectorial Objetivo: El alumno aplicará el álgebra vectorial en la resolución de problemas geométricos. Contenido: 6.1. Cantidades escalares y cantidades vectoriales. Definición de
6. Integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples. 6. Integrales triples. Integral triple en un prisma. El proceso para definir la integral triple f ( xyzdv,, ), de una función continua
GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples. 6. Integrales triples. Integral triple en un prisma. El proceso para definir la integral triple f ( xyzdv,, ), de una función continua
Unidad 1 Teoría de campo
 Unidad Teoría de campo 9 de abril de 28. Campos escalares y vectoriales Un campo es una función matemática del espacio y el tiempo. En particular, un campo escalar es una función que en cada instante de
Unidad Teoría de campo 9 de abril de 28. Campos escalares y vectoriales Un campo es una función matemática del espacio y el tiempo. En particular, un campo escalar es una función que en cada instante de
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
MATEMÁTICAS 2. Curso 2016/17. Integración en varias variables.
 MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
AMPLIACIÓN DE MATEMÁTICAS. Curso 2015/16. Integración en varias variables.
 AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
Vectores. Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica. Unidad Culhuacán.
 Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica. Unidad Culhuacán. Vectores Autor: Ing. Jonathan Alejandro Cortés Montes de Oca. Vectores En el campo de estudio del Cálculo
Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica. Unidad Culhuacán. Vectores Autor: Ing. Jonathan Alejandro Cortés Montes de Oca. Vectores En el campo de estudio del Cálculo
Integración sobre superficies
 Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
El espacio n. Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n :
 El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x 2,, x n ) / x 1,x 2,, x n } A cada uno de los números reales x 1,x 2,, x n que conforman
El espacio n Consideremos el conjunto de todas las n adas ordenadas de números reales, denotado por n : n = {(x 1,x 2,, x n ) / x 1,x 2,, x n } A cada uno de los números reales x 1,x 2,, x n que conforman
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 26 de Junio de 2008 Primera parte. =1, a,b > 0.
 ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
MA2112 Departamento de Matemáticas. f.ds = γ. ABC, con A(1, 0, 2), B(1, 3, 0), C(0, 1, -1) y f = (P, Q, R) = ( z, x+y, x).
 VRANO D 24 UNIVRSIDAD SIMON BOLIVAR P2A.- un segundo examen parcial de alguna fecha anterior. 1.- Calcule la integral : γ f.ds = γ Pdx+Qdy+Rdz, siendo γ la poligonal ABC, con A(1,, 2), B(1, 3, ), C(, 1,
VRANO D 24 UNIVRSIDAD SIMON BOLIVAR P2A.- un segundo examen parcial de alguna fecha anterior. 1.- Calcule la integral : γ f.ds = γ Pdx+Qdy+Rdz, siendo γ la poligonal ABC, con A(1,, 2), B(1, 3, ), C(, 1,
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Práctica 9 Campos conservativos - Teorema de Green
 ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
INDICE 1. Desigualdades 2. Relaciones, Funciones, Graficas 3. La Línea Recta 4. Introducción al Cálculo. Límites
 INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
INDICE 1. Desigualdades 1 1. Desigualdades 1 2. Valor absoluto 8 3. Valor absoluto y desigualdades 11 2. Relaciones, Funciones, Graficas 16 1. Conjunto. Notación de conjuntos 16 2. El plano coordenado.
) + t( a 1 CILINDRO. = { P = Q( u) + ta / t! u! } Γ = Q F 1 ( u), F 2 ( u), F 3. Σ cil. ,a 3 ) / t! u! } ,a 2
 CILINDRO Conjunto de puntos en el espacio en donde se genera una superficie por una recta que se mantiene siempre paralela con respecto a otra, la cual pasa por una superficie plana contenida en alguno
CILINDRO Conjunto de puntos en el espacio en donde se genera una superficie por una recta que se mantiene siempre paralela con respecto a otra, la cual pasa por una superficie plana contenida en alguno
Vectores. Capítulo Escalares y vectores Sistemas de referencia
 Capítulo 2 Vectores 2.1. Escalares y vectores Una cantidad física que pueda ser completamente descrita por un número real, en términos de alguna unidad de medida de ella, se denomina una cantidad física
Capítulo 2 Vectores 2.1. Escalares y vectores Una cantidad física que pueda ser completamente descrita por un número real, en términos de alguna unidad de medida de ella, se denomina una cantidad física
Tema 1: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 1/7 Sistemas de coordenadas
 Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte 1/7 Sistemas de coordenadas Para identificar los puntos del espacio necesitamos
Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte 1/7 Sistemas de coordenadas Para identificar los puntos del espacio necesitamos
Integrales Triples Centro de Masa y Momento de Inercia Integrales Triples en Coordenadas Cilindricas Coordenadas Cilindricas. Integrales Triples
 Integrales Triples Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 30 CONTENIDO Integrales Triples Introducción
Integrales Triples Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 30 CONTENIDO Integrales Triples Introducción
II. Algebra tensorial
 II. Algebra tensorial 2.1 Espacios de N dimensiones. Las coordenadas son un conjunto de números que se utilizan para representar un punto en el espacio; por ejemplo, en el espacio de dos dimensiones representamos
II. Algebra tensorial 2.1 Espacios de N dimensiones. Las coordenadas son un conjunto de números que se utilizan para representar un punto en el espacio; por ejemplo, en el espacio de dos dimensiones representamos
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
MATE1207 Cálculo Vectorial Tarea 2 Individual Entregue a su profesor en la Semana 11 (Ma Vi. 21 de Octubre)
 Universidad de los Andes Departamento de Matemáticas MAT27 Cálculo Vectorial Tarea 2 Individual ntregue a su profesor en la Semana (Ma. 8 - Vi. 2 de Octubre) Segundo xamen Parcial: Sábado 29 de Octubre,
Universidad de los Andes Departamento de Matemáticas MAT27 Cálculo Vectorial Tarea 2 Individual ntregue a su profesor en la Semana (Ma. 8 - Vi. 2 de Octubre) Segundo xamen Parcial: Sábado 29 de Octubre,
Empezaremos por el Álgebra lineal porque:
 Empezaremos por el Álgebra lineal porque: Las soluciones de una ecuación diferencial, como la ecuación de Schroedinger, son base de algún espacio vectorial. Las operaciones de simetría son transformaciones
Empezaremos por el Álgebra lineal porque: Las soluciones de una ecuación diferencial, como la ecuación de Schroedinger, son base de algún espacio vectorial. Las operaciones de simetría son transformaciones
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
EJERCICIOS DEL CAPÍTULO 5 - CAMPOS ESCALARES Y VECTORIALES. C5. 1 Hallar el momento del vector v respecto al punto M (2, 1, 1), siendo v = - grad φ en
 EJERCICIOS DEL CAPÍTULO 5 - CAMPOS ESCALARES Y VECTORIALES C5. 1 Hallar el momento del vector v respecto al punto M (2, 1, 1), siendo v = - grad φ en el punto P (1, 3, 0) y siendo φ=. C5. 2 Dado un campo
EJERCICIOS DEL CAPÍTULO 5 - CAMPOS ESCALARES Y VECTORIALES C5. 1 Hallar el momento del vector v respecto al punto M (2, 1, 1), siendo v = - grad φ en el punto P (1, 3, 0) y siendo φ=. C5. 2 Dado un campo
