qwertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwert yuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopa sdfghjklzxcvbnmqwertyuiopasdf
|
|
|
- Asunción Pereyra Núñez
- hace 5 años
- Vistas:
Transcripción
1 qwertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwert yuiopasdfghjklzxcvbnmqwertyui opasdfghjklzxcvbnmqwertyuiopa PROGRAMACION DE METODOS NUMERICOS sdfghjklzxcvbnmqwertyuiopasdf UNIDAD 3 SISTEMAS DE ECUACIONES LINEALES 01/03/2017 ghjklzxcvbnmqwertyuiopasdfghj M.C. ADA PAULINA MORA GONZALEZ klzxcvbnmqwertyuiopasdfghjklz xcvbnmqwertyuiopasdfghjklzxcv bnmqwertyuiopasdfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqwe rtyuiopasdfghjklzxcvbnmqwerty uiopasdfghjklzxcvbnmqwertyuio pasdfghjklzxcvbnmqwertyuiopas dfghjklzxcvbnmqwertyuiopasdfg hjklzxcvbnmqwertyuiopasdfghjk lzxcvbnmrtyuiopasdfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnmq
2 UNIDAD 3 SISTEMAS DE ECUACIONES LINEALES En la unidad anterior se determinaba el valor de x que satisface a una sola ecuación f(x)=0. Ahora se trata el caso de determinar los valores x1, x2, x3.xn, que satisfaga simultáneamente un conjunto de ecuaciones. f ( x, x,... x ) f ( x, x,... x ) f ( x, x,... x ) 0 n 1 2 En esta son de la FORMA GENERAL n n n Tales sistemas pueden ser tanto lineales como no lineales. unidad se trata de ecuaciones algebraicas lineales que a x + a x a x c n n 1 a x + a x a x c n n a x + a x a x c Donde a= son n1 1 n2 2 nn n constantes. c= son constantes. n= es el numero de ecuaciones. n coeficientes La resolución de sistemas de casi cualquier número de ecuaciones es una realidad hoy gracias a las computadoras, lo cual proporciona un atractivo especial a las técnicas de soluciones directas e iterativas. Sin embargo, todo lo anterior requiere una revisión de los conceptos básicos sobre matrices, ortogonalizacion de vectores y la existencia y unicidad de las soluciones. M.E. Ada Paulina Mora González Página 1
3 MATRICES Una matriz es un conjunto de elementos ordenados en filas y columnas como: a a + a a n + a a n... a + a a m1 m2 mn Los elementos a son números reales. Al conjunto horizontal de elementos se le llama renglón y al conjunto vertical se le llama columna. Al primer subíndice denota el número de renglón y el segundo subíndice denota la columna por ejemplo: a 21 está en el renglón 2 y columna 1. Cuando se hace referencia a una matriz es conveniente especificar el número de filas (m) y columnas(n), así la expresión m x n, indica que se trata de un matriz con m y n dimensiones. Las matrices con dimensión m=1 en el renglón como: [B]= [b1, b2,..bn] se le llama vectores de renglón. Las matrices con dimensión n=1 en la columna, como: c1 [C]= c2 cm TIPOS DE MATRICES A las matrices donde m=n se les llama matrices cuadradas. Porque tienen el mismo número de filas y columnas. Por ejemplo, una matriz 4x4 es a a a a a a a a a a a a a a a a M.E. Ada Paulina Mora González Página 2
4 Una matriz diagonal es una matriz cuadrada donde todos los elementos fuera de la diagonal principal son iguales a cero, como en [A]= a 11 a 22 a 33 a 44 Una matriz identidad es una matriz diagonal donde los elementos de la diagonal principal son iguales a 1, como en: [I]= El símbolo [I] denota la matriz identidad. Una matriz triangular superior es aquella donde todos sus elementos bajo la diagonal principal son cero, como: a a a a a a M.E. Ada Paulina Mora González Página 3
5 Una matriz triangular inferior es aquella donde todos sus elementos arriba de la diagonal principal son ceros, como: a11 a21 a22 a a a REGLAS DE OPERACIÓN SOBRE MATRICES Para sumar dos matrices A y B han de ser de las mismas dimensiones; la suma es una matriz C de iguales dimensiones que A y B, y sus elementos se obtienen sumando los elementos correspondientes de A y B. Ejemplos: Sumar las matrices y = = MULTIIPLICACION DE MATRICES POR UN ESCALAR. Se puede formar el producto de un número real y una matriz. El resultado denotado de A, es la matriz cuyos elementos de A multiplicados por. a a a a a a M.E. Ada Paulina Mora González Página 4
6 Ejemplo: Multiplicar la matriz A α= 2 PROGRAMACION DE METODOS NUMERICOS A= A MULTIPLICACION DE MATRICES Al producto escalar de a y b, esta dado por a*b, necesitamos que a y b tengan el mismo número de componentes. (a1, a2,.., an) * b1 b2.. bn = a1 b1 + a2 b an bn Ejemplo: 1. Sean a= Calcule a*b y b = Solución a*b = (1)(3) + (-2)(-2) + (3)(4)= = Sean a= (2, -3, 4, -6) y b = Calcule a*b 0 3 Solución a*b = (2)(1) + (-3)(2) +(4)(0) + (-6)(3)= = -22 M.E. Ada Paulina Mora González Página 5
7 3. Suponga que un fabricante produce 4 artículos. La demanda para los artículos está dada por el vector de demanda d= (30, 20, 40, 10). Los precios unitarios para los artículos dados por el vector de precios p= ($20, $15, $18, $40). Si satisface su demanda, Cuánto dinero recibirá el fabricante?. Solución: La demanda del primer artículo es de 30 y el fabricante recibe $20 por cada unidad vendida del primer artículo. Por lo tanto recibe, (30)(20) = $600 por la venta del primer artículo. Continuando con este razonamiento vemos que el total de dinero será de d*p. Así sus entradas son (30)(20) + (20)(15) + (40)(18) + (10)(40) = = $2020. Producto de dos matrices. Sea A=(aij) una matriz de m x n cuyo i-esimo renglón denotamos por ai. Sea B =(bij) una matriz de n x p cuya j-esima columna denotamos por bj. Entonces el producto de A y B es una matriz C= (cij) de m x p. donde cij= ai * bj Dos matrices pueden multiplicarse solo si el numero de columnas de la primera es igual al número de renglones de la segunda. A= y B= CALCULE A*B 3 Entonces c11= ( 1 3) * = 3+15 = C12= ( 1 3 ) * = = C21= (-2 4) * = = C22= (-2 4) * = = 28 6 C= Matlab A=[1 3; -2 4]; B=[3-2; 5 6]; disp('c= A*B'); disp(a*b) disp('c=b*a'); disp(b*a) PROGRAMA EN MATLAB A= [1 3; -2 4] B= [3-2; 5 6] disp( C= A*B ) C= A*B disp( C = B*A ) C=B*A M.E. Ada Paulina Mora González Página 6
8 SISTEMAS DE ECUACIONES LINEALES Objetivo: El estudiante debe ser capaz de resolver la mayor parte de problemas que impliquen utilizar ecuaciones algebraicas lineales y poder visualizar sus aplicaciones. Y debe dominar varias técnicas y valorar la confiabilidad de los mismos. Eliminación de incógnitas La eliminación de incógnitas es un esquema algebraico donde se puede ilustrar para un conjunto de ecuaciones a x + a x a x c n n 1 a x + a x a x c n n 2 Donde aij y bj, son números dados. Cada una de estas ecuaciones es la ecuación de una línea recta. Una solución al sistema es un par de números denotados (x,y). Un sistema que no tiene solución se dice que es inconsistente. Si las dos rectas no son paralelas entonces se intersectan en un solo punto y se dice que tiene una solución; si son paralelas entonces nunca se intersectan o son la misma recta se dice que no tienen solución o tienen un numero infinito de soluciones. Solución única A) Rectas no paralelas; un punto de intersección. M.E. Ada Paulina Mora González Página 7
9 Sin solución. B) Rectas paralelas; sin puntos de intersección. Numero infinito de soluciones. C) Rectas que coinciden, numero infinito de puntos de intersección. La estrategia básica es multiplicar las ecuaciones por constantes para que alguna de las incógnitas se elimine al combinar las ecuaciones. El resultado es entonces una ecuación que se pueda resolver para la incógnita restante. Este valor se puede sustituir en alguna de las ecuaciones originales para calcular la otra incógnita. M.E. Ada Paulina Mora González Página 8
10 Por ejemplo si multiplicamos la primera ecuación por a21 y la segunda ecuación por a11 tendremos: a a x a a x c a a a x a a x c a Restando ahora la segunda ecuación por la primera se elimina el término x2, de las ecuaciones para obtener: x 2 a c a a a c a a Este último resultado se puede sustituir en cualquiera de las ecuaciones originales para obtener el valor de x1. La eliminación de incógnitas se puede extender a sistemas grandes de ecuaciones, teniendo en cuenta algunas reglas básicas de operación. Este método extendido se denomina ELIMINACION GAUSSIANA, donde es fácilmente programable. ELIMINACION GAUSSIANA El procedimiento consta de dos pasos: 1. Se reduce por renglón la matriz de coeficientes a la forma escalonada por renglones, se despea el valor de la última incógnita y después se usa la sustitución hacia atrás para las demás incógnitas. La eliminación gaussiana es una de las técnicas más comunes. El procedimiento está planeado para resolver un conjunto de n ecuaciones. a x + a x a x c n n 1 a x + a x a x c n n a x + a x a x c n1 1 n2 2 nn n M.E. Ada Paulina Mora González Página 9 n
11 Eliminación hacia delante de incógnitas. La primera fase reduce el conjunto de ecuaciones a un sistema triangular superior. El paso inicial consiste en dividir la primera ecuación por el coeficiente de la primera incógnita a 11 : a a n X X... X n a11 a11 a11 c A este procedimiento se le conoce como normalización y tiene como finalidad convertir el primer coeficiente de la ecuación normalizada en 1. En seguida se multiplica la ecuación normalizada por el primer coeficiente de la segunda ecuación, a 21 a x a a X... a a n X a n 21 a11 a11 a11 Nótese que el primer término de la primera ecuación es idéntico al primer término de la segunda ecuación. Por consiguiente se puede eliminar la primera incógnita de la segunda ecuación restando la ecuación para obtener: c Ó a a n a a X... a a X c a n 21 n 2 21 a11 a11 a11 a' X... a' X c' n n 2 En donde el apostrofe indica que los elementos han cambiado su valores originales. El proceso se repite hasta que se elimina la primera incógnita de las ecuaciones restantes. La ecuación normalizada se multiplica por a31 y el resultado se resta de la tercera ecuación para obtener: c M.E. Ada Paulina Mora González Página 10
12 a' X a' X... a' X c' n n 3 Se repite el proceso para eliminar la segunda incógnita de las ecuaciones a partir de la tercera ecuación. Para hacerlo, se usa la segunda ecuación normalizándola multiplicando por el primer coeficiente de la tercera ecuación, a32 y restando este resultado de la tercera ecuación, se elimina la segunda incógnita x2. Se sigue eliminando de este modo la segunda incógnita de las restantes ecuaciones y luego se normaliza la tercera ecuación y se elimina la tercera incógnita desde la cuarta ecuación en adelante. El procedimiento se puede continuar hasta llegar a la (n-1)-esima ecuación para eliminar la incógnita Xn-1 de la n-esima ecuación. En este momento el sistema se transforma en un sistema triangular superior. a X a X a X... a X c n n 1 a ' X a ' X.. a ' X c ' n n 2 a ' X.. a ' X c '' n n 3 a (n-1) ( n 1) nn Xn c n SUSTITUCION HACIA ATRÁS La ecuación última del sistema anterior se puede resolver para Xn: a X (n-1) ( n1) nn n n n X c a c ( n1) n (n-1) nn M.E. Ada Paulina Mora González Página 11
13 Ejemplo: Por el método de Gauss resolver la siguiente matriz R1+R R1+R R2+R (1/4) R R2+R3 R2 R3 (1/3)R Sustitución hacia atrás: X3=1 X2-X3=-4 X2= -4+X3 X2= -4+1 = -3 X1+X3= 3 X1= 3 X3 X1=3 1= 2 X1=2, X2= -3, X3= 1 Algoritmo Matlab: %Método de Gauss en matriz de 3x3 format short A=input('Dame la matriz en corchete por filas: ') A(1,:)=A(1,:)/A(1,1) A(2,:)=A(2,:)-A(2,1)*A(1,:) A(3,:)=A(3,:)-A(3,1)*A(1,:) %COLUMNA 1 LISTA A(2,:)=A(2,:)/A(2,2) A(3,:)=A(3,:)-A(3,2)*A(2,:) %COLUMNA 2 LISTA A(3,:)=A(3,:)/A(3,3) disp('las INCOGNITAS SON: ') x3=a(3,4); x2=a(2,4)-a(2,3)*x3; x1=a(1,4)-a(1,2)*x2-a(1,3)*x3; disp(' x3 x2 x1 '); disp([x3 x2 x1]) M.E. Ada Paulina Mora González Página 12
14 Resuelva por el método de Gauss para encontrar las soluciones de los sistemas dados: R1 (-4)+R2 A = R1 (-2)+R3 A = R2 (1/9) A = /9-40/ R2 (-3)+R3 A = /9-40/ /3 4/3 R3 (3/4) A = /9-40/ SOLUCION UNICA X3=1 X2-13/9X3= -40/9 X2= -40/9+ 13/9(1)= X2= -3 X1-2X2+3X3= 11 X1= 11+2(-3)-3(1) X1=2 M.E. Ada Paulina Mora González Página 13
15 R1 (-1/2) A =1-1/ R1 (-5)+R2 A = 1-1/ / R1 (-3)+R3 A = 1-1/ / / R2 (2/5) A =1-1/ /5 58/5 0 7/ R2 (-7/2)+R3 A =1-1/ /5 58/ /5-83/5 R3 (-5/121) A =1-1/ /5 58/ /121 SOLUCION UNICA X3= 83/121 X2+ (46/5) X3= 58/5 X2= (58/5)-(46/5) (83/121) X2= 640/121 X1-(1/2) X2-3X3 = -9 X1= -9 + (1/2) (640/121)+3(83/121) X1= -520/121 M.E. Ada Paulina Mora González Página 14
16 R1 (1/3) A = R1 (-2)+R2 A = R1 (1)+R3 A = R2 (-1/9) A = / R2 (-18)+R3 A = / Hasta aquí se puede llegar; así que se escribe: X3 X2=8/9X3 X1=3-2X2+2X3 X1= 3-2(8/9) X3+ 2X3 X1= 3+ 2/9X3 (Para cualquier valor de X3 quedaría: Si X3=10 X2=80/9 X1=47/9 TIENE INFINITAS SOLUCIONES M.E. Ada Paulina Mora González Página 15
17 R1 (1/3) A = R1 (-2)+R2 A = R1 (-5)+R3 A = R2 (-1/9) A = / R2 (-18)+R3 A = / X3= -23 es imposible ya que EL SISTEMA NO TIENE SOLUCION. El sistema es inconsistente. M.E. Ada Paulina Mora González Página 16
18 R1 (-4)+R2 A = R1 (-2)+R3 A = R2 (-1/5) A = /5 24/ R3 (-1) A = /5 24/ SOLUCION UNICA X3= 14 X2 9/5X3= 24/5 X2= 24/5 + (9/5) (14) X2= 30 X1+ X2 X3 =7 X1= 7 X2 + X3 X1= X1= -9 M.E. Ada Paulina Mora González Página 17
19 R1 (-4)+R2 A = R1 (-6)+R3 A = R2 (-1/5) A = /5 24/ R2 (5)+R3 A = /5 24/ Hasta aquí se puede llegar; así que se escribe: X3 X2=24/5+ 9/5X3 X1=7-X2+X3 X1=7- ((24/5)+ (9/5) X3) + X3 X1= 11/5 4/5X3 (Para cualquier valor de X3 quedaría: Si X3=3 X2=51/5 X1= -1/5 TIENE INFINITAS SOLUCIONES M.E. Ada Paulina Mora González Página 18
20 R1 (-4)+R2 A = R1 (-6)+R3 A = R2 (-1/5) A = /5 24/ R2 (5)+R3 A = /5 24/ X3= -23 es imposible ya que EL SISTEMA NO TIENE SOLUCION. El sistema es inconsistente. M.E. Ada Paulina Mora González Página 19
21 R1 (-4)+R2 A = R1 (-2)+R3 A = R2 (1/9) A = / R2 (-3)+R3 A = / /3 0 R3(3/4) A = / X3=0 X2= 13/9X3 X2= 13/9(0) X2=0 X1= 2X2-3X3 X1= 0 M.E. Ada Paulina Mora González Página 20
22 Para iniciar una matriz se usa el pivoteo parcial que se selecciona el componente de la primera columna con el valor absoluto mayor, a este se le llama pivote. Se rearreaglan los renglones y empieza hacer el procedimiento de reducción de renglones. Se puede hacer el pivoteo en cada uno de los renglones consecuentes con la segunda, tercera columna sucesivamente. R3 R R1 (1/2) A = R1 (-1)+R2 A = R2 (-1/2) A = / R2 (-2)+R3 A = / R3 (1/3) A = / /3 SOLUCION UNICA X3= 11/3 X2= -5/2 X3 X2= -37/6 X1= -1-2X2 X1= -1-2(-37/6) = 34/3 M.E. Ada Paulina Mora González Página 21
23 MATRICES QUE NO SON CUADARADAS APLICANDO EL METODO DE GAUSS EN LA SOLUCION DE LOS SISTEMAS: R1 (-3) +R2 A= R2 (-1/2) A= /2 5/2 R2 (-2)+R1 A= /2 5/2 INFINITAS SOLUCIONES X2= 5/2 +1/2X3 X1= -1 X3 Es x3 una incógnita arbitraria. Se puede escoger cualquier valor. Si x3= -1 La solución seria: X3= -1 X2= 2 X1= -1 M.E. Ada Paulina Mora González Página 22
24 R1 (2)+R2 A= TIENE INFINITAS SOLUCIONES Hasta aquí se puede llegar; así que se escribe: (Para cualquier valor de X3, X2 quedaría: X3, X2 pueden tomar cualquier valor X1= 4-2X2+ 4X3 Si x2=2 y X3= 4 X1= 16 (16, 2,4) R1 (2)+R2 A= X3= -1 es imposible ya que 0 EL SISTEMA NO TIENE SOLUCION. El sistema es inconsistente. M.E. Ada Paulina Mora González Página 23
25 R1 (1/2) R1 (-1)+R2 R1 (3)+R R2 (-1/3) R2 (-11)+R3 R2 (-3)+R / / R3 (-3/13) / /13-45/13 SOLUCION INFINITA X4 es arbitraria puede tomar cualquier valor. X3= -45/13 +9/13X4 X2= -1 +1/3 x3 X2= /3(-45/13 + 9/13x14) X2= -28/13 +3/13X4 X1= 5 +X3 X4 X1= 5 + (-45/13 +9/13X4) X4 X1= 20/13-4/13X4 SI X4 = -2 X3=-63/13 X2= -34/13 X1= 28/13 (28/13, -34/13, -63/13, -2) M.E. Ada Paulina Mora González Página 24
26 DIFICULTADES EN LOS METODOS DE ELIMINACION Hay muchos sistemas de ecuaciones que se pueden resolver con la eliminación de Gauss simple, existen algunas dificultades. DIVISION ENTRE CERO Durante las fases de eliminación y sustitución hacia atrás es posible que ocurra una división entre cero. También se pueden presentar problemas cuando un coeficiente esta muy cercano a cero. La técnica de pivoteo se ha desarrollado para evitar en forma parcial estos problemas. ERRORES DE REDONDEO Cuando se usan números decimales, existe una pequeña discrepancia en el resultado. Se debe al uso de cifras significativas que se manejan durante los cálculos. Si se usan mas cifras significativas, el error en los resultados se reduce considerablemente. SISTEMAS MAL CONDICIONADOS Los sistemas bien condicionados son aquellos en los que un pequeño cambio en uno o más coeficientes provoca un cambio similarmente pequeño en la solución. Y los sistemas mal condicionados son aquellos en donde pequeños cambios en los coeficientes generan grandes cambios en la solución. M.E. Ada Paulina Mora González Página 25
27 METODO DE GAUSS- JORDAN Este método es una variación de la eliminación de Gauss. La principal diferencia es que cuando una incógnita se elimina en el método de Gauss-Jordán, esta se elimina de todas las otras ecuaciones. Además todos los renglones se normalizan al dividirlos entre su elemento pivote. De esta forma, el paso de eliminación genera una matriz identidad en vez de una triangular. No es necesario usar la sustitución hacia atrás para obtener la solución. Aunque el método de Gauss-Jordán y de eliminación gaussiana puede parecer casi idéntico, el primero requiere el 50% más de operaciones. Por lo tanto la eliminación gaussiana es el método por excelencia para la obtención de soluciones exactas de los sistemas de ecuaciones lineales. En un sistema de 3 ecuaciones lineales como el que se muestra se hizo: 1. Se dividió la primera ecuación para hacer el coeficiente de x1 en ella, igual a 1-2. Se eliminaron los términos en x1 de la segunda y tercera ecuaciones. Esto es, los coeficientes de estos términos se hicieron cero multiplicando la primera ecuación por los números adecuados y sumándola a la segunda y tercera ecuación. 3. Se dividió la segunda ecuación para hacer el coeficiente x2 igual a 1 y después se uso la segunda ecuación para eliminar los términos en x2 de la primera y tercera ecuación. 4. Se dividió la tercera ecuación para hacer el coeficiente de x3 igual a 1 y después se uso esta tercera ecuación para eliminar los términos en x3 de la primera y segunda ecuación. M.E. Ada Paulina Mora González Página 26
28 EJEMPLO: Use el método de Gauss-Jordán para resolver el problema: [ ] -4R1+R Solución: -2R1+R X1= -9, X2= 30, X3= 14 (-1/5)R /5 11/5-1R2+R /5 24/ (-4/5)R3+R (9/5)R3+R R Algoritmo en Matlab: %Método de Gauss-Jordán en matriz de 3x3 format rat A=input('Dame la matriz en corchete por filas: ') %HACER UNO EL PRIMER TERMINO A(1,1) Y HACER CEROS LOS TERMINOSA(2,1) Y A(3,1) A(1,:)=A(1,:)/A(1,1) A(2,:)=A(2,:)-A(2,1)*A(1,:) A(3,:)=A(3,:)-A(3,1)*A(1,:) %HACER UNO EL TERMINO A(2,2) Y HACER CEROS LOS TERMINOSA(1,2) Y A(3,2) A(2,:)=A(2,:)/A(2,2) A(1,:)=A(1,:)-A(1,2)*A(2,:) A(3,:)=A(3,:)-A(3,2)*A(2,:) %HACER UNO EL TERCER TERMINO A(3,3) Y HACER CEROS LOS TERMINOSA(1,3) Y A(2,3) A(3,:)=A(3,:)/A(3,3) A(1,:)=A(1,:)-A(1,3)*A(3,:) A(2,:)=A(2,:)-A(2,3)*A(3,:) M.E. Ada Paulina Mora González Página 27
29 EJEMPLO DE APLICACIONES Ejemplo 1 Suponga que un fabricante produce 4 artículos. La demanda para los artículos está dada por el vector de demanda d= (30, 20, 40, 10). Los precios unitarios para los artículos dados por el vector de precios p= ($20, $15, $18, $40). Si satisface su demanda, Cuánto dinero recibirá el fabricante?. Solución: La demanda del primer artículo es de 30 y el fabricante recibe $20 por cada unidad vendida del primer artículo. Por lo tanto recibe, (30)(20) = $600 por la venta del primer artículo. Continuando con este razonamiento vemos que el total de dinero será de d*p. Así sus entradas son (30)(20) + (20)(15) + (40)(18) + (10)(40) = = $2020. Ejemplo 2 Un departamento de pesca y caza del estado proporciona 3 tipos de comida a un lago que alberga a tres especies de peces. Cada pez de la especie 1 consume cada semana un promedio de 1 unidad del alimento 1, 1 unidad del alimento 2 y 2 unidades del alimento 3. Cada pez de la especie 2 consume cada semana un promedio de 3 unidades del alimento 1, 4 del 2 y 5 del 3. Para un pez de la especie 3, el promedio semanal de consumo es 2 unidades del alimento 1, 1 unidad del alimento 2 y 5 unidades del 3. Cada semana se proporciona al lago unidades de alimento 1, unidades del alimento 2 y del 3. Si se supone que los peces comen todo el alimento. Cuántos peces de cada especie pueden coexistir en el lago? Solución: Sean x1, x2, y x3 el numero de peces de cada especie que hay en el lago. Utilizando la información del problema, se observa que x1 peces de la especie 1 consumen x1 unidades del alimento 1, x2 peces de la especie 2 consumen 3x2 del alimento 1. Entonces x1 + 3x2 + 2x3 = = suministro total por semana del alimento 1. Si se obtiene una ecuación similar para los otros dos alimentos se llega a: x 3x 2x x 4x x x 5x 5x M.E. Ada Paulina Mora González Página 28
30 Después de resolver se obtiene R1(-1)+R2 R1(-2)+R R2(-3) + R1 R2 + R Se tiene un número infinito de soluciones X1= x3 X2= x <x3< 8000 M.E. Ada Paulina Mora González Página 29
31 Un ingeniero supervisa la producción de 4 tipos de computadoras. Se requieren 4 clases de recursos: horas/hombre, metales, plásticos y componentes electrónicos; en la producción. Se resumen las cantidades necesarias para cada uno de estos recursos en la producción de cada tipo de computadora. Si se dispone diariamente de 504 horas / hombre, 1970kg de metal, 970 kg de plástico y 601 componentes electrónicos. Cuántas computadoras de cada tipo se puede construir por día? Cuál seria la ganancia por cada computadora producida. Y el total de ganancia? Computadora Horas-hombre Metales kg/computadora Plásticos kg/computad. Componentes, u/computadora La cantidad producida de cada computadora esta restringida al total de recursos disponibles en cada categoría diariamente. Estos recursos totales se distribuyen entre los 4 tipos de computadoras. Sea x1, x2, x3, x4 la cantidad total de computadoras producidas diariamente de cada clase. Se sabe que la cantidad total de horas/hombre es de 504. Por lo tanto, la suma de las distribuciones de horas-hombres en la producción de cada uno de las computadoras debe ser menor o igual a 504. Ganancias por cada computadora 3x 4x 7x 20x En los recursos de material quedaria: 20x 25x 40x 50x x 15x 20x 22x x 8x 10x 15x Computad. $ M.E. Ada Paulina Mora González Página 30
32 Solución con el Algoritmo en Matlab: %Método de Gauss-Jordán en matriz de 4x4 format short B=input('Dame la matriz en corchete por filas') s=length(b) if s==5 B(1,:)=B(1,:)/B(1,1) B(2,:)=B(2,:)-B(2,1)*B(1,:) B(3,:)=B(3,:)-B(3,1)*B(1,:) B(4,:)=B(4,:)-B(4,1)*B(1,:) %COLUMNA 1 LISTA B(2,:)=B(2,:)/B(2,2) B(1,:)=B(1,:)-B(1,2)*B(2,:) B(3,:)=B(3,:)-B(3,2)*B(2,:) B(4,:)=B(4,:)-B(4,2)*B(2,:) %COLUMNA 2 LISTA B(3,:)=B(3,:)/B(3,3) B(1,:)=B(1,:)-B(1,3)*B(3,:) B(2,:)=B(2,:)-B(2,3)*B(3,:) B(4,:)=B(4,:)-B(4,3)*B(3,:) %COLUMNA 3 LISTA B(4,:)=B(4,:)/B(4,4) B(1,:)=B(1,:)-B(1,4)*B(4,:) B(2,:)=B(2,:)-B(2,4)*B(4,:) B(3,:)=B(3,:)-B(3,4)*B(4,:) else disp('la matriz original no es de 4x4') end M.E. Ada Paulina Mora González Página 31
33 B = B = 1 4/3 7/3 20/ B = 1 4/3 7/3 20/ /3-20/3-250/ B = 1 4/3 7/3 20/ /3-20/3-250/ /3-10/3-134/ B = 1 4/3 7/3 20/ /3-20/3-250/ /3-10/3-134/ /3-40/3-155/ B = 1 4/3 7/3 20/ /3-10/3-134/ /3-40/3-155/ B = /3-10/3-134/ /3-40/3-155/ B = / B = / / B = / / / B = / / / / B = / / / B = / / B = / B = B = /3-40/3-155/ B = M.E. Ada Paulina Mora González Página 32
34 METODO GAUSS-SEIDEL Es un método iterativo que es una alternativa a los métodos de eliminación, para aproximar la solución. Este método es el más comúnmente usado. Para una matriz de 3x3, y los elementos de la diagonal principal no son todos ceros, se inicia con las primeras ecuaciones donde a x2 y x3 se les da como valor inicial cero ya después los resultados calculados se utilizan en cada ecuación a resolver. (Si la matriz aumenta de tamaño se usa el mismo procedimiento agregando la ecuación respectiva) (0.1) c1 a12x2 a13x3 x1 a 11 x 2 c a x a x a x 3 c a x a x a Se saca el error aproximado para cada valor de x1, x2, x3. Ejemplo: Use el método de Gauss-Seidel para obtener la solución del sistema: 3x 0.1x 0.2x x 7x 0.3x x 0.2x 10x Primero despejar la incógnita sobre la diagonal para cada una de las ecuaciones x2 0.2x3 x1 3 x x 0.3x x10.2x2 x3 10 M.E. Ada Paulina Mora González Página 33
35 Suponiendo que x2 y x3 al iniciar el cálculo de x1 valdrían cero, y se utilizaría: x x ( ) Se sustituye el valor x1 ya calculado x ( ) 0.2( ) Se sustituye el valor de x1 y x2 ya calculados anteriormente. Esa sería la primera iteración y se procedería a hacer las iteraciones que se necesiten y con el último valor calculado se tomara en cuenta para la nueva sustitución ( ) 0.2( ) x x ( ) 0.( ) x ( ) 0.2( ) Conforme un nuevo valor de x se calcula este se usa inmediatamente en la siguiente ecuación para determinar el otro valor de x. M.E. Ada Paulina Mora González Página 34
36 METODO INVERSA CON GAUSS-JORDAN El cálculo de la matriz inversa por el método de Gauss supone transformar una matriz en otra, equivalente por filas. La demostración rigurosa del procedimiento que a continuación se describe se sale del propósito del presente bloque, aquí se limita a su exposición y comprobación de que efectivamente se obtiene la matriz inversa. En esencia, el método consiste, para una matriz cuadrada de orden n, en: 1. Formar una matriz de orden nx2n tal que las primeras columnas sean las de la matriz A y las otras n las de la matriz identidad de orden n. Mediante las transformaciones elementales de las filas de una matriz, convertir la matriz anterior en otra que tenga en las n primeras columnas la matriz identidad y en las n últimas otra matriz que precisamente será A -1. El método consiste, pues, en colocar juntas la matriz a invertir, y la matriz identidad. (( )) ( ) Por medio de transformaciones elementales, vamos modificando nuestra matriz hasta obtener la matriz identidad. Cada paso que apliquemos a la matriz se lo aplicaremos a la matriz identidad. Cuando hayamos obtenido la matriz identidad, la de la derecha será la inversa. Si no podemos llegar a la matriz identidad (por ejemplo, sale alguna fila de ceros), significa que la matriz no será inversible. Vamos a ver dos ejemplos, uno en el que se puede obtener la inversa y otro en el que la matriz no es inversible. Ojo a lo siguiente, pues es muy importante: hemos de decidir si haremos nuestras transformaciones elementales por filas o por columnas, pues la forma que elijamos debe mantenerse a lo largo de todo el proceso de inversión de la matriz. Las transformaciones elementales son las siguientes: substituir una fila o columna de la matriz por ella misma multiplicada (o dividida) por un número, substituir una fila o columna de la matriz por una combinación lineal de filas o columnas de la matriz (si es fila, filas, y si es columna, columnas), e intercambiar filas o columnas. Por simplicidad en la notación, c indicará columna (ej., 1ª c es 1ª columna) y f indicará fila (ej., 3ª f es 3ª fila). M.E. Ada Paulina Mora González Página 35
37 METODO DE REGLA DE CRAMER Es un método basado en la solución de determinantes que se utiliza para resolver sistemas de ecuaciones lineales con dos o más incógnitas. Para calcular el valor de cada una de las incógnitas del sistema, se resuelve un determinante para cada una de ellas y se divide entre el determinante general. Cuando se plantea el determinante de una incógnita, se elimina la columna de los coeficientes de esa incógnita y se sustituye por la columna de los valores constantes a los que están igualadas las ecuaciones. M.E. Ada Paulina Mora González Página 36
PROGRAMACION DE METODOS NUMERICOS
 PROGRAMACION DE METODOS NUMERICOS UNIDAD 3 M.E. ADA PAULINA MORA GONZALEZ UNIDAD 3 SISTEMAS DE ECUACIONES LINEALES En la unidad anterior se determinaba el valor de x que satisface a una sola ecuación f(x)=0.
PROGRAMACION DE METODOS NUMERICOS UNIDAD 3 M.E. ADA PAULINA MORA GONZALEZ UNIDAD 3 SISTEMAS DE ECUACIONES LINEALES En la unidad anterior se determinaba el valor de x que satisface a una sola ecuación f(x)=0.
SISTEMAS DE ECUACIONES LINEALES Y MATRICES Dos ecuaciones lineales con dos
 de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive
de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive
Elementos de una matriz.
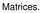 Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
SISTEMAS DE ECUACIONES LINEALES
 APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA SISTEMAS DE ECUACIONES LINEALES REGLA DE CRAMER Esta regla establece que cada incógnita de un sistema de ecuaciones lineales algebraicas puede
APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA SISTEMAS DE ECUACIONES LINEALES REGLA DE CRAMER Esta regla establece que cada incógnita de un sistema de ecuaciones lineales algebraicas puede
Matrices y determinantes
 Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES
 57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
 INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Las matrices se denotarán usualmente por letras mayúsculas, A, B,..., y los elementos de las mismas por minúsculas, a, b,...
 INTRO. MATRICES Y DETERMINANTES Prof. Gustavo Sosa Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas
INTRO. MATRICES Y DETERMINANTES Prof. Gustavo Sosa Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales José Vicente Romero Bauset ETSIT-curso 2009/200 José Vicente Romero Bauset Tema 2.- Sistemas de Ecuaciones Lineales Sistema de ecuaciones lineales Un sistema de ecuaciones
Sistemas de Ecuaciones Lineales José Vicente Romero Bauset ETSIT-curso 2009/200 José Vicente Romero Bauset Tema 2.- Sistemas de Ecuaciones Lineales Sistema de ecuaciones lineales Un sistema de ecuaciones
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS
 UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
 Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Vectores en el plano UNIDAD I: MATRICES. Dirección de un vector. Sentido de un vector
 UNIDAD I: MATRICES Vectores en el plano Un vector,, es un segmento con una dirección que va del punto A (origen) al punto B (etremo).un vector es un segmento orientado que va del punto A (origen) al punto
UNIDAD I: MATRICES Vectores en el plano Un vector,, es un segmento con una dirección que va del punto A (origen) al punto B (etremo).un vector es un segmento orientado que va del punto A (origen) al punto
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Matemáticas Aplicadas a los Negocios
 LICENCIATURA EN NEGOCIOS INTERNACIONALES Matemáticas Aplicadas a los Negocios Unidad 4. Aplicación de Matrices OBJETIVOS PARTICULARES DE LA UNIDAD Al finalizar esta unidad, el estudiante será capaz de:
LICENCIATURA EN NEGOCIOS INTERNACIONALES Matemáticas Aplicadas a los Negocios Unidad 4. Aplicación de Matrices OBJETIVOS PARTICULARES DE LA UNIDAD Al finalizar esta unidad, el estudiante será capaz de:
Unidad 1 Álgebra de matrices
 Unidad Álgebra de matrices Objetivos Al nalizar la unidad, el alumno: Conocerá qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones básicas
Unidad Álgebra de matrices Objetivos Al nalizar la unidad, el alumno: Conocerá qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones básicas
DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES
 ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
Procedimiento para encontrar la inversa de una matriz cuadrada (Método de Gauss-Jordan).
 Ejemplo 19: Demuestre que la matriz A es invertible y escríbala como un producto de matrices elementales. Solución: Para resolver el problema, se reduce A a I y se registran las operaciones elementales
Ejemplo 19: Demuestre que la matriz A es invertible y escríbala como un producto de matrices elementales. Solución: Para resolver el problema, se reduce A a I y se registran las operaciones elementales
Sistemas lineales de ecuaciones
 Sistemas lineales de ecuaciones Conceptos previos a) Sistemas de ecuaciones lineales. b) Solución de un sistema. c) Sistemas triangulares. Resolución de sistemas Métodos directos a) Método de eliminación
Sistemas lineales de ecuaciones Conceptos previos a) Sistemas de ecuaciones lineales. b) Solución de un sistema. c) Sistemas triangulares. Resolución de sistemas Métodos directos a) Método de eliminación
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO FACULTAD DE ECONOMIA LICENCIATURA DE ACTUARIA Algebra Lineal Práctica: Matriz inversa 1 M. en I. Elizabeth Almazán Torres 2 Resultado de Aprendizaje El estudiante
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO FACULTAD DE ECONOMIA LICENCIATURA DE ACTUARIA Algebra Lineal Práctica: Matriz inversa 1 M. en I. Elizabeth Almazán Torres 2 Resultado de Aprendizaje El estudiante
Sistema de ecuaciones lineales
 1 El sistema de ecuaciones lineales Sistema de ecuaciones lineales puede ser escrito en forma matricial como, donde: es llamada matriz de los coeficientes (reales) del sistema es el vector de las incógnitas
1 El sistema de ecuaciones lineales Sistema de ecuaciones lineales puede ser escrito en forma matricial como, donde: es llamada matriz de los coeficientes (reales) del sistema es el vector de las incógnitas
Algebra lineal Matrices
 Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
Matrices y determinantes
 Matrices y determinantes 1 Matrices Una matriz de orden m n es un conjunto de m n números ordenados en m filas y n columnas Por ejemplo, 1 1 2 0 2 0 2 1 1 1 2 1 3 0 2 es una matriz de orden 3 5 Una matriz
Matrices y determinantes 1 Matrices Una matriz de orden m n es un conjunto de m n números ordenados en m filas y n columnas Por ejemplo, 1 1 2 0 2 0 2 1 1 1 2 1 3 0 2 es una matriz de orden 3 5 Una matriz
Matrices, determinantes y sistemas de ecuaciones lineales
 Capítulo 4 Matrices, determinantes y sistemas de ecuaciones lineales DEFINICIÓN DE MATRIZ DE NÚMEROS REALES Una matriz de números reales de tamaño m n es un conjunto ordenado por filas y columnas de números
Capítulo 4 Matrices, determinantes y sistemas de ecuaciones lineales DEFINICIÓN DE MATRIZ DE NÚMEROS REALES Una matriz de números reales de tamaño m n es un conjunto ordenado por filas y columnas de números
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
Sistemas de ecuaciones lineales
 Chapter 2 Sistemas de ecuaciones lineales 2.1 Resolución de sistemas de ecuaciones lineales El problema que se pretende resolver en este capítulo es el de un sistema de m ecuaciones lineales con n incógnitas
Chapter 2 Sistemas de ecuaciones lineales 2.1 Resolución de sistemas de ecuaciones lineales El problema que se pretende resolver en este capítulo es el de un sistema de m ecuaciones lineales con n incógnitas
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
MATRICES. Jaime Garrido Oliver
 MATRICES Jaime Garrido Oliver ÍNDICE DE CONTENIDOS ÍNDICE DE CONTENIDOS... 2 MATRICES... 3 1.1. INTRODUCCIÓN.... 3 2. TIPOS DE MATRICES... 4 2.1. Matriz Fila, Matriz Columna... 4 2.2. Matrices cuadradas...
MATRICES Jaime Garrido Oliver ÍNDICE DE CONTENIDOS ÍNDICE DE CONTENIDOS... 2 MATRICES... 3 1.1. INTRODUCCIÓN.... 3 2. TIPOS DE MATRICES... 4 2.1. Matriz Fila, Matriz Columna... 4 2.2. Matrices cuadradas...
MATRICES. Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas. o simplemente A = (a.
 MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
MATRICES Se denomina matriz de dimensión m n a todo conjunto cuyos elementos están dispuestos en m filas y n columnas A= 2 1 5 0 3 8 A es de dimensión 2 3. a a a En general una matriz de dimensión 2 3
Programa EUROPA Ayuda a la Mejora en el Aprendizaje Matemáticas Cuarta sesión
 1/26 Programa EUROPA Ayuda a la Mejora en el Aprendizaje Matemáticas Cuarta sesión Ramón Esteban y Antonio Pastor Índice 1 Álgebra 3 Sistemas de ecuaciones lineales................ 3 Métodos conocidos...................
1/26 Programa EUROPA Ayuda a la Mejora en el Aprendizaje Matemáticas Cuarta sesión Ramón Esteban y Antonio Pastor Índice 1 Álgebra 3 Sistemas de ecuaciones lineales................ 3 Métodos conocidos...................
Sistema de ecuaciones algebraicas. Eliminación de Gauss.
 Sistema de ecuaciones algebraicas. Eliminación de Gauss. Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com
Sistema de ecuaciones algebraicas. Eliminación de Gauss. Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com
Matrices 1. Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.
 Matrices 1 Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se
Matrices 1 Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se
Introducción a Matrices y Eliminación Gaussiana
 Introducción a Matrices y Eliminación Gaussiana 1 Sistema de Ecuaciones Matricial 2 Definición Una matriz es un arreglo rectangular de valores llamados elementos, organizados por filas y columnas. Ejemplo:
Introducción a Matrices y Eliminación Gaussiana 1 Sistema de Ecuaciones Matricial 2 Definición Una matriz es un arreglo rectangular de valores llamados elementos, organizados por filas y columnas. Ejemplo:
Estos apuntes se han sacado de la página de internet de vitutor con pequeñas modificaciones.
 TEMA 1: MATRICES Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
TEMA 1: MATRICES Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Matrices 3. Matrices. Verónica Briceño V. agosto 2012
 3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Matrices. Primeras definiciones
 Primeras definiciones Una matriz es un conjunto de elementos números ordenado en filas y columnas. En general una matriz se nombra con una letra mayúscula y a sus elementos con letras minúsculas indicando
Primeras definiciones Una matriz es un conjunto de elementos números ordenado en filas y columnas. En general una matriz se nombra con una letra mayúscula y a sus elementos con letras minúsculas indicando
MATEMÁTICAS 2º BACH TECNOL. MATRICES. Profesor: Fernando Ureña Portero MATRICES
 CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
Tema 1: MATRICES. OPERACIONES CON MATRICES
 Tema 1: MATRICES. OPERACIONES CON MATRICES 1. DEFINICIÓN Y TIPO DE MATRICES DEFINICIÓN. Una matriz es un conjunto de números reales dispuestos en filas y columnas. Si en ese conjunto hay m n números escritos
Tema 1: MATRICES. OPERACIONES CON MATRICES 1. DEFINICIÓN Y TIPO DE MATRICES DEFINICIÓN. Una matriz es un conjunto de números reales dispuestos en filas y columnas. Si en ese conjunto hay m n números escritos
Matrices y Determinantes. Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC
 Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
SISTEMAS DE ECUACIONES LINEALES. Método de reducción o de Gauss. 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González.
 SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
TEMA 1: MATRICES Y DETERMINANTES
 TEMA 1: MATRICES Y DETERMINANTES 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales de la forma a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Las líneas horizontales (verticales)
TEMA 1: MATRICES Y DETERMINANTES 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales de la forma a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Las líneas horizontales (verticales)
ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA
 UNIDAD OBJETIVO: Resolverá situaciones y problemas en los que se apliquen ecuaciones de primer grado con una incógnita, sistemas de ecuaciones lineales con dos y tres incógnitas, mediante métodos algebraicos
UNIDAD OBJETIVO: Resolverá situaciones y problemas en los que se apliquen ecuaciones de primer grado con una incógnita, sistemas de ecuaciones lineales con dos y tres incógnitas, mediante métodos algebraicos
Matrices y sistemas de ecuaciones
 Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
MATRICES. Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
 1 MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos horizontales
1 MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos horizontales
MATRICES. TIPOS DE MATRICES Según el aspecto de las matrices, éstas pueden clasificarse en:
 Repaso de Matrices MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos
Repaso de Matrices MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos
INFORMÁTICA MATLAB GUÍA 3 Operaciones con Matrices
 1. ARREGLOS BIDIMENSIONALES (MATRICES) A las matrices también se les conoce como arreglos bidimensionales, y son una colección de números distribuidos en filas y columnas: Usos de las matrices: Electricidad
1. ARREGLOS BIDIMENSIONALES (MATRICES) A las matrices también se les conoce como arreglos bidimensionales, y son una colección de números distribuidos en filas y columnas: Usos de las matrices: Electricidad
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2
 ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS
 1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
puede representarse algebraicamente por una ecuación de la forma
 SISTEMA DE ECUACIONES LINEALES El estudio de los sistemas de ecuaciones lineales y sus soluciones es uno de los temas más importantes del algebra lineal. ECUACIONES LINEALES Una recta en el plano puede
SISTEMA DE ECUACIONES LINEALES El estudio de los sistemas de ecuaciones lineales y sus soluciones es uno de los temas más importantes del algebra lineal. ECUACIONES LINEALES Una recta en el plano puede
Lección 10. Eliminación Gaussiana
 Lección 10. Eliminación Gaussiana MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida. En esta lección analizaremos
Lección 10. Eliminación Gaussiana MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida. En esta lección analizaremos
Matrices 2º curso de Bachillerato Ciencias y tecnología
 MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
Matrices y Determinantes. Un ejemplo: mezcla de fertilizantes
 Matrices y Determinantes Las matrices y los determinantes son objetos matemáticos que permiten simplificar la notación convencional para resolver sistemas de ecuaciones lineales. Por otra parte estos objetos
Matrices y Determinantes Las matrices y los determinantes son objetos matemáticos que permiten simplificar la notación convencional para resolver sistemas de ecuaciones lineales. Por otra parte estos objetos
RESOLUCIÓN DE SISTEMAS LINEALES
 Contenido 1 Métodos de Solución Contenido Métodos de Solución 1 Métodos de Solución Desarrollamos el algoritmo de sustitución regresiva, con el que podremos resolver un sistema de ecuaciones lineales cuya
Contenido 1 Métodos de Solución Contenido Métodos de Solución 1 Métodos de Solución Desarrollamos el algoritmo de sustitución regresiva, con el que podremos resolver un sistema de ecuaciones lineales cuya
Matrices Invertibles y Elementos de Álgebra Matricial
 Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CSI/ITESM 20 de agosto de 2008 Índice 121 Introducción 1 122 Transpuesta 1 123 Propiedades de la transpuesta 2 124 Matrices
Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CSI/ITESM 20 de agosto de 2008 Índice 121 Introducción 1 122 Transpuesta 1 123 Propiedades de la transpuesta 2 124 Matrices
SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
Lección 8. Matrices y Sistemas de Ecuaciones Lineales
 Lección 8 Matrices y Sistemas de Ecuaciones Lineales MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En
Lección 8 Matrices y Sistemas de Ecuaciones Lineales MIGUEL ANGEL UH ZAPATA 1 Análisis Numérico I Facultad de Matemáticas, UADY Septiembre 2014 1 Centro de Investigación en Matemáticas, Unidad Mérida En
Propiedades de los Determinantes
 Propiedades de los Determinantes Departamento de Matemáticas, CCIR/ITESM 26 de mayo de 2010 Índice 19.1. Propiedades............................................... 1 19.2. La adjunta de una matriz cuadrada..................................
Propiedades de los Determinantes Departamento de Matemáticas, CCIR/ITESM 26 de mayo de 2010 Índice 19.1. Propiedades............................................... 1 19.2. La adjunta de una matriz cuadrada..................................
Simulacion Numerica / Metodos Numericos. Unidad III Solución de Ecuaciones Lineales. Ing. Deny González Msc.
 Unidad III Solución de Ecuaciones Lineales Contenido Introducción. Métodos Alternativos para Pequeños Sistemas Método Grafico Regla de Cramer Eliminación de Incógnitas. Eliminación de Gauss Simple Descomposición
Unidad III Solución de Ecuaciones Lineales Contenido Introducción. Métodos Alternativos para Pequeños Sistemas Método Grafico Regla de Cramer Eliminación de Incógnitas. Eliminación de Gauss Simple Descomposición
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
 CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
Tema 5: Sistemas de ecuaciones lineales.
 TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
TEORÍA DE ÁLGEBRA: Tema 5 DIPLOMATURA DE ESTADÍSTICA 1 Tema 5: Sistemas de ecuaciones lineales 1 Definiciones generales Definición 11 Una ecuación lineal con n incognitas es una expresión del tipo a 1
Matrices. En este capítulo: matrices, determinantes. matriz inversa
 Matrices En este capítulo: matrices, determinantes matriz inversa 1 1.1 Matrices De manera informal una matriz es un rectángulo de números dentro de unos paréntesis. A = a 1,1 a 1,2 a 1,3 a 2,1 a 2,2 a
Matrices En este capítulo: matrices, determinantes matriz inversa 1 1.1 Matrices De manera informal una matriz es un rectángulo de números dentro de unos paréntesis. A = a 1,1 a 1,2 a 1,3 a 2,1 a 2,2 a
4.1. Determinante de una matriz cuadrada de orden 2. , entonces el determinante de A es a 21 a 22 a 11 a 12 = a 11a 22 a 12 a 21
 Capítulo 4 Determinante Los determinantes se calculan para matrices cuadradas. Se usan para saber cuando una matriz tiene inversa, en el cálculo de autovalores y también para resolver sistemas de ecuaciones
Capítulo 4 Determinante Los determinantes se calculan para matrices cuadradas. Se usan para saber cuando una matriz tiene inversa, en el cálculo de autovalores y también para resolver sistemas de ecuaciones
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Estrategias de pivoteo
 Estrategias de pivoteo Objetivos. Resolver sistemas de ecuaciones lineales aplicando varias técnicas de pivoteo; programar estos algoritmos. Requisitos. Operaciones elementales, experiencia de resolver
Estrategias de pivoteo Objetivos. Resolver sistemas de ecuaciones lineales aplicando varias técnicas de pivoteo; programar estos algoritmos. Requisitos. Operaciones elementales, experiencia de resolver
ÁLGEBRA DE MATRICES TRASPUESTA DE UNA MATRIZ SUMA Y RESTA DE MATRICES
 ÁLGEBRA DE MATRICES TRASPUESTA DE UNA MATRIZ La traspuesta de una matriz A consiste en intercambiar las filas por las columnas (o las columnas por las filas) y se denota por: A T Así, la traspuesta de
ÁLGEBRA DE MATRICES TRASPUESTA DE UNA MATRIZ La traspuesta de una matriz A consiste en intercambiar las filas por las columnas (o las columnas por las filas) y se denota por: A T Así, la traspuesta de
Sistemas de Ecuaciones Lineales - Métodos Directos -
 Sistemas de Ecuaciones Lineales - Métodos Directos - Contenido Solución de Sistemas de Ecuaciones Sistema de Ecuaciones Método de la Matriz Inversa Método de Cramer Método de Gauss-Jordan Método de Montante
Sistemas de Ecuaciones Lineales - Métodos Directos - Contenido Solución de Sistemas de Ecuaciones Sistema de Ecuaciones Método de la Matriz Inversa Método de Cramer Método de Gauss-Jordan Método de Montante
11.SISTEMAS DE ECUACIONES LINEALES DEFINICIÓN DE ECUACIÓN LINEAL DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN
 ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
PRÁCTICA 3: MATLAB Y LA FORMA REDUCIDA POR FILAS
 PRÁCTICA 3: MATLAB Y LA FORMA REDUCIDA POR FILAS Introducción En esta práctica aprenderemos a manejar el comando rref de MATLAB, que calcula la forma reducida por filas de una matriz; también se verán
PRÁCTICA 3: MATLAB Y LA FORMA REDUCIDA POR FILAS Introducción En esta práctica aprenderemos a manejar el comando rref de MATLAB, que calcula la forma reducida por filas de una matriz; también se verán
APUNTES ALGEBRA SUPERIOR
 1-1-016 APUNTES ALGEBRA SUPERIOR Apuntes del Docente Esp. Pedro Alberto Arias Quintero. Departamento De Ciencias Básicas, Unidades Tecnológicas de Santander. Contenido MATRICES Y DETERMINANTES... ELEMENTOS
1-1-016 APUNTES ALGEBRA SUPERIOR Apuntes del Docente Esp. Pedro Alberto Arias Quintero. Departamento De Ciencias Básicas, Unidades Tecnológicas de Santander. Contenido MATRICES Y DETERMINANTES... ELEMENTOS
MATRICES DETERMINANTES
 MATRICES Y DETERMINANTES INTRODUCCIÓN, MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de
MATRICES Y DETERMINANTES INTRODUCCIÓN, MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de
INGENIERO EN COMPUTACION TEMA: SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: SISTEMAS DE ECUACIONES LINEALES Y MATRICES ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: ENERO
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: SISTEMAS DE ECUACIONES LINEALES Y MATRICES ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: ENERO
TEMA V. Pues bien, a estas caracterizaciones de los sistemas de ecuaciones lineales se las llamó matrices. En el caso del sistema considerado tenemos:
 TEMA V 1. MATRICES Y SISTEMAS DE ECUACIONES LINEALES. Sea el siguiente sistema de ecuaciones lineales: Realmente quien determina la naturaleza y las soluciones del sistema, no son las incógnitas: x, y,
TEMA V 1. MATRICES Y SISTEMAS DE ECUACIONES LINEALES. Sea el siguiente sistema de ecuaciones lineales: Realmente quien determina la naturaleza y las soluciones del sistema, no son las incógnitas: x, y,
Matrices, determinantes y sistemas de ecuaciones lineales
 Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
Matrices, determinantes y sistemas de ecuaciones lineales David Ariza-Ruiz 10 de octubre de 2012 1 Matrices Una matriz es una tabla numérica rectangular de m filas y n columnas dispuesta de la siguiente
ELEMENTOS DE ALGEBRA LINEAL
 ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
Se llama adjunto de un elemento de una matriz A, al número resultante de multiplicar por el determinante de la matriz complementaria
 T.3: MATRICES Y DETERMINANTES 3.1 Determinantes de segundo orden Se llama determinante de a: 3.2 Determinantes de tercer orden Se llama determinante de a: Ejercicio 1: Halla los determinantes de las siguientes
T.3: MATRICES Y DETERMINANTES 3.1 Determinantes de segundo orden Se llama determinante de a: 3.2 Determinantes de tercer orden Se llama determinante de a: Ejercicio 1: Halla los determinantes de las siguientes
Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. ) ( + ( ) ( )
 MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
MATRICES Una matriz es un arreglo rectangular de números. Los números en el arreglo se llaman elementos de la matriz. Ejemplo 1. Algunos ejemplos de matrices ( + ( ) ( + ( ) El tamaño o el orden de una
Sistema de Ecuaciones Lineales - Métodos Iterativos -
 Sistema de Ecuaciones Lineales - Métodos Iterativos - Contenido Métodos Iterativos Método de Jacobi Método de Gauss-Seidel Fórmulas Recursivas Métodos Iterativos Los métodos iterativos son aquellos que
Sistema de Ecuaciones Lineales - Métodos Iterativos - Contenido Métodos Iterativos Método de Jacobi Método de Gauss-Seidel Fórmulas Recursivas Métodos Iterativos Los métodos iterativos son aquellos que
DOCENTE: JESÚS E. BARRIOS P.
 DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
MATRICES. Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.
 MATRICES Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
MATRICES Una matriz es un conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes
 Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
Álgebra y Trigonometría Clase 7 Sistemas de ecuaciones, Matrices y Determinantes CNM-108 Departamento de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Copyleft c 2008. Reproducción
1 ÁLGEBRA DE MATRICES
 1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
Sistemas de Ecuaciones Lineales. Matrices y determinantes.
 Capítulo 3 Sistemas de Ecuaciones Lineales Matrices y determinantes 31 Sistemas de Ecuaciones Lineales El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación
Capítulo 3 Sistemas de Ecuaciones Lineales Matrices y determinantes 31 Sistemas de Ecuaciones Lineales El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación
Matemática II Tema 3: resolución de sistemas de ecuaciones lineales
 Matemática II Tema 3: resolución de sistemas de ecuaciones lineales 2012 2013 Índice Sistemas de ecuaciones lineales 1 Interpretación geométrica y definición 1 Método de eliminación 4 Resolución de sistemas
Matemática II Tema 3: resolución de sistemas de ecuaciones lineales 2012 2013 Índice Sistemas de ecuaciones lineales 1 Interpretación geométrica y definición 1 Método de eliminación 4 Resolución de sistemas
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Tema 5. Matrices y Determinantes
 Tema 5. Matrices y Determinantes 1. Definiciones 2. Operaciones Propiedades 3. Determinantes Orden 2 Orden 3: Regla de Sarrus Orden mayor de 3 Propiedades 4. Matriz inversa Ecuaciones matriciales 5. Rango
Tema 5. Matrices y Determinantes 1. Definiciones 2. Operaciones Propiedades 3. Determinantes Orden 2 Orden 3: Regla de Sarrus Orden mayor de 3 Propiedades 4. Matriz inversa Ecuaciones matriciales 5. Rango
Conceptos Preliminares
 Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Universidad Alonso de Ojeda. Facultad de Ingeniería GUIA DE ESTUDIO ALGEBRA LINEAL.
 UNIDAD III: TÓPICOS DE ANÁLISIS NUMÉRICOS Determinante: El determinante es un número real asociado con una matriz mediante la función determinante. El determinante de una matriz de 1 x 1 es igual a su
UNIDAD III: TÓPICOS DE ANÁLISIS NUMÉRICOS Determinante: El determinante es un número real asociado con una matriz mediante la función determinante. El determinante de una matriz de 1 x 1 es igual a su
Gustavo Rodríguez Gómez. Agosto Dicembre 2011
 Computación Científica Gustavo Rodríguez Gómez INAOE Agosto Dicembre 2011 1 / 46 Capítulo II 2 / 46 1 Introducción Métodos Directos Sistemas Triangulares Sustitución Hacia Atrás Invertibilidad de una Matriz
Computación Científica Gustavo Rodríguez Gómez INAOE Agosto Dicembre 2011 1 / 46 Capítulo II 2 / 46 1 Introducción Métodos Directos Sistemas Triangulares Sustitución Hacia Atrás Invertibilidad de una Matriz
Matrices y determinantes
 Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
Clase. 1. Resolución de sistemas de ecuaciones lineales: preliminares
 Clase 1. Resolución de sistemas de ecuaciones lineales: preliminares 2. Método directo y exacto: Gauss 3. Método directo y exacto (II): descomposición LU 4. Métodos indirectos: Jacobi, Gauss-Seidel 2 Sistemas
Clase 1. Resolución de sistemas de ecuaciones lineales: preliminares 2. Método directo y exacto: Gauss 3. Método directo y exacto (II): descomposición LU 4. Métodos indirectos: Jacobi, Gauss-Seidel 2 Sistemas
Inversa de una matriz
 Capítulo 2 Álgebra matricial 2.1. Inversa de una matriz Inversa de una matriz Para una matriz cuadrada A n n, la matriz B n n que verifica las condiciones AB = I n y B A=I n se denomina inversa de A, y
Capítulo 2 Álgebra matricial 2.1. Inversa de una matriz Inversa de una matriz Para una matriz cuadrada A n n, la matriz B n n que verifica las condiciones AB = I n y B A=I n se denomina inversa de A, y
