Número de Diagonales
|
|
|
- Domingo Contreras Roldán
- hace 9 años
- Vistas:
Transcripción
1 Número de Diagonales Geometría plana Efraín Soto Apolinar aprendematematicas.org.mx 4 de diciembre de 009 Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
2 Definiciones Diagonal: Es el segmento de recta que une dos vértices no consecutivos. Diagonal Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de 009 / 9
3 Definiciones Diagonal: Es el segmento de recta que une dos vértices no consecutivos. Radio: Es el segmento de recta que va del centro del poĺıgono regular a cualquiera de sus vértices. Diagonal Radio Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de 009 / 9
4 Definiciones Diagonal: Es el segmento de recta que une dos vértices no consecutivos. Radio: Es el segmento de recta que va del centro del poĺıgono regular a cualquiera de sus vértices. Apotema: Es el segmento de recta que va del centro del poĺıgono al punto medio de cualquiera de sus lados. Diagonal Radio Apotema Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de 009 / 9
5 Empezamos notando que el poĺıgono regular de n lados tiene n vértices. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
6 Empezamos notando que el poĺıgono regular de n lados tiene n vértices. Fijándonos en uno de los n vértices, podemos formar n 3 diagonales, porque una diagonal no puede ir de un vértice a sí mismo, ni a los vértices más próximos a él: Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
7 Empezamos notando que el poĺıgono regular de n lados tiene n vértices. Fijándonos en uno de los n vértices, podemos formar n 3 diagonales, porque una diagonal no puede ir de un vértice a sí mismo, ni a los vértices más próximos a él: Observa que hay tres nodos que no sirven para trazar una diagonal. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
8 Los dos vecinos porque en lugar de formar una diagonal generan un lado del poĺıgono. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
9 Los dos vecinos porque en lugar de formar una diagonal generan un lado del poĺıgono. El tercer vértice que no nos sirve es sobre el cual nos hemos fijado: una diagonal no puede iniciar y terminar en el mismo vértice. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
10 Los dos vecinos porque en lugar de formar una diagonal generan un lado del poĺıgono. El tercer vértice que no nos sirve es sobre el cual nos hemos fijado: una diagonal no puede iniciar y terminar en el mismo vértice. Entonces, de cada uno de los n vértices podemos trazar n 3 diagonales. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
11 Pero nosotros podemos fijarnos en cualquiera de los n vértices del poĺıgono. Entonces, considerando todos los vértices, podemos trazar n (n 3) diagonales. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
12 Pero nosotros podemos fijarnos en cualquiera de los n vértices del poĺıgono. Entonces, considerando todos los vértices, podemos trazar n (n 3) diagonales. Sin embargo, debemos tener en cuenta que cada diagonal la hemos contado dos veces: Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
13 Pero nosotros podemos fijarnos en cualquiera de los n vértices del poĺıgono. Entonces, considerando todos los vértices, podemos trazar n (n 3) diagonales. Sin embargo, debemos tener en cuenta que cada diagonal la hemos contado dos veces: una cuando el vértice que hemos elegido es inicial Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
14 Pero nosotros podemos fijarnos en cualquiera de los n vértices del poĺıgono. Entonces, considerando todos los vértices, podemos trazar n (n 3) diagonales. Sin embargo, debemos tener en cuenta que cada diagonal la hemos contado dos veces: una cuando el vértice que hemos elegido es inicial y la otra cuando es el punto final de la diagonal. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
15 Es decir, hemos contado dos veces a cada diagonal al hacer la multiplicación: n (n 3). Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
16 Es decir, hemos contado dos veces a cada diagonal al hacer la multiplicación: n (n 3). En otras palabras, si dividimos n (n 3) entre dos, obtenemos el número de diagonales del poĺıgono regular: D = n (n 3) Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
17 Es decir, hemos contado dos veces a cada diagonal al hacer la multiplicación: n (n 3). En otras palabras, si dividimos n (n 3) entre dos, obtenemos el número de diagonales del poĺıgono regular: D = n (n 3) Observa que siempre obtenemos un número entero como resultado porque en el numerador de la fracción siempre tenemos un número par: Cuando n es par, n es divisible entre dos, Y cuando n es impar, n 3 es par. Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
18 Ejemplos D 3 = 3(3 3) = 3(0) = 0 = 0 Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
19 Ejemplos D 3 = 3(3 3) = 3(0) = 0 = 0 D 4 = 4(4 3) = 4(1) = 4 = Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
20 Ejemplos... D 5 = 5(5 3) = 5() = 10 = 5 Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
21 Ejemplos... D 5 = 5(5 3) = 5() = 10 = 5 D 6 = 6(6 3) = 6(3) = 18 = 9 Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
22 Final Quién NO tiene preguntas? Efraín Soto Apolinar (aprendematematicas.org.mx) Número de Diagonales 4 de diciembre de / 9
Definición y Clasificación de Polígonos. Definición
Definición y Clasificación de Polígonos Además del triángulo hay una gran cantidad de otras figuras geométricas delimitadas por segmentos de recta que son importantes en geometría. Definición Polígono
Teorema Isoperimétrico
Teorema Isoperimétrico Geometría plana Efraín Soto Apolinar aprendematematicas.org.mx 23 de Diciembre de 2009 Efraín Soto Apolinar (aprendematematicas.org.mx) Teorema Isoperimétrico 23 de Diciembre de
Trazar un pentágono regular
Trazar un pentágono regular Geometría plana Efraín Soto A. www.aprendematematicas.org.mx 07 de mayo de 2010 Efraín Soto A. (www.aprendematematicas.org.mx) Trazar un pentágono regular 07 de mayo de 2010
1º ESO TEMA 12 FIGURAS PLANAS
1º ESO TEMA 12 FIGURAS PLANAS 1 1.- POLÍGONOS Concepto de polígono POLÍGONO 2 1.- POLÍGONOS Elementos de un polígono Lado: segmento que une dos vértices consecutivos Vértice: punto en común entre dos lados
El punto de unión de cada par de segmentos se denomina ángulo. El numero de lados, ( y por tanto de ángulos) ha de ser mayor o igual a tres.
POLÍGONOS: POLÍGONOS REGULARES y POLÍGONOS REGULARES ESTRELLADOS. Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos. Cada uno de los segmentos
Polígonos Regulares: Definición de polígono:
1 Polígonos Regulares: Definición de polígono: Un polígono es una figura plana cerrada, limitada por segmentos de recta llamados lados del polígono. Los puntos donde se unen dos lados consecutivos se llaman
Contenidos y sub-contenidos
Contenidos y sub-contenidos Definición de perímetro, área y polígono. Polígonos regulares e irregulares. Área de un polígono regular. Polígonos inscrito y circunscrito. Aplicaciones. Analicemos lo siguiente:
A RG. Diédrico 13. Abatimientos Hoja 1/2
menor cota, es horizontal; 2 - El otro vértice, él E, contiguo al A esta en el P; 3 - El pentágono está en el 1º A G R F 2 A 2 F 1 E B 1 2 A LA D 1 0 1 B 1LB 0 menor cota, es horizontal; 2 - El otro vértice,
Colegio San Miguel PLÁSTICA - 3º ESO - Curso 2016/17 Privado Concertado / Bilingual School
CUADERNILLO DE ACTIVIDADES DE RECUPERACIÓN 1ª EVALUACIÓN DE PLÁSTICA 3º Apellidos: Nombre: Fecha: Grupo: Calificación: INSTRUCCIONES: Imprime estas hojas de enunciado y no te olvides de rellenar con tus
1.SISTEMAS DE MEDIDAS: longitud, superficie, volumen. Conversiones.
ÍNDICE DEL TEMA 1.SISTEMAS DE MEDIDAS: longitud, superficie, volumen. Conversiones. 2. FIGURAS PLANAS : 2.1. POLÍGONOS Triángulos Cuadriláteros Polígonos regulares 2.2. CIRCUNFERENCIA Y CÍRCULO: Elementos.
Figuras planas. Definiciones
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
MATEMÁTICA I GEOMETRÍA PLANA. POLÍGONOS DE MÁS DE CUATRO LADOS ING. SANTIAGO FIGUEROA LORENZO
MATEMÁTICA I GEOMETRÍA PLANA. POLÍGONOS DE MÁS DE CUATRO LADOS ING. SANTIAGO FIGUEROA LORENZO LÍNEA POLIGONAL POLÍGONOS Es la figura que esta formado por segmento de recta unido por sus extremos dos a
TORNEOS GEOMÉTRICOS 2015 Segunda Ronda 5º Grado SOLUCIONES
TORNEOS GEOMÉTRICOS 015 Segunda Ronda 5º Grado SOLUCIONES Problema 1- Un paralelogramo de 5 cm de área, tiene por vértices al centro de un hexágono regular y a otros tres vértices del hexágono, como muestra
Geometría Básica 43 UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL
Geometría Básica 43 POLIGONOS UNIVERSIDAD DE LOS ANDES - TÁCHIRA DEPARTAMENTO DE CIENCIAS CARRERA EDUCACIÓN BÁSICA INTEGRAL SEGMENTOS CONCATENADOS Y CONSECUTIVOS Consideremos los segmentos ab y bc, donde
Sesión del día 11 de Marzo del 2011 y tutoría del día 12 de Marzo del 2011
Especialidad La enseñanza de las matemáticas en secundaria Grupo B: Celaya Sesión del día 11 de Marzo del 2011 y tutoría del día 12 de Marzo del 2011 Álgebra Resumen de la sesión anterior. Se añadió que
El polígono es una porción del plano limitado por una línea poligonal cerrada.
UNIDAD 12: GEOMETRÍA PLANA 12.1. Los polígonos: Elementos El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los
A 2 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO TEOREMA DE PITÁGORAS:
TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
Diédrico E3Ip
Diédrico 2001-04 2 Diédrico 2001-04 12 Diédrico 2001-04 14 OPCIÓN II EJERCICIO 1 : SISTEMA DIÉDRICO. Dadas las proyecciones de los puntos A, By C, se pide: 1.- Representar las trazas del plano p definido
INSTITUTO RAÚL SCALABRINI ORTIZ GEOMETRIA POLÍGONOS
GEOMETRIA POLÍGONOS (1) Si un polígono tiene un ángulo central de 45º Cuántos lados tiene? (2) Inscribir en distintas circunferencias los siguientes polígonos: a) Triángulo equilátero b) Pentágono regular
El cubo o hexaedro regular
El cubo o hexaedro regular Como los ángulos de un cuadrado miden 90, solo podemos formar un poliedro de caras cuadradas, tres por cada vértice. La suma de las caras que están unidas en cada vértice será:
Proyecto Guao POLÍGONOS
POLÍGONOS Qué pasaría si te preguntaran cuántos lados tiene un polígono? Cómo describirías el polígono? Después de leer este concepto, vas a poder clasificar un polígono en función de su número de lados.
POLÍGONOS P 6 P 1 P 3. Interior del polígono P 8. P n 1 P 7
POLÍGONOS DEFINICIÓN Sean P 1, P 2,..., P n un conjunto de n puntos distintos de un plano con n 3 y sean los n segmentos P1P 2, P 2 P 3,..., P n 1P n, P n P 1 tales que: (1) Ningún par de segmentos se
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS.
TEMA 11: ÁREA Y FIGURAS GEOMÉTRICAS. LOS POLÍGONOS El polígono es una porción del plano limitado por una línea poligonal cerrada. Un polígono se nombra con las letras mayúsculas situadas en los vértices.
POLÍGONOS REGULARES. Ejemplo: Hexágono 360º / 6 = 60º. TRIÁNGULO 3 120º 60º 180º (3-2)= 180º CUADRADO 4 90º 90º 180º (4-2)= 360º
A B G C F LADO D E A B G C F D E APOTEMA DIAGONALES RADIO 360º / n (180º- ) ELEMENTOS Y PROPIEDADES DE LOS POLÍGONOS REGULARES. (Ilustración nº 1). Diagonal: Es el segmento que une dos vértices no consecutivos.
Distrito escolar de Carson City: Vocabulario matemático CCSS fundamental
Vocabulario matemático fundamental del primer trimestre conmutativa a + b = b + a a x b = b x a En la suma y la multiplicación cambiar el orden no altera la respuesta.( La suma y la resta no son conmutativa)
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
TRIÁNGULOS Y CUADRILÁTEROS
TEMA 8.- POLÍGONOS TRIÁNGULOS Y CUADRILÁTEROS 1.- POLÍGONOS.- La definición de polígono viene dada por POLI= varios y GONO= ángulo. Clasificación de los polígonos según el número de lados: así son los
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( ) 2. g) 0,86 x 0,73 = 1. x = 1 4 3x. = x + + l) ( ) ( )( ) m) ( )( ) ( ) 2
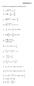1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES GEOMETRÍA: Rama de las matemáticas que se ocupa del estudio de las figuras geométricas, incluyendo puntos, rectas, planos Proviene del Griego GEO (tierra) METRÍA
Triangulación de polígonos
Computación Geométrica Triangulación de polígonos Algoritmos iniciales Introducción a la Geometría Computacional Copyright 2010-2011 Universidad de Alicante 1 Índice Historia Conceptos previos Triangulación
Tema 2 2 Geometría métrica en el pla no
Tema Geometría métrica en el pla no CONCEPTOS BÁSICOS Figuras básicas en el plano: puntos, rectas, semirrectas, segmentos y ángulos Los polígonos y su clasificación según los ángulos internos y según el
Polígonos IES BELLAVISTA
Polígonos IES BELLAVISTA Polígonos: definiciones Un polígono es la porción de plano limitada por rectas que se cortan. Polígono regular: el que tiene todos los lados y ángulos iguales. Polígono irregular:
Objet ivo. Reconocer los elementos del polígono y relacionarlos. en cualquier polígono conociendo su número de lados.
POLÍGONOS I Objet ivo Reconocer los elementos del polígono y relacionarlos en cualquier polígono conociendo su número de lados. DEFINICIÓN Son figuras formadas por segmentos no alineados y de extremos
Profr. Efraín Soto Apolinar. Polígonos
Polígonos En esta sección vamos a utlizar las fórmulas que a conocemos para calcular perímetros áreas de polígonos. Para esto es una buena idea recordar las fórmulas de áreas de los polígonos. alcula el
1. Calcula la razón en cada caso e indica las parejas que pueden formar una proporción:
TEMA 8. PROPORCIONALIDAD NUMERICA 1. Calcula la razón en cada caso e indica las parejas que pueden formar una proporción: 4 5 8 7 12 15 16 14 8 10 80 70 2. Indica qué proporciones son ciertas: 4 10 8 20
Distancia entre un punto y una recta
Distancia entre un punto una recta Frecuentemente en geometría nos encontramos con el problema de calcular la distancia desde un punto a una recta. Distancia de un punto a una recta La fórmula para calcular
POLÍGONOS POLÍGONOS. APM Página 1
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
Lección 6: EXPRESIONES ALGEBRAICAS: MONOMIOS
Lección 6: EXPRESIONES ALGEBRAICAS: MONOMIOS 1.- ÁLGEBRA. EXPRESIONES ALGEBRAICAS Y LENGUAJE ALGEBRAICO ÁLGEBRA es la parte de las matemáticas que estudia las expresiones algebraicas. EXPRESIÓN ALGEBRAICA
SEGUNDA OLIMPIADA ESTATAL DE MATEMÁTICAS
PROBLEMAS PROPUESTOS PARA LA ETAPA DE ZONA PRIMER GRADO 1. Marcos tiene todas las letras del abecedario en tres tamaños: grandes, medianas y pequeñas: A,B,C,D,E,...,Z A,B,C,D,E,...,Z A,B,C,D,E,...,Z Usando
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 2009
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 009 Comisión Académica 1 Nivel Maor Problema 1. Considere 9 puntos en el interior de un cuadrado de lado 1.
GEOMETRÍA PLANA 3º E.S.O. Un polígono es una figura geométrica plana y cerrada limitada por tres o más segmentos llamados lados.
GEOMETRÍA PLANA 3º E.S.O. POLÍGONO.- Un polígono es una figura geométrica plana y cerrada limitada por tres o más segmentos llamados lados. El triángulo (tres lados), el cuadrilátero (cuatro lados), el
GUIA DE TRABAJO Materia: Matemáticas. Tema: Geometría 3- Explorando el polígono. Fecha: Profesor: Fernando Viso
GUIA DE TRABAJO Materia: Matemáticas. Tema: Geometría 3- Explorando el polígono. Fecha: Profesor: Fernando Viso Nombre del alumno: Sección del alumno: CONDICIONES: Marco teórico: Trabajo individual. Sin
PROBLEMA. Cuántas diagonales tiene un triángulo? Y un cuadrilátero? En general, cuántas diagonales tiene un polígono de n lados?
PROBLEMA. Cuántas diagonales tiene un triángulo? Y un cuadrilátero? En general, cuántas diagonales tiene un polígono de n lados? PROPUESTA DE TRABAJO CON LOS ESTUDIANTES: 1. Se tienen claros los conceptos
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº
Cuaderno: LIMPIEZA Y ORGANIZACIÓN Realización de TAREAS SATISFACTORIO ACEPTABLE MEJORABLE TEMA 12 FIGURAS PLANAS Y ESPACIALES ALUMNO/A: Nº Ejercicios TEMA 12 FIGURAS PLANAS Y ESPACIALES (1º ESO) Página
Preguntas Propuestas
reguntas ropuestas 2 ... olígonos 1. alcule la suma de lados de dos polígonos si se sabe que las sumas de las medidas de sus ángulos interiores difieren en 540º y el número de diagonales del polígono de
NIVEL 6 CÓDIGO SECCIÓN 1: ALTERNATIVA MÚLTIPLE. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54?
Problema 1. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54? A. 3 B. 4 C. 5 6 Como 54 = 2 27 = 2 3 3, 9 tiene que dividir a a99b, luego 9 divide a a + b. Además 2 divide
2.- Escribe la lectura o escritura de las siguientes fracciones:
EDUCACIÓN PREESCOLAR 04PJN0020V EDUCACIÓN PRIMARIA Decroly más que un colegio 04PPR0034O EDUCACION SECUNDARIA 04PES0050Z MARATON DE MATEMÁTICAS 1.- Una fracción está compuesta por un numerador y un denominador.
MATEMÁTICAS 1º DE ESO
MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
Clase. Ángulos y polígonos
Clase Ángulos y polígonos Aprendizajes esperados Transformar la medida de un ángulo a los distintos sistemas de medición. Clasificar a los ángulos según su medida. Reconocer relaciones angulares. Clasificar
Capítulo 2: Principio de Inducción Análisis combinatorio Binomio de Newton
Capítulo : Principio de Inducción Análisis combinatorio Binomio de Newton. Escribe usando el símbolo de sumatoria: a) ++9+...+ b) + + + c) 5 7 9 + + + +. 6 8 0. Calcula las siguientes sumas 0 a) ( + )
INSTITUCIÓN EDUCATIVA TÉCNICA SAGRADO CORAZÓN Aprobada según Resolución No NIT DANE SOLEDAD ATLÁNTICO.
Página 1 de 12 GUIA N 2 ÁREA: GEOMETRIA GRADO: 2 DOCENTES: CARMEN MENDOZA-FAISY RODRIGUEZ-IVONNE PRENNET-DILIA BELTRAN PERIODO: 1 IH (en horas): EJE TEMÁTICO LONGITUDES DESEMPEÑO Reconoce el centímetro,
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
Clase N 05 MODULO COMPLEMENTARIO. Ángulos y polígonos
Pre-universitario Manuel Guerrero Ceballos Clase N 05 MODULO COMPLEMENTARIO Ángulos y polígonos Resumen de la clase anterior Tipos de gráficos Probabilidades Histograma Barras De gráfico a tabla Polígono
UNIDAD 2.3 POLIGONOS. Definición.
UNI.3 POLIGONOS. efinición. POLIGONL.- Es un conjunto de segmentos de recta unidos uno a continuación de otro, que solo se cortan en sus extremos. Existen dos tipos de poligonales. Poligonal abierta. E
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA
MINISTERIO DE EDUCACIÓN PÚBLICA DIRECCIÓN DE DESARROLLO CURRICULAR DEPARTAMENTO DE PRIMERO Y SEGUNDO CICLOS ASESORÍA NACIONAL DE MATEMÁTICA Área matemática: Geometría Primer periodo 20XX Habilidad(es)
2.-GEOMETRÍA PLANA O EUCLIDIANA
2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
Compartimos un resumen de las principales fórmulas y formas para calcular el perímetro y área de polígonos. POLÍGONO PERÍMETRO SUPERFICIE o ÁREA
Compartimos un resumen de las principales fórmulas y formas para calcular el perímetro y área de polígonos. POLÍGONO PERÍMETRO SUPERFICIE o ÁREA TRIÁNGULO Se suma lo que miden sus 3 lados. P = a + b +
TEMA 5: GEOMETRÍA PLANA. Contenidos:
Contenidos: - Elementos básicos del plano: punto, recta y segmento. Rectas paralelas y perpendiculares. Ángulos: definición, clasificación y medida. - Instrumentos de dibujo. Construcción de segmentos,
EDUCACIÓN PLÁSTICA Y VISUAL. Trabajo de Recuperación de Pendientes Para 3º ESO. Geometría. IES Ramón Menéndez Pidal DPTO. DE DIBUJO 3º ESO 1
EDUCACIÓN PLÁSTICA Y VISUAL Trabajo de Recuperación de Pendientes Para 3º ESO Geometría IES Ramón Menéndez Pidal DPTO. DE DIBUJO 3º ESO 1 TEOREMA DE THALES El Teorema de Thales sirve para dividir un segmento
Polígono. Superficie plana limitada por una línea poligonal cerrada.
POLÍGONO B C r A d O a l E D Polígono. Superficie plana limitada por una línea poligonal cerrada. r O r =a Elementos, puntos y líneas en los polígonos. (Regulares) LADO Cada uno de los segmentos de la
SOLUCIONES ENERO 2018
Página 1 de 9 SOLUCIONES ENERO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Segundo ciclo de la E. S. O. AUTORES: Colectivo
ENCUENTRO NÚMERO CINCO La circunferencia y el círculo
MODULO III - GEOMETRIA ENCUENTRO NÚMERO CINCO La circunferencia y el círculo 24 DEAGOSTO DE 2014 MANAGUA FINANCIADO POR: FUNDACIÓN UNO 1 Circunferencia: Una circunferencia es una línea curva cerrada cuyos
TALLER No. 17 GEOMETRÍA
TLLER No. 17 GEOMETRÍ ontenidos: Los triángulos Fecha de entrega: Mayo 12 de 2014 1. Investigue sobre las líneas y puntos notables en un triángulo. 2. Responda las siguientes preguntas: a. Qué es un polígono?
Un juego de ángulos SGUICTG001TG31-A16V1
Un juego de ángulos SGUICTG001TG31-A16V1 SECCIÓN: EXPERIMENTANDO Actividad 1 1. Porque la dirección que adquiere el movimiento de las bolas en el billar depende del ángulo con que la bola blanca se golpea.
GEOMETRÍA LLANA: CONCEPTOS BÁSICOS (1ESO)
GEOMETRÍA LLANA: CONCEPTOS BÁSICOS (1ESO) PUNTOS, RECTOS Y PLANES 1.- Punto: Intersección de dos rectos. No tiene dimensiones (ni largo, ni ancho, ni alto). 2.- Recta: Conjunto de puntos con una sola dimensión.
polígono 3 Triángulo 4 Cuadrilátero 5 Pentágono 6 Hexágono 7 Heptágono 8 Octógono 9 Eneágono 10 Decágono 11 Undecágono 12 Dodecágono 20 Icoságono
TEMA: POLÍGONOS Y ÁNGULOS. POLÍGONOS REGULARES. POLÍGONOS Un polígono es una figura cerrada cuyos lados son segmentos. La palabra polígonos se puede interpretar como: figura de muchos ángulos. Los triángulos,
Soluciones de los problemas del taller especial
Soluciones de los problemas del taller especial Este taller fue preparado para satisfacer la inquietud de los docentes que solicitaron más capacitación Olimpiada Akâ Porâ Olimpiada Nacional de Matemáticas
MATEMÁTICAS 2º DE ESO LOE
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
Polígono regular de 3 lados: Triángulo equilátero
Se pueden construir todos los polígonos regulares con regla y compás siguiendo las reglas que hemos establecido para estas construcciones? Vamos a ver la construcción de los mismos partiendo de unos ejes
Dos rectas, r y s, pueden tener un punto en común, ninguno o infinitos. Secantes Paralelas Coincidentes. r r
GEOMETRÍA 1. Puntos y rectas Los puntos y las rectas son dos de los elementos geométricos fundamentales. Los puntos se nombran con letras mayúsculas: A, B, C, La recta está formada por infinitos puntos
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( x ) ( x ) x = x + = x. l) ( ) ( )( ) + = + + o) ( x ) 2.
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
1 1 1 u = u u = + = un vector unitario con la dirección de u será u puesto que u = u = : 1 ( ) ( ) ( ) ( ) ( )
Examen de Geometría analítica del plano Curso 05/6 Ejercicio. a) Halla los dos vectores unitarios que son ortogonales al vector w = ( 3, ) w = 3, ; un vector perpendicular a w será u =,3, puesto que u
PERSPECTIVA ISOMÉTRICA (Construcción de algunos volúmenes)
PERSPECTIVA ISOMÉTRICA (Construcción de algunos volúmenes) Cubo de arista L Para construir un cubo empezamos dibujando la base, que es un cuadrado de lado L. Medimos L en el eje x y desde ese punto dibujamos
DÍA 1 SOLUCIONES BANCO DE PROBLEMAS
XXIX OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP - UNA - UCR - MICITT - UNED - TEC DÍA 1 SOLUCIONES BANCO DE PROBLEMAS Nivel I (7 ) Lunes 13 de noviembre Final 017 GEOMETRÍA 1. Sean ABC un triángulo equilátero
Fracciones. Tipos de fracciones. Impropia. El numerador es más grande o igual que el denominador. 7 3, 9 4, 11 6
Fracciones Es una expresión que representa una o varias partes de la unidad. Numerador y Denominador El denominador indica en cuantas partes se divide la unidad y el numerador indica cuantas partes se
Soluciones - Primer Nivel Juvenil
SOCIEDAD ECUATORIANA DE MATEMÁTICA ETAPA FINAL "VII EDICIÓN DE LAS OLIMPIADAS DE LA SOCIEDAD ECUATORIANA DE MATEMÁTICA" Soluciones - Primer Nivel Juvenil 04 de mayo de 010 1. Cuál es la séptima figura
IGUALDAD. Método de triangulación Método de radiación Método de traslación Método de ángulos y lados Método de coordenadas cartesianas
IGUL INIIÓN ecimos que dos figuras son iguales geométricamente cuando tienen lados y ángulos iguales y están dispuestos en el mismo orden. omo consecuencia de ello, si dos figuras son iguales entonces
Problemas propuestos en el XXXIII Concurso S E V E N E I G H T
Problemas propuestos en el XXXIII Concurso NIVEL I (3º de E.S.O.) Primera parte ( hora 30 minutos) Problema (7 puntos) En la siguiente posible suma cada letra representa un dígito (0,,,, 9), letras diferentes
LA GEOMETRÍA PLANA. Llanos: Si su medida es de 180º. Agudos: Si su medida esta comprendida entre 0 y 90. Rectos: si su medida es 90
LA GEOMETRÍA PLANA La geometría plana trata de aquellos elementos que solo tienen dos dimensiones y, que por lo tanto, se encuentran y operan en un plano. Los elementos básicos con los que se suele trabajar
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
MATEMÁTICAS Y SU DIDÁCTICA
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
Polígonos y Poliedros
09 Lección Apertura Matemáticas Polígonos y s Competencia Socializa sus ideas y llega a acuerdos con los que asimila conceptos relacionados con polígonos y poliedros. Diseño instruccional El maestro aclarará
Plan de Animación para la enseñanza de las Matemáticas
FIGURAS PLANAS CÓMO DETERMINAR AREAS DE FIGURAS PLANAS Las FIGURAS PLANAS son aquellas que están limitadas por líneas rectas o curvas, además de que todos sus puntos están contenidos en un solo plano.
Carrera: Diseño Industrial
POLÍGONOS 1) Dados los siguientes polígonos se pide determinar cuales de ellos son cóncavos y cuales convexos. Justifique sus respuestas. a) b) c) 2) En los polígonos graficados a continuación indique
MYP (MIDDLE YEARS PROGRAMME)
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Las fracciones mixtas
I E YERMO Y PARRES Sección Carlos franco 2 Unidad didáctica periodo tres Las fracciones mixtas Grado 4 Profesora Martha Luz Ospina Muñoz DESCRIPCIÓN: En el desarrollo de esta unidad se pone énfasis en
4º Unir la última división (5) con el extremo B del segmento, y por las demás divisiones trazar paralelas a la recta anterior.
TEM 2: POLÍGONOS TEOREM DE THLES El Teorema de Thales sirve para dividir un segmento en partes iguales. Para ellos seguimos los siguientes pasos. Repite los pasos a la derecha. 1º Dibujar el segmento que
INSTITUTO RAÚL SCALABRINI ORTIZ CUADRILATERO
CUADRILATERO INTRODUCCION Son polígonos de 4 lados. La suma de los ángulos interiores es igual a 360º y la suma de los ángulos exteriores es igual a 360º. Vértices : A, B, C, D Lados : a, b, c, d Ángulos
SOLUCIONES A LOS PROBLEMAS PROPUESTOS
SOLUCIONES A LOS PROBLEMAS PROPUESTOS SOLUCIONES 6. o DE PRIMARIA PROBLEMA 1 : I. 2 x 3 x 4 x 5 x 6 = 720 IV. (1 + 3) x 4 x 5 + 0 = 80 II. (3 + 1) x 4 x 7 x 8 = 896 V. (1+1+1) x 3 x 7 = 63 III. 5 x 6 x
Tema 8: Cuerpos geométricos. Matemáticas Específicas para Maestros 1º Grado en Educación Primaria
Tema 8: Cuerpos geométricos Matemáticas Específicas para Maestros 1º Grado en Educación Primaria Definiciones Cuerpos geométricos Poliedros. Elementos. Clasificaciones: o Poliedros cóncavos y convexos.
UNIDAD II Polígonos y Circunferencia.
UNIDAD II Polígonos y Circunferencia. Objetivo de la unidad: El estudiante: Resolverá problemas relacionados con polígonos y circunferencia, de tipo teórico o prácticos en distintos ámbitos, mediante la
Parábolas con vértice fuera del origen
Parábolas con vértice fuera del origen En este apartado vamos a etender lo que estudiamos en la sección anterior. Ahora vamos a considerar parábolas con vértices fuera del origen. En estos casos, tendremos
Tema 2: --TRAZADOS DE FORMAS POLIGONALES
Tema 2: --TRAZADOS DE FORMAS POLIGONALES 1.- TRIÁNGULOS: - CLASIFICACIÓN Y PUNTOS NOTABLES 2.- CUADRILÁTEROS: PROPIEDADES Y CLASIFICACIÓN 3.- POLÍGONOS REGULARES: CLASIFICACIÓN Y CONSTRUCCIÓN Ø INTRODUCCIÓN:
Lección 1.1: Perímetro y área. Parte A - Figuras regulares e irregulares
Unidad 7.5: Geometría Tema 1: Figuras bidimensionales Lección 1.1: Perímetro y área Parte A - Figuras regulares e irregulares Los polígonos Los ángulos son las regiones que forman los lados al cortarse.
8 GEOMETRÍA DEL PLANO
8 GEOMETRÍ DEL PLNO EJERIIOS PR ENTRENRSE Ángulos y triángulos 8.6 Halla la medida del ángulo p en el siguiente triángulo. 6 4 180 6 p 4 p 180 6 4 11 8.7 alcula la suma de los ángulos interiores de un