Trigonometría esférica
|
|
|
- Xavier Benítez Aguilar
- hace 6 años
- Vistas:
Transcripción
1 Trigonometría esférica Prof. Luis G. López 12 de septiembre de 2013 Resumen Se deducen las tres fórmulas fundamentales de la trigonometría esférica, y otras para los casos particulares de los triángulos rectángulos y rectiláteros. También se ofrecen problemas para aplicarlas, algunos de ellos clásicos, como la transformación de coordenadas astronómicas. Índice 1. Definiciones 2 2. Fórmulas fundamentales Relación del coseno Relación del seno por el coseno o fórmula de los cinco elementos Relación de los senos Observación Fórmulas particulares Triángulo esférico rectángulo Triángulo esférico rectilátero Aplicaciones y problemas Transformación de coordenadas Acimutales a ecuatoriales Ecuatoriales a acimutales Problemas varios Problema N o 76 de [2]
2 Problema N o 168 de [2] Proyección del recorrido solar sobre el ecuador celeste Acimut de salida y puesta de un astro Arco diurno de un astro Respuestas a los problemas A. Cálculo de la hora sidérea 15 A.1. Cálculo del día juliano a las 0hTU A.2. Cálculo de la hora sidérea local A.3. Ejemplo: cálculo de la hora sidérea local B. La trigonometría plana como caso particular de la esférica 18 C. Deducción vectorial de las fórmulas fundamentales Definiciones Se llama triángulo esférico a la figura formada sobre la superficie de una esfera con los arcos de tres círculos máximos (figura 1). A E B c D a b C R O Figura 1: Triángulo esférico Un triángulo esférico se caracteriza por seis ángulos: 2
3 Los tres lados (a, b y c en la figura 1) cuya medida es la medida de su arco. Los tres ángulos diedros entre los planos de los círculos máximos (A, B y C en la figura 1). Resulta natural estudiar sólo los triángulos cuyos ángulos y lados no superen 180 o, en cuyo caso puede demostrarse que la suma de sus ángulos es mayor a 180 o pero menor a 540 o, y la suma de sus tres lados es menor de 360 o. 2. Fórmulas fundamentales 2.1. Relación del coseno Sea O el centro de la esfera sobre la que se forma el triángulo esférico ABC. Tracemos desde A las tangentes AD y AE a los lados b y c hasta su intersección con las prolongaciones de los radios OC y OB. Aplicamos el teorema del coseno de la trigonometría plana a los triángulos OED y AED: DE 2 DE 2 = OD 2 + OE 2 2OD OE cos a = AD 2 + AE 2 2AD AE cos A Restamos ambas ecuaciones y tenemos: 2OD OE cos a = OD 2 AD 2 + OE 2 AE 2 + 2AD AE cos A (1) De los triángulos planos OAE y OAD se deduce: OD 2 AD 2 = R 2 OE 2 AE 2 = R 2 AD = R tg b AE = R tg c OD = R cos b Reemplacemos en (1) y obtenemos: OE = R cos c 2 R R cos b cos c cos a = R2 + R 2 + 2R tg br tg c cos A cos a 2 = tg b tg c cos A cos b cos c 3
4 Multiplicando por (cos b cos c)/2: cos a = cos b cos c + sen b sen c cos A (2) 2.2. Relación del seno por el coseno o fórmula de los cinco elementos La fórmula (2) puede escribirse para el lado b: cos b = cos c cos a + sen c sen a cos B y sustituir en ella el cos a de la ecuación (2): cos b = cos c(cos b cos c + sen b sen c cos A) + sen c sen a cos B cos b = cos 2 c cos b + sen b sen c cos c cos A + sen c sen a cos B cos b(1 cos 2 c) = sen b sen c cos c cos A + sen c sen a cos B Si sustituimos (1 cos 2 c) por sen 2 c y dividimos todo por sen c: sen a cos B = sen c cos b cos c sen b cos A (3) 2.3. Relación de los senos Despejemos cos A de la ecuación (2): cos A = cos a cos b cos c sen b sen c Elevemos al cuadrado y restemos de la unidad ambos miembros: ( cos a cos b cos c 1 cos 2 A = 1 sen b sen c 4 ) 2
5 sen 2 A = 1 cos2 a 2 cos a cos b cos c + cos 2 b cos 2 c sen 2 b sen 2 c sen 2 A = sen2 b sen 2 c cos 2 a + 2 cos a cos b cos c cos 2 b cos 2 c sen 2 b sen 2 c sen 2 A = (1 cos2 b)(1 cos 2 c) cos 2 a + 2 cos a cos b cos c cos 2 b cos 2 c sen 2 b sen 2 c sen 2 A = 1 cos2 c cos 2 b + cos 2 b cos 2 c cos 2 a + 2 cos a cos b cos c cos 2 b cos 2 c sen 2 b sen 2 c Dividamos por sen 2 a: sen 2 A sen 2 a = 1 cos2 a cos 2 b cos 2 c + 2 cos a cos b cos c sen 2 a sen 2 b sen 2 c La expresión anterior es perfectamente simétrica con respecto a a, b y c, por lo que: sen a sen A = sen b sen B = sen c sen C (4) 2.4. Observación Las deducciones precedentes suponen que la construcción de la figura 1 es realizable, lo cual sólo es posible si efectivamente existen los puntos D y E. Para que esto ocurra, es necesario que los lados b y c sean menores que 90 o. Para verificar que las fórmulas anteriores resultan válidas para cualquier triángulo esférico, restan por considerar entonces los siguientes casos particulares: b > 90 o y c > 90 o : Es posible construir (figura 2) sobre los respectivos círculos máximos un triángulo esférico de lados a, 180 o b y 180 o c, con vértices B, C y el punto diametralmente opuesto a A, para el cual resultará válida la construcción, y en el que podemos comprobar que cos a = cos(180 o b) cos(180 o c) + sen(180 o b) sen(180 o c) cos A (puesto que A = A ), lo cual nos conduce a la ecuación (2) teniendo en cuenta que sin(180 o α) = sin α y cos(180 o α) = cos α. 5
6 A C c > 90 o b > 90 o 180 o b A B a C 180 o c 180 o b A Figura 2: b > 90 o y c > 90 o 180 o a c < 90 o b > 90 o B a C Figura 3: b > 90 o y c < 90 o b > 90 o y c < 90 o : Es posible construir un triángulo esférico (figura 3) con vértices en A, B y el punto diametralmente opuesto a C, y lados iguales a 180 o a, 180 o b y c, para el cual nuevamente será válida la construcción de la figura (1), que nos permitirá comprobar nuevamente que la ecuación (2) es válida para el triángulo original efectuando los correspondientes reemplazos (hay que tener en cuenta que el ángulo entre los lados c y 180 o b es 180 o A). A A b = 90 o c < 90 o c > 90 o b = 90 o D A a C B a B D A C Figura 4: b = 90 o y c 90 o (con AD = 90 o ) b = 90 o y c = 90 o : En este caso tanto B como C serán también iguales a 90 o, y a será igual a A, por lo que dicho triángulo verificará la fórmula (2) trivialmente: cos a = cos A. b = 90 o y c 90 o : Unamos C con el punto D, ubicado a 90 o de A y a lo largo del círculo máximo que va desde A hasta B con lo cual 6
7 CD = A. Si CD = 90 o, el punto C será un polo 1 del arco AB (dado que al encontrarse C a 90 o de dos puntos distintos A y D de un mismo círculo máximo, se trata de un polo del mismo). En ese caso, cualquier arco de círculo máximo que lo una al arco AB tendrá también 90 o : en particular, a. Entonces, el triángulo ABC verificará trivialmente la fórmula (2). Si CD 90 o, como también el arco BD 90 o, podemos aplicar al triángulo BCD la fórmula (2): cos a = cos BD cos A+sen BD sen A cos BDC, pero BDC = 90 o y BD = ±(90 o c), con lo cual arribamos a cos a = sen c cos A, que no es otra cosa que la ecuación (2) con b = 90 o. Las ecuaciones (3) y (4) se deducen de la (2), por lo que comprobamos la validez de las tres fórmulas fundamentales para todos los triángulos esféricos posibles. 3. Fórmulas particulares 3.1. Triángulo esférico rectángulo Si uno de los ángulos es igual a 90 o, se dice que el triángulo esférico es rectángulo. Sea A igual a un recto. De la relación del coseno (2) obtenemos: cos a = cos b cos c (5) De la relación del seno por el coseno (3): sen a cos B = sen c cos b sen a = sen c cos b cos B (6) 1 Se llama polo de un círculo máximo porque, si imaginamos a este último como un ecuador de la esfera, se hallará en uno de los polos de la misma. 7
8 Si dividimos (6) y (5): tg a = tg c cos B (7) De la relación de los senos (4): sen a = sen b sen B (8) También de la relación del seno por el coseno (3): sen b cos A = sen c cos a sen a cos c cos B sen c cos a sen a = cos c cos B Y si ahora igualamos el segundo miembro de (8) con el sen a de (9): cos a = sen b tg c tg B (9) (10) Si también igualamos el segundo miembro de (10) con el de (5): cos b cos c = sen b tg c tg B sen c = tg b tg B (11) 3.2. Triángulo esférico rectilátero Si uno de los lados es igual a 90 o, se dice que el triángulo esférico es rectilátero. Sea a igual a un recto. De la relación del coseno (2) obtenemos: cos a = cos b cos c + sen b sen c cos A 8
9 cos A = cotg b cotg c (12) También de la relación del coseno (2): cos b = cos a cos c + sen a sen c cos B cos b = sen c cos B (13) De la relación de los senos (4): sen A = sen B sen b (14) 9
10 4. Aplicaciones y problemas 4.1. Transformación de coordenadas Para deducir las ecuaciones de transformación de coordenadas acimutales a ecuatoriales y viceversa, planteamos el triángulo paraláctico (figura 5), cuyos vértices son el polo celeste visible (PC), el cenit (Z) y el astro ( ). Recordemos que para que la aplicación de las fórmulas anteriores resulte válida, los lados que unen dichos vértices deberán ser arcos de círculos máximos: entre PC y Z el meridiando del lugar, entre Z y el círculo vertical del astro, y entre PC y el meridiano celeste o círculo horario del mismo. Adoptaremos como convención que el acimut se mide desde el sur hacia el oeste, y para la construcción de la figura que el polo visible es el austral. De esta manera, comprobamos que los ángulos con vértice en Z y PC son el acimut (A) y el ángulo horario (t), respectivamente. El ángulo q con vértice en se denomina ángulo paraláctico. Z A 90 o + ϕ 90 o + δ t PC 90 o h q Figura 5: Triángulo paraláctico Como vemos, en el triángulo paraláctico aparece el ángulo horario, y no la ascensión recta, por lo que estrictamente las ecuaciones siguientes vincularán el sistema acimutal con el ecuatorial horario o relativo. Por supuesto, la obtención de la ascensión recta sólo requiere el conocimiento de la hora sidérea (θ s ), ya que: θ s = t + α 10
11 Acimutales a ecuatoriales Por la fórmula (2) aplicada al triángulo paraláctico: cos(90 o + δ) = cos(90 o + ϕ) cos(90 o h) + sen(90 o + ϕ) sen(90 o h) cos A sen δ = sen ϕ sen h cos ϕ cos h cos A (15) Es interesante comprobar que la ecuación (15) nos devuelve la declinación como un arcoseno, función cuyo conjunto imagen es [-90 o ;90 o ], coincidente con los posibles valores que puede tomar la declinación. Si la fórmula, en cambio, nos devolviera el valor del coseno de δ, nos encontraríamos ante una ambigüedad del valor de δ, que deberíamos resolver mediante otra fórmula. También resulta interesante comprobar que la fórmula (15) expresa, como esperábamos, que el valor de la declinación sólo depende de la altura, el acimut y la latitud del lugar de observación. Apliquemos ahora la fórmula (4): sen t sen(90 o h) = sen A sen(90 o + δ) sen A cos h sen t = (16) cos δ Esta fórmula nos permite obtener el seno de t en función de parámetros conocidos (la declinación la obtuvimos previamente gracias a (15)). El inconveniente es que nos encontramos ante una ambigüedad en el valor del ángulo horario: si bien éste puede tomar valores entre 0 o y 360 o2, el arcoseno nos devolverá valores dentro de su conjunto imagen: [-90 o ;90 o ]. Por esta razón, debemos hacer uso de la relación (3): sen(90 o + δ) cos t = sen(90 o + ϕ) cos(90 o h) cos(90 o + ϕ) sen(90 o h) cos A cos ϕ sen h + sen ϕ cos h cos A cos t = (17) cos δ Ahora sí, podemos aprovechar la información que nos ofrecen ambas ecuaciones para conocer inequívocamente el valor de t. Una posible manera de 2 O entre 0 h y 24 h, como con más frecuencia se emplea en Astronomía. 11
12 conseguirlo, es usar primero la ecuación (16), y luego tomando el signo del segundo miembro de (17), ubicar a t en el cuadrante correcto. Observemos también que podemos expresar tg t como un cociente, dividiendo (16) y (17): tg t = sen A cos h cos ϕ sen h + sen ϕ cos h cos A (18) La utilidad de esta fórmula queda de manifiesto al considerar que la mayoría de los lenguajes de programación (incluyendo los que forman parte de las planillas de cálculo) tienen una función arcotangente que admite dos parámetros, que son interpretados por el lenguaje precisamente como el numerador y el denominador de una fracción igual a la tangente del ángulo buscado, devolviendo éste en el cuadrante correcto de manera automática. Resulta interesante observar, nuevamente, que esta fórmula expresa que t depende exclusivamente de la altura, el acimut y la latitud del lugar ( incluso la declinación tuvo la delicadeza de desaparecer en el cociente!) Ecuatoriales a acimutales El problema es en esencia el mismo, pero propuesto para otros ángulos: sen h = sen ϕ sen δ + cos ϕ cos δ cos t (19) cos A = sen t cos δ sen A = cos h sen ϕ cos δ cos t cos ϕ sen δ cos h tg A = sen t cos δ sen ϕ cos δ cos t cos ϕ sen δ (20) Pueden realizarse las mismas observaciones que en el apartado anterior. 12
13 4.2. Problemas varios Problema N o 76 de [2] Expresar la distancia angular d entre dos puntos de la esfera celeste, las coordenadas de los cuales son dadas en el sistema ecuatorial Problema N o 168 de [2] Deducir la fórmula que expresa, para una estrella de declinación δ mayor a la latitud ϕ del lugar (siendo ambas del mismo signo), el valor máximo del acimut A (al este y al oeste del meridiando del lugar) Proyección del recorrido solar sobre el ecuador celeste 1. Expresar la proyección del recorrido α del Sol sobre el ecuador celeste desde un equinoccio, conociendo el valor de su recorrido sobre la eclíptica y, por supuesto, la inclinación de este plano Expresar la proyección del recorrido α del Sol sobre el ecuador celeste desde un equinoccio, conociendo el valor de la declinación solar y, por supuesto, la inclinación de la eclíptica Acimut de salida y puesta de un astro Expresar el valor del acimut de salida y puesta de un astro, conociendo su declinación y la latitud del lugar Arco diurno de un astro Expresar el valor del arco D del recorrido diurno de un astro no circumpolar, conociendo su declinación y la latitud del lugar. 3 Como ejercicio interesante puede el lector usar la solución de este problema para trazar la parte de la ecuación de tiempo debida a la inclinación de la eclíptica. 13
14 Respuestas a los problemas cos d = sen δ 1 sen δ 2 + cos δ 1 cos δ 2 cos α Lo importante es elegir correctamente el triángulo esférico; existe el riesgo de pretender construir uno rectángulo, con la hipotenusa coincidente con la distancia buscada: el problema que puede pasarse por alto es que uno de los catetos, en ese caso, será un arco de paralelo celeste, que (salvo el caso especial del ecuador) no es un círculo máximo, por lo que el pretendido triángulo esférico no es tal, resultando inaplicables a él las ecuaciones deducidas en este apunte. El triángulo esférico que nos permite resolver el problema es el de la figura sen A = cos δ cos ϕ La clave consiste en observar que la condición establecida por el problema se corresponde al momento en que el círculo de altura del astro es tangente a su paralelo celeste, lo que determina un valor del ángulo paraláctico igual a 90 o. P 90 o δ 1 α 90 o δ 2 PC Z A 90 o h 90 o + ϕ 90 o + δ t PC d Q 90 o Figura 6: Problema Figura 7: Problema tg α = tg λ cos i 14
15 Podemos aplicar la relación (7), teniendo en cuenta que la proyección se realiza a lo largo de un meridiano celeste, que es perpendicular al ecuador celeste, por lo que queda determinado un triángulo esférico rectángulo, como se aprecia en la figura 8. Eq i Eclíptica λ Ecuador α celeste δ Figura 8: Proyección del recorrido solar sobre el ecuador celeste desde un equinoccio sen α = tg δ tg i Se utiliza la ecuación (11), válida por las mismas razones del problema anterior. cos A = sen δ cos ϕ Sólo hay que usar la ecuación (2) con h = cos D 2 = tg δ tg ϕ Nuevamente hay que usar la ecuación (2) con h = 0, teniendo en cuenta además que el ángulo buscado es el doble del ángulo horario. A. Cálculo de la hora sidérea Como dijéramos en la sección 4.1, para obtener la ascensión recta de un astro conociendo su ángulo horario es preciso saber la hora sidérea del lugar de observación. En este apéndice se da una receta sin demostración para calcularla. 15
16 A.1. Cálculo del día juliano a las 0hTU En primer lugar, es necesario obtener el valor del día juliano para las 0hTU del día en cuestión. Sean DÍA, MES y AÑO los valores numéricos de la fecha (para enero, febrero, marzo, etc., los valores de MES son 1, 2, 3, etc.). Deben realizarse los siguientes pasos preliminares: 1. Si MES < 3, restar 1 a AÑO y sumar 12 a MES. 2. Calcular A = AÑO/ Calcular B = 2 A + A/4 Finalmente, obtenemos el día juliano a las 0hTU: DJ 0hT U = 365, 25 (AÑO+4716) + 30, 6001 (MES+1) +DÍA+B 1524, 5 A.2. Cálculo de la hora sidérea local Primero debe calcularse, para el día en cuestión: T = DJ 0hT U Entonces la hora sidérea en Greenwich a las 0hTU (θ G,0hT U ) se obtiene así: θ G,0hT U = 6 h 41 m 50 s, s, T + 0 s, T 2 0 s, T 3 Para obtener la hora sidérea en Greenwich a otra hora de tiempo universal (θ G,t ) de ese mismo día, es necesario sumarle dicha hora multiplicada por 1, : ( θ G,t = θ G,0hT U + 1, hora + minutos + segundos ) el operador x devuelve la parte entera de x por truncamiento: 5, 12 = 5; 7, 99 = 7; 3, 14 = 3. 16
17 Finalmente, para obtener la hora sidérea local en ese mismo instante (θ s ), es necesario sumar a θ G,t la longitud (λ) del lugar (expresada en horas), tomada positiva al este de Greenwich y negativa al oeste: θ s = θ G,t + λ A.3. Ejemplo: cálculo de la hora sidérea local Calculemos el valor de la hora sidérea para la ciudad de Buenos Aires (λ = 58 o = 3 h 54 m ) el día 2 de julio de 2012, a las 13:26 hora local (16:26 TU). 1. DÍA = 2, MES = 7 y AÑO = MES > 2, por lo que MES y AÑO mantienen sus valores. 3. A = AÑO/100 = B = /4 = DJ 0hT U = 365, 25 ( ) + 30, 6001 (7 + 1) ( 13) 1524, 5 = , 5 6. T = , = 0, θ G,0hT U = 6 h 41 m 50 s, s, , s, , s, , = 306 h 41 m 57 s 18 h 41 m 57 s (mód 24) ) 8. θ G,t = 18 h 41 m 57 s +1, ( = 35 h 10 m 39 s 11 h 10 m 39 s (mód 24) 9. θ s = 11 h 10 m 39 s + 3 h 54 m = 7 h 16 m 39 s 17
18 B. La trigonometría plana como caso particular de la esférica Si tomamos sobre la esfera triángulos de lados cada vez más pequeños (sin que por eso varíen sus ángulos diedros), resulta natural pensar que iremos obteniendo triángulos cada vez más aplanados. Otra forma de pensarlo es imaginar que la esfera adopta en relación al triángulo de interés un radio tan grande que en el entorno del triángulo su superficie no difiere sensiblemente de un plano 5. En ese sentido resulta interesante intentar obtener fórmulas que sabemos válidas en el plano como casos límite de las fórmulas válidas en la esfera. Si los lados de un triángulo esférico son lo suficientemente pequeños, podremos reemplazar el valor de sus senos y cosenos por las correspondientes aproximaciones según los primeros términos de sus series de Taylor 6 : sen α = α y cos α = 1 α 2 /2. Apliquemos estas relaciones a la ecuación (2): 1 a2 2 = (1 b2 2 ) (1 c2 2 ) + bc cos A 1 a2 2 = 1 c2 2 b2 2 + b2 c 2 + bc cos A 2 2 a 2 = b 2 + c 2 2bc cos A b2 c 2 (21) 2 El lector reconocerá en (21) la famosa fórmula del coseno de la trigonometría plana 7. La aplicación a la fórmula (4) es aún más directa la fórmula del seno: sen A = sen B = sen C a b c Vimos en la sección 3.1 que si A = 90 o, resulta válida la ecuación (5): 5 Resulta inevitable compartir con el lector el ejemplo que sin duda ya adivinó: un triángulo sobre la superficie terrestre, si es de pequeñas proporciones en relación con el tamaño de nuestro planeta, debe dejarse tratar tanto con las fórmulas de la trigonometría plana como con las de la esférica. 6 Naturalmente, con los ángulos expresados en radianes. 7 El término b2 c 2 2 no debería distraernos demasiado, ya que al ser un infinitésimo de orden superior al resto, sería uno de los primeros fantasmas de cantidades evanescentes en desaparecer... 18
19 cos a = cos b cos c Querrá el lector obtener de ella la correspondiente y ubicua fórmula que sin duda ya anticipa? C. Deducción vectorial de las fórmulas fundamentales Podemos formar tres vectores con el centro de una esfera y los tres vértices de un triángulo trazado sobre la misma. Así, el ángulo entre los vectores A y B será igual a c, el ángulo entre A y C será igual a b, y entre B y C será a. También, el ángulo entre el plano que contiene a los vectores A y B y el que contiene a A y C será igual a A (lo propio puede decirse de los restantes planos respectivos). y A c b B a C x z Figura 9: Triángulo esférico De acuerdo a la figura (9), orientaremos los ejes de forma que el vector A coincida con el eje y y el vector B se halle en el plano yz (es fácil ver que esto siempre es posible). En este sistema de coordenadas (y si asumimos sin pérdida de generalidad que la esfera tiene radio unitario), resulta: A = (0, 1, 0), B = (0, cos c, sen c) y C = (sen b sen A, cos b, sen b cos A). 19
20 Por un lado: B C = cos a Por el otro: B C = 0 sen b sen A+cos c cos b+sen c sen b cos A = cos c cos b+sen c sen b cos A Igualando ambos resultados: cos a = cos c cos b + sen c sen b cos A que es la fórmula (2). Y las demás fórmulas pueden deducirse de ésta. Referencias [1] Bakulin, Kononovich, Moroz, Curso de astronomía general, MIR, Moscú, [2] Vorontsov, Veliamínov, Problemas y ejercicios prácticos de astronomía, Mir, Moscú, [3] Asín, Astronomía, Paraninfo, Madrid, [4] Meeus, Astronomical Algorithms, Willmann Bell, Richmond, [5] Todhunter, I., Spherical Trigonometry, MacMillan, Londres,
RESUMEN GEODESIA ASTRONOMICA.-
 RESUMEN GEODESIA ASTRONOMICA.- Esfera Celeste: La esfera celeste es una superficie hipotética de forma abovedada sobre la cual se consideran proyectados todos los astros dispersos en el espacio. Esta bóveda
RESUMEN GEODESIA ASTRONOMICA.- Esfera Celeste: La esfera celeste es una superficie hipotética de forma abovedada sobre la cual se consideran proyectados todos los astros dispersos en el espacio. Esta bóveda
Escuela de Agrimensura
 Escuela de Agrimensura Coordenadas Geográficas Meridianos y paralelos Ecuador Meridiano de Greenwich Coordenada ascendente Longitud: ángulo entre el meridiano de Greenwich y el meridiano del lugar. Coordenada
Escuela de Agrimensura Coordenadas Geográficas Meridianos y paralelos Ecuador Meridiano de Greenwich Coordenada ascendente Longitud: ángulo entre el meridiano de Greenwich y el meridiano del lugar. Coordenada
Sistemas de Coordenadas Astronómicas. Posiciones Especiales de los Astros
 continuación del Tema 1 Sistemas de Coordenadas Astronómicas. Posiciones Especiales de los Astros 1.6- Fórmulas de Nepper para triángulos esféricos Al trabajar con triángulos esféricos es conveniente,
continuación del Tema 1 Sistemas de Coordenadas Astronómicas. Posiciones Especiales de los Astros 1.6- Fórmulas de Nepper para triángulos esféricos Al trabajar con triángulos esféricos es conveniente,
TRIGONOMETRÍA: MEDIDA DE ÁNGULOS
 el blog de mate de aida: trigonometría º ESO pág. 1 TRIGONOMETRÍA: MEDIDA DE ÁNGULOS Ángulo es la porción del plano limitada por dos semirrectas de origen común. Medidas de ángulos Medidas en grados Un
el blog de mate de aida: trigonometría º ESO pág. 1 TRIGONOMETRÍA: MEDIDA DE ÁNGULOS Ángulo es la porción del plano limitada por dos semirrectas de origen común. Medidas de ángulos Medidas en grados Un
CAPITÁN DE YATE MÓDULO DE NAVEGACIÓN ENERO 2017
 CAPITÁN DE YATE MÓDULO DE NAVEGACIÓN ENERO 2017 NOMBRE: APELLIDOS: D.N.I.: TEORÍA DE NAVEGACIÓN 01.- Cuáles de los siguientes puntos de la eclíptica del Sol tienen declinación igual a cero? a) Aries y
CAPITÁN DE YATE MÓDULO DE NAVEGACIÓN ENERO 2017 NOMBRE: APELLIDOS: D.N.I.: TEORÍA DE NAVEGACIÓN 01.- Cuáles de los siguientes puntos de la eclíptica del Sol tienen declinación igual a cero? a) Aries y
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS
 TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
Determinación de la Longitud
 Tema 7 Determinación de la Longitud Geográfica DETERMINACION DE LA LONGITUD DE UNA ESTACION. El objeto de la Astronomía de Posición es la determinación de las coordenadas geográficas terrestres de un Punto
Tema 7 Determinación de la Longitud Geográfica DETERMINACION DE LA LONGITUD DE UNA ESTACION. El objeto de la Astronomía de Posición es la determinación de las coordenadas geográficas terrestres de un Punto
TRIGONOMETRÍA. π radianes. 1.- ÁNGULOS Y SUS MEDIDAS. 1.1 Los ángulos orientados
 TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
TRIGONOMETRÍA.- ÁNGULOS Y SUS MEDIDAS. Los ángulos orientados Son aquellos que además de tener una cierta su amplitud ésta viene acompañada de un signo que nos indica un orden de recorrido (desde la semirrecta
Trigonometría y Análisis Vectorial
 Unidad Educativa enezuela Trigonometría nálisis ectorial Prof. Ronn J. ltuve Unidad Educativa enezuela Trigonometría nálisis ectorial 1. Teorema de Pitágoras: establece que en un triángulo rectángulo el
Unidad Educativa enezuela Trigonometría nálisis ectorial Prof. Ronn J. ltuve Unidad Educativa enezuela Trigonometría nálisis ectorial 1. Teorema de Pitágoras: establece que en un triángulo rectángulo el
Además de la medida, que estudiaremos a continuación, consideraremos que los ángulos tienen una orientación de acuerdo con el siguiente convenio:
 Trigonometría La trigonometría trata sobre las relaciones entre los ángulos y los lados de los triángulos. El concepto fundamental sobre el que se trabaja es el de ángulo. Dos semirrectas con un origen
Trigonometría La trigonometría trata sobre las relaciones entre los ángulos y los lados de los triángulos. El concepto fundamental sobre el que se trabaja es el de ángulo. Dos semirrectas con un origen
Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99, 01, curso cero de física
 VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
Razones trigonométricas.
 Razones trigonométricas. Matemáticas I 1 Razones trigonométricas. Medidas de ángulos. Medidas en grados (Deg.) El grado es el ángulo plano que teniendo su vértice en el centro de un círculo intercepta
Razones trigonométricas. Matemáticas I 1 Razones trigonométricas. Medidas de ángulos. Medidas en grados (Deg.) El grado es el ángulo plano que teniendo su vértice en el centro de un círculo intercepta
RESOLUCIÓN DE TRIÁNGULOS
 RESOLUCIÓN DE TRIÁNGULOS Resolver un triángulo consiste en determinar la longitud de sus tres lados y la amplitud de sus tres ángulos. Vamos a recordar primero la resolución para triángulos rectángulos
RESOLUCIÓN DE TRIÁNGULOS Resolver un triángulo consiste en determinar la longitud de sus tres lados y la amplitud de sus tres ángulos. Vamos a recordar primero la resolución para triángulos rectángulos
Matemáticas Física Curso de Temporada Verano Ing. Pablo Marcelo Flores Jara
 Matemáticas Física Curso de Temporada Verano 2016 Ing. Pablo Marcelo Flores Jara pablofloresjara@gmail.com UNIDAD II: RESOLUCIÓN DE TRIÁNGULO CUALESQUIERA U OBLICUÁNGULOS Ing. Pablo Marcelo Flores Jara
Matemáticas Física Curso de Temporada Verano 2016 Ing. Pablo Marcelo Flores Jara pablofloresjara@gmail.com UNIDAD II: RESOLUCIÓN DE TRIÁNGULO CUALESQUIERA U OBLICUÁNGULOS Ing. Pablo Marcelo Flores Jara
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Examen de Capitán de Yate, Pais Vasco Febrero 2016 Autor: Pablo González de Villaumbrosia García
 Examen de Capitán de Yate, Pais Vasco Febrero 2016 Autor: Pablo González de Villaumbrosia García. 19.03.2016 http://www.villaumbrosia.es Teoría de navegación 21. El horario en Greenwich de un astro cualquiera
Examen de Capitán de Yate, Pais Vasco Febrero 2016 Autor: Pablo González de Villaumbrosia García. 19.03.2016 http://www.villaumbrosia.es Teoría de navegación 21. El horario en Greenwich de un astro cualquiera
intersección de dicho meridiano sobre el Ecuador.
 Tema 6 Determinación de la Latitud Geográfica 5.1 Definiciones De acuerdo a la [Figura 5.1a] siguiente pueden darse tres diferentes definiciones de Latitud (): a) es el arco de meridiano comprendido entre
Tema 6 Determinación de la Latitud Geográfica 5.1 Definiciones De acuerdo a la [Figura 5.1a] siguiente pueden darse tres diferentes definiciones de Latitud (): a) es el arco de meridiano comprendido entre
TRIGONOMETRÍA. CONVERSIÓN DE UN SISTEMA A OTRO Tomando como base la equivalencia de un sistema a otro, podemos establecer la siguiente fórmula:
 Cursos ALBERT EINSTEIN ONLINE Calle Madrid Esquina c/ Av La Trinidad LAS MERCEDES 9937172 9932305! www. a-einstein.com TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS SISTEMA SEXAGESIMAL: Es el que considera
Cursos ALBERT EINSTEIN ONLINE Calle Madrid Esquina c/ Av La Trinidad LAS MERCEDES 9937172 9932305! www. a-einstein.com TRIGONOMETRÍA SISTEMAS DE MEDIDAS DE ÁNGULOS SISTEMA SEXAGESIMAL: Es el que considera
Soluciones Nota nº 1
 Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
GUÍA DE APRENDIZAJE Introducción al álgebra vectorial
 Liceo Juan XXIII V.A Departamento de ciencias Física Prof. David Valenzuela GUÍA DE APRENDIZAJE Introducción al álgebra vectorial www.fisic.jimdo.com Tercero medio diferenciado Magnitudes escalares y vectoriales
Liceo Juan XXIII V.A Departamento de ciencias Física Prof. David Valenzuela GUÍA DE APRENDIZAJE Introducción al álgebra vectorial www.fisic.jimdo.com Tercero medio diferenciado Magnitudes escalares y vectoriales
TRIGONOMETRÍA. MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico. 1.- Ángulos en la Circunferencia.
 TRIGONOMETRÍA MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico 1.- Ángulos en la Circunferencia. 2.- Razones Trigonométricas de un Triángulo Rectángulo. 3.- Valores del Seno, Coseno y Tangente
TRIGONOMETRÍA MATEMÁTICAS I 1º Bachillerato Ciencias de la Salud y Tecnológico 1.- Ángulos en la Circunferencia. 2.- Razones Trigonométricas de un Triángulo Rectángulo. 3.- Valores del Seno, Coseno y Tangente
EJERCICIOS DE GEOMETRÍA PLANA. 1. Hallar las ecuaciones paramétricas de la recta r que pasa por el punto ( 2, 2) tiene como vector director el vector
 EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
Sistemas de coordenadas celestes (resumen)
 istemas de celestes (resumen) suponiendo la tierra homogénea y esférica podemos dar las siguientes definiciones: esfera celeste: esfera imaginaria con centro en el observador y radio arbitrario donde,
istemas de celestes (resumen) suponiendo la tierra homogénea y esférica podemos dar las siguientes definiciones: esfera celeste: esfera imaginaria con centro en el observador y radio arbitrario donde,
= λ + 1 y el punto A(0, 7, 5)
 94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
94 GEOMETRÍA ANALÍTICA DEL ESPACIO en las PAU de Asturias Dados los puntos A(1, 0, 1), B(l, 1, 1) y C(l, 6, a), se pide: a) hallar para qué valores del parámetro a están alineados b) hallar si existen
OPERACIONES GEOMÉTRICAS CON VECTORES
 GUÍA DE APRENDIZAJE Introducción al álgebra vectorial www.fisic.ch Profesor: David Valenzuela Z Magnitudes escalares y vectoriales La gran variedad de cosas medibles (magnitudes) se pueden clasificar en
GUÍA DE APRENDIZAJE Introducción al álgebra vectorial www.fisic.ch Profesor: David Valenzuela Z Magnitudes escalares y vectoriales La gran variedad de cosas medibles (magnitudes) se pueden clasificar en
4, halla sen x y tg x. 5
 TRIGONOMETRÍA 1º.- Sabiendo que 90 º < x < 70 º y que 4, halla sen x y tg x. 5 a) sen x? ; de la fórmula fundamental sen x + cos x 1 se obtiene sen x 1 - cos x. 9 5 de donde sen x 5 3, solución positiva
TRIGONOMETRÍA 1º.- Sabiendo que 90 º < x < 70 º y que 4, halla sen x y tg x. 5 a) sen x? ; de la fórmula fundamental sen x + cos x 1 se obtiene sen x 1 - cos x. 9 5 de donde sen x 5 3, solución positiva
Razones trigonométricas
 RESUMEN TRIGONOMETRIA Para medir ángulos se utilizan las siguientes unidades: 1Grado sexagesimal ( ): Si se divide la circunferencia en 360 partes iguales, el ángulo central correspondiente a cada una
RESUMEN TRIGONOMETRIA Para medir ángulos se utilizan las siguientes unidades: 1Grado sexagesimal ( ): Si se divide la circunferencia en 360 partes iguales, el ángulo central correspondiente a cada una
UNIDAD DE APRENDIZAJE III
 UNIDAD DE APRENDIZAJE III Saberes procedimentales 1. Utiliza correctamente el lenguaje algebraico, geométrico y trigonométrico.. Identifica la simbología propia de la geometría y la trigonometría. Saberes
UNIDAD DE APRENDIZAJE III Saberes procedimentales 1. Utiliza correctamente el lenguaje algebraico, geométrico y trigonométrico.. Identifica la simbología propia de la geometría y la trigonometría. Saberes
ASIGNATURA: MATEMÁTICA. Contenido: TRIGONOMETRÍA I TEORÍA
 ASIGNATURA: MATEMÁTICA Contenido: TRIGONOMETRÍA I TEORÍA Docente: Teneppe María Gabriela Medida de ángulos: Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
ASIGNATURA: MATEMÁTICA Contenido: TRIGONOMETRÍA I TEORÍA Docente: Teneppe María Gabriela Medida de ángulos: Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
Medida de ángulos. Es la medida de un ángulo cuyo arco mide un radio. 2 rad = 360. rad = º rad
 Medida de ángulos Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. El ángulo es positivo si se desplaza
Medida de ángulos Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. El ángulo es positivo si se desplaza
TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS
 IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
4.1. Qué es un número complejo. Representación geométrica.
 Tema Números complejos.. Qué es un número complejo. Representación geométrica. Un número complejo z C C es el conjunto de los números complejos es una expresión de la forma z a + b i en la que a, b R a
Tema Números complejos.. Qué es un número complejo. Representación geométrica. Un número complejo z C C es el conjunto de los números complejos es una expresión de la forma z a + b i en la que a, b R a
Examen de Capitán de Yate, Vigo Septiembre 2015 Autor: Pablo González de Villaumbrosia García
 Examen de Capitán de Yate, Vigo Septiembre 2015 Autor: Pablo González de Villaumbrosia García. 18.03.2016 http://www.villaumbrosia.es Teoría de navegación 1. Cómo se llama el círculo máximo perpendicular
Examen de Capitán de Yate, Vigo Septiembre 2015 Autor: Pablo González de Villaumbrosia García. 18.03.2016 http://www.villaumbrosia.es Teoría de navegación 1. Cómo se llama el círculo máximo perpendicular
TEMA 5 SEMEJANZA Y TRIGONOMETRÍA
 TEMA 5 SEMEJANZA Y TRIGONOMETRÍA. Objetivos / Criterios de evaluación O.5.1 Triángulos semejantes, criterios para la semejanza de triángulos O.5.2 Teorema de Tales. Aplicaciones. O.5.3 Teoremas de Pitágoras,
TEMA 5 SEMEJANZA Y TRIGONOMETRÍA. Objetivos / Criterios de evaluación O.5.1 Triángulos semejantes, criterios para la semejanza de triángulos O.5.2 Teorema de Tales. Aplicaciones. O.5.3 Teoremas de Pitágoras,
UNIDAD III TRIGONOMETRIA
 UNIDAD III TRIGONOMETRIA 1 UNIDAD III TRIGONOMETRIA TEMARIO. 1. Relación del par ordenado en un plano bidimensional. 1.1. El plano coordenado 1.2. Localización de puntos en los cuatro cuadrantes 2. Ángulos
UNIDAD III TRIGONOMETRIA 1 UNIDAD III TRIGONOMETRIA TEMARIO. 1. Relación del par ordenado en un plano bidimensional. 1.1. El plano coordenado 1.2. Localización de puntos en los cuatro cuadrantes 2. Ángulos
TEMA 3. TRIGONOMETRÍA
 TEMA 3. TRIGONOMETRÍA Definiciones: 0 30 45 60 90 180 270 360 Seno 0 1 0-1 0 Coseno 1 0-1 0 1 Tangente 0 1 0 0 Teorema del seno: Teorema del coseno: Fórmulas elementales: FÓRMULAS TRIGONOMÉTRICAS. Suma
TEMA 3. TRIGONOMETRÍA Definiciones: 0 30 45 60 90 180 270 360 Seno 0 1 0-1 0 Coseno 1 0-1 0 1 Tangente 0 1 0 0 Teorema del seno: Teorema del coseno: Fórmulas elementales: FÓRMULAS TRIGONOMÉTRICAS. Suma
Seno (matemáticas) Coseno Tangente
 Seno (matemáticas), una de las proporciones fundamentales de la trigonometría. En un triángulo rectángulo, el valor del seno (que suele abreviarse sen) de un ángulo agudo es igual a la longitud del cateto
Seno (matemáticas), una de las proporciones fundamentales de la trigonometría. En un triángulo rectángulo, el valor del seno (que suele abreviarse sen) de un ángulo agudo es igual a la longitud del cateto
Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula:
 PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
Astrofísica - I Introducción. 2 - La Esfera Celeste
 Astrofísica - I Introducción 2 - La Esfera Celeste Astrofísica - I Introducción 2 - La Esfera Celeste Astronomía de posición Sistema de coordenadas horizontales Movimiento diurno de las estrellas Sistema
Astrofísica - I Introducción 2 - La Esfera Celeste Astrofísica - I Introducción 2 - La Esfera Celeste Astronomía de posición Sistema de coordenadas horizontales Movimiento diurno de las estrellas Sistema
Seminario de problemas-eso. Curso Hoja 14
 Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
CAPÍTULO I TRIGONOMETRÍA ESFÉRICA
 Preliminares Fórmula del coseno Fórmula del seno Otras fórmulas Polaridad Triángulos esféricos CAPÍTULO I TRIGONOMETRÍA ESFÉRICA Índice del capítulo Problemas propuestos Bibliografía 1 1. Trigonometría
Preliminares Fórmula del coseno Fórmula del seno Otras fórmulas Polaridad Triángulos esféricos CAPÍTULO I TRIGONOMETRÍA ESFÉRICA Índice del capítulo Problemas propuestos Bibliografía 1 1. Trigonometría
TRIGONOMETRÍA. 1. Ángulos. 2. Razones trigonométricas de ángulos agudos
 TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
UNIVERSIDAD JOSE CARLOS MARIATEGUI CAPITULO 2 VECTORES
 CAPITULO 2 VECTORES 2.1 Escalares y Vectores Una cantidad física que pueda ser completamente descrita por un número real, en términos de alguna unidad de medida de ella, se denomina una cantidad física
CAPITULO 2 VECTORES 2.1 Escalares y Vectores Una cantidad física que pueda ser completamente descrita por un número real, en términos de alguna unidad de medida de ella, se denomina una cantidad física
meridiano de referencia: círculos máximos que
 coordenadas geográficas meridianos terrestres: meridiano de referencia: círculos máximos que meridiano de Greenwich contienen al eje de P rotación terrestre λ(longitud geográfica)=0h 0h λ 24h + hacia el
coordenadas geográficas meridianos terrestres: meridiano de referencia: círculos máximos que meridiano de Greenwich contienen al eje de P rotación terrestre λ(longitud geográfica)=0h 0h λ 24h + hacia el
Medida de ángulos. Para medir ángulos se utilizan las siguientes unidades:
 Medida de ángulos Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. El ángulo es positivo si se desplaza
Medida de ángulos Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. El ángulo es positivo si se desplaza
SERIE ÁLGEBRA VECTORIAL
 SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
Introducción a la observación astronómica
 Introducción a la observación astronómica Esfera Celeste Werner Omar Chanta Bautista Licenciatura en Física Aplicada, USAC www. astronomia. org. gt 22 de junio de 2012 Werner Chanta (USAC) Observación
Introducción a la observación astronómica Esfera Celeste Werner Omar Chanta Bautista Licenciatura en Física Aplicada, USAC www. astronomia. org. gt 22 de junio de 2012 Werner Chanta (USAC) Observación
EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA 1)
 Colegio Diocesano Asunción de Nuestra Señora Ávila Tema EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA ).- Dados los ángulos = º y = 7º, calcula: a) + b) c) d).- Dados los ángulos = º 7 y = 7º, calcula:
Colegio Diocesano Asunción de Nuestra Señora Ávila Tema EJERCICIOS DE RELACIONES TRIGONOMÉTRICAS (TEMA ).- Dados los ángulos = º y = 7º, calcula: a) + b) c) d).- Dados los ángulos = º 7 y = 7º, calcula:
MOVIMIENTOS DE LA TIERRA
 MOVIMIENTOS DE LA TIERRA Está sujeta a más m s de 10 movimientos Movimiento de rotación Movimiento de traslación 930 millones de km Distancia media al sol 1 U.A. (150 millones km) 30 km por segundo Órbita
MOVIMIENTOS DE LA TIERRA Está sujeta a más m s de 10 movimientos Movimiento de rotación Movimiento de traslación 930 millones de km Distancia media al sol 1 U.A. (150 millones km) 30 km por segundo Órbita
TRIGONOMETRÍA ESFÉRICA 2001 Kepler C k Ikastegia
 TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
TRIGNMETRÍ ESFÉRI 2001 Kepler k Ikastegia 2 1.1 Introducción La Trigonometría es una rama de la Matemática en la que se analiza la medida de las partes de los triángulos, tanto de los triángulos planos
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS
 TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
Ejercicio 1 de la Opción A del modelo 6 de Solución
 Ejercicio 1 de la Opción A del modelo 6 de 2003 [2'5 puntos] Sea la función f : R R definida por f(x) = 2x 3-6x + 4. Calcula el área del recinto limitado por la gráfica de f y su recta tangente en el punto
Ejercicio 1 de la Opción A del modelo 6 de 2003 [2'5 puntos] Sea la función f : R R definida por f(x) = 2x 3-6x + 4. Calcula el área del recinto limitado por la gráfica de f y su recta tangente en el punto
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES
 4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 4.1.1. El teorema de Thales y consecuencias. 4.1.1. El teorema
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 4.1.1. El teorema de Thales y consecuencias. 4.1.1. El teorema
Trigonometría. 1. Ángulos:
 Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
Trigonometría. Ángulos: - Ángulos en posición estándar: se ubican en un sistema de coordenadas XY. El vértice será el origen (0,0) y el lado inicial coincide con el eje X positivo. - Ángulos positivos:
ASTRONOMÍA DE POSICIÓN
 ASTRONOMÍA DE POSICIÓN X Proyección en la esfera celeste Aunque hoy sabemos que los objetos astronómicos están distribuidos en tres dimensiones, sigue siendo cómodo describir sus posiciones en el cielo
ASTRONOMÍA DE POSICIÓN X Proyección en la esfera celeste Aunque hoy sabemos que los objetos astronómicos están distribuidos en tres dimensiones, sigue siendo cómodo describir sus posiciones en el cielo
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS
 TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
TEORÍA DE ECLIPSES, OCULTACIONES Y TRÁNSITOS F. Javier Gil Chica UNIVERSIDAD DE ALICANTE Edita: Publicaciones Universidad de Alicante ISBN: 84-7908-270-4 Depósito Legal: MU-1.461-1996 Edición a cargo de
Examen de Capitán de Yate, Asturias Enero 2016 Autor: Pablo González de Villaumbrosia García
 Examen de Capitán de Yate, Asturias Enero 2016 Autor: Pablo González de Villaumbrosia García. 11.03.2016 http://www.villaumbrosia.es Teoría de navegación 1. La altura de un astro se define como el arco
Examen de Capitán de Yate, Asturias Enero 2016 Autor: Pablo González de Villaumbrosia García. 11.03.2016 http://www.villaumbrosia.es Teoría de navegación 1. La altura de un astro se define como el arco
FORMULARIO DE TRIGONOMETRIA PLANA Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas
 FORMULARIO DE TRIGONOMETRIA PLANA 01.- Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas 03.- Razones trigonometricas de la suma de dos angulos
FORMULARIO DE TRIGONOMETRIA PLANA 01.- Definicion de las seis razones trigonometricas 02.- Relaciones fundamentales entre las razones trigonometricas 03.- Razones trigonometricas de la suma de dos angulos
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS
 11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
Navegación Pesca Y Transporte Marítimo Gobierno del Buque. Tema 2 Coordenadas celestes.
 ÍNDICE 1.1 INTRODUCCIÓN 1.2 COORDENADAS HORIZONTALES 1.3 COORDENADAS HORARIAS 1.4 COORDENADAS URANOGRÁFICAS O ECUATORIALES 1.5 RELACIÓN ENTRE LOS DISTINTOS SISTEMAS DE COORDENADAS QUE SE MIDEN EN EL ECUADOR.
ÍNDICE 1.1 INTRODUCCIÓN 1.2 COORDENADAS HORIZONTALES 1.3 COORDENADAS HORARIAS 1.4 COORDENADAS URANOGRÁFICAS O ECUATORIALES 1.5 RELACIÓN ENTRE LOS DISTINTOS SISTEMAS DE COORDENADAS QUE SE MIDEN EN EL ECUADOR.
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
Se entiende por trigonometría, según su origen griego, la ciencia que tiene por objetivo la medida de los lados y los ángulos de los triángulos.
 Unidad Trigonometría Introducción... Ángulos. Medida de ángulos... Razones trigonométricas de un ángulo... Resolución de triángulos: triángulos rectángulos... Casos concretos... Introducción Se entiende
Unidad Trigonometría Introducción... Ángulos. Medida de ángulos... Razones trigonométricas de un ángulo... Resolución de triángulos: triángulos rectángulos... Casos concretos... Introducción Se entiende
Nociones elementales de trigonometría
 Nociones elementales de trigonometría La parte de la Matemática que se basa en las propiedades especiales de un triángulo rectángulo se llama trigonometría. Muchos conceptos de trigonometría son muy importantes
Nociones elementales de trigonometría La parte de la Matemática que se basa en las propiedades especiales de un triángulo rectángulo se llama trigonometría. Muchos conceptos de trigonometría son muy importantes
MATEMÁTICAS UNIDAD 3 GRADO 10º. IDENTIDADES trigonométricas
 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD GRADO 0º IDENTIDADES trigonométricas Franklin Eduardo Pérez Quintero LOGRO: Utilizar las funciones trigonométricas y las identidades principales para
Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD GRADO 0º IDENTIDADES trigonométricas Franklin Eduardo Pérez Quintero LOGRO: Utilizar las funciones trigonométricas y las identidades principales para
José Antonio Jiménez Nieto
 TRIGONOMETRÍA. UNIDADES PARA MEDIR ÁNGULOS Un ángulo es una porción de plano limitada por dos semirrectas que tienen un origen común. Las unidades que más frecuentemente se utilizan para medir ángulos
TRIGONOMETRÍA. UNIDADES PARA MEDIR ÁNGULOS Un ángulo es una porción de plano limitada por dos semirrectas que tienen un origen común. Las unidades que más frecuentemente se utilizan para medir ángulos
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
Sistema de coordenadas. Plano cartesiano
 Geometría analítica La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.. Actualmente la geometría
Geometría analítica La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.. Actualmente la geometría
IES EL PILES SELECTIVIDAD OVIEDO DPTO. MATEMÁTICAS Geometría
 P.A.U. de. (Oviedo). (junio 994) Dados los puntos A (,0, ), B (,, ), C (,6, a), se pide: i) hallar para qué valores del parámetro a están alineados, ii) hallar si existen valores de a para los cuales A,
P.A.U. de. (Oviedo). (junio 994) Dados los puntos A (,0, ), B (,, ), C (,6, a), se pide: i) hallar para qué valores del parámetro a están alineados, ii) hallar si existen valores de a para los cuales A,
LA RECTA Y SUS ECUACIONES
 UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
27/01/2011 TRIGONOMETRÍA Página 1 de 7
 β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
β 27/01/2011 TRIGONOMETRÍA Página 1 de 7 Notación en un triángulo: En un triángulo cualquiera llamaremos a, b y c a sus lados y A, B y C a sus vértices de forma que A sea el vértice formado por los lados
ovimiento de traslación de la tierra alrededor del sol
 ovimiento de traslación de la tierra alrededor del sol que observamos? el sol se desplaza 1 por día hacia el este con respecto a las estrellas fijas las estrellas salen 4 mas temprano cada día se mueve
ovimiento de traslación de la tierra alrededor del sol que observamos? el sol se desplaza 1 por día hacia el este con respecto a las estrellas fijas las estrellas salen 4 mas temprano cada día se mueve
EJERCICIOS DE GEOMETRÍA
 1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
4º ESO opción B Ejercicios Geometría Analítica
 Geometría Analítica 1) Las coordenadas de un punto A son (3,1) y las del vector AB son (3,4). Cuáles son las coordenadas de punto B? Determina otro punto C de modo que el vector AC tenga el mismo módulo
Geometría Analítica 1) Las coordenadas de un punto A son (3,1) y las del vector AB son (3,4). Cuáles son las coordenadas de punto B? Determina otro punto C de modo que el vector AC tenga el mismo módulo
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
EXAMEN: TEMAS 4 Y 5 BCT 1º OPCIÓN A 25/02/2015
 EXAMEN: TEMAS 4 Y BCT 1º OPCIÓN A 2/02/201 1. (1 punto) Sea M el punto medio del segmento AB. Expresa el vector OM como combinación lineal de los vectores OA y OB. Realizar una construcción gráfica de
EXAMEN: TEMAS 4 Y BCT 1º OPCIÓN A 2/02/201 1. (1 punto) Sea M el punto medio del segmento AB. Expresa el vector OM como combinación lineal de los vectores OA y OB. Realizar una construcción gráfica de
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS
 FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS Objetivo general: Brindar algunas herramientas matemáticas que los estudiantes de física necesitan para su buen desempeño en el curso de
FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS Objetivo general: Brindar algunas herramientas matemáticas que los estudiantes de física necesitan para su buen desempeño en el curso de
Introducción a la trigonometría
 UNIDAD 9: UTILICEMOS LA TRIGONOMETRIA. Introducción Introducción a la trigonometría La trigonometría es el método analítico para estudiar los triángulos y otras figuras. El estudio de la trigonometría
UNIDAD 9: UTILICEMOS LA TRIGONOMETRIA. Introducción Introducción a la trigonometría La trigonometría es el método analítico para estudiar los triángulos y otras figuras. El estudio de la trigonometría
TEMA 03 VECTORES. Prof. Ricardo Nitsche Corvalán
 1 TEMA 03 VECTORES 2 3.1.- LOS VECTORES 3.1.1.- Qué es un vector. Un vector es una cantidad física que se caracteriza por tener dos elementos: a) una magnitud, que al igual que las cantidades escalares
1 TEMA 03 VECTORES 2 3.1.- LOS VECTORES 3.1.1.- Qué es un vector. Un vector es una cantidad física que se caracteriza por tener dos elementos: a) una magnitud, que al igual que las cantidades escalares
ESTATICA. Debajo se encuentran las formulas para calcular las componentes y el ángulo α que determina la dirección de la fuerza.
 ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN
 2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
"Unidad II" Razones trigonométricas. Ing. Arnoldo Campillo Borrego.
 "Unidad II" Razones trigonométricas Ing. Arnoldo Campillo Borrego. 1 ÍNDICE Definición de funciones trigonométricas.pag. 3 Conversión de ángulos..pag. 3 Conversión de grados a radianes pag. 3 Conversión
"Unidad II" Razones trigonométricas Ing. Arnoldo Campillo Borrego. 1 ÍNDICE Definición de funciones trigonométricas.pag. 3 Conversión de ángulos..pag. 3 Conversión de grados a radianes pag. 3 Conversión
ovimiento de traslación de la tierra alrededor del sol
 ovimiento de traslación de la tierra alrededor del sol que observamos? el sol se desplaza 1 por día hacia el este con respecto a las estrellas fijas las estrellas salen 4 mas temprano cada día se mueve
ovimiento de traslación de la tierra alrededor del sol que observamos? el sol se desplaza 1 por día hacia el este con respecto a las estrellas fijas las estrellas salen 4 mas temprano cada día se mueve
Problema a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente.
 Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Tema 11: Problemas Métricos
 ..- Distancia entre dos puntos : Tema : Problemas Métricos B AB A d( A, B) AB La distancia entre dos puntos Aa (, a, a) Bbb (,, b ) es el módulo del vector que une dichos puntos: d( A, B) AB b a b a b
..- Distancia entre dos puntos : Tema : Problemas Métricos B AB A d( A, B) AB La distancia entre dos puntos Aa (, a, a) Bbb (,, b ) es el módulo del vector que une dichos puntos: d( A, B) AB b a b a b
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES
 4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
Existen geodésicas perpendiculares a cada geodésica pasando por cada punto.
 Geometría esférica La geometría de la esfera tiene importancia teórica y también práctica (para la navegación, la aviación y la astronomía). omo todas las esferas tienen la misma forma, basta considerar
Geometría esférica La geometría de la esfera tiene importancia teórica y también práctica (para la navegación, la aviación y la astronomía). omo todas las esferas tienen la misma forma, basta considerar
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
Tema 4 Trigonometría Índice
 Tema 4 Trigonometría Índice 1. Medida de un ángulo... 2 2. Razones trigonométricas en triángulos rectángulos. (Ángulos agudos)... 2 3. Relaciones trigonométricas fundamentales... 3 4. Razones trigonométricas...
Tema 4 Trigonometría Índice 1. Medida de un ángulo... 2 2. Razones trigonométricas en triángulos rectángulos. (Ángulos agudos)... 2 3. Relaciones trigonométricas fundamentales... 3 4. Razones trigonométricas...
UNIDAD DIDÁCTICA 6: Trigonometría
 UNIDAD DIDÁCTICA 6: Trigonometría 1. ÍNDICE 1. Introducción 2. Ángulos 3. Sistemas de medición de ángulos 4. Funciones trigonométricas de un ángulo 5. Teorema de Pitágoras 6. Problemas sobre resolución
UNIDAD DIDÁCTICA 6: Trigonometría 1. ÍNDICE 1. Introducción 2. Ángulos 3. Sistemas de medición de ángulos 4. Funciones trigonométricas de un ángulo 5. Teorema de Pitágoras 6. Problemas sobre resolución
Teoría Tema 9 Vectores, ángulos, vector normal de un plano y simetrías
 página 1/13 Teoría Tema 9 Vectores, ángulos, vector normal de un plano y simetrías Índice de contenido Propiedades de los vectores...2 Ángulo entre dos rectas...4 Bisectriz de dos rectas que se cortan...6
página 1/13 Teoría Tema 9 Vectores, ángulos, vector normal de un plano y simetrías Índice de contenido Propiedades de los vectores...2 Ángulo entre dos rectas...4 Bisectriz de dos rectas que se cortan...6
3. VECTOR UNITARIO DIRECCIONAL. Cada vector tiene su respectivo vector unitario. El vector unitario es paralelo a su respetivo vector de origen.
 ANÁLISIS VECTORIAL Semana 01 1. VECTOR. Se representa mediante un segmento de recta orientado. En física sirve para representar a las magnitudes físicas vectoriales. Se representa por cualquier letra del
ANÁLISIS VECTORIAL Semana 01 1. VECTOR. Se representa mediante un segmento de recta orientado. En física sirve para representar a las magnitudes físicas vectoriales. Se representa por cualquier letra del
Forma de medir los ángulos en números reales
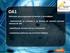 Angulo orientado Un ángulo orientado α consiste de un vértice O, una semirrecta (l i ) de origen O llamada lado inicial, otra semirrecta (l t ) de origen O llamada lado terminal, un giro g alrededor de
Angulo orientado Un ángulo orientado α consiste de un vértice O, una semirrecta (l i ) de origen O llamada lado inicial, otra semirrecta (l t ) de origen O llamada lado terminal, un giro g alrededor de
1. Producto escalar. Propiedades Norma de un vector. Espacio normado. 1.2.Ortogonalidad. Ángulos. 1.4.Producto escalar en V 3.
 . Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
. Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
VECTORES EN EL ESPACIO
 UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
Resuelve. Unidad 4. Vectores en el espacio. BACHILLERATO Matemáticas II. Diagonal de un ortoedro y volumen de un paralelepípedo.
 Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
Si la longitud s del arco MN coincide con la longitud de r, entonces el ángulo subtendido desde el centro O corresponde a 1 radian.
 1 ÁNGULOS EN RADIANES El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del
1 ÁNGULOS EN RADIANES El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia y abarca un arco cuya longitud es igual a la del
Clase 2. Matricula de AIEAS Nª 237/2012 Autor: M.A.R.F Salta
 Clase 2 1 Introducción En esta etapa veremos teoremas y funciones especiales que emplearemos en el desarrollo de los cálculos de las variables eléctricas. Es imprescindible conocer el Teorema de Pitágoras
Clase 2 1 Introducción En esta etapa veremos teoremas y funciones especiales que emplearemos en el desarrollo de los cálculos de las variables eléctricas. Es imprescindible conocer el Teorema de Pitágoras
