Mat r i z in v e r s a
|
|
|
- José Antonio Padilla Maestre
- hace 7 años
- Vistas:
Transcripción
1 Unidad 2 Método de GaUss Mat r i z in v e r s a M U lt i pli cat i va Objetivos: Al inalizar la unidad, el alumno: Representará un sistema de m ecuaciones lineales con n incógnitas mediante una matriz de orden m n. Conocerá y aplicará el método de Gauss para solucionar un sistema de m n. Conocerá y aplicará el método de Gauss-Jordan para solucionar un sistema de n n. Identificará las características de la matriz inversa multiplicativa. Usará el método de Gauss-Jordan para encontrar la matriz inversa multiplicativa. Usará la matriz adjunta para encontrar la matriz inversa multiplicativa. Aplicará el método de la matriz inversa para resolver sistemas de n n.
2
3 Álgebralineal Introducción El problema de solucionar un sistema de m ecuaciones con n incógnitas ha sido objeto de estudio desde hace mucho tiempo. En esta unidad estudiaremos varios métodos para dar solución a dichos sistemas utilizando para ello las matrices y sus propiedades Representación de un sistema mediante matrices En esta sección veremos la representación matricial de un sistema de m n. Recordemos que esto significa que tenemos m ecuaciones, cada una con n incógnitas: a x + a x + + a x = b n n 1 a x + a x + + a x = b n n 2 a x + a x + + a x = b m1 1 m2 2 mn n m Vamos a formar una matriz A de orden m n con todos los coeficientes de las ecuaciones y dos vectores columna, el x formado por las incógnitas y el b formado por los términos independientes. Así, tenemos: a11 a12... a1j... a1 n x1 a21 a22... a2 j... a 2n x A =, x =, ai1 ai2... aij... ain xi am 1 am2... amj... a mn xm b1 b2 b= bi b m Definición 2.1. Si tenemos un sistema de m ecuaciones con n incógnitas. a x + a x + + a x = b n n 1 a x + a x + + a x = b n n 2 = a x + a x + + a x = b m1 1 m2 2 mn n m 67
4 Unidad 2 La representación matricial del sistema es: Ax = b donde A se llama la matriz de los coeficientes, x es el vector columna cuyas entradas son las incógnitas y b es el vector columna cuyas entradas son los términos independientes de las ecuaciones. Ax a11 a12... a1j... a1 n a21 a22... a2 j... a2n = b ai1 ai2... aij... ain am 1 am2... amj... amn x1 b1 x2 b2 = xi bi x m b m 68 Ejemplo 1 Escribe los siguientes sistemas en su representación matricial: a) Con el sistema dado por las siguientes ecuaciones: 2x + 4x + 6x = x + 5x + 6x = x + x 2x = tenemos que A = es la matriz de los coeficientes, x1 x = x2 y x3 Ax = b 18 b= 24 entonces el sistema se puede escribir como x x2 = x 3 4
5 Álgebralineal b) Sea el sistema de ecuaciones dado por: 3a+ 2b 5c+ 6d = 7 4a b+ 3c 2d = 1 a+ 5b 3c+ d = 1 a b tenemos que A = , x = c d el sistema queda representado como a b Ax = b = c d 1 y 7 b = 1 1, entonces Los ejemplos anteriores tienen la característica de que para todos los términos independientes al menos uno es distinto de cero, por lo que son sistemas de ecuaciones no homogéneos, de lo que definiremos cuando todos los términos independientes son iguales a cero. Definición 2.2. Un sistema de ecuaciones de m n se llama homogéneo si el vector b de los términos independientes es el vector cero. Ax Ejemplo 2 2x1 4x2 + x3 0 El sistema x1 3x2 + 4x3 es un sistema homogéneo ya que b = 0 2x1 x2+ x3 0 3x 5x + x = Si tenemos un sistema no homogéneo 2x 3x + 6x = 2 siempre podemos x + 2x 2x = x 5x + x formar un sistema homogéneo asociado a él: 2x1 3x2 + 6x3 poniendo 0 en x1 + 2x2 2x3 los resultados. 69
6 Unidad 2 Las matrices que hemos estudiado son conformadas por los coeficientes de las ecuaciones del sistema, por lo que definiremos las que contienen una columna más, que incluye al vector columna de los valores independientes. Definición 2.3. Se llama matriz aumentada de un sistema m n a la matriz de orden m (n+1) que se obtiene al aumentar a la matriz de los coeficientes una columna formada por los términos independientes. Ejemplo 3 a) Obtén la matriz aumentada del sistema 3x 5x + x = x 3x + 6x = x1 + 2x2 2x3 = Sea A = 2 3 6, entonces la matriz aumentada es B = Nota que A es de orden 3 3 y la matriz aumentada B es de orden x 2y+ z = 9 b) Obtén la matriz aumentada del sistema entonces x 3y+ 6z = A = es la matriz de coeficientes y B = es la matriz aumentada Nota que A es de orden 2 3 y que la matriz aumentada B es de orden
7 Álgebralineal Ejercicio 1 1. De los siguientes sistemas de ecuaciones lineales, encuentra: Su representación matricial. La matriz aumentada. El sistema homogéneo asociado. a) 4x1 + 3x2 5x3 + 3x4 = 4 2x1 4x2 + 7x3 + x4 = 2 7x 6x + 2x + 2x b) 2x1 + 7x2 = 6 3x1 x2 = 1 4x 2x = c) 3x1 + x2 9x3 3x4 = 18 3x + 3x 2x + = Solución de sistemas de orden m n, mediante el método de Gauss Para resolver un sistema de m ecuaciones con n incógnitas usaremos el método de Gauss, para ello necesitamos llevar la matriz a una forma adecuada, de tal manera que podamos obtener inmediatamente el resultado de las incógnitas, las matrices se llevan a ceros en algunos de sus elementos en forma de escalón. Definición 2.4. Una matriz A se encuentra en forma escalonada reducida por renglones si cumple con las siguientes condiciones: i. Todos los renglones cuyos elementos son todos ceros aparecen en la parte inferior de la matriz. ii. El primer número diferente de cero (comenzando por la izquierda) en cualquier renglón cuyos elementos no son todos cero es 1. iii. Si dos renglones sucesivos tienen elementos distintos de cero, entonces el primer 1 en el renglón de abajo está más hacia la derecha que el primer 1 en el renglón de arriba. 71
8 Unidad 2 iv. Cualquier columna que contiene el primer 1 en un renglón, tiene ceros en el resto de sus elementos. El primer número diferente de cero en un renglón se llama pivote de ese renglón. Una matriz se encuentra en forma escalonada por renglones si se cumplen las condiciones (i), (ii) y (iii). Cabe señalar que: a) La forma escalonada reducida por renglones es única. b) Es posible que al cambiar la sucesión de operaciones elementales sobre los renglones se llegue a formas escalonadas distintas. Ejemplo 4 1. Las siguientes matrices están en la forma escalonada reducida por renglones: a) b) c) d) Las siguientes matrices no están en la forma escalonada reducida por renglones: a) Tiene un 4 en el segundo renglón en lugar de b) El tercer renglón tiene 1 a la izquierda del 1 del segundo renglón y debe estar a la derecha.
9 Álgebralineal c) El renglón de puros ceros no está en la parte inferior de la matriz. Observación: Siempre se puede llevar una matriz a la forma escalonada reducida por renglones realizando operaciones elementales con los renglones. Por lo anterior, requerimos conocer cuáles son las operaciones elementales que se pueden realizar con los renglones de una matriz; éstas surgen de convertir una ecuación en otra equivalente realizando ciertas operaciones como son: Definición 2.5. Las operaciones elementales con renglones de una matriz son: i. Multiplicar o dividir un renglón por un número diferente de cero. ii. Sumar un múltiplo de un renglón a otro renglón. iii. Intercambiar dos renglones. El proceso de aplicar las operaciones elementales con renglones para simplificar una matriz aumentada se llama reducción por renglones. Notación: 1. R i cr i significa reemplaza el i-ésimo renglón por ese mismo renglón multiplicado por c. (Para multiplicar un renglón por c, se multiplica cada número del renglón por c). 2. R j R j + cr i significa sustituye el j-ésimo renglón por la suma del renglón j más el renglón i multiplicado por c. 3. R i R j quiere decir intercambiar los renglones i y j. Ejemplo 5 1. Lleva la matriz A= renglones: a la forma escalonada reducida por 73
10 Unidad R2 R2 R R1 R2 R R2 R 2 1 R3 R3 3R R1 R1 R R2 14R / 2 / R3 R3+ 11R R2 R2 R / 2 R3 R / / / R2 R2 R R1 R 1+2R Estamos ya en condiciones de aprender el método de Gauss para resolver un sistema de ecuaciones. Método de eliminación de Gauss para resolver un sistema de ecuaciones. i. Se reduce por renglón la matriz aumentada del sistema a la forma escalonada. ii. Se despeja el valor de la última incógnita. iii. Se usa la sustitución hacia atrás para las demás incógnitas. Ejemplo 6 2x+ 4y+ 6z = Resuelve el sistema 4x+ 5y+ 6z = 24 usando el método de Gauss. 3x+ y 2z = Se forma la matriz de los coeficientes aumentada reduce a su forma escalonada por renglones: y se R1 1 2R / R2 R2 4R R3 R3 3R
11 Álgebralineal R2 13 / R2 R3 R3 5R R2 2 R3 R3 R De aquí regresamos a un sistema de ecuaciones x+ 2y+ 3z = 9 y+ 2z = 4 donde ya tenemos el valor de z = 3; sustituyendo en la segunda z = 3 ecuación obtenemos el valor de y: y + 2(3) = 4 y = 2 ; sustituyendo en la primera ecuación los valores de z y y obtenemos el valor de x: x + 2( 2) + 3(3) = 9 x = 4. Por lo que la solución es (4, 2, 3). x1 + 3x2 5x3 + x4 = 4 2. Resuelve el sistema por el método de Gauss. 2x + 5x 2x + 4x = Se forma la matriz aumentada renglones y se reduce por R R2 R1 R2 R R R 3R Si regresamos al sistema de ecuaciones obtenemos x x x = 2 x2 8x3 2x4 = 2 lo que evidentemente nos muestra que tenemos una infinidad de soluciones, pues los valores de x 3 y x 4 pueden escogerse de manera arbitraria, y para cada par de valores obtenemos los valores de x 1 y de x 2. Como mencionamos en la definición 1.24, un sistema de ecuaciones lineales es inconsistente si no tiene solución y consistente si tiene al menos una solución. Nota. Recordemos los sistemas homogéneos; en ellos los términos independientes son todos cero, por lo tanto podemos decir que un sistema homogéneo siempre tiene al menos una solución: la trivial (donde todas las variables x 1 = x 2 = x 3 = ) y por tanto siempre es consistente. 75
12 Unidad 2 Ejercicio 2 1. Di si las siguientes matrices se encuentran en forma escalonada por renglones (pero no reducida por renglones), en forma escalonada reducida por renglones o ninguna de las dos: a) b) c) d) Usa las operaciones elementales con renglones para reducir las siguientes matrices a la forma escalonada por renglones y a la forma escalonada reducida por renglones: 1 1 a) b) c) d) Encuentra las soluciones (si las hay) de los siguientes sistemas usando el método de Gauss: a) 2x+ 3y z = 3 x 2y+ 2z = 1 3x+ y+ 3z 76
13 Álgebralineal b) 2 x+ 3 y z = 2 x y+ 2z = 1 c) x1 + x2 = 4 2x1 3x2 = 7 3x + 2x = Solución de sistemas de orden m n, mediante el método de Gauss-Jordan El método de Gauss-Jordan para resolver sistemas de ecuaciones es muy similar al método de Gauss, la diferencia es que en éste se pide que la reducción de las matrices sea en la forma escalonada reducida, con lo que se obtienen directamente las soluciones del sistema. Método de Gauss-Jordan para resolver un sistema de ecuaciones lineales. i. Se reduce la matriz aumentada a la forma escalonada reducida por renglones. ii. Se obtienen las soluciones del sistema. Ejemplo 7 1. Resuelve el sistema Jordan: x+ 2y+ 3z = 9 4x+ 5y+ 6z = 24 3x+ y 2z = 4 utilizando el método de Gauss Formamos la matriz aumentada y la llevamos a la forma escalonada reducida por renglones: R2 R2 4R1 R 1 3R / R3 R3 3R R3 R3+ 5R2 R3 R R1 R1 2R
14 Unidad R2 R2 R R1 R1+ R De aquí podemos obtener las soluciones del sistema x = 4; y = 2; z = 3. 3x1 + 6x2 6x3 = 9 2. Resuelve el sistema 2x1 5x2 + 4x3 = 6 usando Gauss-Jordan. x + 16x 14x = Formamos la matriz aumentada y la llevamos a la forma escalonada reducida por renglones: R 2 R 2 2R R 3 R 3 + R R1 R 13 / R3 1/2R R3 R 3+R / 9 3 R2 19 / R2 R1 R1 2R / / Como la matriz tiene un renglón cuyos elementos son todos ceros, podemos concluir que el sistema tiene una infinidad de soluciones, ya que x x 1 2/ 9 3 = 3 x2 8/ 9x3 y por lo tanto x 1 y x 2 dependen del valor de x x+ y z = 7 3. Resuelve el sistema 4x y+ 5z = 4 usando el método de Gauss-Jordan. 6x+ y+ 3z = Llevamos la matriz aumentada a su forma escalonada reducida R2 R2 R R2 R2 4R1 R3 R3 6R1
15 Álgebralineal / 5 13/ 5 R1 R 1+1/5R R2 R Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al mismo tiempo sea cero. Ejercicio 3 1. Encuentra las soluciones (si las hay) de los siguientes sistemas de ecuaciones usando el método de Gauss-Jordan. Explica. a) x1 + x2 x3 = 7 4x1 x2 + 5x3 = 4 2x + 2x 3x b) 3x1 + 6x2 6x3 = 9 2x1 5x2 + 4x3 = 6 5x + 28x 26x = c) x1 2x2 + 3x3 = 11 4x1 + x2 x3 = 4 2x x + 3x = Matriz inversa y matriz adjunta En esta sección definiremos dos tipos de matrices muy importantes que son básicas en la teoría de matrices y que nos son útiles para la solución de sistemas de ecuaciones. Comencemos con un ejemplo sencillo: Sean A = 1 3 y B = 1 2, obtengamos los productos AB y BA. AB = = 0 1 y BA = lo tanto podemos decir que AB = BA = I 2, donde I 2 = identidad de = 0 1, por A la matriz B se le llama matriz inversa de A y se denota B=A 1. es la matriz 79
16 Unidad 2 Definición 2.7. Sean A y B dos matrices de orden n n que satisfacen AB = BA = I donde I es la matriz identidad de orden n n, entonces B se llama matriz inversa de A y se denota por A 1. De donde se tiene que AA 1 = A 1 A = I. En este caso se dice que A es invertible. Así como toda matriz, también existen propiedades para la matriz identidad e inversa. Teorema 2.1. Propiedad de la matriz identidad. Sean A una matriz de orden n n e I la matriz identidad de orden n n, entonces AI = IA = A Teorema 2.2. Propiedades de las matrices invertibles. Sean A y B dos matrices invertibles de orden n n, entonces 1. La inversa es única. 2. (A 1 ) 1 = A 3. (AB) 1 = B 1 A 1 En este momento nos podemos hacer las siguientes preguntas: 1. Todas las matrices cuadradas tienen inversa? 2. Qué matrices tienen inversa? 3. Si una matriz tiene inversa, cómo se puede calcular? En esta parte vamos a contestar esas preguntas. Comenzaremos con el caso de Consideremos la matriz A = 4 5 y vamos a suponer que es invertible. Sea A 1 x y = z w, entonces debe satisfacer que AA 1 = I, por lo tanto: 80
17 Álgebralineal 2 3 AA 1 = 4 5 x z y 2x 3z 2y 3w = w 4x+ 5z 4y+ 5w = Recordemos que dos matrices son iguales si todas sus entradas lo son, por lo cual 2x 3z = 1; 4x + 5z ; 2y 3w ; 4y + 5w = 1. Con esto se forman dos sistemas de ecuaciones lineales: 2x 3z = 1 y 4x+ 5z 2y 3w= 0 4y+ 5w= 1 y para resolverlos vamos a escribirlos en la forma matricial aumentada: y Al 1 0 x reducirlas obtendremos los resultados 0 1 z y 1 0 y 0 1 w Como la matriz original es la misma para ambos sistemas, podemos realizar la reducción por renglones al mismo tiempo considerando la nueva matriz aumentada al hacerlo obtendremos 1 0 x y 0 1 z w R1 12 / R 1 3/ 2 1/ R2 R2+ 4R / 2 1/ 2 0 R R 1 0 5/ 2 3/ R R + / R = x z y w De donde obtenemos las soluciones x = 5/2; z = 2; y = 3/2; w = 1 5/ 2 3/ 2 Entonces A es invertible y su inversa es A 1 = 2 1 Este ejemplo nos ilustra un procedimiento para encontrar la matriz inversa que siempre funciona y que se puede generalizar a matrices de orden n n. 81
18 Unidad 2 Procedimiento para encontrar la inversa de una matriz cuadrada A 1. Se escribe la matriz aumentada ( A I ). 2. Se utiliza la reducción por renglones para poner la matriz A en su forma escalonada reducida por renglones. 3. Se decide si es invertible. a. Si la forma escalonada reducida por renglones de A es la matriz identidad I, entonces A 1 es la matriz que se tiene a la derecha de la barra vertical. b. Si la reducción de A conduce a un renglón de ceros a la izquierda de la barra vertical, entonces A no es invertible. Ejemplo Sea A = 2 4 vamos a determinar si es o no invertible R2 R2 2R Como tiene un renglón de ceros a la izquierda de la barra vertical, A no es invertible Sea A = 4 5 6, vamos a determinar si es o no invertible, y si lo es encontrar A / R1 12R / / R2 R 2 4R R2 1/3R2 R3 R3 3R /
19 Álgebralineal / / 6 2/ / 3 1/ 3 0 R3 R 3 + 5R / 3 1/ 3 0 R1 R1 2R / / 5/ / 3 7/ 3 1 R3 1R / 3 1/ 3 0 R2 R2 2R3 R1 R 1 + R / 6 5/ / 3 7/ / 3 11/ / 5/ 3 1 8/ 3 7/ 3 1 De donde obtenemos la matriz inversa A 1 = 13/ / 2 (*) 11/ 6 5/ / 3 7/ Verificación: AA 1 = / / / 6 5/ Nota: Es importante verificar que AA 1 = I. Veamos algunos resultados importantes acerca de las matrices inversas. Teorema 2.3. Sea A una matriz de orden n n. Entonces A es invertible, si y sólo si, det A 0 Ejemplo 9 1. Consideremos la matriz del ejemplo anterior: A = determinante. sabemos que es invertible, vamos a calcular su det A = = 2( 10 6) 4( 8 18) + 6(4 15) =
20 Unidad 2 det A 0 2. Consideremos la matriz A = det A = y y calculemos su determinante R2 R2 2R invertible. por lo tanto no es Vamos ahora a dar la definición de otra matriz importante en nuestra búsqueda de matrices inversas. Recordemos lo que son los cofactores de una matriz A (Definición 1.22) i j A = ( 1) + M ij ij Si A = entonces sus cofactores son A 11 = 5 6 = 10 6 = 16 A = 4 6 = ( 8 18) = A 13 = = 4 15 = 11 A 21 = = ( 8 6) = 14 A 22 = = 4 18 = 22 A 23 = = (2 12) = 10 A 31 = = = 6 A = = (12 24) = 12 A 33 = = = 6 Con estos cofactores haremos una matriz de orden 3 3 de tal manera que obtendremos una matriz B: B = Habiendo calculado esta matriz podemos definir lo siguiente: 84
21 Álgebralineal Definición 2.8. Sea A una matriz de orden n n y sea B la matriz formada por los cofactores de A. Entonces la adjunta de A, que se denota adj A es la transpuesta de la matriz B, es decir: A11 A21 An 1 A A A adj A = B T n2 = A1 n A2n A nn Ejemplo Vamos a encontrar la adjunta de A = Sea B la matriz de los cofactores de A. A11 A12 A B = A21 A22 A = 10 A31 A32 A entonces adj A =B T = Ya con estos elementos podemos encontrar la inversa de una matriz usando su determinante y su matriz adjunta como nos lo indica el siguiente teorema. Teorema 2.4. Si A es una matriz de orden n n invertible. Entonces A 1 = 1 det A adja Ejemplo 11 Usaremos la matriz anterior A = inversa y vamos a calcular su 85
22 Unidad 2 det A = = 2( 10 6) 4( 8 18) +6(4 15) = = 6 entonces A 1 = 1 6 adj A = = 8/ 3 7/ / / 2 11/ 6 5/ 3 1 Nota que esta matriz inversa ya la habíamos obtenido con el método de Gauss-Jordan.* Observación: Este teorema refuerza el resultado acerca de que una matriz invertible necesariamente debe tener un determinante distinto de cero. Ejercicio 4 1. Encuentra la matriz inversa, si existe, usando el método de Gauss- Jordan. En caso de que no exista la matriz inversa, indica la razón: a) b) c) d) e) Encuentra la matriz inversa, si existe, usando el método de la matriz adjunta. Recuerda calcular primero el determinante para ver si existe o no. * En este momento ya tenemos dos métodos para calcular la matriz inversa, sin embargo, podemos notar que si n > 3, en general es más fácil calcular A 1 con el método de la reducción por renglones que usando la matriz adjunta, pues aun en el caso de 4 4 tenemos que calcular 17 determinantes. 86
23 Álgebralineal a) b) c) Solución de sistemas de n n, mediante la matriz inversa En esta sección encontraremos la solución de un sistema de ecuaciones de n n mediante la matriz inversa. El siguiente resultado nos da una pista acerca de cómo encontrar la solución de un sistema si la matriz de coeficientes asociada es invertible. Teorema 2.5. Sea A la matriz de coeficientes de un sistema de ecuaciones de orden n n. Entonces se cumplen las siguientes condiciones: A es invertible. El sistema Ax = b tiene una solución única que es x = A 1 b El sistema homogéneo asociado Ax tiene una solución única que es x Ejemplo 12 Consideremos el siguiente sistema de ecuaciones: 2x+ 4y+ 3z = 1 y z = 2 formamos la matriz de coeficientes A = 3x+ 5y+ 7z = Vamos a ver si A es invertible, para eso calculamos su determinante: det A = = 2(7+5) ( 4 3) =
24 Unidad 2 Como el determinante es distinto de cero, la matriz es invertible y por lo tanto el sistema tiene solución única. Usando alguno de los métodos vistos con anterioridad encontramos que 4 13/3 7/3 A 1 = 1 5/3 2/3 por lo tanto la solución del sistema será 1 2/3 2/3 4 13/3 7/3 1 x = A 1 b = 1 5/3 2/ /3 2/3 1 = ( / / / ) de donde x = 7/3 2( 7/3)+4(5/3)+3( 1/3) = 1 y = 5/3 comprobando tenemos 5/3 ( 1/3) = 2 z = 1/3 3( 7/3)+5(5/3)+7( 1/3)= 1 Ejercicio 5 1. Considera los siguientes sistemas de ecuaciones lineales y encuentra: 1) El determinante de la matriz de coeficientes asociada. ii) Con base en lo anterior indica si el sistema tiene o no solución única. iii) Encuentra la matriz inversa, si la hay. iv) Encuentra la solución del sistema, si tiene, usando la matriz inversa. a) x1 2x2 + 3x3 4x1 + x2 x3 2x x + 3x b) x+ 6y = 2 4x+ 2y = 1 c) 2x 4y+ 8z = 1 3x+ 5y+ 8z 6x+ 4z = 2 88
25 Álgebralineal Ejercicios resueltos 1. Lleva a la forma escalonada reducida por renglones la matriz R2 R2 R R R R2 R2 2R1 R3 R R2 R3 R R3 R3 3R / R 3 R2 R 3 R3 17 R R 1 R 1 + 7R 2 R 3 1/11R R2 R 2 + 2R R1 R 1 + 2R Considera el siguiente problema: Una compañía quiere comprar maquinaria y recibe de cuatro proveedores los siguientes presupuestos: Proveedor A B C D Núm. compresoras Núm. de medidores Núm. válvulas Núm. reguladores Costo total millones de dólares Si sabemos que todos los proveedores tienen el mismo precio para cada tipo de maquinaria, cuántos millones de pesos cuesta cada una de las máquinas? 89
26 Unidad 2 Para resolver este problema vamos a convertirlo a un sistema de ecuaciones de la siguiente manera: sea x el precio de las compresoras, y el precio de los medidores, z el precio de las válvulas y w el precio de los reguladores, por lo tanto tenemos: 2x+ 4z+ w = y+ 4z+ 2w = x+ 2y+ 2w = 5 Consideremos la matriz aumentada x+ 2y+ 4z = Resolveremos este sistema por el método de Gauss-Jordan: R1 R3 R R 2R R4 R4 R /2 R2 14 / R /2 5/4 2 R3 R 3 + 4R /2 5/4 R1 R1 2R /2 R3 R /2 5/4 18 / /8 1/ /8 22/ /8 9/ /8 1/ /2 3/2 R4 R4 4R3 R2 R2 R3 R1 R 1 + 2R /8 22/ R4 2/3R /8 9/8 4 R 8R R2 8R /8 1/8 R 8R R 3 R 3 + R R / R / 2 1 R 2 R 2 5R4 R2 18 / R2 R 1 R 1 6R R3 18 / R / de donde obtenemos las soluciones x = 2, y = 1/2, z = 1/4, w = 1 por lo tanto el precio de cada máquina es: compresora medidores válvulas reguladores $ 2 millones $ 500 mil $ 250 mil $ 1 millón 90
27 Álgebralineal 3. Encuentra la matriz inversa de A= Gauss-Jordan: con el método de R2 R2 3R R2 R2 R3 R 3 +2R R3 R3 R1 R1 R R R 2 + R R 1 R1 R por lo tanto la matriz inversa es A 1 = Vamos a comprobar: AA 1 = Encuentra la matriz inversa de A= usando la matriz adjunta. Primero vamos a calcular el determinante det A = = 2(1 4) 3(1 2) 1( 2+1) = = 2, entonces sí tiene inversa. Vamos a calcular los cofactores para obtener la adjunta. A 11 = = 1 A 21 = = 1 A 31 = = 5 A 32 = = 3 A 33 = = 1 91
28 Unidad 2 B = entonces adj A = B T = por lo tanto A 1 = / 2 12 / 5/ = / 12 / 3/ 2 12 / 12 / 12 / Vamos a comprobar que efectivamente sea la inversa /2 1/2 5/ /2 1/2 3/ /2 1/2 1/ Resuelve el sistema de ecuaciones lineales usando la inversa. 2x+ 3y z = 1 x y+ 2z = 3 x+ 2y z = 2 Vamos a encontrar su matriz de coeficientes A = Como podemos constatar, se trata de la matriz del ejemplo anterior, por lo tanto sabemos que es invertible, y por lo tanto el sistema tiene una única solución. Usando la matriz inversa obtenemos: x = A 1 b = 3/2 1/2 5/2 1 1/2 1/2 3/2 3 1/2 1/2 1/ = ( ) x = 5, y = 2, z = 3 Comprobamos 2(5)+3( 2 ) 3 = = 1 5 ( 2)+2(3) = = 3 con lo que sabemos que son las soluciones. 5+2( 2) 3 = = 2 92
29 Álgebralineal Ejercicios propuestos 1. Reduce la matriz A a la forma escalonada por renglones: A = Lleva la matriz A a la forma escalonada reducida por renglones: A = Resuelve el sistema de ecuaciones usando el método de Gauss-Jordan: 2x+ 3y z = 3 x 2y+ z 2x+ 2y+ z = 1 4. Di si el siguiente sistema tiene una solución, infinitas soluciones o ninguna solución. Usa el método de Gauss-Jordan: x 3z y+ 2z x+ y z 5. Encuentra la matriz inversa, si existe, usando el método de Gauss- Jordan: En los siguientes ejercicios, haz lo que se te pide: a) Encuentra la matriz adjunta de A = b) Encuentra la inversa de A usando la matriz adjunta. 93
30 Unidad 2 Autoevaluación 1. De las siguientes matrices escoge la que está en la forma escalonada reducida por renglones: a) b) c) d) Cuál es la representación matricial del sistema x 2 a) y = z b) c) x 2 y = 0 z 1 2x+ 3y z = 2 x+ 2y+ 3z? x+ y 2z = 1 d)
31 Álgebralineal 3. De las siguientes afirmaciones elige la que describe la diferencia entre el método de Gauss y el método de Gauss-Jordan: a) No hay diferencia. b) El método de Gauss pide que la matriz esté escalonada por renglones y el método de Gauss-Jordan pide la matriz escalonada reducida por renglones. c) El método de Gauss es para sistemas de ecuaciones y el método de Gauss-Jordan para matrices. d) El método de Gauss-Jordan se usa para matrices de n n y el de Gauss para matrices de m n. 4. Di cuál de las siguientes operaciones con renglones se usó para pasar de la matriz A a la B: A= B a) R 1 R 1 + R 3 b) R 2 R 2 + R 1 c) R 2 R 2 2 R 1 d) R 2 R 2 + 2R 1 5. Cuántas soluciones tiene el sistema 2 x+ 3 y z = 1 3x y+ 2z Gauss)? (utiliza el método de a) No tiene solución. b) Tiene sólo una solución. c) Tiene infinitas soluciones. d) Tiene dos soluciones. 6. Es la solución del sistema Jordan): a) x = 1; y ; z = 1 b) x = 1; y ; z = 1 c) x = 1; y = 1; z = 2 2x+ 3y z = 3 x y+ z x 2y 2z = 3 (utiliza el método de Gauss- 95
32 Unidad 2 d) No tiene solución. 7. Es la matriz adjunta de A = a) b) c) d) Es la matriz inversa de A = a) No tiene inversa b) / c) / / d) : : 9. Es la solución del sistema homogéneo a) x = 1; y = 1; z b) x ; y ; z c) No tiene solución. d) x ; y = 1; z = 1 2x y+ z 3x+ y z x y+ z 96
33 Álgebralineal 10. Elige la opción que diga cuáles de las siguientes afirmaciones son equivalentes: 1. A es invertible 2. det A 3. det A 0 4. El sistema Ax = b tiene solución única. 5. El sistema Ax = b no tiene solución. 6. El sistema Ax =0 sólo tiene la solución trivial. a) 1; 2; 4 b) 1; 3; 4; 6 c) 1; 3; 5; 6 d) 1; 3; 5 97
34
35 Álgebralineal Respuestas a los ejercicios Ejercicio 1 a) La representación matricial es La matriz aumentada es x1 4 x2 = x x 4 El sistema homogéneo asociado es 4x1 + 3x2 5x3 + 3x4 2x1 4x2 + 7x3 + x4 7x 6x + 2x + 2x b) 2 7 x La representación matricial es x La matriz aumentada es El sistema homogéneo asociado es 2x1 + 7x2 3x1 x2 4x 2x = 1 4 c) La representación matricial es x x x x = 54 La matriz aumentada es x1 + x2 9x3 3x4 El sistema homogéneo asociado es 3x + 3x 2x
36 Unidad 2 Ejercicio 2 1. a) Escalonada. b) Escalonada reducida. c) Escalonada reducida. d) Ninguna de las a) 0 1 ; b) / ; / 0 1 9/ c) 0 1; d) ; a) x = 1; y ; z = 1 b) Tiene una infinidad de soluciones. c) No tiene solución. Ejercicio 3 1. a) x 1 = 9; x 2 = 30; x 3 = 14 b) No tiene solución. c) x 1 = 2; x 2 = 3; x 3 = 1 Ejercicio 4 1. a) b) No es invertible porque tiene un renglón de ceros. 100
37 Álgebralineal c) 13 / 13 / 13 / 0 1/ d) No es invertible porque hay un renglón de ceros e) a) 12 / 12 / 14 / 3/ b) c) No es invertible pues su determinante es cero. Ejercicio 5 1. a) det A = 12 El sistema tiene como única solución la trivial (x 1, x 2, x 3 ) (teorema 2.5.) 16 / 14 / 112 / La matriz inversa es 7/ 6 14 / 13/ / 14 / 3/ 4 b) det A = 26 Tiene sólo una solución. 2/ 26 6/ 26 La matriz inversa es 4/ 26 1/ 26 La solución del sistema es x = 10/26; y = 7/26 c) det A = 520 Tiene solución única La matriz inversa es La solución es x = 82/260; y = 38/260; z = 7/
38 Unidad 2 Respuestas a los ejercicios propuestos ) ) ) x= 1; y ; z = 1 4) El sistema tiene una infinidad de soluciones: x = 3z; y = 2z 0 1/ 3 1 5) A 1 = 1 2/ / 3 8 6) a) Adj A = /3 1 b) A 1 = 1 2/ /3 8 Respuestas a la autoevaluación 1. d) 2. a) 3. b) 4. c) 5. c) 6. a) 7. b) 8. a) 9. b) 10. b) 102
1 0 4/ 5 13/
 1 1 1 7 1 0 4/ 5 13/ 5 R1 R 1+1/5R3 0 0 0 2 R2 R3 0 5 9 22 0 5 9 22 0 0 0 2 Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al
1 1 1 7 1 0 4/ 5 13/ 5 R1 R 1+1/5R3 0 0 0 2 R2 R3 0 5 9 22 0 5 9 22 0 0 0 2 Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
MENORES, COFACTORES Y DETERMINANTES
 MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Tema 1. Álgebra lineal. Matrices
 1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
Ejemplo 1. Ejemplo introductorio
 . -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
. -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
Ecuaciones matriciales AX = B y XA = B. Cálculo de la matriz inversa
 Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Matriz sobre K = R o C de dimensión m n
 2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
SISTEMAS DE ECUACIONES LINEALES Y MATRICES Dos ecuaciones lineales con dos
 de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive
de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com de SISTEMAS DE ECUACIONES ES Y MATRICES Dos m con n Sergio Stive
Tema 2. Sistemas de ecuaciones lineales
 Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
Tema 2. Sistemas de ecuaciones lineales Estructura del tema. Definiciones básicas Forma matricial de un sistema de ecuaciones lineales Clasificación de los sistemas según el número de soluciones. Teorema
SISTEMAS DE ECUACIONES LINEALES
 1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
1 SISTEMAS DE ECUACIONES LINEALES Una ecuación es un enunciado o proposición que plantea la igualdad de dos expresiones, donde al menos una de ellas contiene cantidades desconocidas llamadas variables
Procedimiento para encontrar la inversa de una matriz cuadrada (Método de Gauss-Jordan).
 Ejemplo 19: Demuestre que la matriz A es invertible y escríbala como un producto de matrices elementales. Solución: Para resolver el problema, se reduce A a I y se registran las operaciones elementales
Ejemplo 19: Demuestre que la matriz A es invertible y escríbala como un producto de matrices elementales. Solución: Para resolver el problema, se reduce A a I y se registran las operaciones elementales
Matrices. p ij = a ik b kj = a i1 b 1j + a i2 b 2j + + a in b nj.
 Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices escalonadas y escalonadas reducidas
 Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
1.4 SISTEMAS HOMOGÉNEOS DE ECUACIONES. 36 CAPÍTULO 1 Sistemas de ecuaciones lineales y matrices
 36 CAPÍTULO Sistemas de ecuaciones lineales y matrices Escriba, en un comentario, la ecuación del polinomio cúbico que se ajusta a los cuatro puntos. Sea x el vector columna que contiene las coordenadas
36 CAPÍTULO Sistemas de ecuaciones lineales y matrices Escriba, en un comentario, la ecuación del polinomio cúbico que se ajusta a los cuatro puntos. Sea x el vector columna que contiene las coordenadas
Un sistema formado por dos ecuaciones y dos incógnitas, se puede escribir como sigue:
 MATEMÁTICAS EJERCICIOS RESUELTOS DE SISTEMAS LINEALES Juan Jesús Pascual SISTEMA DE ECUACIONES LINEALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA Sistemas de ecuaciones lineales
MATEMÁTICAS EJERCICIOS RESUELTOS DE SISTEMAS LINEALES Juan Jesús Pascual SISTEMA DE ECUACIONES LINEALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA Sistemas de ecuaciones lineales
Sistemas de Ecuaciones y Matrices
 Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Sistemas de Ecuaciones Lineales. Solución de Sistemas de Ecuaciones Lineales. www.math.com.mx. José de Jesús Angel Angel. jjaa@math.com.
 Sistemas de Ecuaciones Lineales Solución de Sistemas de Ecuaciones Lineales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2008 Contenido 1. Sistemas de Ecuaciones Lineales 2
Sistemas de Ecuaciones Lineales Solución de Sistemas de Ecuaciones Lineales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2008 Contenido 1. Sistemas de Ecuaciones Lineales 2
PREPA N o 2. Matriz Inversa y Determinantes.
 UNIVERSIDAD SIMÓN BOLÍVAR MATEMÁTICAS III (MA-1116) Elaborado por Miguel Labrador 12-10423 Ing. Electrónica PREPA N o 2. Matriz Inversa y Determinantes. Sist. de ecuaciones lineales (cierre), cálculo de
UNIVERSIDAD SIMÓN BOLÍVAR MATEMÁTICAS III (MA-1116) Elaborado por Miguel Labrador 12-10423 Ing. Electrónica PREPA N o 2. Matriz Inversa y Determinantes. Sist. de ecuaciones lineales (cierre), cálculo de
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES
 CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
CAPÍTULO 3: DETERMINANTES Y SISTEMAS DE ECUACIONES Parte A: determinantes. A.1- Definición. Por simplificar, consideraremos que a cada matriz cuadrada se le asocia un número llamado determinante que se
Tema 1: Matrices y Determinantes
 Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Instituto Tecnológico Autónomo de México. 1. At =..
 Instituto Tecnológico Autónomo de México TRANSPUESTA DE UNA MATRIZ DEFINICION : Transpuesta Sea A = (a ij ) una matriz de mxn Entonces la transpuesta de A, que se escribe A t, es la matriz de nxm obtenida
Instituto Tecnológico Autónomo de México TRANSPUESTA DE UNA MATRIZ DEFINICION : Transpuesta Sea A = (a ij ) una matriz de mxn Entonces la transpuesta de A, que se escribe A t, es la matriz de nxm obtenida
Tema 5: Sistemas de Ecuaciones Lineales
 Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
ARITMÉTICA Y ÁLGEBRA
 ARITMÉTICA Y ÁLGEBRA 1.- Discutir el siguiente sistema, según los valores de λ: Resolverlo cuando tenga infinitas soluciones. Universidad de Andalucía SOLUCIÓN: Hay cuatro ecuaciones y tres incógnitas,
ARITMÉTICA Y ÁLGEBRA 1.- Discutir el siguiente sistema, según los valores de λ: Resolverlo cuando tenga infinitas soluciones. Universidad de Andalucía SOLUCIÓN: Hay cuatro ecuaciones y tres incógnitas,
Matrices, determinantes, sistemas de ecuaciones lineales.
 UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
Una matriz es una tabla ordenada (por filas y columnas) de escalares a i j de la forma: ... ... a... ...
 MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
Ba s e, d i M e n s i ó n y Mat r i z
 Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Unidad 4 Ba s e, d i M e n s i ó n y Mat r i z de transición Objetivos: Al inalizar la unidad, el alumno: Conocerá la deinición de base de un espacio vectorial Identiicará bases canónicas para algunos
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
 Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
2.- Sistemas de ecuaciones Lineales
 .- Sistemas de ecuaciones Lineales..- Definición, Clasificación de los sistemas lineales y tipos de solución. Definición Una ecuación lineal con las variables escribirse en la forma,..., n es una ecuación
.- Sistemas de ecuaciones Lineales..- Definición, Clasificación de los sistemas lineales y tipos de solución. Definición Una ecuación lineal con las variables escribirse en la forma,..., n es una ecuación
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Matrices, Determinantes y Sistemas de ecuaciones lineales
 Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
Combinación Lineal. Departamento de Matemáticas, CCIR/ITESM. 10 de enero de 2011
 Combinación Lineal Departamento de Matemáticas, CCIR/ITESM 10 de enero de 011 Índice.1. Introducción............................................... 1.. Combinación lineal entre vectores...................................
Combinación Lineal Departamento de Matemáticas, CCIR/ITESM 10 de enero de 011 Índice.1. Introducción............................................... 1.. Combinación lineal entre vectores...................................
Determinante de una matriz
 25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
Una matriz es una arreglo rectangular ordenado de elementos, comúnmente llamados escalares, dispuestos en m renglones y n columnas.
 MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
Definición de la matriz inversa
 Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Matrices y determinantes
 Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
2. SISTEMAS DE ECUACIONES LINEALES. Introducción
 2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 Eliminación gaussiana y otros algoritmos Departamento de Matemáticas ITESM Eliminación gaussiana y otros algoritmos Álgebra Lineal - p. 1/77 En esta lectura veremos procedimientos
Álgebra Lineal Ma1010 Eliminación gaussiana y otros algoritmos Departamento de Matemáticas ITESM Eliminación gaussiana y otros algoritmos Álgebra Lineal - p. 1/77 En esta lectura veremos procedimientos
Inversas Generalizadas
 Inversas Generalizadas Departamento de Matemáticas, CSI/IESM 5 de abril de 2 Índice.. Inversas generalizadas..........................................2. Uso de la inversa generalizada.....................................
Inversas Generalizadas Departamento de Matemáticas, CSI/IESM 5 de abril de 2 Índice.. Inversas generalizadas..........................................2. Uso de la inversa generalizada.....................................
Elementos de una matriz.
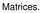 Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices y sistemas de ecuaciones lineales
 Matrices y sistemas de ecuaciones lineales Problemas para examen Antes de resolver un problema en el caso general, se recomienda considerar casos particulares (por ejemplo, n = 4 y n = 50). En el caso
Matrices y sistemas de ecuaciones lineales Problemas para examen Antes de resolver un problema en el caso general, se recomienda considerar casos particulares (por ejemplo, n = 4 y n = 50). En el caso
Dada la proporción =, calcula el producto de extremos menos el producto de medios. 4. Halla los determinantes de las siguientes matrices: Solución:
 3 Determinantes. Determinantes de orden y 3 por Sarrus Piensa y calcula 3 6 Dada la proporción =, calcula el producto de extremos menos el producto de medios. 4 8 3 8 6 4 = 4 4 = 0 Aplica la teoría. Calcula
3 Determinantes. Determinantes de orden y 3 por Sarrus Piensa y calcula 3 6 Dada la proporción =, calcula el producto de extremos menos el producto de medios. 4 8 3 8 6 4 = 4 4 = 0 Aplica la teoría. Calcula
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012. Guía de Estudio y Ejercitación propuesta
 ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
 Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Conceptos Preliminares
 Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
 INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Propiedades de los Determinantes
 Propiedades de los Determinantes Departamento de Matemáticas, CCIR/ITESM 26 de mayo de 2010 Índice 19.1. Propiedades............................................... 1 19.2. La adjunta de una matriz cuadrada..................................
Propiedades de los Determinantes Departamento de Matemáticas, CCIR/ITESM 26 de mayo de 2010 Índice 19.1. Propiedades............................................... 1 19.2. La adjunta de una matriz cuadrada..................................
Sistemas de ecuaciones
 Sistemas de ecuaciones Sistemas de ecuaciones Resolución de un sistema de dos ecuaciones lineales Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones de primer grado con dos incógnitas
Sistemas de ecuaciones Sistemas de ecuaciones Resolución de un sistema de dos ecuaciones lineales Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones de primer grado con dos incógnitas
Capitulo 6. Matrices y determinantes
 Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Matrices Inversas. Rango Matrices Elementales
 Matrices Inversas. Rango Matrices Elementales Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Matrices Matrices identidad La matriz identidad
Matrices Inversas. Rango Matrices Elementales Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Matrices Matrices identidad La matriz identidad
VALOR ABSOLUTO. Definición.- El valor absoluto de un número real, x, se define como:
 VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
Lección 5.1: Matrices y determinantes. Primeros conceptos. Objetivos de esta lección
 Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
Lección 1. Algoritmos y conceptos básicos.
 Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
A cada matriz n-cuadrada A = (ai j ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), A o
 DETERMINANTES A cada matriz n-cuadrada A = (ai j ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), A o Una tabla ordenada n ð n de escalares situada entre dos líneas
DETERMINANTES A cada matriz n-cuadrada A = (ai j ) se le asigna un escalar particular denominado determinante de A, denotado por det (A), A o Una tabla ordenada n ð n de escalares situada entre dos líneas
Sistemas de ecuaciones lineales
 6 Sistemas de ecuaciones lineales 61 Sistemas de ecuaciones lineales Se llama ecuación lineal en n incógnitas sobre R a una expresión de la forma a 1 x 1 + a 2 x 2 + + a n x n = b con los a i en R para
6 Sistemas de ecuaciones lineales 61 Sistemas de ecuaciones lineales Se llama ecuación lineal en n incógnitas sobre R a una expresión de la forma a 1 x 1 + a 2 x 2 + + a n x n = b con los a i en R para
SISTEMAS DE ECUACIONES LINEALES MÉTODO DE LA MATRIZ INVERSA
 MÉTODO DE LA MATRIZ INVERSA Índice Presentación... 3 Método de la matriz inversa... 4 Observaciones... 5 Ejemplo I.I... 6 Ejemplo I.II... 7 Ejemplo II... 8 Sistemas compatibles indeterminados... 9 Método
MÉTODO DE LA MATRIZ INVERSA Índice Presentación... 3 Método de la matriz inversa... 4 Observaciones... 5 Ejemplo I.I... 6 Ejemplo I.II... 7 Ejemplo II... 8 Sistemas compatibles indeterminados... 9 Método
Sistema de ecuaciones algebraicas
 Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES.
 BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales El sistema de ecuaciones lineales como modelo matemático de problemas Los sistemas de ecuaciones lineales permiten el planteamiento de problemas y soluciones que toman en
Sistemas de Ecuaciones Lineales El sistema de ecuaciones lineales como modelo matemático de problemas Los sistemas de ecuaciones lineales permiten el planteamiento de problemas y soluciones que toman en
Valores y Vectores Propios
 Valores y Vectores Propios Departamento de Matemáticas, CSI/ITESM de abril de 9 Índice 9.. Definiciones............................................... 9.. Determinación de los valores propios.................................
Valores y Vectores Propios Departamento de Matemáticas, CSI/ITESM de abril de 9 Índice 9.. Definiciones............................................... 9.. Determinación de los valores propios.................................
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
2 - Matrices y Determinantes
 Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Una forma fácil de recordar esta suma (regla de Sarrus): Primero vamos a estudiar algunas propiedades de los determinantes.
 Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Tema 3 Resolución de Sistemas deecuaciones Lineales
 Tema 3 Resolución de Sistemas de Ecuaciones Lineales E.T.S.I. Informática Indice 1 Introducción 2 Resolución de Sistemas Triangulares Triangulación por el Método de Gauss Variante de Gauss-Jordan Comentarios
Tema 3 Resolución de Sistemas de Ecuaciones Lineales E.T.S.I. Informática Indice 1 Introducción 2 Resolución de Sistemas Triangulares Triangulación por el Método de Gauss Variante de Gauss-Jordan Comentarios
dia G o n a l i z a c i ó n
 Unidad elementos característicos dia G o n a l i z a c i ó n Objetivos: Al inalizar la unidad, el alumno: Encontrará los valores y los vectores característicos de una matriz. Utilizará los elementos característicos
Unidad elementos característicos dia G o n a l i z a c i ó n Objetivos: Al inalizar la unidad, el alumno: Encontrará los valores y los vectores característicos de una matriz. Utilizará los elementos característicos
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales 1 Definiciones Un sistema de m ecuaciones lineales con n incógnitas es un conjunto de expresiones de la forma: a 11 x 1 + a 12 x 2 + + a 1n x n = a 21 x 1 + a 22 x 2 + +
Sistemas de ecuaciones lineales 1 Definiciones Un sistema de m ecuaciones lineales con n incógnitas es un conjunto de expresiones de la forma: a 11 x 1 + a 12 x 2 + + a 1n x n = a 21 x 1 + a 22 x 2 + +
EJERCICIOS RESUELTOS DE SISTEMAS LINEALES
 EJERCICIOS RESUELTOS DE SISTEMAS LINEALES 1. Dado el sistema de ecuaciones lineales: 2x + 3y 3 4x +5y 6 a) Escribir la expresión matricial del sistema. b) Discutir el sistema. c) Resolver el sistema por
EJERCICIOS RESUELTOS DE SISTEMAS LINEALES 1. Dado el sistema de ecuaciones lineales: 2x + 3y 3 4x +5y 6 a) Escribir la expresión matricial del sistema. b) Discutir el sistema. c) Resolver el sistema por
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Sistemas lineales y matrices
 resumen04 1 Sistemas lineales y matrices Sistemas de ecuaciones lineales Un sistema de ecuaciones lineales es de la orma indicada a la izquierda y se suele representar por una matriz una tabla como la
resumen04 1 Sistemas lineales y matrices Sistemas de ecuaciones lineales Un sistema de ecuaciones lineales es de la orma indicada a la izquierda y se suele representar por una matriz una tabla como la
Ecuaciones de segundo grado
 Ecuaciones de segundo grado 11 de noviembre 009 Ecuaciones de segundo grado con una incógnita método de solución, formula general e incompletas Algebra Ecuaciones de segundo grado con una incógnita Las
Ecuaciones de segundo grado 11 de noviembre 009 Ecuaciones de segundo grado con una incógnita método de solución, formula general e incompletas Algebra Ecuaciones de segundo grado con una incógnita Las
Operaciones con matrices
 Operaciones con matrices Problemas teóricos En todos los problemas de esta lista se supone que F es un campo (cuerpo). Si no conoce bien el concepto de campo, entonces puede pensar que F = R. Operaciones
Operaciones con matrices Problemas teóricos En todos los problemas de esta lista se supone que F es un campo (cuerpo). Si no conoce bien el concepto de campo, entonces puede pensar que F = R. Operaciones
Algebra Lineal con Mathematica. Sistemas de Ecuaciones Lineales.
 Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/). Vol. 9, No 2. (Feb., 2009) Algebra Lineal con Mathematica. Sistemas de Ecuaciones Lineales. Carlos Arce S. carce@cariari.ucr.ac.cr
Revista digital Matemática, Educación e Internet (www.cidse.itcr.ac.cr/). Vol. 9, No 2. (Feb., 2009) Algebra Lineal con Mathematica. Sistemas de Ecuaciones Lineales. Carlos Arce S. carce@cariari.ucr.ac.cr
Lección 13: Resolución algebraica de sistemas de ecuaciones
 GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
1 SISTEMAS DE ECUACIONES LINEALES. CONCEPTOS GENERALES
 Sistemas de ecuaciones lineales MTEMÁTICS II 1 1 SISTEMS DE ECUCIONES LINELES. CONCEPTOS GENERLES Definición: Se llama ecuación lineal con n incógnitas x 1, x 2, x 3,., x n a toda ecuación que puede escribirse
Sistemas de ecuaciones lineales MTEMÁTICS II 1 1 SISTEMS DE ECUCIONES LINELES. CONCEPTOS GENERLES Definición: Se llama ecuación lineal con n incógnitas x 1, x 2, x 3,., x n a toda ecuación que puede escribirse
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
ESPACIO NULO DE A: RESOLUCIÓN DE AX = 0 3.2
 3.2 Espacio nulo de A: resolución de Ax = ESPACIO NULO DE A: RESOLUCIÓN DE AX = 3.2 Este tema versa sobre las soluciones espaciales de Ax =. La matriz A puede se cuadrada o rectangular. Una solución inmediata
3.2 Espacio nulo de A: resolución de Ax = ESPACIO NULO DE A: RESOLUCIÓN DE AX = 3.2 Este tema versa sobre las soluciones espaciales de Ax =. La matriz A puede se cuadrada o rectangular. Una solución inmediata
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO FACULTAD DE ECONOMIA LICENCIATURA DE ACTUARIA Algebra Lineal Práctica: Matriz inversa 1 M. en I. Elizabeth Almazán Torres 2 Resultado de Aprendizaje El estudiante
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO FACULTAD DE ECONOMIA LICENCIATURA DE ACTUARIA Algebra Lineal Práctica: Matriz inversa 1 M. en I. Elizabeth Almazán Torres 2 Resultado de Aprendizaje El estudiante
Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291)
 Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291) I. Combinación Lineal Definición: Sean v 1, v 2, v 3,, v n vectores en el espacio vectorial V. Entonces cualquier
Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291) I. Combinación Lineal Definición: Sean v 1, v 2, v 3,, v n vectores en el espacio vectorial V. Entonces cualquier
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel.
 Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
MATRICES. Entonces, A y B son matrices cuadradas de orden 3 y 2 respectivamente.
 1 MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos horizontales
1 MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos horizontales
UNIVERSIDAD CARLOS III DE MADRID
 UNIVERSIDAD CARLOS III DE MADRID Departamento de Economía Tema 1: Matrices y sistemas de ecuaciones lineales Empezaremos por recordar conceptos ya conocidos de álgebra lineal como las matrices, determinantes,
UNIVERSIDAD CARLOS III DE MADRID Departamento de Economía Tema 1: Matrices y sistemas de ecuaciones lineales Empezaremos por recordar conceptos ya conocidos de álgebra lineal como las matrices, determinantes,
MATRICES. TIPOS DE MATRICES Según el aspecto de las matrices, éstas pueden clasificarse en:
 Repaso de Matrices MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos
Repaso de Matrices MATRICES Una matriz es una tabla ordenada de escalares a ij de la forma La matriz anterior se denota también por (a ij ), i =1,..., m, j =1,..., n, o simplemente por (a ij ). Los términos
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Determinantes. Primera definición. Consecuencias inmediatas de la definición
 Determinantes Primera definición Para calcular el determinante de una matriz cuadrada de orden n tenemos que saber elegir n elementos de la matriz de forma que tomemos solo un elemento de cada fila y de
Determinantes Primera definición Para calcular el determinante de una matriz cuadrada de orden n tenemos que saber elegir n elementos de la matriz de forma que tomemos solo un elemento de cada fila y de
1 SISTEMAS DE ECUACIONES LINEALES. CONCEPTOS GENERALES
 Sistemas de ecuaciones lineales MATEMÁTICAS II 1 1 SISTEMAS DE ECUACIONES LINEALES. CONCEPTOS GENERALES o Definición: Un sistema de m ecuaciones con n incógnitas es un conjunto de ecuaciones lineales que
Sistemas de ecuaciones lineales MATEMÁTICAS II 1 1 SISTEMAS DE ECUACIONES LINEALES. CONCEPTOS GENERALES o Definición: Un sistema de m ecuaciones con n incógnitas es un conjunto de ecuaciones lineales que
DETERMINANTES página 251 DETERMINANTES. Por ejemplo: 2 1 8 es un determinante de tres filas y tres columnas.
 DETERMINANTES página 251 DETERMINANTES 13.1 Un determinante es un arreglo numérico en igual número de filas que de columnas del que, a partir de ciertas reglas, se forma un polinomio. El símbolo es un
DETERMINANTES página 251 DETERMINANTES 13.1 Un determinante es un arreglo numérico en igual número de filas que de columnas del que, a partir de ciertas reglas, se forma un polinomio. El símbolo es un
4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES
 57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
57 4 MÉTODOS DIRECTOS PARA RESOLVER SISTEMAS DE ECUACIONES LINEALES En este capítulo se estudia el componente algorítmico y computacional de los métodos directos para resolver sistemas de ecuaciones lineales.
Ecuaciones de primer grado
 Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
Matrices y determinantes
 Matrices y determinantes Matrices y determinantes Matrices Una matriz es un grupo de números organizados en filas y columnas, limitados por un paréntesis: 1 2 3 n columnas a11 a12 a13 a1 n a21 a22 a23
Matrices y determinantes Matrices y determinantes Matrices Una matriz es un grupo de números organizados en filas y columnas, limitados por un paréntesis: 1 2 3 n columnas a11 a12 a13 a1 n a21 a22 a23
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
Contenido. 2 Operatoria con matrices. 3 Determinantes. 4 Matrices elementales. 1 Definición y tipos de matrices
 elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2
 ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
ÁLGEBRA LINEAL I NOTAS DE CLASE UNIDAD 2 Abstract Estas notas conciernen al álgebra de matrices y serán actualizadas conforme el material se cubre Las notas no son substituto de la clase pues solo contienen
MATRICES Y DETERMINANTES MATRIZ INVERSA
 Índice Presentación... 3 Determinante de una matriz... 4 Determinante de matrices de orden 2 y 3... 5 Determinante de una matriz... 6 Ejemplo... 7 Propiedades del cálculo de determinantes... 8 Matriz inversa...
Índice Presentación... 3 Determinante de una matriz... 4 Determinante de matrices de orden 2 y 3... 5 Determinante de una matriz... 6 Ejemplo... 7 Propiedades del cálculo de determinantes... 8 Matriz inversa...
