Capitulo 6. Matrices y determinantes
|
|
|
- María del Pilar Molina Ruiz
- hace 7 años
- Vistas:
Transcripción
1 Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido. 6.1 Definición de matriz y de igualdad de matrices. Operaciones con matrices y sus propiedades: adición, sustracción, multiplicación por un escalar y multiplicación. Matriz identidad. 6.2 Definición y propiedades de la inversa de una matriz. Cálculo de inversa por transformaciones elementales. 6. Ecuaciones matriciales y su resolución. Representación y resolución matricial de los sistemas de ecuaciones lineales. 6.4 Matrices triangulares, diagonales y sus propiedades. Definición de traza de una matriz y sus propiedades. 6.5 Transposición de una matriz y sus propiedades. Matrices simétricas, antisimétricas y ortogonales. Conjugación de una matriz y sus propiedades. Matrices hermitianas, antihermitianas y unitarias. Potencia de una matriz y sus propiedades. 6.6 Definición de determinante de una matriz y sus propiedades. Cálculo de determinantes: Regla de Sarrus, desarrollo por cofactores y método de condensación. Cálculo de la inversa por medio de la adjunta. Regla de Cramer para la resolución de sistemas de ecuaciones lineales de orden superior a tres Definición de matriz.. Matriz: Arreglo rectangular de entes matemáticos (polinomios, funciones, etc.) que usualmente son números. Definición: Una matriz de m x n con elementos en C es un arreglo de la forma: donde a 11, a 12,, a mn C y m, n Z. a 11 a 1n M = a m1 a mn En forma abreviada, M= [a ij ] con i= 1,..., m; j= 1,..., n. AA = 2 + i 0 8 π 4 i x2 1 BB = [1 2 ] 1x CC = 2 x1 DD = i 0 0 i
2 Igualdad de matrices. Definición: Sean A= [a ij ] y B= [b ij ] dos matrices de orden m x n con elementos en C. A y B son iguales si: a ij = b ij ; con i= 1,..., m; j= 1,..., n Operaciones con matrices. Adición de matrices. Si A= [a ij ] mxn y B= [b ij ] mxn entonces A+B=S= [s ij ] mxn donde s ij = a ij + b ij para i= 1,..., m; j= 1,..., n i A = i B = 2 i C = 7 + i 0 2x 2i 4 x2 4 x2 4 A + B = 2 1 2i 0 x2 A + C y B + C no se pueden efectuar NO son conformables para la adición de matrices. Propiedades de la adición de matrices. i) A + (B+C) = (A+B) + C Asociatividad ii) A + B = B + A Conmutatividad iii) A+ 0 = A (Matriz nula del mismo orden) Elemento idéntico iv) A + (-A) =0 Elemento inverso Sustracción de matrices. Si A= [a ij ] mxn y B= [b ij ] mxn entonces A - B se define como A + (-B). Multiplicación por un escalar. Sea A= [a ij ] mxn y α ϵ C. El producto αa es una matriz de m x n definida por: αa = αa ij Teorema: Si A y B son dos matrices de m x n con elementos en C y α, β ϵ C, entonces: i) α(a + B) = αa + αb ii) (α + β)a = αa + βa iii) α(βa) = (αβ)a Multiplicación de matrices. Si A= [a ij ] mxn y B= [b ij ] nxq entonces AB= [p ij ] mxq donde: nn pp iiii = aa iiii bb kkkk kk=1 para i = 1,..., m; j = 1,..., q. 5 1 A = x 2 0 B = 4 1 x2 C = x4
3 2 9 AAAA = xx ; BBBB = xx ; CCCC = xx AC, BA, CB son NO CONFORMABLES para la multiplicación de matrices. AC CA, AB BA y BC CB, la multiplicación de matrices NO siempre es conmutativa. Demostrar que las matrices A, B y C son conmutables para la multiplicación. A = 0 1 1, B = 1 2 4, C = 1 2 AB = 4 6 ; BA = ; AC = ; CA = A y B NO son permutables (conmutables), A y C SI son permutables. Teorema. Sean A, B y C matrices de m x n, n x p y p x q respectivamente, cuyos elementos son números complejos, entonces: A(BC) = (AB)C. Se cumple la ASOCIATIVIDAD en la multiplicación de matrices. Demostrar que las matrices A, B y C cumplen con la asociatividad para la multiplicación. A = 1 2 4, B = , C = Primera forma A(BC): BC = , ABC = Segunda forma (AB)C: AB =, ABC = Teorema. Sean A, B y C matrices de m x n, n x p y p x q respectivamente, y D, E, F, matrices de m x n, m x n y n x p respectivamente, cuyos elementos son números complejos, entonces: i) A(B+C) = AB + AC ii) (D+E)F = DF + EF Matriz identidad. Se conoce como "matriz identidad" de orden n a una matriz cuadrada de n x n de la forma: I n = Definición. Se llama matriz identidad de orden n, a la matriz cuadrada de orden n, I n =[d ij ], tal que: δδ iiii = 1, ssss ii = jj δδ iiii = 0, ssss ii jj
4 La matriz identidad constituye el elemento idéntico en la multiplicación de matrices. Teorema. Si A es una matriz con elementos en C, entonces: i) I m A = A ii) AI n = A 6.2. Inversa de una matriz. Definición. Sea A una matriz de n x n con elementos en C. Una matriz X se dice que es inversa de A si: XA = I n = AX y se representa con A -1. Nota: 1. Para que una matriz A tenga inversa, es condición necesaria que sea cuadrada. A -1 deberá ser cuadrada y del mismo orden que A. 2. NO todas las matrices cuadradas tienen inversa (deta=0).. Singular ( AA 1 ) Matriz No singular ( AA 1 ) 4. Si existe la inversa de una matriz cuadrada, ésta es única (unicidad). Teorema: Si A y B son dos matrices no singulares del mismo orden y λ CC, entonces: i) A 1 es única ii) (AA 1 ) 1 = AA iii) (AAAA) 1 = BB 1 AA 1 iv) (λaa) 1 = 1 λ AA 1, ssss λ 0 Cálculo de la inversa por transformaciones elementales. [A I n ] T 1 T k I n A 1 Transformaciones elementales a) Intercambiar dos renglones. b) Multiplicar un renglón por un escalar diferente de cero. c) Multiplicar un renglón por un escalar diferente de cero y sumarlo a otro renglón, reemplazando este último por el resultado obtenido Ej 1. A = 5 6 ; A 1 = Ej 2. B = ; B 1 = i 1 2 i 2 + i 5 i Ej. C = 0 2 i 1 + i ; C 1 = 0 1 i 0 1 i 0 i 1 + 2i
5 6.. Ecuaciones matriciales. Ej 1. AX+B = X Solución: AX + B = X; X AX = B; (I A)X = B; XX = ( AA) 11 BB X = Ej 2. Dadas las matrices: A = ; B = Resolver la ecuación: AX = B XX = Ej. Dadas las matrices: A = ; B = ; C = Resolver la ecuación: XA + B = C XX = Ej 4. Siendo: A = ; B = ; C = Calcular el valor de X en las siguientes ecuaciones: 1. XA= B+I XX = AX+B= C XX = XA+B= 2C XX = AX+BX= C XX = XAB - XC = 2C XX = Ej 5. Siendo: A = ; B = ; C = Resolver la ecuación matricial: A X + 2 B = C XX =
6 Ej 6. Resolver en forma matricial el sistema: x + y + z = 6 x + 2y + 5z = 12 x + 4y + 25z = 6 X=, Y= 2, Z= Representación matricial de un sistema de ecuaciones lineales. Ecuación matricial: AX = B, donde: A- Matriz de coeficientes X- Vector de incógnitas B- Vector de términos independientes. Resolver el siguiente sistema a través de álgebra matricial. x + z = 2 y - 2z = -1 x + y + 2z = 1 0 x A = ; X = y ; B = 1 ; Solución: A 1 = X = z Tipos especiales de matrices cuadradas. Regiones de una matriz cuadrada. a 11 a 12 a 1n a MM = 21 a 22 Triángulo superior a 2n a n1 a n2 a nn Triángulo inferior Diagonal principal Traza de una matriz Definición: Sea A=[a ij ] una matriz de n x n con elementos en C. Se llama traza de A y se representa con Tr(A), al número: nn aa iiii Teorema: Si A y B son dos matrices de n x n con elementos en C y αα CC. i) tr(a+b) = tr(a) + tr(b) ii) tr(αa) = α tr(a) iii) tr(ab) = tr(ba) ii=1
7 Matrices triangulares Definición: Sea A=[a ij ] una matriz de n x n con elementos en C. Se dice que: i) A es triangular superior si a ij = 0 para i > j. ii) A es triangular inferior si a ij = 0 para i < j. Teorema: Si A y B son dos matrices triangulares superiores (inferiores) del mismo orden y α C, entonces: i) A+B es triangular superior (inferior) ii) αa es triangular superior (inferior) iii) AB es triangular superior (inferior) Se cumple la propiedad de cerradura para este tipo de matrices. Matriz diagonal Los elementos fuera de la diagonal son nulos y distintos entre si. Definición: Sea A=[a ij ] una matriz de n x n con elementos en C. Se dice que A es una matriz diagonal si a ij = 0 para i j, y se representa como: diag (a 11, a 22,..., a nn ) Teorema: Si A y B son dos matrices diagonales tales que A= diag (a 11, a 22,..., a nn ) y B= diag (b 11, b 22,..., b nn ) y α C, entonces: i) A+B = diag (a 11 + b 11, a 22 + b 22,..., a nn + b nn ) ii) αa = diag (αa 11, αa 22,..., αa nn ) iii) AB = diag (a 11 b 11, a 22 b 22,..., a nn b nn ) iv) A -1 = diag (1/a 11, 1/a 22,..., 1/a nn ), si A es no singular. Matriz escalar Los elementos fuera de la diagonal son nulos e iguales entre si, pero diferentes de la unidad. α 0 0 MM = 0 α 0 = αi n 0 0 α
8 Operaciones sobre una matriz 1. Transposición: AA AA TT Si A = A T se tiene una matriz simétrica Si A = A T se tiene una matriz antisimétrica 2. Conjugación: AA AA Si A = AA se tiene una matriz real Si A = AA se tiene una matriz imaginaria. Conjugación - Transposición: AA AA Si A = A se tiene una matriz hermitiana Si A = A se tiene una matriz antihermitiana 4. Potencia enésima: AA AA nn Idempotente Involutoria Nilpotente Periodica 1. Transposición: AA AA TT Los renglones de A T son las columnas de A y las columnas de A T son los renglones de A. Definición: Sea A=[a ij ] una matriz de m x n con elementos en C. Se llama transpuesta de A a la matriz de n x m: AA TT = CC iiii, tal que C ij = a ij 2i 5 2i 0 i A = i, AT = 0 1 i 1 i Propiedades de la transposición Teorema: Si A y B son dos matrices con elementos en C y α C, entonces: i) A T T = A ii) (αa) T = αa T iii) (A + B) T = A T + B T si A + B iv) (AB) T = B T A T si AB Matrices simétricas y antisimétricas (matrices cuadradas) Definición: Sea A una matriz de n x n con elementos en C, se dice que: i) A es simétrica si A T = A ii) A es antisimétrica si A T = A Matriz simétrica i A = 5 i i ; A = A T ; a ij = a ji i, j 2 i i 0
9 Matriz antisimétrica i B = 5 0 i ; B = B T ; b ij = b ji i j; Si i = j, b ii = 0 2 i i 0 Propiedades de las matrices simétrica y antisimétrica. Teorema: Si A y B son dos matrices simétricas (antisimétricas) de n x n y α C, entonces: i) A+B es simétrica (antisimétrica) ii) αa es simétrica (antisimétrica) Teorema: Si A es una matriz de n x n con elementos en C, entonces: i) A + A T es simétrica ii) A A T es antisimétrica 2. Conjugación: AA AA Definición: Sea A=[a ij ] una matriz de m x n con elementos en C. Se llama conjugada de A a la matriz de m x n A = c ij tal que c ij = a. ij 2i 0 i A = i, A = 2i 0 i i Teorema: Si A y B son dos matrices con elementos en C y α C, entonces: i) ( ) A = A ii) αa = α A iii) A + B = A + B si A + B iv) AB = A B si AB Matrices reales e imaginarias. Definición: Sea A una matriz de m x n con elementos en C, se dice que: i) A es real si A = A ii) A es imaginaria si A = A Teorema: Si A es una matriz de m x n con elementos en C, entonces: i) A + A es real ii) A A es imaginaria. Conjugación - Transposición: AA AA La conjugación transposición de una matriz A, se representa con A y está definida como: A = (A ) T = (A T )
10 Propiedades de la conjugación transposición Teorema: Si A y B son dos matrices con elementos en C y α C, entonces: i) (A ) = A ii) (αa) = α A iii) (A + B) = A + B si A + B iv) (AB) = B A si AB Matrices hermitianas y antihermitianas (matrices cuadradas) Definición: Sea A una matriz de n x n con elementos en C, se dice que: i) A es hermitiana si A = A ii) A es antihermitiana si A = A Matriz hermitiana i A = 5 i ; a ij = a ji i, j ; I(a ii ) = 0, Diagonal principal: R 2 i i 0 Matriz antihermitiana i 5 2 i B = 5 i i ; b ij = b ji i, j ; R(a ii ) = 0, Diagonal principal: I 2 i i 0 Teorema: Si A es una matriz de m x n con elementos en C, entonces: i) AA es hermitiana ii) A A es hermitiana iii) A + A es hermitiana (nxn) iv) A A es antihermitiana (nxn) Potencia enésima Teorema: Sea A una matriz de n x n con elementos en C y m, n N, entonces: i) A m A n = A m+n ii) (A m ) n = A mn Una matriz A no singular se dice que: i) Es ortogonal si: A T = A 1 ii) Es unitaria si: A = A 1 Matriz idempotente: Una matriz de n x n es idempotente si se verifica que A 2 = A. Esto implica que A n = A n N. La matriz debe ser simétrica para ser idempotente, no todas las matrices simétricas son idempotentes. 2 A = ; A 1 2 = =
11 Matriz involutoria: Una matriz de n x n es involutoria si se verifica que A 2 = I n. A = ; A2 = = Matriz nilpotente: Una matriz de n x n es nilpotente si se verifica que A 2 = 0 (matriz nula). Esto implica que A n = 0 n N. A = ; A2 = = A = ; A 2 = = Matriz periódica: Una matriz cuadrada A es periódica si existe p N tal que A p+1 = A. Además si p es el menor número natural que cumple A p+1 = A se dice que A es periódica con periodo p. A = ; A = A 2 A ; A 2 = = ; A = Determinantes El concepto de determinante surge antes que el concepto de matriz, en 1750 los trabajos de Cramer orientados a la resolución de sistemas de ecuaciones lineales, dan como resultado el concepto de determinante. Nota: 1. La matriz es un arreglo de números. 2. El determinante es un número. Propiedades de un determinante Teorema: Sea A=[a ij ] una matriz de n x n con elementos en C: 1) Si los elementos de una línea de A (renglón o columna) son todos nulos, entonces det A= 0. 2) Si B se obtiene de A multiplicando los elementos de una de sus líneas por un número λ C entonces det B = λ det A. ) Si B se obtiene de A intercambiando 2 líneas paralelas (renglones o columnas), entonces det B = -det A. 4) Si dos líneas paralelas de A son proporcionales, entonces det A = 0. 5) Si B se obtiene de A sumando a los elementos de una línea, los elementos de una línea paralela multiplicados por un número λ C, entonces det B = det A. Teorema: Si A=[a ij ] y B=[b ij ] son dos matrices de n x n con elementos en C, entonces: i) det A = det A T ii) det λa = λ n det A iii) det AB = det A det B
12 Cálculo de determinantes Regla de Sarrus Éste método se emplea únicamente para calcular determinantes de segundo y tercer orden. Segundo orden: det A = a 11 a 12 a 21 a 22 = a 11 a 22 a 21 a 12 Tercer orden: a 11 a 12 a 1 det A = a 21 a 22 a 2 = a 11 a 22 a + a 21 a 2 a 1 + a 12 a 2 a 1 a 1 a 22 a 1 a 2 a 2 a 11 a a 21 a 12 a 1 a 2 a Determinar el valor de det A y det B. A = ; det A = 7 B = ; det B = Regla de Cramer para la resolución de sistemas de ecuaciones lineales Para encontrar los valores de las incógnitas de sistemas de ecuaciones lineales de orden 2 y, se requiere un cociente de determinantes. El numerador es el determinante que resulta al remplazar en la matriz de coeficientes, la columna de la incógnita por el vector de términos independientes. El denominador es el determinante asociado a la matriz de coeficientes. Resolver a través de la regla de Cramer los siguientes sistemas. a) 5X+Y = 5 4X+7Y = 27 deta = 2 ; X=-2, Y=5 b) X+1 = Y X+4 Y 9 6 = 8 det A = ; X = 4, Y = 9 c) 2X+Y+4Z = 260 X+4Y+8Z = 0 4X+8Y+6Z = 510 det A = -4 ; X = 50, Y = 20, Z = 25
13 Desarrollo por cofactores Aplicable al cálculo de determinantes de cualquier orden y es el fundamento de todos los métodos de aplicación práctica. Definición: Sea A=[a ij ] una matriz de n x n con elementos en C. i) Se llama "menor" (Mij) del elemento aij, al determinante de la matriz que se obtiene suprimiendo en A al renglón ' i ' y a la columna ' j '. ii) Se llama cofactor (Cij) del elemento aij, al producto: CC iiii = ( 11) ii+jj MM iiii Definición: Sea A=[a ij ] una matriz de mxn con elementos en C y r Z, tal que 1 r n, entonces: n i) det A = j=1 a rj c rj n ii) det A = a ir c ir i=1 Calcular el determinante de la matriz A, utilizando el método por cofactores. det A = 2222 CC = A = Cálculo de la inversa por medio de la matriz adjunta Definición: Sea A=[a ij ] una matriz de n x n con elementos en C y sea Cij el cofactor del elemento aij. Se llama matriz adjunta de A, a la matriz: Adj A = [bij], donde bij = Cji Obtener la adjunta de la matriz A A = Adj A = C ji = ; A Adj A = 6I ; det A = 6 ; A AdjA = (det A)I n Teorema: Si A es una matriz de nxn con elementos en C, entonces: A(Adj A)=(Adj A)A = (det A) In Teorema: A -1 existe si y solo si det A 0. A(Adj A) = (det A)I n ; I n = 1 det A (A(Adj A)) ; AA 11 = 11 AAAAAA AA dddddd AA A = 1 4 A 1 =
Una matriz es una tabla ordenada (por filas y columnas) de escalares a i j de la forma: ... ... a... ...
 MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
Matrices, determinantes, sistemas de ecuaciones lineales.
 UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
Teoría de Matrices. Julio Yarasca. 30 de junio de 2015. Julio Yarasca
 30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn
![MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a ] a m1 a m2 a mn](/thumbs/79/78966751.jpg) MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a [ 21 a 22 a 2n ] a m1 a m2 a mn con m renglones y n columnas, donde los a
MATRIZ Una matriz de orden (tamaño) mxn sobre el campo de los complejos es un arreglo rectangular de la forma a 11 a 12 a 1n a [ 21 a 22 a 2n ] a m1 a m2 a mn con m renglones y n columnas, donde los a
Tema 1: Matrices y Determinantes
 Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Matriz sobre K = R o C de dimensión m n
 2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
MENORES, COFACTORES Y DETERMINANTES
 MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
Una matriz es una arreglo rectangular ordenado de elementos, comúnmente llamados escalares, dispuestos en m renglones y n columnas.
 MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
EJERCICIOS DE MATRICES Y DETERMINANTES. Obtención de la Matriz Inversa utilizando transformaciones elementales.
 EJERIIOS DE MATRIES Y DETERMINANTES Obtención de la Matriz Inversa utilizando transformaciones elementales. Recordando: Una matriz elemental se puede obtener aplicando el siguiente procedimiento Ejemplo.
EJERIIOS DE MATRIES Y DETERMINANTES Obtención de la Matriz Inversa utilizando transformaciones elementales. Recordando: Una matriz elemental se puede obtener aplicando el siguiente procedimiento Ejemplo.
Álgebra Lineal, Ejercicios
 Álgebra Lineal, Ejercicios MATRICES 1 Se llama traza de una matriz cuadrada a la suma de los elementos de su diagonal principal Sea G el conjunto de todas las matrices cuadradas de orden n con traza nula
Álgebra Lineal, Ejercicios MATRICES 1 Se llama traza de una matriz cuadrada a la suma de los elementos de su diagonal principal Sea G el conjunto de todas las matrices cuadradas de orden n con traza nula
Ejemplo 1. Ejemplo introductorio
 . -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
. -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
Operaciones con matrices
 Operaciones con matrices Problemas teóricos En todos los problemas de esta lista se supone que F es un campo (cuerpo). Si no conoce bien el concepto de campo, entonces puede pensar que F = R. Operaciones
Operaciones con matrices Problemas teóricos En todos los problemas de esta lista se supone que F es un campo (cuerpo). Si no conoce bien el concepto de campo, entonces puede pensar que F = R. Operaciones
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES.
 BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
 Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
ELEMENTOS DE ALGEBRA LINEAL
 ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
Matrices y determinantes
 Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
Matrices y determinantes 1 Ejemplo Cuál es el tamaño de las siguientes matrices? Cuál es el elemento a 21, b 23, c 42? 2 Tipos de matrices Matriz renglón o vector renglón Matriz columna o vector columna
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; (A ) = A. 2. La inversa de A 1 es A; (A 1 ) 1 = A. 3. (AB) = B A.
 ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
Matrices: Una ordenación de números dispuestos en filas y columnas, encerrados entre corchetes
 Matrices: Una ordenación de números dispuestos en filas y columnas, encerrados entre corchetes Ejemplos: Verifican ciertas reglas o algebra, denominada algebra de matrices.la matriz representa en general
Matrices: Una ordenación de números dispuestos en filas y columnas, encerrados entre corchetes Ejemplos: Verifican ciertas reglas o algebra, denominada algebra de matrices.la matriz representa en general
Matrices. Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas.
 Matrices Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Matrices Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Matrices y Determinantes.
 Matrices y Determinantes. Definición [Matriz] Sea E un conjunto cualquiera, m, n N. Matrices. Generalidades Matriz de orden m n sobre E: a 11 a 12... a 1n a 21 a 22... a 2n...... a m1 a m2... a mn a ij
Matrices y Determinantes. Definición [Matriz] Sea E un conjunto cualquiera, m, n N. Matrices. Generalidades Matriz de orden m n sobre E: a 11 a 12... a 1n a 21 a 22... a 2n...... a m1 a m2... a mn a ij
Métodos Estadísticos Multivariados
 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Matrices y determinantes
 Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
Matrices y determinantes A = ( aij)=a mxn m = nº filas y n = nº columnas Orden o dimensión = mxn Matriz cuadrada m=n Matriz rectangular m n Matriz fila A 1xn Definiciones de Matrices a 11 a 12...a 1n a
MATEMÁTICAS 2º BACH TECNOL. MATRICES. Profesor: Fernando Ureña Portero MATRICES
 CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
CONCEPTO DE MATRIZ Definición: Se denomina matriz A o (a ij ) a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas : Columnas Filas Elemento a ij : Cada uno
Matriz Inversa. donde II es la matriz identidad (matriz diagonal con aa 11 = 1).
 Matriz Inversa Contenido Matriz Inversa Operaciones Elementales de Renglón (o Columna) Matriz Inversa a partir de Operaciones Elementales de Renglón Fórmulas Recursivas para la Inversión de Matrices Matriz
Matriz Inversa Contenido Matriz Inversa Operaciones Elementales de Renglón (o Columna) Matriz Inversa a partir de Operaciones Elementales de Renglón Fórmulas Recursivas para la Inversión de Matrices Matriz
Sistema de ecuaciones algebraicas
 Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.
 TEMA 1.- MATRICES 1.-Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la
TEMA 1.- MATRICES 1.-Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas. Cada uno de los números de que consta la
Algebra lineal Matrices
 Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
Algebra lineal Matrices Una matriz A un arreglo rectangular de números dispuestos en m renglones (filas) y n columnas. Fila 1 La componente o elemento ij de A, denotado por es el número que aparece en
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
INGENIERO EN COMPUTACION TEMA: DETERMINANTES
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: DETERMINANTES ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2017 UNIDAD DE APRENDIZAJE
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: DETERMINANTES ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2017 UNIDAD DE APRENDIZAJE
MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES
 5 de Abril de 2 MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (Clase ) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Puntos a tratar. Definición
5 de Abril de 2 MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (Clase ) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Puntos a tratar. Definición
1. Las matrices se denotan con letras mayúsculas. Por ejemplo, A, B, C, X,...
 CAPÍTULO 1 ALGEBRA MATRICIAL 11 Introducción Definición 111 (Matriz) Definimos una matriz como un arreglo rectangular de elementos, llamados escalares, sobre un álgebra F Más que hacer referencia especifica
CAPÍTULO 1 ALGEBRA MATRICIAL 11 Introducción Definición 111 (Matriz) Definimos una matriz como un arreglo rectangular de elementos, llamados escalares, sobre un álgebra F Más que hacer referencia especifica
a) La adición y la multiplicación de matries cuadradas del mismo orden, están bien definidas.
 MATRICES CUADRADAS Definición: ( Cuadradas Una matriz A es una matriz cuadrada de orden n, si y solo si, A es de oreden n n, es decir, A tiene n filas y n columnas: a 11 a 1n a n1 a nn Observación: a La
MATRICES CUADRADAS Definición: ( Cuadradas Una matriz A es una matriz cuadrada de orden n, si y solo si, A es de oreden n n, es decir, A tiene n filas y n columnas: a 11 a 1n a n1 a nn Observación: a La
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
SISTEMAS Y MATRICES LECCIÓN 8
 SISTEMAS Y MATRICES LECCIÓN 8 Índice: Producto de matrices. Propiedades del producto de matrices. Problemas..- Producto de matrices El producto de una matriz fila de orden n por una matriz columna de orden
SISTEMAS Y MATRICES LECCIÓN 8 Índice: Producto de matrices. Propiedades del producto de matrices. Problemas..- Producto de matrices El producto de una matriz fila de orden n por una matriz columna de orden
MANUAL DE MATRICES Y DETERMINANTES
 Universidad Politécnica Salesiana Carrera de Ingeniería Mecánica MANUAL DE MATRICES Y DETERMINANTES Msc. Wilson Benavides Wilson Benavides MANUAL DE MATRICES Y DETERMINANTES 2012 Carrera de Ingeniería
Universidad Politécnica Salesiana Carrera de Ingeniería Mecánica MANUAL DE MATRICES Y DETERMINANTES Msc. Wilson Benavides Wilson Benavides MANUAL DE MATRICES Y DETERMINANTES 2012 Carrera de Ingeniería
Matemáticas II. Prácticas: Matrices y Determinantes ; C = 1 3 5
 Matemáticas II Prácticas: Matrices y Determinantes. Sean las matrices cuadradas siguientes: 4 5 6 B = 9 8 7 6 5 4 C = 5 7 9 0 7 8 9 Se pide calcular: a A B + C. b A AB + AC. c A B AB + ACB.. Sean las matrices:
Matemáticas II Prácticas: Matrices y Determinantes. Sean las matrices cuadradas siguientes: 4 5 6 B = 9 8 7 6 5 4 C = 5 7 9 0 7 8 9 Se pide calcular: a A B + C. b A AB + AC. c A B AB + ACB.. Sean las matrices:
Matrices. p ij = a ik b kj = a i1 b 1j + a i2 b 2j + + a in b nj.
 Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Elementos de una matriz.
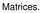 Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
Matrices 2º curso de Bachillerato Matemáticas aplicadas a las ciencias sociales
 MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
2 - Matrices y Determinantes
 Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Tema 5: Sistemas de Ecuaciones Lineales
 Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Definición de la matriz inversa
 Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Matrices. José Vicente Romero Bauset. ETSIT-curso 2009/2010. José Vicente Romero Bauset Tema 1.- Matrices. 1
 Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Determinante de una matriz
 25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
MATRICES. Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden x (que se lee por ).
 1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
1 MATRICES 1 Una matriz es una disposición rectangular de números (Reales); la forma general de una matriz con filas y columnas es Se simboliza tal matriz por y se le llamará una matriz x o matriz de orden
Matrices, Determinantes y Sistemas de ecuaciones lineales
 Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
Tema I. Matrices y determinantes
 Tema I. Matrices y determinantes 2007 Carmen Moreno Valencia 1. Matrices sobre un cuerpo 2. Operaciones con matrices 3. Determinante de una matriz cuadrada 4. Menor complementario y adjunto 5. Cálculo
Tema I. Matrices y determinantes 2007 Carmen Moreno Valencia 1. Matrices sobre un cuerpo 2. Operaciones con matrices 3. Determinante de una matriz cuadrada 4. Menor complementario y adjunto 5. Cálculo
Tema 1. Álgebra lineal. Matrices
 1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
Contenido. 2 Operatoria con matrices. 3 Determinantes. 4 Matrices elementales. 1 Definición y tipos de matrices
 elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Una matriz es un arreglo rectangular de elementos. Por ejemplo:
 1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
Escuela de Matemáticas
 Escuela de Matemáticas Universidad de Costa Rica MA-004: Álgebra Lineal Prácticas Sistemas de ecuaciones lineales, Matrices Determinantes MSc Marco Gutiérrez Montenegro 07 Sistemas de ecuaciones lineales
Escuela de Matemáticas Universidad de Costa Rica MA-004: Álgebra Lineal Prácticas Sistemas de ecuaciones lineales, Matrices Determinantes MSc Marco Gutiérrez Montenegro 07 Sistemas de ecuaciones lineales
Mat r i z in v e r s a
 Unidad 2 Método de GaUss Mat r i z in v e r s a M U lt i pli cat i va Objetivos: Al inalizar la unidad, el alumno: Representará un sistema de m ecuaciones lineales con n incógnitas mediante una matriz
Unidad 2 Método de GaUss Mat r i z in v e r s a M U lt i pli cat i va Objetivos: Al inalizar la unidad, el alumno: Representará un sistema de m ecuaciones lineales con n incógnitas mediante una matriz
DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES
 ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
ALGEBRA DE MATRICES DEFINICIONES TIPOS DE MATRICES DETERMINANTES Y PROPIEDADES OPERACIONES MATRICIALES INVERSA DE UNA MATRIZ SISTEMAS DE ECUACIONES DEFINICIONES 2 Las matrices y los determinantes son herramientas
Lección 1. Algoritmos y conceptos básicos.
 Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Página 1 de 8 Lección 1. Algoritmos y conceptos básicos. Objetivos. La primera lección del curs está dedicada a repasar los conceptos y algoritmos del álgebra lineal, básicos para el estudio de la geometría
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Matemáticas Discretas TC1003
 Matemáticas Discretas TC13 Matrices: Conceptos y Operaciones Básicas Departamento de Matemáticas ITESM Matrices: Conceptos y Operaciones Básicas Matemáticas Discretas - p. 1/25 Una matriz A m n es un arreglo
Matemáticas Discretas TC13 Matrices: Conceptos y Operaciones Básicas Departamento de Matemáticas ITESM Matrices: Conceptos y Operaciones Básicas Matemáticas Discretas - p. 1/25 Una matriz A m n es un arreglo
Conceptos Preliminares
 Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
Conceptos Preliminares Igualdad de matrices Definición: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales. Estas matrices cumplen
UNIVERSIDAD CARLOS III DE MADRID
 UNIVERSIDAD CARLOS III DE MADRID Departamento de Economía Tema 1: Matrices y sistemas de ecuaciones lineales Empezaremos por recordar conceptos ya conocidos de álgebra lineal como las matrices, determinantes,
UNIVERSIDAD CARLOS III DE MADRID Departamento de Economía Tema 1: Matrices y sistemas de ecuaciones lineales Empezaremos por recordar conceptos ya conocidos de álgebra lineal como las matrices, determinantes,
Determinantes. Definiciones básicas sobre determinantes. José de Jesús Angel Angel.
 Determinantes Definiciones básicas sobre determinantes wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2008 Contenido 1 Determinantes 2 11 Propiedades de determinantes 4 2 Inversa
Determinantes Definiciones básicas sobre determinantes wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2008 Contenido 1 Determinantes 2 11 Propiedades de determinantes 4 2 Inversa
de la forma ), i =1,..., m, j =1,..., n, o simplemente por (a i j ).
 INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
INTRODUCCIÓN. MATRICES Y DETERMINANTES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales.
Matrices y determinantes
 Matrices y determinantes Las matrices y los determinantes son herramientas del álgebra de gran utilidad en muchas disciplinas. Los campos de aplicación de la teoría de las matrices y de los determinantes
Matrices y determinantes Las matrices y los determinantes son herramientas del álgebra de gran utilidad en muchas disciplinas. Los campos de aplicación de la teoría de las matrices y de los determinantes
TEMA 2: MATRICES. 2.2.1 Operaciones elementales y matrices elementales. 2.2.2 Proceso de escalonamiento de una matriz no nula.
 TEMA 2: MATRICES 21 Generalidades sobre matrices 211 Definición de matriz Tipos de matrices 212 Operaciones algebraicas con matrices 213 Matriz traspuesta y traspuesta-conjugada 214 Submatrices 22 Proceso
TEMA 2: MATRICES 21 Generalidades sobre matrices 211 Definición de matriz Tipos de matrices 212 Operaciones algebraicas con matrices 213 Matriz traspuesta y traspuesta-conjugada 214 Submatrices 22 Proceso
Matrices 3. Matrices. Verónica Briceño V. agosto 2012
 3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
3 agosto 2012 En esta Presentación... En esta Presentación veremos: Matriz Inversa En esta Presentación... En esta Presentación veremos: Matriz Inversa Determinante En esta Presentación... En esta Presentación
Es decir, det A = producto de diagonal principal producto de diagonal secundaria. Determinante de una matriz cuadrada de orden 3
 1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS.
 TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
TEMA 1. MATRICES, DETERMINANTES Y APLICACIÓN DE LOS DETERMINANTES. 1. MATRICES. CONCEPTO DE MATRIZ. LA MATRIZ COMO EXPRESIÓN DE TABLAS Y GRAFOS. DEFINICIÓN: Las matrices son tablas numéricas rectangulares
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
 Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya
 FUNDAMENTOS DEL ÁLGEBRA LINEAL. EJERCICIOS Y CUESTIONES. SOLUCIONES CON MATHEMATICA Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya ISBN: 978-84-606-6054-5 Depósito legal: BI-355-2015
FUNDAMENTOS DEL ÁLGEBRA LINEAL. EJERCICIOS Y CUESTIONES. SOLUCIONES CON MATHEMATICA Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya ISBN: 978-84-606-6054-5 Depósito legal: BI-355-2015
TEMA 1: MATRICES. Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas ...
 TEMA : MATRICES Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas a a a... a n a a a... an A... am am am... amn A los números reales a ij se les llama elementos
TEMA : MATRICES Una matriz de orden mxn es un conjunto de m n números reales dispuestos en m filas y n columnas a a a... a n a a a... an A... am am am... amn A los números reales a ij se les llama elementos
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes
 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Tema 1: Matrices. Sistemas de ecuaciones. Determinantes José M. Salazar Octubre de 2016 Tema 1: Matrices. Sistemas de ecuaciones. Determinantes Lección 1. Matrices. Sistemas de ecuaciones. Determinantes
Lección 5.1: Matrices y determinantes. Primeros conceptos. Objetivos de esta lección
 Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
PRUEBA MÚLTIPLE ELECCIÓN MATRICES Y DETERMINANTES
 PRUEBA MÚLTIPLE ELECCIÓN MATRICES Y DETERMINANTES 1. Sea una matriz A M n n (R) nilpotente de índice p. r(a) n 1 r(a) =p 1 8 4 2 2. Sea la matriz A = 2 1 1 0 5 2 1 1 r(a) =2 r(a) =3 r(a) =4 3. Sea una
PRUEBA MÚLTIPLE ELECCIÓN MATRICES Y DETERMINANTES 1. Sea una matriz A M n n (R) nilpotente de índice p. r(a) n 1 r(a) =p 1 8 4 2 2. Sea la matriz A = 2 1 1 0 5 2 1 1 r(a) =2 r(a) =3 r(a) =4 3. Sea una
MATRICES OPERACIONES BÁSICAS CON MATRICES
 MATRICES OPERACIONES BÁSICAS CON MATRICES ANTECEDENTES En el año 1850, fueron introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A.
MATRICES OPERACIONES BÁSICAS CON MATRICES ANTECEDENTES En el año 1850, fueron introducidas por J.J. Sylvester El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A.
Ecuaciones matriciales AX = B y XA = B. Cálculo de la matriz inversa
 Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Matrices y Determinantes
 Matrices y Determinantes Definición de matriz Matriz Una matriz es un ente matemático equivalente a una tabla; es decir, es un arreglo de elementos de cualquier naturaleza (aunque, en general, suelen ser
Matrices y Determinantes Definición de matriz Matriz Una matriz es un ente matemático equivalente a una tabla; es decir, es un arreglo de elementos de cualquier naturaleza (aunque, en general, suelen ser
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 MATRICES
 CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
CONTENIDOS MATEMÁTICAS II SEGUNDA EVALUACIÓN CURSO 2017/2018 Unidades: - Matrices (Bloque Álgebra) - Determinantes (Bloque Álgebra) - Sistemas de ecuaciones lineales (Bloque Álgebra) - Vectores (Bloque
Matrices y Determinantes. Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC
 Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
Matrices y Determinantes Prof. Nilsa I. Toro Catedrática Recinto Universitario de Mayagüez Residencial - AFAMaC Origen y Usos Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J.
Matrices y Determinantes. Sistemas Ec. Lineales
 Matrices y Determinantes. Sistemas Ec. Lineales Matrices.- Definiciones.- Se llama matriz de orden nxm a toda ordenación de n.m números ordenados en n filas y m columnas. Se suelen llamar con letras mayúsculas
Matrices y Determinantes. Sistemas Ec. Lineales Matrices.- Definiciones.- Se llama matriz de orden nxm a toda ordenación de n.m números ordenados en n filas y m columnas. Se suelen llamar con letras mayúsculas
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
ÁLGEBRA LINEAL I Práctica 3
 ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
BOLETÍN DE MATRICES 2 IES A Sangriña Curso 2016/ Calcula la matriz inversa, si existe, usando el método de Gauss:
 *** OBLIGATORIOS *** 1. Efectúa todos los posibles productos: 2. Calcula la matriz inversa, si existe, usando el método de Gauss: 3. Sean y. Encuentra X para que cumpla: 3 X 2 A = 5 B 4. Encuentra dos
*** OBLIGATORIOS *** 1. Efectúa todos los posibles productos: 2. Calcula la matriz inversa, si existe, usando el método de Gauss: 3. Sean y. Encuentra X para que cumpla: 3 X 2 A = 5 B 4. Encuentra dos
DOCENTE: JESÚS E. BARRIOS P.
 DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
DOCENTE: JESÚS E. BARRIOS P. DEFINICIONES Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un texto matemático chino que proviene del año 300 A. C. a 200 A. C., Nueve capítulos
Matrices 2º curso de Bachillerato Ciencias y tecnología
 MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
MATRICES Índice:. Introducción-------------------------------------------------------------------------------------- 2. Definición de matriz-----------------------------------------------------------------------------
1 0 4/ 5 13/
 1 1 1 7 1 0 4/ 5 13/ 5 R1 R 1+1/5R3 0 0 0 2 R2 R3 0 5 9 22 0 5 9 22 0 0 0 2 Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al
1 1 1 7 1 0 4/ 5 13/ 5 R1 R 1+1/5R3 0 0 0 2 R2 R3 0 5 9 22 0 5 9 22 0 0 0 2 Como la matriz tiene un renglón (0, 0, 0, 2) indica que el sistema no tiene solución ya que no existe un número que sea 2 y al
ALN. Repaso matrices. In. Co. Facultad de Ingeniería Universidad de la República
 ALN Repaso matrices In. Co. Facultad de Ingeniería Universidad de la República Definiciones básicas - Vectores Definiciones básicas - Vectores Construcciones Producto interno: ( x, y n i x y i i ' α Producto
ALN Repaso matrices In. Co. Facultad de Ingeniería Universidad de la República Definiciones básicas - Vectores Definiciones básicas - Vectores Construcciones Producto interno: ( x, y n i x y i i ' α Producto
Ecuaciones. 3º de ESO
 Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Repaso de álgebra de matrices y probabilidad. Javier Santibáñez (IIMAS, UNAM) Regresión Semestre / 58
 Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
Repaso de álgebra de matrices y probabilidad Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 58 Preliminares Definición (matriz) Una matriz de dimensión m n es un arreglo rectangular de números
TEMA V. Pues bien, a estas caracterizaciones de los sistemas de ecuaciones lineales se las llamó matrices. En el caso del sistema considerado tenemos:
 TEMA V 1. MATRICES Y SISTEMAS DE ECUACIONES LINEALES. Sea el siguiente sistema de ecuaciones lineales: Realmente quien determina la naturaleza y las soluciones del sistema, no son las incógnitas: x, y,
TEMA V 1. MATRICES Y SISTEMAS DE ECUACIONES LINEALES. Sea el siguiente sistema de ecuaciones lineales: Realmente quien determina la naturaleza y las soluciones del sistema, no son las incógnitas: x, y,
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales
 Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
Introducción Las matrices aparecen por primera vez hacia el año 1850, introducidas por J.J. Sylvester. El desarrollo inicial de la teoría se debe al matemático W.R. Hamilton en 1853. En 1858, A. Cayley
1. Matrices. Operaciones con matrices
 REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
REPASO MUY BÁSICO DE MATRICES. Matrices. Operaciones con matrices.. Introducción Las matrices aparecieron por primera vez hacia el año 850, introducidas por el inglés J. J. Sylvester. Su desarrollo se
MATEMÁTICAS 2º BACH CIENCIAS MATRICES. Profesor: Fernando Ureña Portero
 La palabra Álgebra proviene del libro Al-jabr wa l muqabalah, del matemático árabe Al-Jowarizmi (siglo IX). Con dicho nombre se designó en occidente en posteriores siglos a la ciencia que aprendieron del
La palabra Álgebra proviene del libro Al-jabr wa l muqabalah, del matemático árabe Al-Jowarizmi (siglo IX). Con dicho nombre se designó en occidente en posteriores siglos a la ciencia que aprendieron del
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 III 1 / 8 Ejercicios sugeridos para : los temas de las clases del 5 y 7 de mayo de 2009. Temas : Matriz transpuesta. Matriz simétrica. Determinantes; propiedades de los determinantes. Matriz adjunta de
III 1 / 8 Ejercicios sugeridos para : los temas de las clases del 5 y 7 de mayo de 2009. Temas : Matriz transpuesta. Matriz simétrica. Determinantes; propiedades de los determinantes. Matriz adjunta de
