duv = udv + vdu udv = uv vdu
|
|
|
- José Manuel Iglesias Castellanos
- hace 7 años
- Vistas:
Transcripción
1 I. INTEGRACIÓN POR PARTES. Si la integración de una función no es posible encontrarla por alguna de las fórmulas conocidas, es posible que se pueda integrar utilizando el método conocido como integración por partes. Este método tiene como base la integración de la fórmula para la derivada de un producto de dos funciones. Sean u=u() y v=v(). Entonces duv = udv + vdu o udv = uv vdu Al integrar ambos miembros de esta ecuación obtenemos udv = uv vdu (.) Como se puede ver la Integración por partes es la contraparte de la regla del producto de la diferenciación, ya que el integrando en cuestión es el producto de dos funciones (por lo general). En resumen éste es el procedimiento: Para aplicar la fórmula (.) en la práctica, se separa el integrando en dos partes; una de ellas se iguala a u y la otra, junto con d a dv. Por eso se llama integración por partes. Es conveniente considerar los dos criterios siguientes. (a) La parte que se iguala a dv debe ser fácilmente integrable. (b) La vdu no debe de ser más complicada que udv Luego se aplica la fórmula de integración por partes. Este proceso convierte el integrando original - que no se puede integrar - en un integrando que si se puede integrar. Tan claro como el agua, verdad? Vas a aprender la técnica muy rápido si utilizas el acrónimo LIATE y el método del ejemplo de abajo: Para seleccionar la función u, sólo tienes que ir hacia abajo en la lista del acrónimo, la primera función de la lista que coincida con una de tu integrando es la función u. El acrónimo que te ayudará a escoger tu función u es el siguiente: Logarítmica (como Ln) Inversa trigonométrica (como arcsen) Algebraica (como, o +0 ) Trigonométrica (como sen) Eponencial (como 7, o e ) Calcular la integral ln d Tu primer reto en la integración por partes es decidir cuál es la función, (de tu integrando original), que desempeñará el papel de la u en la fórmula. He aquí cómo se hace
2 El integrando contiene una función logarítmica (la primera en LIATE) así que ln es tu función u, el resto d automáticamente es dv. Así pues tienes los términos son: u = ln, dv = d Pero la integral por partes contiene cuatro términos, te faltan los siguientes: du, y v. Estos los encuentras diferenciando u, e integrando dv, es decir: Si u = ln entonces du = d Si dv = d entonces v = dv = d = Esto significa que v se encuentra integrando dv. Ahora, ya tenemos los cuatro elementos que aparecen en la fórmula de integración por partes (.), sustituyendo estos valores ella entonces ln (ln ) ln = d ln ln ln 9 d = uv vdu = d d = + C Problemas resueltos. Ejemplo. Calcular = + C, de donde e d Primero reescribimos la integral así: e d. Por LIATE hacemos u =, y dv = e ; de donde du =, y v = dv = e d = e ( d) = e Bueno ya tenemos los elementos de la integral por partes. u = dv = e d du = d v = e Por tanto aplicando la fórmula (.) se tiene pero la última integral e d = e e d = = e e + C ya se calculó es (v) Ejemplo. Calcular ( sen) d
3 Usando LIATE hacemos u =, y dv = ( sen) d ; de donde du = d, y v = dv = ( sen) d = cos Aplicando la integración por partes obtenemos ( sen) d = ( cos ) ( cos ) d = cos + (cos ) d = cos + se + C Ejemplo. Calcular ln( + 4) d Hacemos u = ln( + 4), y dv = d ; por tanto diferenciado e integrando tenemos u, y d v. du = d( + 4) = , v = d = Por tanto d d + = + = + ln( 4) d ln( 4) ( ) ln( 4) Ahora calculamos la integral d + 4 du u. Recordar que = arctan u + a a a 6 6 d = = = 6 6 arctan d d d = = De donde + d= + + C = C ln( 4) ln( 4) ( 6 arctan ) ln( 4) arctan Ejemplo 4. + d Haciendo u =, y dv = + d ; tendremos du = d, para obtener v hacemos lo siguiente: + ( + ). Por lo tanto v = + d = ( + ) d = = ( + ) ( ) + d = ( + ) ( + ) d = ( + ) + C +. De donde d = ( + ) ( + ) + C 6 Ejemplo 5. Calcular e d
4 Haciendo u =, y dv = e, encontramos u =, du = d du du =, y v = e d = du = e = e du = e d = fórmula de integral por partes obtenemos u u. Aplicando la e e e e e e e e d = d = e d = + C = + C 4 Ejemplo 6. veces. Hacemos cosd. En este ejemplo se aplica la integral por partes dos u =, y dv = cosd, por tanto u =, du = d du du = d, y v = cosd = du = cosu = cosudu = sen d = integral por partes tenemos, sen cos d = sen sen ( d) send = (.). Por la Observa que en la integral send, ha bajado el eponente de la (de a ), lo cual sugiere volver a integrar por partes así que, hacemos aquí u =, y dv = send, y en consecuencia u = du = d du cos du = d, y v= sen d = du = senu = senudu = ( cos ) = d = de donde cos cos cos send = d = cosd cos cos = ( sen) = + sen 9 Sustituyendo este último resultado en (.) tenemos se se cos d = sen d = + sen cos 9 Ejemplo 7. Calcular sen sen cos = + + C 9 7 e d
5 El acrónimo LIATE nos sugiere tomar du = d, y v = e d = e obtenemos e d = e e ( d ) = e e d (.) u =, y dv = e, y por lo tanto, así que aplicando la formula de integral por partes Observa que hemos mejorado nuestra situación, el eponente de la bajó de a, lo cual nos sugiere aplicar de nuevo la integral por partes a la última integral, así que hagámoslo u =, dv = e e d = = e e ( d) = e e d du = d, v = e d = e Si reemplazamos éste último resultado en la ecuación (.) tenemos { } e d = e e d = e e + 6 e d (.4) e d = e e ( d) = e e d) = e e e d Observa que en la última integral de la derecha el eponente de la ahora bajó de a, así que aplicamos de nuevo la integración por partes. u =, dv = e e d = = e e d = e e du = d, v = e d = e Bueno parece que ya terminamos, observa que en la última integral ya no apareció la. Solo falta reemplazar el último resultado en la ecuación (.4) y finalizamos. ed = e e + 6 ed = e e + 6{ e e } + C. Por tanto ed= e e + 6e 6e + C Ejemplo 8. Calcular arcsend Hacemos las sustituciones u = arcsen, dv = d d y tenemos, du = d, v = d = Y ahora arcsend = arcsen d
6 u =, du = d du = = = d = d ( ) d du u Por lo tanto Ejemplo 9. Calcular u = = u = arcsend = arcsen ( ) + C = arcsen + + C arctan d. De acuerdo con el acrónimo LIATE tomamos u = arc tan, dv = d, así entonces d du = y v = d =, +. Por lo tanto la integral por partes es d arctan d d arctan = (arctan ) = + + (.5) Ahora lo único que tenemos que hacer es calcular la integral d + d = = = arctan d d = = En conclusión reemplazando el último resultado en (.5) obtenemos arctan arctan { } arctan d = arctan + C = + arctan + C Ejemplo 0. Calcular sen d sen d = = Así Para integrar separamos ( sen)( sen) d u = sen, dv = send du = cos d, v = send = cos d aplicando la integral por partes sen d = sen ( cos ) ( cos )(cos d ) = sen cos+ cos d (.6) Ahora nuestro problema es calcular la integral cos d que cos = sen, así que cos d = ( sen ) d = d sen d = sen d, es decir, sin embargo recordemos cos d = sen d, reemplacemos esta última ecuación en (.6)
7 sen d = sen cos+ cos d = se n cos + sen d, observa que el último término está restando, así que lo pasamos sumando al inicio de la ecuación y tenemos sen d + sen d = sen cos +, sumamos y sen d = sen +, de donde el pasa dividiendo cos sen cos + sen cos sen d = + C = + + C Ejemplo. Calcular sec d Como en el ejemplo anterior separamos sec = sec sec d sec sec sec =. Por tanto. La parte más complicada del integrando que resulta fácil de integrar porque conocemos una fórmula es sec, por tanto tomamos u = dv = d sec, sec du = sec tan d, v = sec d = tan Aplicando la integral por partes se tiene sec d = sec tan tan (sec tan d ) = sec tan sec tan d (.7) Así que sólo nos queda resolver la integral sec tan sec tan = tan = sec = sec (sec ) d d = (sec sec d ) = sec d sec d Este último resultado lo reemplazamos en la ecuación (.7) d. Manos a la obra { } sec d = sec tan sec tan d = sec tan sec d sec d de donde sec d = sec tan sec d + sec d = sec tan sec d + ln sec + tan, observa que término y tenemos sec d está restando, así que lo pasamos sumando al primer sec d + sec d = sec tan + ln sec + tan, sumando d y finalmente sec = sec tan + ln sec + tan sec tan + ln sec + tan sec tan ln sec + tan sec d = + C = + + C
Integración por Partes II. Integrales Cíclicas
 Integración por Partes II Integrales Cíclicas Para este tema utilizamos la misma fórmula de integración por partes, no hay casi nada nuevo. Para comenzar con esta sección usaré un ejemplo. Ejemplo 1: Integra
Integración por Partes II Integrales Cíclicas Para este tema utilizamos la misma fórmula de integración por partes, no hay casi nada nuevo. Para comenzar con esta sección usaré un ejemplo. Ejemplo 1: Integra
GUÍA: INTEGRALES. Página 1 de 27
 GUÍA: INTEGRALES Área de EET Página de 7 Derechos Reservados Titular del Derecho: INACAP N de inscripción en el Registro de Propiedad Intelectual #. de fecha - -. INACAP 00. Página de 7 . INTEGRALES. La
GUÍA: INTEGRALES Área de EET Página de 7 Derechos Reservados Titular del Derecho: INACAP N de inscripción en el Registro de Propiedad Intelectual #. de fecha - -. INACAP 00. Página de 7 . INTEGRALES. La
1. PRIMITIVA DE UNA FUNCIÓN 2. PROPIEDADES DE LA INTEGRAL INDEFINIDA 3. INTEGRALES INMEDIATAS Ejemplos de integrales inmediatas tipo potencia
 Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
CÁLCULO INTEGRAL INTEGRAL INDEFINIDA
 CÁLCULO INTEGRAL INTEGRAL INDEFINIDA Función primitiva : Una función F( se dice que es primitiva de otra función f( cuando F'( f( Por ejemplo F( es primitiva de f( Otra primitiva de f( podría ser F( +
CÁLCULO INTEGRAL INTEGRAL INDEFINIDA Función primitiva : Una función F( se dice que es primitiva de otra función f( cuando F'( f( Por ejemplo F( es primitiva de f( Otra primitiva de f( podría ser F( +
UNIVERSIDAD DE SEVILLA CALCULO DE PRIMITIVAS. PRIMER CURSO
 UNIVERSIDD DE SEVILL DEPRTMENTO DE ECONOMÍ PLICD I CLCULO DE PRIMITIVS. PRIMER CURSO CLCULO DE PRIMITIVS Conceptos generales. Definición. Dada f : D IR IR decimos que F : D IR IR es una primitiva de f
UNIVERSIDD DE SEVILL DEPRTMENTO DE ECONOMÍ PLICD I CLCULO DE PRIMITIVS. PRIMER CURSO CLCULO DE PRIMITIVS Conceptos generales. Definición. Dada f : D IR IR decimos que F : D IR IR es una primitiva de f
Tema 3. Cálculo de primitivas Conceptos generales.
 Tema Cálculo de primitivas... Conceptos generales. Una primitiva de una función es otra función que la tiene como derivada y la operación que permite obtener esta primitiva a partir de la función original
Tema Cálculo de primitivas... Conceptos generales. Una primitiva de una función es otra función que la tiene como derivada y la operación que permite obtener esta primitiva a partir de la función original
INTEGRACION POR PARTES
 INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
FACULTAD de INGENIERÍA Análisis Matemático A
 FAULTAD de INGENIERÍA Análisis Matemático A TRABAJO PRÁTIO N : Integral Indefinida Definición de antiderivada Se llama a una función F antiderivada(o primitiva) de una función f, si para todo en el dominio
FAULTAD de INGENIERÍA Análisis Matemático A TRABAJO PRÁTIO N : Integral Indefinida Definición de antiderivada Se llama a una función F antiderivada(o primitiva) de una función f, si para todo en el dominio
Un i d a d 7. Objetivos. Al inalizar la unidad, el alumno:
 Un i d a d 7 métodos de integraión Objetivos Al inalizar la unidad, el alumno: Utilizará los métodos de sustitución directa en la resolución de integrales. Resolverá integrales de funciones trigonométricas,
Un i d a d 7 métodos de integraión Objetivos Al inalizar la unidad, el alumno: Utilizará los métodos de sustitución directa en la resolución de integrales. Resolverá integrales de funciones trigonométricas,
Integral. F es primitiva de f F (x) = f(x)
 o Bachillerato, Matemáticas II. Integración. Integrales indefinidas. Métodos de integración. Primitiva de una función. Integral indefinida. Sean f y F dos funciones reales definidas en un mismo dominio.
o Bachillerato, Matemáticas II. Integración. Integrales indefinidas. Métodos de integración. Primitiva de una función. Integral indefinida. Sean f y F dos funciones reales definidas en un mismo dominio.
Tema 3. Cálculo de primitivas Conceptos generales.
 Tema Cálculo de primitivas... Conceptos generales. Una primitiva de una función es otra función que la tiene como derivada y la operación que permite obtener esta primitiva a partir de la función original
Tema Cálculo de primitivas... Conceptos generales. Una primitiva de una función es otra función que la tiene como derivada y la operación que permite obtener esta primitiva a partir de la función original
UNIVERSIDAD ARTURO PRAT IQUIQUE CHILE DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES
 DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES MARIA ELISA VODNIZZA LIRA e-mail : mvodnizz@cec.unap.cl url : www.unap.cl/~mvodnizz SEPTIEMBRE - 00 INTEGRALES Uno de los problemas importantes
DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES MARIA ELISA VODNIZZA LIRA e-mail : mvodnizz@cec.unap.cl url : www.unap.cl/~mvodnizz SEPTIEMBRE - 00 INTEGRALES Uno de los problemas importantes
Técnicas de Integración, preparado por: Gil Sandro Gómez
 Tema II. Técnicas de Integración. Integración por partes. La integración por partes surge del producto de una función trascendente y una algebraica, una inversa trigonométrica y una algébrica, una trigonométrica
Tema II. Técnicas de Integración. Integración por partes. La integración por partes surge del producto de una función trascendente y una algebraica, una inversa trigonométrica y una algébrica, una trigonométrica
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 8. Introducción a la integración INTEGRAL INDEFINIDA
 INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
Repaso de integración
 TABLA DE INTEGRALES INMEDIATAS Repaso de integración. Tabla de integrales inmediatas n d = n+ + C, si n n + f() n f () d = f()n+ n + + C, si n d = ln + C f() f () d = ln f() + C e d = e + C e f() f ()
TABLA DE INTEGRALES INMEDIATAS Repaso de integración. Tabla de integrales inmediatas n d = n+ + C, si n n + f() n f () d = f()n+ n + + C, si n d = ln + C f() f () d = ln f() + C e d = e + C e f() f ()
Ejercicios de Integrales resueltos
 Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
Capítulo 5: Cálculo integral
 Capítulo 5: Cálculo integral 1. Lección 18. La integral indefinida 1.1. Concepto de integral indefinida En el capítulo 3 hemos visto la diferencial de una función: dada y = f(x), su diferencial es una
Capítulo 5: Cálculo integral 1. Lección 18. La integral indefinida 1.1. Concepto de integral indefinida En el capítulo 3 hemos visto la diferencial de una función: dada y = f(x), su diferencial es una
Integración por partes.
 6 Integración por partes. Este método es útil cuando se requiere integrar diferenciales que contienen proctos, diferenciales que contienen logaritmos y diferenciales que contienen funciones trigonométricas
6 Integración por partes. Este método es útil cuando se requiere integrar diferenciales que contienen proctos, diferenciales que contienen logaritmos y diferenciales que contienen funciones trigonométricas
INTEGRACIÓN POR CAMBIO DE VARIABLE
 INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
TEMA 12.- CÁLCULO DE PRIMITIVAS
 TEMA.- CÁLCULO DE PRIMITIVAS.-.- PRIMITIVA DE UNA FUNCIÓN Definición de Función Primitiva Una función F() se dice que es primitiva de otra función f() cuando F'() f() Ejemplos: F() es primitiva de f()
TEMA.- CÁLCULO DE PRIMITIVAS.-.- PRIMITIVA DE UNA FUNCIÓN Definición de Función Primitiva Una función F() se dice que es primitiva de otra función f() cuando F'() f() Ejemplos: F() es primitiva de f()
INTEGRALES INMEDIATAS
 INTEGRALES INMEDIATAS Hay casos en los que la integral indeinida se calcula de orma inmediata, ya que la unción integrando es la derivada de una unción conocida. Se llaman integrales inmediatas a aquellas
INTEGRALES INMEDIATAS Hay casos en los que la integral indeinida se calcula de orma inmediata, ya que la unción integrando es la derivada de una unción conocida. Se llaman integrales inmediatas a aquellas
, pero lím. 1 x3 1. (x 1) x(x + 1) = x = x 1 1 x 3 = que es una forma indeterminada. (x + 2) (1 + x + x 2 ) = 3
 Ana María Albornoz R. Ejercicios resueltos. Calcular los siguientes ites algebraicos + + 5 + + + 0 0 + pero + 0 0 0, pero 0 + + + 4 que es una forma indeterminada. Pero + + + + + + + + + + + + + + + +
Ana María Albornoz R. Ejercicios resueltos. Calcular los siguientes ites algebraicos + + 5 + + + 0 0 + pero + 0 0 0, pero 0 + + + 4 que es una forma indeterminada. Pero + + + + + + + + + + + + + + + +
La integración por partes
 MB0005_M1AAL_Partes Versión: Septiembre 01 La integración por partes Por: Sandra Elvia Pérez Los métodos de integración son necesarios debido a que con frecuencia se presentan integrales que no se pueden
MB0005_M1AAL_Partes Versión: Septiembre 01 La integración por partes Por: Sandra Elvia Pérez Los métodos de integración son necesarios debido a que con frecuencia se presentan integrales que no se pueden
MATEMÁTICAS VI. CÁLCULO INTEGRAL UNIDAD II MÉTODOS DE INTEGRACIÓN
 MÉTODOS DE INTEGRACIÓN UNIDAD II MÉTODOS DE INTEGRACIÓN No todas las funciones en un integrando se pueden resolver mediante reglas inmediatas de integración, y requieren ser tratadas con técnicas especiales.
MÉTODOS DE INTEGRACIÓN UNIDAD II MÉTODOS DE INTEGRACIÓN No todas las funciones en un integrando se pueden resolver mediante reglas inmediatas de integración, y requieren ser tratadas con técnicas especiales.
Cálculo Integral: Guía II
 00 Cálculo Integral: Guía II Profr. Luis Alfonso Rondero García INSTITUTO POLITÉCNICO NACIONAL Departamento de Unidades de Aprendizaje del Área Básica /0/00 Integración de Potencias de Funciones Trigonométricas.
00 Cálculo Integral: Guía II Profr. Luis Alfonso Rondero García INSTITUTO POLITÉCNICO NACIONAL Departamento de Unidades de Aprendizaje del Área Básica /0/00 Integración de Potencias de Funciones Trigonométricas.
Integración de funciones trigonométricas
 Integración de funciones trigonométricas Ya vimos las reglas para calcular integrales de funciones trigonométricas. Ahora vamos a considerar productos de funciones trigonométricas y potencias. Para este
Integración de funciones trigonométricas Ya vimos las reglas para calcular integrales de funciones trigonométricas. Ahora vamos a considerar productos de funciones trigonométricas y potencias. Para este
Desarrollos de Taylor y Primitivas:
 Calculo Diferencial e Integral Profesor: Raúl Uribe Profesor Auiliar: Cristóbal Quiñinao 7 de septiembre de 007 Desarrollos de Taylor y Primitivas: Pregunta.- Sea f : R R definida por f() = e i. Determinar
Calculo Diferencial e Integral Profesor: Raúl Uribe Profesor Auiliar: Cristóbal Quiñinao 7 de septiembre de 007 Desarrollos de Taylor y Primitivas: Pregunta.- Sea f : R R definida por f() = e i. Determinar
Técnicas de Integración. Integración por Partes (I)
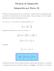 Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
INTEGRAL INDEFINIDA. CÁLCULO DE PRIMITIVAS
 urso 07-08 TEMA 0 INTEGRAL INDEFINIDA. ÁLULO DE PRIMITIVAS ÍNDIE I. INTRODUIÓN II. PRIMITIVA DE UNA FUNIÓN. INTEGRAL INDEFINIDA III. INTEGRALES INMEDIATAS IV. MÉTODOS DE INTEGRAIÓN A. MÉTODO DE SUSTITUIÓN.
urso 07-08 TEMA 0 INTEGRAL INDEFINIDA. ÁLULO DE PRIMITIVAS ÍNDIE I. INTRODUIÓN II. PRIMITIVA DE UNA FUNIÓN. INTEGRAL INDEFINIDA III. INTEGRALES INMEDIATAS IV. MÉTODOS DE INTEGRAIÓN A. MÉTODO DE SUSTITUIÓN.
Funciones Transcendentes
 Funciones Transcendentes Unidad Gil Sandro Gómez Santo Domingo 04 de diciembre de 0 Contenido Introducción....0 Función logaritmo natural... 3. Propiedades de la función logaritmo natural... 3. El número
Funciones Transcendentes Unidad Gil Sandro Gómez Santo Domingo 04 de diciembre de 0 Contenido Introducción....0 Función logaritmo natural... 3. Propiedades de la función logaritmo natural... 3. El número
UNIDAD I. DIFERENCIALES E INTEGRAL INDEFINIDA. Actividad 1. DIFERENCIALES
 CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/ LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO ASIGNATURA PROFESOR SEMESTRE CÁLCULO INTEGRAL L. M. A. JUAN MANUEL VALDEZ CHÁVEZ 0 0 B SEXTO
CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/ LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO ASIGNATURA PROFESOR SEMESTRE CÁLCULO INTEGRAL L. M. A. JUAN MANUEL VALDEZ CHÁVEZ 0 0 B SEXTO
TEMA 5: INTEGRAL INDEFINIDA.
 TEMA : INTEGRAL INDEFINIDA.. Primitivas: propiedades. Integral indefinida.. Integración por partes.. Integración de funciones racionales (denominador con raíces reales simples y múltiples, denominador
TEMA : INTEGRAL INDEFINIDA.. Primitivas: propiedades. Integral indefinida.. Integración por partes.. Integración de funciones racionales (denominador con raíces reales simples y múltiples, denominador
Tema 10: Integral indenida
 Tema 0: Integral indenida May 9, 07 Primitiva de una función Como hemos estudiado, la derivación nos permite encontrar la derivada de una función dada. Por ejemplo, si tenemos la función F () =, su derivada
Tema 0: Integral indenida May 9, 07 Primitiva de una función Como hemos estudiado, la derivación nos permite encontrar la derivada de una función dada. Por ejemplo, si tenemos la función F () =, su derivada
Unidad 5 - Trabajo Práctico 5 Parte 1 Elementos de Matemática
 06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
RELACIONES Y FUNCIONES
 RELACIONES Y FUNCIONES Variables Independiente: Aquella que puede tomar cualquier valor. Dependiente: Depende del valor que tome la variable independiente. Pares ordenados Se representan (a,b) donde: a:
RELACIONES Y FUNCIONES Variables Independiente: Aquella que puede tomar cualquier valor. Dependiente: Depende del valor que tome la variable independiente. Pares ordenados Se representan (a,b) donde: a:
ene 5 12:59 Está basado en la regla de la cadena. Si F(x) y g(x) son funciones derivables, la regla de la cadena nos dice que:
 Métodos de integración: 1) Método de descomposición Para calcular una integral indefinida, usamos las propiedades de las integrales y las igualdades que conozcamos para descomponer la integral en otras
Métodos de integración: 1) Método de descomposición Para calcular una integral indefinida, usamos las propiedades de las integrales y las igualdades que conozcamos para descomponer la integral en otras
El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow.
 INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
Calculo integral. Guía para elaborar el PORTAFOLIO DE EVIDENCIAS PARA EL EXAMEN EXTRAORDINARIO DE
 06 SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DEL BACHILLERATO / LIC. JESUS REYES HEROLES Guía para elaborar el PORTAFOLIO DE EVIDENCIAS PARA EL EXAMEN
06 SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DEL BACHILLERATO / LIC. JESUS REYES HEROLES Guía para elaborar el PORTAFOLIO DE EVIDENCIAS PARA EL EXAMEN
Linealidad. f, para toda función f ytodoescalarα. Primitivas de tipo inmediato. n+1 [f(x)] n f 0 (x)dx = [f(x)]n+1 + K dx =log x + K.
![Linealidad. f, para toda función f ytodoescalarα. Primitivas de tipo inmediato. n+1 [f(x)] n f 0 (x)dx = [f(x)]n+1 + K dx =log x + K. Linealidad. f, para toda función f ytodoescalarα. Primitivas de tipo inmediato. n+1 [f(x)] n f 0 (x)dx = [f(x)]n+1 + K dx =log x + K.](/thumbs/84/90763991.jpg) Tabla de primitivas Linealidad (f + g) = f + g αf = α f, para toda función f todoescalarα Primitivas de tipo inmediato Potencia Logaritmo Eponencial Trigonométricas n d = n+ n+ [f()] n f ()d = [f()]n+
Tabla de primitivas Linealidad (f + g) = f + g αf = α f, para toda función f todoescalarα Primitivas de tipo inmediato Potencia Logaritmo Eponencial Trigonométricas n d = n+ n+ [f()] n f ()d = [f()]n+
Soluciones de la relación de ejercicios del TEMA 0
 Soluciones de la relación de ejercicios del TEMA 0. Indica a que conjunto o conjuntos pertenecen los siguientes números: 0, 9, 4 5, 8, i,, 7, 7, +i,, π, 4 4 56 Para este ejercicio hay que tener en cuenta
Soluciones de la relación de ejercicios del TEMA 0. Indica a que conjunto o conjuntos pertenecen los siguientes números: 0, 9, 4 5, 8, i,, 7, 7, +i,, π, 4 4 56 Para este ejercicio hay que tener en cuenta
2 Métodos de solución de ED de primer orden
 CAPÍTULO 2 Métodos de solución de E de primer orden 2.8 Miscelánea En este apartado queremos responder a la pregunta cómo proceder cuando se nos pide resolver una ecuación diferencial ordinaria de primer
CAPÍTULO 2 Métodos de solución de E de primer orden 2.8 Miscelánea En este apartado queremos responder a la pregunta cómo proceder cuando se nos pide resolver una ecuación diferencial ordinaria de primer
Universidad de Chile Integración por partes. Ingeniería Matemática SEMANA 6: PRIMITIVAS
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
B. Cálculo de primitivas.
 50CAPÍTULO 5. INTEGRAL DEFINIDA. CÁLCULO DE PRIMITIVAS y y f(x) x y y F (x) x F (x) 8 >< >: x si x [0, ] x + six (, ] x si x (, ] Figura 5.5: B. Cálculo de primitivas. 5.. Integración inmediata. Definición
50CAPÍTULO 5. INTEGRAL DEFINIDA. CÁLCULO DE PRIMITIVAS y y f(x) x y y F (x) x F (x) 8 >< >: x si x [0, ] x + six (, ] x si x (, ] Figura 5.5: B. Cálculo de primitivas. 5.. Integración inmediata. Definición
Tabla de integrales inmediatas
 OFIMEGA INTEGRALES Pág. Tabla de integrales inmediatas Inmediatas Cuasi inmediatas d = n+ n n + k f () f'()d = f n+ () n k n + d ln + k f'() d = ln f() +k f() e f() f() d = e + k e f'()d = e + k a d =
OFIMEGA INTEGRALES Pág. Tabla de integrales inmediatas Inmediatas Cuasi inmediatas d = n+ n n + k f () f'()d = f n+ () n k n + d ln + k f'() d = ln f() +k f() e f() f() d = e + k e f'()d = e + k a d =
ECUACIÓN DE CAUCHY-EULER 2013
 ECUACIÓN DE CAUCHY-EULER 3 LA ECUACIÓN DE CAUCHY-EULER Se trata de una ecuación con coeficientes variables cua solución general siempre se puede epresar en términos de potencias, senos, cosenos, funciones
ECUACIÓN DE CAUCHY-EULER 3 LA ECUACIÓN DE CAUCHY-EULER Se trata de una ecuación con coeficientes variables cua solución general siempre se puede epresar en términos de potencias, senos, cosenos, funciones
Métodos de integración
 Integración por partes Métodos de integración De la derivada del producto de dos funciones obtenemos la fórmula de la derivación por partes. (uu. vv) = uu vv + uu vv que se puede escribir dd(uu. vv) =
Integración por partes Métodos de integración De la derivada del producto de dos funciones obtenemos la fórmula de la derivación por partes. (uu. vv) = uu vv + uu vv que se puede escribir dd(uu. vv) =
Universidad Nacional José María Arguedas Carrera Profesional de Administración de Empresas
 Universidad Nacional José María Arguedas Carrera Profesional de Administración de Empresas Cuaderno de ejercicios INTEGRALES Lic. F.M. José Luis Estrada Pantía Andahuaylas - Perú 0 A: Yris Stephany E.
Universidad Nacional José María Arguedas Carrera Profesional de Administración de Empresas Cuaderno de ejercicios INTEGRALES Lic. F.M. José Luis Estrada Pantía Andahuaylas - Perú 0 A: Yris Stephany E.
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
EL CÁLCULO DESARROLLA TU MENTE TRANSFORMA TU VIVIR
 Pág. UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE INGENIERIA CIUDAD OJEDA - ZULIA Guia de Cálculo II EL CÁLCULO DESARROLLA TU MENTE TRANSFORMA TU VIVIR b (Disciplina + Esfuerzo + Consagración)dv = Profesionales
Pág. UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE INGENIERIA CIUDAD OJEDA - ZULIA Guia de Cálculo II EL CÁLCULO DESARROLLA TU MENTE TRANSFORMA TU VIVIR b (Disciplina + Esfuerzo + Consagración)dv = Profesionales
5.1 Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
 INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
Tema 9: Cálculo integral
 Tema 9: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 9: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
MA1112 Secciones 01 y 04 Universidad Simón Bolívar Depto. de Matemáticas VERANO DE 2005 Puras y Aplicadas EJERCICIOS SOBRE INTEGRAL INDEFINIDA.
 MA Secciones y 4 Depto. de Matemáticas VERANO DE 5 EJERCICIOS SOBRE INTEGRAL INDEFINIDA..- Eplique que diferencia hay entre los conceptos de "integral indefinida" y "primitiva". [nota : primitiva es sinónimo
MA Secciones y 4 Depto. de Matemáticas VERANO DE 5 EJERCICIOS SOBRE INTEGRAL INDEFINIDA..- Eplique que diferencia hay entre los conceptos de "integral indefinida" y "primitiva". [nota : primitiva es sinónimo
REPASO DE CÁLCULO I INTEGRAL. Repaso General sobre Métodos de Integración Indefinida Guía Complementaria No.03
 Cálculo II c/geometría Analítica (MAT0), Secc.6 er Trimestre, er Semestre 06; er Parcial Documento Elaborado por: M.Sc. Ing. Julio César López Zerón CICH6 REPASO DE CÁLCULO I INTEGRAL Repaso General sobre
Cálculo II c/geometría Analítica (MAT0), Secc.6 er Trimestre, er Semestre 06; er Parcial Documento Elaborado por: M.Sc. Ing. Julio César López Zerón CICH6 REPASO DE CÁLCULO I INTEGRAL Repaso General sobre
Unidad 2. Técnica de integración, Formas Indeterminadas e Integrales Impropias
 Unidad Técnica de integración, Formas Indeterminadas e Integrales Impropias Gil Sandro Gómez // Unidad : Técnicas de In tegració n, Formas Ind etermi nadas e In tegrale s Impropias Contenido Introducción....
Unidad Técnica de integración, Formas Indeterminadas e Integrales Impropias Gil Sandro Gómez // Unidad : Técnicas de In tegració n, Formas Ind etermi nadas e In tegrale s Impropias Contenido Introducción....
Universidad Icesi Departamento de Matemáticas y Estadística
 Universidad Icesi Departamento de Matemáticas y Estadística Solución del tercer eamen parcial del curso Cálculo una variable Grupo: Uno Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. a. Después
Universidad Icesi Departamento de Matemáticas y Estadística Solución del tercer eamen parcial del curso Cálculo una variable Grupo: Uno Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. a. Después
2.4 Ecuaciones diferenciales de Bernoulli
 .4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
.4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO INTEGRACIÓN POR SUSTITUCIÓN
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO COLEGIO DE CIENCIAS Y HUMANIDADES PLANTEL VALLEJO ÁREA DE MATEMÁTICAS CÁLCULO DIFERENCIAL E INTEGRAL II INTEGRACIÓN POR SUSTITUCIÓN Las formulas de integración inmediatas
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO COLEGIO DE CIENCIAS Y HUMANIDADES PLANTEL VALLEJO ÁREA DE MATEMÁTICAS CÁLCULO DIFERENCIAL E INTEGRAL II INTEGRACIÓN POR SUSTITUCIÓN Las formulas de integración inmediatas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Simplificando los cuadrados con las raíces y sumando términos semejantes y elevando al cuadrado nuevamente:
 . Resolver la siguiente ecuación irracional 6 7 0 Solución: llevando el término con signo negativo al segundo miemro de la ecuación y elevando al cuadrado: 6 7 6 6 7 7 Simplificando los cuadrados con las
. Resolver la siguiente ecuación irracional 6 7 0 Solución: llevando el término con signo negativo al segundo miemro de la ecuación y elevando al cuadrado: 6 7 6 6 7 7 Simplificando los cuadrados con las
Problema de Valor Inicial (PVI):
 Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Universidad Diego Portales Segundo Semestre 2007 Facultad de Ingeniería
 Universidad Diego Portales Segundo Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº Ecuaciones Diferenciales Eactas, Lineales de Primer
Universidad Diego Portales Segundo Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº Ecuaciones Diferenciales Eactas, Lineales de Primer
INTEGRACIÓN POR PARTES
 INTEGRACIÓN POR PARTES Propósitos Reconocer que el método de integración por partes amplía las posibilidades de integrar productos de funciones y saber que se desprende de la derivada de un producto. Utilizar
INTEGRACIÓN POR PARTES Propósitos Reconocer que el método de integración por partes amplía las posibilidades de integrar productos de funciones y saber que se desprende de la derivada de un producto. Utilizar
5.1. Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
Prof. J. Contreras S. Prof. C. del Pino O. Método de cambio de variable. U de Talca
 Sesión Temas Método de sustitución o cambio de variable.. Introducción Capacidades Conocer y comprender el método de cambio de variable. Calcular integrales indefinidas que se pueden obtener aplicando
Sesión Temas Método de sustitución o cambio de variable.. Introducción Capacidades Conocer y comprender el método de cambio de variable. Calcular integrales indefinidas que se pueden obtener aplicando
Tema 10: Cálculo integral
 Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Cálculo de Primitivas
 . Primitivas de una función Sea I un intervalo y f : I IR. Se dice que f tiene tiene una primitiva en I si existe una función G : I IR, continua en I, derivable en el interior de I y verificando que G
. Primitivas de una función Sea I un intervalo y f : I IR. Se dice que f tiene tiene una primitiva en I si existe una función G : I IR, continua en I, derivable en el interior de I y verificando que G
Tema 10: Cálculo Integral
 . Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
. Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Métodos de integración
 Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
Integral indefinida Matemáticas I 1 INTEGRAL INDEFINIDA. Cuando utilizamos la notación diferencial, teniendo en cuenta que
 Primitiva. Integral indefinida INTEGRAL INDEFINIDA Sean f y F dos funciones reales definidas en un mismo dominio. La función F es una función primitiva de f, o simplemente primitiva de f, si F tiene por
Primitiva. Integral indefinida INTEGRAL INDEFINIDA Sean f y F dos funciones reales definidas en un mismo dominio. La función F es una función primitiva de f, o simplemente primitiva de f, si F tiene por
CÁLCULO DE PRIMITIVAS
 CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
du = ln u + NOTA: En las integrales 11, 12, 17 y 18 α significa la raíz cuadrada positiva de α 2. Escribimos
 CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
Matemáticas Empresariales I. Cálculo de Primitivas
 Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Unidad 1 Integrales Indefinidas 1.1 Diferenciales Aproximaciones Anti derivada
 Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3! + x5
 Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
1 Repaso. Cálculo I. 1 o Matemáticas. Curso 2002/2003. Cálculo de Primitivas. (5x 6) f(x) 1 2 f (x) dx, que es inmediata: + 1 x 1
 Cálculo I. o Matemáticas. Curso /. Cálculo de Primitivas Repaso (5 6) d = 5 (5 6) 5 d = 5 (5 6) + C. Nota: Si f() = 5 6 su derivada es 5. En la primera igualdad multiplicamos y dividimos por 5. Así tenemos
Cálculo I. o Matemáticas. Curso /. Cálculo de Primitivas Repaso (5 6) d = 5 (5 6) 5 d = 5 (5 6) + C. Nota: Si f() = 5 6 su derivada es 5. En la primera igualdad multiplicamos y dividimos por 5. Así tenemos
Ejercicios Departamental de marzo del 2016
 Ejercicios Departamental 06 Ciro Fabián Bermúez Márquez 7 de marzo del 06 El siguiente documento tiene la finalidad de revisar los ejercicios del eamen departamental de cálculo integral que se llevo acabo
Ejercicios Departamental 06 Ciro Fabián Bermúez Márquez 7 de marzo del 06 El siguiente documento tiene la finalidad de revisar los ejercicios del eamen departamental de cálculo integral que se llevo acabo
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
Cálculo de primitivas
 73 Fundamentos de Matemáticas : Cálculo integral en R 4. Primitiva de una función Capítulo 4 Cálculo de primitivas Definición 6.- Diremos ue la función F continua en [a, b], es una primitiva de la función
73 Fundamentos de Matemáticas : Cálculo integral en R 4. Primitiva de una función Capítulo 4 Cálculo de primitivas Definición 6.- Diremos ue la función F continua en [a, b], es una primitiva de la función
Cálculo Diferencial e Integral - Integración por partes. Prof. Farith J. Briceño N.
 Cálculo Diferencial e Integral - Integración por partes. Prof. Farith J. Briceño N. Objetivos a cubrir Integración : Integración por partes. Ejemplo : Integre ln d Código : MAT-CDI.6 Ejercicios resueltos
Cálculo Diferencial e Integral - Integración por partes. Prof. Farith J. Briceño N. Objetivos a cubrir Integración : Integración por partes. Ejemplo : Integre ln d Código : MAT-CDI.6 Ejercicios resueltos
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
tiene por límite L cuando la variable independiente x tiende a x , y se nota por L, cuando al acercarnos todo lo que queramos a x lím( x
 UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: TÉCNICAS DE INTEGRACIÓN
 UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
4.2 Reducción de orden
 4. educción de orden 87 Un conjunto de funciones f y ; y g que cumple con la condición anterior se llama un conjunto fundamental de soluciones. Es decir, un conjunto f y ; y g será un conjunto fundamental
4. educción de orden 87 Un conjunto de funciones f y ; y g que cumple con la condición anterior se llama un conjunto fundamental de soluciones. Es decir, un conjunto f y ; y g será un conjunto fundamental
CÁLCULO DE PRIMITIVAS
 2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
SISTEMAS DE ECUACIONES. Un sistema de ecuaciones no lineal es aquel en el que al menos una de las dos ecuaciones no es de primer grado.
 1. SISTEMAS NO LINEALES Un sistema de ecuaciones no lineal es aquel en el que al menos una de las dos ecuaciones no es de primer grado. 3 + = 5 = 3 = + 1 = 3 = 1 + = 5 Resolución: Para resolver un sistema
1. SISTEMAS NO LINEALES Un sistema de ecuaciones no lineal es aquel en el que al menos una de las dos ecuaciones no es de primer grado. 3 + = 5 = 3 = + 1 = 3 = 1 + = 5 Resolución: Para resolver un sistema
Integración por fracciones parciales
 Integración por fracciones parciales El cociente de dos polinomios se denomina función racional. La derivación de una función racional conduce a una nueva función racional que puede obtenerse por la regla
Integración por fracciones parciales El cociente de dos polinomios se denomina función racional. La derivación de una función racional conduce a una nueva función racional que puede obtenerse por la regla
Problemas resueltos del Boletín 4
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES
 INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
Técnicas de Integración
 Técnicas de Integración Índice Capítulo único: Técnicas de Integración. Integración Directa....................................... Integración por Sustitución.................................. Integración
Técnicas de Integración Índice Capítulo único: Técnicas de Integración. Integración Directa....................................... Integración por Sustitución.................................. Integración
Guía de Ejercicios: Métodos de Integración
 Guía de Ejercicios: Métodos de Integración Área Matemática Resultados de aprendizaje Resolver integrales usando diferentes métodos de integración Contenidos 1. Método de sustitución simple 2. Método de
Guía de Ejercicios: Métodos de Integración Área Matemática Resultados de aprendizaje Resolver integrales usando diferentes métodos de integración Contenidos 1. Método de sustitución simple 2. Método de
Antiderivada o Primitiva
 Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
