UNIDAD I. DIFERENCIALES E INTEGRAL INDEFINIDA. Actividad 1. DIFERENCIALES
|
|
|
- Rosario Blázquez Martín
- hace 7 años
- Vistas:
Transcripción
1 CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/ LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO ASIGNATURA PROFESOR SEMESTRE CÁLCULO INTEGRAL L. M. A. JUAN MANUEL VALDEZ CHÁVEZ 0 0 B SEXTO INSTRUCCIONES. CADA ALUMNO DEBE REALIZAR Y ENTREGAR LAS ACTIVIDADES DE FORMA INDIVIDUAL. CADA ACTIVIDAD DEBE ENTREGARSE POR SEPARADO Y EN EL ORDEN INDICADO, EN FORMA CLARA Y LIMPIA. LA FECHA DE ENTREGA SERÁ EL DÍA DEL EXAMEN. NO HABRÁ PRORROGAS. LA ENTREGA DE ESTE TRABAJO TENDRÁ UN VALOR DE UN PUNTO POR CADA UNIDAD, DEPENDIENDO DE LA CALIDAD DEL MISMO, SOBRE LA CALIFICACIÓN DEL EXAMEN EXTRAORDINARIO. DE SER NECESARIO UTILICE LAS HOJAS ADICIONALES QUE SEAN NECESARIAS PARA DARLE UN ESPACIO A CADA PROBLEMA O EJERCICIO. DUDAS EN O EN Encuentre la diferencial dy de la función. 4 y y y y sen5 5. y cot 6. ysec UNIDAD I. DIFERENCIALES E INTEGRAL INDEFINIDA. Actividad. DIFERENCIALES 7. y ln 8. 4 yln y y e e sen II. Calcule y y dy para los valores de y d que se dan.. y,, 0.5. y,, 0.. y e, 0, y cos,, 0.0 III. Resolver los siguientes problemas.. Se midió el radio de una esfera y dio como resultado cm con un posible error de medición de cuando mucho 0.05 cm Cuál es el error máimo si se emplea el valor del radio para calcular el volumen de la esfera?. Use diferenciales para estimar la cantidad de pintura necesaria para aplicar una capa de pintura de 0.05 cm de ancho en un domo hemisférico con un diámetro de 50 m.. El interior de un tanque cilíndrico abierto es de m de diámetro y 8 m de profundidad. El fondo es de cobre y los lados son de acero. Utilice diferenciales para encontrar de manera aproimada cuantos litros de pintura a prueba de agua es necesaria para aplicar una capa de 0.05cm a la parte de acero del interior del tanque.
2 Ejemplo : Encuentre la integral indefinida Actividad. INTEGRAL INDEFINIDA GENERAL d Solución: En este caso se deben aplicar las reglas básicas de integración, además de la propiedad de las integrales que permite separar los términos para integrarlos cada uno por separado. (Consulta tu formulario) d d d 5 Ejemplo : Encuentre la integral indefinida 5 d d C Solución: Recuerda aplicar las reglas básicas de integración d d 5 d d Ejemplo : Encuentre la integral indefinida d Solución: Recuerda aplicar las reglas básicas de integración C 6 5 d 4 d d d d C Ejemplo 4: Encuentre la integral indefinida Solución: Recuerda aplicar las reglas básicas de integración d d d 7 d d 5 d C Ejemplo 5: Encuentre la integral indefinida 5 d Solución: Reescribimos la integral para poder aplicar las reglas básicas de integración. 5 5 d d 5 d d d 5 Ejemplo 6: Encuentre la integral indefinida ln cos 0 e d Solución: Para este tipo de integrales consulta el formulario de integrales básicas, recuerda que en estos casos la integral se obtiene de forma inmediata por el criterio de la antiderivada. ln e cos d ln d e d cos d ln e sen C Ejemplo 7: Encuentre la integral indefinida sec cot d Solución: sec cotd d sec d cotd ln tan ln csc Ejemplo 8: Encuentre la integral indefinida sec tan csc d Solución: sec tan csc d sec tand csc d sec cot C C C
3 EJERCICIOS: Encuentre la integral indefinida general.. 6 d d 7. 4 d 4. 4 d 5. ln 0 d 6. sen sec 7. e d 8. csc 5 d d 9. sec tan sec 0. d e d
4 UNIDAD II. INTEGRAL DEFINIDA Y MÉTODOS DE INTEGRACIÓN. Ejemplo : Evalúe la integral definida 4 Actividad. INTEGRAL DEFINIDA b a d Solución: Recordemos que la integral es f d F b Fa donde F f resolvemos la integral 4, por lo que primero d d d d y evaluamos d F 4 0 Ejemplo : Evalúe la integral definida 4 cos sec d 0 Solución: Resolvemos la integral cos sec cos sec sen tan 4 4 cos sec sen 4 tan 4 sen 0 tan d 0 F d d d y luego evaluamos sen tan.7 0 Ejemplo : Evalúe la integral definida e d Solución: Resolvemos la integral y luego evaluamos e d d e d e e d e e e F EJERCICIOS: I. Evalúe la integral definida.. d. e d 0. e ln d 4. sen d 0 5. sen d 0
5 Actividad 4. INTEGRACIÓN POR SUSTITUCIÓN Recuerda los pasos a seguir para resolver una integral por el método de sustitución o cambio de variable.. Elegir la función u para realizar el cambio de variable.. Obtener du y completar la integral si es necesario.. Sustituir u y du en la integral y simplificar si es necesario. 4. Resolver la integral. 5. Cambiar a la variable original. I.- Evaluar d u du d d d du u lnuc ln C II.- Evaluar sec tan sec d usec du sec tan d sec tan sec d sec sec tan d udu u C sec C d u 4 du 5 d 4 5 III.- Evaluar d 5 d 5 u du
6 4 5 4u 0 C C 5 4 IV.- Evaluar tan d u du d tan tan d d tanudu ln secu C ln sec C EJERCICIOS: I. Evalúe la integral indefinida efectuando la sustitución adecuada.. sec tan d 4. 9 d. ln d 4. e d e 5. cos d
7 Actividad 5. INTEGRACIÓN POR PARTES. Recuerda los pasos a seguir para resolver una integral por partes.. Elegir u y dv.. Obtener du y v.. Sustituir en la integral por partes y simplificar si es necesario. udv uv vdu 4. Resolver la integral resultante. I.- Evaluar e d u dv e d du d v e d e e d e e d e e C II.- Evaluar sec d u dv sec d du d v sec d tan sec d tan tan d tan lnsec C III.- Evaluar d u dv d du d v d ln ln ln ln ln d ln ln ln d d C C ln ln
8 EJERCICIOS. I. Evalúe la integral por partes con la elección indicada para u y dv.. sec d ; u, dv sec d. 5ln d ; u ln, dv d. e d ; u, dv e d 4. e sen d ; u e, dv send II. Evalúe la integral por partes con la elección adecuada para u y dv.. send. cos d. csc d 4. sec tand 5. 0 d
9 Actividad 6. INTEGRACIÓN POR SUSTITUCIÓN TRIGONOMÉTRICA. Recuerda los pasos a seguir para resolver una integral por sustitución trigonométrica.. Determinar el caso que se presenta en la integral y obtener el valor de a.. Determinar el valor de para realizar la sustitución.. Obtener d. 4. Sustituir en la integral y simplificar hasta obtener una integral básica. 5. Resolver la integral resultante. 6. Rotular el triángulo para obtener los valores necesarios de la sustitución. 7. Cambiar a la variable original con los valores obtenidos en el paso anterior. I.- Evaluar 9 d a 9 a sen d cosd 9 sen 9 9 9sen d sen 9 sen 9cos cosd 9sen cosd cosd cos 9sen d 9sen cos 9cos cos d 9sen d 9sen cot d 9 cot d cot 9 cot CA CO recuerda:cos cot sen sen sen arcsen 9 9 d arcsen
10 II.- Evaluar d 4 a 4 a tan d sec d d sec d 4 tan tan 4 d sec tan 4 tan sec d sec tan sec d tan cscd d ln csc cot 4 sec tan 4tan 4 sec tan d 4sec d recuerda: sec csc tan sen cos sen cos csc csc H CO 4 cot cot CA CO d 4 ln C 4
11 III.- Evaluar d 5 a 5 a 5 5sec d 5sec tand d 5sec tand 5sec tan d 5 5sec 5 5sec 5 d 5sec tand 5sec tan d 5tan 5 sec 5sec tand 5tan secd ln sec tan 5 C sec H CA sec 5 tan tan CO CA 5 5 d 5 ln C 5 5 5
12 EJERCICIOS. I. Evalúe la integral usando la sustitución trigonométrica indicada. Dibuje el triángulo rectángulo asociado.., sec 9 d. d, 5tan 5. d, sen 9 II.. Evalúe la integral usando la sustitución trigonométrica adecuada. Dibuje el triángulo rectángulo asociado. 5 d. d 9. d
13 UNIDAD III. APLICACIONES DE LA INTEGRAL Actividad 7. ÁREA BAJO LA CURVA EJEMPLO.- Encuentre el área bajo la curva f en el intervalo, SOLUCIÓN: Por el Teorema fundamental del Cálculo el área bajo la curva f en el intervalo, b f d F b F a, por lo que se debe evaluar la integral, a d y trace la gráfica d f F ab está dada por F b F a EJEMPLO.- Encuentre el área bajo la curva f cos en el intervalo, y trace la gráfica. SOLUCIÓN: Se debe evaluar la integral cos d Recuerda que 80º cos d sen cos sen +cos sen +cos
14 EJEMPLO.- Encuentre el área bajo la curva f en el intervalo SOLUCIÓN: Se debe evaluar la integral primero la parte debajo del eje X, y después la parte que está sobre el eje X. 0, y trace la gráfica. d pero en la gráfica observamos que se debe resolver en dos partes; 0 d d El área total es la suma absoluta de las áreas parciales es decir 4 Ejercicios: Encuentre el área bajo la curva de la función dada en el intervalo indicado. f 9 en 0,.. f en,. f cos en,
15 EJEMPLO.- Trace la región delimitada por las curvas Actividad 8. ÁREA ENTRE CURVAS y 9, y,,. SOLUCIÓN: El área entre las curvas y f, y y g, y entre a y b es b así que al observar la gráfica de estas funciones vemos que se debe evaluar 9 9 d 8d 8 f g d, a d EJEMPLO.- Trace la región delimitada por las curvas y sen, y e, 0,. SOLUCIÓN: Se debe evaluar e sen d. 0 0 e sen d e sen d e cos e cos e cos e 0 e 4.8.8
16 Ejercicios. Trace la región delimitada por las curvas dadas y encuentre su área.. y y, 9,,. y y,,, y cos, y sen, 0,.
CENTRO DE ESTUDIOS DE BACHILLERATO Nº 4/2 LIC. JESÚS REYES HEROLES
CENTRO DE ESTUDIOS DE BACHILLERATO Nº / LIC. JESÚS REYES HEROLES GUÍA DE ESTUDIO DEL EXAMEN EXTRAORDINARIO DE CÁLCULO INTEGRAL ELABORÓ: PROF. L. M. A. JUAN MANUEL VALDEZ CHÁVEZ SEMESTRE: A SEXTO INSTRUCCIONES.
Universidad Icesi Departamento de Matemáticas y Estadística
Universidad Icesi Departamento de Matemáticas y Estadística Solución del tercer eamen parcial del curso Cálculo una variable Grupo: Uno Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. a. Después
GUÍA: INTEGRALES. Página 1 de 27
GUÍA: INTEGRALES Área de EET Página de 7 Derechos Reservados Titular del Derecho: INACAP N de inscripción en el Registro de Propiedad Intelectual #. de fecha - -. INACAP 00. Página de 7 . INTEGRALES. La
TEMA 5: INTEGRAL INDEFINIDA.
TEMA : INTEGRAL INDEFINIDA.. Primitivas: propiedades. Integral indefinida.. Integración por partes.. Integración de funciones racionales (denominador con raíces reales simples y múltiples, denominador
MATEMÁTICAS VI. CÁLCULO INTEGRAL UNIDAD II MÉTODOS DE INTEGRACIÓN
MÉTODOS DE INTEGRACIÓN UNIDAD II MÉTODOS DE INTEGRACIÓN No todas las funciones en un integrando se pueden resolver mediante reglas inmediatas de integración, y requieren ser tratadas con técnicas especiales.
Unidad 5 - Trabajo Práctico 5 Parte 1 Elementos de Matemática
06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
INTEGRACIÓN POR CAMBIO DE VARIABLE
INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
UNIVERSIDAD ARTURO PRAT IQUIQUE CHILE DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES
DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES MARIA ELISA VODNIZZA LIRA e-mail : mvodnizz@cec.unap.cl url : www.unap.cl/~mvodnizz SEPTIEMBRE - 00 INTEGRALES Uno de los problemas importantes
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
Cálculo Integral Enero 2015
Cálculo Integral Enero 015 Laboratorio # 1 Antiderivadas I.- Halle las siguientes integrales indefinidas. 10) ) 6) 1 1 1 1 16) 1 8) 9) 18) II.- Calcule 1.. 1 Cálculo Integral Enero 015 Laboratorio # Aplicaciones
Cálculo Integral Enero 2016
Cálculo Integral Enero 6 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) ( + + ) ) ( + ) ( ) ) ( w + ) (w ) dw ) ( + ) 5) (y ) dy 6) ( +)( 5) 6 7) + 8) ( +) 5 y+ dy ) (y+5
Cálculo Integral: Guía II
00 Cálculo Integral: Guía II Profr. Luis Alfonso Rondero García INSTITUTO POLITÉCNICO NACIONAL Departamento de Unidades de Aprendizaje del Área Básica /0/00 Integración de Potencias de Funciones Trigonométricas.
duv = udv + vdu udv = uv vdu
I. INTEGRACIÓN POR PARTES. Si la integración de una función no es posible encontrarla por alguna de las fórmulas conocidas, es posible que se pueda integrar utilizando el método conocido como integración
RELACIONES Y FUNCIONES
RELACIONES Y FUNCIONES Variables Independiente: Aquella que puede tomar cualquier valor. Dependiente: Depende del valor que tome la variable independiente. Pares ordenados Se representan (a,b) donde: a:
INTEGRALES MÚLTIPLES. 9 xy c) 4
de 6 TRABAJO PRÁCTICO Nº A.M. II - INTEGRALES MÚLTIPLES INTEGRALES DOBLES - Calcule las siguientes integrales: a d d d d d b d d sen e 6 d d --. Grafique la región de integración eprese la integral invirtiendo
El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow.
INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
APELLIDOS Y NOMBRES: C.I.: NOTA: III-
INSTRUCCIONES REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DEL PODER POPULAR PARA LA DEFENSA UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA NÚCLEO BARINAS. Llene todos los datos en
ÁNGULOS, FUNCIONES TRIGONOMÉTRICAS ORIENTADOR: ESTUDIANTE: FECHA:
DEPARTAMENTO DE MATEMÁTICAS ÁREA DE MATEMÁTICAS TEMA: PERÍODO: ORIENTADOR: ESTUDIANTE: E-MAIL: FECHA: ÁNGULOS, FUNCIONES TRIGONOMÉTRICAS SEGUNDO EJES TEMÁTICOS La recta numérica Suma de números enteros
Integración de funciones trigonométricas
Integración de funciones trigonométricas Ya vimos las reglas para calcular integrales de funciones trigonométricas. Ahora vamos a considerar productos de funciones trigonométricas y potencias. Para este
Unidad 1 Integrales Indefinidas 1.1 Diferenciales Aproximaciones Anti derivada
Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
Antiderivada o Primitiva
Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Técnicas de Integración
Técnicas de Integración Índice Capítulo único: Técnicas de Integración. Integración Directa....................................... Integración por Sustitución.................................. Integración
Contenido 1. Integrales Dobles 2. Integrales Triples
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Técnicas de Integración. Integración por Partes (I)
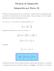Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
INTEGRACION POR PARTES
INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
Ejercicio 1 Relacione convenientemente cada una de las siguientes expresiones: (considere x > 0 ) P Q a b. ax + bxh + h. x bxh
Módulo 1 DERIVADAS 1.1 Reglas de diferenciación Reconocimiento de saberes Ejercicio 1 Relacione convenientemente cada una de las siguientes epresiones: (considere > 0 ) ln ( e ) ln ln ( e ) ln e ln + ln
ejerciciosyexamenes.com
ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
INTEGRACIÓN POR PARTES
INTEGRACIÓN POR PARTES Propósitos Reconocer que el método de integración por partes amplía las posibilidades de integrar productos de funciones y saber que se desprende de la derivada de un producto. Utilizar
Evidentemente, la superficie es un triángulo rectángulo de base 1 y altura también la unidad, por tanto su área es 1/2.
LA INTEGRAL DEFINIDA En los dos temas anteriores se ha hecho el estudio de las primitivas de una función, descubriendo distintos procedimientos para el cálculo de primitivas, es decir, se han encontrado
2 Métodos de solución de ED de primer orden
CAPÍTULO 2 Métodos de solución de E de primer orden 2.8 Miscelánea En este apartado queremos responder a la pregunta cómo proceder cuando se nos pide resolver una ecuación diferencial ordinaria de primer
x 1,9 1,99 1,999 2,001 2,01 2,1 f(x) i) lim j) lim k) lim l) lim m) lim n) lim o) lim p) lim
GUÍA DE ESTUDIO UNIDAD ACADÉMICA UNIDAD TEMÁTICA DEPARTAMENTO DE CIENCIAS BASICAS ASIGNATURA: CALCULO DIFERENCIAL LÍMITES Y CONTINUIDAD DE FUNCIONES COMPETENCIA Deducir resultados mediante procesos de
Antiderivada o Primitiva
Antiderivada o Promitiva agosto 2012 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada. En esta Presentación... En esta Presentación veremos: Definición de Antiderivada.
Definición 1. Definición 3. Un numero critico de una función f es un numero c en el dominio de f tal c ) no existe.
CALCULO DIFERENCIAL Definición. Una función f ( ) tiene un máimo absoluto (o máimo global) en c si f ( c ) f ( ) D, donde D es el dominio de f. El numero f ( c ) se llama valor máimo de f en D. De manera
TEMA 12.- CÁLCULO DE PRIMITIVAS
TEMA.- CÁLCULO DE PRIMITIVAS.-.- PRIMITIVA DE UNA FUNCIÓN Definición de Función Primitiva Una función F() se dice que es primitiva de otra función f() cuando F'() f() Ejemplos: F() es primitiva de f()
El cálculo de la viga superior no presenta mayores problemas, ya que su volumen corresponde al de un prisma recto cuyas dimensiones se indican:
Consideremos el problema: Usted es un ingeniero civil y se le ha encargado la tarea de construir un puente. Para ello necesita cubicar (dimensionar), para saber la cantidad de material necesario para hacer
TRABAJO PARA LA TERCERA EVALUACION PARCIAL DE TRIGONOMETRIA Profra. Dulce Estrella Hernández Hernández.
NEXA A LA NORMAL DE NAUCALPAN TRABAJO PARA LA TERCERA EVALUACION PARCIAL DE TRIGONOMETRIA Profra. Dulce Estrella Hernández Hernández. Contesta a mano en hojas blancas, incluye todos los procedimientos.
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE---V--00-0 CURSO: Matemática Intermedia SEMESTRE: Segundo CÓDIGO DEL CURSO: TIPO DE EXAMEN: Tercer Parcial
Integración múltiple: integrales dobles
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Área La integral definida Propiedades de la integral definida Teorema del valor medio para la integral definida Teoremas fundamentales del cálculo Aplicaciones de la integral definida: Área de una región
Universidad de San Carlos de Guatemala
Clave: 03-2-M-2-00-203 Universidad de San Carlos de Guatemala Facultad de Ingeniería Departamento de matemática Curso: Matemática Básica 2 Código del curso: 03 Semestre: Segundo semestre 203 Tipo de eamen:
Integrales Múltiples.
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Hallar el dominio de las siguientes funciones : 1. log F(x) = 234. F(x) = x F(x) = ln( F(x) = 9 3. x.calcular simplificando
Hallar el dominio de las siguientes funciones : 4. F() = 3 8 0 6 5. F() = 3 7 6. F() = 6 7. F() = 9 4 8. F() = ln 9. F() = e e 30. F() = e 3 3. F() = log 7 3. F() = sen 33. F() = 3 8 34. F() = 3 3 4 35.
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE INGENIERIA CIVIL MATEMATICA II. CARÁCTER: Obligatoria DENSIDAD HORARIA HT HP HS THS/SEM
UNIVERSIDAD CENTROCCIDENTAL LISANDRO ALVARADO DECANATO DE INGENIERIA CIVIL MATEMATICA II CARÁCTER: Obligatoria PROGRAMA: Ingeniería Civil DEPARTAMENTO: Ciencias Básicas CODIGO SEMESTRE DENSIDAD HORARIA
0.Mínimo de alumnos 12, Máximo Saberes teóricos
0.Mínimo de alumnos 12, Máximo 30 1.Saberes teóricos 1. Conceptos de función, límite de funciones, y continuidad. 2. Reglas de diferenciación. 3. Aplicaciones del cálculo de derivadas: Problemas de valores
La integral indefinida
Apuntes Matemáticas º de bachillerato Leibniz Tema 7 La integral indefinida Matemáticas º de bachillerato 7. Introducción Def.: Dadas dos funciones, F() y f(), si se verifica que: F () f(), para un cierto
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA. Calcular las siguientes integrales definidas: b) d e d c) + d d) d e) sen d f) + d d ( ) En primer lugar se ha calculado una primitiva de f() Barrow. y después
UNIDAD I. DIFERENCIALES E INTEGRAL DEFINIDA. Tema: INTEGRAL INDEFINIDA Y REGLAS PARA LA INTEGRACIÓN DE DIERENCIALES
UNIDAD I. DIFERENCIALES E INTEGRAL DEFINIDA Tema: INTEGRAL INDEFINIDA Y REGLAS PARA LA INTEGRACIÓN DE DIERENCIALES INTEGRAL INDEFINIDA Y REGLAS PARA LA INTEGRACIÓN DE DIFERENCIALES ALGEBRAICAS Con fundamento
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integración por Partes II. Integrales Cíclicas
Integración por Partes II Integrales Cíclicas Para este tema utilizamos la misma fórmula de integración por partes, no hay casi nada nuevo. Para comenzar con esta sección usaré un ejemplo. Ejemplo 1: Integra
Guía de Matemática NM 3: Inecuaciones
Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Guía de Matemática NM : Inecuaciones Nombre(s): Curso: Fecha. Contenido:
Cálculo Diferencial e Integral - Integración por partes. Prof. Farith J. Briceño N.
Cálculo Diferencial e Integral - Integración por partes. Prof. Farith J. Briceño N. Objetivos a cubrir Integración : Integración por partes. Ejemplo : Integre ln d Código : MAT-CDI.6 Ejercicios resueltos
1.- Simplifica al máximo la expresión: 2.- Obtener de manera razonada las soluciones de la primera vuelta de la
Colegio del Sagrado Corazón EXAMEN Trigonometría CLASE:1º BACHILLERATO FECHA:9/10/15 tg 1.- Simplifica al máimo la epresión: sen sen sen sen.- Obtener de manera razonada las soluciones de la primera vuelta
Curso Introductorio a las Matemáticas Universitarias
Curso Introductorio a las Matemáticas Universitarias Tema 9: Integración Víctor M. Almeida Lozano Rosa M. Gómez Reñasco Licencia Creative Commons 03 9. INTEGRACIÓN Este tema es una introducción al cálculo
Universidad Icesi Departamento de Matemáticas y Estadística
Universidad Icesi Departamento de Matemáticas y Estadística Solución del examen final del curso Cálculo de una variable Grupo: Once Período: Inicial del año Prof: Rubén D. Nieto C. PUNTO. (x ) sen(x )
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 8. Introducción a la integración INTEGRAL INDEFINIDA
INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
UNIVERSIDAD DIEGO PORTALES CALCULO II. Autores: Sara Arancibia C Viviana Schiappacasse C. Universidad Diego Portales CALCULO II
UNIVERSIDAD DIEGO PORTALES Autores: Sara Arancibia C Viviana Schiappacasse C PROGRAMA OBJETIVOS Comprender y aplicar los conceptos fundamentales del Cálculo Integral y Series Usar el Cálculo Integral y
TEMA 5: LA INTEGRAL DEFINIDA
Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Las funciones trigonométricas
Funciones trigonométricas de ángulos Las funciones trigonométricas Las funciones trigonométricas de ángulos se originaron de triángulos rectángulos que son los que tienen dos ángulos agudos y uno recto.
Cálculo Integral Área de una superficie de revolución. Universidad Nacional de Colombia
Cálculo Integral Área de una superficie de revolución Jeanneth Galeano Peñaloza - Claudio Rodríguez Beltrán Universidad Nacional de Colombia Segundo semestre de 2015 Área de una superficie de revolución
INSTRUCCIONES VERIFIQUE QUE EL FOLLETO ESTÉ BIEN COMPAGINADO Y QUE CONTENGA 60 ÍTEMES.
INSTRUCCIONES VERIFIQUE QUE EL FOLLETO ESTÉ BIEN COMPAGINADO Y QUE CONTENGA 60 ÍTEMES. Para realizar la prueba usted debe contar con Un folleto que contiene 60 ítemes de selección, una tabla de valores
MATEMÁTICAS BÁSICAS DIFERENCIAL DEFINICIÓN DE DIFERENCIAL
MATEMÁTICAS BÁSICAS DIFERENCIAL DEFINICIÓN DE DIFERENCIAL Sea una función f ( ). d Se define como la diferencial de la variable independiente a: Se define como la diferencial de la variable dependiente
Rotaciones alrededor de los ejes cartesianos
Sólido de revolución Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que se contenida en su mismo plano.
Tema 13 La integral definida. Aplicaciones
Tema La integral definida. Aplicaciones. Integral definida. Calcula la integral. ( ) d 4 Calculamos una primitiva de la función f ( ) : G( ) ( ) d Según la regla de Barrow: 4 4 ( ) d G(4) G() 4 8 4 Ahora
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: TÉCNICAS DE INTEGRACIÓN
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
Matemática II Tema 17: integrales dobles en coordenadas polares
Matemática II Tema 7: integrales dobles en coordenadas polares 22 23 Índice Integrales dobles en coordenadas polares Coordenadas polares límites de integración Ejemplos de aplicación 2 Sustitución en integrales
Volumen de Revolución Ejemplo. Se obtiene al hacer girar una región limitada alrededor de un eje. Por ejemplo, si la función: f(x) x el eje 0x:
Volumen de Revolución Ejemplo Se obtiene al hacer girar una región limitada alrededor de un eje. Por ejemplo, si la función: f(x) x 2 1 gira sobre el eje 0x: Sólidos de Revolución conocidos ALGUNAS APLICACIONES
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS Y OBLICUÁNGULOS
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS Y OBLICUÁNGULOS www.cedicaped.com CENTRO DE ESTUDIOS, DIDÁCTICA Y CAPACITACIÓN RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS 1. DEFINICIÓN Se dice que un triángulo es rectángulo
Problemas Tema 3 Enunciados de problemas de Derivabilidad
página / Problemas Tema 3 Enunciados de problemas de Derivabilidad Hoja. Calcula la derivada de f ()= +3 8 +9 +3. Encuentra tres números no negativos que sumen 4 y tales que uno sea doble de otro y la
UNIDAD 5.C :INTEGRALES Y SUPERFICIES DE REVOLUCIÓN
UNIDAD 5.C :INTEGRALES Y SUPERFICIES DE REVOLUCIÓN 5.C.1 Concepto de integral Primitiva de una función: Sea f una función definida en el intervalo (a,b). Llamamos primitiva, antiderivada o integral indefinida
Chapter 1 Integración por partes
Chater 1 Integración or artes Este método de integración se debe a la alicación de la derivada de un roducto de funciones [f ()g()] 0 = f 0 ()g() + f ()g 0 () Puesto que la integración es la oeración inversa
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
Lic. Saúl Villamizar Valencia 53 SÓLIDOS DE REVOLUCIÓN Y ESFERA
Lic. Saúl Villamizar Valencia 53 SÓLIDOS DE REVOLUCIÓN Y ESFERA 54 Actualización Permanente en el Área Matemática 1. Cilindro Definiciones Se llama superficie cilíndrica la engendrada por una recta que
MODELO 1 EXAMEN DE CÁLCULO DIFERENCIAL. siendo a un nº real
MODELO 1 EXAMEN DE CÁLCULO DIFERENCIAL 1. Escribe la ecuación de la recta normal a la curva de ecuación: arcsen abscisa 1. Haz un estudio de todas las asíntotas de la función: 1 e f ( ). Halla los valores
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO PLANTEL IGNACIO RAMIREZ CALZADA GUIA DE ÁLGEBRA Y TRIGONOMETRÍA 1ª Fase Nombre del alumno: No. de Cta.
UNIVERSIDD UTÓNOM DEL ESTDO DE MÉXICO PLNTEL IGNCIO RMIREZ CLZD GUI DE ÁLGER Y TRIGONOMETRÍ 1ª Fase Nombre del alumno: No. de Cta.: Nombre del profesor: Grupo: DESIGULDDES. Resuelve los ejercicios en hojas
Unidad I Funciones Expresar una función. Dominios
Unidad I Funciones Epresar una función 1. Un rectángulo tiene un perímetro de 0m. Eprese el área del rectángulo como función de la longitud de uno de sus lados.. Un rectángulo tiene un área de 16 m. Eprese
f x 41 f x x 2 x 2 19 f x x 3 46 asíntotas verticales: x 2, x 0 47 asíntotas verticales: x 3, x 1 x 1 9 f x 3x x 2 9
4.5 Funciones racionales 35 Ejer. 7-32: Trace la gráfica de f. 7 3 4 8 9 3 2 4 2 3 2 3 4 2 2 3 2 4 5 2 2 6 6 7 4 2 2 8 9 3 2 2 3 3 4 2 5 5 3 3 7 5 3 3 7 2 2 3 2 2 4 2 4 Ejer. 37-44: Simplifique f() trace
CALCULO INTEGRAL. Ejercicios. 1 a Parte: Diferenciales. Rumbo al examen de recuperación. Faus2016. x 1
En los problmas complt la tabla siguint para cada función. d d DIVISION DE INGENIERIA ELECTRONICA.. Rumbo al amn d rcupración a Part: CALCULO INTEGRAL Ejrcicios Difrncials Dfinición. Faus6 Supóngas qu
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
x 3 si 10 <x 6; x si x>6;
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E000 A Primer parcial + 1 +8 1 a Trace su gráfica b Determine su dominio, rango y raíces Sean si 10 < 6; f
UNIDAD III TRIGONOMETRIA
UNIDAD III TRIGONOMETRIA 1 UNIDAD III TRIGONOMETRIA TEMARIO. 1. Relación del par ordenado en un plano bidimensional. 1.1. El plano coordenado 1.2. Localización de puntos en los cuatro cuadrantes 2. Ángulos
Examen de integración Ingeniería Técnica de Obras Públicas (E.T.S.E.C.C.P.B.) x arcsin x. 1 x. u = arcsin x du = v = 1 x 2
Eamen de integración Ingeniería Técnica de Obras Públicas (E.T.S.E.C.C.P.B.).- ( puntos) Calcular las integrales indefinidas siguientes: ln d arcsin (ii) d (iii) e d ln d ln C arcsin (ii) d u arcsin du
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/2 LIC: JESÚS REYES HEROLES
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO / LIC: JESÚS REYES HEROLES GUÍA PARA EL EXAMEN EXTRAORDINARIO DE CÁLCULO DIFERENCIAL JULIO
CAPITULO 5. Integral Indefinida. Licda. Elsie Hernández Saborío. Instituto Tecnológico de Costa Rica Escuela de Matemática
CAPITULO 5 Integral Indefinida 1 Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr) Créditos
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
TEMA 2: CÁLCULO DIFERENCIAL DE UNA VARIABLE.
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Ingeniería Industrial (GITI/GITI+ADE) Ingeniería de Telecomunicación (GITT/GITT+ADE) CÁLCULO Curso 05-06 TEMA : CÁLCULO
1. Efectúa las siguientes operaciones, simplificando el resultado lo máximo posible:
4ºESO 1. Efectúa las siguientes operaciones, simplificando el resultado lo máimo posible: a. 18 50 8 b. 7 3 180 c. 4 3 64 d. e. 3 3 3 5 88 : 1 3 4 7 5. Racionaliza las siguientes epresiones, simplificando
1. PRIMITIVA DE UNA FUNCIÓN 2. PROPIEDADES DE LA INTEGRAL INDEFINIDA 3. INTEGRALES INMEDIATAS Ejemplos de integrales inmediatas tipo potencia
Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
EL CÁLCULO DESARROLLA TU MENTE TRANSFORMA TU VIVIR
Pág. UNIVERSIDAD ALONSO DE OJEDA FACULTAD DE INGENIERIA CIUDAD OJEDA - ZULIA Guia de Cálculo II EL CÁLCULO DESARROLLA TU MENTE TRANSFORMA TU VIVIR b (Disciplina + Esfuerzo + Consagración)dv = Profesionales
1. Resolver las siguientes ecuaciones o inecuaciones.
. Resolver las siguientes ecuaciones o inecuaciones. a) + ; b) + 9 + 6 + ; c) + + ; d) = + + ; e) + = 0; f) 5 < + ; g) + > ; h) < < ; i) + < ; j) + ; b) < ó c) 05 9 05 9 ó < ó > 0
Ejercicios resueltos Matemáticas Universitaras II
Ejercicios resueltos Matemáticas Universitaras II Genaro Luna Carreto Octubre 06 Profesor de la Benemérita Universidad Autónoma de Puebla, Méico. OBJETIVO La finalidad de éste documento es resolver problemas
IES Fco Ayala de Granada Septiembre de 2014 Reserva 2 (Modelo 6) Soluciones Germán-Jesús Rubio Luna
IES Fco Ayala de Granada Septiembre de 01 Reserva (Modelo 6) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 6 Septiembre 01 ['5 puntos] De entre todos los triángulos rectángulos
UNIDAD 2 CALCULO DIFERENCIAL
UNIDAD CALCULO DIFERENCIAL DEFINICION DE FUNCIÓN: una función es una epresión matemática en la que aparecen variables constantes relacionadas. Las variables en este curso serán dos: Una llamada variable
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE INGENIERÍA CICLO BÁSICO DEPARTAMENTO DE MATEMÁTICA APLICADA LABORATORIO:
Fundamentación La matemática es una ciencia esencialmente relacional, estudia las relaciones entre los objetos matemáticos, pero al mismo tiempo es sistemática, es decir tiene organización en el sentido
Integral indefinida Matemáticas I 1 INTEGRAL INDEFINIDA. Cuando utilizamos la notación diferencial, teniendo en cuenta que
Primitiva. Integral indefinida INTEGRAL INDEFINIDA Sean f y F dos funciones reales definidas en un mismo dominio. La función F es una función primitiva de f, o simplemente primitiva de f, si F tiene por
HOJA DE TRABAJO 2. Construyendo las identidades Pitagóricas
INSTITUCIÓN EDUCATIVA RURAL GIOVANNI MONTINI Vereda Colombia Km 41 GUIA DIDÁCTICA CÓDIGO VERSIÓN PÁGINA GAPP01 01 1 de 5 HOJA DE TRABAJO 2. Construyendo las identidades Pitagóricas Nombre del estudiante:
Universidad Icesi Departamento de Matemáticas y Estadística
Universidad Icesi Departamento de Matemáticas y Estadística Solución del primer examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO 1.