Sistemas de ecuaciones lineales
|
|
|
- José Ángel Castillo Acosta
- hace 8 años
- Vistas:
Transcripción
1 7 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica a) En qué punto se cortan la gráfica roja la azul del dibujo de la izquierda? b) Tienen algún punto en común las rectas de la derecha? Cómo son estas rectas? s r s P I E N S A C A L C U L A r a) P(3, 2) b) No. Son paralelas. 1 2 Comprueba que = 2, = 3 es solución del siguiente sistema: Resuelve gráficamente el siguiente sistema: 3 = = ( 3) = = ( 3) = 10 6 = = 4 3 = 5 3 Aplica el criterio que relaciona los coeficientes del siguiente sistema para hallar cuántas soluciones tiene, haz la interpretación gráfica, clasifícalo resuélvelo gráficamente: 2 + = = Criterio: = = Tiene infinitas soluciones. Son rectas coincidentes. Sistema compatible indeterminado. A P L I C A L A T E O R Í A = 1, = 2 P(1, 2) Soluciones: 1 = 1, 1 = 1; 2 = 2, 2 = 3; 3 = 3, 3 = 5, 194 SOLUCIONARIO
2 Aplica el criterio que relaciona los coeficientes del siguiente sistema para hallar cuántas soluciones tiene, haz la interpretación gráfica, clasifícalo resuélvelo gráficamente: 4 3 = = 1 5 Aplica el criterio que relaciona los coeficientes del siguiente sistema para hallar cuántas soluciones tiene. Haz la interpretación gráfica, clasifícalo resuélvelo gráficamente: 2 + = = Criterio: 3 2 Tiene una solución. Son rectas secantes. Sistema compatible determinado Criterio: = No tiene solución. Son rectas paralelas. Sistema incompatible. P( 1, 2) = 1, = 2 6 Escribe un sistema que tenga como solución = 2, = 3 + = 5 = 1 2. Métodos de sustitución e igualación Resuelve mentalmente el siguiente sistema sustituendo el valor de de la primera ecuación en la segunda: = 2 + = = = 150 = 50 = 2 = 2 50 = 100 P I E N S A C A L C U L A UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 195
3 Resuelve por sustitución el siguiente sistema: 10 Resuelve por igualación el siguiente sistema: 2 = = 1 Resuelve el siguiente sistema por igualación: Se despeja de las dos ecuaciones. = 4, = 5 9 Resuelve por sustitución el siguiente sistema: 7 A P L I C A L A T E O R Í A 2 + = = 10 Se despeja de la primera ecuación se sustitue en la segunda. = 2, = = = = 12 5 = 7 Se despeja de las dos ecuaciones. = 1/2, = 1/4 11 Resuelve el siguiente sistema por sustitución: + 3 = = 7 3 Se eliminan los denominadores: + 6 = 22 6 = 21 Se despeja de la primera ecuación se sustitue en la segunda. = 4, = 3 Se despeja de la segunda ecuación se sustitue en la primera. = 3, = 2 12 Resuelve el siguiente sistema por igualación: 0,5 + = 1 0,25 = 0,25 Se despeja de las dos ecuaciones. = 1, = 0,5 196 SOLUCIONARIO
4 3. Reducción qué método utilizar Suma mentalmente las dos ecuaciones del sistema halla el valor de Sustitue mentalmente este valor en la primera ecuación halla el valor de = = 4 P I E N S A C A L C U L A 8 = 16 = = 12 = Resuelve el siguiente sistema por reducción: = = 1 Se suman las dos ecuaciones. = 1, = 2 Resuelve el siguiente sistema por reducción: 3 2 = = 1 Se cambia de signo la primera ecuación se suman. = 2, = 1 Resuelve el siguiente sistema por reducción: = = 3 Se multiplica la primera ecuación por 3 se le resta la segunda. = 2, = 3 Resuelve el siguiente sistema por reducción: 3 2 = = 2 Se multiplica la primera ecuación por 5 la segunda por 2 se suman. = 3, = Resuelve el siguiente sistema por el método más sencillo: Por sustitución. = 2, = 7 Resuelve por el método más sencillo el siguiente sistema: Por reducción, se suman las dos ecuaciones. = 1/2, = 2 Resuelve el siguiente sistema por el método más sencillo: Por igualación. = 9, = 5 = = = = 4 = 2 1 = 3 6 A P L I C A L A T E O R Í A UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 197
5 4. Problemas de sistemas a) 2 CD = 10 1 CD = 5 b) 1 cinta de vídeo = 4 P I E N S A C A L C U L A En el dibujo de la izquierda está planteado un sistema correspondiente a dos ecuaciones con dos incógnitas. a) Suma las dos ecuaciones halla el valor de un CD. b) Observando la primera ecuación sabiendo el valor de un CD, calcula el valor de una cinta de vídeo. 20 Halla dos números sabiendo que uno es el doble del otro que entre los dos suman 51 Primer número: Segundo número: = 2 + = 51 = 17, = A P L I C A L A T E O R Í A El perímetro de un triángulo isósceles mide 65 m, cada uno de los lados iguales mide el doble del lado desigual. Cuánto mide cada lado? Medida del lado desigual: Medida de cada uno de los lados iguales: 21 En un garaje ha 18 vehículos entre coches motos. Sin contar las ruedas de repuesto ha 58 ruedas. Cuántas motos coches ha? Número de coches: Número de motos: + = = 58 Coches: = 11, motos: = = 65 = 2 Lado desigual: = 13 m Cada lado igual: = 26 m 198 SOLUCIONARIO
6 23 El doble de un número más el triple de otro número es igual a 80, el quíntuplo del primero menos la mitad del segundo es igual a 56. De qué números se trata? Primer número: Segundo número: = 80 5 /2 = 56 = 13, = Tres cintas de vídeo 2 CD cuestan 12 ; 4 cintas de vídeo 4 CD cuestan 18. Calcula cuánto cuestan cada cinta de vídeo cada CD. Precio de la cinta de vídeo: Precio del CD: = = 18 Cada cinta de vídeo: = 3 Cada CD: = 1,5 24 Los alumnos de un centro van a ir al teatro. El precio de una entrada sin descuento es de 4,5 con descuento especial para colegios es de 1,5. Se sacan 250 entradas, unas con descuento otras sin descuento, en total se pagan 675. Cuántas entradas se han comprado con descuento? sin descuento? Número de entradas sin descuento: Número de entradas con descuento: + = 250 4,5 + 1,5 = 675 Entradas sin descuento: = 100 entradas. Entradas con descuento: = 150 entradas. 26 Halla la ecuación de la recta a + b = 2 sabiendo que pasa por los puntos A(1, 2) B(3, 7) a + 2b = 2 3a + 7b = 2 a = 10, b = 4 La recta es: 10 4 = = 1 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 199
7 Ejercicios problemas 1. Sistemas lineales. Resolución gráfica Resuelve gráficamente los siguientes sistemas: 30 2 = = 7 = 2, = = 6 3 = 1 = 1, = 4 27 Comprueba que = 1, = 5 es solución del siguiente sistema: = = 1 3 ( 1) = = 13 4 ( 1) + 5 = = 1 P(2, 3) 28 3 = = 4 P(1, 2) = 1, = 2 P( 1, 4) 29 + = 1 2 = = = 2 P( 2, 3) = 2, = 3 = 4, = 2 P(4, 2) 200 SOLUCIONARIO
8 Aplica el criterio que relaciona los coeficientes de los siguientes sistemas para hallar cuántas soluciones tiene, haz la interpretación gráfica, clasifícalo resuélvelo gráficamente: 3 1 Criterio: 1 2 Tiene una solución. Son rectas secantes. Sistema compatible determinado = = = = 9 P(3, 1) Criterio: = = Tiene infinitas soluciones. Son rectas coincidentes. Sistema compatible indeterminado. = 3, = 1 1 = 1, 1 = 2; 2 = 3, 2 = 0; 3 = 5, 3 = = = Criterio: = No tiene solución. Son rectas paralelas. Sistema incompatible = = 4 P( 2, 1) = 2, = 1 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 201
9 Ejercicios problemas = = = = Criterio: = No tiene solución. Son rectas paralelas. Sistema incompatible. 2 1 Criterio: 3 5 Tiene una solución. Son rectas secantes. Sistema compatible determinado. P(5, 1) = 5, = = = Criterio: = = Tiene infinitas soluciones. Son rectas coincidentes. Sistema compatible indeterminado. 40 Escribe un sistema que tenga como solución: = 1, = 2 + = 1 + = 3 2. Métodos de sustitución e igualación Resuelve por el método más sencillo, sustitución o igualación, los siguientes sistemas: = = 1 Soluciones, 1 = 0, 1 = 1; 2 = 1, 2 = 1; 3 = 2, 3 = 3, Se aplica el método de sustitución. Se despeja de la primera ecuación se sustitue en la segunda. = 2, = = = 1 Se aplica el método de sustitución. Se despeja de la segunda ecuación se sustitue en la primera. = 2/3, = 13/3 202 SOLUCIONARIO
10 48 + 0,75 = 3 0,5 = 5 Se aplica el método de igualación. Se despeja de las dos ecuaciones. = 4,2; = 1,6 Se aplica el método de igualación. Se despeja de las dos ecuaciones. = 7, = = = 7 = = 5 4 Se aplica el método de igualación. Se igualan los valores de = 1, = 1 + = = = = 1 Se aplica el método de igualación. Se despeja de las dos ecuaciones. = 6/5, = 7/ = = 17 Se aplica el método de sustitución. Se despeja de la 2ª ecuación se sustitue en la 1ª = 2, = 1 3. Reducción qué método utilizar Resuelve por el método más sencillo los siguientes sistemas: 49 Se aplica el método de reducción. Se suman las dos ecuaciones. = 3, = 4 50 Se aplica el método de sustitución. Se despeja de la 1ª ecuación se sustitue por la 2ª = 2; = = = = = = = 19 Se aplica el método de reducción. Se cambia de signo la segunda ecuación se suman. = 3, = 2 Se eliminan denominadores = 30 2 = 4 Se aplica el método de sustitución. Se despeja de la segunda ecuación se sustitue en la primera. = 21/4, = 13/2 52 = = 5 Se aplica el método de sustitución. Se sustitue el valor de la de la 1ª ecuación en la 2ª = 11/5, = 2/5 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 203
11 Ejercicios problemas = = 5 = = = = 11 Se aplica el método de reducción. m.c.m.(4, 6) = 12 Se multiplica la 1ª ecuación por 3 la 2ª por 2 se suman. = 1, = 0 Se aplica el método de igualación. Se igualan los valores de de las dos ecuaciones. = 3, = 10 Se aplica el método de reducción. Se multiplica la 1ª ecuación por 4 la 2ª por 3 se suman. = 3, = Dos hogazas de pan 8 barras pesan 6 kg 12 barras una hogaza pesan 4 kg. Cuánto pesa cada barra de pan cada hogaza? Peso de la hogaza: Peso de la barra: = = 4 Peso hogaza: = 2,5 kg Peso de la barra: = 0,125 kg = 125 g El triple de un número menos el doble de otro número es igual a 45 el doble del primero menos la cuarta parte del segundo es igual a 43. De qué números se trata? Primer número: Segundo número: 3 2 = 45 2 /4 = 43 = 23, = 12 El perímetro de un romboide mide 42 m un lado mide 7 metros más que el otro. Cuánto mide cada lado? 56 = = 1 Se aplica el método de igualación. Se igualan los valores = 3, = 2 Lado menor: Lado maor: = 42 = + 7 = 7 m, = 14 m 4. Problemas de sistemas 57 Halla dos números sabiendo que uno es el cuádruplo del otro que entre los dos suman 55 Primer número: Segundo número: = 4 + = 55 = 11, = Un ángulo de un rombo mide el doble que el otro. Cuánto mide cada ángulo? Ángulo menor: Ángulo maor: = 2 + = 180 = 60, = SOLUCIONARIO
12 Para ampliar 62 Resuelve gráficamente los sistemas: a) + = 0 b) 2 = 0 = 0 2 = 0 a) = = 5 Se aplica el método de reducción. Se multiplica la 1ª ecuación por 2, la 2ª por 3 se suman. = 3, = 2 O(0, 0) = = 7 = 0, = 0 b) Se aplica el método de sustitución. Se despeja de la 2ª ecuación se sustitue en la 1ª = 3, = 1 67 = = 5 O(0, 0) Se aplica el método de sustitución. Se sustitue el valor de la de la 1ª ecuación en la 2ª = 3, = 4 = 0, = = = 13 Resuelve por el método más sencillo los siguientes sistemas: = = 40 Se aplica el método de reducción. Se multiplica la 1ª ecuación por 5, la 2ª por 3 se suman. = 1, = 2 Se aplica el método de reducción. Se multiplica la 1ª ecuación por 2 se suman. = 4, = = = 1 Se aplica el método de igualación. Se despeja o de las dos ecuaciones se igualan sus valores. = 7, = 9 = = 9 Se eliminan los denominadores. 4 = = = = 9 Se aplica el método de reducción. Se suman las ecuaciones. = 3/2, = 2 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 205
13 Ejercicios problemas + = = Se eliminan los denominadores se simplifica = = = = 4( + 1) Se aplica el método de reducción. Se le resta a la 1ª ecuación la 2ª = 4, = 3 Se eliminan los denominadores, paréntesis se simplifica. + 2 = = 12 Se aplica el método de reducción. Se multiplica por 2 la 2ª ecuación se suman. = 3, = Calcula dos números sabiendo que suman 92 que su diferencia es 22 Primer número: Segundo número: + = 92 = 22 = 57, = 35 Para una fiesta se compran refrescos a 0,85 bolsas de frutos secos a 1,25. Por cada refresco se compran tres bolsas de frutos secos en total se pagan 230. Cuántos refrescos bolsas se han comprado? Nº de refrescos: Nº de bolsas de frutos secos: 0,85 + 1,25 = 230 = 3 Nº de refrescos: = 50 Nº de bolsas de frutos secos: = ,25 + 0,5 = 2 0,75 0,5 = 5 73 Escribe un sistema que tenga la solución: = 3, = 1 + = 2 = 4 74 Calcula el valor de k para que = 2, = 1 sea solución del sistema: = = 4 2k 1 = 9 k = 5 Se aplica el método de reducción. Se suman las ecuaciones = 7, = 0,5 + 2 = 4 k = Halla dos números cua suma sea 12 el primero más el doble del segundo sea igual a 19 Primer número: Segundo número: + = = 19 = 5, = 7 Un ángulo de un rombo mide el triple que el otro. Cuánto mide cada ángulo? Ángulo menor: Ángulo maor: = 3 + = 180 = 45, = SOLUCIONARIO
14 79 Halla la edad de un padre la de su hijo sabiendo que la edad del padre es el triple de la del hijo la diferencia de las edades es de 28 años. Edad del hijo: Edad del padre: = 3 = 28 Edad del hijo: = 14 años. Edad del padre: = 42 años. 81 Un pantalón una camisa cuestan 60 he pagado por ellos 52,8. Si en el pantalón me han hecho el 10% de descuento en la camisa, el 15%, cuánto costaba cada prenda? Precio del pantalón: Precio de la camisa: + = 60 0,9 + 0,85 = 52,8 Coste del pantalón: = 36 Coste de la camisa: = Halla los lados de un rectángulo sabiendo que el perímetro mide 130 m que la base es 3/2 de la altura. Base: Altura: = 130 = 3/2 Base: = 39 m Altura: = 26 m Problemas 82 Se mezcla café de calidad etra de 12 /kg con café normal de 7 /kg para obtener una mezcla de 40 kg a 9 /kg. Cuántos kilos hemos mezclado de cada clase? 83 Precio ( /kg) Peso (kg) + = = 40 9 Café etra Café etra de 12 /kg: = 16 kg Café de 7 /kg: = 24 kg 12 Café normal Halla la ecuación de la recta = a + b sabiendo que pasa por los puntos A(1, 5) B( 1, 1) 7 Mezcla 9 40 a + b = 5 a + b = 1 a = 2, b = 3 La recta es: = José ha comprado en el mercado 3 kg de manzanas 2 kg de higos ha pagado 14. Sabiendo que el kilo de higos cuesta el doble que el de manzanas, halla el precio del kilo de manzanas del kilo de higos. Precio del kilo de manzanas: Precio del kilo de higos: = 14 = 2 Precio del kilo de manzanas: = 2 Precio del kilo de higos: = 4 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 207
15 Ejercicios problemas 85 El perímetro de un triángulo isósceles mide 27,5 m cada uno de los lados iguales mide 2,5 m más que el desigual. Cuánto mide cada lado? 86 Por una camisa un pantalón se han pagado 120, por dos camisas tres pantalones se han pagado 312. Cuánto cuestan cada camisa cada pantalón? Coste de una camisa: Coste de un pantalón: + = = 312 Coste de una camisa: = 48 Coste de un pantalón: = El ángulo desigual de un triángulo isósceles mide la mitad de cada uno de los iguales. Cuánto mide cada uno de los ángulos? Medida del lado desigual: Medida de cada uno de los lados iguales: + 2 = 27,5 = + 2,5 Medida del lado desigual: = 7,5 m Medida de cada uno de los lados iguales: = 10 m Ángulo igual: Cada ángulo desigual: = /2 2 + = 180 Cada uno de los ángulo iguales: = 72 El ángulo desigual: = 36 Precio de un cuaderno: Precio de un bolígrafo: = = 34 Precio de un cuaderno: = 4,5 Precio de un bolígrafo: = 1, Una fábrica hace bicicletas del tipo A, que llevan 1 kg de acero 3 kg de aluminio, otras del tipo B, que llevan 2 kg de acero 2 kg de aluminio. Si la empresa tiene 240 kg de acero 360 kg de aluminio, cuántas bicicletas puede construir de cada modelo? Bicicletas del tipo A: Bicicletas del tipo B: + 2 = = 360 Bicicletas del tipo A: = 60 Bicicletas del tipo B: = 90 Se mezcla aceite puro de oliva de 3,5 el litro con aceite de orujo de 2,5 el litro, para obtener 400 litros de mezcla a 2,75 el litro. Cuántos litros hemos mezclado de cada aceite? Precio ( /l ) Capacidad (l ) Aceite puro 3,5 + = 400 3,5 + 2,5 = 400 2,75 Aceite de oliva: = 100 litros. Aceite de orujo: = 300 litros. Aceite orujo 2,5 Mezcla 2, Pedro María van a comprar cuadernos bolígrafos. Pedro paga 30 por 5 cuadernos 6 bolígrafos, María paga 34 por 7 cuadernos 2 bolígrafos. Cuánto cuestan cada cuaderno cada bolígrafo? 91 Halla dos números sabiendo que al dividir el maor entre el menor se obtiene de cociente 2 de resto 3, que la suma de los dos números es SOLUCIONARIO
16 Número menor: Número maor: + = 39 = Número menor: = 12 Número maor: = Entre conejos gallinas ha 48 animales en un corral. Sabiendo que en total ha 86 patas, cuántos conejos gallinas ha? Interpreta el resultado. Cantidad de conejos: Cantidad de gallinas: + = = 86 Cantidad de conejos: = 5 Cantidad de gallinas: = 53 Interpretación: el número de conejos no puede ser negativo, el problema no tiene solución Reparte 55 proporcionalmente a 2 3 Primera cantidad: Segunda cantidad: + = 55 = 2 3 = 22, = 33 En una tienda, 2 pares de zapatos 3 pares de deportivos cuestan 170, se han pagado por ellos 132. Si en los zapatos han hecho el 25% de descuento en los deportivos el 20%, cuánto costaba cada par? Pares de zapatos: Pares de deportivos: = , ,8 = 132 Pares de zapatos: = 40 Pares de deportivos: = El perímetro de un rectángulo mide 21 m uno de los lados mide el doble del otro. Cuánto mide cada lado? El triple de un número más otro número es igual a 29 el doble del primero menos la mitad del segundo es igual a 10. De qué números se trata? Primer número: Segundo número: 3 + = 29 2 /2 = 10 = 7, = 8 Base: Altura: = 21 = 2 Base: = 7 m Altura: = 3,5 m 97 Dos revistas deportivas una de automóviles cuestan 6. Cuatro revistas deportivas dos de automóviles cuestan 12. Calcula cuánto cuestan cada revista deportiva cada revista de automóviles. Interpreta el resultado que se obtiene. Cantidad de revistas deportivas: Cantidad de revistas de automóviles: 2 + = = 12 Los coeficientes de la segunda ecuación son el doble de los de la primera. El sistema es compatible indeterminado, tiene infinitas soluciones. UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 209
17 Ejercicios problemas Para profundizar 98 Halla dos números tales que su suma sea 25 la seta parte del primero más cinco veces el segundo sea igual a 38 Primer número: Segundo número: + = 25 /6 + 5 = 38 = 18, = 7 99 Entre Juan Antonio hacen un trabajo por el que cobran 654. Si Juan ha hecho los 2/3 del trabajo que ha hecho Antonio, cuánto tiene que cobrar cada uno? Cantidad que cobra Juan: Cantidad que cobra Antonio: + = 654 = 2/3 Juan cobra: = 261,6 Antonio cobra: = 392,4 100 En un puesto se venden melones sandías por unidades. Por la compra de 3 melones 2 sandías se pagan 8, por la compra de 6 melones 4 sandías se pagan 15. Calcula el precio de cada melón de cada sandía e interpreta el resultado que obtengas. Precio de un melón: Precio de una sandía: = = Los coeficientes de las incógnitas de la segunda ecuación son el doble que los de la primera sin embargo el segundo miembro no es el doble. El sistema es incompatible, no tiene solución. Calcula las dimensiones de un rectángulo cuo perímetro es 306 m cua altura mide los 3/4 de la base Se mezcla cebada de 0,15 /kg con trigo de 0,2 /kg para obtener 500 kg de pienso para animales a 0,17 /kg. Cuántos kilos de cebada de trigo hemos mezclado? Precio ( /kg) Masa (kg) + = 500 0,15 + 0,2 = 500 0,17 Cebada: = 300 kg Trigo: = 200 kg El perímetro de un rectángulo mide 24 m la suma de dos lados contiguos mide 12 m. Calcula la longitud de los lados del rectángulo e interpreta el resultado que obtengas. Base: Altura: = 24 + = 12 El sistema es compatible indeterminado, tiene infinitas soluciones porque los coeficientes de la segunda ecuación son la mitad que los de la primera. Halla dos números directamente proporcionales a 5 7 cua suma sea 36 Primer número: Segundo número: = = 36 = 15, = 21 Cebada 0,15 Base: Altura: 2+ 2 = 306 = 3/4 Base: = 612/7 = 87,43 m Altura: = 459/7 = 65,57 m Trigo 0,2 Mezcla 0, SOLUCIONARIO
18 105 La suma de las edades de un padre su hijo es de 75 años la diferencia es de 45 años. Qué edad tienen el padre el hijo? Edad del padre: Edad del hijo: + = 75 = 45 Edad del padre: = 60 años. Edad del hijo: = 15 años. 106 Un número está compuesto de dos cifras que suman 6 unidades. Si cambiamos las dos cifras de orden, el número aumenta en 18 unidades. De qué número se trata? Cifra de las unidades: Cifra de las decenas: + = = = 4, = 2 El número es 24 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 211
19 Aplica tus competencias 107 Dos ciudades, A B, distan entre sí 600 km. De la ciudad A sale hacia la ciudad B un coche a 80 km/h. Al mismo tiempo sale de la ciudad B hacia la ciudad A una moto a 120 km/h. Calcula el tiempo que tardarán en encontrarse la distancia que ha recorrido cada vehículo. A 600 km 80 km/h 120 km/h B 108 Dos ciudades, A B, distan entre sí 800 km. De la ciudad A sale hacia la ciudad B un tren de mercancías a 80 km/h. Tres horas más tarde sale de la misma estación A otro tren de pasajeros a 120 km/h. Calcula el tiempo que tardará el segundo tren en alcanzar al primero la distancia que han recorrido los dos trenes. 80 km/h Tiempo del tren de mercancías: t El tiempo t es el mismo para los dos ha que aplicar la fórmula e = v t A 120 km/h Tiempo del tren de pasajeros: t C B = 80t 600 = 120t t = 3 h, = 240 km El tiempo es el mismo para los dos: 3 h El espacio que recorre el coche que sale de A es de 240 km El espacio que recorre la moto que sale de B es de = 360 km = 80(t + 3) = 120t t = 6 h, = 720 km Comprueba lo que sabes 1 Clasifica un sistema a partir del número de soluciones pon un ejemplo de un sistema incompatible. Un sistema lineal se puede clasificar, según el número de soluciones en: a) Compatible determinado: el sistema tiene una solución las dos rectas se cortan en un punto. b) Incompatible: el sistema no tiene solución las dos rectas son paralelas. c) Compatible indeterminado: el sistema tiene infinitas soluciones las dos rectas son la misma. Ejemplo: = = SOLUCIONARIO
20 Comprueba lo que sabes 2 Resuelve gráficamente el sistema: 2 + = 5 3 = 1 P (2, 1) 5 Resuelve por el método más sencillo el siguiente sistema: = = 4 Se resuelve por reducción. Se multiplica la 1ª por dos se suman. = 2, = 1 = 2, = 1 4 Resuelve por el método más sencillo el siguiente sistema: Resuelve por el método más sencillo el siguiente sistema: 2 + = 2 3 = = = 11 Se resuelve por sustitución. Se despeja en la 1ª ecuación se sustitue en la 2ª = 1, = 3 Se resuelve por reducción. Se suman las dos ecuaciones se obtiene = 1, = Resuelve por el método más sencillo el siguiente sistema: = 2 1 = 3 6 Se resuelve por igualación. = 9, = 5 Ana tiene el triple de dinero que Julio entre los dos tienen 800. Cuánto dinero tiene cada uno? Dinero que tiene Ana: Dinero que tiene Julio: = 3 + = 800 Se resuelve por sustitución. = 600, = 200 Ana tiene: 600 Julio tiene: 200 Un prado tiene forma rectangular. La altura del rectángulo mide 5 m menos que la base el perímetro mide 82 m. Halla el área del prado. Base: = 23 m, altura: = 18 m Área = = 414 m 2 Base: Altura: = = 82 UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 213
21 Windows Derive Paso a paso Resuelve algebraicamente el siguiente sistema clasifícalo a la vista del resultado: + 2 = 8 3 = 3 Resuelto en el libro del alumnado. Resuelve algebraicamente el siguiente sistema clasifícalo a la vista del resultado: = = 3 Resuelto en el libro del alumnado Resuelve algebraicamente el siguiente sistema clasifícalo a la vista del resultado: 3 = = 3 Resuelto en el libro del alumnado. Resuelve gráficamente el siguiente sistema, clasifícalo, si es compatible determinado, halla la solución. 2 + = 9 3 = 1 Resuelto en el libro del alumnado. 113 Internet. Abre la web: elige Matemáticas, curso tema. 214 SOLUCIONARIO
22 Linu/Windows Practica 114 Resuelve algebraicamente los siguientes sistemas clasifícalos a la vista del resultado: = 2 a) b) 5 4 = = = 5 b) P(3, 2) a) = 4, = 5 Sistema compatible determinado. b) No tiene solución. Sistema incompatible. 115 Resuelve algebraicamente los siguientes sistemas clasifícalos a la vista del resultado: 9 6 = 12 a) b) = 4 a) 3 2 = 4 Sistema compatible indeterminado. b) = 3, = 1 Sistema compatible determinado. 116 Resuelve gráficamente los siguientes sistemas, clasifícalos, si son compatibles determinados, halla la solución: = = 12 a) b) = = 5 a) 3 5 = = 7 Plantea los siguientes problemas resuélvelos con auda de DERIVE o Wiris: Sistema compatible determinado. = 3, = 2 Ana tiene el triple de dinero que Julio entre los dos tienen 800. Cuánto dinero tiene cada uno? Planteamiento: = 3 + = 800 Ana tiene: 600 Julio tiene: 200 En un rectángulo, la suma de las longitudes de la base la altura es 35 m la longitud de la base menos la longitud de la altura es 7 m. Cuánto mide cada lado? Planteamiento: + = 35 = 7 La base mide 21 m La altura mide 14 m Sistema incompatible. UNIDAD 7. SISTEMAS DE ECUACIONES LINEALES 215
Sistemas de ecuaciones lineales
 7 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica a) En qué punto se cortan la gráfica roja la azul del dibujo de la izquierda? b) Tienen algún punto en común las rectas de la
7 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica a) En qué punto se cortan la gráfica roja la azul del dibujo de la izquierda? b) Tienen algún punto en común las rectas de la
7. Sistemas de ecuaciones lineales
 76 SOLUCIONARIO 7. Sistemas de ecuaciones lineales 1. SISTEMAS LINEALES. RESOLUCIÓN GRÁFICA PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul del dibujo? s r 3. Aplica el criterio que relaciona
76 SOLUCIONARIO 7. Sistemas de ecuaciones lineales 1. SISTEMAS LINEALES. RESOLUCIÓN GRÁFICA PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul del dibujo? s r 3. Aplica el criterio que relaciona
Sistemas de ecuaciones lineales
 9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
I.E.S. Miguel de Cervantes (Granada) Departamento de Matemáticas GBG 1
 ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
9 Ecuaciones. de primer grado. 1. El lenguaje algebraico
 9 Ecuaciones de primer grado 1. El lenguaje algebraico Calcula el resultado de las siguientes epresiones: a) Tenía 5 y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado mide metros y el
9 Ecuaciones de primer grado 1. El lenguaje algebraico Calcula el resultado de las siguientes epresiones: a) Tenía 5 y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado mide metros y el
Ecuaciones de 1er y 2º grado
 Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN
 Matemáticas Ejercicios Tema 8 3º ESO Bloque II: Álgebra Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN 1.- La base de un rectángulo mide 8 cm
Matemáticas Ejercicios Tema 8 3º ESO Bloque II: Álgebra Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN 1.- La base de un rectángulo mide 8 cm
6Soluciones a los ejercicios y problemas PÁGINA 133
 PÁGINA 33 Pág. P RACTICA Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = 4 3x 4y = 0 a) b) 5x + y = 0 4x + 3y = 5 x y = 4 a) ( ) = 5? 4 No es solución. 5x + y = 0 5 =
PÁGINA 33 Pág. P RACTICA Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = 4 3x 4y = 0 a) b) 5x + y = 0 4x + 3y = 5 x y = 4 a) ( ) = 5? 4 No es solución. 5x + y = 0 5 =
) = 5. Operaciones con polinomios 54 SOLUCIONARIO 1. POLINOMIOS. SUMA Y RESTA 2. MULTIPLICACIÓN DE POLINOMIOS
 54 SOLUCIONARIO 5. Operaciones con polinomios. POLINOMIOS. SUMA RESTA PIENSA CALCULA Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A ( ) = 6 b) V ( ) = CARNÉ CALCULISTA
54 SOLUCIONARIO 5. Operaciones con polinomios. POLINOMIOS. SUMA RESTA PIENSA CALCULA Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A ( ) = 6 b) V ( ) = CARNÉ CALCULISTA
Sistemas de ecuaciones de primer grado con dos incógnitas
 Unidad Didáctica 4 Sistemas de ecuaciones de primer grado con dos incógnitas Objetivos 1. Encontrar y reconocer las relaciones entre los datos de un problema y expresarlas mediante el lenguaje algebraico.
Unidad Didáctica 4 Sistemas de ecuaciones de primer grado con dos incógnitas Objetivos 1. Encontrar y reconocer las relaciones entre los datos de un problema y expresarlas mediante el lenguaje algebraico.
Sistemas de dos ecuaciones lineales con dos incógnitas
 Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
Cuáles son esos números?
 MATEMÁTICAS PROBLEMAS QUE SE RESUELVEN CON ECUACIONES Para resolver un problema de ecuaciones debes seguir los siguientes pasos: a) Identificar el dato desconocido y asignarle el valor x (si hay dos o
MATEMÁTICAS PROBLEMAS QUE SE RESUELVEN CON ECUACIONES Para resolver un problema de ecuaciones debes seguir los siguientes pasos: a) Identificar el dato desconocido y asignarle el valor x (si hay dos o
Sistemas de ecuaciones lineales
 9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
2 Fracciones y. números decimales. 1. Operaciones con fracciones. Realiza mentalmente las siguientes operaciones: Solución: a) b) c) Carné calculista
 Fracciones y números decimales. Operaciones con fracciones Realiza mentalmente las siguientes operaciones: + c) 0 c) P I E N S A Y C A L C U L A Carné calculista : C = ; R = Calcula mentalmente: + c) c)
Fracciones y números decimales. Operaciones con fracciones Realiza mentalmente las siguientes operaciones: + c) 0 c) P I E N S A Y C A L C U L A Carné calculista : C = ; R = Calcula mentalmente: + c) c)
EJERCICIOS DE SISTEMAS DE ECUACIONES
 EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
5Soluciones a los ejercicios y problemas PÁGINA 114
 5Soluciones a los ejercicios y problemas PÁGINA 4 Pág. P RACTICA Ecuaciones: soluciones por tanteo Es o solución de alguna de las siguientes ecuaciones? Compruébalo. a) 5 b) 4 c) ( ) d) 4 4 a)? 0? 5 no
5Soluciones a los ejercicios y problemas PÁGINA 4 Pág. P RACTICA Ecuaciones: soluciones por tanteo Es o solución de alguna de las siguientes ecuaciones? Compruébalo. a) 5 b) 4 c) ( ) d) 4 4 a)? 0? 5 no
1. Ecuaciones lineales 1.a. Definición. Solución.
 Sistemas de ecuaciones Contenidos 1. Ecuaciones lineales Definición. Solución 2. Sistemas de ecuaciones lineales Definición. Solución Número de soluciones 3. Métodos de resolución Reducción Sustitución
Sistemas de ecuaciones Contenidos 1. Ecuaciones lineales Definición. Solución 2. Sistemas de ecuaciones lineales Definición. Solución Número de soluciones 3. Métodos de resolución Reducción Sustitución
PROBLEMAS DE SISTEMAS DE ECUACIONES
 PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
Soluciones a las actividades
 Soluciones a las actividades BLOQUE I Álgebra 1. Sistemas lineales 2. Matrices 3. Determinantes 4. Sistemas lineales con parámetros 1 Sistemas lineales 1. Sistemas de ecuaciones lineales Piensa y calcula
Soluciones a las actividades BLOQUE I Álgebra 1. Sistemas lineales 2. Matrices 3. Determinantes 4. Sistemas lineales con parámetros 1 Sistemas lineales 1. Sistemas de ecuaciones lineales Piensa y calcula
7. Sistemas de ecuaciones lineales
 7. Sistemas de ecuaciones lineales 1. sistemas lineales. Resolución gráfica PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul? s r 3. Aplica el criterio que relaciona los coeficientes del
7. Sistemas de ecuaciones lineales 1. sistemas lineales. Resolución gráfica PIENSA CALCULA a) En qué punto se cortan la gráfica roja la azul? s r 3. Aplica el criterio que relaciona los coeficientes del
7Soluciones a los ejercicios y problemas PÁGINA 159
 7Soluciones a los ejercicios y problemas PÁGINA 159 Pág. 1 S istemas de ecuaciones. Resolución gráfica x + y = 3 1 Representa estas ecuaciones: x y = 1 a) Escribe las coordenadas del punto de corte. b)escribe
7Soluciones a los ejercicios y problemas PÁGINA 159 Pág. 1 S istemas de ecuaciones. Resolución gráfica x + y = 3 1 Representa estas ecuaciones: x y = 1 a) Escribe las coordenadas del punto de corte. b)escribe
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 5 PRACTICA Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución =, =. + 7 = + = a) b) 4 = Sustituimos en cada ecuación =, = operamos: + = a) b) 4 = 0 Comprueba si
Pág. Página 5 PRACTICA Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución =, =. + 7 = + = a) b) 4 = Sustituimos en cada ecuación =, = operamos: + = a) b) 4 = 0 Comprueba si
Para resolver estos problemas podemos seguir tres pasos:
 RESOLUCIÓN DE PROBLEMAS Algunos problemas pueden resolverse empleando sistemas de dos ecuaciones de primer grado con dos incógnitas. Muchas veces se pueden resolver utilizando una sola ecuación con una
RESOLUCIÓN DE PROBLEMAS Algunos problemas pueden resolverse empleando sistemas de dos ecuaciones de primer grado con dos incógnitas. Muchas veces se pueden resolver utilizando una sola ecuación con una
6 SISTEMAS DE ECUACIONES
 6 SISTEMAS DE ECUACIONES EJERCICIOS PROPUESTOS 6.1 Halla las soluciones de la ecuación 2x 6y 28 sabiendo el valor de una de las incógnitas. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28
6 SISTEMAS DE ECUACIONES EJERCICIOS PROPUESTOS 6.1 Halla las soluciones de la ecuación 2x 6y 28 sabiendo el valor de una de las incógnitas. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28
Las fracciones. 1. Concepto de fracción. Cuatro personas se van a comer a partes iguales una tarta. Qué parte le corresponde a cada una?
 Las fracciones. Concepto de fracción Cuatro personas se van a comer a partes iguales una tarta. Qué parte le corresponde a cada una? P I E N S A Y C A L C U L A / Carné calculista 0 : C = 8; R = A P L
Las fracciones. Concepto de fracción Cuatro personas se van a comer a partes iguales una tarta. Qué parte le corresponde a cada una? P I E N S A Y C A L C U L A / Carné calculista 0 : C = 8; R = A P L
Capítulo 5: Ecuaciones de segundo grado y sistemas lineales
 º de ESO Capítulo : Ecuaciones de segundo grado sistemas lineales Autora: Raquel Hernández Revisores: Sergio Hernández María Molero Ilustraciones: Raquel Hernández Banco de Imágenes de INTEF Ecuaciones
º de ESO Capítulo : Ecuaciones de segundo grado sistemas lineales Autora: Raquel Hernández Revisores: Sergio Hernández María Molero Ilustraciones: Raquel Hernández Banco de Imágenes de INTEF Ecuaciones
TEMA: ECUACIONES CON NÚMEROS NATURALES ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA.
 TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
Sistemas de Ecuaciones
 4 Sistemas de Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer y clasificar los sistemas de ecuaciones según su número de soluciones. Obtener la solución de un sistema mediante una tablas.
4 Sistemas de Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer y clasificar los sistemas de ecuaciones según su número de soluciones. Obtener la solución de un sistema mediante una tablas.
k) x - 5 + 6 = 11 l) 5x - 2 = 3x - 1 m) 2x - 3 = 4x - 7 n) 5x + 4 = 6x + 3 ñ) 6x - 1 = 8x - 5 o) 3x + 10 = 5x - 6 p) 4x + 1 = 9x - 64
 Tema : Ecuaciones Resolver las siguientes ecuaciones de primer grado: a) b) c) 0 9 d) - e) f) g) 0 h) i) - j) k) - l) - - m) - - n) ñ) - - o) 0 - p) 9 - q) 9 - r) - 0 s) - - Resolver las siguientes ecuaciones
Tema : Ecuaciones Resolver las siguientes ecuaciones de primer grado: a) b) c) 0 9 d) - e) f) g) 0 h) i) - j) k) - l) - - m) - - n) ñ) - - o) 0 - p) 9 - q) 9 - r) - 0 s) - - Resolver las siguientes ecuaciones
ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES
 ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES La materia se estructurará en dos partes. Los alumnos que tengan en la primera evaluación menos de un cuatro deberán hacer el martes de Febrero
ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES La materia se estructurará en dos partes. Los alumnos que tengan en la primera evaluación menos de un cuatro deberán hacer el martes de Febrero
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES
 PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas
 Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas Recuerda las cuatro fases que tendremos que seguir para resolver un problema: 1.- Comprender el problema. 2.- Plantear el sistema
Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas Recuerda las cuatro fases que tendremos que seguir para resolver un problema: 1.- Comprender el problema. 2.- Plantear el sistema
5 Operaciones. con polinomios P I E N S A Y C A L C U L A A P L I C A L A T E O R Í A. 1. Polinomios. Suma y resta
 5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
Ecuaciones de segundo grado
 3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
ECUACIONES DE PRIMER GRADO
 ECUACIONES DE PRIMER GRADO 1- ECUACION DE PRIMER GRADO CON UNA INCOGNITA Una ecuación de primer grado con una incógnita es una igualdad en la que figura una letra sin eponente y que es cierta para un solo
ECUACIONES DE PRIMER GRADO 1- ECUACION DE PRIMER GRADO CON UNA INCOGNITA Una ecuación de primer grado con una incógnita es una igualdad en la que figura una letra sin eponente y que es cierta para un solo
7 ECUACIONES. SISTEMAS DE ECUACIONES
 EJERCICIOS PROPUESTOS 7. Escribe estos enunciados en forma de ecuación. a) La suma de dos números consecutivos es. La suma de tres números pares consecutivos es 0. c) Un número más su quinta parte es.
EJERCICIOS PROPUESTOS 7. Escribe estos enunciados en forma de ecuación. a) La suma de dos números consecutivos es. La suma de tres números pares consecutivos es 0. c) Un número más su quinta parte es.
RESOLUCIÓN DE PROBLEMAS
 RESOLUCIÓN DE PROBLEMAS La resolución de problemas mediante ecuaciones tiene una serie de dificultades que nos llevan a plantear un tema separado del resto. Las dificultades, llegado este punto en que
RESOLUCIÓN DE PROBLEMAS La resolución de problemas mediante ecuaciones tiene una serie de dificultades que nos llevan a plantear un tema separado del resto. Las dificultades, llegado este punto en que
Polinomios y fracciones
 BLOQUE II Álgebra 3. Polinomios y fracciones algebraicas 4. Resolución de ecuaciones 5. Sistemas de ecuaciones 6. Inecuaciones y sistemas de inecuaciones 3 Polinomios y fracciones algebraicas. Binomio
BLOQUE II Álgebra 3. Polinomios y fracciones algebraicas 4. Resolución de ecuaciones 5. Sistemas de ecuaciones 6. Inecuaciones y sistemas de inecuaciones 3 Polinomios y fracciones algebraicas. Binomio
b) Los lados de un triángulo rectángulo tienen por medida tres números naturales consecutivos. Halla dichos lados.
 Problemas Repaso MATEMÁTICAS APLICADAS A LAS CCSS I Profesor:Féli Muñoz Reduce a común denominador el siguiente conjunto de fracciones: + ; y Común denominador: ( + )( ) MCM + ( )( ) ( )( + )( ) ( ) (
Problemas Repaso MATEMÁTICAS APLICADAS A LAS CCSS I Profesor:Féli Muñoz Reduce a común denominador el siguiente conjunto de fracciones: + ; y Común denominador: ( + )( ) MCM + ( )( ) ( )( + )( ) ( ) (
1. Sistemas lineales. Resolución gráfica
 6 Sistemas de ecuaciones 1. Sistemas lineales. Resolución gráfica Dado el sistema lineal formado por las ecuaciones del gráfico de la parte derecha: a) cuántas soluciones tiene? b) halla la solución o
6 Sistemas de ecuaciones 1. Sistemas lineales. Resolución gráfica Dado el sistema lineal formado por las ecuaciones del gráfico de la parte derecha: a) cuántas soluciones tiene? b) halla la solución o
PARTE 2- Matemáticas pendientes de 3º ESO 2010-11. 2. Indica, para cada representación gráfica, que tipo de sistema de ecuaciones es el representado:
 PARTE - Matemáticas pendientes de 3º ESO 00- NOMBRE: 4º GRUPO:. Resuelve gráficamente los siguientes sistemas de ecuaciones e indica que tipo de sistema son: x x x 3 4. Indica, para cada representación
PARTE - Matemáticas pendientes de 3º ESO 00- NOMBRE: 4º GRUPO:. Resuelve gráficamente los siguientes sistemas de ecuaciones e indica que tipo de sistema son: x x x 3 4. Indica, para cada representación
Sistemas de ecuaciones
 Sistemas de ecuaciones Cuando aparecen varias incógnitas en un problema, resulta más sencillo resolverlo planteando más de una ecuación con más de una incógnita. Un sistema de ecuaciones es un conjunto
Sistemas de ecuaciones Cuando aparecen varias incógnitas en un problema, resulta más sencillo resolverlo planteando más de una ecuación con más de una incógnita. Un sistema de ecuaciones es un conjunto
5. Los números decimales
 40. Los números decimales 6. Representa en la recta los siguientes números a) 0, b) 1,7 c) 2,4 d) 3,2 1. NÚMEROS DECIMALES 3,2 1,7 0, 3 2 1 0 2,4 1 2 3 Escribe la fracción y calcula mentalmente el número
40. Los números decimales 6. Representa en la recta los siguientes números a) 0, b) 1,7 c) 2,4 d) 3,2 1. NÚMEROS DECIMALES 3,2 1,7 0, 3 2 1 0 2,4 1 2 3 Escribe la fracción y calcula mentalmente el número
PROBLEMAS ECUACIONES 1er GRADO
 PROBLEMAS ECUACIONES 1er GRADO 1.- Dos amigos juntan el dinero que tienen, uno tiene el doble que el otro. Se gastan 20, y les quedan 13 Cuánto dinero tiene cada uno? 2.- He comprado 8 cuadernos y he pagado
PROBLEMAS ECUACIONES 1er GRADO 1.- Dos amigos juntan el dinero que tienen, uno tiene el doble que el otro. Se gastan 20, y les quedan 13 Cuánto dinero tiene cada uno? 2.- He comprado 8 cuadernos y he pagado
BLOQUE IV. Funciones. 10. Funciones. Rectas y parábolas 11. Funciones racionales, irracionales, exponenciales y logarítmicas 12. Límites y derivadas
 BLOQUE IV Funciones 0. Funciones. Rectas y parábolas. Funciones racionales, irracionales, exponenciales y logarítmicas. Límites y derivadas 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo
BLOQUE IV Funciones 0. Funciones. Rectas y parábolas. Funciones racionales, irracionales, exponenciales y logarítmicas. Límites y derivadas 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo
a) x 1 = 2 b) x + x 6 = 2 + = + = c) x 9x + 20 = 2 d) x 6x 7 = a) x = 1 y x = 1 b) x = 3 y x = 2 c) x = 4 y x = 5 d) x = 1 y x = 7
 1 Resuelve las siguientes ecuaciones: a) x 1 = x + x 6 = c) x 9x + = d) x 6x 7 = = a) x = 1 y x = 1 x = 3 y x = c) x = 4 y x = 5 d) x = 1 y x = 7 Resuelve las siguientes ecuaciones de primer grado: a)
1 Resuelve las siguientes ecuaciones: a) x 1 = x + x 6 = c) x 9x + = d) x 6x 7 = = a) x = 1 y x = 1 x = 3 y x = c) x = 4 y x = 5 d) x = 1 y x = 7 Resuelve las siguientes ecuaciones de primer grado: a)
1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20
 ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
Proporcionalidad. 1. Calcula:
 Proporcionalidad 1. Calcula:. Resuelve los siguientes problemas: a. Tres kilos de naranjas cuestan,4. Cuánto cuestan dos kilos? b. Seis obreros descargan un camión en tres horas. Cuánto tardarán cuatro
Proporcionalidad 1. Calcula:. Resuelve los siguientes problemas: a. Tres kilos de naranjas cuestan,4. Cuánto cuestan dos kilos? b. Seis obreros descargan un camión en tres horas. Cuánto tardarán cuatro
ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO
 CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
10Soluciones a los ejercicios y problemas PÁGINA 196
 0Soluciones a los ejercicios y problemas PÁGINA 96 Pág. E presiones algebraicas Llamando a un número indeterminado, asocia cada enunciado con la epresión que le corresponde: a) El doble del número. b)
0Soluciones a los ejercicios y problemas PÁGINA 96 Pág. E presiones algebraicas Llamando a un número indeterminado, asocia cada enunciado con la epresión que le corresponde: a) El doble del número. b)
4 Proporcionalidad. 1. Razones y proporciones
 4 Proporcionalidad 1. Razones y proporciones Se han comprado 5 kg de melocotones por 10,5. Calcula mentalmente cuánto cuesta cada kilo. 10,5 : 5 = 2,1 /kg P I E N S A Y C A L C U L A 1 Calcula las razones
4 Proporcionalidad 1. Razones y proporciones Se han comprado 5 kg de melocotones por 10,5. Calcula mentalmente cuánto cuesta cada kilo. 10,5 : 5 = 2,1 /kg P I E N S A Y C A L C U L A 1 Calcula las razones
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES. 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora?
 PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora? Solución : 12 años 2.- Si al doble de un número le restas 13, obtienes
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora? Solución : 12 años 2.- Si al doble de un número le restas 13, obtienes
4 Ecuaciones y sistemas
 Solucionario Ecuaciones y sistemas ACTIVIDADES INICIALES.I. Comprueba si las siguientes ecuaciones tienen como soluciones,,. a) 0 b) 5 () 8 a) 0 () () es solución. 0 8 9 6 0 6 0 0 9 5 5 6 5 es solución.
Solucionario Ecuaciones y sistemas ACTIVIDADES INICIALES.I. Comprueba si las siguientes ecuaciones tienen como soluciones,,. a) 0 b) 5 () 8 a) 0 () () es solución. 0 8 9 6 0 6 0 0 9 5 5 6 5 es solución.
EJERCICIOS SOBRE : ECUACIONES DE PRIMER GRADO
 1.- Igualdades. Las expresiones en donde aparecen el signo =, se llaman igualdades. Ejemplo: 5 = 7-2 ; x + 2 = 9 Toda igualdad consta de dos miembros, el primer miembro ( lo escrito antes del signo igual
1.- Igualdades. Las expresiones en donde aparecen el signo =, se llaman igualdades. Ejemplo: 5 = 7-2 ; x + 2 = 9 Toda igualdad consta de dos miembros, el primer miembro ( lo escrito antes del signo igual
PROBLEMAS RESUELTOS DE OPTIMIZACIÓN
 Problemas de optimiación Ejercicio PROBLEMAS RESUELTOS DE OPTIMIZACIÓN Un banco lana al mercado un plan de inversión cua rentabilidad R(, en euros, viene dada en función de la cantidad invertida, en euros,
Problemas de optimiación Ejercicio PROBLEMAS RESUELTOS DE OPTIMIZACIÓN Un banco lana al mercado un plan de inversión cua rentabilidad R(, en euros, viene dada en función de la cantidad invertida, en euros,
Funciones más usuales 1
 Funciones más usuales 1 1. La función constante Funciones más usuales La función constante Consideremos la función más sencilla, por ejemplo. La imagen de cualquier número es siempre 2. Si hacemos una
Funciones más usuales 1 1. La función constante Funciones más usuales La función constante Consideremos la función más sencilla, por ejemplo. La imagen de cualquier número es siempre 2. Si hacemos una
MATEMÁTICAS-EJERCICIOS DE RECUPERACION PENDIENTES 1º E.S.O. 2º BLOQUE. Nombre y Apellidos:
 TEMA 7. SISTEMA METRICO DECIMAL 1. 2. Para pasar de una medida de superficie inferior a otra inmediatamente superior: a) Se multiplica el resultado de la medida por 100. b) Se multiplica el resultado de
TEMA 7. SISTEMA METRICO DECIMAL 1. 2. Para pasar de una medida de superficie inferior a otra inmediatamente superior: a) Se multiplica el resultado de la medida por 100. b) Se multiplica el resultado de
Problemas de ecuaciones Colección C. MasMates.com Colecciones de ejercicios
 1. En el mercado, Rosa ha comprado 3 kg de guisantes, 4 kg de garbanzos y 5 kg de judías por 48'80 euros. Halla, planteando y resolviendo una ecuación con una incógnita, el precio del kilo de cada tipo
1. En el mercado, Rosa ha comprado 3 kg de guisantes, 4 kg de garbanzos y 5 kg de judías por 48'80 euros. Halla, planteando y resolviendo una ecuación con una incógnita, el precio del kilo de cada tipo
Recuerdas qué es? Constante de proporcionalidad Es el cociente de cualquiera de las razones que intervienen en una proporción.
 Recuerdas qué es? Coordenadas de un punto Un punto del plano viene definido por un par ordenado de números. La primera coordenada es la abscisa del punto, la segunda coordenada es la ordenada del punto.
Recuerdas qué es? Coordenadas de un punto Un punto del plano viene definido por un par ordenado de números. La primera coordenada es la abscisa del punto, la segunda coordenada es la ordenada del punto.
HIgualdades y ecuacionesh. HElementos de una ecuaciónh. HEcuaciones equivalentes. HSin denominadoresh. HCon denominadoresh
 6 Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer situaciones que pueden resolverse con ecuaciones Traducir al lenguaje matemático enunciados del lenguaje ordinario. Conocer los elementos
6 Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer situaciones que pueden resolverse con ecuaciones Traducir al lenguaje matemático enunciados del lenguaje ordinario. Conocer los elementos
EJERCICIOS PROPUESTOS. Copia y completa de modo que estas expresiones sean igualdades numéricas. a) 5 2 13 c) 2 32 b) 4 5 17 d) 4 6 18 10
 5 ECUACIONES EJERCICIOS PROPUESTOS 5.1 Copia y completa de modo que estas epresiones sean igualdades numéricas. a) 5 1 c) b) 5 17 d) 6 1 10 a) 5 10 1 c) 16 b) 5 17 d) 6 1 10 5. Sustituye las letras por
5 ECUACIONES EJERCICIOS PROPUESTOS 5.1 Copia y completa de modo que estas epresiones sean igualdades numéricas. a) 5 1 c) b) 5 17 d) 6 1 10 a) 5 10 1 c) 16 b) 5 17 d) 6 1 10 5. Sustituye las letras por
9 Geometría. analítica. 1. Vectores
 9 Geometría analítica 1. Vectores Dibuja en unos ejes coordenados los vectores que nacen en el origen de coordenadas y tienen sus extremos en los puntos: A(, ), B(, ), C(, ) y D(, ) P I E N S A C A L C
9 Geometría analítica 1. Vectores Dibuja en unos ejes coordenados los vectores que nacen en el origen de coordenadas y tienen sus extremos en los puntos: A(, ), B(, ), C(, ) y D(, ) P I E N S A C A L C
8 Geometría. analítica. 1. Vectores
 Geometría analítica 1. Vectores Dibuja en unos ejes coordenados los vectores que nacen en el origen de coordenadas y tienen sus extremos en los puntos: A(, ), B(, ), C(, ) y D(, ) P I E N S A C A L C U
Geometría analítica 1. Vectores Dibuja en unos ejes coordenados los vectores que nacen en el origen de coordenadas y tienen sus extremos en los puntos: A(, ), B(, ), C(, ) y D(, ) P I E N S A C A L C U
EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7
 I.E.S. Humanes Junio de 007 EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7 1º) Resuelve: 3 x ( x 3) = 7x 3 ( x + 4) x x + 4 º) Resuelve: = 3 1 3º) Resuelve: ( x 1) = ( x 1 ) ( x + ) x 4º) Resuelve:
I.E.S. Humanes Junio de 007 EXAMEN DE POLINOMIOS, ECUACIONES Y SISTEMAS 6-3-7 1º) Resuelve: 3 x ( x 3) = 7x 3 ( x + 4) x x + 4 º) Resuelve: = 3 1 3º) Resuelve: ( x 1) = ( x 1 ) ( x + ) x 4º) Resuelve:
PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES 3º ESO 2009. 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible.
 PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES º ESO 009 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible. 1 A = 8 1 + 1 B = A = 8 1 = 8 = 8 = 6 4 B = = 4 4 = 4 16
PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES º ESO 009 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible. 1 A = 8 1 + 1 B = A = 8 1 = 8 = 8 = 6 4 B = = 4 4 = 4 16
Problemas de ecuaciones de primer grado
 Problemas de ecuaciones de primer grado 1. La suma de dos números pares consecutivos es 102. Halla esos números. (50 y 52) 2. La suma de tres números impares consecutivos es 69. Busca los números. (21,23
Problemas de ecuaciones de primer grado 1. La suma de dos números pares consecutivos es 102. Halla esos números. (50 y 52) 2. La suma de tres números impares consecutivos es 69. Busca los números. (21,23
EJERCICIOS DE REPASO 2º ESO
 NOMBRE: CURSO: 0-0 EJERCICIOS DE REPASO º ESO.- Calcula, poniendo los pasos que haces, no sólo el resultado: a ) - ( - ) + 8 ( - ) = b) ( - 8 ) [ 7 + ( - 9 ) ] = c) 7 ( 8 ) + : ( - + 7 ) = d) 6 : ( 8 )
NOMBRE: CURSO: 0-0 EJERCICIOS DE REPASO º ESO.- Calcula, poniendo los pasos que haces, no sólo el resultado: a ) - ( - ) + 8 ( - ) = b) ( - 8 ) [ 7 + ( - 9 ) ] = c) 7 ( 8 ) + : ( - + 7 ) = d) 6 : ( 8 )
CUADERNO DE VERANO 3º ESO FRACCIONES. 1. Efectúa las siguientes operaciones: 5 = 7 = 1 1 = c) 2 3 + = d) 5 29 : = e) 4. f) 24
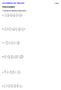 CUADERNO DE VERANO º ESO FRACCIONES. Efectúa las siguientes operaciones: a) 0 9 9 b) 0 0 7 c) d) 8 e) 7 9 : f) 9 9 7 : : ) El aire es una mezcla de gases. En la capa más próima a la superficie de la Tierra,
CUADERNO DE VERANO º ESO FRACCIONES. Efectúa las siguientes operaciones: a) 0 9 9 b) 0 0 7 c) d) 8 e) 7 9 : f) 9 9 7 : : ) El aire es una mezcla de gases. En la capa más próima a la superficie de la Tierra,
Colegio Las Tablas Tarea de verano Matemáticas 3º ESO
 Colegio Las Tablas Tarea de verano Matemáticas º ESO Nombre: C o l e g i o L a s T a b l a s Tarea de verano Matemáticas º ESO Resolver la siguiente ecuación: 5 5 6 Multiplicando por el mcm(,,6) = 6 y
Colegio Las Tablas Tarea de verano Matemáticas º ESO Nombre: C o l e g i o L a s T a b l a s Tarea de verano Matemáticas º ESO Resolver la siguiente ecuación: 5 5 6 Multiplicando por el mcm(,,6) = 6 y
1º BACHILLERATO MATEMÁTICAS CCSS
 PÁGINA 87, EJERCICIO 48 1º BACHILLERATO MATEMÁTICAS CCSS PROBLEMAS TEMA 4 - ECUACIONES Y SISTEMAS La suma de los cuadrados de dos números naturales impares consecutivos es 170. Calcula el valor del siguiente
PÁGINA 87, EJERCICIO 48 1º BACHILLERATO MATEMÁTICAS CCSS PROBLEMAS TEMA 4 - ECUACIONES Y SISTEMAS La suma de los cuadrados de dos números naturales impares consecutivos es 170. Calcula el valor del siguiente
3 Polinomios y fracciones algebráicas
 Solucionario 3 Polinomios y fracciones algebráicas ACTIVIDADES INICIALES 3.I. Para cada uno de los siguientes monomios, indica las variables, el grado y el coeficiente, y calcula el valor numérico de los
Solucionario 3 Polinomios y fracciones algebráicas ACTIVIDADES INICIALES 3.I. Para cada uno de los siguientes monomios, indica las variables, el grado y el coeficiente, y calcula el valor numérico de los
ACTIVIDADES DE REPASO. MATEMÁTICAS 1º ESO
 ACTIVIDADES DE REPASO. MATEMÁTICAS º ESO NÚMEROS NATURALES. Calcula: a) 4 6 5 + 3 4 b) (4 6 5) + 3 4 c) 4 6 (5 + 3 4) d) 4 (6 5) + 3 4 e) (5 + 0) 8 f) (73 37) : 6. Calcula: a) 987 + 5 + 3 784 b) 3 978
ACTIVIDADES DE REPASO. MATEMÁTICAS º ESO NÚMEROS NATURALES. Calcula: a) 4 6 5 + 3 4 b) (4 6 5) + 3 4 c) 4 6 (5 + 3 4) d) 4 (6 5) + 3 4 e) (5 + 0) 8 f) (73 37) : 6. Calcula: a) 987 + 5 + 3 784 b) 3 978
1º E.S.O. NÚMEROS ENTEROS:
 1º E.S.O. NÚMEROS ENTEROS: 1. Los números naturales. Sistema de numeración decimal. Orden y representación de los números naturales. Los números grandes: millones, millardos, billones. Suma, resta y multiplicación.
1º E.S.O. NÚMEROS ENTEROS: 1. Los números naturales. Sistema de numeración decimal. Orden y representación de los números naturales. Los números grandes: millones, millardos, billones. Suma, resta y multiplicación.
9 FUNCIONES DE PROPORCIONALIDAD DIRECTA E INVERSA
 9 FUNCINES DE PRPRCINALIDAD DIRECTA E INVERSA EJERCICIS PRPUESTS 9. Dibuja la gráfica de la función que eprese que el precio del litro de gasolina en los últimos 6 meses ha sido siempre de 0,967 euros.
9 FUNCINES DE PRPRCINALIDAD DIRECTA E INVERSA EJERCICIS PRPUESTS 9. Dibuja la gráfica de la función que eprese que el precio del litro de gasolina en los últimos 6 meses ha sido siempre de 0,967 euros.
5 Proporcionalidad. 1. Razón y proporción. Una pescadería cobra 160 por 8 kg de bogavantes. Cuánto cobrará por un kilo? Solución: 160 : 8 = 20 /kg
 5 Proporcionalidad 1. Razón y proporción Una pescadería cobra 160 por 8 kg de bogavantes. Cuánto cobrará por un kilo? P I E N S A Y C A L C U L A 160 : 8 20 /kg Carné calculista 1 409,6 : 68 C 6,02; R
5 Proporcionalidad 1. Razón y proporción Una pescadería cobra 160 por 8 kg de bogavantes. Cuánto cobrará por un kilo? P I E N S A Y C A L C U L A 160 : 8 20 /kg Carné calculista 1 409,6 : 68 C 6,02; R
SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS
 SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS Sistemas de dos ecuaciones con dos incógnitas. Un sistema lineal de dos ecuaciones con dos incógnitas es de la forma: a b c ' ' ' con a b c a b c números reales
SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS Sistemas de dos ecuaciones con dos incógnitas. Un sistema lineal de dos ecuaciones con dos incógnitas es de la forma: a b c ' ' ' con a b c a b c números reales
Matemáticas pendiente de 3º ESO IES PLAYAMAR Curso 2015-2016
 Matemáticas pendiente de º ESO IES PLAYAMAR Curso -6 ºEVALUACIÓN FECHA DEL EXAMEN: 7 DE NOVIEMBRE DE A LAS : (SALÓN DE ACTOS) INSTRUCCIONES o o Las actividades realizadas deben entregarse obligatoriamente
Matemáticas pendiente de º ESO IES PLAYAMAR Curso -6 ºEVALUACIÓN FECHA DEL EXAMEN: 7 DE NOVIEMBRE DE A LAS : (SALÓN DE ACTOS) INSTRUCCIONES o o Las actividades realizadas deben entregarse obligatoriamente
Serie 5 - Problemas de enunciado
 Serie 5 - Problemas de enunciado Nombre:...Curso: 4ºD Resuelve los siguientes problemas. El proceso a seguir es como en el problema resuelto: [1º] Definir adecuadamente la(s) incógnita(s) [2º] Realizar
Serie 5 - Problemas de enunciado Nombre:...Curso: 4ºD Resuelve los siguientes problemas. El proceso a seguir es como en el problema resuelto: [1º] Definir adecuadamente la(s) incógnita(s) [2º] Realizar
PROBLEMAS ORIENTATIVOS PARA EL EXAMEN DE INGRESO AL CICLO FORMATIVO DE GRADO MEDIO
 OPERACIONES BÁSICAS CON NÚMEROS NATURALES, ENTEROS, DECIMALES Y FRACCIONES (SUMA, RESTA, MULTIPLICACIÓN Y DIVISIÓN) Y OPERACIONES COMBINADAS DE LAS ANTERIORES. 1. Realizar las siguientes operaciones con
OPERACIONES BÁSICAS CON NÚMEROS NATURALES, ENTEROS, DECIMALES Y FRACCIONES (SUMA, RESTA, MULTIPLICACIÓN Y DIVISIÓN) Y OPERACIONES COMBINADAS DE LAS ANTERIORES. 1. Realizar las siguientes operaciones con
BOLETIN Nº 5 MATEMÁTICAS 3º ESO Ecuaciones y sistemas Curso 2011/12
 BOLETIN Nº MATEMÁTICAS º ESO Ecuaciones sistemas Curso / ) ( ) ) ( ) 8 ( ) ) ) 8 ( ) ( ) ) ( )( ) ) ( )( ) ( ) ) ( ) ( ) ( ) ( ) 8) ( ) 8( ) ( ) ) ( ) ( 8) ( ) ) (8 ) ( ) ( ) ) ( ) ( ) (8 ) ) ( ) ( ) (
BOLETIN Nº MATEMÁTICAS º ESO Ecuaciones sistemas Curso / ) ( ) ) ( ) 8 ( ) ) ) 8 ( ) ( ) ) ( )( ) ) ( )( ) ( ) ) ( ) ( ) ( ) ( ) 8) ( ) 8( ) ( ) ) ( ) ( 8) ( ) ) (8 ) ( ) ( ) ) ( ) ( ) (8 ) ) ( ) ( ) (
Matemáticas. 4º Primaria Repaso Segundo Trimestre. Nombre:
 Escribe como se leen estas fracciones 1 4 6 1 6 7 1 9 9 Escribe las fracciones Dos sextos Un quinto Un medio Dos octavos Tres cuartos Cuatro tercios 40 X = + = Completa En una fracción, el indica las partes
Escribe como se leen estas fracciones 1 4 6 1 6 7 1 9 9 Escribe las fracciones Dos sextos Un quinto Un medio Dos octavos Tres cuartos Cuatro tercios 40 X = + = Completa En una fracción, el indica las partes
4. Cuáles son los dos números?
 Problemas algebraicos 1 PROBLEMAS (SISTEMAS LINEALES) 1.1 PROBLEMAS (SISTEMAS NO LINEALES) 1.- La razón de dos números es tres quintos y si aumentamos el denominador una unidad y disminuimos el numerador
Problemas algebraicos 1 PROBLEMAS (SISTEMAS LINEALES) 1.1 PROBLEMAS (SISTEMAS NO LINEALES) 1.- La razón de dos números es tres quintos y si aumentamos el denominador una unidad y disminuimos el numerador
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Potencias, radicales y logaritmos
 Potencias, radicales y logaritmos 1. Potencias de exponente natural y entero Calcula mentalmente las siguientes potencias: a) b) ( ) c) d) ( ) P I E N S A Y C A L C U L A a) 8 b) 8 c) 8 d) 8 1 Calcula
Potencias, radicales y logaritmos 1. Potencias de exponente natural y entero Calcula mentalmente las siguientes potencias: a) b) ( ) c) d) ( ) P I E N S A Y C A L C U L A a) 8 b) 8 c) 8 d) 8 1 Calcula
9. Ecuaciones de 1. er grado
 9 9. Ecuaciones de 1. er grado 1. EL LENGUAJE ALGEBRAICO PIENSA Y CALCULA Calcula el resultado de las siguientes epresiones: a) Tenía y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado
9 9. Ecuaciones de 1. er grado 1. EL LENGUAJE ALGEBRAICO PIENSA Y CALCULA Calcula el resultado de las siguientes epresiones: a) Tenía y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado
Ecuaciones e Inecuaciones. 83 Ejercicios para practicar con soluciones. 1 Resuelve las siguientes ecuaciones bicuadradas:
 Ecuaciones e Inecuaciones. 83 Ejercicios para practicar con soluciones 1 Resuelve las siguientes ecuaciones bicuadradas: 4 a) x 13x + 36 = 0 4 b) x 6x + 5 = 0 a) Realizando el cambio de variable: x = z
Ecuaciones e Inecuaciones. 83 Ejercicios para practicar con soluciones 1 Resuelve las siguientes ecuaciones bicuadradas: 4 a) x 13x + 36 = 0 4 b) x 6x + 5 = 0 a) Realizando el cambio de variable: x = z
BLOQUE III Funciones
 BLOQUE III Funciones 8. Funciones 9. Continuidad, límites y asíntotas 0. Cálculo de derivadas. Aplicaciones de las derivadas. Integrales 8 Funciones. Estudio gráfico de una función Piensa y calcula Indica
BLOQUE III Funciones 8. Funciones 9. Continuidad, límites y asíntotas 0. Cálculo de derivadas. Aplicaciones de las derivadas. Integrales 8 Funciones. Estudio gráfico de una función Piensa y calcula Indica
Ecuaciones de primer y segundo grado
 Igualdad Ecuaciones de primer y segundo grado Una igualdad se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2.
Igualdad Ecuaciones de primer y segundo grado Una igualdad se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2.
UNIDAD 7 Sistemas de ecuaciones
 Pág. 1 de 3 1 La diagonal de un rectángulo mide 37 cm, y el perímetro, 94 cm. Calcula los lados del rectángulo. 37 y + y = 94 = 37 Solución: Los lados del rectángulo miden 1 cm y 35 cm. La raíz cuadrada
Pág. 1 de 3 1 La diagonal de un rectángulo mide 37 cm, y el perímetro, 94 cm. Calcula los lados del rectángulo. 37 y + y = 94 = 37 Solución: Los lados del rectángulo miden 1 cm y 35 cm. La raíz cuadrada
CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO
 CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO Potencias y raíces. Expresa en forma de potencia: a) 7 7 7 7 = b) 8 8 8 8 8 8 8 = c) 6 6 6 6 6 = d) 5 5 5 5 = e) 9 9 9 = f) 3 3 = Calcula las siguientes potencias:
CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO Potencias y raíces. Expresa en forma de potencia: a) 7 7 7 7 = b) 8 8 8 8 8 8 8 = c) 6 6 6 6 6 = d) 5 5 5 5 = e) 9 9 9 = f) 3 3 = Calcula las siguientes potencias:
Sistema de ecuaciones e inecuaciones
 5 Sistema de ecuaciones e inecuaciones 1. Sistemas lineales. Resolución gráfica Piensa y calcula Indica, en cada caso, cómo son las rectas y en qué puntos se cortan: c) r r s P r s s Las rectas r y s son
5 Sistema de ecuaciones e inecuaciones 1. Sistemas lineales. Resolución gráfica Piensa y calcula Indica, en cada caso, cómo son las rectas y en qué puntos se cortan: c) r r s P r s s Las rectas r y s son
Sistemas de ecuaciones lineales
 José María Martíne Mediano (SM, www.profes.net) de ecuaciones lineales CTJ5. Resuelve el siguiente sistema de ecuaciones: 9 Lo resolvemos por el método de Gauss. 9 7 6 E E E E 7 6 La solución es: = ; =
José María Martíne Mediano (SM, www.profes.net) de ecuaciones lineales CTJ5. Resuelve el siguiente sistema de ecuaciones: 9 Lo resolvemos por el método de Gauss. 9 7 6 E E E E 7 6 La solución es: = ; =
NÚMEROS Y OPERACIONES
 NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
NÚMEROS Y OPERACIONES NUESTRO SISTEMA DE NUMERACIÓN Para escribir un número usamos sólo diez cifras, que son: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 El número 2 1 403.745 está formado por siete órdenes de unidades.
REPASO DE LA PRIMERA EVALUACIÓN
 REPASO DE LA PRIMERA EVALUACIÓN º ESO. Escribe todos los divisores de: 7,, 8, y Sol: a),,,, 6, 8, 9,, 8,, 6, 7 b),,,, 6, 8,, c),,, 7,, 8 d),,, 9,, d),,, 6, 9, 8, 7,. Descompón en factores primos: 800,
REPASO DE LA PRIMERA EVALUACIÓN º ESO. Escribe todos los divisores de: 7,, 8, y Sol: a),,,, 6, 8, 9,, 8,, 6, 7 b),,,, 6, 8,, c),,, 7,, 8 d),,, 9,, d),,, 6, 9, 8, 7,. Descompón en factores primos: 800,
SOLUCIONES. Matemáticas 3 EDUCACIÓN SECUNDARIA 1 3 1 1 3, 4 2,3 + : a) Expresamos N = 2,3 en forma de fracción: 10 N = 23,333 N = 2,333 21 7 = + = =
 Matemáticas EDUCACIÓN SECUNDARIA Opción A SOLUCIONES Evaluación: Fecha: Ejercicio nº 1.- a) Opera y simplifica: 1 1 1, 4, + : 5 b) Reduce a una sola potencia: 4 1 5 5 0 a) Expresamos N =, en forma de fracción:
Matemáticas EDUCACIÓN SECUNDARIA Opción A SOLUCIONES Evaluación: Fecha: Ejercicio nº 1.- a) Opera y simplifica: 1 1 1, 4, + : 5 b) Reduce a una sola potencia: 4 1 5 5 0 a) Expresamos N =, en forma de fracción:
2. Haz los dos gráficos anteriores, uno al lado del otro para facilitar su comparación. Qué conclusión te permite obtener esta gráfica?
 2. Haz los dos gráficos anteriores, uno al lado del otro para facilitar su comparación. Qué conclusión te permite obtener esta gráfica 3. Haz las dos gráficas correspondientes a las dos mezclas del segundo
2. Haz los dos gráficos anteriores, uno al lado del otro para facilitar su comparación. Qué conclusión te permite obtener esta gráfica 3. Haz las dos gráficas correspondientes a las dos mezclas del segundo
MATEMÁTICAS 2ºESO Curso: 2011-2012 ACTIVIDADES PARA ALUMNOS DE 3º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE 2º E.S.O. PRIMERA PARTE 1.
 MATEMÁTICAS ºESO Curso: 011-01 ACTIVIDADES PARA ALUMNOS DE º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE º E.S.O. PRIMERA PARTE 1. Calcula: a 6 8 1 10 6 1 1 8 + + + ( ( ( + ( ( ( + + ( ( 7 8 6 9 7 d. Realiza
MATEMÁTICAS ºESO Curso: 011-01 ACTIVIDADES PARA ALUMNOS DE º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE º E.S.O. PRIMERA PARTE 1. Calcula: a 6 8 1 10 6 1 1 8 + + + ( ( ( + ( ( ( + + ( ( 7 8 6 9 7 d. Realiza
EJERCICIOS DE MATEMÁTICAS 1º ESO
 EJERCICIOS DE MATEMÁTICAS 1º ESO Realiza estos ejercicios y entrégaselos a tu profesor de Matemáticas en septiembre antes del examen. Te servirán para repasar toda la asignatura. 1.- Calcula: a) 3 4 +
EJERCICIOS DE MATEMÁTICAS 1º ESO Realiza estos ejercicios y entrégaselos a tu profesor de Matemáticas en septiembre antes del examen. Te servirán para repasar toda la asignatura. 1.- Calcula: a) 3 4 +
