6Soluciones a los ejercicios y problemas PÁGINA 133
|
|
|
- Juan José Sosa Mendoza
- hace 8 años
- Vistas:
Transcripción
1 PÁGINA 33 Pág. P RACTICA Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = 4 3x 4y = 0 a) b) 5x + y = 0 4x + 3y = 5 x y = 4 a) ( ) = 5? 4 No es solución. 5x + y = 0 5 = 9? 0 3x 4y = 0 3 4( ) = 0 b) Sí es solución de este sistema. 4x + 3y = ( ) = 5 Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución x = 3, y = /: x 3x + y = + y = a) b) x 4y = x y = x + y = ( ) = 9 = a) x 4y = 3 4( ) = 3 + = 5 3 x = + y = b) 7 x y = 3 + = 3 a) Busca dos soluciones de la ecuación 3x y =. b) Representa gráficamente la recta 3x y =. c) Un punto cualquiera de la recta es solución de la ecuación? a) 3x y = Si x = : 3 y = y = Si x = 0: 3 0 y = y = b) Y (, ) 3 4 X (0, ) x + y = 7 x y = 3x + y = x 4y = 5 c) Todos los puntos de la recta son soluciones de la ecuación.
2 4 a) Representa gráficamente en los mismos ejes las dos rectas siguientes: x + y = 3 x y = 3 b) Di cuál es la solución de este sistema: x + y = 3 x y = 3 a) x + y = 3 x y = 3 x 0 y 3 x 0 y 3 Y x + y = 3 (, ) x y = 3 X Pág. x + y = 3 b) x y = 3 La solución del sistema es x =, y =, que corresponde al punto de corte de ambas rectas. 5 Resuelve gráficamente los siguientes sistemas de ecuaciones: 3x y = 3x y = 0 x + 3y = 5 x 3y = 4 a) b) c) d) x +y = 5 3x + y = 6 x y = 4 x +y = 3x y = a) x +y = 5 3x y = x +y = 5 x 0 y Solución: x =, y = x y 3 Y 3 P(, ) X 3x y = 0 b) 3x + y = 6 3x y = 0 3x + y = 6 Y X x 0 y 0 3 x 0 y 6 0 P(, 3) Solución: x =, y = 3 x + 3y = 5 c) x y = 4 x + 3y = 5 x y = 4 x y Solución: x =, y = x 0 y 4 Y P(, ) X
3 x 3y = 4 d) x +y = x 3y = 4 x +y = x y 0 Solución: x =, y = 0 x 6 y 0 Y 4 6 X Pág. 3 6 Resuelve por sustitución. x + 3y = 0 a) b) x + y = 5 7x y = 6 x + 6 = y c) d) 4x +3y = 3 y 3x = 6 a) 6y + y = 5 5y = 5 y = x = 3 = 3 Solución: x = 3, y = x 3y = 5 b) x 5y = 7 x = 7 + 5y ( 7 + 5y) 3y = y 3y = 5 37y = y = 3 x = = Solución: x =, y = 3 c) x + 3y = 0 x + y = 5 7x y = 6 4x +3y = 3 4x + x + = 3 5x = 5 x = 5 = y = = 9 ( 5 ) 5 Solución: x = 3, y = x + 6 = y d) y 3x = 6 x = 3y ( 3y)+y = 5 7x +6 = y 4x + 3(7x + 6) = 3 x + 6 y = = x + (x + ) 3x = 6 x 3y = 5 x 5y = 7 x + 6 3x = 6 x = 0 x = 0 y = Solución: x = 0, y =
4 7 Resuelve por igualación. a) x = 4 x y = 6 Pág. 4 x +3y = 4 b) x y = 6 c) y = 6x 7x = y 5 3x 4y = 4 d) x + y = x = 4 x = 4 a) 6 + y = 4 y = x y = 6 x = 6 + y Solución: x = 4, y = x +3y = 4 x = 4 3y b) 4 3y = 6 + y 4 6 = 5y x y = 6 x = 6 + y y = x = 4 3( ) = Solución: x =, y = y = 6x y = 6x c) 7x + 5 6x = 7x + 5 x = 7x + 5 5x = 5 7x = y 5 y = x = y = 6 = 6 Solución: x =, y = 6 3x + 4 3x 4y = 4 y = d) 4 3x + 4 = x 3x + 4 = 4 x x + y = 4 y = x x = x = y = = 5 ( ) Solución: x =, y = 5
5 Resuelve por reducción. x + y = 0 3x y = 0 a) b) x y = 3x + y = 6 Pág. 5 4x 3y = x + y = c) d) x + y = 4 3x y = 7 x 3y = e) f) 3x +6y = a) x + y = 0 x y = x = x =, y = Solución: x =, y = 3x y = 0 b) 3x + y = 6 6x = 6 x =, y = 3 Solución: x =, y = 3 4x 3y = 4x 3y = c) x + y = 4 6x + 3y = 0x = 0 x = ( ) + y = 4 y = Solución: x =, y = x + y = x + y = d) 7x = 5 x = 5 5 +y = 3x y = 7 6x y = y = 5/7 = 4 7 Solución: x = 5, y = x 3y = x 6y = e) 5x = 4 x = 4 4 3y = 3x +6y = 3x +6y = 5 5 Solución: x = 4, y = 5 5 3x + y = 3 3x + y = 3 f) x = 3 4 = + y = 7 x + y = 7/6 x y = 4/ Solución: x =, y = 3 y = 4/5 = 3 5 3x + y = 3 x + y = 7/6 y = 7 = 6 3
6 9 Resuelve estos sistemas por el método que consideres más adecuado: a) x y = 4x 3y = Pág. 6 3x = + y b) 3 + y = 0x c) d) x +5y = 4x 3y = 3x y = x + 4y = 5/3 x y = x = + y a) Por sustitución: 4x 3y = 4( + y) 3y = 4 + 4y 3y = y = 4 x = + 4 = 5 Solución: x = 5, y = 4 3x = + y b) Por sustitución: 3 + y = 0x 3 + 6x = 0x = 4x x = y = 3 = Solución: x =, y = 4 4 x +5y = 4x 0y = c) Por reducción: 4x 3y = 4x 3y = 3y = 0 y = 0 x = x = Solución: x =, y = 0 3x y = 6x 4y = 4 d) Por reducción: x + 4y = 5/3 x + 4y = 5/3 y = 3x 3 + (3x ) = 0x 7x = 7 x = 3 y = y = y = Solución: x =, y = 3
7 6Soluciones a los ejercicios y problemas 0 Resuelve los sistemas siguientes: a) x y = 4 b) 3 x y + = 4 c) d) x + y = 0 5x 3 = 9y 3 (3x ) = y 3(x + y) + (x y) = y x + = 4 3 x y = 5 Pág. 7 x + y = 0 a) Por sustitución: y = x 5x 3 = 9( x) 3 5x 3 = 9y 3 5x 3 = x 3 3x = 0 x = 0 y = 0 = 0 Solución: x = 0, y = 0 x y = 4 x 3y = 4 b) 3 x 3y = 4 Por reducción: x y x + y = x y = + = 4 4y = 6 y = 4 x 3( 4) = 4 x = x = 6 Solución: x = 6, y = 4 (3x ) = y c) 3(x + y)+(x y) = Por reducción: x = x = 6 y = 3 y = 3 Solución: x =, y = 3 y x + = 4x + y = 6 d) 4 4x + y = 4 Por reducción: 3 x 3y = 0 x 3y = 0 x y = 5 6x 4 = y 3x +3y +x y = 5x + y = 6x y = 3 5x + y = x + 3y = 4x = x = 3 y = 5 y = 5 = x 3y = 0 3/ Solución: x =, y =
8 Observa las ecuaciones que forman los siguientes sistemas y di cuál de ellos tiene una única solución, cuál no tiene solución y cuál tiene infinitas soluciones. Compruébalo representando las rectas que los forman: x y = x y = 5 5x + y = x y = 5 a) b) c) d) 4x y = x 4y = 0 4x y = 7 x 4y = 3 Pág. x y = a) 4x y = No tiene solución x y = 4x y = x y = 4 x 0 y 3 x 0 y 4 0 Y X x y = 5 b) x 4y = 0 Tiene infinitas soluciones x y = 5 x 4y = 0 x y = 5 x 3 y Es la misma recta Y 3 X 5x + y = c) 4x y = 7 Tiene una solución, x =, y = 3. 5x +y = 4x y = 7 x y 3 x y 3 Y 3 P(, 3) X x y = 5 d) No tiene solución x 4y = 3 Y x y = 5 x 4y = 3 x y 3 x 3 y 5/4 9/4 X Completa los siguientes sistemas de modo que el primero tenga la solución x = 3, y = ; el segundo sea incompatible y el tercero y el cuarto sean indeterminados: 3x + y = x + y = 5 3x y = 4 x +y = 7 a) b) c) d) y = x +y = 6x 4y = 4y = 3x + y = ( ) = 5 a) Solución: y = = + y = = 6 3x +y = 5 6x y =
9 x + y = 5 b) Puede ser cualquier número distinto de 0. x +y = Pág. 9 Por ejemplo: x + y = 5 x +y = 3x y = 4 c) 6x 4y = x + y = 7 d) 4y = 3x y = 4 6x 4y = x + y = 7 x 4y = 4 PÁGINA 34 3 Representa los pares de rectas correspondientes a cada sistema y di si son equivalentes: a) x + y = 3 x y = 3 y + = 0 b) 3x 4y = 0 x + y = 3 a) x y = 3 x + y = 3 x y = 3 x 0 y 3 Solución: x =, y = x 0 y 3 Y (, ) X y + = 0 b) 3x 4y = 0 y = 3x 4y = 0 x 0 y,5 Y X Solución: x =, y = Los sistemas son equivalentes, porque tienen la misma solución.
10 4 Resuelve los siguientes sistemas de ecuaciones, aplicando dos veces el método de reducción para despejar cada una de las incógnitas: 3x y = 5 9x 3y = 54 a) b) 7x 4y = 9 x 7y = Pág. 0 3x y = 5 9x 56y = 05 a) 6y = y = 7x 4y = 9 9x + y = 7 x y = 0 6x = 3 x = 56x + y = 7 Solución: x = 3, y = 9x 3y = 54 99x 43y = 594 b) 0y = 396 y = 99 x 7y = 99x + 63y = x 9y = 37 0x = 9 x = 3 43x +9y = 6 0 Solución: x = 3, y = Resuelve los siguientes sistemas de ecuaciones. Para ello, simplifica previamente las ecuaciones que los forman: x + y = a) 3 b) x + y + = 3 6 x 3 + y + = c) 3 6 d) 3x + y = 6 9 x + + y = 3 x 3 + y = 4 x y + + = 4 x y + = 6 x + y = x +3y = 3 a) 3 x +3y = 3 x + y (x + ) + y = 6 x + y = 7 + = 3 6 x + 3y = 3 y = 4 y = x y = 7 x + = x = 3 = 9 3 /3 Solución: x = 9, y = 3
11 x + + y = b) 3 x + +3y = 3 x + 3y = x 3 x 3 + y = 4 x +y = 7 + y = 4 x + 3y = 5y = 5 y = x y = 7 x + + = x = 3 Solución: x =, y = Pág. x 3 + y + = ( x) y = c) 3 6 3x + y 3( 3x) ( + y) = 36 = x y = x + y = 5 4 9x 4 y = 36 9x y = 6 Solución: x =, y = 4x +y = 0 3x = 6 x = 9x y = 6 ( ) y = 3 + y = y = y = 6 3 x y + + = d) 4 (x ) + y + = 4 x y + 3(x ) (y + ) = 6 = 6 x + y + = 4 x + y = 5 6x 3 y = 6 6x y = 0 Solución: x =, y = 4x +y = 0 0x = 0 x = 6x y = 0 + y + = y + = y = 4 4
12 6 Resuelve los siguientes sistemas. Indica si alguno de ellos es incompatible o indeterminado. a) b) c) x 5y = 3,5x,5y = 0,x,7y = 6, 3x + y = 9 3(x ) + y = 0 3(x +)+y = 5 x + y = 4 y d) 3x 5 = 7 6y Pág. x 5y = x 5y = a) Por reducción: 3,5x,5y = 6,5x + 5y = 6 4,5x = x = 4 4 5y = 0 = 5y y = Solución: x = 4, y = 0,x,7y = 6, b) Por sustitución: y = 9 3x 3x + y = 9 0,x,7 9 3x = 6, 0,x 5,3 5,x ( = 6, ) 0,4x 5,3 + 5,x =, 5,5x = 7,5 x = 5 y = = 3 Solución: x = 5, y = 3 3(x ) + y = 0 3x 3 + y = 0 c) 3(x +)+y = 5 3x +3 +y = 5 No tiene solución. Es incompatible. x + y = 4 y x +y = 4 d) 3x 5 = 7 6y 3x +6y = Tiene infinitas soluciones. Es indeterminado. 3x + y = 3 3x + y = P IENSA Y RESUELVE 7 Halla dos números tales que su suma sea 60, y su diferencia, 34. Llamamos x e y a los números. x + y = 60 x = 94 x = y = 60 y = 63 x y = 34 Los números son 97 y 63.
13 Por dos bolígrafos y tres cuadernos he pagado 7,0 ; por cinco bolígrafos y cuatro cuadernos, pagué 3,. Cuál es el precio de un bolígrafo? Y de un cuaderno? x es el precio de un bolígrafo e y es el precio de un cuaderno. x +3y = 7,0 5x +4y = 3, 7,0 3y x = 7,0 3y 5 ( ) +4y = 3, Pág y +y = 6,4 7y =,6 y =, x = 7,0 3, =, Un bolígrafo cuesta,, y un cuaderno,,. 9 Un librero ha vendido 45 libros, unos a 3 y otros a. Obtuvo por la venta 36. Cuántos libros vendió de cada clase? x son los libros de 3 e y son los de. x + y = 45 y = 45 x 3x +y = 36 3x + (45 x) = 36 3x + 60 x = 36 4x = 0 x = 7 y = 45 7 = Vendió 7 libros de 3 y libros de. 0 En un corral hay conejos y gallinas que hacen un total de 9 cabezas y 9 patas. Cuántos animales hay de cada clase? x es el número de gallinas, e y, el de conejos. x + y = 9 y = 9 x x + 4y = 9 x + 4(9 x) = 9 x + 6 4x = 9 x = 4 x = y = 9 = 7 Hay gallinas y 7 conejos. Un examen tipo test consta de 50 preguntas y hay que contestar a todas. Por cada acierto se obtiene un punto y por cada fallo se restan 0,5 puntos. Si mi nota ha sido 4,5, cuántos aciertos y cuántos fallos he tenido? x es el número de aciertos, e y, el de fallos. x + y = 50 x y = 50,5y = 5,5 y = 7 x = 33 x 0,5y = 4,5 x 0,5y = 4,5 He tenido 33 aciertos y 7 fallos.
14 Una cooperativa ha envasado 000 l de aceite en botellas de,5 l y l. Si ha utilizado 00 botellas, cuántas se han necesitado de cada clase? x son las botellas de,5 l, e y, las de l. x + y = 00 x y = 00,5x +y = 000,5x +y = 000 0,5x = 00 x = 400 y = = 700 Se han utilizado 400 botellas de,5 l y 700 de l. Pág. 4 3 Halla dos números naturales tales que su suma sea 54, y su cociente,. 3 Llamamos x e y a los números. x + y = 54 y = 54 x x 3x = (54 x) 3x = 3 x = 3x = y y 3 x = 3 x = y = 54 = 4 Los números son y 4. 4 Halla dos números naturales que suman 40 y tales que al dividir el mayor entre el menor obtenemos de cociente y 4 de resto. Recuerda: Dividendo = divisor Ò cociente + resto. Los números son x e y. x + y = 40 y y = 40 3y = 6 y = 4 x = y +4 x = = 9 9 y 4 son los números buscados. 5 La suma de las edades de una madre y su hijo es 56 años. Hace 0 años, la edad de la madre era el quíntuple de la edad que tenía el hijo. Cuál es la edad actual de cada uno? HOY HACE 0 AÑOS MADRE x x 0 HIJO y y 0 56 x 0 = 5(y 0) x + y = 56 x + y = 56 y = 56 x x 0 = 5(y 0) x 0 = 5y 50 x 0 = 5(56 x) 50 x 0 = 0 5x 50 6x = 40 x = 40 y = = 6 La madre tiene 40 años, y el hijo, 6 años.
15 6 Hace tres años la edad de Nuria era el doble de la de su hermana Marta. Dentro de 7 años, será los 4 de la que entonces tenga Marta. Calcula la edad actual de cada 3 una. Pág. 5 x 3 = (y 3) 4 x +7 = (y +7) 3 HOY HACE 3 AÑOS DENTRO DE 7 AÑOS NURIA x x 3 x + 7 MARTA y y 3 y +7 x 3 = y 6 x = y 3 3x + = 4y + 3(y 3) 4y = 7 6y 9 4y = 7 y = 6 y = x = 3 Nuria tiene 3 años, y Marta, años. 7 La base menor de un trapecio isósceles mide 6 m y la base mayor mide lo mismo que los lados iguales juntos. Si el perímetro del trapecio es 3 m, cuánto mide cada lado? x 6 y x y = x 6 + x + y = x +x = 3 4x = 3 x = m y = 6 m La base mayor mide 6 m, y los lados oblicuos, m, respectivamente. He cambiado un montón de monedas de 0 céntimos por monedas de, de manera que ahora tengo 4 monedas menos que antes. Cuántas monedas de 0 céntimos tenía? Tengo x monedas de 0,0. El número de monedas de es y. x 0, = y 0,x = x 4 4 = 0,x x = 30 y = 30 4 = 6 y = x 4 Tenía 30 monedas de 0, y las he cambiado por 6 monedas de. 9 Si Álvaro regala a Rita 4 de sus discos, ella tendrá el doble que él. Si Rita da 6 de sus discos a Álvaro, entonces será él el que tenga el doble que ella. Cuántos discos tiene cada uno? Discos de Álvaro: x Discos de Rita: y (x 4) = y +4 x = y + 4 y = x x + 6 = (y 6) x + 6 = y x + 6 = (x ) x + 6 = 4x 4 3x = 4 x = 4 y = 4 = 6 Álvaro tiene 4 discos, y Rita, 6.
16 PÁGINA Problema resuelto He pagado 55,7 por una camiseta y un pantalón que costaban 70 entre los dos. En la camiseta me han hecho un % de descuento, y en el pantalón, un %. Cuál era el precio original de cada artículo? La camiseta vale x; con la rebaja del % pago 0,x. El pantalón vale y; con la rebaja del % pago 0,7y. Por tanto: x + y = 70 y = 70 x 0,x + 0,7y = 55,7 0,x + 0,7(70 x) = 55,7 0,x + 54,6 0,7x = 55,7 0,04x =, x = y = 70 = 4 La camiseta vale, y el pantalón, = 70 Comprobación:,96 + 3,76 = 55,7 Pág. 6 3 Por unos zapatos y una chaqueta he pagado 6. Si el precio de los zapatos aumentara en un 4%, entonces sería igual al 75% del precio de la chaqueta. Cuánto he pagado por cada uno? Precio de los zapatos: x; precio de la chaqueta: y ; x + y = 6 y = 6 x,4x = 0,75y,4x = 0,75(6 x),4x = 94,5 0,75x,9x = 94,5 x = 50 y = 76 He pagado 50 por los zapatos y 76 por la chaqueta. 3 Los alumnos de un centro escolar son 40 entre ESO y Bachillerato. El 4% de ESO y el 5% de Bachillerato son chicas, lo que supone un total de 96 mujeres. Calcula cuántos estudiantes hay en ESO y cuántos en Bachillerato. x es el número de alumnos de ESO e y los de Bachillerato. x + y = 40 y = 40 x 0,4x + 0,5y = 96 0,4x + 0,5(40 x) = 96 0,4x 0,5x = 96,4 0,x =,4 x = 4 y = 40 4 = 96 Son 4 alumnos en la ESO y 96 en Bachillerato.
17 33 Un comerciante compró 35 juegos de un tipo y 5 de otro pagando por ellos 0. Con la venta de los primeros ganó un 5% y con los segundos perdió el 5%, de forma que obtuvo 70 de ganancia sobre el precio de compra. Calcula el precio de compra de cada tipo de juego. Precios de compra de cada tipo de juego: x e y. 35x + 5y = 0 7x +5y = 44,5 35x + 0,95 5y = ,75x + 3,75y = 390 y = 44 7x 43,75x x = ( 5 ) 43,75x ,5x = 390 0,5x = 3 x = y = 44 7 = 5 Los precios de compra fueron y, respectivamente. Pág Problema resuelto Un autobús sale de A a 90 km/h. Cuando ha recorrido 5 km, sale de A un coche a 0 km/h que quiere alcanzar al autobús. Cuánto tiempo tarda en hacerlo y qué distancia recorre hasta conseguirlo? A AUTOBÚS: 90 km/h 5 km x B A COCHE: 0 km/h 5 + x B Sabemos que espacio = velocidad tiempo. x = 90t 5 + x = 0t Tarda,5 h y recorre 37,5 km t = 0t 0t = 5 t =,5 x =,5 35 Un tren regional sale de una estación a 5 km/h. Media hora más tarde sale otro más rápido en la misma dirección a 0 km/h. Calcula el tiempo que tardará en alcanzarlo y la distancia recorrida hasta lograrlo. t : tiempo que tarda en alcanzarlo. x : distancia que recorre el tren regional hasta el alcance. 4,5 5 km/h ESPACIO VELOCIDAD TIEMPO AUTOBÚS x 90 t COCHE 5 + x 0 t x + 4,5 x 5 0,5 = 4,5
18 x = 5t 5t + 4,5 = 0t 5t = 4,5 x + 4,5 = 0t t =,7 x = 44,5 44,5 + 4,5 = 7 Tarda h 4 min y recorre 7 km. Pág. 36 Dos ciudades, A y B, distan 34 km. De A sale un autobús en dirección a B y simultáneamente sale de B un tren en dirección a A. Tardan en cruzarse hora y 30 minutos. Cuál es la velocidad de cada uno sabiendo que la del autobús supera a la del tren en 5 km/h? A v x x v B x = v,5 34,5v =,5v 7,5 34 x = (v + 5),5 34 7,5 = 3v v = 6,5 = 75,5 km/h 3 El tren va a 75,5 km/h, y el autobús, a 0,5 km/h. 37 Un automóvil tarda dos horas en recorrer la distancia entre dos ciudades. Si su velocidad hubiera sido superior en 30 km/h, habría tardado una hora y cuarto. Cuál es la distancia entre las dos ciudades? x es la distancia que tiene que recorrer y v la velocidad que lleva. x = v v =,5v + 37,5 0,75v = 37,5 x =,5(v + 30) v = 50 km/h x = 50 = 00 La distancia es 00 km. 3 Un autobús escolar hace la ruta entre dos pueblos, A y B. Cuando va con niños, lleva una velocidad media de 60 km/h y tarda un cuarto de hora más que si va vacío con una velocidad de 00 km/h. Cuál es la distancia entre A y B? 60 km/h x 00 km/h x = 60t 60t = 00t 5 40t = 5 x = 00(t 0,5) t = 0,65 x = 60 0,65 = 37,5 La distancia entre A y B es 37,5 km. 39 Hemos mezclado aceite de oliva de 3,5 /l con aceite de girasol de /l para obtener 50 l de mezcla a 3,0 /l. Calcula la cantidad de aceite de oliva y de aceite de girasol que hemos mezclado.
19 Pág. 9 CANTIDAD PRECIO OLIVA x 3,5 GIRASOL y MEZCLA 50 3,0 x + y = 50 y = 50 x 3,5x +y = 50 3,0 3,5x + (50 x) = 54 3,5x + 00 x = 54,5x = 54 x = 36 y = 4 36 l de aceite de oliva y 4 l de girasol. 40 Si en un depósito que contiene agua a 50 C añadimos agua a 5 C, obtenemos 50 l a 36 C. Cuántos litros había en el depósito y cuántos hemos añadido? x son los litros de agua que había en el depósito. y son los litros que hemos añadido. x + y = 50 y = 50 x 50x + 5y = x + 5(50 x) = x x = x = 3 50 x = 90 y = = 60 Había 90 l de agua a 50 y hemos añadido 60 l de agua a 5. 4 Problema resuelto Las dos cifras de un número suman 7. Si invertimos el orden de estas, obtenemos otro número que es igual al doble del anterior más unidades. Cuál es el número inicial? Cifra de las decenas: x Cifra de las unidades: y Número inicial: 0x + y Número invertido: 0y + x. a condición: x + y = 7. a condición: 0y + x = (0x + y)+ x + y = 7 x + y = 7 0y + x = (0x + y)+ 0y + x = 0x +y + El número buscado es 5. y = 7 x 0(7 x)+x = 0x + (7 x) x + x = 0x + 4 x + 7x = 54 x = y = 5
20 PÁGINA 36 Pág. 0 4 Un número de tres cifras es capicúa y sus cifras suman 0. Si a dicho número le sumamos 0 veces la cifra de las decenas, el resultado es 6. Cuál es el número? x es la cifra de las unidades. y es la cifra de las decenas. x es la cifra de las centenas. x + y = 0 y = 0 x 00x + 0y + x +0y = 6 0x + 0(0 x) = 6 0x x = 6 6x = 6 x = y = 0 = El número es. 43 Si a un número de dos cifras le restamos el que resulta de invertir el orden de estas, obtenemos el doble de la cifra de las decenas del número inicial. Halla dicho número sabiendo que sus cifras suman 6. x es la cifra de las decenas. y es la cifra de las unidades. x + y = 6 y = 6 x (0x + y) (0y + x) = x 0x + 6 x 0(6 x) x = x 0x + 6 x x x = x 6x = 44 x = 9 y = 7 El número es 97. R EFLEXIONA SOBRE LA TEORÍA 44 Escribe un sistema de dos ecuaciones con dos incógnitas cuya única solución sea x =, y =. 3x +y = 4 x y = ( ) = 4 x =, y = es solución. ( ) = 3 45 Comprueba si x = 3, y = es solución de alguno de estos sistemas de ecuaciones: x + y = 4 x y = a) x y = b) x 3y = 3 x 6y = 0 x + y = 5 x + y = = 4 a) x y = 3 = x = 3, y = es la solución de ese sistema. x 6y = = 0
21 x y = 3 = b) x 3y = = 3 x = 3, y = no es solución de ese sistema. x + y = = 4? 5 Pág. 46 Observa la representación de las rectas r, r, r 3 y responde sin resolver. r y x = 0 5y x = r r 3 x + y = a) Cuál es la solución de los siguientes sistemas de ecuaciones?: y x = 0 I) II) x +y = b) Cuál es la solución de este sistema?: y x = 0 5y x = x + y = 5y x = y x = 0 a) I) Solución: x = 7, y = 3 II) Solución: x = 7, y = 3 b) Solución: x = 7, y = 3 47 Observa la representación de las rectas r, r, r 3 y responde sin resolver. 4 r 3 : 7y x = 6 4 r : x y = 4 r : x + y = 0 a) Cuál es la solución de los sistemas siguientes?: x + y = 0 x + y = 0 x y = I) II) III) x y = 7y x = 6 7y x = 6
22 b) Tiene alguna solución este sistema?: x + y = 0 x y = 7y x = 6 Pág. x + y = 0 a) I) x y = Solución: x =, y = x + y = 0 II) 7y x = 6 Solución: x =, y = x y = III) 7y x = 6 Solución: x = 5, y = 3 b) No, porque las tres rectas no tienen ningún punto en común. 4 Considera este sistema: 3x +y = 5 ax + by = 5 Qué valores deben tomar a y b para que el sistema tenga infinitas soluciones? Busca tres soluciones del sistema. Para que tenga infinitas soluciones, la segunda ecuación debe ser proporcional a la primera. 3x + y = 5 Así: a = 9 y b = 6 ax + by = 5 Soluciones: Damos valores a x para obtener puntos de la recta 3x +y = 5: x =, y = ; x = 0, y = 5 ; x =, y = 4 49 Observa el sistema de ecuaciones siguiente: 3x +y = c 6x +4y = d Qué condición deben cumplir c y d para que el sistema no tenga solución? El sistema no tendrá solución cuando las dos rectas sean paralelas, es decir, cuando d? c. 50 Cuál debe ser el valor de m para que los sistemas a) y b) sean equivalentes? x 3y = x y = m a) b) x + y = y = 3 La solución de a) es x = 5, y = 3. b) debe tener la misma solución: 5 3 = m m =
23 PÁGINA 37 Pág. 3 PROFUNDIZA 5 Ejercicio resuelto x y = Resolver por sustitución: x + y = 5 Despejamos y en la. a ecuación y sustituimos en la. a : y = x x +(x ) = 5 5x x 4 = 0 ± x = = ± 3 x = x = /5 Si x = 4, y = 4 = 6. Si x =, y = = 34 ( ) Resuelve por sustitución. x + y = 4 y x = 0 a) b) x + y = 7 x + y = 47 x y = x + y = c) d) x y = 6 x y = x + y = 4 a) x + y = 7 y = 4 x x + 4 x = 7 x ± x 3 = 0 x = = Si x = 3, y = 4 3 =. Si x =, y = 4 ( ) = 6. ± 4 x = 3 x = y x = 0 b) x + y = 47 Si x = 7, y = 7. Si x = 7, y = 7. y = x x + x = 47 3x = 47 x = 49 x = 7 x = 7 x y = y = x c) x y = 6 x (x ) = 6 x x + 4x 4 = 6 4x = 0 x = 5 y = 3 Solución: x = 5, y = 3
24 x + y = y = x d) x y = x ( x) = x + x x = x + x 3 = 0 ± 4 + x = x = = ± 4 x = 3 Si x =, y = 0. Si x = 3, y = ( 3) = 4. Pág La diferencia de dos números es, y la de sus cuadrados, 0. Halla esos números. Los números son x e y. x y = x = + y x y = 0 ( + y) y = y + y y = 0 4y = 6 y = 4 x = 6 Los números son 6 y Halla dos números cuya suma es, y la de sus cuadrados, 0. Los números son x e y. x + y = y = x x + y = 0 x + ( x) = 0 x x + x = 0 x 4x + 64 = 0 x x + 3 = 0 ± x = = Si x =, y = 4. Si x = 4, y =. Los números son y 4. ± 4 x = x = 4 55 La diagonal de un rectángulo mide 5 cm, y su perímetro, 4 cm. Calcula sus lados. x +y = 4 x + y = 5 x + y = x + y = 5 5 x y y = x x + ( x) = 5 x x + x = 5 x 4x + 6 = 0 x x + 0 = 0 ± x = x = = ± 3 x = 9 Si x =, y = = 9. Si x = 9, y = 9 =. Los lados del rectángulo miden 9 cm y cm, respectivamente.
25 56 El perímetro de un rectángulo es 6 m, y su área, 40 m. Halla sus lados. y Pág. 5 x + y = 6 xy = 40 x + y = 34 y = 34 x xy = 40 x (34 x) = 40 34x x = 40 x 34x = 40 = 0 x 34 ± 34 x = 40 4 = 34 ± 4 Si x = 0, y = 34 0 = 4. Si x = 4, y = 34 4 = 0. Los lados del rectángulo miden 0 cm y 4 cm, respectivamente. x = 4 x = 0 57 Las diagonales de un rombo se diferencian en 6 cm y su área es 56 cm. Calcula la medida de las diagonales. x x y = 6 x = 6 + y x y = 56 (6 + y)y = 6y + y = y +6y = 0 6 ± y = y = = 6 ± y = 4 (No vale). Si y =, x = 6 + = 4. Las diagonales miden cm y 4 cm, respectivamente. y 5 El perímetro de un triángulo isósceles es 36 m. La altura relativa al lado desigual mide m. Calcula la medida de los lados iguales. Si llamas x a la mitad de la base, se simplifican los cálculos. y y x x x +y = 36 x + y = y = x y x = y x = 44 ( x) x = x + x x = 44 36x = 0 x = 5 y = 5 = 3 Los lados iguales miden 3 cm.
26 59 Los lados de un triángulo miden 5 cm, 7 cm y 0 cm, respectivamente. Calcula la altura relativa al lado más largo y halla el área del triángulo. Ten en cuenta que la altura h divide al triángulo original en dos triángulos rectángulos. Pág. 6 5 h 7 x 0 x h + x = 5 h + (0 x) = 7 h + x = 5 h x + x = 49 h = 5 x 5 x x + x = 49 0x = 76 x = 3, h = 5 3, = 0,56 3,5 cm A = 0 3,5 = 6,5 La altura mide 3,5 cm, y el área, 6,5 cm. 60 En una parcela rectangular de 60 m de perímetro se hace un jardín rectangular bordeado por un camino de m de ancho. Calcula las dimensiones de la parcela sabiendo que el área del jardín es m. x y x +y = 60 (x 4)(y 4) = x + y = 30 xy 4x 4y + 6 = y = 30 x x (30 x) 4x 4(30 x) + 6 = 30x x 4x 0 + 4x + 6 = x +30x 6 = 0 x 30x + 6 = 0 30 ± 30 x = 4 6 = = 30 ± 6 x = y = x = y = Las dimensiones de la parcela son m y m, respectivamente.
27 6 Varios amigos se van a repartir un premio de 00 a partes iguales. Dos de ellos deciden renunciar a su parte y de esta forma los demás reciben 0 más cada uno. Cuántos amigos son? Cuánto recibe cada uno? Son x amigos; y es el dinero que corresponde a cada uno. xy = 00 (x )(y + 0) = 00 xy = 00 xy +0x y 40 = 00 Pág y = x x + 0x 40 = 00 x x x = 00 x 0x x = 0 x x 0 = 0 ± x = +4 0 = ± x = 0 x = No vale. x = 0 y = 00 = 0 0 Son 0 amigos. Como renuncian a su parte, a los restantes les corresponde Si la base de un rectángulo disminuye cm y la altura aumenta 4 cm, se convierte en un cuadrado. Si la base disminuye 4 cm y la altura aumenta cm, su área disminuye cm. Calcula los lados del rectángulo. x 4 y + y x = y +4 x = y +6 (x 4)(y + ) = xy xy + x 4y = xy (y + 6) 4y = y + 4y = y = 6 y = x = 4 Los lados del rectángulo miden cm y 4 cm, respectivamente. x
28 63 Resuelve este sistema de tres ecuaciones y dos incógnitas y comprueba gráficamente su solución: x + y = x y = 5 x + y = Halla la solución de las dos primeras ecuaciones y comprueba si verifica la tercera. Pág. x + y = x y = 5 x + y = x + y = 3x = 6 x = y = 4 = 3 x y = 5 Comprobamos si se verifica la tercera ecuación: + ( 3) = La solución del sistema es x =, y = Resuelve los siguientes sistemas de ecuaciones: x 3 = 0 3x y + z = 4 x + y = z x + y = 5 a) x 3y = 9 b) x + y = 5 c) x y = z d) x + y + z = 3 x + y z = z 3 = x + z = 4 y + z = x 3 = 0 x = 3 a) x 3y = 9 3 3y = 9 3y = 3 y = x + y z = 3 + ( ) z = z = z = Solución: x = 3, y =, z = 3x y + z = 4 3x y + 4 = 4 b) x + y = 5 x + y = 5 z 3 = z = 4 3x y = 0 3x y = 0 x + y = 5 x +y = 0 5x = 0 x = + y = 5 y = 3 Solución: x =, y = 3, z = 4 x + y = z x + y = z c) x y = z x = z x = z z + z = 4 x y = z x + z = 4 z = 4 z = + y = y = 0 Solución: x =, y = 0, z = x + y = 5 x = 5 y x = 5 4 = d) x + y + z = 3 5 y + y + z = 3 z = y + z = y + z = y + ( ) = y = 4 Solución: x =, y = 4, z =
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 5 PRACTICA Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución =, =. + 7 = + = a) b) 4 = Sustituimos en cada ecuación =, = operamos: + = a) b) 4 = 0 Comprueba si
Pág. Página 5 PRACTICA Completa los siguientes sistemas de ecuaciones para que ambos tengan la solución =, =. + 7 = + = a) b) 4 = Sustituimos en cada ecuación =, = operamos: + = a) b) 4 = 0 Comprueba si
5Soluciones a los ejercicios y problemas PÁGINA 114
 5Soluciones a los ejercicios y problemas PÁGINA 4 Pág. P RACTICA Ecuaciones: soluciones por tanteo Es o solución de alguna de las siguientes ecuaciones? Compruébalo. a) 5 b) 4 c) ( ) d) 4 4 a)? 0? 5 no
5Soluciones a los ejercicios y problemas PÁGINA 4 Pág. P RACTICA Ecuaciones: soluciones por tanteo Es o solución de alguna de las siguientes ecuaciones? Compruébalo. a) 5 b) 4 c) ( ) d) 4 4 a)? 0? 5 no
EJERCICIOS DE SISTEMAS DE ECUACIONES
 EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
EJERCICIOS DE SISTEMAS DE ECUACIONES Ejercicio nº 1.- a) Resuelve por sustitución: 5x y 1 3x 3y 5 b) Resuelve por reducción: x y 6 4x 3y 14 Ejercicio nº.- a) Resuelve por igualación: 5x y x y b) Resuelve
Sistemas de dos ecuaciones lineales con dos incógnitas
 Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
Sistemas de dos ecuaciones lineales con dos incógnitas Una ecuación lineal con dos incógnitas es una epresión de la forma a b c donde a, b c son los coeficientes (números) e son las incógnitas. Gráficamente
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
Pág. Página 9 PRACTICA Sistemas lineales Comprueba si el par (, ) es solución de alguno de los siguientes sistemas: x + y 5 a) x y x y 5 x + y 8 El par (, ) es solución de un sistema si al sustituir x
Sistemas de ecuaciones lineales
 7 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica a) En qué punto se cortan la gráfica roja la azul del dibujo de la izquierda? b) Tienen algún punto en común las rectas de la
7 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica a) En qué punto se cortan la gráfica roja la azul del dibujo de la izquierda? b) Tienen algún punto en común las rectas de la
6Soluciones a los ejercicios y problemas
 PÁGINA Pág. P R A C T I C A Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = x y = 0 a) b) 5x + y = 0 x + y = 5 x y = a) ( ) = 5? No es solución. 5x + y = 0 5 = 9? 0 x
PÁGINA Pág. P R A C T I C A Comprueba si x =, y = es solución de los siguientes sistemas de ecuaciones: x y = x y = 0 a) b) 5x + y = 0 x + y = 5 x y = a) ( ) = 5? No es solución. 5x + y = 0 5 = 9? 0 x
Sistemas de ecuaciones de primer grado con dos incógnitas
 Unidad Didáctica 4 Sistemas de ecuaciones de primer grado con dos incógnitas Objetivos 1. Encontrar y reconocer las relaciones entre los datos de un problema y expresarlas mediante el lenguaje algebraico.
Unidad Didáctica 4 Sistemas de ecuaciones de primer grado con dos incógnitas Objetivos 1. Encontrar y reconocer las relaciones entre los datos de un problema y expresarlas mediante el lenguaje algebraico.
Para resolver estos problemas podemos seguir tres pasos:
 RESOLUCIÓN DE PROBLEMAS Algunos problemas pueden resolverse empleando sistemas de dos ecuaciones de primer grado con dos incógnitas. Muchas veces se pueden resolver utilizando una sola ecuación con una
RESOLUCIÓN DE PROBLEMAS Algunos problemas pueden resolverse empleando sistemas de dos ecuaciones de primer grado con dos incógnitas. Muchas veces se pueden resolver utilizando una sola ecuación con una
Cuáles son esos números?
 MATEMÁTICAS PROBLEMAS QUE SE RESUELVEN CON ECUACIONES Para resolver un problema de ecuaciones debes seguir los siguientes pasos: a) Identificar el dato desconocido y asignarle el valor x (si hay dos o
MATEMÁTICAS PROBLEMAS QUE SE RESUELVEN CON ECUACIONES Para resolver un problema de ecuaciones debes seguir los siguientes pasos: a) Identificar el dato desconocido y asignarle el valor x (si hay dos o
PROBLEMAS DE SISTEMAS DE ECUACIONES
 PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
PROBLEMAS DE SISTEMAS DE ECUACIONES Problema nº 1.- Calcula un número sabiendo que la suma de sus dos cifras es 10; y que, si invertimos el orden de dichas cifras, el número obtenido es 36 unidades mayor
Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN
 Matemáticas Ejercicios Tema 8 3º ESO Bloque II: Álgebra Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN 1.- La base de un rectángulo mide 8 cm
Matemáticas Ejercicios Tema 8 3º ESO Bloque II: Álgebra Tema 8: Problemas con ecuaciones y sistemas. INTENTA RESOLVER TODOS ESTOS PROBLEMAS PLANTEANDO UNA ECUACIÓN 1.- La base de un rectángulo mide 8 cm
7Soluciones a los ejercicios y problemas PÁGINA 159
 7Soluciones a los ejercicios y problemas PÁGINA 159 Pág. 1 S istemas de ecuaciones. Resolución gráfica x + y = 3 1 Representa estas ecuaciones: x y = 1 a) Escribe las coordenadas del punto de corte. b)escribe
7Soluciones a los ejercicios y problemas PÁGINA 159 Pág. 1 S istemas de ecuaciones. Resolución gráfica x + y = 3 1 Representa estas ecuaciones: x y = 1 a) Escribe las coordenadas del punto de corte. b)escribe
1. Ecuaciones lineales 1.a. Definición. Solución.
 Sistemas de ecuaciones Contenidos 1. Ecuaciones lineales Definición. Solución 2. Sistemas de ecuaciones lineales Definición. Solución Número de soluciones 3. Métodos de resolución Reducción Sustitución
Sistemas de ecuaciones Contenidos 1. Ecuaciones lineales Definición. Solución 2. Sistemas de ecuaciones lineales Definición. Solución Número de soluciones 3. Métodos de resolución Reducción Sustitución
Sistemas de ecuaciones lineales
 9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
9 Sistemas de ecuaciones lineales 1. Sistemas lineales. Resolución gráfica Comprueba si = 2, = 3 es solución del siguiente sistema: 2 + 4 3 = 14 5 2 + 3 = 13 P I E N S A C A L C U L A + 4 = 14 5 + = 13
Ecuaciones de 1er y 2º grado
 Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
Ecuaciones de er y º grado. Ecuaciones de er grado Resuelve mentalmente: a) + = b) = c) = d) = P I E N S A Y C A L C U L A a) = b) = c) = d) = Carné calculista, : C =,; R = 0, Resuelve las siguientes ecuaciones:
k) x - 5 + 6 = 11 l) 5x - 2 = 3x - 1 m) 2x - 3 = 4x - 7 n) 5x + 4 = 6x + 3 ñ) 6x - 1 = 8x - 5 o) 3x + 10 = 5x - 6 p) 4x + 1 = 9x - 64
 Tema : Ecuaciones Resolver las siguientes ecuaciones de primer grado: a) b) c) 0 9 d) - e) f) g) 0 h) i) - j) k) - l) - - m) - - n) ñ) - - o) 0 - p) 9 - q) 9 - r) - 0 s) - - Resolver las siguientes ecuaciones
Tema : Ecuaciones Resolver las siguientes ecuaciones de primer grado: a) b) c) 0 9 d) - e) f) g) 0 h) i) - j) k) - l) - - m) - - n) ñ) - - o) 0 - p) 9 - q) 9 - r) - 0 s) - - Resolver las siguientes ecuaciones
9 Ecuaciones. de primer grado. 1. El lenguaje algebraico
 9 Ecuaciones de primer grado 1. El lenguaje algebraico Calcula el resultado de las siguientes epresiones: a) Tenía 5 y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado mide metros y el
9 Ecuaciones de primer grado 1. El lenguaje algebraico Calcula el resultado de las siguientes epresiones: a) Tenía 5 y me han dado 7. Cuántos euros tengo? b) En un rectángulo, un lado mide metros y el
a) x 1 = 2 b) x + x 6 = 2 + = + = c) x 9x + 20 = 2 d) x 6x 7 = a) x = 1 y x = 1 b) x = 3 y x = 2 c) x = 4 y x = 5 d) x = 1 y x = 7
 1 Resuelve las siguientes ecuaciones: a) x 1 = x + x 6 = c) x 9x + = d) x 6x 7 = = a) x = 1 y x = 1 x = 3 y x = c) x = 4 y x = 5 d) x = 1 y x = 7 Resuelve las siguientes ecuaciones de primer grado: a)
1 Resuelve las siguientes ecuaciones: a) x 1 = x + x 6 = c) x 9x + = d) x 6x 7 = = a) x = 1 y x = 1 x = 3 y x = c) x = 4 y x = 5 d) x = 1 y x = 7 Resuelve las siguientes ecuaciones de primer grado: a)
Sistemas de Ecuaciones
 4 Sistemas de Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer y clasificar los sistemas de ecuaciones según su número de soluciones. Obtener la solución de un sistema mediante una tablas.
4 Sistemas de Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer y clasificar los sistemas de ecuaciones según su número de soluciones. Obtener la solución de un sistema mediante una tablas.
I.E.S. Miguel de Cervantes (Granada) Departamento de Matemáticas GBG 1
 ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
ECUACIONES Y SISTEMAS. PROBLEMAS 1. El lado de un cuadrado mide 3 m más que el lado de otro cuadrado. Si la suma de las dos áreas es 89 m, calcula las dimensiones de los cuadrados.. La suma de dos números
ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES
 ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES La materia se estructurará en dos partes. Los alumnos que tengan en la primera evaluación menos de un cuatro deberán hacer el martes de Febrero
ALUMNOS DE CUARTO DE ESO CON MATEMÁTICAS DE TERCERO PENDIENTES La materia se estructurará en dos partes. Los alumnos que tengan en la primera evaluación menos de un cuatro deberán hacer el martes de Febrero
RESOLUCIÓN DE PROBLEMAS
 RESOLUCIÓN DE PROBLEMAS La resolución de problemas mediante ecuaciones tiene una serie de dificultades que nos llevan a plantear un tema separado del resto. Las dificultades, llegado este punto en que
RESOLUCIÓN DE PROBLEMAS La resolución de problemas mediante ecuaciones tiene una serie de dificultades que nos llevan a plantear un tema separado del resto. Las dificultades, llegado este punto en que
7 ECUACIONES. SISTEMAS DE ECUACIONES
 EJERCICIOS PROPUESTOS 7. Escribe estos enunciados en forma de ecuación. a) La suma de dos números consecutivos es. La suma de tres números pares consecutivos es 0. c) Un número más su quinta parte es.
EJERCICIOS PROPUESTOS 7. Escribe estos enunciados en forma de ecuación. a) La suma de dos números consecutivos es. La suma de tres números pares consecutivos es 0. c) Un número más su quinta parte es.
11 Resuelve los siguientes sistemas de ecuaciones, aplicando dos veces el método de reducción para despejar cada una de las incógnitas:
 PÁGINA 22 Pág. Resuelve los siguientes sistemas de ecuaciones, aplicando dos veces el método de reducción para despejar cada una de las incógnitas: a) 3x y = 5 7x 4y = 9 b) 9x 3y = 54 x 7y = 22 a) 3x y
PÁGINA 22 Pág. Resuelve los siguientes sistemas de ecuaciones, aplicando dos veces el método de reducción para despejar cada una de las incógnitas: a) 3x y = 5 7x 4y = 9 b) 9x 3y = 54 x 7y = 22 a) 3x y
Matemáticas pendiente de 3º ESO IES PLAYAMAR Curso 2015-2016
 Matemáticas pendiente de º ESO IES PLAYAMAR Curso -6 ºEVALUACIÓN FECHA DEL EXAMEN: 7 DE NOVIEMBRE DE A LAS : (SALÓN DE ACTOS) INSTRUCCIONES o o Las actividades realizadas deben entregarse obligatoriamente
Matemáticas pendiente de º ESO IES PLAYAMAR Curso -6 ºEVALUACIÓN FECHA DEL EXAMEN: 7 DE NOVIEMBRE DE A LAS : (SALÓN DE ACTOS) INSTRUCCIONES o o Las actividades realizadas deben entregarse obligatoriamente
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
REPASO DE LA PRIMERA EVALUACIÓN
 REPASO DE LA PRIMERA EVALUACIÓN º ESO. Escribe todos los divisores de: 7,, 8, y Sol: a),,,, 6, 8, 9,, 8,, 6, 7 b),,,, 6, 8,, c),,, 7,, 8 d),,, 9,, d),,, 6, 9, 8, 7,. Descompón en factores primos: 800,
REPASO DE LA PRIMERA EVALUACIÓN º ESO. Escribe todos los divisores de: 7,, 8, y Sol: a),,,, 6, 8, 9,, 8,, 6, 7 b),,,, 6, 8,, c),,, 7,, 8 d),,, 9,, d),,, 6, 9, 8, 7,. Descompón en factores primos: 800,
SOLUCIONES. Matemáticas 3 EDUCACIÓN SECUNDARIA 1 3 1 1 3, 4 2,3 + : a) Expresamos N = 2,3 en forma de fracción: 10 N = 23,333 N = 2,333 21 7 = + = =
 Matemáticas EDUCACIÓN SECUNDARIA Opción A SOLUCIONES Evaluación: Fecha: Ejercicio nº 1.- a) Opera y simplifica: 1 1 1, 4, + : 5 b) Reduce a una sola potencia: 4 1 5 5 0 a) Expresamos N =, en forma de fracción:
Matemáticas EDUCACIÓN SECUNDARIA Opción A SOLUCIONES Evaluación: Fecha: Ejercicio nº 1.- a) Opera y simplifica: 1 1 1, 4, + : 5 b) Reduce a una sola potencia: 4 1 5 5 0 a) Expresamos N =, en forma de fracción:
De dos incógnitas. Por ejemplo, x + y 3 = 4. De tres incógnitas. Por ejemplo, x + y + 2z = 4. Y así sucesivamente.
 3 Ecuaciones 17 3 Ecuaciones Una ecuación es una igualdad en la que aparecen ligados, mediante operaciones algebraicas, números y letras Las letras que aparecen en una ecuación se llaman incógnitas Existen
3 Ecuaciones 17 3 Ecuaciones Una ecuación es una igualdad en la que aparecen ligados, mediante operaciones algebraicas, números y letras Las letras que aparecen en una ecuación se llaman incógnitas Existen
BOLETIN Nº 5 MATEMÁTICAS 3º ESO Ecuaciones y sistemas Curso 2011/12
 BOLETIN Nº MATEMÁTICAS º ESO Ecuaciones sistemas Curso / ) ( ) ) ( ) 8 ( ) ) ) 8 ( ) ( ) ) ( )( ) ) ( )( ) ( ) ) ( ) ( ) ( ) ( ) 8) ( ) 8( ) ( ) ) ( ) ( 8) ( ) ) (8 ) ( ) ( ) ) ( ) ( ) (8 ) ) ( ) ( ) (
BOLETIN Nº MATEMÁTICAS º ESO Ecuaciones sistemas Curso / ) ( ) ) ( ) 8 ( ) ) ) 8 ( ) ( ) ) ( )( ) ) ( )( ) ( ) ) ( ) ( ) ( ) ( ) 8) ( ) 8( ) ( ) ) ( ) ( 8) ( ) ) (8 ) ( ) ( ) ) ( ) ( ) (8 ) ) ( ) ( ) (
EJERCICIOS SOBRE : ECUACIONES DE PRIMER GRADO
 1.- Igualdades. Las expresiones en donde aparecen el signo =, se llaman igualdades. Ejemplo: 5 = 7-2 ; x + 2 = 9 Toda igualdad consta de dos miembros, el primer miembro ( lo escrito antes del signo igual
1.- Igualdades. Las expresiones en donde aparecen el signo =, se llaman igualdades. Ejemplo: 5 = 7-2 ; x + 2 = 9 Toda igualdad consta de dos miembros, el primer miembro ( lo escrito antes del signo igual
LAS FUNCIONES ELEMENTALES
 UNIDAD LAS FUNCIONES ELEMENTALES Página 98. Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con ellas. Las ecuaciones correspondientes
UNIDAD LAS FUNCIONES ELEMENTALES Página 98. Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con ellas. Las ecuaciones correspondientes
TEMA: ECUACIONES CON NÚMEROS NATURALES ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA.
 TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
TEMA: ECUACIONES CON NÚMEROS NATURALES INTRODUCCIÓN: Las ecuaciones sirven, básicamente, para resolver problemas ya sean matemáticos, de la vida diaria o de cualquier ámbito- y, en ese caso, se dice que
Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas
 Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas Recuerda las cuatro fases que tendremos que seguir para resolver un problema: 1.- Comprender el problema. 2.- Plantear el sistema
Problemas de Sistemas de Ecuaciones de Primer Grado con dos Incógnitas Recuerda las cuatro fases que tendremos que seguir para resolver un problema: 1.- Comprender el problema. 2.- Plantear el sistema
b) Los lados de un triángulo rectángulo tienen por medida tres números naturales consecutivos. Halla dichos lados.
 Problemas Repaso MATEMÁTICAS APLICADAS A LAS CCSS I Profesor:Féli Muñoz Reduce a común denominador el siguiente conjunto de fracciones: + ; y Común denominador: ( + )( ) MCM + ( )( ) ( )( + )( ) ( ) (
Problemas Repaso MATEMÁTICAS APLICADAS A LAS CCSS I Profesor:Féli Muñoz Reduce a común denominador el siguiente conjunto de fracciones: + ; y Común denominador: ( + )( ) MCM + ( )( ) ( )( + )( ) ( ) (
1º BACHILLERATO MATEMÁTICAS CCSS
 PÁGINA 87, EJERCICIO 48 1º BACHILLERATO MATEMÁTICAS CCSS PROBLEMAS TEMA 4 - ECUACIONES Y SISTEMAS La suma de los cuadrados de dos números naturales impares consecutivos es 170. Calcula el valor del siguiente
PÁGINA 87, EJERCICIO 48 1º BACHILLERATO MATEMÁTICAS CCSS PROBLEMAS TEMA 4 - ECUACIONES Y SISTEMAS La suma de los cuadrados de dos números naturales impares consecutivos es 170. Calcula el valor del siguiente
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES. 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora?
 PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora? Solución : 12 años 2.- Si al doble de un número le restas 13, obtienes
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1.- Qué edad tiene Rita sabiendo que dentro de 24 años tendrá el triple de la que tiene ahora? Solución : 12 años 2.- Si al doble de un número le restas 13, obtienes
PARTE 2- Matemáticas pendientes de 3º ESO 2010-11. 2. Indica, para cada representación gráfica, que tipo de sistema de ecuaciones es el representado:
 PARTE - Matemáticas pendientes de 3º ESO 00- NOMBRE: 4º GRUPO:. Resuelve gráficamente los siguientes sistemas de ecuaciones e indica que tipo de sistema son: x x x 3 4. Indica, para cada representación
PARTE - Matemáticas pendientes de 3º ESO 00- NOMBRE: 4º GRUPO:. Resuelve gráficamente los siguientes sistemas de ecuaciones e indica que tipo de sistema son: x x x 3 4. Indica, para cada representación
Serie 5 - Problemas de enunciado
 Serie 5 - Problemas de enunciado Nombre:...Curso: 4ºD Resuelve los siguientes problemas. El proceso a seguir es como en el problema resuelto: [1º] Definir adecuadamente la(s) incógnita(s) [2º] Realizar
Serie 5 - Problemas de enunciado Nombre:...Curso: 4ºD Resuelve los siguientes problemas. El proceso a seguir es como en el problema resuelto: [1º] Definir adecuadamente la(s) incógnita(s) [2º] Realizar
2 Fracciones y. números decimales. 1. Operaciones con fracciones. Realiza mentalmente las siguientes operaciones: Solución: a) b) c) Carné calculista
 Fracciones y números decimales. Operaciones con fracciones Realiza mentalmente las siguientes operaciones: + c) 0 c) P I E N S A Y C A L C U L A Carné calculista : C = ; R = Calcula mentalmente: + c) c)
Fracciones y números decimales. Operaciones con fracciones Realiza mentalmente las siguientes operaciones: + c) 0 c) P I E N S A Y C A L C U L A Carné calculista : C = ; R = Calcula mentalmente: + c) c)
El primero puso: 12 El segundo puso: 12 + 3 = 15. Entre los dos primeros juntaron: 12 + 15 = 27. El tercero puso: 40 27 = 13.
 Ejercicios de números naturales con soluciones 1 Tres amigos han juntado 40 para comprar un regalo a otro amigo. El primero puso 12 y el segundo, 3 más que el primero. Cuánto puso el tercero? El primero
Ejercicios de números naturales con soluciones 1 Tres amigos han juntado 40 para comprar un regalo a otro amigo. El primero puso 12 y el segundo, 3 más que el primero. Cuánto puso el tercero? El primero
10Soluciones a los ejercicios y problemas PÁGINA 196
 0Soluciones a los ejercicios y problemas PÁGINA 96 Pág. E presiones algebraicas Llamando a un número indeterminado, asocia cada enunciado con la epresión que le corresponde: a) El doble del número. b)
0Soluciones a los ejercicios y problemas PÁGINA 96 Pág. E presiones algebraicas Llamando a un número indeterminado, asocia cada enunciado con la epresión que le corresponde: a) El doble del número. b)
Ecuaciones de segundo grado
 3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
3 Ecuaciones de segundo grado Objetivos En esta quincena aprenderás a: Identificar las soluciones de una ecuación. Reconocer y obtener ecuaciones equivalentes. Resolver ecuaciones de primer grado Resolver
Proporcionalidad. 1. Calcula:
 Proporcionalidad 1. Calcula:. Resuelve los siguientes problemas: a. Tres kilos de naranjas cuestan,4. Cuánto cuestan dos kilos? b. Seis obreros descargan un camión en tres horas. Cuánto tardarán cuatro
Proporcionalidad 1. Calcula:. Resuelve los siguientes problemas: a. Tres kilos de naranjas cuestan,4. Cuánto cuestan dos kilos? b. Seis obreros descargan un camión en tres horas. Cuánto tardarán cuatro
Resuelve problemas PÁGINA 75
 PÁGINA 7 Pág. 1 Resuelve problemas 9 Una empresa de alquiler de coches cobra por día y por kilómetros recorridos. Un cliente pagó 10 por días y 400 km, y otro pagó 17 por días y 00 km. Averigua cuánto
PÁGINA 7 Pág. 1 Resuelve problemas 9 Una empresa de alquiler de coches cobra por día y por kilómetros recorridos. Un cliente pagó 10 por días y 400 km, y otro pagó 17 por días y 00 km. Averigua cuánto
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA
 4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
4º ESO 1. ECUAC. 2º GRADO Y UNA INCÓGNITA Una ecuación con una incógnita es de segundo grado si el exponente de la incógnita es dos. Ecuaciones de segundo grado con una incógnita son: Esta última ecuación
Sistemas de ecuaciones
 Sistemas de ecuaciones Cuando aparecen varias incógnitas en un problema, resulta más sencillo resolverlo planteando más de una ecuación con más de una incógnita. Un sistema de ecuaciones es un conjunto
Sistemas de ecuaciones Cuando aparecen varias incógnitas en un problema, resulta más sencillo resolverlo planteando más de una ecuación con más de una incógnita. Un sistema de ecuaciones es un conjunto
Ejercicios para repasar y recuperar el. Área de Matemáticas de 1º ESO
 Octubre 01 º Cuadernillo Ejercicios para repasar y recuperar el Área de Matemáticas de 1º ESO Nota: Debes de presentarlo el día del º Parcial. ALUMNO: 1 1. Efectúa: a) 5 5 1 : 5 = b) 1 = c) 7 5 8 1 10
Octubre 01 º Cuadernillo Ejercicios para repasar y recuperar el Área de Matemáticas de 1º ESO Nota: Debes de presentarlo el día del º Parcial. ALUMNO: 1 1. Efectúa: a) 5 5 1 : 5 = b) 1 = c) 7 5 8 1 10
ACTIVIDADES DE REPASO. MATEMÁTICAS 1º ESO
 ACTIVIDADES DE REPASO. MATEMÁTICAS º ESO NÚMEROS NATURALES. Calcula: a) 4 6 5 + 3 4 b) (4 6 5) + 3 4 c) 4 6 (5 + 3 4) d) 4 (6 5) + 3 4 e) (5 + 0) 8 f) (73 37) : 6. Calcula: a) 987 + 5 + 3 784 b) 3 978
ACTIVIDADES DE REPASO. MATEMÁTICAS º ESO NÚMEROS NATURALES. Calcula: a) 4 6 5 + 3 4 b) (4 6 5) + 3 4 c) 4 6 (5 + 3 4) d) 4 (6 5) + 3 4 e) (5 + 0) 8 f) (73 37) : 6. Calcula: a) 987 + 5 + 3 784 b) 3 978
4. Cuáles son los dos números?
 Problemas algebraicos 1 PROBLEMAS (SISTEMAS LINEALES) 1.1 PROBLEMAS (SISTEMAS NO LINEALES) 1.- La razón de dos números es tres quintos y si aumentamos el denominador una unidad y disminuimos el numerador
Problemas algebraicos 1 PROBLEMAS (SISTEMAS LINEALES) 1.1 PROBLEMAS (SISTEMAS NO LINEALES) 1.- La razón de dos números es tres quintos y si aumentamos el denominador una unidad y disminuimos el numerador
Soluciones a las actividades
 Soluciones a las actividades BLOQUE I Álgebra 1. Sistemas lineales 2. Matrices 3. Determinantes 4. Sistemas lineales con parámetros 1 Sistemas lineales 1. Sistemas de ecuaciones lineales Piensa y calcula
Soluciones a las actividades BLOQUE I Álgebra 1. Sistemas lineales 2. Matrices 3. Determinantes 4. Sistemas lineales con parámetros 1 Sistemas lineales 1. Sistemas de ecuaciones lineales Piensa y calcula
Ejercicios resueltos de porcentajes
 Ejercicios resueltos de porcentajes 1) Calcula los siguientes porcentajes: a) 30% de 600 b) 45% de 81 c) 50% de 340 d) 25% de 48 2) Calcula el término que falta en las siguientes expresiones: a) 40% de
Ejercicios resueltos de porcentajes 1) Calcula los siguientes porcentajes: a) 30% de 600 b) 45% de 81 c) 50% de 340 d) 25% de 48 2) Calcula el término que falta en las siguientes expresiones: a) 40% de
SISTEMAS DE ECUACIONES. 3 o
 SISTEMAS DE ECUACIONES. 3 o EJERCICIOS I 1- Busca dos soluciones de la ecuación 3 y = 1. Representa gráficamente la recta 3 y = 1. Un punto cualquiera de la recta, es solución de la ecuación? 2- Representa
SISTEMAS DE ECUACIONES. 3 o EJERCICIOS I 1- Busca dos soluciones de la ecuación 3 y = 1. Representa gráficamente la recta 3 y = 1. Un punto cualquiera de la recta, es solución de la ecuación? 2- Representa
1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20
 ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
ACTIVIDADES DE REPASO MATEMÁTICAS 1º ESO NOMBRE: GRUPO:. Actividades a realizar: 1) Tacha los números que no sean naturales: 12-4 23-5 36 29-1 -15 13-20 2) Calcula: a) 4 6 + 3 + 9-2 3 = b) 6 (3 + 7) -
PROBLEMAS ECUACIONES 1er GRADO
 PROBLEMAS ECUACIONES 1er GRADO 1.- Dos amigos juntan el dinero que tienen, uno tiene el doble que el otro. Se gastan 20, y les quedan 13 Cuánto dinero tiene cada uno? 2.- He comprado 8 cuadernos y he pagado
PROBLEMAS ECUACIONES 1er GRADO 1.- Dos amigos juntan el dinero que tienen, uno tiene el doble que el otro. Se gastan 20, y les quedan 13 Cuánto dinero tiene cada uno? 2.- He comprado 8 cuadernos y he pagado
2Soluciones a los ejercicios y problemas PÁGINA 61
 PÁGINA 61 Pág. 1 P RACTICA Fracciones y decimales 1 Expresa como un número decimal las siguientes fracciones: 9 1 1 5 1 5 9 6 00 990 9 5 5 1 0,6; 1, ;,8 ; 0,085 9 6 0, 185; 0,5 00 ; 1 0,590 990 Clasifica
PÁGINA 61 Pág. 1 P RACTICA Fracciones y decimales 1 Expresa como un número decimal las siguientes fracciones: 9 1 1 5 1 5 9 6 00 990 9 5 5 1 0,6; 1, ;,8 ; 0,085 9 6 0, 185; 0,5 00 ; 1 0,590 990 Clasifica
Problemas de ecuaciones de primer grado
 Problemas de ecuaciones de primer grado 1. La suma de dos números pares consecutivos es 102. Halla esos números. (50 y 52) 2. La suma de tres números impares consecutivos es 69. Busca los números. (21,23
Problemas de ecuaciones de primer grado 1. La suma de dos números pares consecutivos es 102. Halla esos números. (50 y 52) 2. La suma de tres números impares consecutivos es 69. Busca los números. (21,23
ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO
 CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
CURSO 10-11 ACTIVIDADES DE RECUPERACIÓN MATEMÁTICAS 1º ESO NOMBRE: GRUPO:.; Nº:. Los contenidos mínimos para la prueba extraordinaria de septiembre se encuentran en la programación, que se puede consultar
HIgualdades y ecuacionesh. HElementos de una ecuaciónh. HEcuaciones equivalentes. HSin denominadoresh. HCon denominadoresh
 6 Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer situaciones que pueden resolverse con ecuaciones Traducir al lenguaje matemático enunciados del lenguaje ordinario. Conocer los elementos
6 Ecuaciones Objetivos En esta quincena aprenderás a: Reconocer situaciones que pueden resolverse con ecuaciones Traducir al lenguaje matemático enunciados del lenguaje ordinario. Conocer los elementos
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES
 PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES 1º) El perímetro de un triángulo isósceles mide 15 cm. El lado desigual del triángulo es la mitad de cada uno de los lados iguales. Halla la longitud de cada uno
6 SISTEMAS DE ECUACIONES
 6 SISTEMAS DE ECUACIONES EJERCICIOS PROPUESTOS 6.1 Halla las soluciones de la ecuación 2x 6y 28 sabiendo el valor de una de las incógnitas. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28
6 SISTEMAS DE ECUACIONES EJERCICIOS PROPUESTOS 6.1 Halla las soluciones de la ecuación 2x 6y 28 sabiendo el valor de una de las incógnitas. a) x 5 c) y 1 e) y 3 b) x 10 d) y 0 f) x 1 2 a) x 5 2 5 6y 28
EJERCICIOS DE REPASO 2º ESO
 NOMBRE: CURSO: 0-0 EJERCICIOS DE REPASO º ESO.- Calcula, poniendo los pasos que haces, no sólo el resultado: a ) - ( - ) + 8 ( - ) = b) ( - 8 ) [ 7 + ( - 9 ) ] = c) 7 ( 8 ) + : ( - + 7 ) = d) 6 : ( 8 )
NOMBRE: CURSO: 0-0 EJERCICIOS DE REPASO º ESO.- Calcula, poniendo los pasos que haces, no sólo el resultado: a ) - ( - ) + 8 ( - ) = b) ( - 8 ) [ 7 + ( - 9 ) ] = c) 7 ( 8 ) + : ( - + 7 ) = d) 6 : ( 8 )
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 3 Ecuaciones y sistemas. Inecuaciones Elaborado por la Profesora Doctora
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 3 Ecuaciones y sistemas. Inecuaciones Elaborado por la Profesora Doctora
Matemáticas 3º ESO Problemas de Sistemas de Ecuaciones 1. 1.- La suma de dos números es 25 y su diferencia 1. Calcula los dos números.
 Matemáticas 3º ESO Problemas de Sistemas de Ecuaciones 1 Problemas tipo A (A: poca dificultad; B: media y C: alta) 1.- La suma de dos números es 25 y su diferencia 1. Calcula los dos números. 2.- Un librero
Matemáticas 3º ESO Problemas de Sistemas de Ecuaciones 1 Problemas tipo A (A: poca dificultad; B: media y C: alta) 1.- La suma de dos números es 25 y su diferencia 1. Calcula los dos números. 2.- Un librero
Ecuaciones Problemas Ejercicios resueltos
 Ecuaciones Problemas Ejercicios resueltos 1. En el siguiente dibujo todos los autos son iguales: Determinar el largo de cada auto. Sea x el largo de cada auto. De acuerdo a la figura, la ecuación que modela
Ecuaciones Problemas Ejercicios resueltos 1. En el siguiente dibujo todos los autos son iguales: Determinar el largo de cada auto. Sea x el largo de cada auto. De acuerdo a la figura, la ecuación que modela
CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO
 CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO Potencias y raíces. Expresa en forma de potencia: a) 7 7 7 7 = b) 8 8 8 8 8 8 8 = c) 6 6 6 6 6 = d) 5 5 5 5 = e) 9 9 9 = f) 3 3 = Calcula las siguientes potencias:
CUADERNILLO DE VERANO MATEMÁTICAS 1º ESO Potencias y raíces. Expresa en forma de potencia: a) 7 7 7 7 = b) 8 8 8 8 8 8 8 = c) 6 6 6 6 6 = d) 5 5 5 5 = e) 9 9 9 = f) 3 3 = Calcula las siguientes potencias:
EJERCICIOS PROPUESTOS. Copia y completa de modo que estas expresiones sean igualdades numéricas. a) 5 2 13 c) 2 32 b) 4 5 17 d) 4 6 18 10
 5 ECUACIONES EJERCICIOS PROPUESTOS 5.1 Copia y completa de modo que estas epresiones sean igualdades numéricas. a) 5 1 c) b) 5 17 d) 6 1 10 a) 5 10 1 c) 16 b) 5 17 d) 6 1 10 5. Sustituye las letras por
5 ECUACIONES EJERCICIOS PROPUESTOS 5.1 Copia y completa de modo que estas epresiones sean igualdades numéricas. a) 5 1 c) b) 5 17 d) 6 1 10 a) 5 10 1 c) 16 b) 5 17 d) 6 1 10 5. Sustituye las letras por
5 SISTEMAS DE ECUACIONES
 5 SISTEMAS DE ECUACINES EJERCICIS PRPUESTS 5. Escribe estos enunciados en forma de una ecuación con dos incógnitas. a) Un número más el doble de otro es. La diferencia de dos números es 5. c) Un número
5 SISTEMAS DE ECUACINES EJERCICIS PRPUESTS 5. Escribe estos enunciados en forma de una ecuación con dos incógnitas. a) Un número más el doble de otro es. La diferencia de dos números es 5. c) Un número
) = 5. Operaciones con polinomios 54 SOLUCIONARIO 1. POLINOMIOS. SUMA Y RESTA 2. MULTIPLICACIÓN DE POLINOMIOS
 54 SOLUCIONARIO 5. Operaciones con polinomios. POLINOMIOS. SUMA RESTA PIENSA CALCULA Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A ( ) = 6 b) V ( ) = CARNÉ CALCULISTA
54 SOLUCIONARIO 5. Operaciones con polinomios. POLINOMIOS. SUMA RESTA PIENSA CALCULA Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A ( ) = 6 b) V ( ) = CARNÉ CALCULISTA
Problemas de ecuaciones Colección C. MasMates.com Colecciones de ejercicios
 1. En el mercado, Rosa ha comprado 3 kg de guisantes, 4 kg de garbanzos y 5 kg de judías por 48'80 euros. Halla, planteando y resolviendo una ecuación con una incógnita, el precio del kilo de cada tipo
1. En el mercado, Rosa ha comprado 3 kg de guisantes, 4 kg de garbanzos y 5 kg de judías por 48'80 euros. Halla, planteando y resolviendo una ecuación con una incógnita, el precio del kilo de cada tipo
PROPORCIONALIDAD - teoría
 PROPORCIONALIDAD RAZÓN: razón de dos números es el cociente indicado de ambos. Es decir, la razón de los dos números a y b es a:b, o lo que es lo mismo, la fracción b a. PROPORCIÓN: es la igualdad de dos
PROPORCIONALIDAD RAZÓN: razón de dos números es el cociente indicado de ambos. Es decir, la razón de los dos números a y b es a:b, o lo que es lo mismo, la fracción b a. PROPORCIÓN: es la igualdad de dos
PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES 3º ESO 2009. 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible.
 PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES º ESO 009 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible. 1 A = 8 1 + 1 B = A = 8 1 = 8 = 8 = 6 4 B = = 4 4 = 4 16
PRUEBA DE CONOCIMIENTOS Y DESTREZAS INDISPENSABLES º ESO 009 1) Calcula el valor de A y B, dando el resultado de la forma más sencilla posible. 1 A = 8 1 + 1 B = A = 8 1 = 8 = 8 = 6 4 B = = 4 4 = 4 16
FUNCIONES DE PROPORCIONALIDAD
 UNIDAD 2 PROPORCIONALIDAD. FUNCIONES DE PROPORCIONALIDAD 1.- INTRODUCCIÓN Continuamente hacemos uso de las magnitudes físicas cuando nos referimos a diversas situaciones como medida de distancias (longitud),
UNIDAD 2 PROPORCIONALIDAD. FUNCIONES DE PROPORCIONALIDAD 1.- INTRODUCCIÓN Continuamente hacemos uso de las magnitudes físicas cuando nos referimos a diversas situaciones como medida de distancias (longitud),
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. Página 4 En la última semana, los 0 monos de un parque natural han comido 0 kg de fruta. Acaban de traer monos más y disponemos de 080 kg de fruta. Para cuántos días tenemos? (Averigua previamente
Pág. Página 4 En la última semana, los 0 monos de un parque natural han comido 0 kg de fruta. Acaban de traer monos más y disponemos de 080 kg de fruta. Para cuántos días tenemos? (Averigua previamente
CUADERNO DE VERANO 3º ESO FRACCIONES. 1. Efectúa las siguientes operaciones: 5 = 7 = 1 1 = c) 2 3 + = d) 5 29 : = e) 4. f) 24
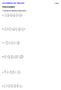 CUADERNO DE VERANO º ESO FRACCIONES. Efectúa las siguientes operaciones: a) 0 9 9 b) 0 0 7 c) d) 8 e) 7 9 : f) 9 9 7 : : ) El aire es una mezcla de gases. En la capa más próima a la superficie de la Tierra,
CUADERNO DE VERANO º ESO FRACCIONES. Efectúa las siguientes operaciones: a) 0 9 9 b) 0 0 7 c) d) 8 e) 7 9 : f) 9 9 7 : : ) El aire es una mezcla de gases. En la capa más próima a la superficie de la Tierra,
Recuerdas qué es? Constante de proporcionalidad Es el cociente de cualquiera de las razones que intervienen en una proporción.
 Recuerdas qué es? Coordenadas de un punto Un punto del plano viene definido por un par ordenado de números. La primera coordenada es la abscisa del punto, la segunda coordenada es la ordenada del punto.
Recuerdas qué es? Coordenadas de un punto Un punto del plano viene definido por un par ordenado de números. La primera coordenada es la abscisa del punto, la segunda coordenada es la ordenada del punto.
Problemas Tema 1 Enunciados de problemas de Repaso 4ºESO
 página / Problemas Tema Enunciados de problemas de Repaso 4ºESO Hoja. Calcula las medidas de un rectángulo cuya superficie es de 40 metros cuadrados, sabiendo que el largo es 6 metros mayor que el triple
página / Problemas Tema Enunciados de problemas de Repaso 4ºESO Hoja. Calcula las medidas de un rectángulo cuya superficie es de 40 metros cuadrados, sabiendo que el largo es 6 metros mayor que el triple
4 Ecuaciones y sistemas
 Solucionario Ecuaciones y sistemas ACTIVIDADES INICIALES.I. Comprueba si las siguientes ecuaciones tienen como soluciones,,. a) 0 b) 5 () 8 a) 0 () () es solución. 0 8 9 6 0 6 0 0 9 5 5 6 5 es solución.
Solucionario Ecuaciones y sistemas ACTIVIDADES INICIALES.I. Comprueba si las siguientes ecuaciones tienen como soluciones,,. a) 0 b) 5 () 8 a) 0 () () es solución. 0 8 9 6 0 6 0 0 9 5 5 6 5 es solución.
gastado 1/3 del combustible que llevábamos. Si al final quedaron 20 l, cuál es la capacidad del depósito?
 FICHA 4: 58 problemas de planteamiento de ecuaciones y sistemas RECORDAR: A la hora de resolver un problema que requiera el planteamiento de una ecuación o un sistema se recomienda: Leer atentamente el
FICHA 4: 58 problemas de planteamiento de ecuaciones y sistemas RECORDAR: A la hora de resolver un problema que requiera el planteamiento de una ecuación o un sistema se recomienda: Leer atentamente el
HOJA 5 SUCESIONES Y PROGRESIONES
 HOJA 5 SUCESIONES Y PROGRESIONES Sucesión: Término general 1.- Calcula el término general de las sucesiones: a) -1, 2, 5, 8, 11, b) 3, 3/2, ¾, 3/8, c) 1, 4, 9, 16, 25, 2.- Halla el término general de cada
HOJA 5 SUCESIONES Y PROGRESIONES Sucesión: Término general 1.- Calcula el término general de las sucesiones: a) -1, 2, 5, 8, 11, b) 3, 3/2, ¾, 3/8, c) 1, 4, 9, 16, 25, 2.- Halla el término general de cada
Capítulo 5: Ecuaciones de segundo grado y sistemas lineales
 º de ESO Capítulo : Ecuaciones de segundo grado sistemas lineales Autora: Raquel Hernández Revisores: Sergio Hernández María Molero Ilustraciones: Raquel Hernández Banco de Imágenes de INTEF Ecuaciones
º de ESO Capítulo : Ecuaciones de segundo grado sistemas lineales Autora: Raquel Hernández Revisores: Sergio Hernández María Molero Ilustraciones: Raquel Hernández Banco de Imágenes de INTEF Ecuaciones
Carrera: Técnico Superior en Programación
 1 Sistema de dos ecuaciones lineales Resolver los siguientes sistemas de dos ecuaciones lineales en forma analítica y gráfica. Verificar los resultados obtenidos. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
1 Sistema de dos ecuaciones lineales Resolver los siguientes sistemas de dos ecuaciones lineales en forma analítica y gráfica. Verificar los resultados obtenidos. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
UNIDAD 7 Sistemas de ecuaciones
 Pág. 1 de 3 1 La diagonal de un rectángulo mide 37 cm, y el perímetro, 94 cm. Calcula los lados del rectángulo. 37 y + y = 94 = 37 Solución: Los lados del rectángulo miden 1 cm y 35 cm. La raíz cuadrada
Pág. 1 de 3 1 La diagonal de un rectángulo mide 37 cm, y el perímetro, 94 cm. Calcula los lados del rectángulo. 37 y + y = 94 = 37 Solución: Los lados del rectángulo miden 1 cm y 35 cm. La raíz cuadrada
Página 123 EJERCICIOS Y PROBLEMAS PROPUESTOS. Dominio de definición PARA PRACTICAR UNIDAD. 1 Halla el dominio de definición de estas funciones: 2x + 1
 Página 3 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: 3 x a) y = y = x + x (x ) c) y = d) y = e) y = x + x + 3 5x x f) y = x x
Página 3 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: 3 x a) y = y = x + x (x ) c) y = d) y = e) y = x + x + 3 5x x f) y = x x
1. HABILIDAD MATEMÁTICA
 HABILIDAD MATEMÁTICA SUCESIONES, SERIES Y PATRONES. HABILIDAD MATEMÁTICA Una serie es un conjunto de números, literales o dibujos ordenados de tal manera que cualquiera de ellos puede ser definido por
HABILIDAD MATEMÁTICA SUCESIONES, SERIES Y PATRONES. HABILIDAD MATEMÁTICA Una serie es un conjunto de números, literales o dibujos ordenados de tal manera que cualquiera de ellos puede ser definido por
Cajón de Ciencias. Problemas resueltos de sistemas de ecuaciones
 Problemas resueltos de sistemas de ecuaciones 1) En una granja se crían gallinas y conejos. En total hay 50 cabezas y 134 patas Cuántos animales hay de cada clase? 2) En un taller hay vehículos de 4 y
Problemas resueltos de sistemas de ecuaciones 1) En una granja se crían gallinas y conejos. En total hay 50 cabezas y 134 patas Cuántos animales hay de cada clase? 2) En un taller hay vehículos de 4 y
MATEMÁTICAS 2ºESO Curso: 2011-2012 ACTIVIDADES PARA ALUMNOS DE 3º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE 2º E.S.O. PRIMERA PARTE 1.
 MATEMÁTICAS ºESO Curso: 011-01 ACTIVIDADES PARA ALUMNOS DE º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE º E.S.O. PRIMERA PARTE 1. Calcula: a 6 8 1 10 6 1 1 8 + + + ( ( ( + ( ( ( + + ( ( 7 8 6 9 7 d. Realiza
MATEMÁTICAS ºESO Curso: 011-01 ACTIVIDADES PARA ALUMNOS DE º E.S.O. QUE TIENEN PENDIENTE MATEMÁTICAS DE º E.S.O. PRIMERA PARTE 1. Calcula: a 6 8 1 10 6 1 1 8 + + + ( ( ( + ( ( ( + + ( ( 7 8 6 9 7 d. Realiza
Tema 4: Problemas Aritméticos
 Tema 4: Problemas Aritméticos 4.1 Proporcionalidad simple. Vamos a en primer lugar a responder a dos preguntas: Cuándo se dice que dos magnitudes son directamente proporcionales? Se dice que son directamente
Tema 4: Problemas Aritméticos 4.1 Proporcionalidad simple. Vamos a en primer lugar a responder a dos preguntas: Cuándo se dice que dos magnitudes son directamente proporcionales? Se dice que son directamente
EJERCICIOS SOBRE : PROBLEMAS ECUACIONES DE PRIMER GRADO
 1) Calcular tres números consecutivos cuya suma sea 1. ) Las edades de dos hermanos suman 49 años. Calcularlas sabiendo que la edad de uno es superior en años a la del otro. ) Descomponer el número 171
1) Calcular tres números consecutivos cuya suma sea 1. ) Las edades de dos hermanos suman 49 años. Calcularlas sabiendo que la edad de uno es superior en años a la del otro. ) Descomponer el número 171
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS
 UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
UNIDAD 6. POLINOMIOS CON COEFICIENTES ENTEROS Unidad 6: Polinomios con coeficientes enteros. Al final deberás haber aprendido... Expresar algebraicamente enunciados sencillos. Extraer enunciados razonables
http://www.youtube.com/watch?v=puen0s0idwc http://www.youtube.com/watch?v=fhmvwv5wfuo http://www.youtube.com/watch?v=38nysgkjxdg
 .- Sistema ecuaciones lineales por Gauss Resuelve por Gauss 3 7 3 3 3 3 6 http://www.outube.com/watch?vpuen0s0idwc.- Sistema ecuaciones lineales por Gauss Resuelve por Gauss 3-3 5-3 -0 0 http://www.outube.com/watch?vfhmvwv5wfuo
.- Sistema ecuaciones lineales por Gauss Resuelve por Gauss 3 7 3 3 3 3 6 http://www.outube.com/watch?vpuen0s0idwc.- Sistema ecuaciones lineales por Gauss Resuelve por Gauss 3-3 5-3 -0 0 http://www.outube.com/watch?vfhmvwv5wfuo
Funciones lineales. Objetivos. Antes de empezar. 1.Función de proporcionalidad directa pág. 170 Definición Representación gráfica
 10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
Examen de Matemáticas 2 o de Bachillerato Mayo 2003
 Examen de Matemáticas o de Bachillerato Mayo 00 1. Expresar el número 60 como suma de tres enteros positivos de forma que el segundo sea el doble del primero y su producto sea máximo. Determinar el valor
Examen de Matemáticas o de Bachillerato Mayo 00 1. Expresar el número 60 como suma de tres enteros positivos de forma que el segundo sea el doble del primero y su producto sea máximo. Determinar el valor
4 ECUACIONES Y SISTEMAS
 4 ECUACIONES Y SISTEMAS PARA EMPEZAR 1 Indica si las siguientes igualdades son identidades o ecuaciones, y resuelve estas últimas. a) 5 1 4 c) ( )( ) 4 b) 5 d) 7 5 10 a) Identidad c) Identidad b) Ecuación.
4 ECUACIONES Y SISTEMAS PARA EMPEZAR 1 Indica si las siguientes igualdades son identidades o ecuaciones, y resuelve estas últimas. a) 5 1 4 c) ( )( ) 4 b) 5 d) 7 5 10 a) Identidad c) Identidad b) Ecuación.
Sistemas de ecuaciones lineales
 José María Martíne Mediano (SM, www.profes.net) de ecuaciones lineales CTJ5. Resuelve el siguiente sistema de ecuaciones: 9 Lo resolvemos por el método de Gauss. 9 7 6 E E E E 7 6 La solución es: = ; =
José María Martíne Mediano (SM, www.profes.net) de ecuaciones lineales CTJ5. Resuelve el siguiente sistema de ecuaciones: 9 Lo resolvemos por el método de Gauss. 9 7 6 E E E E 7 6 La solución es: = ; =
2. Si P(x)= x 3 -x 2-3x+1, Q(x)= 2x 2-2x+1 y R(x)= 2x 3-6x 2 +6x-1, opera: a) P+Q; b) P-Q+R; c) 2P-3R; d) P.Q-R; e) P+Q-R; f) Q.
 ejerciciosyeamenes.com POLINOMIOS 1. Si P()= - +1 y Q()= -+, opera: a) P-Q b) P+Q c) P+Q P.Q Sol: a) P-Q= -6 +-1 b) P+Q= 1 - -6+7 c) P+Q= -+ P.Q= 1 5-1 +17 - -+. Si P()= - -+1, Q()= -+1 y R()= -6 +6-1,
ejerciciosyeamenes.com POLINOMIOS 1. Si P()= - +1 y Q()= -+, opera: a) P-Q b) P+Q c) P+Q P.Q Sol: a) P-Q= -6 +-1 b) P+Q= 1 - -6+7 c) P+Q= -+ P.Q= 1 5-1 +17 - -+. Si P()= - -+1, Q()= -+1 y R()= -6 +6-1,
