Ecuaciones Diferenciales
|
|
|
- David Espinoza Belmonte
- hace 6 años
- Vistas:
Transcripción
1 1.- Resolver la siguiente ecuación diferencial: (x + y -4) dx + (5y -1) dy=0.- Obtener la solución general de la ecuación diferencial (x-1) y dx + x (y+1) dy = 0. Hallar la solución particular que pasa por el punto (1,1). 3.-a. Hallar la solución general de la ecuación diferencial: (3x + y - 5)dx + (6x + y - l)dy = 0 b. Hallar la solución particular que pasa por el punto (1, ). 4.- Dada la ecuación diferencial y 3 dx - x (y + x)dy = O. Se pide: a) Clasificarla. b) Resolverla utilizando la función de DERIVE adecuada. c) Hallar la solución particular que pasa por el punto (1,3) 5.- a) Clasificar y resolver la siguiente ecuación diferencial con la función de Derive específica para este tipo de ecuaciones: (x 4 + x + xy + l)dx - (1 + x )dy = 0. b) Hallar la solución particular que pasa por el pimío (,3). 6.- Indicar de qué tipo es la siguiente ecuación diferencial y resolverla utilizando la función de Derive específica para este tipo de ecuaciones: y y xdx y cos dx x cos dy 0 x x 7.-. Hallar la solución general de la ecuación diferencial: (3x - y - l)dx + (5x - y- 3)dy = 0 xyln ydx x y y 1 dy Resolver la ecuación diferencial 9.- Resolver la ecuación diferencial dy ycosx sen(x) dx 10.- Resolver la ecuación diferencial (x 3 +y 4 )dx+8xy 3 dy= Esta nevando con regularidad a las 1 sale una máquina quitanieves que recorre en la 1ªhora km y en la segunda 1 km. A qué hora empezó a nevar? (Se admitirá como hipótesis que la cantidad de nieve quitada por la máquina en la unidad de tiempo es uniforme, de modo que su velocidad de avance resulta inversamente proporcional a la altura de la nieve encontrada) U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 1
2 1.- a) Clasificar y resolver la siguiente ecuación diferencial con la función de DERIVE específica para este tipo de ecuaciones: y' x y xy y b) Hallar la solución particular que pasa por el punto (0, 1). 13.-Para las siguientes ecuaciones diferenciales, clasificarlas y resolverlas, con la función específica de DERIVE para cada tipo. Calcular también la solución particular que pasa por el punto indicado: a) (xy - 4x) dx + dy = 0. Punto (, ). b) (x 3 + 3y) dx + (3x + y -1)dy = 0. Punto (1, 0). c) y = x y. Punto (1,1). y x d) (3y - 5) dx+ x 1 dy = 0. Punto (, ). e) (xy - 4x) dx + dy = 0. Punto (, ). f) (x 3 + 3y) dx + (3x + y -1) dy = 0. Punto (1, 0) Resolver las ecuaciones diferenciales siguientes reduciéndolas a una ecuación de variables separables o a una ecuación homogénea, según proceda: a.- (x + y) dx + (3x +3y 4) dy = 0 b.- (x + y-) dx + (x -y +4) dy = 0 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos
3 1.- Resolver la siguiente ecuación diferencial: (x + y -4) dx + (5y -1) dy=0 Solución: #: DSOLVE1( x + y - 4, 5 y - 1, x, y, c) #3: inapplicable #4: SOLVE([ x + y - 4 = 0, 5 y - 1 = 0], [x, y]) 19 1 #5: x = y = 10 5 Efectuamos el cambio de variable: u=x-19/10, v=y-1/ #6: u + + v #7: u + v 1 #8: 5 v #9: 5 v La nueva ecuación a resolver es: #11: ( u + v) d u + (5 v) d v = 0 que es homogénea: u + v #13: HOMOGENEOUS_GEN -, u, v, c 5 v u 39 (u + 10 v) LN #14: 39 ATAN 39 u u + u v + 5 v + = LN(u) + c 39 Deshacemos el cambio de variable y queda: x y ATAN #15: x x - 10 LN x - + x - y y = 19 LN x - + c 10 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 3
4 .- Obtener la solución general de la ecuación diferencial (x-1) y dx + x (y+1) dy = 0. Hallar la solución particular que pasa por el punto (1,1). Solución: (x - 1) y #1: SEPARABLE_GEN, -, x, y, c y + 1 x x + c x - 1 #: LN(y) + y = LN(x) - x (x - 1) y #3: SEPARABLE, -, x, y, 1, 1 y + 1 x x - x - 1 #4: LN(y) + y = LN(x) - x U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 4
5 3.-a. Hallar la solución general de la ecuación diferencial: (3x + y - 5)dx + (6x + y - l)dy = 0 b. Hallar la solución particular que pasa por el punto (1, ). Solución: a) Solución general de la ecuación diferencial (3x+y-5)dx+(6x+y-l)dy=0 #1: DSOLVEl_GEN(3-x + y - 5, 6-x + -y - 1, x, y, c) #: inapplicable Hay que efectuar un cambio de variable antes de resolverla con DERIVE: u = 3 x + y, y = u 3 x, dy = du 3 dx (u-5)dx+(u-l)(du-3dx)=0, (-5u-)dx+(u-l)du=0, u'=(5u-)/(u-l) que ya es de variables separadas. 5 u - #3: SEPARABLE_GEN 1,, x, u, c u - 1 LN(5 u - ) u #4: - = -x - c 5 5 LN(15 x + 5 y - ) (3 x + y) #5: - = -x - c 5 5 b) Solución particular que pasa por el punto (1,) Si x=l, y=, entonces, u=3x+y=5 5 u - #6: SEPARABLE 1,, x, u, 1, 5 u - 1 LN(5 u - ) u LN(3) #7: - = -x LN(15 x + 5 y - ) (3 x + y) LN(3) #8: - = -x U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 5
6 4.- Dada la ecuación diferencial y 3 dx - x (y + x)dy = O. Se pide: a) Clasificarla. b) Resolverla utilizando la función de DERIVE adecuada. c) Hallar la solución particular que pasa por el punto (1,3) Solución: a) Es una ecuación diferencial ordinaria de primer orden homogénea. b) 3 y #1: HOMOGENEOUS_GEN, x, y, c x ( y + x) 1 x ( - 1) + y #: - LN x 4 1 y - x ( + 1) y LN + LN = - LN(x) - c x x b) 3 y #3: HOMOGENEOUS, x, y, 1, 3 x ( y + x) 1 x ( - 1) + y #4: - LN x 4 1 y - x ( + 1) y x LN + LN = - LN - + x x LN() LN( - 1) + - LN( + 1) - 4 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 6
7 5.- a) Clasificar y resolver la siguiente ecuación diferencial con la función de Derive específica para este tipo de ecuaciones: (x 4 + x + xy + l)dx - (1 + x )dy = 0. b) Hallar la solución particular que pasa por el pimío (,3) Solución: a) La ecuación puede escribirse en la forma dy 1x xy xy y' dx 1x 1x 1x Que es una ecuación lineal x LINEAR1_GEN -, 1 + x, x, y, c #1: 1 + x #: y = (x + c) (x + 1) b) x LINEAR1 -, 1 + x, x, y,, 3 #3: 1 + x (x + 1) (5 x - 7) #4: y = 5 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 7
8 6.- Indicar de qué tipo es la siguiente ecuación diferencial y resolverla utilizando la función de Derive específica para este tipo de ecuaciones: y y xdx y cos dx x cos dy 0 x x Solución: Vemos que no puede tratarse de una ecuación diferencial de variables separables pues es imposible separar x e y. Para ver si es homogénea despejamos y. y ycos x y y dy x y 1 xdx ycos dx x cos dy 0 y ' x x dx y x y xcos cos x x Sustituyendo x por xt e y por yt, obtenemos ty 1 y 1 y' tx ty x y cos cos tx x Se trata de una ecuación homogénea y y COS - x x #1: HOMOGENEOUS_GEN, x, y, c y x COS x y #: SIN = - LN(x) - c x U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 8
9 7.-. Hallar la solución general de la ecuación diferencial: (3x - y - l)dx + (5x - y- 3)dy = 0 Solución: #1: DSOLVE1_GEN(3 x - y - 1, 5 x - y - 3, x, y, c) #: inapplicable #3: SOLVE([3 x - y - 1, 5 x - y - 3], [x, y]) #4: [x = 1 y = ] Realizamos el cambio: u=x-1 con du=dx v=y- con dv=dy 3x y l dx 5x y 3 dy 0 3 u 1 v l du 5 u 1 v 3 dv 0 3u v 3u vdu 5u vdv 0 v ' 5u v 3 u - v #5: HOMOGENEOUS_GEN -, u, v, c 5 u - v u ( 7 - ) + v 1 #6: + LN u 3 7 v - u ( 7 + ) LN = - LN(u) - c 14 u x ( 7 - ) + y #7: + LN x x ( 7 + ) - y - 7 LN = - LN(x - 1) - c x U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 9
10 8.- Resolver la ecuación diferencial xy ln ydx x y y 1 dy 0 Solución: La ecuación M(x,y)dx+N(x,y)dy=0 se llama ecuación diferencial exacta o ecuación en diferenciales totales si M(x,y) y N(x,y) son funciones continuas y derivables que verifican: M y N siendo M N, continuas en un cierto dominio. x y x M N x ln y 1 x y x En nuestro caso, no es diferencial exacta, sin embargo mediante un factor integrante se transforma en: Mdx+Ndy=0 diferencial exacta. Para 1 x y y 1 y x ln ydx dy 0 y y Obtenemos Aplicando la solución general Mdx x ln ydx x ln y Mdx x ln y y y y x Mdx N Mdx dy C y N Mdx dy dy y y 1dy y 1 y y y 3 x y y 1 x 1 Resulta 1 3/ 3 x lny y 1 C 3/ U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 10
11 dy 9.- Resolver la ecuación diferencial ycosx sen(x) dx Solución: dy Se trata de una ecuación lineal no homogénea p(x)y q(x) dx q(x)=sen(x) siendo p(x) = -cosx; Haciendo y=u(x)v(x) en la ecuación dada: y' u'vuv' uvcosxsen(x) u'vu v' vcosx senx Resolvemos senx v' v' vcosx 0 cosx v e y sustituyendo en la anterior v senx senx senx u 'e senx u sen(x)e dx C e (senx ) C que junto con v se obtiene y uv (senx) Ce senx U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 11
12 10.- Resolver la ecuación diferencial (x 3 +y 4 )dx+8xy 3 dy=0. Solución: Consideramos P P(x, y) x y 4y y Q Q(x, y) 8xy 8y x 3 3 Utilizamos un factor integrante P Q 3 3 y x 4y 8y / ln lnx 3 x Q 8xy x x Obtenemos la ecuación diferencial exacta x y 8xy dx dy 0 x x Resolvemos 8xy xy F(x, y) dy h(y) h(y) xy h(y) x x Por último, F 1 x y y h'(x) h'(x) x h(x) x x x x / 7/ 4 F(x, y) xy h(y) 7 4 7/ xy x C U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 1
13 11.- Esta nevando con regularidad a las 1 sale una máquina quitanieves que recorre en la 1ªhora km y en la segunda 1 km. A qué hora empezó a nevar? (Se admitirá como hipótesis que la cantidad de nieve quitada por la máquina en la unidad de tiempo es uniforme, de modo que su velocidad de avance resulta inversamente proporcional a la altura de la nieve encontrada) Solución: ds Consideramos que la v=k 1 /h, siendo h la altura de la nieve y v la velocidad. Si dt llamamos t 0 el instante en que empezó a nevar la altura de la nieves quedará h=k (t-t 0 ), luego ds k1 k1 k k v ds dt s kln tt0 C dt h k tt tt tt Teniendo en cuenta las soluciones particulares del enunciado. t 1;s0kln1t0 C0 t 11;skln13t0 C t 1;s1kln14t0 C3 Haciendo el cambio T=1-t 0 kln T C0 T1 ln 3 kln T1ln T T T1 T kln T1C klnt lnt 3 T 3 T T kln T C 3 ln T Y simplificando T 1 T T T 3T 3T 1 T 4T T T T 1 0 T Deshaciendo el cambio nos quedamos con 1 5 t0 1 T Empezó a nevar a las 11h m 55s U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 13
14 1.- a) Clasificar y resolver la siguiente ecuación diferencial con la función de DERIVE específica para este tipo de ecuaciones: y' x y xy y b) Hallar la solución particular que pasa por el punto (0, 1). Solución a) La ecuación puede escribirse en la forma: x y dx xy ydy 0 Es una ecuación diferencial exacta pues: x y xy y y y x #1: EXACT_GEN(x - y, - x y - y, x, y, c) x y #: - x y - = c b) Solución particular que pasa por (0, 1) #3: EXACT(x - y, - x y - y, x, y, 0, 1) x y - 1 #4: - x y - = 0 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 14
15 13.-Para las siguientes ecuaciones diferenciales, clasificarlas y resolverlas, con la función específica de DERIVE para cada tipo. Calcular también la solución particular que pasa por el punto indicado: a) (xy - 4x) dx+dy = 0. Punto (, ). b) (x 3 + 3y) dx+(3x + y -1)dy = 0. Punto (1, 0). c) y = x y. Punto (1,1). y x d) (3y - 5) dx+ x 1 dy = 0. Punto (, ). e) (xy - 4x) dx + dy = 0. Punto (, ). f) (x 3 + 3y) dx + (3x + y -1) dy = 0. Punto (1, 0). Solución a) Es una ecuación diferencial lineal pues puede escribirse en la forma: y + x y = 4 x #1: LINEAR1_GEN( x, 4 x, x, y, c) #: - x y = c e + Solución particular: #3: LINEAR1( x, 4 x, x, y,, ) #4: y = b) Es una ecuación diferencial exacta pues: x 3 3y 3x y 1 3 y x 3 #4: EXACT_GEN( x + 3 y, 3 x + y - 1, x, y, c) 4 x y #5: + 3 x y + - y = c 3 #6: EXACT( x + 3 y, 3 x + y - 1, x, y, 1, 0) 4 x y 1 #7: + 3 x y + - y = c) Es una ecuación diferencial homogénea pues está escrita en la forma y = r(x, y), siendo r(x, y) una función homogénea de grado 0. También porque puede escribirse como U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 15
16 x y dx xydy 0 mismo grado. Ecuaciones Diferenciales, siendo los coeficientes de dx y de dy polinomios homogéneos del x y #1: HOMOGENEOUS_GEN +, x, y, c y x y #: = LN(x) + c x x y #3: HOMOGENEOUS_GEN +, x, y, 1, 1 y x y #4: = LN(x) + x d) Es una ecuación diferencial lineal pues puede escribirse en la forma y + p(x) y = q(x), concretamente, y + 3xy = 5x #5: LINEAR1_GEN(3 x, 5 x, x, y, c) - 3 x / 5 #6: y = c e + 3 #7: LINEAR1(3 x, 5 x, x, y,, 3) 6-3 x / #8: 4 e 5 y = e) (xy - 4x) dx + dy = 0. Punto (, ). Es una ecuación diferencial lineal pues puede escribirse en la forma: y + x y = 4 x #: LINEAR1_GEN( x, 4 x, x, y, c) #3: - x y = c e + Solución particular: #8: LINEAR1( x, 4 x, x, y,, ) #9: y = f) (x 3 + 3y) dx + (3x + y -1) dy = 0. Punto (1, 0). U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 16
17 Es una ecuación diferencial exacta pues: Ecuaciones Diferenciales x 3 3y 3x y 1 3 y 3 #1: EXACT_GEN( x + 3 y, 3 x + y - 1, x, y, c) 4 x y #: + 3 x y + - y = c Solución particular: 3 #3: EXACT( x + 3 y, 3 x + y - 1, x, y, 1, 0) 4 x y 1 #4: + 3 x y + - y = x U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 17
18 14.- Resolver las ecuaciones diferenciales siguientes reduciéndolas a una ecuación de variables separables o a una ecuación homogénea, según proceda: a.- (x + y) dx + (3x +3y 4) dy = 0 b.- (x + y-) dx + (x -y +4) dy = 0 Solución a.- (x + y) dx + (3x +3y 4) dy = 0 Las rectas x y 0 3x + 3 y son rectas paralelas. Se efectúa el cambio de variable: u = x + y Sustituyendo en la ecuación queda: du = dx + dy, y = u x, dy = du - dx. (x + (u x)) dx + (3x + 3(u - x) - 4) (du dx) = 0 u 4dx 3u 4du 0 u 4 u 43u 4u ' 0 u ', que ya es una ecuación de variables separadas. 4 3u u - 4 #5: SEPARABLE_GEN 1, -, x, u, c 4-3 u 3 u #6: LN(u - ) + = x + c Deshaciendo el cambio de variable, se obtiene: 3 (x + y) #7: LN((x + y) - ) + = x + c b.- (x + y-) dx + (x -y +4) dy = 0 x y 0 Las rectas se cortan en el punto (- x y , 8 ), que se calcula sin más que 3 resolver el sistema formado por sus dos ecuaciones. Se efectúa el cambio de variables: u = x v = y - 3 du = dx, dv = dy x = u y = v + 3. Sustituyendo en la ecuación queda: U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 18
19 8 8 (( u - ) + ( v + ) ) du + (( u - ) ( v + ) + 4) dv = u v uvduuvdv0 v', que ya es una ecuación homogénea. u v u + v #1: HOMOGENEOUS_GEN -, u, v, c u - v 13 1 u ( 13-3) + v 1 #: + LN u 13 v - u ( ) LN = - LN(u) - c 6 u Deshaciendo el cambio de variable, se obtiene: 8 x + ( 13-3) + y #3: + LN x y - - x + ( ) LN = - LN x + - c 6 3 x x ( 13-3) + (3 y ) 1 #4: + LN x + 13 (3 y ) - 3 x ( ) LN = x + 3 x + LN - c 3 U. D. de Matemáticas de la ETSITGC Asignatura: Métodos Matemáticos 19
20 Ecuación diferencial Es toda ecuación que incluya una función, que es la incógnita, y alguna de sus derivadas o diferenciales. Las ecuaciones diferenciales se clasifican según su: tipo: Ordinarias si la función incógnita es de una sola variable independiente. En derivadas parciales si la función incógnita depende de dos o más orden: El de la derivada de mayor orden que aparece en la ecuación. Ecuación diferencial ordinaria de primer orden Es una ecuación de la forma F(x,y,y )=0. A veces la ecuación anterior se puede expresar en la forma y =G(x,y), diremos que la ecuación diferencial viene expresada en forma normal. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 70
21 Ecuación de Bernouilli Es toda ecuación diferencial de la forma dy p(x)y q(x)y n donde n0,1, ya que en dx dichos casos sería lineal U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 71
22 Ecuación lineal Se llama ecuación lineal a una ecuación de la forma: a1x1 a x... a n x n b, donde los coeficientes a 1,a,..., a n, así como el término independiente b, son escalares de un cuerpo conmutativo K, y x, x,..., son las incógnitas. 1 x n U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 73
23 Ecuaciones diferenciales exactas La ecuación M(x,y)dx+N(x,y)dy=0 se llama ecuación diferencial exacta o ecuación en diferenciales totales si M(x,y) y N(x,y) son funciones continuas y derivables que verifican: M y N siendo M N, continuas en un cierto dominio. x y x U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 75
24 Ecuaciones lineales de primer orden Se llama ecuación diferencial lineal de primer orden a la que es lineal respecto de la función incógnita y su derivada. Es de la forma: dy dx p(x)y q(x) 1. Si q(x)=0 la ecuación se denomina lineal homogénea y es de variables separables; entonces: dy p(x)y 0 dx. Si q(x)0 la ecuación se denomina lineal no homogénea. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 76
25 Ecuaciones con variables separadas y ecuaciones reducibles a ellas Toda ecuación de la forma f(y)dy=g(x)dx se llama ecuación de variables separadas. La solución general es de la forma f( y) dy g( x) dx C Las ecuaciones de la forma f(y)h(x)dy=g(x)m(y)dx donde los coeficientes de las diferenciales se descomponen en factores que dependen solo de x, o solo de y, se llaman ecuaciones con variables separables. Dividiendo por h(x)m(y) la anterior ecuación, se obtiene una de variables separadas: f( y) my dy gx ( ) ( ) hx ( ) dx f( y) my ( ) dy gx ( ) hx ( ) dx Observación. La división por h(x)m(y) puede dar lugar a que se pierdan las soluciones particulares que anulan el producto h(x) m(y). U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 78
26 Ecuaciones homogéneas Toda ecuación diferencial que pueda escribirse de la forma dy dx F y se dice x que es homogénea. También puede venir dada en la forma P(x,y)dx+Q(x,y)dy=0 siendo P(x,y), Q(x,y) funciones homogéneas del mismo grado. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 80
Ecuaciones Diferenciales
 1.- Resolver la siguiente ecuación diferencial: (x + y -4) dx + (5y -1) dy=0.- Obtener la solución general de la ecuación diferencial (x-1) y dx + x (y+1) dy = 0. Hallar la solución particular que pasa
1.- Resolver la siguiente ecuación diferencial: (x + y -4) dx + (5y -1) dy=0.- Obtener la solución general de la ecuación diferencial (x-1) y dx + x (y+1) dy = 0. Hallar la solución particular que pasa
+ = 0, siendo z=f(x,y).
 Ecuaciones diferenciales de primer orden ECUACIONES DIFERENCIALES Definición. Se llama ecuación diferencial a toda ecuación que inclua una función, que es la incógnita, alguna de sus derivadas o diferenciales.
Ecuaciones diferenciales de primer orden ECUACIONES DIFERENCIALES Definición. Se llama ecuación diferencial a toda ecuación que inclua una función, que es la incógnita, alguna de sus derivadas o diferenciales.
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
1. ECUACIONES DIFERENCIALES ORDINARIAS
 1 1. ECUACIONES DIFERENCIALES ORDINARIAS 1.1. PRIMERAS DEFINICIONES. PROBLEMA DEL VALOR INICIAL Definición 1.1. Una ecuación diferencial es una ecuación en la que intervienen una variable dependiente y
1 1. ECUACIONES DIFERENCIALES ORDINARIAS 1.1. PRIMERAS DEFINICIONES. PROBLEMA DEL VALOR INICIAL Definición 1.1. Una ecuación diferencial es una ecuación en la que intervienen una variable dependiente y
ECUACIONES DIFERENCIALES
 ECUACIONES DIFERENCIALES DEFINICIÓN Ecuación Diferencial es una ecuación que contiene las derivadas o diferenciales de una función de una o más variables. 1. Si hay una sola variable independiente, las
ECUACIONES DIFERENCIALES DEFINICIÓN Ecuación Diferencial es una ecuación que contiene las derivadas o diferenciales de una función de una o más variables. 1. Si hay una sola variable independiente, las
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos. Ecuaciones diferenciales ordinarias
 Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
Ecuaciones diferenciales en la Química. Modelos.
 Capítulo 1 Ecuaciones diferenciales en la Química. Modelos. 1.1 Introducción. Muchos fenómenos naturales (físicos, químicos, biológicos, etc. ) responden, en sus resultados, a formulaciones matemáticas
Capítulo 1 Ecuaciones diferenciales en la Química. Modelos. 1.1 Introducción. Muchos fenómenos naturales (físicos, químicos, biológicos, etc. ) responden, en sus resultados, a formulaciones matemáticas
1. ECUAC. DIFERENCIALES ORDINARIAS
 1 1. ECUAC. DIFERENCIALES ORDINARIAS Variables separables. 1. Hallar la solución general de la ecuación de variables separables (x 2 + 4) dy dx = xy. Al separar variables, queda la expresión 1 y dy = ambos
1 1. ECUAC. DIFERENCIALES ORDINARIAS Variables separables. 1. Hallar la solución general de la ecuación de variables separables (x 2 + 4) dy dx = xy. Al separar variables, queda la expresión 1 y dy = ambos
Contenidos. Grupo EDUMATICUS. Departamento de Matemática Aplicada. Universidad de Málaga 2
 Tema 2 Ecuaciones diferenciales ordinarias de primer orden Definiciones generales Problema de Cauchy Contenidos Resolución de ecuaciones diferenciales ordinarias de primer orden Resolución de ecuaciones
Tema 2 Ecuaciones diferenciales ordinarias de primer orden Definiciones generales Problema de Cauchy Contenidos Resolución de ecuaciones diferenciales ordinarias de primer orden Resolución de ecuaciones
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Ecuaciones Diferenciales
 Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II
 4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
CAPÍTULO 1 INTRODUCCION
 CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS.
 160 LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS. JUSTIFICACIÓN En esta lección centraremos nuestro estudio en aquellas ecuaciones diferenciales homogéneas mediante
160 LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS. JUSTIFICACIÓN En esta lección centraremos nuestro estudio en aquellas ecuaciones diferenciales homogéneas mediante
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5
 Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
Variables separables
 Definición: Variables separables Si el segundo miembro de una ecuación expresada de la forma: puede expresar como una función que depende solamente de x, multiplicada por una función que depende solamente
Definición: Variables separables Si el segundo miembro de una ecuación expresada de la forma: puede expresar como una función que depende solamente de x, multiplicada por una función que depende solamente
Tema 6: Ecuaciones diferenciales lineales.
 Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial
 Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial Sergio Blanes http://personales.upv.es/ serblaza Instituto de Matemtica Multidisciplinar Universidad Politécnica de Valencia Edificio 8-G, entrada
Matemáticas II: Segundo del Grado en Ingeniería Aeroespacial Sergio Blanes http://personales.upv.es/ serblaza Instituto de Matemtica Multidisciplinar Universidad Politécnica de Valencia Edificio 8-G, entrada
EJERCICIOS UNIDADES 1, 2 Y 3
 EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
Herramientas digitales de auto-aprendizaje para Matemáticas
 ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
2.4 Ecuaciones diferenciales de Bernoulli
 .4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
.4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO
 MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
MATEMÁTICAS AVANZADAS PARA LA INGENIERÍA EN SISTEMAS CLAVE: MIS 206 PROFESOR: MTRO. ALEJANDRO SALAZAR GUERRERO 1 1. SISTEMAS LINEALES DISCRETOS Y CONTINUOS 1.1. Modelos matemáticos 1.2. Sistemas 1.3. Entrada
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 17/01/2013
 MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
MATEMÁTICAS II - EXAMEN SEGUNDO PARCIAL - 7// Código: Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio. Considera la región R del primer cuadrante que
2.3 Ecuaciones diferenciales lineales
 .3 Ecuaciones diferenciales lineales 45.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos la atención
.3 Ecuaciones diferenciales lineales 45.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos la atención
2.11. Diferencial de funciones vectoriales.
 2 Diferencial de funciones vectoriales Definición 2 Una función vectorial es una aplicación f : D R n R m tal que a cada vector x = (x, x 2,, x n D R n le hace corresponder un vector y = (y, y 2,, y m
2 Diferencial de funciones vectoriales Definición 2 Una función vectorial es una aplicación f : D R n R m tal que a cada vector x = (x, x 2,, x n D R n le hace corresponder un vector y = (y, y 2,, y m
4.2 Reducción de orden
 4. educción de orden 87 Un conjunto de funciones f y ; y g que cumple con la condición anterior se llama un conjunto fundamental de soluciones. Es decir, un conjunto f y ; y g será un conjunto fundamental
4. educción de orden 87 Un conjunto de funciones f y ; y g que cumple con la condición anterior se llama un conjunto fundamental de soluciones. Es decir, un conjunto f y ; y g será un conjunto fundamental
1.9 Sustituciones diversas 49
 1.9 Sustituciones diversas 49 1.9 Sustituciones diversas En ocasiones tenemos ecuaciones diferenciales que no corresponden a ninguna forma de ecuación conocida, donde, para resolverlas fácilmente recurrimos
1.9 Sustituciones diversas 49 1.9 Sustituciones diversas En ocasiones tenemos ecuaciones diferenciales que no corresponden a ninguna forma de ecuación conocida, donde, para resolverlas fácilmente recurrimos
Selectividad Matemáticas II septiembre 2014, Andalucía
 Selectividad Matemáticas II septiembre 14, Andalucía Pedro González Ruiz 17 de septiembre de 14 1. Opción A Problema 1.1 Sabiendo que lím x cos(3x) e x +ax xsen(x) Sea l el límite pedido. Tenemos: es finito,
Selectividad Matemáticas II septiembre 14, Andalucía Pedro González Ruiz 17 de septiembre de 14 1. Opción A Problema 1.1 Sabiendo que lím x cos(3x) e x +ax xsen(x) Sea l el límite pedido. Tenemos: es finito,
Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Ecuaciones Diferenciales Ordinarias
 Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
1. Ecuaciones Exactas. M(x, y)x + N(x, y) = 0 (1.4)
 1. Ecuaciones Exactas Consideremos la ecuación diferencial M(x, y) + N(x, y)y = 0 (1.1) en donde la variable independiente es x y la variable dependiente es y. Vamos a asociar a esta ecuación diferencial
1. Ecuaciones Exactas Consideremos la ecuación diferencial M(x, y) + N(x, y)y = 0 (1.1) en donde la variable independiente es x y la variable dependiente es y. Vamos a asociar a esta ecuación diferencial
TRABAJO DE MATEMÁTICAS. PENDIENTES DE 3º ESO. (2ª parte)
 TRABAJO DE MATEMÁTICAS PENDIENTES DE 3º ESO. (2ª parte) 1 OPERACIONES CON POLINOMIOS 1.-) Dados los polinomios: P(x) = 3x 2 + 3x - 1, Q(x) = 3x 2 + 2x + 1 y R(x) = -x 3 + 2x 2 +1. Calcular: a) P - Q R
TRABAJO DE MATEMÁTICAS PENDIENTES DE 3º ESO. (2ª parte) 1 OPERACIONES CON POLINOMIOS 1.-) Dados los polinomios: P(x) = 3x 2 + 3x - 1, Q(x) = 3x 2 + 2x + 1 y R(x) = -x 3 + 2x 2 +1. Calcular: a) P - Q R
INTEGRALES INDEFINIDAS
 INTEGRALES INDEFINIDAS Índice: 1. Primitiva de una función--------------------------------------------------------------------------- 2 2. Interpretación geométrica. Propiedades de la integral indefinida--------------------------
INTEGRALES INDEFINIDAS Índice: 1. Primitiva de una función--------------------------------------------------------------------------- 2 2. Interpretación geométrica. Propiedades de la integral indefinida--------------------------
Ecuaciones diferenciales de primer orden
 Práctica Ecuaciones diferenciales de primer orden.. Introducción Para resolver una ecuación diferencial en la forma F (x, y, y ) = 0, o bien y = f(x, y) (.) el Mathematica dispone del comando DSolve, cuya
Práctica Ecuaciones diferenciales de primer orden.. Introducción Para resolver una ecuación diferencial en la forma F (x, y, y ) = 0, o bien y = f(x, y) (.) el Mathematica dispone del comando DSolve, cuya
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
P R I M E R B L O Q U E E C. D I F E R E N C I A L E S
 P R I M E R B L O Q U E E C. D I F E R E N C I A L E S Os proponemos una serie de ejercicios tipo examen de la asignatura Matemáticas II del Grado de Industriales. 1. y = t y t 1 + y ; y(0) = 1 2. Resolver
P R I M E R B L O Q U E E C. D I F E R E N C I A L E S Os proponemos una serie de ejercicios tipo examen de la asignatura Matemáticas II del Grado de Industriales. 1. y = t y t 1 + y ; y(0) = 1 2. Resolver
Ecuaciones Diferenciales
 UNIVERSIDAD DIEGO PORTALES Ecuaciones Diferenciales 1 ECUACIONES DIFERENCIALES Una ecuación diferencial contiene una función desconocida y algunas de sus derivadas. He aquí algunos ejemplos: (1) y ' =
UNIVERSIDAD DIEGO PORTALES Ecuaciones Diferenciales 1 ECUACIONES DIFERENCIALES Una ecuación diferencial contiene una función desconocida y algunas de sus derivadas. He aquí algunos ejemplos: (1) y ' =
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
Integrales indenidas
 Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas.
 Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas. 1.- El polinomio p 3 (x) = 2 (x + 1) + x(x + 1) 2x(x + 1)(x 1) interpola a los primeros cuatro datos de la tabla x
Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas. 1.- El polinomio p 3 (x) = 2 (x + 1) + x(x + 1) 2x(x + 1)(x 1) interpola a los primeros cuatro datos de la tabla x
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M.
 Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
Soluciones de ecuaciones de primer orden
 GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
CÁLCULO DE PRIMITIVAS
 CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
CÁLCULO DE PRIMITIVAS David Ariza-Ruiz Departamento de Análisis Matemático Seminario I 7 de noviembre de 202 (Universidad de Sevilla) David Ariza Ruiz 7 de noviembre de 202 / 42 Definición y propiedades
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Cálculo I Aplicaciones de las Derivadas: Linealización y Diferenciales. Julio C. Carrillo E. * 1. Introducción 1. 2.
 4.7. Aplicaciones de las Derivadas: Linealización y Diferenciales Julio C. Carrillo E. * Índice 1. Introducción 1 2. Errores 2 3. Linealización 4 4. Diferenciales 10 A. Teorema de Taylor (Opcional) 17
4.7. Aplicaciones de las Derivadas: Linealización y Diferenciales Julio C. Carrillo E. * Índice 1. Introducción 1 2. Errores 2 3. Linealización 4 4. Diferenciales 10 A. Teorema de Taylor (Opcional) 17
Universidad de Chile Integración por partes. Ingeniería Matemática SEMANA 6: PRIMITIVAS
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
Contenidos de los preliminares
 Preliminares del tema Contenidos de los preliminares Propiedades de los logaritmos Un par de primitivas elementales Algunas ideas sobre la función arcotangente Funciones hiperbólicas Descomposición en
Preliminares del tema Contenidos de los preliminares Propiedades de los logaritmos Un par de primitivas elementales Algunas ideas sobre la función arcotangente Funciones hiperbólicas Descomposición en
Jorge Mozo Fernández Dpto. Matemática Aplicada
 Álgebra y Ecuaciones Diferenciales Lineales y Matemáticas II E.T.S. Ingenieros de Telecomunicación I.T. Telecomunicación Esp. Telemática y Sistemas de Telecomunicación Curso 2009-2010 Tema 6: Introducción
Álgebra y Ecuaciones Diferenciales Lineales y Matemáticas II E.T.S. Ingenieros de Telecomunicación I.T. Telecomunicación Esp. Telemática y Sistemas de Telecomunicación Curso 2009-2010 Tema 6: Introducción
4 Ecuaciones diferenciales de orden superior
 CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4. educción de orden allar un método para encontrar soluciones que formen un conjunto fundamental de la ED será nuestro trabajo en las siguientes secciones.
CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4. educción de orden allar un método para encontrar soluciones que formen un conjunto fundamental de la ED será nuestro trabajo en las siguientes secciones.
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Septiembre 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-5-V-2-00-2013 CURSO: Matemática Intermedia III SEMESTRE: Segundo CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN:
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-5-V-2-00-2013 CURSO: Matemática Intermedia III SEMESTRE: Segundo CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN:
Tema 1 Generalidades sobre Ecuaciones Diferenciales Ordinarias (E.D.O.)
 Tema 1 Generalidades sobre Ecuaciones Diferenciales Ordinarias (E.D.O.) 1.1 Definiciones Se llama ecuación diferencial a toda ecuación que contiene las derivadas de una o más variables dependientes respecto
Tema 1 Generalidades sobre Ecuaciones Diferenciales Ordinarias (E.D.O.) 1.1 Definiciones Se llama ecuación diferencial a toda ecuación que contiene las derivadas de una o más variables dependientes respecto
3. Ecuaciones diferenciales. Mayo, 2009
 Cálculo 3. Ecuaciones diferenciales Mayo, 2009 Clasificación de las ecuaciones diferenciales 1. Ecuaciones diferenciales ordinarias 1.a Ecuaciones diferenciales ordinarias de primer orden Nociones generales
Cálculo 3. Ecuaciones diferenciales Mayo, 2009 Clasificación de las ecuaciones diferenciales 1. Ecuaciones diferenciales ordinarias 1.a Ecuaciones diferenciales ordinarias de primer orden Nociones generales
Problema de Valor Inicial (PVI):
 Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 201 Capítulo 4 Año 200 4.1. Modelo 200 - Opción A Problema 4.1.1 2 puntos Determinar los valores
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 201 Capítulo 4 Año 200 4.1. Modelo 200 - Opción A Problema 4.1.1 2 puntos Determinar los valores
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
INTEGRACION POR PARTES
 INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
Tema 6: Derivada de una función
 Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
1. Utilizando el cambio de variable y = z α y eligiendo adecuadamente α integrar el problema de valor inicial dy dx = xy 3x 2 y 4 y(2) = 1
 1 Ecuaciones diferenciales homogéneas 1 Utilizando el cambio de variable y = z α y eligiendo adecuadamente α integrar el problema de valor inicial = xy 3x y 4 y() = 1 Solution 1 Utilizamos el cambio de
1 Ecuaciones diferenciales homogéneas 1 Utilizando el cambio de variable y = z α y eligiendo adecuadamente α integrar el problema de valor inicial = xy 3x y 4 y() = 1 Solution 1 Utilizamos el cambio de
Lecturas Ecuaciones Diferenciales Ordinarias (I) Ampliación de Matemáticas. Grado en Ingeniería Civil Curso
 1 / 34 Lecturas Ecuaciones Diferenciales Ordinarias (I) Ampliación de Matemáticas. Grado en Ingeniería Civil Curso 2012-13 Octubre 2012 2 / 34 Motivación: Existen infinidad de problemas en Ciencia e Ingeniería
1 / 34 Lecturas Ecuaciones Diferenciales Ordinarias (I) Ampliación de Matemáticas. Grado en Ingeniería Civil Curso 2012-13 Octubre 2012 2 / 34 Motivación: Existen infinidad de problemas en Ciencia e Ingeniería
Métodos de solución de ED de primer orden
 CAPÍTULO 2 Métodos de solución de ED de primer orden 2.6 Ecuaciones diferenciales exactas Antes de abordar este tema, sugerimos al lector revise la última sección de este capítulo, la cual trata sobre
CAPÍTULO 2 Métodos de solución de ED de primer orden 2.6 Ecuaciones diferenciales exactas Antes de abordar este tema, sugerimos al lector revise la última sección de este capítulo, la cual trata sobre
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
Unidad Temática Cálculo de primitivas
 Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
Unidad Temática 5 5.1 Análisis Matemático (Ingeniería Informática) Departamento de Matemática Aplicada Facultad de Informática Universidad Politécnica de Valencia Contenidos 1 Integración Primitiva Integración
Terceras Jornadas Investigaciones en la Facultad de Ciencias Económicas y Estadística, octubre de 1998
 PLUSS, ILEANA Departamento de Matemática, Escuela de Estadística UNIDAD DE ENSEÑANZA. ECUACIONES DIFERENCIALES DE 1 ORDEN. APLICACIONES DE DERIVE EN LA RESOLUCIÓN DE UN PROBLEMA MICROECONÓMICO SOBRE RELACIÓN
PLUSS, ILEANA Departamento de Matemática, Escuela de Estadística UNIDAD DE ENSEÑANZA. ECUACIONES DIFERENCIALES DE 1 ORDEN. APLICACIONES DE DERIVE EN LA RESOLUCIÓN DE UN PROBLEMA MICROECONÓMICO SOBRE RELACIÓN
Tema 1.- ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN
 Tema 1.- ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN Ampliación de Matemáticas Ingeniería Técnica Industrial. Especialidad en Electrónica Industrial. Índice General 1 Ecuaciones diferenciales ordinarias.
Tema 1.- ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN Ampliación de Matemáticas Ingeniería Técnica Industrial. Especialidad en Electrónica Industrial. Índice General 1 Ecuaciones diferenciales ordinarias.
ETSI de Topografía, Geodesia y Cartografía
 ETSI de Topografía, Geodesia Cartografía LÍMITES, CONTINUIDAD Y DIFERENCIABILIDAD DE FUNCIONES DE VARIAS VARIABLES REALES Prueba de Evaluación Continua Grupo ºA 3-Octubre-04.- Sea la función 5 si (,) 4
ETSI de Topografía, Geodesia Cartografía LÍMITES, CONTINUIDAD Y DIFERENCIABILIDAD DE FUNCIONES DE VARIAS VARIABLES REALES Prueba de Evaluación Continua Grupo ºA 3-Octubre-04.- Sea la función 5 si (,) 4
LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS
 195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 3 puntos.
 Opción A. Ejercicio 1. Valor: 3 puntos. Dado el sistema de ecuaciones lineales: { x ay = 2 se pide: ax y = a + 1 a) (2 puntos) Discutir el sistema según los valores del parámetro a. Resolverlo cuando la
Opción A. Ejercicio 1. Valor: 3 puntos. Dado el sistema de ecuaciones lineales: { x ay = 2 se pide: ax y = a + 1 a) (2 puntos) Discutir el sistema según los valores del parámetro a. Resolverlo cuando la
INTEGRAL INDEFINIDA. Hemos estudiado la derivada de una función. Ahora vamos a determinar una función F(x) conociendo su derivada.
 1. INTEGRAL INDEFINIDA INTEGRAL INDEFINIDA Hemos estudiado la derivada de una función. Ahora vamos a determinar una función F(x) conociendo su derivada. Ejm: La función F x = x es una primitiva de f x
1. INTEGRAL INDEFINIDA INTEGRAL INDEFINIDA Hemos estudiado la derivada de una función. Ahora vamos a determinar una función F(x) conociendo su derivada. Ejm: La función F x = x es una primitiva de f x
Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos
 Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M.
Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M.
TEMA 3. Algebra. Teoría. Matemáticas
 1 1 Las expresiones algebraicas Las expresiones algebraicas son operaciones aritméticas, de suma, resta, multiplicación y división, en las que se combinan letras y números. Para entenderlo mejor, vamos
1 1 Las expresiones algebraicas Las expresiones algebraicas son operaciones aritméticas, de suma, resta, multiplicación y división, en las que se combinan letras y números. Para entenderlo mejor, vamos
EXAMEN DE SEPTIEMBRE, MATEMÁTICAS I. 1. (2.5 ptos) Sean f y g funciones con derivadas primeras y segundas continuas de las que se sabe que
 EXAMEN DE SEPTIEMBRE, MATEMÁTICAS I DEBE CONTESTAR ÚNICAMENTE A 4 DE LOS SIGUIENTES 5 EJERCICIOS 1. (.5 ptos) Sean f y g funciones con derivadas primeras y segundas continuas de las que se sabe que Sea
EXAMEN DE SEPTIEMBRE, MATEMÁTICAS I DEBE CONTESTAR ÚNICAMENTE A 4 DE LOS SIGUIENTES 5 EJERCICIOS 1. (.5 ptos) Sean f y g funciones con derivadas primeras y segundas continuas de las que se sabe que Sea
ECUACIONES DIFERENCIALES ORDINARIAS
 ECUACIONES DIFERENCIALES ORDINARIAS Introducción y métodos elementales de resolución 7.1. Generalidades Llamamos ecuación diferencial a toda ecuación que relacione una o más variables independientes,
ECUACIONES DIFERENCIALES ORDINARIAS Introducción y métodos elementales de resolución 7.1. Generalidades Llamamos ecuación diferencial a toda ecuación que relacione una o más variables independientes,
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO Opción A
 IES Fco Ayala de Granada Modelo 1 del 1999. Germán-Jesús Rubio Luna PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 1998999. Opción A Ejercicio 1, Opción A, Modelo 1 de 1999. x si x
IES Fco Ayala de Granada Modelo 1 del 1999. Germán-Jesús Rubio Luna PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 1998999. Opción A Ejercicio 1, Opción A, Modelo 1 de 1999. x si x
Examen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos
 Eamen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Dadas las matrices 2 4 2 2 0 A = 1 m m ; B = 0 X = y O = 0 1 2 1 1 z 0 (1 punto). Estudiar el rango
Eamen de Matemáticas II (Modelo 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Dadas las matrices 2 4 2 2 0 A = 1 m m ; B = 0 X = y O = 0 1 2 1 1 z 0 (1 punto). Estudiar el rango
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES
 INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Ecuaciones lineales de segundo orden
 Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (12y - 6x + 1) dy = 0. Será ésta una ecuación diferencial reducible a homogénea?
 82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Ecuaciones diferenciales de orden superior
 CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4.7 Variación de parámetros El método de variación de parámetros es un procedimiento útil para la obtención de una solución particular y p.x/ de la
CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4.7 Variación de parámetros El método de variación de parámetros es un procedimiento útil para la obtención de una solución particular y p.x/ de la
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2008 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 8 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 8 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio,
Apellidos: Nombre: para x 1, determina sus asíntotas. 4. Halla el valor de los parámetros m y n para que la función f sea continua en todo.
 EXAMEN DE MATEMÁTICAS CONTINUIDAD Y DERIVABILIDAD Apellidos: Nombre: Curso: º Grupo: C Día: 3- II- 6 CURSO 05-6. Halla el dominio de definición y recorrido de las funciones a) f(x)= 9 b) g(x)= 4. Calcula
EXAMEN DE MATEMÁTICAS CONTINUIDAD Y DERIVABILIDAD Apellidos: Nombre: Curso: º Grupo: C Día: 3- II- 6 CURSO 05-6. Halla el dominio de definición y recorrido de las funciones a) f(x)= 9 b) g(x)= 4. Calcula
Tema 16. Ecuaciones diferenciales
 Tema 16. Ecuaciones diferenciales Juan Medina Molina 12 de mayo de 2005 Introducción Dedicaremos el último tema del curso a resolver ecuaciones diferenciales de orden uno y lineales de orden superior.
Tema 16. Ecuaciones diferenciales Juan Medina Molina 12 de mayo de 2005 Introducción Dedicaremos el último tema del curso a resolver ecuaciones diferenciales de orden uno y lineales de orden superior.
Cálculo Diferencial - Parcial No. 2
 Cálculo Diferencial - Parcial No. 2 Departamento de Matemáticas - Universidad de los Andes Marzo 18 de 2010 Juro solemnemente abstenerme de copiar o de incurrir en actos que puedan conducir a la trampa
Cálculo Diferencial - Parcial No. 2 Departamento de Matemáticas - Universidad de los Andes Marzo 18 de 2010 Juro solemnemente abstenerme de copiar o de incurrir en actos que puedan conducir a la trampa
Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1
 Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1 Ejercicio 1: Estudiar el dominio, asíntotas, signo, crecimiento, decrecimiento, máximos y mínimos relativos de la función f(x) = e 2x
Matemáticas Primer Examen Parcial, 18 de Noviembre de 2004, Prueba 1 Ejercicio 1: Estudiar el dominio, asíntotas, signo, crecimiento, decrecimiento, máximos y mínimos relativos de la función f(x) = e 2x
Técnicas de Integración. Integración por Partes (I)
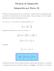 Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
(1.5 p.) 2) Hallar el polinomio de Taylor de grado 3 de la función g(x) = e 1 x2 centrado en x 0 = 1 y usarlo para dar una aproximación de e 5/4.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Examen final 0 de enero de 0.75 p. Se considera la función escalar de una variable real fx = lnlnx. lnx a Calcular el
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Examen final 0 de enero de 0.75 p. Se considera la función escalar de una variable real fx = lnlnx. lnx a Calcular el
