MÉTODO DE BISECCIÓN. El método de bisección se basa en el Teorema del Valor Intermedio
|
|
|
- Agustín del Río Valenzuela
- hace 8 años
- Vistas:
Transcripción
1 El método de bisección se basa en el Teorema del Valor Intermedio Básicamente el Teorema del Valor Intermedio nos dice que toda función continua en un intervalo cerrado, una vez que alcanzó ciertos valores en los extremos del intervalo, entonces debe alcanzar todos los valores intermedios. En particular, si f(a) y f(b) tienen signos opuestos, entonces un valor intermedio es precisamente z = 0, y por lo tanto, el Teorema del Valor Intermedio nos asegura que debe existir x o Є (a,b) tal que f(x o )=0, es decir, debe haber por lo menos una raíz de f(x) en el intervalo (a,b). 1
2 En el método de bisección se ejecutan los siguientes pasos: Sea f(x) continua, (i) Encontrar valores iniciales Xa y Xb tales que f(xa) y f(xb) tengan signos opuestos, es decir: f(xa) * f(xb) < 0 (ii) La primera aproximación a la raíz se toma igual al punto medio entre Xa y Xb Xr = (Xa + Xb) 2 2
3 (iii) Evaluar f(xr). Puede darse uno de los siguientes casos: f(xa) * f(xr) < 0 En este caso, tenemos que f(xa) y f(xr) tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo [Xa, Xr]. f(xa) * f(xr) > 0 En este caso, tenemos que f(xa) y f(xr) tienen el mismo signo, y de aquí que f(xr) y f(xb) tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo [Xr, Xb]. f(xa) * f(xr) = 0 En este caso, se tiene que f(xr) = 0 y se ha localizado la raíz. 3
4 El proceso se vuelve a repetir con el nuevo intervalo, hasta que Es decir, Er < Tolerancia (Xnueva - Xanterior) Xnueva < Tolerancia 4
5 Ejemplo 1. Aproximar la raíz de f(x) = e - ln (x) Hasta que el error relativo porcentual sea menor al 1% Analizando la función (Usar el programa) vemos que un intervalo útil es (1, 1.5), garantizando un intervalo con raíz única. -x -1-1 En efecto, tenemos que f(1) = e - ln (1) = e > 0-1,5 Mientras que f(1,5) = e - ln (1,5) = < 0 Cabe mencionar que la función f(x) es continua en el intervalo [1, 1.5] Así pues, tenemos todos los requisitos satisfechos para aplicar el método de bisección. Comenzamos: 5
6 (i) Calculamos el punto medio (De hecho, es la primera aproximación a la raíz) Xanterior = (a + b) / 2 = ( ) / 2 = (ii) Evaluamos f(1.25) = e - ln (1.25) = > 0 (iii) Para identificar mejor en cual de los 2 sub-intervalos se encuentra la raíz, hacemos la siguiente figura: f(1) f(1.25) f(1.5) Por lo tanto, vemos que la raíz se encuentra en el intervalo [1.25, 1.5] En este punto, vemos que todavía no podemos calcular ningún error relativo, puesto que solamente tenemos la primera aproximación. Así, repetimos el proceso con el nuevo intervalo [1.25, 1.5] 6
7 Calculamos el punto medio del nuevo sub-intervalo (Es la segunda aproximación a la raíz) Xnueva = ( ) / 2 = Aquí podemos calcular el error relativo porcentual, puesto que contamos ya con la aproximación nueva y la aproximación anterior Erp = Xnueva - Xanterior Xnueva * 100% = 9.09% Puesto que no se ha logrado el objetivo, continuamos con el proceso Dado que Xnueva no sirvió, se reasigna como Xanterior 7
8 Evaluamos f(1.375) = e - ln (1.375) = < 0 y elaboramos la figura: f(1.25) f(1.375) f(1.5) Por lo tanto, vemos que la raíz se encuentra en el intervalo [1.25, 1.375] Calculamos el punto medio del nuevo sub-intervalo: Xnueva = ( ) / 2 = Calculamos el nuevo error relativo porcentual: Erp = Xnueva - Xanterior Xnueva * 100% = * 100% = 4.76% El proceso debe seguir hasta lograr el objetivo 8
9 En la siguiente tabla resumimos los resultados que se obtienen: Aproximación a la raíz 1.25 Error relativo porcentual Así, obtenemos como aproximación a la raíz X =
10 ======================================================================= Para encontrar una solución de f(x) = 0 dada la función f en el intervalo [a, b] donde f(a) y f(b) tienen signos opuestos (y garantizando que haya raíz única) Entradas: extremos a y b, tolerancia TOL, número máximo de iteraciones N Salida: Solución aproximada Xnueva ó mensaje de fracaso Paso 1: tomar i = 1. (La variable i es la contadora de iteraciones). Paso 2: Calcular el primer punto medio y evaluar en cuál sub-intervalo continuar Xanterior = (a + b)/2 si f(a)*f(xanterior)>0 entonces tomar a=xanterior, si no, tomar b=xanterior Paso 3: Mientras (i<=n) seguir pasos 4 a 7: Paso 4: Cálculo de nueva raíz y del error relativo Xnueva = (a + b)/2; er = (Xnueva - Xanterior)/Xnueva; Paso 5: si f(xnueva) = 0 ó (error relativo < TOL) entonces mostrar Xnueva y PARAR Paso 6: tomar i = i + 1 Paso 7: Redefinición del intervalo y actualización de raíz. Si f(a)*f(xnueva)>0 entonces tomar a=xnueva, si no, tomar b=xnueva. Tomar Xanterior = Xnueva Paso 8: SALIDA. El método ha fracasado después de N iteraciones y PARAR ======================================================================= 10
EL MÉTODO DE LA BISECCIÓN
 EL MÉTODO DE LA BISECCIÓN Teorema de Bolzano Sea f : [a, b] IR IR una función continua en [a, b] tal que f(a) f(b) < 0, es decir, que tiene distinto signo en a y en b. Entonces, existe c (a, b) tal que
EL MÉTODO DE LA BISECCIÓN Teorema de Bolzano Sea f : [a, b] IR IR una función continua en [a, b] tal que f(a) f(b) < 0, es decir, que tiene distinto signo en a y en b. Entonces, existe c (a, b) tal que
1. Ecuaciones no lineales
 1. Ecuaciones no lineales 1.1 Ejercicios resueltos Ejercicio 1.1 Dada la ecuación xe x 1 = 0, se pide: a) Estudiar gráficamente sus raíces reales y acotarlas. b) Aplicar el método de la bisección y acotar
1. Ecuaciones no lineales 1.1 Ejercicios resueltos Ejercicio 1.1 Dada la ecuación xe x 1 = 0, se pide: a) Estudiar gráficamente sus raíces reales y acotarlas. b) Aplicar el método de la bisección y acotar
Tema 2 Resolución de Ecuaciones No Lineales
 Tema 2 Resolución de Ecuaciones No Lineales Índice 1. Introducción 2. Método de Bisección 2.1 Algoritmo del Método de Bisección 2.2 Análisis de Método de Bisección 3. Método de Regula-Falsi 3.1 Algoritmo
Tema 2 Resolución de Ecuaciones No Lineales Índice 1. Introducción 2. Método de Bisección 2.1 Algoritmo del Método de Bisección 2.2 Análisis de Método de Bisección 3. Método de Regula-Falsi 3.1 Algoritmo
SISTEMAS DE ECUACIONES LINEALES
 SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice Dada una función f : D R R y un intervalo I D
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice Dada una función f : D R R y un intervalo I D
Estudio de ceros de ecuaciones funcionales
 Capítulo 1 Estudio de ceros de ecuaciones funcionales Problema 1.1 Calcular el número de ceros de la ecuación arctang(x) = 4 x, dando un intervalo 5 donde se localicen. Solución: Denimos f(x) = arctan(x)
Capítulo 1 Estudio de ceros de ecuaciones funcionales Problema 1.1 Calcular el número de ceros de la ecuación arctang(x) = 4 x, dando un intervalo 5 donde se localicen. Solución: Denimos f(x) = arctan(x)
EJERCICIOS RESUELTOS DE LOS TEOREMAS DEL VALOR MEDIO
 MATEMÁTICAS EJERCICIOS RESUELTOS DE LOS TEOREMAS DEL VALOR MEDIO Juan Jesús Pascual TEOREMAS DEL VALOR MEDIO. Es aplicable el teorema de Rolle a la función f( x) = x 5x 6 en [ 0, 5 ]? El teorema de Rolle
MATEMÁTICAS EJERCICIOS RESUELTOS DE LOS TEOREMAS DEL VALOR MEDIO Juan Jesús Pascual TEOREMAS DEL VALOR MEDIO. Es aplicable el teorema de Rolle a la función f( x) = x 5x 6 en [ 0, 5 ]? El teorema de Rolle
1. Dominio, simetría, puntos de corte y periodicidad
 Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
La Lección de Hoy es Distancia entre dos puntos. El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1
 La Lección de Hoy es Distancia entre dos puntos El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1 La formula de la distancia dada a dos pares es: d= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 De
La Lección de Hoy es Distancia entre dos puntos El cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1 La formula de la distancia dada a dos pares es: d= (x 2 -x 1 ) 2 + (y 2 -y 1 ) 2 De
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
ETS Caminos Santander. Curso 2012. Ejercicios de introducción a la programación.
 Ejercicio 1. Saludo. El programa preguntará el nombre al usuario y a continuación le saludará de la siguiente forma "Hola, NOMBRE" donde NOMBRE es el nombre del usuario. Ejercicio 2. Suma. El programa
Ejercicio 1. Saludo. El programa preguntará el nombre al usuario y a continuación le saludará de la siguiente forma "Hola, NOMBRE" donde NOMBRE es el nombre del usuario. Ejercicio 2. Suma. El programa
Ecuaciones e Inecuaciones
 5 Ecuaciones e Inecuaciones Objetivos En esta quincena aprenderás a: Resolver ecuaciones de primer y segundo grado. Resolver ecuaciones bicuadradas y factorizadas. Identificar y resolver inecuaciones de
5 Ecuaciones e Inecuaciones Objetivos En esta quincena aprenderás a: Resolver ecuaciones de primer y segundo grado. Resolver ecuaciones bicuadradas y factorizadas. Identificar y resolver inecuaciones de
PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.
![PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2. PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.](/thumbs/27/11795036.jpg) PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
MEDIDAS DE TENDENCIA CENTRAL
 CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx
 La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx Resumen Se dan algunas definiciones básicas relacionadas con la divisibilidad
La nueva criba de Eratóstenes Efraín Soto Apolinar 1 F.I.M.E. U.A.N.L. San Nicolás, N.L. México. efrain@yalma.fime.uanl.mx Resumen Se dan algunas definiciones básicas relacionadas con la divisibilidad
Actualización en módulo NÓMINA
 Actualización en módulo NÓMINA La nueva actualización del módulo de Nómina permite la asignación de configuraciones que facilitaran el proceso de facturación. Lo invitamos a seguir el siguiente tutorial.
Actualización en módulo NÓMINA La nueva actualización del módulo de Nómina permite la asignación de configuraciones que facilitaran el proceso de facturación. Lo invitamos a seguir el siguiente tutorial.
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 FUNCIONES CONTINUAS. La mayor parte de las funciones que manejamos, a nivel elemental, presentan en sus gráficas una propiedad característica que es la continuidad. La continuidad de una función definida
FUNCIONES CONTINUAS. La mayor parte de las funciones que manejamos, a nivel elemental, presentan en sus gráficas una propiedad característica que es la continuidad. La continuidad de una función definida
Funciones de varias variables
 Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Para la oblicua hacemos lo mismo, calculamos el límite en el menos infinito : = lim. 1 ( ) = = lim
 ) Sea la función: f(x) = ln( x ): a) Dar su Dominio y encontrar sus asíntotas verticales, horizontales y oblicuas. b) Determinar los intervalos de crecimiento y decrecimiento, los máximos y mínimos, los
) Sea la función: f(x) = ln( x ): a) Dar su Dominio y encontrar sus asíntotas verticales, horizontales y oblicuas. b) Determinar los intervalos de crecimiento y decrecimiento, los máximos y mínimos, los
Ejemplo: Resolvemos Sin solución. O siempre es positiva o siempre es negativa. Damos un valor cualquiera Siempre + D(f) =
 T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
a) Buscar dominio, crecimiento, decrecimiento y máximos absolutos. b) Buscar el área delimitada por la función y el eje '0X'.
 .- Dada la función: f(x) = x 9 x a) Buscar dominio, crecimiento, decrecimiento y máximos absolutos. b) Buscar el área delimitada por la función y el eje '0X'..a.- Lo primero que hacemos es buscar el dominio,
.- Dada la función: f(x) = x 9 x a) Buscar dominio, crecimiento, decrecimiento y máximos absolutos. b) Buscar el área delimitada por la función y el eje '0X'..a.- Lo primero que hacemos es buscar el dominio,
ANÁLISIS ECONÓMICO DE INVERSIONES.
 ANÁLISIS ECONÓMICO DE INVERSIONES. José Ignacio González Soriano Agosto 2013 INDICE 1. FORMULAS FINANCIERAS.... 2 1.1.- VALOR ACTUAL NETO.... 3 1.1.1.- DEFINICIÓN... 3 1.1.2.- CASO GENERAL... 3 1.1.3.-
ANÁLISIS ECONÓMICO DE INVERSIONES. José Ignacio González Soriano Agosto 2013 INDICE 1. FORMULAS FINANCIERAS.... 2 1.1.- VALOR ACTUAL NETO.... 3 1.1.1.- DEFINICIÓN... 3 1.1.2.- CASO GENERAL... 3 1.1.3.-
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO
 EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
EJERCICIOS RESUELTOS SOBRE ERRORES DE REDONDEO 1º) Considérese un número estrictamente positivo del sistema de números máquina F(s+1, m, M, 10). Supongamos que tal número es: z = 0.d 1 d...d s 10 e Responde
mcd y mcm Máximo Común Divisor y Mínimo Común múltiplo www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx
 mcd y mcm Máximo Común Divisor y Mínimo Común múltiplo www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2008 Contenido 1. Divisores de un número entero 2 2. Máximo común divisor
mcd y mcm Máximo Común Divisor y Mínimo Común múltiplo www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2008 Contenido 1. Divisores de un número entero 2 2. Máximo común divisor
CREAR TICKETS DE SOPORTE
 CREAR TICKETS DE SOPORTE El Sistema de Soporte por Tickets, permite que el centro de asistencia técnica reciba su consulta y responda sobre la misma o solicite mayor información cuando sea necesario. De
CREAR TICKETS DE SOPORTE El Sistema de Soporte por Tickets, permite que el centro de asistencia técnica reciba su consulta y responda sobre la misma o solicite mayor información cuando sea necesario. De
UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA DECANATO DE POSTGRADO Maestría en Matemática Mención Educación Matemática MÉTODOS NUMÉRICOS
 Bisección Newton-Raphson Secante UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA DECANATO DE POSTGRADO Maestría en Matemática Mención Educación Matemática Material digital para la Asignatura: MÉTODOS NUMÉRICOS
Bisección Newton-Raphson Secante UNIVERSIDAD NACIONAL EXPERIMENTAL DEL TÁCHIRA DECANATO DE POSTGRADO Maestría en Matemática Mención Educación Matemática Material digital para la Asignatura: MÉTODOS NUMÉRICOS
Cómo?: Resolviendo el sistema lineal homógeneo que satisfacen las componentes de cualquier vector de S. x4 = x 1 x 3 = x 2 x 1
 . ESPACIOS VECTORIALES Consideremos el siguiente subconjunto de R 4 : S = {(x, x 2, x 3, x 4 )/x x 4 = 0 x 2 x 4 = x 3 a. Comprobar que S es subespacio vectorial de R 4. Para demostrar que S es un subespacio
. ESPACIOS VECTORIALES Consideremos el siguiente subconjunto de R 4 : S = {(x, x 2, x 3, x 4 )/x x 4 = 0 x 2 x 4 = x 3 a. Comprobar que S es subespacio vectorial de R 4. Para demostrar que S es un subespacio
Registro de MSDN Academic Alliance
 Microsoft Caribe, Centroamerica. Registro de MSDN Academic Alliance Guia de registro de MSDN Academic Alliance Liz Romero(liz.romero@microsoft.com) y Marco Zanabria 7 de diciembre de 2006 Para efectuar
Microsoft Caribe, Centroamerica. Registro de MSDN Academic Alliance Guia de registro de MSDN Academic Alliance Liz Romero(liz.romero@microsoft.com) y Marco Zanabria 7 de diciembre de 2006 Para efectuar
Activación de Producto
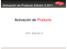 Activación de Producto 2011 Edición 2 Pantalla de inicio Informa al usuario que debe activar el software. Este cuadro de diálogo, o asistente, aparecerá después de completarse la instalación y de realizarse
Activación de Producto 2011 Edición 2 Pantalla de inicio Informa al usuario que debe activar el software. Este cuadro de diálogo, o asistente, aparecerá después de completarse la instalación y de realizarse
Control Estadístico del Proceso. Ing. Claudia Salguero Ing. Alvaro Díaz
 Control Estadístico del Proceso Ing. Claudia Salguero Ing. Alvaro Díaz Control Estadístico del Proceso Es un conjunto de herramientas estadísticas que permiten recopilar, estudiar y analizar la información
Control Estadístico del Proceso Ing. Claudia Salguero Ing. Alvaro Díaz Control Estadístico del Proceso Es un conjunto de herramientas estadísticas que permiten recopilar, estudiar y analizar la información
Capítulo 1. MANUAL DE USUARIO
 Capítulo 1. MANUAL DE USUARIO 1.1 SUCESIONES GRÁFICAS Lo primero que se hará es mostrar la pantalla que se encontrará el usuario cuando ejecute la aplicación, indicando las zonas en las que se divide esta:
Capítulo 1. MANUAL DE USUARIO 1.1 SUCESIONES GRÁFICAS Lo primero que se hará es mostrar la pantalla que se encontrará el usuario cuando ejecute la aplicación, indicando las zonas en las que se divide esta:
INVENTARIOS FISICOS. 2. Se deberá de contar con todas las localizaciones en los artículos sujetos al conteo.
 El siguiente documento detallara el procedimiento correcto para hacer un levantamiento de inventarios físicos. Los principales puntos a recordar son 2: 1. No se deberán tener piezas Reservadas en Traspasos
El siguiente documento detallara el procedimiento correcto para hacer un levantamiento de inventarios físicos. Los principales puntos a recordar son 2: 1. No se deberán tener piezas Reservadas en Traspasos
innovadora y simple tres etapas Inicial, Intermedia y Final
 Pontificia Universidad Católica de Chile IIC2100 Taller de Herramientas Computacionales para Ingeniería Profesor: Ignacio Casas. Ayudantes: Consuelo Pavón, Constanza Gómez Proyecto Semestral Modelación
Pontificia Universidad Católica de Chile IIC2100 Taller de Herramientas Computacionales para Ingeniería Profesor: Ignacio Casas. Ayudantes: Consuelo Pavón, Constanza Gómez Proyecto Semestral Modelación
Guía para la elaboración de Proyectos de Formación Sindical Ambiental e Investigación en Trabajo y Desarrollo Sustentable
 Guía para la elaboración de Proyectos de Formación Sindical Ambiental e Investigación en Trabajo y Desarrollo Sustentable 1- Denominación del Proyecto Esto se hace indicando, de manera sintética y mediante
Guía para la elaboración de Proyectos de Formación Sindical Ambiental e Investigación en Trabajo y Desarrollo Sustentable 1- Denominación del Proyecto Esto se hace indicando, de manera sintética y mediante
Unidad 6 Cálculo de máximos y mínimos
 Unidad 6 Cálculo de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Utilizará la derivada para decidir cuándo una función es creciente o decreciente. Usará la derivada para calcular los etremos
Unidad 6 Cálculo de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Utilizará la derivada para decidir cuándo una función es creciente o decreciente. Usará la derivada para calcular los etremos
Informática Bioingeniería
 Informática Bioingeniería Representación Números Negativos En matemáticas, los números negativos en cualquier base se representan del modo habitual, precediéndolos con un signo. Sin embargo, en una computadora,
Informática Bioingeniería Representación Números Negativos En matemáticas, los números negativos en cualquier base se representan del modo habitual, precediéndolos con un signo. Sin embargo, en una computadora,
Matemática I Extremos de una Función. Definiciones-Teoremas
 Universidad Centroccidental Lisandro Alvarado Decanato de Agronomía Programa Ingeniería Agroindustrial Departamento de Gerencia Estudios Generales Matemática I Etremos de una Función. Definiciones-Teoremas
Universidad Centroccidental Lisandro Alvarado Decanato de Agronomía Programa Ingeniería Agroindustrial Departamento de Gerencia Estudios Generales Matemática I Etremos de una Función. Definiciones-Teoremas
5.4 Consultas. 5.4.1. Crear una consulta
 Tutoriales de Ayuda al docente: 5.4. Consultas 5.4 Consultas Las consultas nos permite recabar la opinión del grupo (profesores/as y alumnos/as) sobre un tema, planteando una sencilla pregunta y ofreciendo
Tutoriales de Ayuda al docente: 5.4. Consultas 5.4 Consultas Las consultas nos permite recabar la opinión del grupo (profesores/as y alumnos/as) sobre un tema, planteando una sencilla pregunta y ofreciendo
Métodos Iterativos para Resolver Sistemas Lineales
 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
LABORATORIO Nº 2 GUÍA PARA REALIZAR FORMULAS EN EXCEL
 OBJETIVO Mejorar el nivel de comprensión y el manejo de las destrezas del estudiante para utilizar formulas en Microsoft Excel 2010. 1) DEFINICIÓN Una fórmula de Excel es un código especial que introducimos
OBJETIVO Mejorar el nivel de comprensión y el manejo de las destrezas del estudiante para utilizar formulas en Microsoft Excel 2010. 1) DEFINICIÓN Una fórmula de Excel es un código especial que introducimos
Uso del Programa Gantt Project
 Uso del Programa Gantt Project Presentación En esta práctica guiada aprenderás varias cosas relacionadas con el uso de Gantt Project, que es una aplicación de ayuda a la gestión de proyectos: Especificar
Uso del Programa Gantt Project Presentación En esta práctica guiada aprenderás varias cosas relacionadas con el uso de Gantt Project, que es una aplicación de ayuda a la gestión de proyectos: Especificar
www.clublineexpress.com/admin
 MANUAL CLUBLINE EXPRESS: ZONA DE GESTIÓN PARA DELEGADOS 1. ACCESO AL GESTOR E INTERFACE Para acceder al Gestor de Socios para delegaciones será necesario acceder a esta dirección web: www.clublineexpress.com/admin
MANUAL CLUBLINE EXPRESS: ZONA DE GESTIÓN PARA DELEGADOS 1. ACCESO AL GESTOR E INTERFACE Para acceder al Gestor de Socios para delegaciones será necesario acceder a esta dirección web: www.clublineexpress.com/admin
Aproximación local. Plano tangente. Derivadas parciales.
 Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Tema 5. Aproximación funcional local: Polinomio de Taylor. 5.1 Polinomio de Taylor
 Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
AHORRO ENERGÉTICO DOMÉSTICO. NIVEL DE IMPLANTACIÓN.
 AHORRO ENERGÉTICO DOMÉSTICO. NIVEL DE IMPLANTACIÓN. Juan Manuel Boronat Giner F. P. A. PATERNA Valencia Introducción Cada día consumimos más energía. En los últimos 25 años nuestro consumo energético se
AHORRO ENERGÉTICO DOMÉSTICO. NIVEL DE IMPLANTACIÓN. Juan Manuel Boronat Giner F. P. A. PATERNA Valencia Introducción Cada día consumimos más energía. En los últimos 25 años nuestro consumo energético se
CAPÍTULO III. FUNCIONES
 CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
TEMA 4 FRACCIONES MATEMÁTICAS 1º ESO
 TEMA 4 FRACCIONES Criterios De Evaluación de la Unidad 1 Utilizar de forma adecuada las fracciones para recibir y producir información en actividades relacionadas con la vida cotidiana. 2 Leer, escribir,
TEMA 4 FRACCIONES Criterios De Evaluación de la Unidad 1 Utilizar de forma adecuada las fracciones para recibir y producir información en actividades relacionadas con la vida cotidiana. 2 Leer, escribir,
Eduardo Kido 26-Mayo-2004 ANÁLISIS DE DATOS
 ANÁLISIS DE DATOS Hoy día vamos a hablar de algunas medidas de resumen de datos: cómo resumir cuando tenemos una serie de datos numéricos, generalmente en variables intervalares. Cuando nosotros tenemos
ANÁLISIS DE DATOS Hoy día vamos a hablar de algunas medidas de resumen de datos: cómo resumir cuando tenemos una serie de datos numéricos, generalmente en variables intervalares. Cuando nosotros tenemos
FUENTES DE ALIMENTACION
 FUENTES DE ALIMENTACION INTRODUCCIÓN Podemos definir fuente de alimentación como aparato electrónico modificador de la electricidad que convierte la tensión alterna en una tensión continua. Remontándonos
FUENTES DE ALIMENTACION INTRODUCCIÓN Podemos definir fuente de alimentación como aparato electrónico modificador de la electricidad que convierte la tensión alterna en una tensión continua. Remontándonos
Práctica 4 Diseño de circuitos con puertas lógicas.
 Práctica 4 Diseño de circuitos con puertas lógicas. Descripción de la práctica: -Esta práctica servirá para afianzar los conocimientos adquiridos hasta ahora de simplificación, e implementación de funciones,
Práctica 4 Diseño de circuitos con puertas lógicas. Descripción de la práctica: -Esta práctica servirá para afianzar los conocimientos adquiridos hasta ahora de simplificación, e implementación de funciones,
Fundamentos de Investigación de Operaciones Investigación de Operaciones 1
 Fundamentos de Investigación de Operaciones Investigación de Operaciones 1 1 de agosto de 2003 1. Introducción Cualquier modelo de una situación es una simplificación de la situación real. Por lo tanto,
Fundamentos de Investigación de Operaciones Investigación de Operaciones 1 1 de agosto de 2003 1. Introducción Cualquier modelo de una situación es una simplificación de la situación real. Por lo tanto,
PLAN DE DESARROLLO PERSONAL GESTIÓN POR COMPETENCIAS DEL PAS DE LA UCA
 PLAN DE DESARROLLO PERSONAL GESTIÓN POR COMPETENCIAS DEL PAS DE LA UCA Diciembre, 2009 ÍNDICE Introducción... 3 1. Plan de Desarrollo Personal: Análisis Jefe / Empleado... 3 2. Plan de Desarrollo Personal:
PLAN DE DESARROLLO PERSONAL GESTIÓN POR COMPETENCIAS DEL PAS DE LA UCA Diciembre, 2009 ÍNDICE Introducción... 3 1. Plan de Desarrollo Personal: Análisis Jefe / Empleado... 3 2. Plan de Desarrollo Personal:
GUIA APLICACIÓN DE SOLICITUDES POR INTERNET. Gestión de Cursos, Certificados de Aptitud Profesional y Tarjetas de Cualificación de Conductores ÍNDICE
 ÍNDICE ACCESO A LA APLICACIÓN... 2 1.- HOMOLOGACIÓN DE CURSOS... 4 1.1.- INICIAR EXPEDIENTE... 4 1.2.- CONSULTA DE EXPEDIENTES... 13 1.3.- RENUNCIA A LA HOMOLOGACIÓN... 16 2.- MECÁNICA DE CURSOS... 19
ÍNDICE ACCESO A LA APLICACIÓN... 2 1.- HOMOLOGACIÓN DE CURSOS... 4 1.1.- INICIAR EXPEDIENTE... 4 1.2.- CONSULTA DE EXPEDIENTES... 13 1.3.- RENUNCIA A LA HOMOLOGACIÓN... 16 2.- MECÁNICA DE CURSOS... 19
FORMACIÓN DE EQUIPOS DE E-LEARNING 2.0 MÓDULO DE DISEÑO Y PRODUCCIÓN DE MATERIALES UNIDAD 6 B
 141 1 FORMACIÓN DE EQUIPOS DE E-LEARNING 2.0 Unidad 6 B 142 2 Índice SEGUIMIENTO DE PERSONAS 1 INFORMES 2 143 3 SEGUIMIENTO DE PERSONAS E INFORMES EN MOODLE El seguimiento de los participantes en Moodle
141 1 FORMACIÓN DE EQUIPOS DE E-LEARNING 2.0 Unidad 6 B 142 2 Índice SEGUIMIENTO DE PERSONAS 1 INFORMES 2 143 3 SEGUIMIENTO DE PERSONAS E INFORMES EN MOODLE El seguimiento de los participantes en Moodle
CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES
 CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES Para la valuación de opciones hay dos modelos ampliamente reconocidos como son el modelo binomial y el modelo de Black
CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES Para la valuación de opciones hay dos modelos ampliamente reconocidos como son el modelo binomial y el modelo de Black
Unidad III: Programación no lineal
 Unidad III: Programación no lineal 3.1 Conceptos básicos de problemas de programación no lineal Programación no lineal (PNL) es el proceso de resolución de un sistema de igualdades y desigualdades sujetas
Unidad III: Programación no lineal 3.1 Conceptos básicos de problemas de programación no lineal Programación no lineal (PNL) es el proceso de resolución de un sistema de igualdades y desigualdades sujetas
Funciones polinomiales de grados 3 y 4
 Funciones polinomiales de grados 3 y 4 Ahora vamos a estudiar los casos de funciones polinomiales de grados tres y cuatro. Vamos a empezar con sus gráficas y después vamos a estudiar algunos resultados
Funciones polinomiales de grados 3 y 4 Ahora vamos a estudiar los casos de funciones polinomiales de grados tres y cuatro. Vamos a empezar con sus gráficas y después vamos a estudiar algunos resultados
EJERCICIOS DE MATEMÁTICAS I HOJA 4. Ejercicio 1. Se consideran los vectores
 EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
1-Comportamiento de una función alrededor de un punto:
 Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
INCREMENTOS CAPÍTULO 2 2.1 CONCEPTO
 CAPÍTULO INCREMENTOS. CONCEPTO Supóngase que se tiene una función cualquiera, por ejemplo x, a la cual se le asigna arbitrariamente cualquier valor inicial como x = 3, de donde corresponde que 9. Se quiere
CAPÍTULO INCREMENTOS. CONCEPTO Supóngase que se tiene una función cualquiera, por ejemplo x, a la cual se le asigna arbitrariamente cualquier valor inicial como x = 3, de donde corresponde que 9. Se quiere
1. Números Reales 1.1 Clasificación y propiedades
 1. Números Reales 1.1 Clasificación y propiedades 1.1.1 Definición Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero,
1. Números Reales 1.1 Clasificación y propiedades 1.1.1 Definición Número real, cualquier número racional o irracional. Los números reales pueden expresarse en forma decimal mediante un número entero,
Una función f es derivable en un punto a de su dominio si existe el límite. f(x) f(a) Si f y g son derivables en a, entonces fg es derivable en a y
 4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
Movimiento Rectilíneo Uniforme
 Movimiento Rectilíneo Uniforme 1. Teoría La mecánica es la parte de la física encargada de estudiar el movimiento y el reposo de los cuerpos, haciendo un análisis de sus propiedades y causas. La mecánica
Movimiento Rectilíneo Uniforme 1. Teoría La mecánica es la parte de la física encargada de estudiar el movimiento y el reposo de los cuerpos, haciendo un análisis de sus propiedades y causas. La mecánica
Es necesario actualizar el software del medidor FreeStyle InsuLinx. Lea este documento antes de comenzar.
 Es necesario actualizar el software del medidor FreeStyle InsuLinx. Lea este documento antes de comenzar. Los pasos que se describen a continuación lo guiarán por el proceso para descargar e instalar la
Es necesario actualizar el software del medidor FreeStyle InsuLinx. Lea este documento antes de comenzar. Los pasos que se describen a continuación lo guiarán por el proceso para descargar e instalar la
DIVISIBILIDAD SOLUCIÓN:
 DIVISIBILIDAD 1. Si a, b y c son números naturales tales que c = a. b, se dice: a) c es divisor de a y de b. b) c es múltiplo de a y de b. c) a y b son múltiplos de c. Todo número descompuesto en un producto
DIVISIBILIDAD 1. Si a, b y c son números naturales tales que c = a. b, se dice: a) c es divisor de a y de b. b) c es múltiplo de a y de b. c) a y b son múltiplos de c. Todo número descompuesto en un producto
MANUAL PARA LA ACTUALIZACIÓN Y CREACIÓN DE DEPENDENCIAS EN EL SISTEMA CREG ENTREGA-RECEPCIÓN
 MANUAL PARA LA ACTUALIZACIÓN Y CREACIÓN DE DEPENDENCIAS EN EL SISTEMA CREG ENTREGA-RECEPCIÓN Para la configuración de dependencias debe ingresar al menú Configuración del Sistema, después a Dependencias
MANUAL PARA LA ACTUALIZACIÓN Y CREACIÓN DE DEPENDENCIAS EN EL SISTEMA CREG ENTREGA-RECEPCIÓN Para la configuración de dependencias debe ingresar al menú Configuración del Sistema, después a Dependencias
Evaluación. del desempeño
 Evaluación del desempeño 9Claves para la ISO 9001-2015 BLOQUE 9: Evaluación del desempeño Viene a corresponder con el capítulo 8. Medición, análisis y mejora que incluye los apartados: 8.1. Generalidades,
Evaluación del desempeño 9Claves para la ISO 9001-2015 BLOQUE 9: Evaluación del desempeño Viene a corresponder con el capítulo 8. Medición, análisis y mejora que incluye los apartados: 8.1. Generalidades,
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de
 CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
Estas visiones de la información, denominadas vistas, se pueden identificar de varias formas.
 El primer paso en el diseño de una base de datos es la producción del esquema conceptual. Normalmente, se construyen varios esquemas conceptuales, cada uno para representar las distintas visiones que los
El primer paso en el diseño de una base de datos es la producción del esquema conceptual. Normalmente, se construyen varios esquemas conceptuales, cada uno para representar las distintas visiones que los
Apertura administrativa del ejercicio 2015
 Apertura administrativa del ejercicio 2015 1 La apertura administrativa del nuevo ejercicio.... 4 2 Cierre contable.... 7 2.1 Asiento de regularización.... 7 2.2 Asiento de cierre.... 8 2.3 Asiento de
Apertura administrativa del ejercicio 2015 1 La apertura administrativa del nuevo ejercicio.... 4 2 Cierre contable.... 7 2.1 Asiento de regularización.... 7 2.2 Asiento de cierre.... 8 2.3 Asiento de
1. Derivadas parciales
 Análisis Matemático II. Curso 2009/2010. Diplomatura en Estadística/Ing. Téc. en Inf. de Gestión. Universidad de Jaén TEMA 3. ABLES DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARI- 1. Derivadas parciales Para
Análisis Matemático II. Curso 2009/2010. Diplomatura en Estadística/Ing. Téc. en Inf. de Gestión. Universidad de Jaén TEMA 3. ABLES DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARI- 1. Derivadas parciales Para
MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE
 MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE Índice de contenidos: 1. Ley Financiera de capitalización a interés vencido. 1.1. Equivalencia de capitales. 1.2. Tipos de interés equivalentes.
MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE Índice de contenidos: 1. Ley Financiera de capitalización a interés vencido. 1.1. Equivalencia de capitales. 1.2. Tipos de interés equivalentes.
MICROECONOMÍA II. PRÁCTICA TEMA II: Equilibrio parcial
 MICROECONOMÍA II PRÁCTICA TEMA II: Equilibrio parcial EJERCICIO 1 A) En equilibrio, la cantidad demandada coincide con la cantidad ofrecida, así como el precio de oferta y demanda. Por lo tanto, para hallar
MICROECONOMÍA II PRÁCTICA TEMA II: Equilibrio parcial EJERCICIO 1 A) En equilibrio, la cantidad demandada coincide con la cantidad ofrecida, así como el precio de oferta y demanda. Por lo tanto, para hallar
Departamento de Matemáticas
 MA5 Clase 9: Campos Direccionales, Curvas Integrales. Eistencia y Unicidad Elaborado por los profesores Edgar Cabello y Marcos González La ecuación y = f(, y) determina el coeficiente angular de la tangente
MA5 Clase 9: Campos Direccionales, Curvas Integrales. Eistencia y Unicidad Elaborado por los profesores Edgar Cabello y Marcos González La ecuación y = f(, y) determina el coeficiente angular de la tangente
MANUAL DE USUARIO DE GESTIÓN DE ALEGACIONES
 MANUAL DE USUARIO DE GESTIÓN DE ALEGACIONES Tal y como se viene haciendo hasta ahora, entramos en la aplicación Web a través de la pantalla principal: Figura 1: Pantalla de inicio del portal de Bolsa de
MANUAL DE USUARIO DE GESTIÓN DE ALEGACIONES Tal y como se viene haciendo hasta ahora, entramos en la aplicación Web a través de la pantalla principal: Figura 1: Pantalla de inicio del portal de Bolsa de
Hacer obligatorio tener persona de contacto.
 Hacer obligatorio tener persona de contacto. Resumen Modulo Sistema B1 Validación, Funciones Universales. Nivel Medio. Requerimientos 2.7.3.0 o superior. Escenario. El cliente desea que no se puedan generar
Hacer obligatorio tener persona de contacto. Resumen Modulo Sistema B1 Validación, Funciones Universales. Nivel Medio. Requerimientos 2.7.3.0 o superior. Escenario. El cliente desea que no se puedan generar
La ventana de Microsoft Excel
 Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
Resortes y fuerzas. Analiza la siguiente situación. Ley de Hooke. 2do Medio > Física Ley de Hooke. Qué aprenderé?
 2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3. Espacios vectoriales
 Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES
 GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES Tema: Cartas de Servicios Primera versión: 2008 Datos de contacto: Evaluación y Calidad. Gobierno de Navarra. evaluacionycalidad@navarra.es
GUÍA TÉCNICA PARA LA DEFINICIÓN DE COMPROMISOS DE CALIDAD Y SUS INDICADORES Tema: Cartas de Servicios Primera versión: 2008 Datos de contacto: Evaluación y Calidad. Gobierno de Navarra. evaluacionycalidad@navarra.es
1.4.- D E S I G U A L D A D E S
 1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
Para cada cada valor de la función original lo multiplicas por 3 lo recorres 45 a la derecha y lo subes 5 unidades.
 3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
Empezamos abriendo el ClonyXXL que nos mostrara la ventana de abajo:
 Tutorial Copiar CDs protegidos con Alcohol 120% o CloneCD Usaremos 4 programas en este tutorial, que son: 1. ClonyXXL v2.0.1.5 2. Alcoholer v4.1 3. CloneCD 4. Alcohol 120% Empezamos abriendo el ClonyXXL
Tutorial Copiar CDs protegidos con Alcohol 120% o CloneCD Usaremos 4 programas en este tutorial, que son: 1. ClonyXXL v2.0.1.5 2. Alcoholer v4.1 3. CloneCD 4. Alcohol 120% Empezamos abriendo el ClonyXXL
4. EVALUACIÓN DEL PROGRAMA DE CAPACITACIÓN
 4. EVALUACIÓN DEL PROGRAMA DE CAPACITACIÓN La etapa final del proceso de capacitación es la evaluación de los resultados obtenidos, mediante este proceso se puede responder a las siguientes preguntas:
4. EVALUACIÓN DEL PROGRAMA DE CAPACITACIÓN La etapa final del proceso de capacitación es la evaluación de los resultados obtenidos, mediante este proceso se puede responder a las siguientes preguntas:
ANÁLISIS DE FUNCIONES RACIONALES
 ANÁLISIS DE FUNCIONES RACIONALES ( x 9) Dada la función f( x) = x 4 DETERMINE: Dominio, asíntotas, intervalos de crecimiento, intervalos de concavidad, extremos relativos y puntos de inflexión, representar
ANÁLISIS DE FUNCIONES RACIONALES ( x 9) Dada la función f( x) = x 4 DETERMINE: Dominio, asíntotas, intervalos de crecimiento, intervalos de concavidad, extremos relativos y puntos de inflexión, representar
CAPITULO 4. Requerimientos, Análisis y Diseño. El presente capítulo explica los pasos que se realizaron antes de implementar
 CAPITULO 4 Requerimientos, Análisis y Diseño El presente capítulo explica los pasos que se realizaron antes de implementar el sistema. Para esto, primero se explicarán los requerimientos que fueron solicitados
CAPITULO 4 Requerimientos, Análisis y Diseño El presente capítulo explica los pasos que se realizaron antes de implementar el sistema. Para esto, primero se explicarán los requerimientos que fueron solicitados
1. Objetivos. 2. Idea Principal. Teoría de Autómatas y Lenguajes Formales. Boletín de Autoevaluación 3: Cómo se minimiza un AFD?.
 Teoría de Autómatas y Lenguajes Formales Boletín de Autoevaluación 3: Cómo se minimiza un AFD?.. Objetivos. El objetivo de este boletín es ilustrar uno de los métodos ue permiten obtener el Autómata Finito
Teoría de Autómatas y Lenguajes Formales Boletín de Autoevaluación 3: Cómo se minimiza un AFD?.. Objetivos. El objetivo de este boletín es ilustrar uno de los métodos ue permiten obtener el Autómata Finito
ACCESO AL APLICATIVO
 Tarifa Mobile en Línea es una APP desarrollada por RECO S.A. de C.V., puede ser descargada a través del Play Store de Google el cual permite la consulta en línea de toda la información necesaria para la
Tarifa Mobile en Línea es una APP desarrollada por RECO S.A. de C.V., puede ser descargada a través del Play Store de Google el cual permite la consulta en línea de toda la información necesaria para la
BÚSQUEDA DE DOCUMENTOS DIGITALIZADOS
 Notarnet S.L. BÚSQUEDA DE DOCUMENTOS DIGITALIZADOS Cualquier documento digitalizado y registrado en DigiFactIn se puede localizar desde el formulario Búsqueda de Documentos. Haciendo clic en el botón Buscar
Notarnet S.L. BÚSQUEDA DE DOCUMENTOS DIGITALIZADOS Cualquier documento digitalizado y registrado en DigiFactIn se puede localizar desde el formulario Búsqueda de Documentos. Haciendo clic en el botón Buscar
Hacer clic sobre la figura, para extraer todos los registros o presionar la tecla F2.
 b) Adicionar grados Para llevar a cabo esta operación el usuario deberá realizar los siguientes pasos: Recuperar la información, para realizar esta operación el usuario puede hacerla de las siguientes
b) Adicionar grados Para llevar a cabo esta operación el usuario deberá realizar los siguientes pasos: Recuperar la información, para realizar esta operación el usuario puede hacerla de las siguientes
Los polinomios. Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x
 Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
(A) Primer parcial. si 1 x 1; x 3 si x>1. (B) Segundo parcial
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
DESARROLLO DE HABILIDADES DEL PENSAMIENTO LÓGICO
 I. SISTEMAS NUMÉRICOS DESARROLLO DE HABILIDADES DEL PENSAMIENTO LÓGICO LIC. LEYDY ROXANA ZEPEDA RUIZ SEPTIEMBRE DICIEMBRE 2011 Ocosingo, Chis. 1.1Sistemas numéricos. Los números son los mismos en todos
I. SISTEMAS NUMÉRICOS DESARROLLO DE HABILIDADES DEL PENSAMIENTO LÓGICO LIC. LEYDY ROXANA ZEPEDA RUIZ SEPTIEMBRE DICIEMBRE 2011 Ocosingo, Chis. 1.1Sistemas numéricos. Los números son los mismos en todos
Pasos para cambiar URL, imágenes, Titulos, etc.
 Pasos para cambiar URL, imágenes, Titulos, etc. 1. Como cambiar la URL Cambiar el menú Padre Para comenzar tomaremos de ejemplo el primer menú, que vendría siendo: Nuestra Empresa => Quienes somos. En
Pasos para cambiar URL, imágenes, Titulos, etc. 1. Como cambiar la URL Cambiar el menú Padre Para comenzar tomaremos de ejemplo el primer menú, que vendría siendo: Nuestra Empresa => Quienes somos. En
CAPITULO V. SIMULACION DEL SISTEMA 5.1 DISEÑO DEL MODELO
 CAPITULO V. SIMULACION DEL SISTEMA 5.1 DISEÑO DEL MODELO En base a las variables mencionadas anteriormente se describirán las relaciones que existen entre cada una de ellas, y como se afectan. Dichas variables
CAPITULO V. SIMULACION DEL SISTEMA 5.1 DISEÑO DEL MODELO En base a las variables mencionadas anteriormente se describirán las relaciones que existen entre cada una de ellas, y como se afectan. Dichas variables
FUNDACION NIC-NIIF www.nicniif.org
 NORMAS INTERNACIONALES DE INFORMACION FINANCIERA NIC-NIIF Identificación de un contrato de seguro, para que sea de aplicación la NIFF 4 o bien en su defecto otra norma con la NIC 39 si por ejemplo se trata
NORMAS INTERNACIONALES DE INFORMACION FINANCIERA NIC-NIIF Identificación de un contrato de seguro, para que sea de aplicación la NIFF 4 o bien en su defecto otra norma con la NIC 39 si por ejemplo se trata
Base de datos en Excel
 Base de datos en Excel Una base datos es un conjunto de información que ha sido organizado bajo un mismo contexto y se encuentra almacenada y lista para ser utilizada en cualquier momento. Las bases de
Base de datos en Excel Una base datos es un conjunto de información que ha sido organizado bajo un mismo contexto y se encuentra almacenada y lista para ser utilizada en cualquier momento. Las bases de
