Unidad 11. Cuerpos geométricos
|
|
|
- Marta Lagos Aguilar
- hace 6 años
- Vistas:
Transcripción
1 a las Enseñanzas cadémicas Página 07 Resuelve 1. Busca información sore los sólidos arquimedianos: a) Cuántos triángulos y cuántos cuadrados forman la superficie de un romicuoctaedro? ) Escrie el nomre de otros tres sólidos arquimedianos. a) La superficie de un romicuoctaedro está formada por 8 triángulos y 18 cuadrados. ) Cuoctaedro, icosidodecaedro, romicosidodecaedro.. Calcula, al estilo de rquímedes, la fórmula del volumen de una esfera, teniendo en cuenta las siguientes ayudas: La suma de los volúmenes de varias pirámides con la misma altura es: = 1 (suma de las superficies de las ases) ltura El volumen de la esfera se calcula aplicando la fórmula anterior a la suma de todas las finísimas pirámides, de vértice O y altura r, en que se puede descomponer la esfera. El área de la superficie esférica es 4π r. La suma de la superficie de las ases de las pirámides coincide con la superficie esférica, 4πr. La altura de cada pirámide es muy próima al radio de la esfera, r. V = 1 (Suma de las superficies de las ases) ltura = 1 (4πr ) = 4 πr 1
2 a las Enseñanzas cadémicas 1 Poliedros regulares y semirregulares Página Hemos señalado en rojo los centros de las caras frontales de estos poliedros, y en color más claro, los centros de algunas caras ocultas. Uniéndolos convenientemente se otienen los poliedros duales. Hazlo en tu cuaderno. octaedro cuo dodecaedro icosaedro tetraedro tetraedro
3 a las Enseñanzas cadémicas Página 09. Haz una tala con el número de caras, vértices y aristas de los cinco poliedros regulares. tetr. cuo oct. dodec. icos. caras vértices aristas a) Compruea que los cinco cumplen la fórmula de Euler. ) Compruea que el dodecaedro y el icosaedro cumplen las condiciones necesarias para ser duales. c) Compruea que el tetraedro cumple las condiciones para ser dual de sí mismo. tetr. cuo oct. dodec. icos. caras vértices aristas a) Tetraedro = Cuo = Octaedro = Dodecaedro = Icosaedro = ) l unir mediante segmentos los centros de cada dos caras contiguas de un dodecaedro, se forma un icosaedro. Si hiciéramos lo mismo con un icosaedro, otendríamos un dodecaedro. demás, el número de caras del dodecaedro coincide con el número de vértices del icosaedro, y viceversa. mos tienen el mismo número de aristas. Por tanto, son poliedros duales. c) l unir mediante segmentos los centros de cada dos caras contiguas de un tetraedro, se forma otro tetraedro. demás, el número de caras y de vértices en un tetraedro son iguales. El tetraedro es dual de sí mismo.. Hemos visto que esta figura no es un poliedro regular. Es semirregular? Esta figura no es un poliedro semirregular porque en todos los vértices no concurren los mismos polígonos.
4 a las Enseñanzas cadémicas 4. Esta pirámide truncada cuyas ases son cuadrados, es un poliedro semirregular? Por qué? No es un poliedro semirregular porque sus aristas no son todas iguales. 5. Eplica por qué las aristas de un poliedro semirregular tienen que ser todas iguales. Las aristas de un poliedro semirregular tienen que ser todas iguales porque son como poliedros regulares, solo se diferencian en que los primeros no tienen todas las caras iguales. 4
5 a las Enseñanzas cadémicas Truncando poliedros Página Vamos a truncar, dando cortes que pasen por los puntos medios de las aristas adyacentes, los restantes poliedros regulares. a) l truncar de este modo un tetraedro, se otiene una figura conocida. Cuál? ) El resultado de truncar el octaedro tamién es conocido. Comprendes, ahora, por qué a esta figura se le llama cuoctaedro? c) Qué figura resulta de truncar un icosaedro? Compárala con el resultado de truncar un dodecaedro que has visto antes y eplica por qué es un poliedro semirregular (recuerda, se llama icosidodecaedro). d) Relaciona los resultados anteriores con la dualidad de poliedros estudiada en el epígrafe anterior. a) La figura que se otiene es un octaedro. ) La figura que se otiene es un cuoctaedro. c) l truncar un icosaedro se otiene un icosidodecaedro, que se compone de pentágonos regulares y de triángulos equiláteros. En cada vértice confluyen dos pentágonos y dos triángulos (es un poliedro semirregular). l truncar un dodecaedro tamién se otiene un icosidodecaedro. d) La figura que resulta al truncar dos poliedros duales es la misma. 5
6 a las Enseñanzas cadémicas. Eplica por qué al truncar los poliedros regulares, ecepto el tetraedro, se otienen siempre poliedros semirregulares. Otenemos poliedros semirregulares porque al truncar siguiendo el patrón que se indica en la teoría, las caras que aparecen son dos tipos de polígonos regulares y en todos los vértices concurren el mismo número de caras.
7 a las Enseñanzas cadémicas Página 11. qué distancia del vértice hemos de cortar los triángulos pequeños para que el heágono resultante sea regular? = 1 l, donde l es el lado del triángulo. 4. Descrie el tetraedro truncado. Cuántas caras tiene? Cuántas son de cada tipo? Cuántos vértices? Cuántas aristas? Cuánto mide la arista del tetraedro truncado con relación a la del tetraedro original? Tiene 8 caras, 4 heágonos regulares y 4 triángulos equiláteros. Tiene 1 vértices donde concurren dos heágonos y un triángulo. Tiene 18 aristas que miden 1 l, siendo l la medida de la arista del tetraedro original. 5. Descrie el octaedro truncado. Caras, tipos. Vértices. ristas. Tiene 14 caras, 8 heágonos y cuadrados. Tiene 4 vértices donde concurren dos heágonos y un cuadrado. Tiene aristas que miden 1 l, siendo l la medida de la arista del octaedro original.. Conociendo las características de un dodecaedro (caras, vértices), descrie cómo será el dodecaedro truncado. Tiene caras, 1 decágonos regulares y 0 triángulos equiláteros. Tiene 0 vértices donde concurren dos decágonos y un triángulo. Tiene 90 aristas. 7. Conocidas las características de un icosaedro, descrie cómo será el icosaedro truncado. Tiene caras, 0 heágonos y 1 pentágonos. Tiene 0 vértices donde concurren dos heágonos y un pentágono. Tiene 90 aristas que miden 1 l, siendo l la medida de la arista del icosaedro original. 7
8 a las Enseñanzas cadémicas Planos de simetría de una figura Página 1 1. Qué condiciones dee cumplir un plano para ser plano de simetría del tetraedro? Cuántos planos de simetría tiene el tetraedro? Para que un plano sea plano de simetría del tetraedro tiene que contener una arista y ser perpendicular a dos caras. El tetraedro tiene planos de simetría, uno por cada arista.. Diuja un prisma heagonal regular. Cuántos planos de simetría tiene? Y cuántos tiene una pirámide heagonal regular? El prisma heagonal regular tiene seis planos de simetría, uno por cada eje de simetría de sus ases, y otro plano de simetría paralelo a las dos ases. La pirámide heagonal regular tiene seis planos de simetría, uno por cada eje de simetría de sus ases.. Recuerda la relación de dualidad entre el cuo y el octaedro (caras-vértices). Basándote en los planos de simetría del cuo, descrie todos los planos de simetría del octaedro. Todos los planos de simetría del cuo inscrito en el octaedro son tamién planos de simetría del octaedro. Por tanto, el octaedro y el cuo tienen el mismo número de planos de simetría. 4. Qué planos de simetría tiene un cono? Y una esfera? Cualquier plano que contiene al eje del cono es plano de simetría de este. Hay, pues, infinitos. Cualquier plano que contenga al centro de la esfera es un plano de simetría de esta. Hay, pues, infinitos. O 8
9 a las Enseñanzas cadémicas 4 Ejes de giro de una figura Página 1 1. Qué ejes de giro tiene una pirámide heagonal regular? De qué órdenes son? Y un prisma heagonal regular? (No pases por alto algunos de orden ). pirámide heagonal Hay solo un eje de giro de orden. Pasa por el centro de la ase y el vértice de la pirámide. prisma heagonal Hay un eje de giro de orden, el que pasa por el centro de las dos ases. Hay ejes de giro de orden : todos ellos son paralelos a las ases. de ellos pasan por el punto medio de las dos caras latelares opuestas, y los otros, por las aristas opuestas.. Qué ejes de giro tiene un ortoedro con las tres dimensiones distintas? De qué órdenes son? e 1 e Hay tres ejes de giro de orden, e 1, e y e. e. Estudia los ejes de giro del octaedro. Puedes asarte en los del cuo. Todos los ejes de giro del cuo son tamién ejes de giro del octaedro inscrito en él. Por tanto, el octaedro y el cuo tienen el mismo número de ejes de giro y de los mismos órdenes. Es decir: Tres ejes de giro de orden cuatro, que pasan por dos vértices opuestos. Seis ejes de giro de orden dos, que pasan por los puntos medios de dos aristas opuestas. Cuatro ejes de giro de orden tres, que pasan por los centros de dos caras opuestas. l comparar estos ejes de giro con los del cuo, se puede oservar la dualidad (caras vértices, aristas aristas): Los ejes que en el cuo pasan por los centros de caras opuestas, en el octaedro pasan por vértices opuestos. Los ejes que en el cuo pasan por aristas opuestas, en el octaedro pasan por aristas opuestas. Los ejes que en el cuo pasan por dos vértices opuestos del cuo, en el octaedro pasan por los centros de caras opuestas. 9
10 a las Enseñanzas cadémicas 5 Superficie de los cuerpos geométricos Página Calcula el área de estos poliedros otenidos a partir de un cuo de 1 cm de arista: 1 B C D Si hacemos el desarrollo de la figura, queda: Ò + 4 Ò FIG. + Ò FIG. 1 cm FIG. 1 1 cm 1 cm 1 cm fig. 1 = 1 + = 108 cm fig. = 1 = 7 cm fig. = 1 = 144 cm total = = 79 cm B Si hacemos el desarrollo de la figura, queda: 1 cm Ò + Ò FIG. + 1 cm FIG. 1 1 cm FIG. 1 cm 1 cm 1 cm = ,97 cm fig. 1 = 1 = 7 cm fig. = 1 = 144 cm fig. = 1 1,97 = 0,4 cm total = ,4 = 5,4 cm 10
11 a las Enseñanzas cadémicas C Si hacemos el desarrollo de la figura, queda: FIG. 1 1 cm h + Ò FIG. + Ò 1 cm FIG. 1 cm 1 cm 1,97 cm (ver B ); h = l 14,70 cm fig. 1 = = 1, 97 14, 70 14,7 cm fig. = 1 = 144 cm fig. = 7 cm total = 14, = 77,7 cm D Si hacemos el desarrollo de la figura, queda: FIG. 1 z Ò + + Ò z = + 8,49 cm potema del heágono regular: ap = z fig. 1 = 18 cm fig. = 8, 49 75, = 187,0 cm z FIG. z ap z = fig. = 1 1 fig. 1 = 144 7,5 = 1,5 cm total = 7, ,0 + 1,5 = 19, cm 1 cm z z l 7,5 cm FIG. 1 cm. Otén la medida de la superficie del prisma y de la pirámide. La ase de amos es un heágono regular. 8 cm B 8 cm z 10 cm 1 cm arista ase 8 cm altura prisma 10 cm arista ase 8 cm arista lateral 1 cm 11
12 a las Enseñanzas cadémicas a = 8 4,9 cm 8 cm 4 cm a ase = 8, 9 = 1, cm lateral = 8 10 = 480 cm total = 1, = 81,4 cm B ase = 1, cm potema de la pirámide = h = ,1 cm lateral = 8 111, = 71,44 cm total = 1, + 71,44 = 47,7 h 4 cm 1 cm. Calcula el área de estos cuerpos: B C 1 cm 1 cm total = π 1 + π 78,58 cm B g = 1+ 1,4 cm total = π 1,4 + π,0 C total = 4π 45,9 cm 4. Calcula el área de los siguientes cuerpos: 10 cm B 5 cm 17 cm 17 cm 1 cm ase grande = = 7 ase pequeña = 10 = 100 cm h = 17 8 = 15 cm 17 cm 10 cm lateral = = 1080 cm 8 cm total = = 185 B = π 1 + π 5 + π(1 + 5) 17 = 50,9 + 78, , = 1 570,8 cm h 1
13 a las Enseñanzas cadémicas 5. Calcula el área total del cono, del cuerpo que resulta de partirlo por la mitad y del tronco de cono otenido al cortar por una sección paralela a la ase, a 5 cm de la misma. B C 0 cm 8 cm 5 cm g = ,54 cm total = π 8 1,54 + π 8 = 74,4 cm B ase = π 8 100,5 cm ; 1/ lateral = π 8 154, 70,8 cm triángulo = 1 0 = 10 cm total = 100,5 + 70, = 51,1 cm C 5 cm 0 cm 15 cm 1,54 cm z y 8 cm 0 = 15 = 8 y = 8 = cm z = 5+ 5,9 cm total = π (8 + ) 5,9 + π 8 + π 551, cm. En una esfera de 0 cm de diámetro, calcula: a) El área de una zona esférica de de altura. ) El área de un casquete esférico cuya ase tiene un radio de 1 cm. a) zona esférica = π 15 55,49 cm 15 cm ) 1 cm = 15 1 = 9 cm y = 15 9 = 15 cm 1 cm y casquete esférico = π 15 55,49 cm 1
14 a las Enseñanzas cadémicas 7. Halla el área de: a) Un prisma recto cuya ase es un romo de diagonales 1 cm y 0 cm, saiendo que su arista lateral mide 4 cm. ) Una pirámide recta con la misma ase y la misma arista lateral que el prisma anterior. c) Un cuoctaedro de 10 cm de arista. d) Un dodecaedro truncado de 10 cm de arista. l 0 l = 10+ = 1 = 11, romo = 0 1 = 10 cm P romo = 4,5 cm 1 a) prisma = romo + P romo 4 = 1 59, ) Cara lateral de la pirámide: 4 cm l ap 4 cm potema de la pirámide: ap = = 4,97 lateral = 4 l ap/ = 115,90 cm ase = 10 cm pirámide = 5,9 cm c) cuadrados 1 = 10 = 00 cm 8 triángulos = 8 (10 10 /) : = 4,41 cm total = 94,41 cm d) 1 pentágonos y 0 heágonos. Área de un pentágono de lado 10 cm: 1 = 5 10, 88 = 17 cm Área de un heágono de lado 10 cm: = 10 8, = 59,80 cm total = = 7 0 cm 14
15 a las Enseñanzas cadémicas Volumen de los cuerpos geométricos Página Calcula el volumen de estos prismas, otenidos cortando un cuo de 1 cm de arista: 1 B C V = 1 = 84 cm B V = 1 = 19 C V = 4. Calcula el volumen de estas pirámides cuyas ases son polígonos regulares: 1 = 84 cm B 8 cm 15 cm 1 cm 15 cm = + 8,49 cm 15 cm h 1 cm h = 15 84, 1,7 cm V = 1 1 1,7 59,7 B 8 cm h = ,9 cm = 8 4,9 cm h 15 cm V = 1 8, 9 1,9 70,5 cm 15
16 a las Enseñanzas cadémicas. Calcula el volumen del tronco de cono y el del tronco de pirámide. B 5 cm 5 cm cm 8 cm 5 = = 15 cm V cono mayor = 1 π 8 0 = 1 40,41 cm V cono menor = 1 π 15 = 55,49 cm 5 8 V tronco de cono = 1 40,41 55,49 = 774,9 cm B = 8 4,9 cm 8 cm 8 cm V pirámide mayor = 1 8, 9 0 = 1108,8 cm 4 cm y y = 5, cm V pirámide menor = 1 5, 15 = 48 cm V tronco de pirámide = 1108,8 48 = 40,8 cm 4. Se corta una esfera de de diámetro por dos planos paralelos: uno pasa por el centro y el otro dista 1 cm del centro Calcula el volumen de cada una de las tres porciones en las que ha quedado dividida la esfera. 1
17 a las Enseñanzas cadémicas ) V porción (1) cilindro = π 18 1 = 888π cm V tronco (1) cono = 1 π 1 1 = 57π cm V porción (1) esfera = 888π 57π 10404,95 cm ) V porción () cilindro = π 18 = 1944π cm V porción () cono = 1 π π 1 1 = 18π cm V porción () esfera = 1944π 18π 1809, ) V porción () esfera = 4 π 18 = 1 14,51 cm 17
18 a las Enseñanzas cadémicas 7 Coordenadas geográficas Página 1 Hazlo tú Halla, en kilómetros, la medida del paralelo 45. r = radio del paralelo 45 r + r = R r =, r = 4501,58 km Perímetro = π 4501,58 = 884, km R 45 r 45 r 1. El metro, unidad de medida de longitud, se definía antiguamente como la diezmillonésima parte de un cuadrante de meridiano terrestre. Es decir, un meridiano terrestre tiene de metros. Según esto: a) Calcula el radio de la Tierra en kilómetros. ) Su superficie en kilómetros cuadrados. c) Su volumen en kilómetros cúicos. d) Calcula el área de un huso horario. a) Meridiano = Perímetro = π R = m = km R, km ) Superficie = 4π (,) = ,1 km c) Volumen = 4 π (,) = 1, km d) Área huso horario = , 1 = 1 074,5 km 4. Un arco va de un punto, situado en las costas de África a 0 latitud norte y 10 longitud oeste, a otro punto B, con la misma latitud y 80 de longitud oeste, siguiendo el paralelo común. a) Qué distancia ha recorrido? ) Qué distancia recorrería si la diferencia de longitudes de los dos puntos fuera de 180? a) Entre y B hay un arco de = 70 Como hemos visto en el prolema resuelto de esta página, el perímetro del paralelo 0 es 441,1 km. Por tanto, la distancia de a B es 4 41, ,77 km. 0 ) 4 41, 1 = 170,55 km 18
19 a las Enseñanzas cadémicas. En Río de Janeiro (4 O) son las 7 de la mañana. Qué hora es en Hiroshima (1 E)? Río de Janeiro 4 Oeste Hiroshima 1 Este Hay 1 horas de diferencia. Por tanto, en Hiroshima son las 7 de la tarde. Otra forma de hacerlo es: 1 = Hiroshima está en el huso horario número 9 al este. 4 = Río de Janeiro está en el huso horario número al oeste. Están, pues, a 1 husos horarios de diferencia. Por tanto, en Hiroshima son las 7 de la tarde (19 h). 19
20 a las Enseñanzas cadémicas Página Hazlo tú Calcula la distancia a la que tenemos que mirar una esfera de 40 cm de diámetro para ver la cuarta parte de su superficie. B = 0 10= = d (d + 10) = 00 d = 0 Tenemos que mirar a 0 cm de distancia. 0 cm O B d 10 cm P Hazlo tú Halla el área total y el volumen de un tronco de cono de de altura cuyos radios miden y 4 cm. 4 cm g = + = = 4 = 1 4 V tronco = V cono grande V cono pequeño = 1 π 18 1 π ,5 cm g = +, cm total = π( + 4), + π + π 4 1,91 cm 0
21 a las Enseñanzas cadémicas Ejercicios y prolemas Página Practica Áreas y volúmenes de cuerpos geométricos 1. Calcula el área y el volumen de los siguientes cuerpos geométricos: a) ) 1 cm 0 cm 1 cm 1 cm 15 cm 10 cm 10 cm a) Calculamos primero la altura de la ase, h. h = ,1 cm _ 0 81, 1, cm BSES = = ` cm LTERL = + = + = a V = 8,1 15 = 14,5 cm ) Calculamos primero la apotema, m, y la altura, h, de la pirámide. m = 1 5 = 1 cm; h = ,91 cm _ cm BSE = = ` = = 40 cm total = = 40 cm LTERL a V = ,91,7 cm. Calcula el área y el volumen de los cuerpos geométricos siguientes: total = = 85 a) Prisma de altura 0 cm y cuya ase es un romo de diagonales 18 cm y 1 cm. ) Pirámide heagonal regular de arista lateral 18 cm y arista ásica. c) Octaedro regular de 10 cm de arista. d) Cilindro de altura 7 cm y cuya circunferencia ásica mide 44 cm de longitud. e) Cono de radio 9 cm y generatriz 15 cm. f) Semiesfera de 10 cm de radio. g) Esfera inscrita en un cilindro de 1 m de altura. h) Casquete esférico de 7 cm de altura de una esfera de radio 1 cm. 1
22 a las Enseñanzas cadémicas a) Calculamos primero el lado del romo, l. l = ,8 cm _ BSES = = ` 4 108, 0 85, LTERL = = total = , = 1081, a V = = 10 cm ) Calculamos primero la apotema de la ase,, y la de la pirámide, m. = 5, cm; m = cm _ 5, 9, BSE = = ` = 17 total = 9, + 0 = 99, = 0 LTERL a Calculamos la altura de la pirámide y el volumen: h = 17 5, 1,19 cm V = 1 9, 1,19 = 505,18 cm c) Calculamos la altura de las caras, m, y el área: m = , = , = 4,4 cm Para calcular el volumen del octaedro calcularemos el volumen de una pirámide de ase cuadrada y lo multiplicaremos por dos. h = 8, 5 7,1 cm V pirámide = ,1,7 cm V octaedro =,7 = 47,4 cm d) Calculamos primero el radio de la ase, r. r = 44 7 cm π = π 7 07, 88 cm = 44 7 = 1188 cm BSES LTERL 4 total = 07, = cm V = 15,94 7 = 415,8 cm e) Calculamos primero la altura del cono, h. h = 15 9 = 1 cm π 9 54, 47 cm BSE = = π 9 15 = 44, 1 cm4 total = 54, ,1 = 78,59 cm LTERL V = 1 54,47 1 = 1 017,88 cm f) = 4π 10 8, cm 4 π 10 V = 094,4 cm
23 a las Enseñanzas cadémicas g) = 4π ,9 cm V = 4 π ,78 cm h) = π ,79 cm 7 cm 7 cm 1 cm 1 cm 1 cm 7 cm 5 cm 7 cm 5 cm 5 cm 1 cm V porción cilindro = π 1 7 1,7 cm V tronco de cono = 1 π π , V casquete = 1,7 178, = 1488,07 cm. Halla el área y el volumen de estos cuerpos geométricos: a) ) 8 cm 4 cm 0 cm c) d) 0 cm 10 cm 0 a) Primero calculamos el radio de la ase inclinada, r. d = + 8 = 10 cm r = 5 cm _ π 4 π 5 18, 81 cm BSES = + π 4 ` 75, 4 cm LTERL = = a V = π 4 = 150,8 cm total = 18, ,4 = 04,1 cm
24 a las Enseñanzas cadémicas ) Calculamos primero la generatriz, g. g = + 8 = 10 cm _ π 10 π, 7 cm BSES = + π 10 π 10 7, 99 cm LTERL = + ` total =,7 + 7,99 = 70,7 cm a Para calcular el volumen del tronco de cono restaremos el volumen del cono grande del volumen del cono pequeño. Para ello deemos conocer la altura del cono pequeño,. = + 10 = 1 + = 1,5 cm 10 V tronco de cono = 1 π 10 7,5 1 π 4 1,5 = 1 π 7 70,7 cm c) Calculamos la apotema de la ase, ap, la apotema de la pirámide, m, y la altura de la pirámide, h. ap = 5, cm m = 10 9,54 cm h = 954, 5, 8 cm _ 5, 9, BSE = = ` 9, , 7 cm LTERL = = a V = 1 9, 8 = 49, total = 9, + 171,7 = 5, cm d) Deemos oservar que la porción de esfera que estamos eliminando es 0 = 1 de la 0 1 esfera completa, y que al calcular el área deemos añadir dos semicírculos de radio 0 cm. = 11 4π 0 + π 0 407,7 + 15,4 = 584,1 cm 1 V = π ,79 cm 4. Haciendo girar un triángulo rectángulo cuyos catetos miden 9 cm y 1 cm alrededor de cada uno de ellos, se otienen dos conos. Diújalos y halla el área y el volumen de cada uno de ellos. 1 cm 9 cm g = 1+ 9 = 15 cm π 9 54, 47 cm BSE = = π , 1 cm LTERL V = 1 54, ,88 cm 4 total = 54, ,1 = 78,59 cm 4
25 a las Enseñanzas cadémicas 9 cm 1 cm g = 15 cm LTERL BSE = π 1 45, 9 cm = π , 49 cm4 total = 45,9 + 55,49 = 1017,88 cm V = 1 45, ,17 cm 5. Calcula la superficie de: a) Un prisma recto pentagonal regular cuyas aristas miden, todas, 10 cm. ) Un dodecaedro regular de arista 10 cm. Recuerda que la apotema de un pentágono regular de lado l mide 0,88 l. a) potema del pentágono =,88 cm S ase = 5 10, 88 = 17 cm S lateral = = 500 cm S total = = 844 cm ) S total = S pentágono 1 = 17 1 = 04 cm. Calcula el área total de los siguientes poliedros regulares y semirregulares de 8 cm de arista: B C D E F G Saemos que la suma de las áreas de las figuras y F es igual al triple del área de la figura B. Decimos, entonces que: + F = B Compruea cuáles de estas afirmaciones son ciertas: a) C + D = G ) B + C = G c) B + C = D d) F + B + C = E 5
26 a las Enseñanzas cadémicas Para las figuras y B, primero calculamos la altura de los triángulos de las caras, h. h = 8 4,9 cm Figura a = 4 8, 9 = 4 7,7 = 110,88 cm Figura B = 8 7,7 = 1,7 Figura C c = 8 = 84 cm Figura D d = ,7 = ,7 = 05,7 Figura E ap heágono = h =,9 cm e = 8 8 9, + 8 = 10, = 1714,5 Figura F f = 0 8, 9 = 554,4 cm Figura G g = , 9 = 17,7 Todas las afirmaciones son ciertas. 7. Halla las áreas y los volúmenes de estos prismas regulares. En amos, la arista ásica mide 10 cm, y la altura, 8 cm. 10 cm 10 cm = 10 5 = 75 = 8, perímetro apotema ase = = , = 1, 5 cm lateral = P h = = 400 cm total = ase + lateral = 1, = 8 cm V = ase h = 1,5 8 = 17 cm En este caso el apotema de este prisma es el mismo que el anterior. perímetro apotema ase = = , = 4,4 cm lateral = P h = = 40 cm total = ase + lateral = 4, = 1,8 cm V = ase h = 4,4 8 = 771, cm
27 a las Enseñanzas cadémicas Página 4 8. Calcula las áreas y los volúmenes de los siguientes cuerpos geométricos: a) ) 4 m 10 m 5 m 15 m m 8 m c) d) 1 m 15 m 4 m,5 m 8 m 14 m 1 m 5 m a) Descomponemos el cuerpo en un cono, un cilindro y una semiesfera. Calculamos primero la generatriz del cono, g. g = 5+ 5,8 cm = πrg + πrh + 4πr = π 5,8 + π 5 + 4π 05,74 cm V = 1 πr h + πr h + 4 πr = 1 π 5 + π π 07,5 cm ) Descomponemos el cuerpo en dos cilindros, uno dentro de otro. = (πr πr ) + πrh + πrh = π(r r ) + πh(r + r) = = π(4 ) + π15(4 + ) 40,88 cm V = πr h πr h = πh(r r ) = π15(4 ) 55,49 cm c) Descoponemos el cuerpo en un prisma y una pirámide triangular. Calculamos primero la altura de la ase de la pirámide, h. h = 1 7 9,75 cm = V = , 1 = 445 cm , = 144,5 cm d) La figura resulta de quitarle al cilindro de radio,5 cm y altura 8 cm un cuarto del mismo. _ π, 5 97, cm BSES = π, , 78 cm` LTERL = + 4 total = 9,7 + 1,78 = 71,05 cm a V = π, ,81 cm 4 7
28 a las Enseñanzas cadémicas 9. Halla el área y el volumen de este tetraedro regular: B D 8 cm D H h O O C C Para hallar la altura H, recuerda que O = h, donde h es la altura de una cara. Calculamos lo que mide la altura h: D h O C h = 8 4 = 48 h =,9 cm ase = h = 8, 9 = 7, 7 cm total = 4 ase = 110,88 cm Calculamos lo que mide la altura H del tetraedro: H = 8 c 9, m = 4, H =,5 cm V = 1 H 1 BSE = 7, 7 5, = 04, cm 10. La ase de un ortoedro tiene dimensiones 40 cm 44 cm. Su volumen es 1 5,5 dm. Calcula las diagonales de sus caras y la diagonal principal. D 40 cm = 4 dm 44 cm = 4,4 dm 40 dm 44 cm V = ase h 1 5,5 = 4 4,4 h h = 11,7 dm d 11,7 dm d = 11,7 + 4 d =,7 dm 40 dm d' 11,7 dm d ' = 4,4 + 11,7 d ' = 1,5 dm 4,4 dm D = 4 + 4,4 + 11,7 D = 7,0 dm 8
29 11. Calcula el volumen del siguiente tronco de pirámide de ases cuadradas: Calculamos las alturas de las pirámides que forman el tronco: h 10 8 = = 0 + = h = 1 a las Enseñanzas cadémicas 10 m 1 m m V tronco = V pirámide mayor V pirámide menor = = 1 9, m 1. Cortamos una esfera de 4 cm de radio por dos planos paralelos: uno que pase por el centro y otro a 1 de este. Halla las superficies y los volúmenes de las tres porciones otenidas ) = π ,74 cm _ V π π cm PORCIÓN CILINDRO = = V 1 ` = π , π cm TRONCO CONO a V porción esfera = 91π 15,π 4,1 cm ) = π ,7 cm V V PORCIÓN CILINDRO TRONCO CONO = = π 4 8= 408π cm 1 π π 1 1 4, 7π cm V porción esfera = 4 08π 4,7π 4 89,1 cm _ ` a ) = 4π 4 19,11 cm ; V porción esfera = 4 π ,9 cm 1. Se corta una esfera de 50 cm de diámetro por dos planos paralelos a 8 cm y 15 cm del centro, respectivamente. Halla el volumen de la porción de esfera comprendida entre amos planos
30 a las Enseñanzas cadémicas V porción cilindro = π 50 (15 8) = π cm V tronco de cono = 1 π π 50 8 = 5 8,π cm V porción esfera = V porción cilindro V tronco de cono = Coordenadas geográficas = π 5 8,π = 11,7π cm 51,9 cm 14. Cuando en el huso 0 son las 8 a.m., qué hora es en el tercer huso al E? Y en el quinto al O? En el huso E son tres horas más, es decir, las 11 a.m. En el huso 5 O son cinco horas menos, es decir, las a.m. 15. Saemos que en Bilao (longitud O) son las 9 de la mañana. Utilizando el siguiente esquema, indica qué hora será en Monterrey (longitud 100 O). M 11 0' ' 0 7 0' B En Monterrey serán las de la mañana. 1. Roma está en el primer huso al E y Nueva York, en el quinto al O. Si un avión sale de Roma a las 11 p.m. y el vuelo dura 8 h, cuál será la hora local de llegada a Nueva York? = horas menos en Nueva York que en Roma. 11 p.m. + 8 = 19 7 a.m. hora de Roma. 19 = 1 p.m. = 1 a.m. es la hora de llegada a Nueva York. 17. Si en La Haana (8 O) son las 8 p.m., asigna su hora a cada ciudad en tu cuaderno: Maputo (Mozamique) p.m. Natal (Brasil) a.m. staná (Kazajistán) 8 p.m. Temuco (Chile) 0 a.m. Honolulú (Hawái) 11 a.m. Dakar (Senegal) 11 p.m. Katmandú (Nepal) a.m. Melourne (ustralia) 7 a.m. Maputo ( E) a.m. Natal 11 p.m. staná (71 E) a.m. Temuco (7 O) 8 p.m. Honolulú (158 O) p.m. Dakar (1 O) 0 a.m. Katmandú (85 E) 7 a.m. Melourne (144 E) 11 a.m. 0
31 a las Enseñanzas cadémicas 18. Dos ciudades tienen la misma longitud, 15 E, y sus latitudes son 7 5' N y 5' S. Cuál es la distancia entre ellas? R a α = 7 5' β = 5' Tenemos que hallar la longitud del arco correspondiente a un ángulo de α + β = 7 5' + 5' = 0 Distancia = πr 0 = π ,5 km La milla marina es la distancia entre dos puntos del ecuador cuya diferencia de longitud es 1'. Calcula la longitud de una milla marina. 1' = 0 1 grados; radio de la Tierra: R 70 km Milla marina πr π π = R 70 1,85 km Un avión tiene que ir de a B, dos lugares diametralmente opuestos en el paralelo 45. Puede hacerlo siguiendo el paralelo (PB) o siguiendo la ruta polar (NB). Calcula la distancia que se recorrería en cada trayecto. N B P 45 R Hallamos el radio del paralelo 45 : R = + = = R = R = R S = ,7 km 1. lejandría, Nueva Orleans y Houston tienen todas la misma latitud, 0 N. Sus longitudes son, respectivamente, 0 E, 90 O y 95 O. Qué distancia recorrería un avión que va de lejandría a Nueva Orleans por el paralelo 0 N? Y de lejandría a Houston? Utilizando el ejercicio resuelto de la página 1, saemos que el paralelo 0 tiene una longitud de 4 4 km aproimadamente. Entre lejandría y Nueva Orleans hay un arco de 90 0 = 0 ; por tanto, la distancia entre ellos es , km. 0 Entre lejandría y Houston hay un arco de 95 0 = 5, por lo que la distancia entre ellos es , km. 0 1
PÁGINA 98. a) Tetraedro = 2 Cubo = 2 Octaedro = 2 Dodecaedro = 2 Icosaedro = 2
 PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
PÁGINA 98 Pág. 1 1 Haz una tabla con el número de caras, vértices y aristas de los cinco poliedros regulares. a) Comprueba que los cinco cumplen la fórmula de Euler. [Recuerda: c + v = a + ]. b) Comprueba
1 Poliedros y cuerpos de revolución
 Unidad 1. Figuras en el espacio a las Enseñanzas Aplicadas 1 Poliedros y cuerpos de revolución Página 155 1. Describe cada uno de los cinco poliedros de abajo diciendo cómo son sus caras (por ejemplo,
Unidad 1. Figuras en el espacio a las Enseñanzas Aplicadas 1 Poliedros y cuerpos de revolución Página 155 1. Describe cada uno de los cinco poliedros de abajo diciendo cómo son sus caras (por ejemplo,
11Soluciones a los ejercicios y problemas
 Soluciones a los ejercicios y problemas PÁGINA 9 Pág. P R A C T I C A D e s a r r o l l o s y á r e a s Dibuja el desarrollo plano y calcula el área total de los siguientes cuerpos geométricos: a) b) cm
Soluciones a los ejercicios y problemas PÁGINA 9 Pág. P R A C T I C A D e s a r r o l l o s y á r e a s Dibuja el desarrollo plano y calcula el área total de los siguientes cuerpos geométricos: a) b) cm
2πr r = πr. Aplica la fórmula: para obtener el volumen de la esfera.
 10 Soluciones a las actividades de cada epígrafe PÁGIN 191 Pág. 1 PR EMPEZR Calcula al estilo de rquímedes ÁRE DEL CÍRCULO Cuál es la suma de sus bases? Cuál es la altura de todos ellos? Sustituye y obtendrás
10 Soluciones a las actividades de cada epígrafe PÁGIN 191 Pág. 1 PR EMPEZR Calcula al estilo de rquímedes ÁRE DEL CÍRCULO Cuál es la suma de sus bases? Cuál es la altura de todos ellos? Sustituye y obtendrás
UNIDAD 11 Figuras en el espacio
 Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
Pág. 1 de 5 I. Conoces de cursos anteriores los poliedros regulares y algunas de sus características. Has reforzado ese conocimiento y lo has ampliado a los poliedros semirregulares? 1 Dibuja, a partir
2πr r = πr. Aplica la fórmula: para obtener el volumen de la esfera.
 10 Soluciones a las actividades de cada epígrafe PÁGIN 191 Pág. 1 PR EMPEZR Calcula al estilo de rquímedes ÁRE DEL CÍRCULO Cuál es la suma de sus bases? Cuál es la altura de todos ellos? Sustituye y obtendrás
10 Soluciones a las actividades de cada epígrafe PÁGIN 191 Pág. 1 PR EMPEZR Calcula al estilo de rquímedes ÁRE DEL CÍRCULO Cuál es la suma de sus bases? Cuál es la altura de todos ellos? Sustituye y obtendrás
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
2 Calcula la superficie total de cada cuerpo:
 8 Pág. Calcula la superficie total de cada cuerpo: A cm B C D cm A Área lateral πrh π,5 5π Área bases (πr ) π,5,5π Área total 5π +,5π 7,5π 86, B Área lateral πrg π 5 5π Área base πr π 9π Área total 5π
8 Pág. Calcula la superficie total de cada cuerpo: A cm B C D cm A Área lateral πrh π,5 5π Área bases (πr ) π,5,5π Área total 5π +,5π 7,5π 86, B Área lateral πrg π 5 5π Área base πr π 9π Área total 5π
Tema 11 Cuerpos geométricos
 Tema 11 Cuerpos geométricos 11.1 Poliedros regulares y semirregulares Tareas 11/11/: todos los ejercicios de la página 08. Además, completa la tabla análoga de los poliedros duales para el icosaedro y
Tema 11 Cuerpos geométricos 11.1 Poliedros regulares y semirregulares Tareas 11/11/: todos los ejercicios de la página 08. Además, completa la tabla análoga de los poliedros duales para el icosaedro y
PÁGINA Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de A a B en cada caso.
 PÁGIN 213 Pág. 1 0 Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de a en cada caso. 1 m 1 m 3 m En el tercer caso, y son centros de dos caras en una pirámide
PÁGIN 213 Pág. 1 0 Describe y calcula la longitud del trayecto más corto que debe recorrer la lagartija para ir de a en cada caso. 1 m 1 m 3 m En el tercer caso, y son centros de dos caras en una pirámide
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
POLIEDROS. Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
MATEMÁTICAS 2º DE ESO LOE
 MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
MATEMÁTICAS º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS REDONDOS Poliedros: o Elementos. o Tipos. Poliedros regulares. Cubos. Prismas: elementos, clases. Pirámides: elementos, clases. Áreas laterales y
CUERPOS GEOMÉTRICOS. Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas.
 CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
CUERPOS GEOMÉTRICOS CUERPOS GEOMÉTRICOS.- Los cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. Clasificamos, en el siguiente esquema, los cuerpos geométricos: POLIEDROS.-
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
CUERPOS GEOMÉTRICOS. 2º E.S.O. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS
 CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
CUERPOS GEOMÉTRICOS. PUNTOS, RECTAS Y PLANOS EN EL ESPACIO 2º E.S.O. DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de puntos: DETERMINACIÓN DE PUNTOS, RECTAS Y PLANOS Determinación de una recta:
TEMA 4. Geometría. Teoría. Matemáticas
 1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
RESUMEN BÁSICO DEL BLOQUE DE GEOMETRÍA Matemáticas 3º de ESO
 RESUMEN ÁSICO DEL LOQUE DE GEOMETRÍA Matemáticas 3º de ESO 1-. Conceptos fundamentales. Punto Recta Plano Semirrecta: porción de recta limitada en un extremo por un punto Semiplano: es cada una de las
RESUMEN ÁSICO DEL LOQUE DE GEOMETRÍA Matemáticas 3º de ESO 1-. Conceptos fundamentales. Punto Recta Plano Semirrecta: porción de recta limitada en un extremo por un punto Semiplano: es cada una de las
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS REGULARES ESFERA
 ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
ESQUEMA GENERAL DE LA CLASIFICACIÓN DE LOS CUERPOS GEOMÉTRICOS POLIEDROS REGULARES Tetraedro ( 4 triángulos equiláteros) Hexaedro o cubo( 6 cuadrados) Octaedro( 8 triángulos equiláteros) Dodecaedro ( 12
Elementos del cilindro
 Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
Definición de cilindro Un cilindro es un cuerpo geométrico engendrado por un rectángulo que gira alrededor de uno de sus lados. Desarrollo del cilindro Elementos del cilindro Eje Es el lado fijo alrededor
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
 EXAMEN A: Ejercicio nº 1.- Página 1 de 25 Indica el valor de los ángulos señalados en cada figura: Ejercicio nº 2.- La siguiente figura es una esfera de centro C y radio 3 unidades. Cómo definirías dicha
EXAMEN A: Ejercicio nº 1.- Página 1 de 25 Indica el valor de los ángulos señalados en cada figura: Ejercicio nº 2.- La siguiente figura es una esfera de centro C y radio 3 unidades. Cómo definirías dicha
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
FIGURAS DEL ESPACIO. ÁREAS Y VOLÚMENES
 POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
POLIEDROS : Cuerpo sólido limitado por polígonos, llamados caras; en la que algunas de las caras confluyen en líneas rectas, llamadas aristas; y algunas de las aristas confluyen en puntos,llamados vértices.
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
FICHA TEMA 9: CUERPOS GEOMETRICOS NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro:
 FICHA TEMA 9: CUERPOS GEOMETRICOS CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº 2.- Cuáles de las siguientes figuras
FICHA TEMA 9: CUERPOS GEOMETRICOS CURSO: 2 FECHA: NOMBRE Y APELLIDOS: Ejercicio nº 1.-Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº 2.- Cuáles de las siguientes figuras
14 CUERPOS GEOMÉTRICOS. VOLÚMENES
 EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
EJERCICIOS PARA ENTRENARSE Poliedros 14.33 Calcula la suma de los ángulos de las caras que concurren en un vértice de los poliedros regulares. Qué observas? TETRAEDO: En un vértice concurren tres triángulos
1 Indica, en la ilustración, dos edificios que sean poliedros y tengan formas diferentes. PÁGINA 186
 PÁGINA 186 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los cuerpos de revolución han sido elevados a la categoría
PÁGINA 186 En la Casa de la Cultura se ha montado una exposición fotográfica. En ella se recogen modernos edificios en los que los poliedros y los cuerpos de revolución han sido elevados a la categoría
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Perímetros, áreas y volúmenes de figuras y cuerpos geométricos.
 Perímetros, áreas y volúmenes de figuras y cuerpos geométricos. Perímetros y áreas de polígonos Triángulo El triángulo es un polígono con tres lados P = b + c + d ( Perímetro es igual a la suma de las
Perímetros, áreas y volúmenes de figuras y cuerpos geométricos. Perímetros y áreas de polígonos Triángulo El triángulo es un polígono con tres lados P = b + c + d ( Perímetro es igual a la suma de las
PERÍMETROS ÁREAS - VOLÚMENES
 ERÍMETROS ÁREAS - VOLÚMENES 1.- OLÍGONOS olígono: arte del plano limitada por una línea poligonal cerrada. Lado: Segmento que une dos vértices consecutivos. En un polígono el número de lados y el número
ERÍMETROS ÁREAS - VOLÚMENES 1.- OLÍGONOS olígono: arte del plano limitada por una línea poligonal cerrada. Lado: Segmento que une dos vértices consecutivos. En un polígono el número de lados y el número
Figura plana Área Ejemplo Cuadrado. Área =
 ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
ersión: Septiembre 01 Áreas y volúmenes Por Sandra Elvia Pérez Márquez Áreas de figuras planas Las aplicaciones de las figuras planas requieren, por lo general, conocer (o calcular) dos características
OBJETIVO 1 CONOCER LOS POLIEDROS Y DIFERENCIAR LOS POLIEDROS REGULARES NOMBRE: CURSO: FECHA:
 OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
OJETIVO 1 CONOCER LOS POLIEDROS Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
INSTITUCION EDUCATIVA DIVERSIFICADO DE CHIA TALLER DE VOLUMENES Y POLIEDROS
 Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones. 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides.
 Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
Cuerpos Geométricos. 100 Ejercicios para practicar con soluciones 1 Indica cuáles de las siguientes figuras son prismas y cuáles son pirámides. a) b) c) Prisma es un poliedro que tiene por caras dos bases
IES FONTEXERÍA MUROS. 14-II-2014 Nombre y apellidos:.
 IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
IES FONTEXERÍA MUROS MATEMÁTICAS º E.S.O-A (Desdoble 1) 1º Examen (ª Evaluación) 14-II-014 Nombre y apellidos:. 1. Completa las siguientes definiciones: a) Un poliedro es un cuerpo geométrico tridimensional
5to Parcial de Geometría Euclidiana. 2) Sea p un polígono tal que se puede descomponer en n polígonos simples
 5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
5to Parcial de Geometría Euclidiana AREAS y VOLUMENES Definición 55 (Área) Se define el área como una función A definida del conjunto de todos los polígonos P en R + (A : P R + ), con las siguientes propiedades:
unidad 10 Cuerpos geométricos
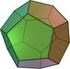 unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
unidad 10 Cuerpos geométricos Poliedros. Características Página 1 Poliedro es un cuerpo cerrado limitado por caras planas que son polígonos. Aristas son los lados de las caras. Cada dos caras contiguas
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
P RACTICA. 1 Di cuáles de estos triángulos son: 2 Di cómo son, según sus lados y según sus ángulos, los triángulos siguientes:
 P RCTIC Polígonos: clasificación 1 Di cuáles de estos triángulos son: a) cutángulos. b) Rectángulos. c) Obtusángulos isósceles. B C D G E a) cutángulos: C, F y G. b) Rectángulos: D y E. c) Obtusángulos
P RCTIC Polígonos: clasificación 1 Di cuáles de estos triángulos son: a) cutángulos. b) Rectángulos. c) Obtusángulos isósceles. B C D G E a) cutángulos: C, F y G. b) Rectángulos: D y E. c) Obtusángulos
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
1. Calcula el área y volumen de los siguientes cuerpos geométricos:
 1. Calcula el área y volumen de los siguientes cuerpos geométricos: 2.- Dibuja los siguientes cuerpos geométricos y calcula su área. a) Prisma de altura 24 cm y cuya base es un rombo de diagonales 18 y
1. Calcula el área y volumen de los siguientes cuerpos geométricos: 2.- Dibuja los siguientes cuerpos geométricos y calcula su área. a) Prisma de altura 24 cm y cuya base es un rombo de diagonales 18 y
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
CUADERNO Nº 8 NOMBRE: FECHA: / /
 Cuerpos geométricos Contenidos 1. Poliedros regulares Definiciones Desarrollos Planos de simetría Poliedros duales 2. Otros poliedros Prismas Pirámides Planos de simetría Poliedros semirregulares 3. Cuerpos
Cuerpos geométricos Contenidos 1. Poliedros regulares Definiciones Desarrollos Planos de simetría Poliedros duales 2. Otros poliedros Prismas Pirámides Planos de simetría Poliedros semirregulares 3. Cuerpos
Geometría en el espacio
 Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
Geometría en el espacio 3º E.S.O. PARTE TEÓRICA 1.- Define los siguientes conceptos: Poliedro: Vértice de un poliedro: Cara de un poliedro: Arista de un poliedro: Poliedro regular: 2.- Di cuáles son los
IDEAS PREVIAS. 1. Planos paralelos. 2.Planos perpendiculares
 IDEAS PREVIAS 1. Planos paralelos..planos perpendiculares .Planos oblicuos. CUERPO GEOMÉTRICO Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa
IDEAS PREVIAS 1. Planos paralelos..planos perpendiculares .Planos oblicuos. CUERPO GEOMÉTRICO Un Sólido o Cuerpo Geométrico es una figura geométrica de tres dimensiones (largo, ancho y alto), que ocupa
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
EJERCICIOS PROPUESTOS
 7 PROBLEMAS MÉTRICOS EJERCICIOS PROPUESTOS 7.1 La hipotenusa y uno de los catetos de un triángulo rectángulo miden 4 y centímetros, respectivamente. Halla las medidas de sus ángulos. cm B 4 cm Cp arc 4
7 PROBLEMAS MÉTRICOS EJERCICIOS PROPUESTOS 7.1 La hipotenusa y uno de los catetos de un triángulo rectángulo miden 4 y centímetros, respectivamente. Halla las medidas de sus ángulos. cm B 4 cm Cp arc 4
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Autor: 2º ciclo de E.P.
 1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
1 Autor: 2º ciclo de E.P. Una línea recta es una línea que no tiene principio ni fin. Una semirrecta es una línea que tiene principio pero no tiene final. o Un punto divide a una recta en dos semirrectas.
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES
 OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
OBJETIVO 1 ELEMENTOS DE UN POLIEDRO. PRINCIPALES POLIEDROS REGULARES NOMBRE: CURSO: ECHA: CONCEPTO DE POLIEDRO Vértice Arista Cara Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
Área del rectángulo y del cuadrado
 59 Área del rectángulo y del cuadrado El área del rectángulo es el producto de su base por su altura. El área del cuadrado es su lado elevado al cuadrado. 1. Mide con una regla y completa. Área del rectángulo:
59 Área del rectángulo y del cuadrado El área del rectángulo es el producto de su base por su altura. El área del cuadrado es su lado elevado al cuadrado. 1. Mide con una regla y completa. Área del rectángulo:
Cuerpos geométricos POLIEDROS CUERPOS DE REVOLUCIÓN POLIEDROS PIRÁMIDES PRISMAS REGULARES ÁREA TOTAL ÁREA TOTAL. A T = P B h+2a B = ESFERA
 11 Cuerpos geométricos POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES ÁREA TOTAL A T = P B h+a B A T ÁREA TOTAL PB a PB a' = + CUERPOS DE REVOLUCIÓN CILINDRO CONO ESFERA ÁREA TOTAL A T = πrh+πr ÁREA TOTAL
11 Cuerpos geométricos POLIEDROS POLIEDROS REGULARES PRISMAS PIRÁMIDES ÁREA TOTAL A T = P B h+a B A T ÁREA TOTAL PB a PB a' = + CUERPOS DE REVOLUCIÓN CILINDRO CONO ESFERA ÁREA TOTAL A T = πrh+πr ÁREA TOTAL
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Programa Entrenamiento MT-22
 Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
CUERPOS DE REVOLUCIÓN
 PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
11 CUERPOS GEOMÉTRICOS. PROPIEDADES MÉTRICAS
 A C T I V I D A D E S D E L O S E P Í G R A F E S Poliedros y cuerpos redondos P A R A P R A C T I C A R 11.1 Completa la tabla. Comprueba si se verifica la igualdad: Número de caras número de vértices
A C T I V I D A D E S D E L O S E P Í G R A F E S Poliedros y cuerpos redondos P A R A P R A C T I C A R 11.1 Completa la tabla. Comprueba si se verifica la igualdad: Número de caras número de vértices
6Soluciones a los ejercicios y problemas PÁGINA 139
 ÁGIN 9 ág. RTI Figuras semejantes uáles de estas figuras son semejantes? uál es la razón de semejanza? F F F F es semejante a F. La razón de semejanza es. a) Son semejantes los triángulos interior y eterior?
ÁGIN 9 ág. RTI Figuras semejantes uáles de estas figuras son semejantes? uál es la razón de semejanza? F F F F es semejante a F. La razón de semejanza es. a) Son semejantes los triángulos interior y eterior?
CUERPOS GEOMÉTRICOS. VOLÚMENES. 3º E.S.O. ( ) SUPERFICIE DE UN PRISMA SUPERFICIE DE UN ORTOEDRO SUPERFICIE DE UN PRISMA
 CUERPOS GEOMÉTRICOS. ÁRES Y VOLÚMENES. º E.S.O. SUPERFICIE DE UN PRISM ÁRE LTERL = Perímetro de la base altura ÁRE TOTL = ÁRE LTERL + ÁRE DE L BSE SUPERFICIE DE UN PRISM Hallar el área total de una celda
CUERPOS GEOMÉTRICOS. ÁRES Y VOLÚMENES. º E.S.O. SUPERFICIE DE UN PRISM ÁRE LTERL = Perímetro de la base altura ÁRE TOTL = ÁRE LTERL + ÁRE DE L BSE SUPERFICIE DE UN PRISM Hallar el área total de una celda
3. Si la diferencia de volúmenes de los cilindros A) 2 3 B) En el gráfico se tiene un tronco de cilindro. A) 196p B) 200p C) 250p
 ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
POLIEDROS, PRISMAS Y PIRÁMIDES
 POLIEDROS, PRISMAS Y PIRÁMIDES 1. Completa la siguiente tabla. 2. Indica si son verdaderas o falsas (V o F) las siguientes afirmaciones. a) La suma de las caras y los vértices del cubo es 12. b) El menor
POLIEDROS, PRISMAS Y PIRÁMIDES 1. Completa la siguiente tabla. 2. Indica si son verdaderas o falsas (V o F) las siguientes afirmaciones. a) La suma de las caras y los vértices del cubo es 12. b) El menor
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos
 Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
Matemáticas 3º E.S.O. 2013/14
 Matemáticas º E.S.O. 01/14 TEM 6: Cuerpos geométricos Repaso eamen 1.- Estoy construyendo una piscina de 5 metros de largo, 15 metros de ancho y metros de alto. Quiero cubrir las paredes y el fondo con
Matemáticas º E.S.O. 01/14 TEM 6: Cuerpos geométricos Repaso eamen 1.- Estoy construyendo una piscina de 5 metros de largo, 15 metros de ancho y metros de alto. Quiero cubrir las paredes y el fondo con
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
10 FIGURAS Y CUERPOS GEOMÉTRICOS EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10. Completa la siguiente tabla. Caras (C ) Vértices (V )
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Pág. 1 PÁGINA 246 REFLEXIONA En la inauguración de la Casa de la Cultura observamos, entre otras, las siguientes figuras: Todas ellas son polígonos. Cuáles crees que son regulares? Explica por qué crees
Halla los siguientes perímetros y áreas:
 73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
1 Calcula en la siguiente figura el elemento que falta: 2 Calcula en la siguiente figura el elemento que falta:
 1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
Problemas geométricos
 Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
2º. La diagonal de un cuadrado mide 1 metro. Cuántos centímetros mide el lado?
 FIGURAS PLANAS. ÁREAS 1º. De las siguientes ternas de números, cuáles son pitagóricas? (Es decir cumplen el teorema de Pitágoras) a) 3, 4, 5 b) 4, 5, 6 c) 5, 12, 13 d) 6, 8, 14 e) 15, 20, 25 2º. La diagonal
FIGURAS PLANAS. ÁREAS 1º. De las siguientes ternas de números, cuáles son pitagóricas? (Es decir cumplen el teorema de Pitágoras) a) 3, 4, 5 b) 4, 5, 6 c) 5, 12, 13 d) 6, 8, 14 e) 15, 20, 25 2º. La diagonal
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGIN 212 Recorta en cartulina cada una de estas figuras y sujétalas en palillos de dientes. Sosteniendo el palillo entre los dedos y soplando en el lateral, qué ves en cada caso? Triángulo ono
Pág. 1 PÁGIN 212 Recorta en cartulina cada una de estas figuras y sujétalas en palillos de dientes. Sosteniendo el palillo entre los dedos y soplando en el lateral, qué ves en cada caso? Triángulo ono
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Matemáticas 3º Eso.
 Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
MATEMÁTICAS 3º ESO PENDIENTES HOJA 1 GEOMETRÍA PLANA. 1.- Calcular el área y el perímetro de los siguientes polígonos:
 MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
9 Cuerpos geométricos
 9 Cuerpos geométricos RELACIONA Y CONTESTA Platón, filósofo griego, había sostenido un modelo geométrico para explicar la estructura del Universo. Los cinco poliedros regulares, los sólidos platónicos,
9 Cuerpos geométricos RELACIONA Y CONTESTA Platón, filósofo griego, había sostenido un modelo geométrico para explicar la estructura del Universo. Los cinco poliedros regulares, los sólidos platónicos,
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014
 E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
E S C U E L A T É C N I C A S U P E R I O R D E A R Q U I T E C T U R A U N I V E R S I D A D D E N A V A R R A Preguntas tipo OLIMPIADA DE DIBUJO TÉCNICO MARZO 2014 G E O M E T R Í A M É T R I C A. T
