Electrostática: Definición.
|
|
|
- Xavier Blanco Acuña
- hace 9 años
- Vistas:
Transcripción
1 lectcdad y Magetsmo / lectostátca efcó Los coductoes e electostátca. Campo de ua caga putual. Aplcacoes de la Ley de Gauss Itegales de supeposcó. Potecal electostátco. efcó e Itepetacó. cuacoes de Posso y Laplace. Codcoes de Itefase. Itegales de supeposcó. Codcoes de eguladad. Teoema de ucdad, teoema del alo medo. Campo y potecal eléctco e putos alejados: dpolo, mometo dpola,... Polaacó de mateales. Método de las mágees. stemas de coductoes. Codesadoes. egía y Fueas. ym 3a- J.L. Feáde Jamba lectostátca: efcó. s el caso más smple de las cuacoes de Maxwell. Codcoes: No hay aacó co el tempo: d No hay mometo de cagas: J dt» sta últma codcó es ecesaa: Puede habe coetes auue d dt jemplo: esfea co caga ufome ue ga alededo de uo de sus dámetos. Cometaos: No puede exst stuacoes estátcas desde u puto de sta estcto:» Los campos pecsa de u tempo fto paa alcaa su alo estátco.» empe hay coetes de coduccó e los medos. No obstate, es ua buea apoxmacó paa muchos casos e ue las coetes y las elocdades de las cagas so peueñas. J.L. Feáde Jamba ym 3a- lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a
2 lectcdad y Magetsmo / Campo státco estas codcoes las ecuacoes de Maxwell se smplfca otablemete: B (, t), t t, t H, t J, t + t H t J B, t, t B, t (, t) J J, t + t B µ H (, t) (, t) B(, t) µ H (, t) σ J (, t) σ(, t) Puede supoese s poblema ue el campo magétco es ulo, auue o se sgue dectamete de sus ecuacoes. Las ecuacoes de la electostátca so: σ ym 3a-3 J.L. Feáde Jamba l campo electostátco e el teo de los coductoes. Ates de pasa al estudo e pofuddad de las ecuacoes de la electostátca coee aala el compotameto de los coductoes. Puesto ue las coetes so ulas y la coductdad de los coductoes o es ula, el campo eléctco e los coductoes es ulo: J J σ» Patedo de la ley de Ohm geealada: σ σ, J» Paa cosegu este efecto la caga del coducto se dstbuye sobe su supefce de foma ue cacela cualue campo exteo.» La caga eta e el teo del + coducto es ula: ( ) J.L. Feáde Jamba ym 3a σ σ lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a
3 lectcdad y Magetsmo / lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 3 J.L. Feáde Jamba ym 3a-5 e tata de aplca las codcoes de fotea sabedo ue e el teo de los coductoes el campo es ulo: upoedo ue el coducto es el medo : Resulta ue el campo e la pate exteo de la supefce de los coductoes es omal a la supefce. Po comoddad se suele deoma al campo e la pate exteo de la supefce de los coductoes como campo e la supefce del coducto. t l campo electostátco e la supefce de los coductoes. σ, σ J.L. Feáde Jamba ym 3a-6 Campo de ua caga putual e espaco lbe s ecesao paa justfca la utlacó de las smetías e la aplcacó de la Ley de Gauss. Plateameto del poblema: e supoe ue la caga está e el oge de coodeadas. Po la lealdad del medo: e cooce ue: Luego: k O d O k d π π π
4 lectcdad y Magetsmo / Campo de ua caga putual e espaco lbe La expesó del campo ceado po ua caga e el oge de coodeadas es: 4π ( ) Popedades: s adal. u módulo sólo depede (del eso del cuadado) de la dstaca ete la caga y el puto de obseacó. J.L. Feáde Jamba ym 3a-7 Aplcacoes dectas de la Ley de Gauss. La ley de Gauss e su foma tegal pemte e detemadas codcoes calcula el campo ceado po ua dstbucó de caga. geeal se euee u coocmeto peo del compotameto del campo e la supefce e ue se aplca la ley de Gauss. ste compotameto se suele fe a pat de» Las smetías ue pesete el sstema.» l hecho de ue el campo debdo a ua caga putual es adal. Impotate: La ley de Gauss se puede aplca sempe. Las smetías sólo so ecesaas paa pode utla la Ley de Gauss paa obtee el campo eléctco. J.L. Feáde Jamba ym 3a-8 lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 4
5 lectcdad y Magetsmo / Ley de Gauss: stbucoes co smetía esféca. Ua dstbucó tee smetía esféca cuado d d sólo hay aacó co la coodeada esféca : dθ dϕ Bajo estas codcoes el campo eléctco es adal y sólo depede de la coodeada esféca : emostacó:» ado u puto abtao paa el cálculo del campo y u d abtao, sempe esulta posble ecota oto d tal ue su cotbucó al campo total cacele las compoetes o adales del pme d : d d d + d d d» l campo o depede de las coodeadas θ y ϕ: ua caga eía la dstbucó de gual foma al aa estas coodeadas. ym 3a-9 J.L. Feáde Jamba Ley de Gauss: stbucoes co smetía esféca. () Co estos pesupuestos basta aplca la ley de Gauss a ua supefce esféca cetada e el ceto de smetía de la dstbucó: dv d d 4π V 4π 4π 4π ode () es la caga eceada e la supefce de ado. jemplo: l campo ceado po ua bola de caga de ado R y desdad de caga es: 3 4π ; R ; R 3 3 dv 3 V 4πR 3 ; R 4π 3 R 3 R J.L. Feáde Jamba ym 3a- ; lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 5
6 lectcdad y Magetsmo / Ley de Gauss: stbucoes aates e ua deccó co smetía de eolucó. Ua dstbucó tee smetía de eolucó alededo de u eje, el eje Z, y es aate e esa deccó cuado sólo hay aacó co la coodeada clídca : Bajo estas codcoes el campo eléctco es adal y sólo depede de la coodeada clídca : emostacó: d dϕ ado u puto abtao paa el cálculo del campo y u d abtao, sempe esulta posble ecota oto d tal ue su cotbucó al campo total cacele las compoetes o adales del pme d : Ua caga eía la dstbucó de la msma foma auue aíe ϕ y. d d d d d d d + d ym 3a- J.L. Feáde Jamba Ley de Gauss: stbucoes aates e ua deccó co smetía de eolucó. () Co estos pesupuestos basta aplca la ley de Gauss a ua supefce clídca co eje el el eje de smetía de logtud abtaa L: dv L d d + d d πl L V L, lat Tapas lat Obseese ue el flujo a taés de las tapas es ulo poue el campo eléctco es tagecal a la supefce. L L L π π π $ $ ode L es la caga po udad de logtud deto del cldo de ado. jemplo: stbucó leal de caga λ a lo lago del eje : $ λ π ym 3a- J.L. Feáde Jamba L L $ $ $ lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 6
7 lectcdad y Magetsmo / Ley de Gauss: stbucoes co aacó e ua deccó. stas dstbucoes sólo depede de ua coodeada leal, s ésta es la coodeada : o defdas e las deccoes a la coodeada de la ue depede. Paa comea su estudo coee empea po el caso más smple: ua dstbucó de caga supefcal costate e el plao. l campo tee sólo compoete omal a la dstbucó: dado u d sempe se puede ecota oto, e poscó smétca, de foma ue se cacela las compoetes del campo paalelas al plao de la dstbucó. Paa putos smétcos especto del plao, uo a u lado y el oto al oto lado, el campo tee el msmo módulo y setdos cotaos: cuestó de smetía. d dx d dy l módulo del campo o depede de la dstaca a la dstbucó: ym 3a-3 J.L. Feáde Jamba s Ley de Gauss: stbucoes co aacó e ua deccó. () l módulo del campo o depede de la dstaca a la dstbucó:» Basta co toma ua supefce de Gauss como la de la fgua: u cldo co ecto co sus tapas paalelas a la dstbucó y e poscoes smétcas especto a ellas. l flujo a taés de la supefce lateal es ulo ya ue el campo es tagecal. l flujo a taés de las caas se suma debdo a la smetía del campo y de las omales. d d d + lat 443 ( ) ( h) ( h) d ( h) d + ( h) ( h) ( h) d d ; < ( h) ; < ym 3a-4 J.L. Feáde Jamba ( h) h $ lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 7
8 lectcdad y Magetsmo / Ley de Gauss: stbucoes co aacó e ua deccó. (3) l campo es costate a cada lado de la dstbucó supefcal y co el msmo módulo y setdos cotaos a cada lado. caso de dstbucoes mas complejas, debe ecodase ue cada d defe u elemeto ftesmal de caga eualete a ua dstbucó supefcal de caga de desdad: d y ue la smetía de los campos debe mateese fuea de la dstbucó. -a a Z -a a a a a Z a 3a ym 3a-5 J.L. Feáde Jamba Campo poducdo po u sstema de cagas putuales upogamos u cojuto de cagas putuales e el acío. l campo poducdo po ellas seá la suma de los ue poduce cada ua de ellas po sepaado, es dec: ' ( ) R 3 ' ' 4π 4π sedo el campo poducdo po la caga -ésma. Total O J.L. Feáde Jamba ym 3a-6 lectostátca: Itoduccó, Aplcacó de la Ley de Gauss ym 3-a 8
Se entiende por sistema de fuerzas a un conjunto de fuerzas como se indica
CDENADAS VECTIALES DE LS SISTEAS DE FUEZAS Se etede po sstema de fuezas a u cojuto de fuezas como se dca La esultate geeal del sstema se obtee sumado los vectoes equpoletes de cada ua de las compoetes
FUNDAMENTOS FÍSICOS Y TECNOLÓGICOS DE LA INFORMÁTICA
FUNDAMENTOS FÍSIOS Y TENOLÓGIOS DE LA INFORMÁTIA TEMA I.- ELETROSTÁTIA FUNDAMENTOS FÍSIOS Y TENOLÓGIO DE LA INFORMÁTIA Tema.ELETROSTÁTIA- Tecología de omputadoes-datsi-fi-upm-madd - M. A. Pascual Iglesas
ALGUNAS CUESTIONES DE ELECTROMAGNETISMO LECCIONES 1 A 10 ( )
ALGUNAS CUESTIONES DE ELECTROMAGNETISMO LECCIONES 1 A 1 (24-25) 1. E ua esfea de adio a teemos ua caga Q distibuida de modo que cea u campo eléctico adial de itesidad: k E, < < a 2 siedo k ua costate.
Bibliografía. Bibliografía. Fundamentos Físicos de la Ingeniería. Tema 3 Mc Graw Hill. - Tipler. "Física". Cap. 23. Reverté.
Tema.- POTENCIAL ELÉCTRICO. Potencal eléctco. (3.).. Potencal eléctco debdo a un sstema de cagas puntuales. (3.).. Potencal eléctco debdo a dstbucones contnuas de caga. (3.4)..3 Detemnacón del campo eléctco
Bolilla 4: Rotación de los cuerpos rígidos. Movimiento circular
Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula Bollla 4: Rotacó de los cueos ígdos. Movmeto ccula 4. Vaables Agulaes Las vaables agulaes sve aa eeseta e foma mas smle e dóea al movmeto de otacó. La
q q q q q q n r r r qq k r q q q q
urso: FISIA II B 30 00 I Profesor: JOAQIN SALEDO [email protected] Eergía potecal electrostátca. S traemos ua carga desde ua dstaca fta el trabajo ecesaro es ulo. 0 trate ua fumadta, grats,, te vto S luego
MEDIDAS DE FORMA: ASIMETRÍA Y CURTOSIS. MOMENTOS
Julo Olva Coteo Estadístca TEMA 6 MEDIDA DE FORMA: AIMETRÍA Y CURTOI. MOMETO. Moetos de ua dstbucó Los oetos de ua dstbucó so eddas obtedas a pat de todos sus datos y de sus fecuecas absolutas. Estas eddas
Estadística Tema 9. Modelos de distribuciones. Pág. 1
Estadístca Tema 9. Modelos de dstbucoes. Pág. 9 Modelos de dstbucoes. 9. Modelos dscetos de vaables aleatoas. 9.. Epemetos y dstbucó de Beoull. 9.. Dstbucó bomal. 9.. Dstbucó ufome dsceta. 9.. Dstbucó
Momento lineal: Momento lineal: p = mv Principio de conservación del momento lineal: pi = p
Julá oeo este www.julweb.es tlf. 69886 Chuletao de físca º de Bachlleato y 4º de ESO Cemátca: ( t) + vt v ( t) v v v a( ) Cemátca del movmeto ccula: θ θ () t θ + ωt+ αt ω() t ω + αt ω ω α( θ θ) π π v f
dq de x r CAMPO DE UN ANILLO CON CARGA UNIFORME r α P de y de x
y a dsdq AMPO D UN ANILLO ON AGA UNIFOM P d y l campo d debdo a dq es: d dq dq a d d Un segmento en la pate nfeo del anllo cea un capo eléctco d con componente d y gual y opuesta, así que sólo contbuyen
CAPÍTULO 6 TEOREMAS ENERGÉTICOS
CPÍTULO 6 TEORES ENERGÉTICOS L ENERGÍ ELÁSTIC EXPRESD EN UNCIÓN DE LS CRGS PLICDS Hasta ahoa, habíamos utlao la sguete epesó e la esa e eegía elástca: ( σ ε σ ε σ ε τ γ τ γ τ γ ) ω Que, tegaa a lo lago
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Números Complejos PREGUNTAS MÁS FRECUENTES
Repaso de º de Bachllerato Números Complejos PREGUNTAS MÁS FRECUENTES. Qué es la udad magara? Es u elemeto del que coocemos úcamete su cuadrado:.obvamete, o se trata de u úmero real.. Qué es u úmero complejo?
CAPÍTULO II LEY DE GAUSS
Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
PROBLEMAS DE ÓPTICA. FÍSICA 2 BACHILLERATO. Profesor: Félix Muñoz Jiménez
PROBEMS DE ÓPTIC. FÍSIC BCHIERTO. Pofeo: Félx Muñoz Jméez Poblema º Calcula el ídce de efaccó elatvo del vdo al acete. Halla la velocdad de popagacó y la logtud de oda, e el acete y e el vdo de u ayo de
MANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA PROPAGACIÓN DE ERRORES. Escuela de Geociencias y Medio Ambiente
ANUAL DE PRÁCTICAS DE LABORATORIO DE HIDRÁULICA 35 ANEXO A5 PROPAGACIÓN DE ERRORES Ramo abello Péez Escuela de Geocecas y edo Ambete 36 ANEXO 5 A5 PROPAGACIÓN DE ERRORES Tomado de la Ref. [0] Las magtudes
LEY DE GAUSS. Este enunciado constituye en realidad una de las principales leyes del Electromagnetismo.
LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
Matemáticas Aplicadas CC. SS. I -- I. E. S. Sabinar
Matemátcas Aplcadas. SS. I -- I. E. S. Saba MATEMÁTIAS INANIERAS EN 1º BTO.. SS. 1. PORENTAJES 1.1 Aumetos y dsmucoes pocetuales. Ídce de vaacó 1.2 Aumetos y dsmucoes pocetuales ecadeados. Ídce de vaacó
TEMA 2: LOS NÚMEROS COMPLEJOS
Matemátcas º Bachllerato. Profesora: María José Sáche Quevedo TEMA : LOS NÚMEROS COMPLEJOS. LOS NÚMEROS COMPLEJOS Relacó etre los úmeros complejos y los putos del plao. Afjo de u úmero complejo. Cojugado
3.5 Factores y Coeficientes de Forma
Autoes: Patco Covalá Vea Jame eáez Palma 3.5 Factoes y Coecetes e Foma A es el slo XIX, Towa esaolla la ea e los actoes e oma como ua espuesta a las cultaes suas el uso e los sólos e evolucó. La ea e Towa
Práctica 11. Calcula de manera simbólica la integral indefinida de una función. Ejemplo:
PRÁCTICA SUMAS DE RIEMAN Práctcas Matlab Práctca Objetvos Calcular tegrales defdas de forma aproxmada, utlzado sumas de Rema. Profudzar e la compresó del cocepto de tegracó. Comados de Matlab t Calcula
Capítulo 2 Análisis de datos (Bivariados( Bivariados) Estadística Computacional I Semestre 2006 Parte II
Uvesdad Técca Fedeco Sata Maía Uvesdad Técca Fedeco Sata Maía Depatameto de Iomátca ILI-80 Capítulo Aálss de datos (Bvaados( Bvaados) Estadístca Computacoal I Semeste 006 Pate II Poesoes: Calos Valle ([email protected])
La inferencia estadística es primordialmente de naturaleza
VI. Ifereca estadístca Ifereca Estadístca La fereca estadístca es prmordalmete de aturaleza ductva y llega a geeralzar respecto de las característcas de ua poblacó valédose de observacoes empírcas de la
E r = 0). Un campo irrotacional proviene de un campo escalar; es el gradiente de un campo escalar. En el caso del campo electrostático,
L OTNIAL LÉTRIO l campo electostático es iotacional ( = ). Un campo iotacional poiene de un campo escala; es el gadiente de un campo escala. n el caso del campo electostático, esta función se denomina
1. ESPACIOS VECTORIALES
Espacios Vectoiales Heamietas ifomáticas paa el igeieo e el estudio del algeba lieal. ESPACIOS VECTORIALES.. ESTRUCTURA DE ESPACIO VECTORIAL... Defiició..2. Ejemplos de espacios vectoiales..3. Popiedades
La Carga Eléctrica Puntual, es una partícula cuya masa se supone está concentrada en un punto, y en el mismo se concentra su carga eléctrica.
LEY DE COULOMB La Ley de Coulomb es la pmea ue se estuda en Electcdad ella consttuye una LEY UNIVERSAL poue es posble deducla del expemento y s ese expemento se ealza bajo las msmas condcones físcas cualuea
ESPACIOS VECTORIALES SUBESPACIOS FINITAMENTE GENERADOS:
SUBESPACIOS FINITAMENTE GENERADOS: Teorema S G={v, v,, v } es u sstema fto de geeradores de u subespaco S V K-EV, etoces G`= {v, v,, v,w} sedo w combacó leal de vectores de G, també geera a S. Demostracó
2. Medición de Índices de Refracción. Neil Bruce
. Medició de Ídices de Refacció Neil Buce Laboatoio de Optica Aplicada, Ceto de Ciecias Aplicadas y Desaollo Tecológico, U.N.A.M., A.P. 70-86, México, 0450, D.F. Objetivos Istumeta e el laboatoio métodos
Momento cuadrupolar eléctrico
Depatamento de Físca Fac. Cencas Eactas - UNLP Momento cuadupola eléctco El núcleo y sus adacones Cuso 0 Págna S el pomedo tempoal de la dstbucón de caga dento del núcleo se desvía de la smetía esféca,
Solucionario de las actividades propuestas en el libro del alumno
Soluconao de las actvdades popuestas en el lbo del alumno 7.. LEY DE COULOMB Págna 47. La dstanca que sepaa ente sí los dos potones de un núcleo de helo es del oden de fm (0 5 m). a) Calcula el módulo
Apuntes de Electrostática Prof. J. Martín ETSEIT ELECTROESTÁTICA I CAMPO ELECTRICO EN EL ESPACIO LIBRE
LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
5. Estimación puntual. Curso Estadística
5. stmacó utual Cuso - stadístca Poblacó % DFCTUOSA Pobabldad Coocdo cuato vale? Muesta Nº Defectuosa Coocdo cuato vale? Ifeeca stmacó utual N Paámetos? MUSTRA... Datos Coocdos? stmacó utual 3 sesoes de
Potencial eléctrico. Física II Grado en Ingeniería de Organización Industrial Primer Curso. Departamento de Física Aplicada III Universidad de Sevilla
Potencal eléctco Físca II Gado en Ingeneía de Oganzacón Industal Pme Cuso Joaquín enal Méndez Cuso 11-1 Depatamento de Físca plcada III Unvesdad de Sevlla Índce Intoduccón: enegía potencal electostátca
Al estar la fuerza dirigida hacia arriba y la intensidad del campo eléctrica hacia abajo, la carga de la esfera es negativa:
PROLMS CMPO LÉCTRICO. FÍSIC CHILLRTO. Pofeso: Féli Muñoz Jiménez Poblema 1 Detemina la caga de una peueña esfea cagada de 1, mg ue se encuenta en euilibio en un campo eléctico unifome de 000 N /C diigido
TEMA 5 SISTEMAS DE N GRADOS DE LIBERTAD. Sistemas de N Grados de Libertad
Sstemas de N Gados de Lbetad ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 5. - ELEMENTOS DE MÁQUINAS Y VIBRACIONES - 5. - 5. Plateameto matcal Se va a extede los esultados de gdl al caso geeal de N gdl. El estudo
INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DE QUIBDÓ. CINEMÁTICA DEL MOVIMIENTO EN EL PLANO: dos dimensiones, horizontal y vertical.
MCOSPB CIENCIS NTULES FÍSIC -- 10 -- 013. N.S.Q INSTITUCIÓN EDUCTIV ESCUEL NOML SUPEIO DE QUIBDÓ CINEMÁTIC DEL MOVIMIENTO EN EL PLNO: dos dimesioes, hoizotal y vetical. O sea: Esfea: cayedo de ua mesa
Electromagnetismo: Electrostática
lectomagnetsmo: lectostátca 1.1 Intoduccón La electcdad está pesente en nuestas vdas cotdanas. asta pensa en desaollos tecnológcos como la ed de alumbado eléctco o los electodoméstcos, o en fenómenos meteoológcos
Experimento 1 Medición de Índices de Refracción
Expemeto Medcó de Ídces de Refccó Objetvos Istumet e el lbotoo métodos de medcó de ídces de efccó de sustcs tspetes que puede est e estdo líqudo o sóldo, tles como vdo, luct, gu, glce, etc. Relz u álss
Polarización. Propagación de la luz en medios anisótropos
Polaizació Popagació de la luz e medios aisótopos Polaizació de ua oda Popiedad de las odas tasvesales: La vibació es pepedicula a la diecció de popagació Se defie la diecció de polaizació como la diecció
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN
VARIABLE ALEATORIA Y FUNCIÓN DE DISTRIBUCIÓN - INTRODUCCIÓN E este tema se tratará de formalzar umércamete los resultados de u feómeo aleatoro Por tato, ua varable aleatora es u valor umérco que correspode
Tema 2: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 4/7 Leyes de la electrostática
Tema : Pincipios de la electostática 1, Antonio Gon nzález Fená ández Antonio González Fenández Depatamento de Física Aplicada III Univesidad de Sevilla Pate 4/7 Leyes de la electostática Leyes de la electostática:
x x x x x Y se seguía operando
. INTRODUCCIÓN. DEFINICIONES UNIDAD : Números complejos Cuado se teta resolver ecuacoes de segudo grado como por ejemplo x 4x 0, se observa que o 4 6 5 4 6 tee solucoes reales x x, pues o exste raíces
Intensidad de campo eléctrico Se define como la fuerza que actúa por unidad de carga. Es una magnitud vectorial. F q E k q d se mide en N C
Campo eléctico Campo eléctico es la pate el espacio en la ue apaecen fuezas e atacción o e epulsión ebio a la pesencia e una caga. Caacteísticas e las cagas: Hay os tipos e cagas: positivas y negativas.
CAPÍTULO IV NÚMEROS COMPLEJOS E INDUCCIÓN MATEMÁTICA
NÚMEROS COMPLEJOS E INDUCCIÓN MATEMATICA 55 CAPÍTULO IV NÚMEROS COMPLEJOS E INDUCCIÓN MATEMÁTICA 4. INTRODUCCIÓN Los úmeros Complejos costtuye el mímo cojuto C, e el que se puede resolver la ecuacó x a
Soluciones de los ejercicios de Selectividad sobre Inferencia Estadística de Matemáticas Aplicadas a las Ciencias Sociales II
Solucoes de los ejeccos de Selectvdad sobe Ifeeca Estadístca de Matemátcas Aplcadas a las Cecas Socales II Atoo Facsco Roldá López de Heo * Covocatoa de 007 Las sguetes págas cotee las solucoes de los
Cinemática del Robot Industrial
Cemátca del Robot Idustal M.C. Mguel de J. Ramíe C. CMfgT Automatacó de Sstemas de Maufactua Adatacó: Glbeto Reoso Estuctua Mecáca del Robot Idustal Mecácamete u obot es ua cadea cemátca fomada de eslaboes
Lección 2. El campo de las cargas en reposo: campo electrostático.
Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
TEMA 3. Medidas de variabilidad y asimetría. - X mín. X máx
TEMA 3 Meddas de varabldad y asmetría 1. MEDIDAS DE VARIABILIDAD La varabldad o dspersó hace refereca al grado de varacó que hay e u cojuto de putuacoes. Por ejemplo: etre dos dstrbucoes que preseta la
Hotel Burj Al Arab, Dubai, Emiratos Árabes Unidos
Hotel Buj Al Aab Dubai Emiato Áabe Unido Pedo ami Bofill-Gaet Poyecto de paametiación Ampliación de Matemática Intoducción Paa ete poyecto e ha ecogido como upeficie el lujoo hotel Buj al Aab de Dubai.
Tema 4.-Potencial eléctrico
Tema 4: Potencial eléctico Fundamentos Físicos de la Ingenieía Pime cuso de Ingenieía Industial Cuso 6/7 Dpto. Física plicada III Univesidad de Sevilla 1 Índice Intoducción: enegía potencial electostática
Variables aleatorias
Vaables aleatoas M. e A. Vícto D. Plla Moá Facultad de Igeeía, UNAM Resume El cocepto de vaable aleatoa como abstaccó de u eveto aleatoo y su defcó. vaable aleatoa dsceta: fucó de pobabldad, sus popedades
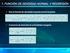
Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).
![Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).](/thumbs/76/73987868.jpg "Electromagnetismo I. 1. Problema: (20pts) El potencial en la superficie de una esfera de radio R está dado por. Alm r l + B lm r (l+1)] Y lm (θ, ϕ).")
Electomagnetismo I Semeste: 25-2 Pof. Alejando Reyes Coonado Ayud. Calos Albeto Maciel Escudeo Ayud. Chistian Espaza López Solución a la Taea 5 Solución po Calos Maciel Escudeo. Poblema: 2pts El potencial
Electrostática. Campo electrostático y potencial
Electostática Campo electostático y potencial 1. Caga eléctica Electostática estudio de las cagas elécticas en eposo ++ +- -- epulsión atacción Unidad de caga el electón e 1.602177x 10-19 19 C 1.1 Constituyentes
3. Campo eléctrico de distribuciones continuas de carga. M.A.Monge / B. Savoini Dpto. Física UC3M
Campo eléctico II: Ley de Gau 1. Intoducción 2. Ditibucione continua de caga. 3. Campo eléctico de ditibucione continua de caga. 4. Flujo del campo eléctico. 5. Ley de Gau. 6. Aplicacione de la ley de
Figura 1.63: letra i superpuesta con los símbolos = e. Figura 2.1: donde dice δc debe decir δs.
Fe de eatas Debido a poblemas técicos duate la impesió de esta pimea edició de lectomagetismo elemetal, vaias iguas peseta eoes ue o existía e el mauscito oigial pesetado po el auto. uellas e las cuales
Aplicaciones de Balances de Energía en Reactores Batch
plcacoes de Balaces de Eergía e Reactores Batch Para u reactor batch, el BdeM se epresa como la ecuacó para determar el tempo de resdeca: t N ( rv Separado varables: V N Esta es ua ecuacó dferecal ordara
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO.
Tema 3. DINÁMICA DE UN SÓLIDO RÍGIDO. CONTENIDOS: 3.1 Intoduccón 3. Cnemátca de la otacón alededo de un eje fjo. 3.3 Momento de una fueza y de un sstema de fuezas. 3.4 Momento angula del sóldo ígdo. 3.5
Energía del campo eléctrico.
Enegía del camp eléctc. Cagas puntuales en el vací. Enegía ptencal de un pa de cagas (I). En el ema, dms ue la enegía ptencal de una caga puntual, en pesenca de ta caga puntual es:,, O Dnde, es el ptencal
REGRESIÓN LINEAL SIMPLE
RGRIÓN LINAL IMPL l aálss de regresó es ua técca estadístca para vestgar la relacó fucoal etre dos o más varables, ajustado algú modelo matemátco. La regresó leal smple utlza ua sola varable de regresó
LAZOS DE AMARRE DE FASE
LAZOS DE AMARRE DE FASE Maco Atoio Péez Ciseos *, Mak Readma * Divisió de Electóica Computació, CUCEI, Uivesidad de Guadalajaa, México. Cosulto Cotol Sstems Piciples RESUMEN: Este atículo peteece a la
TEMA 2 MEDIDAS DE CENTRALIZACIÓN
D37 ESTADÍSTICA. Tema TEMA MEDIDAS DE CETRALIZACIÓ. Caacteístcas de las meddas de poscó cetal.. Meddas de cetalzacó: meda atmétca, medaa y moda. Popedades. Relacó ete meda, medaa y moda..3 Cuatles: cuatles,
MOVIMIENTO DE UNA PARTICULA EN EL CAMPO GRAVITACIONAL REAL
MOVIMIENTO DE N PRTICL EN EL CMPO RVITCIONL REL Consdeaemos el movmento de una patícula en el campo gavtaconal Real donde el Sstema de Laboatoo es despecado poque se toma en cuenta la geodesa de la tea
CAMPO ELÉCTRICO { } ( ) ( ) ( ) ( ) { } 2 { } ( ) ( ) ( ) ( ) ( ) ( ) C
MPO LÉTRIO Septembe 0. Pegunta B.- Dos esfeas peueñas tenen caga postva. uano se encuentan sepaaas una stanca e cm, exste una fueza epulsva ente ellas e 0,0. alcule la caga e caa esfea y el campo eléctco
OPTICA REFLEXIÓN Y REFRACCIÓN
OPTICA REFLEXIÓN Y REFRACCIÓN IES La Magdalea. Avlés. Astuas La eflexó se poduce cuado ua oda ecueta ua supefce cota la cual ebota. E la eflexó el ayo cdete y el eflejado se popaga e el msmo medo. La velocdad
Transformada Z. Definición y Propiedades Transformada Inversa Función de Transferencia Discreta Análisis de Sistemas
5º Curso-Tratameto Dgtal de Señal Trasformada Z Defcó y Propedades Trasformada Iversa Fucó de Trasfereca Dscreta Aálss de Sstemas 7//99 Capítulo 7: Trasformada Z Defcó y Propedades 5º Curso-Tratameto Dgtal
Analogía para derivar un teorema extendido de Pitágoras para N dimensiones
Igeeía Ivestgacó y Tecología. ol. III, Núm.,, 75-84 ISSN 45-7743 FI-UNM atículo abtado alogía paa deva u teoema exteddo de Ptágoas paa N dmesoes alogy to Deve a Exteded Pytagoea Teoem to N Dmesos costa-robledo
ÁLGEBRA II (LSI PI) VALORES Y VECTORES PROPIOS UNIDAD Nº 6. Facultad de Ciencias Exactas y Tecnologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO
6 ÁLGEBRA II (LSI PI) UNIDAD Nº 6 VALORES Y VECTORES PROPIOS Facultad de Cecas Exactas y Tecologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO aa Error! No hay texto co el estlo especfcado e el documeto.
GENERALIDADES SOBRE MÓDULOS
GENERALIDADES SOBRE MÓDULOS Presetar el Z -módulo Z como cocete de u Z -módulo lbre Hacer lo msmo para el grupo de Kle Calcular los auladores de los sguetes módulos: a) El Z -módulo Z Z 6 b) El Z -módulo
TEMA 4: VALORACIÓN DE RENTAS
TEMA 4: ALORACIÓN DE RENTAS 1. Cocepto y valor facero de ua reta 2. Clasfcacó de las retas. 3. aloracó de Retas dscretas. Temporales. 4. aloracó de Retas dscretas. Perpetuas. 5. Ejerccos tema 4. 1. Cocepto
Emilio Benitez Aguado Y Luis García-Asenjo Villamayor Ingeniero en Geodesia y Cartografía Ingeniero en Geodesia y Cartografía
Emlo Betez Agado Ls Gacía-Aseo Vllamayo Igeeo e Geodesa y Catogafía Igeeo e Geodesa y Catogafía Ig. ec. e opogafía Ig. ec. e opogafía Pofeso asocado a tempo pacal, Depatameto de Pofeso tla del Depatameto
(Feb03-1ª Sem) Problema (4 puntos). Se dispone de un semiconductor tipo P paralepipédico, cuya distribución de impurezas es
(Feb03-ª Sem) Problema (4 putos). Se dspoe de u semcoductor tpo P paraleppédco, cuya dstrbucó de mpurezas es ( x a) l = A 0 dode A y 0 so mpurezas/volume, l es u parámetro de logtud y a la poscó de ua
APÉNDICE 1 1. Sistemas de coordenadas
APÉNDICE. Sstemas de coodenadas El naldad de un sstema de coodenadas es la de consegu una adecuada descpcón de un punto de una cuva o de una supece en el espaco. De los dstntos tpos de sstemas de coodenadas