UN EJEMPLO DE GEOMETRIAS METRICAS EUCLIDIANAS EN CUALQU.IER DIMENSION EN LAS QUE JO RIGE EL AXIOMA DE PARALELISMO DE EUCLIDES. Heinz-Reiner Friedlein
|
|
|
- Mercedes Contreras Barbero
- hace 5 años
- Vistas:
Transcripción
1 Revista de la Unian Matemática Argentina Vlumen 27, UN EJEMPLO DE GEOMETRAS METRCAS EUCLDANAS EN CUALQU.ER DMENSON EN LAS QUE JO RGE EL AXOMA DE PARALELSMO DE EUCLDES Heinz-Reiner Friedlein Pr ls aximas en (2) 6 (4) es psible cnstruir gemetrías en cualquier dimensi6n. Adjuntams a ls aximas de (2) el siguient"e: EUC. Para g 1 h existe un punt S 1 g, h Y ds rectas que pasan pr S, cn s 1 t tales que g 1 s 1 t 1 h. Se dice que las rectas s, h 6 g, t est~n en una escalera. Decims que la gemetría así descrita es una gemetría métrica euclidiana. Es cncid que ciertas gemetrías afines sn gemetrías m~tricas.euclidianas. Ahra querems cnstruir un ejempl de una gemetría m~trica eucli diana que n es gemetría afín. El ejempl que vams a cnstruir es una genera1izaci6n de un ejempl para el plan métric euclidian que figura en[ 1). Designarems ls punts y las rectas de las gemetrías pr letras mayúsculas y minúsculas, respectivamente. Un haz prpi cn sp~ te P es el cnjunt de tdas las rectas que pasan pr P. El terema principal en (2) ns muestra que es psible extender cada gemetría m~trica euclidiana a una gemetría pryectiva bien que la gemetría métrica euclidiana es sumergible en una geq metría pryectiva, que se dice gemetría pryectiva euclidiana. TEOREMA 1. a) En un espai m4t~i euzidian tds Zs haes p~pis tienen 1.a misma a~dinaudad. b) Además, ada has de Za gemet~la p~yetiva euzidiana tiene Za misma a~dinazidad que un has p~pi en Za gemetrla m4t~ia euzidiana. Un haz de la gemetría pryectiva euclidiana es definid en frma anuga a un haz prpi de una gemetría euclidiana. DemBt~ai~n. a) Sean ds haces diferentes que tienen cm sprtes ls punts diferentes O y P respectivamente. Sea g O; según
2 163 [2] existe exactamente un h P Y perpendicular a g. Est implica un mape biyectiv del cnjunt de las rectas del haz determinad pr O sbre el cnjunt de las rectas que pasan pr P. b) Sea G un haz que cntiene rectas pryectivas, que n sn rectas métricas. Elegims un punt métric O cm centr de un "snail map" (cmparar [3]). Existen en G ds reqtas métricas euclidianas diferentes a, b, tal que a, b n tienen ni un punt métric ni una recta métrica euclidiana en cmún que sea rtgnal a las ds; entnces existe un "snai1 map" cn centr O tal que la imagen G' de G baj este mape es un haz prpi. Las preimágenes de las rectas de, G' sn - pr cnstrucción (cmparar [3]) - rectas pryectivas y están en crrespndencia 1-1 cn el snai1 map. Queda pr demstrar que ls haces G cn la prpiedad que tdas las rectas de G sn perpendiculares a un hiperp1an de la gemetría métrica euclidiana que 'pasa pr O tienen la misma cardinalidad. Per cm estams en una gemetría pryectiva, se sabe que ls haces de esta gemetría tienen la misma cardinalidad. DEFNCON. Una gemetr!a af!n que ea una gemetr!a métrica eucti diana ae ttama gemetr!a euctidiana. Desde 1ueg,n tda gemetría afín es una gemetría euclidiana. Pr ejempl, las gemetrías afines cn crdenadas en un cuerp n cnmutativ n' sn gemetrías euclidianas (cmpa.rar [1]). TEOREMA 2. Cada gemetr!a métrica euctidiana ea aumergibte en una gemetr!a euczidiana. Dematración. Según [2] ó [3] cada gemetría métrica euclidiana es sumergible en una gemetría métrica pryectiva Ep' Elegims en Ep subcnjunts T ' r de punts y rectas respectivamente. T = {P E Ep ~ g.. h, g, h P tal que g, h 1 H, H hiperp1an y g, h rectas en la gemetría métrica euclidiana} r = {r E Ep Q, R E T ' Q.. R Y Q, R r} Entnces T yr determinan una gemetría afín y tds ls punts métrics euclidians se encuentran en T y tdas las rectas métri cas euclidianas pertenec~n a r. Según [3] cada recta de r es eje de una reflexión. Est implica que T ' r determinan una gemetría euclidiana [3]. Cn este resultad pdems cnstruir nuestr ejempl. Cnsiderems el anill e = ({l/p p = 2, 4l + 1, l E N} )
3 164 Sea H.: = {(al'...,an,... ) al'",an,... E Ca} un cnjunt de pu!!. ts cuyas crdenadas pertenecen a e. Es clar queh es un sub.. cnjunt de ls punts de una cierta gemetría euclidiana A (R) cn crdenadas enr. Adem&s A (R) es una gemetría afín y el espaci vectrial cn prduct intern crrespndiente es un espaci de Hilbert. NOTA. Es psible demstrar que la gemetría métrica euclidiana de termina este prduct interir (cmparar [2]). Cm cnjunt r de rectas definims: Si P es un punt de H entnces las rectas de r sn las rectas g de A (R) cn la siguiente prpiedad: g es la unión de P cn un punt Q E rr y Q ~ P. Ahra querems demstrar que (rr, r, ) es una gemetría métrica euclidiana per n una gemetría euclidiana. TEOREMA 3. (rr, r, ) determina una gemetria métria eulidiana en la que n vale el a~ima de paralelism de Euclides. Demstración. Usams ls aximas de [21. Ests aximas exigen tam bién para la gemetría métrica euclidiana una relaci6n 1 y reflexi~ nes en punts y rectas. Per A (R) tiene estas prpiedades. Axima 1 de [21 se cumple pues rr,r sn subcnjunts de ls punts y rectas en A (R). Axima 2. Sean g' ha, J' a ' gl' J reflexines en A (R) cn ejes g' ha, j' a ' gl' j respectivamente y g' ha, j A; ha, gl' j B; A, B. Entnces tenems g. n a A Y J. ha. Y = al cn al B. Axima 3. Dads ls punts y rectas cm en el dibuj J = a cn p P ""'=::: ;2::...- p 2 a.. e = a cn a, b P implica según [21 que a, b, c se encuentran en un plan métric euclidian. Sea t P3 la recta per-
4 165 pendicular a b pr P~ tal que crta la recta a en Pi' Falta demstrar que Pi, Pz E n. Per est sale de [11,pág. 288/299,f6rm~ la (1) y (3). Axima 4. Sean g = (P, P'), h = (P,Q') diferentes y (P,P') t (P,Q'). Entnces (P,P'), (P,Q') determinan un plan euclidian Az (R) de A (R). Se sabe que en A2 (R) la reflexi6n P en el punt P es el prduct g.r cn r 1 g, r E A2 (R). Análgamente cm en la demstraci6n para axima 3, existe un punt A 1 r y A E n tal que (A, Q') t r. El terema de tres reflexines [11 implica que (P,P'). (P,Q').r es una reflexi6n en una cierta recta d 1 P. El axima 5 sigue inmediatamente de la demstraci6n de ls aximas 3 y 4. Aximas 6 y 7 se satisfacen, pues estams en A (R). Axima 8 es trivial pues en A (R) n existen punts P,Q distints cn P.Q = Q. P. Axima 9. La existencia de tres punts que n se encuentran en una sla recta es trivial (ver la demstraci6n del axima 4) y des de lueg ds punts diferentes se encuentran sbre cada. recta. Además la gemetría cnstruída cumple trivialmente Euc. Pr tant n,r sn ls cnjunts de punts y rectas respectivamente de una gemetría métrica euclidiana. Ahra vams a demstrar que esta gemetría n satisface el terema de las paralelas de Euclides. Cm cada gemetría afín satisface este terema, estams lists cn la demstraci6n si hems encntrad ds rectas distintas g,h cn g, h 1 E, x n g = 0, x n h = 0; g, h E r, P E n. Cm 1/3 é e entnces (1/3,0,... ) é n per 0, E' = (1,1,0,... ) En.. Además sabems que ls ejes crdenads x e y pertenecen a r. Per en el ~lan euclidian que determinan x e y se tienen ds rectas diferentes g, h que pasan pr E' y que n crtan la recta x. Elegims g cm la recta rtgnal a y cn g 1 E' Y cm h la recta y le' g (3/2,0, ) en el plan euclidian de ecuaci6n y x 3/2 x - 1/2, h pertenece a
5 166 r pues (0,-1/2,0,... ) y E' se encuentran sbre h y E'. (0,-1/2,0,...,0,... ) E n per la intersección cn x es (3/2,0,0,... ) ~ n. REFERENC las [1] F. BACRMANN, Au6bau de~ Geame~4ie au~ dem Spiegelu~g~begAi66, Berlin [2] G. EWALD, Spiegelung~geame~Ai~che Kennzeichnung eu~lidi~che und nich~eu~lidi~chea Raume beliebige~ Vimen~ian, Math. Abh Sem. Ramburg 41 (1974). [3] R.R. FREDLEN, Enbe~~ung beliebig dimen~ianalea me~ai~che~ Raume mi~ Hil6e van Halbd~ehungen. [4] SMTR, O~~haganal Geame~Aie~ 1,11, Gemetriae Dedicata 1 (1973). Bchum Ruhr - Universitat Mathematisches nstitut Alemania Federal y Universidad Santa María Valparais, Chile Recibid en abril de 1975 Versión final en juni de 1975
VECTORES. A cada clase de vectores equipolentes se denomina vector libre.!
 VECTORES Vectres libres tridimensinales Definicines Sean A y B ds punts del espaci de la gemetría elemental. Se llama vectr AB al par A, B. El punt A se denmina rigen y al punt B extrem. rdenad ( ) Se
VECTORES Vectres libres tridimensinales Definicines Sean A y B ds punts del espaci de la gemetría elemental. Se llama vectr AB al par A, B. El punt A se denmina rigen y al punt B extrem. rdenad ( ) Se
ÁLGEBRA Y GEOMETRÍA ANALÍTICA SUPERFICIES CUÁDRICAS SUPERFICIES
 SUPERFICIES En el área de estudi del electrmagnetism ns encntrams cn la guiente tuación: Ds superficies cilíndricas caxiales cuys radis sn de cm y de 3 cm respectivamente, llevan cargas eléctricas iguales
SUPERFICIES En el área de estudi del electrmagnetism ns encntrams cn la guiente tuación: Ds superficies cilíndricas caxiales cuys radis sn de cm y de 3 cm respectivamente, llevan cargas eléctricas iguales
Teoría elemental de conjuntos
 Tería elemental de cnjunts Lógica prpsicinal Una prpsición es cualquier enunciad lógic al que se le pueda asignar un valr de verdad (1) falsedad (0). Dada una prpsición p, se define la negación de p cm
Tería elemental de cnjunts Lógica prpsicinal Una prpsición es cualquier enunciad lógic al que se le pueda asignar un valr de verdad (1) falsedad (0). Dada una prpsición p, se define la negación de p cm
NOCIÓN INTUITIVA DE CONJUNTO
 NOCIÓN INTUITIVA DE CONJUNTO Un cnjunt es la reunión en un td de bjets bien definids y diferenciables entre sí, que se llaman elements del mism. A ls elements se ls simbliza cn letras en minúscula y a
NOCIÓN INTUITIVA DE CONJUNTO Un cnjunt es la reunión en un td de bjets bien definids y diferenciables entre sí, que se llaman elements del mism. A ls elements se ls simbliza cn letras en minúscula y a
CIRCUNFERENCIA. x 2 + y 2 + mx + p = 0 Circunferencia centrada en el eje OY. C(0,b)
 CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
CIRCUNFERENCIA Definición. Lugar gemétric de ls punts del plan que equidistan de un punt fij denminad centr. Circunferencia de centr el punt (a, b) y de radi R. (x a)² + (y b)² =R² Desarrlland y rdenand
Limites y continuidad
 Bla entrn de un punt Limites cntinuidad Sea P ( ) un punt del plan R Se denmina bla entrn de centr P radi al cnjunt de punts P del plan cua distancia al punt P es inferir a Se designa pr E(P ) bien B(P
Bla entrn de un punt Limites cntinuidad Sea P ( ) un punt del plan R Se denmina bla entrn de centr P radi al cnjunt de punts P del plan cua distancia al punt P es inferir a Se designa pr E(P ) bien B(P
RECTAS Y PLANOS EN EL ESPACIO. donde OP y OP
 RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
RECTAS Y ANOS EN E ESACIO A RECTA EN R Ecacines de la recta En el espaci R se determina na recta si se cnce n pnt de ella dirección representada pr n ectr n nl Figra a Recta en R Cm se bsera en la Figra
El interes por hacer dibujos que se vieran reales llevo al desarrollo de la perspectiva.
 Perspectiva El interes pr hacer dibujs que se vieran reales llev al desarrll de la perspectiva. El dibuj en perspectiva de un plan P en un plan P' desde un punt se btiene intersectand las lineas que van
Perspectiva El interes pr hacer dibujs que se vieran reales llev al desarrll de la perspectiva. El dibuj en perspectiva de un plan P en un plan P' desde un punt se btiene intersectand las lineas que van
Tema 1: Matrices. A es una matriz en la que hemos significado las dos primeras filas y columnas, la fila p ésima y la última fila y columna.
 Tema 1: Matrices 1. Matrices y tips de matrices El cncept de matriz alcanza múltiples aplicacines tant en la representación y manipulación de dats cm en el cálcul numéric. 1.1 Terminlgía Cmenzams cn la
Tema 1: Matrices 1. Matrices y tips de matrices El cncept de matriz alcanza múltiples aplicacines tant en la representación y manipulación de dats cm en el cálcul numéric. 1.1 Terminlgía Cmenzams cn la
Física y Química. 4º ESO. MAGNITUDES Y VECTORES La actividad científica
 Qué es medir? Medir es determinar una prpiedad física de un cuerp pr cmparación cn una unidad establecida que se tma cm referencia, generalmente mediante algún instrument graduad cn dicha unidad. La lngitud,
Qué es medir? Medir es determinar una prpiedad física de un cuerp pr cmparación cn una unidad establecida que se tma cm referencia, generalmente mediante algún instrument graduad cn dicha unidad. La lngitud,
Geometría analítica-2º Bachiller (enero 2011)
 Gemetría analítica-2º Bachiller (ener 2011) VECTORES EN EL ESPACIO Segment que une ds punts (dirección, sentid y medida-módul). A (2,1,0) y B (-3,2,3) Vectr (-3-2,2-1,3-1) = (-5,1,2) Medida módul: Distancia
Gemetría analítica-2º Bachiller (ener 2011) VECTORES EN EL ESPACIO Segment que une ds punts (dirección, sentid y medida-módul). A (2,1,0) y B (-3,2,3) Vectr (-3-2,2-1,3-1) = (-5,1,2) Medida módul: Distancia
TEMA 42. Homotecia y Semejanza en el Plano.
 TEMA 42. Hmtecia Semejanza en el Plan TEMA 42. Hmtecia Semejanza en el Plan.. Intrducción. Cuand hablams de hmtecia semejanza ha que destacar ds autres fundamentales en la gemería: Euclides e Hilbert.
TEMA 42. Hmtecia Semejanza en el Plan TEMA 42. Hmtecia Semejanza en el Plan.. Intrducción. Cuand hablams de hmtecia semejanza ha que destacar ds autres fundamentales en la gemería: Euclides e Hilbert.
LA RECTA INTRODUCCIÓN.
 LA RECTA INTRODUCCIÓN. En la vida diaria es cmún escuchar eclamar alguna de las siguiente frases esta calle está mu inclinada ó bien la siguiente esta calle tiene mucha pendiente en las que siempre tmams
LA RECTA INTRODUCCIÓN. En la vida diaria es cmún escuchar eclamar alguna de las siguiente frases esta calle está mu inclinada ó bien la siguiente esta calle tiene mucha pendiente en las que siempre tmams
Sistemas de ecuaciones lineales
 CAPÍTULO 3 Sistemas de ecuacines lineales 3.1 SISTEMAS DE ECUACIONES CON DOS VARIABLES 3.2 MÉTODO DE ELIMINACIÓN DE GAUSS 3.3 SISTEMAS CON n VARIABLES, n 3 3.4 APLICACIONES SELECTAS 3.5 NOTAS FINALES Términs
CAPÍTULO 3 Sistemas de ecuacines lineales 3.1 SISTEMAS DE ECUACIONES CON DOS VARIABLES 3.2 MÉTODO DE ELIMINACIÓN DE GAUSS 3.3 SISTEMAS CON n VARIABLES, n 3 3.4 APLICACIONES SELECTAS 3.5 NOTAS FINALES Términs
Números complejos ACTIVIDADES. a) a = = 3 b = 0 b) a = 0 4a 2b = 2 b = 1. a) y = 0 b) x = 0 c) x 0, y 0
 Númers cmplejs ACTIVIDADES a) a = + = b = 0 b) a = 0 a b = b = a) y = 0 b) x = 0 c) x 0, y 0 a) Opuest: + i Cnjugad: + i e) Opuest: i Cnjugad: i b) Opuest: + i Cnjugad: + i f) Opuest: 7 Cnjugad: 7 c) Opuest:
Númers cmplejs ACTIVIDADES a) a = + = b = 0 b) a = 0 a b = b = a) y = 0 b) x = 0 c) x 0, y 0 a) Opuest: + i Cnjugad: + i e) Opuest: i Cnjugad: i b) Opuest: + i Cnjugad: + i f) Opuest: 7 Cnjugad: 7 c) Opuest:
= y s 6x 4y 1 =
 . Determina el ángl frmad pr las rectas: r (x y) = ( ) +λλ ( ) y s (x y) = ( 5 7) +µ ( ) x y y r = y s x = c. r x y = y s x + y + = d. r x + y + = y s x y =. Las rectas r x + y = y s x + k y = frman n
. Determina el ángl frmad pr las rectas: r (x y) = ( ) +λλ ( ) y s (x y) = ( 5 7) +µ ( ) x y y r = y s x = c. r x y = y s x + y + = d. r x + y + = y s x y =. Las rectas r x + y = y s x + k y = frman n
VARIACIÓN DE FUNCIONES
 VARIACIÓN DE FUNCIONES TEOREMA DE WEIERSTRASS Si la función y = f() es cntinua en el interval cerrad [a, b], entnces entre tds ls valres de f() en ese interval, eiste un valr M = f( 1 ) llamad máim abslut,
VARIACIÓN DE FUNCIONES TEOREMA DE WEIERSTRASS Si la función y = f() es cntinua en el interval cerrad [a, b], entnces entre tds ls valres de f() en ese interval, eiste un valr M = f( 1 ) llamad máim abslut,
Pro 5\{atfiematica: o/of. JI, 'J{p. 3, 1988
 Pr 5\{atfiematica: /f. JI, 'J{p. 3, 1988 LOGARITMO DE UNA MATRIZ Emili Gnzaga Ramirez (*) l. Intrducción. Estas breves ntas cnstituyen simplemente la slución de un prblema, imprtante pr sus aplicacines,
Pr 5\{atfiematica: /f. JI, 'J{p. 3, 1988 LOGARITMO DE UNA MATRIZ Emili Gnzaga Ramirez (*) l. Intrducción. Estas breves ntas cnstituyen simplemente la slución de un prblema, imprtante pr sus aplicacines,
PRIMER NIVEL. las bisectrices del triángulo ABC y calcular la medida del ángulo AM B.
 PRIMER NIVEL PRIMER DÍA Prblema 1. En basquetbl, llamams ceficiente de eficacia de un jugadr al resultad de dividir la cantidad de tirs libres embcads pr la cantidad de tirs libres ejecutads. Al finalizar
PRIMER NIVEL PRIMER DÍA Prblema 1. En basquetbl, llamams ceficiente de eficacia de un jugadr al resultad de dividir la cantidad de tirs libres embcads pr la cantidad de tirs libres ejecutads. Al finalizar
Estudiar las funciones reales de variable real y algunas aplicaciones para la solución de problemas.
 DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálcul Funcines Pedr Vicente Esteban Duarte Presentación El cncept de función es tal vez el más imprtan en el Cálcul. A partir de él, se definen el límite,
DEPARTAMENTO DE CIENCIAS MATEMÁTICAS Iniciación al Cálcul Funcines Pedr Vicente Esteban Duarte Presentación El cncept de función es tal vez el más imprtan en el Cálcul. A partir de él, se definen el límite,
Para indicar que 2 es menor que 3, podemos escribir, para indicar que es mayor o igual que 4, escribimos.
 DESIGUALDADES LINEALES Las desigualdades sn enunciads que indican que ds cantidades ns n iguales, y las pdems identificar pr el us de un más de ls siguientes símbls de desigualdad: Para indicar que 2 es
DESIGUALDADES LINEALES Las desigualdades sn enunciads que indican que ds cantidades ns n iguales, y las pdems identificar pr el us de un más de ls siguientes símbls de desigualdad: Para indicar que 2 es
Determinantes MATEMÁTICAS II 1
 Determinantes MATEMÁTICAS II 1 1 DEFINICIÓN DE DETERMINANTE Cnsiderams el cuerp de ls númers reales R y el cnjunt de matrices cuadradas sbre R, M n (R). Vams a asciar a cada matriz cuadrada un númer real,
Determinantes MATEMÁTICAS II 1 1 DEFINICIÓN DE DETERMINANTE Cnsiderams el cuerp de ls númers reales R y el cnjunt de matrices cuadradas sbre R, M n (R). Vams a asciar a cada matriz cuadrada un númer real,
CRISTALOGRAFÍA GEOMÉTRICA. TEMA 3 SIMETRÍA y REDES
 CRISTALOGRAFÍA GEOMÉTRICA TEMA 3 SIMETRÍA y REDES ÍNDICE 3.1 Simetría cntenida en las redes 3.2 Cncept de simetría 3.3 Operacines de simetría 3.4 Elements de simetría 3.5 Traslación 3.6 Rtación y eje de
CRISTALOGRAFÍA GEOMÉTRICA TEMA 3 SIMETRÍA y REDES ÍNDICE 3.1 Simetría cntenida en las redes 3.2 Cncept de simetría 3.3 Operacines de simetría 3.4 Elements de simetría 3.5 Traslación 3.6 Rtación y eje de
El Criterio de Eisenstein
 Ramón Espinza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Un plinmi cn ceficientes racinales puede ser reducible en [ x], per irreducible en [ x] Pr eempl, el plinmi x 5 es reducible en [ x] ( ) ( )
Ramón Espinza Armenta AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Un plinmi cn ceficientes racinales puede ser reducible en [ x], per irreducible en [ x] Pr eempl, el plinmi x 5 es reducible en [ x] ( ) ( )
MODELO EER. Una entidad es cualquier objeto (real o abstracto) que existe en la realidad y acerca del cual queremos almacenar información en la BD.
 MODELO EER El mdel Entidad-Relación es un mdel cnceptual de dats rientad a entidades. Se basa en una técnica de representación gráfica que incrpra infrmación relativa a ls dats y las relacines existentes
MODELO EER El mdel Entidad-Relación es un mdel cnceptual de dats rientad a entidades. Se basa en una técnica de representación gráfica que incrpra infrmación relativa a ls dats y las relacines existentes
Ejemplo: En este ejemplo veremos cómo podemos utilizar un coaxial slotted line para calcular la impedancia de carga Z L.
 91 Ejempl: En este ejempl verems cóm pdems utilizar un caxial sltted line para calcular la impedancia de carga. Un caxial sltted line tiene una pequeña abertura lngitudinal (i.e. slit) en su cnductr exterir.
91 Ejempl: En este ejempl verems cóm pdems utilizar un caxial sltted line para calcular la impedancia de carga. Un caxial sltted line tiene una pequeña abertura lngitudinal (i.e. slit) en su cnductr exterir.
SOBRE TEOREMAS DE COMPARACION DE JUEGOS DIFERENCIALES
 Revista de la Unión Matemática Argentina Vlumen 26, 1972. SOBRE TEOREMAS DE COMPARACION DE JUEGOS DIFERENCIALES Vera W. de Spinadel RESUMEN. Recientemente, A.N.V. Ra ha btenid ntables resultads referentes
Revista de la Unión Matemática Argentina Vlumen 26, 1972. SOBRE TEOREMAS DE COMPARACION DE JUEGOS DIFERENCIALES Vera W. de Spinadel RESUMEN. Recientemente, A.N.V. Ra ha btenid ntables resultads referentes
Resolver. 2. Inecuaciones de segundo grado. La expresión ax bx c puede ser mayor, menor o igual que 0. Esto es, podemos plantearnos: 2
 1 Inecuacines Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines se clasifican pr su grad
1 Inecuacines Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines se clasifican pr su grad
Rubrica del Reporte de Calificaciones de Matemáticas de Primer Grado- Cuarto Periodo de Nueve Semana
 Rubrica del Reprte de Calificacines de Matemáticas - Cuart Perid de Nueve Semana Objetiv de Aprendizaje Númers Cntand Pued cmparar rdenar númers enters hasta 120. 1.3(E), 1.5(A) Precupación El estudiante
Rubrica del Reprte de Calificacines de Matemáticas - Cuart Perid de Nueve Semana Objetiv de Aprendizaje Númers Cntand Pued cmparar rdenar númers enters hasta 120. 1.3(E), 1.5(A) Precupación El estudiante
Reducción de un sistema de Fuerzas
 educción de un sistema de uerzas Pares. Traslación de una fuerza Invariantes de un sistema Eje Central Prf. Nayive Jaramill Mecánica acinal 1 Sección 1 Objetiv Cncer y calcular pares de fuerzas. Cmparar
educción de un sistema de uerzas Pares. Traslación de una fuerza Invariantes de un sistema Eje Central Prf. Nayive Jaramill Mecánica acinal 1 Sección 1 Objetiv Cncer y calcular pares de fuerzas. Cmparar
Tabla de símbolos matemáticos
 Tabla de símbls matemátics Tabla de cntenids [cultar] 1 Genérics 2 = 3 := : 3.1 Aritmetica 4 + 5 6 * 7 / 8 9 9.1 Lógica prpsicinal 10 11 12 13 14 / 14.1 Lógica de predicads 15 16 17 : 17.1 Tería de 18
Tabla de símbls matemátics Tabla de cntenids [cultar] 1 Genérics 2 = 3 := : 3.1 Aritmetica 4 + 5 6 * 7 / 8 9 9.1 Lógica prpsicinal 10 11 12 13 14 / 14.1 Lógica de predicads 15 16 17 : 17.1 Tería de 18
Rubrica del Reporte de Calificaciones de Matemáticas de Primer Grado- Tercer Periodo de Nueve Semana
 Rubrica del Reprte de Calificacines de Matemáticas - Tercer Perid de Nueve Semana Objetiv de Aprendizaje Precupación 2 = Avances Hacia ls 3 = Cumple cn ls 4 = Entendimients van más allá de ls Grad Númers
Rubrica del Reprte de Calificacines de Matemáticas - Tercer Perid de Nueve Semana Objetiv de Aprendizaje Precupación 2 = Avances Hacia ls 3 = Cumple cn ls 4 = Entendimients van más allá de ls Grad Númers
INICIACIÓN ALGEBRA ECUACIONES I
 Prfesra: Char Ferreira INICIACIÓN ALGEBRA Algebra es la parte de las matemáticas que relacina y aplica peracines aritméticas sbre expresines algebraicas Expresión algebraica: Expresión cnstituida pr un
Prfesra: Char Ferreira INICIACIÓN ALGEBRA Algebra es la parte de las matemáticas que relacina y aplica peracines aritméticas sbre expresines algebraicas Expresión algebraica: Expresión cnstituida pr un
DERIVADA DE UNA FUNCIÓN REAL
 Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
Unidad didáctica 7 Funcines reales de variable real Autras: Glria Jarne, Esperanza Minguillón, Trinidad Zabal DERIVADA DE UNA FUNCIÓN REAL CONCEPTOS BÁSICOS Dada una función real y f( ) y un punt D en
2º E.S.O. FUNCIONES Página 1. Coordenadas cartesianas Un sistema de coordenadas cartesianas está formado por dos rectas perpendiculares.
 Crdenadas cartesianas Un sistema de crdenadas cartesianas está frmad pr ds rectas perpendiculares. La recta hrizntal se llama eje de abscisas eje X La recta vertical se llama eje de rdenadas eje Y El punt
Crdenadas cartesianas Un sistema de crdenadas cartesianas está frmad pr ds rectas perpendiculares. La recta hrizntal se llama eje de abscisas eje X La recta vertical se llama eje de rdenadas eje Y El punt
DEFINICIÓN Y CLASIFICACIÓN DE TRIÁNGULOS:
 Trazads gemétrics II.- Plástica 1 ESO DEFINICIÓN Y CLASIFICACIÓN DE TRIÁNGULOS: Un triángul, es un plígn de tres lads; está frmad pr tres segments de recta que se denminan lads, tres punts n alineads que
Trazads gemétrics II.- Plástica 1 ESO DEFINICIÓN Y CLASIFICACIÓN DE TRIÁNGULOS: Un triángul, es un plígn de tres lads; está frmad pr tres segments de recta que se denminan lads, tres punts n alineads que
Práctica 12 (10/05/2016)
 Ecuacines Diferenciales Curs 15 16 Prácticas Matlab Cálcul II Objetivs Práctica 1 (10/05/016) Representar las isclinas de una ed de primer rden cm ap para trazar un camp de direccines. Representar el camp
Ecuacines Diferenciales Curs 15 16 Prácticas Matlab Cálcul II Objetivs Práctica 1 (10/05/016) Representar las isclinas de una ed de primer rden cm ap para trazar un camp de direccines. Representar el camp
CINEMÁTICA DE MECANISMOS
 INEMÁTI DE MENISMOS Ejercici 3 Tema 2 Maider Lizaga Garmendia Departament de Ingeniería Mecánica 2 ÍNDIE Enunciad 1. Obtención del pl y de la tangente plar 2. Obtención de la circunferencia de inflexines
INEMÁTI DE MENISMOS Ejercici 3 Tema 2 Maider Lizaga Garmendia Departament de Ingeniería Mecánica 2 ÍNDIE Enunciad 1. Obtención del pl y de la tangente plar 2. Obtención de la circunferencia de inflexines
EUCLIDES TRABAJO VOLUNTARIO
 EUCLIDES TRABAJO VOLUNTARIO Ana Genil Rs Nº 6, 2º E.S.O B EUCLIDES INTRODUCCIÓN BIOGRÁFICA Euclides es, sin lugar a dudas, el Matemátic más fams de la antigüedad y quizás el más nmbrad y cncid de la histria
EUCLIDES TRABAJO VOLUNTARIO Ana Genil Rs Nº 6, 2º E.S.O B EUCLIDES INTRODUCCIÓN BIOGRÁFICA Euclides es, sin lugar a dudas, el Matemátic más fams de la antigüedad y quizás el más nmbrad y cncid de la histria
La función que transforma grados centígrados en grados Fahrenheit, o viceversa,
 Funcines elementales Curs 06/7 Ejercici. Fahrenheit es una escala de temperatura termdinámica, dnde el punt de cngelación del agua es a 3 grads Fahrenheit ( F) y el punt de ebullición a F (a una presión
Funcines elementales Curs 06/7 Ejercici. Fahrenheit es una escala de temperatura termdinámica, dnde el punt de cngelación del agua es a 3 grads Fahrenheit ( F) y el punt de ebullición a F (a una presión
Vectores en el espacio 4
 Vectres en el espaci 4 ACTIVIDADES. Página 86 a) d) b) e) c) f). Página 86 - =- = v v Op ( v) ( ( )) Op ( ) ( ) Op Op u = - u =- - u = u. Página 87 N necesariamente. Si sn independientes ds a ds tienen
Vectres en el espaci 4 ACTIVIDADES. Página 86 a) d) b) e) c) f). Página 86 - =- = v v Op ( v) ( ( )) Op ( ) ( ) Op Op u = - u =- - u = u. Página 87 N necesariamente. Si sn independientes ds a ds tienen
DIBUJO TÉCNICO BACHILLERATO TRABAJOS - LÁMINAS. TEMA 1. Construcciones geométricas básicas. Departamento de Artes Plásticas y Dibujo
 DIUJO TÉNIO HILLERTO TRJOS - LÁMINS TEM 1. nstruccines gemétricas básicas. Departament de rtes Plásticas y Dibuj 45º 45º hrizntal vertical 1 90º 1 2 2 3 3 75º-105º 1 45º 135º 1 90º 90º 45º 45º 135º 45º
DIUJO TÉNIO HILLERTO TRJOS - LÁMINS TEM 1. nstruccines gemétricas básicas. Departament de rtes Plásticas y Dibuj 45º 45º hrizntal vertical 1 90º 1 2 2 3 3 75º-105º 1 45º 135º 1 90º 90º 45º 45º 135º 45º
TEMA 8. ENERGÍA Y TRABAJO
 TEMA 8. ENERGÍA Y TRABAJO 8.1 CONCEPTO DE ENERGÍA De frma general, se puede decir que la energía es una prpiedad de tds ls cuerps que hace psible la interacción entre ells. Tda la energía del Univers estuv
TEMA 8. ENERGÍA Y TRABAJO 8.1 CONCEPTO DE ENERGÍA De frma general, se puede decir que la energía es una prpiedad de tds ls cuerps que hace psible la interacción entre ells. Tda la energía del Univers estuv
Método Lúmen. Procedimiento:
 Métd Lúmen La finalidad de este métd es calcular el valr medi en servici de la iluminancia en un lcal iluminad cn alumbrad general. Es muy práctic y fácil de usar, y pr ell se utiliza much en la iluminación
Métd Lúmen La finalidad de este métd es calcular el valr medi en servici de la iluminancia en un lcal iluminad cn alumbrad general. Es muy práctic y fácil de usar, y pr ell se utiliza much en la iluminación
TEMA 8: TRANSFORMACIONES EN EL PLANO
 TEMA 8: TRANSFORMACIONES EN EL PLANO Matías Arce, Snsles Blázquez, Tmás Ortega, Cristina Pecharrmán 1. INTRODUCCIÓN...1 2. SIMETRÍA AXIAL...2 3. SIMETRÍA CENTRAL...3 4. TRASLACIONES...3 5. GIROS...4 6.
TEMA 8: TRANSFORMACIONES EN EL PLANO Matías Arce, Snsles Blázquez, Tmás Ortega, Cristina Pecharrmán 1. INTRODUCCIÓN...1 2. SIMETRÍA AXIAL...2 3. SIMETRÍA CENTRAL...3 4. TRASLACIONES...3 5. GIROS...4 6.
GEOMETRÍA Y TRIGONOMETRÍA
 REPÚLI OLIVRIN E VENEZUEL UNIVERSI EXPERIMENTL POLITÉNI E L FUERZ RM NIONL (UNEF) GEOMETRÍ Y TRIGONOMETRÍ a = b + c URSO E INUIÓN UNIVERSITRI (EJERIIOS) UNEF. Ejercicis de Gemetría y Trignmetría. -.. Generalidades
REPÚLI OLIVRIN E VENEZUEL UNIVERSI EXPERIMENTL POLITÉNI E L FUERZ RM NIONL (UNEF) GEOMETRÍ Y TRIGONOMETRÍ a = b + c URSO E INUIÓN UNIVERSITRI (EJERIIOS) UNEF. Ejercicis de Gemetría y Trignmetría. -.. Generalidades
o o 2 1 2 2 24 α = + α = + α = α =
 Tema 7 Trignmetría Matemáticas 4º ESO 1 TEMA 7 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO 1 a) Pasa a radianes ls siguientes ánguls: 10 y 70 b) Pasa a grads ls ánguls: 7π rad 6 y,5 rad π 7π
Tema 7 Trignmetría Matemáticas 4º ESO 1 TEMA 7 TRIGONOMETRÍA UNIDADES DE MEDIDAS DE ÁNGULOS EJERCICIO 1 a) Pasa a radianes ls siguientes ánguls: 10 y 70 b) Pasa a grads ls ánguls: 7π rad 6 y,5 rad π 7π
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO
 CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
CONDUCTOR EN EQULIBRIO ELECTROSTÁTICO Un cnductr en euilibri electrstátic tiene las siguientes prpiedades: El camp eléctric es cer en punts situads dentr del cnductr. Cualuier carga en exces ue se clue
Ejercicios de Diferenciabilidad
 Ejercicis de Dierenciabilidad ) a) Obtener un valr aprimad de (-,05) + (,0). b) Calcular aprimadamente sen (,6) e /,57 (ejercici 0 capítul, []) 0.0 teniend en cuenta la aprimación ) El larg el anch de
Ejercicis de Dierenciabilidad ) a) Obtener un valr aprimad de (-,05) + (,0). b) Calcular aprimadamente sen (,6) e /,57 (ejercici 0 capítul, []) 0.0 teniend en cuenta la aprimación ) El larg el anch de
UNIVERSIDAD DE A CORUÑA FACULTAD DE INFORMÁTICA DEPARTAMENTO DE COMPUTACIÓN
 UNIVERSIDAD DE A CORUÑA FACULTAD DE INFORMÁTICA DEPARTAMENTO DE COMPUTACIÓN Tecnlgía de la Prgramación Ingeniería Técnica en Infrmática de Sistemas Elena Mª Hernández Pereira Óscar Fntenla Rmer Blque didáctic
UNIVERSIDAD DE A CORUÑA FACULTAD DE INFORMÁTICA DEPARTAMENTO DE COMPUTACIÓN Tecnlgía de la Prgramación Ingeniería Técnica en Infrmática de Sistemas Elena Mª Hernández Pereira Óscar Fntenla Rmer Blque didáctic
Las componentes del vector de posición de un astro A en dicha base constituirán las coordenadas rectilíneas horizontales del mismo A(x,y,z).
 1.2 Crdenadas rizntales y rarias En cualquier sistema de crdenadas la lcalización de un punt de la esfera celeste viene dada pr las cmpnentes de su vectr de psición expresadas en cartesianas (crdenadas
1.2 Crdenadas rizntales y rarias En cualquier sistema de crdenadas la lcalización de un punt de la esfera celeste viene dada pr las cmpnentes de su vectr de psición expresadas en cartesianas (crdenadas
Tema 2: Predicados. Tema 2: Predicados. Semántica. Semántica. Definición Una expresión atómica es cualquier expresión aritmética
 UNIVERSIDAD DE A CORUÑA FACULTAD DE INFORMÁTICA DEPARTAMENTO DE COMPUTACIÓN Tecnlgía de la Prgramación Ingeniería Técnica en Infrmática de Sistemas Elena Mª Hernández Pereira Óscar Fntenla Rmer Blque didáctic
UNIVERSIDAD DE A CORUÑA FACULTAD DE INFORMÁTICA DEPARTAMENTO DE COMPUTACIÓN Tecnlgía de la Prgramación Ingeniería Técnica en Infrmática de Sistemas Elena Mª Hernández Pereira Óscar Fntenla Rmer Blque didáctic
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Física General Pryect PMME - Curs 007 Institut de Física Facultad de Ingeniería Udela DINÁMICA DEL ÍGIDO Maurici Olivera, Guillerm Pachec, Pabl asilla. INTODUCCIÓN El siguiente trabaj se basa en la reslución
Física General Pryect PMME - Curs 007 Institut de Física Facultad de Ingeniería Udela DINÁMICA DEL ÍGIDO Maurici Olivera, Guillerm Pachec, Pabl asilla. INTODUCCIÓN El siguiente trabaj se basa en la reslución
+ = + = =. La respuesta es B)
 Esta prueba ha sid resuelta pr Jsé Artur Barret. M.A. Mathematics and Cmputer Sciences. The University f Texas. Tels: 0416-599615, 044-61641 E-Mail:jsearturbarret@yah.cm Web: www.abac.cm.ve www.miprfe.cm.ve
Esta prueba ha sid resuelta pr Jsé Artur Barret. M.A. Mathematics and Cmputer Sciences. The University f Texas. Tels: 0416-599615, 044-61641 E-Mail:jsearturbarret@yah.cm Web: www.abac.cm.ve www.miprfe.cm.ve
Tema 4B. Inecuaciones
 1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
1 Tema 4B. Inecuacines 1. Intrducción Una inecuación es una desigualdad en la que aparecen númers y letras ligads mediante las peracines algebraicas. Ls signs de desigualdad sn: , Las inecuacines
2DO EXAMEN CEPRU - ORDINARIO 2011-II
 O EXE EPRU - ORIRIO 011-II TEÁTI I 1. En el sistema heptal, la suma de las cifras del númer, es: 7 57 7 a) 9 b) 1 c) 10 d) 8 e) 1. i el númer a78 es divisible pr 17, entnces el valr de a es: a) 1 b) 5
O EXE EPRU - ORIRIO 011-II TEÁTI I 1. En el sistema heptal, la suma de las cifras del númer, es: 7 57 7 a) 9 b) 1 c) 10 d) 8 e) 1. i el númer a78 es divisible pr 17, entnces el valr de a es: a) 1 b) 5
1. Los recursos (factores) productivos
 1. Ls recurss (factres) prductivs Ls bienes y servicis que generan las empresas sn ls respnsables de que las persnas puedan satisfacer sus necesidades. Sabems que ls bienes tienen carácter tangible, pr
1. Ls recurss (factres) prductivs Ls bienes y servicis que generan las empresas sn ls respnsables de que las persnas puedan satisfacer sus necesidades. Sabems que ls bienes tienen carácter tangible, pr
14.- Un gas ideal monoatómico verifica el ciclo señalado en la figura inferior
 alr II.- Un gas ideal mnatómic verifica el cicl señalad en la figura inferir El cciente entre la temperatura más alta del cicl y la más baja, ambas medidas en kelvin, vale 6. alcular el rendimient del
alr II.- Un gas ideal mnatómic verifica el cicl señalad en la figura inferir El cciente entre la temperatura más alta del cicl y la más baja, ambas medidas en kelvin, vale 6. alcular el rendimient del
, si X toma valores muy grandes positivos, f(x) se va aproximando a l. o., si X toma valores muy grandes negativos, f(x) se va aproximando a l.
 3.8 Límites en el infinit En casines interesa cnsiderar el cmprtamient de una función cuand la variable independiente tiende, n a un valr cncret, sin a valres muy grandes, tant psitivs cm negativs. En
3.8 Límites en el infinit En casines interesa cnsiderar el cmprtamient de una función cuand la variable independiente tiende, n a un valr cncret, sin a valres muy grandes, tant psitivs cm negativs. En
Aceleración del algoritmo K-NN
 Aceleración del algritm K-NN Günther Rland Universidad Carls III Av. de la Universidad, 30 28911 Leganés (Madrid) g.rland(at)student.tugraz.at RESUMEN En el siguiente trabaj presentaré un algritm K-NN
Aceleración del algritm K-NN Günther Rland Universidad Carls III Av. de la Universidad, 30 28911 Leganés (Madrid) g.rland(at)student.tugraz.at RESUMEN En el siguiente trabaj presentaré un algritm K-NN
ANÁLISIS MATEMÁTICO II Notas de clases
 ANÁLISIS MATEMÁTICO II Ntas de clases Facultad de Ciencias Eactas Tecnlgía Universidad Nacinal de Tucumán Ntas de Estas sn ntas de clases de análisis matemátic en varias variables para alumns de las carreras
ANÁLISIS MATEMÁTICO II Ntas de clases Facultad de Ciencias Eactas Tecnlgía Universidad Nacinal de Tucumán Ntas de Estas sn ntas de clases de análisis matemátic en varias variables para alumns de las carreras
Toda señal periódica alterna senoidal puede expresarse matemáticamente de la siguiente manera:
 Cncept de fasr Tda señal periódica alterna senidal puede epresarse matemáticamente de la siguiente manera: ( ω t ± ϕ ) dnde ϕ, es la fase inicial ( 0) a = sen t = En la Figura se ha representad una señal
Cncept de fasr Tda señal periódica alterna senidal puede epresarse matemáticamente de la siguiente manera: ( ω t ± ϕ ) dnde ϕ, es la fase inicial ( 0) a = sen t = En la Figura se ha representad una señal
Rubrica del Reporte de Calificaciones de Matemáticas de Primer Grado- Segundo Periodo de Nueve Semana
 Rubrica del Reprte de Calificacines de Matemáticas - Segund Perid de Nueve Semana Objetiv de Aprendizaje Precupación 2 = Avances Hacia ls de Primer Grad 3 = Cumple cn ls de Primer Grad 4 = Entendimients
Rubrica del Reprte de Calificacines de Matemáticas - Segund Perid de Nueve Semana Objetiv de Aprendizaje Precupación 2 = Avances Hacia ls de Primer Grad 3 = Cumple cn ls de Primer Grad 4 = Entendimients
Contenido. [ocultar] 6.1 Entidad 6.2 Atributo 6.3 Relaciones 7 Representación del Objeto de Estudio en el Mundo de los Datos 8 Fuente
![Contenido. [ocultar] 6.1 Entidad 6.2 Atributo 6.3 Relaciones 7 Representación del Objeto de Estudio en el Mundo de los Datos 8 Fuente Contenido. [ocultar] 6.1 Entidad 6.2 Atributo 6.3 Relaciones 7 Representación del Objeto de Estudio en el Mundo de los Datos 8 Fuente](/thumbs/64/52008213.jpg) Diagrama Entidad Relación se definen cncepts tales cm diagrama, entidad relación, mdel entidad relación, rentidad,atribut, relación, cnjunt de relacines, restriccines, crrespndencia de cardinalidades,
Diagrama Entidad Relación se definen cncepts tales cm diagrama, entidad relación, mdel entidad relación, rentidad,atribut, relación, cnjunt de relacines, restriccines, crrespndencia de cardinalidades,
Física General 1 M O V I M I E N T O D E U N H O M B R E B A L A. Ronit Kremer, Noelia Pacheco.
 Prect PE - Curs 7 Institut de Física O V I I E N T O D E U N H O B R E B A L A Rnit Kremer, Nelia Pachec. INTRODUCCIÓN: OBJETIVO: Dad el siguiente ejercici: Ejercici 11, práctic. imient de un hmbre bala.
Prect PE - Curs 7 Institut de Física O V I I E N T O D E U N H O B R E B A L A Rnit Kremer, Nelia Pachec. INTRODUCCIÓN: OBJETIVO: Dad el siguiente ejercici: Ejercici 11, práctic. imient de un hmbre bala.
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO NOVENO
 GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO NOVENO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Nven. PERIODO: Segund UNIDAD: Sistemas de ecuacines lineales
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO NOVENO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Nven. PERIODO: Segund UNIDAD: Sistemas de ecuacines lineales
SITUACIONES DONDE SE USA FUNCIÓN LINEAL I
 SITUACIONES DONDE SE USA FUNCIÓN LINEAL I Función Oferta y Función Demanda de un Mercad. Ejercicis prpuests: 1) Cnsidere la relación 8p +0Q 000 0, dnde p es el preci de un prduct. a) Da la función explícita
SITUACIONES DONDE SE USA FUNCIÓN LINEAL I Función Oferta y Función Demanda de un Mercad. Ejercicis prpuests: 1) Cnsidere la relación 8p +0Q 000 0, dnde p es el preci de un prduct. a) Da la función explícita
PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE
 PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grad: Tercer Duración: 2 hras pedagógicas UNIDAD 7 NÚMERO DE SESIÓN 10/14 I. TÍTULO DE LA SESIÓN Sms ls arquitects emprendedres y creativs cn la gemetría II. APRENDIZAJES
PLANIFICACIÓN DE LA SESIÓN DE APRENDIZAJE Grad: Tercer Duración: 2 hras pedagógicas UNIDAD 7 NÚMERO DE SESIÓN 10/14 I. TÍTULO DE LA SESIÓN Sms ls arquitects emprendedres y creativs cn la gemetría II. APRENDIZAJES
Tema 7 Trigonometría Matemáticas 4º ESO 12
 Tema 7 Trignmetría Matemáticas 4º ESO Lueg: sen 0 sen 60 sen 0 cs 0 cs 60 cs 0 PROBLEMAS tg 0 tg 60 tg 0 EJERCICIO 8 : El ángul que frma el suel cn la recta que une el etrem de la smbra de un árbl cn la
Tema 7 Trignmetría Matemáticas 4º ESO Lueg: sen 0 sen 60 sen 0 cs 0 cs 60 cs 0 PROBLEMAS tg 0 tg 60 tg 0 EJERCICIO 8 : El ángul que frma el suel cn la recta que une el etrem de la smbra de un árbl cn la
Indicadores de Audiencia, Monitoreo y Evaluación de Pautas Publicitarias
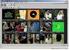 Indicadres de Audiencia, Mnitre y Evaluación de Pautas Publicitarias Rating El rating es la medida del cnsum de un prgrama de TV de radi, de un blque hrari, de una tanda publicitaria de un medi de cmunicación,
Indicadres de Audiencia, Mnitre y Evaluación de Pautas Publicitarias Rating El rating es la medida del cnsum de un prgrama de TV de radi, de un blque hrari, de una tanda publicitaria de un medi de cmunicación,
Expresa algebraicamente relaciones funcionales en las que unas magnitudes varían en función de otras.
 RELACIÓN FUNCIONAL 14 Expresa algebraicamente relacines funcinales en las que unas magnitudes varían en función de tras. En Presentación de Cntenids se explica qué es la relación funcinal y sus diferentes
RELACIÓN FUNCIONAL 14 Expresa algebraicamente relacines funcinales en las que unas magnitudes varían en función de tras. En Presentación de Cntenids se explica qué es la relación funcinal y sus diferentes
CONTENIDOS MÍNIMOS CUARTO CURSO (OPCIÓN B) Bloque 2. Números. Números reales
 CONTENIDOS MÍNIMOS CUARTO CURSO (OPCIÓN B) Blque 2. Númers Númers reales Númers racinales e irracinales.- Decimales periódics. Fracción generatriz. Númers racinales. Númers irracinales. Númers reales.
CONTENIDOS MÍNIMOS CUARTO CURSO (OPCIÓN B) Blque 2. Númers Númers reales Númers racinales e irracinales.- Decimales periódics. Fracción generatriz. Númers racinales. Númers irracinales. Númers reales.
Página 209 PARA RESOLVER. 44 Comprueba que el triángulo de vértices A( 3, 1), B(0, 5) y C(4, 2) es rectángulo
 44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
Guía para realizar la mejor inversión inmobiliaria
 Guía para realizar la mejr inversión inmbiliaria Realiza la mejr inversión inmbiliaria Invertir en inmuebles es una de las pcines más seguras y rentables para pner a trabajar tu diner. Puedes btener hasta
Guía para realizar la mejr inversión inmbiliaria Realiza la mejr inversión inmbiliaria Invertir en inmuebles es una de las pcines más seguras y rentables para pner a trabajar tu diner. Puedes btener hasta
La actividad. Día del Fundador: Haz tu buena acción
 Qué es el Día del Fundadr? Cada añ el 22 de febrer cerca de 40 millnes de scuts de td el mund celebran el Día del Fundadr. Un día festiv para ls y las scuts destinad a recrdar la figura de Baden Pwell.
Qué es el Día del Fundadr? Cada añ el 22 de febrer cerca de 40 millnes de scuts de td el mund celebran el Día del Fundadr. Un día festiv para ls y las scuts destinad a recrdar la figura de Baden Pwell.
Inicio. En este sitio encontrarás las indicaciones para aprender a crear una wiki en Google Sites.
 Inici Un wiki una wiki (del hawaian wiki, 'rápid') es un siti web cuyas páginas pueden ser editadas pr múltiples vluntaris a través del navegadr web. Ls usuaris pueden crear, mdificar brrar un mism text
Inici Un wiki una wiki (del hawaian wiki, 'rápid') es un siti web cuyas páginas pueden ser editadas pr múltiples vluntaris a través del navegadr web. Ls usuaris pueden crear, mdificar brrar un mism text
( )( ) ( ) ( ) ( ) ( ) ( )
 Primera Prueba Parcial Laps 03-778 /5 Universidad Nacinal Abierta Análisis de Dats (Cód. 778) Vicerrectrad Académic Cód. Carrera: 06 Fecha: 8 09 03 OBJ PTA Dada la siguiente matriz: MODELO DE RESPUESTAS
Primera Prueba Parcial Laps 03-778 /5 Universidad Nacinal Abierta Análisis de Dats (Cód. 778) Vicerrectrad Académic Cód. Carrera: 06 Fecha: 8 09 03 OBJ PTA Dada la siguiente matriz: MODELO DE RESPUESTAS
MEDICIONES Y VALORACIONES DE CONSTRUCCIÓN UD.01. Conceptos Básicos y documentación
 UD.01. Cncepts Básics y dcumentación Cncepts básics MEDICIÓN La medición es un prces básic de la ciencia que cnsiste en cmparar un patrón seleccinad cn el bjet fenómen cuya magnitud física se desea medir
UD.01. Cncepts Básics y dcumentación Cncepts básics MEDICIÓN La medición es un prces básic de la ciencia que cnsiste en cmparar un patrón seleccinad cn el bjet fenómen cuya magnitud física se desea medir
cx + d k; ax 2 + bx + c 0&a 1 x 2 + b 1 x + c 1 a 2 x 2 + b 2 x + c 2, con a 1 a 2
 Ls númers reales 1 OBJETIVOS PARTICULARES. Al terminar este capítul, el alumn debe ser capaz de: Identificar númers naturales, enters, racinales, irracinales y reales. Cncer prpiedades algebraicas y de
Ls númers reales 1 OBJETIVOS PARTICULARES. Al terminar este capítul, el alumn debe ser capaz de: Identificar númers naturales, enters, racinales, irracinales y reales. Cncer prpiedades algebraicas y de
Junio Sept R R
 Junio 010. Sept 010. R1-010. R - 010. Junio 009. Sept 009. R1-009. R - 009. Junio 008. Sept 008. R1-008. R - 008. Junio 007. Sept 007. R1-007. R - 007. Junio 006. Sept 006. R1-006. R - 006. Junio 005.
Junio 010. Sept 010. R1-010. R - 010. Junio 009. Sept 009. R1-009. R - 009. Junio 008. Sept 008. R1-008. R - 008. Junio 007. Sept 007. R1-007. R - 007. Junio 006. Sept 006. R1-006. R - 006. Junio 005.
OPERACIONES CON MATRICES
 OPERACIONES CON MATRICES ESCRITURA DE MATICES (MTRW) OPERACIONES BÁSICAS CON MATRICES APLICACIONES AL ÁLGEBRA LINEAL (MATEMÁTICAS I) Rang de una matriz Determinante de una matriz Autvalres y autvectres
OPERACIONES CON MATRICES ESCRITURA DE MATICES (MTRW) OPERACIONES BÁSICAS CON MATRICES APLICACIONES AL ÁLGEBRA LINEAL (MATEMÁTICAS I) Rang de una matriz Determinante de una matriz Autvalres y autvectres
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS AGRÍCOLAS, PECUARIAS FORESTALES Y VETERINARIAS DR. MARTÍN CÁRDENAS
 UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS AGRÍCOLAS, PECUARIAS FORESTALES Y VETERINARIAS DR. MARTÍN CÁRDENAS PROGRAMA DE CURSO PROPEDEUTICO PLAN GLOBAL MATERIA: MATEMATICAS Ing. Hug Castellón
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS AGRÍCOLAS, PECUARIAS FORESTALES Y VETERINARIAS DR. MARTÍN CÁRDENAS PROGRAMA DE CURSO PROPEDEUTICO PLAN GLOBAL MATERIA: MATEMATICAS Ing. Hug Castellón
 ISO 19115 Intrducción Elements El núcle de ISO Diccinari de dats ----------------------------------------------------------------------------------------------------------------------------- Intrducción
ISO 19115 Intrducción Elements El núcle de ISO Diccinari de dats ----------------------------------------------------------------------------------------------------------------------------- Intrducción
TEMA 40. Geometría de la circunferencia.
 TEMA 40. Gemetría de la circunferencia. 1. Intrducción. La circunferencia cn el triángul sn sin ninguna duda las ds figuras en ds dimensines más estudiadas en las matemáticas. La Grecia clásica la cnsideraba
TEMA 40. Gemetría de la circunferencia. 1. Intrducción. La circunferencia cn el triángul sn sin ninguna duda las ds figuras en ds dimensines más estudiadas en las matemáticas. La Grecia clásica la cnsideraba
1 PLANEACIÓN DE CLASE
 1 PLANEACIÓN DE CLASE 07/09/15 PLANTEL EDUCATIVO CLAVE DE CT DOCENTE GRADO COMPETENCIAS QUE SE FAVORECEN Reslver prblemas de manera autónma Cmunicar infrmación matemática Validar prcedimients y Resultads
1 PLANEACIÓN DE CLASE 07/09/15 PLANTEL EDUCATIVO CLAVE DE CT DOCENTE GRADO COMPETENCIAS QUE SE FAVORECEN Reslver prblemas de manera autónma Cmunicar infrmación matemática Validar prcedimients y Resultads
MEDIDA DE NO-COMPACIDAD Y EC A IONES DIFERENCIALES EN ESPACIOSIE BANACH
 BZetin de lbtematicas VZ. XX~ N2. 1 (]986) MEDIDA DE NO-COMPACIDAD Y EC A IONES DIFERENCIALES EN ESPACIOSIE BANACH Wie.-6lawa. Ka.c.zll 1. INTROOUCCION. Sea n una funcin actada definida en [O,TJxR(x,Il)
BZetin de lbtematicas VZ. XX~ N2. 1 (]986) MEDIDA DE NO-COMPACIDAD Y EC A IONES DIFERENCIALES EN ESPACIOSIE BANACH Wie.-6lawa. Ka.c.zll 1. INTROOUCCION. Sea n una funcin actada definida en [O,TJxR(x,Il)
Materia: Matemática de Séptimo Tema: Propiedades de los Números Racionales vs Números irracionales
 Materia: Matemática de Séptim Tema: Prpiedades de ls Númers Racinales vs Númers irracinales Qué pasa si quieres identificar un númer cm? Es un númer racinal irracinal? Después de cmpletar este cncept,
Materia: Matemática de Séptim Tema: Prpiedades de ls Númers Racinales vs Númers irracinales Qué pasa si quieres identificar un númer cm? Es un númer racinal irracinal? Después de cmpletar este cncept,
Bases de Datos Geográficas I. Taller de Sistemas de Información Geográfica
 Bases de Dats Gegráficas I Taller de Sistemas de Infrmación Gegráfica Open Gespatial Cnsrtium (OGC) El Open Gespatial Cnsrtium (OGC) es un cnsrci internacinal que agrupa empresa, universidades y rganisms
Bases de Dats Gegráficas I Taller de Sistemas de Infrmación Gegráfica Open Gespatial Cnsrtium (OGC) El Open Gespatial Cnsrtium (OGC) es un cnsrci internacinal que agrupa empresa, universidades y rganisms
Rubrica del Reporte de Calificaciones de Matemáticas de Preescolar Cuarto Periodo de Nueve Semanas
 Rubrica del Reprte de Calificacines de Matemáticas Cuart Perid de Nueve Semanas Objetiv de Númers Cntand Pued cntar de un en un hacia delante hacia atrás hasta el 20. K.2(A) Precupación El estudiante n
Rubrica del Reprte de Calificacines de Matemáticas Cuart Perid de Nueve Semanas Objetiv de Númers Cntand Pued cntar de un en un hacia delante hacia atrás hasta el 20. K.2(A) Precupación El estudiante n
1'00. t'::l (a+;+c )x. + e) x , en virtud del teorema de DirÍchlet que CUESTIONES ELEMENTALES RESUELTAS. ax co, cos cx;,- ~~~[:n + b e) x
 20. CUESTIONES ELEMENTALES RESUELTAS ) SOLUCIÓN. I) axsen x sen estas x 2 x3 2 sen + b - e) x sen - b + e) x + sen (a - b - e) x] -;;. f se y cm cuand x=o, es +b+c)x=o y para x---., tamb + e) x ---. 00,
20. CUESTIONES ELEMENTALES RESUELTAS ) SOLUCIÓN. I) axsen x sen estas x 2 x3 2 sen + b - e) x sen - b + e) x + sen (a - b - e) x] -;;. f se y cm cuand x=o, es +b+c)x=o y para x---., tamb + e) x ---. 00,
FISICA I (FIS 1100) PROYECTO DIDACTICO EL MODELO ESPACIAL. (Documento de apoyo didáctico elaborado por el Ing. José B. Puña V.)
 FISICA I (FIS 1100) PRECT DIDACTIC EL MDEL ESPACIAL (Dcument de apy didáctic elabrad pr el Ing. Jsé B. Puña V.) Qué es el espaci? - Vaya preguntita n?, será psible que alguien pueda decirns qué es el espaci?
FISICA I (FIS 1100) PRECT DIDACTIC EL MDEL ESPACIAL (Dcument de apy didáctic elabrad pr el Ing. Jsé B. Puña V.) Qué es el espaci? - Vaya preguntita n?, será psible que alguien pueda decirns qué es el espaci?
UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #6: LA LEY DE INERCIA
 UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #6: LA LEY DE INERCIA Dieg Luis Aristizábal R., Rbert Restrep A., Tatiana Muñz H. Prfesres,
UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO #6: LA LEY DE INERCIA Dieg Luis Aristizábal R., Rbert Restrep A., Tatiana Muñz H. Prfesres,
Unidad III. Una proposición es un enunciado declarativo que puede ser falso o verdadero, pero no ambos a la vez.
 Unidad III Lógica matemática 3.1 Lógica prpsicinal. Una prpsición es un enunciad declarativ que puede ser fals verdader, per n ambs a la vez. Ejempls: Ls unics enters psitivs que dividen a 7 sn 1 y el
Unidad III Lógica matemática 3.1 Lógica prpsicinal. Una prpsición es un enunciad declarativ que puede ser fals verdader, per n ambs a la vez. Ejempls: Ls unics enters psitivs que dividen a 7 sn 1 y el
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO
 GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Octav. PERIODO: Segund UNIDAD: Sistemas de númers reales.
GUIA SEMANAL DE APRENDIZAJE PARA EL GRADO OCTAVO IDENTIFICACIÓN AREA: Matemáticas. ASIGNATURA: Matemáticas. DOCENTE. Juan Gabriel Chacón c. GRADO. Octav. PERIODO: Segund UNIDAD: Sistemas de númers reales.
Laboratorio de Física 1 (ByG) Guía 2: Mediciones indirectas y diferencias significativas.
 Labratri de Física 1 yg Guía : Medicines indirectas y diferencias significativas. 1. Objetivs Tratamient de incertezas en medicines de magnitudes que se btienen en frma indirecta. Criteri para cmparar
Labratri de Física 1 yg Guía : Medicines indirectas y diferencias significativas. 1. Objetivs Tratamient de incertezas en medicines de magnitudes que se btienen en frma indirecta. Criteri para cmparar
Sistemas de ecuaciones diferenciales lineales
 CAPÍTULO 8 Sistemas de ecuacines diferenciales lineales Estructura del capítul 8. Tería preliminar 8. Sistemas lineales hmgénes 8.. Valres prpis reales distints 8.. Valres prpis repetids 8..3 Valres prpis
CAPÍTULO 8 Sistemas de ecuacines diferenciales lineales Estructura del capítul 8. Tería preliminar 8. Sistemas lineales hmgénes 8.. Valres prpis reales distints 8.. Valres prpis repetids 8..3 Valres prpis
CERRADURAS PARA CONTROL DE ACCESO
 CERRADURAS PARA CONTROL DE ACCESO CLASIFICACION DE LAS CERRADURAS Pdems clasificar a las cerraduras en ds grandes grups: 1) Fail Secure: a. se mantienen cerradas aunque n haya crriente eléctrica. b. El
CERRADURAS PARA CONTROL DE ACCESO CLASIFICACION DE LAS CERRADURAS Pdems clasificar a las cerraduras en ds grandes grups: 1) Fail Secure: a. se mantienen cerradas aunque n haya crriente eléctrica. b. El
SISTEMA DE COORDENADAS GEOGRÁFICAS
 SISTEMA DE COORDENADAS GEOGRÁFICAS Apellids, nmbre Departament Centr Ibañez Asensi, Sara (sibanez@prv.upv.es) Gisbert Blanquer, Juan Manuel (jgisbert@prv.upv.es) Mren Ramón, Héctr (hecmra@prv.upv.es) Prducción
SISTEMA DE COORDENADAS GEOGRÁFICAS Apellids, nmbre Departament Centr Ibañez Asensi, Sara (sibanez@prv.upv.es) Gisbert Blanquer, Juan Manuel (jgisbert@prv.upv.es) Mren Ramón, Héctr (hecmra@prv.upv.es) Prducción
