Homogeneización de problemas (elasto)hidrodinámicos en lubricación
|
|
|
- Julia Díaz Coronel
- hace 8 años
- Vistas:
Transcripción
1 XX Congreso de Ecuaciones Diferenciales y Aplicaciones X Congreso de Matemática Aplicada Sevilla, 4-8 septiembre 7 pp. 8 Homogeneización de problemas elastohidrodinámicos en lubricación G. Bayada, S. Martin, C. Vázquez 3 Centre de Maths, INSA de Lyon Bat. L. da Vinci, INSA de Lyon, 6968-Villeurbanne Cede. Guy.Bayada@insa-lyon.fr Dépt. Mathématiques, Université Paris Sud, sebastien.martin@math.u-psud.fr. 3 Dpto. de Matemáticas, Univ. de A Coruña, Campus Elvina s/n, 57-A Coruna. carlosv@udc.es. Palabras clave: Lubricación elastohidrodinámica, homogeneización, simulación numérica Resumen El presente trabajo trata sobre la homogeneización de un problema de lubricación, utilizando técnicas de doble escala. Se plantea un problema acoplado de tipo Reynolds- Hertzcon cavitación Elrod-Adams, que contempla la presencia de efectos debidos a superficies rugosas con oscilaciones periódicas. La geometría de la rugosidad depende de un pequeño parámetro asociado a la frecuencia de la misma. Entre las dificultades para la homogeneización del problema elastohidrodinámico destacamos el caracter no lineal asociado a la frontera libre del modelo de cavitación, los aspectos no locales del modelo de Hertz y la ley de viscosidad no lineal. Además de establecer los resultados de convergencia al problema homogeneizado, para un problema con datos reales se presentan resultados obtenidos con métodos numéricos adecuados, comparando el modelo dependiente del pequeño parámetro y el modelo homogeneizado.. Modelo matemático La creciente presencia de dispositivos industriales, que conllevan contactos lubricados por capas delgadas de fluido, motiva el interés por proponer los modelos matemáticos más adecuados para la simulación numérica de los mismos [6]. En muchas situaciones prácticas es interesante la introducción de rugosidades periódicas en las superficies deformables o no durante la fabricación. En el marco de contactos lubricados entre superficies rugosas, se mostrará como las técnicas de homogeneización permiten obtener modelos matemáticos adecuados para la simulación numérica eficiente de los procesos. Los modelos matemáticos se basan en ecuaciones de tipo Reynolds para la presión del lubricante, relaciones no
2 G. Bayada, S. Martin, C.Vázquez lineales presión-saturación para la cavitación y leyes elásticas para la relación presióndeformación. Para plantear el modelo de lubricación consideramos el dominio =] l, l[ ] l, l[; la frontera de alimentación de lubricante Γ = { l} ] l, l[ y Γ = \ Γ. Además, suponemos las siguientes aproimaciones parabólicas para la separación entre superficies rígidas en los contactos esfera-plano y cilindro-plano [6]: h r = h + + R, esfera-plano h + R, cilindro-plano Las condiciones < h h r h, siendo h y h constantes, se verifican en. Siguiendo la teoría del contacto hertziano, la relación presión-separación está dada por h[p] = h r + k, zpz dz,, donde h r tiene la epresión y k, z viene dada por c log c z k, z = z c z + z cilindro-plano esfera-plano, 3, donde c > y c má{ }. Claramente k es positiva y eiste K > tal que k,. K 4 L uniformemente respecto de. Además, suponemos la relación presión-viscosidad de Barus: : µ = µ e αp, α, µ > 5 La formulación fuerte del problema consiste en encontrar p, θ tal que: + h 3 [p] e αp p = 6µ : s θ h[p] p > and θ = θ h[p] = p = and θ h 3 [p] e αp p n Σ : p = con las condiciones de contorno = 6µ s θh[p] cos n, i 6µ s θh[p] h 3 [p] e αp p n = 6µ s θ h[p] en Γ, p = en Γ,
3 Homogeneización en lubricación elastrohidrodinámica donde s denota la velocidad relativa de la superficie inferior en la dirección, θ [, ] es un parámetro de alimentación, n es el vector unitario normal a Σ eterior a e i es el vector unitario en la dirección. Asimismo, los conjuntos son: + = {, p > } región lubricada, = {, p = } región cavitada, Σ = + frontera libre Entonces, una formulación variacional del problema está dada por: Encontrar p, θ V L tal que: P h 3 [p] e αp v p v = 6µ s θ h[p] + θ h[p] v, v V Γ p, p θ =, θ c.p.d. en donde V = { v H, v Γ = } y θ L Γ, θ z, c.p.d. en Γ. Para modelar el caso de superficies rugosas, introducimos el conjunto Y =], [ ], [, de modo que la separación sin deformación se escribe: h ε r = h r + λ ε donde h r se define en y el patrón de rugosidad, λ, verifica: i λ C Y = { v C Y, v es Y periódica }, ii λ má >, λ λ L má < h. Y A continuación se definen las separaciones efectivas: Definición Para q L, sean h[q] y h ε [q] las funciones: h[q], y = h r + λy + k, zqz dz,, y Y, h ε [q] = h[q],,. 6 ε Se introduce una formulación variacional del problema rugoso: Find p ε, θ ε V L such that: P ε h 3 ε[p ε ]e αp ε p ε v = 6µ s θ ε h ε [p ε ] v + θ h ε [p ε ] v, v V Γ p ε, p ε θ ε =, θ ε c.p.d. en Teorema Con las notaciones y condiciones precedentes y cierta hipótesis técnica, para cada ε >, el problema P ε tiene solución p ε, θ ε verificando las estimaciones: L p ε C L 3, p ε C L 4, θ ε 7 donde C 3 y C 4 solo dependen de µ, s, α, h λ L, h, K, θ,, Γ, r. 3
4 G. Bayada, S. Martin, C.Vázquez. Modelo homogeneizado En esta sección se establece el problema homogeneizado, que se obtiene utilizando las técnicas de desdoblamiento periódico [5]. Las demostraciones de los siguientes resultados se puede encontrar en [3]. En primer lugar, se tiene: Lema Eiste p V tal que p ε p en H y p ε p en L. Además, se tiene el resultado de convergencia de doble-escala: i La sucesión p ε converge en doble escala a p. Además, eiste p L ; H Y /R y una subsucesión ε, también denotada ε, tal que p ε converge en doble escala a p + y p. ii Eiste θ L Y y una subsucesión ε, denotada ε, tal que θ ε converge en doble escala a θ. Además, p c.p.d. en. La demostración es consecuencia de las estimaciones del Teorema y lemas previos que aparecen en [3]. Además se tiene el siguiente resultado para el par p, θ : θ y p θ = c.p.d. en Y. Teorema El problema homogeneizado se puede escribir en la forma: Encontrar p, Ξ, Ξ V L L tal que: P e αp A[p ] p φ = 6µ s b [p ] φ + θ ĥ[p ] φ, φ V Γ p and p Ξ i =, i =, c.p.d. en con f = f, y dy, y A[p ] = Y [ a[p ] a[p ] W ] y [ a[p ] W ] y con las notacionesi =, : [ a[p ] W ] y [ a[p ] a[p ] W ], b [p ] = y h i [p ] = b[p [ ] a[p ] χ ] [ i, h i [p ] = ] θ b[p ] y i y definiendo los siguientes cocientesi =, : Ξ i [p ] = h i [p ] h i [p ] Ξ [p ] h [p ] Ξ [p ] h [p ] [ a[p ] χ ] i, y i A continuación se garantiza la eistencia de soluciones del problema con saturación isotrópica. Teorema 3 El problema P admite una solución p, Ξ, Ξ con p Ξ = y Ξ c.p.d. en., 4
5 Homogeneización en lubricación elastrohidrodinámica 3. Ejemplos numéricos En esta sección, la simulación numérica de contactos micro-elastohidrodinámicos ilustra los resultados teóricos de convergencia de la sección anterior. Para la solución del problema dependiente de ε y el homogeneizado correspondiente, se usa una iteración de punto fijo entre el problema hidrodinámico y el elástico. Además, el hidrodinámico se resuelve mediante un método de características para el término convectivo combinado con elementos finitos y un método de dualidad para el operador maimal monótono asociado al modelo de Elrod-Adams. El problema elástico se aproima mediante una fórmula de cuadratura apropiada en la epresión con los puntos medios de las aristas como nodos de cuadratura. Estas técnicas se han usado en [7] en ausencia de rugosidad. En los ejemplos abordamos la simulación de un contacto bola-plano que, escrito en variables adimensionales en el dominio =] 4, [ ], [, plantea el problema: Encontrar p ε, θ ε V L tal que: h 3 ε[p ε ] e αp ε v p ε v = β θ ε h ε [p ε ] + θ h ε [p ε ] v, v V Γ p ε, p ε θ ε =, θ ε c.p.d. in, donde la separación efectiva se escribe en la forma h ε [p ε ] = h ε r + h d [p ε ], siendo h ε r = h + + π + 4 8π + + α sin + α sin, ε ε h d [p ε ] = p ε z π z + z dz. con los parámetros h =,6, α, α =,85h, para la rugosidad transversal y α, α =,,85h para la rugosidad longitudinal. Se consideran α =,4, β =,6 y θ =,3. De este modo el problema homogeneizado puede escribirse en la forma Encontrar p, Ξ V L tal que: e αp a [p ] p a [p ] φ = β Ξb[p ] φ + θ c[p ]φ, φ V. Γ p, p Ξ =, Ξ, c.p.d. en En la Tabla presentamos los coeficientes funcionales a, a, b y c del problema homogenizado para los casos de rugosidad transversal y longitudinal obtenidos mediante MATHEMATICA. La separación en el caso rígido sin rugosidad viene dada por: h r = h + +. En este resumen sólo mostramos el caso de rugosidad transversal y remitimos al trabajo [3] para el caso de rugosidad longitudinal. Aunque se ha verificado la convergencia con el uso de distintas malla, simplemente presentamos los resultados para =,5 y =,5 384 triángulos y 95 vértices. Además, se toma el paso de tiempo artificial t = ; los test de parada en todos los algoritmos son δ = 5 en error relativo en la norma L discreta entre dos 5
6 G. Bayada, S. Martin, C.Vázquez Rugosidad transversal Rugosidad longitudinal h[p], y h r + h d [p] + α sin πy h r + h d [p] + α sin πy hr + h d [p] α 5/ a [p ] h r + h d [p] + h h r + h d [p] r h r + h d [p] α a [p ] h r + h d [p] h r + h d [p] α hr + h d [p] α 5/ h r + h d [p] + α b[p ] h r + h d [p] h r + h d [p] α h r + h d [p] + α h r + h d [p] c[p ] h r + h d [p] h r + h d [p] Tabla : Coeficientes homogenizados.5.45 ε=/ ε=/3 Homogenized Pressure Pressure Figura : Izda:Comparación de presiones en =. Dcha:Presión homogeneizada. iteraciones. A la izquierda en la Figura, se muestra la convergencia fuerte en presión al problema homogeneizado cuando ε tiende a, representando para =, la presión para diferentes valores de ε y la presión del problema homogeneizado. A la derecha, se presenta la presión del homogeneizado en todo el dominio. En la Figura, se presentan resultados análogos para la deformación. En la Figura 3, se muestran los resultados para la saturación, ilustrando su convergencia débil ligada a la presencia de oscilaciones que no se amortiguan con el decrecimiento de ε, a diferencia de la presión y la deformación. A continuación, se ilustra la influencia del comportamiento elástico en los efectos debidos a la rugosidad en presencia de rugosidades transversales. Para ello comparamos los resultados de los casos hidrodinámico y elastohidrodinámico. En la Figura 4 se muestran la presión y saturación correspondientes a los problemas hidrodinámico sin rugosidad α = α = k =, hidrodinámico homogeneizado α, α = k =, elastohidrodinámico sin rugosidad α = α =, k y elastohidrodinámico homogeneizado α, α =, k. Las simulaciones numéricas permiten observar la influencia de la rugosidad sobre la distribución de presiones en régimen hidrodinámico y elastohidrodinámico, así como en la presión máima. Es claro que la presencia de rugosidad influye más en el caso hidrodinámico. En la Figura 5 se observa como la rugosidad conlleva un aumento de las deformaciones. 6
7 Homogeneización en lubricación elastrohidrodinámica.35 ε=/ ε=/3 Homogenized Deformation.5. Deformation Figura : Izda:Comparación de deformaciones en =. Dcha:Deformación homogeneizada... ε=/ ε=/3 Homogenized Saturation Saturation Figura 3: Izda:Comparación de saturaciones en =. Dcha:Saturación homogeneizada..6 HD, homogenized HD, roughless EHL, homogenized EHL, roughless. HD, homogenized HD, roughless EHL, homogenized EHL, roughless Pressure.3 Saturation Figura 4: Influencia de la contribución elástica sobre la rugosidad en presión izda y saturación dcha. 7
8 G. Bayada, S. Martin, C.Vázquez.35 EHL, homogenized EHL, roughless.3.5 Deformation Figura 5: Deformación del caso sin rugosidad y del homogeneizado. Las demostraciones de los resultados teóricos se pueden encontrar en [3]. Las técnicas de doble escala de [] se han utilizado previamente en problemas hidrodinámicos [] y las técnicas de homogeneización y métodos numéricos permiten abordar otros dispositivos como el eje-cojinete o patrones de rugosidad más generales [4]. Agradecimientos Este trabajo ha sido parcialmente financiado por el MEC mediante el proyecto de investigación MTM C-. Referencias [] G. Allaire, Homogenization and two-scale convergence. SIAM J. Math. Anal., 3, 99, [] G. Bayada, S. Martin, C. Vázquez, Two-scale homogenization of Elrod-Adams model. Asymp. Anal., 44, 5, 75. [3] G. Bayada, S. Martin, C. Vázquez, Homogenization of a nonlocal elastohydrodynamic lubrication problem: a new free boundary model. Math. Mod. Meth. Appl. Sci., 5, 5, [4] G. Bayada, S. Martin, C. Vázquez, Micro-roughness effects in elastohydrodynamic lubrication including a mass-flow preserving cavitation model. Tribology International, 39, 6, [5] D. Cioranescu, A. Damlamian, G. Griso, Periodic unfolding and homogenization. C.R.A.S. Paris, 335,, [6] D. Dowson, J. R. Higgison, Elastohydrodynamic lubrication, Pergamon Press, Oford, 977. [7] J. Durany, G. García, C. Vázquez, Numerical simulation of a lubricated Hertzian contact problem under imposed load. Finite Elem. Anal. Des., 38,,
1-Comportamiento de una función alrededor de un punto:
 Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Métodos generales de generación de variables aleatorias
 Tema Métodos generales de generación de variables aleatorias.1. Generación de variables discretas A lo largo de esta sección, consideraremos una variable aleatoria X cuya función puntual es probabilidad
Tema Métodos generales de generación de variables aleatorias.1. Generación de variables discretas A lo largo de esta sección, consideraremos una variable aleatoria X cuya función puntual es probabilidad
2.2 Transformada de Laplace y Transformada. 2.2.1 Definiciones. 2.2.1.1 Transformada de Laplace
 2.2 Transformada de Laplace y Transformada 2.2.1 Definiciones 2.2.1.1 Transformada de Laplace Dada una función de los reales en los reales, Existe una función denominada Transformada de Laplace que toma
2.2 Transformada de Laplace y Transformada 2.2.1 Definiciones 2.2.1.1 Transformada de Laplace Dada una función de los reales en los reales, Existe una función denominada Transformada de Laplace que toma
Variables aleatorias continuas
 Variables aleatorias continuas Hemos definido que una variable aleatoria X es discreta si I X es un conjunto finito o infinito numerable. En la práctica las variables aleatorias discretas sirven como modelos
Variables aleatorias continuas Hemos definido que una variable aleatoria X es discreta si I X es un conjunto finito o infinito numerable. En la práctica las variables aleatorias discretas sirven como modelos
Ejercicios de Programación Lineal
 Ejercicios de Programación Lineal Investigación Operativa Ingeniería Informática, UCM Curso 8/9 Una compañía de transporte dispone de camiones con capacidad de 4 libras y de 5 camiones con capacidad de
Ejercicios de Programación Lineal Investigación Operativa Ingeniería Informática, UCM Curso 8/9 Una compañía de transporte dispone de camiones con capacidad de 4 libras y de 5 camiones con capacidad de
INTERCAMBIADORES DE CALOR
 1 OBJETO: INTERCAMBIADORES DE CALOR Estudio del comportamiento de un cambiador de calor de carcasa y tubos. Determinación de su coeficiente global de transmisión de calor, DMLT, F, eficiencia, NUT, y pérdidas
1 OBJETO: INTERCAMBIADORES DE CALOR Estudio del comportamiento de un cambiador de calor de carcasa y tubos. Determinación de su coeficiente global de transmisión de calor, DMLT, F, eficiencia, NUT, y pérdidas
Tema 07. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
T.1 CONVERGENCIA Y TEOREMAS LÍMITE
 T.1 CONVERGENCIA Y TEOREMAS LÍMITE 1. CONVERGENCIA DE SUCESIONES DE VARIABLES ALEATORIA CONVERGENCIA CASI-SEGURA CONVERGENCIA EN PROBABILIDAD CONVERGENCIA EN MEDIA CUADRÁTICA CONVERGENCIA EN LEY ( O DISTRIBUCIÓN)
T.1 CONVERGENCIA Y TEOREMAS LÍMITE 1. CONVERGENCIA DE SUCESIONES DE VARIABLES ALEATORIA CONVERGENCIA CASI-SEGURA CONVERGENCIA EN PROBABILIDAD CONVERGENCIA EN MEDIA CUADRÁTICA CONVERGENCIA EN LEY ( O DISTRIBUCIÓN)
x : N Q 1 x(1) = x 1 2 x(2) = x 2 3 x(3) = x 3
 3 Sucesiones - Fernando Sánchez - - Cálculo I de números racionales 03 10 2015 Los números reales son aproximaciones que se van haciendo con números racionales. Estas aproximaciones se llaman sucesiones
3 Sucesiones - Fernando Sánchez - - Cálculo I de números racionales 03 10 2015 Los números reales son aproximaciones que se van haciendo con números racionales. Estas aproximaciones se llaman sucesiones
Algebra Lineal -III: Álgebra Vectorial en R2 and R 3
 Algebra Lineal -III: Álgebra Vectorial en R2 and R 3 José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingeniería, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@ugto.mx
Algebra Lineal -III: Álgebra Vectorial en R2 and R 3 José María Rico Martínez Departamento de Ingeniería Mecánica División de Ingeniería, Campus Irapuato-Salamanca Universidad de Guanajuato email: jrico@ugto.mx
Funciones de varias variables
 Capítulo 2 Funciones de varias variables 1. Definiciones básicas En este texto consideraremos funciones f : A R m, A R n. Dichas funciones son comúnmente denominadas como funciones de varias variables,
Capítulo 2 Funciones de varias variables 1. Definiciones básicas En este texto consideraremos funciones f : A R m, A R n. Dichas funciones son comúnmente denominadas como funciones de varias variables,
Tema 3: Aplicaciones de la diagonalización
 TEORÍA DE ÁLGEBRA II: Tema 3. DIPLOMATURA DE ESTADÍSTICA 1 Tema 3: Aplicaciones de la diagonalización 1 Ecuaciones en diferencias Estudiando la cría de conejos, Fibonacci llegó a las siguientes conclusiones:
TEORÍA DE ÁLGEBRA II: Tema 3. DIPLOMATURA DE ESTADÍSTICA 1 Tema 3: Aplicaciones de la diagonalización 1 Ecuaciones en diferencias Estudiando la cría de conejos, Fibonacci llegó a las siguientes conclusiones:
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Problemas teóricos Sistemas de ecuaciones lineales con parámetros En los siguientes problemas hay que resolver el sistema de ecuaciones lineales para todo valor del parámetro
Sistemas de ecuaciones lineales Problemas teóricos Sistemas de ecuaciones lineales con parámetros En los siguientes problemas hay que resolver el sistema de ecuaciones lineales para todo valor del parámetro
Nivelación de Matemática MTHA UNLP 1. Vectores
 Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES
 CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
Funciones vectoriales de variable vectorial. Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m
 Funciones vectoriales de variable vectorial Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m x y x = (x 1, x 2,, x n ), y = (y 1, y 2,, y m ) e y j = f j (x 1, x 2,, x n ), 1 j n n =
Funciones vectoriales de variable vectorial Son aplicaciones entre espacios eucĺıdeos, IR n, f : X IR n Y IR m x y x = (x 1, x 2,, x n ), y = (y 1, y 2,, y m ) e y j = f j (x 1, x 2,, x n ), 1 j n n =
Valores y vectores propios de una matriz. Juan-Miguel Gracia
 Juan-Miguel Gracia Índice 1 Valores propios 2 Polinomio característico 3 Independencia lineal 4 Valores propios simples 5 Diagonalización de matrices 2 / 28 B. Valores y vectores propios Definiciones.-
Juan-Miguel Gracia Índice 1 Valores propios 2 Polinomio característico 3 Independencia lineal 4 Valores propios simples 5 Diagonalización de matrices 2 / 28 B. Valores y vectores propios Definiciones.-
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1,0, la recta x 1 y z
 GEOMETRÍA Junio 94. 1. Sin resolver el sistema, determina si la recta x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1. Razónalo. [1,5 puntos]. Dadas las ecuaciones de los
GEOMETRÍA Junio 94. 1. Sin resolver el sistema, determina si la recta x 3y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1. Razónalo. [1,5 puntos]. Dadas las ecuaciones de los
Tema 5. Aproximación funcional local: Polinomio de Taylor. 5.1 Polinomio de Taylor
 Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Tema 8: Análisis Discriminante. Clasificación. Aurea Grané Departamento de Estadística Universidad Carlos III de Madrid. Análisis discriminante
 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Análisis discriminante Tema 8: Análisis Discriminante y Clasificación Aurea
Aurea Grané. Máster en Estadística. Universidade Pedagógica. 1 Aurea Grané. Máster en Estadística. Universidade Pedagógica. 2 Análisis discriminante Tema 8: Análisis Discriminante y Clasificación Aurea
Inversión en el plano
 Inversión en el plano Radio de la circunferencia x 2 + y 2 + Ax + By + D = 0 Circunferencia de centro (a, b) y radio r: (x a) 2 + (y b) 2 = r 2. Comparando: x 2 + y 2 2ax 2by + a 2 + b 2 r 2 = 0 con x
Inversión en el plano Radio de la circunferencia x 2 + y 2 + Ax + By + D = 0 Circunferencia de centro (a, b) y radio r: (x a) 2 + (y b) 2 = r 2. Comparando: x 2 + y 2 2ax 2by + a 2 + b 2 r 2 = 0 con x
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 7 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 7 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Resistencia de Materiales
 Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
Curso: Métodos de Monte Carlo Unidad 2, Sesión 6: Integración por Monte Carlo
 Curso: Métodos de Monte Carlo Unidad 2, Sesión 6: Integración por Monte Carlo Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad de la República, Montevideo,
Curso: Métodos de Monte Carlo Unidad 2, Sesión 6: Integración por Monte Carlo Departamento de Investigación Operativa Instituto de Computación, Facultad de Ingeniería Universidad de la República, Montevideo,
Mecánica Racional 20 TEMA 3: Método de Trabajo y Energía.
 INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
Comenzaremos recordando algunas definiciones y propiedades estudiadas en el capítulo anterior.
 Capítulo 2 Matrices En el capítulo anterior hemos utilizado matrices para la resolución de sistemas de ecuaciones lineales y hemos visto que, para n, m N, el conjunto de las matrices de n filas y m columnas
Capítulo 2 Matrices En el capítulo anterior hemos utilizado matrices para la resolución de sistemas de ecuaciones lineales y hemos visto que, para n, m N, el conjunto de las matrices de n filas y m columnas
CAPÍTULO 3. ALGORITMOS DE PREVISIÓN BASADOS EN LA EXTRAPOLACIÓN DE LOS DATOS MÁS RECIENTES
 CAPÍTULO 3. ALGORITMOS DE PREVISIÓN BASADOS EN LA EXTRAPOLACIÓN DE LOS DATOS MÁS RECIENTES El objetivo de esta tesina es la introducción de mejoras en la previsión meteorológica a corto plazo. El punto
CAPÍTULO 3. ALGORITMOS DE PREVISIÓN BASADOS EN LA EXTRAPOLACIÓN DE LOS DATOS MÁS RECIENTES El objetivo de esta tesina es la introducción de mejoras en la previsión meteorológica a corto plazo. El punto
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
NÚMEROS NATURALES Y NÚMEROS ENTEROS
 NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
Lógica Proposicional IIC2212. IIC2212 Lógica Proposicional 1 / 56
 Lógica Proposicional IIC2212 IIC2212 Lógica Proposicional 1 / 56 Inicio de la Lógica Originalmente, la Lógica trataba con argumentos en el lenguaje natural. Ejemplo Es el siguiente argumento válido? Todos
Lógica Proposicional IIC2212 IIC2212 Lógica Proposicional 1 / 56 Inicio de la Lógica Originalmente, la Lógica trataba con argumentos en el lenguaje natural. Ejemplo Es el siguiente argumento válido? Todos
Problemas Resueltos de Ecuaciones en Derivadas Parciales
 Problemas Resueltos de Ecuaciones en Derivadas Parciales Alberto Cabada Fernández 4 de diciembre de. Índice general Introducción I. Ecuaciones de primer orden.. Método de las bandas características...................
Problemas Resueltos de Ecuaciones en Derivadas Parciales Alberto Cabada Fernández 4 de diciembre de. Índice general Introducción I. Ecuaciones de primer orden.. Método de las bandas características...................
1 Límites de funciones
 Héctor Palma Valenzuela. Dpto. de Matemática UdeC. 1 1 Límites de funciones En general, en la recta real R podemos considerar la noción de distancia entre dos puntos y a dada por la fórmula d (, a) = a
Héctor Palma Valenzuela. Dpto. de Matemática UdeC. 1 1 Límites de funciones En general, en la recta real R podemos considerar la noción de distancia entre dos puntos y a dada por la fórmula d (, a) = a
Prácticas de Algebra con Mathematica II (Ingeniería Industrial). Jose Salvador Cánovas Peña. Departamento de Matemática Aplicada y Estadística.
 Prácticas de Algebra con Mathematica II (Ingeniería Industrial). Jose Salvador Cánovas Peña. Departamento de Matemática Aplicada y Estadística. Índice General 1 PRACTICAS CON MATHEMATICA 2 1.1 Introducción...
Prácticas de Algebra con Mathematica II (Ingeniería Industrial). Jose Salvador Cánovas Peña. Departamento de Matemática Aplicada y Estadística. Índice General 1 PRACTICAS CON MATHEMATICA 2 1.1 Introducción...
Selectividad Septiembre 2013 OPCIÓN B
 Pruebas de Acceso a las Universidades de Castilla y León ATEÁTICAS APLICADAS A LAS CIENCIAS SOCIALES EJERCICIO Nº páginas Tablas OPTATIVIDAD: EL ALUNO DEBERÁ ESCOGER UNA DE LAS DOS OPCIONES Y DESARROLLAR
Pruebas de Acceso a las Universidades de Castilla y León ATEÁTICAS APLICADAS A LAS CIENCIAS SOCIALES EJERCICIO Nº páginas Tablas OPTATIVIDAD: EL ALUNO DEBERÁ ESCOGER UNA DE LAS DOS OPCIONES Y DESARROLLAR
Análisis Real: Primer Curso. Ricardo A. Sáenz
 Análisis Real: Primer Curso Ricardo A. Sáenz Índice general Introducción v Capítulo 1. Espacios Métricos 1 1. Métricas 1 2. Métricas en espacios vectoriales 4 3. Topología 9 Ejercicios 17 Capítulo 2.
Análisis Real: Primer Curso Ricardo A. Sáenz Índice general Introducción v Capítulo 1. Espacios Métricos 1 1. Métricas 1 2. Métricas en espacios vectoriales 4 3. Topología 9 Ejercicios 17 Capítulo 2.
Teóricas de Análisis Matemático (28) - Práctica 4 - Límite de funciones. 1. Límites en el infinito - Asíntotas horizontales
 Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
Unidad III: Programación no lineal
 Unidad III: Programación no lineal 3.1 Conceptos básicos de problemas de programación no lineal Programación no lineal (PNL) es el proceso de resolución de un sistema de igualdades y desigualdades sujetas
Unidad III: Programación no lineal 3.1 Conceptos básicos de problemas de programación no lineal Programación no lineal (PNL) es el proceso de resolución de un sistema de igualdades y desigualdades sujetas
Cálculo de las Acciones Motoras en Mecánica Analítica
 Cálculo de las Acciones Motoras en Mecánica Analítica 1. Planteamiento general El diseño típico de la motorización de un sistema mecánico S es el que se muestra en la figura 1. Su posición viene definida
Cálculo de las Acciones Motoras en Mecánica Analítica 1. Planteamiento general El diseño típico de la motorización de un sistema mecánico S es el que se muestra en la figura 1. Su posición viene definida
TEMA 2: FUNCIONES CONTINUAS DE VARIAS VARIABLES
 TEMA 2: FUNCIONES CONTINUAS DE VARIAS VARIABLES ÍNDICE 1. Funciones de varias variables 1 2. Continuidad 2 3. Continuidad y composición de funciones 4 4. Continuidad y operaciones algebraicas 4 5. Carácter
TEMA 2: FUNCIONES CONTINUAS DE VARIAS VARIABLES ÍNDICE 1. Funciones de varias variables 1 2. Continuidad 2 3. Continuidad y composición de funciones 4 4. Continuidad y operaciones algebraicas 4 5. Carácter
Series y Probabilidades.
 Series y Probabilidades Alejandra Cabaña y Joaquín Ortega 2 IVIC, Departamento de Matemática, y Universidad de Valladolid 2 CIMAT, AC Índice general Sucesiones y Series Numéricas 3 Sucesiones 3 2 Límites
Series y Probabilidades Alejandra Cabaña y Joaquín Ortega 2 IVIC, Departamento de Matemática, y Universidad de Valladolid 2 CIMAT, AC Índice general Sucesiones y Series Numéricas 3 Sucesiones 3 2 Límites
Ejercicios 2.2 Usando aritmética de cuatro dígitos de precisión, sume la siguiente expresión
 CAPÍTULO EJERCICIOS RESUELTOS: ARITMÉTICA DE ORDENADORES Y ANÁLISIS DE ERRORES Ejercicios resueltos Ejercicios.1 Calcula la suma y la resta de los números a = 0.453 10 4, y b = 0.115 10 3, con una aritmética
CAPÍTULO EJERCICIOS RESUELTOS: ARITMÉTICA DE ORDENADORES Y ANÁLISIS DE ERRORES Ejercicios resueltos Ejercicios.1 Calcula la suma y la resta de los números a = 0.453 10 4, y b = 0.115 10 3, con una aritmética
Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004
 Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004. Estudia si existe alguna función de variable compleja f() entera cuya parte real sea x
Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004. Estudia si existe alguna función de variable compleja f() entera cuya parte real sea x
LÍMITES DE FUNCIONES. CONTINUIDAD
 LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Tema 4: Representación de funciones Índice:. Información obtenida de la función... Dominio de la función.. Simetrías..3. Periodicidad.4. Puntos de corte con los ejes..5. Ramas
REPRESENTACIÓN DE FUNCIONES Tema 4: Representación de funciones Índice:. Información obtenida de la función... Dominio de la función.. Simetrías..3. Periodicidad.4. Puntos de corte con los ejes..5. Ramas
1 Introducción... 2. 2 Distribución exponencial... 2. 3 Distribución Weibull... 6. 4 Distribuciones Gamma y k-erlang... 10
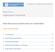 Asignatura: Ingeniería Industrial Índice de Contenidos 1 Introducción... 2 2 Distribución exponencial... 2 3 Distribución Weibull... 6 4 Distribuciones Gamma y k-erlang... 10 5 Distribución log-normal...
Asignatura: Ingeniería Industrial Índice de Contenidos 1 Introducción... 2 2 Distribución exponencial... 2 3 Distribución Weibull... 6 4 Distribuciones Gamma y k-erlang... 10 5 Distribución log-normal...
5.3 Esfuerzos y deformaciones producidos por flexión. Puente grúa. 5.3.1 Flexión pura
 5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
1. Limite de Funciones
 1. Limite de Funciones 1.1. Introducción. Consideremos la función f() = { 1+ 2 si > 0 1 2 si < 0 Se observa que la función no está definida en 0 = 0. Sin embargo, se observa que cuando se consideran valores
1. Limite de Funciones 1.1. Introducción. Consideremos la función f() = { 1+ 2 si > 0 1 2 si < 0 Se observa que la función no está definida en 0 = 0. Sin embargo, se observa que cuando se consideran valores
Una función f es derivable en un punto a de su dominio si existe el límite. f(x) f(a) Si f y g son derivables en a, entonces fg es derivable en a y
 4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
MÓDULO 2 CURVAS INTENSIDAD DURACIÓN FRECUENCIA
 MÓDULO 2 CURVAS INTENSIDAD DURACIÓN FRECUENCIA Autores: Dr. Ing. Roberto Pizarro T. Ing. Juan Pablo Flores V. Ing. Claudia Sangüesa P. Ing. Enzo Martínez A. 1. INTRODUCCIÓN El estudiar las precipitaciones
MÓDULO 2 CURVAS INTENSIDAD DURACIÓN FRECUENCIA Autores: Dr. Ing. Roberto Pizarro T. Ing. Juan Pablo Flores V. Ing. Claudia Sangüesa P. Ing. Enzo Martínez A. 1. INTRODUCCIÓN El estudiar las precipitaciones
Interpolación polinómica
 9 9. 5 9. Interpolación de Lagrange 54 9. Polinomio de Talor 57 9. Dados dos puntos del plano (, ), (, ), sabemos que ha una recta que pasa por ellos. Dicha recta es la gráfica de un polinomio de grado,
9 9. 5 9. Interpolación de Lagrange 54 9. Polinomio de Talor 57 9. Dados dos puntos del plano (, ), (, ), sabemos que ha una recta que pasa por ellos. Dicha recta es la gráfica de un polinomio de grado,
Soluciones a los problemas Olimpiada de Matemáticas Fase local Extremadura Enero de 2015
 Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
Funciones de varias variables
 Tema 5 Funciones de varias variables Supongamos que tenemos una placa rectangular R y determinamos la temperatura T en cada uno de sus puntos. Fijado un sistema de referencia, T es una función que depende
Tema 5 Funciones de varias variables Supongamos que tenemos una placa rectangular R y determinamos la temperatura T en cada uno de sus puntos. Fijado un sistema de referencia, T es una función que depende
Tema 2 Límites de Funciones
 Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Ampliación de Matemáticas. Integrales de línea
 Ampliación de Matemáticas Integrales de línea En Física la idea intuitiva de trabajo queda recogida en la fórmula Trabajo = Fuerza x Espacio Si f(x) es la fuerza aplicada, a lo largo del eje x, a un objeto
Ampliación de Matemáticas Integrales de línea En Física la idea intuitiva de trabajo queda recogida en la fórmula Trabajo = Fuerza x Espacio Si f(x) es la fuerza aplicada, a lo largo del eje x, a un objeto
Funciones de varias variables
 Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Fundamentos físicos de la teledetección
 Tema 1 Fundamentos físicos de la teledetección 1.1 La radiación electromagnética Dada la importancia que la radiación electromagnética tiene como transmisor de información en todas las formas de teledetección,
Tema 1 Fundamentos físicos de la teledetección 1.1 La radiación electromagnética Dada la importancia que la radiación electromagnética tiene como transmisor de información en todas las formas de teledetección,
Contenido. 1 Definiciones y propiedades. 2. Método de la potencia. 3. Método de la potencia inversa. 4. Método de la potencia inversa desplazada.
 Métodos Numéricos: Resumen y ejemplos Tema 7: Valores y vectores propios Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 9 Versión 7 Contenido
Métodos Numéricos: Resumen y ejemplos Tema 7: Valores y vectores propios Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 9 Versión 7 Contenido
1.4.1. Residuos pesados
 1.4. Métodos de aproximación de ED 1.4.1. Residuos pesados El método de los residuos pesados es un método general y poderoso para obtener soluciones aproximadas de ecuaciones diferenciales ordinarias (EDO)
1.4. Métodos de aproximación de ED 1.4.1. Residuos pesados El método de los residuos pesados es un método general y poderoso para obtener soluciones aproximadas de ecuaciones diferenciales ordinarias (EDO)
Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años.
 MATEMÁTICAS para Mayores de 25 años Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años. Curso 2014-2015 Conviene recordar que los contenidos y criterios
MATEMÁTICAS para Mayores de 25 años Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años. Curso 2014-2015 Conviene recordar que los contenidos y criterios
LÍMITES Y CONTINUIDAD
 UNIDAD 5 LÍMITES Y CONTINUIDAD Páginas 0 y Describe las siguientes ramas: a) f () b) f () no eiste c) f () d) f () + e) f () f) f () + g) f () h) f () no eiste; f () 0 i) f () + f () + j) f () 5 4 f ()
UNIDAD 5 LÍMITES Y CONTINUIDAD Páginas 0 y Describe las siguientes ramas: a) f () b) f () no eiste c) f () d) f () + e) f () f) f () + g) f () h) f () no eiste; f () 0 i) f () + f () + j) f () 5 4 f ()
Propiedades de los límites
 SECCIÓN 3 Cálculo analítico de ites 59 3 Cálculo analítico de ites Evaluar un ite mediante el uso de las propiedades de los ites Desarrollar usar una estrategia para el cálculo de ites Evaluar un ite mediante
SECCIÓN 3 Cálculo analítico de ites 59 3 Cálculo analítico de ites Evaluar un ite mediante el uso de las propiedades de los ites Desarrollar usar una estrategia para el cálculo de ites Evaluar un ite mediante
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE
 Capítulo 4 Algoritmos de Aprendizaje 26 CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE En este capítulo se proporcionan las descripciones matemáticas de los principales algoritmos de aprendizaje para redes neuronales:
Capítulo 4 Algoritmos de Aprendizaje 26 CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE En este capítulo se proporcionan las descripciones matemáticas de los principales algoritmos de aprendizaje para redes neuronales:
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 3 espacios vectoriales Objetivos: Al inalizar la unidad, el alumno: Describirá las características de un espacio vectorial. Identiicará las propiedades de los subespacios vectoriales. Ejempliicará
Unidad 3 espacios vectoriales Objetivos: Al inalizar la unidad, el alumno: Describirá las características de un espacio vectorial. Identiicará las propiedades de los subespacios vectoriales. Ejempliicará
Programa de Nuevos Dominios Genéricos de Alto Nivel (gtld): Variantes de Nombres de Dominio Internacionalizados (IDN)
 Programa de Nuevos Dominios Genéricos de Alto Nivel (gtld): Variantes de Nombres de Dominio Internacionalizados (IDN) Febrero de 2010 Introducción Las comunidades lingüísticas que planean utilizar Nombres
Programa de Nuevos Dominios Genéricos de Alto Nivel (gtld): Variantes de Nombres de Dominio Internacionalizados (IDN) Febrero de 2010 Introducción Las comunidades lingüísticas que planean utilizar Nombres
Aplicaciones Lineales
 Aplicaciones Lineales Ejercicio Dada la matriz A = 0 2 0 a) Escribir explícitamente la aplicación lineal f : 2 cuya matriz asociada con respecto a las bases canónicas es A. En primer lugar definimos las
Aplicaciones Lineales Ejercicio Dada la matriz A = 0 2 0 a) Escribir explícitamente la aplicación lineal f : 2 cuya matriz asociada con respecto a las bases canónicas es A. En primer lugar definimos las
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
9. Límites que involucran funciones exponenciales y logarítmicas
 Métodos para evaluación de ites Yoel Monsalve 77 9 Límites que involucran funciones eponenciales y logarítmicas 9 El número e como un ite El ite: + n) n 9) se conoce como el número e Su valor aproimado,
Métodos para evaluación de ites Yoel Monsalve 77 9 Límites que involucran funciones eponenciales y logarítmicas 9 El número e como un ite El ite: + n) n 9) se conoce como el número e Su valor aproimado,
Tema 7: Valores y vectores propios
 Tema 7: es y clausura s Espacios y Permutaciones es y clausura Una permutación p = {p 1, p 2,..., p n } de los números {1, 2,..., n} es una nueva ordenación de los elementos {1, 2,..., n}, es decir, un
Tema 7: es y clausura s Espacios y Permutaciones es y clausura Una permutación p = {p 1, p 2,..., p n } de los números {1, 2,..., n} es una nueva ordenación de los elementos {1, 2,..., n}, es decir, un
Colisión de dos partículas
 Capítulo 14 Colisión de dos partículas 14.1 Descripción de un proceso de colisión en el sistema centro de masa En el capítulo anterior describimos la colisión de un proyectil contra un centro de fuerza
Capítulo 14 Colisión de dos partículas 14.1 Descripción de un proceso de colisión en el sistema centro de masa En el capítulo anterior describimos la colisión de un proyectil contra un centro de fuerza
SESION 4. 1. El comando Integrate 2. Aproximación de integrales definidas 3. Integración de funciones racionales
 SESION. El comando Integrate. Aproimación de integrales definidas. Integración de funciones racionales . El comando Integrate El cálculo de integrales definidas e indefinidas en MATHEMATICA es sencillo
SESION. El comando Integrate. Aproimación de integrales definidas. Integración de funciones racionales . El comando Integrate El cálculo de integrales definidas e indefinidas en MATHEMATICA es sencillo
Congruencias de Grado Superior
 Congruencias de Grado Superior Capítulo 3 3.1 Introdución En el capítulo anterior vimos cómo resolver congruencias del tipo ax b mod m donde a, b y m son enteros m > 1, y (a, b) = 1. En este capítulo discutiremos
Congruencias de Grado Superior Capítulo 3 3.1 Introdución En el capítulo anterior vimos cómo resolver congruencias del tipo ax b mod m donde a, b y m son enteros m > 1, y (a, b) = 1. En este capítulo discutiremos
Álgebra Vectorial. Principios de Mecánica. Licenciatura de Física. Curso 2007-2008. 1
 Álgebra Vectorial Principios de Mecánica. Licenciatura de Física. Curso 2007-2008. 1 Indice. 1. Magnitudes Escalares y Vectoriales. 2. Vectores. 3. Suma de Vectores. Producto de un vector por un escalar.
Álgebra Vectorial Principios de Mecánica. Licenciatura de Física. Curso 2007-2008. 1 Indice. 1. Magnitudes Escalares y Vectoriales. 2. Vectores. 3. Suma de Vectores. Producto de un vector por un escalar.
7. MODELADO EN DINAMICA DE SISTEMAS
 7. MODELADO EN DINAMICA DE SISTEMAS 7.1. Dinámica de Sistemas El origen de la dinámica de sistemas se encuentra ligado al desarrollo de una aplicación para analizar los pedidos de una empresa fabricante
7. MODELADO EN DINAMICA DE SISTEMAS 7.1. Dinámica de Sistemas El origen de la dinámica de sistemas se encuentra ligado al desarrollo de una aplicación para analizar los pedidos de una empresa fabricante
RECOMENDACIÓN UIT-R S.1559
 Rec. UIT-R S.1559 1 RECOMENDACIÓN UIT-R S.1559 Metodología para el cálculo de la distribución geográfica de los niveles de la densidad de flujo de potencia equivalente de enlace descendente máximos generados
Rec. UIT-R S.1559 1 RECOMENDACIÓN UIT-R S.1559 Metodología para el cálculo de la distribución geográfica de los niveles de la densidad de flujo de potencia equivalente de enlace descendente máximos generados
Integrales paramétricas e integrales dobles y triples.
 Integrales paramétricas e integrales dobles y triples. Eleonora Catsigeras * 19 de julio de 2006 PRÓLOGO: Notas para el curso de Cálculo II de la Facultad de Ingeniería. Este texto es complementario al
Integrales paramétricas e integrales dobles y triples. Eleonora Catsigeras * 19 de julio de 2006 PRÓLOGO: Notas para el curso de Cálculo II de la Facultad de Ingeniería. Este texto es complementario al
Métodos Iterativos para Resolver Sistemas Lineales
 Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
Métodos Iterativos para Resolver Sistemas Lineales Departamento de Matemáticas, CCIR/ITESM 17 de julio de 2009 Índice 3.1. Introducción............................................... 1 3.2. Objetivos................................................
AMPLIACIÓN DE MATEMÁTICAS. REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros
 AMPLIACIÓN DE MATEMÁTICAS REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto
AMPLIACIÓN DE MATEMÁTICAS REPASO DE MATEMÁTICAS DISCRETA. CONGRUENCIAS. En el conjunto de los números enteros Z = {..., n,..., 2, 1, 0, 1, 2, 3,..., n, n + 1,...} tenemos definidos una suma y un producto
Laboratorio de Mecánica de Fluidos. Práctica de Laboratorio 2 FLUJO DE AIRE A TRAVÉS DE TUBERÍAS Y TOBERAS
 Universidad de Navarra Escuela Superior de Ingenieros Nafarroako Unibertsitatea Ingeniarien Goi Mailako Eskola Laboratorio de Mecánica de Fluidos Práctica de Laboratorio FLUJO DE AIRE A TRAVÉS DE TUBERÍAS
Universidad de Navarra Escuela Superior de Ingenieros Nafarroako Unibertsitatea Ingeniarien Goi Mailako Eskola Laboratorio de Mecánica de Fluidos Práctica de Laboratorio FLUJO DE AIRE A TRAVÉS DE TUBERÍAS
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
Juegos Cooperativos. Core
 Curso : Juegos Cooperativos Core J. Oviedo Universidad Nacional de San Luis 1. Juegos Cooperativos En estos juegos se permite la comunicación entre los jugadores, también pueden firmar contratos de cooperación.
Curso : Juegos Cooperativos Core J. Oviedo Universidad Nacional de San Luis 1. Juegos Cooperativos En estos juegos se permite la comunicación entre los jugadores, también pueden firmar contratos de cooperación.
Diferenciabilidad de funciones de R n en R m
 Diferenciabilidad de funciones de R n en R m Cálculo II (2003) En este capítulo generalizamos la noción de diferenciabilidad para funciones vectoriales de variable vectorial, que también llamamos aplicaciones.
Diferenciabilidad de funciones de R n en R m Cálculo II (2003) En este capítulo generalizamos la noción de diferenciabilidad para funciones vectoriales de variable vectorial, que también llamamos aplicaciones.
Estructuras algebraicas
 Tema 2 Estructuras algebraicas básicas 2.1. Operación interna Definición 29. Dados tres conjuntos A, B y C, se llama ley de composición en los conjuntos A y B y resultado en el conjunto C, y se denota
Tema 2 Estructuras algebraicas básicas 2.1. Operación interna Definición 29. Dados tres conjuntos A, B y C, se llama ley de composición en los conjuntos A y B y resultado en el conjunto C, y se denota
Selectividad Septiembre 2009 SEPTIEMBRE 2009. Opción A
 SEPTIEMBRE 2009 Opción A 1.- Como cada año, el inicio del curso académico, una tienda de material escolar prepara una oferta de 600 cuadernos, 500 carpetas y 400 bolígrafos para los alumnos de un IES,
SEPTIEMBRE 2009 Opción A 1.- Como cada año, el inicio del curso académico, una tienda de material escolar prepara una oferta de 600 cuadernos, 500 carpetas y 400 bolígrafos para los alumnos de un IES,
Límites y Continuidad de funciones
 CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
Operaciones lineales en R 3 y sus propiedades
 Operaciones lineales en R 3 y sus propiedades Ejercicios Objetivos. Aprender a demostrar propiedades de las operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las
Operaciones lineales en R 3 y sus propiedades Ejercicios Objetivos. Aprender a demostrar propiedades de las operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las
2. Integrales dobles sobre regiones no rectangulares.
 GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples.. Integrales dobles sobre regiones no rectangulares. Supongamos que tenemos una función f :(, ) f(, ) continua positiva cuo dominio
GRADO DE INGENIERÍA AEROESPACIAL. CRSO 0. Lección. Integrales múltiples.. Integrales dobles sobre regiones no rectangulares. Supongamos que tenemos una función f :(, ) f(, ) continua positiva cuo dominio
CARACTERIZACIÓN ESTADÍSTICA DE RECURSO EÓLICO CON FINES ENERGÉTICOS
 CARACTERIZACIÓN ESTADÍSTICA DE RECURSO EÓLICO CON FINES ENERGÉTICOS Ing. BONOLI ESCOBAR, MARIANO; UTN FRH GESE ; mbonoli@fi.uba.ar Lic. GOGNI, VALERIA; UTN FRH GESE ; Valeria.gogni@gmail.com Ing. EDWARDS,
CARACTERIZACIÓN ESTADÍSTICA DE RECURSO EÓLICO CON FINES ENERGÉTICOS Ing. BONOLI ESCOBAR, MARIANO; UTN FRH GESE ; mbonoli@fi.uba.ar Lic. GOGNI, VALERIA; UTN FRH GESE ; Valeria.gogni@gmail.com Ing. EDWARDS,
S n = 3n + 2 n + 4. ln(1 + a n ) (3) Decidir, para cada una de las siguientes series, si es convergente o divergente.
 CÁLCULO HOJA 1 INGENIERO TÉCNICO EN INFORMÁTICA DE SISTEMAS GRUPO DE MAÑANA, MÓSTOLES, 2008-09 (1) De la serie a n se sabe que la sucesión de sumas parciales viene dada por: S n = 3n + 2 n + 4. Encontrar
CÁLCULO HOJA 1 INGENIERO TÉCNICO EN INFORMÁTICA DE SISTEMAS GRUPO DE MAÑANA, MÓSTOLES, 2008-09 (1) De la serie a n se sabe que la sucesión de sumas parciales viene dada por: S n = 3n + 2 n + 4. Encontrar
ADALINE Y PERCEPTRON
 Tema 3: Adaline y Perceptron Sistemas Conexionistas 1 ADALINE Y PERCEPTRON 1. Adaline 1.1. Características. 1.. Regla de Aprendizaje (LMS). Regla Delta. 1.3. Aplicaciones. 1.3.1. Clasificación de vectores.
Tema 3: Adaline y Perceptron Sistemas Conexionistas 1 ADALINE Y PERCEPTRON 1. Adaline 1.1. Características. 1.. Regla de Aprendizaje (LMS). Regla Delta. 1.3. Aplicaciones. 1.3.1. Clasificación de vectores.
Cálculo Simbólico también es posible con GeoGebra
 www.fisem.org/web/union ISSN: 1815-0640 Número 34. Junio de 2013 páginas 151-167 Coordinado por Agustín Carrillo de Albornoz Cálculo Simbólico también es posible con GeoGebra Antes de exponer las posibilidades
www.fisem.org/web/union ISSN: 1815-0640 Número 34. Junio de 2013 páginas 151-167 Coordinado por Agustín Carrillo de Albornoz Cálculo Simbólico también es posible con GeoGebra Antes de exponer las posibilidades
LÍMITES DE FUNCIONES. CONTINUIDAD
 LÍMITES DE FUNCIONES. CONTINUIDAD Página 7 REFLEXIONA Y RESUELVE Visión gráfica de los ites Describe análogamente las siguientes ramas: a) f() b) f() no eiste c) f() d) f() +@ e) f() @ f) f() +@ g) f()
LÍMITES DE FUNCIONES. CONTINUIDAD Página 7 REFLEXIONA Y RESUELVE Visión gráfica de los ites Describe análogamente las siguientes ramas: a) f() b) f() no eiste c) f() d) f() +@ e) f() @ f) f() +@ g) f()
TEMA V TEORÍA DE CUADRIPOLOS LINEALES. 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto.
 TEMA V TEORÍA DE CUADRIPOLOS LINEALES 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto. 5.3.-Parámetros de Admitancia a cortocircuito. 5.4.-Parámetros Híbridos (h, g). 5.5.-Parámetros
TEMA V TEORÍA DE CUADRIPOLOS LINEALES 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto. 5.3.-Parámetros de Admitancia a cortocircuito. 5.4.-Parámetros Híbridos (h, g). 5.5.-Parámetros
Cadenas de Markov y Perron-Frobenius
 Cadenas de Markov y Perron-Frobenius Pablo Lessa 10 de octubre de 2014 1. Cadenas de Markov En 1996 Larry Page y Sergey Brin, en ese momento en Stanford, inventaron una manera de asignar un ranking de
Cadenas de Markov y Perron-Frobenius Pablo Lessa 10 de octubre de 2014 1. Cadenas de Markov En 1996 Larry Page y Sergey Brin, en ese momento en Stanford, inventaron una manera de asignar un ranking de
5. Introducción a la Formulación Lagrangiana y Hamiltoniana
 5. Introducción a la Formulación Lagrangiana y Hamiltoniana Introducción Definiciones: coordenadas, momentos y fuerzas generalizados. Función Lagrangiana y ecuaciones de Euler-Lagrange. Coordenadas cíclicas.
5. Introducción a la Formulación Lagrangiana y Hamiltoniana Introducción Definiciones: coordenadas, momentos y fuerzas generalizados. Función Lagrangiana y ecuaciones de Euler-Lagrange. Coordenadas cíclicas.
Funciones definidas a trozos
 Concepto de función Dominio de una función Características de las funciones Intersecciones con los ejes Crecimiento y decrecimiento Máximos y mínimos Continuidad y discontinuidad Simetrías Periodicidad
Concepto de función Dominio de una función Características de las funciones Intersecciones con los ejes Crecimiento y decrecimiento Máximos y mínimos Continuidad y discontinuidad Simetrías Periodicidad
