Las funciones exponencial y logarítmica
|
|
|
- Pablo Ponce Ortiz
- hace 7 años
- Vistas:
Transcripción
1 Las funciones eponencial y logarítmica
2 Las funciones eponenciales y logarítmicas Las funciones eponenciales Una función eponencial de base a es la que se define a partir de las potencias de los números. Su epresión es de la forma: a, siendo a > 0 Sus características son: Dominio: (,+ ). Imagen: (0,+ ). No tienen ni máimos ni mínimos. Pasan por el punto (0,1). a > 1 a < 1 Función creciente si tiende a, la función tiende a 0 si tiende a +, la función tiende a + Función decreciente si tiende a, la función tiende a + si tiende a +, la función tiende a0 a y (1/a) son simétricas respecto del eje Y Una de las funciones eponenciales más importantes es e, es decir, función eponencial cuya base es el número e =, Ecuaciones eponenciales Una ecuación eponencial es una ecuación que incluye funciones eponenciales. Para resolver una ecuación eponencial deben agruparse al máimo las potencias para sustituir la ecuación eponencial por una ecuación lineal o cuadrática. Por ejemplo, los pasos para resolver: = 793 son: = ( ) = = = 793/57 = 49 por lo tanto: = resuelve = 793. El mismo procedimiento debe seguirse para resolver un sistema de ecuaciones eponencial. Para resolver: y 5 = 5 65 y = 56 Se deben seguir estos pasos: 5 = 5 y y = 5 4 y = 8 +y = 8 el sistema inicial se convierte en y = 4 + y = 8 cuya solución es = 6 e y =, que son también soluciones del primer sistema.
3 Composición de funciones y función inversa La composición de la función f con la función g es otra función, designada como gof, que cumple: (gof)() = g(f()) Dos funciones, f y g, se dice que son inversas una de la otra, si (gof)() =, y (fog)() = La función inversa de f se denota f 1. El logaritmo y sus propiedades El logaritmo en base a (a > 0) de un número real positivo,, se calcula de la siguiente manera: log a = y si = a y y tiene las siguientes propiedades: 1. log a a = 1 log a 1 = 0.. El logaritmo del producto es igual a la suma de logaritmos: log a ( y) = log a + log a y 3. El logaritmo de una potencia es igual al producto del eponente por el logaritmo de la base: log a y = y log a 4. El logaritmo de un cociente es el logaritmo del numerador menos el logaritmo del denominador: log a = loga loga y y 5. Es posible relacionar logaritmos de diferentes bases, a y b, con esta fórmula: 1 logb = logb log b a Las funciones logarítmicas La función logaritmo de base a (a > 0, a 1) es la función inversa de la función eponencial de base a; y = log a si = a y Sus características son: Dominio: (0,+ ). Imagen: (,+ ). No tienen ni máimos ni mínimos. Pasan por el punto (1,0). a > 1 a < 1 Función creciente si tiende a 0, la función tiende a si tiende a +, la función tiende a + Función decreciente si tiende a 0, la función tiende a + si tiende a +, la función tiende a las gráficas de log a y log 1/a son simétricas respecto al eje X Una de las funciones logarítmicas más importantes es ln, función logaritmo neperiano, es decir, función logarítmica cuya base es el número e =,
4 Relación entre las gráficas de las funciones eponenciales y logarítmicas Las gráficas de las funciones eponenciales y logarítmicas de la misma base son simétricas respecto a la recta y = a > 1 a < 1 Las ecuaciones logarítmicas Una ecuación logarítmica es una ecuación con funciones logarítmicas. Para resolver una ecuación logarítmica deben agruparse al máimo los logaritmos para sustituir la ecuación logarítmica por una ecuación lineal o cuadrática. Por ejemplo, los pasos para resolver: log log ( 16) = son: log log ( 16) = log log ( 16) = log 16 log = log = = 0 las soluciones son = 0 y = 80 De la misma manera, pueden resolverse sistemas de ecuaciones logarítmicos, convirtiéndolos en sistemas de ecuaciones lineales, manipulando convenientemente los logaritmos. Por ejemplo, los pasos para resolver: + y = 65 log + log y = 3 son: log + log y = log( y) = 3 = log 1000 así, pues, se debe resolver: + y = 65 y = 1000 cuyas soluciones son = 40 e y = 5, o bien, = 5 e y = 40.
5 Los orígenes del logaritmo El origen del concepto de logaritmo se encuentra en un problema de matemáticas aplicadas: se trata de simplificar la pesada tarea de los calculadores, ecesivamente complicada cuando se trata de hacer multiplicaciones, divisiones, incluso potencias o etracción de raíces, en problemas relacionados en principio con la agrimensura y la astronomía, en particular en sus aplicaciones a la navegación. A Arquímedes se debe la idea fundamental que generaría los logaritmos, idea que encontramos en su obra Arenario. Ahora bien, no es hasta John Napier cuando se aprovecha esta idea lanzada por Arquímedes. John Napier (de cuyo nombre procede el calificativo neperiano) nació en Procedente de la baja nobleza escocesa, mostró toda su vida un espíritu curioso y dinámico, a pesar de una vida alejada de los centros culturales de la época. La introducción de los logaritmos no es su única aportación, puesto que escribió también un teto sobre las ecuaciones e imaginó además un sistema de cálculo por medio de regletas graduadas (Rabdología). En 1614 publicó el Mirifici logarithmorun canonis descriptio, donde pone en relación una progresión geométrica con una progresión aritmética. La primera es la de las distancias recorridas con velocidades proporcionales a ellas mismas, la segunda, la de las distancias recorridas con velocidad constante; éstas son entonces los "logaritmos" de las primeras (el neologismo es del propio Napier). La unidad elegida es 10 7, y la obra comprende una tabla de logaritmos de senos, con los ángulos variando de minuto en minuto. En 1619 apareció una segunda obra, Mirifici logarithmorum canonis constructio, donde el autor eplica cómo calcular los logaritmos. Esta obra es póstuma, puesto que Napier murió en Mientras tanto, un eminente matemático de Londres, Henry Briggs, había descubierto la importancia de estos trabajos y viajó a Escocia para encontrarse con el autor. Retomando la idea fundamental, pero considerando una progresión geométrica simple, la de las potencias de 10, publica en 1617 una primera tabla, con 8 decimales. El logaritmo de un número es, por lo tanto, definido como el eponente n de 10, tal que sea igual a 10 elevado a n. Siguieron otras tablas que permitieron la difusión del método, en particular en el continente. En realidad, la idea estaba en el aire; un colaborador de Kepler, el suizo Bürgi, proponía en la misma época, para simplificar los cálculos que debía realizar, hacer corresponder una progresión aritmética (en números rojos) y una progresión geométrica (en números negros); sin embargo, sus trabajos no fueron publicados hasta 160. La difusión en el continente europeo de esta nueva noción se debe sobre todo a las tablas publicadas por el flamenco Adrien Ulacq, en 168, retomando las tablas de Griggs. El objetivo era realizar un tratado de cálculo práctico, en particular para uso de los agrimensores. Las primeras tablas fueron seguidas por otras, cada vez más precisas, y en ellas se menciona que su principal aplicación son los cálculos trigonométricos. Los logaritmos como herramienta serán de gran ayuda para el nacimiento de la física matemática a finales del siglo XVII. Así ocurre con el Discurso sobre la causa de la gravedad de Huygens, y también con los diferentes trabajos sobre la presión atmosférica, en particular los de Mariotte. Los logaritmos, surgidos de una idea de hecho muy simple, continúan siendo un instrumento tal vez modesto, pero a pesar de todo esencial para el conocimiento científico. John Napier
6 Qué es una función eponencial y cuáles son sus características? Una función eponencial es la que se define a partir de las potencias de los números. Su epresión es de la forma a, siendo a > 0. El dominio de estas funciones son todos los números reales y su imagen son todos los números positivos. La función es siempre creciente si a > 1, y siempre decreciente si a < 1. Estas funciones no tienen máimos ni mínimos. Las funciones eponenciales resultan muy útiles en el estudio de procesos de crecimiento/decrecimiento de poblaciones, por ejemplo. La función eponencial de base a se define a partir de las potencias de números. Así, por ejemplo, la función eponencial de base 3 es igual a g() = 3 En este caso, pues, g(0) = 3 0 = 1, g(1) = 3 1 = 3, g() = 3 = 9, g( 1) = 3 1 = 1/3, g(1/) = 3 1/ = 3, etc. En general, si a es un número positivo, la función eponencial de base a es igual a a Si representamos algunos de los puntos de la gráfica de la función g() = 3 obtendremos una gráfica como ésta: Es evidente que cualquier valor de la función es siempre positivo porque la potencia de un número siempre es un número positivo. Así pues, la gráfica de una función eponencial siempre se representará por encima del eje X. Es decir: El dominio de cualquier función eponencial es (,+ ). La imagen de cualquier función eponencial (a 1) es (0,+ ). Observando la anterior representación, no es difícil deducir la gráfica de la función eponencial de base 3: Podemos observar que la gráfica de una función eponencial siempre contiene el punto (0,1), y la función siempre es positiva. Además, también puede afirmarse que: Si la base a es mayor que 1: o o Si la base a es menor que 1: si < y, entonces, a < a y, es decir, la función crece al aumentar la variable; dicho de otra manera, la función es creciente. Además, el crecimiento es mayor cuanto mayor es la base; cuanto menor es la, el valor de a más se acerca a 0, aunque nunca llega a alcanzarlo. Esto puede comprobarse en las gráficas de la izquierda: más a la izquierda de, pongamos por caso, = 1, el valor de las funciones se aproima muy rápidamente a 0, pero nunca es 0.
7 o o si < y, entonces, a > a y, es decir, la función decrece al aumentar la variable; dicho de otro modo, la función es decreciente. Además, el decrecimiento es mayor cuanto menor es la base; cuanto mayor es la, el valor de a más se acerca a 0, sin llegar a alcanzarlo nunca. Esto puede comprobarse en las gráficas de la derecha: más a la derecha de, pongamos por caso, = 1, el valor de las funciones se aproima rápidamente a 0, pero nunca es 0. Evidentemente, si la base es 1, la función es una constante, ya que 1 = 1. Se pueden comprobar estos hechos en estas gráficas: la gráfica de la izquierda contiene las gráficas de 4, 3, y (3/) ; la otra gráfica contiene las gráficas de (1/4), (1/3), (1/) y (/3). Podemos observar que las gráficas de 4, 3, y (3/) ; son simétricas, respectivamente de (1/4), (1/3), (1/) y (/3), lo que es evidente, ya que, (1/a) = a La función eponencial es una de las funciones más importantes por sus aplicaciones, ya que es capaz de describir una gran variedad de fenómenos, especialmente, los de crecimiento; a veces, estas funciones también se denominan funciones de crecimiento. Se trata de aplicaciones tan importantes como el crecimiento de una población de bacterias en un laboratorio, el crecimiento demográfico del número de animales, el modo como decrece la materia radiactiva (crecimiento negativo), la razón con la que un obrero aprende cierto proceso, el aumento en adquirir eperiencia sobre cómo escribir a máquina o nadar mediante la práctica y la razón con la que una enfermedad contagiosa se disemina con el tiempo. Las funciones eponenciales también desempeñan una importante función en el cálculo del interés obtenido en una cuenta bancaria, es decir, describen el aumento monetario a un interés compuesto, etc. Una de las funciones eponenciales principales es la que tiene como base el número e, que, como sabemos, es un número irracional cuyos primeros decimales son:, Cuando no se dice lo contrario, se entiende por función eponencial la función e. Qué es una ecuación eponencial y cómo se resuelve? Una ecuación eponencial es una ecuación con funciones eponenciales. Para resolver una ecuación eponencial deben agruparse al máimo las potencias para sustituir la ecuación eponencial por una ecuación lineal o cuadrática. De la misma manera, pueden resolverse sistemas de ecuaciones eponenciales, convirtiéndolos en sistemas de ecuaciones lineales, manipulando convenientemente las potencias. Una ecuación eponencial es una ecuación con funciones eponenciales. Por ejemplo, una ecuación eponencial puede ser: +1 =. En este caso, es muy sencilla la resolución, observando que las bases son iguales y, por lo tanto, los eponentes deben ser iguales; es decir, + 1 =, por lo que = 1. Puede comprobarse este hecho: efectivamente, 1+1 =. La ecuación puede ser más complicada. Por ejemplo: = 793 En este caso, debe intentar sacarse 7 como factor común, recordando las propiedades de las potencias: = ( ) = 793 se operan los elementos entre paréntesis: 7 57 = 793 por lo tanto: 7 = 793/57 = 49 Es evidente que =.
8 Incluso puede complicarse más: = + 5 En este caso debe intentarse, en primer lugar, eliminar el denominador, multiplicándolo todo por 5 : = 5 +3 operando = 0 puede reescribirse de la siguiente forma: = 0 agrupando 5(5 ) 5 3 = 0 Se trata pues de una ecuación de segundo grado, cuya incógnita es 5 = y, es decir: 5y y 3 = 0 Las soluciones son: y = 1, y = 3/5. Esta última es imposible, ya que 5 no puede ser negativo. Para la otra solución obtenemos que: 5 = 1 = 5 0 por lo tanto, = 0; es decir, =. Así pues, para resolver una ecuación eponencial, deben agruparse al máimo las potencias para intentar sustituir la ecuación eponencial por una ecuación lineal o cuadrática. De la misma manera, también pueden resolverse sistemas de ecuaciones eponenciales, convirtiéndolos en sistemas de ecuaciones lineales, manipulando convenientemente las potencias. Por ejemplo, para resolver el sistema: y 5 = 5 65 y = 56 se puede reescribir la primera ecuación: 5 = 5 y y = 5 4 y también la segunda ecuación: y = 8 +y = 8 es fácil sustituir el primer sistema por éste: y = 4 + y = 8 cuya solución es = 6 e y =. Qué es la composición de funciones y la inversa de una función? La composición de la función f con la función g es otra función, designada como gof, que a cada elemento del domino le hace corresponder g(f()). Dos funciones, f y g, se dice que son inversas una de la otra si (gof)() =, y (fog)() =. La función inversa de f se denota f 1. Dadas dos funciones f y g, se puede definir la función f compuesta con g, o composición de f con g, gof, de la siguiente manera: (gof)() = g(f()) Debe tenerse en cuenta que para que pueda calcularse la composición de f con g en un punto a, f(a), debe pertenecer al dominio de g. Por ejemplo, si f() = y g() =, entonces: (gof)() = g(f()) = g( ) = (fog)() = f(g()) = f() = 4 Puede observarse, en este ejemplo, cómo la composición de funciones no es conmutativa, es decir, gof no suele ser igual a fog; dicho de otra manera, no es lo mismo la composición de f con g, que la composición de g con f. A partir del concepto de composición de funciones puede definirse el concepto de función inversa de otra función. Si f es una función, se dice que g es la función inversa de f si (gof)() = para perteneciente al dominio de f y (fog)() = para perteneciente al dominio de g Debe cumplirse, por tanto, que el dominio de f sea igual a la imagen de g.
9 Veamos qué significa este hecho. Si, por ejemplo, f es una función tal que f(3) = 5, sabemos que debe cumplirse: (gof)(3) = 3 esto es (gof)(3) = g(f(3)) = g(5) = 3 Es decir, si la imagen del 3 en la función f es 5, entonces, la imagen del 5 en la función g es el 3. Y así para cualquier valor de f. En definitiva, g es la inversa de f si se cumple lo siguiente: si f() = y entonces g(y) = La función inversa de f se denota f 1. Finalmente, puede demostrarse que si una función tiene inversa, ambas funciones deben ser biyectivas. Qué es el logaritmo y cuáles son sus propiedades? El logaritmo en base a de un número es la operación inversa a la potencia de base a. Por ello, el logaritmo sólo puede calcularse para números positivos y, además, la base sólo puede ser positiva. Las propiedades de los logaritmos se derivan de las propiedades de las potencias. El logaritmo en base a (a > 0) de un número real positivo,, se calcula de la siguiente manera: log a = y si = a y log a indica precisamente esta operación: el logaritmo en base a. Por ejemplo, el logaritmo en base de 8 es igual a 3 porque 3 = 8; es decir: log 8 = 3 porque 3 = 8 Otros ejemplos, con diferentes bases: log 3 81 = 4 porque 3 4 = 81 log 5 5 = porque 5 = 5 log 7 49 = porque 7 = 49 Las propiedades del logaritmo se derivan de manera sencilla de las propiedades de las potencias, por la relación entre ambas operaciones, sea cual sea el valor de a > 0, y son las siguientes: 1. log a a = 1 log a 1 = 0.. El logaritmo del producto es igual a la suma de logaritmos: log a ( y) = log a + log a y ya que log a( y ) loga logb y loga + loga y a = y = a a = a 3. El logaritmo de una potencia es igual al producto del eponente por el logaritmo de la base: log a y = y log a ya que y log a( ) log y y a y loga a = = ( a ) = a 4. El logaritmo de un cociente es el logaritmo del numerador menos el logaritmo del denominador: log a = loga loga y y ya que 1 1 loga = loga( y ) = loga + loga y = loga loga y y 5. Es posible relacionar logaritmos de diferentes bases, a y b, con esta fórmula: 1 logb = logb loga b ya que si denominamos y = log a, z = log b = a y = b z además, como log a b b = a podemos decir que log a ( ) y b y loga b a a a = = es decir log a = y = z log a b = log b log a b, y de aquí se deduce la propiedad enunciada.
10 Qué son las funciones logaritmo y cuáles son sus características? La función logaritmo de base a es la función inversa de la función eponencial de base a. Su epresión es de la forma log a, siendo a > 0. El dominio de estas funciones son todos los números reales positivos, y su imagen son todos los número reales. La función es siempre creciente si a > 1, y siempre decreciente si a < 1. Estas funciones no tienen máimos ni mínimos. Las funciones logarítmicas son muy útiles en el estudio de procesos de descomposición radioactiva, por ejemplo. La función logaritmo de base a (a > 0, a 1) es la función inversa de la función eponencial de base a. Es decir, y = log a si = a y En otras palabras, la función logaritmo de base a es la función inversa de la función eponencial de base a. Así pues: El dominio de la función logaritmo de base a es igual a (0,+ ), ya que corresponde a la imagen de la función eponencial de base a. La imagen de la función logaritmo de base a es igual a todos los números reales, es decir, (,+ ), ya que éste es el dominio de la función eponencial de base a. Si se realiza la gráfica de una tabla de la función logaritmo en base, se obtendrá un conjunto de puntos como éste: Así pues, la gráfica de la función logaritmo en base en el dominio [0,3] es Podemos observar que la gráfica de una función logarítmica siempre contiene el punto (1,0). Además, también puede afirmarse que: Si la base a es mayor que 1, o o si < y, entonces, log a < log a y, es decir, la función crece al aumentar la variable; dicho de otra manera, la función es creciente. Además, no hay límite para el crecimiento de la función: cuando aumenta, la y aumenta también. Este crecimiento es mayor cuanto menor es la base; cuanto más cerca de 0 se encuentra la, el valor de log a es menor, sí que eiste límite; por ello se dice que la función log a tiende a cuando la tiende a 0. Esto puede comprobarse en las gráficas de la izquierda: más a la izquierda de, pongamos por caso, = 1, el valor de las funciones decrecen muy rápidamente, sin que haya límite alguno.
11 Si la base a es menor que 1: o o si < y, entonces, log a > log a y, es decir, la función decrece al aumentar la variable; dicho de otro modo, la función es decreciente. Además, no hay límite para el decrecimiento de la función. Este decrecimiento es mayor cuanto mayor es la base; cuanto mayor es la, el valor de a más se acerca a 0, sin llegar a alcanzarlo nunca. Esto puede comprobarse en las gráficas de la derecha: más a la derecha de, pongamos por caso, = 1, el valor de las funciones se aproima rápidamente a 0, pero nunca es 0. Se pueden comprobar estos hechos en estos gráficos: el gráfico de la izquierda contiene las gráficas de log, ln, log, log 0 ; el otro gráfico contiene las gráficas de los logaritmos con las bases inversas a los anteriores (es decir, las bases son: ½, 1/e, 1/10 y 1/0). Cabe destacar que ln es el logaritmo cuya base es el número e, y se denomina logaritmo neperiano, mientras que log (sin indicar la base) significa que se trata el logaritmo de base 10. Podemos observar que las gráficas de log a y log 1/a son simétricas respecto al eje X; lo que es justificable porque: log 1/a = log a Las funciones logarítmicas son muy importantes para el estudio de muchos fenómenos físicos, por ejemplo, la descomposición radioactiva. Cuál es la relación entre las gráficas de las funciones eponenciales y logarítmicas? Las gráficas de la función logarítmica de base a y la función eponencial de la misma base son simétricas respecto a la recta y =. De hecho, si f y g son dos funciones cualesquiera, inversas una de la otra, entonces, sus gráficas son simétricas respecto a la recta y =. Esto es así porque la función inversa intercambia los papeles de la y la y de la función original. Eiste una íntima relación entre las gráficas de una función eponencial y una función logarítmica con la misma base. Por ejemplo, si se considera la función logaritmo neperiano, ln, y la función e, sus gráficas son: La gráfica de una función debe analizarse con precaución porque siempre es aproimada y, por ello, es posible malinterpretarla. En el caso de las funciones eponenciales y logarítmicas, podría parecer que las gráficas acaban uniéndose a los ejes, la primera al eje X, la segunda al eje Y, lo que es imposible por la propia
12 Puede observarse cómo ambas funciones son simétricas respecto a la recta y =. Es decir, si se dobla el papel con las dos funciones por la recta y =, entonces ambas rectas coincidirán después de plegado. De la misma manera, si las funciones tienen la base menor que 1, sucede eactamente lo mismo; por ejemplo, las funciones (1/3) y log 1/3 tienen estas gráficas: Se puede observar que las funciones son también simétricas respecto a la recta y =. Este hecho no es solamente aplicable a estas funciones. Si dos funciones cualesquiera son inversas una de la otra, sus gráficas cumplen esta propiedad: son simétricas respecto a la recta y =. Esto es fácil de eplicar, ya que la inversa de una función intercambia los papeles de la y la y. Por lo tanto, la función inversa debe tener la misma forma que la función original, sólo que los ejes X e Y se deben intercambiar. Qué es una ecuación logarítmica y cómo se resuelve? Una ecuación logarítmica es una ecuación con funciones logarítmicas. Para resolver una ecuación logarítmica deben agruparse al máimo los logaritmos, para sustituir la ecuación logarítmica por una ecuación lineal o cuadrática. De la misma manera, pueden resolverse sistemas de ecuaciones logarítmicos, convirtiéndolos en sistemas de ecuaciones lineales, manipulando convenientemente los logaritmos. Una ecuación logarítmica es una ecuación en la que aparecen funciones logarítmicas. Para su resolución, deben aplicarse las propiedades de los logaritmos convenientemente, para agrupar las epresiones y, así, poder sustituirla por una ecuación lineal o cuadrática. Por ejemplo, para resolver: log log ( 16) = se deben agrupar los términos de la izquierda. Se cumple que log = log, por lo tanto: log log ( 16) = aplicando la propiedad del logaritmo del cociente: log log ( 16) = log 16 y ya que = log 100, se llega a la ecuación: log = log es decir: = Por lo tanto, se trata de resolver = 0; las soluciones son = 0 y = 80, y observamos que ambas pueden aplicarse en la ecuación inicial. También pueden resolverse sistemas de ecuaciones logarítmicas intentando siempre agrupar los logaritmos para convertir las ecuaciones iniciales en ecuaciones lineales o cuadráticas. Por ejemplo: + y = 65 log + log y = 3 La primera ecuación ya es lineal; intentemos transformar la segunda en una ecuación lineal: log + log y = log( y) = 3 = log 1000
13 por lo tanto, se debe sustituir la ecuación logarítmica por: y = 1000 así, pues, se debe resolver: + y = 65 y = 1000 cuyas soluciones son = 40 e y = 5, o bien, = 5 e y = 40.
14 Ejercicios 1. Encuentra una función eponencial del tipo f( ) = a que cumpla que f (6) = 64.. Cuáles de estas funciones son crecientes y cuáles decrecientes: f( ) = 11, g= ( ) 13, h ( ) = 0.1 y t= ( ) 0.3? Ordénalas de mayor a menor crecimiento. 3. Considera estas funciones: f( ) = 3+ 1, g ( ) = 3+ 1 y h ( )= e. Realiza estas composiciones: a. fog( ) b. gof ( ) c. foh( ) d. hogof ( ) 4. Calcula estos logaritmos sin usar la calculadora: 3 log 3, log9 81, log5 5, log Encuentra una función logarítmica del tipo f( ) = log a que cumpla que f (15) = Cuáles de estas funciones son crecientes y cuáles decrecientes: f( ) = log3, g ( ) = log 0., h ( ) = log13 y t ( ) = log0.1? Ordénalas de mayora a menor crecimiento. 7. Encuentra las funciones inversas de f( ) 3 = e y g ( ) ln(4 3) = Encuentra la que cumpla estas igualdades: 3 log4 = 4, log 7 =, log 1 4 =, log3 = 9. Resuelve estas ecuaciones paso a paso: a = 36 b. log 10 - log(1 4) = 10. Resuelve estas ecuaciones logarítmicas y eponenciales: a. ln + ln(-1) = 0 b. log - log = log 7
15 Soluciones 1. Se debe cumplir que f = =, por lo tanto, a =. 6 (6) a 64. f( ) = 11 y g= ( ) 13 son crecientes ya que su base es mayor que 1. Las otras son decrecientes. De mayora a menor crecimiento:: g= ( ) 13, f( ) = 11, t= ( ) 0.3 y h ( ) = a. fog( ) = b. gof ( ) = c. foh( ) = (e ) 3e + 1 d. hogof ( ) = e log 3 = log = 5log = = 9 = 3 5 = log 81 log 9 log 5 3 1/ 5 1/ 5/ 5 log3 43 = log343 = log 3(3 ) = log33 = 5. f( ) = log3. 6. Crecientes son f( ) = log3 i h ( ) = log13. De mayor a menor crecimiento: f( ) = log 3, h ( ) = log13, t ( ) = log0.1 y g ( ) = log /3 1 3 f ( ) = ln y ( ) e g = log4 = 4 = 56 log 7 = = 7 por lo tanto = 3 log 1 4 = log 3 3 = 1 = 4 por lo tanto, = 3/ = 3 por lo tanto, 3 = 3 9. a. =
16 3 5 3 = 36 ( ) = 0 se trata de una ecuación de segundo grado con incógnita 3, cuyas soluciones son 9 y 4. Esta última no es posible. Por lo tanto, 3 = 9 = 3. Así, =, como puede comprobarse fácilmente. b. log 10 - log(1 4) = Aplicando las diversas propiedades de los logaritmos: log 100 log(1 4) = log log = log por lo tanto, 100 = =1 1 4 = = 0 cuyas soluciones son =, = -6. La solución =-6 no es posible porque log 10 = log -60 es una epresión errónea.
17 en cambio =, sí que es una solución correcta: log 10 - log(1 4 ) = log 0 log 4 = 10. a. ln + ln(-1) = 0 ln((-1)) = 0 (-1)= = 0 1± 5 = b. log - log = log 7 log(/ )=log 7 / = 7 = 7 = 1/7
INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente acompañado de las tablas logarítmicas y del estudio de conceptos tales como el
INTRODUCCIÓN. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente acompañado de las tablas logarítmicas y del estudio de conceptos tales como el
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
 FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
1. Conocimientos previos. 1 Funciones exponenciales y logarítmicas.
 . Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
. Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
= y. Así pues, el domino lo forman los números x para los cuales existe el valor de f (x)
 UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
3.3 Funciones crecientes y decrecientes y el criterio de la primera derivada
 SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
Logaritmos. Cuál es la etimología de la palabra logaritmo? Proviene del griego Lógos: estilo, manera, relación, razón Arithmós: número
 Logaritmos La invención de los logaritmos se debe al matemático escocés John Neper quien, a principios del siglo XVII, intentó idear un método que aliviara los complejos cálculos que debían realizarse
Logaritmos La invención de los logaritmos se debe al matemático escocés John Neper quien, a principios del siglo XVII, intentó idear un método que aliviara los complejos cálculos que debían realizarse
Expresiones algebraicas
 Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA.
 UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA Históricamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes,
UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA Históricamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes,
Funciones algebraicas
 Funciones algebraicas Las funciones polinomiales tienen una gran aplicación en la elaboración de modelos que describen fenómenos reales. Algunos de ellos son: la concentración de una sustancia en un compuesto,
Funciones algebraicas Las funciones polinomiales tienen una gran aplicación en la elaboración de modelos que describen fenómenos reales. Algunos de ellos son: la concentración de una sustancia en un compuesto,
Ecuaciones de primer y segundo grado
 Ecuaciones de primer y segundo grado Las ecuaciones de primer y segundo grado es una ecuación porque es una igualdad entre expresiones algebraicas. Ecuaciones de primer grado con una incógnita Ejemplo
Ecuaciones de primer y segundo grado Las ecuaciones de primer y segundo grado es una ecuación porque es una igualdad entre expresiones algebraicas. Ecuaciones de primer grado con una incógnita Ejemplo
TEMA 1: Funciones elementales
 MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra.
 Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
Contenidos mínimos 4B ESO. 1. Contenidos. Bloque I: Aritmética y álgebra. 1. Clasificar distintos tipos de números: naturales, enteros, racionales y reales. 2. Operar con números reales y aplicar las propiedades
2.1. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable x)
 Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Los números naturales
 Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Guía Práctica N 14: Función Logarítmica
 Fuente: Pre Universitario Pedro de Valdivia Guía Práctica N 4: Función Logarítmica LOGARITMOS FUNCIÓN LOGARÍTMICA DEFINICIÓN El logaritmo de un número real positivo b en base a, positiva y distinta de,
Fuente: Pre Universitario Pedro de Valdivia Guía Práctica N 4: Función Logarítmica LOGARITMOS FUNCIÓN LOGARÍTMICA DEFINICIÓN El logaritmo de un número real positivo b en base a, positiva y distinta de,
y = f(x) = (10,000)2 x
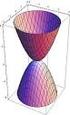 SESION. EXPONENTES Y LOGARITMOS.. Eponentes.. Importancia de los eponentes Funciones eponenciales 0,000 = (0,000) 40,000 = (0,000) 80,000 = (0,000) 3 Usamos b > 0 para evitar las raíces de números negativos,
SESION. EXPONENTES Y LOGARITMOS.. Eponentes.. Importancia de los eponentes Funciones eponenciales 0,000 = (0,000) 40,000 = (0,000) 80,000 = (0,000) 3 Usamos b > 0 para evitar las raíces de números negativos,
Funciones exponencial, logarítmica e hiperbólicas
 Funciones exponencial, logarítmica e hiperbólicas Introducción Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente unido de las tablas logarítmicas. En la actualidad, con la creciente
Funciones exponencial, logarítmica e hiperbólicas Introducción Tradicionalmente, el estudio de los logaritmos ha ido inevitablemente unido de las tablas logarítmicas. En la actualidad, con la creciente
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
FUNCIONES LINEALES Y AFINES
 www.matesronda.net José A. Jiménez Nieto FUNCIONES LINEALES Y AFINES. LA FUNCIÓN LINEAL = m El tren AVE lleva una velocidad media de 40 km/h. La siguiente tabla nos da el espacio que recorre en función
www.matesronda.net José A. Jiménez Nieto FUNCIONES LINEALES Y AFINES. LA FUNCIÓN LINEAL = m El tren AVE lleva una velocidad media de 40 km/h. La siguiente tabla nos da el espacio que recorre en función
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
Universidad de Antioquia
 Introducción Funciones eponenciales Instituto de Matemáticas * Facultad de Ciencias Eactas Naturales Unviersidad de Anquioquia Medellín, de julio de 0 El número e es un número real trascendente, es decir
Introducción Funciones eponenciales Instituto de Matemáticas * Facultad de Ciencias Eactas Naturales Unviersidad de Anquioquia Medellín, de julio de 0 El número e es un número real trascendente, es decir
Límites y continuidad
 Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
operaciones inversas Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
 Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Funciones Exponenciales y Logarítmicas
 Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
3. Resolver triángulos rectángulos utilizando las definiciones de las razones trigonométricas.
 Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
MATE 3031. Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 77
 MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
FUNCIONES TRIGONOMÉTRICAS, EXPONENCIALES Y LOGARÍTMICAS
 UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
Funciones exponenciales y logarítmicas
 Funciones exponenciales y logarítmicas - Funciones exponenciales y sus gráficas Un terremoto de 85 grados en la escala de Richter es 00 veces más potente que uno de 65, por qué?, cómo es la escala de Richter?
Funciones exponenciales y logarítmicas - Funciones exponenciales y sus gráficas Un terremoto de 85 grados en la escala de Richter es 00 veces más potente que uno de 65, por qué?, cómo es la escala de Richter?
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
MATEMÁTICAS. ESTÁNDARES 2º DE ESO
 16 Ejercicios y Problemas de Matemáticas de 1º a 3º de ESO Población: Alumnos de ESO de tu centro. Variable: Edad. Población: Coches aparcados en tu calle. Variable: Marca. Población: Familias de tu calle.
16 Ejercicios y Problemas de Matemáticas de 1º a 3º de ESO Población: Alumnos de ESO de tu centro. Variable: Edad. Población: Coches aparcados en tu calle. Variable: Marca. Población: Familias de tu calle.
FUNCIONES TRIGONOMÉTRICAS, EXPONENCIALES Y LOGARÍTMICAS
 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES LOGARÍTMICAS Página 9 REFLEIONA RESUELVE A vueltas con la noria Modificando la escala, representa la función: : tiempo transcurrido y: distancia al suelo correspondiente
FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES LOGARÍTMICAS Página 9 REFLEIONA RESUELVE A vueltas con la noria Modificando la escala, representa la función: : tiempo transcurrido y: distancia al suelo correspondiente
y con la semiamplitud δ =1. 2.
 LÍMITE DE UNA FUNCIÓN UNIDAD II II. ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
LÍMITE DE UNA FUNCIÓN UNIDAD II II. ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
Problemas de 4 o ESO. Isaac Musat Hervás
 Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Sistemas de ecuaciones
 Sistemas de ecuaciones Sistemas de ecuaciones Resolución de un sistema de dos ecuaciones lineales Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones de primer grado con dos incógnitas
Sistemas de ecuaciones Sistemas de ecuaciones Resolución de un sistema de dos ecuaciones lineales Un sistema de dos ecuaciones lineales es un conjunto de dos ecuaciones de primer grado con dos incógnitas
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
 Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE MATEMÁTICAS LOGARITMOS
 LOGARITMOS Introducción El empleo de los logaritmos es de gran utilidad para entender muchos de los desarrollos que se analizan en la Matemática, y para explicar una variedad muy extensa de problemas que
LOGARITMOS Introducción El empleo de los logaritmos es de gran utilidad para entender muchos de los desarrollos que se analizan en la Matemática, y para explicar una variedad muy extensa de problemas que
RELACIONES Y FUNCIONES FUNCIÓN
 1 RELACIONES Y FUNCIONES FUNCIÓN, en matemáticas,el término es usado para indicar la relación o correspondencia entre dos o más cantidades. El término función fue usado por primera vez en 1637 por el matemático
1 RELACIONES Y FUNCIONES FUNCIÓN, en matemáticas,el término es usado para indicar la relación o correspondencia entre dos o más cantidades. El término función fue usado por primera vez en 1637 por el matemático
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714)
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 1 (FUNCIONES) Profesora: Yulimar Matute Octubre 2011 Función Constante: Se
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 1 (FUNCIONES) Profesora: Yulimar Matute Octubre 2011 Función Constante: Se
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
Unidad 1. Las fracciones.
 Unidad 1. Las fracciones. Ubicación Curricular en España: 4º, 5º y 6º Primaria, 1º, 2º y 3º ESO. Objetos de aprendizaje. 1.1. Concepto de fracción. Identificar los términos de una fracción. Escribir y
Unidad 1. Las fracciones. Ubicación Curricular en España: 4º, 5º y 6º Primaria, 1º, 2º y 3º ESO. Objetos de aprendizaje. 1.1. Concepto de fracción. Identificar los términos de una fracción. Escribir y
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 3.- FUNCIONES ELEMENTALES
 1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 3.- FUNCIONES ELEMENTALES 1 1.- FUNCIONES. CARACTERÍSTICAS Concepto de función. Una función es una forma de hacerle corresponder a un valor x un único
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 3.- FUNCIONES ELEMENTALES 1 1.- FUNCIONES. CARACTERÍSTICAS Concepto de función. Una función es una forma de hacerle corresponder a un valor x un único
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
MODULO DE LOGARITMO. 1 log 2 4 16. log N x b N N se llama antilogaritmo, b > 0 y b 1. Definición de Logaritmo. Liceo n 1 Javiera Carrera 2011
 MODULO DE LOGARITMO Nombre:.. Curso : Medio Los aritmos están creados para facilitar los cálculos numéricos. Por aritmo podemos convertir los productos en sumas, los cocientes en restas, las potencias
MODULO DE LOGARITMO Nombre:.. Curso : Medio Los aritmos están creados para facilitar los cálculos numéricos. Por aritmo podemos convertir los productos en sumas, los cocientes en restas, las potencias
Tema Contenido Contenidos Mínimos
 1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Lección 13: Resolución algebraica de sistemas de ecuaciones
 GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
1.5 Límites infinitos
 SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
FECHA OBJETIVO CONTENIDO 12 DE MARZO. Introducir el tema de funciones
 Página 1 de 11 INA Turismo Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO 12 DE MARZO Introducir el tema de funciones inicio de clases
Página 1 de 11 INA Turismo Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO 12 DE MARZO Introducir el tema de funciones inicio de clases
APUNTES DE FUNCIONES PARA 4º ESO
 APUNTES DE FUNCIONES PARA 4º ESO - DEFINICIÓN: Una función es una relación entre dos magnitudes, X e Y, de forma que a cada valor de la magnitud X corresponde un único valor y de la magnitud Y. : variable
APUNTES DE FUNCIONES PARA 4º ESO - DEFINICIÓN: Una función es una relación entre dos magnitudes, X e Y, de forma que a cada valor de la magnitud X corresponde un único valor y de la magnitud Y. : variable
1. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de Matemáticas I)
 . NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
DESCOMPOSICIÓN FACTORIAL
 6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
Ecuaciones de primer grado
 Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
TEMAS 10 LAS FUNCIONES ELEMENTALES 1º BACH MATE I
 TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas Función Derivada Función compuesta Derivada y f x y f x y f g x
 Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES
 MATEMÁTICAS EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES Juan Jesús Pascual ECUACIONES LOGARÍTMICAS Y EXPONENCIALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA
MATEMÁTICAS EJERCICIOS RESUELTOS DE ECUACIONES LOGARÍTMICAS Y EXPONENCIALES Juan Jesús Pascual ECUACIONES LOGARÍTMICAS Y EXPONENCIALES A. Introducción teórica B. Ejercicios resueltos A. INTRODUCCIÓN TEÓRICA
FECHA OBJETIVO CONTENIDO Semana. Introducir el tema de funciones ( tentativo)
 Página 1 de 11 INA Uruca Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO Semana Introducir el tema de funciones ( tentativo) inicio de
Página 1 de 11 INA Uruca Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO Semana Introducir el tema de funciones ( tentativo) inicio de
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
El problema de la recta tangente. 96 CAPÍTULO 2 Derivación
 96 CAPÍTULO Derivación. La derivada el problema de la recta tangente Hallar la pendiente de la recta tangente a una curva en un punto. Usar la definición de ite para calcular la derivada de una función.
96 CAPÍTULO Derivación. La derivada el problema de la recta tangente Hallar la pendiente de la recta tangente a una curva en un punto. Usar la definición de ite para calcular la derivada de una función.
UNIDAD 4.- INECUACIONES Y SISTEMAS (tema 4 del libro)
 UNIDAD 4. INECUACIONES Y SISTEMAS (tema 4 del libro) 1. INECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA Definición: Se llama desigualdad a toda relación entre epresiones numéricas o algebraicas unidas por
UNIDAD 4. INECUACIONES Y SISTEMAS (tema 4 del libro) 1. INECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA Definición: Se llama desigualdad a toda relación entre epresiones numéricas o algebraicas unidas por
Teoría Tema 1 Propiedades de funciones elementales. Ejemplos exponencial y logaritmo
 página 1/9 Teoría Tema 1 Propiedades de funciones elementales. Ejemplos exponencial y logaritmo Índice de contenido Dominio de una función...2 Rango o recorrido de una función...3 Simetría...4 Periodicidad...5
página 1/9 Teoría Tema 1 Propiedades de funciones elementales. Ejemplos exponencial y logaritmo Índice de contenido Dominio de una función...2 Rango o recorrido de una función...3 Simetría...4 Periodicidad...5
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
HOMOGENEIDAD DIMENSIONAL
 HOMOGENEIDAD DIMENSIONAL Los observables que podemos medir se agrupan en conjuntos caracterizados por una propiedad que llamamos magnitud. Existe la magnitud tiempo, la magnitud velocidad, la magnitud
HOMOGENEIDAD DIMENSIONAL Los observables que podemos medir se agrupan en conjuntos caracterizados por una propiedad que llamamos magnitud. Existe la magnitud tiempo, la magnitud velocidad, la magnitud
Cálculos aproximados y estimaciones. Logaritmos
 Cálculos aproximados y estimaciones. Logaritmos J Güémez Facultad de Ciencias Universidad de Cantabria Enero 21, 2015 1 Estimaciones Cómo estimar la longitud de un objeto? Método de la media geométrica.
Cálculos aproximados y estimaciones. Logaritmos J Güémez Facultad de Ciencias Universidad de Cantabria Enero 21, 2015 1 Estimaciones Cómo estimar la longitud de un objeto? Método de la media geométrica.
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
( ) es aceptable. El grado del
 POLINOMIOS 8.1.1 8.1.3 El capítulo eplora funciones polinómicas en maor profundidad. Los alumnos aprenderán cómo bosquejar funciones polinómicas sin su herramienta de graficación, utilizando la forma factorizada
POLINOMIOS 8.1.1 8.1.3 El capítulo eplora funciones polinómicas en maor profundidad. Los alumnos aprenderán cómo bosquejar funciones polinómicas sin su herramienta de graficación, utilizando la forma factorizada
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
Complejos, C. Reales, R. Fraccionarios
 NÚMEROS COMPLEJOS Como ya sabemos, conocemos distintos cuerpos numéricos en matemáticas como por ejemplo el cuerpo de los números racionales, irracionales, enteros, negativos,... Sin embargo, para completar
NÚMEROS COMPLEJOS Como ya sabemos, conocemos distintos cuerpos numéricos en matemáticas como por ejemplo el cuerpo de los números racionales, irracionales, enteros, negativos,... Sin embargo, para completar
DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x):
 FUNCIONES ELEMENTALES 0. CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, Dom, le hace corresponder un único número real, f(): Lo denotamos por : f : Dom -----> R ----->
FUNCIONES ELEMENTALES 0. CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, Dom, le hace corresponder un único número real, f(): Lo denotamos por : f : Dom -----> R ----->
FUNCIONES Y GRÁFICAS
 FUNCIONES Y GRÁFICAS 1. DEPENDENCIA ENTRE MAGNITUDES Relaciones dadas por tablas En una clase de laboratorio un alumno ha medido la temperatura de un líquido según se calentaba. Los resultados del eperimento
FUNCIONES Y GRÁFICAS 1. DEPENDENCIA ENTRE MAGNITUDES Relaciones dadas por tablas En una clase de laboratorio un alumno ha medido la temperatura de un líquido según se calentaba. Los resultados del eperimento
Ecuaciones. 3º de ESO
 Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Teoría Tema 3 Teoremas de derivabilidad
 página 1/10 Teoría Tema 3 Teoremas de derivabilidad Índice de contenido Teorema de Rolle...2 Teorema del valor medio de Lagrange (o de los incrementos finitos)...4 Teorema de Cauchy...6 Regla de L'Hôpital...8
página 1/10 Teoría Tema 3 Teoremas de derivabilidad Índice de contenido Teorema de Rolle...2 Teorema del valor medio de Lagrange (o de los incrementos finitos)...4 Teorema de Cauchy...6 Regla de L'Hôpital...8
Se dice que una ecuación es entera cuando las incógnitas esta sometidas únicamente a las operaciones de suma, resta y multiplicación.
 III. UNIDAD : ECUACIONES DE PRIMER GRADO III.. ECUACIONES DE PRIMER GRADO III... Ecuaciones de Primer Grado con una incógnita Se dice que una ecuación es entera cuando las incógnitas esta sometidas únicamente
III. UNIDAD : ECUACIONES DE PRIMER GRADO III.. ECUACIONES DE PRIMER GRADO III... Ecuaciones de Primer Grado con una incógnita Se dice que una ecuación es entera cuando las incógnitas esta sometidas únicamente
Las superficies serán: Tapa y superficie lateral S 1 = ( x 2 +4xy ) cm 2 Superficie de la base: S 2 = x 2 cm 2
 MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
Unidad 1: Números reales.
 Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 4. Números reales y números complejos
 CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
CONCEPTOS NÚMEROS COMPLEJOS En el conjunto de los números reales, una ecuación tan sencilla como x + = 0 no se puede resolver ya que es equivalente a x = - y no existe ningún número real cuyo cuadrado
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
21. Círculo y recta Matemáticas II, 2012-II. Por qué el círculo y la recta son tan importantes?
 . Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
. Círculo recta Matemáticas II, -II. Círculo recta Por qué el círculo la recta son tan importantes? Los dos objetos geométricos más importantes aparte del punto son sin duda la recta el círculo. La recta
Gráficas de las funciones racionales
 Gráficas de las funciones racionales Ahora vamos a estudiar de una manera geométrica las ideas de comportamiento de los valores que toma la función cuando los valores de crecen mucho. Es importante que
Gráficas de las funciones racionales Ahora vamos a estudiar de una manera geométrica las ideas de comportamiento de los valores que toma la función cuando los valores de crecen mucho. Es importante que
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
TEMA 6 ECUACIONES DE PRIMER GRADO
 Nueva del Carmen,. 0 Valladolid. Tel 98 9 6 9 Fa 98 89 96 Matemáticas º ESO TEMA 6 NOMBRE Y APELLIDOS... HOJA - FECHA... Comenzamos en este tema a resolver ecuaciones. Primero de Primer grado. Luego vendrán
Nueva del Carmen,. 0 Valladolid. Tel 98 9 6 9 Fa 98 89 96 Matemáticas º ESO TEMA 6 NOMBRE Y APELLIDOS... HOJA - FECHA... Comenzamos en este tema a resolver ecuaciones. Primero de Primer grado. Luego vendrán
2. SISTEMAS DE ECUACIONES LINEALES. Introducción
 2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
2. SISTEMAS DE ECUACIONES LINEALES Introducción El presente curso trata sobre álgebra lineal. Al buscarla palabra lineal en un diccionario se encuentra, entre otras definiciones la siguiente: lineal, perteneciente
Las funciones polinómicas
 Las funciones polinómicas 1 Las funciones polinómicas Una función polinómica es aquella que tiene por expresión un polinomio. En general, suelen estudiarse según el grado del polinomio: Las funciones afines
Las funciones polinómicas 1 Las funciones polinómicas Una función polinómica es aquella que tiene por expresión un polinomio. En general, suelen estudiarse según el grado del polinomio: Las funciones afines
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
Ecuaciones de segundo grado
 Ecuaciones de segundo grado 11 de noviembre 009 Ecuaciones de segundo grado con una incógnita método de solución, formula general e incompletas Algebra Ecuaciones de segundo grado con una incógnita Las
Ecuaciones de segundo grado 11 de noviembre 009 Ecuaciones de segundo grado con una incógnita método de solución, formula general e incompletas Algebra Ecuaciones de segundo grado con una incógnita Las
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 A-09 - Incorporado a la Enseñanza Oficial COLEGIO SAN PATRICIO - 0 - Prof. Celia R. Sánchez MATEMÁTICA - TRABAJO PRÁCTICO Nº 8 AÑO FUNCIÓN EXPONENCIAL Y LOGARÍTMICA - ECUACIONES POTENCIACIÓN: Ejercicio
A-09 - Incorporado a la Enseñanza Oficial COLEGIO SAN PATRICIO - 0 - Prof. Celia R. Sánchez MATEMÁTICA - TRABAJO PRÁCTICO Nº 8 AÑO FUNCIÓN EXPONENCIAL Y LOGARÍTMICA - ECUACIONES POTENCIACIÓN: Ejercicio
Anexo C. Introducción a las series de potencias. Series de potencias
 Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Funciones exponencial y logarítmica
 Funciones eponencial y logarítmica El estudiante: Resolverá problemas con funciones eponenciales y logarítmicas, teóricos o prácticos, utilizando su relación como funciones inversas y sus propiedades algebraicas,
Funciones eponencial y logarítmica El estudiante: Resolverá problemas con funciones eponenciales y logarítmicas, teóricos o prácticos, utilizando su relación como funciones inversas y sus propiedades algebraicas,
Método de fórmula general
 Método de fórmula general Ahora vamos a utilizar el método infalible. La siguiente fórmula, que llamaremos «fórmula general» nos ayudará a resolver cualquier ecuación cuadrática. Fórmula General La fórmula
Método de fórmula general Ahora vamos a utilizar el método infalible. La siguiente fórmula, que llamaremos «fórmula general» nos ayudará a resolver cualquier ecuación cuadrática. Fórmula General La fórmula
