Funciones reales de variable real
|
|
|
- Laura Hernández Macías
- hace 7 años
- Vistas:
Transcripción
1 84 Matemáticas I : Cálculo diferencial en IR Tema 8 Funciones reales de variable real 8. Los números reales Los números reales son de sobra conocidos, sus operaciones básicas así como su identificación con los puntos de la recta real, por lo que sólo vamos a mencionar aquí algunas de sus propiedades (la mayoría conocidas) que son imprescindibles en el desarrollo de este tema. Propiedades de orden 74.- Denotaremos por IR + = x IR : x > 0 y IR = x IR : x < 0.- Antisimétrica: Si x y e y x = x = y..- Transitiva: Si x y e y z = x z. 3.- Total: Para cualesquiera x, y IR: o bien x y, o bien y x. 4.- Si x y, entonces x + z y + z para todo z IR (si x < y = x + z < y + z ). 5.- Si x y, entonces x z y z para todo z IR + (si x < y = x z < y z ). 6.- Si x y, entonces x z y z para todo z IR (si x < y = x z > y z ). 7.- Si 0 < x < y, entonces 0 < y < x. Las propiedades de acotación siguientes garantizan que los números reales llenan la recta real, lo que nos permite decir que recorremos de manera continua un subconjunto de IR. Definición 75.- Sea A IR, diremos que el conjunto A está acotado superiormente si existe algún K IR tal que x K, para todo x A; es decir, todos los elementos de A son menores que K. Del valor K diremos que es una cota superior de A. Análogamente, A está acotado inferiormente si existe k IR tal que k x, para todo x A y diremos que k es una cota inferior de A. Diremos que A está acotado si lo está superior e inferiormente. Propiedad del extremo superior 76.- Todo subconjunto no vacío A IR y acotado superiormente admite una cota superior mínima, es decir, Γ IR tal que: a) x Γ; x A b) Si K < Γ, entonces x A verificando que K < x Γ. Se dice que Γ es el extremo superior o supremo de A y se denota por sup A ó ext sup A. Si Γ pertenece a A, se dice que Γ es el máximo de A, y escribiremos máx A = Γ. Propiedad del extremo inferior 77.- Todo subconjunto no vacío A IR acotado inferiormente admite una cota inferior máxima, es decir, γ IR tal que: a) γ x; x A b) Si γ < k, entonces x A verificando que γ x < k. Se dice que γ es el extremo inferior o ínfimo de A y se denota por inf A ó ext inf A. Si γ pertenece a A, se dice que γ es el mínimo de A, y escribiremos mín A = γ. Nota: Que Γ = sup A es equivalente a que para cada ε > 0 existe x A con Γ ε < x Γ. Es decir, que para cualquier valor más pequeño que el superior hay algún elemento del conjunto más grande que él. Análogamente, γ = inf A para cada ε > 0 existe x A con γ x < γ + ε. El conjunto A = n : n IN =,, 3, 4,... está acotado superior e inferiormente.
2 85 Matemáticas I : Cálculo diferencial en IR 8. Los números reales En efecto, n < para todo n, luego es una cota superior del conjunto (de hecho, cualquier número mayor o igual a lo es). También está acotado inferiormente, pues n es positivo luego 0 < n para todo n y 0 es una cota inferior de A (cualquier número negativo es también una cota inferior). Luego A es un conjunto acotado y tiene supremo e ínfimo: como el supremo es la mínima cota superior, sup A =, pues es una cota superior y si K <, existe el A tal que K < sup A = luego K no es una cota y es la más pequeña. Como el ínfimo es la máxima cota inferior, inf A = 0, pues es una cota y para cualquier k > 0, puedo encontrar un n suficientemente grande para que 0 < n < k (por ejemplo, para k = , se tiene que 0 < 0000 < = k ). Además, sup A = A luego máx A = ; lo que no ocurre con el ínfimo, pues inf A = 0 / A, luego mín A. 8.. Valor absoluto de un número real Definición 78.- Sea a IR, se llama valor absoluto de a, y se representa por a, al número real dado por a = + a, si a 0 a = a, si a < 0 Propiedades del valor absoluto 79.- a) a 0, a y a = 0 a = 0 b) ab = a b c) a = a d) a k k a k e) a + b a + b f) a b a b El valor absoluto y su uso como distancia es clave en las definiciones de conjuntos y conceptos como el límite y la continudad, la derivación e integración. Nota: Con el valor absoluto, diremos que A es acotado existe K > 0 tal que x K, x A. El conjunto A =,, 3, 4,... del ejemplo anterior está acotado pues para todo n. n 8.. Intervalos y entornos en IR Los subconjuntos de IR, están formados por puntos separados o por intervalos ( trozos ) de la recta real o por uniones de ellos; pero no sólo eso, sino que la validez de algunos resultados depende del tipo de intervalo usado. Pero además, los intervalos centrados en un punto (que llamaremos entornos) son básicos en la construcción de la mayoría de los conceptos del Cálculo. Definición 80.- Dados los números reales a y b con a b, se llama intervalo abierto de extremos a y b, y se representa por (a, b), al conjunto: (a, b) = x IR : a < x < b. Se llama intervalo cerrado de extremos a y b, y se representa por [a, b], al conjunto: [a, b] = x IR : a x b. Análogamente se definen: (a, b] = x IR : a < x b y [a, b) = x IR : a x < b y los intervalos no acotados: (a, + ) = x IR : a < x y [a, + ) = x IR : a x (, b) = x IR : x < b y (, b] = x IR : x b En los intervalos cerrados, inf[a, b] = mín[a, b] = a y sup[a, b] = máx[a, b] = b, mientras que en los abiertos inf(a, b) = a y sup(a, b) = b pero no tiene ni máximo ni mínimo. En los no acotados, como [a, + ), se tiene inf[a, + ) = mín[a, + ) = a pero no existe el superior (a veces se escribe sup A = +, para indicar que el conjunto no está acotado superiomente). Naturalmente, IR es también un intervalo IR = (, + ). Y, [a, a] = a pero (a, a) = (a, a] = [a, a) =. Definición 8.- Llamaremos entorno de centro a y radio ε > 0, y escribiremos E(a, ε), al conjunto: E(a, ε) = x IR : x a < ε = x IR : a ε < x < a + ε = (a ε, a + ε). Llamaremos entorno reducido de centro a y radio ε > 0, E (a, ε), al conjunto E (a, ε) = E(a, ε) a = x IR : 0 < x a < ε.
3 86 Matemáticas I : Cálculo diferencial en IR 8. Funciones reales de variable real 8..3 Algunas operaciones con números reales Potencias racionales y reales de un número real Las potencias racionales, x r, se definen paulatinamente a partir de las potencias naturales: para n IN y x IR, definimos x n = x x n) x. para z Z y x IR 0, definimos x 0 = y si z < 0, x z = (x ) z. para n IN y x IR +, definimos x n = n x como el α IR tal que α n = x para r = z n, con z Z y n IN, y x IR+, definimos x z n = n x z. y se verifican las siguientes propiedades: () x r y r = (xy) r () x r x s = x r+s (3) (x r ) s = x rs (4) Si 0 < x < y, entonces 0 < x r < y r si r > 0 y 0 < y r < x r si r < 0 (5) Si r < s se tiene que x r < x s cuando x > y x s > x r cuando 0 < x <. n Antes de terminar, un pequeño apunte sobre las raices n-ésimas, x para x 0: si n es impar, existe un único número real α > 0 tal que α n = x; y si n es par, existe un único número real α > 0 tal que α n = x y ( α) n = x. Por ello, si n es par siempre se escribe n x > 0 y n x < 0 para distinguir entre el valor positivo y el negativo. Potencias reales.- Las potencias reales de un número real, x α, con x > 0 y α IR se extienden de las racionales (aunque no de manera sencilla) y verifican las mismas propiedades de () a (5) que las potencias racionales Exponencial real de base e La exponencial de base e que a cada x IR le asigna el número real e x. Las propiedades de las potencias, establecen la validez de: () e x+y = e x e y () Si x < y se tiene que e x < e y (3) e x > 0 (Genéricamente, tenemos exponenciales de base a, para cualquier a > 0, con propiedades similares.) Logaritmo neperiano real Para cada x (0, + ), se define el logaritmo neperiano, ln x como el valor real α tal que e α = x; es decir, la operación recíproca a la exponencial. () ln(xy) = ln x + ln y () ln(x y ) = y ln x (3) Si 0 < x < y se tiene ln x < ln y (Genéricamente, para cada exponencial a x, tenemos el logaritmo en base a, log a x.) 8. Funciones reales de variable real Definición 8.- Llamaremos función real de variable real, a cualquier aplicación f: A IR, donde A IR. Al conjunto A lo denominaremos dominio de f y escribiremos A = Dom(f). Si x A escribiremos y = f(x) para indicar que y IR es la imagen de x por medio de f. El recorrido o conjunto imagen de f, que suele denotarse por f(a), será: f(a) = f(x) IR : x A = y IR : x A con y = f(x) = Img f Nota: Si la función viene dada sólo por la expresión y = f(x), sobreentenderemos que el dominio es el máximo subconjunto de IR para el cual f(x) IR, es decir, Dom(f) = x IR : f(x) IR Sea f: [, ] IR dada por f(x) = x. Se tiene que: Dom(f) = [, ]: pues x [, ] = 0 x = x 0 = x = f(x) IR.
4 87 Matemáticas I : Cálculo diferencial en IR 8. Funciones reales de variable real f([, ]) [0, ], ya que x [, ] = 0 x = x 0 = 0 x = 0 x y, si k [0, ], se tiene k = f ( k ) ; luego f([, ]) = [0, ]. Para f dada por f(x) = x, su dominio se obtendrá de: f(x) IR x IR x 0 x x ± luego Dom(f) = IR, = (, ) (, ) (, + ). Además, Img(f) = IR [0, ). Definición 83.- Llamaremos gráfica de la función dada por y = f(x), y lo denotaremos por graf(f), al subconjunto de IR graf(f) = (x, y) IR : x Dom(f) e y =f(x) = (x, f(x)) IR : x Dom(f) f(a) f(c) f(b) y graf(f) (a, f(a)) (c, f(c)) (b, f(b)) a b c x Definición 84 (Operaciones con funciones).- Sea f y g funciones reales de variable real. Entonces son funciones reales de variable real las siguientes:.- (Suma) (f +g)(x) = f(x) + g(x).- (Producto) (fg)(x) = f(x) g(x) ( ) 3.- (Cociente) f g (x) = f(x) g(x) 4.- (Composición) (g f)(x) = g(f(x)) en los conjunto donde tenga sentido. Es decir: ( Dom(f +g) = Dom(f) Dom(g) Dom(f/g) = Dom(fg) = Dom(f) Dom(g) Dom(g f) = ) Dom(f) Dom(g) x : g(x) = 0 x Dom(f) : f(x) Dom(g) Sean f(x) = x y g(x) = x. Se tiene que Dom f = x IR : x 0 = x IR : x = (, ] Dom g = x IR : x 0 = x IR : x = (, ] [, + ) = IR (, ) Luego el dominio de (f + g)(x) = x + x es Dom(f + g) = Dom f Dom g = (, ] ( ) (, ] [, + ) = (, ] [, ] que coincide con el de (fg)(x) = x x. Para el dominio de ( f g )(x) = x, como g(x) = 0 si x x = 0, es decir, si x = ±, ( ) ( ) Dom f g = (Dom f Dom g), = (, ] [, ], = (, ) (, ] y, finalmente el dominio de (g f)(x) = ( x) = x será Dom(g f) = x (, ] : x Dom g () = x (, ] : x = x (, ] : x = x (, ] : x = (, ] () como x 0, se tiene x Dom g si x [, + ), es decir, si x. Dominio de algunas funciones elementales 85.- Raíz: f(x) = n x y Dom f = [0, + ). Con n x = 0 x = 0. Potencia real: f(x) = x α y Dom f = (0, + ). Con x α > 0 para todo x. Exponencial: f(x) = e x y Dom f = IR. Con e x > 0 para todo x. Logaritmo neperiano: f(x) = ln(x) y Dom f = (0, + ). Con ln x = 0 x =.
5 88 Matemáticas I : Cálculo diferencial en IR 8. Funciones reales de variable real Seno: f(x) = sen(x) y Dom f = IR. Con sen x = 0 x = kπ con k Z, Coseno: f(x) = cos(x) y Dom f = IR. Con cos x = 0 x = π + kπ con k Z. Tangente: f(x) = tg(x) = sen x cos x y Dom f = IR π + kπ : k Z = ( π k Z + kπ, π + kπ). Seno hiperbólico: Coseno hiperbólico: Tangente hiperbólica: f(x) = sh(x) = ex e x y Dom f = IR. Con sh x = 0 x = 0. f(x) = ch(x) = ex +e x y Dom f = IR. Con ch x para todo x. f(x) = th(x) = sh x ch x y Dom f = IR. α < α > f(x) = x α 0 < α < < α < 0 α = f(x) = e x f(x) = ln(x) ch(x) sh(x) th(x) π π sen(x) cos(x) tg(x) Fig. 8.. Gráficas de algunas funciones elementales. Definición 86.- Sea f: A IR, con A IR. Diremos que f es una función acotada si el conjunto imagen f(a) está acotado. Es decir, si existe K > 0 tal que f(x) K para todo x A. El seno y el coseno están acotadas en IR, pues sen x y cos x para todo x IR. La función f: IR 0 IR, con f(x) = x x, está acotada en su dominio pues para todo x IR, se tiene x x x, y para todo x 0, x x. (De hecho, f(x) =, x 0.) La función th(x) está acotada en IR. En efecto, si x 0, se cumple que e x e = e x, luego x 0 e x e x < e x + e x y entonces 0 ex e x e x +e <. Como th( x) = th(x) (comprobarlo), cuando x x < 0, se tiene < th(x) < 0, por lo que th(x) <, para todo x IR. 8.. Monotonía. Funciones inversas Definición 87.- Sea f: A IR diremos que f es creciente o monótona creciente en el conjunto A, si para cualesquiera x, y A, con x < y, se verifica que f(x) f(y). Diremos que f es decreciente o monótona decreciente en el conjunto A, si para cualesquiera x, y A, con x < y, se verifica que f(x) f(y). Diremos que f es creciente (resp. decreciente) en el punto a A, si existe un entorno E(a, δ) tal que x, y E(a, δ) con x < a < y se cumple f(x) f(a) f(y) (resp. f(x) f(a) f(y)). Nota: Si las desigualdades son estrictas, diremos estrictamente creciente y estrictamente decreciente. Por las propiedades enunciadas anteriormente, las funciones e x, ln x y x α con α > 0 son estrictamente crecientes en sus dominios; y si α < 0, x α decrece estrictamente en (0, + ) (ver gráficas arriba). La función f(x) = x es estrictamente decreciente en cada punto de su dominio IR 0, pero no es monótona decreciente en el conjunto (ya que < pero f( ) = < f() =.) Definición 88.- Se dice que f: A IR es inyectiva en A si f(x) f(y) para todo x, y A, con x y. Las funciones estrictamente crecientes o estrictamente decrecientes en un conjunto son inyectivas. La función f(x) = x es inyectiva en [0, ] y también en [, 0], pero no lo es en el conjunto [, ] puesto que f( ) = = f() con.
6 89 Matemáticas I : Cálculo diferencial en IR 8.3 Ejercicios Definición 89.- Sean f: A IR y B = f(a). Si f es inyectiva en A, llamaremos función inversa de f en A, y la denotaremos por f, a la función f : B A tal que f (f(x)) = x, para todo x A. 90 La función f: [0, ) IR con f(x) = x, tiene inversa en ese conjunto (es estrictamente creciente en él) y es f : [0, ) [0, ) dada por f (y) = y. [ f (f(x)) = x = x = x ] La función f: (, 0] IR con f(x) = x, tiene inversa en ese conjunto (es estrictamente decreciente en él), que es f : [0, ) (, 0] dada por f (y) = y. [ f (f(x)) = x = x = x ] La función f: (0, + ) IR con f(x) = x α, tiene inversa en el conjunto (es estr. creciente si α > 0 y decreciente si α < 0), que es f : (0, ) IR dada por f (y) = y α. [ f (f(x)) = (x α ) α = x = x ] La función f: IR (0, ) con f(x) = e x, tiene inversa en IR (es estrictamente creciente en él), que es f : (0, ) IR dada por f (y) = ln y. [ f (f(x)) = ln(e x ) = x ln(e) = x ] La función f(x) = sen x, tiene inversa en el conjunto [ π, π ] (es estrictamente creciente en él), la función f : [, ] [ π, π ] que llamaremos arcoseno y denotaremos f (y) = arcsen y. (El seno no tiene inversa en [0, π], pues no es inyectiva en ese conjunto) La función f(x) = cos x, tiene inversa en el conjunto [0, π] (es estrictamente decreciente en él), la función f : [, ] [0, π] que llamaremos arcocoseno y denotaremos f (y) = arccos y. La función f(x) = tg x, tiene inversa en el conjunto [ π, π ] (es estrictamente creciente en él), la función f : IR [ π, π ] que llamaremos arcotangente y denotaremos f (y) = arctg y. La función f(x) = sh x, f: IR IR, tiene inversa en IR (es estrictamente creciente en él), la función f : IR IR que llamaremos argumento del sh y denotaremos f (y) = argsh y = ln(y + y + ). La función f(x) = ch x, tiene inversa en [0, ) (estrictamente creciente), la función f : [, ) [0, ) que llamaremos argumento del ch y denotaremos f (y) = argch y = ln( y + y + ). La función th: IR (, ), tiene inversa en IR (estrictamente creciente), la función f : (, ) IR que llamaremos argumento de la th y denotaremos f (y) = argth y = ln y+ y. Nota: La gráfica de f es simétrica, respecto de la bisectriz del primer cuadrante, a la gráfica de f. En efecto, si (x, y) graf(f) con y = f(x), entonces, el punto (y, f (y)) graf(f ) es de la forma (y, f (y)) = (y, f (f(x))) = (y, x). Puede observarse esto en la figura 8. de la página 88, para e x y su inversa ln(x) y x α y su inversa x α. 8.3 Ejercicios 8.90 Usar las Propiedades del orden 74 y las de las operaciones descritas en el apartado 8..3, para probar que: a) si 0 < x < y, entonces 0 < x < y b) si y < x < 0, entonces 0 < x < y c) si 0 < x < y, entonces 0 < x < y d) si y < x < 0, entonces 0 < x < y e) si 0 < x <, entonces 0 < x < x f) si < x, entonces < x < x g) si y < x < 0, entonces x < y < 0 h) si y < x < 0, entonces 0 < y < x i) si 0 < x < y, entonces 0 < x < y j) si 0 < x < y, entonces y < x < Hallar el dominio de las funciones reales de variable real dadas por: (i) f (x) = x x (ii) f (x) = x x (iii) f 3 (x) = x x+ (iv) f 4 (x) = ln x (v) f 5 (x) = ln x (vi) f 6 (x) = ln( x ) (vii) f (x) + f (x) (viii) f 3 (x) f (x) (ix) f (x) + f 3 (x) (x) f 7 (x) = x x+ (xi) f 8 (x) = ln(f 6 (x)) (xii) f 9 (x) = x x+ (xiii) f 3 (x) f 3 (x) (xiv) f 9 (x) f 7 (x) (xv) (xvi) f 6 (x) f + f (x) (x) f 6(x) f 4 (x)+f 5 (x) f 8 (x) (xvii) (f 5 f 8 )(x) (xviii) (f f 4 f )(x)
7 90 Matemáticas I : Cálculo diferencial en IR 8.3 Ejercicios a) Expresar la funciones f y f 4 como funciones definidas a trozos. b) Por qué los dominios de f 3 y de f 7 son distintos? c) Cuál será el dominio de la función f f? Obtener su expresión. 8.9 Sean f y g dos funciones reales de variable real monótonas. Probar que: a) Si f es (estrictamente) creciente, las funciones f( x) y f(x) son (estric.) decrecientes. b) Si f es (estrictamente) decreciente, las funciones f( x) y f(x) son (estric.) crecientes. c) Si f es (estric.) creciente y positiva, la función f(x) es (estric.) decreciente. d) Si f es (estric.) decreciente y positiva, la función f(x) es (estric.) creciente. Qué ocurrirá en este caso y en el anterior si la función f es negativa? e) Si f y g son crecientes (decrecientes), f + g es creciente (decreciente). f) Buscar una función f creciente y una g decreciente tales que f + g sea creciente; y otras para que f + g sea decreciente. g) Si g es creciente y f es creciente (decreciente), g f es creciente (decreciente). h) Si g es decreciente y f es creciente (decreciente), g f es decreciente (creciente). Que ocurrira si la monotonía de g es estricta? Y si lo es la de f? Y si lo son ambas? 8.93 Usar los resultados del ejercicio anterior, para probar lo siguente: a) Probar que f(x) = x + es creciente en (, 0) y decreciente en (0, + ). b) Sabiendo que e x es esctirtamente creciente en IR y que x = e ln x, probar que sh(x) y ln(x) son crecientes. c) Probar que f(x) = x x + es creciente en (0, + ) y usarlo para probar que th(x) es creciente en IR Sea f: IR IR, se dice que f es par si f( x) = f(x), y que es impar si f( x) = f(x). a) Comprobar si sen x, cos x, tg x, sh x, ch x, th x y x n, para n = 0, ±, ±,..., son pares o impares. b) Si f es par y creciente en (0, + ), será también creciente en (, 0)? c) Si f es impar y creciente en (0, + ), será también creciente en (, 0)? d) Que característica especial cumplen las gráficas de las funciones pares? Y las de las funciones impares? Justificar la respuesta 8.95 Para las funciones que aparecen en el 90 anterior, dibujar su gráfica y la de su inversa en los dominios indicados. Si una función f: A B es creciente (decreciente) en A, dirías que su inversa f : B A también es creciente (decreciente) en B? Probarlo en el caso de creer que es cierto, o en el caso de creer que es falso, justificarlo con un ejemplo Sean las funciones f, g y h, funciones reales definidas por: f(x) = x, si x 0, si x > 0 ; g(x) =, si x (, ] x, si x (, 0) 3 x, si x [0, ) ; h(x) = x 3 x, si x + x + x+4, si x + > a) Describir la casuística de f y h mediante la pertenencia de x a intervalos (como la función g ) b) Describir la casuística de g y h mediante desigualdades de x (como la función f ) c) Obtener su dominio y el de las funciones f, g, f +g y f h. d) Hallar las expresiones de f, g, f +g y f h, como funciones definidas a trozos. e) Encontrar el dominio y la expresión de las funciones compuestas f(x ) y g( x). f) Encontrar el dominio y la expresión de las funciones g f y f g.
82 Matemáticas I. Parte III. Cálculo diferencial en IR. I.T.I. en Electricidad. Prof: José Antonio Abia Vian
 8 Matemáticas I Parte III Cálculo diferencial en IR 83 Matemáticas I : Cálculo diferencial en IR Tema 8 Funciones reales de variable real 8. Los números reales Los números reales son de sobra conocidos,
8 Matemáticas I Parte III Cálculo diferencial en IR 83 Matemáticas I : Cálculo diferencial en IR Tema 8 Funciones reales de variable real 8. Los números reales Los números reales son de sobra conocidos,
Funciones, ĺımites y continuidad
 5 Matemáticas : Preliminares Capítulo 3 Funciones, ĺımites y continuidad 3. Funciones reales de variable real 3.. Los números reales Los números reales son de sobra conocidos, sus operaciones básicas así
5 Matemáticas : Preliminares Capítulo 3 Funciones, ĺımites y continuidad 3. Funciones reales de variable real 3.. Los números reales Los números reales son de sobra conocidos, sus operaciones básicas así
25 Fundamentos de Matemáticas. Unidad I. Cálculo diferencial en R
 5 Fundamentos de Matemáticas Unidad I Cálculo diferencial en R Prof: José Antonio Abia Vian Grado de Ing. en Diseño Industrial y Desarrollo de producto : Curso 07 08 6 Fundamentos de Matemáticas : Cálculo
5 Fundamentos de Matemáticas Unidad I Cálculo diferencial en R Prof: José Antonio Abia Vian Grado de Ing. en Diseño Industrial y Desarrollo de producto : Curso 07 08 6 Fundamentos de Matemáticas : Cálculo
83 Matemáticas I. Parte III. Cálculo diferencial en IR. I.T.I. en Electricidad. Prof: José Antonio Abia Vian
 83 Matemáticas I Parte III Cálculo diferencial en IR 84 Matemáticas I : Cálculo diferencial en IR Tema 8 Funciones reales de variable real 8. Los números reales Los números reales son de sobra conocidos,
83 Matemáticas I Parte III Cálculo diferencial en IR 84 Matemáticas I : Cálculo diferencial en IR Tema 8 Funciones reales de variable real 8. Los números reales Los números reales son de sobra conocidos,
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Funciones, Límites y Continuidad
 Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
Tema Funciones, Límites y Continuidad Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real, así como de los límites en dichas
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real
 Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real En la primera parte de este tema vamos a tratar con funciones reales de variable real, esto es, funciones
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.1. Generalidades sobre funciones reales de variable real En la primera parte de este tema vamos a tratar con funciones reales de variable real, esto es, funciones
Fundamentos matemáticos. Tema 4 Funciones de una y varias variables
 Grado en Ingeniería agrícola y del medio rural Tema 4 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 4 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Tema 7: Funciones de una variable. Límites y continuidad.
 Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
Tema 7: Funciones de una variable. Límites y continuidad. José M. Salazar Noviembre de 2016 Tema 7: Funciones de una variable. Límites y continuidad. Lección 8. Funciones de una variable. Límites y continuidad.
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
f : R R Definición 2. Se llama dominio de una función f (lo denotaremos por Dom f) al conjunto de valores para los que está bien definida f(x) :
 Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
Resumen Tema 2: Funciones Concepto de función. Gráficas Definición. Se llama función (real de variable real) a toda aplicación f : R R que a cada número le hace corresponder otro valor f(). f() Definición
FUNCIONES REALES 1º DE BACHILLERATO CURSO
 FUNCIONES REALES 1º DE BACHILLERATO CURSO 2007-2008 Funciones reales Definición Clasificación Igual de funciones Dominio Propiedades Monotonía Extremos relativos Acotación. Extremos absolutos Simetría
FUNCIONES REALES 1º DE BACHILLERATO CURSO 2007-2008 Funciones reales Definición Clasificación Igual de funciones Dominio Propiedades Monotonía Extremos relativos Acotación. Extremos absolutos Simetría
Tema 1. Números reales y funciones reales de variable real. Números complejos. Departamento de Análisis Matemático Universidad de Granada
 Tema 1. Números reales y funciones reales de variable real. Números complejos Departamento de Análisis Matemático Universidad de Granada Números reales Números reales Universidad de Granada Septiembre,
Tema 1. Números reales y funciones reales de variable real. Números complejos Departamento de Análisis Matemático Universidad de Granada Números reales Números reales Universidad de Granada Septiembre,
Contenidos. Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada
 Contenidos Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada Máximo, mínimo Función par o impar Función periódica Función Potencial
Contenidos Concepto de aplicación Dominio e Imagen Igualdad Función Compuesta Función Inversa Crecimiento. Decrecimiento Función Acotada Máximo, mínimo Función par o impar Función periódica Función Potencial
Funciones reales de variable real
 Capítulo 2 Funciones reales de variable real 2.. Definición. Dominio, imagen y gráfica. Informalmente, una función entre dos conjuntos A y B es una regla que a ciertos elementos del conjunto A les asigna
Capítulo 2 Funciones reales de variable real 2.. Definición. Dominio, imagen y gráfica. Informalmente, una función entre dos conjuntos A y B es una regla que a ciertos elementos del conjunto A les asigna
UNIVERSIDAD CARLOS III DE MADRID. Departamento de Matemáticas CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 2010 2011 Elaborado por Elena Romera Índice general
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción En este primer tema del Bloque de Cálculo tendremos como objetivo fundamental el recordar conceptos ya conocidos acerca de las funciones reales de variable
Tema Funciones reales de variable real Introducción En este primer tema del Bloque de Cálculo tendremos como objetivo fundamental el recordar conceptos ya conocidos acerca de las funciones reales de variable
Nociones básicas. Febrero, 2005
 Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Febrero, 2005 Índice general Funciones es de variable Derivación de funciones es de variable Funciones es de variable Derivación de funciones es de variable Conjuntos de números IN Z Q IR C Densidad de
Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad.
 TEMA 1 Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Polinomio de Taylor.
TEMA 1 Objetivos. Conjuntos numéricos. Funciones reales de una variable real. Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Polinomio de Taylor.
Por extensión, también se puede hablar de la preimagen de un conjunto. Si B 0 B, la preimagen de B 0 es
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
1. Nociones básicas. Oct, 2007
 Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2007 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
1 NÚMEROS REALES. Tema 1 Números reales. Curso 2017/ El conjunto R.
 Tema Números reales. Curso 07/8 NÚMEROS REALES El Cálculo Innitesimal centran su trabajo en las funciones y sus propiedades. Pero para poder estudiarlas, previamente es esencial conocer con detalle las
Tema Números reales. Curso 07/8 NÚMEROS REALES El Cálculo Innitesimal centran su trabajo en las funciones y sus propiedades. Pero para poder estudiarlas, previamente es esencial conocer con detalle las
Funciones. A.1 Definiciones. Dominio, rango e imagen A.1.1
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Cálculo:Notas de preliminares
 Cálculo:Notas de preliminares Antonio Garvín Curso 04/05 1 Recordando cosas Recordaremos los conjuntos con los que vamos a trabajar, en especial R y R n. A fin de cuentas el cálculo trata basicamente de
Cálculo:Notas de preliminares Antonio Garvín Curso 04/05 1 Recordando cosas Recordaremos los conjuntos con los que vamos a trabajar, en especial R y R n. A fin de cuentas el cálculo trata basicamente de
El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.
 Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
Concepto de función Función real de variable real es toda correspondencia f que asocia a cada elemento de un determinado subconjunto de números reales, llamado dominio, otro número real (uno y sólo uno).
MATEMÁTICAS II. Apuntes
 MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
MATEMÁTICAS II. Apuntes Curso preparatorio para el acceso a la universidad para mayores de 5 años Tema 1 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas Índice general
f: D IR IR x f(x) v. indep. v. dependiente, imagen de x mediante f, y = f(x). A x se le llama antiimagen de y por f, y se denota por x = f -1 (y).
 TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
TEMA 8: FUNCIONES. 8. Función real de variable real. 8. Dominio de una función. 8.3 Características de una función: signo, monotonía, acotación, simetría y periodicidad. 8.4 Operaciones con funciones:
Cálculo I, GIEAI. Rafael Bravo de la Parra. Curso U. D. Matemáticas, Universidad de Alcalá
 , GIEAI U. D. Matemáticas, Universidad de Alcalá Curso 2014-15 Índice Tema1 Tema2 Tema3 Reales Complejos 1 TEMA 1: Conjuntos de números: operaciones y representación. 2 TEMA 2: Funciones: operaciones y
, GIEAI U. D. Matemáticas, Universidad de Alcalá Curso 2014-15 Índice Tema1 Tema2 Tema3 Reales Complejos 1 TEMA 1: Conjuntos de números: operaciones y representación. 2 TEMA 2: Funciones: operaciones y
1 El número x = 0, es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x.
 El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
1.- CONCEPTO DE FUNCIÓN. DOMINIO Y RECORRIDO
 1.- CONCEPTO DE FUNCIÓN. DOMINIO Y RECORRIDO Definición: Una función es una relación entre dos conjuntos X e Y, que asocia a cada elemento x X un único elemento y Y. Diremos que y es la imagen del elemento
1.- CONCEPTO DE FUNCIÓN. DOMINIO Y RECORRIDO Definición: Una función es una relación entre dos conjuntos X e Y, que asocia a cada elemento x X un único elemento y Y. Diremos que y es la imagen del elemento
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica Esquivel
 Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
Fundamentos de Matemáticas - Grado en Ingeniería Agrícola - Profª. Mónica squivel Tema 1 FUNCION RAL D VARIABL RAL. CONTINUIDAD. DRIVABILIDAD 1.1. Funciones reales de variable real: generalidades I V R
CONTINUIDAD DE FUNCIONES
 CONTINUIDAD CONTINUIDAD DE FUNCIONES CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO Una función f es continua en a si y sólo si se cumplen las tres condiciones siguientes: 1) Existe f(a), es decir, a Dom f. 2)
CONTINUIDAD CONTINUIDAD DE FUNCIONES CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO Una función f es continua en a si y sólo si se cumplen las tres condiciones siguientes: 1) Existe f(a), es decir, a Dom f. 2)
FUNCIONES REALES DE VARIABLE REAL
 FUNCIONES REALES DE VARIABLE REAL Definición. donde D R. Se define función real de variable real a una aplicación f : D R [, [. Ejemplo. Si consideramos f(x) = x entonces el dominio máximo de f es D =
FUNCIONES REALES DE VARIABLE REAL Definición. donde D R. Se define función real de variable real a una aplicación f : D R [, [. Ejemplo. Si consideramos f(x) = x entonces el dominio máximo de f es D =
1. Nociones básicas. Oct, 2008
 Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Cálculo 1. Nociones básicas Oct, 2008 Nociones básicas Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial y logarítmica Funciones
Función Real de variable Real. Definiciones
 Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
Función Real de variable Real Definiciones Función Sean A y B dos conjuntos cualesquiera. Una aplicación de A en B es una relación que asocia a cada elemento (x=variable independiente) de A un único valor
EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable
 EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
Funciones elementales. A.1 Funciones potenciales. A.2 Función exponencial
 Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas
 UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
FUNCIONES POLINÓMICAS
 PRÁCTICAS CON DERIVE 28 NUM.de MATRÍCULA FECHA... APELLIDOS /Nombre...PC PRÁCTICA CUATRO. FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS Dado un entero n 0, la función f(x) =a 0 x n + a 1 x n 1 + a 2 x n
PRÁCTICAS CON DERIVE 28 NUM.de MATRÍCULA FECHA... APELLIDOS /Nombre...PC PRÁCTICA CUATRO. FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS Dado un entero n 0, la función f(x) =a 0 x n + a 1 x n 1 + a 2 x n
2. FUNCIONES CONTINUAS.
 . FUNCIONES CONTINUAS. En este capítulo nos centraremos en el estudio de las funciones continuas. Para ello, necesitamos estudiar el concepto de ite y algunas de sus propiedades..1. Límites de una función.1.1.
. FUNCIONES CONTINUAS. En este capítulo nos centraremos en el estudio de las funciones continuas. Para ello, necesitamos estudiar el concepto de ite y algunas de sus propiedades..1. Límites de una función.1.1.
TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
2009 TEMA 8: FUNCIONES. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 1º E.S.O. TEMA 08: Funciones. TEMA 08: FUNCIONES. 1. Correspondencia.
Función real de variable real, hallar g f y
 1.- Si 3 f() e y g() cos( ) Función real de variable real, hallar g f y f g..- Hallar el dominio de las siguientes funciones: 1 a) f() ln(sen) b) f() 1 c) f() 1 1 3.- Hallar la inversa de las siguientes
1.- Si 3 f() e y g() cos( ) Función real de variable real, hallar g f y f g..- Hallar el dominio de las siguientes funciones: 1 a) f() ln(sen) b) f() 1 c) f() 1 1 3.- Hallar la inversa de las siguientes
RESUMEN DE FUNCIONES. MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I
 RESUMEN DE FUNCIONES. MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1.- INTRODUCCIÓN Definición: Una función real de variable real es una aplicación entre dos subconjuntos de los números reales, de modo
RESUMEN DE FUNCIONES. MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I 1.- INTRODUCCIÓN Definición: Una función real de variable real es una aplicación entre dos subconjuntos de los números reales, de modo
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
Conjuntos numéricos. Sucesiones. Funciones
 Conjuntos numéricos. Sucesiones. Funciones Conjuntos numéricos 1. Pertenece el número real 2.15 al entorno de centro 2.2 y radio 0.1? 2. Representa gráficamente el conjunto de puntos tales que (a) x+6
Conjuntos numéricos. Sucesiones. Funciones Conjuntos numéricos 1. Pertenece el número real 2.15 al entorno de centro 2.2 y radio 0.1? 2. Representa gráficamente el conjunto de puntos tales que (a) x+6
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Funciones de una variable (I)
 Funciones de una variable (I) Sesión teórica 7 5 de octubre de 2010 1 Preliminares 2 Funciones polinómicas y racionales 3 Función exponencial y logarítmica 4 Funciones trigonométricas Función Definición
Funciones de una variable (I) Sesión teórica 7 5 de octubre de 2010 1 Preliminares 2 Funciones polinómicas y racionales 3 Función exponencial y logarítmica 4 Funciones trigonométricas Función Definición
4. Probar que la suma de dos funciones crecientes en su dominio es creciente en su dominio.
 1. Definir función de A en B, conjunto imagen y gráfica de una función. 2. Definir función inyectiva. 3. Probar que una función lineal con pendiente negativa es decreciente. 4. Probar que la suma de dos
1. Definir función de A en B, conjunto imagen y gráfica de una función. 2. Definir función inyectiva. 3. Probar que una función lineal con pendiente negativa es decreciente. 4. Probar que la suma de dos
Tema 6: Límites y continuidad
 Tema 6: Límites y continuidad March 25, 217 Contents 1 *Conceptos relativos a funciones 2 1.1 Dominio de funciones usuales........................................ 2 1.2 Funciones periódicas.............................................
Tema 6: Límites y continuidad March 25, 217 Contents 1 *Conceptos relativos a funciones 2 1.1 Dominio de funciones usuales........................................ 2 1.2 Funciones periódicas.............................................
En este tema vamos a trabajar sobre el conjunto de números reales.
 1. Introducción. 1.1. Subconjuntos de ΙΡ. 1.2. Cotas de subconjuntos. 2. Concepto de función. 3. Operaciones con funciones. 3.1. Suma de funciones. 3.2. Producto de funciones. 3.3. Producto de una función
1. Introducción. 1.1. Subconjuntos de ΙΡ. 1.2. Cotas de subconjuntos. 2. Concepto de función. 3. Operaciones con funciones. 3.1. Suma de funciones. 3.2. Producto de funciones. 3.3. Producto de una función
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites. Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites
 Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
Capítulo 2. Funciones
 Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
Capítulo 1: Números y funciones
 (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Números Primeras clases de números Números reales Operaciones con números reales Ecuaciones e
(Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Números Primeras clases de números Números reales Operaciones con números reales Ecuaciones e
TEMA 0 FUNCIONES ***************
 TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
Tema 1: Repaso de conocimientos previos. Funciones elementales y sus gráficas. Límites. Continuidad.
 Tema 1: Repaso de conocimientos previos.... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Outline Relaciones trigonométricas 1 Relaciones trigonométricas 2 3 4 5 6 Outline Relaciones
Tema 1: Repaso de conocimientos previos.... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Outline Relaciones trigonométricas 1 Relaciones trigonométricas 2 3 4 5 6 Outline Relaciones
Tema 7.0. Repaso de números reales y de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Repaso de números reales y de funciones 47 Tema 70 Repaso de números reales y de funciones El conjunto de los números reales El conjunto de los números
Matemáticas II (Bachillerato de Ciencias) Análisis: Repaso de números reales y de funciones 47 Tema 70 Repaso de números reales y de funciones El conjunto de los números reales El conjunto de los números
FUNCIONES REALES DE VARIABLE REAL
 Pag. 1 FUNCIONES REALES DE VARIABLE REAL 1.- Aplicaciones y Funciones. Definiciones. 2.- Tipos de funciones. 3.-Operaciones con funciones. 4.-Composición de funciones. 5.- Función identidad y funciones
Pag. 1 FUNCIONES REALES DE VARIABLE REAL 1.- Aplicaciones y Funciones. Definiciones. 2.- Tipos de funciones. 3.-Operaciones con funciones. 4.-Composición de funciones. 5.- Función identidad y funciones
E.T.S.I. Industriales y Telecomunicación Curso PRUEBAS DE EVALUACIÓN
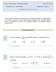 E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones. 1. Estudiar la acotación de las siguientes funciones:
 Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García. UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior
 INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
INGENIERÍAS TÉCNICAS INDUSTRIALES TEORIA DE CÁLCULO I Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento
FUNCIONES REALES DE VARIABLE REAL.
 -CONTENIDOS: FUNCIONES REALES DE VARIABLE REAL. 1.1 Definición y terminología. 1. Funciones conocidas. 1. Operaciones con funciones. 1.4 Funciones recíprocas. 1.5 Funciones monótonas y funciones acotadas.
-CONTENIDOS: FUNCIONES REALES DE VARIABLE REAL. 1.1 Definición y terminología. 1. Funciones conocidas. 1. Operaciones con funciones. 1.4 Funciones recíprocas. 1.5 Funciones monótonas y funciones acotadas.
TEMA 3: Funciones de varias variables: ĺımites y continuidad
 TEMA 3: Funciones de varias variables: ĺımites y continuidad Cálculo Ingeniero de Telecomunicación Cálculo () TEMA 3 Ingeniero de Telecomunicación 1 / 69 1 Funciones Elementales 2 El conjunto R n Estructuras
TEMA 3: Funciones de varias variables: ĺımites y continuidad Cálculo Ingeniero de Telecomunicación Cálculo () TEMA 3 Ingeniero de Telecomunicación 1 / 69 1 Funciones Elementales 2 El conjunto R n Estructuras
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FUNCIONES ELEMENTALES.
 Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
CÁLCULO ELEMENTAL PROBLEMAS. Valor absoluto. Funciones y sus gráficas
 CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN
 UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN 46 OBJETIVOS DIDÁCTICOS En esta unidad aprenderás a:. Analizar si una gráfica es o no función.. Analizar las
UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN 46 OBJETIVOS DIDÁCTICOS En esta unidad aprenderás a:. Analizar si una gráfica es o no función.. Analizar las
Documento 2 : Nuevas funciones a partir de otras
 Unidad 4: Funciones reales de una variable real Temas: Algebra de funciones. Composición de funciones. Funciones inyectivas, sobreyectivas, biyectivas. Función inversa. Capacidades. Manejar conceptos y
Unidad 4: Funciones reales de una variable real Temas: Algebra de funciones. Composición de funciones. Funciones inyectivas, sobreyectivas, biyectivas. Función inversa. Capacidades. Manejar conceptos y
Curso 0: Matemáticas Año académico
 Curso 0: Matemáticas Año académico 2014-2015 Ana García González Miguel Martínez Panero Luis Carlos Meneses Poncio Teresa Peña García UniversidaddeValladolid Departamento de Economía Aplicada 1. Aritmética
Curso 0: Matemáticas Año académico 2014-2015 Ana García González Miguel Martínez Panero Luis Carlos Meneses Poncio Teresa Peña García UniversidaddeValladolid Departamento de Economía Aplicada 1. Aritmética
Por ser un cociente entre dos longitudes, el radián no tiene dimensión. De la definición obtenemos la relación entre radianes y grados:
 E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. f : R R
 TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
f ( x)= Indica el dominio y recorrido de estas funciones: a) f(x)= 2x-1; b) g(x)= 3x²; c) h(x)=1/x
 FUNCIONES REALES DE VARIABLE REAL. CONCEPTO DE FUNCIÓN Una función f del conjunto A en el conjunto B es una relación de dependencia entre dos magnitudes A y B, de tal manera que a cada valor de la primera
FUNCIONES REALES DE VARIABLE REAL. CONCEPTO DE FUNCIÓN Una función f del conjunto A en el conjunto B es una relación de dependencia entre dos magnitudes A y B, de tal manera que a cada valor de la primera
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Conjuntos, números y propiedades básicas. Conjuntos
 Conjuntos, números y propiedades básicas Conjuntos Entenderemos que un CONJUNTO es una colección de objetos. Dichos objetos pueden ser de diferente naturaleza, tanto objetos tangibles como abstracciones
Conjuntos, números y propiedades básicas Conjuntos Entenderemos que un CONJUNTO es una colección de objetos. Dichos objetos pueden ser de diferente naturaleza, tanto objetos tangibles como abstracciones
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1. x = x + 5 si x < 0.
 Matemática Aplicada - Licenciatura de Farmacia - Curso 005/006 - HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1 1) Estudiemos cada caso: x = x+5 a) El único número que verifica la condición es x =
Matemática Aplicada - Licenciatura de Farmacia - Curso 005/006 - HOJA 1 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 1 1) Estudiemos cada caso: x = x+5 a) El único número que verifica la condición es x =
C alculo Septiembre 2010
 Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Cálculo Septiembre 2010 Funciones reales de variable real Conjuntos de números Números complejos Funciones reales de variable real Valor absoluto Funciones polinómicas y racionales Función exponencial
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Funciones Reales de Variable real
 Semana05[1/29] 30 de marzo de 2007 Funciones Definición de funciones Semana05[2/29] Sean A y B dos conjuntos no vacios de naturaleza arbitraria. Una función de A en B es una correspondencia entre los elementos
Semana05[1/29] 30 de marzo de 2007 Funciones Definición de funciones Semana05[2/29] Sean A y B dos conjuntos no vacios de naturaleza arbitraria. Una función de A en B es una correspondencia entre los elementos
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
du = ln u + NOTA: En las integrales 11, 12, 17 y 18 α significa la raíz cuadrada positiva de α 2. Escribimos
 CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
CÁLCULO I CÁLCULO DE PRIMITIVAS: Integrales Inmediatas 3 5 7 9 3 5 7 u m du = um+ + C, m m + du = ln u + C u u du = u + C 4 a u du = au + C, a > 0, a ln a sen u du = cos u + C 6 cos u du = sen u + C cos
x y = x x y = x
 FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
10.1 LAS FUNCIONES DESCRIBEN FENÓMENOS REALES
 TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 LAS FUNCIONES DESCRIBEN FENÓMENOS REALES Las funciones describen fenómenos cotidianos, económicos, psicológicos,
TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 LAS FUNCIONES DESCRIBEN FENÓMENOS REALES Las funciones describen fenómenos cotidianos, económicos, psicológicos,
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
Temas preliminares de Análisis Real
 Temas preliminares de Análisis Real Problemas para examen Usamos la notación A B en el siguiente sentido: A es un subconjunto de B, puede ser que A = B. Propiedades de las operaciones con conjuntos 1.
Temas preliminares de Análisis Real Problemas para examen Usamos la notación A B en el siguiente sentido: A es un subconjunto de B, puede ser que A = B. Propiedades de las operaciones con conjuntos 1.
FUNCIONES. 4º E.S.O. Opción B CONCEPTO DE FUNCIÓN
 CONCEPTO DE FUNCIÓN FUNCIONES 4º E.S.O. Opción B Una función es una relación entre dos magnitudes en la que a cada valor de la primera se le asocia un único valor de la segunda que se llama imagen. La
CONCEPTO DE FUNCIÓN FUNCIONES 4º E.S.O. Opción B Una función es una relación entre dos magnitudes en la que a cada valor de la primera se le asocia un único valor de la segunda que se llama imagen. La
Resumen 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial
 Resumen 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial 1 La recta real R R, el conjunto de los números reales, son los números decimales
Resumen 8: La recta real y el espacio métrico R n. Funciones de una variable: límites, continuidad y cálculo diferencial 1 La recta real R R, el conjunto de los números reales, son los números decimales
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Análisis Matemático I: Numeros Reales y Complejos
 Contents : Numeros Reales y Complejos Universidad de Murcia Curso 2008-2009 Contents 1 Definición axiomática de R Objetivos Definición axiomática de R Objetivos 1 Definir (y entender) R introducido axiomáticamente.
Contents : Numeros Reales y Complejos Universidad de Murcia Curso 2008-2009 Contents 1 Definición axiomática de R Objetivos Definición axiomática de R Objetivos 1 Definir (y entender) R introducido axiomáticamente.
Funciones de Variable Real
 Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Conjuntos. Relaciones. Aplicaciones
 Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
DERIVADAS. TVM (a, b) = = h. La tasa de variación media se puede interpretar como la pendiente de la recta AB de la figura siguiente:
 Tasa de variación media DERIVADAS La tasa de variación media TVM de una unción ( en un intervalo (x, x se deine como: TVM (a, b ( x ( x x x Si consideramos x x + h, podemos expresar la TVM como: Interpretación
Tasa de variación media DERIVADAS La tasa de variación media TVM de una unción ( en un intervalo (x, x se deine como: TVM (a, b ( x ( x x x Si consideramos x x + h, podemos expresar la TVM como: Interpretación
Matemáticas II: Cálculo diferencial
 Matemáticas II: Cálculo diferencial Javier Segura Universidad de Cantabria Javier Segura (Universidad de Cantabria) Matemáticas II: Cálculo diferencial 1 / 22 Tema 1 1. NÚMEROS REALES, SUCESIONES Y SERIES.
Matemáticas II: Cálculo diferencial Javier Segura Universidad de Cantabria Javier Segura (Universidad de Cantabria) Matemáticas II: Cálculo diferencial 1 / 22 Tema 1 1. NÚMEROS REALES, SUCESIONES Y SERIES.
GLOSARIO DE REGLAS DE DERIVACIÓN
 CÁLCULO GLOSARIO DE REGLAS DE DERIVACIÓN RESUMEN 1. Derivadas de funciones elementales o Derivada de una constante o Derivada de una función potencial (monomio) o Derivada de una raíz cuadrada (caso particular
CÁLCULO GLOSARIO DE REGLAS DE DERIVACIÓN RESUMEN 1. Derivadas de funciones elementales o Derivada de una constante o Derivada de una función potencial (monomio) o Derivada de una raíz cuadrada (caso particular
Funciones. Las funciones no tienen una forma única de expresión, y sin embargo, de todas ellas podemos extraer propiedades.
 7 Funciones LECTURA INICIAL Las funciones no tienen una forma única de expresión, y sin embargo, de todas ellas podemos extraer propiedades. G. W. Leibniz Busca en la web El calculo Trabajando por separado
7 Funciones LECTURA INICIAL Las funciones no tienen una forma única de expresión, y sin embargo, de todas ellas podemos extraer propiedades. G. W. Leibniz Busca en la web El calculo Trabajando por separado
