TEMA 3: Funciones de varias variables: ĺımites y continuidad

Transcripción

1 TEMA 3: Funciones de varias variables: ĺımites y continuidad Cálculo Ingeniero de Telecomunicación Cálculo () TEMA 3 Ingeniero de Telecomunicación 1 / 69

2 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 2 / 69

3 Índice 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 3 / 69

4 Función exponencial Dado un número real a > 0, f : R R x a x Propiedades Dom(f ) = R, Im(f ) = f es continua en R. { R + si a 1 1 si a = 1 f es derivable en R, con f (x) = a x ln a. Si a 1, f es creciente. Si 0 < a < 1, f es decreciente. a 0 = 1 a x a y = a x+y a x a y = ax y Cálculo () TEMA 3 Ingeniero de Telecomunicación 4 / 69

5 Función exponencial Dado un número real a > 0, f : R R x a x Cálculo () TEMA 3 Ingeniero de Telecomunicación 4 / 69

6 Función logarítmica Sea a > 0, a 1. Se llama función logarítmica de base a, f (x) = log a (x), a la función inversa de la exponencial a x. a log a (x) = x log a (a x ) = x Si a = e, hablamos del logaritmo neperiano, denotado ln x. Propiedades Dom(f ) = R +, Im(f ) = R f es continua en R +. f es derivable, con f (x) = 1 x ln a. Si a 1, f es creciente. Si 0 < a < 1, f es decreciente. log a (1) = 0. log a (xy) = log a (x) + log a (y), x, y, R +. log a (x y ) = y log a (x), x, y, R +. log a ( x y ) = log a(x) log a (y), x, y, R + ; 0. Cálculo () TEMA 3 Ingeniero de Telecomunicación 5 / 69

7 Función logarítmica Sea a > 0, a 1. Se llama función logarítmica de base a, f (x) = log a (x), a la función inversa de la exponencial a x. a log a (x) = x log a (a x ) = x Si a = e, hablamos del logaritmo neperiano, denotado ln x. Cálculo () TEMA 3 Ingeniero de Telecomunicación 5 / 69

8 Función seno f : R [ 1, 1] x sin x Propiedades Dom(f ) = R, Im(f ) = [ 1, 1]. sin x es continua en R. sin x es derivable, con f (x) = cos x. sin x es una función impar. sin(x + 2π) = sin x. Cálculo () TEMA 3 Ingeniero de Telecomunicación 6 / 69

9 Función coseno f : R [ 1, 1] x cos x Propiedades Dom(f ) = R, Im(f ) = [ 1, 1]. cos x es continua en R. cos x es derivable, con f (x) = sin x. cos x es una función par. cos(x + 2π) = cos x. Cálculo () TEMA 3 Ingeniero de Telecomunicación 7 / 69

10 Función tangente f : R R x tan x = sin x cos x Propiedades Dom(f ) = R { π 2 +kπ, k Z}, Im(f ) = R. tan x es continua en su dominio. tan x es derivable, con f (x) = 1 cos 2 x. tan x es una función impar. tan(x + π) = tan x. Cálculo () TEMA 3 Ingeniero de Telecomunicación 8 / 69

11 Función cosecante Propiedades Dom(f ) = R {kπ, k Z}, Im(f ) =], 1] [1, + [. cosec x es continua en su dominio. cosec x es derivable, con f (x) = cosec x cot x. cosec x es una función impar. cosec(x + 2π) = cosec x. f : R R x cosec x = 1 sin x Cálculo () TEMA 3 Ingeniero de Telecomunicación 9 / 69

12 Función secante Propiedades Dom(f ) = R { π 2 +kπ, k Z}, Im(f ) =], 1] [1, + [. sec x es continua en su dominio. sec x es derivable, con f (x) = sec x tan x. sec x es una función par. sec(x + 2π) = sec x. f : R R x sec x = 1 cos x Cálculo () TEMA 3 Ingeniero de Telecomunicación 10 / 69

13 Función cotangente Propiedades Dom(f ) = R {kπ, k Z}, Im(f ) = R. cot x es continua en su dominio. cot x es derivable, con f (x) = cosec 2 x. cot x es una función impar. cot(x + π) = cot x. f : R R x cot x = cos x sin x Cálculo () TEMA 3 Ingeniero de Telecomunicación 11 / 69

14 Función arcoseno Para cada x [ 1, 1], se define arcsin x como el único y [ π 2, π 2 ] tal que sin(y) = x. arcsin(sin x) = x sin(arcsin x) = x Propiedades Dom(f ) = [ 1, 1], Im(f ) = [ π 2, π 2 ]. arcsin x es continua en [ 1, 1]. arcsin x es derivable, con f 1 (x) =. 1 x 2 arcsin x es una función impar. Cálculo () TEMA 3 Ingeniero de Telecomunicación 12 / 69

15 Función arcocoseno Para cada x [ 1, 1], se define arccos x como el único y [0, π] tal que cos(y) = x. arccos(cos x) = x cos(arccos x) = x Propiedades Dom(f ) = [ 1, 1], Im(f ) = [ π, π]. arccos x es continua en [ 1, 1]. arccos x es derivable, con f (x) = 1 1 x 2. arccos x es una función par. Cálculo () TEMA 3 Ingeniero de Telecomunicación 13 / 69

16 Función arcotangente Para cada x R, se define arctan x como el único y ] π 2, π 2 [ tal que tan(y) = x. arctan(tan x) = x tan(arctan x) = x Propiedades Dom(f ) = R, Im(f ) =] π 2, π 2 [. arctan x es continua en R. arctan x es derivable, con f (x) = x 2. arctan x es una función impar. Cálculo () TEMA 3 Ingeniero de Telecomunicación 14 / 69

17 Relaciones trigonométricas 1 sin 2 x + cos 2 x = 1. 2 sin(x + y) = sin x cos y + cos x sin y; sin(2x) = 2 sin x cos x. 3 cos(x + y) = cos x cos y sin x sin y; cos(2x) = cos 2 x sin 2 x. 4 tan(x + y) = 5 sin 2 x = 1 cos(2x) 2. 6 cos 2 x = 1+cos(2x) 2. 7 sec 2 x = 1 + tan 2 x. tan x+tan y 1 tan x tan y. Cálculo () TEMA 3 Ingeniero de Telecomunicación 15 / 69

18 Índice 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 16 / 69

19 El conjunto R n Definición El conjunto R n es el producto cartesiano R n = R R R, es decir R n = {(x 1, x 2,..., x n ) x j R, para j = 1, 2,..., n} El conjunto R n con las operaciones usuales de suma y producto por escalares, es decir: x + y = (x 1 + y 1, x 2 + y 2,..., x n + y n ) λ x = (λx 1, λx 2,..., λx n x n ) siendo x = (x 1, x 2,..., x n ), y = (y 1, y 2,..., y n ) y λ R, tiene estructura de espacio vectorial, cuya dimensión es n. Cálculo () TEMA 3 Ingeniero de Telecomunicación 17 / 69

20 Distancia eucĺıdea Norma de un vector Si se define el producto escalar ordinario como x y = x 1 y 1 + x 2 y x n y n R n tiene estructura de espacio eucĺıdeo, pudiéndose definir la norma de un vector como x = x x = x1 2 + x x n 2 Definición La distancia eucĺıdea entre dos vectores x = (x 1, x 2,..., x n ) y y = (y 1, y 2,..., y n ) se define como d( x, y) = x y = (x 1 y 1 ) 2 + (x 2 y 2 ) (x n y n ) 2 Cálculo () TEMA 3 Ingeniero de Telecomunicación 18 / 69

21 Topología en R n Bola con centro a y radio r Dado el vector a de R n, la bola con centro a y radio r es el conjunto B r (a) = { x R n d( x, a) = x a < r} Ejemplo La bola de R 2 con centro el vector a = (a 1, a 2 ) y radio r es precisamente el conjunto de los puntos interiores a la circunferencia con centro a y radio r. B r ( a) = {(x 1, x 2) R 2 (x 1 a 1) 2 + (x 2 a 2) 2 < r} = {(x 1, x 2) R 2 (x 1 a 1) 2 + (x 2 a 2) 2 < r 2 } Cálculo () TEMA 3 Ingeniero de Telecomunicación 19 / 69

22 Topología en R n Punto interior y conjunto abierto Un punto x = (x 1,..., x n ) R n se dice que es un punto interior del conjunto A (x int(a)) si existe una bola con centro x totalmente contenida en A, es decir, x punto interior de A si B r (x) A Ejemplo Se dice que el conjunto A es abierto si todos sus puntos son interiores. El conjunto A = {(x, y) R 2 (x 1) 2 + (y + 1) 2 < ( 1 2 )2 } es abierto. El conjunto B = {(x, y) R 2 x 2 + y } no es abierto. Cálculo () TEMA 3 Ingeniero de Telecomunicación 20 / 69

23 Topología en R n Punto frontera Nota Un punto x = (x 1,..., x n ) R n se dice que es un punto frontera del conjunto A (x Fr(A)) si toda bola con centro x contiene puntos de A y puntos no pertenecientes a A. El conjunto frontera de A está formado por todos los puntos frontera de A. Un punto frontera de A no pertenece necesariamente a A. Ejemplo Siendo A y B los conjuntos del ejemplo anterior, Fr(A) = {(x, y) R 2 (x 1) 2 +(y+1) 2 = ( 1 2 )2 } Fr(B) = {(x, y) R 2 x 2 + y 2 = 1 3 }. Cálculo () TEMA 3 Ingeniero de Telecomunicación 21 / 69

24 Topología en R n Conjunto cerrado Se dice que el conjunto A es cerrado si contiene a todos sus puntos frontera. Ejemplo En muchos de los problemas de optimización, los dominios estarán definidos por una o más desigualdades. Por ejemplo, si p, q y m son parámetros positivos, el conjunto de los puntos (x, y) que verifican las desigualdades es cerrado. px + qy m, x 0, y 0 Cálculo () TEMA 3 Ingeniero de Telecomunicación 22 / 69

25 Topología en R n Conjunto cerrado Se dice que el conjunto A es cerrado si contiene a todos sus puntos frontera. Importante En general, si g(x) = g(x 1,,..., x n ) es una función continua de n variables y c es un número real, los tres conjuntos {x R n g(x) c} {x R n g(x) c} {x R n g(x) = c} son cerrados. Si sustituimos por > ó por <, los conjuntos correspondientes son abiertos. Ejemplo El conjunto C = {(x, y) 2x 3y 12} es cerrado. El conjunto D = {(x, y) 2x 3y < 12} es abierto. Cálculo () TEMA 3 Ingeniero de Telecomunicación 23 / 69

26 Topología en R n Conjunto acotado Se dice que el conjunto A es acotado si existe una bola que lo contenga. Ejemplo El conjunto {(x, y) 4 < x 2 + y 2 9} es acotado. Cálculo () TEMA 3 Ingeniero de Telecomunicación 24 / 69

27 Topología en R n Conjunto acotado Se dice que el conjunto A es acotado si existe una bola que lo contenga. Ejemplo El conjunto {(x, y) 4 < x 2 + y 2 } no es acotado. Cálculo () TEMA 3 Ingeniero de Telecomunicación 24 / 69

28 Topología en R n Conjunto compacto Se dice que el conjunto A es compacto si es cerrado y acotado. Ejemplo El conjunto {(x, y) 4 < x 2 + y 2 9} no es compacto, pues es acotado pero no cerrado. Sin embargo, el conjunto {(x, y) 4 x 2 + y 2 9} sí es compacto. Cálculo () TEMA 3 Ingeniero de Telecomunicación 25 / 69

29 Topología en R n Conjunto compacto Se dice que el conjunto A es compacto si es cerrado y acotado. Ejemplo El conjunto {(x, y) 4 x 2 + y 2 } no es compacto, pues es cerrado pero no acotado. Cálculo () TEMA 3 Ingeniero de Telecomunicación 25 / 69

30 Coordenadas en R 2 Coordenadas en R 2 Coordenadas cartesianas: Un punto P tiene como coordenadas cartesianas (x, y), siendo x la abcisa e y la ordenada del punto P. Coordenadas polares: Un punto P tiene como coordenadas polares (ρ, θ), siendo ρ es la distancia del punto P al origen, es decir ρ = x 2 + y 2. θ [0, 2π[ es el ángulo que forma el vector OP con el semieje positivo de las x. Cálculo () TEMA 3 Ingeniero de Telecomunicación 26 / 69

31 Coordenadas en R 2 C.cartesianas C.polares Dado un punto (x, y) en coordenadas cartesianas, obtenemos (r, θ) como C.polares C.cartesianas Dado un punto (r, θ) en coordenadas cartesianas, obtenemos (x, y) como ρ = x 2 + y 2 θ = arctan y x x = ρ cos θ y = ρ sin θ Cálculo () TEMA 3 Ingeniero de Telecomunicación 27 / 69

32 Coordenadas en R 2 C.cartesianas C.polares Dado un punto (x, y) en coordenadas cartesianas, obtenemos (r, θ) como C.polares C.cartesianas Dado un punto (r, θ) en coordenadas cartesianas, obtenemos (x, y) como ρ = x 2 + y 2 θ = arctan y x x = ρ cos θ y = ρ sin θ Ejemplos El punto de R 2 cuyas coordenadas cartesianas son ( 2, 2) tiene como expresión en coordenadas polares (2, π 4 ). La circunferencia de radio 1 y centrada en el origen, x 2 + y 2 = 1, viene expresada como ρ = 1 en coordenadas polares. Cálculo () TEMA 3 Ingeniero de Telecomunicación 27 / 69

33 Coordenadas en R 3 Coordenadas cartesianas en R 3 Un punto P tiene como coordenadas cartesianas (x, y, z). Cálculo () TEMA 3 Ingeniero de Telecomunicación 28 / 69

34 Coordenadas en R 3 Coordenadas ciĺındricas en R 3 Un punto P tiene como coordenadas ciĺındricas (ρ, θ, z), siendo (ρ, θ) las coordenadas polares del punto Q proyección de P sobre el plano OXY. Cálculo () TEMA 3 Ingeniero de Telecomunicación 29 / 69

35 Coordenadas en R 3 C.cartesianas C.ciĺındricas Dado un punto (x, y, z) en c.cartesianas, obtenemos (ρ, θ, z) como C.ciĺındricas C.cartesianas Dado un punto (ρ, θ, z) en coordenadas ciĺındricas, obtenemos (x, y, z) como ρ = x 2 + y 2 θ = arctan y x z = z x = ρ cos θ y = ρ sin θ z = z Cálculo () TEMA 3 Ingeniero de Telecomunicación 30 / 69

36 Coordenadas en R 3 C.cartesianas C.ciĺındricas Dado un punto (x, y, z) en c.cartesianas, obtenemos (ρ, θ, z) como C.ciĺındricas C.cartesianas Dado un punto (ρ, θ, z) en coordenadas ciĺındricas, obtenemos (x, y, z) como ρ = x 2 + y 2 θ = arctan y x z = z x = ρ cos θ y = ρ sin θ z = z Ejemplos El punto de R 3 cuyas coordenadas cartesianas son ( 3, 3, 3) tiene como expresión en coordenadas ciĺındricas ( 6, π 4, 3). El cilindro de radio 1 con eje el eje z, x 2 + y 2 = 1, viene expresado como ρ = 1 en coordenadas ciĺındricas. Cálculo () TEMA 3 Ingeniero de Telecomunicación 30 / 69

37 Coordenadas en R 3 Coordenadas esféricas en R 3 Un punto P tiene como coordenadas ciĺındricas (ρ, θ, ϕ), donde ρ 0, 0 θ < 2π y 0 ϕ < π, siendo: ρ el módulo del vector OP, es decir, ρ es la distancia del punto P al origen. OQ con el semieje positivo de OX, θ es el ángulo formado por el vector siendo Q el punto proyección de P sobre el plano OXY. ϕ es el ángulo formado por OP y el eje OZ. Cálculo () TEMA 3 Ingeniero de Telecomunicación 31 / 69

38 Coordenadas en R 3 C.cartesianas C.esféricas Dado un punto (x, y, z) en coordenadas cartesianas, obtenemos (ρ, θ, ϕ) como ρ = x 2 + y 2 + z 2 θ = arctan y x ϕ = arccos z x 2 + y 2 + z 2 C.esféricas C.cartesianas Dado un punto (ρ, θ, ϕ) en coordenadas esféricas, obtenemos (x, y, z) como x = ρ cos θ sin ϕ y = ρ sin θ sin ϕ z = ρ cos ϕ Cálculo () TEMA 3 Ingeniero de Telecomunicación 32 / 69

39 Coordenadas en R 3 Ejemplos El punto (3, π 4, π 4 ) en coordenadas esféricas tiene como coordenadas cartesianas ( 3 2, 3 2, ). La esfera de radio 1 centrada en el origen, x 2 + y 2 + z 2 = 1, viene expresado como ρ = 1 en coordenadas esféricas. Cálculo () TEMA 3 Ingeniero de Telecomunicación 33 / 69

40 Índice 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 34 / 69

41 Funciones de varias variables Definición Una función f : A R n R m es una aplicación que a cada punto x A R n le hace corresponder y R m f (x 1, x 2,..., x n ) = (y 1, y 2,..., y m ) R m Cálculo () TEMA 3 Ingeniero de Telecomunicación 35 / 69

42 Funciones de varias variables Definición Una función f : A R n R m es una aplicación que a cada punto x A R n le hace corresponder y R m f (x 1, x 2,..., x n ) = (y 1, y 2,..., y m ) R m Ejemplo Si expresamos el área de un triángulo en función de la base y de la altura, tendremos una función de dos variables: A = 1 2bh = A = f (b, h) Cálculo () TEMA 3 Ingeniero de Telecomunicación 35 / 69

43 Funciones de varias variables Definición Una función f : A R n R m es una aplicación que a cada punto x A R n le hace corresponder y R m f (x 1, x 2,..., x n ) = (y 1, y 2,..., y m ) R m Si m = 1, se denomina función escalar y si m > 1, función vectorial. Cálculo () TEMA 3 Ingeniero de Telecomunicación 35 / 69

44 Dominio e Imagen Definición Dada f : R n R m, se define su dominio como Ejemplos Dom(f ) = {(x 1, x 2,..., x n ) R n f (x 1, x 2,..., x n ) R m } Si f (x, y) = x + y, entonces Dom(f ) = {(x, y) R 2 x + y 0} y Si g(x, y) = (sin(xy), x 2 + y 2, entonces Dom(g) = R2 {(0, 0)} e x 2 +8 Si h(x, y) = ln(x + y 1), entonces Dom(h) = {(x, y) R 2 x + y 1 > 0, x + y 2}. Si l(x, y) = (x, log y, arcsin x), entonces Dom(l) = {(x, y) R 2 y > 0} {(x, y) R 2 x 1}. Cálculo () TEMA 3 Ingeniero de Telecomunicación 36 / 69

45 Dominio e Imagen Definición Sea f : R n R m. La imagen de f se define por Im(f ) = {(y 1, y 2,..., y m) R m (x 1, x 2,..., x n) R n con f (x 1, x 2,..., x n) = (y 1, y 2,..., y m Ejemplos Si f (x, y) = x + y, entonces Im(f ) = [0, + [ Si g(x, y) = ln(xy), entonces Im(g) = R Si h(x, y) = sin(x + y), entonces Im(h) = [ 1, 1]. Si h(x, y) = (ln(x + y 1), e xy, sin(x y), 2x 1 x y ), entonces Dom(h) = Cálculo () TEMA 3 Ingeniero de Telecomunicación 37 / 69

46 Función compuesta y función inversa Definición Sean f : R n R m y g : R m R p. Si Im(f ) Dom(g), se define la función compuesta (g f ) : R n R p como R n f R m g R p (g f )(x) = g(f (x)) Ejemplos Sean f : R 2 R 3 definida por f (x, y) = (x + y, x y, x 2 ) g : R 3 R definida por g(x, y, z) = x 2 + y 2 + z 2 Entonces, (g f )(x) = (x + y) 2 + (x y) 2 + x 4 Cálculo () TEMA 3 Ingeniero de Telecomunicación 38 / 69

47 Función compuesta y función inversa. Función acotada Definición Sea f : R n R m. Si f es inyectiva, se puede definir la función inversa f 1 : Im(f ) R m R n de modo que, (f 1 f )(x) = f 1 (f (x)) = x x Dom(f ) Ejemplos Sea f : R 2 R definida por f (x, y) = e x+y. Entonces, f 1 (z) = ln z Si g : R R está definida por g(x) = sin x, entonces g 1 (x) = arcsin x Si h : R R está definida por h(x) = cos x, entonces h 1 (x) = arccos x Cálculo () TEMA 3 Ingeniero de Telecomunicación 39 / 69

48 Función acotada Definición Sea f : A R n R. f está acotada en A si M R tal que f (x) M x A, o equivalentemente, Im(f ) es un subconjunto acotado de R. Ejemplos Sea f : R 2 R definida por f (x, y) = sin 2 (x + y) cos(x e y ). Entonces, f está acotada, pues f (x, y) 1 (x, y) R 2. Si g : R 3 R está definida por g(x, y, z) = e x+y + z, entonces g no está acotada. Cálculo () TEMA 3 Ingeniero de Telecomunicación 40 / 69

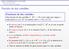
49 Curvas de nivel Funciones escalares Para representar funciones escalares f : R n R, necesitamos n+1 dimensiones. Por ello, analizaremos principalmente funciones f : R 2 R. Dada una función f : R 2 R, el conjunto de puntos de la forma (x, y, z) con z = f (x, y) (grafo de una función), es una superficie en R 3 que denominaremos representación gráfica de f. Definición Curvas de nivel Dada la función f : A R 2 R y una constante c, la curva de nivel c de la superficie z = f (x, y) es el conjunto T c = {(x, y) A : f (x, y) = c} Cálculo () TEMA 3 Ingeniero de Telecomunicación 41 / 69

50 Curvas de nivel Cálculo () TEMA 3 Ingeniero de Telecomunicación 42 / 69

51 Índice 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 43 / 69

52 Límite de una función de dos variables Definición Sea f : R 2 R. Entonces, lim f (x, y) = L (x,y) (a,b) si y sólo si para cada ɛ > 0 existe un correspondiente δ > 0 tal que f (x, y) L < ɛ, siempre que 0 < (x a) 2 + (y b) 2 < δ Cálculo () TEMA 3 Ingeniero de Telecomunicación 44 / 69

53 Límite de una función de dos variables Significado El ĺımite de una función en un punto P = (a, b) es L si los valores que toma la función en los alrededores de P = (a, b) están tan cerca de L como queramos. Es importante tener en cuenta que el valor que la función tome en P no interesa a la hora de calcular el ĺımite. Cálculo () TEMA 3 Ingeniero de Telecomunicación 45 / 69

54 Límite de una función de dos variables El estudio de los ĺımites de funciones de dos variables es mucho más complejo que el de funciones de una variable, pues en éste únicamente se tienen dos caminos para acercarse a un punto, por la derecha o por la izquierda. Sin embargo, en el caso de dos variables, existe una infinidad de caminos para acercarnos al punto (a, b), como muestra la siguiente figura. Cálculo () TEMA 3 Ingeniero de Telecomunicación 46 / 69

55 Propiedades Sean f : R n R, g : R n R tales que los ĺımites lim f (x) y lim g(x) existen y x x0 x x0 valen L y M, respectivamente. Entonces: 1 lim x x0 (f + g)(x) existe y vale L + M. 2 lim λf (x) existe y vale λl, λ R. x x0 f (x) 3 lim f (x) existe y vale L. lim x x0 x x0 g(x) existe y vale L M 4 lim f (x) = L. x x lim (f g)(x) exixste y vale L M. x x0 6 lim x x0 f (x) = 0 lim x x0 f (x) = 0, si M 0. Cálculo () TEMA 3 Ingeniero de Telecomunicación 47 / 69

56 Límites iterados o reiterados Definición Dada una función f : R 2 R, los ĺımites iterados de f en (a, b) se definen, si existen, como ( ) ( ) lim lim f (x, y) = L 1 y lim lim f (x, y) = L 2 x a y b y b x a ( ) Para calcular el ĺımite iterado lim lim f (x, y) = L 2, en primer lugar fijamos la y b x a variable y, y hacemos que la variable x se aproxime al punto a. Al hacer este ĺımite, obtenemos una función de una variable, que depende únicamente de y. Calculamos entonces el ĺımite de dicha función cuando y se acerca a b. Cálculo () TEMA 3 Ingeniero de Telecomunicación 48 / 69

57 Límites iterados o reiterados Definición Dada una función f : R 2 R, los ĺımites iterados de f en (a, b) se definen, si existen, como ( ) ( ) lim lim f (x, y) = L 1 y lim lim f (x, y) = L 2 x a y b y b x a Ejemplos Los ĺımites reiterados de f (x, y) = xy en (1, 2) son: x + y ( ) xy 2x lim lim = lim x 1 y 2 x + y x 1 x + 2 = 2 3 ( lim lim y 2 x 1 ) xy = lim x + y y 2 y 1 + y = 2 3 Cálculo () TEMA 3 Ingeniero de Telecomunicación 48 / 69

58 Límites iterados o reiterados Definición Dada una función f : R 2 R, los ĺımites iterados de f en (a, b) se definen, si existen, como ( ) ( ) lim lim f (x, y) = L 1 y lim lim f (x, y) = L 2 x a y b y b x a Ejemplos Los ĺımites reiterados de f (x, y) = x 2 + y 3 ( lim lim x 0 y 0 x 2 en (0, 0) son: + y 2 ) x 2 + y 3 x 2 + y 2 = lim x 0 1 = 1 ( x 2 + y 3 ) lim lim y 0 x 0 x 2 + y 2 = lim y = 0 y 0 Cálculo () TEMA 3 Ingeniero de Telecomunicación 48 / 69

59 Límites iterados o reiterados Nota Sea f : R 2 R. Si existe el ĺımite doble ĺımites reiterados, lim x a ( ) lim f (x, y) = L 1 y lim y b lim f (x, y) = L, y existen los (x,y) (a,b) y b ( ) lim f (x, y) = L 2 x a entonces los tres ĺımites deben ser iguales, es decir, L = L 1 = L 2. Importante Aunque f : R 2 R tenga los ĺımites iterados iguales ( ) lim lim f (x, y) = L 1 = L 2 = lim x a y b eso no significa que exista lim f (x, y). (x,y) (a,b) y b ( ) lim f (x, y) x a Cálculo () TEMA 3 Ingeniero de Telecomunicación 49 / 69

60 Límites iterados o reiterados Importante Si f : R 2 R verifica que lim x a ( lim f (x, y) y b entonces no existe el ĺımite doble ) = L 1 L 2 = lim y b ( lim f (x, y). (x,y) (a,b) ) lim f (x, y) x a Ejemplo Como los ĺımites reiterados de son distintos, f (x, y) = x + y x y lim (x,y) (0,0) x + y x y Cálculo () TEMA 3 Ingeniero de Telecomunicación 50 / 69

61 Límites iterados o reiterados Importante Si f : R 2 R verifica que lim x a ( lim f (x, y) y b entonces no existe el ĺımite doble ) = L 1 L 2 = lim y b ( lim f (x, y). (x,y) (a,b) ) lim f (x, y) x a Ejemplos Como los ĺımites reiterados de f (x, y) = x 2 + y 3 ( lim lim x 0 y 0 tenemos que no existe x 2 + y 2 ) x 2 + y 3 = lim 1 = 1 lim x 2 + y 2 x 0 y 0 x 2 + y 3 lim (x,y) (0,0) x 2 + y. 2 en (0, 0) son distintos, ( lim x 0 ) x 2 + y 3 = lim y = 0 x 2 + y 2 y 0 Cálculo () TEMA 3 Ingeniero de Telecomunicación 51 / 69

62 Límites iterados o reiterados Importante Si f : R 2 R verifica que lim x a ( lim f (x, y) y b entonces no existe el ĺımite doble ) = L 1 L 2 = lim y b ( lim f (x, y). (x,y) (a,b) ) lim f (x, y) x a Ejemplos Como los ĺımites reiterados de f (x, y) = x y en (0, 0) son distintos, x + y ( ) ( ) x y x y lim lim = lim 1 = 1 lim lim = lim 1 = 1 x 0 y 0 x + y x 0 y 0 x 0 x + y y 0 tenemos que no existe x y lim (x,y) (0,0) x + y. Cálculo () TEMA 3 Ingeniero de Telecomunicación 51 / 69

63 Límites direccionales Teorema Sea f : R 2 R. Si lim f (x, y) = L, entonces para toda función continua (x,y) (x 0,y 0) y = g(x) tal que g(x 0 ) = y 0, se tiene: lim (x, y) (x 0, y 0 ) y = g(x) f (x, y) = lim x x0 f (x, g(x)) = L Similarmente, para toda función continua x = h(y) tal que h(y 0 ) = x 0, se tiene: lim (x, y) (x 0, y 0 ) x = h(y) f (x, y) = lim y y0 f (h(y), y) = L Cálculo () TEMA 3 Ingeniero de Telecomunicación 52 / 69

64 Límites direccionales Ejemplos xy Vamos a probar que el ĺımite lim (x,y) (0,0) x 2 no existe. + y 2 Si nos acercamos al origen a través de la recta y = mx, obtenemos que lim (x, y) (0, 0) y = mx xy x 2 + y 2 = lim x 0 mx 2 x 2 + (mx) 2 = m 1 + m 2 Como el ĺımite a través de la recta y = mx, depende de la pendiente de ésta, tenemos que xy lim (x,y) (0,0) x 2 + y 2 Cálculo () TEMA 3 Ingeniero de Telecomunicación 53 / 69

65 Teorema del Sandwich o de compresión Teorema Sean f, g, h : A R n R y a R n, verificando g(x) f (x) h(x) x A y lim x a g(x) = lim x a h(x) = L. Entonces, lim f (x) = L x a Cálculo () TEMA 3 Ingeniero de Telecomunicación 54 / 69

66 Teorema del Sandwich o de compresión Ejemplo Estudiar la existencia del ĺımite en el origen para la función f (x, y) = x 2 y x 2 + y 2 Como entonces: x = x 2 x 2 + y 2 y = y 2 x 2 + y 2 Ahora bien, como Sandwich: f (x, y) = x 2 y x 2 + y 2 (x 2 + y 2 ) x 2 + y 2 x 2 + y 2 = x 2 + y 2 lim x 2 + y 2 = 0, entonces, aplicando el Teorema del (x,y) (0,0) lim (x,y) (0,0) x 2 y x 2 + y 2 = 0 Cálculo () TEMA 3 Ingeniero de Telecomunicación 55 / 69

67 Teorema del Sandwich o de compresión Corolario Sean f, g : A R n R y a R n, verificando f (x) acotada y lim x a g(x) = 0 Entonces, lim f (x)g(x) = 0 x a Ejemplos 1 lim xy sin( ) = 0, ya que (x,y) (0,0) xy 1 sin( 1 xy ) 1 y lim xy = 0 (x,y) (0,0) Cálculo () TEMA 3 Ingeniero de Telecomunicación 56 / 69

68 Teorema del Sandwich o de compresión Corolario Sean f, g : A R n R y a R n, verificando f (x) acotada y lim x a g(x) = 0 Entonces, lim f (x)g(x) = 0 x a Ejemplos lim (x,y) (0,0) x 2 y x 2 + y 2 cos(x y 2 ) = 0, ya que 1 cos(x y 2 x 2 y ) 1 y lim (x,y) (0,0) x 2 + y = 0 2 Cálculo () TEMA 3 Ingeniero de Telecomunicación 56 / 69

69 Infinitésimos equivalentes Definición Sea f : R n R. Diremos que f (x) es un infinitésimo en a R n si Definición lim f (x) = 0 x a Sean f, g : R n R infinitésimos en a. Diremos que f (x) es de orden superior, f (x) igual o inferior a g en x = a si lim = l con l = 0, l R {0} ó, x a g(x) respectivamente. Cálculo () TEMA 3 Ingeniero de Telecomunicación 57 / 69

70 Infinitésimos equivalentes Definición Sean f, g : R n R infinitésimos en a. Diremos que f (x) y g(x) son infinitésimos f (x) equivalentes en a si lim = 1. En este caso, escribiremos f (x) g(x) si x a g(x) x a. Tabla de infinitésimos equivalentes Si ɛ(x) es un infinitésimo en a (es decir, lim x a ɛ(x) = 0, entonces: ɛ(x) sin ɛ(x) tan ɛ(x) ɛ(x) arcsin ɛ(x) arctan ɛ(x) ln(1 + ɛ(x)) ɛ(x) 1 cos(ɛ(x)) 1 2 (ɛ(x))2 (1 + ɛ(x)) p 1 pɛ(x) a ɛ(x) 1 ɛ(x) ln a Cálculo () TEMA 3 Ingeniero de Telecomunicación 58 / 69

71 Princinpio de sustitución Principio de sustitución Sean f, g : R n R infinitésimos en a y ψ : R R. Entonces Ejemplos lim (x,y) (0,0) lim ψ(x)f (x) = lim ψ(x)g(x) x a x a ψ(x) lim x a f (x) = lim ψ(x) x a g(x) sin 2 (xy) 1 cos(x) = lim (xy) 2 (x,y) (0,0) 1 ln(1 + (x y)) lim (x,y) (1,1) tan(x y) lim (x,y) (2,1) = lim (x,y) (1,1) x 2y (1 + (x 2y)) 3 1 = lim (x,y) (2,1) 2 x = lim y 2 = 0 2 (x,y) (0,0) x y x y = 1 x 2y 3(x 2y) = 1 3 Cálculo () TEMA 3 Ingeniero de Telecomunicación 59 / 69

72 Cambio a coordenadas polares Teorema lim f (x, y) = L si y sólo si exixte una función G(ρ) 0 tal que (x,y) (0,0) G(ρ) = 0 y de forma que: lim ρ 0 Importante f (ρ cos θ, ρ sin θ) L G(ρ) Si lim f (ρ sin θ, ρ cos θ) = L depende del ángulo θ, entonces el ĺımite doble ρ 0 f (x, y) no existe. lim (x,y) (0,0) El cambio a coordenadas polares se emplea únicamente cuando calculamos ĺımites para (x, y) (0, 0). Cálculo () TEMA 3 Ingeniero de Telecomunicación 60 / 69

73 Cambio a coordenadas polares Ejemplos x 2 y x 2 + y 2 = 0 Pasando a coordenadas polares: lim (x,y) (0,0) lim ρ 0 lim (x,y) (0,0) (ρ cos θ) 2 (ρ sin θ) (ρ cos θ) 2 + (ρ sin θ) 2 = lim ρ 3 cos 2 θ sin θ ρ 0 ρ 2 = lim ρ cos 2 θ sin θ = 0 ρ 0 xy x 2 no existe. + y 2 Pasando a coordenadas polares: lim ρ 0 (ρ cos θ)(ρ sin θ) (ρ cos θ) 2 + (ρ sin θ) 2 = lim ρ 2 cos θ sin θ ρ 0 ρ 2 = lim cos θ sin θ = cos θ sin θ ρ 0 EL LÍMITE DEPENDE DEL ÁNGULO!!, luego no existe el ĺımite doble Cálculo () TEMA 3 Ingeniero de Telecomunicación 61 / 69

74 Caracterización sucesional del ĺımite Teorema Sea f : A R n R. Entonces, son equivalentes: lim f (x) = L x a Para cualquier sucesión {x n } n N A {a} convergente a a, se tiene que la sucesión {f (x n )} converge a L. Ejemplo Demostrar que lim x 0 sin( 1 x ) En efecto, consideremos las siguientes sucesiones convergentes a 0: {x n} n N = { 1 nπ } 1 n N e {y n} n N = { π } n N 2 + 2nπ Entonces, lim sin( 1 ) = lim n x sin(nπ) = 0 n n mientras que lim ) = lim n y n n 2 + 2nπ) = 1 Cálculo () TEMA 3 Ingeniero de Telecomunicación 62 / 69

75 Cálculo práctico de ĺımites de funciones vectoriales Teorema Sea f : A R n R m. Sean f 1, f 2,..., f m las funciones coordenadas de f, esto es, f (x) = (f 1 (x), f 2 (x),..., f m (x)) y L = (L 1, L 2,..., L m ) R m. Entonces, son equivalentes: lim f (x) = L x a lim f i(x) = L i R x a i Importante Para calcular el ĺımite de una función vectorial en un punto a R n, basta con calcular por separado el ĺımite de cada una de sus funciones coordenadas en a R n. Cálculo () TEMA 3 Ingeniero de Telecomunicación 63 / 69

76 Cálculo práctico de ĺımites de funciones vectoriales Teorema Sea f : A R n R m. Sean f 1, f 2,..., f m las funciones coordenadas de f, esto es, f (x) = (f 1 (x), f 2 (x),..., f m (x)) y L = (L 1, L 2,..., L m ) R m. Entonces, son equivalentes: lim f (x) = L x a lim f i(x) = L i R x a i Ejemplo Sea F : R 2 R 3 definida por F (x, y) = (1 + y sin( x y ), lim F (x, y) = (1, 0, 0) (x,y) (0,0) x 2 y x 2, xy). Entonces, + y 2 Cálculo () TEMA 3 Ingeniero de Telecomunicación 63 / 69

77 Índice 1 Funciones Elementales 2 El conjunto R n Estructuras en R n Principales tipos de coordenadas en R 2 Principales tipos de coordenadas en R 3 3 Funciones de varias variables Dominio e Imagen de una función Función inversa. Función compuesta 4 Límites de funciones escalares Límite de una función de dos variables Cálculo práctico de ĺımites de funciones escalares Propiedades de los ĺımites Límites iterados Límites direccionales Teorema de compresión Infinitésimos equivalentes Cálculo del ĺımite por cambio a coordenadas polares Caracterización sucesional del ĺımite Cálculo práctico de ĺımites de funciones vectoriales 5 Funciones continuas Funciones continuas en compactos Cálculo () TEMA 3 Ingeniero de Telecomunicación 64 / 69

78 Funciones continuas Definición Decimos que f : A R n R m es una función continua en el punto a Dom(f ) si existe el ĺımite de f cuando x tiende a a y además coincide con f (a), lim x a f (x) = f (a). Definición Decimos que f : A R n R m es una función continua en A si es continua en cualquier punto a A Cálculo () TEMA 3 Ingeniero de Telecomunicación 65 / 69

79 Funciones continuas Las siguientes funciones son continuas en su dominio: Funciones constantes. (Ej: f (x, y) = 2) Polinomios. (Ej: f (x, y) = x 2 + xy + 2) Exponenciales. (Ej: f (x, y) = e x y ) Seno, coseno, tangente... (Ej: f (x, y) = sin(x 2 + y)) Logaritmos. (Ej: f (x, y) = ln(x 2 + y 2 )) Cálculo () TEMA 3 Ingeniero de Telecomunicación 66 / 69

80 Propiedades de las funciones continuas Teorema Sean f, g : A R n R m. Sea h : A R n R. Sea a A. Si f, g y h son continuas en a, entonces: 1 f es continua en a. 2 αf + βg, f g y hf son continuas en a. 3 Si h(x) 0 x A, entonces 1 h es continua en a. Cálculo () TEMA 3 Ingeniero de Telecomunicación 67 / 69

81 Composición de funciones continuas Teorema Consideremos las funciones f : R n R m, g : R m R p y sea a Dom(g f ). Si f es continua en a y g es continua en f (a) Dom(g), entonces g f : f : R n R p es continua en a. Ejemplos sin(x y) f (x, y) = x 2 + y 2 es continua en R 2 {(0, 0)}. g(x, y) = ln(x + y 2 ) es continua en {(x, y) R 2 x + y 2 > 0}. h(x, y) = e tan(xy) es continua en {(x, y) R 2 cos(xy) 0}. Cálculo () TEMA 3 Ingeniero de Telecomunicación 68 / 69

82 Funciones continuas en compactos Teorema de Weierstrass Sea f : R n R m una función continua y K Dom(f ) un conjunto compacto. Entonces, f tiene un máximo absoluto y un mínimo absoluto en K. Cálculo () TEMA 3 Ingeniero de Telecomunicación 69 / 69