En este grabado de Alberto Durero (Núremberg 1471 Núremberg 1528) titulado Melancolía I puedes ver un cuadrado mágico de constante
|
|
|
- Clara San Segundo López
- hace 7 años
- Vistas:
Transcripción
1 Tema 1 ENTEROS Y DECIMALES. REVISIÓN DE OPERACIONES En este grabado de Alberto Durero (Núremberg 1471 Núremberg 1528) titulado Melancolía I puedes ver un cuadrado mágico de constante 34. Es muy interesante observar como la constante (34) aparece en otras muchas partes del cuadrado. Por ejemplo: En las cuatro cantidades centrales En los cuadrados de las esquinas La suma de los números de las esquinas es 34 6 Además, las dos cifras centrales de la última fila, 1514, muestran su fecha de elaboración.
2 S 1 CUADRADO MÁGICO De 1º a 2 º PRACTICA Completa el cuadrado siguiente para que sea mágico para la suma. Recuerda: un cuadrado es mágico para la suma cuando se obtiene el mismo resultado sumando cada fila, cada columna o cada diagonal ,5 1,5-0,5-3,5 2 CUBO MÁGICO Coloca los números 1, 2, 3, 4, 1, 2, 3 y 4 en los vértices del cubo para que el producto de los cuatro números de cada cara del cubo sea el mismo. 3 JUEGA CON LOS SIGNOS En la siguiente expresión puedes ver tres números y dos cuadrados en los que deberás colocar los signos +, -, 3 y 4. Encuentra todos los resultados diferentes que puedes obtener. 4 VERDADERO O FALSO? 1 c 4 c 2 a) = 0 b) = 0 c) -8,5-1, = 0 d) -11,5 + 13,2-1,7 = 0 P ap S R e Re S P R O O e a P a
3 e NTe ROS Y De CImaL e S. Re VISIÓN De OPe R a CIONe S 1 Los números enteros Vocabulario números opuestos Recuerda que el conjunto de los números enteros se designa por Z y es: Z = { 4, 3, 2, 1, 0, 1, 2, 3, 4.} y se representan gráficamente en la llamada recta entera. Z enteros Z - enteros negativos Z + enteros positivos Los números 4 y 4, 3 y 3 y en general a y a se dice que son opuestos. Dos números opuestos se encuentran a la misma distancia del cero y se dice que tienen igual valor absoluto. El valor absoluto de un número es el que tiene prescindiendo del signo y se expresa escribiendo el número entre barras. Por ejemplo: 3 = +3 = 3; +4 = 4 = 4; 0 = 0 La recta entera sirve también para comparar números enteros: dados dos números enteros cualesquiera, el mayor es el que está situado más a la derecha. a a < b b EJERCICIOS Escribe los opuestos de los siguientes números: a) 1; b) 5; c) 25; d) 0 Halla el valor del número x en las siguientes igualdades: a) x = 2; b) x + 5 = 8; c) 3 x+1 =0 Ordena en forma creciente los siguientes números (el más pequeño primero): 6; 1; 5; 0; 4; 1; 3; 10; 6. 8
4 T e m a 1 2 Los números decimales Un número decimal está formado por una parte entera seguida de una parte decimal separada por una coma. Por ejemplo, los números 3,45; 12,07; 0,03 son números decimales. El número 42,325 es un número decimal. Su parte entera es 42 y su parte decimal es 325. Se lee cuarenta y dos enteros y trescientas veinticinco milésimas. RECUERDA QUE... En la calculadora la coma decimal se sustituye por un punto. Una fracción decimal tiene por numerador un número entero y por denominador es la unidad seguida de ceros. Una fracción decimal se puede escribir como un número decimal. Son fracciones decimales las fracciones 3 10 ; ; Las fracciones 37 10, , 27 son fracciones decimales que se 1000 pueden escribir como números decimales. LOS DECIMALES EN LA VIDA ORDINARIA 1 euro = 166,386 ptas 1 litro gasolina = 1,348 Record 100 m = 8,94 s Un boli = 1,75 π = 3, Billete bus = 1,50 s Así: = 3,7 (tres enteros y siete décimas). = 2,53 (dos enteros y cincuenta y tres centésimas). = 0,027 (veintisiete milésimas). A) Descomposición polinómica de un decimal Un número decimal puede descomponerse polinómicamente de las siguientes formas: 15,251 = ,2 + 0,05 + 0,001 = B) Comparación de decimales Dados dos números decimales, es menor el que tiene menor parte entera. 4,58 < 8,2 pues 4 < 8 Si los decimales tiene igual parte entera, es menor el que tiene menor parte decimal. 16,348 < 16,52 pues 3 < 5 ; 1,362 < 1,369 pues 2 < 9 9
5 e NTe ROS Y De CImaL e S. Re VISIÓN De OPe R a CIONe S Un número decimal no varía si se añaden ceros a su parte decimal. 16,52 = 16,520 = 16,5200 =. Por tanto también puedes comparar decimales con la misma parte entera usando este resultado y así: 16,348 < 16,52 pues 348 < 520 EJERCICIOS 4 5 Escribe los siguientes números y haz su descomposición polinómica. a) cuatro enteros y dos centésimas; b) treinta enteros y doscientas cuarenta y tres milésimas; c) quince diezmilésimas; d) cien enteros y cien milésimas. Ordena de menor a mayor los siguientes números: a) 3,25; b) 4,3; c) 12,1; d) 12,02; e) tres enteros y cien milésimas. 3 Operaciones con números enteros RECUERDA QUE... Para sumar dos números enteros de igual signo se suman sus valores absolutos. El signo del resultado es el de ambos sumandos. Para sumar dos números enteros de distinto signo se restan sus valores absolutos, el mayor menos el menor. El signo del resultado es el del que tiene mayor valor absoluto. A) Adiciones y sustracciones En una serie de adiciones y sustracciones, las operaciones se realizan una tras otra de izquierda a derecha, en el sentido de la escritura = = = 29 7 = 22 También puedes sumar los positivos y los negativos por separado y restar después ambos resultados = ( ) (8 + 7) = = 22 B) Multiplicaciones y divisiones. Regla de los signos. Recuerda la regla de los signos para multiplicaciones y divisiones: Multiplicación + + = + + _ = + = _ = + División + : + = + + : _ = : + = : _ = + 10
6 T e m a 1 En una operación debes de tener presente que: Si sólo hay multiplicaciones y divisiones, las operaciones se realizan de izquierda a derecha en el sentido de la escritura. 48 : 8 : = 6 : = = 10 En una serie de operaciones combinadas, las multiplicaciones y divisiones se realizan antes que las adiciones y sustracciones : 2 = = = = 11 CUIDADO No olvides utilizar paréntesis para separar los signos. En matemáticas es incorrecto escribir dos signos seguidos sin separación es incorrecto ( 4) = 8 es correcto EJERCICIOS 6 Calcula los números A, B, C, D, E y F siguientes: A = B = C = : 6 8 D = 75 : : 30 E = 4 ( 8) : ( 5) F = 32 : 4 : ( 25) 4 Operaciones con números decimales A) Suma y resta de decimales Se colocan uno debajo de otro de forma que coincidan las comas y las unidades de igual orden, luego se suman o restan como si fueran números enteros y se coloca la coma decimal bajo la coma de los sumandos. Si un número tiene menos cifras decimales que otro se completa este con ceros, para que ambos tengan las mismas cifras decimales. Para hallar 23, ,38 y 23,457 10,38 se hace: B) Multiplicación de decimales Se multiplican como si fueran números enteros. El producto tiene tantas cifras decimales como tengan entre los dos factores. Así: 12,35 3 3,2 es: 23, ,380-23,457 10,380 33,837 13,077 12,35 3 3, ,520 11
7 e NTe ROS Y De CImaL e S. Re VISIÓN De OPe R a CIONe S SI SE MULTIPLICA EL DIVIDENDO Y EL DIVISOR POR UN MISMO NÚMERO, EL COCIENTE NO VARÍA. FÍJATE TÚ! C) División de decimales Para dividir dos números decimales puedes multiplicar ambos por la unidad seguida de los ceros necesarios para que se conviertan en enteros y luego se realiza la división. También puedes añadir los ceros necesarios en la parte decimal para que ambos tengan el mismo número de cifras decimales. EJEMPLO 1 Haz la división 42, 25 : 12,6 con tres cifras decimales. Para dividir 42,25 entre 12,6 multiplicaremos ambos números por 100 para convertir ambos en enteros: 42, = ,6 100 = ,25 : 12, ,353 cociente resto = 0,0022 El resto es 0,0022. La línea discontinua indica dónde estaba la coma decimal. EJERCICIOS 7 8 Calcula a mano : a) 325, ,0056 b) 590,86 409,3 c) 12,603 7,21 d) 0,386 0,042 Halla el cociente de las siguientes divisiones, con dos cifras decimales: a) 36,4 : 2,5 b) 100 : 8,2 c) 2,514 : 1,02 d) 3,456 : 0,011 5 Propiedades de las operaciones En el cuadro adjunto te recordamos algunas propiedades de las operaciones: Conmutativa Asociativa Elemento neutro Distributiva de la multiplicación respecto de la adición ADICIÓN a + b = b + a a + (b + c) = (a + b) + c Es el cero. a + 0 = 0 + a = a a (b + c) = a b + a c MULTIPLICACIÓN a b = b a a (b c) = (a b) c Es el uno. a 1 = 1 a = a Además ya sabes que, en la adición, el opuesto del número a es a pues verifica que a + ( a) = 0. 12
8 T e m a 1 6 Prioridad de operaciones A) Operaciones combinadas sin paréntesis En una serie de operaciones combinadas sin paréntesis s las mul- tiplicaciones y divisiones se efectúan antes que las sumas y las restas. Una vez resueltas, la operación se efectúa de izquierda a derecha, en el sentido de la escritura. EJEMPLO 2 Calcula: : 5 4, Según lo dicho anteriormente, el proceso es: : 5 4, = , = = , = 4, = 5, 8 B) Operaciones combinadas con paréntesis En una operación combinada con paréntesis, s éstos son los primeros que se resuelven. Una vez resueltos, la operación se realiza como en el caso anterior. EJEMPLO 3 Calcula: 5 3 ( ,25) [5,4 (7 3,5)] Al haber paréntesis encajados se comienza resolviendo los más interiores. 5 ( ,25) + 2 [5,4 (7 3,5)] = 5 (6 + 12,75) + 2 [5,4 24,5] = 5 18, ( 19,1) = = 93,75 38,2 = 55,55 EL ORDEN PARA EFECTUAR UNA SERIE DE OPERACIONES COMBINADAS ES: 1º. RESUELVE LOS PARÉNTESIS. SI ÉSTOS ESTÁN ENCAJADOS, COMIENZA POR LOS MÁS INTERIORES. 2º. RESUELVE LAS MULTIPLICACIONES Y DIVISIONES. 3º. POR ÚLTIMO HAZ LAS SUMAS Y RESTAS. EJERCICIOS Calcula los números A, B, C y D siguientes: A = ,5 + 1; B = : 6 8 C = ; D = : 0, Comprueba que: (51 : 3) (25 (4 3)) (5 2) + 60 = 54 Pon los paréntesis necesarios para que las siguientes expresiones sean correctas: a) = 1 b) : = 1 c) =
9 ENTEROS Y DECIMALES. REVISIÓN DE OPERACIONES Fracciones decimales En resumen Una fracción decimal tiene por numerador un número entero y su denominador es la unidad seguida de ceros. 43 = , (cuatro enteros y tres décimas); = , 213 (doscientas trece milésimas) Descomposición de un decimal: , = (veintitrés enteros y diecisiete centésimas) Operaciones con números enteros y decimales A) Adición Para sumar dos decimales del mismo signo: - se suman sus valores absolutos - el signo del resultado es el de ambos sumandos 6 + ( 3,5) = 9, ,5= + 9,5 Se calcula 6 + 3,5 = 9,5 y se escribe el signo común delante del resultado Para sumar dos decimales de distinto signo: - se restan sus valores absolutos (el mayor menos el menor) - el signo del resultado es el del que tiene mayor valor absoluto. M N E E E R S U R M U R US E 14 RN B) Sustracción +2,6 + ( 6) = 3,4 Se calcula 6 2,6 = 3,4 y se escribe signo pues 6 > 2,6 Para restar dos números se le suma al primero el opuesto del segundo. suma del opuesto de (+8) 6 (+8) = 6 + ( 8) = 2 ( 2,6) + 6 = +3,4 Se calcula 6 2,6 =3,4 y se escribe el signo + pues 6 > 2,6 suma del opuesto de ( 9) 5 ( 9) = 5 + (+9) = 4
10 C) Serie de adiciones y sustracciones En resumen En una serie de adiciones y sustracciones, las operaciones se realizan una tras otra de izquierda a derecha, en el sentido de la escritura. A = 12,6 3, T E M A A = 9, D) Multiplicación y división A = 17,1 3 = 14,1 Para multiplicar o dividir dos decimales cualesquiera debes tener en cuenta la regla de los signos de la página 10. Prioridad de operaciones A) Operaciones combinadas sin paréntesis En ausencia de paréntesis, las multiplicaciones y divisiones se realizan antes que las adiciones y las sustracciones. P = : ( 4) = = = 5 5 = 0 B) Operaciones combinadas con paréntesis En una operación combinada con paréntesis se efectúan en primer lugar los cálculos entre paréntesis. Q = 2 + [ 16 + ( 4) 3 ( 9)] : ( 5) Q = 2 + ( ) : ( 5) Q = : ( 5) Q = 2 + ( 4) Q = 2 Efectúa en primer lugar los cálculos entre paréntesis (o corchetes. Para ello se calcula en primer lugar el producto ( 4) 3 ( 9). Se terminan los cálculos entre paréntesis. Se efectúa la división (pues tiene prioridad). Se termina el cálculo. M 15 N E E E R S U R M U NRN R E US
11 ENTEROS Y DECIMALES. REVISIÓN DE OPERACIONES EJERCICIOS LECTURA Y ESCRITURA DE NÚMEROS Encuentra en cada caso el número k tal que: a 7 + k = 8 b k + 9 = 5 c 8 + k = 16 d 16 + k = 16 e 8 k = 10 f k 5 = 1 Un frío día de Enero en Albacete el termómetro marcaba 8 C. Ese mismo día Tenerife tenía una temperatura máxima de 19 C. Qué diferencia de temperatura había entre ambas capitales? 21 Completa los muros. Cada número es la suma de los dos lados que tiene debajo Copia y completa la tabla siguiente: Ordena de menor a mayor los números siguientes. Usa el símbolo <. 7, 4, 10, 3, 5, 9, 11, 7 Representa los números anteriores en la recta entera. 15 Ordena de mayor a menor los siguientes números. Usa el símbolo > 8; 1,2; 3,1; 3,01; 10; 10; 6, 25; 0 16 Utiliza los signos +,, y : en el primer miembro para que las siguientes igualdades sean ciertas, usa paréntesis si es necesario: = = = = 3 Intenta encontrar otros resultados. 17 Escribe todos los enteros x que verifiquen: 3 < x < Qué enteros x verifican que x 6 = 4? 19 Qué enteros x verifican que x = 2? 20 Calcula el valor de los números: P = Q = 3 ( 2) : ( 4) a b c a + b + c Haz la descomposición polinómica de los siguientes números a 15, 28 b 241, 205 c 10,01 d 638,345 e 25,6 f 0, Qué número decimal corresponde a cada una de las siguientes fracciones decimales? a b c d Escribe como una fracción decimal los siguientes números: a 3,2 b 7,35 c 0,45 d 0,0034 e 481,9267 f 3, a Escribe cinco números decimales comprendidos entre 8,4 y 8,5. b Escribe cinco números decimales comprendidos entre 8,4 y 8,45. c Escribe cinco números decimales comprendidos entre 8,4 y 8,41. 16
12 T E M A 1 OPERACIONES 27 Calcula mentalmente: a 3,18 + 5,82 b 0, ,55 c 5,25 + 0,65 + 1,1 d 6, 42 3, 2 e 25, , 01 f 5, 7 2, Realiza los siguientes productos: a 32,045 1,03 b 3, 54 0,02 c 6,52 12,045 d 0,032 0,48 e 2,025 0,3 f 5,12 0, Halla los siguientes cocientes con tres cifras decimales: a 12,3 : 4, 2 b 5,634 : 2,12 c 0,248 : 0,21 d 51,05 : 16, 346 e 116,32335 : 54,23 f 2,651 : 0, Calcula: a 5 + [15 (8 2)] b 12 5 (8 2) + [44 3 (6 9)] c 14 (6 4) [7 (12 1) + 1] d [ ( )] : 3 e (32 [6 (16 + 8)]) : f (48 100) : : (5 4 1) 31 Completa cada cuadrado por el número que corresponda. a 4 (3 12) = 4 = b 3 ( 6 + 9) = 3 = c 24 : ( ) = 24 : ( ) = d 5 ( : 8) + 34 : ( ) = = 5 (8 + ) + 34 : ( + 32) = : = 32 Completa cada símbolo con el signo de operación, +,,, :, adecuado: a 3 ( 4) 4 = 13 b 10 3 : ( 1) = 13 c 3 + ( 1) ( 10) = 13 d 6 2 ( 5) = 2 e 5 ( 8) 2 = 80 f 5 3 ( 6) = 21 g 10 [3 : ( 1)] = 7 h [ 10 ( 1)] 3 = Usa tu calculadora para hallar el valor de los siguientes números: A = ( 6, 28) 32,05 ( 6,21 48,322) B = 54, ,57 ( 6,15 + 8, 2) C = [ 57 ( )] 43 ( 15) D = ( 13,01) (12,6 + 8,88) 32 (15,96 : 3,8) 34 Sea el número A = 6 ( 5) + 3 ( 4) + 10 a Calcula A b Pon los paréntesis necesarios en la expresión de A para que el resultado sea: a) 58 ; b) Calcula: a ( 5) b ( 7 + 2) ( 5) c 8 : ( 2) d [ 8 : 4 + 6] ( 2) 36 Copia en tu cuaderno y completa la tabla siguiente: a b a b a : b Copia en tu cuaderno y completa la tabla. a b c a b c b a : c Copia en tu cuaderno y completa la tabla. a b c d a b c d (a b c) : d
13 ENTEROS Y DECIMALES. REVISIÓN DE OPERACIONES 39 Calcula: a (18 12) (5 9) (7 4) + (1 3) b 1 (0,1 1) + ( 1 + 1,1) c ( ,5) + 2,5 8 ( 6,5 + 11) d 14 + (5 6,2) ( 6 + 3,4) Calcula: a 3 + [ 16 + ( 4) ( 9)] : ( 5) b 9 + [ ( 2)] : ( 4) c 14 [5 12 : ( 4)] ( 2) + [12 ( 3) 5] : d [ 24 + ( 2) ( 4)] : ( 2) [20 + ( 4) ( 9)] : ( 8) 41 Calcula: a 30 : ( 6) 6 : ( 1) b ( 32) : ( 4) 2 5 c ( 4) d ( 3) e 22 3 ( 1) ( 7) f 7 28 : ( 4) 42 Calcula los siguientes números: A = : 8 8 B = C = 7 ( 2) + 25 : 5 ( 4) D = 32 : 4 : Calcula: A = : B = C = : D = : 6 44 Mismo ejercicio: A = : 15 B = : : 4 C = 240 : 12 : D = Estrellas mágicas. Una estrella se dice que es mágica para la suma cuando el resultado de sumar los números de cada línea es constante. Análogamente se puede hablar de estrellas mágicas para el producto. Completa las estrellas mágicas siguientes sabiendo que la primera es mágica para la suma y la segunda lo es para el producto Cuadrados mágicos. 6 2,5 12 Un cuadrado es mágico para la multiplicación cuando el producto de los elementos de sus filas, columnas o diagonales son iguales.) a Verifica que el siguiente cuadrado es mágico. 16 0, , ,25 b Completa las celdas vacías para que los siguientes cuadrados sean mágicos con el mismo criterio que el anterior ,25 0, ,5 18
14 T E M A 1 47 Coloca los paréntesis necesarios para que los siguientes resultados sean correctos: a = 88 b 25 4 : = 3 c : = 5 d = 31 e = 8 f : 50 = 4 52 Esquemas. Completa: Calcula: a 16 ( ) (4 7) b ((4 (7 2)) ) 43 c 24 ((37 + 4) 3) 5 7 d ( ) : 7 (3 4 9) Calcula cuando a = 2, b = 3, c = 4 (sabes que el producto a b se suele escribir ab). A = ab + ac + bc B = abc C = a(b c) ab + ac D = ab ac bc 50 Si a = 2, b = 4, c = 6. Calcula: A = ab 3c B = abc C = 2a 3b 4c D = a(2b 5c) + 3 (a + 4c) 51 Con la serie de números 1, 2, 3, 4, 5, 6, 7, 8, 9 y utilizando, o no, signos de operaciones entre ellos se obtiene un número. Por ejemplo el 61 pues: = 61; o el 0: (1 + 2) ((7 + 8) 9) = : 6 Escribe en línea el cálculo escrito en los esquemas anteriores. 53 Es frecuente no indicar el símbolo de multiplicar ( ó ) cuando un número va delante de un paréntesis. Teniendo en cuenta esta forma de representar un producto, calcula: a 5 4 ( ) + 50 : (2 5) b 2(8 2,5 3) + 5 ( 4 2) + 15 c : 12 5 (32 6 3) (2 ( )) d 24 : 6 : 2 ( ) (7 27) Puedes obtener 45 como resultado? Y 100? 19
15 ENTEROS Y DECIMALES. REVISIÓN DE OPERACIONES 54 Si a = 6, b = 1,2 y c = 5, calcula las expresiones siguientes: a a bc b (a c) b c a b : c d (a b) : c 55 Las cartas. Utiliza cada vez tres de las cuatro cartas siguientes y encuentra el resultado propuesto. = 1 + = 13 + = 8 = 1 Propón a tu compañero otros cáculos. 56 Oymyakon es un pueblo de la república rusa de Yakutia y tiene fama de ser una de las ciudades más frías del mundo. En 1926 batió el record de temperatura más baja alcanzada en zona habitada con 71,2 ºC. Las temperaturas medias mensuales figuran en esta tabla: E 50 F 44 M 32 A 15 M 2 Jun 11 a Calcula la media anual de las temperaturas de esta ciudad. b Calcula la temperatura media en los meses de invierno. 57 En una librería se han adquirido libros a tres precios diferentes (5,25 euros, 3,8 euros y 4,3 euros respectivamente cada ejemplar). El importe total de la factura ha sido de 606 euros. Sabiendo que han comprado triple cantidad del segundo que del primero y doble del tercero que del primero. Cuántos ejemplares se han adquirido de cada clase? 58 Para comprar 42 bolígrafos me faltan 7,3 euros, y si compro 35 me sobran 14,75 euros. Cuánto cuesta cada bolígrafo y cuánto dinero tengo? 59 Laura ha recibido 80 por su cumpleaños. Con este dinero piensa comprar tres CD que cuestan 18,65 cada uno y un jersey que cuesta 22,34. Laura se aprovecha de un descuento de 7,55 en el jersey por ser rebajas de verano. Escribe la expresión que permite calcular lo que le queda de su dinero inicial y efectúa después los cálculos. Jul A S O N D
16 T e m a 1 AUTOEVALUACIÓN 1 El opuesto del número 25 es: a 25. b 25. c 0. d Nada de lo anterior. 2 Los posibles valores de x tales que x = 8 son: a x = 8 ó x = 8. b Sólo x = 8. c x = 8 y x = 8. d Nada de lo anterior. 3 El número 12,003 se lee: a Doce enteros y tres décimas. b Doce enteros y tres centésimas. c Doce enteros y tres milésimas. d Nada de lo anterior. 4 La fracción decimal representa al número: a 1,2045. b 120,45. c 1204,5. d Nada de lo anterior. 5 El número es: a 23,72. b 23,702. c 23,072. d Nada de lo anterior. 6 El valor del número A = 3 3 ( 2) : ( 8) es: a 17. b 0. c 17. d Nada de lo anterior. 7 El número B tal que 4,58 3 B = 28,396 es: a 6,2. b 130, c 7, 04. d Nada de lo anterior. 8 El número C tal que C 45,065 = 10,24 es: a 34,825. b 55,305. c 55,305. d Nada de lo anterior. 9 El valor del número D = 23 [72 : 9 (4 3 2,5)] ,5 es: a 40. b 73. c 37. d Nada de lo anterior. 10 Para que : 4 = 8 hay que escribir: a (8 5) 8 : 4 = 8. b 8 5 (8 : 4) = 8. c [8 5 8] : 4 = 8. d Nada de lo anterior. 21
UNIDAD 7: NÚMEROS DECIMALES Y OPERACIONES
 UNIDAD 7: NÚMEROS DECIMALES Y OPERACIONES ÍNDICE 7.1 Unidad decimal. 7.2 Escritura, lectura y descomposición de números decimales. 7.2.1 Escritura de números decimales. 7.2.2 Lectura de números decimales.
UNIDAD 7: NÚMEROS DECIMALES Y OPERACIONES ÍNDICE 7.1 Unidad decimal. 7.2 Escritura, lectura y descomposición de números decimales. 7.2.1 Escritura de números decimales. 7.2.2 Lectura de números decimales.
Semana 1: Números Reales y sus Operaciones
 Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
Semana 1: Números Reales y sus Operaciones Taller de Preparación para Prueba PLANEA Ing. Jonathan Quiroga Tinoco Conalep Tehuacán P.T.B. en ADMO, SOMA y EMEC UNIDAD 04 Los números enteros y sus operaciones
NÚMEROS DECIMALES. Teoría 3 er Ciclo Primaria Colegio Romareda 2011/2012 Página 28
 Teoría 3 er Ciclo Primaria Colegio Romareda 20/202 Página 28 NÚMEROS DECIMALES Los números decimales nacen como una forma especial de escritura de las fracciones decimales, de manera que la coma separa
Teoría 3 er Ciclo Primaria Colegio Romareda 20/202 Página 28 NÚMEROS DECIMALES Los números decimales nacen como una forma especial de escritura de las fracciones decimales, de manera que la coma separa
UNIDAD DIDÁCTICA #1 CONTENIDO
 UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
NUMEROS ENTEROS ( Z)
 NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
MATEMÁTICAS UNIDAD 4 GRADO 6º. Números naturales
 1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 6º Números naturales 1 2 Franklin Eduardo Pérez Quintero LOGRO: Estudiar, analizar y profundizar las operaciones y propiedades de los números
1 Franklin Eduardo Pérez Quintero MATEMÁTICAS UNIDAD 4 GRADO 6º Números naturales 1 2 Franklin Eduardo Pérez Quintero LOGRO: Estudiar, analizar y profundizar las operaciones y propiedades de los números
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
LOS NÚMEROS DECIMALES
 1 LOS NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 5 5 0,; 1,5;,15 10 4 8 C D U d c m dm, 1 5 Parte entera Parte decimal Tres unidades, ciento
1 LOS NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 5 5 0,; 1,5;,15 10 4 8 C D U d c m dm, 1 5 Parte entera Parte decimal Tres unidades, ciento
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL. Mate 3041 Profa. Milena R. Salcedo Villanueva
 NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL Mate 3041 Profa. Milena R. Salcedo Villanueva 1 FRACCIONES Una fracción tiene dos términos: numerador y denominador Denominador indica las veces que se divide
NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL Mate 3041 Profa. Milena R. Salcedo Villanueva 1 FRACCIONES Una fracción tiene dos términos: numerador y denominador Denominador indica las veces que se divide
5º EP [NUMERACIÓN Y CÁLCULO] Matemáticas COLEGIO SAN JOSÉ
![5º EP [NUMERACIÓN Y CÁLCULO] Matemáticas COLEGIO SAN JOSÉ 5º EP [NUMERACIÓN Y CÁLCULO] Matemáticas COLEGIO SAN JOSÉ](/thumbs/72/66410635.jpg) 5º EP Matemáticas COLEGIO SAN JOSÉ [NUMERACIÓN Y CÁLCULO] 1 Observa y completa: 234 = 2 C + 3 D + 4 U = 200 + 30 + 4 970 = 307 = 766 = 2 Utiliza todas estas cifras para escribir cuatro números distintos.
5º EP Matemáticas COLEGIO SAN JOSÉ [NUMERACIÓN Y CÁLCULO] 1 Observa y completa: 234 = 2 C + 3 D + 4 U = 200 + 30 + 4 970 = 307 = 766 = 2 Utiliza todas estas cifras para escribir cuatro números distintos.
Divisibilidad I. Nombre Curso Fecha
 Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Suma y resta de números decimales
 35 Suma y resta de números decimales Para sumar o restar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Después, se suman o se restan como si fueran
35 Suma y resta de números decimales Para sumar o restar números decimales, se colocan de forma que coincidan en la misma columna las cifras del mismo orden. Después, se suman o se restan como si fueran
Tema 05: Números Decimales, Fracciones y Porcentajes Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco.
 2009 Tema 05: Números Decimales, Fracciones y Porcentajes Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco. Manuel González de León. mgdl 0/0/2009 INDICE: 0. UNIDADES DECIMALES: 02. DESCOMPOSICIÓN
2009 Tema 05: Números Decimales, Fracciones y Porcentajes Primero de Educación Secundaria Obligatoria. I.e.s Fuentesaúco. Manuel González de León. mgdl 0/0/2009 INDICE: 0. UNIDADES DECIMALES: 02. DESCOMPOSICIÓN
TEMA 3 NÚMEROS DECIMALES
 TEMA 3 NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 3 10 5 25 = 0,3; = 1,25; = 3,125 4 8 C D U d c m dm 3, 1 2 5 Parte entera Parte decimal
TEMA 3 NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 3 10 5 25 = 0,3; = 1,25; = 3,125 4 8 C D U d c m dm 3, 1 2 5 Parte entera Parte decimal
Números decimales OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 8 _ 0-088.qxd //0 09: Página Números decimales INTRODUCCIÓN El estudio de los números decimales comienza recordando el sistema de numeración decimal, que es la base de la expresión escrita de los números
8 _ 0-088.qxd //0 09: Página Números decimales INTRODUCCIÓN El estudio de los números decimales comienza recordando el sistema de numeración decimal, que es la base de la expresión escrita de los números
6º PRIMARIA. Números decimales.
 6º PRIMARIA Números decimales. Qué son los números decimales? Los números decimales son los que vienen después de la coma ejemplo: 2, 8. El número 2 es un entero, el número que viene después de la coma,
6º PRIMARIA Números decimales. Qué son los números decimales? Los números decimales son los que vienen después de la coma ejemplo: 2, 8. El número 2 es un entero, el número que viene después de la coma,
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
NÚMEROS DECIMALES. PORCENTAJES
 NÚMEROS DECIMALES. PORCENTAJES E.S.O.. UNIDADES DECIMALES. SISTEMA DE NUMERACIÓN DECIMAL En los números decimales se tiene en cuenta el valor posicional de las cifras al igual que en los números naturales
NÚMEROS DECIMALES. PORCENTAJES E.S.O.. UNIDADES DECIMALES. SISTEMA DE NUMERACIÓN DECIMAL En los números decimales se tiene en cuenta el valor posicional de las cifras al igual que en los números naturales
Una fracción decimal tiene por denominador la unidad. Número decimal. Es aquel que se puede expresar mediante una fracción
 Fracción decimal Una fracción decimal tiene por denominador la unidad seguida de ceros. Número decimal decimal. Es aquel que se puede expresar mediante una fracción Consta de dos partes: entera y decimal.
Fracción decimal Una fracción decimal tiene por denominador la unidad seguida de ceros. Número decimal decimal. Es aquel que se puede expresar mediante una fracción Consta de dos partes: entera y decimal.
2º Se lee número que hay antes de la coma, se añade la palabra coma y luego se lee la parte decimal
 Qué son los decimales? Los decimales son una manera distinta de escribir fracciones con denominadores como 10, 100 y 1,000. Tanto los decimales como las fracciones indican una parte de un entero. Un decimal
Qué son los decimales? Los decimales son una manera distinta de escribir fracciones con denominadores como 10, 100 y 1,000. Tanto los decimales como las fracciones indican una parte de un entero. Un decimal
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
Bloque 1. Aritmética y Álgebra 2. Los números enteros 1. Los números enteros Es el conjunto de los números negativos, el cero y los positivos, y se representan como: Z...,-5,-4,-3,-2,-1,0, 1, 2, 3, 4,
UNIDAD 6: FRACCIONES ÍNDICE. 6.1 Conocimiento de fracciones: Términos de las fracciones Representación. 6.1.
 UNIDAD 6: FRACCIONES ÍNDICE 6. Conocimiento de fracciones: 6.. Términos de las fracciones. 6.. Representación 6.. Interpretación 6. Lectura y escritura de fracciones. 6. Comparación de fracciones. 6..
UNIDAD 6: FRACCIONES ÍNDICE 6. Conocimiento de fracciones: 6.. Términos de las fracciones. 6.. Representación 6.. Interpretación 6. Lectura y escritura de fracciones. 6. Comparación de fracciones. 6..
OBJETIVO 1 EL CONCEPTO DE NÚMERO DECIMAL
 COMPRENDER OBJETIVO 1 EL CONCEPTO DE NÚMERO DECIMAL NOMBRE: CURSO: ECHA: SIGNIICADO DE LOS NÚMEROS DECIMALES En nuestra vida diaria medimos, calculamos, comparamos, etc. Hablamos de cantidades que no son
COMPRENDER OBJETIVO 1 EL CONCEPTO DE NÚMERO DECIMAL NOMBRE: CURSO: ECHA: SIGNIICADO DE LOS NÚMEROS DECIMALES En nuestra vida diaria medimos, calculamos, comparamos, etc. Hablamos de cantidades que no son
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS
 TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS VALOR ABSOLUTO Es la distancia que existe entre un número y el 0-3 -2-1 0 1 2 3 Z -3 = 3, 3 = 3 DEFINICIÓN:
C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS VALOR ABSOLUTO Es la distancia que existe entre un número y el 0-3 -2-1 0 1 2 3 Z -3 = 3, 3 = 3 DEFINICIÓN:
TRABAJO DE MATEMÁTICAS. PENDIENTES DE 2º E.S.O. (1ª parte)
 TRABAJO DE MATEMÁTICAS PENDIENTES DE º E.S.O. (ª parte) NÚMEROS ENTEROS.-) Realiza las operaciones siguientes () (0) (-) ( ) (-) ( -) (-) ( -) (-) () - - - -0 - - - ( -) ( ) ( -) ( ) ( ) ( - ) ( - ) (
TRABAJO DE MATEMÁTICAS PENDIENTES DE º E.S.O. (ª parte) NÚMEROS ENTEROS.-) Realiza las operaciones siguientes () (0) (-) ( ) (-) ( -) (-) ( -) (-) () - - - -0 - - - ( -) ( ) ( -) ( ) ( ) ( - ) ( - ) (
Los números enteros Z = {,-3, -2, -1, 0, 1, 2, 3, }
 Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
Los números enteros La unión de los números naturales y los enteros negativos forma el conjunto de los números enteros, que se designa con la palabra Z. Está constituido por infinitos elementos y se representan
UNIDAD III NÚMEROS FRACCIONARIOS
 UNIDAD III NÚMEROS FRACCIONARIOS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica los números fraccionarios y realiza operaciones con ellos. Identifica los porcentajes, decimales y fraccionarios y realiza
UNIDAD III NÚMEROS FRACCIONARIOS COMPETENCIAS E INDICADORES DE DESEMPEÑO Identifica los números fraccionarios y realiza operaciones con ellos. Identifica los porcentajes, decimales y fraccionarios y realiza
62,415 = ,4 + 0,01 + 0,005
 NOMBRE:... Nivel:... FECHA:... LOS NÚMEROS DECIMALES LAS UNIDADES DECIMALES 1 0,1 1 0 0,01 0,1 una décima (d) 0,01 una centésima (c) 0,001 una milésima (m) 1 U = d = 0 c = 1.000 m 1 1.000 0,001 D U, d
NOMBRE:... Nivel:... FECHA:... LOS NÚMEROS DECIMALES LAS UNIDADES DECIMALES 1 0,1 1 0 0,01 0,1 una décima (d) 0,01 una centésima (c) 0,001 una milésima (m) 1 U = d = 0 c = 1.000 m 1 1.000 0,001 D U, d
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
UNIDAD 6 AULA 360. Números decimales
 UNIDAD 6 Números decimales 1. Números decimales. Ordenación y representación 2. Tipos de números decimales 3. Conversión de decimal a fracción 4. Operaciones con números decimales 1. Números decimales
UNIDAD 6 Números decimales 1. Números decimales. Ordenación y representación 2. Tipos de números decimales 3. Conversión de decimal a fracción 4. Operaciones con números decimales 1. Números decimales
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO)
 PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO) 1 NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación correspondiente
PLAN DE RECUPERACIÓN DE MATEMÁTICAS 1º ESO (Para alumnos de 2º de ESO) 1 NOMBRE: Para aprobar las matemáticas pendientes de cursos anteriores es obligatorio realizar el plan de recuperación correspondiente
Números fraccionarios y decimales
 Unidad didáctica Números fraccionarios y decimales .- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Unidad didáctica Números fraccionarios y decimales .- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
MATEMÁTICAS 1º DE ESO LOMCE TEMA I : NÚMEROS NATURALES Sistema de numeración romano. Los números naturales. Números naturales como cardinales y ordinales. o Recta numérica. El sistema de numeración decimal.
3 Números decimales OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Significado de los números decimales. Representación en la recta numérica.
 829485 _ 024-008.qxd 12/9/07 15:10 Página 27 Números decimales INTRODUCCIÓN RESUMEN DE LA UNIDAD En esta unidad estudiamos el sistema de numeración decimal, e introducimos las denominaciones de la parte
829485 _ 024-008.qxd 12/9/07 15:10 Página 27 Números decimales INTRODUCCIÓN RESUMEN DE LA UNIDAD En esta unidad estudiamos el sistema de numeración decimal, e introducimos las denominaciones de la parte
TEMA 1. Los números enteros. Matemáticas
 1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
1 Introducción En esta unidad veremos propiedades de los números enteros, como se opera con ellos (con y sin calculadora), los números primos, máximo común divisor y mínimo común múltiplo y por últimos
La multiplicación y la división
 La multiplicación y la división La multiplicación y sus propiedades Completa las siguientes oraciones. La multiplicación cumple las propiedades, conmutativa asociativa y distributiva respecto de la adición
La multiplicación y la división La multiplicación y sus propiedades Completa las siguientes oraciones. La multiplicación cumple las propiedades, conmutativa asociativa y distributiva respecto de la adición
NÚMEROS DECIMALES. 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal.
 NÚMEROS DECIMALES 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal. Parte entera, Décimas Centésimas Milésimas Diezmilésimas Cienmilésimas
NÚMEROS DECIMALES 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal. Parte entera, Décimas Centésimas Milésimas Diezmilésimas Cienmilésimas
NÚMEROS DECIMALES. 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal.
 NÚMEROS DECIMALES 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal. Parte entera, Décimas Centésimas Milésimas Diezmilésimas Cienmilésimas
NÚMEROS DECIMALES 1 LECTURA Y ORDENACIÓN DE NÚMEROS DECIMALES Todo número decimal se compone de una parte entera, la coma y la parte decimal. Parte entera, Décimas Centésimas Milésimas Diezmilésimas Cienmilésimas
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones. Prof. Kyria A. Pérez
 7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
7.1 Números Racionales: números enteros, propiedades de los números y orden de operaciones Prof. Kyria A. Pérez Estándares de contenido y expectativas N.SO.7.2.1- Modela la suma, Resta, multiplicación
Indica el coeficiente, parte literal y grado de estos monomios.
 Polinomios EJERCICIOS 001 Indica el coeficiente, parte literal y grado de estos monomios. a) y z 4 b) 5b c c) 15 y d) y 5 a) Coeficiente: Parte literal: y z 4 Grado: + + 4 9 b) Coeficiente: 5 Parte literal:
Polinomios EJERCICIOS 001 Indica el coeficiente, parte literal y grado de estos monomios. a) y z 4 b) 5b c c) 15 y d) y 5 a) Coeficiente: Parte literal: y z 4 Grado: + + 4 9 b) Coeficiente: 5 Parte literal:
Números Racionales. Repaso para la prueba. Profesora: Jennipher Ferreira Curso: 7 B
 Números Racionales Repaso para la prueba Profesora: Jennipher Ferreira Curso: 7 B Tipos de Fracciones Fracciones propias: Son aquellas en las que el denominador es mayor al numerador, y su valor es menor
Números Racionales Repaso para la prueba Profesora: Jennipher Ferreira Curso: 7 B Tipos de Fracciones Fracciones propias: Son aquellas en las que el denominador es mayor al numerador, y su valor es menor
Apuntes de matemáticas 2º ESO Curso
 Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde a un número menor
Unidad 1 Los números de todos los días
 CUENTAS ÚTILES Módulo nivel intermedio. 3ra. Edición. Primaria Unidad 1 Los números de todos los días Los números naturales son aquellos que utilizamos para contar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
CUENTAS ÚTILES Módulo nivel intermedio. 3ra. Edición. Primaria Unidad 1 Los números de todos los días Los números naturales son aquellos que utilizamos para contar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
Operaciones con números enteros
 Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
Operaciones con números enteros Suma de números enteros Cuando tienen el mismo signo: Se suman los valores y se deja el signo que tengan, si son positivos signo positivo y si son negativos signo negativo.
TEMA Nº 1. Conjuntos numéricos
 TEMA Nº 1 Conjuntos numéricos Aprendizajes esperados: Utilizar y clasificar los distintos conjuntos numéricos en sus diversas formas de expresión, tanto en las ciencias exactas como en las ciencias sociales
TEMA Nº 1 Conjuntos numéricos Aprendizajes esperados: Utilizar y clasificar los distintos conjuntos numéricos en sus diversas formas de expresión, tanto en las ciencias exactas como en las ciencias sociales
OBJETIVO 1 COMPRENDER EL CONCEPTO DE NÚMERO DECIMAL NOMBRE: CURSO: FECHA: Centena Decena Unidad Décima Centésima Milésima.
 OBJETIVO COMPRENDER EL CONCEPTO DE NÚMERO DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: unidades de un orden forman unidad del orden siguiente..
OBJETIVO COMPRENDER EL CONCEPTO DE NÚMERO DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: unidades de un orden forman unidad del orden siguiente..
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
MATEMÁTICAS 1º DE ESO LOMCE TEMA III : LOS NÚMEROS ENTEROS Los números negativos. Su necesidad. El conjunto de los números enteros. Valor absoluto de un número entero. Opuesto de un número entero. Suma
TEMA 4 NÚMEROS ENTEROS
 TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
2º. Representa en una recta numérica los números: (+4), (-3), (0), (+7), (-2), (+2) y luego escríbelos de forma ordenada.
 TEMA 01 - NÚMEROS ENTEROS 1º. Indica el número que corresponde a cada letra. º. Representa en una recta numérica los números: (+) (-) (0) (+7) (-) (+) y luego escríbelos de forma ordenada. º. En un museo
TEMA 01 - NÚMEROS ENTEROS 1º. Indica el número que corresponde a cada letra. º. Representa en una recta numérica los números: (+) (-) (0) (+7) (-) (+) y luego escríbelos de forma ordenada. º. En un museo
Números fraccionarios y decimales
 Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Teoría (resumen) Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12, 15, 18, ; los múltiplos de 2 son: 2, 4, 6, 8, 10, 12, ; o sea los números pares.
 1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
1.- Divisibilidad Teoría (resumen) Múltiplos de un número. Son aquellos que se obtienen al multiplicar dicho número por los números naturales 1, 2, 3,. Por ejemplo, los múltiplos de 3 son: 3, 6, 9, 12,
Números Naturales. Cero elemento neutro: = 12 Sucesión fundamental : se obtiene el siguiente número = 9
 Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
Números Naturales Cuando comenzamos a contar los objetos, los años, etc, nos hemos encontrado con los números de forma natural; por eso a este conjunto de números así aprendidos se les denomina números
CONJUNTO DE LOS NÚMEROS NATURALES
 República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
República Bolivariana de Venezuela Ministerio de la Defensa Universidad Nacional Experimental de las Fuerzas Armadas Curso de Inducción Universitaria CIU Cátedra: Razonamiento Matemático CONJUNTO DE LOS
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA V : LOS NÚMEROS DECIMALES El Sistema de Numeración Decimal: órdenes de unidades decimales y equivalencias. Números decimales y fracciones decimales. Tipos de números decimales
MATEMÁTICAS 1º DE ESO LOE TEMA V : LOS NÚMEROS DECIMALES El Sistema de Numeración Decimal: órdenes de unidades decimales y equivalencias. Números decimales y fracciones decimales. Tipos de números decimales
PRIMER CURSO AÑO LECTIVO El módulo de la multiplicación es el 0 V F. 4. La división de Z si cumple la propiedad conmutativa V F
 BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
BANCO DE PREGUNTAS PRIMER SEMESTRE PRIMER CURSO AÑO LECTIVO 007-008 I. Establezca si las siguientes proposiciones son verdaderas o falsas 1. En el ejercicio 1 + 4 48 el factor común es 1 V F. Los términos
* Debes hacer los ejercicios en una libreta. * Es mejor hacer todos los días un poco. * No olvides poner la fecha cada día que hagas el Cuadernillo.
 Matemáticas 5º Recuerda: * Debes hacer los ejercicios en una libreta * Es mejor hacer todos los días un poco. * No olvides poner la fecha cada día que hagas el Cuadernillo. * Conviene que tengas cerca
Matemáticas 5º Recuerda: * Debes hacer los ejercicios en una libreta * Es mejor hacer todos los días un poco. * No olvides poner la fecha cada día que hagas el Cuadernillo. * Conviene que tengas cerca
UNIDAD: NÚMEROS Y PROPORCIONALIDAD. Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números
 GUÍA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS NÚMEROS NATURALES (ln) Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números naturales NÚMEROS ENTEROS (Z) Los elementos
GUÍA Nº 2 UNIDAD: NÚMEROS Y PROPORCIONALIDAD NÚMEROS ENTEROS NÚMEROS NATURALES (ln) Los elementos del conjunto IN = {1, 2, 3, 4, 5, 6, 7,...} se denominan números naturales NÚMEROS ENTEROS (Z) Los elementos
CONJUNTO DE LOS NÚMEROS NATURALES
 CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
CONJUNTO DE LOS NÚMEROS NATURALES 1.- DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS NATURALES (Conjunto N): Un número natural es cualquier número que se puede usar para contar los elementos de un conjunto finito.
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: PENSAMIENTO NUMÉRICO Y ALGEBRAICO I
 ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
ARITMÉTICA 1. Números naturales 2. Divisibilidad 3. Números enteros 4. Números decimales 5. Fracciones y números racionales 6. Proporcionalidad 7. Sistema métrico decimal 8. Sistema sexagesimal 9. Números
TEMA 1 CONJUNTOS NUMÉRICOS
 TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
Los números naturales
 I.E.S. Los números naturales Contenidos 1. Números naturales Sistema de numeración decimal Escritura Orden y redondeo 2. Operaciones Suma y resta Multiplicación y división Jerarquía de las operaciones
I.E.S. Los números naturales Contenidos 1. Números naturales Sistema de numeración decimal Escritura Orden y redondeo 2. Operaciones Suma y resta Multiplicación y división Jerarquía de las operaciones
TEMA 2. FRACCIONES Y NÚMEROS DECIMALES
 TEMA 2. FRACCIONES Y NÚMEROS DECIMALES ÍNDICE 1. Operaciones con fracciones 2. Operaciones con números decimales 3. Fracciones y números decimales 4. Fracción generatriz Tema 2. Fracciones y números decimales
TEMA 2. FRACCIONES Y NÚMEROS DECIMALES ÍNDICE 1. Operaciones con fracciones 2. Operaciones con números decimales 3. Fracciones y números decimales 4. Fracción generatriz Tema 2. Fracciones y números decimales
LOGRO: Reconoce distintas representaciones de los números reales y usa sus propiedades para resolver Problemas.
 ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
ESTANDARES Utilizo números reales en sus diferentes representaciones y en diversos contextos. Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones
POTENCIACIÓN Y RADICACIÓN
 LECCIÓN 3: POTENCIACIÓN Y RADICACIÓN 3.1.- POTENCIAS La potenciación es la operación que permite obtener el valor de una potencia. Una potencia es un producto de factores iguales. TÉRMINOS DE UNA POTENCIA
LECCIÓN 3: POTENCIACIÓN Y RADICACIÓN 3.1.- POTENCIAS La potenciación es la operación que permite obtener el valor de una potencia. Una potencia es un producto de factores iguales. TÉRMINOS DE UNA POTENCIA
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
UNIDAD DE APRENDIZAJE II NÚMEROS RACIONALES Jerarquía de Operaciones En matemáticas una operación es una acción realizada sobre un número (en el caso de la raíz y potencia) o donde se involucran dos números
Actividades para vacaciones
 Actividades para vacaciones Colegio Virgen del Carmen Números y operaciones 1.- Coloca el símbolo mayor que ( ) o menor que ( ) entre estos pares de números números: 44.999 45.712 7.136 6.905 4.080 8.040
Actividades para vacaciones Colegio Virgen del Carmen Números y operaciones 1.- Coloca el símbolo mayor que ( ) o menor que ( ) entre estos pares de números números: 44.999 45.712 7.136 6.905 4.080 8.040
TEMA 2. Números racionales. Teoría. Matemáticas
 1 1.- Números racionales Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Las fracciones también pueden
1 1.- Números racionales Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Las fracciones también pueden
INSTITUCIÓN EDUCATIVA JORGE ROBLEDO PLAN DE APOYO
 FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
FECHA:07-0-204 Página de 4 ÁREA/ASIGNATURA: ARITMÉTICA PARA LA PROMOCIÓN ANTICIPADA GRADO: SEXTO AÑO: 207 INSTRUCCIONES: La entrega de la solución, por escrito y bien presentada, es requisito indispensable
COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS
 COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS GRADO: 5 ASIGNATURA: Matemática PERIODO: I PROFESOR: María Raquel Vigil. UNIDAD Nº 1 NOMBRE DE LA UNIDAD: JUGUEMOS CON
COLEGIO AUGUSTO WALTE INFORMACIÓN DE ASIGNATURA I PERÍOD DESCRIPCIÓN DE CONTENIDOS GRADO: 5 ASIGNATURA: Matemática PERIODO: I PROFESOR: María Raquel Vigil. UNIDAD Nº 1 NOMBRE DE LA UNIDAD: JUGUEMOS CON
TEMA 2: NÚMEROS ENTEROS
 TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
TEMA : NÚMEROS ENTEROS 1. NÚMEROS ENTEROS Los números naturales se utilizan para expresar matemáticamente multitud de situaciones cotidianas. Sin embargo, a veces no sirven para cuantificar las situaciones
Soluciones a la autoevaluación
 1 Soluciones a la autoevaluación Conoces algunos de los sistemas de numeración utilizados a lo largo de la historia? Pág. 1 1 Aquí tienes una cantidad escrita en distintos sistemas de numeración: 3 290
1 Soluciones a la autoevaluación Conoces algunos de los sistemas de numeración utilizados a lo largo de la historia? Pág. 1 1 Aquí tienes una cantidad escrita en distintos sistemas de numeración: 3 290
Los números enteros. Dado que los enteros contienen los enteros positivos, se considera a los números naturales son un subconjunto de los enteros.
 Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Los números enteros Con los números naturales no era posible realizar diferencias donde el minuendo era menor que el que el sustraendo, pero en la vida nos encontramos con operaciones de este tipo donde
Operaciones con fracciones I
 Matemáticas.º ESO Unidad Ficha 1 Operaciones con fracciones I La suma y resta de fracciones con igual denominador es otra fracción que tiene por: - Numerador: la suma o resta de los numeradores. - Denominador:
Matemáticas.º ESO Unidad Ficha 1 Operaciones con fracciones I La suma y resta de fracciones con igual denominador es otra fracción que tiene por: - Numerador: la suma o resta de los numeradores. - Denominador:
CONJUNTOS NUMÉRICOS. La noción de número es tan antigua como el hombre mismo ya que son necesarios para resolver situaciones de la vida diaria.
 CONJUNTOS NUMÉRICOS La noción de número es tan antigua como el hombre mismo ya que son necesarios para resolver situaciones de la vida diaria. Por ejemplo, usamos números para contar una determinada cantidad
CONJUNTOS NUMÉRICOS La noción de número es tan antigua como el hombre mismo ya que son necesarios para resolver situaciones de la vida diaria. Por ejemplo, usamos números para contar una determinada cantidad
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 0
 Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
AULA MATEMÁTICA - ACTIVIDADES DE AMPLIACIÓN NÚMEROS DECIMALES
 AULA MATEMÁTICA - ACTIVIDADES DE AMPLIACIÓN Abel Martín NÚMEROS DECIMALES Lee los siguientes números y escríbelos con letra: 00 (a) 7.2 (b) 7.2 (c) 7.23 (d) 7.234 (e) 7.2345 (f) 7.23453 (g) 8.0523 (a)
AULA MATEMÁTICA - ACTIVIDADES DE AMPLIACIÓN Abel Martín NÚMEROS DECIMALES Lee los siguientes números y escríbelos con letra: 00 (a) 7.2 (b) 7.2 (c) 7.23 (d) 7.234 (e) 7.2345 (f) 7.23453 (g) 8.0523 (a)
TEMA 1 MATEMÁTICAS 1º E.S.O.
 TEMA 1 MATEMÁTICAS 1º E.S.O. NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN El conjunto de los números naturales es ilimitado y está formado por: N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, El sistema de numeración decimal
TEMA 1 MATEMÁTICAS 1º E.S.O. NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN El conjunto de los números naturales es ilimitado y está formado por: N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, El sistema de numeración decimal
TEMA 1. Números Reales. Teoría. Matemáticas
 1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
Escribe en tu cuaderno dos situaciones donde se utilicen los números y explica qué significado tienen en cada caso MANUEL
 UNIDAD AR Escribe en tu cuaderno dos situaciones donde se utilicen los números y explica qué significado tienen en cada caso. 2 Escribe con cifras y con letras los números representados: CM DM UM C D U
UNIDAD AR Escribe en tu cuaderno dos situaciones donde se utilicen los números y explica qué significado tienen en cada caso. 2 Escribe con cifras y con letras los números representados: CM DM UM C D U
Tema 3: Multiplicación y división.
 Tema 3: Multiplicación y división. SELECCIÓN DE EJERCICIOS RESUELTOS 2. Determina el menor número natural que multiplicado por 7 nos da un número natural que se escribe usando únicamente la cifra 1. Y
Tema 3: Multiplicación y división. SELECCIÓN DE EJERCICIOS RESUELTOS 2. Determina el menor número natural que multiplicado por 7 nos da un número natural que se escribe usando únicamente la cifra 1. Y
Opuesto de un número +3 + (-3) = (+5) = 0. N = 0,1, 2,3,4, Conjunto de los números naturales
 Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
Números enteros Opuesto de un número Los números enteros son una extensión de los números naturales, de tal forma, que los números enteros tienen signo positivo (+) ó negativo (-). Los números positivos
5 REPASO Y APOYO OBJETIVO 1
 REPASO Y APOYO OBJETIVO 1 COMPARAR Y ORDENAR NÚMEROS DECIMALES El sistema de numeración decimal tiene dos características: 1. a Es decimal: 10 unidades de un orden forman 1 unidad del orden siguiente.
REPASO Y APOYO OBJETIVO 1 COMPARAR Y ORDENAR NÚMEROS DECIMALES El sistema de numeración decimal tiene dos características: 1. a Es decimal: 10 unidades de un orden forman 1 unidad del orden siguiente.
Fracciones: lectura y escritura
 Fracciones: lectura y escritura PLAN DE MEJORA Ficha La fracción que representa la parte sombreada es: Número de partes sombreadas Número de partes iguales de la figura La fracción se lee: un medio. Escribe
Fracciones: lectura y escritura PLAN DE MEJORA Ficha La fracción que representa la parte sombreada es: Número de partes sombreadas Número de partes iguales de la figura La fracción se lee: un medio. Escribe
Los números enteros y racionales
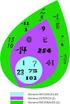 Los números enteros y racionales Objetivos En esta quincena aprenderás a: Representar y ordenar números enteros Operar con números enteros Aplicar los conceptos relativos a los números enteros en problemas
Los números enteros y racionales Objetivos En esta quincena aprenderás a: Representar y ordenar números enteros Operar con números enteros Aplicar los conceptos relativos a los números enteros en problemas
Los Números Enteros (Z)
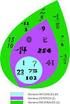 Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
Los Números Enteros (Z) Los números enteros: representación gráfica, orden, modulo o valor absoluto. Operaciones en Z, procedimientos y propiedades de estas. Prioridades de operaciones y paréntesis. Problemas
LOS NÚMEROS NATURALES. Los números están formados por cifras. El valor de cada cifra depende de la posición que ocupa en el número.
 LOS NÚMEROS NATURALES Los números están formados por cifras. El valor de cada cifra depende de la posición que ocupa en el número. Ejemplo: En el número 25.628 2 DM = 20.000 U 2 D = 20 U Para ordenar varios
LOS NÚMEROS NATURALES Los números están formados por cifras. El valor de cada cifra depende de la posición que ocupa en el número. Ejemplo: En el número 25.628 2 DM = 20.000 U 2 D = 20 U Para ordenar varios
*Número natural, el que sirve para designar la cantidad de. *El cero, a veces, se excluye del conjunto de los números
 *Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
*Número natural, el que sirve para designar la cantidad de elementos que tiene un cierto conjunto, y se llama cardinal de dicho conjunto. *Los números naturales son infinitos. El conjunto de todos ellos
TEMA 1: LOS NÚMEROS ENTEROS. Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León.
 TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
TEMA 1: LOS NÚMEROS ENTEROS Segundo Curso de Educación Secundaria Obligatoria. I.E.S de Fuentesaúco. Manuel González de León. CURSO 2011-2012 1. Los Números Enteros. 2. Suma y resta de números enteros.
INSTITUCIÓN EDUCATIVA TÉCNICA SAGRADO CORAZÓN Aprobada según Resolución No NIT DANE SOLEDAD ATLÁNTICO.
 Página 1 de 24 GUÍA N 3 ÁREA:MATEMATICAS GRADO:QUINTO Docente; RAMIRO OSORIO GUTIERREZ PERIODO:SEGUNDO IH (en horas): 20 EJE TEMÁTICO OPERACIONES CON NUMEROS DECIMALES DESEMPEÑO Resolver situaciones problemas
Página 1 de 24 GUÍA N 3 ÁREA:MATEMATICAS GRADO:QUINTO Docente; RAMIRO OSORIO GUTIERREZ PERIODO:SEGUNDO IH (en horas): 20 EJE TEMÁTICO OPERACIONES CON NUMEROS DECIMALES DESEMPEÑO Resolver situaciones problemas
UNIDAD 3: NÚMEROS DECIMALES
 UNIDAD 3: NÚMEROS DECIMALES Si dividimos la unidad en 10 partes iguales, cada parte es una DÉCIMA. Cuando necesitamos expresar cantidades más pequeñas que la unidad, utilizamos LAS UNIDADES DECIMALES.
UNIDAD 3: NÚMEROS DECIMALES Si dividimos la unidad en 10 partes iguales, cada parte es una DÉCIMA. Cuando necesitamos expresar cantidades más pequeñas que la unidad, utilizamos LAS UNIDADES DECIMALES.
FICHAS DE TRABAJO REFUERZO
 FICHAS DE TRABAJO REFUERZO DEPARTAMENTO DE MATEMATICAS CONTENIDO 1. Números naturales a. Leer y escribir números naturales b. Orden de cifras c. Descomposición polinómica d. Operaciones combinadas e. Potencias
FICHAS DE TRABAJO REFUERZO DEPARTAMENTO DE MATEMATICAS CONTENIDO 1. Números naturales a. Leer y escribir números naturales b. Orden de cifras c. Descomposición polinómica d. Operaciones combinadas e. Potencias
OBJETIVO 1 CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: FECHA: Unidad de millar. Decena de millar
 OBJETIVO CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: 0 unidades de un orden forman unidad del
OBJETIVO CONOCER LA ESTRUCTURA DEL SISTEMA DE NUMERACIÓN DECIMAL NOMBRE: CURSO: ECHA: El sistema de numeración decimal tiene dos características:. a Es decimal: 0 unidades de un orden forman unidad del
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 5 / 08 / 15 Guía Didáctica 3-6 Desempeños: * Resuelve operaciones y polinomios
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS GRADO:6 O DOCENTE: Nubia E. Niño C. FECHA: 5 / 08 / 15 Guía Didáctica 3-6 Desempeños: * Resuelve operaciones y polinomios
UNIDAD 1 CONCEPTOS BÁSICOS. Números naturales, Números enteros, Números racionales, números irracionales y números reales. Dr. Daniel Tapia Sánchez
 UNIDAD 1 CONCEPTOS BÁSICOS Números naturales, Números enteros, Números racionales, números irracionales y números reales Dr. Daniel Tapia Sánchez 1.1 Números Naturales (N) 1.1.1 Consecutividad numérica
UNIDAD 1 CONCEPTOS BÁSICOS Números naturales, Números enteros, Números racionales, números irracionales y números reales Dr. Daniel Tapia Sánchez 1.1 Números Naturales (N) 1.1.1 Consecutividad numérica
Asignatura: Pensamiento Lógico
 GIMNASIO MODERNO CASTILLA Asignatura: Pensamiento Lógico Docentes: Mariela Pinzón y Luz Stella Valdez Nota: Grado: TALLER DE RECUPERACIÓN III Y IV PERIODO 2016 4TO A Y B NOMBRE: Instrucciones para la entrega
GIMNASIO MODERNO CASTILLA Asignatura: Pensamiento Lógico Docentes: Mariela Pinzón y Luz Stella Valdez Nota: Grado: TALLER DE RECUPERACIÓN III Y IV PERIODO 2016 4TO A Y B NOMBRE: Instrucciones para la entrega
Y LOS ELEMENTOS QUE FORMAN UN POLINOMIO. Nombre: Curso: Fecha: F Cómo es el polinomio, completo o incompleto?
 REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
REPASO Y APOYO OBJETIVO 1 3 RECONOCER EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO Nombre: Curso: echa: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los
TEMA 4: LAS FRACCIONES
 TEMA : LAS FRACCIONES Hasta ahora has trabajado con números naturales, enteros y decimales, pero sigue habiendo situaciones que no podemos expresar con estos números, por ejemplo, cuando decimos: Medio
TEMA : LAS FRACCIONES Hasta ahora has trabajado con números naturales, enteros y decimales, pero sigue habiendo situaciones que no podemos expresar con estos números, por ejemplo, cuando decimos: Medio
