3.1 OPERADORES DIFERENCIALES a) Gradiente de un c. escalar, U:
|
|
|
- Elisa Peña Lozano
- hace 6 años
- Vistas:
Transcripción
1 Obs.: Dfrncal d na mantd varabl n 3(ó 2) 1) En nral (Análss): S f dpnd d (y 1, y m ), df := y1 f dy ym f dy m Lo msmo ocrr s s trata d na mantd vctoral d n componnts, F: df := y1 F dy ym F dy m. El df o l df son los térmnos d prmr ordn n l dsarrollo d Taylor d f o d F alrddor dl pnto y consttyn na apro. dl f o F 2) En 3 : Dfrncal dl vctor poscón r(p) n cart. y n crv. df.: En cartsanas, al pasar d P(,y,z) a Q(+d, y+dy, z+dz), s dfn dr = d + dy + dz = d = PQ = dsplazamnto vctoral ral = r = OQ OP En crvlínas, al pasar d P(,v,w) a Q(+d, v+dv, w+dw), l Análss asra: dr = r r r d v dv w dw d PQ = r El dr s, ps, análoo, pro rslta l dsarrollo contravarant dl vctor dr, y sólo s aproma () l dsplazamnto ral, r, n lar d concdr con él. Pro l vctor dr s ntrínsco (l msmo vctor, prsado n los dos sstmas) porq: col. ª J 1 d r d d d d Obs. (!!!): la prsón d n prodcto scalar dr n crvlínas ncsta las componnts covas dl campo, para oprar con las componnts contras dl dr. Así: dr = d = 1 ( 1, 2, 3 ) d ( 1, 2, 3 ) d ( 1, 2, 3 ) d 3 ; na contraccón T dr ncsta componnts t ( 1, 2, 3 ) para prodcr contras dl rsltado. 3.1 OPERADORES a) Gradnt d n c. scalar, U: 1) dfncón: dado U : 3, n 3 con rfrs. cartsana {O; } y crvlína {O; } asocadas n n pnto orn O d crta rón. S stda la varacón d U rspcto dl pnto P, o sa, al varar la poscón dl pnto n l spaco. D Cálclo sabmos: l ncr. d U: U := U(+d, y+dy, z+dz) U(,y,z) U U U d dy d: z = du y z s análoo n crvlínas, con du = U U U d dv dw U. n ambos casos s pd ntndr du como rsltado (scalar) d la accón d n tnsor d ordn 1 (forma lnal) sobr l vctor dr: n cart.: du = ( U + yu + z U ) dr y n crv. : du = ( 1U 1 + 2U 2 + 3U 3 ) (d ) ( Obs.: prfactor n covas!) S obsrva q s trata dl msmo vctor prsado n los dos sst. S llama vctor radnt d U y s l vctor: fla d J a covas U U U U U U U U + y z l símbolo nabla,, (o atld ) s la dlta may. ra nvrtda, dbdo a Hamlton Métodos - matmátcas /
2 2) Propdads dl radnt d n c. scalar d clas C 1 : ) Prop. fndamntal: l vctor U rla la varacón d U n l spaco, pq. U du=u dr, como s ha vsto. ) Natralza tnsoral: porq la drvada drcconal U(P) d n c. sc. d clas 1 n calqr drccón tomada n P s: U(P) = U(P) U( Pλ ) U( P) U( P) λ dm: U ( P): lm lm U ( P) λ0 λ λ0 λ y sto sr consdrarlo como n tnsor d prmr ordn: U Î (1). ) las lín. d campo d U son ortoonals a las sprf. socantas U = ct. dm: s s tant. a la sp. {U = c} n P, ntoncs U(P) = 0, lo U(P) = 0 Como ocrr " tt. A la sp., rslta q U(P) tt (P) v) la máma drvada drcconal d U n P s U(P) n la propa dr. U dl radnt U(P). dm: U(P) = U(P) = U(P) cos U(P), mámo s l lánlo s 0. 3) El oprador dfrncal nabla: : Es vntaoso consdrar como n oprador dfrncal vctoral q prodc l radnt al "mltplcars" por campos scalars. Las Rlas d actacón d sobr campos scalars q s opran ntr sí: son las msmas d la drvada, s dcr: / lnaldad frnt a comb. ln. con cof. constants, a, b: (au+bv) = a U + b V radnt dl prodcto o cocnt d campos scalars (UV) = (U) V + U (V), (U/V) = [(U)V U (V)]/V 2 radnt d na potnca: (U m ) = mu m-1 U otras rlas d actacón n b) opradors rlaconados con Emplos: 1) En cartsanas s cmpl = 2) En crvlínas: = (altrnatva para calclar ) 3) n cl.: z cos sn z 4) (a r+c), dond a s n vc. ct. y c = ct. scalar: (a r+c) = a 5) (a r /r 2 ) =... D Pr2.12, apartados:1, 2, 3, y 7 Métodos - matmátcas /
3 b) Opradors dfrncals rlaconados con nabla S llama oprador nabla al vctor smbólco: := + y + z =, q rslta al abstrar l campo sc. U dl radnt U. En crv. s análoo: := = + v v + w w ( covas!) o sa: : + y z v w Cando actúa sobr n campo scalar da l radnt U y la forma d tratarlo s: vctor smbólco cyas componnts s "mltplcan" por U prodcndo la drvada parcal q ndcan. En crv. s covarant pro s ntnd al. Otros opradors: l oprador s combna con otros prodctos * d vctors o tnsors y la accón dl oprador rsltant s dtrmna n nral así: 1º) s drva l 2º factor n carts. s dfn: * := * : * 2º ) s fcta l prodcto q.sa n crv. s análoo: * := Casos más mportants: op. dvrnca := op. rotaconal := op. laplacano := = 2 op. radnt-tnsor: 1º) s drva (drv. covarant) * : * 2º ) s fcta l prodcto s aplca la norma nral antror y rslta: S = U = =, s tn: 1) dvrnca d : =... U U U U U y U z carts.:... : y z crv.:... h h :, h, h,,1,2,3 1 Forma práctca n crv. formlº: obs: sa contras d! dm: s obsrva: 1), =, = [ + h h] = + h h 2) (± ) = [ 1, 2, 3 ] = [ 1, 2, 3 ] + [ 1, 2, 3 ] + [ 1, 2, 3 ] = = [ 1 1 +, 2 +, 3 = ± ( = ± h 1, 2, 3 ] [ 1 2 2, 3 ] [ 1, ] 3) h y s ddc: (± ) = ± h h ± = ± (,) = 1/ [ ( )], c.q.d. yz Emplos: Calclar la dvrnca d: 1) F(,y,z) = ; 2) Msmo campo n y z sfércas ; 3) (,, z) = + + z z ( oo, no s r!) PR2.12, apartados 4 y 9 Métodos - matmátcas /
4 2) rotaconal d = U = : =... U U n cart.: U U U : y z y z n crv.: 1 :...,, 1 q. condc a la frmla. práctca (formlº): obs.: covas d! Emplos: Calclar a l rotaconal o a d los campos consdrados n l mplo antror: yz 1) F(,y,z) = ; y z 2) Msmo mplo pasándolo a sfércas ; 3) (,, z) = + + z z 4) PR2.13, cstón. PR2.18, cstón 3) laplacano := U := (U) = 2 U n cartsanas: n crvlínas: U U U U ( U)... y z 1 U U ( U) 4) radnt-tnsor := = U n cartsanas: U n crvlínas:, obs: l dfrncal d n campo vctoral s: d = = () Rlas d actacón d los opradors sobr prodctos formlaro! Emplo: Calclar dv(ar) sndo a n c. vctoral constant dl spaco 3. Otros rccos: PR212, cstons d los problmas PR2.13, 15, 18 Métodos - matmátcas /
5 c) Opradors dfrncals n bas físca crvlína Las fórmlas para calclar los op. dfrncals d campos n bas físca s adaptan con sncllz, cambando las bass o componnts nrals a aqélla : h :=, a = â ê, = h h v h w, = ê /h (para cada ), a = â /h (para cada ), a = h â (para cada ). Así: 1 U 1 U 1 U U ˆ ˆ ˆ h h v h w 1 a aˆ h h h aˆ h h h aˆ hhh a 1 hhh h ˆ h vˆv hwˆw haˆ haˆ h aˆ v v w w 1 hh U hh U hh U v w w v U U h h v h w h v h v v w h w w Emplos y rccos 1) y sndo { = p(+v), y = p(v), z = w} solcón: n contras s (1,0,0); y n covas, s 1 = 1 = (2 Ch2v, 2 Sh2v, 0) lo: (campo rrotaconal) 2 2 Ch2v 2 Sh2v 0 2) Práctca 2b: Erccos: PR2.14, y PR2.15 Problmas d amn: PR2.16, PR2.17, PR2.18. (FIN DE LA MATERIA DEL PRIMER PARCIAL) Métodos - matmátcas /
Si v y w son ambos vectores, entonces el resultado de las operaciones v + w y v w son. Dichas operaciones cumplen con propiedades conmutativas y
 Crso nzdo d Fnómnos d Trnsport Dr. Jn Cros Frro Gonzáz Dprtmnto d Ingnrí Qímc Insttto Tcnoógco d Cy Oprcons con Vctors Adcón y sbstrccón d ctors S y w son mbos ctors, ntoncs rstdo d s oprcons w y w son
Crso nzdo d Fnómnos d Trnsport Dr. Jn Cros Frro Gonzáz Dprtmnto d Ingnrí Qímc Insttto Tcnoógco d Cy Oprcons con Vctors Adcón y sbstrccón d ctors S y w son mbos ctors, ntoncs rstdo d s oprcons w y w son
Administración de inventarios. Ejercicio práctico.
 Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
Admnstracón d nvntaros. Ejrcco práctco. La Cía. GOMA REDONDA S.A. llva n nvntaro un crto tpo d numátcos, con las sgunts caractrístcas: Vntas promdo anuals: 5000 numátcos Costo d ordnar: $ 40/ ordn Costo
Transformada de Laplace
 Tranformada d alac CIPQ Marga Marco, Itzar Caban, Eva Portllo, 6 Tranformada d alac f(t funcón tmoral f(t f(t ara t < [ f (t] F( f (t t σ jω varabl comlja d alac t f(t g(t [ f (t] [ g(t ] F( G( Cambo d
Tranformada d alac CIPQ Marga Marco, Itzar Caban, Eva Portllo, 6 Tranformada d alac f(t funcón tmoral f(t f(t ara t < [ f (t] F( f (t t σ jω varabl comlja d alac t f(t g(t [ f (t] [ g(t ] F( G( Cambo d
3. DINÁMICA DEL SÓLIDO RÍGIDO
 3. DINÁMICA DEL SÓLIDO RÍIDO 3.1. Dnámca la partícula La sguna ly Nwton stablc qu n una partícula masa constant m sobr la qu actúa una furza F s vrfca F p (3.1) on p s l momnto lnal qu s fn como l proucto
3. DINÁMICA DEL SÓLIDO RÍIDO 3.1. Dnámca la partícula La sguna ly Nwton stablc qu n una partícula masa constant m sobr la qu actúa una furza F s vrfca F p (3.1) on p s l momnto lnal qu s fn como l proucto
Tabla 3 Diámetro de la Nombre Perímetro de la muñeca muñeca (aprox.) Cierre: (20 minutos) Perímetro de Nombre Tal a o

Masa y composición isotópica de los elementos
 Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
Masa y composición isotópica de los elementos www.vaxasoftware.com Z Sím A isótopo Abndancia natral Vida Prodcto 1 H 1 1,00782503207(10) 99,9885(70) 1,00794(7) estable D 2 2,0141017780(4) 0,0115(70) estable
LECCIÓN 6 AMPLIFICADORES OPERACIONALES
 LEIÓN 6. mplfcaor Opraconal LEIÓN 6 MPLIFICDOES OPECIONLES mplfcaor frncal mplfcaor opraconal. El O al plcacon lnal lo O plcacon no lnal lo O Caractrítca ral lo O LEIÓN 6. mplfcaor Opraconal mplfcaor frncal
LEIÓN 6. mplfcaor Opraconal LEIÓN 6 MPLIFICDOES OPECIONLES mplfcaor frncal mplfcaor opraconal. El O al plcacon lnal lo O plcacon no lnal lo O Caractrítca ral lo O LEIÓN 6. mplfcaor Opraconal mplfcaor frncal
Matemáticas II TEMA 8 Derivadas. Teorema. Regla de L Hôpital Problemas Propuestos
 Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
Matmáticas II TEMA 8 Drivadas Torma Rgla d L Hôpital Problmas Propustos Drivada d una función n un punto Utilizando la dfinición, calcula la drivada d f ( ) n l punto = Utilizando la dfinición, halla la
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
En imprenta: Anuario Martiano. Revista del Centro de Estudios Martianos. (La Habana, Cuba). Sección Estudios y aproximaciones
 Publicado en: Revista Cubana de Filosofía. Edición Digital No. 15. Junio - Septiembre 2009. ISSN: 1817-0137 En: http://revista.filosofia.cu/articulo.php?id=549 En imprenta: Anuario Martiano. Revista del
Publicado en: Revista Cubana de Filosofía. Edición Digital No. 15. Junio - Septiembre 2009. ISSN: 1817-0137 En: http://revista.filosofia.cu/articulo.php?id=549 En imprenta: Anuario Martiano. Revista del
Lección 3. Cálculo vectorial. 4. Integrales de superficie.
 GRAO E INGENIERÍA AEROEPACIAL CURO 0 MATEMÁTICA II PTO E MATEMÁTICA APLICAA II 4 Integrales de sperficie Nestro último paso en la etensión del concepto de integral es el estdio de las integrales de sperficie,
GRAO E INGENIERÍA AEROEPACIAL CURO 0 MATEMÁTICA II PTO E MATEMÁTICA APLICAA II 4 Integrales de sperficie Nestro último paso en la etensión del concepto de integral es el estdio de las integrales de sperficie,
MODELOS DE SUBASTAS Y SU APLICACIÓN A LOS CONCURSOS
 Modlos d sbastas y s aplaón a los onrsos. MODELOS DE SUBASTAS Y SU APLICACIÓN A LOS CONCURSOS Jan Momparlr, Maro Hdalgo Jam I, UTEM RESUMEN En st trabao ralzamos na ntrodón hstóra a la Toría d sbastas
Modlos d sbastas y s aplaón a los onrsos. MODELOS DE SUBASTAS Y SU APLICACIÓN A LOS CONCURSOS Jan Momparlr, Maro Hdalgo Jam I, UTEM RESUMEN En st trabao ralzamos na ntrodón hstóra a la Toría d sbastas
Tema 2. Termodinámica Estadística. Problemas
 ma. rmodnámca Estadístca Problmas jrccos. La apromacón d trlng (ln! ln - ) prmt valuar l logartmo d factorals d númros grands con un rror puño. Calcula y rprsnta l rror rlatvo (n %) obtndo al utlzar la
ma. rmodnámca Estadístca Problmas jrccos. La apromacón d trlng (ln! ln - ) prmt valuar l logartmo d factorals d númros grands con un rror puño. Calcula y rprsnta l rror rlatvo (n %) obtndo al utlzar la
b-h s:= )EE F "fif E(e )kq r 7: 60 su) ) { ; ;l ec_ .A nf ;c"t {d<r \-{ o+ qtrc s;.., Yts f F{ q )'6 =O (U LU o- )) $fi 3 -tue ah ;.
 l l ll l l,l " l l '( i '( (. j /, 1 l l.l l *l.t..., T 0!. ^. L \ \ \.>. i. L \ L L 1 ( i > ' K i!! : l ( 1 bh Q,Lj 5 T QD 1..,4 ' 0 0 L > L L? 4 u l! i5 0, ul l l l i' l (l (l > * Y { '* {! : ( l } D
l l ll l l,l " l l '( i '( (. j /, 1 l l.l l *l.t..., T 0!. ^. L \ \ \.>. i. L \ L L 1 ( i > ' K i!! : l ( 1 bh Q,Lj 5 T QD 1..,4 ' 0 0 L > L L? 4 u l! i5 0, ul l l l i' l (l (l > * Y { '* {! : ( l } D
Contactores TeSys. Referencias 5. Bobinas en corriente alterna para contactores tri o tetrapolares TeSys d
 Referencias 5 537496 Para contactores a LC1 D09...D38 y LC1 DT0 DT40 Llamada (cos ϕ = 0,75) 70 VA. Mantenimiento (cos ϕ = 0,3) 50 Hz: 7 VA, 60 Hz: 7,5 VA. Campo de funcionamiento (θ y 60 C): 50 Hz: 0,8
Referencias 5 537496 Para contactores a LC1 D09...D38 y LC1 DT0 DT40 Llamada (cos ϕ = 0,75) 70 VA. Mantenimiento (cos ϕ = 0,3) 50 Hz: 7 VA, 60 Hz: 7,5 VA. Campo de funcionamiento (θ y 60 C): 50 Hz: 0,8
IPC PLAN 6º EPO 2 nd TERM
 IP PLAN 6º EPO 2 d TERM ONTENT UNIT 3: GROWING UP! ASSESSMENT I S, w fdg : Hw d f d gw d dp A h hg h k p dg py f y d g Hw h pd Hw y dp d h A dff hd f p I Sy, w fdg : A dff yp f hp A h p d f h f fy d A
IP PLAN 6º EPO 2 d TERM ONTENT UNIT 3: GROWING UP! ASSESSMENT I S, w fdg : Hw d f d gw d dp A h hg h k p dg py f y d g Hw h pd Hw y dp d h A dff hd f p I Sy, w fdg : A dff yp f hp A h p d f h f fy d A
F U N D A D O POR DON 0SE B A T l L E Y O R D O Ñ E Z EL > 6 DE J U N I O DE « '»eriarclóo 0 E O O A4 I N C O A LLAMENOS CHURRASOUERA
 $ Ñ $ $ & $ [ & Ó Ü Ó É & à # ú Î à Ö # Ç # # Î# ~ ì & & # ~ ì ï + ú Ü ö Ù ì ï # Û à Ö Ö Ä # ç & Ú Î Ü æ ~ ò ú ì ] ~ ~ ì ~ à ì Ì & û ú ~ # ~ ò & Î # Ì Ï = ~ = = ~ ò ô Î & ï à Á û ô ß æ + ì ] Ä ò æ Ï ]
$ Ñ $ $ & $ [ & Ó Ü Ó É & à # ú Î à Ö # Ç # # Î# ~ ì & & # ~ ì ï + ú Ü ö Ù ì ï # Û à Ö Ö Ä # ç & Ú Î Ü æ ~ ò ú ì ] ~ ~ ì ~ à ì Ì & û ú ~ # ~ ò & Î # Ì Ï = ~ = = ~ ò ô Î & ï à Á û ô ß æ + ì ] Ä ò æ Ï ]
Parte I: Propagación de ondas
 desarrollo de experencas ddáctcas 5 Anmando la Físca Parte I: Propagacón de ondas Oleg V. Nagornov, Roberto E. Calgars, Georgna B. Rodrígez y Marta G. Calgars Calqer profesor qe trate de enseñar físca
desarrollo de experencas ddáctcas 5 Anmando la Físca Parte I: Propagacón de ondas Oleg V. Nagornov, Roberto E. Calgars, Georgna B. Rodrígez y Marta G. Calgars Calqer profesor qe trate de enseñar físca
Ejercicios de Integrales resueltos
 Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
Ejercicios de Integrales resueltos. Resuelve la integral: Ln Ln Llamemos I Ln u du Aplicamos partes: dv v I Ln t t 4 t t t 4 t t 4 t 4 4 4t 4 t t t A t B t A( t) B( t) A ; B 4 t t Ln t Ln t t C Deshaciendo
Colección de problemas de. Poder de Mercado y Estrategia
 de Poder de Mercado y Estrategia urso 3º Grado en Economía 0-03 ñaki guirre Jaromir Kovarik Marta San Martín Fundamentos del nálisis Económico Universidad del País Vasco UPV/EU Tema. Teoría de Juegos y
de Poder de Mercado y Estrategia urso 3º Grado en Economía 0-03 ñaki guirre Jaromir Kovarik Marta San Martín Fundamentos del nálisis Económico Universidad del País Vasco UPV/EU Tema. Teoría de Juegos y
OBJETIVOS: Definir Límites. Realizar demostraciones formales de límites. Describir gráficamente los límites. Calcular límites.
 Cap. Límites de Fnciones. LÍMITE EN UN PUNTO. LÍMITES LATERALES. TEOREMAS SOBRE LÍMITES.4 CÁLCULO DE LÍMITES.5 LÍMITES AL INFINITO.6 LÍMITES INFINITOS.7 OTROS LÍMITES OBJETIVOS: Definir Límites. Realizar
Cap. Límites de Fnciones. LÍMITE EN UN PUNTO. LÍMITES LATERALES. TEOREMAS SOBRE LÍMITES.4 CÁLCULO DE LÍMITES.5 LÍMITES AL INFINITO.6 LÍMITES INFINITOS.7 OTROS LÍMITES OBJETIVOS: Definir Límites. Realizar
CAPÍTULO 2. Ecuación paraxial de Helmholtz.
 CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
CAPÍTLO Ecuacón paraal d Hlmholt. S dscut la posbldad d vsualar mdant un procsador óptco [1] a las solucons d la cuacón paraal d Hlmholt. Para llo s rala una comparacón d los rsultados obtndos consdrando
EJERCICIO. Dadas las rectas y
 EJERCICIO Dadas las rectas x4 y1 z y z 8 r : y s: x1 1 3 se pide: a) Comprueba que las rectas r y s se cruzan. b) Determina la ecuación de la perpendicular común. c) Calcula la distancia entre ambas. Perpendicular
EJERCICIO Dadas las rectas x4 y1 z y z 8 r : y s: x1 1 3 se pide: a) Comprueba que las rectas r y s se cruzan. b) Determina la ecuación de la perpendicular común. c) Calcula la distancia entre ambas. Perpendicular
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS
 CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
CAPÍTULO 14: LAS EXPECTATIVAS: LOS INSTRUMENTOS BÁSICOS 14-1 Los tipos d intrés nominals y rals Slid 14.2 Los tipos d intrés xprsados n unidads d la monda nacional s dnominan tipos d intrés nominals. Los
TEOREMAS DE CIRCUITOS ELÉCTRICOS. 2.1 Teoremas de THEVENIN Y NORTON y MILLMAN. Pasivado de fuentes
 TOMS D IUITOS LTIOS TOMS D IUITOS LÉTIOS. Teoremas de VNIN Y NOTON y MILLMN Pasvado de fentes Una fente qeda pasvada cando el módlo de s magntd eléctrca se hace cero (No tene más capacdad de aportar energía
TOMS D IUITOS LTIOS TOMS D IUITOS LÉTIOS. Teoremas de VNIN Y NOTON y MILLMN Pasvado de fentes Una fente qeda pasvada cando el módlo de s magntd eléctrca se hace cero (No tene más capacdad de aportar energía
DISEÑO ÓPTIMO SIMULTÁNEO DE TOPOLOGÍA Y GEOMETRÍA DE ESTRUCTURAS ARTICULADAS MEDIANTE TÉCNICAS DE CRECIMIENTO
 UNIVERSIDAD POLITÉCNICA DE CARTAGENA DEPARTAMENTO DE ESTRUCTURAS Y CONSTRUCCIÓN DISEÑO ÓPTIMO SIMULTÁNEO DE TOPOLOGÍA Y GEOMETRÍA DE ESTRUCTURAS ARTICULADAS MEDIANTE TÉCNICAS DE CRECIMIENTO Pdro Jsús Martínz
UNIVERSIDAD POLITÉCNICA DE CARTAGENA DEPARTAMENTO DE ESTRUCTURAS Y CONSTRUCCIÓN DISEÑO ÓPTIMO SIMULTÁNEO DE TOPOLOGÍA Y GEOMETRÍA DE ESTRUCTURAS ARTICULADAS MEDIANTE TÉCNICAS DE CRECIMIENTO Pdro Jsús Martínz
ú
 ť ú ú ď ř Ž ú ť ě ř ú Í ú ř Í ú ř ř ú č Ó ú ě Í Ť ý ř ú Í ŤÉ ř š ú Í ť ť ů ú ť ť Á Á Ř ř ú Ú Í ě ě Ó Í ě ě ě Í ú ú ú É ú ú ú Í ú ř ú ú ú ú Í Í Á Ť Ž Ř Í ú ú ú Í ú ů ř Í ě ú ú ú Í ú ú
ť ú ú ď ř Ž ú ť ě ř ú Í ú ř Í ú ř ř ú č Ó ú ě Í Ť ý ř ú Í ŤÉ ř š ú Í ť ť ů ú ť ť Á Á Ř ř ú Ú Í ě ě Ó Í ě ě ě Í ú ú ú É ú ú ú Í ú ř ú ú ú ú Í Í Á Ť Ž Ř Í ú ú ú Í ú ů ř Í ě ú ú ú Í ú ú
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
 III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
bunes 17 de Enero de 1021 No se reparten esquelas. D o n QUE FALLECIO EN SALAMANCA EL DIA 18 DE ENERO DE 1920
 P ñ: jc q v * C ú 2 5 ú- ú 37 P HW8KB vv : q 4 2 é ú 67 C v Z é XXX 235 7 2 "j Z 42 P Y B - 26 C j x - P v - j F C P C q - P j - v j j J Ñ P h 6 5 92 é B P G h: F h * B ñ ú v vv F: 7 v ñ q: ñ C C v: C
P ñ: jc q v * C ú 2 5 ú- ú 37 P HW8KB vv : q 4 2 é ú 67 C v Z é XXX 235 7 2 "j Z 42 P Y B - 26 C j x - P v - j F C P C q - P j - v j j J Ñ P h 6 5 92 é B P G h: F h * B ñ ú v vv F: 7 v ñ q: ñ C C v: C
Campo eléctrico. Líneas de campo. Teorema de Gauss. El campo de las cargas en reposo. Campo electrostático
 qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
qco sθ qz Ez= 4 zπε0 2+ R2 = 4πε0 [z2 +R2 ]3/ 2 El campo de las cargas en reposo. Campo electrostátco ntroduccón. Propedades dferencales del campo electrostátco. Propedades ntegrales del campo electromagnétco.
EVIDENCIA EMPÍRICA DE LA COMBINACIÓN DE PSICOTERAPIA Y TRATAMIENTO FARMACOLÓGICO DE LA FOBIA SOCIAL (TRASTORNO DE ANSIEDAD SOCIAL)
 Y FACULTAD DE PSICOLOGÍA - UBA / SECRETARÍA DE INVESTIGACIONES / ANUARIO DE INVESTIGACIONES / VOLUMEN XX EVIDENCIA EMPÍRICA DE LA COMBINACIÓN DE PSICOTERAPIA Y TRATAMIENTO FARMACOLÓGICO DE LA FOBIA SOCIAL
Y FACULTAD DE PSICOLOGÍA - UBA / SECRETARÍA DE INVESTIGACIONES / ANUARIO DE INVESTIGACIONES / VOLUMEN XX EVIDENCIA EMPÍRICA DE LA COMBINACIÓN DE PSICOTERAPIA Y TRATAMIENTO FARMACOLÓGICO DE LA FOBIA SOCIAL
2º Bachillerato: ejercicios modelo para el examen de las lecciones 11, 12 y 13
 º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
LÍMITES, CONTINUIDAD Y DERIVADAS
 LÍMITES, CONTINUIDAD Y DERIVADAS ÍNDICE. Concepto de límite. Propiedades de los límites 3. Definición de continidad 4. Tipos de continidad 5. Concepto de derivada 6. Tabla de derivadas 7. Crecimiento y
LÍMITES, CONTINUIDAD Y DERIVADAS ÍNDICE. Concepto de límite. Propiedades de los límites 3. Definición de continidad 4. Tipos de continidad 5. Concepto de derivada 6. Tabla de derivadas 7. Crecimiento y
A1. ELEMENTOS DE VIGA DE EULER BERNOULLI LIBRES DE ROTACIÓN
 Anass d acas y amna 34 ANEJO I A. ELEMENOS DE VIGA DE EULER ERNOULLI LIRES DE ROACIÓN La toría d vgas d Eur-rnou s robabmnt uno d os robmas modo más sms d a formuacón rstrngda d a astcdad na. La rstrccón
Anass d acas y amna 34 ANEJO I A. ELEMENOS DE VIGA DE EULER ERNOULLI LIRES DE ROACIÓN La toría d vgas d Eur-rnou s robabmnt uno d os robmas modo más sms d a formuacón rstrngda d a astcdad na. La rstrccón
Problemas Resueltos. el radio de la órbita circular, y la energía tiene el valor GMm 2 = a GM. 0. Es decir, 2 T 4π. GMm
 Problmas sultos.0 Un satélit dscrib una órbita circular n torno a la Tirra. Si s cambia d rpnt la dircción d su vlocidad, pro no su módulo, studiar l cambio n su órbita y n su príodo. Al cambiar sólo la
Problmas sultos.0 Un satélit dscrib una órbita circular n torno a la Tirra. Si s cambia d rpnt la dircción d su vlocidad, pro no su módulo, studiar l cambio n su órbita y n su príodo. Al cambiar sólo la
() t ( )exp( ) 2. La transformada de Fourier
 1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen, 7 de Septiembre de 2004 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicción Exmen, 7 de Septiembre de 24 Primer prte Ejercicio. Clculr ls coordends de los puntos P y Q de l prábol y x 2, tles que el triángulo formdo por el eje
CÁLCULO Primer curso de Ingeniero de Telecomunicción Exmen, 7 de Septiembre de 24 Primer prte Ejercicio. Clculr ls coordends de los puntos P y Q de l prábol y x 2, tles que el triángulo formdo por el eje
producto exterior y derivada de 1-formas
 producto exterior y derivada de 1-formas Jana Rodriguez Hertz Cálculo 3 IMERL 9 de junio de 2011 introducción introducción campo asociado a una 2-forma ω = adydz + bdzdx + cdxdy introducción introducción
producto exterior y derivada de 1-formas Jana Rodriguez Hertz Cálculo 3 IMERL 9 de junio de 2011 introducción introducción campo asociado a una 2-forma ω = adydz + bdzdx + cdxdy introducción introducción
c i I a a C " a l 2 C C N I M amico t e s a r b o S c i e d d 7
 www.. ó P M L " 5 1 0 2 M O A H N A M B y u S.. www j b P 2015 b p S 7 PREMO DEL OM MANHAOM 2015 P. Obj. v P Só ó L M MANHAÓM 2015 Sgu. Su, pz y ug pó. 1. L u pá gú qu ju Ax y qu á pb wb www.. E é uy pb
www.. ó P M L " 5 1 0 2 M O A H N A M B y u S.. www j b P 2015 b p S 7 PREMO DEL OM MANHAOM 2015 P. Obj. v P Só ó L M MANHAÓM 2015 Sgu. Su, pz y ug pó. 1. L u pá gú qu ju Ax y qu á pb wb www.. E é uy pb
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
CONTENIDO FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS. Campos escalares y vectoriales. Gradiente y rotacional. Campos conservativos.
 CONTENIDO FUERZS CONSERVTIVS Y NO CONSERVTIVS Campos escalaes y vectoiales Gadiente y otacional Campos consevativos. Potencial Tabajo ealizado po una fueza consevativa Fuezas no consevativas: Fueza de
CONTENIDO FUERZS CONSERVTIVS Y NO CONSERVTIVS Campos escalaes y vectoiales Gadiente y otacional Campos consevativos. Potencial Tabajo ealizado po una fueza consevativa Fuezas no consevativas: Fueza de
( ) ( ) ( x ) ( ) ( ) ( ) v( x) u( x) ( ) EJERCICIOS RESUELTOS. 1. Calcula F a) ( x) en los siguientes casos: f ( t) = e. = x
 Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
Alro Enro Cond Mi Gonzálz Jrrro L ingrl y ss pliccions Clcl F ) d) n los sigins csos: F cos d RESUELTOS ) ( + ) d ) ( + ) F cos F d c) F( ) + d f) F d + F d g) v( ) F d h) F + f ( ) d i) F( ) ( ) cos d
HASTA EL TOPE RAÍZ DE LOS 63% INDEPENDIENTES Qué tan independientes son los candidatos que van sin partido a la Constituyente? Cómo SEMANAL MAYO
 H P 3 1 3 41 18 $1423 x $6 H é é q x G q 1-16 Y x @_ wwwx 216 / 22 RÍZ D DPD Qé q? 63% j q? q á x #PP Pí GRU D P á : U j é í ñ q x á á á j G Á j B q Pá á 3 á 7 25 j é ; j ú 8 V? P í í í í q á H q 2 9 ú:
H P 3 1 3 41 18 $1423 x $6 H é é q x G q 1-16 Y x @_ wwwx 216 / 22 RÍZ D DPD Qé q? 63% j q? q á x #PP Pí GRU D P á : U j é í ñ q x á á á j G Á j B q Pá á 3 á 7 25 j é ; j ú 8 V? P í í í í q á H q 2 9 ú:
A C T I N O M IC O S I S Ó r g a n o : M u c o s a b u c a l T é c n i ca : H / E M i c r o s c o p í a: L o s c o r t e s h i s t o l ó g i c oms u e
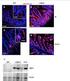 T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l
LEO COMERCIAL DE EQUIPOS SA. DE C.V. NORTE 24 No. 67 COL INDUSTRIAL CP 07800 MÉXICO D.F. TEL: 5739 0717 FAX: 9112 3126 leo.comercial@leocomercial.
 DISTRIBUIDOR: LEO COMERCIAL DE EQUIPOS SA. DE C.V. NORTE 24 No. 67 COL INDUSTRIAL CP 07800 MÉXICO D.F. TEL: 5739 0717 FAX: 9112 3126 leo.comercial@leocomercial.com DISTRIBUIDOR: LEO COMERCIAL DE EQUIPOS
DISTRIBUIDOR: LEO COMERCIAL DE EQUIPOS SA. DE C.V. NORTE 24 No. 67 COL INDUSTRIAL CP 07800 MÉXICO D.F. TEL: 5739 0717 FAX: 9112 3126 leo.comercial@leocomercial.com DISTRIBUIDOR: LEO COMERCIAL DE EQUIPOS
CAPITULO 2 LA TABLA PERIODICA
 1.0079 1 H HIDROGENO 6.941 3 Li LITIO 22.989 11 Na SODIO 30.098 19 K POTASIO CAPITULO 2 LA TABLA PERIODICA ORDENAMIENTO ACTUAL GRUPOS Y PERIODOS PROPIEDADES PERIODICAS TAMAÑO POTENCIAL DE IONIZACION AFINIDAD
1.0079 1 H HIDROGENO 6.941 3 Li LITIO 22.989 11 Na SODIO 30.098 19 K POTASIO CAPITULO 2 LA TABLA PERIODICA ORDENAMIENTO ACTUAL GRUPOS Y PERIODOS PROPIEDADES PERIODICAS TAMAÑO POTENCIAL DE IONIZACION AFINIDAD
SIMULACIÓN NUMÉRICA DE UNA CÁMARA DE COMBUSTIÓN DE ALTA VELOCIDAD CON DOS CONFIGURACIONES DE INYECCIÓN DE COMBUSTIBLE
 SIMULAIÓN NUMÉRIA DE UNA ÁMARA DE OMBUSIÓN DE ALA VELOIDAD ON DOS ONFIGURAIONES DE INYEIÓN DE OMBUSIBLE NUMERIAL SIMULAION OF HIGH SPEED OMBUSION HAMBER USING WO FUEL INJEION ONFIGURAIONS HENRY OPEE Grpo
SIMULAIÓN NUMÉRIA DE UNA ÁMARA DE OMBUSIÓN DE ALA VELOIDAD ON DOS ONFIGURAIONES DE INYEIÓN DE OMBUSIBLE NUMERIAL SIMULAION OF HIGH SPEED OMBUSION HAMBER USING WO FUEL INJEION ONFIGURAIONS HENRY OPEE Grpo
Notas de NdeCColaboración
 Notas de Colaboración Notas de NdeCColaboración LA INFORMACIÓN GEOGRÁFICA EN LA APLICACIÓN DE LA LEY 13/2015: REPRESENTACIÓN GRÁFICA GEORREFERENCIADA. Por Carmen Femenia-Ribera. Ingeniera Técnica en Topografía.
Notas de Colaboración Notas de NdeCColaboración LA INFORMACIÓN GEOGRÁFICA EN LA APLICACIÓN DE LA LEY 13/2015: REPRESENTACIÓN GRÁFICA GEORREFERENCIADA. Por Carmen Femenia-Ribera. Ingeniera Técnica en Topografía.
NOMBRE: VECTORES EN EL PLANO. Ángel de la Llave Canosa
 NOMBRE: VECTORES EN EL PLANO Ángel de la Llave Canosa 1 VECTORES EN EL PLANO VECTOR FIJO Un vector fijo AB es n segmento orientado, qe está definido por dos pntos: Un pnto origen y n pnto extremo. Los
NOMBRE: VECTORES EN EL PLANO Ángel de la Llave Canosa 1 VECTORES EN EL PLANO VECTOR FIJO Un vector fijo AB es n segmento orientado, qe está definido por dos pntos: Un pnto origen y n pnto extremo. Los
TRABAJO MECÁNICO (FUERZA VARIABLE. RESORTES)
 TRABAJO MECÁNICO (FUERZA VARIABLE. RESORTES) En sicions rls l frz no s consn, sino q vri cndo l ojo s mv sor n lín rc. w = fd Δ w = f )( Δ w f )( Si l frz s mid n l. y l disnci n pis noncs Si l frz s mid
TRABAJO MECÁNICO (FUERZA VARIABLE. RESORTES) En sicions rls l frz no s consn, sino q vri cndo l ojo s mv sor n lín rc. w = fd Δ w = f )( Δ w f )( Si l frz s mid n l. y l disnci n pis noncs Si l frz s mid
Tipo de Concepto (1 Percepción, (2 Deducciones, (3 Prestamos del ISSSTE. Partida. Partida. Partida Antecedente. Presupuestal. Descripción.
 Catalogo de s de Percepciones y Deducciones Tipo de (1 Percepción, 1103 1 07 00 SUELDOS BASE 1306 1 24 GA AGUINALDO O GRATIF. DE FIN DE AÑO (PERS. ACTIVO) 1306 1 24 BA AGUINALDO O GRATIF. DE FIN DE AÑO
Catalogo de s de Percepciones y Deducciones Tipo de (1 Percepción, 1103 1 07 00 SUELDOS BASE 1306 1 24 GA AGUINALDO O GRATIF. DE FIN DE AÑO (PERS. ACTIVO) 1306 1 24 BA AGUINALDO O GRATIF. DE FIN DE AÑO
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES 1 Módlo: Indica la intensidad, iene dado por la longitd de la flecha
VECTORES EN EL ESPACIO (,4,3) MATEMÁTICAS II º Bachillerato Alfonso Gonále IES Fernando de Mena Dpto. de Matemáticas I. DEFINICIONES 1 Módlo: Indica la intensidad, iene dado por la longitd de la flecha
Tipo de Concepto (1 Percepción, (2 Deducciones, (3 Prestamos del ISSSTE. Partida. Partida Antecedente. Presupuestal. Partida. Descripción.
 Catalogo de s de Percepciones y Deducciones Tipo de (1 1202 1 02 00 SUELDOS COMPACTADOS A PERSONAL EVENTUAL 02 00 SUELDOS COMPACTADOS A PERSONAL EVENTUAL 1103 1 07 00 SUELDOS BASE 07 00 SUELDOS BASE 1306
Catalogo de s de Percepciones y Deducciones Tipo de (1 1202 1 02 00 SUELDOS COMPACTADOS A PERSONAL EVENTUAL 02 00 SUELDOS COMPACTADOS A PERSONAL EVENTUAL 1103 1 07 00 SUELDOS BASE 07 00 SUELDOS BASE 1306
Teoría de Lenguajes. Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014
 Teoría de Lenguajes Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014 aterial compilado por el Profesor Julio Jacobo, a lo largo de distintas ediciones
Teoría de Lenguajes Clase Teórica 7 Autómatas de Pila y Lenguajes Independientes del Contexto Primer cuartimestre 2014 aterial compilado por el Profesor Julio Jacobo, a lo largo de distintas ediciones
Telf
 I ó z y b y S. v p y C A, 1,5k. p Eá ú b Vy y py Rg Cb. N v p p gp, v, p /, T Bg p p, v,. x pk 2, 10.000 C á, pb á p A) y v Wp (H v Bbb S, q j p p. v p v pá pk. T. 647 975 975 www.x v A H Wp Aá g 25. x
I ó z y b y S. v p y C A, 1,5k. p Eá ú b Vy y py Rg Cb. N v p p gp, v, p /, T Bg p p, v,. x pk 2, 10.000 C á, pb á p A) y v Wp (H v Bbb S, q j p p. v p v pá pk. T. 647 975 975 www.x v A H Wp Aá g 25. x
F I C H A D E P R O G R A M A S
 G D MDD D MDD F H D G M FÓ: DÓ D MDD GM: ÁM D : ÁM D D MDD D MDD Ó: ÁM D D GM: D D ÁM D. M D G GM/Í D G D GM M % /. G D. G Y V. G F. F. V. F D. V F. V F......,,,,....., ) Función fiscalizadora de la actividad
G D MDD D MDD F H D G M FÓ: DÓ D MDD GM: ÁM D : ÁM D D MDD D MDD Ó: ÁM D D GM: D D ÁM D. M D G GM/Í D G D GM M % /. G D. G Y V. G F. F. V. F D. V F. V F......,,,,....., ) Función fiscalizadora de la actividad
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
UNIVERSIDAD POLITÉCNICA DE VALENCIA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN DEPARTAMENTO DE COMUNICACIONES TESIS DOCTORAL
 UNIVERSIDAD POLITÉCNICA DE VALENCIA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN DEPARTAMENTO DE COMUNICACIONES TESIS DOCTORAL MÉTODOS DE MALLADO Y ALGORITMOS ADAPTATIVOS EN DOS Y TRES DIMENSIONES
UNIVERSIDAD POLITÉCNICA DE VALENCIA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE TELECOMUNICACIÓN DEPARTAMENTO DE COMUNICACIONES TESIS DOCTORAL MÉTODOS DE MALLADO Y ALGORITMOS ADAPTATIVOS EN DOS Y TRES DIMENSIONES
TEMA 0: Herramientas matemáticas
 1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO Para poder isalizar los elementos de R 3 ={(x,y,z)/x,y,z R}, primero fijamos n sistema de coordenadas, eligiendo n pnto en el espacio llamado el origen qe denotaremos por O, y tres
VECTORES EN EL ESPACIO Para poder isalizar los elementos de R 3 ={(x,y,z)/x,y,z R}, primero fijamos n sistema de coordenadas, eligiendo n pnto en el espacio llamado el origen qe denotaremos por O, y tres
ALGEBRA LINEAL GUÍA No. 4 - VECTORES Profesor: Benjamín Sarmiento
 ALGEBRA LINEAL GUÍA No. 4 - VECTORES Profesor: Benjamín Sarmiento VECTORES EN R n.. OPERACIONES CON VECTORES VECTORES EN R 2 : Un vector v en el plano R 2 = XY es un par ordenado de números reales .
ALGEBRA LINEAL GUÍA No. 4 - VECTORES Profesor: Benjamín Sarmiento VECTORES EN R n.. OPERACIONES CON VECTORES VECTORES EN R 2 : Un vector v en el plano R 2 = XY es un par ordenado de números reales .
Análisis Estadístico de Datos Climáticos
 Aálss Estadístco d Datos Clmátcos Rgrsó lal smpl (Wlks, cap. 6.) Vo Storch ad Zwrs (Cap. 8) 05 Rgrsó La rgrsó, gral, s utlza habtualmt para stmar modlos paramétrcos d la rlacó tr varabls ua scala cotua,
Aálss Estadístco d Datos Clmátcos Rgrsó lal smpl (Wlks, cap. 6.) Vo Storch ad Zwrs (Cap. 8) 05 Rgrsó La rgrsó, gral, s utlza habtualmt para stmar modlos paramétrcos d la rlacó tr varabls ua scala cotua,
R e a l i z a r p r e g u n t a s y r e s p u e s t a s e n u n e n t o r n o d e c o m p r a s R e c o n o c e r s a l u d o s s e n c i l l o s R e
 ACCIÓN FORMATIVA: INGLÉS INTERMEDIO MODALIDAD: Di s t a n c i a DU R AC IÓ N : 2 5 0 h o r a s N º h o r a s t e ó r i c a s : 1 1 6 h o r a s N º h o r a s p r á c t i c a s : 1 3 4 h o r a s DE S T IN
ACCIÓN FORMATIVA: INGLÉS INTERMEDIO MODALIDAD: Di s t a n c i a DU R AC IÓ N : 2 5 0 h o r a s N º h o r a s t e ó r i c a s : 1 1 6 h o r a s N º h o r a s p r á c t i c a s : 1 3 4 h o r a s DE S T IN
ARCHIVO. inumen ARCHIVO DE MUESTRA PROMOCIONAL DE ARCHIVO DE MUESTRA PROMOCIONAL DE ARCHIVO DE MUESTRA PROMOCIONAL DE
 www..s s gs (B1) é spñ p xjs b y p:... Gp / cs:... Fch:... bsvcs pfs: b ccs p: x sc B1, www..s www..s www..s s gs (B1) 1. psó v b ccs p: x sc www..s 1.1. scch y s ág. c hc, f s pbs. scch y scíbs. [1],
www..s s gs (B1) é spñ p xjs b y p:... Gp / cs:... Fch:... bsvcs pfs: b ccs p: x sc B1, www..s www..s www..s s gs (B1) 1. psó v b ccs p: x sc www..s 1.1. scch y s ág. c hc, f s pbs. scch y scíbs. [1],
DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL
 DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL DISEÑO MECÁNICO PRÁCTICA Nº 4 METROLOGÍA Y CALIDAD. CALIBRACIÓN DE UN PIE DE REY Metrología y Caldad. Calbracón de n pe de rey. INDICE 1. OBJETIVOS
DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL DISEÑO MECÁNICO PRÁCTICA Nº 4 METROLOGÍA Y CALIDAD. CALIBRACIÓN DE UN PIE DE REY Metrología y Caldad. Calbracón de n pe de rey. INDICE 1. OBJETIVOS
TEMA 3 Trabajo y Energía
 ESCUEL DE INGENIERÍS INDUSTRILES. UNIVERSIDD DE VLLDOLID FÍSIC I. CURSO 013-014 TEM 3 Trabajo y Energía 1.- Trabajo, energía cinética y potencia.- Energía potencial. Fuerzas conservativas y no conservativas
ESCUEL DE INGENIERÍS INDUSTRILES. UNIVERSIDD DE VLLDOLID FÍSIC I. CURSO 013-014 TEM 3 Trabajo y Energía 1.- Trabajo, energía cinética y potencia.- Energía potencial. Fuerzas conservativas y no conservativas
1.2 TÉCNICAS DE LA DERIVACIÓN.
 . TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
. TÉCNICAS DE LA DERIVACIÓN... DERIVACIÓN DE FUNCIONES ALGEBRAICAS Generalmente la derivación se lleva acabo aplicando fórmlas obtenidas mediante la regla general de la derivación y qe calclaremos a continación,
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
Fandaáoí y Éifeete?, J U t i i a S e c o d e. de San Juan. los Tristes; arrancando de nuevo desde
 T B I F D CBIZOH x - x 8 f( f RIÓDICO BHTTHIO f F Éf O F I C I N R C 8 T H Z F D Q OBTTOBI8 INDNDINT Nú T B I F D CONICDO D D T R 9 N - D f f H - ñ f f - f f z é ñ f x f - - f ñ H x ú f C Y f z x T C O
T B I F D CBIZOH x - x 8 f( f RIÓDICO BHTTHIO f F Éf O F I C I N R C 8 T H Z F D Q OBTTOBI8 INDNDINT Nú T B I F D CONICDO D D T R 9 N - D f f H - ñ f f - f f z é ñ f x f - - f ñ H x ú f C Y f z x T C O
LÍMITES DE FUNCIONES. CONTINUDAD
 LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
LÍMITES DE FUNCIONES. CONTINUDAD Signiicado dl it Ejrcicio nº.- Rprsnta gráicamnt y plica l gniicado d la prón: Ejrcicio nº.- Eplica l gniicado d la guint prón y rprséntalo gráicamnt: 9 Ejrcicio nº.- Escrib
12.3. El producto punto. 674 Capítulo 12: Los vectores y la geometría del espacio. Ángulo entre vectores
 674 Capítlo 1: Los ectores la geometría del espacio c. Obtenga las coordenadas del pnto donde se cortan las medianas del DABC. De acerdo con el ejercicio 17 de la sección 6.6, este pnto es el centro de
674 Capítlo 1: Los ectores la geometría del espacio c. Obtenga las coordenadas del pnto donde se cortan las medianas del DABC. De acerdo con el ejercicio 17 de la sección 6.6, este pnto es el centro de
 s S ä k E l e k t r i s k s ä k e r h e t I n s t a l l a t i o n s s ä k e r h e t R e n g ö r i n g s s ä k e r h e t S p l k L C D d s k ä P l l k P l a c e r i n g I n s t a l l a t i o n E x t e r
s S ä k E l e k t r i s k s ä k e r h e t I n s t a l l a t i o n s s ä k e r h e t R e n g ö r i n g s s ä k e r h e t S p l k L C D d s k ä P l l k P l a c e r i n g I n s t a l l a t i o n E x t e r
Tema 1. Repaso de Teoría de Circuitos
 Tma. paso d Toría d rcuos Joaquín aquro ópz Elcrónca, 7 Joaquín aquro ópz paso d Toría d rcuos: índc. oncpos prlmars. oncpo d crcuo, lmnos d un crcuo. ys fundamnals d los crcuos lécrcos: ys d Krchhoff.3
Tma. paso d Toría d rcuos Joaquín aquro ópz Elcrónca, 7 Joaquín aquro ópz paso d Toría d rcuos: índc. oncpos prlmars. oncpo d crcuo, lmnos d un crcuo. ys fundamnals d los crcuos lécrcos: ys d Krchhoff.3
ANÁLISIS DE SISTEMAS ELECTRÓNICOS REALIMENTADOS
 ANÁLISIS DE SISTEMAS ELECTÓNICOS EALIMENTADOS DESANECIMIENTO J.M. Mlá d la oca P. EDITOIAL MIL 6 CAACAS Esta obra s ncuntra rvsón; cualqur obsrvacón qu UD tnga s l agradc comuncarla al autor. jmmladroca@hotmal.com
ANÁLISIS DE SISTEMAS ELECTÓNICOS EALIMENTADOS DESANECIMIENTO J.M. Mlá d la oca P. EDITOIAL MIL 6 CAACAS Esta obra s ncuntra rvsón; cualqur obsrvacón qu UD tnga s l agradc comuncarla al autor. jmmladroca@hotmal.com
CAMPOS: CIRCULACIÓN Y FLUJO
 AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA CAMPOS Y ONDAS
 Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA Análisis Vectorial 1. Algebra vectorial: suma, resta y multiplicación de vectores. 2. Sistemas de coordenadas ortogonales:
Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA Análisis Vectorial 1. Algebra vectorial: suma, resta y multiplicación de vectores. 2. Sistemas de coordenadas ortogonales:
INF-VALPARAÍSO-02. Asistencia solicitada por: COE REGIÓN DE VALPARAÍSO, COE NACIONAL
 EFETOS DEL INENDIO DEL 12 AL 16 DE ABRIL DE 2014, OUNA DE VALPARAÍSO, REGIÓN DE VALPARAÍSO: ÁREAS DE RIESGO POR REOIONES EN ASA SEGÚN INSTRUENTOS DE PLANIFIAIÓN VIGENTES Y ESTUDIO DE PELIGRO DE SERNAGEOIN.
EFETOS DEL INENDIO DEL 12 AL 16 DE ABRIL DE 2014, OUNA DE VALPARAÍSO, REGIÓN DE VALPARAÍSO: ÁREAS DE RIESGO POR REOIONES EN ASA SEGÚN INSTRUENTOS DE PLANIFIAIÓN VIGENTES Y ESTUDIO DE PELIGRO DE SERNAGEOIN.
Método de los Elementos Finitos para Análisis Estructural. Alisado de tensiones
 Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
Método d los Elmntos Finitos para Análisis Estructural Alisado d tnsions Campo d tnsions Tnsions n cualquir punto dl lmnto, sgún l MEF: = Dε= DBδ Matriz B contin las drivadas d las N: no son continuas
Opción A Ejercicio 1 opción A, modelo Septiembre 2011
 IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
IES Fco Ayala d Granada Sptimbr d 0 (Modlo ) Grmán-Jsús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 0-0 MATEMÁTICAS II Opción A Ejrcicio opción A, modlo Sptimbr 0 k si
I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l. U l a d i s l a o G á m e z S o l a n o
 1 A n t o l o g í a : P r o m o c i ó n y A n i m a c i ó n d e l a l e c t u r a M i n i s t e r i o d e E d u c a c i ó n P ú b l i c a I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l.
1 A n t o l o g í a : P r o m o c i ó n y A n i m a c i ó n d e l a l e c t u r a M i n i s t e r i o d e E d u c a c i ó n P ú b l i c a I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l.
SISTEMA DE RECONOCIMIENTO DE IMÁGENES COMO INTÉRPRETE DEL LENGUAJE DE SEÑAS
 SISTE DE RECOOCIIETO DE IÁGEES COO ITÉRPRETE DEL LEGUJE DE SEÑS Ordóñz Ortíz Edgar _ordonz@.org Escla Spror Poltécnca d Chmborazo Robamba-Ecador BSTRCT.- Th prsnt work rass a proct appld to th rcognton
SISTE DE RECOOCIIETO DE IÁGEES COO ITÉRPRETE DEL LEGUJE DE SEÑS Ordóñz Ortíz Edgar _ordonz@.org Escla Spror Poltécnca d Chmborazo Robamba-Ecador BSTRCT.- Th prsnt work rass a proct appld to th rcognton
APUNTE Y PROBLEMAS DE FÍSICA III
 APUE Y PROBLEMAS DE FÍSICA III CARRERA: LICECIAURA E QUÍMICA PROFESOR Mg. CARLOS A. CAAEO AUILIAR Lc. ERIQUE M. BIASOI COEIDOS: Mcáca Clásca: Mcáca Cuátca: Mcáca Estadístca: Problmas: Cmátca Dámca Prcpos
APUE Y PROBLEMAS DE FÍSICA III CARRERA: LICECIAURA E QUÍMICA PROFESOR Mg. CARLOS A. CAAEO AUILIAR Lc. ERIQUE M. BIASOI COEIDOS: Mcáca Clásca: Mcáca Cuátca: Mcáca Estadístca: Problmas: Cmátca Dámca Prcpos
1. Distancia entre puntos y rectas en el espacio. 3. Calcula la distancia existente entre las rectas: Solución: d(r, s) =
 7 Espacio métrico. Distancia entre puntos y rectas en el espacio Piensa y calcula Dados los puntos A, 4, ) y B5,, 4), halla las coordenadas del vector: AB AB,5,) Aplica la teoría. Calcula la distancia
7 Espacio métrico. Distancia entre puntos y rectas en el espacio Piensa y calcula Dados los puntos A, 4, ) y B5,, 4), halla las coordenadas del vector: AB AB,5,) Aplica la teoría. Calcula la distancia
Cualquier transformador puede diseñarse haciendo uso de tres ecuaciones generales.
 7. Transformaors Cállo ransformaors S s onsrano n oro qvaln. Calqr ransformaor p sñars hano so rs aons nrals. Prmra aón. Dfnón nsa fljo manéo (nón ampo manéo). B A Sna aón. y Ampèr. l I 7. Transformaors
7. Transformaors Cállo ransformaors S s onsrano n oro qvaln. Calqr ransformaor p sñars hano so rs aons nrals. Prmra aón. Dfnón nsa fljo manéo (nón ampo manéo). B A Sna aón. y Ampèr. l I 7. Transformaors
Examen de Estadística Ingeniería de Telecomunicación
 Examen de Estadística Ingeniería de Telecomunicación 8 de Mayo de 3 Cuestiones solucion h C. (.5p) El equipo directivo de cierta empresa del sector de hostelería está constituido por 5 personas de las
Examen de Estadística Ingeniería de Telecomunicación 8 de Mayo de 3 Cuestiones solucion h C. (.5p) El equipo directivo de cierta empresa del sector de hostelería está constituido por 5 personas de las
Comprobación de limitación de condensaciones superficiales e intersticiales en los cerramientos
 Mnstro d Fomnto Scrtaría d Estado d Infrastructuras, Transport y Vvnda Drccón Gnral d Arqutctura, Vvnda y Sulo Documnto d Apoyo al Documnto Básco DB-HE Ahorro d nrgía Códgo Técnco d la Edfcacón DA DB-HE
Mnstro d Fomnto Scrtaría d Estado d Infrastructuras, Transport y Vvnda Drccón Gnral d Arqutctura, Vvnda y Sulo Documnto d Apoyo al Documnto Básco DB-HE Ahorro d nrgía Códgo Técnco d la Edfcacón DA DB-HE
 ACCIÓN FORMATIVA: INGLÉS AVANZADO MODALIDAD: DISTANCIA DU R AC IÓ N : 2 5 0 h o r a s Nº h o r a s t e ó r i ca s : 1 1 6 h o r a s Nº h o r a s p r á ct i ca s : 1 3 4 h o r a s DE S T IN AT AR IOS :
ACCIÓN FORMATIVA: INGLÉS AVANZADO MODALIDAD: DISTANCIA DU R AC IÓ N : 2 5 0 h o r a s Nº h o r a s t e ó r i ca s : 1 1 6 h o r a s Nº h o r a s p r á ct i ca s : 1 3 4 h o r a s DE S T IN AT AR IOS :
Una viga se encuentra sometida a Flexión Pura cuando el momento Flector es la única fuerza al interior de la sección.
 3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
EJERCICIOS RESUELTOS
 FUNAMENTOS MATEMÁTICOS E LA INGENIEÍA Ingerierí Técnic Industril. Esecilidd en Mecánic. Boletin 7. Integrción Múltile EJECICIOS ESUELTOS Curso -. Clculr ls siguientes integrles iterds: Z Z Z y ( + y)dyd.
FUNAMENTOS MATEMÁTICOS E LA INGENIEÍA Ingerierí Técnic Industril. Esecilidd en Mecánic. Boletin 7. Integrción Múltile EJECICIOS ESUELTOS Curso -. Clculr ls siguientes integrles iterds: Z Z Z y ( + y)dyd.
Carpintería y elementos de seguridad. Precios unitarios descompuestos
 Carpintería y elementos de seguridad Precios unitarios descompuestos Capítulo 11: CARPINTERÍA Y ELEMENTOS DE SEGURIDAD Y PROTECCIÓN Subcapítulo 11A: ACERO Apartado 11AM: Mamparas Grupo 11AMA: Abatibles
Carpintería y elementos de seguridad Precios unitarios descompuestos Capítulo 11: CARPINTERÍA Y ELEMENTOS DE SEGURIDAD Y PROTECCIÓN Subcapítulo 11A: ACERO Apartado 11AM: Mamparas Grupo 11AMA: Abatibles
MATEMÁTICAS II PRUEBAS DE ACCESO A LA UNIVERSIDAD DE OVIEDO
 MTEMÁTICS II PRUEBS DE CCESO L UNIVERSIDD DE OVIEDO.- NÁLISIS ª PRTE.- Cálclo Intgral.- MODELO DE PRUEB Dada la parábola, s corta por la rcta d cación ; n los pntos d intrscción s trazan las tangnts a
MTEMÁTICS II PRUEBS DE CCESO L UNIVERSIDD DE OVIEDO.- NÁLISIS ª PRTE.- Cálclo Intgral.- MODELO DE PRUEB Dada la parábola, s corta por la rcta d cación ; n los pntos d intrscción s trazan las tangnts a
 Reglamento de D i v er s i ones y E s p ec tá c u los P ú b li c os Ayuntamiento Constitucional de Zapotlanejo 2007-2009 e n t e M u n i c i Z a t n e j o, J a o, a h a t a n t e m u n i c i o h a g o
Reglamento de D i v er s i ones y E s p ec tá c u los P ú b li c os Ayuntamiento Constitucional de Zapotlanejo 2007-2009 e n t e M u n i c i Z a t n e j o, J a o, a h a t a n t e m u n i c i o h a g o
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas y x 12x 2 y log 2 x ln x e e y ln 1 x
 . Drivar las siguints funcions simplificar l rsultado n la mdida d lo posibl. ) 4) 7) ) 4 5 5 5 7 5) 8) ) 5 6) 5 9) 4 5 0) ) 7 ) ) 4) 4 5) 6) 7) 8) 9) ) 5) 0) 4 ln ) ln log 6) ln 8) ln ) 9) ) 5) 4) 7)
. Drivar las siguints funcions simplificar l rsultado n la mdida d lo posibl. ) 4) 7) ) 4 5 5 5 7 5) 8) ) 5 6) 5 9) 4 5 0) ) 7 ) ) 4) 4 5) 6) 7) 8) 9) ) 5) 0) 4 ln ) ln log 6) ln 8) ln ) 9) ) 5) 4) 7)
3.2 EL PRODUCTO ESCALAR Y LAS PROYECCIONES EN R 2
 34 CAPÍTULO 3 Vectores en R R 3 ais sqare a=ais; ais([min(a([1,3])),ma(a([,4])),min(a([1,3])),ma(a([,4]))]) % hold off Una ez qe se haa escrito la fnción en n archio con nombre lincomb.m, dé el comando
34 CAPÍTULO 3 Vectores en R R 3 ais sqare a=ais; ais([min(a([1,3])),ma(a([,4])),min(a([1,3])),ma(a([,4]))]) % hold off Una ez qe se haa escrito la fnción en n archio con nombre lincomb.m, dé el comando
Unidad 4 : DERIVADAS PARCIALES. dy dt. d dt. z x. = dt
 Unidad DEIVADAS PACIALES Tma. gla d la Cadna (Edia la Scción. n l Sa ª Edición Hac la Taa No. ) gla d la Cadna paa na nción d na aiabl q a dpnd d oa aiabl. d d d d Si g nonc d d d d d d Ejmplo d n co d
Unidad DEIVADAS PACIALES Tma. gla d la Cadna (Edia la Scción. n l Sa ª Edición Hac la Taa No. ) gla d la Cadna paa na nción d na aiabl q a dpnd d oa aiabl. d d d d Si g nonc d d d d d d Ejmplo d n co d
Análisis de la eficiencia técnica y asignativa a través de las fronteras estocásticas de costes: una aplicación a los hospitales del INSALUD
 Unversdad de Valladold Análss de la efcenca técnca y asgnatva a través de las fronteras estocástcas de costes: na aplcacón a los hosptales del INSALUD Carmen García Preto Tess de Doctorado Facltad: Drector:
Unversdad de Valladold Análss de la efcenca técnca y asgnatva a través de las fronteras estocástcas de costes: na aplcacón a los hosptales del INSALUD Carmen García Preto Tess de Doctorado Facltad: Drector:




