Matemticas V: Cálculo diferencial
|
|
|
- Alejandro Rivero Muñoz
- hace 5 años
- Vistas:
Transcripción
1 Matemticas V: Cálculo iferencial Soluciones Tarea 8. Para caa una e las siguientes ecuaciones encuentra la ecuación e la recta tangente a la curva en el punto ao p. (a) x y + xy, p (, ). Suponemos que cerca el punto p la curva en cuestión es la gráfica e una función y(x). Necesitamos calcular la erivaa e icha función en x, sabieno que y(). Para ello erivamos implícitamente la ecuación e la curva: Luego 0 x x [ x y(x) + xy(x) ] ( ) ( ) ( ) ( ) x x y(x) + x x y(x) + x x y(x) + x x y(x) xy(x) + x y (x) + y(x) + y(x)y (x). 0 y() + y () + y() + y()y () + y () y (). Por lo tanto la ecuación e la recta tangente que pasa por p es e la forma y x + b. Sabieno que las coorenaas el punto p satisfacen tal ecuación obtenemos el valor e b: + b b. Por lo tanto la ecuación e la recta tangente en el punto p es y x +. Incluiremos en caa inciso las gráficas que se pien en el ejercicio 4.
2 (b) x + xy y, p (, ). x y (x) ( ) ( ) x x + x x y(x) + x x y(x) Sustituyeno los valores el punto p: y(x) y (x) x + y(x) + xy (x) ( ) y (/) que al simplificarse nos a la ecuación ( ) ( + ) y (/) y (/), ( ) y (/), cuya solución es y (/). Luego la ecuación e la recta tangente es e la forma y x + b, sustituyeno las coorenaas e p, que eben ser solución e esa ecuación, se transforma en + b b. y por consiguiente la ecuación e la recta tangente es y x. (c) y + x y x x, p (, 0). Derivamos con respecto a x como antes: ( ) ( ) x y (x) + x x y + x x y(x) x x x x y(x)y (x) + xy(x) + x y (x) x y()y () + y() + y () y (). Luego la recta tangente es e la forma y x + b y tomano x, y 0 obtenemos 0 + b, es ecir, b. Por lo tanto la ecuación e la recta tangente a la curva en el punto p es y x.
3 () x + xy + y x y, p (, ). x + xy(x) + y(x) x y(x) x (x + xy(x) + y(x) ) x (x y(x) ) Sustituyeno las coorenaas e p en la última expresión obtenia: x + y(x) + xy (x) + y(x) y (x) x y(x)y (x). ( ) ( + y ( /) + ) ( y ( /) + y ( y ) ( /) ) 4 y ( /) + 4 y ( /) y ( /) + y ( /) 4 y ( /) y ( /) 4 4 y ( /) 5 4 y ( /) 5. y ( /) y ( /) ( ) y (/) Resolvieno la ecuación corresponiente obtenemos que la recta tangente a la curva en el punto p tiene por ecuación y 5 x +.
4 (e) ye xy, p (0, ). y(x)e xy(x) x [y(x)exy(x) ] 0 Sustituyeno x 0 y y en la ecuación anterior obtenemos ( ) ( ) x y(x) e xy(x) + y(x) x exy(x) 0 y (x)e xy(x) + y(x)e xy y (0) + 0 y (0). Como la recta tiene ecuación y x + b, tomano x 0 y y se sigue que b. Por lo tanto la ecuación e la recta tangente a la curva en el punto p es y x +. 4
5 5. Si os curvas se intersectan en un punto p ecimos que su ángulo e intersección es el ángulo que forman sus rectas tangentes en p. (a) Encuentra la ecuación e la elipse con focos (-,0) y (,0) y suma constante igual a 4. Dao un punto p (x, y), las istancias el punto p a los puntos f (, 0) y f (, 0) están aas por (p, f ) (x + ) + y, (p, f ) (x ) + y. Sabemos que para los puntos p en la elipse la suma e ichas istancias es constante e igual a 4: (p, f ) + (p, f ) (x + ) + y + (x ) + y 4. Escribimos la ecuación anterior como (x + ) + y 4 (x ) + y y elevamos al cuarao para obtener (x + ) + y 6 8 (x ) + y + (x ) + y. Expanieno obtenemos x + x + + y 6 8 (x ) + y + x x + + y, y al simplificar Elevano nuevamente al cuarao: 4x 6 8 (x ) + y. 6x 8x (x x + + y ). Simplificano la expresión anterior obtenemos la ecuación e la elipse: x + 4y. (b) Encuentra la ecuación e la hipérbola con focos (-,0) y (,0) y e iferencia constante igual a. Tomamos los focos f y f como en el inciso anterior. Entonces p está en la hipérbola si y sólo si (p, f ) (p, f ) ±, one usamos el signo ± para evitar liiar con valores absolutos; más aelante éste esaparecerá. Expresano las istancias en función e las coorenaas e p: (x + ) + y (x ) + y ±, que es equivalente a (x + ) + y ± + (x ) + y. Elevano ambos extremos al cuarao obtenemos (x + ) + y ± (x ) + y + (x ) + y. Expanieno los binomios al cuarao x + x + + y ± (x ) + y + x x + + y y simplificano 4x ± (x ) + y. Elevano nuevamente al cuarao esaparece el signo ± y obtenemos 6x 8x + 4[(x ) + y ] 4x 8x y. Simplificano la expresión anterior obtenemos la ecuación e la hipérbola: x 4y. El valor ao originalmente era, pero la hipérbola con esa constante resulta egeneraa. 5
6 (c) Encuentra el punto e intersección e las os cónicas anteriores que está en el primer cuarante (es ecir, que tenga ambas entraas positivas). Un punto e intersección e ambas cónicas será solución e sus respectivas ecuaciones e manera simultánea: x + 4y y x 4y. De la ecuación e la elipse espejamos 4y x. Sustituyeno en la ecuación e la hipérbola: x 4y x ( x ) 5x 5x 5 x. La solución positiva e esta última ecuación es x. Por otra parte 4y x 9 y 9 4 con lo que y. Y el punto e intersección en el primer cuarante es P (, ). () Encuentra las rectas tangentes a ambas cónicas en el punto P que hallaste en el inciso anterior. Suponremos que cerca el punto p, la elipse y la hipérbola son gráficas e funciones y e (x) y y h (x) respectivamente. Éstas satisfacen las ecuaciones Derivano implícitamente: y espejano las erivaas e y e y y h : x + 4y e (x) 4 y x 4y h (x). 6x + 8y e (x)y e(x) 0 y 4x 8y h (x)y h(x) 0 y e(x) 4 x y e (x) y y h(x) x y h (x) Sabieno que para y e () y h (), sustituimos x en las ecuaciones anteriores y obtenemos que y e() y y h(). Luego las ecuaciones e las rectas tangentes a la elipse y la hipérbola en el punto p son respectivamente y x + b e y y x + b h. Sustituyeno las coorenaas el punto P en ambas ecuaciones obtenemos + b e y + b h, e one espejamos b e y b h. Entonces la ecuación e la recta tangente a la elipse en P es y y +. Y la ecuación e la recta tangente a la hipérbola en P es y x. (e) Verifica que estas curvas se intersectan ortogonalmente en P. Es un resultao conocio e geometría analítica que os rectas se intersectan ortogonalmente si el proucto e sus penientes es igual a, lo cual se verifica en las tangentes que hemos encontrao. A continuación graficamos las cónicas junto con sus tangentes. 6
7 6. Encuentra la erivaa e las siguientes funciones: (a) f(x) xe x, (b) f(x) e cos(x), (c) f(x) x log(x), () f(x) ex + e x e x e x, ( ) ( ) x (xex ) x x e x + x x ex e x + x e x e x + xe x. f (x) exp (cos(x)) cos (x) e cos(x) sen(x). f (x) (x) log(x) + x log (x) log(x) + x log(x) +. x f (x) (ex + e x ) (e x e x ) (e x + e x )(e x e x ) (e x e x ) (ex e x )(e x e x ) (e x + e x )(e x + e x ) (e x e x ) (ex ) e x e x + (e x ) [(e x ) + e x e x + (e x ) ] (e x e x ) 4 (e x e x ). (e) f(x) log(x + ), f (x) log (x + ) (x + ) x + (x) x x +. 7
8 (f) f(x) tan(log(x )), f (x) tan (log(x )) (log(x )) sec (log(x )) log (x ) (x ) sec (log(x )) x (x) sec (log(x )) x (g) f(x) e ex, f (x) exp (e x ) (e x ) e ex e x e x+ex (h) f(x) x x. Comenzamos observano que a b exp(b log(a)). Luego Aplicano la regla e la caena: f(x) x x exp( x log(x) ). f (x) exp (x log(x)) (x log(x)) exp(x log(x)) [(x ) (log(x)) + (x )(log(x)) ] [ x x x log(x) + x ] x x x (x log(x) + x). (i) f(x) sen(x ), f (x) sen (x ) (x ) cos(x )(x) x cos(x ). (j) f(x) log(log(log(x))), f (x) log (log(log(x))) [log(log(x))] log(log(x)) log (log(x)) [log(x)] log(log(x)) log(x) x x log(x) log(log(x)). 7. Determina si la función f aa es solución a la ecuación funcional que se muestra: (a) f f, f(x) e x. f(x) e x f (x) e x f(x). (b) f f, f(x) cos(x). f(x) cos(x) f (x) sen(x) f (x) cos(x) f f. Puesto que cos(0) cos(0) concluímos que f(x) cos(x) no es solución e f f. (c) f f 0, f(x) x. f(x) x f (x) f (x) 0 f (x) f(x) 0. () f f 0, f(x) e x. f(x) e x f (x) e x f (x) e x f (x) f(x) e x e x 0. 8
9 (e) f(f ), f(x) x. f(x) x x f (x) x x f(f (x)) x 4 x. Es claro que la función x 4 x no es igual a la constante, con lo que f(x) x no es solución e f(f ). 8. Determina los posibles valores e A para que f(x) e Ax satisfaga f + f + f 0. En primer lugar f + f + f ( ) x x eax + x (eax ) + e Ax x (AeAx ) + Ae Ax + e Ax A e Ax + Ae Ax + e Ax e Ax (A + A + ). Puesto que e Ax 0 para cualesquiera A y x, concluímos que f + f + f 0 si y sólo si A + A + 0, lo cual reuce el problema a resolver una ecuación e seguno grao. Observano que A +A+ (A+)(A+) concluímos que los posibles valores e A son A y A. 9
Información importante
 Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Cálculo I Derivadas de Funciones Trascendentes. Julio C. Carrillo E. * 1. Introducción Derivadas de funciones trigonométricas inversas 7
 3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
3.3. Derivaas e Funciones Trascenentes Julio C. Carrillo E. * Ínice. Introucción 2. Derivaas e funciones trigonométricas 3. Derivaas e funciones trigonométricas inversas 7 4. Derivaas e la función exponencial
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS. S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO: 207 PERÍODO: PRIMER TÉRMINO MATERIA: Cálculo e una variable PROFESOR: EVALUACIÓN:
Cálculo I. Índice Reglas Fundamentales para el Cálculo de Derivadas. Julio C. Carrillo E. * 1. Introducción 1. 2.
 3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Geometría Analítica Agosto 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. 1) A(3, 3), B( 3, 1), C(0, 3) 2) O( 2, 3), P(2, 3), Q(0, 2) 3) R(4, 4), S(7, 4), T(6,
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. 1) A(3, 3), B( 3, 1), C(0, 3) 2) O( 2, 3), P(2, 3), Q(0, 2) 3) R(4, 4), S(7, 4), T(6,
Unidad 1 Ecuaciones Diferenciales de Primer Orden. 1.1 Definiciones (Ecuación Diferencial, Orden, Grado, Linealidad)
 . Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) Unia Ecuaciones Diferenciales e Primer Oren. Definiciones (Ecuación Diferencial, Oren, Grao, Linealia) En iversas áreas como son la ingeniería,
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE--4-M---7 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: TIPO DE EXAMEN: Eamen Final FECHA DE
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
( ) 2 +( 1) 2. BLOQUE III Geometría analítica plana. Resoluciones de la autoevaluación del libro de texto
 Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
INTEGRAL INDEFINIDA. Una pregunta inicial para hacerse. Cuál es una función F(x), que al haber sido derivada se obtuvo f ( x) B?.
 es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
es INTEGRAL INDEFINIDA UConcepto e antierivaau: Una pregunta inicial para hacerse. Cuál es una función F(), que al haber sio erivaa se obtuvo f ( ) =?. La repuesta es: F ( ) =. Una nueva pregunta. Es la
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
La esfera. Haciendo los cuadrados y agrupando se obtiene la ecuación implícita:
 José María Martíne Meiano La esfera La superficie esférica la esfera es el conjunto e puntos el espacio que equiistan e otro punto fijo, llamao centro Si el centro es el punto Oa, b, c el raio vale r,
José María Martíne Meiano La esfera La superficie esférica la esfera es el conjunto e puntos el espacio que equiistan e otro punto fijo, llamao centro Si el centro es el punto Oa, b, c el raio vale r,
Regla de la cadena. Ejemplo 1. y = f (g(x)) Como las funciones son diferenciables son suaves.
 1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
1 Regla e la caena Hasta aquí hemos erivao funciones que no son compuestas. El problema surge cuano tenemos una función que es compuesta, por ejemplo, igamos que el precio e la gasolina epene el precio
UNIVERSIDAD DIEGO PORTALES GUÍA N 11 CÁLCULO I. Profesor: Carlos Ruz Leiva DERIVADAS. Derivadas de orden superior. Ejemplos
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V
 GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
GUIA PARA EL EXAMEN EXTRAORDINARIO DE MATEMATICAS V 1) Determinar el dominio de las siguientes funciones dando el resultado en parentesis para:. y = x + 4. y = 3x c). y = x 3 x+ ) Obtener el rango para
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
UNIDAD I CÁLCULO DIFERENCIAL
 Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Vicerrectorao Acaémico Faculta e Ciencias Aministrativas Licenciatura en Aministración Mención Gerencia y Mercaeo Unia Curricular: Matemática I UNIDAD I CÁLCULO DIFERENCIAL Elaborao por: Ing. Ronny Altuve
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada
![Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada](/thumbs/71/65048770.jpg) Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
FUNCIONES DE UNA VARIABLE Una función es una regla que a cada número x R le asigna un único valor f x) R El dominio de f son los puntos en los que está definida Dom f ) = {x R/ f x)} La gráfica de f es
30. La tangente paralela a la bisectriz del segundo cuadrante tendrá pendiente 1. y' = 2x= 1 x= El punto pedido es :, 4
 PÁGINA 96 1 SOLUCIONES 0 La tangente paralela a la bisectriz del segundo cuadrante tendrá pendiente 1 Por tanto: 1 La solución queda: 1 1 1 y' = x= 1 x= El punto pedido es :, 4 La ecuación de la elipse
PÁGINA 96 1 SOLUCIONES 0 La tangente paralela a la bisectriz del segundo cuadrante tendrá pendiente 1 Por tanto: 1 La solución queda: 1 1 1 y' = x= 1 x= El punto pedido es :, 4 La ecuación de la elipse
Tema 6: Ecuaciones diferenciales lineales.
 Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) y = ex cos y. e x cos y e x sin y. y 2.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
f(x,y) = e x+y cos(xy)
 Universia e los Anes Departamento e Matemáticas MATE1207 Cálculo Vectorial Tarea 1 Iniviual Entregue en clase a su profesor e la MAGISTRAL la semana 6 (Lu. 3 Sep. Vi. 7 Sep.) 1. Consiere la función f efinia
Universia e los Anes Departamento e Matemáticas MATE1207 Cálculo Vectorial Tarea 1 Iniviual Entregue en clase a su profesor e la MAGISTRAL la semana 6 (Lu. 3 Sep. Vi. 7 Sep.) 1. Consiere la función f efinia
Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones. 1. Estudiar la acotación de las siguientes funciones:
 Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Fundamentos Matemáticos para la Ingeniería. Curso 2015-2016. Tema 3. Hoja 1 Tema 3. FUNCIONES. CÁLCULO DIFERENCIAL. Funciones 1. Estudiar la acotación de las siguientes funciones: (a) y = 2x 1; (b) y =
Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos
 página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Reglas de derivación
 1 CAPÍTULO 6 Reglas e erivación 6.6 erivación imlícita 1 Hasta aquí la alabra erivaa ha sio asociaa a funciones efinias exlícitamente meiante una iguala e la forma y f.x/, one una e las variables.y/ aarece
1 CAPÍTULO 6 Reglas e erivación 6.6 erivación imlícita 1 Hasta aquí la alabra erivaa ha sio asociaa a funciones efinias exlícitamente meiante una iguala e la forma y f.x/, one una e las variables.y/ aarece
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Curso: 2º Bachillerato Examen II
 Nombre: Nota Curso: º Bachillerato Examen II Fecha: de Octubre de 015 La mala o nula explicación de cada ejercicio implica una penalización de hasta el 5% de la nota. 1.- Se sabe que la función f :[0,5]
Nombre: Nota Curso: º Bachillerato Examen II Fecha: de Octubre de 015 La mala o nula explicación de cada ejercicio implica una penalización de hasta el 5% de la nota. 1.- Se sabe que la función f :[0,5]
ALGUNOS EJERCICIOS DE C. DIF.
 1 ALGUNOS EJERCICIOS DE C. DIF. 1.-Concepto de función Algunos ejercicios 1.1==En una circunferencia de radio 10 m, se inscribe un rectangulo. Expresar el area del rectangulo en funcion del lado x de la
1 ALGUNOS EJERCICIOS DE C. DIF. 1.-Concepto de función Algunos ejercicios 1.1==En una circunferencia de radio 10 m, se inscribe un rectangulo. Expresar el area del rectangulo en funcion del lado x de la
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Creciente y decreciente.
 Creciente y decreciente. Estrictamente creciente. Función creciente en un intervalo Función estrictamente decreciente en un intervalo Función decreciente de un intervalo. Si un punto A (x,y) escribe
Creciente y decreciente. Estrictamente creciente. Función creciente en un intervalo Función estrictamente decreciente en un intervalo Función decreciente de un intervalo. Si un punto A (x,y) escribe
3 Aplicaciones de primer orden
 CAPÍTULO 3 Aplicaciones de primer orden 3.7.1 Traectorias ortogonales Si consideramos la familia de curvas C c; con c > 0; podemos decir que esta familia es el conjunto de las circunferencias de radio
CAPÍTULO 3 Aplicaciones de primer orden 3.7.1 Traectorias ortogonales Si consideramos la familia de curvas C c; con c > 0; podemos decir que esta familia es el conjunto de las circunferencias de radio
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
Unidad 6 GEOMETRIA ANALITICA
 Profesor: Blas Torres Suárez. Versión.0 Unidad 6 GEOMETRIA ANALITICA Competencias a desarrollar: Determinar distancia y el punto medio de entre dos puntos dados Encontrar la ecuación de una recta si se
Profesor: Blas Torres Suárez. Versión.0 Unidad 6 GEOMETRIA ANALITICA Competencias a desarrollar: Determinar distancia y el punto medio de entre dos puntos dados Encontrar la ecuación de una recta si se
Ecuación vectorial de la recta en el plano y su ecuación cartesiana
 iceo Técnico Aolfo Matthei ierano la Eucación Técnico Profesional Docente: Cristian Casas. GUIA MATEMATICA Departamento e Matemática Curso: 4 Meio Fecha : Puntos : NOMBRE: Nota : Ecuación vectorial e la
iceo Técnico Aolfo Matthei ierano la Eucación Técnico Profesional Docente: Cristian Casas. GUIA MATEMATICA Departamento e Matemática Curso: 4 Meio Fecha : Puntos : NOMBRE: Nota : Ecuación vectorial e la
Práctico 4: Funciones inversas
 Práctico 4: Funciones inversas 1. Averiguar acerca e la inyectivia e las siguientes funciones en sus ominios naturales: 1.- y = ax + bx + c con a 6= 0.- y = x + ax + b con a>0.- y = x + ax + b con a
Práctico 4: Funciones inversas 1. Averiguar acerca e la inyectivia e las siguientes funciones en sus ominios naturales: 1.- y = ax + bx + c con a 6= 0.- y = x + ax + b con a>0.- y = x + ax + b con a
Soluciones de los ejercicios del examen de Cálculo del 29 de junio de 2007 Primero de Ingeniería de Telecomunicación
 Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Soluciones de los ejercicios del examen de del 29 de junio de 27 Primero de Ingeniería de Telecomunicación Ejercicio a Justifica que la ecuación x 2 = x sen x+ cos x tiene exactamente dos soluciones reales.
Resolución de ecuaciones y sistemas.
 PRÁCTICAS MATEMÁTICAS I Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Práctica 4: Resolución de ecuaciones Cálculo de derivadas y Problemas de
PRÁCTICAS MATEMÁTICAS I Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Práctica 4: Resolución de ecuaciones Cálculo de derivadas y Problemas de
4.1. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS
 Escuela Colombiana e Ingeniería 4.. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS Derivaa e y La erivaa e y se puee obtener como: y + Lim 0 Para calcular este límite se utilizan los siguientes conceptos previamente
Escuela Colombiana e Ingeniería 4.. DERIVADAS DE LAS FUNCIONES TRIGONOMETRICAS Derivaa e y La erivaa e y se puee obtener como: y + Lim 0 Para calcular este límite se utilizan los siguientes conceptos previamente
TEMA 4 TERCER TURNO (09/10/2017)
 TEMA 4 Ejercicio 1 (2 puntos) Determinar el valor de la constante a R para que se verifique que la recta de ecuación y = 2 sea una asíntota horizontal de la función f(x) = 20x2 x + 7 2ax 2 + 1 Hallar la
TEMA 4 Ejercicio 1 (2 puntos) Determinar el valor de la constante a R para que se verifique que la recta de ecuación y = 2 sea una asíntota horizontal de la función f(x) = 20x2 x + 7 2ax 2 + 1 Hallar la
TEMA 1 TERCER TURNO (09/10/2017) Ejercicio 1 (2 puntos) Dadas las funciones. determinar todos los valores de x R para los cuales (g f)(x) = f(36)
 TEMA 1 Ejercicio 1 (2 puntos) Dadas las funciones f(x) = x 3 ; g(x) = 2(x 5) 2 + 1 determinar todos los valores de x R para los cuales (g f)(x) = f(36) Primero debemos hallar la expresión de la función
TEMA 1 Ejercicio 1 (2 puntos) Dadas las funciones f(x) = x 3 ; g(x) = 2(x 5) 2 + 1 determinar todos los valores de x R para los cuales (g f)(x) = f(36) Primero debemos hallar la expresión de la función
DERIVADAS. Problemas con Solución.
 DERIVADAS. Problemas con Solución. Aplica la definición de derivada como un límite, para calcular f siendo fx = x + x +. 4. Sea la función fx = x/x, halla la derivada de f en el punto de abcisa usando
DERIVADAS. Problemas con Solución. Aplica la definición de derivada como un límite, para calcular f siendo fx = x + x +. 4. Sea la función fx = x/x, halla la derivada de f en el punto de abcisa usando
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900 (1) La posición vertical de una pelota está dada por h(t) = 128 + 16t 16t 2 en donde t se mide en segundos y h(t) se mide en pies. Durante
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E0900 (1) La posición vertical de una pelota está dada por h(t) = 128 + 16t 16t 2 en donde t se mide en segundos y h(t) se mide en pies. Durante
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-13-5-M-1--17 CURSO: Matemática Básica SEMESTRE: Primero CÓDIGO DEL CURSO: 13 TIPO DE EXAMEN: Primera Retrasaa
() 25 de mayo de / 9
 DEFINICION. Una función es iferenciable en a si f (a) existe, y iremos que es iferenciable en un intervalo abierto si es iferenciable en caa uno e los puntos el intervalo. NOTA. Para las funciones que
DEFINICION. Una función es iferenciable en a si f (a) existe, y iremos que es iferenciable en un intervalo abierto si es iferenciable en caa uno e los puntos el intervalo. NOTA. Para las funciones que
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Función de dos variables
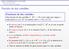 Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable
 EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Cálculo 10. Semestre A Rectas y Cónicas
 Cálculo 10. Semestre A-017 Prof. José Prieto Correo: prieto@ula.ve. Rectas Cónicas Problema.1 Hallar las distancia entre los siguientes pares de puntos P Q, además encontrar el punto medio que los une:
Cálculo 10. Semestre A-017 Prof. José Prieto Correo: prieto@ula.ve. Rectas Cónicas Problema.1 Hallar las distancia entre los siguientes pares de puntos P Q, además encontrar el punto medio que los une:
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Fundamentos matemáticos. Tema 5 Derivación de funciones de una y varias variables
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
2 Estudio local de funciones de varias variables.
 a t e a PROBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CURSO 2009 2010 2 Estudio local de funciones de varias variables. 2.1 Derivadas de orden superior. Problema 2.1 Sea
a t e a PROBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CURSO 2009 2010 2 Estudio local de funciones de varias variables. 2.1 Derivadas de orden superior. Problema 2.1 Sea
3 DERIVADAS ALGEBRAICAS
 DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Autoevaluación. Bloque III. Geometría. BACHILLERATO Matemáticas I * 8 D = (3, 3) Página Dados los vectores u c1, 1m y v (0, 2), calcula:
 Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
CÁLCULO DE PRIMITIVAS
 2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
Temas 4 y 5. Teoremas de inversión local. Extremos.
 Problemas de Diferenciación de Funciones de Varias Variables Curso 2013-2014 Temas 4 y 5. Teoremas de inversión local. Extremos. 1. Sea U R n abierto convexo y f : U R. Decimos que f es convexa si: f(tx+(1
Problemas de Diferenciación de Funciones de Varias Variables Curso 2013-2014 Temas 4 y 5. Teoremas de inversión local. Extremos. 1. Sea U R n abierto convexo y f : U R. Decimos que f es convexa si: f(tx+(1
Coordinación de Matemática I (MAT021) Taller 10
 Coordinación de Matemática I MAT01 Taller 10 Primer semestre de 01 Semana 11: Lunes 0 viernes 08 de junio Ejercicios Ejercicio 1 Calcular las derivadas de las siguientes funciones: 1. cos x ln x. x + x
Coordinación de Matemática I MAT01 Taller 10 Primer semestre de 01 Semana 11: Lunes 0 viernes 08 de junio Ejercicios Ejercicio 1 Calcular las derivadas de las siguientes funciones: 1. cos x ln x. x + x
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
MATE 3013 LA REGLA DE LA CADENA
 MATE 3013 LA REGLA DE LA CADENA La composición e funciones DEFINICION: La composición función f g, e f con g, se efine f g f ( g( x)) La composición e funciones Ejemplo : Para Hallar f (x) x 3 y g(x) 1
MATE 3013 LA REGLA DE LA CADENA La composición e funciones DEFINICION: La composición función f g, e f con g, se efine f g f ( g( x)) La composición e funciones Ejemplo : Para Hallar f (x) x 3 y g(x) 1
x = 1 y que la recta tangente a la gráfica de la función en el punto de abcisa x=0 tiene la a)estudia y calcula las asístontas de la gráfica de f.
 Jueves 9 de noviembre de 17 Ejercicio 1. Problema de optimización. Se considera una ventana rectangular en la que el lado de arriba se ha sustituido por un triángulo equilátero. Calcula la longitud de
Jueves 9 de noviembre de 17 Ejercicio 1. Problema de optimización. Se considera una ventana rectangular en la que el lado de arriba se ha sustituido por un triángulo equilátero. Calcula la longitud de
Docente Matemáticas. Marzo 11 de 2013
 Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Pauta Prueba Parcial 1 de Matemáticas 2
 Pauta Prueba Parcial 1 de Matemáticas Programa de Bachillerato. Universidad de Chile. Sábado 17 de Diciembre, 011 1. Demuestre que f : R R es derivable en x 0, donde { cos( x) cos( 3x) f(x) x si x 0 0
Pauta Prueba Parcial 1 de Matemáticas Programa de Bachillerato. Universidad de Chile. Sábado 17 de Diciembre, 011 1. Demuestre que f : R R es derivable en x 0, donde { cos( x) cos( 3x) f(x) x si x 0 0
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
IES RAFAEL PUGA RAMÓN DERIVADA Y APLICACIONES Calcula el valor de a para que la gráfica de la función y= x a cumpla que la recta
 BOLETÍN DE DERIVADAS Y RECTA TANGENTE 1. Aplicando la definición, calcula la derivada de f(x)=2x 2 -x en x=1 2. Pon tres ejemplos de funciones cuya derivada sea x 2. Cuántas existen?. Existe alguna función
BOLETÍN DE DERIVADAS Y RECTA TANGENTE 1. Aplicando la definición, calcula la derivada de f(x)=2x 2 -x en x=1 2. Pon tres ejemplos de funciones cuya derivada sea x 2. Cuántas existen?. Existe alguna función
4. Mecánica en la Medicina Derivar e Integrar
 4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
4. Mecánica en la Meicina Derivar e Integrar Teoría Dr. Willy H. Gerber Instituto e Ciencias Físicas y Matemáticas, Universia Austral, Valivia, Chile 17.04.2011 W. Gerber 4. Mecánica en la Meicina - Matemática
La derivada de las funciones trascendentes
 La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
La erivaa e las funciones trascenentes Manuel Barahona, Eliseo Martínez Diciembre 205 Muchos fenómenos e la naturaleza son moelaos meiante funciones eponeciales, logarítimicas, trigonométricas y combinaciones
2.1. Derivada de una función en un punto
 Capítulo 2 Diferenciación 1 2.1. Derivaa e una función en un punto Ritmo (o razón, o tasa) e cambio e una función en un momento ao. Peniente e la recta tangente. Aproximación por la peniente e las rectas
Capítulo 2 Diferenciación 1 2.1. Derivaa e una función en un punto Ritmo (o razón, o tasa) e cambio e una función en un momento ao. Peniente e la recta tangente. Aproximación por la peniente e las rectas
2. Sea f(x, y) = x 2 2xy+y 2. Aquí el discriminante es igual a cero. Qué son los puntos críticos: mínimos locales, máximos locales o puntos silla?
 1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
Examen final Junio 2012
 1 Matemáticas 1 Bachillerato de Ciencias y Tecnología I.E.S. José Hierro Getafe) 1ª Evaluación 1. *) Calcular los siguientes límites: a) n Examen final Junio 01 n +1 1)n n +1 n 1) c) n n x 5. *) Resolver
1 Matemáticas 1 Bachillerato de Ciencias y Tecnología I.E.S. José Hierro Getafe) 1ª Evaluación 1. *) Calcular los siguientes límites: a) n Examen final Junio 01 n +1 1)n n +1 n 1) c) n n x 5. *) Resolver
MATEMÁTICAS I Modalidad Ciencias y Tecnología
 CUADERNO DE ACTIVIDADES CURSO 016/017 MATEMÁTICAS I Modalidad Ciencias y Tecnología 1º curso de Bachillerato I.E.S. Victoria Kent (Marbella) Departamento de Matemáticas Bloque de Aritmética y álgebra Ejercicio
CUADERNO DE ACTIVIDADES CURSO 016/017 MATEMÁTICAS I Modalidad Ciencias y Tecnología 1º curso de Bachillerato I.E.S. Victoria Kent (Marbella) Departamento de Matemáticas Bloque de Aritmética y álgebra Ejercicio
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
ELEMENTOS DE GEOMETRIA ANALITICA
 ELEMENTOS DE GEOMETRIA ANALITICA Derecho básico de aprendizaje: Explora y describe las propiedades de los lugares geométricos y de sus transformaciones a partir de diferentes representaciones. (ver DBA
ELEMENTOS DE GEOMETRIA ANALITICA Derecho básico de aprendizaje: Explora y describe las propiedades de los lugares geométricos y de sus transformaciones a partir de diferentes representaciones. (ver DBA
Tema 5. Introducción a las ecuaciones diferenciales ordinarias. senx + C 2. x es solución de la ecuación diferencial
 1 Tema 5. Introducción a las ecuaciones diferenciales ordinarias 1.- Comprobar que la función y = C 1 senx + C 2 x es solución de la ecuación diferencial (1 - x cotgx) d2 y dx 2 - x dy dx + y = 0. 2.-
1 Tema 5. Introducción a las ecuaciones diferenciales ordinarias 1.- Comprobar que la función y = C 1 senx + C 2 x es solución de la ecuación diferencial (1 - x cotgx) d2 y dx 2 - x dy dx + y = 0. 2.-
E.T.S.I. Industriales y Telecomunicación Curso PRUEBAS DE EVALUACIÓN
 E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
E.T.S.I. Industriales y Telecomunicación Curso 00-0 A continuación se presentan 5 preguntas con 4 respuestas posibles. En cada pregunta hay una única respuesta correcta. Cada pregunta acertada y bien justificada
x 2 y si x 3y 2 si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.
 FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P. 8 x 2 + y 2 + xy3 x 4 =1
 CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P (1) Obtener la ecuación de la tangente a la curva en el punto (2, 2). x 2 + y 2 + xy3 x 4 =1 (2) Se requiere construir un
CÁLCULO DIFERENCIAL E INTEGRAL I TERCERA EVALUACIÓN PARCIAL E0600 TRIMESTRE 00-P (1) Obtener la ecuación de la tangente a la curva en el punto (2, 2). x 2 + y 2 + xy3 x 4 =1 (2) Se requiere construir un
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas
 UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas a t e a t i c a s PROBLEMAS, CÁLCULO I, er CURSO 2. CÁLCULO DIFERENCIAL DE UNA VARIABLE GRADO EN INGENIERÍA EN:
Lección 51. Funciones III. Funciones lineales
 Lección 51 Funciones III Funciones lineales Una función lineal es una función de la forma f (x) = mx + b, donde m y b son constantes. Se llama lineal porque su gráfica es una línea recta, en el plano R
Lección 51 Funciones III Funciones lineales Una función lineal es una función de la forma f (x) = mx + b, donde m y b son constantes. Se llama lineal porque su gráfica es una línea recta, en el plano R
FUNCIONES. Ejemplo: F(x) = 3x + 2
 FUNCIONES Una función es una regla que asocia a cada elemento de un conjunto, uno y solo un elemento de otro conjunto. Una función es un conjunto de parejas ordenadas de números (x, y) en el cual dos parejas
FUNCIONES Una función es una regla que asocia a cada elemento de un conjunto, uno y solo un elemento de otro conjunto. Una función es un conjunto de parejas ordenadas de números (x, y) en el cual dos parejas
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
4.1 Antiderivadas o primitivas e integración indefinida
 48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
48 CAPÍTULO 4 Integración 4. Antierivaas o primitivas e integración inefinia Escribir la solución general e una ecuación iferencial. Usar la notación e la integral inefinia para las antierivaas o primitivas.
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Ecuaciones de la tangente y la normal
 Ecuaciones de la tangente la normal Ahora que sabemos cómo calcular la pendiente de una recta tangente a una curva dada su ecuación, independientemente de que ésta sea una función o no lo sea, podemos
Ecuaciones de la tangente la normal Ahora que sabemos cómo calcular la pendiente de una recta tangente a una curva dada su ecuación, independientemente de que ésta sea una función o no lo sea, podemos
Problema 1. Calcula las derivadas parciales de las siguientes funciones: (d) f(x, y) = arctan x + y. (e) f(x, y) = cos(3x) sin(3y),
 Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
