Conjuntos, Aplicaciones y Relaciones
|
|
|
- José Ignacio Alcaraz Chávez
- hace 5 años
- Vistas:
Transcripción
1 Capítulo 2 Conjuntos, plicaciones y Relaciones 2.1. Conjuntos Se partirá, en esta introducción, de la existencia intuitiva de unos entes matemáticos que se denominarán conjuntos. Definición 3. Un conjunto es una colección de objetos bien definidos y diferenciables entre sí. los objetos que constituyen un conjunto se les denomina elementos del mismo. Los conjuntos se designan, habitualmente, por letras latinas mayúsculas:, B,... y los elementos por letras latinas minúsculas: a, b,...; si a es un elemento del conjunto, se dirá que a pertenece al conjunto, y se escribirá a. En caso contrario, se dirá que el elemento no pertenece al conjunto y se denotará a. 1 l conjunto que carece de elementos se le denomina conjunto vacío, y se denota por o por { }. Ejemplo 17. La proposición Todos los alumnos que aprobarán Matemáticas en junio no define adecuadamente un conjunto puesto que, dado un alumno, no se puede afirmar de antemano si aprobará o no en junio. Un conjunto puede ser definido por extensión, enumerando todos y cada uno de sus elementos, o por compresión, diciendo cuál es la propiedad que los caracteriza. 1 Un conjunto está bien definido cuando, dado un elemento cualquiera x, es cierta una y sólo una, de las proposiciones x y x. 23
2 24 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES B Figura 2.1: Inclusión de Conjuntos, B. Ejemplo 18. lgunos conjuntos definidos por comprensión: = {x Z ; x 2 16} B = {x N ; x divide a 20} = { } Ejemplo 19. Los mismos conjuntos definidos por extensión: = {0, 1, 2, 3, 4, 1, 2, 3, 4} B = {1, 2, 4, 5, 10, 20} Como se aprecia en este ejemplo, se utilizan las llaves { y } para delimitar los elementos que componen un conjunto Inclusión Definición 4. Dados dos conjuntos y B, se dice que es un subconjunto de B, y se expresa B, cuando todos los elementos de son también elementos de B, es decir: x [x = x B] se dirá que está incluído o contenido en B. Cuando no está contenido en B, se escribirá B (lo cual quiere decir que existe a tal que a B). Cualquier conjunto, siempre admite como subconjuntos al conjunto vacío y a. Estos se denominan subconjuntos impropios o triviales. En otro caso, se dice que B es un subconjunto propio de. Si B y B, se dice que B está contenido estrictamente en y se denota B.
3 2.1. CONJUNTOS 25 En la figura 2.1 se muestra, mediante Diagramas de Venn, 2 un conjunto subconjunto de otro B. Definición 5. El conjunto formado por todos los subconjuntos de uno dado se denomina partes de o conjunto potencia, y se denota P() o 2. Ejemplo 20. Se exponen a continuación dos conjuntos sencillos, y sus partes: Si = {a, b} P() = {, {a}, {b}, }. Si = {a, b, c} P() = {, {a}, {b}, {c}, {a, b}, {a, c}, {b, c }, }. Debe quedar claro que si y B son dos conjuntos cualesquiera, se verifica que B P() B Ejemplo 21. Las afirmaciones I), III), IV ), V ), V III), IX) y XI) son verdaderas. i). ii) iii) { } iv) { } v) {a, b} {a, b, c, {a, b, c}} vi) {a, b} {a, b, c, {a, b, c}} vii) {a, } {a, {a, }} viii) {a, } {a, {a, }} ix) N Z x) N Z xi) {2} P(Z) xii) {2} P(Z) 2 Los Diagramas de Venn fueron introducidos en 1880 por John Venn ( ). Básicamente, se trata de una colección de curvas simples y cerradas, dibujadas en el plano. Son muy útiles para visualizar relaciones entre conjuntos.
4 26 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES U Figura 2.2: Complementario de respecto a U. Definición 6. Un conjunto es finito si tiene un número finito de elementos; este número se llama cardinal y se denota o #. En caso contrario, se dice que es no finito. Es fácil comprobar que si es un conjunto finito, tambien lo es P() 3 y, además, P() = 2. Definición 7. Dos conjuntos y B son iguales si, simultáneamente, se verifica B y B, es decir: = B B B 2.2. Operaciones entre conjuntos Complementación Definición 8. Dado un conjunto U 4 y un subconjunto U se llama complementario del conjunto, y se denota 5 Ā, al subconjunto de U formado por todos los elementos que no pertenecen a, es decir: Ā = {x U ; x } Obsérvese que la propiedad que determina al complementario de es la negación de la propiedad que determina a los elementos de. 3 Si = {a 1, a 2,..., a n } tiene n elementos, a cada uno de sus subconjuntos B le asociamos una cadena c B de 0 s y 1 s de longitud n. Cada cadena binaria tendrá un 1 en la posición i-ésima (i = 1,...,n) si, y sólo si, el elemento a i B, con lo que el cardinal de P() es el número de cadenas binarias de longitud n, es decir 2 n. 4 Cuando, en un contexto determinado, se consideran siempre conjuntos que son subconjuntos de uno dado U, a dicho conjunto de referencia U se le denomina conjunto universal o universo 5 Puede usarse tambien la notación o C U ()
5 2.2. OPERCIONES ENTRE CONJUNTOS 27 B B Figura 2.3: Unión de conjuntos: B. Figura 2.4: Intersección de conjuntos: B. En la figura 2.2 en la página anterior se muestra, en la zona rayada, el conjunto complementario de respecto a U. Propiedades 1. Dado un conjunto U y dos subconjuntos suyos y B, se verifican las siguientes propiedades: i) = U. ii) Ū =. iii) Ā =. iv) B B Ā Unión Definición 9. Dados dos conjuntos y B se llama unión de y B, y se representa B, al conjunto formado por los elementos que pertenecen a o a B: B = {x ; x x B} En la figura 2.3, la zona rayada reprsenta el conjunto B. Propiedades 2. Dados los conjuntos, B y C, subconjuntos de U, la unión de conjuntos verifica las siguientes propiedades: i) ( B), B ( B). ii) B B = B. iii) C B C ( B) C. iv) = (Propiedad Idempotente).
6 28 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES v) B = B (Propiedad Conmutativa). vi) (B C) = ( B) C (Propiedad sociativa). vii) U = U viii) = Intersección Definición 10. Dados dos conjuntos y B se llama intersección de y B, y se representa B, al conjunto formado por los elementos que pertenecen a y a B, es decir: B = {x ; x x B} De la definición se sigue que un elemento pertenece a la intersección si pertenece a los dos conjuntos. En la figura 2.4 en la página anterior la zona rayada indica el conjunto intersección B. Propiedades 3. Dados tres conjuntos,b y C, subconjuntos de U, la intersección verifica las siguientes propiedades: i) ( B), ( B) B. ii) B B =. iii) C ( B) C. 6 iv) C C B C ( B). v) = (Propiedad Idempotente). vi) B = B (Propiedad Conmutativa). vii) (B C) = ( B) C (Propiedad sociativa). viii) U = (U es el conjunto universal). ix) =. Propiedades 4. Con la notación anterior, la unión y la intersección verifican además las siguientes propiedades conjuntas: 6 Nótese que puede suceder que B C y, sin embargo, C y B C. Es el caso de = {a, x}, B = {b, x} y C = {x, y}.
7 2.2. OPERCIONES ENTRE CONJUNTOS 29 B C B C Figura 2.5: (B C). Figura 2.6: (B C). i) (B C) = ( B) ( C) (Ver figura 2.5). ii) (B C) = ( B) ( C) (Ver figura 2.6). iii) Ā = U. iv) Ā =. v) ( B) = Ā B (Primera Ley de De Morgan). vi) ( B) = Ā B (Segunda Ley de De Morgan). Como consecuencia, si, B U son dos subconjuntos de U, se verifica que = U = (B B) = ( B) ( B) Definición 11. Si dos conjuntos no tienen ningún elemento en común, se dice que son disjuntos, es decir: Diferencia y B son disjuntos B = Definición 12. Dados dos conjuntos y B se llama diferencia entre y B, y se representa \B o B, al conjunto formado por los elementos de que no pertenecen a B: \B = {x ; x B} En la figura 2.7(a) en la página siguiente se muestran dos conjuntos y B y, representado por el área rayada, el conjunto B. Se aprecia con
8 30 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES B B (a) Diferencia: \B. (b) Diferencia simétrica: B. Figura 2.7: Diferencia de conjuntos facilidad que \B y B\ son, en general, distintos. Por otro lado, es claro que \B = B demás, se verifica que \B = B B = B Ā B\ = B Definición 13. Dados dos conjuntos y B se llama diferencia simétrica entre y B, y se representa B, al conjunto de los elementos que están en uno y, sólo uno de los conjuntos o B. B = ( B) \ ( B) En la figura 2.7(b) se muestran dos conjuntos y B, y en el área rayada, el conjunto diferencia simétrica B. Es fácil ver que B = B y, además: B = ( B) \ ( B) = (\B) (B\) Tambien se puede comprobar que =, =, Ā = U y U = Ā Producto Cartesiano Definición 14. Dados dos conjuntos y B, se llama producto cartesiano de por B, y se denota B, al conjunto constituido por pares ordenados de elementos, el primero perteneciente al conjunto y el segundo al B. Esto es: B = {(a, b) ; a b B} Ejemplo 22. El producto cartesiano B de los conjuntos = {1, 2, 3} y B = {a, b} es el conjunto: B = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)}
9 2.3. PLICCIONES 31 B b a (1, b) (1, a) (2, b) (2, a) (3, b) (3, a) Figura 2.8: Representación gráfica de B Cuando sea posible, es útil representar gráficamente el producto cartesiano por medio de diagramas de coordenadas cartesianas. Para ello se toman dos rectas OX y OY, perpendiculares u oblicuas, de forma que el punto O es la intersección de ambas. Este punto recibe el nombre de origen, la recta OX es el eje de abscisas y la OY es el eje de ordenadas. El conjunto se representa linealmente en OX, y el B en OY. Los elementos (a, b) de B se representan por puntos resultantes de la intersección de la paralela a OY por a con la paralela a OX por b. En la figura 2.8 se muestra la representación en coordenadas cartesianas del ejemplo anterior. Dos pares ordenados (a, b) y (c, d), elementos del producto cartesiano B, son iguales si a = c y b = d. Es claro que, en general, B B. Se puede extender la definición de producto cartesiano a n conjuntos. Definición 15. Dados n conjuntos 1, 2,..., n se define su producto cartesiano como: 1 2 n = {(a 1, a 2,..., a n ) ; a i i, i = 1, 2,..., n} Finalmente, si y B son conjuntos finitos, tambien lo es B y se tiene que: B =. B 2.3. plicaciones El concepto de aplicación (función) es de gran importancia en Informática. Una función es el modo más natural de implementar la correspondencia entre los datos y el resultado de un proceso de cálculo en un ordenador. Los llamados lenguajes funcionales como OCML, HSKELL, etc., se fundamentan en este concepto y suelen identificar programa y función.
10 32 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES Definición 16. Sean y B dos conjuntos no vacíos. Una aplicación f de en B es una regla que asocia a cada elemento a de un único elemento de B que se denomina imagen de a y se denota f(a). El conjunto se llama conjunto inicial, y el B conjunto final. La relación entre a y b debida a f se suele representar de la forma: f : B a f (a) = b Se suele denominar función 7 a la correspondencia f : B si y B son conjuntos numéricos. Con frecuencia, se utiliza la letra x para denotar los elementos del conjunto inicial de f, y la letra y para los elementos del conjunto final. rojo naranja verde amarillo azul violeta 4, 28 4, 63 5, 17 5, 35 6, 12 6, 97 7, 49 Hz Figura 2.9: plicación del espectro visible Ejemplo 23. i) Se puede considerar que el arco iris define una aplicación que asocia a cada rango de frecuencias del espectro electromagnético, un color de los que percibimos tal como se muestra en la figura 2.9. ii) El horario de un ferrocarril define una aplicación que asocia a cada estación a, b, c,... un número que sirve para expresar la medida del tiempo (8h, 8h30m, 8h57m,...) que invertirá el tren en llegar a cada estación. Puesto que a cada estación sólo le puede corresponder una hora de llegada del tren, esta correspondencia entre estaciones y horarios sea efectivamente una aplicación. iii) Una tabla de seguros de vida es una función que asocia cada edad del solicitante (1 año, 2 años, 3 años, etc.) el importe de las primas que ha de pagar para suscribir tal seguro. 7 En el contexto del nálisis Matemático es frecuente utilizar la palabra función para referirse a una correspondencia f : B, es decir una regla que asocia a algunos elementos de un elemento en B. Esos elementos de que tienen imagen en B forman un subconjunto de llamado dominio de f y que coincide con cuando f es una aplicación.
11 2.3. PLICCIONES 33 iv) La regla que permite calcular el perímetro p de una circunferencia multiplicando su diámetro 2r (siendo r el radio) por la constante π, es una función real de variable real, ya que el conjunto inicial es el de los números reales, R, y coincide con el de llegada. Se representa: p = f(r) = 2πr Dos aplicaciones f : B y g : C D son iguales si = C, B = D y f(a) = g(a), para cualquier elemento a de. Si y B son dos conjuntos cualesquiera, se denota por B al conjunto: B = {f : B ; f es una aplicación}. Cuando y B son conjuntos son finitos, también lo es B y se verifica que B = B. Definición 17. Sea f : B una aplicación y sean 1 y B 1 B dos subconjuntos de y B respectivamente. Definimos la imagen por f del conjunto 1 como: f( 1 ) := {f(a) ; a 1 } B y la imagen recíproca por f del conjunto B 1 como: f 1 (B 1 ) := {a ; f(a) B 1 } Si tomamos como 1 =, al conjunto f() = Imf le denominamos conjunto imagen. Ejemplo 24. Sea f : = {1, 2, 3} B = {x, y, z, t} la aplicación dada por f(1) = x, f(2) = z, f(3) = z. Es claro que y, por otro lado, f({1}) = {x}, f({2}) = {z}, f({3}) = {z} f 1 ({x, y}) = {1} y f 1 ({y, t}) =. Propiedades 5. Sea f : B una aplicación y sean 1, 2 y B 1, B 2 B subconjuntos de y B respectivamente. Se verifica: i) f( ) =, f 1 ( ) = y f 1 (B) = ii) Si 1 2, entonces f( 1 ) f( 2 )
12 34 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES iii) Si B 1 B 2, entonces f 1 (B 1 ) f 1 (B 2 ) iv) f( 1 2 ) f( 1 ) f( 2 ) La igualdad no es cierta, en general. Basta tomar 1 = {2} y 2 = {3} en el el ejemplo 24. v) f( 1 2 ) = f( 1 ) f( 2 ) vi) f 1 (B 1 B 2 ) = f 1 (B 1 ) f 1 (B 2 ) vii) f 1 (B 1 B 2 ) = f 1 (B 1 ) f 1 (B 2 ) viii) 1 f 1 (f( 1 )) Si tomamos 1 = {2} en el ejemplo 24 comprobamos que {2} f 1 (f({2}) = f 1 ({z}) = {2, 3} ix) f (f 1 (B 1 )) B 1 Si tomamos B 1 = B = {x, y, z, t} en el ejemplo 24 comprobamos que f(f 1 ({x, y, z, t}) = f({1, 2, 3}) = {x, z} {x, y, z, t}. Definición 18. Sea f : B una aplicación y sea 1 un subconjunto de. Llamamos restricción de f a 1 y denotamos f /1 a la aplicación f restringida al conjunto 1, es decir, f definida sólo para los elementos de 1. Definición 19. Se dice que una aplicación f : B entre y B es: i) inyectiva si dos elementos distintos de tienen diferente imagen en B, esto es: a 1, a 2 [f(a 1 ) = f(a 2 ) = a 1 = a 2 ] ii) sobreyectiva, suprayectiva o exhaustiva si todo elemento de B es imagen, al menos, de un elemento de, es decir: b B, a [f (a) = b] iii) biyectiva o biunívoca si es a la vez inyectiva y sobreyectiva. Es interesante destacar que si los conjuntos y B son finitos y f : B es una aplicación entre ellos, se verifica que:
13 2.3. PLICCIONES 35 Si f es inyectiva 8, entonces B Si f es sobreyectiva, entonces B Si f es biyectiva 9, entonces = B Ejemplo 25. Una empresa proporciona a sus 513 empleados un código que consta de nueve cifras entre 0 y 9, por ejemplo 23/130/0467. Dos códigos son coincidentes en ceros si, en cada posición, uno tiene un cero si, y sólo si, lo tiene el otro. sí, los códigos 20/560/0503 y 10/730/0804 son coincidentes en ceros. Demuestra que al menos dos empleados tendrán códigos de usuario coincidentes en ceros. 10 demás, se verifica también el siguiente resultado que será de utilidad en la práctica: Proposición 1. Si y B son dos conjuntos finitos con el mismo cardinal y f : B es una aplicación entre ellos, son equivalentes: f es inyectiva f es sobreyectiva f es biyectiva Demostración. Si = {a 1,...,a n }, entonces f() = {f(a 1 ),..., f(a n )} y, al ser f inyectiva, f() = = B. Puesto que f() B y tienen el mismo cardinal, es obvio que f() = B, es decir f es sobreyectiva. Recíprocamente, si f es sobreyectiva y f(a 1 ) = f(a 2 ) con a 1 a 2, entonces f() < = B, lo que contradice la sobreyectividad de f. Definición 20. Dados tres conjuntos, B y C, y dos aplicaciones f y g tales que f : B g : B C a f (a) = b b g (b) = c 8 Este principio se conoce como Principio de Palomar. Es claro que si tenemos un conjunto de n palomas y otro conjunto de m nidos, con n > m, y definimos una aplicación entre ellos que consiste en enviar cada paloma a su nido, al menos dos palomas comparten un nido, es decir la aplicación no es inyectiva. 9 Conviene destacar que, si bien no todas las aplicaciones que se pueden definir entre conjuntos con el mismo cardinal son biyectivas, siempre es posible encontrar una aplicación biyectiva entre ellos. 10 cada empleado (paloma) le hacemos corresponder el subconjunto de {1, 2,..., 9} (nido) correspondiente a las posiciones en las que su código tiene un cero. Como hay más palomas que nidos (el número de subconjuntos posibles es 2 9 = 512), dos palomas al menos comparten el nido.
14 36 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES se llama composición de f con g a la aplicación g f : C a (g f)(a) = g [f (a)] = g (b) = c Ejemplo 26. Sea = {1, 2, 3, 4, 5} y sean f, g : las aplicaciones definidas por f(1) = f(2) = f(3) = f(4) = f(5) = 1 y g(1) = 5, g(2) = 4, g(3) = 3, g(4) = 2 y g(5) = 1. Es evidente que (g f)(a) = 5 y (f g)(a) = 1, para todo a. Por lo tanto, g f f g. La composición de aplicaciones tiene la propiedad asociativa, es decir, dadas tres aplicaciones f : B, g : B C y h : C D : h (g f) = (h g) f Proposición 2. Sean f : B y g : B C dos aplicaciones cualesquiera. Se verifica que: Si f y g son inyectivas, también lo es g f Si f y g son sobreyectivas, también lo es g f Si f y g son biyectivas, también lo es g f Demostración. Si f y g son inyectivas y a 1, a 2 son dos elementos de tales que (g f)(a 1 ) = (g f)(a 2 ), entonces g(f(a 1 )) = g(f(a 2 )) (por definición de composición). Puesto que g es inyectiva, se verifica que f(a 1 ) = f(a 2 ) y, la inyectividad de f permite concluir que a 1 = a 2. La demostración de las otras dos afirmaciones es un sencillo ejercicio. Definición 21. Se llama aplicación identidad a una aplicación I de a de la forma: I : a I (a) = a Es inmediato comprobar que dada cualquier aplicación f : B se verifica que f I = f = I B f Definición 22. Sea f : B una aplicación. Se llama aplicación inversa de f, y se denota por f 1, a una aplicación f 1 : B tal que, si b es un elemento de B, f 1 (b) = a b = f(a) Puede que no exista aplicación inversa de f.
15 2.3. PLICCIONES 37 Z N Figura 2.10: Representación gráfica de la aplicación γ : N Z Proposición 3. Dada una aplicación f : B, f admite inversa si, y sólo si, f es biyectiva. demás, Si f es inversible, su inversa f 1 es la única aplicación verificando f f 1 = I B y f 1 f = I Si f es inversible, su inversa f 1 también lo es y (f 1 ) 1 = f Si f : B y g : B C son dos aplicaciones inversibles, entonces g f también lo es y (g f) 1 = f 1 g Conjuntos numerables Decimos que un conjunto es numerable si es finito o existe una biyección entre y N. Se comprende fácilmente que si es finito y n =, existe una biyección entre el conjunto y {1,...,n}. Son numerables los conjuntos N y Z ya que la aplicación γ : N Z { n/2, si n es par n γ (n) = (n 1)/2, si n es impar es biyectiva. En la figura 2.10 se muestra un diagrama en el que se aprecia el funcionamiento de esta aplicación. Los naturales pares son asignados a los enteros positivos, y los naturales impares a los enteros negativos. Es evidente, a la vista de la figura, que esta aplicación no tiene por qué ser única. También es cierto que el conjunto de los números racionales Q es numerable. No son numerables ni R ni C.
16 38 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES B R b a r R Figura 2.11: Representación gráfica de R B Figura 2.12: Representación gráfica de C R R 2.4. Relaciones Definición 23. Dados dos conjuntos y B, una relación binaria 11 de en B es un subconjunto cualquiera R del producto cartesiano B. Si el par ordenado (a, b) pertenece a R, se dirá que a está relacionado con b, y se denotará arb. Ejemplo 27. i) Para los conjuntos y B del ejemplo 22, se tiene que B = {(1, a),(1, b),(2, a),(2, b),(3, a),(3, b)}. Una posible relación sería R = {(1, a),(2, b),(3, a)}. En la figura 2.11 se muestran, mediante puntos, los elementos de B, y mediante círculos los de R. ii) Para el producto cartesiano R R, serán = B = R. Una posible relación podría ser C = {(x, y) R R ; x 2 + y 2 = r 2 }, siendo r un número real positivo. En la figura 2.12 se muestran los conjuntos y B (los ejes cartesianos), y toda la superficie del papel, en la que se encuentran los ejes, que constituye el producto cartesiano B = R R = R 2. Los elementos de la relación C serán los puntos de ese plano que verifiquen la ecuación que la caracteriza. En la figura, esos puntos se encuentran sobre la línea fina que, como se aprecia, forma una circunferencia de radio r. iii) El estado de una partida de un juego de barcos se determina, habitualmente, en un tablero cuadrado de 100 casillas, ordenadas en 10 filas y 11 En general si tenemos n conjuntos, i con i = 1,...,n, se dice que un subconjunto R 1 n es una relacion n-aria sobre 1, 2,..., n.
17 2.4. RELCIONES 39 B C D E F G H I J B C D E F G H I J Figura 2.13: Tablero de una partida de barcos: X Y. Figura 2.14: Flota de barcos (F) y torpedos disparados (T ) en un tablero de barcos (X Y ). 10 columnas numeradas respectivamente del 1 al 10 y de la a la J, tal como se muestra en la figura Si llamamos X al conjunto de las filas del tablero e Y al de las columnas, las casillas del tablero serán pares ordenados de la forma (x, y) X Y. La situación de la flota de barcos en el tablero bien puede considerarse una relación F X Y. En concreto, los barcos que se muestran en el tablero de la figura 2.14 constituyen la relación: F = {(B, 2), (B, 3),(B, 4),(E, 8),(F, 8),(G, 8),(H, 3),(H, 4),(H, 5)} Por otra parte, los sucesivos intentos de hundir la flota, indicados en la figura 2.14 mediante torpedos, constituyen otra relación T de la forma: T = {(D, 6),(E, 2),(F, 8),(H, 5),(I, 9)} Los impactos que los torpedos han producido en los barcos, serán la relación intersección entre ambas: I = F T = {(F, 8), (H, 5)}. Definición 24. Dado un conjunto, se llama relación binaria en a cualquier subconjunto R de. 12 Una relación binaria en es, por tanto, una relación en la que coinciden el conjunto inicial y el final. Si el conjunto es finito, se puede representar una relación binaria en con un grafo dirigido. Para ello, se dibujan tantos puntos como elementos tenga y una flecha de a a b si (a, b) R o, lo que es lo mismo, si arb. 12 Si es finito, el número de relaciones binarias en es 2 2.
18 40 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES Propiedades de una relación binaria Sea un conjunto y R una relación binaria en, Se dice que R es i) Reflexiva si a ara ii) Simétrica si a 1, a 2 [a 1 Ra 2 = a 2 Ra 1 ] iii) ntisimétrica si iv) Transitiva si a 1, a 2 [(a 1 Ra 2 ) (a 2 Ra 1 ) = a 1 = a 2 ] a 1, a 2, a 3 [(a 1 Ra 2 ) (a 2 Ra 3 ) = a 1 Ra 3 ] Ejemplo 28. i) Dado cualquier conjunto, la relación ( ) estar contenido en definida en P() es reflexiva, antisimétrica y transitiva. ii) Si = N, Z, Q o R, la relación ( ) ser menor o igual que es también reflexiva, antisimétrica y transitiva. iii) Dados dos números enteros a y b, se dice que a divide a b y se denota a b, si existe un número entero m tal que b = am. Es fácil comprobar que es reflexiva y transitiva. Cuando la restringimos a un subconjunto de números enteros del mismo signo (es decir Z + o Z ), verifica, además la propiedad antisimétrica Relación de Equivalencia Definición 25. Una relación de equivalencia en un conjunto es una relación binaria R que satisface las propiedades reflexiva, simétrica y transitiva. En adelante, utilizaremos el símbolo para referirnos a una relación de equivalencia. Ejemplo 29. En Z, la relación: a 2 b a b es un múltiplo de 2 es una relación de equivalencia. Esta relación se puede extender, considerando cualquier entero positivo m y definiendo: a m b a b es un múltiplo de m
19 2.4. RELCIONES 41 Las relaciones de equivalencia permiten agrupar elementos relacionados entre sí en subconjuntos llamados clases de equivalencia: Definición 26. Dado un conjunto dotado de una relación de equivalencia, se llama clase de equivalencia del elemento a, y se denota por [a] al conjunto de los elementos de que están relacionados con a mediante, es decir: [a] = {x ; x a} La relación de equivalencia del ejemplo que hemos visto antes divide a los elementos del conjunto Z en dos clases de equivalencia, una formada por los números pares, y la otra por los impares. Cuando la relación es m, tenemos m clases de equivalencia 13 [0], [1],...,[m 1]. Propiedades 6. Las clases de equivalencia verifican las siguientes propiedades: i) Dos elementos a 1 y a 2 están relacionados entre sí (a 1 a 2 ) si, y sólo si, determinan la misma clase de equivalencia ([a 1 ] = [a 2 ]) 14. Demostración. Si a 1 a 2 y a [a 1 ], entonces a a 1 y a 1 a 2, nos permiten deducir que a a 2, es decir a [a 2 ]. Recíprocamente, si las clases coinciden, entonces a 1 [a 1 ] = [a 2 ], es decir a 1 a 2. ii) Dos elementos a 1 y a 2 no están relacionados si, y sólo si, [a 1 ] [a 2 ] =. Demostración. Si a 1 a 2 y a [a 1 ] [a 2 ], entonces a 1 a y a a 2, así que a 1 a 2, lo que contradice la hipótesis de partida. El recíproco es análogo. Definición 27. una familia { i } i I de subconjuntos no vacíos de que verifica: = i I i i j =, para todo i j se le llama partición de. 13 Un número entero x pertenece a la clase de equivalencia [r], con 0 r m 1, si r es el resto de la división de x entre m. 14 Teniendo esto en cuenta, una clase de equivalencia puede representarse por cualquiera de sus elementos.
20 42 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES Es fácil comprobar que una partición define una relación de equivalencia 15 y viceversa. Definición 28. Dada una relación de equivalencia definida en un conjunto, se llama conjunto cociente de respecto a, y se denota /, al conjunto cuyos elementos son las clases de equivalencia determinadas en por. En el ejemplo que estamos manejando, el conjunto cociente Z/ m tiene m elementos. Este conjunto se denota Z m y se llama conjunto de restos módulo m Relación de orden Definición 29. Si es una relación binaria en reflexiva, antisimétrica y transitiva, se dice que es una relación de orden. Si a b se dice que a es anterior a b o menor o igual que 16 b. Una relación de orden en un conjunto es de orden total si dados dos elementos cualesquiera a, b de, siempre se pueden comparar, es decir a b o b a. Un ejemplo de relación de orden total es la relación en N, Z, Q o R, mientras que las relaciones y divide a definidas anteriormente no son de orden total. Definición 30. Un poset (, ) es un conjunto y una relación de orden definida en él. Ejemplo 30. i) Son ejemplos de posets (P(), ) y (N, ). ii) Sea (L, ) un alfabeto, es decir un conjunto finito totalmente ordenado y sea L el conjunto de palabras que se pueden formar con los elementos de L. El orden de L se puede extender a L siendo la relación de orden resultante de orden total y llamada orden lexicográfico por ser el orden del diccionario. sí, las palabras l 1 l 2...l p y l 1 l 2...l q están relacionadas y verifican que l 1 l 2...l p l 1l 2...l q, si ocurre: para algún k < p, se tiene que l i = l i (con i = 1,...k), l k+1 l k+1 y l k+1 l k+1 (por ejemplo casa y caso) p q y l i = l i, para i = 1...p (por ejemplo casa y casas). 15 Si { i } i I es una partición de y a, b, se dice que a b si, y sólo si, existe i I tal que a, b i. 16 De la relación de orden nace, por ejemplo, el ordenamiento de los números reales. No es de extrañar el parecido entre el símbolo y el símbolo (o, a veces, ) utilizado para ordenar de menor a mayor los números reales.
21 2.4. RELCIONES 43 Cuando (, ) es un poset finito, se puede representar con un diagrama de Hasse que consiste en un conjunto de vértices (denotando los elementos de ) y una serie de aristas (sin flecha). Dibujaremos una arista ascendente de x a y si y cubre a x, es decir, x y y no hay elementos intermedios entre ambos, es decir, si z es tal que x z y, entonces z = x o z = y. Definición 31. Dos posets (, ) y (B, ) son isomorfos si existe una aplicación biyectiva f : B, de modo que: a a f(a) f(a ). Ejemplo 31. Los posets (P({a, b, c}), ), (D 30 = {1, 2, 3, 5, 6, 10, 15, 30}, ) 17 y ({0, 1} 3, R) son isomorfos D Elementos distinguidos en un poset Sea (P, ) un poset. Definición 32. Un elemento m P es un maximal si 19 p P [(m p) (m p)], es decir, no hay elementos en P estrictamente mayores que m. Definición 33. Un elemento n P es un minimal si 20 p P [(p n) (n p)], es decir, no hay elementos en P estrictamente menores que n. 17 D m denota el conjunto de divisores positivos de m. 18 R es la relación dada por (a, b, c) (a, b, c ) (a a ) (b b ) (c c ) 19 Equivalentemente, p P [(m p) (m = p)]. 20 Equivalentemente, p P [(p n) (n = p)].
22 44 CPÍTULO 2. CONJUNTOS, PLICCIONES Y RELCIONES Un poset puede tener varios maximales y varios minimales y, si es finito, tiene al menos un maximal y al menos un minimal. Si P es un poset finito, dado p P existe al menos un maximal m de P (respectivamente, un minimal n de P) tal que p m (respectivamente, n p). Definición 34. Un elemento M P es máximo de P si p M, para todo p P. Definición 35. Un elemento m P es mínimo de P si m p, para todo p P. Proposición 4. Se verifican los siguientes enunciados: i) El máximo, si existe, es único. ii) El mínimo, si existe, es único. iii) Si P es finito, P tiene máximo si, y sólo si, tiene un un único maximal. iv) Si P es finito, P tiene mínimo si, y sólo si, tiene un un único minimal. Sea ahora Q P un subconjunto de P. Definición 36. Un elemento a P es una cota superior de Q en P si q a, para cualquier q Q. Definición 37. Un elemento b P es una cota inferior de Q en P si b q, para cualquier q Q. Definición 38. Un elemento a P es supremo de Q si a es una cota superior de Q en P, es decir, q a, para todo q Q. Si b es otra cota superior de Q en P, necesariamente a b. Queda claro que, si el conjunto de cotas superiores de Q en P es no vacío, entonces el supremo es el mínimo de dicho conjunto. Definición 39. Un elemento c P es ínfimo de Q si c es una cota inferior de Q en P, es decir, c q, para todo q Q. Si d es otra cota inferior de Q en P, necesariamente d c. Igual que ocurre con el supremo, si el conjunto de cotas inferiores de Q en P es no vacío, entonces el ínfimo es el máximo de dicho conjunto. Proposición 5. Se verifican los siguientes enunciados:
23 2.4. RELCIONES 45 i) El supremo de Q, si existe, es único. ii) El ínfimo de Q, si existe, es único. iii) Existe el máximo de Q si, y sólo si, existe el supremo y éste es un elemento de Q. iv) Existe el mínimo de Q si, y sólo si, existe el ínfimo y éste es un elemento de Q. Ejemplo 32. En el conjunto P = {1, 2, 3, 4, 5, 6, 8, 10, 12, 20}, se considera la relación de orden parcial de divisibilidad y el subconjunto Q = {1, 2, 4, 10}. Es fácil ver que Q no tiene máximo porque tiene dos maximales (4 y 10). El supremo de Q en P es 20. Por otro lado, el único minimal 1 es mínimo e ínfimo. Por su parte, P tiene tres maximales (8, 12 y 20), no tiene máximo y su mínimo es P
Conjuntos, relaciones y grafos
 Capítulo 2 Conjuntos, relaciones y grafos 2.1. Conjuntos Se partirá de la noción intuitiva de objeto y de unos entes matemáticos que se denominarán conjuntos. Definición 12. Un conjunto es una colección
Capítulo 2 Conjuntos, relaciones y grafos 2.1. Conjuntos Se partirá de la noción intuitiva de objeto y de unos entes matemáticos que se denominarán conjuntos. Definición 12. Un conjunto es una colección
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2016
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2017
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2018
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Capítulo 4: Conjuntos
 Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
2. Estructuras Algebraicas
 2. Estructuras Algebraicas 2.1. Conjuntos Un conjunto es una reunión en un todo de determinados objetos bien definidos y diferentes entre sí. Llamamos elementos a los objetos que lo forman. Requisitos:
2. Estructuras Algebraicas 2.1. Conjuntos Un conjunto es una reunión en un todo de determinados objetos bien definidos y diferentes entre sí. Llamamos elementos a los objetos que lo forman. Requisitos:
Una manera de describir un conjunto es por extensión y consiste en enumerar sus elementos entre llaves
 CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
Tema 1: Fundamentos.
 Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Contenido. BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática
 Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Conjuntos, Aplicaciones y Relaciones
 Conjuntos, Aplicaciones y Relaciones Curso 2017-2018 1. Conjuntos Un conjunto será una colección de objetos; a cada uno de estos objetos lo llamaremos elemento del conjunto. Si x es un elemento del conjunto
Conjuntos, Aplicaciones y Relaciones Curso 2017-2018 1. Conjuntos Un conjunto será una colección de objetos; a cada uno de estos objetos lo llamaremos elemento del conjunto. Si x es un elemento del conjunto
PRELIMINARES. En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura.
 1 PRELIMINARES 1. CONJUNTOS En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura. 1.1 Def:. Se define un conjunto como una colección de objetos.
1 PRELIMINARES 1. CONJUNTOS En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura. 1.1 Def:. Se define un conjunto como una colección de objetos.
Definiciones Un conjunto es una colección de objetos distintos. Notaremos. A = {a, b, c, d, } por extensión
 CONJUNTOS Definiciones Un conjunto es una colección de objetos distintos. Notaremos A = {a, b, c, d, } por extensión A = {x / x tiene la propiedad P} por comprensión El cardinal de un conjunto es el número
CONJUNTOS Definiciones Un conjunto es una colección de objetos distintos. Notaremos A = {a, b, c, d, } por extensión A = {x / x tiene la propiedad P} por comprensión El cardinal de un conjunto es el número
Si un objeto x es elemento de un conjunto A, se escribe: x A.
 Conjuntos. Dentro de la teoría se consideran como primitivos o términos no definidos los conjuntos y los elementos. En general, se designan los conjuntos usando letras latinas mayúsculas y los elementos
Conjuntos. Dentro de la teoría se consideran como primitivos o términos no definidos los conjuntos y los elementos. En general, se designan los conjuntos usando letras latinas mayúsculas y los elementos
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
y exámenes. Temas 3 y 4
 U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2017/2018. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2017/2018. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
Capítulo 2 Conjuntos. 2.1 Introducción. 2.2 Determinación de conjuntos. Definición:
 Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
Capítulo 2 Conjuntos 2.1 Introducción El concepto de conjunto, de singular importancia en la ciencia matemática y objeto de estudio de una de sus disciplinas más recientes, está presente, aunque en forma
y exámenes. Temas 3 y 4
 U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2016/2017. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2016/2017. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 3 Conjuntos, Relaciones y Funciones Conjuntos y Operaciones Los conjuntos se representan con letras mayúsculas,
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 3 Conjuntos, Relaciones y Funciones Conjuntos y Operaciones Los conjuntos se representan con letras mayúsculas,
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
ÁLGEBRA I. Curso Grado en Matemáticas
 ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
Conjuntos. Relaciones. Aplicaciones
 Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
TEMA 2. TEORÍA DE CONJUNTOS
 TEMA 2. TEORÍA DE CONJUNTOS 1. Introducciónalalógica de proposiciones 1.1 Definición. Una proposición es una oración declarativa de la cual se puede decir sin ambigüedad si es verdadera o falsa. 1.2 Definición.
TEMA 2. TEORÍA DE CONJUNTOS 1. Introducciónalalógica de proposiciones 1.1 Definición. Una proposición es una oración declarativa de la cual se puede decir sin ambigüedad si es verdadera o falsa. 1.2 Definición.
TEMA 1. Teoría de Conjuntos. Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos:
 TEMA 1 Teoría de Conjuntos Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos: i) A = { }, B = {{ }} ii) A = {, { }}, B = {, {, { }}} iii) A = {{ }, {, { }}}, B = {{ }} Ejercicio 1.2. Dar
TEMA 1 Teoría de Conjuntos Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos: i) A = { }, B = {{ }} ii) A = {, { }}, B = {, {, { }}} iii) A = {{ }, {, { }}}, B = {{ }} Ejercicio 1.2. Dar
Preliminares. 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros.
 CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4. ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas
 ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4 ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas 1. Decir, justificando adecuadamente, si las siguientes afirmaciones son verdaderas o falsas: (a) { } (b) { }
ÁLGEBRA (Ciencias) año 2014 PRÁCTICA N 4 ELEMENTOS DE TEORÍA DE CONJUNTOS: nociones básicas 1. Decir, justificando adecuadamente, si las siguientes afirmaciones son verdaderas o falsas: (a) { } (b) { }
Álgebra Lineal y Estructuras Matemáticas. J. C. Rosales y P. A. García Sánchez. Departamento de Álgebra, Universidad de Granada
 Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 1 Conjuntos, relaciones y aplicaciones 1. Conjuntos La idea de conjunto
Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 1 Conjuntos, relaciones y aplicaciones 1. Conjuntos La idea de conjunto
Definición : Es una colección de objetos bien definidos y diferenciables entre si que se llaman elementos.
 1 CONJUNTOS Y APLICACIONES Conjunto : Es una colección de objetos bien definidos y diferenciables entre si que se llaman elementos. Representación Suelen emplearse letras mayusculas para los conjuntos
1 CONJUNTOS Y APLICACIONES Conjunto : Es una colección de objetos bien definidos y diferenciables entre si que se llaman elementos. Representación Suelen emplearse letras mayusculas para los conjuntos
Matemáticas Discretas Relaciones y funciones
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
1. Conjuntos y funciones
 PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
Práctico 1 Conjuntos, Relaciones y Funciones
 1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas: i) 1 A ii) {1} A iii){2, 1} A iv) {1, 3} A v){2} A. 2. Dado el conjunto A = {1, 2, {3}, {1, 2}}, determinar
1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas: i) 1 A ii) {1} A iii){2, 1} A iv) {1, 3} A v){2} A. 2. Dado el conjunto A = {1, 2, {3}, {1, 2}}, determinar
Taller matemático (Cálculo) Venancio Tomeo Universidad Complutense
 Taller matemático (Cálculo) Venancio Tomeo Universidad Complutense Parte II: 6: Conjuntos y operaciones 7: Funciones y gráficas 8: Exponencial y logaritmica 9: Funciones trigonométricas 10: Límites de
Taller matemático (Cálculo) Venancio Tomeo Universidad Complutense Parte II: 6: Conjuntos y operaciones 7: Funciones y gráficas 8: Exponencial y logaritmica 9: Funciones trigonométricas 10: Límites de
TEMA 3 Elementos de la teoría de los conjuntos. *
 TEM 3 Elementos de la teoría de los conjuntos. * Conjuntos. Un conjunto es cualquier colección, bien definida, de objetos llamadas elementos o miembros del conjunto. Una manera de describir un conjunto
TEM 3 Elementos de la teoría de los conjuntos. * Conjuntos. Un conjunto es cualquier colección, bien definida, de objetos llamadas elementos o miembros del conjunto. Una manera de describir un conjunto
Ejemplo No. 2 Empleando esta notación, los conjuntos del ejemplo anterior se pueden escribir como:
 UNIDAD 1: CONJUNTOS NUMÉRICOS En esta unidad se ofrece una información general sobre los diferentes conjuntos de números que se utilizaran en el desarrollo de este curso. Comencemos con un breve repaso
UNIDAD 1: CONJUNTOS NUMÉRICOS En esta unidad se ofrece una información general sobre los diferentes conjuntos de números que se utilizaran en el desarrollo de este curso. Comencemos con un breve repaso
Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones
 Conjuntos Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones 1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas i) 1 A ii) {1} A iii) {2, 1} A iv)
Conjuntos Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones 1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas i) 1 A ii) {1} A iii) {2, 1} A iv)
MÉTODOS MATEMÁTICOS DE LA FÍSICA I
 MÉTODOS MATEMÁTICOS DE LA FÍSICA I Ignacio Sánchez Rodríguez Curso 2006-07 TEMA PRELIMINAR ÍNDICE 1. Lenguaje matemático 2 2. Conjuntos 6 3. Aplicaciones 10 4. Relaciones 12 5. Estructuras algebraicas
MÉTODOS MATEMÁTICOS DE LA FÍSICA I Ignacio Sánchez Rodríguez Curso 2006-07 TEMA PRELIMINAR ÍNDICE 1. Lenguaje matemático 2 2. Conjuntos 6 3. Aplicaciones 10 4. Relaciones 12 5. Estructuras algebraicas
CONJUNTOS. Por ejemplo, el E del ejemplo 2 se escribe.
 CONJUNTOS La teoría de conjuntos nos permite describir de forma precisa conjuntos de números, de personas, de objetos, etc que comparten una propiedad común. Esto puede ser de gran utilidad al establecer
CONJUNTOS La teoría de conjuntos nos permite describir de forma precisa conjuntos de números, de personas, de objetos, etc que comparten una propiedad común. Esto puede ser de gran utilidad al establecer
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación. Lecturas en Ciencias de la Computación ISSN
 Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Introducción a la Matemática Discreta
 Introducción a la Matemática Discreta Teoría de Conjuntos Luisa María Camacho Camacho Introd. a la Matemática Discreta 1 / 20 Introducción a la Matemática Discreta Temario Tema 1. Teoría de Conjuntos.
Introducción a la Matemática Discreta Teoría de Conjuntos Luisa María Camacho Camacho Introd. a la Matemática Discreta 1 / 20 Introducción a la Matemática Discreta Temario Tema 1. Teoría de Conjuntos.
Operaciones extendidas de conjuntos
 234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
Conjuntos, relaciones de equivalencia y aplicaciones
 CAPíTULO 1 Conjuntos, relaciones de equivalencia y aplicaciones 1. Conjuntos La idea de conjunto es una de las más significativas en Matemáticas. La mayor parte de los conceptos matemáticos están construidos
CAPíTULO 1 Conjuntos, relaciones de equivalencia y aplicaciones 1. Conjuntos La idea de conjunto es una de las más significativas en Matemáticas. La mayor parte de los conceptos matemáticos están construidos
CONJUNTOS TEORIA BASICA DE CONJUNTOS
 Repasamos CONJUNTOS TEORIA BASICA DE CONJUNTOS Cualquier colección de objetos o individuos se denomina conjunto. El termino conjunto no tiene una definición matemática, sino que es un concepto primitivo.
Repasamos CONJUNTOS TEORIA BASICA DE CONJUNTOS Cualquier colección de objetos o individuos se denomina conjunto. El termino conjunto no tiene una definición matemática, sino que es un concepto primitivo.
3.3. TEORÍA BÁSICA DE CONJUNTOS Utilizar tablas de verdad para comprobar la equivalencia lógica p q p q.
 3.3. TEORÍA BÁSICA DE CONJUNTOS 83 a) p q b) p q c) q p 7. Sabiendo que la proposición compuesta ( q) (q p) es falsa, indicar cuál es el valor de verdad de las proposiciones p y q. 8. Utilizar tablas de
3.3. TEORÍA BÁSICA DE CONJUNTOS 83 a) p q b) p q c) q p 7. Sabiendo que la proposición compuesta ( q) (q p) es falsa, indicar cuál es el valor de verdad de las proposiciones p y q. 8. Utilizar tablas de
TEMA II TEORÍA INTUITIVA DE CONJUNTOS
 TEMA II TEORÍA INTUITIVA DE CONJUNTOS Policarpo Abascal Fuentes TEMA II Teoría intuitiva de conjuntos p. 1/4 TEMA II 2. TEORÍA INTUITIVA DE CONJUNTOS 2.1 CONJUNTOS 2.1.1 Operaciones con conjuntos 2.2 RELACIONES
TEMA II TEORÍA INTUITIVA DE CONJUNTOS Policarpo Abascal Fuentes TEMA II Teoría intuitiva de conjuntos p. 1/4 TEMA II 2. TEORÍA INTUITIVA DE CONJUNTOS 2.1 CONJUNTOS 2.1.1 Operaciones con conjuntos 2.2 RELACIONES
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES
 SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
En matemáticas el concepto de conjunto es considerado primitivo y no se da una definición de este, por lo tanto la palabra CONJUNTO debe aceptarse
 En matemáticas el concepto de conjunto es considerado primitivo y no se da una definición de este, por lo tanto la palabra CONJUNTO debe aceptarse lógicamente como un término no definido. Un conjunto se
En matemáticas el concepto de conjunto es considerado primitivo y no se da una definición de este, por lo tanto la palabra CONJUNTO debe aceptarse lógicamente como un término no definido. Un conjunto se
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA NOCIONES PRELIMINARES DE MATEMÁTICAS
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA NOCIONES PRELIMINARES DE MATEMÁTICAS A. 1 Conjuntos. A. TEORÍA DE CONJUNTOS. Un conjunto
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA NOCIONES PRELIMINARES DE MATEMÁTICAS A. 1 Conjuntos. A. TEORÍA DE CONJUNTOS. Un conjunto
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
Pregunta 1 Es correcta esta definición? Por qué?
 TEORÍA DE CONJUNTOS. En un libro de COU de 1975 puede leerse la siguiente definición de conjunto: Un conjunto es una colección de objetos, cualquiera que sea su naturaleza. Pregunta 1 Es correcta esta
TEORÍA DE CONJUNTOS. En un libro de COU de 1975 puede leerse la siguiente definición de conjunto: Un conjunto es una colección de objetos, cualquiera que sea su naturaleza. Pregunta 1 Es correcta esta
CAPÍTULO III RELACIONES Y FUNCIONES
 RELACIONES Y FUNCIONES 41 CAPÍTULO III RELACIONES Y FUNCIONES 3.1 RELACIONES 1 Una relación R de un conjunto A a un conjunto B asigna a cada par (a,b) en A x B exactamente uno de los enunciados siguientes:
RELACIONES Y FUNCIONES 41 CAPÍTULO III RELACIONES Y FUNCIONES 3.1 RELACIONES 1 Una relación R de un conjunto A a un conjunto B asigna a cada par (a,b) en A x B exactamente uno de los enunciados siguientes:
DEFINICIÓN: Se define el conjunto vacio como el complementario de en, don de es un conjunto. Se representa por :
 CONJUNTOS Y APLICACIONES CONCEPTOS BÁSICOS: DEFINICIÓN: Conjunto es una colección de objetos a los que llamo elementos. n dos conjuntos, entonces se dice que es un subconjunto de, se escribe, si para todo
CONJUNTOS Y APLICACIONES CONCEPTOS BÁSICOS: DEFINICIÓN: Conjunto es una colección de objetos a los que llamo elementos. n dos conjuntos, entonces se dice que es un subconjunto de, se escribe, si para todo
UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS
 UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
Recordemos que utilizaremos, como es habitual, la siguiente notación para algunos conjuntos de números que son básicos.
 Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Capítulo 1 Preliminares Vamos a ver en este primer capítulo de preliminares algunos conceptos, ideas y propiedades que serán muy útiles para el desarrollo de la asignatura. Se trata de resultados sobre
Relaciones de orden. Álgebras de Boole
 Relaciones de orden. Álgebras de Boole MATEMÁTICA DISCRETA I F. Informática. UPM MATEMÁTICA DISCRETA I () Relaciones de orden. Álgebras de Boole F. Informática. UPM 1 / 52 Conjuntos y relaciones entre
Relaciones de orden. Álgebras de Boole MATEMÁTICA DISCRETA I F. Informática. UPM MATEMÁTICA DISCRETA I () Relaciones de orden. Álgebras de Boole F. Informática. UPM 1 / 52 Conjuntos y relaciones entre
Conjuntos. 17 {perro, gato, 17, x 2 }
 Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Relaciones Binarias. Matemática Discreta. Agustín G. Bonifacio UNSL. Relaciones Binarias
 UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
Teoría de Conjuntos DEFINICION DE CONJUNTO
 Teoría de Conjuntos Teoría de Conjuntos Teoría de conjuntos es un instrumento matemático adecuado para la sistematización de nuestra forma de pensar, y permitir nuestra capacidad de análisis y comprensión
Teoría de Conjuntos Teoría de Conjuntos Teoría de conjuntos es un instrumento matemático adecuado para la sistematización de nuestra forma de pensar, y permitir nuestra capacidad de análisis y comprensión
Espacios Vectoriales. Tema Introducción. 1.2 Repaso de Estructuras Algebraicas
 Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas se han escrito con el ánimo de facilitar al estudiante una guía para el estudio de la asignatura, y no como un libro de texto o manual de Álgebra
Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas se han escrito con el ánimo de facilitar al estudiante una guía para el estudio de la asignatura, y no como un libro de texto o manual de Álgebra
CONJUNTOS. Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas.
 CONJUNTOS CPR. JORGE JUAN Xuvia-Narón Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas. Un conjunto está formado por una serie de elementos susceptibles de poseer
CONJUNTOS CPR. JORGE JUAN Xuvia-Narón Los conjuntos son conceptos primitivos que representan una totalidad, una reunión de cosas. Un conjunto está formado por una serie de elementos susceptibles de poseer
UNIDAD DE APRENDIZAJE I
 UNIDAD DE APRENDIZAJE I Saberes procedimentales GEOMETRÍA ANALÍTICA 1. Define e identifica los tipos de conjuntos y las operaciones entre ellos. 2. Emplea de manera sistemática conceptos algebraicos, trigonométricos
UNIDAD DE APRENDIZAJE I Saberes procedimentales GEOMETRÍA ANALÍTICA 1. Define e identifica los tipos de conjuntos y las operaciones entre ellos. 2. Emplea de manera sistemática conceptos algebraicos, trigonométricos
Matemática I C.F.E. I.N.E.T. Profesorado de Informática Conjuntos
 Conjuntos Conceptos primitivos: CONJUNTO, ELEMENTO, PERTENECE. Pertenecer- Elemento Sea el conjunto de los ríos del Uruguay. El Río Negro es un río del Uruguay. Entonces, este río es un elemento del conjunto
Conjuntos Conceptos primitivos: CONJUNTO, ELEMENTO, PERTENECE. Pertenecer- Elemento Sea el conjunto de los ríos del Uruguay. El Río Negro es un río del Uruguay. Entonces, este río es un elemento del conjunto
Capítulo 2. Funciones
 Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
Capítulo 2. Funciones Objetivo: El alumno analizará las características principales de las funciones reales de variable real y formulará modelos matemáticos. Contenido: 2.1 Definición de función real de
Estructuras Discretas. Conjuntos. Conjuntos & Funciones. Especificación de Conjuntos.
 Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
mi la sol fa si Un conjunto está bien definido si se puede establecer sin dudar si un elemento pertenece o no al conjunto.
 CONJUNTOS LENGUJE SIMÓLICO Cada día, en nuestra conversación, por la televisión, en la lectura de por ejemplo un diario, o en el trabajo está presente la idea de conjunto. En matemática utilizaremos la
CONJUNTOS LENGUJE SIMÓLICO Cada día, en nuestra conversación, por la televisión, en la lectura de por ejemplo un diario, o en el trabajo está presente la idea de conjunto. En matemática utilizaremos la
CONJUNTOS Y NÚMEROS. HOJA 2
 CONJUNTOS Y NÚMEROS. HOJA 2 Conjuntos 1) Vamos a demostrar que, dado un conjunto B de n búhos, todos los búhos de B son del mismo color. Lo haremos por inducción sobre n. a) Si n = 1 sólo hay un búho,
CONJUNTOS Y NÚMEROS. HOJA 2 Conjuntos 1) Vamos a demostrar que, dado un conjunto B de n búhos, todos los búhos de B son del mismo color. Lo haremos por inducción sobre n. a) Si n = 1 sólo hay un búho,
Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación.
 NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
NÚMEROS REALES Conjuntos Los conjuntos se emplean en muchas áreas de las matemáticas, de modo que es importante una comprensión de los conjuntos y de su notación. Un conjunto es una colección bien definida
Definición 1 Un semigrupo es un conjunto E provisto de una operación binaria asociativa sobre E, se denota por (E, ).
 ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
ALGEBRA La primera parte del presente libro está dedicada a las estructuras algebraicas. En esta parte vamos a iniciar agregándole a los conjuntos operaciones. Cuando las operaciones tienen determinadas
P(f) : P(B) P(A) (A.2)
 TEMA 2. APLICACIONES 227 Tema 2. Aplicaciones Definición A.2.1. Una correspondencia entre dos conjuntos A y B es un subconjunto del producto cartesiano A B. Una aplicación f entre dos conjuntos A y B es
TEMA 2. APLICACIONES 227 Tema 2. Aplicaciones Definición A.2.1. Una correspondencia entre dos conjuntos A y B es un subconjunto del producto cartesiano A B. Una aplicación f entre dos conjuntos A y B es
Un elemento de un monoide se dice que es inversible si tiene elemento inverso.
 Tema 1: Semigrupos 1 Tema 1: Semigrupos 1. Semigrupos: Conceptos fundamentales. Recordemos que un sistema algebraico es un conjunto S con una o varias operaciones sobre él, siendo una operación ó ley de
Tema 1: Semigrupos 1 Tema 1: Semigrupos 1. Semigrupos: Conceptos fundamentales. Recordemos que un sistema algebraico es un conjunto S con una o varias operaciones sobre él, siendo una operación ó ley de
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2007 Ciencias Computacionales INAOE Dr. Luis Villaseñor Pineda villasen@inaoep.mx http://ccc.inaoep.mx/~villasen
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2007 Ciencias Computacionales INAOE Dr. Luis Villaseñor Pineda villasen@inaoep.mx http://ccc.inaoep.mx/~villasen
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
Tema 1 Espacios Vectoriales 1.1 Introducción Estas notas están elaboradas pensando simplemente en facilitar al estudiante una guía para el estudio de la asignatura, y en consecuencia se caracterizan por
GUÍA DE TRABAJO No.4
 INSTITUCIÓN EDUCATIVA JOSÉ JOAQUIN FLOREZ HERNANDEZ JORNADA TARDE ALUMNO: CÓDIGO : GRADO: 9 C - D ASIGNATURA : MATEMÁTICAS FECHA : UNIDAD 2: RELACIONES Y FUNCIONES PERÍODO : 2 GUÍA DE TRABAJO No.4 Definición
INSTITUCIÓN EDUCATIVA JOSÉ JOAQUIN FLOREZ HERNANDEZ JORNADA TARDE ALUMNO: CÓDIGO : GRADO: 9 C - D ASIGNATURA : MATEMÁTICAS FECHA : UNIDAD 2: RELACIONES Y FUNCIONES PERÍODO : 2 GUÍA DE TRABAJO No.4 Definición
Fundamentos de Lógica y Teoría de Conjuntos
 Índice general 1. Lógica y Teoría de conjuntos 3 1.1. Introducción a la Lógica............................ 3 1.1.1. Repaso histórico (Ref. Grimaldi pág. 187).............. 3 1.1.2. Conceptos básicos (Ref.
Índice general 1. Lógica y Teoría de conjuntos 3 1.1. Introducción a la Lógica............................ 3 1.1.1. Repaso histórico (Ref. Grimaldi pág. 187).............. 3 1.1.2. Conceptos básicos (Ref.
b) Sea una relación de equivalencia en A y una operación en A. Decimos que y son compatibles si a b a c b c y c a c b para todo a, b, c A
 APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
APENDICE Relaciones y Operaciones Compatibles 1 Definición: a) Sea A un conjunto y una relación entre elementos de A. Decimos que es una relación de equivalencia si es: i Reflexiva: a A, a a. ii Simétrica:
Curso de conjuntos y números. Versión corregida de los Apuntes. Juan Jacobo Simón Pinero
 Curso de conjuntos y números. Versión corregida de los Apuntes Juan Jacobo Simón Pinero Curso 2012/2013 Índice general I Conjuntos 3 1. Conjuntos y elementos 4 1.1. Sobre el concepto de conjunto y elemento..............
Curso de conjuntos y números. Versión corregida de los Apuntes Juan Jacobo Simón Pinero Curso 2012/2013 Índice general I Conjuntos 3 1. Conjuntos y elementos 4 1.1. Sobre el concepto de conjunto y elemento..............
CONCEPTOS BÁSICOS DE LA TEORÍA DE CONJUNTOS. ESTRUCTURAS ALGEBRAICAS.
 TEMA 11 ÍNDICE CONCEPTOS BÁSICOS DE LA TEORÍA DE CONJUNTOS. ESTRUCTURAS ALGEBRAICAS. 1. INTRODUCCIÓN 2. CONJUNTOS 3. SUBCONJUNTOS 4. OPERACIONES 4.1 UNIÓN 4.2 INTERSECCIÓN 4.3 COMPLEMENTO 4.4 DIFERENCIA
TEMA 11 ÍNDICE CONCEPTOS BÁSICOS DE LA TEORÍA DE CONJUNTOS. ESTRUCTURAS ALGEBRAICAS. 1. INTRODUCCIÓN 2. CONJUNTOS 3. SUBCONJUNTOS 4. OPERACIONES 4.1 UNIÓN 4.2 INTERSECCIÓN 4.3 COMPLEMENTO 4.4 DIFERENCIA
Probabilidad y Estadística
 Probabilidad y Estadística M.C. Marcos Samuel López Rivera Conjuntos. Un conjunto puede considerarse como una colección de objetos, llamados miembros o elementos del conjunto. Denotamos un conjunto por
Probabilidad y Estadística M.C. Marcos Samuel López Rivera Conjuntos. Un conjunto puede considerarse como una colección de objetos, llamados miembros o elementos del conjunto. Denotamos un conjunto por
Conjuntos Parcialmente Ordenados y Reticulados. Matemática Discreta. Agustín G. Bonifacio UNSL. Conjuntos Parcialmente Ordenados y Reticulados
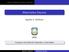 y UNSL y y y Capítulo 4 del libro de B. Kolman, R. Busby y S. Ross. Definición Una relación R sobre un conjunto X es un orden orden parcial si es reflexiva, antisimétrica y transitiva. El conjunto A con
y UNSL y y y Capítulo 4 del libro de B. Kolman, R. Busby y S. Ross. Definición Una relación R sobre un conjunto X es un orden orden parcial si es reflexiva, antisimétrica y transitiva. El conjunto A con
En general, un conjunto A se define seleccionando los elementos de un cierto conjunto U de referencia que cumplen una determinada propiedad.
 nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
nidad 3: Conjuntos 3.1 Introducción Georg Cantor [1845-1918] formuló de manera individual la teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de formalizar las matemáticas
LEYES, ESTRUCTURAS BÁSICAS Y COCIENTES CONJUNTOS Y GRUPOS
 Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
MATEMÁTICAS BÁSICAS. Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño
 MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2014 Universidad Nacional de Colombia
MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2014 Universidad Nacional de Colombia
{ } Listado de elementos del conjunto
 CONJUNTOS Qué es un conjunto? Un conjunto es un grupo no ordenado de elementos que comparte una o más características. Nomenclatura en los conjuntos Los conjuntos siempre se nombran con letras mayúsculas,
CONJUNTOS Qué es un conjunto? Un conjunto es un grupo no ordenado de elementos que comparte una o más características. Nomenclatura en los conjuntos Los conjuntos siempre se nombran con letras mayúsculas,
John Venn Matemático y filósofo británico creador de los diagramas de Venn
 Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
John Venn Matemático y filósofo británico creador de los diagramas de Venn
 Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
Georg Cantor Matemático Alemán creador de la teoría de conjuntos John Venn Matemático y filósofo británico creador de los diagramas de Venn August De Morgan Matemático ingles creador de leyes que llevan
1. Números reales. Análisis de Variable Real
 1. Números reales Análisis de Variable Real 2014 2015 Índice 1. Sistemas numéricos 2 1.1. Números naturales. Principio de Inducción... 2 1.2. Números enteros... 4 1.3. Números racionales... 6 2. Los números
1. Números reales Análisis de Variable Real 2014 2015 Índice 1. Sistemas numéricos 2 1.1. Números naturales. Principio de Inducción... 2 1.2. Números enteros... 4 1.3. Números racionales... 6 2. Los números
Capítulo 6. Relaciones. Continuar
 Capítulo 6. Relaciones Continuar Introducción Una relación es una correspondencia entre dos elementos de dos conjuntos con ciertas propiedades. En computación las relaciones se utilizan en base de datos,
Capítulo 6. Relaciones Continuar Introducción Una relación es una correspondencia entre dos elementos de dos conjuntos con ciertas propiedades. En computación las relaciones se utilizan en base de datos,
Guía N 1 Introducción a las Matemáticas
 Glosario: Guía N 1 Introducción a las Matemáticas - Aritmética: Es la rama de las matemáticas que se dedica al estudio de los números y sus propiedades bajo las operaciones de suma, resta, multiplicación
Glosario: Guía N 1 Introducción a las Matemáticas - Aritmética: Es la rama de las matemáticas que se dedica al estudio de los números y sus propiedades bajo las operaciones de suma, resta, multiplicación
Definiciones Una relación R en un conjunto A es una relación de orden si verifica las propiedades reflexiva, antisimétrica y transitiva.
 RELACIONES DE ORDEN Definiciones Una relación R en un conjunto A es una relación de orden si verifica las propiedades reflexiva, antisimétrica y transitiva. Un conjunto parcialmente ordenado ( A, R ) es
RELACIONES DE ORDEN Definiciones Una relación R en un conjunto A es una relación de orden si verifica las propiedades reflexiva, antisimétrica y transitiva. Un conjunto parcialmente ordenado ( A, R ) es
Álgebra y Trigonometría
 Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
Álgebra y Trigonometría Conceptos fundamentales del Álgebra Universidad de Antioquia Departamento de Matemáticas 1. Números Reales El conjunto de los números reales está constituido por diferentes clases
BLOQUE 1. LOS NÚMEROS
 BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
BLOQUE 1. LOS NÚMEROS Números naturales, enteros y racionales. El número real. Intervalos. Valor absoluto. Tanto el Cálculo como el Álgebra que estudiaremos en esta asignatura, descansan en los números
Conjuntos, aplicaciones y
 0 Conjuntos, aplicaciones y números En este capítulo presentamos los conceptos fundamentales sobre la teoría de conjuntos que nos serán muy útiles en el desarrollo de la asignatura. En primer lugar recordamos
0 Conjuntos, aplicaciones y números En este capítulo presentamos los conceptos fundamentales sobre la teoría de conjuntos que nos serán muy útiles en el desarrollo de la asignatura. En primer lugar recordamos
1.1 Conceptos básicos de la teoría de conjuntos
 Copyright 204. Grupo Editorial Patria. ll rights reserved. NIDD. Conceptos básicos de la teoría de conjuntos La expresión conjunto es un término matemático introducido en 879, por Georg Cantor (845-98).
Copyright 204. Grupo Editorial Patria. ll rights reserved. NIDD. Conceptos básicos de la teoría de conjuntos La expresión conjunto es un término matemático introducido en 879, por Georg Cantor (845-98).
UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS
 UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
NOCIONES PRELIMINARES (*) 1
 CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
CONJUNTOS NOCIONES PRELIMINARES (*) 1 Conjunto no es un término definible, pero da idea de una reunión de cosas ( elementos ) que tienen algo en común. En matemática los conjuntos se designan con letras
