Integral doble 1.- Calcular el área representada en el gráfico mediante una integral doble.
|
|
|
- Aarón Herrero Montoya
- hace 5 años
- Vistas:
Transcripción
1 Integral doble 1.- Calcular el área representada en el gráfico mediante una integral doble..- Colocar los límites de integración en uno y otro orden, en la integral doble: f(x,y)dxdy para los recintos: a) es un paralelogramo cuyos vértices son A(1,), B(,4), C(,7) y D(1,5). b) es un sector circular, con centro en (,) y cuyo arco tiene sus extremos en los puntos (1,1) y (-1,1). 3.- Demostrar Γ(p) Γ(q) β (p,q) = siendo p, q>. Γ (p + q) 1 x Probar que I = e dx = 1. π 1 x 1 Nota: f(x) = e dx es la función de densidad de la distribución N(,1). π 5.- Hallar el área de la superficie de un cilindro interceptada por otra superficie cilíndrica igual de eje perpendicular. 6.- Calcular (4 x y )dxdy siendo el recinto limitado por las rectas x=, x=1, y=, y=3/. 7.- Dada la integral (x + y + 1)dxdy siendo el cuadrado de vértices (1,), (,1), (1,) y (,1). a) Calcular dicha integral. b) Efectuar el cambio de variable u=y-x, v=y+x y evaluar la nueva integral. 8.- Invertir el orden de integración en: 3 I dy f(x,y)dx =. 1 y 9.- Calcular el volumen del cilindroide limitado por el plano XY, la superficie z=x +y, y los cilindros parabólicos x=y, y=x. x 1.- Hallar el volumen del cuerpo limitado por el plano XY, la superficie z =, y y el cilindro cuya sección recta es una elipse del plano XY de semiejes a y b paralelos a los OX, y OY y centro (a,b). U. D. de Matemáticas de la ETSITGC 1
2 Integral doble 11.- Hallar r cos αdrdα en el interior de la cardioide r = 1 + cos α. 1.- Volumen del cilindroide limitado por el plano XY, el parabóloide el cilindro x + y = a. x y + = z y p q 13.- Hallar + y )dxdy en el recinto x + y a (x Calcular (x y)dxdy en el recinto limitado por x, y, la circunferencia x + y = a y la elipse x 4a y + = 1. a 15.- Hallar xy(x y)dxdy en el rectángulo x a, y b En el supuesto de que la integral doble de una función positiva f, sobre una región, se reduzca a la integral iterada: a) 1 1 x f(x,y)dy dx 1 1 x, 1 x x b) ( f(x,y)dy ) dx + 1 ( ) f(x,y)dy dx, π senx c) x f(x,y)dy dx sen epresentar la región e invertir el orden de integración 17.- Hallar + y )dxdy en el recinto (x xy k,a y b. U. D. de Matemáticas de la ETSITGC
3 Integral doble 1.- Calcular el área representada en el gráfico mediante una integral doble. Solución: Puede ser: A = dy dx = 4 4y 1/ , o bien, x /4 A = dx dy = 7 4 U. D. de Matemáticas de la ETSITGC 3
4 Integral doble.- Colocar los límites de integración en uno y otro orden, en la integral doble: f(x,y)dxdy para los recintos: a) es un paralelogramo cuyos vértices son A(1,), B(,4), C(,7) y D(1,5). b) es un sector circular, con centro en (,) y cuyo arco tiene sus extremos en los puntos (1,1) y (-1,1). Solución: a) Obtenemos las rectas AB que es y=x y la recta CD que es y=x+3 3+ x 4 y/ 5 f (x, y)dxdy = dx f (x, y)dy = 1 dy f (x, y)dx + dy f (x, y)dx x b) Sector circular de la circunferencia x +y = f (x, y)dxdy x 1 x = dx f (x, y)dy + dx f (x, y)dy = 1 x x 1 y y dy f (x, y)dx + dy f (x, y)dx y 1 y U. D. de Matemáticas de la ETSITGC 4
5 Γ(p) Γ(q) (p q) Integral doble 3.- Demostrar β (p,q) = siendo p, q>. Γ + Solución: p 1 x q 1 x p 1 q 1 x y (p) (q) x e dx y e dy dx x y e dy Γ Γ = = = ealizamos el cambio de variable: x x x = r cos α r α r cos α r cos αsenα 3 J 4r s en cos = = = α α y = r s en α y y r s en α r s enαcos α r α / p 1 q 1 x y π p 1 q 1 p+ q 1 r Γ(p) Γ (q) = dx x y e dx = dα 4 cos αsen α r e dr = 1 1/ Haciendo el cambio r = t dr = t dt π/ / p 1 q 1 1 π p+ q 1 t p 1 q 1 p+ q 1 t Γ(p) Γ (q) = 4 cos αsen αdα t e dt = cos αsen αdα t e dt = β(p,q) Γ (p+ q) Y haciendo el cambio s en α= x senα cos αdα= dx π/ 1 p 1 q 1 p 1 q 1 Γ(p) Γ (q) =Γ (p + q) cos αsen αd α =Γ (p + q) x (1 x) dx =Γ (p + q) β(p,q) Γ(p) Γ(q) Luego, β (p,q) = c.q.d. Γ (p + q) U. D. de Matemáticas de la ETSITGC 5
6 4.- Probar que 1 x 1 I = e dx = 1. π Integral doble 1 x 1 Nota: f(x) = e dx es la función de densidad de la distribución N(,1). π Solución: Por la simetría respecto el eje de ordenadas: 1 x 1 x 1 x 1 I e dx e dx π = = e dx I = π π Efectuando el producto x y (x y ) = + e dx e dy e dydx ealizamos el cambio a polares: x x x = r cos α r α cos α rsenα J = = = r y = r s enα y y s enα r cos α r α π x y (x y ) r r π + e π e dx e dy = e dydx = e rdr dα= dα= 1 x π π Luego, e dx = = I I = 1 c.q.d. U. D. de Matemáticas de la ETSITGC 6
7 Integral doble 5.- Hallar el área de la superficie de un cilindro interceptada por otra superficie cilíndrica igual de eje perpendicular. Solución: Sea r el radio de los cilindros. La superficie es: x + z = r z x = x r x z = y Para calcular el área calculamos la parte en rojo que es 1/16 por simetría. z z x r = 1+ + dxdy = dxdy = 16 dxdy = D x y r x r x Área ( ) 1 r x dy r x = 16r dxdy = 16r dx = 16r dx = r x r x r x 16r U. D. de Matemáticas de la ETSITGC 7
8 Integral doble 6.- Calcular (4 x y )dxdy siendo el recinto limitado por las rectas x=, x=1, y=, y=3/. Solución: ( ) 3 3/ 1 3/ 1 1 y 3 9 (4 x y )dxdy = (4 x y )dy dx = 4y x y dx = 6 x dx = = x dx x x = = U. D. de Matemáticas de la ETSITGC 8
9 Integral doble 7.- Dada la integral (x + y + 1)dxdy siendo el cuadrado de vértices (1,), (,1), (1,) y (,1). a) Calcular dicha integral. b) Efectuar el cambio de variable u=y-x, v=y+x y evaluar la nueva integral. Solución: a) (x + y + 1)dxdy = + ( ) ( ) 3 1+ x 3 3 x 1 1 x 3 x 1 y y = (x + y + 1)dy dx + (x + y + 1)dy dx = x y + + y dx + x y + + y dx = 3 3 b) 1 x 1 x x x 1 ( ) ( ) ( ) ( ) ( ) ( ) x 1 x = x ( 1+ x) + + ( 1+ x) x ( 1 x) + + ( 1 x) dx ( ) x x 1 ( ) + x 3 x x x x x 1 dx = ( ) ( ) = 14x + 1x dx + 14x + 36x 36x + 4 dx = 1 v u y = x+ 1 u = 1 x = u = y x y = 1 x v = 1 v = y+ x v+ u y = 3 x+ 1 v = 3 y = y = x 1 u = = x + 6x + x + 1x 18x + 4x = y el jacobiano 9 x x 1 1 u v 1 J = = = y y 1 1 u v + + = + + = = (3v vu 3u 4)dv du = = 6u - 8u + 34 du = 1 3 v u v+ u (x y 1)dxdy ( 1)dv J du ( ) 9 U. D. de Matemáticas de la ETSITGC 9
10 8.- Invertir el orden de integración en: Integral doble 3 = 1. y I dy f(x,y)dx Solución: Dibujamos el recinto con los límites de integración: y=1; y=3; x= y; x= 3 3 x 3 1 y I = dy f (x, y)dx = dx f (x, y)dy + dx f (x, y)dy U. D. de Matemáticas de la ETSITGC 1
11 Integral doble 9.- Calcular el volumen del cilindroide limitado por el plano XY, la superficie z=x +y, y los cilindros parabólicos x=y, y=x. Solución: x 1 x 1 x / 1 3/ ( ) V = zdxdy = dx zdy = dx x + y dy = x y + y dx = x + x x x dx = x x x 1 7/ 5/ = x + x x x = U. D. de Matemáticas de la ETSITGC 11
12 Integral doble 1.- Hallar el volumen del cuerpo limitado por el plano XY, la superficie z x =, y el cilindro cuya sección recta es una elipse del plano XY de semiejes a y b paralelos a los OX, y OY y centro (a,b). Solución: y ( ) ( ) x a x b a + = = ± a b b ( ) 1 x a b y b a a a a+ b ( y b ) b a+ b ( y b) x b 1 a+ b ( y b) b b b b 1 a a a b ( y b) a b ( y b) a b y y b a b ( y b) b V = zdxdy = dy dx = dy xdx = x dy = b 1 a 1 a = 4 b y b dy = b ydy = * b b y ealizamos el cambio: b ( ) ( ) b y t dy tdt = = y = t = b y = b t = b a b a 4a 1 3 4a 1 (*) b ydy t( t)dt t ( b ) = = = = = b b b b 3 b a b 3 U. D. de Matemáticas de la ETSITGC 1
13 Integral doble 11.- Hallar r cos αdrdα en el interior de la cardioide r = 1 + cos α. Solución: 3 1+ cos α π 1+ cos α π r 1 π 3 4 ( ) r cos αdrdα= cos αdα r dr = cos αdα = cos α+ 3cos α+ 3cos α+ cos α dα= = α α+ α α+ α α+ α α = 3 3 π π π π 3 4 ( cos ) d ( cos ) d ( cos ) d ( cos ) d (*) = 5 4 π Calculando las cuatro integrales por separado: [ ] π π cos αdα= senα = ( ) 1+ cos α 1 1 senα cos αdα= dα= dα+ cos αdα = α+ =π π π π π ( ) π 3 π π cos αdα= cos αcos αdα= cos α 1 sen α dα= 3 π π π sen α = cos αdα cos αsen αdα= = cos α 1 4( ) π π π [ sen ] d ( d cos 4 d ) π π π π π cos αdα= dα= dα+ cos αdα+ cos αdα = 1 π 1 1+ cos 4α π 1 π 1 sen4α 3π = α+ α + α= + α+ α α = + α+ = π π sustituyendo en la igualdad 13π (*) = +π+ + = π U. D. de Matemáticas de la ETSITGC 13
14 Integral doble 1.- Volumen del cilindroide limitado por el plano XY, el parabóloide y el cilindro x + y = a. Solución: Por simetría calculamos la cuarta parte: a a x a a x x y x y x y V = zdxdy = + dxdy = 4 dx dy dx dy p q + = + = p q p q ( a x ) 3 a x 3 a a x 1y x 1 = dx y + = a x + dx = (*) p 3q p 3 q x y + = z p q ealizamos el cambio: x = asent dx = a cos tdt x = t = π x = a t = ( ) 3 a (asent) 3 3 π/ (asent) / 1 π a a 3 (*) = a (asent) + a cos tdt = sen t cos t + cos t a cos tdt = p 3 q p 3q π/ / π = a sen t cos t + cos t dt = a ( 1 cos t) cos t cos t dt p 3q + = p 3q π/ / / / 4 1 π π π 4 = a cos tdt + cos tdt a cos tdt a cos tdt (**) p + = + + = p 3q p p 3q Calculando las integrales por separado: π ( ) / π / 1+ cos t 1 π / π cos tdt dt dt / π = cos tdt = + = 4 π/ π/ / / / 4 1+ cos t 1 π π π cos tdt = dt = ( dt + cos dt + cos tdt 4 ) = π/ 1 π / 1 π/ 1+ cos 4t π 1 π/ π/ π 1 sen4t 3π = [ t + sent] + dt ( dt cos 4tdt ) t 4 4 = = + + = sustituyendo en la igualdad 1 π 1 1 3π (**) a a p 4 p 3q = + + = 4 π 1 1 a + 4 p q U. D. de Matemáticas de la ETSITGC 14
15 Integral doble 13.- Hallar (x + y )dxdy en el recinto x y a Solución: 1 p = x y I = (x + y )dxdy = dxdy + p q 1 q = 4 π π I= a + = a + = a π 4 p q 4 1/ 1/ +. según el ejercicio 1 U. D. de Matemáticas de la ETSITGC 15
16 Integral doble Calcular (x y)dxdy en el recinto limitado por x, y, la circunferencia x y x + y = a y la elipse + = 1. 4a a Solución: x y 1 + = 1 y = 4a x 4a a x + y = a y = a x I = 3 (x y)dxdy 1 1 a 4a x a 4a x 3 3 a x a = x dx ydy + x dx ydy = I + I 1 Por separado: a 4a x a 4a x a a a I1 = x dx ydy = x y dx x ( 4a x ) ( a x ) dx x dx a x = = = a x a 4a x a a a a a x a I = x dx ydy = x y dx x ( 4a x ) dx x dx x dx a a = = = a 4 a 8 a a 1 4 a a 15a 63a 9a = x x 4 a 8 6 = = a Y ahora, 6 6 a 9a I= I1+ I = + = a 8 U. D. de Matemáticas de la ETSITGC 16
17 15.- Hallar Solución: Integral doble xy(x y)dxdy en el rectángulo x a, y b. a b a b xy(x y)dxdy = x ydxdy xy dxdy = x dx ydy xdx y dy = a a = x b dx x b dx = a b a b = 1 a b ab ( ) U. D. de Matemáticas de la ETSITGC 17
18 Integral doble 16.- En el supuesto de que la integral doble de una función positiva f, sobre una región, se reduzca a la integral iterada: 1 1 x a) f(x,y)dy dx 1 1 x 1 x x b) ( f(x,y)dy ) dx + 1 ( ) c) π senx x f(x,y)dy dx sen f(x,y)dy dx epresentar la región e invertir el orden de integración. Solución: a) x = 1 y = 1 x x 1 y 1 x y = ± 1 x x + y = 1 x = ± 1 y = = I 1 1 x f (x, y)dy dx dy 1 y f (x, y)dx 1 dy 1 y f (x, y)dx 1 dy 1 y = f (x, y)dx 1 1 x = + = 1 1 y 1 y 1 1 y b) x = 1 y = x y = x; x = y = x y = x x = y x = y = x = 1 y = c) ( ) ( ) 1 x x 1 y I = f (x, y)dy dx + f (x, y)dy dx = dy f (x, y)dx 1 y y = senx x = π x = arcseny x x = y = sen x = arcseny π senx π 1 π arcseny I = x f (x, y)dy dx dy f (x, y)dy dy f (x, y)dx sen = + 1 arceny arcseny U. D. de Matemáticas de la ETSITGC 18
19 Integral doble 17.- Hallar (x + y )dxdy en el recinto xy k,a y b. Solución: xy k x = k / y k /y 6 b k /y b b 1 3 k k a a a 3 3 3y y (x + y )dxdy == dy (x + y )dx = dy x + y x = + y dy = 6 6 b b 6 b b dy k ydy k b a a 3 a y y b a a a k 1 k 1 y k 1 1 k = + = + = + ( ) = k 6a b 6 = + ( b a ) k U. D. de Matemáticas de la ETSITGC 19
20 Definición: Integral doble Si f(x,y) es una función de dos variables definida en una región D que tenga área, se descompone D en n partes que no se solapen, D1, D,..., Dn y se forma la suma n f(x,y)area(d ) donde (xi,yj) es un punto de la región Di. Llamando C al área del i1 i cuadrado más pequeño que contenga a todos los Di, el límite de aquella suma al tender C a cero es, si existe, la integral doble de la función en el recinto D y se denota f (x, y)dd f (x, y)dxdy D D. Si la región D se puede escribir D=[a,b]x[c,d] y f(x,y) es una función continua sobre el rectángulo, entonces Volumen= b d d b D a c c a f(x,y)dxdy f(x,y)dy dx f(x,y)dx dy U. D. de Matemáticas de la ETSITGC 1
21 Área del paralelogramo. Paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos entre sí. Área b h Área ABAD El área del paralelogramo cuyos vértices son A ( a1, a, a3 ), B ( b1, b, b3 ), C ( c1, c, c3 ) y D ( d1, d, d3 ), puede calcularse mediante la fórmula: 3 3 b a b a d a d a b a b a d a d a b a b a d a d a 1 1 U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 1
22 Área del sector circular Sector: porción de círculo comprendida entre un arco y los dos radios que pasan por sus extremidades. 1 Área r Longitud del Arco (s) r U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 11
23 Función beta de Euler 1 p1 q1 Sea p,q, p,q>. Sea (p,q) x (1 x) dx la función beta de Euler. Esta integral es convergente y recibe el nombre de Integral Euleriana de ª especie. Función gamma de Euler x p 1 (p) e x dx Sea p, p>. Sea la función gamma de Euler. Esta integral es convergente y recibe el nombre de Integral Euleriana de 1ª especie. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía
24 Función de densidad Una variable aleatoria con función de distribución F(x), se dice que es una variable aleatoria continua si F(x) es una función absolutamente continua (o simplemente continua) de x cuya derivada F (x) = f(x) existe y es continua salvo, como mucho, en un número finito de puntos. La función f(x) definida, se denomina función de densidad de. Verifica: f(x) para todo x, y además f(x)dx1 U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 88
25 Distribución Normal. Una variable aleatoria continua se dice que tiene una distribución normal o de Laplace- 1(x ) 1 Gauss de media y desviación típica : f(x) e es su función de densidad. es la llamada campana de Gauss. 1(x ) x 1 La función de distribución es: F(x) P( x) e.dx La esperanza matemática o media es y la varianza es. Se denota N(, ). Distribución normal típificada La media y la desviación típica son los dos parámetros de la distribución N(, ). Si queremos calcular una probabilidad determinada: 1 x 1 b Pa ( b) e. dx a debemos hacer uso de las tablas, pero sólo existen tablas de la N(,1), es decir, de la distribución normal de media y desviación típica 1. Por lo que, tendremos que realizar una transformación de la variable N(, ) a la variable N( 1, ) que recibe el nombre de distribución normal tipificada. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 57
26 Volumen del cilindro Cilindro: cuerpo limitado por una superficie cilíndrica cerrada y dos planos que la cortan. Volumen r h Área lateral r h U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 178
27 Área de una superficie de revolución Sea la curva y=f(x) siendo f(x)> para todo x[a, b] y f continua en [a, b], el área de la superficie de revolución engendrada al girar la curva y=f(x) alrededor del eje OX entre los valores de abscisa a y b es: b a S f x 1 f x dx x x t Sea la curva donde las funciones x e y tienen derivada continua en el intervalo y y t [t,t1]. El área de la superficie de revolución engendrada al girar, alrededor del eje OX, el arco de dicha curva entre los valores del parámetro t y t1 es: t1 t S y t x t y t dt Si la curva esta expresada en coordenadas polares r f, y gira alrededor de su eje polar la superficie de revolución del arco de la curva entre los argumentos y 1 con 1 es: 1. S f sen f f d U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 9
28 Volúmenes de cuerpos de revolución Se llama sólido de revolución al generado por la rotación de una región del plano alrededor de un eje situado en él. Si la región está definida por y=f(x), x=a, x=b y f(x) es continua en ab, el volumen es: b a) V f ( x) dx alrededor del eje OX. a d c b) V x dy alrededor del eje OY. c) Si la generatriz es una curva cerrada, V ( f ( x) f ( x)) dx. a b d) Si la curva viene dada en paramétricas x x(t) t1, V y t x t dt y y(t) () '() t e) Si la curva viene dada en coordenadas polares r f( ), al girar alrededor del eje polar se 3 obtiene: V r sen d U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 18
29 Elipse La suma de las distancias de un punto cualquiera de la elipse a los focos es igual al doble de su semieje mayor. x y Sea la elipse de ecuación reducida 1, entonces: a b c Excentricidad: e 1 a Vértices: A(a,); A (-a,); B(,b); B (,-b). Semieje mayor: a; semieje menor: b. Focos: F(c,); F (-c,). a Directrices: x c Ejes de simetría: x=; y=; eje focal o eje mayor: y=. Centro: O(,) punto de intersección de los ejes de simetría. Distancia focal: d(f,f )=c. Parámetro focal: p b /a U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 69
30 Semiejes En una elipse son las distancias entre los vértices dividas por dos: Semieje mayor: a Semieje menor: b U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 155
31 Es el lugar descrito por un punto fijo P de una circunferencia que rueda sin deslizarse sobre otra circunferencia que tiene el mismo radio. Las ecuaciones paramétricas, en coordenadas cartesianas, son: x r (sen t - sent) y r ( cos t - cos t) En coordenadas polares: ρ=a(1+cosα)=acos (α/) Cardioide U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 1
32 Cilindroide Conoide de Plücker es un conoide recto cuya directriz es una elipse contenida en un cilindro de revolución, la arista es la generatriz rectilínea del cilindro que pasa por un extremo del eje mayor de la elipse, y el plano director es perpendicular a la arista. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 3
33 Paraboloide Cuádrica cuyas intersecciones con planos secantes son siempre o bien parábolas o bien elipses o bien hipérbolas. Si el eje del paraboloide es el eje z, entonces la ecuación del paraboloide elíptico es: x a y cz b y la ecuación del paraboloide hiperbólico es: x a y cz b Silla de montar U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 13
34 ectángulo Paralelogramo que tiene los cuatro ángulos rectos y los lados contiguos desiguales. U.D. de Matemáticas de la E.T.S.I. en Topografía, Geodesia y Cartografía 149
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
De x = 1 a x = 6, la recta queda por encima de la parábola.
 Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Área entre curvas El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo. Ejemplos 1. Calcular el área
Tema 2. Ejercicios propuestos
 Tema 2. Ejercicios propuestos 1.- - Calcular 2.- - Calcular 3.- - Sea = x2 y2 dx dy, siendo = {(x, y) 2 : 1 x y 2, x y 4x}. (x2 +y2 )dx dy, donde = (x, y) 2 : x2 + y2 2y, x2 + y2 1, x 0. (x, y) 2 1 x 2
Tema 2. Ejercicios propuestos 1.- - Calcular 2.- - Calcular 3.- - Sea = x2 y2 dx dy, siendo = {(x, y) 2 : 1 x y 2, x y 4x}. (x2 +y2 )dx dy, donde = (x, y) 2 : x2 + y2 2y, x2 + y2 1, x 0. (x, y) 2 1 x 2
Área entre curvas. Ejercicios resueltos. 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x.
 Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
Área entre curvas Ejercicios resueltos 1. Calcular el área limitada por la curva y = x 2 5x + 6 y la recta y = 2x. En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites
INTEGRACION EN VARIAS VARIABLES: Integrales dobles. 1. e x+y dy dx. 3. Evaluar las siguientes integrales en los recintos que se indican:
 INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
INTEGACION EN VAIAS VAIABLES: Integrales dobles.. Evaluar las siguientes integrales iteradas: (x y + y )dy dx xye x+y dy dx ( x ln y)dy dx ln [((x + )(y + )] dx dy. 3 ; ; ; ln. 5. Sea I = [, ] [, 3]. Calcular
Integración múltiple: integrales dobles
 Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Problemas propuestos con solución Integración múltiple: integrales dobles ISABEL MAEO epartamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice. Integrales iteradas 2. Teorema
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
3 Integración en IR n
 a t e a POBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CUSO 29 21 3 Integración en I n 3.1 Integral múltiple. Problema 3.1 Calcula f en los siguientes casos: Q i) f(x, y) =
a t e a POBLEMAS DE CÁLCULO II t i c a s 1 o Ings. Industrial y de Telecomunicación CUSO 29 21 3 Integración en I n 3.1 Integral múltiple. Problema 3.1 Calcula f en los siguientes casos: Q i) f(x, y) =
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO
 PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA
 SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
EJERCICIOS DE CA LCULO II PARA GRADOS DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera
 EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
EJECICIOS E CA LCULO II PAA GAOS E INGENIEI A Elaborados por omingo Pestana y Jose Manuel odrı guez, con Arturo de Pablo y Elena omera 3 3. Integracio n en n Integral mu ltiple. f en los siguientes casos:
5º Prueba de Evaluación continua (CÓNICAS) 5 de junio de 2012
 Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.
 REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Rotaciones alrededor de los ejes cartesianos
 Sólido de revolución Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que se contenida en su mismo plano.
Sólido de revolución Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que se contenida en su mismo plano.
Pauta Auxiliar N 10 Aplicaciones de la Integral I Viernes 1 de Junio de 2012
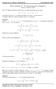 Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Integrales Dobles. Hermes Pantoja Carhuavilca. Matematica II. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
Integrales Dobles Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 76 CONTENIDO Integrales Dobles Introducción
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
GEOMETRÍA ANALÍTICA PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES
 PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
1. L U G A R E S G E O M É T R I C O S E N E L P L A N O
 L U G A R E S G E O M É T R I C O S. C Ó N I C A S 1. L U G A R E S G E O M É T R I C O S E N E L P L A N O Se define un lugar geométrico como el conjunto de puntos del plano que cumplen una determinada
L U G A R E S G E O M É T R I C O S. C Ó N I C A S 1. L U G A R E S G E O M É T R I C O S E N E L P L A N O Se define un lugar geométrico como el conjunto de puntos del plano que cumplen una determinada
Lugares geométricos. Cónicas
 ACTIVIDADES Si el plano es perpendicular a la generatriz del cilindro, la sección es una circunferencia. Si no es perpendicular, la sección es una elipse. Porque el plano solo corta a uno de los conos
ACTIVIDADES Si el plano es perpendicular a la generatriz del cilindro, la sección es una circunferencia. Si no es perpendicular, la sección es una elipse. Porque el plano solo corta a uno de los conos
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Vectores. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo equivalente a QP.
 Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Tema 1.- Cónicas y Cuádricas.
 Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
1 + r, y = y 1 + ry Si P es el punto medio del segmento P 1 P 2, entonces x = x 1 + x 2 2
 CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
Geometría Analítica Agosto 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. 1) A(3, 3), B( 3, 1), C(0, 3) 2) O( 2, 3), P(2, 3), Q(0, 2) 3) R(4, 4), S(7, 4), T(6,
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. 1) A(3, 3), B( 3, 1), C(0, 3) 2) O( 2, 3), P(2, 3), Q(0, 2) 3) R(4, 4), S(7, 4), T(6,
Integrales de lı nea y de superficie
 EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
Geometría Analítica Enero 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
x y z x y z x y z z z z z z z
 . Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
. Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
Opción A Ejercicio 1.- [2 5 puntos] Una ventana normanda consiste en un rectángulo coronado con un semicírculo. De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco
TEMA 6 CÓNICAS CÓNICAS TEMA 6. 1.º BACHILLERATO - CIENCIAS. 1. La circunferencia. Ecuación de una circunferencia. (x - a) + (y - b) = r.
 TEMA 6 CÓNICAS Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen
TEMA 6 CÓNICAS Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice, se obtienen
Unidad 8 Lugares geométricos. Cónicas
 Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
 La Parábola La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz. Características geométricas. a) Vértice. Es el
La Parábola La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz. Características geométricas. a) Vértice. Es el
A pesar de la importancia de las cónicas como secciones de una superficie cónica, para estudiar los elementos y propiedades de cada una de ellas en
 SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 2009 PRIMER PARCIAL
 EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
Guía de Integrales Definidas. Matemáticas II Prof. Wilson Herrera.
 Wilson Herrera 1 Guía de Integrales Definidas. Matemáticas II Prof. Wilson Herrera. 1. Calcular las siguientes integrales: a) b) c) d) e) f ) g) h) 1 8 4 1 6 3 3 1 ( + 3) ( + 3 ) 1 + y dy y 5 + 3 1 + 3
Wilson Herrera 1 Guía de Integrales Definidas. Matemáticas II Prof. Wilson Herrera. 1. Calcular las siguientes integrales: a) b) c) d) e) f ) g) h) 1 8 4 1 6 3 3 1 ( + 3) ( + 3 ) 1 + y dy y 5 + 3 1 + 3
Gu ıa Departamento Matem aticas U.V.
 Universidad de Valparaíso Instituto de Matemáticas Guía de Cálculo en Varias Variables Integración. Sean = [,] [,] {(x,y) : (x,y) < } y f : continua. a) Escriba lafuncióncaracterísticaχ demedianteunafunciónporparte,análogamente
Universidad de Valparaíso Instituto de Matemáticas Guía de Cálculo en Varias Variables Integración. Sean = [,] [,] {(x,y) : (x,y) < } y f : continua. a) Escriba lafuncióncaracterísticaχ demedianteunafunciónporparte,análogamente
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
Primer octante Segundo octante Tercer octante Cuarto octante P ( X, Y, Z ) P (-X, Y, Z ) P (-X,-Y, Z ) P ( X,-Y, Z )
 Capítulo VI. Álgebra vectorial Objetivo: El alumno aplicará el álgebra vectorial en la resolución de problemas geométricos. Contenido: 6.1. Cantidades escalares y cantidades vectoriales. Definición de
Capítulo VI. Álgebra vectorial Objetivo: El alumno aplicará el álgebra vectorial en la resolución de problemas geométricos. Contenido: 6.1. Cantidades escalares y cantidades vectoriales. Definición de
Funciones reales de varias variables
 PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
+ ax 2 + bx) x. ( 2 sen(x) 0 (a + b sen(x) sen(2x))2 dx sea mínima.
 Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
Facultad de Ingeniería - IMERL Cálculo - Curso. Práctico 8. Integrales paramétricas e integrales iteradas dobles y triples. Integrales múltiples. Cambio de variables, áreas, volúmenes, sumas de Riemann
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
Capítulo 3. Integración multidimensional. 1. Integrales de Riemann en rectángulos
 Capítulo 3 Integración multidimensional 1. Integrales de Riemann en rectángulos Definición (Partición de rectángulos). Consideremos el rectángulo [a, b] [c, d] y sean P 1 = {a = x 0, x 1,..., x n = b}
Capítulo 3 Integración multidimensional 1. Integrales de Riemann en rectángulos Definición (Partición de rectángulos). Consideremos el rectángulo [a, b] [c, d] y sean P 1 = {a = x 0, x 1,..., x n = b}
Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos
 página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
página 1/9 Problemas Tema 7 Solución a problemas de ampliación de los Temas 5 y 6 - Hoja 13 - Todos resueltos Hoja 13. Problema 1 1. Sea una circunferencia de centro (0,) y radio unidades. Sea una segunda
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
ETSII Febrero Análisis Matemático.
 Departamento de Análisis Matemático ETSII Febrero 2000. Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese
Departamento de Análisis Matemático ETSII Febrero 2000. Análisis Matemático. Problema 1. (1 punto) Calcular los siguientes ites: e x e senx x 0 x senx x π/4 (tgx)tg2x Problema 2. (2 puntos) Considérese
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones:
 APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto.
![1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto. 1. Sea f una función definida en I = [1, 2] [1, 4] del siguiente modo: (x + y) 2, x y 2x, 0, en el resto.](/thumbs/40/20516327.jpg) La integral múltiple Problemas resueltos. Sea f una función definida en I [, ] [, 4] del siguiente modo: { (x + y), x y x, f(x, y), en el resto. Indique, mediante un dibujo, la porción A del rectángulo
La integral múltiple Problemas resueltos. Sea f una función definida en I [, ] [, 4] del siguiente modo: { (x + y), x y x, f(x, y), en el resto. Indique, mediante un dibujo, la porción A del rectángulo
APLICACIONES DE LA INTEGRAL DEFINIDA
 CAPÍTULO XI. APLICACIONES DE LA INTEGRAL DEFINIDA SECCIONES A. Áreas de figuras planas. B. Cálculo de volúmenes. C. Longitud de curvas planas. D. Ejercicios propuestos. 37 A. ÁREAS DE FIGURAS PLANAS. En
CAPÍTULO XI. APLICACIONES DE LA INTEGRAL DEFINIDA SECCIONES A. Áreas de figuras planas. B. Cálculo de volúmenes. C. Longitud de curvas planas. D. Ejercicios propuestos. 37 A. ÁREAS DE FIGURAS PLANAS. En
MÉTODOS MATEMÁTICOS II
 MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
APLICACIONES GEOMÉTRICAS DE LA INTEGRAL DEFINIDA
 APLICACIONES GEOMÉTRICAS DE LA INTEGRAL DEFINIDA APLICACIONES GEOMÉTRICAS DE LA INTEGRAL DEFINIDA [8.] Calcular el área del dominio plano definido en el primer cuadrante por: Determinemos los puntos de
APLICACIONES GEOMÉTRICAS DE LA INTEGRAL DEFINIDA APLICACIONES GEOMÉTRICAS DE LA INTEGRAL DEFINIDA [8.] Calcular el área del dominio plano definido en el primer cuadrante por: Determinemos los puntos de
Sesión No. 13. Elipse. Objetivo
 Sesión No. 13 Elipse Objetivo Identificar la ecuación de una Elipse, con eje focal paralelo a los ejes coordenados, y reconocer sus características esenciales, en los casos de Elipse con vértice fuera
Sesión No. 13 Elipse Objetivo Identificar la ecuación de una Elipse, con eje focal paralelo a los ejes coordenados, y reconocer sus características esenciales, en los casos de Elipse con vértice fuera
Ejercicios de Álgebra y Geometría Analítica
 Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
Ejercicios de Álgebra y Geometría Analítica Profr. Fausto Cervantes Ortiz Recta Dibujar las rectas indicadas 1. y = x + 1 2. y = 2x + 5 2 3. y = x + 2 4. y = x + 2 5. y = 2x 3 2 6. y = 3 2 x + 1 2 7. y
Geometría Analítica. Ecuación de una recta que pasa por un punto y tiene una pendiente dada:
 Geometría Analítica Definición de línea recta: Llamamos línea recta al lugar geométrico de los puntos tales que tomados dos puntos diferentes cualesquiera y del lugar, el valor de la pendiente m calculado
Geometría Analítica Definición de línea recta: Llamamos línea recta al lugar geométrico de los puntos tales que tomados dos puntos diferentes cualesquiera y del lugar, el valor de la pendiente m calculado
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
Parametrización de curvas Integrales de linea. h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/
 Parametrización de curvas Integrales de linea h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Curvas en el espacio En el espacio, una curva se define por el corte de dos superficies. La forma más general
Parametrización de curvas Integrales de linea h"p://www.sc.ehu.es/sqwpolim/metodos_matema6cos/ Curvas en el espacio En el espacio, una curva se define por el corte de dos superficies. La forma más general
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-2011 CUESTIONES TIPO TEST
 MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
UTalca - Versión Preliminar
 1. Definición La elipse es el lugar geométrico de todos los puntos del plano cuya suma de las distancias a dos puntos fijos es constante. Más claramente: Dados (elementos bases de la elipse) Dos puntos
1. Definición La elipse es el lugar geométrico de todos los puntos del plano cuya suma de las distancias a dos puntos fijos es constante. Más claramente: Dados (elementos bases de la elipse) Dos puntos
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
