MOVIMIENTO RECTILÍNEO DEL PUNTO EN UN CAMPO DE FUERZAS ESTACIONARIO. ESTUDIO CUALITATIVO
|
|
|
- Lorenzo Paz Jiménez
- hace 7 años
- Vistas:
Transcripción
1 MOVIMIENTO RECTILÍNEO DEL PUNTO EN UN CAMPO DE FUERZAS ESTACIONARIO. ESTUDIO CUALITATIVO Índice 1. Introducción 2 2. Ecuación del movimiento y su solución 2 3. Análisis cualitativo de movimiento mediante interpretación gráfica del diagrama energético y del plano de fases Diagrama energético del movimiento Puntos de parada Zonas permitidas y zonas prohibidas del movimiento Valor de la velocidad Valor de la Fuerza Espacios y mapas de fases Definición de espacio de fases Definición de diagrama o mapa de fases Definición de plano de fases Plano de fases de un sistema conservativo Ejemplo: caso potencial de movimiento rectilíneo Estabilidad lineal en el plano de fases Estabilidad Movimiento oscilatorio en un pozo de potencial Otros movimientos posibles Analogía de la curva lisa Generalización del estudio cualitativo 16
2 1. Introducción 2 Se considera el movimiento de una partícula de masa m por una recta sometida a una fuerza que tiene la dirección de la recta y que sólo es función de la posición que ocupa la partícula. 2. Ecuación del movimiento y su solución Se elige un sistema cartesiano cuyo eje de coordenadas O contiene la trayectoria, para epresar las magnitudes vectoriales. La fuerza que actúa sobre la partícula puede representarse por F = F() ı. Unas condiciones iniciales arbitrarias son: { (t0 ) = t = t 0 : 0 ẋ(t 0 ) = ẋ 0 La ecuación de cantidad de movimiento será: F() = mẍ El campo de fuerzas definido de esta forma es irrotacional en toda la recta O, por lo tanto el trabajo realizado por la fuerza F() cuando la partícula se mueve desde un punto = a a otro = b no depende del camino recorrido y sí de las posiciones inicial y final. Esto implica que F() es un campo de fuerzas potencial y por tanto el sistema considerado es conservativo. Se define la función potencial del mismo como: V() = a F()d donde = a puede ser cualquier punto regular de la primitiva, que se denomina origen del potencial (o nivel nulo), y que no tiene repercusión en el movimiento. La ecuación de la energía nos conduce, en este caso, a la integral de la energía: T +V = E 1 2 mẋ2 +V() = E = 1 2 mẋ2 0 +V( 0 ) Donde E = E( 0,ẋ 0 ) es una constante de integración que se determina con las condiciones iniciales y que físicamente representa la energía mecánica que se conserva en este tipo de movimientos. Esta ecuación diferencial ordinaria de primer orden debe ser resuelta. Despejando se tiene: d dt = ±( 2 [E V()])1/2 v = v() m y separando las variables obtenemos: m dt = ± 2 d [E V()] 1/2 Integrando la ecuación entre ( 0,t 0 ) y (,t) se tiene: m dξ t t 0 = ± t = t() 2 [E V(ξ)] 1/2 0 que es esencialmente la solución de la ecuación del movimiento, reducida a una cuadratura 1. Aparece, en principio, una indeterminación del signo ligada a la etracción de la raíz cuadrada y asociada al signo de la velocidad. Para deshacerla hay que seleccionar el signo apropiado en cada instante. Para discutir el signo en la fase inicial se desarrolla la velocidad en serie de Taylor en torno al instante inicial: ẋ(t) ẋ 0 +ẍ 0 (t t 0 ) Se dice que la solución de un sistema de EDO queda reducida a cuadraturas cuando podemos epresar las variables dependientes en términos de integrales indefinidas de la variable independiente.
3 3 Conclusiones: Si ẋ 0 0 se acude al signo de la velocidad inicial: Si ẋ 0 > 0 se elige el signo +. Si ẋ 0 < 0 se elige el signo. Si ẋ 0 = 0 se acude al signo de la aceleración inicial ẍ 0, o con su equivalente de acuerdo con la ecuación de cantidad de movimiento, el de la fuerza en la posición inicial F( 0 ): Si F( 0 ) > 0 se elige el signo +. Si F( 0 ) < 0 se elige el signo. Si F( 0 ) = 0 este tratamiento no tiene sentido, porque la partícula tiene inicialmente velocidad y aceleración nulas y por tanto va a permanecer en reposo indefinidamente (posición de equilibrio). Una elección de signo sólo es válida hasta la siguiente anulación de la velocidad, en la que de nuevo hay que replantearse si hay cambio de signo de la velocidad y si hay que elegir el signo opuesto. Si la funciónv() fuera conocida y si eistiera una primitiva elemental de la función del integrando de la última cuadratura podríamos obtener la representación de la función t = t(). Si además eistiera una función inversa elemental de esta última función, se podría obtener = (t).
4 3. Análisis cualitativo de movimiento mediante interpretación gráfica del diagrama energético y del plano de fases Aunque no seamos capaces de encontrar la función = (t) es posible hacer una interpretación cualitativa del movimiento a partir de las características del diagrama energético y del plano de fases del sistema. Unas condiciones iniciales arbitrarias son: { (t0 ) = t = t 0 : 0 ẋ(t 0 ) = ẋ 0 El valor de la energía mecánica será: E( 0,ẋ 0 ) = 1 2 mẋ2 0 +V( 0) Diagrama energético del movimiento Se denomina diagrama energético a la representación gráfica de la función potencial y de la energía mecánica (que, como se conserva, denominaremos nivel energético) en función de la posición de la partícula. El nivel energético se representa por una recta horizontal. E V V() GRAFICA DEL POTENCIAL NIVEL ENERGÉTICO PER PRO PER PRO 0 PER PRO PUNTOS DE PARADA Puntos de parada Se denominan puntos de parada a aquellas posiciones en las que se anula la velocidad de la partícula. Se calculan resolviendo la ecuación V() = E y son los puntos de corte del nivel energético con la gráfica de la función potencial en el diagrama energético.
5 Zonas permitidas y zonas prohibidas del movimiento Como la energía cinética es siempre no negativa, es imposible que la partícula se encuentre en una región donde V > E. A estas regiones se las conoce como zonas prohibidas. A las regiones donde V E se las denomina zonas permitidas. Los puntos de parada separan diferentes zonas, tanto del mismo tipo como de tipos opuestos. La posición del punto correspondiente a las condiciones iniciales de un movimiento real debe estar necesariamente dentro de una zona permitida. La partícula se mueve única y eclusivamente por esa zona inicial permitida. El tiempo t p que se tarda en alcanzar un punto de parada = p a partir de unas condiciones iniciales arbitrarias que conducen a la partícula hacia él viene dado por la epresión: m t p t 0 = ± 2 p 0 d [E V()] 1/2 Por ser = p punto de parada, es una raíz de la ecuación E V() = 0 de orden de multiplicidad arbitrario. Esta epresión está presente en el denominador del integrando y hace que dicha integral sea impropia por integrando no acotado. El tiempo de acceso será finito o infinito dependiendo de si esta integral impropia es convergente o divergente. Para analizar la convergencia de la integral se utiliza el criterio de comparación con las integrales impropias del tipo: a 0 d α (a,α R,a > 0) { convergente si α < 1 divergente si α 1 En las proimidades del punto de parada se tiene: E V() = ( p ) β φ() lím p φ() 0 β < 2 CONVERGENTE Punto de parada accesible en tiempo finito β 2 DIVERGENTE Punto de parada no accesible en tiempo finito El tiempo que se tarda en alcanzar el infinito accesible a partir de unas condiciones iniciales arbitrarias que conducen a la partícula hacia él viene dado por la epresión: m t( ± ) = t 0 ± 2 lím dξ ± [E V(ξ)] 1/2 0 La integral es impropia porque el intervalo de integración no está acotado. El tiempo de acceso al infinito será finito o infinito dependiendo de si esta integral impropia es convergente o divergente. Para analizar la convergencia de la integral se utiliza el criterio de comparación con las integrales impropias del tipo: a d α (a,α R,a > 0) De acuerdo al mismo se tiene: { convergente si α > 1 divergente si α 1 E V() = β Φ() lím Φ() 0, ± ± β > 2 CONVERGENTE Infinito accesible en tiempo finito β 2 DIVERGENTE Infinito no accesible en tiempo finito Valor de la velocidad El módulo de la velocidad de la partícula en una posición se determina mediante la siguiente epresión: v() = ( 2 [E V()])1/2 m
6 Una indicación del valor del módulo de la velocidad en el diagrama energético es la diferencia de cotas entre el nivel energético y la gráfica de la función potencial. A mayor diferencia, mayor velocidad. En los puntos de parada, obviamente, esta diferencia es nula Valor de la Fuerza La fuerza que actúa sobre la partícula en una determinada posición puede ser determinada mediante la relación: F() = dv d Esto significa que el valor de la fuerza está representado en el diagrama energético por el opuesto de la pendiente de la gráfica de la función potencial. Por la segunda ley de Newton, la fuerza y la aceleración son directamente proporcionales y además del mismo signo. En los puntos donde la pendiente es positiva (resp. negativa) la fuerza y la aceleración tienen sentidos negativos (resp. positivos). En los puntos donde la pendiente es nula no se aplica fuerza alguna sobre la partícula y se denominan puntos de aceleración nula Espacios y mapas de fases Definición de espacio de fases Sea X un sistema mecánico formado por N partículas (i = 1,...,N). Su estado cinemático en un instante es el conjunto de todas las posiciones y velocidades de sus partículas: {( r i, v i ); i = 1,...,N}. Sean {q j ; j = 1,...,n} las coordenadas generalizadas del mismo (introducidas para considerar sus ligaduras geométricas), y { q j ; j = 1,...,n} las velocidades generalizadas. Se demuestra que el estado cinemático queda definido por {(q j, q j ); j = 1,...,n}. Supongamos que X está sometido a fuerzas directamente aplicadas que derivan del potencial V(q j,t) y que T(q j, q j,t) es su energía cinética. El espacio de fases (phase space) de X es un espacio 2n-dimensional cuyas coordenadas son las variables canónicas de estado del sistema en el formalismo Hamiltoniano: {(q j,p j ); j = 1,...,n}, donde p j = L q j son los momentos generalizados conjugados y L(q j, q j,t) = T V es la función lagrangiana asociada al sistema. Hay un isomorfismo entre los posibles estados cinemáticos del sistema y los puntos del espacio de fases. De ahí su utilidad Definición de diagrama o mapa de fases El mapa de fases (phase portrait) es la representación gráfica de las trayectorias posibles del punto representativo del sistema en el espacio de fases, considerado como cartesiano. Por cada punto regular del espacio de fases pasa una única trayectoria que se recorre en un único sentido. La evolución concreta de un sistema estará determinada por la trayectoria que pasa por el punto representativo del estado inicial del sistema Definición de plano de fases El único mapa de fases representable es el correspondiente a n = 1, que se denomina plano de fases (phase plane). Es habitual sustituir la coordenada momento conjugado p correspondiente a la coordenada generalizada q por q, ya que suelen ser proporcionales (lo que es equivalente a reescalar los parámetros del sistema para que los coeficientes de proporcionalidad de momento frente a velocidad generalizada valgan la unidad).
7 3.3. Plano de fases de un sistema conservativo 7 Las trayectorias en el plano de fases de un sistema conservativo corresponden con las curvas isoenergéticas del mismo. Dicho de otra forma, en un sistema conservativo la integral de la energía es una representación implícita de la familia uniparamétrica de trayectorias en el plano de fases cuyo parámetro es la energía mecánica del sistema. A cada punto del plano de fases le corresponde un único valor de la energía mecánica y al estado inicial le corresponde fijar la energía mecánica de la trayectoria real que seguirá el punto representativo del sistema en el espacio de fases Ejemplo: caso potencial de movimiento rectilíneo Definiciones: T = 1 2 mẋ2 V() = a F(ξ)dξ n = 1 q 1 = p 1 = T q 1 = mẋ Como m > 0, vamos a trabajar en el plano cartesiano de coordenadas (,ẋ). Partimos de la integral de la energía: 1 2 mẋ2 +V() = E( 0,ẋ 0 ) diferenciando obtenemos el valor de la pendiente de la trayectoria en cada punto: mẋdẋ+v ()d = 0 dẋ d = V () mẋ Consecuencias: (Pendiente de la curva isoenergética) En un punto crítico del potencial ( : V ( ) = 0) la pendiente de la trayectoria en el plano de fases se anula y la velocidad alcanza un valor crítico. En un punto de parada ( p : ẋ( p ) = 0) se tiene: E V() = ( p ) β φ() : φ( p ) 0 E V() p β 2 ẋ = ± m [E V()] ẋ p β/2 V () = φ ()( p ) β +βφ()( p ) β 1 V () p β 1 Con lo que la pendiente de la curva isoenergética en los puntos de parada es: dẋ φ() d = β sign(ẋ) 2m ( p) β 2 1 dẋ d p β 2 1 Se presentan los siguientes casos: 0 < β < 2 pendiente infinita β = 2 pendiente finita y no nula 2 < β pendiente nula
8 8 Puntos de parada característicos: 1. Puntos de parada y cambio de sentido (β = 1) ẋ β = 1 Figura 1: Caso β = 1 2. Puntos de parada perpetua (1 < β < 2) ẋ 1 < β < 2 3. Puntos de parada asintóticos (β = 2) Figura 2: Caso 1 < β < 2 ẋ β = 2 Figura 3: Caso β = 2
9 3.4. Estabilidad lineal en el plano de fases (Solo leer) 9 Plano de fases para un SEDO lineal bidimensional: } ( { = a+by y {X} = [A]{X} {X} = = c+dy y El polinomio característico de [A] será: P A (λ) = det(a λi) = λ 2 tr(a)λ+det(a) Además, factorizando las raíces se obtiene: 2 2 P A (λ) = (λ λ i ) = λ 2 λ λ i + i=1 i=1 Identificando coeficientes resulta: 2 tr(a) = λ i = λ 1 +λ 2 det(a) = i=1 A la inversa: λ 1,λ 2 = tr(a) tr(a) 2 ± det(a) 2 4 Los autovalores serán: complejos no reales si det(a) > tr(a)2 4 reales e iguales si det(a) = tr(a)2 4 reales y distintos si det(a) < tr(a)2 4 2 i=1 λ i 2 λ i = λ 1 λ 2 i=1 } [ a b, [A] = c d ] ) ( ) tr(a) = a+d, det(a) = ad bc El comportamiento del sistema está determinado por los autovalores λ 1,λ 2 de la matriz [A]. Las solución general será de la forma: c 1 e λ1t {A 1 }+c 2 e λ2t {A 2 }, si son distintos; c {X} = 1 e λt {A}, {A} R 2 si son iguales y [A] es escalar; e λt [(c 1 +c 2 t){a 1 }+c 2 {B}] : : ([A] λ[i]){b} = {A 1 }, si son iguales y [A] no es escalar. La casuística que aparece se estudia en un plano cartesiano cuyos ejes de abscisas y ordenadas son tr(a) y det(a) respectivamente. Las curvas separatrices (casos críticos) se corresponden con: 1. det(a) = tr(a)2 4, que es una parábola de dicho plano; 2. tr(a) = 0, que es el eje de ordenadas; NODOS ESTABLES FOCOS ESTABLES det(a) NODOS det(a) = tr(a)2 4 DEGENERADOS FOCOS INESTABLES NODOS INESTABLES tr(a) 3. det(a) = 0, que es el eje de abscisas. CENTROS SILLAS LINEA CRITICA SILLAS
10 10 Estos son los casos no degenerados: Punto silla dos autovalores reales no nulos y de distinto signo: det(a) < 0 Nodo dos autovalores reales no nulos y del mismo signo: 0 < det(a) < tr(a)2 4. inestable dos autovalores reales positivos: det(a) > 0, tr(a) > 0 estable dos autovalores reales negativos: det(a) > 0, tr(a) < 0 Foco, Espiral o Vórtice dos autovalores complejos con parte real no nula: tr(a)2 4 < det(a). inestable dos autovalores complejos con parte real positiva: tr(a) > 0 estable dos autovalores complejos con parte real negativa: tr(a) < 0 Además hay tres casos degenerados (puntos de las separatrices): Centro un par de autovalores imaginarios puros: tr(a) = 0. Las trayectorias locales del plano de fases son elipses (salvo la degenerada del centro). Nodo degenerado dos autovalores reales idénticos: det(a) = tr(a) 2 /4. Las trayectorias locales concurren al nodo y pueden ser: a) estrelladas radiales, si [A] es diagonal (estables si tr(a) < 0, inestables si tr(a) > 0); b) estrelladas equitangentes, si [A] no es diagonal (estables si tr(a) < 0, inestables si tr(a) > 0). Punto de línea crítica un autovalor nulo: det(a) = 0 En el último caso degenerado hay una infinidad de puntos fijos que corresponden al autovector con autovalor nulo. Así, esos puntos fijos forman una línea del plano. Hay varios conceptos importantes que son bastante bien ilustrados por el simple sistema lineal Estabilidad Todos los sistemas lineales pertenecen a una de estas categorías: Asintóticamente estables soluciones atenuadas (nodos, focos y estrellas estables) lím{x(t)} = {0} : tr(a) < 0, det(a) > 0 t Neutralmente estables soluciones periódicas (centros) tr(a) = 0, det(a) > 0 Inestables soluciones amplificadas (Puntos silla, nodos y focos inestables)
11 3.5. Movimiento oscilatorio en un pozo de potencial 11 Llamamos puntos de cambio de sentido (del inglés turning points ) a puntos de parada que no son de aceleración nula. Si = p es un punto de cambio de sentido entonces es una raíz simple (de orden de multiplicidad uno) de la ecuación E V() = 0. Esta ecuación está presente en el denominador del integrando y hace que dicha integral sea impropia. Como el cero del denominador es de orden 1/2 dicha integral impropia es convergente. Esto significa que el tiempo se tarda en acceder al punto de cambio de sentido es finito. Cuando la partícula se encuentra en una zona permitida limitada por dos puntos de cambio de sentido vamos a comprobar que nos encontramos en presencia de un movimiento oscilatorio periódico. Para ilustrar la aparición de movimiento oscilatorio en estas condiciones vamos a utilizar un ejemplo de diagrama energético representado en la figura 4: DIAGRAMA ENERGETICO V() E V(),E ẋ Figura 4: DIAGRAMAS ENERGÉTICO Y DE FASES (Ejemplo 1) Supongamos que la partícula se encuentra inicialmente (t = t 0 ) en la posición = 0 con una velocidad ẋ = ẋ 0 > 0. En nuestro caso, los límites donde hay cambio de sentido son 3 y 2, con 3 < 2. La partícula se mueve primeramente hacia la derecha con velocidad creciente (acelerada en sentido positivo porque la pendiente es negativa) hasta que alcanza el punto de aceleración nula 1. A partir de éste continua moviéndose hacia la derecha pero con aceleración en sentido negativo (siendo frenada). Luego la partícula alcanza el punto de parada = 2 en tiempo finito y se detiene. Como
12 en él la pendiente del potencial es positiva se produce una fuerza de sentido negativo (y por tanto una aceleración de sentido negativo) que impide a la partícula permanecer en reposo en el punto de parada. Por esto abandona el punto de parada y retrocede. Puede realizarse un análisis similar del movimiento hacia el punto de cambio de sentido de la izquierda. Cuando se alcanza el punto = 3 la partícula igualmente se para y cambia de sentido, iniciándose un movimiento hacia la derecha, en el que alcanza el punto 0 en unas condiciones idénticas a las iniciales. A partir de este momento se repite cíclicamente todo el proceso. Se denomina ciclo a la parte del movimiento de la partícula delimitada por dos pasos consecutivos por el mismo estado cinemático. Al tiempo de duración de un ciclo se denomina periodo de oscilación del movimiento. El periodo se calcula duplicando el tiempo que tarda la partícula en pasar del punto 3 al 2, y viene dado por la epresión: T = 2 d 2m E V() 3 que es una integral impropia en ambos etremos, pero convergente. 12
13 3.6. Otros movimientos posibles 13 En este apartado se estudian los casos que se presentan cuando algún punto de parada (en la frontera de una zona permitida) es de aceleración nula. En la figura 5 el punto = 2 es un punto de la gráfica de la función potencial con tangente horizontal. DIAGRAMA ENERGETICO V() E V(),E ẋ < β < 2 ẋ β = 2 Figura 5: DIAGRAMAS ENERGÉTICO Y DE FASES (Ejemplo 2)
14 El razonamiento anterior sobre el movimiento sería valido ecepto en un entorno del mismo. Dicho punto es una raíz de orden de multiplicidad mayor que la unidad de la ecuación E V() = 0. A continuación se tiene que analizar si estos puntos de parada son accesibles en tiempo finito. Se pueden presentar dos casos: 1. Si la raíz es de orden mayor que uno y menor que dos el denominador es un cero de orden menor que uno y la integral es convergente. En este caso la partícula se aproima a = 2 cada vez más lentamente pero llegando a alcanzar el punto de parada en tiempo finito y permaneciendo en él indefinidamente, ya que la aceleración en el mismo es cero. Este caso es bastante raro, puesto que V() no es desarrollable en serie de Taylor en dicho punto. Lo denominaremos punto de parada perpetua. 2. Si la raíz es de orden mayor o igual a dos el denominador es un cero de orden mayor o igual que uno y la integral es divergente. En este caso la partícula se aproima al punto de parada = 2 cada vez más lentamente sin llegar a alcanzarlo en tiempo finito. A este tipo de movimiento se le denomina movimiento asintótico, porque se presenta una asíntota en la representación gráfica de la curva en función de t. Cuando las condiciones iniciales son tales que abandonamos en reposo la partícula en un punto crítico de la función potencial estamos haciendo que el nivel energético sea tangente a la gráfica de la función potencial en dicho punto. Como dejamos la partícula en reposo en un punto de aceleración nula permanecerá en reposo indefinidamente, debido a que se encuentra en equilibrio. Se denominan a estos puntos posiciones de equilibrio. 14 DIAGRAMA ENERGETICO Ejemplo 3a Ejemplo 3b Ejemplo 3c Ejemplo 4 E V(),E Figura 6: DIAGRAMA ENERGÉTICO (Ejemplos 3 y 4) En estas condiciones aparecen otras dos situaciones: 1. Cuando la posición es un máimo relativo (Figura 6: ejemplo 3a) a ambos lados eisten zonas permitidas. Cuando la posición es un punto de infleión con tangente horizontal (Figura 3: ejemplos 3b y 3c) solo en un lado eiste una zona permitida. Si eistieran perturbaciones tendentes a sacar la partícula de su posición de equilibrio subirían verticalmente el nivel energético y la partícula se movería hacia una de las zonas permitidas colindantes. En estos casos hablamos de posiciones de equilibrio inestable porque el movimiento resultante de la perturbación es radicalmente distinto del reposo del que se parte.
15 2. Cuando la posición es un mínimo relativo (Figura 3, ejemplo 4) a ambos lados eisten zonas prohibidas. Si eistieran perturbaciones tendentes a sacar la partícula de su posición de equilibrio subirían verticalmente el nivel energético y la partícula quedaría moviéndose con movimiento oscilatorio confinado en las proimidades del punto en cuestión. En este caso hablamos de posición de equilibrio estable porque el movimiento resultante de la perturbación es próimo al reposo de partida. Sea = un punto de equilibrio y sean = c t = t t c ( c,t c magnitudes características del problema) las variables adimensionales del problema. Se dice que la posición de equilibrio es estable en el sentido de Lagrange si y solo si se satisface la siguiente condición matemática { } { } ( t 0 ) < δ ( t) < ǫ ǫ > 0, δ > 0 d d t ( t 0 ) < δ 3.7. Analogía de la curva lisa d d t ( t) < ǫ t > t 0 Con todo lo epuesto anteriormente podemos descubrir la siguiente analogía: El movimiento de la partícula en las condiciones anteriores es cualitativamente equivalente al que se produce al abandonar en condiciones cinemáticas equivalentes un abalorio pesado en un punto de una curva lisa contenida en un plano vertical y de ecuación z() = V()/mg. 15 V = mgz() T = 1 2 mẋ2 (1+[z ()] 2 ) } m t t 0 = ± [z ()] 2 E mgz() d La simple inspección del diagrama energético permite deducir de una forma rápida los aspectos cualitativos más importantes del movimiento.
16 4. Generalización del estudio cualitativo 16 Todo este estudio cualitativo del movimiento rectilíneo del punto sometido a un campo de fuerzas que admite función potencial es generalizable a aquellas situaciones en las que disponemos de una ecuación que puede escribirse en la forma: ( dy d )2 = C f(y) Donde y, son respectivamente las variables dependiente e independiente y C es una constante de integración. A la función f(y) se la denomina potencial efectivo por analogía con lo anterior y se la representa generalmente por V ef (y). La constante C juega el papel de nivel energético. Por la analogía de las ecuaciones, la evolución cualitativa de la variable dependiente puede analizarse de la misma forma que la realizada en el movimiento rectilíneo del punto sometido a un campo potencial estacionario. También puede realizarse un estudio cualitativo en el caso de ecuaciones del tipo: ( dy d )2 = ϕ(y) sin más que identificar con el caso anterior: E = 0, V ef (y) = ϕ(y)
Sistemas autónomos. Introducción a la teoría cualitativa.
 Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Tema II: Dinámica en el espacio de fases
 Tema II: Dinámica en el espacio de fases 1. Las ecuaciones de Hamilton Para sistemas autónomos en los que H no depende de t, es una constante del movimiento por lo que H(p, q = α (1.1 Esta ecuación determina
Tema II: Dinámica en el espacio de fases 1. Las ecuaciones de Hamilton Para sistemas autónomos en los que H no depende de t, es una constante del movimiento por lo que H(p, q = α (1.1 Esta ecuación determina
Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización.
 TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
TEMA 1 Límites de funciones. Continuidad de funciones. Derivabilidad. Propiedades de las funciones derivables. Optimización. Límite finito en un punto: Consideremos una función f definida en las proimidades
MECÁNICA CLÁSICA CINEMATICA. FAyA Licenciatura en Química Física III año 2006
 Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Física III año 26 CINEMATICA MECÁNICA CLÁSICA La cinemática estudia el movimiento de los cuerpos, sin tener en cuenta las causas que lo producen. Antes de continuar establezcamos la diferencia entre un
Las raíces del polinomio característico P (λ) = λ 2 + 4λ + 3 son
 Tiempo total: 2 horas 4 minutos Problema 1 [2 puntos]. Colgamos una masa m de un muelle vertical cuya constante de Hooke es λ. El medio ofrece una resistencia igual a µ veces la velocidad instantánea.
Tiempo total: 2 horas 4 minutos Problema 1 [2 puntos]. Colgamos una masa m de un muelle vertical cuya constante de Hooke es λ. El medio ofrece una resistencia igual a µ veces la velocidad instantánea.
DIAGRAMAS DE FASE DE SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN
 DIAGRAMAS DE FASE DE SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN Alejandro Lugon 26 de mayo de 2010 1. Ecuaciones planares: dos dimensiones Las soluciones del sistema homogéneo: ẋ = ax
DIAGRAMAS DE FASE DE SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN Alejandro Lugon 26 de mayo de 2010 1. Ecuaciones planares: dos dimensiones Las soluciones del sistema homogéneo: ẋ = ax
Numericamente idénticas, pero conceptualmente distintas en Mecánica Clásica. Numérica y conceptualmente distintas en Relatividad General.
 FUNDAMENTOS FÍSICOS DE LA INGENIERÍA. CURSO 22/23. PRIMERO INGENIERO DE TELECOMUNICACIÓN. PRIMERA PRUEBA DE SOBRENOTA: MECÁNICA SOLUCIÓN DETALLADA. Las masas inerte y gravitatoria son: Numérica y conceptualmente
FUNDAMENTOS FÍSICOS DE LA INGENIERÍA. CURSO 22/23. PRIMERO INGENIERO DE TELECOMUNICACIÓN. PRIMERA PRUEBA DE SOBRENOTA: MECÁNICA SOLUCIÓN DETALLADA. Las masas inerte y gravitatoria son: Numérica y conceptualmente
Aplicaciones de los S.E.D.O.
 Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
TIRO CON RESISTENCIA
 TIRO CON RESISTENCIA Índice 1. Planteamiento del problema 1. Replanteamiento óptimo y resolución del problema 3. Análisis cualitatio del comportamiento de la hodógrafa 3.1. Puntos singulares de la hodógrafa..........................
TIRO CON RESISTENCIA Índice 1. Planteamiento del problema 1. Replanteamiento óptimo y resolución del problema 3. Análisis cualitatio del comportamiento de la hodógrafa 3.1. Puntos singulares de la hodógrafa..........................
b) Calcular sus cuatro puntos de equilibrio y estudiar la estabilidad en cada uno por el método de linealización.
 Examen Final de EDOs Fecha: 14 de enero de 2013 Problemas Tiempo total: 2 horas y 30 minutos 1. Es un problema largo, pero casi todos los apartados son de tipo estándar. La interdependencia entre apartados
Examen Final de EDOs Fecha: 14 de enero de 2013 Problemas Tiempo total: 2 horas y 30 minutos 1. Es un problema largo, pero casi todos los apartados son de tipo estándar. La interdependencia entre apartados
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
A = α cuyos VAPs son λ = 2 y λ ± = α ± i. (No hace falta que comprobeis este dato.) a) Calcular la solución general real del sistema x = Ax.
 Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
No usar por academias
 ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
ECUACIONES DIFERENCIALES I Grupo D 1 de septiembre de 003 Apellidos: Nombre: D.N.I.: Firma: 1. Considérese la ecuación y = 1 + y x. i) Hallar su solución general. ii) Dibujar aproximadamente sus curvas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Matemáticas aplicadas a las CC.SS. II
 Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
Profesores de Enseñanza Secundaria. MATEMÁTICAS. ANDALUCÍA 2018
 ANDALUCÍA 8 PROBLEMA Dados la matriz A R, el vector b R, α R y el subespacio F de R A =, b = y F + = α + + = α a) Discutir y resolver cuando sea compatible el sistema AX=b con X R. b) Sea E el espacio
ANDALUCÍA 8 PROBLEMA Dados la matriz A R, el vector b R, α R y el subespacio F de R A =, b = y F + = α + + = α a) Discutir y resolver cuando sea compatible el sistema AX=b con X R. b) Sea E el espacio
Examen de Selectividad Matemáticas JUNIO Andalucía OPCIÓN A
 Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto.
 Un i d a d Lí m i t e s Objetivos Al inalizar la unidad, el alumno: Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto. Calculará límites de funciones
Un i d a d Lí m i t e s Objetivos Al inalizar la unidad, el alumno: Mostrará la convergencia o divergencia de funciones mediante el criterio de límite de una función en un punto. Calculará límites de funciones
Posición de un Cuerpo. Elementos para la descripción del movimiento. Vector de Posición y Vector Desplazamiento
 1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
1 Bárbara Cánovas Conesa 637 70 113 www.clasesalacarta.com 1 Cinemática Posición de un Cuerpo Coordenadas Cartesianas Coordenadas Polares Vector de Posición (,, z) r, q r Elementos para la descripción
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Modelización por medio de sistemas
 SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las opciones
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las opciones
OPCIÓN A. El sistema homogéneo tiene infinitas soluciones cuando la matriz de los coeficientes tenga rango 3 y para ello: x y
 OPCIÓN A 1. Hallar los valores del parámetro a para que el sistema de ecuaciones soluciones [1,5 puntos]. Resolverlo en cada uno de esos casos [1 punto]. z 0 a y z 0 (a 1)y az 0 admita infinitas El sistema
OPCIÓN A 1. Hallar los valores del parámetro a para que el sistema de ecuaciones soluciones [1,5 puntos]. Resolverlo en cada uno de esos casos [1 punto]. z 0 a y z 0 (a 1)y az 0 admita infinitas El sistema
Para qué x de ese intervalo alcanza F su valor máximo? Y el valor mínimo?
 Análisis I (A y B) febrero9 Consideremos f() = sen() arctg( 3 Calcular el límite de f cuando tiende a Sea la sucesión ) a n = cosn Es convergente? Determinar el límite, si eiste, de la sucesión {f(a n
Análisis I (A y B) febrero9 Consideremos f() = sen() arctg( 3 Calcular el límite de f cuando tiende a Sea la sucesión ) a n = cosn Es convergente? Determinar el límite, si eiste, de la sucesión {f(a n
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato
 página 1/17 Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato Índice de contenido Ecuación vectorial, paramétrica, cartesiana y general de la recta en dos dimensiones...2 Pendiente
página 1/17 Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato Índice de contenido Ecuación vectorial, paramétrica, cartesiana y general de la recta en dos dimensiones...2 Pendiente
1. Es un problema largo, pero casi todos los apartados son de tipo estándar. Consideramos el sistema no lineal 2D cuadrático dado por
 Fecha: 7 de enero de 24 Problemas Tiempo total: 2 horas y 3 minutos Es un problema largo, pero casi todos los apartados son de tipo estándar Consideramos el sistema no lineal 2D cuadrático dado por { x
Fecha: 7 de enero de 24 Problemas Tiempo total: 2 horas y 3 minutos Es un problema largo, pero casi todos los apartados son de tipo estándar Consideramos el sistema no lineal 2D cuadrático dado por { x
CONSIDERACIONES GENERALES SOBRE ESTÁTICA
 CONSIDERACIONES GENERALES SOBRE ESTÁTICA Índice 1. CONCEPTOS ÚTILES 2 1.1. Configuración geométrica de un sistema....................... 2 1.2. Ligaduras....................................... 2 1.3. Coordenadas
CONSIDERACIONES GENERALES SOBRE ESTÁTICA Índice 1. CONCEPTOS ÚTILES 2 1.1. Configuración geométrica de un sistema....................... 2 1.2. Ligaduras....................................... 2 1.3. Coordenadas
5 Estabilidad de soluciones de equilibrio
 Prácticas de Ecuaciones Diferenciales G. Aguilar, N. Boal, C. Clavero, F. Gaspar Estabilidad de soluciones de equilibrio Objetivos: Clasificar y analizar los puntos de equilibrio que aparecen en los sistemas
Prácticas de Ecuaciones Diferenciales G. Aguilar, N. Boal, C. Clavero, F. Gaspar Estabilidad de soluciones de equilibrio Objetivos: Clasificar y analizar los puntos de equilibrio que aparecen en los sistemas
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
CUESTIONES RESUELTAS 3. INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA
 CUESTIONES RESUELTAS INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS º GRADO GESTIÓN AERONAÚTICA INTEGRAL DEFINIDA REGLA DE BARROW Sea f() una función discontinua en = y continua en el resto de puntos del intervalo
CUESTIONES RESUELTAS INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS º GRADO GESTIÓN AERONAÚTICA INTEGRAL DEFINIDA REGLA DE BARROW Sea f() una función discontinua en = y continua en el resto de puntos del intervalo
Prof. Virginia Mazzone - Mariana Suarez
 SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
SISTEMAS NO LINEALES SISTEMAS DE SEGUNDO ORDEN Prof. Virginia Mazzone - Prof. Mariana Suarez 1 Introducción Método de isoclinas Ejemplos 3 Introducción Un sistema de segundo orden autónomo está representado
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA APELLIDOS:
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
Análisis de funciones
 Análisis de funciones Tiempo atrás, en nuestro curso, hemos analizado algunas funciones para determinar la forma de la gráfica de manera estimativa y sin una tabla de valores estricta. En este mismo sentido,
Análisis de funciones Tiempo atrás, en nuestro curso, hemos analizado algunas funciones para determinar la forma de la gráfica de manera estimativa y sin una tabla de valores estricta. En este mismo sentido,
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Breve revisión de estabilidad de sistemas dinámicos
 Breve revisión de estabilidad de sistemas dinámicos Estabilidad de Sistemas Eléctricos de Potencia Pablo Monzón Instituto de Ingeniería Eléctrica (IIE) Facultad de Ingeniería-Universidad de la República
Breve revisión de estabilidad de sistemas dinámicos Estabilidad de Sistemas Eléctricos de Potencia Pablo Monzón Instituto de Ingeniería Eléctrica (IIE) Facultad de Ingeniería-Universidad de la República
SEPTIEMBRE b) (1 punto) Calcular el valor de a 0 para el cual se verifica la igualdad = 2
 SEPTIEMBRE INSTRUCCIONES: El eamen presenta dos opciones A B; el alumno deberá elegir una de ellas contestar raonadamente a los cuatro ejercicios de que consta dicha opción en h. min. OPCIÓN A Ejercicio.
SEPTIEMBRE INSTRUCCIONES: El eamen presenta dos opciones A B; el alumno deberá elegir una de ellas contestar raonadamente a los cuatro ejercicios de que consta dicha opción en h. min. OPCIÓN A Ejercicio.
Representación de Funciones Reales
 Representación de Funciones Reales Curso 0 Universidad Rey Juan Carlos «Conceptos Básicos» Curso Académico 16/17 1. Notación Se utilizan dos notaciones: y = f(x): variable independiente = x y variable
Representación de Funciones Reales Curso 0 Universidad Rey Juan Carlos «Conceptos Básicos» Curso Académico 16/17 1. Notación Se utilizan dos notaciones: y = f(x): variable independiente = x y variable
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Ecuaciones diferenciales
 de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
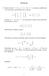 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
GEOMETRÍ A ANALÍ TÍCA
 GEOMETRÍ A ANALÍ TÍCA En este tema estudiaremos vectores (definición, características, operaciones) de forma geométrica y analítica. Además veremos los conceptos de vector director, pendiente de una recta
GEOMETRÍ A ANALÍ TÍCA En este tema estudiaremos vectores (definición, características, operaciones) de forma geométrica y analítica. Además veremos los conceptos de vector director, pendiente de una recta
Alonso Fernández Galián
 Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Ecuaciones Diferenciales II. Tema 3: El entorno de los puntos críticos
 Ecuaciones Diferenciales II Tema 3: El entorno de los puntos críticos José C. Sabina de Lis Universidad de La Laguna La Laguna, 24 de febrero de 2013 1.Puntos críticos no degenerados. Se considera la ecuación
Ecuaciones Diferenciales II Tema 3: El entorno de los puntos críticos José C. Sabina de Lis Universidad de La Laguna La Laguna, 24 de febrero de 2013 1.Puntos críticos no degenerados. Se considera la ecuación
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
MATEMÁTICA - 6 A C y D - Prof. Sandra M. Corti
 TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
Física Ondas 10/11/06
 Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales
 Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales Profesor: Axel Osses, Auxiliares: Jorge Lemus,Oscar Peredo 7 de Noviembre del 2005 1. Definiciones y Propiedades Definición 1 (SNLA). Dado
Ecuaciones Diferenciales Ordinarias MA26A Sistemas No Lineales Profesor: Axel Osses, Auxiliares: Jorge Lemus,Oscar Peredo 7 de Noviembre del 2005 1. Definiciones y Propiedades Definición 1 (SNLA). Dado
10.APLICACIÓN DE LAS DERIVADAS
 .APLICACIÓN DE LAS DERIVADAS. DERIVADAS SUCESIVAS Antes de introducirnos en algunas importantes aplicaciones de las derivadas, vamos a ver una ampliación de los puntos estudiados en el tema anterior que
.APLICACIÓN DE LAS DERIVADAS. DERIVADAS SUCESIVAS Antes de introducirnos en algunas importantes aplicaciones de las derivadas, vamos a ver una ampliación de los puntos estudiados en el tema anterior que
Teoría Tema 6 Ecuaciones de la recta
 página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
BACHILLERATO FÍSICA B. REPASO DE MECÁNICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA B. REPASO DE MECÁNICA R. Artacho Dpto. de Física y Química B. REPASO DE MECÁNICA ÍNDICE 1. Las magnitudes cinemáticas 2. Movimientos en una dimensión. Movimientos rectilíneos 3. Movimientos
BACHILLERATO FÍSICA B. REPASO DE MECÁNICA R. Artacho Dpto. de Física y Química B. REPASO DE MECÁNICA ÍNDICE 1. Las magnitudes cinemáticas 2. Movimientos en una dimensión. Movimientos rectilíneos 3. Movimientos
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
E.T.S.I. Agrónomos Grado en Biotecnología Matemáticas II 2 a prueba de la evaluación continua: soluciones
 E.T.S.I. Agrónomos Grado en Biotecnología Matemáticas II a prueba de la evaluación continua: soluciones 6 de mayo de 14 Es importante que escribáis con claridad y expreséis con precisión los argumentos
E.T.S.I. Agrónomos Grado en Biotecnología Matemáticas II a prueba de la evaluación continua: soluciones 6 de mayo de 14 Es importante que escribáis con claridad y expreséis con precisión los argumentos
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES El estudio de la derivada de una función, junto con otras consideraciones sobre las funciones tales como el estudio de su campo de eistencia (dominio), de sus puntos de corte
REPRESENTACIÓN DE FUNCIONES El estudio de la derivada de una función, junto con otras consideraciones sobre las funciones tales como el estudio de su campo de eistencia (dominio), de sus puntos de corte
7. Sistemas autónomos planos. ( Chema Madoz, VEGAP, Madrid 2009)
 7. Sistemas autónomos planos Chema Madoz, VEGAP, Madrid 009 Curvas solución "sin una solución" Podemos estudiar EDOs de primer orden analizándolas cualitativamente. d/d = 0. = f, a Pendientes: Debido a
7. Sistemas autónomos planos Chema Madoz, VEGAP, Madrid 009 Curvas solución "sin una solución" Podemos estudiar EDOs de primer orden analizándolas cualitativamente. d/d = 0. = f, a Pendientes: Debido a
B. REPASO DE MECÁNICA ÍNDICE
 BACHILLERATO FÍSICA B. REPASO DE MECÁNICA R. Artacho Dpto. de Física y Química B. REPASO DE MECÁNICA ÍNDICE 1. Las magnitudes cinemáticas 2. Movimientos en una dimensión. Movimientos rectilíneos 3. Movimientos
BACHILLERATO FÍSICA B. REPASO DE MECÁNICA R. Artacho Dpto. de Física y Química B. REPASO DE MECÁNICA ÍNDICE 1. Las magnitudes cinemáticas 2. Movimientos en una dimensión. Movimientos rectilíneos 3. Movimientos
Análisis cualitativo de sistemas no lineales
 Análisis cualitativo de sistemas no lineales Ecuaciones Diferenciales Ordinarias Andrés Iturriaga J. Departamento de Ingeniería Matemática Universidad de Chile Primavera 2011 Andrés Iturriaga J. (DIM)
Análisis cualitativo de sistemas no lineales Ecuaciones Diferenciales Ordinarias Andrés Iturriaga J. Departamento de Ingeniería Matemática Universidad de Chile Primavera 2011 Andrés Iturriaga J. (DIM)
Energía potencial gravitatoria (largo alcance) Comparo con el caso general. Se acostumbra tomar nula a la energía potencial gravitatoria cuando r
 Energía potencial gravitatoria (largo alcance) Comparo con el caso general Se acostumbra tomar nula a la energía potencial gravitatoria cuando r 1 Propiedades de los campos de fuerzas conservativos independiente
Energía potencial gravitatoria (largo alcance) Comparo con el caso general Se acostumbra tomar nula a la energía potencial gravitatoria cuando r 1 Propiedades de los campos de fuerzas conservativos independiente
Tratamiento newtoniano de los fenómenos impulsivos: percusiones
 Tratamiento newtoniano de los fenómenos impulsivos: percusiones Índice 1. Introducción 2 2. Modelo matemático y físico de los fenómenos impulsivos 4 2.1. Preliminares matemáticos..............................
Tratamiento newtoniano de los fenómenos impulsivos: percusiones Índice 1. Introducción 2 2. Modelo matemático y físico de los fenómenos impulsivos 4 2.1. Preliminares matemáticos..............................
Funciones, límites y continuidad
 8/0/016 Funciones, límites y continuidad C U R S O 0 1 5-0 1 6 Funciones, limites y continuidad Los puntos rojos son los que entran en el eamen de º evaluación 1) Concepto de función. Dominio y recorrido.
8/0/016 Funciones, límites y continuidad C U R S O 0 1 5-0 1 6 Funciones, limites y continuidad Los puntos rojos son los que entran en el eamen de º evaluación 1) Concepto de función. Dominio y recorrido.
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase
 Matemáticas Aplicadas MA101 Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Sistemas de coeficientes
Matemáticas Aplicadas MA101 Semana 13 Análisis cualitativo de Sistemas No Lineales Retratos de Fase Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Sistemas de coeficientes
Problemas. Laboratorio. Física moderna 09/11/07 DEPARTAMENTO DE FÍSICA E QUÍMICA. Nombre:
 Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
Física moderna 9/11/7 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: 1. Un muelle de constante k =, 1 3 N/m está apoyado en una superficie horizontal sin rozamiento. A 1, m hay un bucle vertical de
Práctico 2: Mecánica lagrangeana
 Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
Mecánica Anaĺıtica Curso 2016 Práctico 2: Mecánica lagrangeana 1. La polea y la cuerda de la figura son ideales y los bloques deslizan sin roce. Obtenga las aceleraciones de los bloques a partir de las
tiene una rama infinita cuando x, f(x) o ambas al mismo tiempo crecen infinitamente. De esta manera el punto ( x, f ( x))
 Matemáticas II Curso 03-04 6. Asíntotas Se dice que una función y f ( tiene una rama infinita cuando, f( o ambas al mismo tiempo crecen infinitamente. De esta manera el punto (, f ( ) se aleja infinitamente
Matemáticas II Curso 03-04 6. Asíntotas Se dice que una función y f ( tiene una rama infinita cuando, f( o ambas al mismo tiempo crecen infinitamente. De esta manera el punto (, f ( ) se aleja infinitamente
Tema 5: Funciones. Límites de funciones
 Tema 5: Funciones. Límites de funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar
Tema 5: Funciones. Límites de funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar
El estudio del movimiento de los cuerpos generalmente se divide en dos fases, por conveniencia: la cinemática y la dinámica.
 Tema 1: Cinemática. Introducción. Describir el movimiento de objetos es una cuestión fundamental en la mecánica. Para describir el movimiento es necesario recurrir a una base de conceptos o ideas, sobre
Tema 1: Cinemática. Introducción. Describir el movimiento de objetos es una cuestión fundamental en la mecánica. Para describir el movimiento es necesario recurrir a una base de conceptos o ideas, sobre
2 = ( ) = con vértice en (0, 3) y cortes con el. Tomando la parte continua de cada una de ellas se obtiene la grafica de la función.
 Septiembre. Ejercicio B. Puntuación máima: puntos) Se considera la función real de variable real definida por: a si f ) Ln ) si > b) Represéntese gráficamente la función para el caso a. Nota: Ln denota
Septiembre. Ejercicio B. Puntuación máima: puntos) Se considera la función real de variable real definida por: a si f ) Ln ) si > b) Represéntese gráficamente la función para el caso a. Nota: Ln denota
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
TEMA 2. CINEMÁTICA OBJETIVOS
 OBJETIVOS Definir y relacionar las variables que describen el movimiento de una partícula (desplazamiento, velocidad y aceleración). Justificar la necesidad del carácter vectorial de las variables cinemáticas.
OBJETIVOS Definir y relacionar las variables que describen el movimiento de una partícula (desplazamiento, velocidad y aceleración). Justificar la necesidad del carácter vectorial de las variables cinemáticas.
CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen
 CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
CINEMÁTICA CONCEPTO DE CINEMÁTICA: es el estudio del movimiento sin atender a las causas que lo producen CONCEPTO DE MOVIMIENTO: el movimiento es el cambio de posición, de un cuerpo, con el tiempo (este
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones
 (Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
el blog de mate de aida 4º ESO: apuntes de funciones elementales pág. 1
 el blog de mate de aida 4º ESO: apuntes de funciones elementales pág. 1 FUNCIONES LINEALES 1.- FUNCIÓN CONSTANTE Una función constante es aquella en la cual el valor de la variable dependiente siempre
el blog de mate de aida 4º ESO: apuntes de funciones elementales pág. 1 FUNCIONES LINEALES 1.- FUNCIÓN CONSTANTE Una función constante es aquella en la cual el valor de la variable dependiente siempre
c) Calcular la solución general y dibujar un croquis preciso del sistema cuando µ = 4.
 Examen Final de Ecuaciones Diferenciales Fecha: 10 de enero de 2013 3 Problemas 75 puntos Tiempo total: 2 horas 30 minutos Problema 1 [25 puntos] Consideramos el sistema lineal x = Ax, donde 2µ 4 1, µ
Examen Final de Ecuaciones Diferenciales Fecha: 10 de enero de 2013 3 Problemas 75 puntos Tiempo total: 2 horas 30 minutos Problema 1 [25 puntos] Consideramos el sistema lineal x = Ax, donde 2µ 4 1, µ
UNIVERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO # 11: CINEMÁTICA -CONCEPTOS BÁSICOS-
 UNIERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO # 11: CINEMÁTICA -CONCEPTOS BÁSICOS- Diego Luis Aristizábal R., Roberto Restrepo A., Tatiana
UNIERSIDAD NACIONAL DE COLOMBIA SEDE MEDELLÍN FACULTAD DE CIENCIAS-ESCUELA DE FÍSICA FÍSICA MECÁNICA MÓDULO # 11: CINEMÁTICA -CONCEPTOS BÁSICOS- Diego Luis Aristizábal R., Roberto Restrepo A., Tatiana
TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL
 Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos
 página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
página 1/12 Problemas Tema 1 Solución a problemas de Repaso de Matemáticas I - Hoja 26 - Todos resueltos Hoja 26. Problema 1 1. a) Calcula el número real m que cumple lim 0 ln(1+m ) sen(2 ) =. b) Obtener
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
UNIDAD II Ecuaciones diferenciales con variables separables
 UNIDAD II Ecuaciones diferenciales con variables separables UNIDAD ECUACIONES DIFERENCIALES CON VARIABLES SEPARABLES Ecuaciones diferenciales de primer orden y de primer grado. Una ecuación diferencial
UNIDAD II Ecuaciones diferenciales con variables separables UNIDAD ECUACIONES DIFERENCIALES CON VARIABLES SEPARABLES Ecuaciones diferenciales de primer orden y de primer grado. Una ecuación diferencial
FUNCIONES ELEMENTALES
 FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS.- Son aquellas cuya expresión algebraica es un polinomio. El grado del polinomio es el grado de la función polinómica. Ejemplos.- f ( x) = 3 g ( x) = x + 1 h
FUNCIONES ELEMENTALES FUNCIONES POLINÓMICAS.- Son aquellas cuya expresión algebraica es un polinomio. El grado del polinomio es el grado de la función polinómica. Ejemplos.- f ( x) = 3 g ( x) = x + 1 h
MATEMÁTICAS ESPECIALES II PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden.
 MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
MATEMÁTICAS ESPECIALES II - 8 PRÁCTICA 5 Parte I - Sistemas de ecuaciones diferenciales de primer orden. Considere el sistema de ecuaciones diferenciales ordinarias (EDOs) de primer orden dx dt = f (t,
MOVIMIENTO ARMÓNICO SIMPLE
 MOVIMIENTO ARMÓNICO SIMPLE Estudio del movimiento armónico simple. Desde el punto de vista dinámico, es el movimiento de una partícula que se mueve sobre una recta, sometida a la acción de una fuerza atractiva
MOVIMIENTO ARMÓNICO SIMPLE Estudio del movimiento armónico simple. Desde el punto de vista dinámico, es el movimiento de una partícula que se mueve sobre una recta, sometida a la acción de una fuerza atractiva
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES El estudio de la derivada de una función, junto con otras consideraciones sobre las funciones tales como el estudio de su campo de eistencia (dominio), de sus puntos de corte
REPRESENTACIÓN DE FUNCIONES El estudio de la derivada de una función, junto con otras consideraciones sobre las funciones tales como el estudio de su campo de eistencia (dominio), de sus puntos de corte
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 003 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva, Ejercicio 1, Opción A
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 003 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva, Ejercicio 1, Opción A
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
Boletín II. Cálculo diferencial de funciones de una variable
 CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. (NUEVO) Utiliza la definición de derivada para demostrar que f () = 10 para 5 2. ( ) sin() 2. Sea arctan. Calcula
CÁLCULO Boletín II. Cálculo diferencial de funciones de una variable Ejercicios básicos 1. (NUEVO) Utiliza la definición de derivada para demostrar que f () = 10 para 5 2. ( ) sin() 2. Sea arctan. Calcula
Universidad Carlos III de Madrid
 Ejercicio 3 4 5 6 7 8 total Puntos Universidad Carlos III de Madrid Departamento de Economía Eamen final de Matemáticas I 0 de septiembre de 007 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO : Dada
Ejercicio 3 4 5 6 7 8 total Puntos Universidad Carlos III de Madrid Departamento de Economía Eamen final de Matemáticas I 0 de septiembre de 007 APELLIDOS: NOMBRE: DNI: Titulación: Grupo: MODELO : Dada
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Unidad 6 Funciones algebraicas PÁGINA 102
 Unidad 6 Funciones algebraicas PÁGINA 10 SOLUCIONES Evaluar polinomios. a) b) c) d) Raíces de un polinomio. Usando el teorema del factor: Resolver ecuaciones de segundo grado. a) b) c) PÁGINA 104 SOLUCIONES
Unidad 6 Funciones algebraicas PÁGINA 10 SOLUCIONES Evaluar polinomios. a) b) c) d) Raíces de un polinomio. Usando el teorema del factor: Resolver ecuaciones de segundo grado. a) b) c) PÁGINA 104 SOLUCIONES
Matemáticas para estudiantes de Química
 Matemáticas para estudiantes de Química PROYECTO EDITORIAL BIBLIOTECA DE QUÍMICAS Director: Carlos Seoane Prado Catedrático de Química Orgánica Universidad Complutense de Madrid Matemáticas para estudiantes
Matemáticas para estudiantes de Química PROYECTO EDITORIAL BIBLIOTECA DE QUÍMICAS Director: Carlos Seoane Prado Catedrático de Química Orgánica Universidad Complutense de Madrid Matemáticas para estudiantes
