CUESTIONES RESUELTAS 3. INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA
|
|
|
- Hugo Alvarado Ávila
- hace 5 años
- Vistas:
Transcripción
1 CUESTIONES RESUELTAS INTEGRACIÓN FUNDAMENTOS DE MATEMÁTICAS º GRADO GESTIÓN AERONAÚTICA INTEGRAL DEFINIDA REGLA DE BARROW Sea f() una función discontinua en = y continua en el resto de puntos del intervalo [-,] Entonces f() es integrable en [-,] y tiene primitiva en dicho intervalo a Falso, la función f ( ) = verifica las condiciones del enunciado, no es integrable en [-,] y no tiene primitivas en este intervalo b Es cierto que la función es integrable en [-,] ya que cumple la condición suficiente de integrabilidad en el intervalo, n embargo no tiene primitiva en [-,] ya que no es continua en = c Verdadero, f() es integrable en [-,] ya que cumple la condición suficiente de integrabilidad, y una de sus primitivas es su función integral en dicho intervalo Sea f( ) una función continua en el intervalo [-,] tal que f ( ) d = Entonces, se verifica que la función g()= f() es integrable en [-,] y además g( ) d = a Verdadero, ya que g() es continua (y, por tanto, integrable) en [-,], al ser compoción de funciones continuas pues g()=h(f()) donde h()= Además, aplicando las propiedades de las funciones integrables, resulta que g( ) d = f ( ) d = f ( ) d = b Es falso, ya que aunque g() es integrable en [-,], no es cierto que g( ) d = como lo demuestra la función f()= para la cual d = y, n embargo d = ( ) d d + = + = c Falso, pues bajo las hipótes del enunciado no podemos garantizar la integrabilidad de la función g() en el intervalo [-,] Sean las funciones f() y F() definidas por + < f ( ) = ; F( ) = 6 6 Entonces, F() es una primitiva de f() en [,] < a Falso, pues F() no es la función integral de f() en el intervalo [,] ya que F()= b Verdadero, pues f es continua, F() es su función integral en [,] y por tanto por el Teorema Fundamental del Cálculo F() es una de sus primitivas en [,] c Verdadero, pues F() es continua y derivable en [,] y F ()=f() en dicho intervalo d Falso, pues F() no es continua en [,] ( + ) La función F ( ) = Ln + Ln es una función primitiva de [,] 6 f ( ) = en el intervalo
2 a Falso, F no puede ser la primitiva de f en [,] porque F no es continua b Verdadero, pues F() es derivable en el intervalo [,] y además se verifica que F '( ) = f ( ) en el intervalo [,] c Falso, pues f() no está acotada en = y en consecuencia no puede ser integrable en el intervalo [,] ni tener una primitiva en dicho intervalo e Sea f( ) = entonces ( ) ln( ) < e f d = (a) Falso, dado que la integral representa el área de una región del plano y no puede ser negativa (b) Verdadero, f es continua en el intervalo [,e], F( ) = es una función ( ln( )) < e primitiva de f en [,e] y aplicando la regla de Barrow, se tiene que e f ( ) d = F ( e ) F () = e e (c) Verdadero, pues ( ) d = y ( ln( )) d = [ ln + ] = = = (d) Falso, la función f no es integrable por no ser continua 6 La función f ( ) = < es integrable en el intervalo [-,] + a Verdadero, pues como f ( ) para todo [,] entonces f es acotada en [-,] y toda función acotada es integrable b Falso, ya que f no es continua en el intervalo [-,] c Verdadero, dado que f es una función acotada y discontinua en =- y =, por tanto en un número finito de puntos de [-,], luego es integrable 7 Sean las funciones f() y F() definidas por < < f ( ) = ; F( ) = + Entonces, F() es la función integral de f() en el intervalo [-,] y F() es una primitiva de f() en dicho intervalo a Falso, pues f() no es continua y, por tanto, no es integrable en [-,] por lo que no eiste su función integral También es falso que F() sea primitiva de f() en [-,] ya que F ( ) b Verdadero, pues f es continua, F() es su función integral en [-,] y por tanto por el Teorema Fundamental del Cálculo F() es una de sus primitivas en [-,] c Falso F() no es la función integral de f() pues F(-)=-/ Tampoco es una primitiva de f() en [-,], ya que F() no es derivable en = e + 8 Sea f ( ) = se verifica que: + < a f () es integrable en el intervalo [, ] ya que es continua en dicho intervalo e + + b F( ) = es la función integral de f () en el intervalo [, ] + + < c La función (), ya que no es continua en = f no tiene primitiva en [ ]
3 9 Sean las funciones f() y F () definidas por: f ( ) = + < Entonces se verifica: F ( ) = + < a no tiene primitiva en el intervalo [,] b F () es una primitiva de f () puesto que f () es integrable en [,] F '( ) = f ( ) para todo [,] c f () es integrable en el intervalo [,] que es la función CÁLCULO DE PRIMITIVAS Sea la función 6 G ( ) = + 6 < f ( ) = e se verifica que: = C f ( ) d = e C a F ( ) = e + 7 es una primitiva de f () ya que F '( ) = f ( ) b f ( ) d e + c + y se verifica que por lo que eiste función integral en dicho intervalo La función F ( ) = ln es una función primitiva de f ( ) = en el intervalo [,] + (a) Falso, pues como F()=ln(-)-ln(+) entonces F () f() (b) Falso, F no puede ser la primitiva de f en [,] porque F no es derivable en [,] pues no es continua en dicho intervalo (c) Verdadero, pues la integral indefinida de f es Dada la integral f ( ) d = d = d = + = ln( ) ln( + ) + C = ln + C + sen cos d se verifica que sen sen sen cos d = + C (a) Verdadero, pues efectuando el cambio de variable t = sen( ) se verifica que dt = cos( ) d y por dt tanto despejando d se tiene que d = por lo que cos( ) t t sen sen sen cos d = t ( t ) dt = ( t t ) dt = + C = + C (b) Falso, pues la función f ( ) = sen cos no tiene primitivas ya que se trata de una función no integrable (c) Falso, pues aplicando el método de descompoción por partes, tomamos por cos u = sen cos y por dv = cos d se obtiene que du = d y v=sen() por tanto sen cos sen cos d = ( sen cos )( sen) sen d = sen = ( sen cos ) cos d = ( sen cos ) sen + C sen sen + C
4 sen ( ) Se verifica que cos d = sen( ) + C, sen ( ) sen (a) Falso, ya que sen( ) + = + cos( ) = sen + cos cos (b) Falso, pues cos ( ) no tiene primitivas (c) Verdadero, pues efectuando el cambio de variable t = sen( ), dt = cos( ) d y teniendo en cuenta que sen + cos = entonces t sen ( ) cos d = ( t )( dt) = t + C = sen( ) + C INTEGRALES IMPROPIAS Dada la función f( ) =, entonces se verifica que f ( ) d es convergente (a) Verdadero, puesto que d = β (, ), y por tanto es convergente (b) Falso, ya que = y como ( )d es convergente y d es divergente, entonces resulta que la integral de la suma es divergente (c) Falso, la función F( ) = ln( ) es una primitiva de f en (,], y como entonces la integral dada es divergente (d) Verdadero, pues para todo (,] se verifica que, y como la integral ( ) d es convergente, por el criterio de comparación se tiene que d es convergente Sea f() una función continua en [, ) tal que para todo se cumple: < f( ) Entonces podemos asegurar que la integral e I = d es divergente f( ) e e (a) Verdadero, pues como entonces, eiste, lim y por tanto distinto de cero; f( ) f( ) por ello la integral es divergente e (b) Falso, pues f( ) = entonces d = e d =Γ () = f( ) (c) Verdadero, pues f( ) = e entonces e d = d f( ) y esta integral es divergente 6 Sea f() una función acotada e integrable en [,b] para todo b tal que lim f ( ) = Entonces f ( ) d es convergente (a) Verdadero, pues se cumple la condición necesaria de convergencia (b) Falso, pues f ( ) = verifica las hipótes del enunciado y n embargo no es convergente (c) Falso, pues f ( ) = verifica las hipótes del enunciado y n embargo no es convergente (d) Falso, aunque sería cierto lim F( b) < endo F() una primitiva de f() en [,b] para todo b b e
5 7 La integral = I = d a Verdadero, pues como lim =, entonces I es convergente b Verdadero, pues I = d = = = + = c Falso, f ( ) = no es una función acotada en [-,], al no estar definida en = (= es una asíntota vertical de f()) Así, I es una integral impropia que puede escribirse como = I d + d y como estas dos integrales son divergentes, I también es divergente 8 La integral I = e d es convergente a Verdadero, pues F ( + ) lim F ( ) = lim = lim = e e b Verdadero, pues I = Γ( ) =! = ( ) = ( + ) e es una primitiva de f ( ) = e en, ) ( y c Falso, ya que lim e = y, por tanto, no cumple la condición necesaria de convergencia APLICACIONES CÁLCULO DE AREAS 9 Determinar qué integral o integrales definidas habría que calcular para obtener el área limitada por las curvas y=, = e y=/ tal y como se muestra en la guiente figura: (a) d + d
6 (b) + (c) y ( ) dy ( y) dy y y ( ) dy + d Determinar qué integral o integrales definidas habría que calcular para obtener el área limitada por las curvas y =, y = +, = - y = / tal y como se muestra en la guiente figura: / (a) ( + ) d (b) ( y y) dy / ( ( y) dy (c) + ) d + ( y ( )) dy + / Sea el área limitada por las curvas y = 9, y = 6, =, y = continuación: tal y como se muestra a
7 Determina qué integrales definidas habría que calcular para obtener el área sombreada y delimitada por estas curvas: ( 9 (6 )) + (9 a d d 9 b 9 ( 9 ) d (6 ) d c ( 9 ) d (6 ) d 9 )
CUESTIONES RESUELTAS 2. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA CURSO
 CUESTIONES RESUELTAS. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. º GRADO GESTIÓN AERONAÚTICA CURSO 0-0. CONCEPTOS DE DOMINIO, RECORRIDO Y GRÁFICA e. Sea f() definida por: f ( ) Entonces
CUESTIONES RESUELTAS. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. º GRADO GESTIÓN AERONAÚTICA CURSO 0-0. CONCEPTOS DE DOMINIO, RECORRIDO Y GRÁFICA e. Sea f() definida por: f ( ) Entonces
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA
 EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA. Calcular las siguientes integrales definidas: b) d e d c) + d d) d e) sen d f) + d d ( ) En primer lugar se ha calculado una primitiva de f() Barrow. y después
EJERCICIOS RESUELTOS DE INTEGRAL DEFINIDA. Calcular las siguientes integrales definidas: b) d e d c) + d d) d e) sen d f) + d d ( ) En primer lugar se ha calculado una primitiva de f() Barrow. y después
( ) ( ) ( ) f h f h h h h. h 0 h h 0 h h 0 h h 0. f h f h h h h
 Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
Eamen de cálculo diferencial e integral /4/9 Opción A Ejercicio. (Puntuación máima: puntos) Sea la función f ( ) = 4 a. Estudiar su continuidad y derivabilidad. b. Dibujar su gráfica. c. Calcular el área
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA APELLIDOS:
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
RESUMEN DE ANÁLISIS MATEMÁTICAS II
 RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
RESUMEN DE ANÁLISIS MATEMÁTICAS II 1. DOMINIO DE DEFINICIÓN Y CONTINUIDAD 1.1. FUNCIONES ELEMENTALES (No tienen puntos angulosos) Tipo de función f (x) Dom (f) Continuidad Polinómicas P(x) R Racional P(x)/Q(x)
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
ANÁLISIS DE FUNCIONES
 ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
ANÁLISIS MATEMÁTICO I TEMA V : INTEGRALES Hoja 1. A) Calcular las siguientes integrales definidas aplicando la Regla de Barrow: 4x dx 3) I= π 0
 ANÁLISIS MATEMÁTICO I TEMA V : INTEGRALES Hoja A) Calcular las siguientes integrales definidas aplicando la Regla de Barrow: ) I= ( + ) ) I= / 4 π 0 cos 4) I= e ( + ) 6) I= 4 0 ( y) / dy B) Hallar el valor
ANÁLISIS MATEMÁTICO I TEMA V : INTEGRALES Hoja A) Calcular las siguientes integrales definidas aplicando la Regla de Barrow: ) I= ( + ) ) I= / 4 π 0 cos 4) I= e ( + ) 6) I= 4 0 ( y) / dy B) Hallar el valor
Nombre y Apellidos: si x 0 f(x) = e x 1 1 si x = 0
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Diciembre 2 de Diciembre de 25 Nombre y Apellidos: DNI: (2.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Diciembre 2 de Diciembre de 25 Nombre y Apellidos: DNI: (2.5 p.) ) Se considera la función f : R R definida
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
Unidad 15 Integrales definidas. Aplicaciones 3 SOLUCIONES 1. La suma superior es: La suma inferior es:. La suma superior es: s ( P) = ( 1) 3 + (3 ) 10 = 3 + 10 = 13 La suma inferior es: s ( P) = ( 1) 1+
1. INTEGRALES DEFINIDAS E IMPROPIAS
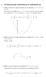 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráca de y = con el eje OX son los valores de tales que =, esto es, = y =. El
Unidad 5 - Trabajo Práctico 5 Parte 1 Elementos de Matemática
 06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
OPCIÓN A. MATEMÁTICAS 2º BACHILLERATO B Lo que te llevará al final, serán tus pasos, no el camino. Fito y los Fitipaldis
 MATEMÁTICAS º BACHILLERATO B 9--4 Lo que te llevará al final, serán tus pasos, no el camino Análisis Fito y los Fitipaldis OPCIÓN A.- a) Hallar las dimensiones que hacen mínimo el coste de un contenedor
MATEMÁTICAS º BACHILLERATO B 9--4 Lo que te llevará al final, serán tus pasos, no el camino Análisis Fito y los Fitipaldis OPCIÓN A.- a) Hallar las dimensiones que hacen mínimo el coste de un contenedor
INTEGRACIÓN DE FUNCIONES REALES DE UNA VARIABLE REAL RESUMEN
 INTEGRACIÓN DE FUNCIONES REALES DE UNA VARIABLE REAL RESUMEN 1.- INTRODUCCIÓN. 1.1 Definición de Primitiva F es función primitiva de f Para todo elemento del Dom(f) F (x)=f(x) 1.2 Representación de Primitivas
INTEGRACIÓN DE FUNCIONES REALES DE UNA VARIABLE REAL RESUMEN 1.- INTRODUCCIÓN. 1.1 Definición de Primitiva F es función primitiva de f Para todo elemento del Dom(f) F (x)=f(x) 1.2 Representación de Primitivas
Nombre y Apellidos: x e 1 x 1 x f(x) = ln(x) x
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
ln x dx = x ln x 2x ln x + 2x = (e 2e + 2e) 2 = (e 2) u
 Tema: Integrales definidas. Áreas Ejercicios PAU - JUNIO GENERAL Ejercicio.- Calcule d + Sea F() = d = + = + d d ln ln + = ln ln ln 5 + ln = A B + = + + = A( + ) + B = = A = = B A =, B = d = ln ln ln 5
Tema: Integrales definidas. Áreas Ejercicios PAU - JUNIO GENERAL Ejercicio.- Calcule d + Sea F() = d = + = + d d ln ln + = ln ln ln 5 + ln = A B + = + + = A( + ) + B = = A = = B A =, B = d = ln ln ln 5
Unidad 9 Integrales indefinidas
 Unidad 9 Integrales indefinidas PÁGINA SOLUCIONES. La solución es: a) F ( ) + 8; F( ), 5 b) F() cos ; F( ) cos + c) F ( ) e + ; F( ) e d) F ( ) ln( + ) + 5; F( ) ln( + ). La solución en cada caso: a) F
Unidad 9 Integrales indefinidas PÁGINA SOLUCIONES. La solución es: a) F ( ) + 8; F( ), 5 b) F() cos ; F( ) cos + c) F ( ) e + ; F( ) e d) F ( ) ln( + ) + 5; F( ) ln( + ). La solución en cada caso: a) F
Nombre y Apellidos: x (1 + ln(x)) si x > 0 f(x) = 0 si x = 0.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre de Septiembre de 008 Nombre y Apellidos: DNI: (6.5 p.) ) Se considera la función f : [0,
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL Septiembre de 00 APELLIDOS: NOMBRE: DNI CUESTIONARIO DE RESPUESTA MÚLTIPLE (50%) (Cada respuesta incorrecta
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL Septiembre de 00 APELLIDOS: NOMBRE: DNI CUESTIONARIO DE RESPUESTA MÚLTIPLE (50%) (Cada respuesta incorrecta
EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A
 Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
PROBLEMAS DE INTEGRALES INDEFINIDAS
 PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
PROBLEMAS DE INTEGRALES INDEFINIDAS Integración por partes. Mediante la integración por partes, hallar una primitiva de la función y = Ln (1 + x) Calcular una primitiva de una función, es hallar su
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Unidad 10 Integrales definidas. Aplicaciones
 Unidad Integrales definidas. Aplicaciones PÁGINA 5 SOLUCIONES. Las áreas quedan: A u A u A 5 u. El área del recinto viene dada por : ( ) ( ) Área d,5 u PÁGINA 9 SOLUCIONES. La solución queda: Directo:
Unidad Integrales definidas. Aplicaciones PÁGINA 5 SOLUCIONES. Las áreas quedan: A u A u A 5 u. El área del recinto viene dada por : ( ) ( ) Área d,5 u PÁGINA 9 SOLUCIONES. La solución queda: Directo:
Unidad 15 Integrales definidas. Aplicaciones
 Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
Unidad 15 Integrales definidas. Aplicaciones PÁGINA 363 SOLUCIONES 1. La solución: Lo que nos pide el problema es hallar el área del recinto rayado. Este recinto es un trapecio y su area es:. Queda: x
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Para saber si tiene asíntotas horizontales hacemos los límites en los infinitos.
 1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
1.- Considerad las funciones: f(x) = x + 2 2x x + 2 g(x) = 2 x + 2 a) Determinar el dominio de la función f(x) y calcular sus asíntotas (horizontales, verticales y oblicuas) en caso de que existan. b)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua.
 Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
Apellidos: Nombre: Curso: 2º Grupo: Día: CURSO
 EXAMEN DE MATEMATICAS II ª ENSAYO (ANÁLISIS) Apellidos: Nombre: Curso: º Grupo: Día: CURSO 56 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios
EXAMEN DE MATEMATICAS II ª ENSAYO (ANÁLISIS) Apellidos: Nombre: Curso: º Grupo: Día: CURSO 56 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios
a) p = ½. b) p = 0. c) Ninguna de las anteriores. Solución: Para que sea continua en x = 0 debe cumplirse que lím
 Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
Soluciones de la relación de ejercicios del TEMA 4
 Soluciones de la relación de ejercicios del TEMA. Aplica el Teorema Fundamental del Cálculo Integral, para resolver: (a) d ( +t dt) d Sean f,g,h :, definidas por h() = +t dt, f(t) = +t y g() =. Como f
Soluciones de la relación de ejercicios del TEMA. Aplica el Teorema Fundamental del Cálculo Integral, para resolver: (a) d ( +t dt) d Sean f,g,h :, definidas por h() = +t dt, f(t) = +t y g() =. Como f
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:...CURSO:...
 EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: 4 5 NOTA Condición mínima de aprobación (4 puntos): 5% del eamen correctamente
EXÁMENES PARCIALES Y FINALES DE ANÁLISIS MATEMÁTICO I ANÁLISIS MATEMÁTICO I ANUAL - Primer Parcial TURNO MAÑANA APELLIDO NOMBRE:CURSO: 4 5 NOTA Condición mínima de aprobación (4 puntos): 5% del eamen correctamente
S E) 10 S B) S D) S C) o D) o 1 B) , x 2x 1. , D) x, 1, 5 MATEMÁTICAS VI (AREAS 3 Y 4) VERSIÓN 31
 MATEMÁTICAS VI (AREAS Y ). Una suma de $ se deposita en una casa de bolsa con una tasa de interés compuesto anual de % En cuánto se convertirá esta suma al inal del quinto año?.. Encuentra la suma de la
MATEMÁTICAS VI (AREAS Y ). Una suma de $ se deposita en una casa de bolsa con una tasa de interés compuesto anual de % En cuánto se convertirá esta suma al inal del quinto año?.. Encuentra la suma de la
La integral indefinida
 Apuntes Matemáticas º de bachillerato Leibniz Tema 7 La integral indefinida Matemáticas º de bachillerato 7. Introducción Def.: Dadas dos funciones, F() y f(), si se verifica que: F () f(), para un cierto
Apuntes Matemáticas º de bachillerato Leibniz Tema 7 La integral indefinida Matemáticas º de bachillerato 7. Introducción Def.: Dadas dos funciones, F() y f(), si se verifica que: F () f(), para un cierto
Evidentemente, la superficie es un triángulo rectángulo de base 1 y altura también la unidad, por tanto su área es 1/2.
 LA INTEGRAL DEFINIDA En los dos temas anteriores se ha hecho el estudio de las primitivas de una función, descubriendo distintos procedimientos para el cálculo de primitivas, es decir, se han encontrado
LA INTEGRAL DEFINIDA En los dos temas anteriores se ha hecho el estudio de las primitivas de una función, descubriendo distintos procedimientos para el cálculo de primitivas, es decir, se han encontrado
Análisis Matemático I (Lic. en Cs. Biológicas)
 Análisis Matemático I (Lic. en Cs. Biológicas) Segundo cuatrimestre 7 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g () = (ii) g () = (iii) g () = sen (iv)
Análisis Matemático I (Lic. en Cs. Biológicas) Segundo cuatrimestre 7 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g () = (ii) g () = (iii) g () = sen (iv)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2001 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Opción A. teorema se puede aplicar también si sale /, y cuando x. Como. , la recta x = 0 es una A.V. de la función f.
 Opción A 1 Ejercicio 1. [ 5 puntos] Sea f la función definida, para 0, por f e. Determina las asíntotas de la gráfica de f. La recta = a es una asíntota vertical (A.V.) de la función f si lim f Veamos
Opción A 1 Ejercicio 1. [ 5 puntos] Sea f la función definida, para 0, por f e. Determina las asíntotas de la gráfica de f. La recta = a es una asíntota vertical (A.V.) de la función f si lim f Veamos
Soluciones del Segundo Parcial 22 de diciembre de 2015
 Grado M+I Curso 2015-2016 Apellidos: Nombre: Cálculo I Soluciones del Segundo Parcial 22 de diciembre de 2015 Matemática Aplicada ETSIINF-UPM Nota: /10 Parte 1. Teoría (2 puntos). 1. Enuncia el teorema
Grado M+I Curso 2015-2016 Apellidos: Nombre: Cálculo I Soluciones del Segundo Parcial 22 de diciembre de 2015 Matemática Aplicada ETSIINF-UPM Nota: /10 Parte 1. Teoría (2 puntos). 1. Enuncia el teorema
Selectividad hasta el año incluido = 0. Página 1 de 13 ANÁLISIS
 ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
ANÁLISIS Selectividad hasta el año 9- incluido Ejercicio. Calificación máima: puntos. (Junio 99 A) Hallar la longitud de los lados del triángulo isósceles de área máima cuyo perímetro sea 6 m. Ejercicio.
lim x sen(x) Apellidos: Nombre: Curso: 2º Grupo: A Día: 23-II-2015 CURSO Instrucciones:
 EXAMEN DE MATEMATICAS II ª EVALUACIÓN Apellidos: Nombre: Curso: º Grupo: A Día: II5 CURSO 5 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª EVALUACIÓN Apellidos: Nombre: Curso: º Grupo: A Día: II5 CURSO 5 Instrucciones: a) Duración: HORA y MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
ejerciciosyexamenes.com
 ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad
 PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
PRIMITIVAS E INTEGRAL DEFINIDA Ejercicios de selectividad Sea f : R R la función definida por f() = e /. (a) En qué punto de la gráfica de f la recta tangente a ésta pasa por el origen de coordenadas?
EJERCICIOS DE ANÁLISIS PRIMERA EVALUACIÓN - MATEMÁTICAS II 2 BACH A Soluciones en Ejercicios resueltos de la PAU
 EJERCICIOS DE ANÁLISIS PRIMERA EVALUACIÓN - MATEMÁTICAS II 2 BACH A Soluciones en Ejercicios resueltos de la PAU Problema 1 (2 puntos) De una función derivable f (x) se conoce que pasa por el punto A(-1,
EJERCICIOS DE ANÁLISIS PRIMERA EVALUACIÓN - MATEMÁTICAS II 2 BACH A Soluciones en Ejercicios resueltos de la PAU Problema 1 (2 puntos) De una función derivable f (x) se conoce que pasa por el punto A(-1,
a) Se trata de integrar una función racional cuyo denominador tiene raíces reales simples. Por tanto, se descompone en fracciones simples:
 . a.sen() e Sabiendo que lim es finito, calcula el valor de a y el de dicho límite. lim L'Hôpital a.sen() e a.cos (e e ) lim L'Hôpital a. sen e (e e ) a. sen e e lim lim L'Hôpital El parámetro a puede
. a.sen() e Sabiendo que lim es finito, calcula el valor de a y el de dicho límite. lim L'Hôpital a.sen() e a.cos (e e ) lim L'Hôpital a. sen e (e e ) a. sen e e lim lim L'Hôpital El parámetro a puede
, se denomina primitiva de esta función a otra F(x)
 1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx
![INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx](/thumbs/56/39119384.jpg) INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
EJERCICIOS UNIDADES 3 y 4: INTEGRACIÓN DE FUNCIONES
 IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES a. (6-M-A-) (.5 puntos) Calcula el valor de a > para el que se verifica d. +. (6-M-B-) (.5 puntos) Considera la función : R R f
IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES a. (6-M-A-) (.5 puntos) Calcula el valor de a > para el que se verifica d. +. (6-M-B-) (.5 puntos) Considera la función : R R f
(Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS
 (Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS En integración se pide que la función sea continua en el intervalo considerado que además éste sea finito. En este tema se pretende
(Apuntes en revisión para orientar el aprendizaje) INTEGRALES IMPROPIAS En integración se pide que la función sea continua en el intervalo considerado que además éste sea finito. En este tema se pretende
Límites. Regla de L'Hôpital
 Matemáticas II Ejercicios resueltos de los eámenes de Selectividad propuestos en Castilla-La Mancha Límites. Regla de L'Hôpital. Calcular tg 8 sec + (Septiembre 999) tg 8 sec + da lugar a una indeterminación
Matemáticas II Ejercicios resueltos de los eámenes de Selectividad propuestos en Castilla-La Mancha Límites. Regla de L'Hôpital. Calcular tg 8 sec + (Septiembre 999) tg 8 sec + da lugar a una indeterminación
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
a) Calcular las asíntotas, el máximo y el mínimo absolutos de f (x). 4. (SEP 04) Sabiendo que una función f (x) tiene como derivada
 Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Cálculo Integral LA INTEGRAL DEFINIDA DE RIEMANN: UNA APROXIMACIÓN CON DERIVE.
 Cálculo Integral 85 6. CÁLCULO INTEGRAL. 6.. LA INTEGRAL DEFINIDA DE RIEMANN: UNA APROXIMACIÓN CON DERIVE. La integral definida de Riemann surge a partir del problema del cálculo de áreas de superficies
Cálculo Integral 85 6. CÁLCULO INTEGRAL. 6.. LA INTEGRAL DEFINIDA DE RIEMANN: UNA APROXIMACIÓN CON DERIVE. La integral definida de Riemann surge a partir del problema del cálculo de áreas de superficies
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
Convocatoria de Septiembre 9 de Septiembre de Nombre y Apellidos: (6 p.) 1) Se considera la función f : R R definida por
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre 9 de Septiembre de 26 Nombre y Apellidos: DNI: (6 p. Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Convocatoria de Septiembre 9 de Septiembre de 26 Nombre y Apellidos: DNI: (6 p. Se considera la función f : R R definida
Análisis Matemático I (Lic. en Cs. Biológicas) Práctica 6: Integración. Primer cuatrimestre de (e) f(x) = cos x. F(x) = arccosx. Ejercicio 1.
 Análisis Matemático I (Lic. en Cs. Biológicas) Primer cuatrimestre de 29 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g () = 2 (ii) g () = (iii) g () = sen
Análisis Matemático I (Lic. en Cs. Biológicas) Primer cuatrimestre de 29 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g () = 2 (ii) g () = (iii) g () = sen
TERCER EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
MATEMÁTICAS II G. I. T. I.) TERCER EXAMEN 4 EJERCICIOS RESUELTOS EJERCICIO. ) Dibuja la región limitada por la circunferencia de ecuación r = r θ) = senθ) y la lemniscata de ecuación r = r θ) = cosθ).
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES
 INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
INTEGRAL INDEFINIDA E INTEGRAL DEFINIDA. APLICACIONES. a) Eplicar el concepto de función primitiva. b) Sea f () = e + 8, justificar si es primitiva de alguna de las siguientes funciones: g () = e + 8 h
U de Talca. Funciones y series de potencias Introducción. Temas Métodos para determinar series de potencias de nuevas funciones.
 Sesión 28 Funciones y series de potencias Temas Métodos para determinar series de potencias de nuevas funciones. 28. Introducción Colin Maclaurin Escocés. (698-6. Capacidades Conocer y aplicar el método
Sesión 28 Funciones y series de potencias Temas Métodos para determinar series de potencias de nuevas funciones. 28. Introducción Colin Maclaurin Escocés. (698-6. Capacidades Conocer y aplicar el método
Matemáticas II TEMA 11 La integral definida Problemas Propuestos
 Análisis Integral Indefinida Matemáticas II TEMA La integral definida Problemas Propuestos Integrales definidas Halla el valor de: a) d b) 7 c) d 5 d d) e d Calcula la integral e ln( ) d Utilizando el
Análisis Integral Indefinida Matemáticas II TEMA La integral definida Problemas Propuestos Integrales definidas Halla el valor de: a) d b) 7 c) d 5 d d) e d Calcula la integral e ln( ) d Utilizando el
Análisis Matemático 1 para estudiantes de Ingeniería
 Alejandro E. García Venturini - Mónica Scardigli Análisis Matemático 1 para estudiantes de Ingeniería EDICIONES COOPERATIVAS , INDICE 505 NOCIONES PREVIAS... 7 Los conjuntos numéricos... 9 Conjuntos de
Alejandro E. García Venturini - Mónica Scardigli Análisis Matemático 1 para estudiantes de Ingeniería EDICIONES COOPERATIVAS , INDICE 505 NOCIONES PREVIAS... 7 Los conjuntos numéricos... 9 Conjuntos de
PROBLEMAS DE CÁLCULO I
 INGENIERÍAS TÉCNICAS INDUSTRIALES PROBLEMAS DE CÁLCULO I UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas ING. TEC. IND. MECANICA, ELECTRICIDAD Y ELECTRÓNICA 24
INGENIERÍAS TÉCNICAS INDUSTRIALES PROBLEMAS DE CÁLCULO I UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica Superior Departamento de Matemáticas ING. TEC. IND. MECANICA, ELECTRICIDAD Y ELECTRÓNICA 24
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1600) I. RELACIONES Y FUNCIONES
 INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
Matemáticas II. * Análisis III: Integrales * o) x x. p) 3. q) 5. r) 1. s) e 2x 3 dx. t) 5 dx. u) x2 5 x 4. v) x3 3x 2 x 1. z) 3
 I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Análisis III: Integrales *. Integrales inmediatas (o casi inmediatas): a) 4 2 5 7 b) 3 3 5 2 +3 +4 c) 2 7 d) 5 e) sen f) sen +7cos g) tg 2 h)
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las opciones
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2013 MATEMÁTICAS II. CÓDIGO 158 OBSERVACIONES IMPORTANTES: El alumno deberá responder a todas las cuestiones de una de las opciones
U.P.N.A. SELECTIVIDAD MATEMÁTICAS II JUNIO 2000
 U.P.N.A. SELECTIVIDAD MATEMÁTICAS II JUNIO 000 Grupo Opción c) c) Calcula y epresa lo más simplificadamente posible la derivada de las siguientes funciones: + tag ( ) e ( puntos) c) Utilizando el cambio
U.P.N.A. SELECTIVIDAD MATEMÁTICAS II JUNIO 000 Grupo Opción c) c) Calcula y epresa lo más simplificadamente posible la derivada de las siguientes funciones: + tag ( ) e ( puntos) c) Utilizando el cambio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
( ) ( ) ( ) ( ) ( ) Opción A ( ) ( ) ( ) ( ) Examen. 2ª evaluación 4/03/2008. Obtener el valor del siguiente límite: a b entonces la función
 Eamen. ª evaluación 4//8 Oción A Ejercicio. (Puntuación máima: untos) Obtener el valor del siguiente límite: lim ( + ) t ln 4t dt 5 Alicación del teorema fundamental del cálculo integral: Si f ( ) es continua
Eamen. ª evaluación 4//8 Oción A Ejercicio. (Puntuación máima: untos) Obtener el valor del siguiente límite: lim ( + ) t ln 4t dt 5 Alicación del teorema fundamental del cálculo integral: Si f ( ) es continua
Análisis Matemático I (Lic. en Cs. Biológicas)
 Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Problemas Tema 2 Enunciados de problemas de Límite y Continuidad
 página /2 Problemas Tema 2 Enunciados de problemas de Límite y Continuidad Hoja. Estudiar la continuidad y derivabilidad de la función f ()=. solución: continua en toda la recta real. Punto anguloso en
página /2 Problemas Tema 2 Enunciados de problemas de Límite y Continuidad Hoja. Estudiar la continuidad y derivabilidad de la función f ()=. solución: continua en toda la recta real. Punto anguloso en
Apéndice 10: Integral de Riemann
 Apéndice : Integral de Riemann. Otras aplicaciones geométricas.. Volúmenes mediante secciones planas transversales Supongamos que tenemos un sólido del que se conoce (), el área de la sección plana obtenida
Apéndice : Integral de Riemann. Otras aplicaciones geométricas.. Volúmenes mediante secciones planas transversales Supongamos que tenemos un sólido del que se conoce (), el área de la sección plana obtenida
PRIMER PARCIAL 8 de febrero de 2007
 PRIMER PARCIAL 8 de febrero de 7 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta:. puntos. Respuesta incorrecta: -. puntos Respuesta en blanco: puntos.- La suma de los ángulos de un
PRIMER PARCIAL 8 de febrero de 7 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta:. puntos. Respuesta incorrecta: -. puntos Respuesta en blanco: puntos.- La suma de los ángulos de un
Integrales impropias múltiples
 Integrales impropias múltiples ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Caracterización de la integrabilidad impropia 2 3.
Integrales impropias múltiples ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Caracterización de la integrabilidad impropia 2 3.
Cálculo Infinitesimal: grupo piloto
 Tema : La derivada. Cálculo Infinitesimal: grupo piloto Curso 6/7 A. Objetivos. Al finalizar el tema, los estudiantes deberán ser capaces de: Calcular la derivada de una función utilizando la definición
Tema : La derivada. Cálculo Infinitesimal: grupo piloto Curso 6/7 A. Objetivos. Al finalizar el tema, los estudiantes deberán ser capaces de: Calcular la derivada de una función utilizando la definición
Primer Parcial MA1002 Cálculo II ExMa
 Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
Primer Parcial MA1002 Cálculo II ExMa Cualquiera de los siguientes objetivos puede ser evaluado en el primer parcial. 1. Demostrar proposiciones que se cumplen para infinidad de números naturales, aplicando
ACTIVIDADES INICIALES. 14.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 25, 25 5,...
 Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
III BLOQUE III ANÁLISIS. Página Estudia las asíntotas, intervalos de crecimiento y de decrecimiento y extremos
 III BLOQUE III ANÁLISIS Página 9 Estudia las asíntotas, intervalos de crecimiento y de decrecimiento y etremos de la función y =, y represéntala gráficamente. Asíntotas: Vertical: = Posición: = @ 8 8 +
III BLOQUE III ANÁLISIS Página 9 Estudia las asíntotas, intervalos de crecimiento y de decrecimiento y etremos de la función y =, y represéntala gráficamente. Asíntotas: Vertical: = Posición: = @ 8 8 +
Matemáticas II Hoja 9: Derivadas y Aplicaciones. Representación de Funciones.
 Profesor: Miguel Ángel Baeza Alba (º Bachillerato) Matemáticas II Hoja 9: Derivadas y Aplicaciones Representación de Funciones Ejercicio 1: (Continuación del Ejercicio 1 de la Hoja 8) + 1 a 1 e < 0 0 Para
Profesor: Miguel Ángel Baeza Alba (º Bachillerato) Matemáticas II Hoja 9: Derivadas y Aplicaciones Representación de Funciones Ejercicio 1: (Continuación del Ejercicio 1 de la Hoja 8) + 1 a 1 e < 0 0 Para
Cálculo Diferencial e Integral
 Cálculo Diferencial e Integral (Junio-96 Un comerciante vende un determinado producto Por cada unidad de producto cobra la cantidad de 5 pesetas No obstante, se le encargan más de unidades, decide disminuir
Cálculo Diferencial e Integral (Junio-96 Un comerciante vende un determinado producto Por cada unidad de producto cobra la cantidad de 5 pesetas No obstante, se le encargan más de unidades, decide disminuir
EJERCICIOS UNIDADES 3 y 4: INTEGRACIÓN DE FUNCIONES
 IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES (5-M-A-) (5 puntos) Calcula el valor de a > sabiendo que el área del recinto comprendido entre la parábola y + a y la recta y es
IES Padre Poveda (Guadi) EJERCICIOS UNIDADES y : INTEGRACIÓN DE FUNCIONES (5-M-A-) (5 puntos) Calcula el valor de a > sabiendo que el área del recinto comprendido entre la parábola y + a y la recta y es
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 003 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva, Ejercicio 1, Opción A
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 003 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva, Ejercicio 1, Opción A
MATEMÁTICAS II - P.A.U. CÁLCULO INTEGRAL CUESTIONES
 MATEMÁTICAS II - P.A.U. CÁLCULO INTEGRAL CUESTIONES. Calcular d sen (S9) 6 + C 5 cos 5Cos. Qué diferencias eisten entre integral definida e integral indefinida?. Calcula ln d cos. Define primitiva. Calcula
MATEMÁTICAS II - P.A.U. CÁLCULO INTEGRAL CUESTIONES. Calcular d sen (S9) 6 + C 5 cos 5Cos. Qué diferencias eisten entre integral definida e integral indefinida?. Calcula ln d cos. Define primitiva. Calcula
INTEGRALES DEFINIDAS. CÁLCULO DE ÁREAS
 INTEGRALES DEFINIDAS. CÁLCULO DE ÁREAS. Dada la función f() = -. Calcular f () d. a) Representar y = ( ) 3. b b) Calcular la integral indefinida ( 3 ) d a c) Justificar el resultado de b en función de
INTEGRALES DEFINIDAS. CÁLCULO DE ÁREAS. Dada la función f() = -. Calcular f () d. a) Representar y = ( ) 3. b b) Calcular la integral indefinida ( 3 ) d a c) Justificar el resultado de b en función de
Cálculo Integral Enero 2016
 Cálculo Integral Enero 6 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) ( + + ) ) ( + ) ( ) ) ( w + ) (w ) dw ) ( + ) 5) (y ) dy 6) ( +)( 5) 6 7) + 8) ( +) 5 y+ dy ) (y+5
Cálculo Integral Enero 6 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) ( + + ) ) ( + ) ( ) ) ( w + ) (w ) dw ) ( + ) 5) (y ) dy 6) ( +)( 5) 6 7) + 8) ( +) 5 y+ dy ) (y+5
Problemas tipo examen
 Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
Problemas tipo examen La división en temas no es exhaustiva. Las referencias (H n- m) indican el problema m de la hoja n y las referencias (A- cd), con A en números romanos indican un examen del mes A
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula
![x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula x 2 dx. 2x 2-2x-4 1. [2014] [EXT-A] Calcula x dx. (Sugerencia: integración por partes) cos 2 x 2. [2014] [EXT-B] Calcula](/thumbs/55/37833821.jpg) . [] [ET-A] Calcula d. --. [] [ET-B] Calcula / d. (Sugerencia: integración por partes) cos. [] [JUN-A] Sean f: y g: las funciones definidas respectivamente por: f() = y g() = +. a) Esboza las gráficas
. [] [ET-A] Calcula d. --. [] [ET-B] Calcula / d. (Sugerencia: integración por partes) cos. [] [JUN-A] Sean f: y g: las funciones definidas respectivamente por: f() = y g() = +. a) Esboza las gráficas
3.3 Propiedades locales de una función derivable: continuidad, crecimiento y decrecimiento.
 DERIVADAS. Función derivable en un punto. laterales. Interpretación geométrica de la derivada. Ecuaciones de las rectas tangente normal a la gráfica de una función en un punto.. Concepto de función derivada.
DERIVADAS. Función derivable en un punto. laterales. Interpretación geométrica de la derivada. Ecuaciones de las rectas tangente normal a la gráfica de una función en un punto.. Concepto de función derivada.
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
FACULTAD de INGENIERÍA Análisis Matemático A
 FAULTAD de INGENIERÍA Análisis Matemático A TRABAJO PRÁTIO N : Integral Indefinida Definición de antiderivada Se llama a una función F antiderivada(o primitiva) de una función f, si para todo en el dominio
FAULTAD de INGENIERÍA Análisis Matemático A TRABAJO PRÁTIO N : Integral Indefinida Definición de antiderivada Se llama a una función F antiderivada(o primitiva) de una función f, si para todo en el dominio
Integración en una variable
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) er. Cuatrimestre - 7 Práctica 8: Integración Integración en una variable. Calcular: xsen x. sen x cos x. xe x. e x sen x. (f) 3x x + x.
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) er. Cuatrimestre - 7 Práctica 8: Integración Integración en una variable. Calcular: xsen x. sen x cos x. xe x. e x sen x. (f) 3x x + x.
