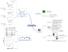
Electromagnetismo. lamparita. bobina. imán

Transcripción

1 Elecromagesmo E ese capíulo veremos los feómeos y cocepos falaes para complear ua vsó geeral de la elecroámca clásca. Haca 183 Mchael Faraday, bráco, y Joseph Hery, oreamercao, descubrero la duccó elecromagéca, algua de cuyas mafesacoes veremos a couacó. lampara má boba Supogamos eer como e la fgura ua boba co ua lampara e sere (o cualquer oro sesor de fuerza elcromoríz). S la boba y el má esá e reposo relavo y el cojuo esá lbre de oras eraccoes la lampara permaecerá apagada; s e cambo el má se acerca bruscamee a la boba la lampara desellará cado que sobre ella aparecó ua fuerza elecromoríz ducda por el movmeo del má. La lampara permaecerá eceda e ao se maega el movmeo del má; s ese se deee, o mpora cuá cerca de la boba, la lampara se apagará. S el má ahora se aleja de la boba, la lampara ecederá uevamee hasa que ése vuelva a deeerse. La lampara será más brllae cuao más rápdo sea el movmeo del má ω lampara má boba S ahora maeemos queo el má y hacemos roar la boba, de modo que su saca promeo al má es cosae pero el flujo de campo magéco sobre ella varía, la lampara ecederá meras esa roacó se maega. E los expermeos descrpos mas arrba los efecos se magfca proporcoalmee al úmero de espras que ega la boba. El má puede ser reemplazado por u elecromá, o sea ua boba crculada por corree que ya sabemos producrá u campo magéco que sabemos calcular. Esos y oros expermeos llevaro a la coclusó de que cuado e u crcuo varía el flujo del campo magéco se duce ua fuerza elecromoríz. Eedemos aquí por crcuo ua curva 1

2 cerrada esé o o maeralzada por u coducor; la fereca resde e que raádose de u crcuo coducor, al haber ua fem, crculará corree. Movmeo de u coducor e u campo magéco. Hemos vso que cuado cargas elécrcas se mueve e u campo magéco aparece sobre ellas fuerzas por ese solo hecho (la fuerza de Lorez). S u maeral coducor se mueve e u campo magéco aparecerá fuerzas sobre las cargas que lo egra erormee y, como hemos scudo, pare de esas cargas so fjas y oras so móvles; como es de esperar las cargas móvles se desplazará sguedo las fuerzas que acúa sobre ellas reubcádose e el seo del coducor hasa que o haya fuerza ea sobre las cargas, excepo como ya vmos, e la superfce del coducor y perpecular a ésa. Veamos e parcular u caso geomércamee smple como es ua barra coducora de logud l movédose co velocdad cosae perpecular a ella msma y a u campo magéco uforme. Es decr la barra, su velocdad y la duccó magéca so perpeculares ere sí. + v^ v v - E=V/l Las cargas móvles (supuesas posvas) se moverá e la reccó de la fuerza de Lorez hasa crear u campo elécrco que produzca a su vez ua fuerza sobre las cargas que compese la fuerza de Lorez. Al ser los vecores v y, perpeculares ere sí y perpeculares a la barra, edremos qv = qe V v = E = l y eoces V = lv (N.) Las cargas esará e equlbro e esas cocoes y o se requerrá fuerza exera para que la barra sga movédose co velocdad cosae e el campo magéco. Mofquemos ahora la cofuguracó cerrado u crcuo plao pepecular al campo magéco + I v (N.1) v v A() E que perma la crculacó de corree pero sedo sempre uesra barra el úco elemeo móvl.

3 Ahora crculado corree e u campo magéco acuará sobre la msma, como ya sabemos, ua fuerza ea de valor F = l que deberemos compesar exeramee para maeer la barra e movmeo. El área A ecerrada por la espra varía co el empo como da = lvd por lo cual el flujo de la duccó magéca a ravés de la msma varía como dφ = lvd dφ (N.3) = lv d Comparado co la ecuacó (N.) vemos que la fereca de poecal o fuerza elecromoríz geeradas e la barra so guales a la varacó de flujo de la duccó magéca a ravés de la espra cerrada por la barra o al área barrda por la msma e el caso del crcuo abero. E el caso del crcuo cerrado, la resseca del msmo lmará la corree al valor I = V / R co lo que la ley de Ohm se cumplrá como e cualquer oro crcuo. Ley de Faraday. E u crcuo cerrado se produce ua fuerza elecromoríz proporcoal a la varacó emporal del flujo que elaza Ley de Lez. La fuerza elecromoríz ducda es al que ede a OPONERSE a la causa que la produce La ley de Faraday y la Ley de Lez puede combarse e la sguee ecuacó dφ ε = (N.4) d sedo ε la fuerza elecromoríz ducda y Φ el flujo de la duccó magéca. E el Ssema Ieracoal de Udades (y el SIMELA) la cosae de proporcoaldad ere la fuerza elecromoríz y la dervada del flujo de la duccó magéca es la udad (que omamos como egava) y [ ] ε = V = Wb. s S S Φ =. ds S e la forma usual, la ecuacó (N.4) os ce que s el flujo de la duccó magéca aumea, ya sea porque aumea la esdad de la msma, el área de la curva, o varía la oreacó relava ere ambas, la fuerza elecromoríz ducda haría crcular ua corree covecoal (cargas dl (N.5) 3

4 posvas) e el sedo coraro al marcado e el bujo para el sedo de crculacó (opuesa a dl ). Por el coraro, s el flujo magéco smuye, la fuerza elecromoríz ducda edrá el sgo opueso favorecedo ua corree que refuerce el flujo exsee. E u crcuo cerrado, poedo el pulgar de la mao derecha e la reccó de la duccó magéca, la fem edra el sedo de los demás dedos s el flujo smuye y sedo opueso s el flujo aumea. Comearo: como veremos, e 1876 J.C. Maxwell propuso que la Ley de Gauss Elécrca, la Ley de Gauss Magéca, la Ley de Ampère (co algú agregado) y la Ley de Faraday era sufcees para descrbr el elecromagesmo. Lo que veremos de aquí e más so aplcacoes de esas leyes. Correes de Foucaul. Las leyes de Faraday y de Lez os ce que s e u crcuo varía el flujo de la duccó magéca, se geera e él ua fuerza elecromoríz ducda (fem) de al sedo que raa de opoerse a la causa que lo produce. Ese crcuo puede ser smplemee ua curva deal e el vacío, e cuyo caso la fem o producrá gú efeco deecable, pero para uesra descrpcó elecromagéca del espaco e base a campos es gualmee válda. S e cambo el crcuo resula maeralzado por u meo que perme el desplazameo de cargas, la fem producrá correes que se llama correes de Foucaul. Esas correes puede resular buscadas o deseadas segú los casos, y e cosecueca se las favorece o fcula segú covega. Cuado las correes de Foucaul o so ulzadas se las llama ambé correes parásas que sólo provoca pérdas de eergía por efeco Joule (caleameo de compoees) y campos magécos parásos o rudo magéco. Las correes de Foucaul se lma aumeado la ressvdad del meo (como e las chapas de Fe-S para rasformadores) o apaallado los campos magécos. Ua aplcacó de las correes de Foucaul so ferees pos de freos magécos ulzados e moores elécrcos, rees, ec. y e moores elécrcos como los llamados de jaula de arlla o los moderos aleradores de auomóvl. Iduccó muua. N ; I N 1; I 1 Supogamos eer dos crcuos 1 y recorrdos respecvamee por correes de esdades I 1 e I y e reposo relavo. Sabemos ya que cada uo de ellos geerará u campo magéco e el 4

5 espaco y e parcular dode se halle el oro crcuo, que e cosecueca elazará u flujo magéco debdo a la corree crculae por el prmero. Vmos ambé que cada corbucó al campo magéco obedece al prcpo de superposcó e cuao a las correes que los produce. S uesros crcuos 1 y eoces, esá aslados, el flujo elazado por el crcuo debdo a I 1 depederá del valor de ésa y de la cofguracó geomérca. Tedremos y smlarmee N Φ = M. I (N.6),1 1 N Φ = M. I (N.7) 1 1 1, Recordemos que es lo msmo varar la corree e u crcuo o varar proporcoalmee el úmero de vuelas del msmo para los efecos magécos producdos. El coefcee de duccó muua puede defrse ambé cluyedo el úmero de vuelas e ambos crcuos, lo que deberá observarse s se ulza ferees exos. E el vacío y por aproxmacó e meos o magécamee acvos, como are, alumo, cobre, ec., como veremos e dealle, pero o e preseca de maerales magécamee acvos como ferromagécos, ferrmagécos, ec. Resula ser M = M = M (N.8),1 1, El coefcee M de duccó muua resula ser úco para la cofguracó geomérca y el flujo elazado por el crcuo por udad de corree e el crcuo 1 es gual al flujo elazado por el crcuo 1 por udad de corree e el crcuo. Los crcuos puede ser de cualquer po y forma, auque cuado se busca efecos de duccó se ulza bobas apropadas. Sempre que hay crcuos de corree se produce duccoes muuas, a veces o deseadas; veremos mas adelae alguas éccas para evar esos casos. De (N.6), (N.7) y (N.8), resula N Φ N Φ M I1 I S las correes varía co el empo e alguo de los crcuos varía el flujo elazado por el oro y se geera e el msmo ua fuerza elecromoríz ducda. dφ1 ε1 = N1 = M d d dφ 1 ε = N = M d d E el fuuro usaremos, como e la ecuacó (N.1) leras músculas para los valores saáeos de magudes que varía co el empo y mayúsculas para valores, cosaes, promeos, ec. Auoducaca. 1 1 = = (N.9) (N.1) U crcuo recorrdo por corree elaza u flujo debdo al campo magéco que el msmo geera, como hemos vso ya e el caso de bobas plaas, soleodes, orodes, ec..e ese caso defmos el coefcee de auoducaca L como L NΦ I = (N.11) 5

6 sedo Φ el flujo elazado por cada vuela del crcuo, N su úmero de vuelas e I la corree que lo crcula. Ora vez s la corree es varable, será dφ ( ) ε = = L (N.1) d d Los compoees fabrcados para geerar auoducaca se llama ducores, auque vulgarmee se los suele car ambé como ducacas o auoducacas. Udades: Tao el coefcee de ducaca muua como el de auoducaca ee udades de flujo de duccó sobre esdad de corree, lo que recbe el ombre especal de Hero [ Φ] Wb V. s J. s [ M ] = [ L] = = = = Ω. s = = H (N.13) I A A C [ ] Ua vez más, el Hero es ua udad muy grade y ormalmee se ulza submúlplos. Ejemplos. Soleode. Hemos calculado que la duccó magéca dero de u soleode largo y de pequeña seccó N( ) rasversal es ( ) = µ s esá recorrdo por ua corree varable, de dode l µ N( ) AN µ N A Φ ( ) = = ( ) l l µ N A L = l (N.14) y la fem ducda será ( ) µ N A ( ) ε = L = (N.15) d l d oba de Tesla. Supogamos ahora que sobre el msmo soleode bobamos oro arrollameo de N vuelas. Ese segudo bobado elazará u flujo µ N1NA NΦ = ( ) = M( ) l NΦ µ N1N A M = = ( ) l Las fem ducdas e cada bobado será eoces 1 (N.16) 6

7 ( ) µ N 1A ( ) ε1 = L = d l d ( ) µ N N A ( ) ε = = 1 M d l d (N.17) co el mporae resulado de que ε N ε = 1 N (N.18) 1 La boba de Tesla es el aecedee del rasformador y fue uo de los prmeros méodos ulzados para obeer esoes aleras de muy alo volaje, para lo que basa co que N sea mucho mayor que N 1. Ua varae de la boba de Tesla es la boba de ecedo de los moores de dos empos o de cclo Oo y perme obeer esoes de uos 14kV (ecedo covecoal) a 3kV (ecedo elecróco) a parr de la esó de 1V omales de la baería. Torode. Recordado que las ecuacoes para u orode era las msmas que para u soleode (co l=πr), ambé so váldos para u orode los resulados que acabamos de obeer, co la veaja de que al obvar los efecos de borde de los exremos de del soleode es aú mas efcee y geera meos rudos. Es mporae remarcar que o hemos cosderado por ahora el efeco de la crculacó de corree por el segudo bobado y que auralmee afecará a odo el ssema. Eergía magéca. La fereca de poeca ere exremos de ua ducaca, recorrda por ua corree crecee que era por bore a y sale por el bore b, es Vab = L. S d d >, V ab = Vb Va > y las cargas crculaes por la ducaca aumea su eergía al recorrerla. La poeca saáea que las fuees exeras erega a esas cargas es P( ) = Vab( ) = L (N.19) d y la eergía eregada e u ervalo de empo d será dw = L (N.) y s la corree crece desde hasa u valor fal L W = L = (N.1) S se raa de u orode e el vacío, la ecuacó (N.1) puede reescrbrse eedo e cuea la ec. (N.14) como W (N.) µ N A = (N.3) π r 7

8 Esa eergía se debe al campo magéco ecerrado e el volume del orode. La eergía por udad de volume es eoces y recordado que dero del orode e el vacío w µ N = (N.4) ( π r) µ N π r w µ =, falmee = (N.5) La expresó (N.5), obeda aquí para ua cofguracó parcular es válda para cualquer cofguracó que produzca u campo e el vacío y como se verá e breve e meos magécamee leales. Asocacó de auoduccoes. S coecamos auoduccoes e sere, como ya hemos vso co las ressecas será recorrdas por la msma corree y la suma de las caídas de esó sobre cada ua, será la caída de esó sobre el cojuo V = V = L = L eq = 1 d = 1 d (N.6) Las auoduccoes o auoducacas so ormalmee arrollameos de coducores. Présese aecó a que la ec. (N.6) o es afecada por el hecho de que cada ducaca esé bobada e uo u oro sedo, ya que la Ley de Lez os asegura que cada ua raará de opoerse a la varacó de la corree geerado ua fem y fereca de poecal e el msmo sedo. U cojuo de auoduccoes coecadas e paralelo, e cambo maedrá la msma fereca de poecal ere sus bores y la corree se reparrá ere ellas de modo de maeer esa suacó. Recordado que la dervada es u operador leal podemos escrbr d 1 V k = V = d L L k= 1 k= 1 k eq 1 1 = L L eq k= 1 k (N.7) y la versa de la ducaca equvalee es gual a la suma de las versas de las ducacas duales, es decr gual que sucede co las resseca y smércamee a lo que sucede co las capacdades. Corree de cerre y aperura de u crcuo. La esó ere bores de ua ducaca es segú acabamos de ver V L d de dode = (N.8) 8

9 lm V = lm L = d d d (N.9) que os ce que s ua corree se aplca o errumpe súbamee e ua ducaca se producrá ere sus bores ua fereca de poecal muy ala. Cuado aplca o se errumpe bruscamee la crculacó de corree por u crcuo ducvo como u moor fucoado (secador de cabello, aladro, ubo fluorescee, ec.) se observa ua srupcó o chspa debdo a que se supera la rgdez elécrca del are. Esa srupcó o chspa produce deeroros de los coacos de los errupores, fchas de almeacó y escobllas de los moores (los coacos que lleva la corree a sus bobados) y e lo posble se la eva aplcado la corree e forma gradual a ravés de ua resseca decrecee e el empo o colocado codesadores e paralelo. E oros casos ese efeco se ulza provechosamee para obeer esoes muy alas como e el ssema de ecedo de los moores de cclo Oo o de dos empos, o e bobas del po Tesla o Rumkorf para obeer ua descarga srupva e u meo. Crcuo RL. Cosderemos el crcuo de la fgura, formado por ua fuee de fuerza elecromoríz, ua resseca, ua ducaca y los errupores S 1 y S. S cerramos el errupor S 1 crculará corree por la resseca y la ducaca y edremos Vε R L = d V R ε = L R d (N.3) que reordeado e egrado da R = d V L ε R Vε R l R = Vε L R (N.31) 9

10 R V V ε ε L = e R R R V V ε L ε τ = 1 e = 1 e R R (N.3) τ=l/r se llama cosae de empo del crcuo RL () V ε /R V() V ε Al prcpo como se ve, la ducaca geera ua fereca de poeca que mpde el paso de la corree y luego esa aumea, hasa que a empo fo la ducaca es u corocrcuo y la corree esá sólo lmada por la resseca. S luego de u empo muy largo, lo que e esos caos quere decr varas veces τ, abrmos el errupor S 1 y cerramos el S la suacó será R = L d R d = d = L τ = l ( ) = e τ = τ d τ (N.33) () V() Al cerrarse el crcuo de descarga la ducaca se opodrá a la smucó rápda de la corree que la crcula geerado lo que suele llamarse ua fuerza coraelecromoríz.. A meda que la 1

11 eergía almaceada e la ducaca es spada e la resseca la corree y la esó smuye expoecalmee 11